Basal mass balance and prevalence of ice tongues in the Western ross sea

Ice tongues at the fringes of the Antarctic ice sheet lose mass primarily through both basal melting and calving. They are sensitive to ocean conditions which can weaken the ice both mechanically or through thinning. Ice tongues, which are laterally unconfined, are likely to be particularly sensitive to ocean-induced stresses. Here we examine ice tongues in the Western Ross Sea, by looking into the factors affecting their stability. We calculate the basal mass change of twelve Antarctic ice tongues using a flux gate approach, deriving thickness from ICESat-2 height measurements and ice surface velocities from Sentinel-1 feature-tracking over the same period (October 2018 to December 2021). The basal mass balance ranges between −0.14 ± 0.07 m yr⁻¹ and −1.50 ± 1.2 m yr⁻¹. The average basal mass change for all the ice tongues is −0.82 ± 0.68 m of ice yr⁻¹. Low values of basal melt suggest a stable mass balance condition in this region, with low thermal ocean forcing, as other studies have shown. We found a heterogeneous basal melt pattern with no latitudinal gradient and no clear driver in basal melt indicating that local variables are important in the persistence of ice tongues in the absence of a strong oceanographic melting force. Moreover, thanks to the temporal resolution of the data we were able to resolve the seasonal variability of Drygalski and Aviator Ice Tongues, the two largest ice tongues studied.

1 Introduction

Antarctic ice tongues are the floating extensions of marine-terminating glaciers beyond their protected embayments. Considered unconstrained ice shelves, they are potentially more exposed to oceanic and atmospheric forcing (Truffer and Motyka, 2016). Their dynamics are influenced by different types of ice-ocean interaction; either directly by tides, coastal currents, and waves (Holdsworth, 1985; Squire et al., 1994; Legrésy et al., 2004) or indirectly by fast-ice persistence (Massom et al., 2010; Gomez-Fell et al., 2022). Motyka et al. (2011) found that the most important control of ice tongue stability is basal melt. The notable absence of ice tongues in Greenland, where basal melting is much higher, confirms basal melt as an important factor (Motyka et al., 2011; Truffer and Motyka, 2016). The basal melt of ice tongues is driven by ocean temperature and turbulent mixing from tides and currents (Jenkins et al., 2010; Stevens et al., 2014), but it is also a function of the local melting point as a result of the ice tongue draft (Lindbäck et al., 2019). The highest basal melt rates on ice shelves and ice tongues are usually found near the grounding line (Pritchard et al., 2012; Rignot et al., 2013) and the ice edge (Stewart et al., 2019; Adusumilli et al., 2020). In addition to basal mass loss, the dynamic variability of Parker Ice Tongue due to fast ice extent illustrates the sensitivity of ice tongues to environmental conditions compared to fully constrained ice shelves (Gomez-Fell et al., 2022). In this work, we focus on the stability of ice tongues and their basal mass balance, as sentinels of change, in the Western Ross Sea. We use the term stability to reflect the long-term persistence of ice tongues in the region over time in view of mass balance processes.

Ice tongues along the Victoria Land Coast in the Western Ross Sea are characteristic coastal features that have been stable over the last 60 years with regular periods of retreat and re-advance (Frezzotti, 1997; Fountain et al., 2017; Lovell et al., 2017). Frezzotti (1997) found that the ice tongues south of Terra Nova Bay maintained their relative shape and position during the 20th century, while the ones north of Terra Nova Bay have a 10–15 years calving cycle. Currently, it is hypothesized that non-climatic variables are the primary regulators of frontal position at the fringes of Victoria Land (Fountain et al., 2017; Lovell et al., 2017; Baumhoer et al., 2021). The prevalence of these ice tongues is likely influenced by the cold Victoria Land Coastal Current (VLCC) as a result of ice shelf water (ISW) outflow (Stevens et al., 2017; Jendersie et al., 2018), but the basal mass balance has only been estimated at a few places because it is particularly hard to measure (Holdsworth, 1982; Wuite et al., 2009; Stevens et al., 2014; Han and Lee, 2015). The reason why this region of Antarctica has a large group of ice tongues which do not occur in the same way elsewhere is unclear and deserves further study. The VLCC influence could be one possibility for the ice tongue persistence and growth in this sector of Antarctica (Debenham, 1965; Frezzotti, 1997).

Ice tongues tend to have relatively larger variations in frontal position than ice shelves and marine-terminating glaciers (Lovell et al., 2017). Frontal calving of ice tongues can be triggered by collision with icebergs (MacAyeal et al., 2008; Young et al., 2010), influenced by ocean temperatures (Motyka et al., 2011; Miles et al., 2020), or oceanic waves (Squire et al., 1994; Brunt et al., 2011). Frezzotti (1997) found that floating glaciers along the Victoria Land Coast went through a phase of retreat during the 1950s and 1960s, followed by a period of growth during the 1980s and 1990s. More recent studies have found that on average frontal positions of ice tongues have been fairly stable, with short periods of advance and retreat (Fountain et al., 2017). Changes in the frontal position of ice tongues in this region of Antarctica tend to be related to larger irregular calving events, rather than continuous ice loss (Frezzotti and Mabin, 1994; Stevens et al., 2013; Gomez-Fell et al., 2022). Local geomorphological settings and external environmental factors have an important role in ice tongue stability (Frezzotti, 1997; Massom et al., 2015). All of this seems to indicate that glacier terminus variations in the Western Ross Sea during the last 60 years are associated with non-climatic drivers than more obvious atmospheric and oceanic forcing (Lovell et al., 2017).

Antarctic ice sheet mass depends largely on two antagonistic processes: snow accumulation in the interior and ice loss that is driven by the ocean processes on the margins (Smith et al., 2020). There is large interannual and spatial variability in basal mass loss around Antarctica (Adusumilli et al., 2020). Fluctuations in the basal melt of ice shelves over time can be indicators of shifts in ocean processes (Adusumilli et al., 2018). Understanding the processes driving mass loss under ice tongues and ice shelves is fundamental to better constrain the present and future of Antarctic ice.

There are three main basal melt processes (Jacobs et al., 1992). The first is driven by the formation of sea ice on the ocean surface, creating a dense salty brine that intrudes deeply into the ice shelves or ice tongues cavity (High Salinity Shelf Water, HSSW) generating melt at the grounding line. This mode is most common during the austral autumn and the beginning of winter when most of the sea ice is starting to form (Stevens et al., 2020). The second occurs when warm and dense Circumpolar Deep Water (CDW) penetrates under the ice shelf or ice tongue creating melt at mid-depth. This phenomenon is driving mass loss under glaciers such as Pine Island and Thwaites Glacier draining into the Amundsen Sea in West Antarctica (Holland et al., 2019). The third mode is related to the loss of sea ice and the warming of the surface waters during the summer months generating melt close to the surface of the ice shelf or ice tongue (Lindbäck et al., 2019; Stewart et al., 2019). Under the ice tongues of the Western Ross Sea processes 1, and 3 are expected to be prevalent (Wuite et al., 2009; Stevens et al., 2017). The interactions between water masses, ice tongues, and potential thresholds are not well understood (Stevens et al., 2017).

Oceanographic patterns in the Ross Sea are complex. Every winter polynyas build up at the front of the Ross Ice Shelf, in McMurdo Sound, and in Terra Nova Bay, creating an important mass of sea ice that is mainly exported toward the Southern Ocean (Sansiviero et al., 2017). Part of this new sea ice can pile up against the coastal regions generating areas of thick coastal sea ice (Rack et al., 2021) that could strengthen land-fast sea ice protecting ice tongues from calving. Polynya efficiency has been related to land-fast sea ice extent and persistence (Mezgec et al., 2017). The Western Ross Sea is modulated by colder water masses, generated mainly by sea ice formation (HSSW) or by the melting of glaciers at the grounding line (Ice Shelf Water, ISW) (Orsi and Wiederwohl, 2009), that in turn mixes with warmer waters creating modified Shelf Water (mSW) that has been observed in autumn and winter near the Victoria Land Coast (Piñones et al., 2019). Similarly, CDW mixes with colder waters creating modified CDW (mCDW), that could reach the western margins of the Ross Sea (Orsi and Wiederwohl, 2009). The intrusion of warm CDW into the Ross Sea is mainly confined to a deep trough at the centre and west of the continental shelf and has a seasonal variability with a peak intrusion over the late winter months (Piñones et al., 2019).

The study of seasonal change variability at an individual glacier scale can help to better understand the processes driving such variability (Miles et al., 2022). We know that terminus variations along the Victoria Land Coast are not principally driven by climatic or oceanic forcing (Fountain et al., 2017; Lovell et al., 2017), but this is not yet clear for basal melting. Therefore, we explore some environmental and geographical variables to investigate possible relations with the basal mass balance of ice tongues in this Antarctic sector. Few studies have considered the seasonality of basal melt of ice shelves or ice tongues around Antarctica. Most of these studies are from point measurements (e.g., Arzeno et al., 2014; Stewart et al., 2019; Rosevear et al., 2022). Here we use ICESat-2 laser altimetry repeat pass frequency and resolution, combined with the consistent temporal acquisition of synthetic aperture radar satellite imaging, making it possible to study basal melt at a smaller scale at remote locations. In this study, we consider the spatial and temporal basal ice tongue mass changes in the Victoria Land Coast (Figure 1). We present first an overview of the study area, followed by the data and methods, main results, and a discussion on seasonal and spatial variability and possible links to environmental and geographical variables.

FIGURE 1

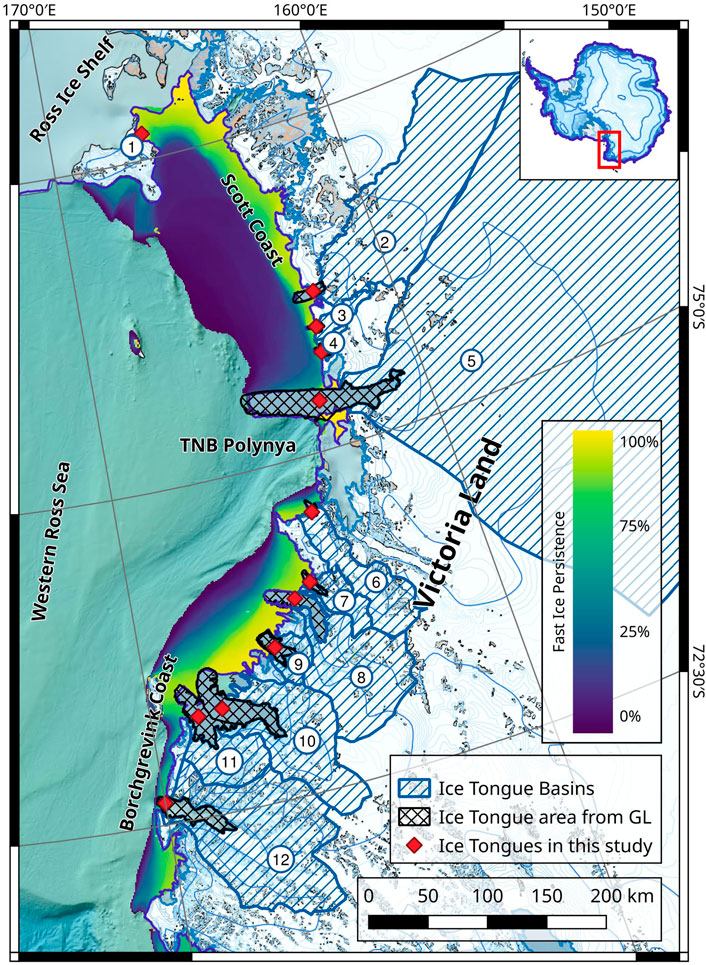
FIGURE 1. Red diamonds indicate the Ice tongues included in this study, their areas from the grounding line are cross-hatched in black. Numbers indicate the ice tongues and basins as they are shown in tables and figures in this article. The catchment areas of the different ice tongues are shown in hatched blue. The percentage of sea ice persistence in the areas surrounding the ice tongues over the 2000–2018 period was averaged from Fraser et al. (2021) data. Yellow indicates areas with year-round land-fast sea ice, and blue areas with sporadic land-fast sea ice.

2 Study area

Victoria Land on the western margin of the Ross Sea has a coastline that spans more than 600 km. It is the third largest North-South oriented coastline in Antarctica, behind the Western and Eastern sides of the Antarctic Peninsula. There are 30 major marine-terminating glaciers located along the coast which can be subdivided into the Borchgrevink Coast, Terra Nova Bay, Scott Coast, and McMurdo Sound (Frezzotti, 1997). There is an important concentration of glaciers with ice tongues protruding away from the coastline. Here, we investigate the mass balance of twelve of the largest ice tongues along the margins of the Western Ross Sea (Frezzotti, 1997; Stevens et al., 2014). These are, from south to north: Erebus, Nordenskjold, Harbord, Cheetham, Drygalski, Campbell, Tinker, Aviator, Icebreaker, Mariner, Borchgrevink and Tucker Ice Tongues (The basins of the ice tongues are labelled 1 to 12 on Figure 1). The largest is Drygalski with a length of 135 km and a floating area of 2,500 km² from the grounding line. The smallest is the Erebus Ice Tongue with a length of 10 km and a floating area of 17 km² from the grounding line. Nine ice tongues were selected due to latitudinal coverage, ICESat-2 data availability, and ice tongue orientation with respect to ICESat-2 ascending and descending orbits. We added three more ice tongues using already available thickness and velocity datasets to extend the latitudinal coverage.

About half of these ice tongues are a continuation of fjord-type glaciers with grounding lines set back from the point where the ice extends as an ice tongue towards the sea. These fjords tend to be very deep, for example, the Drygalski Ice Tongue with thicknesses at the grounding line larger than 2,000 m or Aviator, Mariner and Borchgrevink with thicknesses at the grounding line larger than 1,000 m (Morlighem et al., 2019). These thicknesses are comparable with some of the large glaciers that drain into the Ross Ice Shelf such as Byrd Glacier. Catchment basins also vary, with the larger Drygalski Ice Tongue occurring at the outlet of David Glacier with a basin of 2,24 ,000 km² and at the other end of the spectrum Erebus glacier with a basin of 16 km².

3 Data and methods

We calculate the basal mass loss of twelve ice tongues in the Western Ross Sea. Basal mass loss for nine of them is calculated using ICESat-2 derived thickness and Sentinel-1 surface velocities, while for the remaining three, we used the BedMachine version 2 derived thickness (Morlighem, 2020). We use a flux-gate approach, where each ICESat-2 track is considered a gate. Then we fit a weighted least squares regression model to the flux data. An average ice flux was derived along the ice tongue using the statistical ice flux model and new gates were defined. Finally, average basal mass loss amidst gates was calculated for each ice tongue and inter-cycle variability was estimated for Aviator and Drygalski ice tongues. We used other ready-available datasets to create a baseline for our results and for calculating the basal mass loss.

3.1 Satellite-derived surface velocity

We use freely available synthetic aperture radar (Sentinel-1) data to derive surface velocities and the hydrostatic equilibrium line of the ice tongues. Sentinel-1 is a synthetic aperture radar in a repeat polar orbit of 12 days over the study region. We derive surface velocities from feature tracking processed on Vertex—the on-demand cloud computing platform from Alaska Satellite Facility (ASF), using the autoRIFT algorithm (Lei et al., 2021). We used the autoRIFT feature tracking algorithm for all but three ice tongues (Mariner, Borchgrevink and Campbell), and we used the MEaSUREs Phased-Based Antarctica Ice Velocity data set for the other three (Mouginot et al., 2019a). In order to separate the areas that are freely floating we define the hydrostatic line (Bindschadler et al., 2011) using alpha maps (Wild et al., 2019; Alley et al., 2021) based on the MEaSUREs 2011 grounding line (Rignot et al., 2016). Then we corroborate the hydrostatic line using three-pass differential interferometry (DInSAR) (see Supplementary Figure S2) where the hydrostatic line is defined as the seaward limit of the fringe pattern of the differential interferogram (DInSAR-defined) (Wild et al., 2019).

3.2 Satellite-derived thickness

ICESat-2 was launched in 2018, with its first measurements in October of the same year. It consists of three pairs of laser beams that measure the Earth’s surface height from the ellipsoid. Each pair follows a track separated perpendicular to the others by 3 km. We use each available laser beam to calculate freeboard and ice thickness. Tracks were separated in ascending and descending orbits to create different flux gates across the ice tongues. Separating the different tracks allowed us to avoid crossovers between gates. ICESat-2 covers the Earth in a 91-day cycle, with almost exact repeat passes over the polar regions. We used data from 13 cycles, spanning from October 2018 to December 2021. A more detailed overview of the mission can be found in Neumann et al. (2019). ICESat-2 has different product levels with different corrections and aims. Here we used the ATL06 land height product (Smith et al., 2019). The ATL06 product from ICESat-2 has enough granularity to resolve surface changes and comes with ancillary parameters to assess the quality and uncertainty of the measurement (Smith et al., 2019). We applied the ATL06 quality flag to the data collected in order to be sure that only high-quality measurements were used.

3.2.1 ICESat-2 ice tongue freeboard to thickness

We derived the ice tongue mass-equivalent ice thickness from ICESat-2 height data using Eq. 1 and assuming hydrostatic equilibrium. First, we define the ice tongue freeboard from the ICESat-2 point data using an ocean surface reference for each track. We used two methods depending on if the ICESat-2 track passed over the ocean or if the satellite track was inland. In most cases, it was the former (Figure 2C). But there were cases near the hydrostatic line where the track never passed over the ocean. For the first case, we used the lowest point of each ICESat-2 track in a 5 km buffer zone outside of the margins of the ice tongue. This method has the advantage of not needing surface correction for the barometric effect or ocean tides, as we have a real-time ocean surface measurement. But is only valid for the tracks that are on the ocean side of the coastal margin. For ice tongues that were surrounded by land-fast sea ice, there could be an impact on the final basal melt calculations, this is discussed in the mass balance and associated uncertainties section with a sensitivity analysis. The second case is if the track transits over the interior of the ice tongue in its embayment or fjord, then the ocean surface reference is defined by the mean value of all the ICESat-2 data points that are in the surrounding 5 km buffer around the ice tongue. This value is corrected for the tidal range using the CATS2008 model (Padman et al., 2002; 2003; 2008) and the barometric effect using the ICESat-2 accompanying dynamic atmosphere correction data. The difference between the ATL06 height product and the defined ocean reference gives the freeboard of the ice tongue.

FIGURE 2

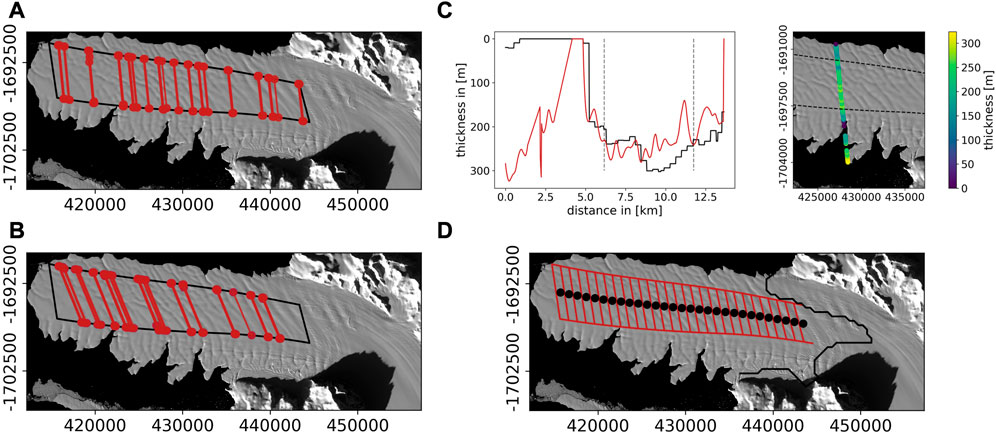
FIGURE 2. Aviator Ice Tongue flux gates from ICESat-2 (A) descending paths and (B) ascending paths in red with a black polygon showing the area between flowlines calculated using velocity trajectories. The polygon area is used to calculate the basal melt. Panel (C) shows on the left the comparison between the ICESat-2 derived thickness in red and BedMachine in black over one ICESat-2 track (1,098 cycle 13 from 03 December 2021) across the ice tongue. The flowlines are shown as dashed grey lines. On the right the same track is overlaid over a Sentinel-2 greyscale image, the colour map indicates the thickness and the dashed lines are the derived flowlines. On panel, (D) in red the final gates and areas that are used for the basal melt calculations using the modelled ice flux. Black dots mark the centre of each polygon associated with distance in the x-axis of Figures 5A–C and Figures 6A–C. Sentinel-2 greyscale image from 07 March 2020 in the back of all panels.

In order to derive thickness from ice tongue freeboard (h_f), we calculate the mass-equivalent ice thickness using the following formula from Moholdt et al. (2014):

$M={\left(\frac{1}{{\rho }_i}-\frac{1}{{\rho }_w}\right)}^{-1}\left(h_f-H_a\right)(1)$

Where ρ_i is the density of pure ice (917 kg m⁻³) and ρ_w is the density of ocean water (1,028 kg m⁻³). H_a is the firn air content of the ice column in metres. To get the ice equivalent thickness we divided M by the ice density ρ_i. Our overall ICESat-2 data thicknesses are in agreement with BedMachine version 2 (Morlighem, 2020) data thicknesses. As an example, we show a cross-section of the Aviator Ice tongue in Figure 2C, where differences at the ice tongue margin can be seen due to the movement of the edge indentations through time and some variability in the central area caused by the advection of crevasses and surface undulations. The ICESat-2 freeboard and derived thickness can be affected by factors such as the temporal and spatial variability in snowfall, seasonality in firn compaction, snow redistribution by wind, ice advection, and surface topography (e.g., crevasses). To take this into account we first estimate the error using the error propagation (Supplementary Material S1.1), which will be used as a weight for the regression of the ice flux (Section 3.3). Uncertainties are further investigated in Section 4.3.

3.3 Flux gate method for basal mass balance derivations

In the absence of precise and repeat surface elevation models, we make use of an input-output method or fluxgate approach (Wuite et al., 2009). This allows us to use sparse data to derive basal mass change over a relatively larger area and can give us better glaciological insight than the altimetry method as it depends on the ice dynamics instead of surface elevation changes. We choose this methodology over the more common altimetry method (e.g., Moholdt et al., 2014; Berger et al., 2017; Smith et al., 2020). We found that interpolation of available ICESat-2 data was not possible to resolve basal mass change spatially and temporally over these relatively small ice tongues.

We use the method to calculate the basal mass change of twelve ice tongues in the Victoria Land Coast. The first step of the methodology is obtaining the ice flux values over gates across the different ice tongues. For the calculations, an ice surface velocity field and the thickness of the ice tongue are required. The gates were defined using the ICESat-2 tracks between two parallel ice trajectories defined by the autoRIFT ice velocity field (Figures 2A, B). The use of glacier flow trajectories as limits for the flux gates has two main advantages. First, it allows us to avoid uncertainties over mass loss due to calving at the margins of the ice tongue, and secondly, simplifies the areas used between gates for mass change estimations. The ice flow trajectories used were visually compared with surface glacier flowlines for correctness.

3.3.1 Ice flux calculations

The ice flux is calculated at different gates defined by the ICESat-2 ascending and descending tracks between two defined flowlines (Figures 2A, B). We generated the flowline seeding points at a defined distance over the DInSAR-defined hydrostatic line and then manually chose the ones with the best area coverage over the ice tongue. The velocity field-derived flowlines were generated from the autoRIFT velocity fields, except for Campbell, Mariner and Borchgrevink Ice Tongues. For those three cases, the MEaSUREs Phase-based Antarctica Ice Velocity dataset (Mouginot et al., 2019b) was used.

The individual velocity fields obtained from October 2018 to December 2021 for the different ice tongues using the autoRIFT algorithm were stacked, time-averaged and filtered. Creating a velocity field that matches the timing of the ICESat-2 data acquisition. We decided to use a time-average velocity field, instead of trying to overlap ICESat-2 measurements with velocities, due to the temporal variability of the individual velocity fields and the ICESat-2 data. We used two different Gaussian filters to smooth the time average velocity fields and resample the resolution from 120 to 360 m. In general, velocity magnitudes were similar to the MEaSUREs data set, with some exceptions.

We separated ascending and descending paths to avoid cross-over of the tracks/gates for the flux calculations. For every gate, we used the mean values of thickness and ice velocity. To account for any distortion due to the angle of the tracks against the main ice flow, we calculate the velocity components perpendicular to the gate using the following equation:

$V_{\perp }=\mid \text{sin}\theta \mid \sqrt{{\widehat{u}}^2+{\widehat{v}}^2}(2)$

Where V_⊥ is the perpendicular velocity component of the magnitude at each segment, θ is the angle of the track relative to the flowline and $\widehat{u}$ and $\widehat{v}$ are the mean components of the velocity at each ICESat-2 measurement. The perpendicular component of the magnitude is used for the flux calculations, this accounts for any deviation of the gates from the main velocity component and is necessary due to the oblique orientations of the ICESat-2 tracks versus the ice flow. The flux at each gate Φ_i is then calculated by the multiplication of the length of the gate (W), the mean thickness of all the ICESat-2 measurements, and the mean perpendicular velocity along with that gate, using the following equation:

${\mathrm{\Phi }}_i=\overline{V_{\perp i}}\overline{H_i}{W}_i(3)$

Where $\overline{V_{\perp i}}$ is the perpendicular velocity component of the magnitude at each segment, $\overline{H_i}$ is the thickness and W_i is the length of the gate between the two flowlines, at each segment (Figure 3).

FIGURE 3

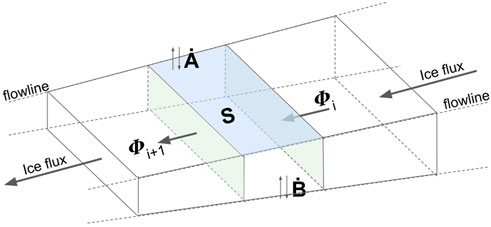
FIGURE 3. Ice tongue section depicting the main components of Eq. 4. Basal mass balance $(\dot{B})$, surface mass balance $(\dot{A})$, ice flux at the gate i (Φ_i) and i +1 (Φ_i+1) and the area between gates S. For clarity, the surface area has been coloured pale blue and the gate areas have been coloured pale green.

The amount of ICESat-2 tracks and data available at each ice tongue was a decisive factor when choosing the nine ice tongues (Erebus, Nordenskjold, Harbord, Cheetham, Drygalski, Tinker, Aviator, Icebreaker and Tucker). In addition, the orientation of the ascending and descending tracks of the satellite was also considered when doing the selection. For the other three ice tongues (Mariner, Borchgrevink and Campbell) ice flux was calculated using the same method with the BedMachine ice thickness and the MEaSUREs Phased-Based Ice Velocity datasets. The main difference was that the gates were defined every kilometre and from each gate the integrated thickness and velocity over the gate were calculated, using the same Eq. 3. The reason for using ICESat-2 data to derive the thickness instead of using BedMachine is that we know the precise date of acquisition required to compute seasonal ice fluxes. That allows us to compute seasonal mass change variability.

3.4 Basal mass balance derivation

We calculate the mean basal mass loss at different time periods using the flux gate results. Due to the inherent variability of the data used and the consequent variability of the ice flux for each ice tongue we favoured a linear regression over a higher-order regression model as a more conservative, simple and consistent approach to the data analysis. Without additional field data, the interrelation between complex mass balance processes is masked and cannot get separated at the required accuracy. In the linear regression, this is reflected by a larger confidence interval of the results and lower statistical parameters. Using this approach we can define new gates perpendicular to the flux and derivate the average flux of each gate. Then we can calculate the basal mass balance for the areas between gates using Eq. 4.

For each ice tongue, a weighted least square (WLS) linear regression was fitted over the ICESat-2 calculated ice flux data as a function of the distance from the defined hydrostatic line. The weight was defined as one divided by the squared variance of the propagated error from the flux calculations $\frac{1}{{({\sigma }_{\varphi })}^2}$. From the regression formula, the mass flux between the two-seeded flowlines can be determined for any defined gate. For Drygalski and Aviator ice tongues, there was sufficient data to fit a linear regression model for every ICESat-2 cycle. For the other ice tongues, an average for the whole period was calculated. For each ice tongue, the basal mass loss $\dot{B}$ was derived from the ice flux linear models, using the following equation (Wuite et al., 2009):

$\dot{B}=\frac{{\mathrm{\Phi }}_i-{\mathrm{\Phi }}_{i+1}}{S}+\dot{A}(4)$

where Φ_i is the mass flux through a flux gate, S is the surface area between gates and $\dot{A}$ is the mean accumulation rate. In the specific cases of Drygalski and Aviator ice tongues, when the basal melt for each cycle is calculated we used the accumulation rate from ERA5-Land as $\dot{A}$. A schematic of the equation is shown in Figure 3. For the yearly calculations, we used the average 1979 to 2016 RACMO2 surface mass balance data. For the flux difference, new gates were defined and set every kilometre for all the ice tongues except Drygalski Ice Tongue (Aviator is shown as an example in Figure 2D). Drygalski gates were set every 4 km because of the ice tongue length. In the case of Mariner, Borchgrevink and Campbell ice tongues because of the method, there was no need for a linear regression model as the fluxes were directly obtained from BedMachine and MEaSUREs Phased-Based ice velocity products.

3.5 Surface processes supporting data sets

When looking into seasonal variability of mass change the densification of snow during the summer months and the penetration of the signal in the snow can play a significant role in the altimetry measurement introducing surface uncertainties related to density changes of the firn layer. Today one of the standard methods to account for firn densification is to use modelled depth for the firn layer and add this to the freeboard calculations (e.g., Griggs and Bamber, 2011; Moholdt et al., 2014). We used the average between 1979 and 2016 of the firn air content model (Ligtenberg et al., 2011) forced with RACMO2.3p2 (van Wessem et al., 2018) that comes as a companion data set for BedMachine (Morlighem, 2020).

For the mass change derivations, we used two different datasets to account for the surface processes. One was snow accumulation from the ERA5-Land reanalysis from the Copernicus Climate Change Service (Muñoz-Sabater, 2019; Muñoz-Sabater et al., 2021). ERA5-Land snow accumulation performs better than other reanalyses over Antarctica (Gossart et al., 2019). We choose to use ERA5-land snow accumulation values as they cover the same time period as the ICESat-2 data. From the ERA5-Land monthly averaged data from 1950 to the present product, the coincident months with every cycle were taken, averaged and converted into metres of ice per year. The land mask for ERA5-Land is coarse along the Antarctic coast, masking out some of the floating ends of ice tongues. Non-etheless, when calculating inter-annual temporal variability of mass change we used ERA5-land snow accumulation data due to the temporal coincidence with the ICESat-2 data. But, in the case when we use all the ICESat-2 data from every cycle we used the average surface mass balance data from 1979 to 2016 for each ice tongue from the regional atmospheric climate model (RACMO2.3p2) (Lenaerts et al., 2018), as it will represent better the surface processes affecting the ice tongues.

3.6 Error estimation

The error in the ICESat-2 measurement is relatively small, with an accuracy lower than 0.1 m for flat surfaces and generally lower than 1 m for rough surfaces (Smith et al., 2019). Variability can be incorporated into the ICESat-2 freeboard calculations due to the ice tongue crevassed areas and undulated terrain. The firn model, surface ice velocities, surface mass balance and snow accumulation values all introduce uncertainties to the results. The error is driven by the measurement uncertainties, whereas the confidence interval is driven by the natural variability of the measurables. The former can be quantified as part of the measurement bias, while the latter is mostly driven by surface changes and properties. For example, we noticed that surfaces tend to get smoother towards the tips of the ice tongues and that there are undulations at various spatial scales (e.g., crevasses or snow dunes). There is also temporal variability caused by the advection of ice and the Eulerian nature of the measurement.

This variability is taken into account by the linear model confidence interval taken from the gate fluxes results and transferred analytically to the basal mass balance results. This gave us a 95% confidence interval for the possible range of basal melt results. We used error propagation to define the total errors of each ICESat-2 flux gate (Supplementary materials) and used them as weights for our linear regression.

4 Mass balance and associated uncertainties

The basal mass balance of twelve Victoria Land Coast representative ice tongues is presented in this section. The results are divided into four sections. First, the spatial distribution of mean basal mass loss along the Victoria Land Coast, secondly the seasonal and spatial variability observed over Aviator ice tongue and Drygalski ice tongue, third a sensitivity analysis of the uncertainties and lastly a correlation assessment of different environmental variables and basal mass loss.

4.1 Victoria land coast spatial distribution of basal mass change

We derived ice flux results from the ICESat-2 height data for nine ice tongues using a weighted least square regression (Erebus, Nordenskjold, Harbord, Cheetham, Drygalski, Tinker, Aviator, Icebreaker and Tucker Ice Tongues). The statistics of each regression are presented in Supplementary Table S1 of the supplements. Using the BedMachine ice thickness data set we were able to add three more ice tongues to the total count (Campbell, Mariner and Borchgrevink). Other ice tongues (Moubray, Ironside, Wylde, Marin, Fry and Mackay ice tongues) could not be included due to inaccuracies in the ice thickness or velocities data sets, or insufficient ICESat-2 data.

With the available ICESat-2 data, we fitted nine weighted least squares linear regressions, which gave a good representation of the ice flux over the selected gates at each ice tongue. There were three ice tongues with low R² values. These are, Nordenslkjold (R² = 0.152), Tinker (R² = 0.126) and Erebus (R² = 0.064), all three have relatively small RMSE but significant F-test p-values (Supplementary Table S1). The R values imply that the modelled regression of the ice flux is not an accurate prediction. But, as the F-test shows the fit is a good and significant representation of the data. These shortcomings are reflected in the large confidence intervals of the three ice tongues (Figure 4). All the other ice tongue flux regressions have better R square results with significant p-values for the F-test (Supplementary Table S1).

FIGURE 4

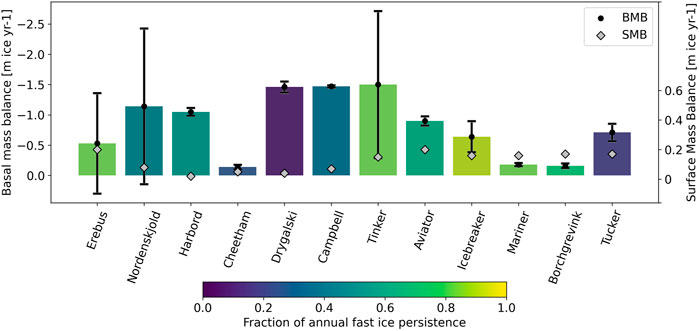
FIGURE 4. Basal melt rates (with confidence intervals) of ice tongues along the Victoria Land Coast. Ice tongues are ordered from South to North. The colour scale represents the land-fast sea ice permanence surrounding the ice tongue, colours as per Figure 1. The average surface mass balance van Wessem et al. (2014) is shown as grey diamonds with an exaggerated scale.

The flux regressions were used to calculate new flux gates (Eq. 3) and then a basal mass change of each ice tongue using Eq. 4. Values are displayed in Table 1 and Figure 4. The values of basal mass change range between (−0.14 ± 0.07 m of ice yr⁻¹) for Cheetham to (−1.5 ± 1.21 m of ice yr⁻¹) for Tinker. The average basal mass change for all the ice tongues is (−0.82 ± 0.68 m of ice yr⁻¹). The three largest basal mass loss is from Tinker (−1.50 ± 2.43 m of ice yr⁻¹), Campbell (−1.47 ± 0.03 m of ice yr⁻¹). Other ice tongues presented mean values of less than or close to a metre (Table 1; Figure 4).

TABLE 1

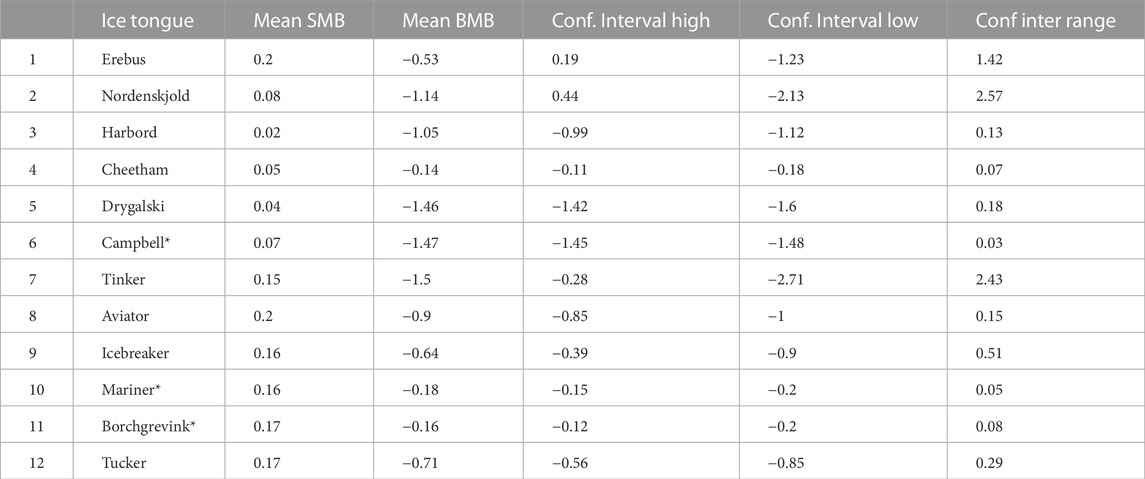
TABLE 1. Annual mean of surface mass balance and basal mass balance with confidence intervals of all the ice tongues in this study (m of ice yr⁻¹). *: basal melt derived using BedMachine thickness and MEaSUREs velocity data with confidence intervals calculated by error propagation (see text).

4.2 Aviator and Drygalski ice tongues temporal variations of basal melt

Aviator and Drygalski ice tongues had measurements over every ICESat-2 cycle with good spatial coverage. With the data, a temporal analysis of the basal mass change of these two ice tongues was done. Figures 5A, B show the spatial distribution of basal mass change and ice flux over the Dryglski Ice Tongue. With relatively larger basal mass change values (−1.80 ± 0.22 m of ice yr⁻¹ at 3 km from the Hydrostatic Line (HL)) near the HL and getting more stable (−1.40 ± 0.17 m of ice yr⁻¹ at 60 km from HL) as the ice tongue goes into the ocean. The same can be done for each cycle, with all the different derived fluxes from ICESat-2 gates shown in Figure 5C. All the WLS regression models done over the different cycles are significant, and only three (cycles 2, 10 and 13) of the 13 cycles have R² values lower than 0.3. We then calculate the modelled ice flux at every 4 km, for each cycle and use the average basal melt rate of each period. We found some variability over the different cycles, with most values between −1.0 and −1.30 m of ice yr⁻¹ (Figure 5D) and with a mean value plus minus standard deviation for all cycles of −1.1 ± 0.37 m of ice yr⁻¹. With the largest basal mass changeil in, April-June 2020–1.57 ± 0.31 m of ice yr⁻¹ and the lowest in Jilan-March 2021–0.38 ± 0.43 m of ice yr⁻¹. The April-Jun cycles have the largest values with April-June 2019–1.36 ± 0.29 m of ice yr⁻¹, April-June 2020–1.57 ± −0.31 m of ice yr⁻¹ and April-June 2021–1.30 ± 0.31 m of ice yr⁻¹. Also, the July-September 2021 cycle had a similar large value of −1.31 ± 0.33 m of ice yr⁻¹. The mean range of the confidence interval considering all cycles is 0.74 m of ice yr⁻¹ with a standard deviation of 0.13 m of ice yr⁻¹.

FIGURE 5

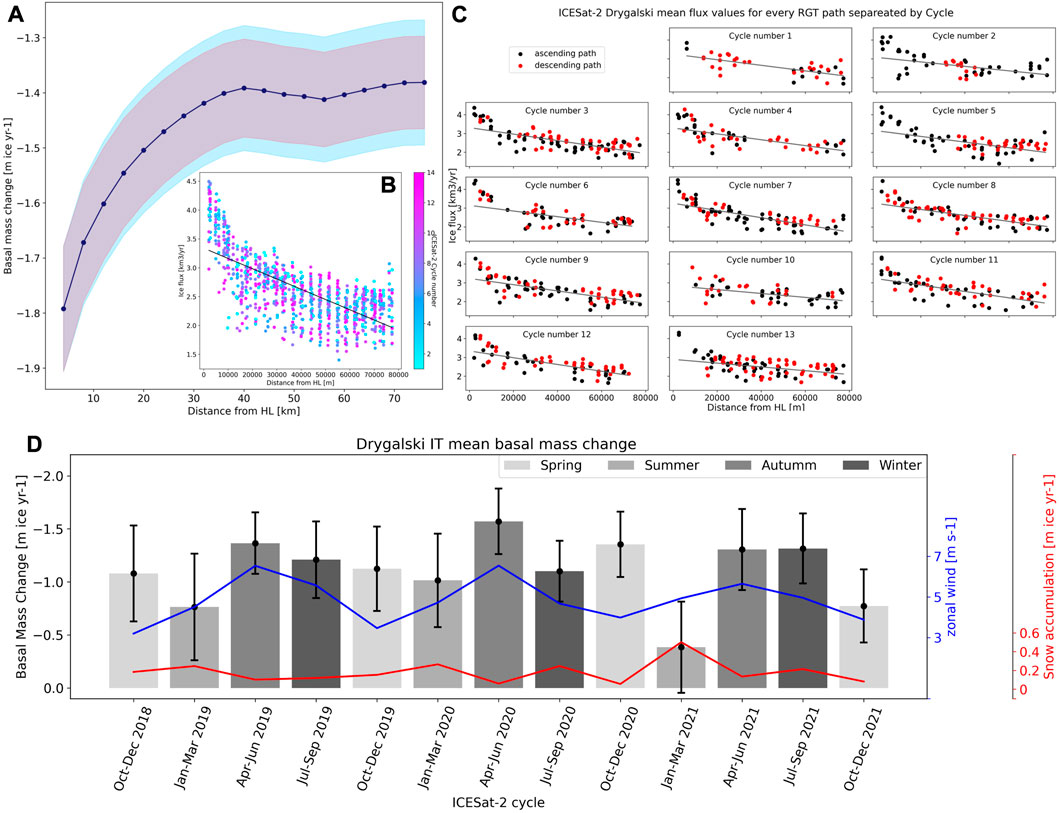
FIGURE 5. Drygalski (A) Basal melt between flowlines over the free-floating area of the ice tongue, derived from all the ICESat-2 data. The basal melt derived from the linear model confidence interval is shown in red, and the standard deviation of the basal melt is in light blue. (B) Ice flux derived from all cycles with fitted linear regression in black. The different cycles are shown in a colour map from cycle-1 in light blue to cycle-13 in pink. (C) Ice flux per cycle for every ICESat-2 track, with red showing the descending tracks and in black the ascending tracks. Every cycle has a fitted linear regression shown in grey. (D) Drygalski spatially averaged basal melt rates, with the axis inverted for clarity. Where more negative numbers imply larger mass loss, and the different seasons are depicted in a grey colour scheme. With darker grey for winter and lighter grey for summer. The snow accumulation rate in m of ice over the same period is shown in red. The snow accumulation values are derived from ERA5-land and are scaled to the same period as the ICESat-2 cycles.

The lower basal mass loss from cycle 10 (Jan-March 2021) could be influenced by the relatively large snow accumulation reported for that period by ERA5-land (0.5 m of ice yr⁻¹) and the relative fewer ICESat-2 data points near the HL compared to other cycles (Figure 5C). These could skew the results toward the lower basal melt values registered at the tip of the ice tongue. Drygalski Ice Tongue ice flux shows a non-linear relationship with distance, which may be caused by a different basal ablation regime close to its grounding line inside the fjord-like embayment. The selection of a linear model for the representation of this relationship is most probably underestimating the BMB near the HL and overestimating the BMB closer to the tip. Overall average results for BMB from linear or third-order polynomial regression are, however, similar in magnitude (−1.46 m of ice yr⁻¹ and −1.79 m of ice yr⁻¹, respectively).

For Aviator ice tongue each point in Figure 6B shows the mean flux at one gate on a given ICESat-2 cycle with the linear regression fitted to the data. The modelled flux was used to derive the spatial basal melt of the ice tongue (Figure 6A). The curve shows a similar spatial pattern with lower basal melt values near the front (−0.86 ± 0.07 m of ice yr⁻¹ at 26 km from the HL) and larger closer to the HL (−1.14 ± 0.09 m of ice yr⁻¹ at 2 km from the HL), with a steep curve that flattens as the flux approaches the ice tongue tip. When we do the same ice flux modelling for each cycle (Figure 6C), all the WLS regression models are significant, and only three (cycles 6 and 11) of the 13 cycles have R² values lower than 0.6. We then calculate the modelled ice flux at every 1 km (Figure 2D) for each cycle and use the average basal melt rate of each period. When the different cycles are taken independently, intra-annual variability appears (Figure 6D). With the largest values during Jan-March 2019 (−1.00 ± 0.22 m of ice yr⁻¹), Apr-June 2020 (−1.09 ± 0.22 m of ice yr⁻¹), Jan-March 2021 (−1.10 ± 0.47 m of ice yr⁻¹) and Jul-September 2021 (−1.19 ± 0.27 m of ice yr⁻¹).

FIGURE 6

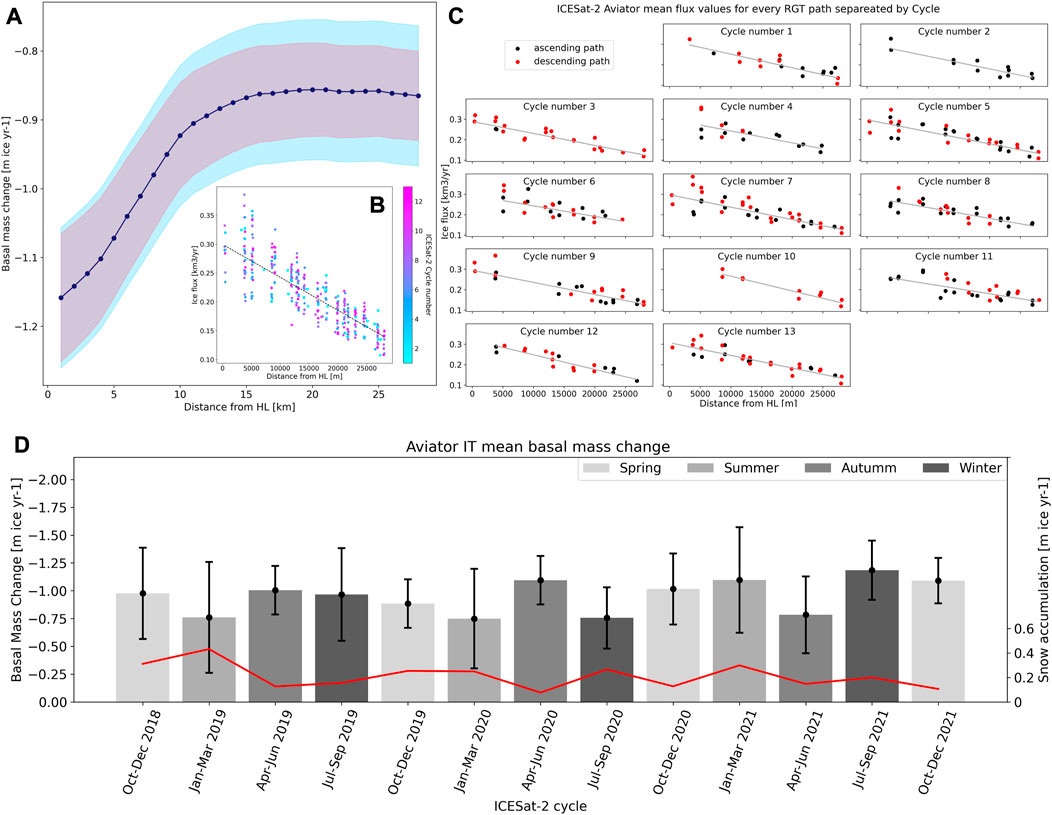
FIGURE 6. Aviator (A) Basal melt between flowlines over the free-floating area of the ice tongue, derived from all the ICESat-2 data. The basal melt derived from the linear model confidence interval is shown in red, and the standard deviation of the basal melt is in light blue. (B) Ice flux derived from all cycles with fitted linear regression in black. The different cycles are shown in a colour map from cycle-1 in light blue to cycle-13 in pink. (C) Ice flux per cycle for every ICESat-2 track, with red showing the descending tracks and in black the ascending tracks. Every cycle has a fitted linear regression shown in grey. (D) Aviator spatially averaged basal melt rates, with the axis inverted for clarity. More negative numbers imply larger mass loss, and the different seasons are depicted in a grey colour scheme. With darker grey for winter and lighter grey for summer. The snow accumulation rate in m of ice over the same period is shown in red. The snow accumulation values are derived from ERA5-land and are scaled to the same period as the ICESat-2 cycles.

4.3 Uncertainty and sensitivity analysis

There are several uncertainties in the method associated with different surface processes that are important to address: Temporal and spatial variability in snowfall, seasonality in firn compaction, snow redistribution by wind, ice advection and surface topography, and sparse measurement in time and space in the same cycle. Also, changes in the ocean surface reference due to land-fast sea ice. All these uncertainties are taken into account by the confidence interval of the results. The confidence interval of the basal melt change was derived analytically using the regression model and low and high values of the confidence intervals as inputs in Eq. 4. The range of the confidence intervals is roughly the same order of magnitude as the basal mass change. Understanding the processes and the limitations of the method could give us a better notion of what is needed to narrow down the overall uncertainties associated with the physical processes. In order to assess some of these uncertainties, we looked into surface velocity changes and the effect of land-fast sea ice on freeboard changes via sensitivity analysis.

4.3.1 Seasonal ice surface velocities

It has been observed that surface velocities on ice tongues can vary between seasons (Zhou et al., 2014; Greene et al., 2018; Gomez-Fell et al., 2022). When computing ice surface velocities over some ice tongues, we found small seasonal variations, particularly on the component of the velocity perpendicular to Drygalski and Aviator ice tongues ice flow. In order to take this variability into account, we calculated the basal mass loss using a seasonal average that covers the study period (2018–2021). We found that using a seasonal mean versus a 4-year average covering the same period had little impact on the final results. A slightly higher mass loss was observed for both ice tongues, 0.5% for Drygalski and 1.5% for Aviator. Because the values are still in between the error given by the confidence interval, we used the 4-year average covering the same period for all the ice tongues. In the case of Drygalski and Aviator ice tongues, the difference was not significant. But, because the variability could be higher, we did a small sensitivity analysis and observed what would happen if we changed both of the velocity components by 10%. We found that the overall mass loss increases by 12%, with a 10% increase in velocity. Therefore, if a large seasonal surface ice velocity is observed or if the velocity product used is from a different epoch than the surface height values, there could be a noticeable impact on the basal mass change calculations.

4.3.2 Snow accumulation and land-fast sea ice effect over derived freeboard

Snow accumulation has a spatial and temporal variability that is hard to resolve with the method (Supplementary Figure S3). Each ICESat-2 cycle has 91 days between repeat passes. This means that the combined values used to define the ice height are spatially distributed over the three months. The snowfall is not evenly distributed over the surface during those months. Additionally, redistribution of snow by wind might happen, or snow compaction during the summer months. Another process that affects freeboard derivations from laser altimeters over ice tongues is the growth and decay of annual land-fast sea ice.

Land-fast sea ice attached to the ice tongues can distort the freeboard derivations by lowering it by tens of centimetres, biassing the seasonal variability to values of larger basal melt during the winter/spring months compared to the summer and autumn months. This would only happen on ice tongues that are surrounded by ice during winter and are ice-free during the summer. This does not happen yearly for every ice tongue, not for the entire length of all the ice tongues. Aviator Ice Tongue tend to be surrounded by ice from Apr-Jun to Jan-Feb. Because this could bias the basal mass loss during the free-ice periods and explain, in part, lower values during the periods of Jan-March 2019 and 2020. We decided to do a sensitivity analysis and add 0.5 m to the freeboard, accounting for an additional 5 m in thickness. When adding this value uniformly over the ice tongue, it impacts 0.7% of the overall mass change. Therefore, we disregard a seasonal effect in the overall basal mass balance due to changes in freeboard because of land-fast sea ice.

4.4 Correlation of mass balance with environmental variables

Having derived the mass balance of twelve ice tongues along the Victoria Land Coast, the correlation to eleven environmental variables is analysed: snow accumulation (SA), surface temperature (Ts), ice tongue mass turnover (MT), ice tongue to catchment area ratio (AR), surface mass balance (SMB), fast ice persistence (FIP), ice tongue width to length ratio (WLR), meridional wind (MW), ice tongue latitude (IL), ice tongue area (IA), ice tongue basin area (ICA), and zonal wind (ZW). To define FIP, we used the occurrence and classification of fast ice from Fraser et al. (2020). Every pixel classified as fast ice was averaged in time, and then a ratio between 0 and 1 was created. We call FIP the percentage of time the pixel was classified as fast ice. We used a Pearson correlation, and the values ranged from 0.8 to −0.41 (Figure 6). Seven of the 13 correlations reveal significance values (p-value) lower than 0.25 (Figure 6). We use a p-value of 0.25 as a significant coefficient due to the small sample set. This result is the basis for a further discussion about the wider geographic context of ice tongue characteristics and stability (Section 5.3).

We looked into the correlation between basal melt and some climatological and geomorphological variables (Figure 7 and Supplementary Figure S1). We used four climatological variables from ERA5-Land (Muñoz-Sabater et al., 2021) SA, Ts, ZW and MW and SMB from RACMO2.3p2 (van Wessem et al., 2018). Four of them had a significant correlation with basal mass loss SA (0.63), SMB (0.38), Ts (0.5) and ZW (−0.41). It was expected that SA and SMB would have a positive correlation with basal mass loss as both have the same order of magnitude and are directly related to the mass balance of the ice tongue.

FIGURE 7

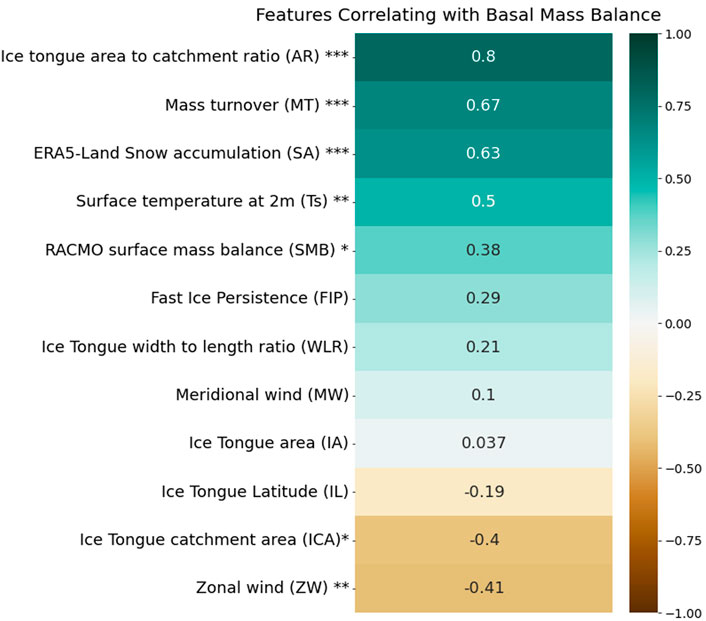
FIGURE 7. Correlation coefficients of different environmental and geomorphological variables with ice tongues basal mass balance. The variables are snow accumulation (SA), surface temperature (Ts), ice tongue mass turnover (MT), ice tongue to catchment area ratio (AR), surface mass balance (SMB), fast ice persistence (FIP), ice tongue width to length ratio (WLR), meridional wind (MW), ice tongue latitude (IL), ice tongue area (IA), ice tongue basin area (ICA), and zonal wind (ZW). The colour code indicates the correlation values. The significance level of the correlation is given by: (***) 95%, (**) 85%, (*) 75%. Correlation values are annotated in each cell, colour scale indicates a correlation from −1 to 1.

The geomorphological variables used are MT, defined as the relation between the volume of ice divided by the flux of ice that crosses the first gate. The volume was calculated as the area between the defined flowlines and the first and last gate multiplied by the mean thickness of the ice tongue over that area. MT has a correlation value of 0.66; as expected ice tongues with larger basal mass loss will have shorter turnover rates. IA is the complete outline of the ice tongue from the grounding line to the tip. The polygon was manually drawn from a 2019 Sentinel-1 SAR image. According to the results, the total area of the ice tongue does not have a difference over the basal mass change in the outward part of the ice tongue. The ICA (shown in Figure 1) (Frezzotti, 1997) has a significant negative correlation (−0.4) with basal mass change, meaning that ice tongues with larger catchment areas will have a relatively larger basal mass loss.

We also compound some of these metrics to examine the ratios between some geomorphological characteristics. The AR was calculated for all the ice tongues dividing the IA by the ICA values. We found that this measurement presents a relatively high positive correlation (0.8). This means that the relative size of the ice tongue to its catchment area could be an important factor in its overall glaciological persistence. The other ratio calculated was WLR, calculated as the width divided by the length of the ice tongue. The width was taken at a representative point, and the length was measured from the hydrostatic line to the tip of the ice tongue. The result of this correlation was low (0.21) and not significant.

The last two parameters analysed were the relation of basal mass loss with latitude and land-fast sea ice. The relation of basal mass loss with IL was negative (−0.19) but not significant. If ocean forcing is the main driver of basal mass loss, this could mean that the oceanographic conditions along the coast are similar for all the ice tongues. Lastly, FIP had a positive but not significant correlation (0.29), suggesting that areas that have persistent land-fast sea ice over time have a lower basal mass loss. Non-etheless, we were expecting the relation with FIP to be stronger than what we found.

5 Discussion

In the following sections, we compare our ice tongue basal mass balance results with previous ice tongue studies. Then we explore the seasonal variability and look into the various environmental variables that potentially influence ice tongue stability. Followed by comparisons with pan-Antarctic basal melt rates, potential gaps in our study and future research directions are highlighted.

5.1 Victoria land ice tongues basal mass loss previous studies

When compared with specific ice tongue studies, we found that there are very few studies that look into the basal mass balance of ice tongues in the region. From South to North we have the Erebus, Drygalski and Campbell ice tongues. Erebus Ice Tongue has a very comprehensive glaciological study from Holdsworth (1974, 1982). In his study, the ice tongue thickness was obtained from radio-echo-sounding and airborne radar data. Surface displacement and surface mass balance were calculated from direct measurements. Basal mass loss was then calculated from the mass balance equation obtaining the following values −1.2 ± 0.5 m of ice yr⁻¹. This is slightly higher than our result (−0.53 ± 0.71 m of ice yr⁻¹) but still within the limits of the confidence interval of both measurements. In our result, the biggest uncertainty is the firn layer. The modelled firn does not possess enough spatial resolution to resolve the ice tongue firn values. To resolve this we used the mean firn value of each track at every ICESat-2 point. When using this firn value the thickness is well resolved if compared with previous observational data (e.g., Holdsworth, 1974; Holdsworth, 1982; Stevens et al., 2014).

The Drygalski ice tongue, the largest ice tongue in the Western Ross Sea, has two mass balance studies. We compare our average basal mass loss of −1.46 ± 0.09 m of ice yr⁻¹ with the average values from Wuite et al. (2009), at gates 5–10), −0.834 ± 1.4 m of ice yr⁻¹, and from Frezzotti et al. (2000), at gates D9-D10 to D11-D12), −1.0 ± 0.5 m of ice yr⁻¹. Both investigations used a flux-gate approach. The difference between them is that the thickness and velocity data are obtained from different measurements. Both studies have measurements deep inside the fjord, near the grounding line. For our comparison, we consider the same area of the ice tongue and our results are slightly larger but in the 95% confidence interval. They show the same spatial pattern from larger ice loss near the fjord-type embayment and then stabilised at lower values through the mid-to-tip section (Figure 5). The difference, more than a bias of the sensor (ICESat vs. ICESat-2) or methodology in the thickness derivation, is most likely related to the width of the gates and the area averaged. There is presumably a variability in basal melt values between the Southern and Northern sides of Drygalski ice tongue, as has been shown in other ice tongues (Holdsworth, 1982). This would make basal melt values vary depending on how the location of the gates has been chosen. Stevens et al. (2017) observed a difference in water temperatures between the Northern and Southern sides of the ice tongue suggesting a gradient in the basal melt. In the Stevens et al. (2017) study a source of ISW was also detected on the southwest side of the ice tongue, which is coming from inside the Drygalski ice tongue cavity and they found summer meltwater only on the northern side of the ice tongue.

The other ice tongue with a specific basal mass balance study is Campbell Ice Tongue. Here Han and Lee (2015) used a mass conservation approach and found an average basal mass balance of −2.46 ± 1.07 m of ice yr⁻¹. While our result of −1.47 ± 0.02 m of ice yr⁻¹ is at the lower end of their confidence intervals. They used a very precise InSAR surface velocity product, but the main uncertainties are related to the assumption of overall thickness and average thickness change derived from a few ICESat tracks. Overall, previous measurements are in the confidence range of our results. This indicates that over the last 50 years, the ice melt driven by ocean forcing has remained stable for these ice tongues. However, we are now able to extend the measurements to larger areas at higher temporal resolution.

5.2 Seasonal patterns on basal melt change/seasonality of intra-annual variability

Sufficient satellite data coverage justified the calculation of the temporal mass balance variability of Drygalski and Aviator ice tongues. Drygalski ice tongue had larger values over autumn and lower during summer, while over Aviator ice tongue there is not a clear pattern. Because of the short time series, these results do not allow us to draw firm conclusions about a seasonal mass-balance pattern. But, it gives a picture of the intra-annual variations and the importance of local seasonal processes on ice tongue basal melt. We found that the main uncertainty is the snow accumulation product that defines the surface processes and directly impacts the basal mass change calculations. On the other hand, as we have already shown, it seems that variability in ice flow does not have a big impact on basal melt variability.

If we compare the coefficient of variation of Aviator and Drygalski basal mass loss (Figure 5D, Figure 6D). Over the three years of the study, there is a relatively larger variability in the basal mass loss with Drygalski (28.6%) compared to Aviator (15.8%). It would be expected that variability in basal melt is driven by large melt rates during summer and lower during winter, similar to the front west of the Ross Ice Shelf (Stewart et al., 2019). Changes in the ocean surface and climatic conditions vary yearly and regionally creating variability in the ice tongues ocean forcing (Piñones et al., 2019). Another cause of variability could be the seasonal intrusion of mCDW as modelled by Jendersie et al. (2018). In their results, mCDW has the largest intrusion during the winter months when sea ice production is at its highest. This could explain peaks of basal mass loss in Autumn or Winter.

Drygalski Ice Tongue northern flank is open to the year-round ice-free Terra Nova Bay polynya. Sea ice formation and HSSW may play a larger role in the basal melt of the Drygalski ice tongue near the grounding line (Stevens et al., 2017). Large polynya events driven by katabatic winds may have an influence over Drygalski basal melt variability. ERA5-Land shows that katabatic winds picked over the Drygalski Ice Tongue at the same periods of the larger basal mass loss. In this three-year case that was Apr-June 2019, 2020 and 2021 (Figure 5D).

There is no clear pattern over Aviator ice tongue basal mass loss variability during the three years (Figure 6D). The observed variation is most likely the inherent intrinsic variability of the system (Orsi and Wiederwohl, 2009) and related to the stability of the area (Frezzotti, 1997). It is an indication that there is not a clear process driving the basal mass loss of Aviator ice tongue. All these points towards a stable ice tongue helped by a low annual and seasonal basal mass loss. This differs from other parts of Antarctica where basal melt under ice shelves has shown strong seasonal variability over the summer months (Lindbäck et al., 2019; Stewart et al., 2019).

5.3 Spatial relations between basal mass balance and geographical and environmental variables

The applied satellite analysis is restricted to ice tongues with sufficient size and adequate orientation with respect to ICESat-2 overpasses (9) or large enough that the basal melt could be derived with available thickness and velocity products (3). The total sample size for the correlation analysis is therefore restricted to twelve ice tongues. We, therefore, focus the discussion on variables revealing confidence levels $<$ 0.3. These variables are ice tongue area to catchment ratio (AR), mass turnover (MT), snow accumulation (SA), Surface temperature (Ts), surface mass balance (SMB), fast ice persistence (FIP), zonal wind (ZW) and ice tongue glacier catchment area (ICA) (Figure 7).

The ice tongues used in this study are well distributed along the Victoria Land Coast (Figure 1). We found that the latitudinal position of the different ice tongues does not correlate with the rate of basal melt. This suggests that ocean temperatures along the coastal areas of Victoria Land are fairly uniform and that intrusions of warmer waters over the Ross Sea (Piñones et al., 2019; Tinto et al., 2019) are not occurring near the coast or not driving the basal melt of these ice tongues. More likely is that the VLCC, a cold coastal current transporting ISW from the Ross and McMurdo Ice Shelves (Hughes et al., 2014; Stevens et al., 2017; Jendersie et al., 2018) is stabilizing these features.

In the absence of a strong driver of basal mass loss, other geomorphological parameters seem to have an important role in the maintenance of an ice tongue. Of all the parameters analysed, we found that AR (0.8, with a p-value $<$ 0.05) correlates well with BMB. This implies that relatively small catchment areas with relatively large ice tongues are sustainable over time at a low BMB regime. Meaning that ice tongues formed from small catchments are potentially more unstable than relatively small ice tongues from relatively large catchments. This has the potential to use AR as a proxy for changes in BMB over the Western Ross Sea region.

On the other hand, our results show that the larger the ICA, the larger the basal mass loss (−0.4 with a p-value $<$ 0.2). This is easier to comprehend as larger catchment areas will have more mass to discharge into the ocean and thicker draft areas, all of this contributing to larger basal melt rates. The opposite happens with MT, where a larger MT will mean lower basal melt rates. As expected, the larger MT (0.67 with a p-value $<$ 0.05) were related to the lower BMB values. MT could also be used as a proxy for changes in BMB. Another feature that correlates positively with BMB is FIP. Land-fast sea ice grows between ice tongues and grounded icebergs (Massom et al., 2001) and can last for several years (Fraser et al., 2021). It has been hypothesised that ISW could enhance FIP (Massom et al., 2010). This would link cold water outflows with FIP and lower BMB. FIP varies along the Victoria Land Coast (Figure 1) and depends on other factors (Brett et al., 2020), not just lower ocean temperatures.

We observed that climatic variables, such as SA, Ts, ZW and SMB, had significant correlations (p-values $<$ 0.2) with BMB (Figure 7). SA and SMB are directly related to BMB calculations, but they help understand other relationships between the correlation matrix. The ZW in this area of Antarctica is related to the katabatic winds coming from the Transantarctic Mountains (Bromwich and Kurtz, 1984). Models of basal melt have shown that katabatic winds can increase the melting of ice shelves (Hazel and Stewart, 2020). In the case of the Western Ross Sea, the katabatic winds are the drivers of polynya events over Terra Nova Bay (Bromwich and Kurtz, 1984), enhancing vertical mixing and convection (Morales Maqueda et al., 2004). BMB correlation with Ts is less clear, annual mean temperatures range between −22 and −18°C and there is a strong relation between Ts and SA (Supplementary Figure S1). The correlation is probably due to a relation between SA and Ts.

Other variables did not have a significant correlation with basal melt (Figure 7). MW wind in this area of Antarctica follows the coast, as ZW is perpendicular to the coast. This implies that along-shore winds do not have an effect on basal melt in this region, the opposite has been observed in other areas of Antarctica (Hirano et al., 2020). As for the relation between IA and BMB, we can say that changes in the size of an ice tongue are not necessarily a good indicator of an overall stable region. The same can be said for the WLR.

The mass balance of the ice tongues is in a delicate balance between ocean forcing and catchment-wide accumulation. Ice tongues in this region of Antarctica have not yet been affected by the intrusion of mCDW waters over the shelf. The size and persistence of ice tongues in the absence of a strong ocean or atmospheric forcing are controlled by external factors such as fast ice extent or other size-limiting factors. We found that ice tongues with larger catchment areas have a larger basal mass loss, and they are normally thicker, while ice tongues with large MT have low basal melt rates.

Other processes that have been found to have an influence over ice shelves are basal roughness and polynyas. Watkins et al. (2021) found that the roughness of ice shelves was correlated with basal melt rates, as interesting as it is Larter (2022) addressed that more measurements around Antarctica are necessary to corroborate that the correlation holds. Non-etheless, Bianchi et al. (2001) carried out an assessment of the underlying roughness of 10 ice tongues and ice shelves in the Western Ross sea and Pennel Coast. Of those, we have a basal mass loss of five (Harbord, Drygalski, Campbell, Aviator and Mariner). When comparing our results with their estimated roughness we found that the flat morphology (Harbord and Mariner ice tongue) corresponds to relatively low basal mass loss, and the rippled morphology (Drygalski, Campbell and Aviator) corresponds to relatively larger basal mass loss. Our results indicate that the link between roughness and basal mass loss might be applicable to ice tongues and that might be a desirable avenue for further basal melt studies.

Polynyas tend to form on the leeward side of ice tongues and ice shelves Nihashi and Ohshima (2015). Katabatic winds that drive most of the polynyas around Antarctica help mix the upper ocean layer introducing warmer surface water underneath the front of ice shelves and ice tongues (Khazendar et al., 2013; Stewart et al., 2019). Is plausible to believe that the same process is valid for ice tongues near polynyas as the Drygalski ice tongue where we did observe a seasonality in its basal mass loss. This contrasts with the lack of a clear pattern over variability in the basal mass loss that we found for the Aviator ice tongue. This could indicate that a seasonal climatic process does not drive Aviator ice tongue basal melt.

When we compare the ice tongue basal mass balance with results from Pan-Antarctic ice shelves studies, we found that our estimations are in general lower. Adusumilli et al. (2020) had a mean value of basal melt rates between 1994 and 2018 of 1.9 ± 0.9 m of ice yr⁻¹ for Drygalski and 1.1 ± 1.7 m of ice yr⁻¹ for Mariner and Borchgrevink, both higher than our calculated basal mass loss. Depoorter et al. (2013) inform a value of basal mass loss of −2.5 ± 0.5 m of ice yr⁻¹ for Drygalski, while Rignot et al. (2013) present melt rates of 3.3 ± 0.5 m of ice yr⁻¹ for Drygalski, and also give values for Aviator (1.7 ± 0.3 m of ice yr⁻¹) and Mariner (0.9 ± 0.2 m of ice yr⁻¹).

The differences between our results and Pan-Antarctic studies are related either to the measurement or the method used. Because, this area of Antarctica has remained stable over the last 60 years (Frezzotti, 1997; Miles et al., 2013; Fountain et al., 2017; Lovell et al., 2017), glaciers in the Victoria Land Coast have deep bed troughs (Bianchi et al., 2001; Morlighem et al., 2019), the bias that tidal flexure can create on floating ice thickness measurements (Rack et al., 2017; Wild et al., 2019), and that our results focus on the greater part of the ocean side of the ice tongue as defined by the DInSAR-derived hydrostatic line. Is most probable that the methodology and definition of the area of interest are the main reason for the basal mass loss differences. Seasonality could be another factor to consider when building a Pan-Antarctic product as basal mass loss can vary between summer and winter. If we want to understand variability at a local scale for relatively small ice tongues, Pan-Antarctic basal melt rate products might not apply. Because spatial and temporal resolutions of such studies might not resolve temporal variability in forcing and local geomorphology that is important for basal mass loss and varies between different glacier catchments.

We provide a new picture of the overall mass balance of ice tongues in the VLC by addressing the prevalence of ice tongues and their value as sentinels of change. We found a heterogeneous distribution of basal melt rates along the coast. From our study, it is not possible to narrow down the determining factor of ice tongue stability in the region. But we can hypothesise that the VLCC has a strong influence in maintaining these features stables over time, with the added support of favourable local geomorphological conditions. There are shortcomings of this study that should be addressed in future research; one is the number of ice tongues studied and their representativity outside the VLC, and the lack of ground measurements to validate the results. Using a combination of satellite remote sensing of basal mass loss time series with in situ measurements (e.g., ApRES) would help validate the observations. There are other areas that if improved would allow to better derive basal mass balance of small ice tongues. Some of these are: Oceanographic measurements around ice tongues in the Victoria Land Coast are sparse, a better understanding of the oceanographic climatological and seasonal oceanographic conditions near the ice tongues of Victoria Land Coast would help bridge the glaciological understanding of the seasonality of ice tongue basal mass loss; Longer time series of satellite laser altimeters will allow elucidating seasonal drivers of basal melt; The knowledge of the thickness of the northern Victoria Land glacier valleys and fjords is poor and downscaling firn and surface mass balance models at the fringes of Antarctica would help to reconcile high-resolution satellite measurements and low-resolution Antarctic models. More data on all these fronts would help constrain better the mass balance of the Western Ross Sea Ice Tongues.

6 Conclusion

Using freely available laser altimeter data from ICESat-2 combined with Sentinel-1 synthetic aperture radar imagery, we extended previous studies of ice tongue mass balance. A much-improved satellite coverage allows for the quantification of the basal melt of twelve Antarctic ice tongues in the Western Ross Sea using the flux-gate method as a basis for further geospatial analysis. The favourable ICESat-2 repeated pass cycles also enabled the quantification of intra-annual variations in the basal mass loss for two of the larger ice tongues.

The values of basal mass loss range from −0.14 ± 0.04 m of ice yr⁻¹ to −1.5 ± 1.2 m of ice yr⁻¹, with the low values comparing well to cold cavity ice shelves in the area. These can be explained by the outflow-modified ISW originating in the ice shelf and ice tongue cavities in the Western Ross Sea region and explain the observed stability of most of the ice tongues in the area. A number of environmental and geomorphological parameters were used to further explore the drivers of ice tongue mass balance. We found that the relative size of the ice tongue with respect to its catchment is a good indicator for basal melt in this region of Antarctica, as relatively large catchment basins are able to sustain relatively large ice tongues even with higher basal melt rates. For the environmental variables, an example of a strong negative correlation of ice tongue melt is found with katabatic winds in the area. This is also closely related to the occurrence of polynyas and the prevalence of land-fast sea ice. Basal melt values are relatively heterogeneous along the coast, with no clear latitudinal gradient. This signals that even though Victoria Land Coast is one of the largest stretches of North-South oriented coastline in Antarctica, this is not reflected in a basal melt latitudinal gradient. This suggests that local processes and geomorphology are important for the stability of ice tongues in the absence of a strong oceanographic melting force.

The capability to obtain seasonal or intra-annual variations in basal melt from satellite remote sensing is a significant progress for the study of ice tongue stability. The combination of our applied method with in situ time series of basal melt, for example, using phase-sensitive radars, would enable further improvements in our understanding of the processes behind the temporal mass balance sensitivity of ice tongues in this area.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://doi.org/10.5281/zenodo.7127099.

Author contributions

RG-F conceived the research project and performed the data analysis and processing and led the manuscript writing. CW assisted with the initial coding and produced the alpha maps. WR, OM, and HP provided discussion and feedback during the different project stages. All authors participated in the writing and revision of the article and approved the final manuscript.

Funding

The New Zealand Antarctic Science Platform (ASP) and the Antarctic and High Latitude Climate Project (NIWA) partially funded WR.

Acknowledgments

RG-F acknowledges the support of the University of Canterbury and the Antarctic New Zealand Sir Robin Irvine Doctoral Scholarships. We thank Shelley MacDonell for her advice and comments during the research process.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1057761/full#supplementary-material

References

Adusumilli, S., Fricker, H. A., Medley, B., Padman, L., and Siegfried, M. R. (2020). Interannual variations in meltwater input to the Southern Ocean from Antarctic ice shelves. Nat. Geosci. 13, 616–620. doi:10.1038/s41561-020-0616-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Adusumilli, S., Fricker, H. A., Siegfried, M. R., Padman, L., Paolo, F. S., and Ligtenberg, S. R. (2018). Variable basal melt rates of antarctic peninsula ice shelves, 1994-2016. Geophys. Res. Lett. 45, 4086–4095. doi:10.1002/2017GL076652

CrossRef Full Text | Google Scholar

Alley, K. E., Wild, C. T., Luckman, A., Scambos, T. A., Truffer, M., Pettit, E. C., et al. (2021). Two decades of dynamic change and progressive destabilization on the Thwaites Eastern Ice Shelf. Cryosphere 15, 5187–5203. doi:10.5194/tc-15-5187-2021

CrossRef Full Text | Google Scholar

Arzeno, I. B., Beardsley, R. C., Limeburner, R., Owens, B., Padman, L., Springer, S. R., et al. (2014). Ocean variability contributing to basal melt rate near the ice front of Ross Ice Shelf, Antarctica. J. Geophys. Res. Oceans 119, 4214–4233. doi:10.1002/2014JC009792

CrossRef Full Text | Google Scholar

Baumhoer, C. A., Dietz, A. J., Kneisel, C., Paeth, H., and Kuenzer, C. (2021). Environmental drivers of circum-Antarctic glacier and ice shelf front retreat over the last two decades. Cryosphere 15, 2357–2381. doi:10.5194/tc-15-2357-2021

CrossRef Full Text | Google Scholar

Berger, S., Drews, R., Helm, V., Sun, S., and Pattyn, F. (2017). Detecting high spatial variability of ice shelf basal mass balance, Roi Baudouin Ice Shelf, Antarctica. Cryosphere 11, 2675–2690. doi:10.5194/tc-11-2675-2017

CrossRef Full Text | Google Scholar

Bianchi, C., Chiappini, M., Tabacco, I., Passerini, A., Zirizzotti, A., and Zuccheretti, E. (2001). Morphology of bottom surfaces of glacier ice tongues in the East Antarctic region. Roma, Italy: Istituto Nazionale di Geofisica e Vulcanologia. doi:10.4401/ag-3609

CrossRef Full Text | Google Scholar

Bindschadler, R., Choi, H., Wichlacz, A., Bingham, R., Bohlander, J., Brunt, K., et al. (2011). Getting around Antarctica: New high-resolution mappings of the grounded and freely-floating boundaries of the Antarctic ice sheet created for the International Polar Year. Cryosphere 5, 569–588. doi:10.5194/tc-5-569-2011

CrossRef Full Text | Google Scholar

Brett, G. M., Irvin, A., Rack, W., Haas, C., Langhorne, P. J., and Leonard, G. H. (2020). Variability in the distribution of fast ice and the sub-ice platelet layer near McMurdo ice shelf. J. Geophys. Res. Oceans 125, 1–21. doi:10.1029/2019JC015678

CrossRef Full Text | Google Scholar

Bromwich, D. H., and Kurtz, D. D. (1984). Katabatic wind forcing of the Terra Nova Bay polynya. J. Geophys. Res. 89, 3561. doi:10.1029/JC089iC03p03561

CrossRef Full Text | Google Scholar

Brunt, K. M., Okal, E. A., and MacAyeal, D. R. (2011). Antarctic ice-shelf calving triggered by the Honshu (Japan) earthquake and tsunami, March 2011. J. Glaciol. 57, 785–788. doi:10.3189/002214311798043681

CrossRef Full Text | Google Scholar

Debenham, F. (1965). The Glacier tongues of McMurdo Sound. Geogr. J. 131, 369. doi:10.2307/1794191

CrossRef Full Text | Google Scholar

Depoorter, M. A., Bamber, J. L., Griggs, J. A., Lenaerts, J., Ligtenberg, S. R., Van Den Broeke, M. R., et al. (2013). Calving fluxes and basal melt rates of Antarctic ice shelves. Nature 502, 89–92. doi:10.1038/nature12567

PubMed Abstract | CrossRef Full Text | Google Scholar

Fountain, A. G., Glenn, B., and Scambos, T. (2017). The changing extent of the glaciers along the Western Ross Sea, Antarctica. Geology 45, 927–930. doi:10.1130/G39240.1

CrossRef Full Text | Google Scholar

Fraser, A. D., Massom, R. A., Handcock, M. S., Reid, P., Ohshima, K. I., Raphael, M. N., et al. (2021). Eighteen-year record of circum-Antarctic landfast-sea-ice distribution allows detailed baseline characterisation and reveals trends and variability. Cryosphere 15, 5061–5077. doi:10.5194/tc-15-5061-2021

CrossRef Full Text | Google Scholar

Fraser, A. D., Massom, R. A., Ohshima, K. I., Willmes, S., Kappes, P. J., Cartwright, J., et al. (2020). High-resolution mapping of circum-Antarctic landfast sea ice distribution, 2000–2018. Earth Syst. Sci. Data 12, 2987–2999. doi:10.5194/essd-12-2987-2020

CrossRef Full Text | Google Scholar

Frezzotti, M. (1997). Ice front fluctuation, iceberg calving flux and mass balance of Victoria Land glaciers. Antarct. Sci. 9, 61–73. doi:10.1017/s0954102097000096

CrossRef Full Text | Google Scholar

Frezzotti, M., and Mabin, M. (1994). 20th century behaviour of Drygalski ice tongue, Ross Sea, Antarctica. Ann. Glaciol. 20, 397–400. doi:10.3189/1994aog20-1-397-400

CrossRef Full Text | Google Scholar

Frezzotti, M., Tabacco, I. E., and Zirizzotti, A. (2000). Ice discharge of eastern Dome C drainage area, Antarctica, determined from airborne radar survey and satellite image analysis. J. Glaciol. 46, 253–264. doi:10.3189/172756500781832855

CrossRef Full Text | Google Scholar

Gomez-Fell, R., Rack, W., Purdie, H., and Marsh, O. (2022). Parker ice tongue collapse, Antarctica, triggered by loss of stabilizing Land-Fast Sea Ice. Geophys. Res. Lett. 49, 1–11. doi:10.1029/2021GL096156

PubMed Abstract | CrossRef Full Text | Google Scholar

Gossart, A., Helsen, S., Lenaerts, J. T., Vanden Broucke, S., van Lipzig, N. P., and Souverijns, N. (2019). An evaluation of surface climatology in state-of-the-art reanalyses over the Antarctic Ice Sheet. J. Clim. 32, 6899–6915. doi:10.1175/JCLI-D-19-0030.1

CrossRef Full Text | Google Scholar

Greene, C. A., Young, D. A., Gwyther, D. E., Galton-Fenzi, B. K., and Blankenship, D. D. (2018). Seasonal dynamics of Totten Ice Shelf controlled by sea ice buttressing. Cryosphere 12, 2869–2882. doi:10.5194/tc-12-2869-2018

CrossRef Full Text | Google Scholar

Griggs, J., and Bamber, J. (2011). Antarctic ice-shelf thickness from satellite radar altimetry. J. Glaciol. 57, 485–498. doi:10.3189/002214311796905659

CrossRef Full Text | Google Scholar

Han, H., and Lee, H. (2015). Tide-corrected flow velocity and mass balance of Campbell Glacier Tongue, East Antarctica, derived from interferometric SAR. Remote Sens. Environ. 160, 180–192. doi:10.1016/j.rse.2015.01.014

CrossRef Full Text | Google Scholar

Hazel, J. E., and Stewart, A. L. (2020). Bistability of the filchner-ronne ice shelf cavity circulation and basal melt. J. Geophys. Res. Oceans 125, 1–21. doi:10.1029/2019JC015848

CrossRef Full Text | Google Scholar

Hirano, D., Tamura, T., Kusahara, K., Ohshima, K. I., Nicholls, K. W., Ushio, S., et al. (2020). Strong ice-ocean interaction beneath shirase glacier tongue in east Antarctica. Nat. Commun. 11, 4221–4312. doi:10.1038/s41467-020-17527-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Holdsworth, G. (1982). Dynamics of Erebus glacier tongue. Ann. Glaciol. 3, 131–137. doi:10.1017/s0260305500002652

CrossRef Full Text | Google Scholar

Holdsworth, G. (1974). Erebus Glacier tongue, mcmurdo Sound, Antarctica. J. Glaciol. 13, 27–35. doi:10.1017/s0022143000023340

CrossRef Full Text | Google Scholar

Holdsworth, G. (1985). “Some effects of ocean currents and wave motion on the dynamics of floating glacier tongues,” in Oceanology of the Antarctic Continental Shelf. Editor S. S. Jacobs (Washington, DC, United States: American Geophysical Union, Antarctic Research Series), 235–271.

CrossRef Full Text | Google Scholar

Holland, P. R., Bracegirdle, T. J., Dutrieux, P., Jenkins, A., and Steig, E. J. (2019). West Antarctic ice loss influenced by internal climate variability and anthropogenic forcing. Nat. Geosci. 12, 718–724. doi:10.1038/s41561-019-0420-9

CrossRef Full Text | Google Scholar

Hughes, K. G., Langhorne, P. J., Leonard, G. H., and Stevens, C. (2014). Extension of an Ice Shelf Water plume model beneath sea ice with application in McMurdo Sound, Antarctica. J. Geophys. Res. Oceans 119, 8662–8687. doi:10.1002/2013JC009411

CrossRef Full Text | Google Scholar

Jacobs, S. S., Helmer, H., Doake, C. S. M., Jenkins, A., and Frolich, R. M. (1992). Melting of ice shelves and the mass balance of Antarctica. J. Glaciol. 38, 375–387. doi:10.3189/S0022143000002252

CrossRef Full Text | Google Scholar

Jendersie, S., Williams, M. J. M., Langhorne, P. J., and Robertson, R. (2018). The density-driven winter intensification of the Ross Sea circulation. J. Geophys. Res. Oceans 123, 7702–7724. doi:10.1029/2018JC013965

CrossRef Full Text | Google Scholar

Jenkins, A., Nicholls, K. W., and Corr, H. F. (2010). Observation and parameterization of ablation at the base of ronne ice shelf, Antarctica. J. Phys. Oceanogr. 40, 2298–2312. doi:10.1175/2010JPO4317.1

CrossRef Full Text | Google Scholar

Khazendar, A., Schodlok, M., Fenty, I., Ligtenberg, S., Rignot, E., and van den Broeke, M. (2013). Observed thinning of Totten Glacier is linked to coastal polynya variability. Nat. Commun. 4, 2857. doi:10.1038/ncomms3857

PubMed Abstract | CrossRef Full Text | Google Scholar

Larter, R. D. (2022). Basal melting, roughness and structural integrity of ice shelves. Geophys. Res. Lett. 49, 1–5. doi:10.1029/2021GL097421

PubMed Abstract | CrossRef Full Text | Google Scholar

Legrésy, B., Wendt, A., Tabacco, I., Rémy, F., and Dietrich, R. (2004). Influence of tides and tidal current on Mertz Glacier, Antarctica. J. Glaciol. 50, 427–435. doi:10.3189/172756504781829828

CrossRef Full Text | Google Scholar

Lei, Y., Gardner, A., and Agram, P. (2021). Autonomous repeat image feature tracking (Autorift) and its application for tracking ice displacement. Remote Sens. 13, 749–820. doi:10.3390/rs13040749

CrossRef Full Text | Google Scholar

Lenaerts, J. T., Ligtenberg, S. R., Medley, B., Van De Berg, W. J., Konrad, H., Nicolas, J. P., et al. (2018). Climate and surface mass balance of coastal West Antarctica resolved by regional climate modelling. Ann. Glaciol. 59, 29–41. doi:10.1017/aog.2017.42

CrossRef Full Text | Google Scholar

Ligtenberg, S. R., Helsen, M. M., and Van Den Broeke, M. R. (2011). An improved semi-empirical model for the densification of Antarctic firn. Cryosphere 5, 809–819. doi:10.5194/tc-5-809-2011

CrossRef Full Text | Google Scholar

Lindbäck, K., Moholdt, G., Nicholls, K. W., Hattermann, T., Pratap, B., Thamban, M., et al. (2019). Spatial and temporal variations in basal melting at Nivlisen ice shelf, East Antarctica, derived from phase-sensitive radars. Cryosphere 13, 2579–2595. doi:10.5194/tc-13-2579-2019

CrossRef Full Text | Google Scholar

Lovell, A. M., Stokes, C. R., and Jamieson, S. S. (2017). Sub-decadal variations in outlet glacier terminus positions in Victoria land, oates land and george v land, east Antarctica (1972-2013). Antarct. Sci. 29, 468–483. doi:10.1017/S0954102017000074

CrossRef Full Text | Google Scholar

MacAyeal, D. R., Okal, M. H., Thom, J. E., Brunt, K. M., Kim, Y.-J., and Bliss, A. K. (2008). Tabular iceberg collisions within the coastal regime. J. Glaciol. 54, 371–386. doi:10.3189/002214308784886180

CrossRef Full Text | Google Scholar

Massom, R. A., Giles, A. B., Fricker, H. A., Warner, R. C., Legrésy, B., Hyland, G., et al. (2010). Examining the interaction between multi-year landfast sea ice and the Mertz Glacier Tongue, East Antarctica: Another factor in ice sheet stability? J. Geophys. Res. Oceans 115, 1–15. doi:10.1029/2009JC006083

CrossRef Full Text | Google Scholar

Massom, R. A., Giles, A. B., Warner, R. C., Fricker, H. A., Legrésy, B., Hyland, G., et al. (2015). External influences on the mertz glacier tongue (east Antarctica) in the decade leading up to its calving in 2010. J. Geophys. Res. Earth Surf. 120, 490–506. doi:10.1002/2014JF003223

CrossRef Full Text | Google Scholar

Massom, R. A., Hill, K. L., Lytle, V. I., Worby, A. P., Paget, M. J., and Allison, I. (2001). Effects of regional fast-ice and iceberg distributions on the behaviour of the Mertz Glacier polynya, East Antarctica. Ann. Glaciol. 33, 391–398. doi:10.3189/172756401781818518

CrossRef Full Text | Google Scholar

Mezgec, K., Stenni, B., Crosta, X., Masson-Delmotte, V., Baroni, C., Braida, M., et al. (2017). Holocene sea ice variability driven by wind and polynya efficiency in the Ross Sea. Nat. Commun. 8, 1334. doi:10.1038/s41467-017-01455-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Miles, B. W. J., Stokes, C. R., Jamieson, S. S. R., Jordan, J. R., Gudmundsson, G. H., and Jenkins, A. (2022). High spatial and temporal variability in Antarctic ice discharge linked to ice shelf buttressing and bed geometry. Sci. Rep. 12, 10968. doi:10.1038/s41598-022-13517-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Miles, B. W., Stokes, C. R., Jenkins, A., Jordan, J. R., Jamieson, S. S., and Gudmundsson, G. H. (2020). Intermittent structural weakening and acceleration of the Thwaites Glacier tongue between 2000 and 2018. J. Glaciol. 66, 485–495. doi:10.1017/jog.2020.20

CrossRef Full Text | Google Scholar

Miles, B. W., Stokes, C. R., Vieli, A., and Cox, N. J. (2013). Rapid, climate-driven changes in outlet glaciers on the Pacific coast of East Antarctica. Nature 500, 563–566. doi:10.1038/nature12382

PubMed Abstract | CrossRef Full Text | Google Scholar

Moholdt, G., Padman, L., and Fricker, H. A. (2014). Basal mass budget of Ross and Filchner-Ronne ice shelves, Antarctica, derived from Lagrangian analysis of ICESat altimetry. J. Geophys. Res. Earth Surf. 119, 2361–2380. doi:10.1002/2014JF003171

CrossRef Full Text | Google Scholar

Morales Maqueda, M. A., Willmott, A. J., and Biggs, N. R. (2004). Polynya dynamics: A review of observations and modeling. Rev. Geophys. 42. doi:10.1029/2002RG000116

CrossRef Full Text | Google Scholar

Morlighem, M. (2020). MEaSUREs BedMachine Antarctica. Bolder, United States: NASA National Snow and Ice Data Center Distributed Active Archive Center. [Data Set]. Accessed January 13, 2022. doi:10.5067/E1QL9HFQ7A8M

CrossRef Full Text | Google Scholar

Morlighem, M., Rignot, E., Binder, T., Blankenship, D., Drews, R., Eagles, G., et al. (2019). Deep glacial troughs and stabilizing ridges unveiled beneath the margins of the Antarctic ice sheet. Nat. Geosci. 13, 132–137. doi:10.1038/s41561-019-0510-8

CrossRef Full Text | Google Scholar

Motyka, R. J., Truffer, M., Fahnestock, M., Mortensen, J., Rysgaard, S., and Howat, I. (2011). Submarine melting of the 1985 Jakobshavn Isbræ floating tongue and the triggering of the current retreat. J. Geophys. Res. Earth Surf. 116, 1–17. doi:10.1029/2009JF001632

CrossRef Full Text | Google Scholar

Mouginot, J., Rignot, E., and Scheuchl, B. (2019a). Continent-wide, interferometric SAR phase, mapping of antarctic ice velocity. Geophys. Res. Lett. 46, 9710–9718. doi:10.1029/2019GL083826

CrossRef Full Text | Google Scholar

Mouginot, J., Rignot, E., and Scheuchl, B. (2019b). MEaSUREs phase-based Antarctica ice velocity map. Bolder, United States: NASA National Snow and Ice Data Center Distributed Active Archive Center. [Data Set]. Accessed August 3, 2020. doi:10.5067/PZ3NJ5RXRH10

CrossRef Full Text | Google Scholar

Muñoz-Sabater, J., Dutra, E., Agustí-Panareda, A., Albergel, C., Arduini, G., Balsamo, G., et al. (2021). ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 13, 4349–4383. doi:10.5194/essd-13-4349-2021

CrossRef Full Text | Google Scholar

Muñoz-Sabater, J. (2019). ERA5-Land monthly averaged data from 1981 to present. Copernic. Clim. Change Serv. (C3S). doi:10.24381/cds.68d2bb3

CrossRef Full Text | Google Scholar

Neumann, T. A., Martino, A. J., Markus, T., Bae, S., Bock, M. R., Brenner, A. C., et al. (2019). The ice, cloud, and land elevation satellite – 2 mission: A global geolocated photon product derived from the advanced topographic laser altimeter system. Remote Sens. Environ. 233, 111325. doi:10.1016/j.rse.2019.111325

CrossRef Full Text | Google Scholar

Nihashi, S., and Ohshima, K. I. (2015). Circumpolar mapping of Antarctic coastal polynyas and landfast sea ice: Relationship and variability. J. Clim. 28, 3650–3670. doi:10.1175/JCLI-D-14-00369.1

CrossRef Full Text | Google Scholar

Orsi, A. H., and Wiederwohl, C. L. (2009). A recount of Ross Sea waters. Deep-Sea Res. Part II Top. Stud. Oceanogr. 56, 778–795. doi:10.1016/j.dsr2.2008.10.033

CrossRef Full Text | Google Scholar

Padman, L., Erofeeva, S., and Joughin, I. (2003). Tides of the Ross Sea and Ross ice shelf cavity. Antarct. Sci. 15, 31–40. doi:10.1017/S0954102003001032

CrossRef Full Text | Google Scholar

Padman, L., Erofeeva, S. Y., and Fricker, H. A. (2008). Improving Antarctic tide models by assimilation of ICESat laser altimetry over ice shelves. Geophys. Res. Lett. 35, L22504. doi:10.1029/2008GL035592

CrossRef Full Text | Google Scholar

Padman, L., Fricker, H. A., Coleman, R., Howard, S., and Erofeeva, L. (2002). A new tide model for the Antarctic ice shelves and seas. Ann. Glaciol. 34, 247–254. doi:10.3189/172756402781817752

CrossRef Full Text | Google Scholar

Piñones, A., Hofmann, E. E., Costa, D. P., Goetz, K., Burns, J. M., Roquet, F., et al. (2019). Hydrographic variability along the inner and mid-shelf region of the Western Ross Sea obtained using instrumented seals. Prog. Oceanogr. 174, 131–142. doi:10.1016/j.pocean.2019.01.003

CrossRef Full Text | Google Scholar

Pritchard, H., Ligtenberg, S., Fricker, H., Vaughan, D., van den Broeke, M., and Padman, L. (2012). Antarctic ice-sheet loss driven by basal melting of ice shelves. Nature 484, 502–505. doi:10.1038/nature10968

PubMed Abstract | CrossRef Full Text | Google Scholar

Rack, W., King, M. A., Marsh, O., Wild, C. T., and Floricioiu, D. (2017). Analysis of ice shelf flexure and its InSAR representation in the grounding zone of the southern McMurdo Ice Shelf. Cryosphere 11, 2481–2490. doi:10.5194/tc-11-2481-2017

CrossRef Full Text | Google Scholar

Rack, W., Price, D., Haas, C., Langhorne, P. J., and Leonard, G. H. (2021). Sea Ice thickness in the western Ross Sea. Geophys. Res. Lett. 48. doi:10.1029/2020GL090866

CrossRef Full Text | Google Scholar

Rignot, E., Jacobs, S. S., Mouginot, J., and Scheuchl, B. (2013). Ice-shelf melting around Antarctica. Science 341, 266–270. doi:10.1126/science.1235798

PubMed Abstract | CrossRef Full Text | Google Scholar

Rignot, E., Mouginot, J., and Scheuchl, B. (2016). MEaSUREs antarctic grounding line from differential satellite radar interferometry, version 2 [data set]. Bolder, United States: NASA National Snow and Ice Data Center Distributed Active Archive Center. (Accessed March 2, 2017). doi:10.5067/IKBWW4RYHF1Q

CrossRef Full Text | Google Scholar

Rosevear, M. G., Gayen, B., and Galton-Fenzi, B. K. (2022). Regimes and transitions in the basal melting of Antarctic ice shelves. J. Phys. Oceanogr. 1, 2589–2608. doi:10.1175/jpo-d-21-0317.1

CrossRef Full Text | Google Scholar

Sansiviero, M., Morales Maqueda, M., Fusco, G., Aulicino, G., Flocco, D., and Budillon, G. (2017). Modelling sea ice formation in the Terra Nova Bay polynya. J. Mar. Syst. 166, 4–25. doi:10.1016/j.jmarsys.2016.06.013

CrossRef Full Text | Google Scholar

Smith, B., Fricker, H. A., Gardner, A. S., Medley, B., Nilsson, J., Paolo, F. S., et al. (2020). Pervasive ice sheet mass loss reflects competing ocean and atmosphere processes. Science 368, 1239–1242. doi:10.1126/science.aaz5845

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, B., Fricker, H. A., Holschuh, N., Gardner, A. S., Adusumilli, S., Brunt, K. M., et al. (2019). Land ice height-retrieval algorithm for NASA’s ICESat-2 photon-counting laser altimeter. Remote Sens. Environ. 233, 111352. doi:10.1016/j.rse.2019.111352

CrossRef Full Text | Google Scholar

Squire, V. A., Robinson, W. H., Meylan, M., and Haskell, T. G. (1994). Observations of flexural waves on the Erebus Ice Tongue, McMurdo Sound, Antarctica, and nearby sea ice. J. Glaciol. 40, 377–385. doi:10.3189/S0022143000007462

CrossRef Full Text | Google Scholar

Stevens, C., Hulbe, C., Brewer, M., Stewart, C., Robinson, N., Ohneiser, C., et al. (2020). Ocean mixing and heat transport processes observed under the Ross Ice Shelf control its basal melting. Proc. Natl. Acad. Sci. 117, 16799–16804. doi:10.1073/pnas.1910760117

PubMed Abstract | CrossRef Full Text | Google Scholar

Stevens, C., McPhee, M. G., Forrest, A. L., Leonard, G. H., Stanton, T., and Haskell, T. (2014). The influence of an Antarctic glacier tongue on near-field ocean circulation and mixing. J. Geophys. Res. Oceans 119, 2344–2362. doi:10.1002/2013JC009070

CrossRef Full Text | Google Scholar

Stevens, C., Sang Lee, W., Fusco, G., Yun, S., Grant, B., Robinson, N., et al. (2017). The influence of the Drygalski Ice Tongue on the local ocean. Ann. Glaciol. 58, 51–59. doi:10.1017/aog.2017.4

CrossRef Full Text | Google Scholar

Stevens, C., Sirguey, P., Leonard, G. H., and Haskell, T. (2013). Brief communication: ”The 2013 Erebus glacier tongue calving event. Cryosphere 7, 1333–1337. doi:10.5194/tc-7-1333-2013

CrossRef Full Text | Google Scholar

Stewart, C., Christoffersen, P., Nicholls, K. W., Williams, M. J., and Dowdeswell, J. A. (2019). Basal melting of Ross Ice Shelf from solar heat absorption in an ice-front polynya. Nat. Geosci. 1, 435–440. doi:10.1038/s41561-019-0356-0

CrossRef Full Text | Google Scholar

Tinto, K. J., Padman, L., Siddoway, C. S., Springer, S. R., Fricker, H. A., Das, I., et al. (2019). Ross Ice Shelf response to climate driven by the tectonic imprint on seafloor bathymetry. Nat. Geosci. 12, 441–449. doi:10.1038/s41561-019-0370-2

CrossRef Full Text | Google Scholar

Truffer, M., and Motyka, R. J. (2016). Where glaciers meet water: Subaqueous melt and its relevance to glaciers in various settings. Rev. Geophys. 54, 220–239. doi:10.1002/2015RG000494

CrossRef Full Text | Google Scholar

van Wessem, J. M., Reijmer, C. H., Morlighem, M., Mouginot, J., Rignot, E., Medley, B., et al. (2014). Improved representation of East Antarctic surface mass balance in a regional atmospheric climate model. J. Glaciol. 60, 761–770. doi:10.3189/2014JoG14J051

CrossRef Full Text | Google Scholar

van Wessem, J. M., van de Berg, W. J., Noël, B. P. Y., van Meijgaard, E., Amory, C., Birnbaum, G., et al. (2018). Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 2: Antarctica (1979–2016). Cryosphere 12, 1479–1498. doi:10.5194/tc-12-1479-2018

CrossRef Full Text | Google Scholar

Watkins, R. H., Bassis, J. N., and Thouless, M. D. (2021). Roughness of ice shelves is correlated with basal melt rates. Geophys. Res. Lett. 48, 1–8. doi:10.1029/2021GL094743

CrossRef Full Text | Google Scholar

Wild, C. T., Marsh, O. J., and Rack, W. (2019). Differential interferometric synthetic aperture radar for tide modelling in Antarctic ice-shelf grounding zones. Cryosphere 13, 3171–3191. doi:10.5194/tc-13-3171-2019

CrossRef Full Text | Google Scholar

Wuite, J., Jezek, K. C., Wu, X., Farness, K., and Carande, R. (2009). The velocity field and flow regime of David Glacier and Drygalski ice tongue, Antarctica. Polar Geogr. 32, 111–127. doi:10.1080/10889370902815499

CrossRef Full Text | Google Scholar

Young, N. W., Legresy, B., Coleman, R., and Massom, R. (2010). Mertz Glacier tongue unhinged by giant iceberg. Canberra, Australia: Australian Antarctic Division.

Google Scholar

Zhou, C., Zhou, Y., Deng, F., Ai, S., Wang, Z., and Dongchen, E. (2014). Seasonal and interannual ice velocity changes of polar record glacier, east Antarctica. Ann. Glaciol. 55, 45–51. doi:10.3189/2014AoG66A185

CrossRef Full Text | Google Scholar