Late quaternary glacial history of the La Ji Shan: Implications for the LGM on the northeastern Tibetan Plateau

Previous studies have suggested that the Bayan Har Shan and Lake Donggi Cona areas on the northeastern Tibetan Plateau were not glaciated during the Last Glacial Maximum (LGM; MIS2). However, the La Ji Shan, which is at a lower elevation than the Bayan Har Shan and Lake Donggi Cona areas but has similar annual precipitation, experienced a glacial event during the LGM. To investigate this discrepancy, factors controlling glacier development in the Bayan Har Shan, Lake Donggi Cona, and La Ji Shan were examined. First, a coupled mass balance and ice flow model was used to reconstruct the LGM climatic conditions in the La Ji Shan, and then the factors controlling glacier development were assessed based on the modeled LGM climatic conditions. With LGM precipitation being 70%–80% of present-day values, the modeled LGM temperature decrease was 3.9°C–4.3°C, which is consistent with other reconstructed LGM climatic conditions on the Tibetan Plateau. A comparison of the topography and climate of the La Ji Shan, Bayan Har Shan and Lake Donggi Cona areas indicates that a lower LGM summit height above the LGM equilibrium line altitude (ELA) and LGM annual precipitation at the LGM ELA are the main reason for the lack of LGM glacial expansion in the Bayan Har Shan and Lake Donggi Cona areas.

1 Introduction

The topography and abundant precipitation due to the Asian monsoon and westerlies have made the Tibetan Plateau the most prominent glaciated region outside of the polar regions (Shi et al., 2006; Wang et al., 2013). The Tibetan Plateau is sensitive to global climatic changes due to its high altitude, steep terrain and vast area (An et al., 2001; Wang et al., 2006; Heyman et al., 2011; Kirchner et al., 2011), and thus is an ideal region to investigate glacial changes due to climate fluctuations. During the Quaternary, glaciers advanced and retreated periodically due to climate changes, and abundant glacial features (e.g., moraines, trimlines and U-shaped valleys) are preserved on the Tibetan Plateau (Dortch et al., 2013; Murari et al., 2014). The extent, type, and age of a paleo-glacier can be determined from these preserved glacial features (e.g., Owen and Dortch, 2014), along with the nature of the paleo-cryosphere. Moreover, both paleo-temperature and precipitation proxy-data can be derived from glacial features (Shi et al., 2006; Refsnider et al., 2008; Xu et al., 2013; Xu, 2014; Xu et al., 2014; Xu and Glasser, 2015; Xu et al., 2016; Xu et al., 2017a; Xu et al., 2017b; Xu and Yi, 2017; Eaves et al., 2019; Xu et al., 2020a; Xu et al., 2020b; Cui et al., 2020; Doughty et al., 2021).

Previous studies have shown that the Bayan Har Shan (Heyman et al., 2011) and Lake Donggi Cona (Rother et al., 2017) areas, which are located in the interior of the northeastern Tibetan Plateau (Figure 1A), were unglaciated during the Last Glacial Maximum (LGM). However, on the northeastern Tibetan Plateau, based on ¹⁰Be exposure ages, glacial advance occurred during the LGM in some regions (e.g., Qilian Shan (Cui, 2017; Owen et al., 2003c) and the Anyemaqen area (Owen et al., 2003a). Rother et al. (2017) suggested that this was because of the drier and lower altitudes of the Bayan Har Shan and Lake Donggi Cona areas, compared with these two regions. However, the La Ji Shan, which is also located in the northeastern Tibetan Plateau, experienced a glacial advance during the LGM (Owen et al., 2003b; Murari et al., 2014). The annual precipitation in the La Ji Shan (200–400 mm; Owen et al., 2003b) is similar to that in the Bayan Har Shan (300–500 mm; Heyman et al., 2011) and Lake Donggi Cona (300–350 mm; Rother et al., 2017) areas, although the highest peak in the La Ji Shan (4898 m asl) is lower than that in the Bayan Har Shan (5267 m asl) and Lake Donggi Cona (5029 m asl) areas (Figure 1B). As such, other factors (e.g., relief and temperature) should be considered to determine the reason for the lack of the LGM glacial advance in the Bayan Har Shan and Lake Donggi Cona areas. Shi et al. (2011) proposed that the development of glaciers is dominated by the slope above the equilibrium line altitude (ELA) (S_ELA), the summer (June, July, and August) average temperature (T_JJA) and annual precipitation (P_a) at the ELA, and the summit height above the ELA (SH_ELA). A higher SH_ELA leads to a larger glacier size (Shi et al., 2011). A lower T_JJA, higher P_a at the ELA, and gentler SH_ELA are favorable for the development of glaciers (Ramage et al., 2005; Shi et al., 2011; Wang et al., 2015; Cui et al., 2018). As such, the SH_ELA, S_ELA, LGM ELA, and T_JJA and P_a at the LGM are essential for modeling glacier development during the LGM. In this study, our main objective was to understand the mechanisms responsible for the different glacial evolution during the last glacial period in the La Ji Shan, Bayan Har Shan, and Lake Donggi Cona areas. To do this, based on a coupled mass balance and ice flow model, the LGM climatic conditions were derived from glacial landforms in the La Ji Shan. The estimated LGM paleoclimatic conditions were then used to assess the factors controlling glacier development.

FIGURE 1

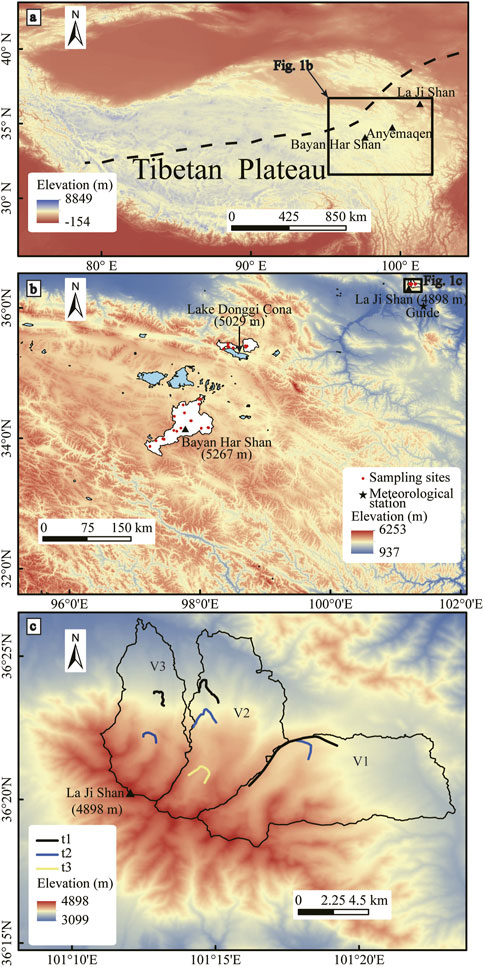
FIGURE 1. (A) Digital elevation model (DEM) of the Tibetan Plateau. The dashed black line represents the limit of the modern Asian summer monsoon (modified after Chen et al., 2008). (B) The spatial distribution of meteorological stations close to the La Ji Shan, Bayan Har Shan, and Lake Donggi Cona areas. White areas are where samples were collected in the La Ji Shan, Bayan Har Shan, and Lake Donggi Cona areas for ¹⁰Be exposure dating. (C) Locations of the three moraine groups in the La Ji Shan (modified after Owen et al., 2003b).

2 Study area

2.1 La Ji Shan

The La Ji Shan is located in the transitional area between the monsoon region and westerlies on the northeastern Tibetan Plateau (Figure 1A). There are no present-day glaciers in the La Ji Shan, but the La Ji Shan was extensively glaciated during the Quaternary and past glacial features are preserved down to 3900 m asl (Owen et al., 2003b). The climate of the La Ji Shan is controlled by the Asian monsoons (Owen et al., 2003b; Zhang et al., 2011). Climate data sets from the Guide climatological station (Figure 1B), which is located in the southeastern La Ji Shan (∼40 km southeast of the highest peak), suggest that the current average annual temperature and precipitation are 7.6°C and 253.1 mm, respectively (http://data.cma.cn). The precipitation from May to September accounts for 88% of the annual precipitation, based on the monthly mean temperature and precipitation data for the period 1981–2010 (Figure 2).

FIGURE 2

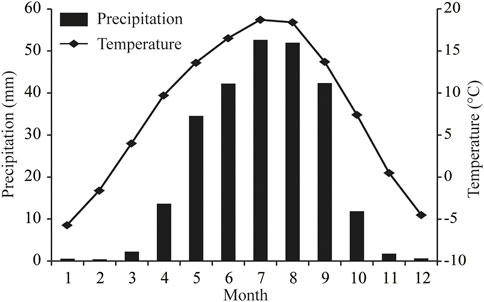
FIGURE 2. Monthly averaged temperature and precipitation data for the period 1981–2010 at the Guide meteorological station (36°1.8ʹN, 101°25.8ʹE, and 2237 m asl).

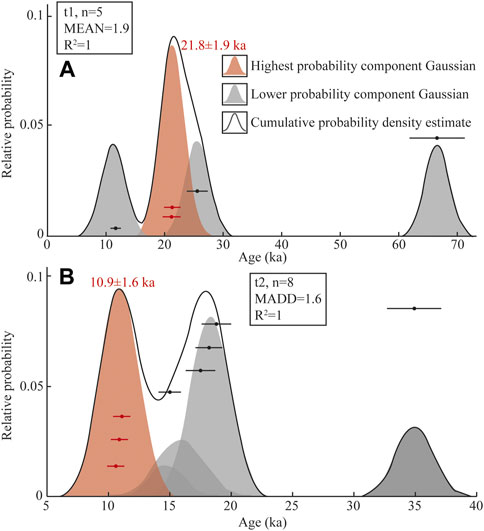
There are three moraine groups (t1, t2, and t3) in the three studied valleys (V1, V2, and V3, from east to west) along the northern margin of the La Ji Shan (Figure 1C). Past glacial features are preserved down to 3900 m asl (Owen et al., 2003b). Although the weathering characteristics of t1, t2, and t3 are similar, the relative ages of t1, t2, and t3 could be identified on the basis of their morphostratigraphy (Owen et al., 2003b). t1 and t3 are the oldest and youngest moraine groups, respectively, and t2 is of intermediate age. The ¹⁰Be exposure ages of 15 samples were obtained for t1, t2, and t3, and there were large ranges of exposure ages for t1 and t2 (the ¹⁰Be exposure ages in the La Ji Shan were recalculated based on the CRONUS-Earth web-based calculator version 3; http://hess.ess.washington.edu/math/; Balco et al., 2008; Table 1) (Owen et al., 2003b). As such, Owen et al. (2003b) could only suggest that three glacial advances in the La Ji Shan occurred during the LGM and/or Late Glacial, or the early Holocene. Based on Student’s t-test, Murari et al. (2014) suggested that the ages of t2 and t1 correspond to the Older Dryas (17.1 ± 4.5 ka) and the Heinrich 2 event (23.1 ± 5.9 ka), respectively, and the two ¹⁰Be exposure ages for t3 are erroneous due to geological factors. However, Dortch et al. (2022) argued that most previous approaches were not optimized for analysis of terrestrial cosmogenic nuclide (TCN) datasets owing to them being mean- or median-based, a failure to adequately propagate measurement or production rate uncertainties, and a lake of geological context. To address these limitations, the Probabilistic Cosmogenic Age Analysis Tool (P-CAAT) was introduced to detect outliers and analyze landform ages for each group of ¹⁰Be ages [sample number (n) ≥ 3] (Dortch et al., 2022). The bandwidth value was determined by the largest Chi-squared value from three patterns (MEAN, MADD and STD/IQR) and appropriate sample sizes for each pattern suggested by the P-CAAT. The highest peak age of the Gaussian curves was the most likely value for ages younger than 21 ka, whereas the oldest peak age that contains ≥3 ¹⁰Be exposure ages was used for group ages older than 21 ka (Dortch et al., 2013). As such, the ages of t1 and t2 were 21.8 ± 1.9 and 10.9 ± 1.6 ka (Figure 3), respectively, corresponding to the LGM and the 10.3 event. Therefore, it was inferred that t1 was deposited during the LGM, and then the glacial extent of t1 was reconstructed to derive the LGM climatic conditions.

TABLE 1

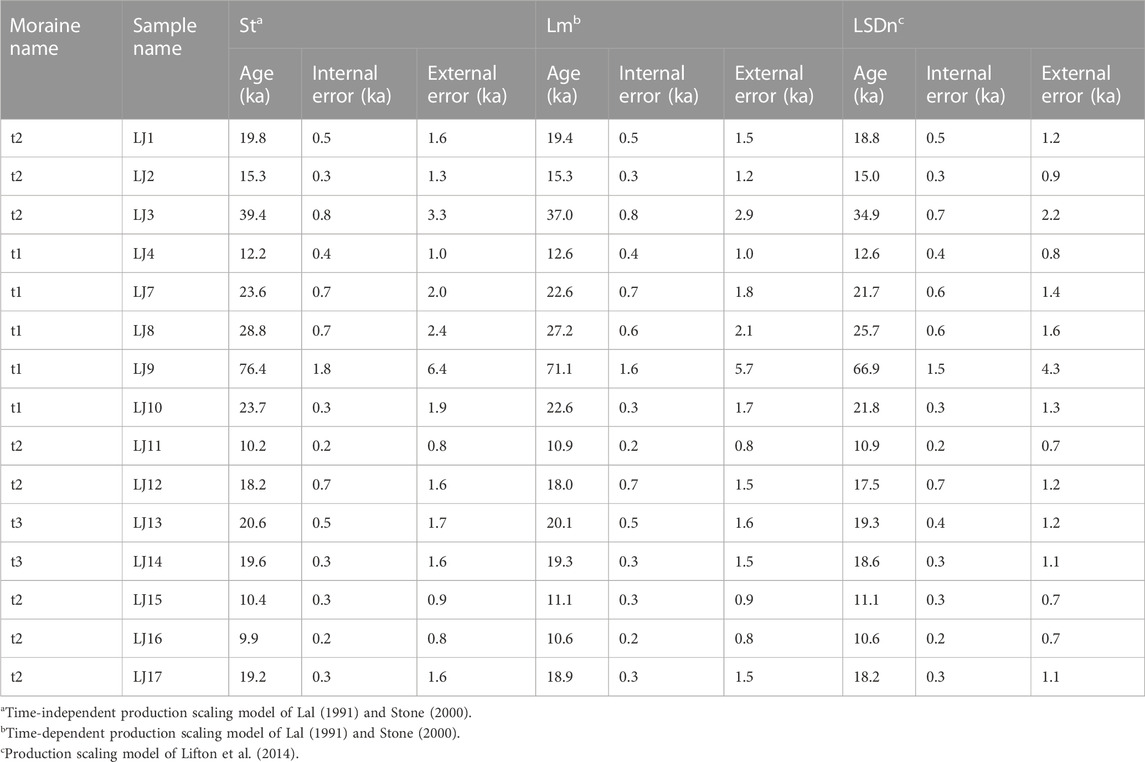
TABLE 1. Recalculated¹⁰Be exposure ages (Owen et al., 2003b) for the La Ji Shan.

FIGURE 3

FIGURE 3. Gaussian separation curves for all ¹⁰Be exposure ages for moraines (A) t1 and (B) t2.

2.2 Bayan Har Shan and Lake Donggi Cona areas

The highest peaks of the Bayan Har Shan and Lake Donggi Conas areas are 5267 and 5029 m asl, respectively (Figure 1B) and there are no glaciers in these areas today. The climate is dominated by the East and South Asian monsoons (Zhang et al., 2011). The annual precipitation at the mountain summits in the Lake Donggi Cona area is 450–500 mm (Rother et al., 2017), and the annual precipitation in the Bayan Har Shan is 300–500 mm (Heyman et al., 2011). Based on the ¹⁰Be exposure ages, Rother et al. (2017) suggested that four glacial advances occurred in the Lake Donggi Cona area during ≥MIS6, late MIS6/MIS5, late MIS5/early MIS4, and late MIS4/early MIS3. The youngest moraine in the Bayan Har Shan was deposited prior to MIS3, and two older glaciations in the Bayan Har Shan have minimum ages of 100–60 and 165–95 ka, based on ¹⁰Be exposure ages (Heyman et al., 2011). The Bayan Har Shan and Lake Donggi Cona areas remained ice free during the LGM.

3 Methods

In this study, we used a coupled mass balance and ice flow model to reconstruct the LGM paleoclimatic conditions in the La Ji Shan. Then on the basis of the modeled LGM climate, the mechanisms responsible for the differences in glacier development in the La Ji Shan, Bayan Har Shan, and Lake Donggi Cona areas were examined.

3.1 Coupled mass balance and ice flow model

The coupled mass balance and ice flow model is designed to simulate glacier dynamics and thermodynamic processes by running on a digital elevation model (DEM) of the bedrock (Plummer and Phillips, 2003; Refsnider et al., 2008). Detailed information regarding the model was described in Xu et al. (2013, 2016, 2020b). In this paper, the model input data sets and parameters are briefly described.

The input data sets are the DEM of the bedrock and monthly averaged temperature and precipitation data for different altitudes in the La Ji Shan. A DEM for the study area with 30 × 30 m spatial resolution was downloaded from the Geospatial Data Cloud (http://www.gscloud.cn) and trimmed to the watersheds of the model domain (Figure 1C). Given that the La Ji Shan is not presently glaciated, the model can be run directly on the present-day DEM. For the mass balance model, altitudinal gradients of monthly averaged temperature and precipitation were obtained from the global climate dataset created by Fick and Hijmans (2017) (Table 2). The mass balance model simulates the glacier mass balance in the model domain with these altitudinal gradients of monthly averaged temperature and precipitation. Clearly, this is the present-day climate pattern in the study area. To reconstruct the paleoclimate conditions that produced the glacial extent of t1, the difference in the mean monthly air temperature from the present-day conditions (ΔT) and fractional value of the present-day precipitation (F_p) were adjusted to match the positions of t1 (i.e., stepwise changes in ΔT of .1°C and F_p of .1).

TABLE 2

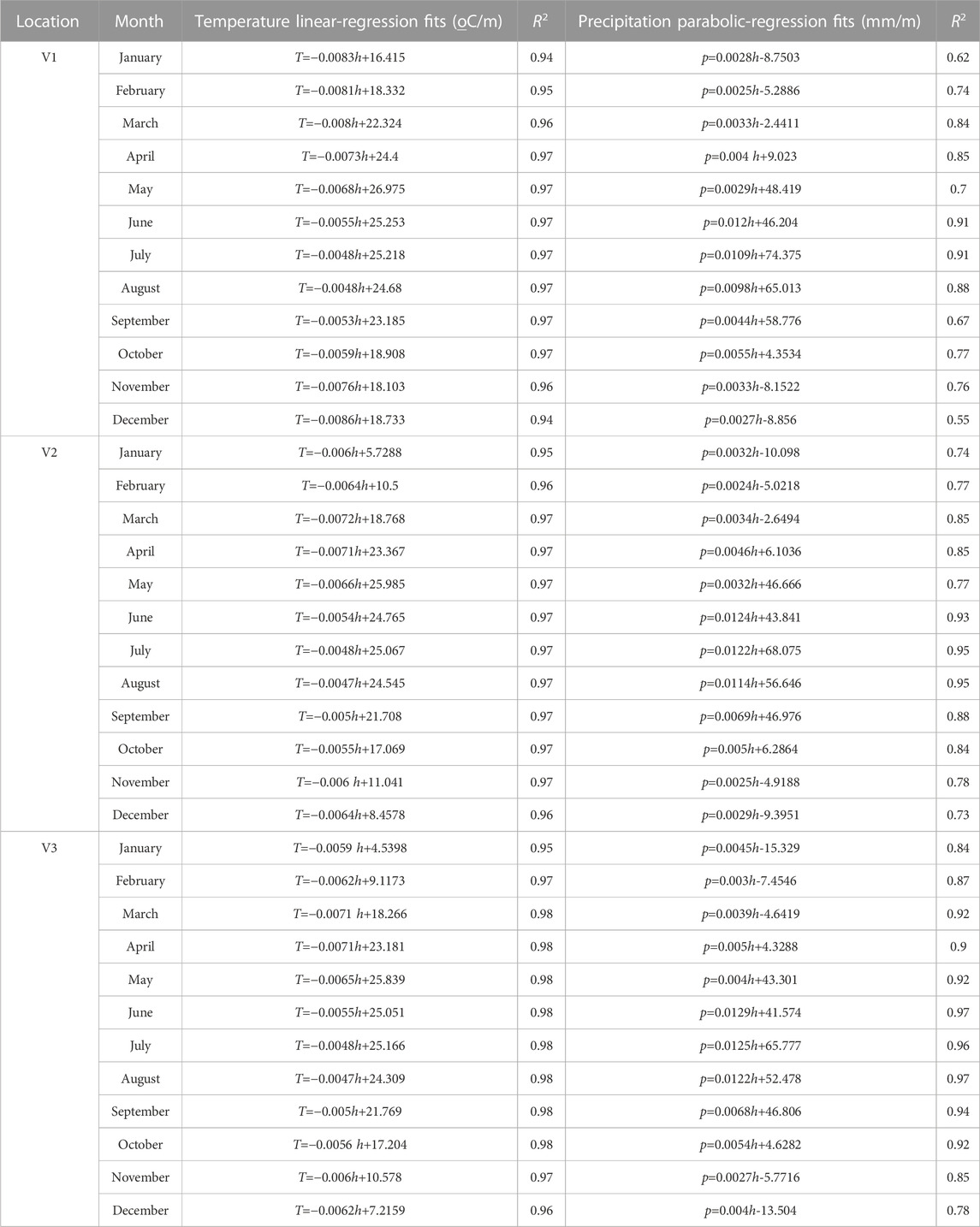
TABLE 2. Regression equations for the monthly mean climate data at the elevation used to simulate the glacier mass balance over the entire model domain.

The main model parameters used in this study are the degree-day factor (DDF), snowfall threshold (T_s), ice deformation (A) and sliding (B) coefficients, and ice deformation versus sliding factor (f). Given that there are no glaciers in the La Ji Shan, we cannot directly obtain a precise value for DDF. Based on an analysis of the spatial distribution of DDF values on the Tibetan Plateau and surrounding areas, Zhang et al. (2006) suggested that the DDF value on the northeastern Tibetan Plateau is 6–9 mm d⁻¹°C⁻¹, with an average of 7.2 mm d⁻¹°C⁻¹. Observations of Qiyi Glacier, which is located in the Qilian Shan on the northeastern Tibetan Plateau (∼440 km northwest of the La Ji Shan), suggest the DDF value of Qiyi Glacier is 7.2 mm d⁻¹°C⁻¹ (Kayastha et al., 2003; Wang et al., 2011). Therefore, a DDF value of 7.2 mm d⁻¹°C⁻¹ was used to simulate the glacier mass balance in the model. A T_s value of 1°C was used to determine the monthly proportion of precipitation that falls as snow (Anderson et al., 2006). When the monthly mean temperature of a DEM cell is below T_s, the monthly mean precipitation of the DEM cell is equal to the monthly accumulation of the glacier in the DEM cell, which allows glacier growth to be estimated. With the steady-state glacier simulation used in this study, changes in glacial extent are controlled by the net mass balance gradient, and changes in ice deformation and sliding only affect the glacier shape (Paterson, 1994; Kessler et al., 2006). As such, we did not attempt to vary the A and B values in this steady-state glacier simulation, because this would only cause minor changes in the model results. Based on previous studies, the A, B, and f values used in this study are 1.0 × 10⁻⁷ a⁻¹ kPa⁻³, 1.5 × 10⁻³ m a⁻¹ kPa⁻², and .5, respectively (Plummer and Phillips, 2003; Refsnider et al., 2008). The DDF value is the main model parameter that controls the uncertainties on the model results owing to its larger variations compared with T_s, on the Tibetan Plateau (Xu et al., 2020b). To test the effects of the DDF values on our model results, different DDF values (6–9 mm d⁻¹°C⁻¹) were used to test the model sensitivity to changes in DDF.

3.2 Glacier development

The peak height and S_ELA values of the La Ji Shan, Bayan Har Shan, and Lake Donggi Cona areas were derived from a 30 × 30 m DEM downloaded from the Geospatial Data Cloud (http://www.gscloud.cn; Figure 1A). The S_ELA values for the La Ji Shan were the sum of those of V1, V2, and V3. The peak heights of V1, V2, V3, the Lake Donggi Cona area, and the Bayan Har Shan are 4868, 4876 , 4898, 5029, and 5276 m asl, respectively (Table 3). Furthermore, the estimation of S_ELA, the T_JJA and P_a at the ELA, and SH_ELA were all based on the ELA. Given that the Bayan Har Shan and Lake Donggi Cona areas were not glaciated during the LGM, it is necessary to estimate the LGM theoretical ELA (ELAt). The LGM ELAt of the Bayan Har Shan and Lake Donggi Cona areas were obtained using the ELAt method developed by Wang et al. (2015). To apply this method, the altitudinal gradients of T_JJA and P_a need to be known. Monthly averaged temperature and precipitation data were derived from the global climate dataset created by Fick and Hijmans (2017). Assuming the changes in T_JJA and P_a during the LGM were the same at each of our study sites, the LGM T_JJA and P_a at the LGM ELAt can be determined from the present-day T_JJA and P_a at the LGM ELAt minus the changes in the LGM T_JJA and P_a. Finally, the LGM ELAt of the Bayan Har Shan and Lake Donggi Cona areas were determined. The changes in the LGM T_JJA and P_a were derived from the results of the coupled mass balance and ice flow model and other paleo climatic data (discussed below). In addition, the LGM ELA in the La Ji Shan was also estimated using this method to compare with the results of the coupled mass balance and ice flow model.

TABLE 3

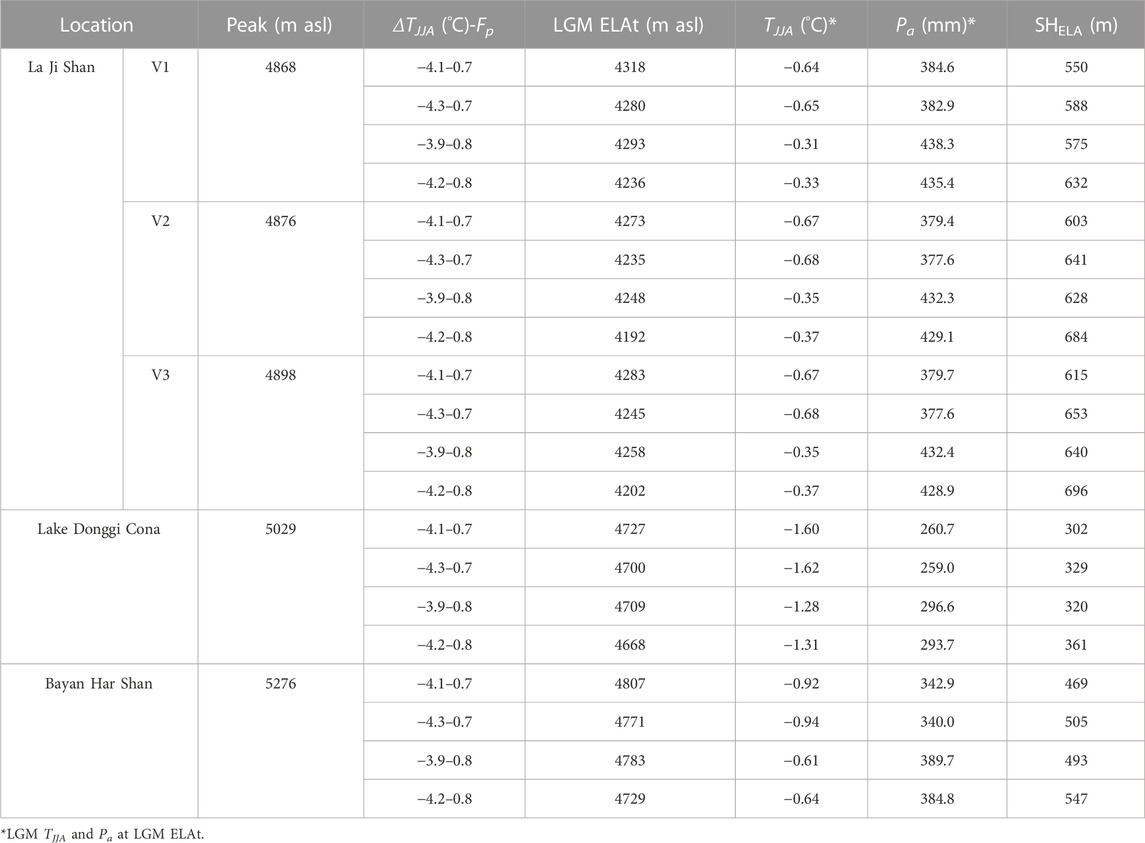
TABLE 3. Factors controlling glacier development in the La Ji Shan, Bayan Har Shan, and Lake Donggi Cona.

4 Results

4.1 Paleoclimate reconstruction corresponding to t1 in the La Ji Shan

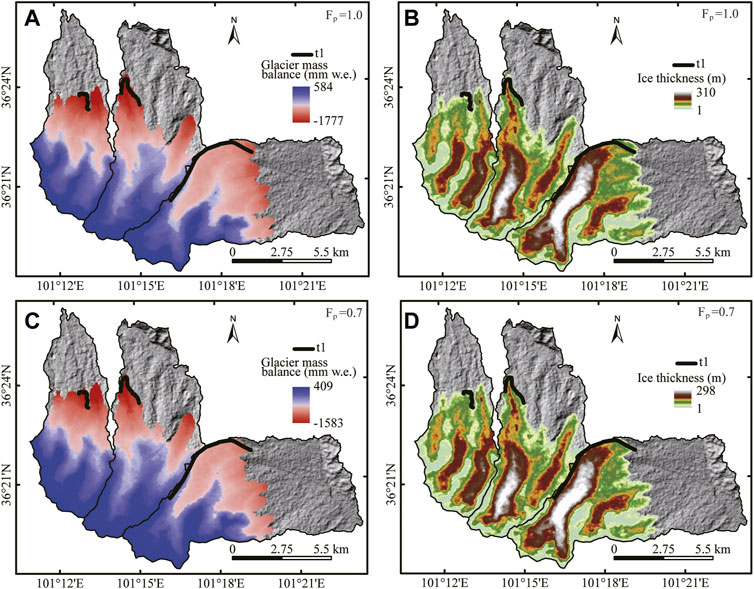
The modeled LGM temperatures were ∼2.9°C–6.0°C, ∼3.0°C–7.0°C, and ∼2.7°C–6.3°C lower than those of the present day in V1, V2, and V3, respectively, with F_p = .1–2 (Figure 4A). The ΔT values of V1, V2, and V3 are consistent with each other. All ΔT–F_p combinations shown in Figure 4A match the position of t1 and reproduce similar glacial extents (∼33 km², ∼29 km², and ∼24 km² in V1, V2, and V3, respectively; Figures 5B, D) in each valley. The net mass balance was largest at the peak and smallest at the lowest elevations in the three valleys (Figures 5A, C). With present-day precipitation (F_p = 1.0), the temperature drops during the LGM were 3.9°C, 4.0°C, and 3.7°C in V1, V2, and V3, respectively (Figure 4A). The modeled ELAs in V1, V2, and V3 under this climate condition were 4215, 4198, and 4247 m asl, respectively. With a more realistic F_p value of .7, the LGM temperature decreases in V1, V2, and V3 were 4.2°C, 4.3°C, and 4.1°C, respectively. The modeled ELAs in V1, V2, and V3 were 4185 m asl, 4196 m asl, and 4197 m asl, respectively.

FIGURE 4

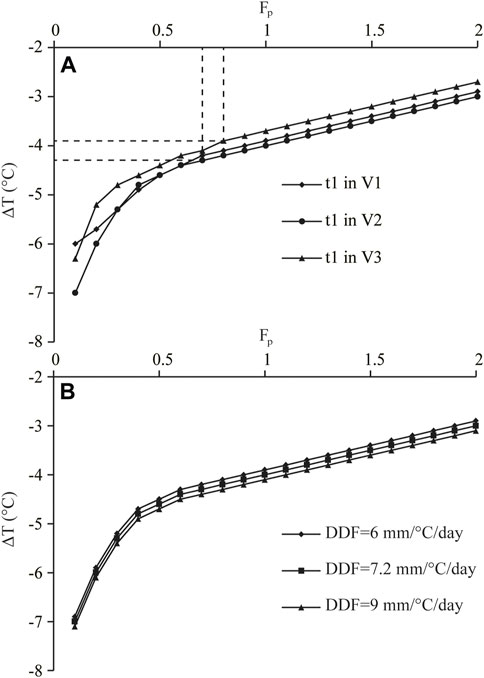
FIGURE 4. Plots of the ΔT–F_p combinations that (A) yield the glacial extent of t1 and (B) show a sensitivity test for t1 in V2.

FIGURE 5

FIGURE 5. Simulated glacier mass balances and extents for the LGM with F_p of (A,B) .9 and (C,D) .7.

4.2 Factors controlling glacier development in the La Ji Shan, Bayan Har Shan, and Lake Donggi Cona areas

Based on the method of Wang et al. (2015) and climate data sets, the LGM ELAt for the La Ji Shan, Bayan Har Shan and Lake Donggi Cona areas were 4192–4318, 4729–4807, and 4668–4727 m asl at F_p = .7–.8, respectively (Table 3). The LGM T_JJA at the LGM ELAt of the La Ji Shan was higher than that of the Bayan Har Shan and Lake Donggi Cona areas, and the LGM T_JJA at the LGM ELAt of the Lake Donggi Cona area was the lowest (Table 3). The LGM P_a at the LGM ELAt of the Bayan Har Shan and Lake Donggi Cona areas were lower than that of the La Ji Shan (Table 3). The LGM SH_ELA values of La Ji Shan was higher than that of Lake Donggi Cona area and Bayan Har Shan (Table 3). The LGM S_ELA values of the Bayan Har Shan are the gentlest, followed by those of the Lake Donggi Cona and La Ji Shan areas (Figure 6).

FIGURE 6

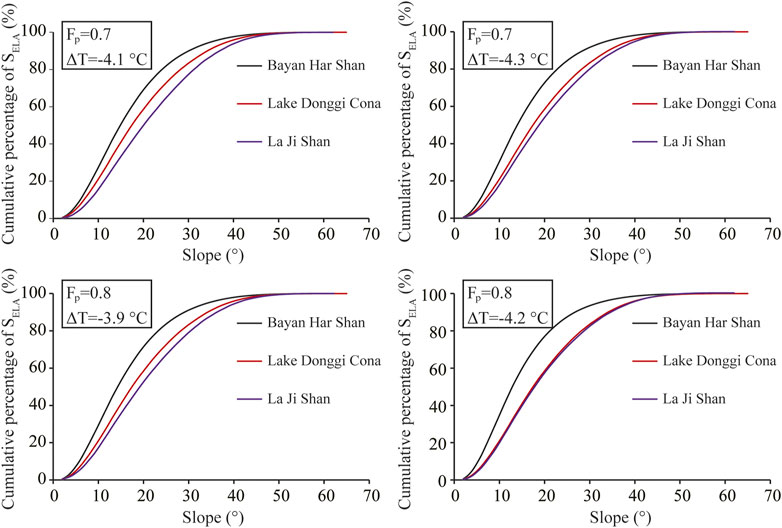
FIGURE 6. Cumulative percentages of the LGM S_ELA in the study area for different LGM climatic conditions.

5 Discussion

5.1 Model sensitivity and uncertainties

Previous studies have indicated that DDF and T_s values have the greatest effect on the paleoclimate reconstructions from the coupled mass balance and ice flow model (Xu et al., 2014; 2017a; b, 2020b). An experiment was conducted to test the model sensitivity to changes in DDF based on simulations of t1 in V2. With DDF values of 6 and 9 mm d⁻¹°C⁻¹, the difference in the modeled ΔT values was <.3°C (Figure 4B). Xu et al. (2014, 2017a, b, 2020b) suggested that changes in DDF of ± .5 mm d⁻¹°C⁻¹ and ± 1°C in T_s had approximately the same influence on paleoclimate estimates from the coupled mass balance and ice flow model. As such, we adopted this approach, in that variations of ± 1°C in T_s should yield changes of <.1 °C on the model results. In addition to the model parameters, inaccuracies in the details of the ice motion physics and model input data sets are potential sources of uncertainties. Errors in the details of the ice motion physics have only a minor effect on our modeled paleoclimate estimates due to the assumption of a steady-state paleoglacier (Paterson, 1994; Kessler et al., 2006). The model input data sets (i.e., altitudinal gradients of temperature and precipitation) were derived from a small number of meteorological stations. In addition, the effects of second-order climate factors (e.g., cloudiness, relative humidity, and wind speed) were not taken into account in our model. Although we did not evaluate the inaccuracies caused by the model input data sets, Plummer (2002) suggested that uncertainties in the model input data sets produce errors for ΔT and F_p of ± .5°C and ± .3, respectively. Therefore, we are confident that the errors on our model results do not exceed these values, because Plummer (2002) used a similar model to reconstruct paleoclimate conditions to that used in this study. In addition, with F_p = .7–.8, the LGM ELAs (4185–4239 m asl) derived from the coupled mass balance and ice flow model agree well with the LGM ELAt (4192–4318 m asl, Table 3) in the La Ji Shan. Moreover, using an accumulation area ratio (AAR) of .5–.8, Owen et al. (2003b) suggested that the LGM and Late Glacial ELA were at 4300–4400 m asl, which is consistent with our results. As such, we consider that our estimated results are reliable.

5.2 LGM paleoclimate in the La Ji Shan

δD values of the Antarctic Dome C ice core (EPICA Community Members, 2004) (Figure 7A) and δ¹⁸O values of the Guliya ice core (Thompson et al., 1997) (Figure 7B) and the LR04 (Lisiecki and Raymo, 2005) (Figure 7C) show that the LGM temperature was lower than the present-day (Figures 7A, B). δ¹⁸O values for the Asian monsoon region suggest that the LGM precipitation was lower than the present-day (Cheng et al., 2016) (Figure 7D). On the Tibetan Plateau, the LGM was colder and drier than the present-day, based on periglacial features, ice core data, and pollen assemblages (Shi et al., 1997; Shi et al., 2001). On the northeastern Tibetan Plateau, Jiang et al. (2011) suggested that the LGM precipitation was 70%–80% of present day values based on PMIP simulations. Considering the LGM precipitation being 70%–80% of present day (F_p = .7–.8), our model results suggest that the LGM temperature was 3.9°C–4.3°C lower than the present-day (Figure 4A). On the Tibetan Plateau, the LGM temperature decreases were 3.3°C–4.4°C in the Payuwang Valley on the northern slopes of the western Nyaiqentanggulha Shan (Xu and Glasser, 2015), 2.9°C–4.6°C in four valleys on the southern slopes of the western Nyaiqentanggulha Shan (Xu et al., 2017b), and 3.1°C–4.3°C in Quemuqu Valley on the southern slopes of the western Nyaiqentanggulha Shan (Xu et al., 2020b), based on a similar glacier–climate model. On the basis of altitudinal vegetation belt shifts, Herzschuh et al. (2006) suggested that the LGM temperature was about 4°C–7°C lower than present day on the northeastern Tibetan Plateau. These estimates of LGM temperature decreases are consistent with our modeled LGM paleoclimate, and thus our model results represent the LGM climatic conditions in the study area.

FIGURE 7

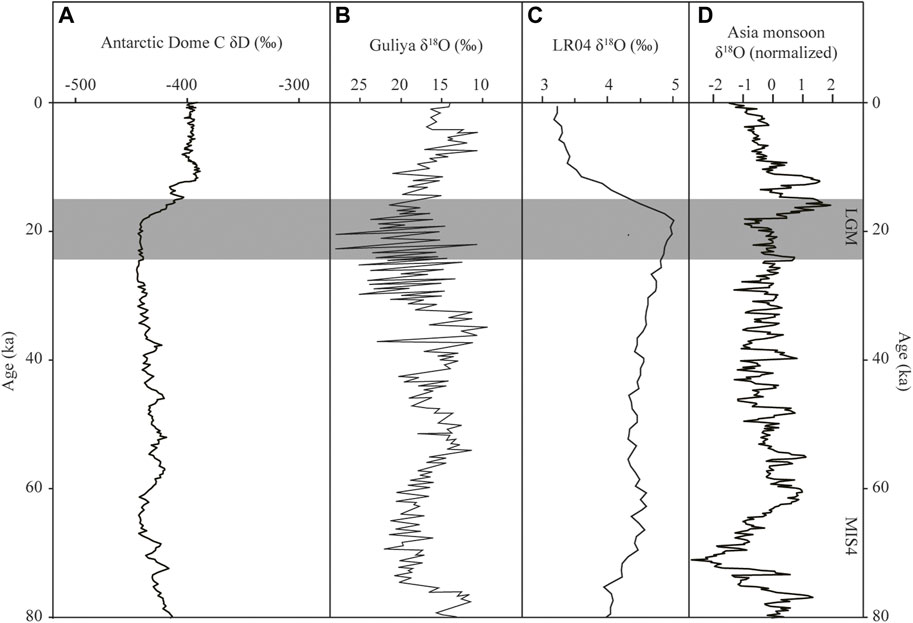
FIGURE 7. (A) δD record of the Antarctic Dome C ice core (EPICA Community Members, 2004). (B) δ¹⁸O record of the Guliya ice core (modified after Thompson et al., 1997). (C) The LR04 benthic δ¹⁸O record (Lisiecki and Raymo, 2005). (D) Speleothem δ¹⁸O record from Hulu Cave (Cheng et al., 2016).

5.3 Why was there no expansion in the interior of the northeastern Tibetan Plateau during the LGM?

Figure 6 shows that the LGM S_ELA of the Bayan Har Shan and Lake Donggi Cona areas are gentler than those of the La Ji Shan, which suggests that the former are more favorable for glacier development. If other factors (e.g., temperature, precipitation, and relief) in these regions are the same, then a glacial advance during the LGM, which have been identified in the La Ji Shan, should also have occurred in the Bayan Har Shan and Lake Donggi Cona areas. However, this is not the case. The differences in the LGM S_ELA values of these regions are not the reason that there was no glacial advance during the LGM in the Bayan Har Shan and Lake Donggi Cona areas. Moreover, the LGM T_JJA and P_a values at the LGM ELAt in the Bayan Har Shan and Lake Donggi Cona areas are lower than those of the La Ji Shan (Table 3). Although lower LGM T_JJA values at the LGM ELAt in the Bayan Har Shan and Lake Donggi Cona areas were more favorable for glacier development than those of the La Ji Shan and the La Ji Shan experienced a LGM glacial advance, the Bayan Har Shan and Lake Donggi Cona areas were unglaciated during the LGM. The lower LGM P_a values at the LGM ELAt in the Bayan Har Shan and Lake Donggi Cona areas than those of La Ji Shan were not favorable for glacier development. As such, drier climatic conditions at the LGM ELAt were responsible for no LGM glacial advance in the Bayan Har Shan and Lake Donggi Cona areas. In addition, the LGM SH_ELA values in the Bayan Har Shan and Lake Donggi Cona areas are smaller than those of the La Ji Shan (Table 3), which suggests that the extents of the LGM glacial advances in the Bayan Har Shan and Lake Donggi Cona areas were smaller than that in the La Ji Shan. A larger LGM SH_ELA value reflects a larger accumulation area for glacier formation. In fact, only the La Ji Shan was glaciated during the LGM. The LGM glacier size in the La Ji Shan was larger than those in the Bayan Har Shan and Lake Donggi Cona areas (i.e., where there was no glaciation during the LGM) because of its larger LGM SH_ELA value. On the Tibetan Plateau, although the LGM temperature was colder than the present–day, the F_p of the LGM was only .7–.8 (discussed above), which was not favorable for glacier development in regions with low SH_ELA values. Therefore, the low LGM SH_ELA and LGM P_a values at the LGM ELAt are the main reasons why there was no LGM glacial advance in the Bayan Har Shan and Lake Donggi Cona areas.

6 Conclusion

On the basis of published chronological data from the La Ji Shan and P-CAAT, two glacial events occurred at 21.8 ± 1.9 ka and 10.9 ± 1.6 ka (Figure 3), corresponding to the LGM and the 10.3 ka event, respectively. Using a coupled mass balance and ice flow model, the glacial extent constrained by t1 was simulated along with the different ΔT–F_p combinations that can sustain such a glacial advance during the LGM. Based on PMIP simulations, the LGM precipitation was tentatively constrained to be 70%–80% of present-day values. Under these precipitation amounts, the modeled LGM temperature changes were –−4.3°C to −3.9°C. The modeled results are consistent with generally accepted LGM climatic conditions on the Tibetan Plateau. Using our modeled LGM climatic conditions, factors controlling glacier development in the study area were assessed. The LGM S_ELA values of the La Ji Shan are the steepest and its LGM T_JJA values at the LGM ELAt were the highest, which is not favorable for glacier development, but its high LGM SH_ELA and LGM P_a values at the LGM ELAt caused a glacial advance during the LGM. Based on this, we infer that the lower LGM SH_ELA and LGM P_a values at the LGM ELAt in the Bayan Har Shan and Lake Donggi Cona areas limited the development of glaciers during the LGM.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

HC conducted most of the research and wrote the manuscript. HM and TJ processed data and edited the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (42161003, 41801032).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, Z., Kutzbach, J. E., Prell, W. L., and Porter, S. C. (2001). Evolution of Asian monsoons and phased uplift of the Himalaya-Tibetan Plateau since late Miocene times. Nature 411, 62–66. doi:10.1038/35075035

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, B., Lawson, W. J., Owens, I. F., and Goodsell, B. (2006). Past and future mass balance of ‘ka Roimata o hine Hukatere’ franz Josef Glacier, New Zealand. J. Glaciol. 52, 597–607. doi:10.3189/172756506781828449

CrossRef Full Text | Google Scholar

Balco, G., Stone, J. O., Lifton, N. A., and Dunai, T. J. (2008). A complete and easily accessible means of calculating surface exposure ages or erosion rates from ¹⁰Be and ²⁶Al measurements. Quat. Geochronol. 3, 174–195. doi:10.1016/j.quageo.2007.12.001

CrossRef Full Text | Google Scholar

Chen, F., Yu, Z., Yang, M., Ito, E., Wang, S., Madsen, D. B., et al. (2008). Holocene moisture evolution in arid central Asia and its out-of-phase relationship with Asian monsoon history. Quat. Sci. Rev. 27, 351–364. doi:10.1016/j.quascirev.2007.10.017

CrossRef Full Text | Google Scholar

Cheng, H., Edwards, R. L., Sinha, A., Spötl, C., Yi, L., Chen, S., et al. (2016). The Asian monsoon over the past 640,000 years and ice age terminations. Nature 534, 640–646. doi:10.1038/nature18591

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, H. (2017). Paleo-glaciations and paleoclimate reconstruction of the Qilan Shan. Ph.D Thesis. (in Chinese with English abstract).

Google Scholar

Cui, H., Wang, J., Yu, B., Hu, Z., Yao, P., and Harbor, J. M. (2018). Marine Isotope Stage 3 paleotemperature inferred from reconstructing the Die Shan ice cap, northeastern Tibetan Plateau. Quat. Res. 89 (2), 494–504. doi:10.1017/qua.2017.115

CrossRef Full Text | Google Scholar

Cui, H., Cao, G., BadingquiyingChen, K., Guo, H., and Jiang, G. (2020). Climates since late quaternary glacier advances: Glacier-climate modeling in the Kunlun Pass area, Burhan Budai Shan, northeastern Tibetan Plateau. Quat. Int. 553, 53–59. doi:10.1016/j.quaint.2020.05.050

CrossRef Full Text | Google Scholar

Dortch, J. M., Owen, L. A., and Caffee, M. W. (2013). Timing and climatic drivers for glaciation across semi-arid Western Himalayan–Tibetan orogen. Quat. Sci. Rev. 78, 188–208. doi:10.1016/j.quascirev.2013.07.025

CrossRef Full Text | Google Scholar

Dortch, J. M., Tomkins, M. D., Saha, S., Murari, M. K., Schoenbohm, L. M., and Crul, D. (2022). A tool for the ages: The probabilistic cosmogenic age analysis tool (P-caat). Quat. Geochronol. 71, 101323. doi:10.1016/j.quageo.2022.101323

CrossRef Full Text | Google Scholar

Doughty, A. M., Kelly, M. A., Russell, J. M., Jackson, M. S., Anderson, B. M., Chipman, J., et al. (2021). Modeling glacier extents and equilibrium line altitudes in the Rwenzori Mountains, Uganda, over the last 31,000 yr. Untangling Quat. Period A Leg. Stephen C. Porter 548, 175.

Google Scholar

Eaves, S. R., Mackintosh, A. N., and Anderson, B. M. (2019). Climate amelioration during the Last Glacial Maximum recorded by a sensitive mountain glacier in New Zealand. Geology 47 (4), 299–302. doi:10.1130/G45543.1

CrossRef Full Text | Google Scholar

EPICA Community Members (2004). Eight glacial cycles from an Antarcticice core. Nature 429, 623–628. doi:10.1038/nature02599

PubMed Abstract | CrossRef Full Text | Google Scholar

Fick, S. E., and Hijmans, R. J. (2017). WorldClim 2: New 1km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 37 (12), 4302–4315. doi:10.1002/joc.5086

CrossRef Full Text | Google Scholar

Herzschuh, U., Kurschner, H., and Mischke, S. (2006). Temperature variability and vertical vegetation belt shifts during the last ∼50,000 yr in the Qilian Mountains (NE margin of the Tibetan Plateau, China). Quat. Res. 66, 133–146. doi:10.1016/j.yqres.2006.03.001

CrossRef Full Text | Google Scholar

Heyman, J., Stroeven, A. P., Caffee, W. M., Hättestrand, C., Harbor, J. M., Li, Y., et al. (2011). Palaeoglaciology of bayan har Shan, NE Tibetan plateau: Exposure ages reveal a missing LGM expansion. Quat. Sci. Rev. 30, 1988–2001. doi:10.1016/j.quascirev.2011.05.002

CrossRef Full Text | Google Scholar

Jiang, D., Lang, X., Tian, Z., and Guo, D. (2011). Last glacial maximum climate over China from PMIP simulations. Palaeogeogr. Palaeoclimatol. Palaeoecol. 309, 347–357. doi:10.1016/j.palaeo.2011.07.003

CrossRef Full Text | Google Scholar

Kayastha, R. B., Ageta, Y., Nakawo, M., Fujita, K., and Matsuda, Y. (2003). Positive degree-day factors for ice ablation on four glaciers in the Nepalese Himalayas and Qinghai-Tibetan Plateau. Bull. Glaciol. Res. 20, 7–14.

Google Scholar

Kessler, M. A., Anderson, R. S., and Stock, G. M. (2006). Modeling topographic and climatic control of east-west asymmetry in Sierra Nevada glacier length during the last glacial maximum. J. Geophys. Res. 111, F02002. doi:10.1029/2005JF000365

CrossRef Full Text | Google Scholar

Kirchner, N., Greve, R., Stroeven, A. P., and Heyman, J. (2011). Paleoglaciological reconstructions for the Tibetan Plateau during the last glacial cycle: Evaluating numerical ice sheet simulations driven by GCM-ensembles. Quat. Sci. Rev. 30, 248–267. doi:10.1016/j.quascirev.2010.11.006

CrossRef Full Text | Google Scholar

Lal, D. (1991). Cosmic ray labeling of erosion surfaces: In situ nuclide production rates and erosion models. Earth Planet. Sci. Lett. 104, 424–439. doi:10.1016/0012-821X(91)90220-C

CrossRef Full Text | Google Scholar

Lifton, N. A., Sato, T., and Dunai, T. J. (2014). Scaling in situ cosmogenic nuclide production rates using analytical approximations to atmospheric cosmic-ray fluxesfluxes. Earth Planet. Sci. Lett. 386, 149–160. doi:10.1016/j.epsl.2013.10.052

CrossRef Full Text | Google Scholar

Lisiecki, L. E., and Raymo, M. E. (2005). A Pliocene-Pleistocene stack of 57 globally distributed benthic δ¹⁸O records. Paleoceanography 20, A1003. doi:10.1029/2004pa001071

CrossRef Full Text | Google Scholar

Murari, M. K., Owen, L. A., Dortch, J. M., Caffee, M. W., Dietsch, C., Fuchs, M., et al. (2014). Timing and climatic drivers for glaciation across monsoon-influenced regions of the Himalayan-Tibetan orogen. Quat. Sci. Rev. 88, 159–182. doi:10.1016/j.quascirev.2014.01.013

CrossRef Full Text | Google Scholar

Owen, L. A., and Dortch, J. M. (2014). Nature and timing of Quaternary glaciation in the Himalayan–Tibetan orogen. Quat. Sci. Rev. 88, 14–54. doi:10.1016/j.quascirev.2013.11.016

CrossRef Full Text | Google Scholar

Owen, L. A., Finkel, R. C., Ma, H., Spencer, J. Q., Derbyshire, E., Barnard, P. L., et al. (2003a). Timing and style of late Quaternary glaciation in northeastern Tibet. Geol. Soc. Am. Bull. 115, 1356–1364. doi:10.1130/B25314.1

CrossRef Full Text | Google Scholar

Owen, L. A., Ma, H., Derbyshire, E., Spencer, J. Q., and Caffee, M. W. (2003b). The timing and style of late quaternary glaciation in the La Ji mountains, NE Tibet: Evidence for restricted glaciation during the latter part of the last glacial. Z. Geomorphol. 47, 263–276. doi:10.1016/S0277-3791(02)00164-6

CrossRef Full Text | Google Scholar

Owen, L. A., Spencer, J. Q., Ma, H., Barnard, P. L., Derbyshire, E., Finkel, R. C., et al. (2003c). Timing of late quaternary glaciation along the southwestern slopes of the qilian Shan, Tibet. Boreas 32, 281–291. doi:10.1080/03009480310001632

CrossRef Full Text | Google Scholar

Paterson, W. S. B. (1994). The physics of glaciers, thirded. Oxford: Pergamon.

Google Scholar

Plummer, M. A. (2002). Paleoclimate conditions during the last deglaciation inferred from combined analysis of pluvial and glacial records. Ph.D Thesis.

Google Scholar

Plummer, M. A., and Phillips, F. M. (2003). A 2-D numerical model of snow/ice energy balance and ice flow for paleoclimatic interpretation of glacial geomorphic features. Quat. Sci. Rev. 22 (14), 1389–1406. doi:10.1016/S0277-3791(03)00081-7

CrossRef Full Text | Google Scholar

Ramage, J. M., Smith, J. A., Rodbell, D. T., and Seltzer, G. O. (2005). Comparing reconstructed Pleistocene equilibrium-line altitudes in the tropical Andes of central Peru. J. Quat. Sci. 20, 777–788. doi:10.1002/jqs.982

CrossRef Full Text | Google Scholar

Refsnider, K. A., Laabs, B. J. C., Plummer, M. A., Mickelson, D. M., Singer, B. S., and Caffee, M. W. (2008). Last Glacial Maximum climate inferences from cosmogenic dating and glacier modeling of the Western Uinta ice field, Uinta Mountains, Utah. Quat. Res. 69 (1), 130–144. doi:10.1016/j.yqres.2007.10.014

CrossRef Full Text | Google Scholar

Rother, H., Stauch, G., Loibl, D., Lehmkuhl, F., and Freeman, S. P. H. T. (2017). Late Pleistocene glaciations at Lake Donggi Cona, eastern Kunlun Shan (NE Tibet): Early maxima and a diminishing trend of glaciation during the last glacial cycle. Boreas 46, 503–524. doi:10.1111/bor.12227

CrossRef Full Text | Google Scholar

Shi, Y., Zheng, B., and Yao, T. (1997). Glaciers and environments during the last glacial maximum (LGM) on the Tibetan plateau. J. Glaciol. Geocryol. 19, 97–113. (in Chinese, with English Abstract).

Google Scholar

Shi, Y., Yu, G., Liu, X., Li, B., and Yao, T. (2001). Reconstruction of the 30-40 ka BP enhanced Indian monsoon climate based on geological records from the Tibetan Plateau. Palaeogeogr. Palaeoclimatol. Palaeoecol. 169, 69–83. doi:10.1016/s0031-0182(01)00216-4

CrossRef Full Text | Google Scholar

Shi, Y., Cui, Z., and Su, Z. (2006). The quaternary glaciations and environmental variations in China. Shijiazhuang: Hebei Science and Technology Press. (in Chinese).

Google Scholar

Shi, Y., Zhao, J., and Wang, J. (2011). New understanding of quaternary glaciations in China. Shanghai: Shanghai Popular Science Press. (in Chinese with English abstract).

Google Scholar

Stone, J. O. (2000). Air pressure and cosmogenic isotope production. J. Geophys. Res. Solid Earth 105, 23753–23759. doi:10.1029/2000JB900181

CrossRef Full Text | Google Scholar

Thompson, L. G., Yao, T., Davis, M. E., Henderson, K. A., Thompson, E. M., Lin, P. N., et al. (1997). Tropical climate instability: The last glacial cycle from a Qinghai-Tibetan ice core. Science 276, 1821–1825. doi:10.1126/science.276.5320.1821

CrossRef Full Text | Google Scholar

Wang, J., Raisbeck, G., Xu, X., Francios, Y., and Bai, S. (2006). In situ cosmogenic 10Be dating of the quaternary glaciations in the southern Shaluli Mountain on the southeastern Tibetan plateau. Sci. China Ser. D. Earth Sci. 49 (12), 1291–1298. doi:10.1007/s11430-006-2026-5

CrossRef Full Text | Google Scholar

Wang, S., Pu, J., and Wang, N. (2011). Study of mass balance and sensibility to climate change of Qiyi Glaicer in Qilian Mountains. J. Glaciol. Geocryol. 33 (6), 1214–1221. (in Chinese with English abstract).

Google Scholar

Wang, J., Kassab, C., Harbor, J. M., Caffee, M. W., Cui, H., and Zhang, G. (2013). Cosmogenic nuclide constraints on late Quaternary glacial chronology on the Dalijia Shan, northeastern Tibetan Plateau. Quat. Res. 79, 439–451. doi:10.1016/j.yqres.2013.01.004

CrossRef Full Text | Google Scholar

Wang, J., Cui, H., Harbor, J. M., Zheng, L., and Yao, P. (2015). Mid-MIS3 climate inferred from reconstructing the Dalijia Shan ice cap, north-eastern Tibetan Plateau. J. Quat. Sci. 30 (6), 558–568. doi:10.1002/jqs.2802

CrossRef Full Text | Google Scholar

Xu, X. (2014). Climates during late Quaternary glacier advances: Glacier-climate modeling in the Yingpu Valley, eastern Tibetan plateau. Quat. Sci. Rev. 101, 18–27. doi:10.1016/j.quascirev.2014.07.007

CrossRef Full Text | Google Scholar

Xu, X., and Glasser, N. F. (2015). glacier sensitivity to equilibrium line altitude and reconstruction for the last glacial cycle: Glacier modeling in the Payuwang Valley, Western Nyaiqentanggulha Shan, Tibetan plateau. Palaeogeogr. Palaeoclimatol. Palaeoecol. 440, 614–620. doi:10.1016/j.palaeo.2015.09.025

CrossRef Full Text | Google Scholar

Xu, X., and Yi, C. (2017). Timing and configuration of the Gongga II glaciation in the Hailuogou valley, eastern Tibetan plateau: A glacier-climate modeling methodfiguration of the Gongga II glaciation in the Hailuogou valley, eastern Tibetan plateau: A glacier-climate modeling method. Quat. Int. 44, 151–156. doi:10.1016/j.quaint.2017.01.011

CrossRef Full Text | Google Scholar

Xu, X., Hu, G., and Qiao, B. (2013). Last glacial maximum climate based on cosmogenic ¹⁰Be exposure ages and glacier modeling for the head of Tashkurgan Valley, northwest Tibetan Plateau. Quat. Sci. Rev. 80, 91–101. doi:10.1016/j.quascirev.2013.09.004

CrossRef Full Text | Google Scholar

Xu, X., Dong, G., and Pan, B. (2014). Modelling glacier advances and related climate conditions during the last glaciation cycle in the Kuzigun Valley, Tashkurgan catchment, on the north-west Tibetan Plateau. J. Quat. Sci. 29 (3), 279–288. doi:10.1002/jqs.2701

CrossRef Full Text | Google Scholar

Xu, X., Muhammad, A. Q., and Pan, B. (2016). Late-Holocene glacier advances and related climate conditions in the Hailuogou catchment, Gongga Shan, eastern Tibetan Plateau. Holocene 26 (12), 1897–1903. doi:10.1177/0959683616646181

CrossRef Full Text | Google Scholar

Xu, X., Dong, G., Pan, B., Hu, G., Bi, W., Liu, J., et al. (2017a). Late Glacial glacier-climate modeling in two valleys on the eastern slope of Samdainkangsang Peak, Nyaiqentanggulha Mountains. Sci. China Earth Sci. 60 (1), 135–142. doi:10.1007/s11430-016-0110-x

CrossRef Full Text | Google Scholar

Xu, X., Pan, B., Dong, G., Yi, C., and Glasser, N. F. (2017b). Last Glacial climate reconstruction by exploring glacier sensitivity to climate on the southeastern slope of the Western Nyaiqentanglha Shan, Tibetan Plateau. J. Glaciol. 63 (238), 361–371. doi:10.1017/jog.2016.147

CrossRef Full Text | Google Scholar

Xu, X., Yao, T., Xu, B., Yi, C., Pan, B., Zeng, X., et al. (2020a). Glacial events during the last glacial termination in the Pagele valley, Qiongmu Gangri peak, southern Tibetan Plateau, and their links to oceanic and atmospheric circulation. Quat. Res. 95, 129–141. doi:10.1017/qua.2020.7

CrossRef Full Text | Google Scholar

Xu, X., Yao, T., Xu, B., Zhang, L., Sun, Y., and Pan, B. (2020b). Last glacial Maximum glacier modelling in the Quemuqu Valley, southern Tibetan plateau, and its climatic implications. Boreas 49 (2), 286–295. doi:10.1111/bor.12422

CrossRef Full Text | Google Scholar

Zhang, Y., Liu, S., and Ding, Y. (2006). Observed degree-day factors and their spatial variation on glaciers in Western China. Ann. Glaciol. 43, 301–306. doi:10.3189/172756406781811952

CrossRef Full Text | Google Scholar

Zhang, J., Chen, F., Holmes, J., Li, H., Guo, X., Wang, J., et al. (2011). Holocene monsoon climate documented by oxygen and carbon isotopes from lake sediments and peat bogs in China: A review and synthesis. Quat. Sci. Rev. 30, 1973–1987. doi:10.1016/j.quascirev.2011.04.023

CrossRef Full Text | Google Scholar