Atomic structure and physical properties of peridotite glasses at 1 bar

Earth’s mantle, whose bulk composition is broadly peridotitic, likely experienced periods of extensive melting in its early history that formed magma oceans and led to its differentiation and formation of an atmosphere. However, the physical behaviour of magma oceans is poorly understood, as the high liquidus temperatures and rapid quench rates required to preserve peridotite liquids as glasses have so far limited their investigation. In order to better characterize the atomic structure and estimate the physical properties of such glasses, we examined the Raman spectra of quenched peridotite melts, equilibrated at 1900 °C ± 50 °C at ambient pressure under different oxygen fugacities (fO₂), from 1.9 log units below to 6.0 log units above the Iron-Wüstite buffer. Fitting the spectra with Gaussian components assigned to different molecular entities (Q-species) permits extraction of the mean state of polymerisation of the glass. We find that the proportions of Q¹ (0.36–0.32), Q² (0.50–0.43), and Q³ (0.16–0.23) vary with Fe³⁺/Fe^TOT (Fe^TOT = Fe²⁺ + Fe³⁺), where increasing Fe³⁺/Fe^TOT produces an increase in Q³ at the expense of Q² at near-constant Q¹. To account for the offset between Raman-derived NBO/T (2.06–2.27) with those determined by assuming Fe²⁺ exists entirely as a network modifier and Fe³⁺ a network former (2.10–2.44), ∼2/3 of the ferric iron and ∼90% of the ferrous iron in peridotite glasses must behave as network modifiers. We employ a deep neural network model, trained to predict alkali and alkaline-earth aluminosilicate melts properties, to observe how small variations in the atomic structure of peridotite-like melts affect their viscosity. For Fe-free peridotite-like melts, the model yields a viscosity of ∼ −1.75 log Pa s at 2000 °C, similar to experimental determinations for iron-bearing peridotite melts. The model predicts that changes in the peridotite melt atomic structure with Fe³⁺/Fe^TOT yield variations in melt viscosity lower than 0.1 log Pa s, barely affecting the Rayleigh number. Therefore, at the high temperatures typical of magma oceans, at least at 1 bar, small changes in melt structure from variations in oxidation state are unlikely to affect magma ocean fluid dynamics.

1 Introduction

Soon after their accretion or following giant impacts, several clues suggest the existence of extended magma oceans at the surface of terrestrial planets (Elkins-Tanton, 2012 and references therein). On Earth, the Earth-Theia Moon-forming collision would deposit sufficient energy to cause widespread melting (e.g., Tonks and Melosh, 1993; Abe, 1997; Canup, 2004; Canup, 2012). The convective dynamics of such a magma ocean would have been critical for the formation and evolution of the Earth’s early atmosphere, the segregation of its core and the crystallisation of its mantle (Schaefer and Fegley Jr, 2004; Labrosse et al., 2007; Rubie et al., 2007; Elkins-Tanton, 2012; Deguen et al., 2014; Canup et al., 2015; Landeau et al., 2016; Sossi et al., 2020). A key physical parameter of silicate liquids relevant to the dynamics of magma oceans is their viscosity, owing to its influence on the timescales over which convection, settling of crystals and metal-silicate emulsion occur (e.g., see reviews by Rubie et al., 2007; Elkins-Tanton, 2012). For instance, for a canonical Moon-forming impact, the impactor’s core is expected to emulsify in the Earth’s magma ocean post-collision (Karato and Murthy, 1997; Rubie et al., 2007). The viscosity of the magma ocean is thought to have been low enough (∼0.1 Pa·s Liebske et al., 2005) to give rise to turbulent (hard) convection, characterized by a very high Rayleigh number, the non-dimensional ratio of thermal buoyancy forces to viscous and diffusive dissipative effects, in the 10²⁸–10³⁰ range (Solomatov, 2007; Elkins-Tanton, 2012):

$R_a=\frac{\rho g\alpha \mathit{\Delta }T{L}^3}{\eta \kappa }.(1)$

where ρ is the fluid density in kg m⁻³, g is the gravitational acceleration in m s⁻², α is the thermal expansivity in K⁻¹, ΔT is the temperature range across the fluid that drives the convection in K, L is a characteristic length scale for the fluid body in m, η is dynamic viscosity in Pa·s, and κ is the thermal diffusivity in m² s⁻¹. This should favour the emulsion of the impactor metal core, controlled by the ratio of the silicate melt viscosity ${\eta }_{silicate}$ and the metal viscosity ${\eta }_{metal}$ (Wacheul et al., 2014):

$r_{\mu }=\frac{{\eta }_{silicate}}{{\eta }_{metal}}.(2)$

The size of the metal droplets will depend on the equilibrium between inertial and surface tension forces; it is estimated to be in the centimeter range (Karato and Murthy, 1997; Wacheul et al., 2014).

Equations 1, 2 illustrate the importance of liquid viscosity in the various processes that shaped the evolution of a magma ocean(s) on the early Earth. To date, however, our understanding of melt viscosity for magma ocean-relevant melts is incomplete. For the Earth, assuming it was fully molten following a giant impact, likely had a magma ocean of peridotitic composition. However, there are few measurements of the viscosity of peridotite melt. Dingwell et al. (2004) determined the viscosity of komatiitic- to peridotitic melt (∼32 wt% MgO) at 1 bar in air by concentric cylinder viscometry, finding log η ∼ −0.95 Pa·s at 1860 K. They fit their data as a function of temperature to the Vogel–Fulcher–Tammann (VFT) equation;

$\mathit{log}\eta =A+\frac{B}{T-C},(3)$

where A = −4.31, B = 3703 and C = 761.7, and T the temperature in K. At higher pressures, up to 13 GPa, Liebske et al. (2005) determined the viscosity of peridotitic melts by the falling sphere method. They fit their data to a modified VFT equation to account for the effect of pressure, obtaining η between −1 and −2 log Pa·s up to 2500 K and 14 GPa. The recent measurements of Xie et al. (2021), which benefit from the latest advances in high speed camera (1,000 fps) determination of falling sphere velocities, indicate that the effect of pressure on the viscosity of peridotite melt is limited at temperatures above 2000 K. In particular, along the liquidus, the viscosity decreases from 38 ± 2 mPa·s (log η = −1.42) at 2173 ± 100 K to 17 ± 1 mPa·s (log η = −1.77) at 2773 ± 150 K (Xie et al., 2021). These values are in line with falling sphere velocities determined by Cochain et al. (2017), applying in situ X-ray radiography of melts in the system MSiO₃ (where M = Ca or Mg), which show a modest decrease from ∼200 mPa·s for CaSiO₃ and ∼100 mPa·s for MgSiO₃ with increasing pressure from 1 bar up to ∼7 GPa at temperatures near 2000 K. Viscosities of a variety of silicate melts, including peridotite and Fe₂SiO₄, converge to a common value near 20–30 mPa·s (log η = −1.6 ± 0.1) at 12–14 GPa (Spice et al., 2015; Cochain et al., 2017).

However, these measurements were performed under conditions that may not necessarily reflect those of a superficial magma ocean. For example, the experiments of Dingwell et al. (2004) were conducted without any control of fO₂, meaning the Fe³⁺/Fe²⁺ ratios in their liquids were unconstrained. This is important as the Fe³⁺/Fe²⁺ ratio in turn modifies melt viscosity, because ferric and ferrous iron occupy different structural roles in silicate melts (Dingwell et al., 1988; Dingwell and Virgo, 1988; 1989; Dingwell, 1991; Liebske et al., 2003; Chevrel et al., 2013). Indeed, in silicate melts, it is widely accepted that Fe³⁺ acts as a network former, participating more readily in the construction of the aluminosilicate polyhedral disordered network due to its preference for tetrahedral coordination, whereas Fe²⁺ acts as a network modifier that breaks T-O-T bonds (T = Si, Al), tending to occupy octahedral sites (see Le Losq et al., 2021b for a review). However, the coordination number (CN) of Fe²⁺ and Fe³⁺ varies as a function of composition, temperature, and pressure (e.g., Jackson et al., 2005; Zhang et al., 2017), implying that the relationship between melt structure, and, hence, viscosity with iron oxidation state, may not be straightforward. As a result, these variables need to be understood in order to ensure accurate prediction of silicate melt viscosities.

To evaluate how iron oxidation state could influence the rheology of silicate melts in magma oceans, we determine the atomic structure of peridotite glasses equilibrated at 1 bar and 1900 °C under different oxygen fugacities. The glasses were prepared by laser-heating aerodynamic levitation, under conditions representative of the surface of a terrestrial magma ocean (Sossi et al., 2020). Raman spectroscopy (Mysen et al., 1982; McMillan, 1984; McMillan et al., 1992; Neuville et al., 2014) was used to investigate the atomic structure of the glasses as a function of their Fe³⁺/Fe^TOT. Such data permit better constraints to be placed on the role of iron and the atomic structure of peridotite melts at the surface of magma oceans, and, hence, inform models of the rheology of magma oceans and mineral-melt partition coefficients of elements like Fe and Mg.

2 Materials and methods

2.1 Glass synthesis

The glass samples were presented in the study of Sossi et al. (2020). The starting peridotite composition was synthesised by mixing and grinding a combination of oxide powders (>99.95% pure), MgO, SiO₂, Fe₂O₃, Al₂O₃, and CaCO₃ three times under ethanol in an agate mortar. The mixture was then decarbonated for 24 h in air at ∼1,000 °C, and the resultant powder was pressed into pellets. Roughly 20-mg pieces of the pellet were placed into the conical nozzle of the furnace, from which was fluxed a gas-mixture providing sufficient buoyancy to cause the molten silicate bead to levitate. Heating was achieved by a continuous wave 125-W CO₂ laser focused by gold-coated mirrors to a spot diameter of ∼5 mm. All samples were melted once at 1900 °C ± 50 °C for 30 s in pure O₂ to achieve complete fusion and quenched to glass. Subsequently, the glass beads (diameters 1.45–2.05 mm) were equilibrated under different CO₂/H₂ gas mixtures diluted with 92% Ar, at temperatures of 1900 °C ± 50 °C, continuously recorded by an optical pyrometer. Quenching below the glass transition was achieved by switching off the laser, resulting in cooling rates of ∼800 °C per second.

2.2 Glass characterisation

Glass compositions were measured by electron probe microanalysis (Sossi et al., 2020). On average, the composition, in wt%, is 46.5 ± 0.03 SiO₂, 4.37 ± 0.04 Al₂O₃, 8.4 ± 0.03 FeO, 38.0 ± 0.4 MgO, and 2.06 ± 0.05 CaO, with Na₂O and K₂O being both lower than 0.01. The oxidation state of the glasses was determined using Fe K-edge X-ray Absorption Near Edge Structure (XANES) spectroscopy at beamline 13IDE of the Advanced Photon Source, Argonne National Laboratories (IL, United States). All details are provided in Sossi et al. (2020). Table 1 provides the chemical composition and iron oxidation state of the samples investigated in this study.

TABLE 1

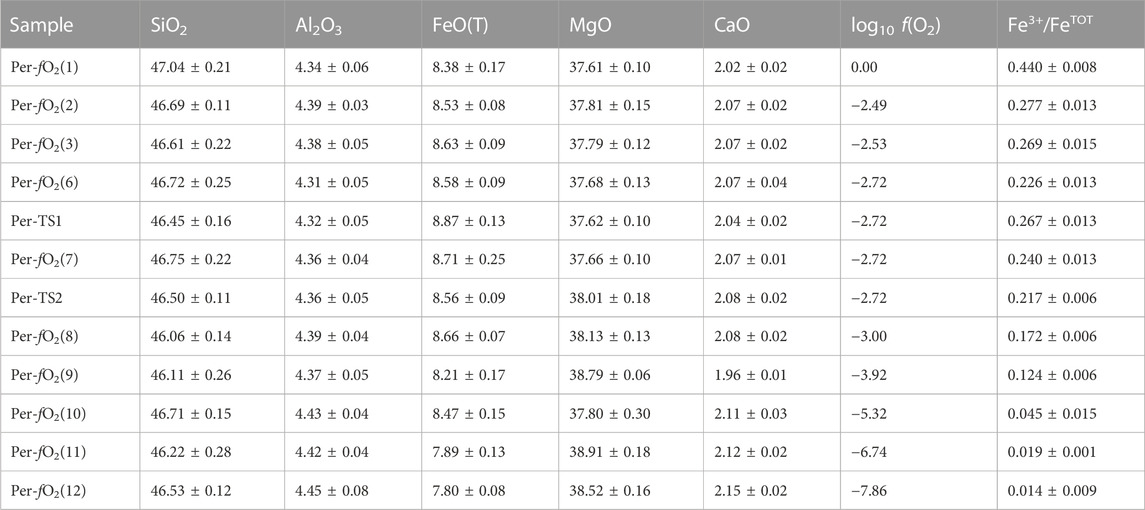
TABLE 1. Chemical composition in wt%, synthesis fO₂ and resulting Fe oxidation state, expressed as Fe³⁺/Fe^TOT with Fe^TOT = [Fe²⁺] + [Fe³⁺], of the samples investigated in this study.

2.3 Raman spectroscopy

In total, there are 12 different peridotite glasses with Fe³⁺/Fe^TOT ranging from 0.01 to 0.44 (Sossi et al., 2020). Their Raman spectra were recorded using a Renishaw inVia spectrometer at the Australian National University. This Raman spectrometer is equipped with a Peltier-cooled detector, a 2400 lines/mm grating and a confocal system. Samples were excited using a 532 nm laser line focused ∼3 µm below the surface using a ×100 Leica objective; laser power on the sample was ∼1.2 mW. The spatial resolution was <1 mm, and the spectral resolution ∼1.2 cm⁻¹. Five spectra were recorded from different points for each sample. They were treated separately during the data reduction process. The combination of a laser power less than 5 mW (Di Genova et al., 2016) with a relatively short counting time of 120 s, and the analysis at five different points, was used to prevent Fe oxidation during spectral acquisition (Le Losq et al., 2019).

Pre-processing of the Raman spectra was done using the Rampy library in the Python programming language (Le Losq et al., 2019). The raw data were corrected from a linear background that was fit to the 1,180–1,300 cm⁻¹ portions of the Raman spectra that are devoid of signal. Corrected spectra were normalized to the area under the curve.

To gather quantitative structural information from the Raman spectra, peak fitting was performed on the 700–1,300 cm⁻¹ portion of the corrected Raman signals using the Bayesian approach described in Le Losq et al. (2022). In the Bayesian framework, the log posterior probability of a model is calculated from the sum of the log likelihood with the log prior. While the former describes how well a particular model fits the data, the latter embeds our initial knowledge about the problem, in the form of a priori probability distributions on model parameters. In this study, we used a single model composed of five peaks to fit all the spectra simultaneously. The choice of the number of peaks was made after observation of the spectra and consideration of results from previous studies on similar materials. The rationale for the number of peaks will be discussed in more detail in the Results section.

Gaussian, pseudo-Voigts and Lorentzian functions were tested to determine the most appropriate peak shapes to fit the data. The fits with the highest likelihoods are obtained using Gaussian peaks, in agreement with previous Raman studies of alkaline-earth alumino-silicate glasses (e.g., Mysen et al., 1982; Mysen et al., 1985a; Neuville, 2006). In the present model, we assume that Fe³⁺/Fe^TOT has no influence on the frequencies and widths of the Gaussian peaks assigned to (Si,Al)-O stretching in Qⁿ units and Fe³⁺-O stretching (see Results for details on attributions). Furthermore, while the intensities of the other peaks were considered as independent adjustable parameters, that of the peak assigned to Fe³⁺-O stretching was calculated by multiplying the Fe³⁺/Fe^TOT ratio by an adjustable parameter, θ^Fe3+-O. This parameter can be considered as the equivalent of the Raman cross section of the signal assigned to Fe³⁺-O. The log likelihood of the model is thus calculated using the 12 observed mean spectra of the 12 samples and those calculated using the model. The prior distributions of model parameters (intensities, positions, and widths) were set up using truncated Gaussian distributions, with means and standard deviations adjusted according to properties based on the decomposition of Raman spectra of depolymerised silicate glass compositions (e.g., from the studies of Mysen et al., 1982; Seifert et al., 1982; Neuville, 2006). Table 2 lists the prior mean and standard deviation values that were used.

TABLE 2

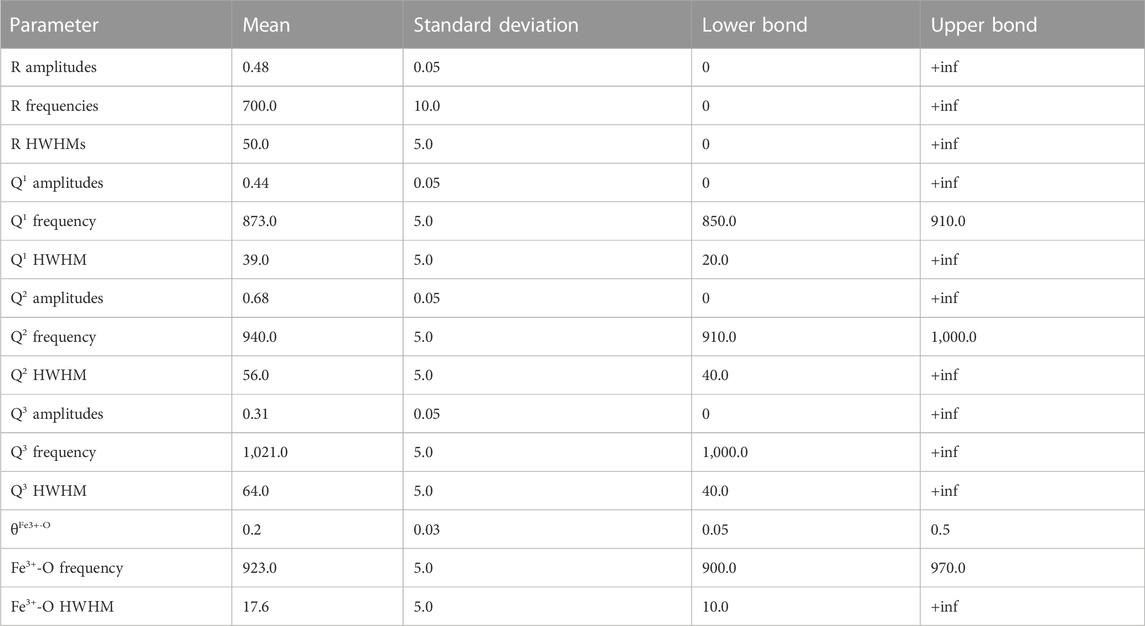
TABLE 2. Prior values of the truncated normal distributions of amplitudes, frequencies and half width at half maximum (HWHM) of the peaks in the model.

The goal of the Bayesian approach adopted here is to obtain a sample of models, in which their statistical occurrence actually reflects their true probability distribution. Various methods allow obtaining this sample of models by sampling from the log posterior probability distribution. Here, we used the No-U-TurnS (NUTS) sampler (Hoffman and Gelman, 2014), implemented in the Python PyMC3 library (Salvatier et al., 2016), that relies on the Hamiltonian Monte Carlo (HMC) algorithm (Neal, 2012). The latter performs a random walk guided by Hamiltonian dynamics. After sampling one thousand models (initialization advi-map, 200,000 init steps, 2000 tuning steps), statistics on the different model parameters were estimated. Convergence was checked via a visual inspection of the chains for each parameter, and via the Gelman-Rubin diagnostic criterion that was around one for each parameter. All subsequent calculations performed with model parameters (e.g., for calculating peak areas, Qⁿ unit fractions, etc.) were done using the full sample of models, such that reported results automatically take into account the propagation of errors. In this article, we report either the mean and σ values for parameters which distribution is approximately a normal one, or their median, and 2.5% and 97.5% quantiles in the other case.

3 Results

3.1 Glass Raman spectra

The Raman spectra of the glasses show two main large asymmetric bands located near 720 and 900–1,000 cm⁻¹ (Figure 1). The first band can be assigned to a combination of inter-tetrahedral and rocking vibrations in the glass network (e.g., McMillan, 1984 and references therein). The second asymmetric band can be assigned to Si-O, Al-O and Fe³⁺-O stretching in the polyhedral units building the glass aluminosilicate network. As the glass Fe³⁺/Fe^TOT ratio increases, we observe an increase in the intensity of the ∼720 cm⁻¹ peak at the expense of the ∼900 cm⁻¹ band (Figure 1). In the 800–1,300 cm⁻¹ portion of the Raman signals, the spectra of the reduced glasses define a clear maximum near 908 cm⁻¹ and a shoulder near 950 cm⁻¹. With the oxidation of Fe, the intensity maximum shifts to ∼930 cm⁻¹ at Fe³⁺/Fe^TOT = 0.44 and the signal intensity in the 1,000–1,150 cm⁻¹ range increases.

FIGURE 1

FIGURE 1. Raman spectra of the peridotite glasses. The color bar indicates the glass Fe³⁺/Fe^TOT.

From the Raman spectra, quantitative information on the effect of the iron oxidation state on the glass structure can be gleaned by examining the 800–1,300 cm⁻¹ portion of the spectra, which contains the signals assigned to (Si,Al)-O stretching in the SiO₄-AlO₄ tetrahedral units that constitute the glasses. In the following, such structures are referred to as the Qⁿ tetrahedral units, with n their number of bridging oxygens (Schramm et al., 1984). Fully polymerized glasses like silica (pure SiO₂) are comprised exclusively of Q⁴ units. In such a glass, Si⁴⁺ is a network former cation, as it participates in building a 3D tetrahedral network interconnected through bridging oxygens (BOs). Other potential network formers include Al³⁺ and Ti⁴⁺. Adding monovalent or divalent metal cations M^{+, 2+}, such as Mg²⁺ or Na⁺, to silica disrupts Si-O-Si bridges, and thus results in the formation of non-bridging oxygens (NBOs). As such, Qⁿ units with n < 4 characterise these depolymerized glasses, in proportions that depend on the bulk composition of the glass (e.g., Maekawa et al., 1991).

To quantify the degree of depolymerization, a useful parameter is the mean number of non-bridging oxygens per tetrahedral units, NBO/T, of the network. It ranges from 0 in fully polymerized glasses composed only of Q⁴ units, to four in fully depolymerized glasses composed only of Q⁰ units. Similarly, the NBO/T of Q¹ units is 3, that of Q² is 2, and that of Q³ is 1. Regarding Fe²⁺ and Fe³⁺, existing data generally indicate that the first acts as a network modifier cation, whereas the second acts as a network former cation (e.g., see the review in Le Losq et al., 2021b). Assuming such roles for Fe²⁺ and Fe³⁺, the present glasses have an estimated NBO/T (calculated from composition as [2O-4T]/T with T the tetrahedral cations Si⁴⁺, Al³⁺ and Fe³⁺) that ranges from ∼2.10 (Fe³⁺/Fe^TOT = 0.44) to ∼2.44 (Fe³⁺/Fe^TOT = 0.01). Such an increase in NBO/T as Fe³⁺/Fe^TOT decreases is in qualitative agreement with the decreasing intensity of the 700 cm^-1 band that reflects a decrease in T-O-T bridging in the glass network.

Given the NBO/Ts of the present peridotite glasses, their atomic structure should mostly be composed of Q² units, with lower fractions of Q¹ and Q³ units (e.g., see Maekawa et al., 1991). Considering that the peridotite glasses are also rich in MgO (38 wt%), a similar Q-species distribution to that of MgSiO₃ glass, with NBO/T = 2.00, might be expected. Enstatite glass comprises ∼20–25% Q¹, ∼39–42% Q², ∼26–33% Q³ and ∼7–8% Q⁴ (Sen et al., 2009; Spiekermann et al., 2013). This distribution is consistent with the shape of the 800–1,200 cm⁻¹ portion of the peridotite glass spectra, where three different features (such as peak maxima, shoulders, and slope breaks) visible near 900, 950 and 1,050 cm⁻¹ can be assigned to signals from T-O stretching in Q¹, Q² and Q³ units, respectively (Brawer and White, 1975; Brawer and White, 1977; Virgo et al., 1980; Furukawa et al., 1981; Mysen et al., 1982; McMillan, 1984; Spiekermann et al., 2013). Furthermore, upon increasing Fe³⁺/Fe^TOT, the intensity maximum near 900 cm⁻¹ shifts to ∼930 cm⁻¹, suggesting the presence of another vibrational mode near 920–930 cm⁻¹ that could be assigned to Fe³⁺-O stretching (Virgo et al., 1982; Magnien et al., 2004; Roskosz et al., 2008; Di Muro et al., 2009; Di Genova et al., 2016; Le Losq et al., 2019), seeing as the bulk composition of the glass remains otherwise unchanged.

3.2 Spectral model

Given the aforementioned considerations, the joint fit of the 700–1,200 cm⁻¹ region of the spectra can be achieved with one peak near 700 cm⁻¹, hereafter named the R peak, to properly account for the background near 800 cm⁻¹, then four additional peaks in the 800–1,200 cm⁻¹ range assigned to T-O (T = Si, Al) stretching in Q¹, Q² and Q³ units as well as Fe³⁺-O stretching in Fe³⁺O₄ tetrahedral units. In order to assess the statistical number of Gaussian peaks required to fit the observed spectra, a principal component analysis (PCA) was undertaken (Figure 2). This exercise demonstrates that three to four components account for most of the variance in the 700–1,200 cm⁻¹ region of the spectra (Figure 2), with additional components assigned to noise. Here, as independent constraints on the Fe³⁺/Fe^TOT of the glasses are afforded via XANES (Sossi et al., 2020) we choose to decompose the spectra using a model with five discrete peaks, including one assigned to Fe³⁺-O stretching that is constrained to covary with the Fe³⁺/Fe^TOT of the glasses. In this manner, the degrees of freedom in the fits do not increase relative to the number (3—4) required by the PCA analysis, and the variation in Fe³⁺-O contribution is instructive to isolate the effect of this variable on the Raman spectra.

FIGURE 2

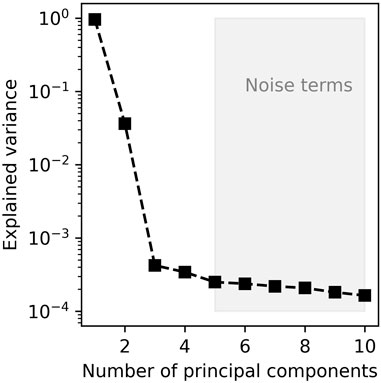
FIGURE 2. Principal component analysis of the 700–1,300 cm⁻¹ portion of the Raman spectra. Before the PCA analysis, preprocessing was done by removing the mean of the data.

The model reproduces the Raman spectra of the samples to an excellent level of agreement (Figure 3). The addition of more peaks, which could be assigned to Q⁰ or Q⁴ units for instance, does not result in significant improvements in the fits (cf. Figure 2). The peak at ∼873.4 cm⁻¹ is assigned to T-O stretching in Q¹ units, that at ∼941.6 cm⁻¹ to T-O stretching in Q² units, and that at ∼1,023.9 cm⁻¹ to Q³ units (Brawer and White, 1975; Brawer and White, 1977; Virgo et al., 1980; Furukawa et al., 1981; Mysen et al., 1982; McMillan, 1984; Mysen et al., 1985a; Spiekermann et al., 2013). The peak at ∼926.0 cm⁻¹ is assigned to Fe³⁺-O stretching in Fe³⁺O₄ tetrahedral units (Mysen et al., 1980; Virgo et al., 1982; Mysen et al., 1985a; 1985b; Cochain et al., 2012). The positions and widths of the peaks are provided in Table 3.

FIGURE 3

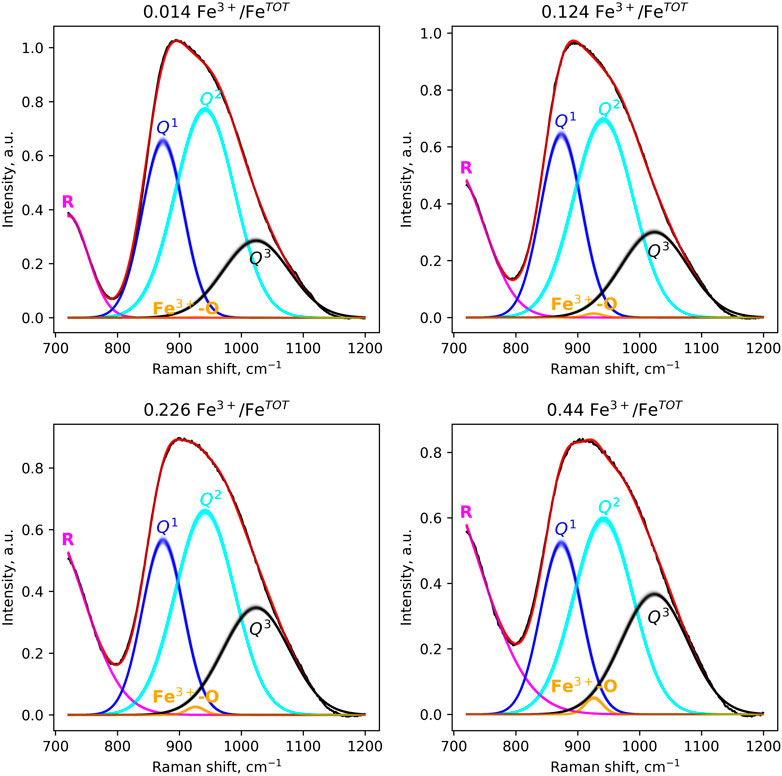
FIGURE 3. Peak-fitting models of the 800–1,200 cm⁻¹ portion of Raman spectra of four peridotite glasses spanning the range of Fe³⁺/Fe^TOT ratios. A subset of 200 posterior models, obtained by NUTS sampling (see Methods), are shown. The curves are affected by transparency coefficients, so that a more intense color means a higher density of models, and therefore a higher probability. All spectra are fit with a single model (see text). For one spectrum, the sum of its Gaussian components (pink, blue, cyan, black and orange lines) yields its fit (red line). The R band at ∼720 cm⁻¹ was used as a way to model properly the minimum in signal near 800 cm⁻¹.

TABLE 3

TABLE 3. Median, 2.5 and 97.5 quantiles of the parameters of the Gaussian peaks used to model the spectra (see also Figure 2). As the R band was only used as a way to model properly background, no parameters are reported for this band.

The intensities of the peaks vary with the glass Fe³⁺/Fe^TOT in a continuous manner (Figure 4A). As Fe³⁺/Fe^TOT increases, the intensities of the Q¹ and Q² peaks decrease, whereas those of the Q³ and Fe³⁺O₄^5- peaks increase. The calculated areas of the peaks vary similarly (Figure 4B). We note that the area of the Fe³⁺O₄⁵⁻ peak is very small, nearly negligible compared to that of the other Qⁿ units. In general, the observations from Figure 4 indicate that increasing Fe³⁺/Fe^TOT leads to increasing the fractions of Q³ units at the expense of those of Q¹ and Q² units.

FIGURE 4

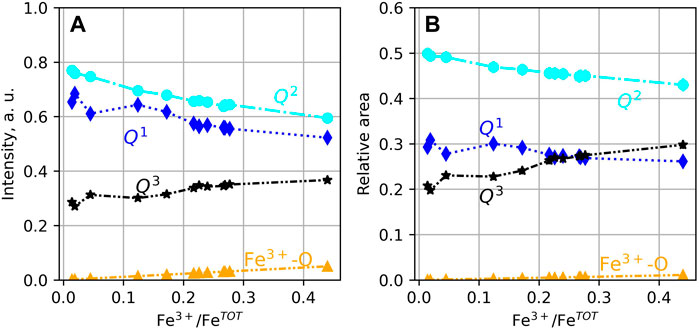
FIGURE 4. (A) Intensity and (B) areas of the peaks assigned to (Si,Al)-O and Fe³⁺-O stretching. If not visible, error bars are smaller than symbol size.

Using conversion coefficients θⁿ, it is possible to convert the areas A(Qⁿ) of the Raman peaks assigned to the different Qⁿ units (Figure 4B) into species concentrations [Qⁿ] (e.g., Mysen and Frantz, 1993):

$\left[Q^n\right]={\theta }^n\mathrm{A}\left({\mathrm{Q}}^{\mathrm{n}}\right).(4)$

The determination of θⁿ values requires the knowledge of [Qⁿ], generally obtained from ²⁹Si Nuclear Magnetic Resonance (NMR) spectroscopy data. Using such an approach, Mysen (2007) determined that θ³ = 1.05 ± 0.04 in sodium aluminosilicate glasses, and θ³ = 1.06 ± 0.04 in hydrous sodium silicate glasses. From the analysis of their glass series; Mysen (2007) also proposed two values for θ²: 1.06 ± 0.07 and 0.84 ± 0.07 for sodium aluminosilicate and hydrous sodium silicate compositions, respectively. Finally, from the study of Raman spectra of depolymerised hydrous sodium silicate glasses; Mysen (2007) proposed θ¹ = 0.22 ± 0.06. From the study of lithium silicate glasses, Umesaki et al. (1993) found that θ³, θ², θ¹ and θ⁰ values were 1.04, 1.02, 1.15 and 0.90, respectively. Recently, Nesbitt et al. (2021) proposed θ³ = 0.95 and θ² = 1.12 from the analysis of a sodium silicate glass with 40 mol% Na₂O.

To the best of our knowledge, there are no reported θⁿ values for complex iron-bearing alkaline-earth alumino-silicate compositions. Furthermore, it is uncertain whether θⁿ values determined in alkali silicate- and aluminosilicate glasses are applicable to peridotite glasses. To test their applicability, we derive θⁿ values from the fit of the Raman spectrum of enstatite MgSiO₃ glass. Indeed, its Mg-rich composition and NBO/T of two resemble those of the peridotite glasses, making it a suitable simplified analogue. Furthermore, the fractions of the different Qⁿ units in the enstatite glass have been determined precisely from 1D and 2D ²⁹Si Nuclear Magnetic Resonance (NMR) spectroscopy (Sen et al., 2009). Peak fitting the Raman spectrum of enstatite glass in the same manner as that of the peridotite glasses allows the quantification of the contributions from Q¹ to Q⁴ units (Figure 5). The θⁿ values are then simply obtained from the ratio between the true fraction of the Qⁿ unit and their normalized Raman peak areas. Using this approach, we determine θ¹ =1.24 ± 0.07, θ² =1.02 ± 0.06, θ³ = 0.77 ± 0.04 and θ⁴ = 1.42 ± 0.09.

FIGURE 5

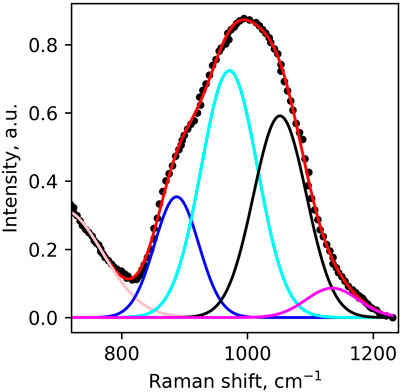
FIGURE 5. Peak fitting modeling of the Raman spectrum of enstatite glass. Original spectrum digitized from Kalampounias et al. (2009).

Using the enstatite-derived θⁿ values and Eq. 4, we convert the relative areas of the Raman peaks to fractions of Qⁿ units. The result is shown in Figure 6A. As Fe³⁺/Fe^TOT increases from 0.01 to 0.44, the fraction of Q¹ units decreases from ∼0.36 to ∼0.32, that of Q² units decreases from ∼0.50 to ∼0.43, and that of Q³ increases from ∼0.16 to ∼0.23. The subsequent NBO/T is given by

$\mathrm{N}\mathrm{B}\mathrm{O}/\mathrm{T}=3\left[Q^1\right]+2\left[Q^2\right]+1\left[Q^3\right].(5)$

FIGURE 6

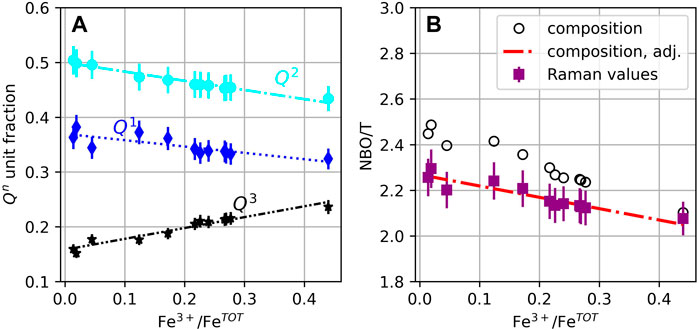
FIGURE 6. (A) Qⁿ unit fractions determined from the Raman data; lines are polynomial fits to the data. (B) Mean non-bridging oxygen atoms per tetrahedral units (NBO/T) calculated from the glass composition (black circles) and from the Raman-derived Qⁿ unit fractions in A (see Eq. 4, purple squares). The red dashed line marks the adjusted compositional trend, calculated assuming that ∼66% of all Fe³⁺ cations act as network modifiers, and ∼94% of all Fe²⁺ act as network modifiers (see discussion); the trend was corrected from a 0.15 absolute shift between stoichiometric and spectroscopic NBO/T values, observed for enstatite glass (Sen et al., 2009). If not visible, error bars are smaller than symbol size.

Neglecting the influence of the Fe³⁺O₄ peak as its contribution is very small and does not significantly affect the calculation of the NBO/T (Figures 2, 3), the NBO/T value decreases from ∼2.26 to ∼2.07 as Fe³⁺/Fe^TOT increases from 0.01 to 0.44. These values can be compared with the NBO/T calculated from melt composition, assuming that Fe²⁺ acts only as a network modifier, and that Fe³⁺ acts only as a network former. The comparison shows that the compositionally determined NBO/T of reduced glasses are higher by ∼0.2 compared to the Raman-determined values (Figure 6B). Furthermore, the slope d(NBO/T)/d(Fe³⁺/Fe^TOT) is steeper (i.e., a larger change in NBO/T for a given change in Fe³⁺/Fe^TOT) than that of Raman-derived values.

4 Discussion

4.1 Raman modeling

The above analysis relies on the validity of the modeling of the broad signal assigned to Si-O and Al-O stretching in the 800–1,300 cm⁻¹ portion of the spectra. In this study, we chose to follow the conventional approach that relies on using a limited number of symmetric peaks to decompose the observed signals (e.g., following the milestone study of Mysen et al., 1982). Each peak is assigned to T-O stretching in specific Qⁿ units and to Fe³⁺-O stretching.

In detail, we consider this model a simplification of reality. Indeed, the true peak shapes of the T-O stretching signals assigned to Q², Q³ and Q⁴ units are not purely symmetric, as documented by studies of the Raman signals of silicate glasses relying on linear spectral decomposition (e.g., Zotov et al., 1999; Zakaznova-Herzog et al., 2007; Malfait, 2009; Herzog and Zakaznova-Herzog, 2011), atomistic simulations (Spiekermann et al., 2013), and peak fitting involving multiple symmetric peaks per Qⁿ units (e.g., see You et al., 2005; Osipov et al., 2015; Nesbitt et al., 2019; Nesbitt et al., 2021). The study of Spiekermann et al. (2013) presents simulation results on enstatite glass, and is thus particularly pertinent for our purposes. Their simulations reveal that the shape of the tetrahedral symmetric stretching signals (υ₁^TET) is, in general, asymmetric in the vibrational density of state of enstatite glass, particularly for Q² units. Therefore, the use of symmetric peaks in our peak-fitting model clearly is an approximation, but it was necessary because we could not determine the true shape of T-O stretching signals from Q², Q³ and Q⁴ units in the present peridotite glasses.

In the model, we also neglect the contributions of the asymmetric stretching of bridging oxygens in Qⁿ units, also referred to as υ₃^BO in Spiekerman et al. (2013), T_2s in Le Losq et al. (2022), or BO in Mysen et al. (1982). This simplification was made because the attempts at modeling the enstatite and peridotite spectra with an additional υ₃^BO peak were not successful. This may be explained by the fact that υ₃^BO occurs at a frequency of ∼950–1,050 cm⁻¹ (Spiekermann et al., 2013) and thus strongly overlaps with the T-O stretching signals from Q² and Q³ units in the spectra (Figures 3, 5). While it is usually possible to extract this signal from Raman spectra of relatively polymerized glasses (e.g., see Le Losq et al., 2022), here the signals in the 800–1,300 cm⁻¹ portion of the Raman spectra of peridotite and enstatite glasses are broad and featureless. Because of this, attempts at introducing a new υ₃^BO/T_2s band resulted in model instability and convergence failure. It was not possible to add a new υ₃^BO/T_2s band without imposing strong constraints, and, hence, new sources of possible errors. Iron-bearing peridotite glasses present an even greater challenge, as the small Fe³⁺-O signal overlaps part of the υ₁^TET Q² signal (Figure 3). The omission of the υ₃^BO/T_2s peak may result in a systematic bias in the Q¹, Q², Q³ and Q⁴ peak areas, and hence in the θⁿ values used for conversion of peak areas in [Qⁿ] (Eq. 4). Therefore, given that we use the same model to fit the Raman spectra of both enstatite and peridotite glasses, the omission of the υ₃^BO/T_2s peak results in no systematic change in Qⁿ species as any area offset is subsumed by the calibration of the θⁿ values. Furthermore, several studies of depolymerized silicate glasses reveal near-negligible contributions of υ₃^BO/T_2s signals in their Raman spectra (e.g., see Nesbitt et al., 2019; Nesbitt et al., 2021).

Despite the simplicity of the model employed herein, it produces excellent fits of the Raman spectra of peridotite and enstatite glasses (Figures 3, 5) and returns coherent Qⁿ unit concentrations and NBO/T values (see Results section and Figure 6). For the peridotite glasses, the number of introduced components also is consistent with the results of PCA (Figure 2). Together, these results indicate a robust and representative decomposition of Raman spectra of peridotite and enstatite glasses.

4.2 Structural role of iron in peridotite glasses

The conventional wisdom on the role of Fe²⁺ and Fe³⁺ in the atomic structure of silicate melts states that the former acts as a network modifier cation, breaking T-O-T bonds and creating NBOs, while the latter acts as a network former cation, like Al³⁺, and participates in constructing the polyhedral network of the melt (e.g., see Le Losq et al., 2021b for a review). This structural picture is broadly corroborated by variations in the viscosity of silicate melts upon changing the redox state of iron. That is, at a given temperature, melt viscosity decreases as Fe³⁺ is reduced to Fe²⁺ (Dingwell et al., 1988; Dingwell, 1989; Liebske et al., 2003; Chevrel et al., 2013; Le Losq et al., 2021b). However, this general picture still is subject to debate because the coordination numbers (CNs) of Fe³⁺ and Fe²⁺ may vary with melt composition, which can, in turn, induce variations in melt properties.

In particular, while Fe³⁺ in CN 4 will act as a network former, forming true coordination polyhedra in the sense of Pauling (strong covalency of Fe-O bonds), Fe³⁺ that exists partially in CN 5 or 6 may not. Such considerations are important because multiple experimental studies support a mean Fe³⁺ CN higher than four in reduced glasses (e.g., Mysen et al., 1985a; Hannoyer et al., 1992; Farges et al., 2004; 2005; Jayasuriya et al., 2004; Liu and Lange, 2006; Wilke et al., 2007; Alderman et al., 2017; Zhang et al., 2018; Le Losq et al., 2020). For instance, XANES spectra collected by Wilke et al. (2004) showed that the average CN of Fe³⁺ in sodium silicate and basaltic glasses is closer to 4.5 or 4.6. This agrees with earlier findings of Mysen et al. (1985b), Mysen et al. (1985a) and Virgo and Mysen (1985), all of whom suggested that, in reduced glasses with Fe³⁺/Fe^TOT < ∼0.5–0.6, Fe³⁺O₄⁵⁻ units coexist with Fe³⁺·O₆⁹⁻. Such a conclusion is also supported by the more recent Mossbaüer and XANES studies of Jayasuriya et al. (2004), Alderman et al. (2017) and Zhang et al. (2018). These authors argue that the low Mossbaüer quadrupole splitting and isomer shift values in reduced glasses suggest that Fe³⁺ exists in CN higher than 4.

Similarly, Fe²⁺ dos not solely occupy octahedral coordination but has an average CN around ∼5 in many silicate glasses, as indicated by Fe K-edge XANES studies (e.g., Wilke et al., 2004; 2007; Jackson et al., 2005; Le Losq et al., 2020) and Mossbaüer studies (e.g., Mysen, 2006; Zhang et al., 2018). In their diffraction study, Drewitt et al. (2013) confirm this assignment, showing that in ferrosilite, hedenbergite and fayalite liquids, Fe²⁺ is present in both CN 4 and CN 6, in proportions of roughly 50% FeO₄⁶⁻ and 50% FeO₆¹⁰⁻, with negligible FeO₅^8-. Regardless of its CN, ferrous iron is generally considered as a network modifier because of its low valence and its well-characterised effect on melt viscosity (e.g., Dingwell, 1991).

Here, information on the mean CNs of Fe²⁺ and Fe³⁺ was obtained from Fe K-edge X-Ray Absorption Near-Edge Structure (XANES) spectra of the peridotite glasses reported in Sossi et al. (2020). Indeed, relative to Raman spectroscopy, the Fe K-edge XANES region provides complementary information as to the structural and electronic environment of Fe in silicate glasses (e.g.; Berry et al., 2003; Wilke et al., 2004). In particular, the pre-edge feature that arises due to electronic transitions between bound- and excited states (in this case, the 1s → 3 d transition, Waychunas et al., 1983) can be used to estimate Fe³⁺/Fe²⁺ and its mean coordination number. Bajt et al. (1994) demonstrated that the mean area-weighted centroid energies for Fe²⁺- and Fe³⁺-bearing compounds occur at ∼7,112 eV and 7,113.5 eV, respectively, independent of their coordination environment. On the other hand, the pre-edge intensity of the ferrous- and ferric iron-related transitions depends on the coordination geometry of the site. In detail, centrosymmetric octahedral geometries result in low integrated intensities, whereas sites of low symmetry, such as tetrahedrally-coordinated Fe, produce higher intensity transitions for a given valence state of Fe (Wilke et al., 2001; Berry et al., 2003). One method used to calibrate the effect of oxidation state and coordination number on the pre-edge is predicated on the XANES measurement of minerals (Wilke et al., 2001; Wilke et al., 2004) to produce a variogram (Figure 7). Combinations of two discrete coordination geometries of different Fe valence states result in curvilinear mixing lines weighted towards the larger relative intensity contribution of the low symmetry site to the mean centroid energy. The use of the variogram to derive absolute oxidation states and coordination environments for glasses is subject to the caveat that, unlike minerals, glasses do not preserve long-range order. Therefore, we consider it as a guide, rather than as an absolute measure of bonding environment in glasses. This point is illustrated by the Anorthite-Diopside eutectic (ADeu) glass sample of Berry et al. (2003) synthesised at logfO₂ = +4.8 at 1,409 °C, which plots outside the calibration range defined by the mineral end members (Figure 7).

FIGURE 7

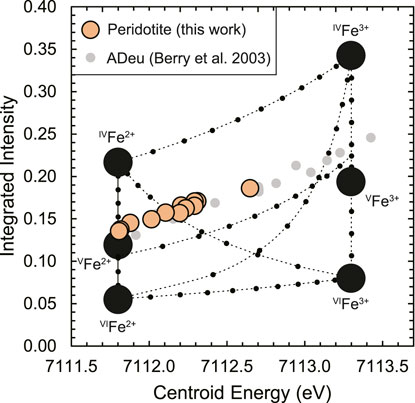
FIGURE 7. A variogram (after Wilke et al., 2004) that defines boundaries of iron valence state and coordination number as a function of the normalised integrated intensity of the XANES Fe K-edge pre-edge (1s → 3 d) feature against its mean centroid energy. The centroid energy of the variogram is shifted downwards by 0.2 eV to match the energy calibration used for the XANES spectra of Sossi et al. (2020). The end member compositions (large black points) are deduced based on Fe bonding environments in minerals, with the dashed curves representing mixing lines between them (at increments of 0.1, small black points). Data for peridotite glasses (orange points, this work) are shown together with literature data for glasses of Anorthite-Diopside eutectic (ADeu) composition (Berry et al., 2003), shifted downwards by 0.3 eV to match the centroid energy of the peridotite glasses when both sets have Fe³⁺/(Fe²⁺ + Fe³⁺) = 0. Error bars on points are smaller than the circles.

Nevertheless, the value of the variogram lies in the capacity for direct comparison with other silicate glasses. The XANES spectra of the peridotite glasses were fit according to the method outlined in Sossi et al. (2020) and results are shown in Table 4 and Figure 7. The glasses overlap, within uncertainty, with the trend defined by ADeu glasses synthesised at ∼500 °C lower temperatures and with a considerably MgO-depleted, CaO-enriched composition with respect to peridotite. This result suggests the structural and electronic environment of Fe exhibits no resolvable, systematic differences as a function of composition or temperature of synthesis among ADeu and peridotitic glasses. The other prevailing trend, commonly observed in silicate glasses (Knipping et al., 2015; Alderman et al., 2017), is the tendency for Fe²⁺ to exist in higher mean coordination environments than Fe³⁺. The variogram (Figure 7) indicates a mean coordination number of ∼5.1 for Fe²⁺, compared with ∼4.7 for Fe³⁺.

TABLE 4

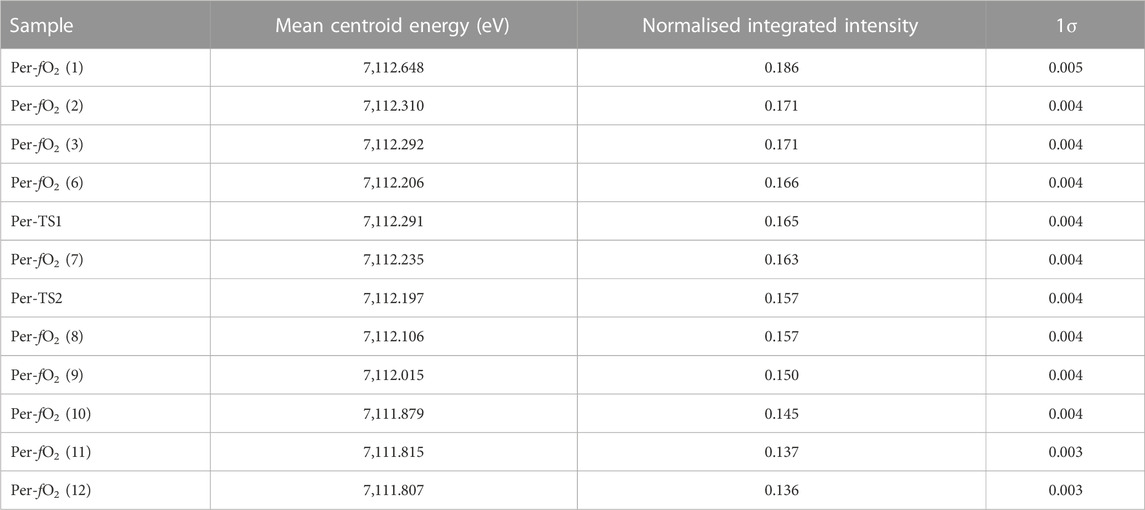
TABLE 4. Mean centroid energy (eV) and normalised integrated intensity in peridotite glasses. See Sossi et al. (2020) for methods.

As these CN do not correspond to a discrete coordination environment, Fe²⁺ and Fe³⁺ must reside in a distribution of environments in peridotite glasses. This observation is important because the extent to which each valence state affects NBO/T relates to the structural roles they assume in melts, whereas the compositional method for calculating NBO/T is binary, applying the same weighting coefficient to each element (e.g., see footnote two in Mysen et al., 1985). That is, each element is assumed to contribute equally to either network formation or destruction. In contrast, Fe³⁺ is proposed to show amphoteric behaviour on chemical grounds; it can act either as an acidic or basic oxide, depending on the basicity of the melt (Ottonello et al., 2001; Moretti, 2005; Ottonello, 2005; Moretti and Ottonello, 2022). Hence, it can react with both bridging and non-bridging oxygens, thus leading to variations in its local environment as reflected by a variable CN (Moretti and Ottonello, 2022 and references cited therein).

We observe that, upon increasing Fe³⁺/Fe^TOT, the Raman-derived NBO/T decreases to a lesser extent than expected, should all Fe³⁺ cations play a network-forming role (Figure 6B). This observation indicates that Fe³⁺ may behave in an amphoteric manner in the peridotite glasses. That is, some of the Fe³⁺ cations act as network formers, while others do not and can be considered as network modifiers. We can formalise this behaviour by, first, taking into account the reaction between the three kinds of oxygen atoms present in the melt atomic network (Fincham and Richardson, 1954):

$2{\mathrm{O}}_{\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{-}={\mathrm{O}}_{\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{2-}+{\mathrm{O}}_{\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^0,(6)$

with O⁻ the NBOs, O⁰ the BOs and O²⁻ the free (unbound) oxygens in the glass/melt. Upon glass synthesis, oxygen fugacity is imposed (Table 1) such that the equilibrium constant of the reaction (Moretti, 2005):

${\mathrm{F}\mathrm{e}}_{\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{2+}+¼1/4{{\mathrm{O}}_2}_{\left(\mathrm{g}\mathrm{a}\mathrm{s}\right)}={\mathrm{F}\mathrm{e}}_{\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{3+}+½1/2{\mathrm{O}}_{\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{2-},(7)$

is defined. Reaction (7) accounts for the oxidation-reduction reaction between network modifiers Fe²⁺ and Fe³⁺, but not for that involving Fe³⁺ in tetrahedral coordination (Ottonello et al., 2001; Moretti, 2005; Ottonello, 2005; Moretti and Ottonello, 2022). Another reaction is required to do so (Moretti and Ottonello, 2022):

${\mathrm{F}\mathrm{e}}_{\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{2+}+7/2{\mathrm{O}}_{\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{2-}+1/4{\mathrm{O}}_{2\left(\mathrm{g}\mathrm{a}\mathrm{s}\right)}={\mathrm{F}\mathrm{e}}^{3+}{\mathrm{O}}_{4\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{5-},(8)$

with Fe³⁺O₄⁵⁻ as a Fe³⁺ network former in tetrahedral coordination. It is the Fe³⁺-O vibrations in such Fe³⁺O₄⁵⁻ units that yield the signal observed near 925 cm⁻¹ in the Raman spectra (Figure 3). By the same token, a continued increase in aO²⁻ implies equilibria of the form

${\mathrm{F}\mathrm{e}}^{3+}{\mathrm{O}}_{4\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{5-}+{\mathrm{O}}_{\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{2-}={\mathrm{F}\mathrm{e}}^{3+}{\mathrm{O}}_{5\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{7-},(\mathrm{9a})$

${\mathrm{F}\mathrm{e}}^{3+}{\mathrm{O}}_{4\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{5-}+2{\mathrm{O}}_{\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{2-}={\mathrm{F}\mathrm{e}}^{3+}{\mathrm{O}}_{6\left(\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}\right)}^{9-},(\mathrm{9b})$

that control the distribution of IV-fold (Fe³⁺O₄⁵⁻), V-fold (Fe³⁺O₅⁷⁻) and VI-fold (Fe³⁺O₆⁹⁻) coordinated Fe³⁺ in the liquid. Hence, the oxidation of Fe²⁺ can produce both network forming (Eq. 8) and modifying (Eqs 9a, b) Fe³⁺. The activity of free oxygens O²⁻, driven by melt basicity and, hence, composition, will drive the equilibrium constants of reactions (7) to (9), and determine the different quantities of Fe³⁺O₄⁵⁻, Fe³⁺O₅⁷⁻ and Fe³⁺O₆⁹⁻ at given Fe³⁺/Fe^TOT (Moretti and Ottonello, 2022). Upon oxidation, Eq. 8 will shift to the right-hand side, and be accompanied by network polymerisation (Figure 6A)

$Q^1+Q^2=2Q^3,(10)$

to an extent controlled by the equilibrium constants of reactions (9 a, b). The proposed amphoteric behaviour of Fe³⁺ in the alumino-silicate network of peridotite melts would explain the NBO/T versus Fe³⁺/Fe^TOT trend derived from Raman data (Figure 6B), as well as the observed CN of Fe³⁺ (Figure 7). Indeed, as the formation of Fe³⁺O₄⁵⁻, Fe³⁺O₅⁷⁻ and Fe³⁺O₆⁹⁻ complexes occurs upon oxidation and with the increase in O²⁻ activity (Eqs 7–9), the fraction of NBO converted to BO must be lower than expected if assuming all Fe³⁺ were to play a network-forming role. As a consequence, the slope of the NBO/T versus Fe³⁺/Fe^TOT trend based on the Raman spectra should be lower than predicted by the computationally derived NBO/T value. This prediction is borne out in Figure 6B, and suggests the coexistence of network former Fe³⁺O₄⁵⁻ with network modifier Fe³⁺ in CN 5 or 6 (Fe³⁺O₅⁷⁻ and Fe³⁺O₆⁹⁻ complexes in Eq. 9; Figure 7).

To quantify the proportions of Fe²⁺ and Fe³⁺ that act as network modifiers and formers, we reassign fractions of ferrous and ferric iron to tetrahedral T species $f_T^{{Fe}^{2+}}$ and $f_T^{{Fe}^{3+}}$, respectively), until the slope and intercept of the compositionally-derived calculation matches those of the Raman, using non-linear least-squares fitting. A systematic correction factor to the NBO/T of the Raman data of +0.15 is applied, given by the difference between the stoichiometric and NMR-derived NBO/T for enstatite glass (from the data of Sen et al., 2009). There are two simultaneous equations, each with one unknown fraction $f_T^{{Fe}^{3+}}$ and $f_T^{{Fe}^{2+}}$, where $f_{modifier}^{{Fe}^{3+}}$ = $1-f_T^{{Fe}^{3+}}$ and $f_{modifier}^{{Fe}^{2+}}$ = $1-f_T^{{Fe}^{2+}}$. In order to fit the Raman NBO/T data (red line, Figure 6B) by solving for $f_T^{{Fe}^{3+}}$ and $f_T^{{Fe}^{2+}}$ indicates that, in the reduced, depolymerised peridotite glasses, most Fe²⁺ cations play a network modifier role (∼94%), and, in fact, so too do most Fe³⁺ cations (∼66% of total Fe³⁺). Such values are consistent with the mean coordination number of Fe³⁺ given by XANES (∼4.7; Figure 7). Indeed, if we assume that 34% of network former Fe³⁺ is in CN 4% and 66% of network modifier Fe³⁺ is in CN 5, then the mean CN of Fe³⁺ is expected to be ∼4.7. Similarly, 6% of network former Fe²⁺ in CN 4 coexisting with ∼78% CN 5 and ∼16% CN 6 network-modifying Fe²⁺ yields the observed average CN of 5.1 (Figure 7). As noted above, the variogram should be used only as a guide, however, irrespective of the exact proportions of the coordination environments of Fe, the Raman and Fe K-edge XANES data point toward a significant fraction of Fe³⁺ acting as a network modifier in peridotite melts.

The equilibrium constants of reactions 7 to 9 should be strong functions of temperature and melt composition (Moretti, 2005; Moretti and Ottonello, 2022). In particular, with increasing temperature, we expect the equilibrium

$2Q^2=Q^1+Q^3,(11)$

to shift to the right-hand side (e.g., Mysen and Frantz, 1993; Mysen, 1995; Mysen, 1996; Mysen, 1999). As temperature changes, this could influence the progress of reaction (10), such that we expect the ratio of Fe³⁺O₄⁵⁻_former/Fe³⁺_modifier to be temperature dependent. Comparison of aerodynamically levitated melts with their quenched counterparts show only marginal evidence for a temperature dependence of Eq. 9 (Alderman et al., 2017). However, XANES spectra of ultramafic compositions in the MgO-FeO-SiO₂ system are suggestive of an increase in CN in both Fe²⁺ and Fe³⁺ in melts with higher NBO/T, as expected from Eq. 9 and its ferrous iron equivalent.

High pressure conditions may also favour network modifier Fe³⁺, as pressure tends to promote higher coordination environments for cations in silicate melts (e.g., Sanloup et al., 2013a; b; Wang et al., 2014; Drewitt et al., 2015; Sanloup, 2016) owing to their denser packing arrangements and therefore smaller molar volumes. In addition, pressure favours the conversion of Fe³⁺ to Fe²⁺ at given fO₂ (e.g., O’Neill et al., 2006; Zhang et al., 2017), at least up to ∼9 GPa, above which the trend is reversed (Armstrong et al., 2019; Deng et al., 2020). Interestingly, the inflection point in Fe³⁺/Fe²⁺ ratios observed in Armstrong et al. (2019) coincides with the viscosity decrease in the experiments of Liebske et al. (2005). Considering both effects, Fe in silicate melts at high pressures should be present at a significantly lower degree of polymerization (higher CN) relative to their low pressure counterparts. Indeed, ab-initio molecular dynamics (AIMD) simulations show evidence for higher mean Fe-O CN in peridotitic melts at 4000 K, from an average near ∼4.5 at 1 bar to and reaching ∼6 by 100 GPa (Huang et al., 2022). As a result, we speculate that, upon decompression, melt polymerization may occur as a result of pressure-induced oxidation of Fe²⁺ to Fe³⁺ and the subsequent transition of Fe³⁺_modifier to Fe³⁺O₄⁵⁻_former as Fe³⁺ CN decreases, and that this melt polymerization should result in an increase in viscosity. Independent evidence for this comes from other AIMD simulations on basaltic melts, in which such liquids, at 2200 K, exhibit decreasing viscosities up to ∼10 GPa before undergoing a drastic increase above these pressures (Bajgain et al., 2022). Such hypothesis is also in accord with the conclusions of Spice et al. (2015). Those authors observed that viscosity of molten fayalite at 1850 °C increases by a factor of 2.5 when pressure decreases from 9.5 GPa to ambient. They reconciled their observations with the increase in <Fe-O> coordination with pressure observed by Sanloup et al. (2013a). Experimental investigation of glass or melt viscosities above 25 GPa would be key to reconciling structural changes with viscosity variations in deep magma oceans.

4.3 Evolution of the properties of peridotite melts in an early magma ocean

In an early magma ocean on Earth, the changing Fe redox state with temperature and fO₂ will yield variations in melt properties, including viscosity and density, that can affect the nature of convection. Previous viscosity measurements were performed at fixed or unconstrained fO₂ conditions, meaning these effects were not systematically investigated. The data at superliquidus temperatures on the CaFeSi₂O_x composition indicate that its viscosity changes by less than 0.2 log Pa·s as Fe³⁺/Fe^TOT increases from ∼0.10 to ∼0.85 (Dingwell, 1991). Taking this composition as an analogue for peridotite melts, only very limited variations in viscosity at superliquidus temperatures are expected, of the order of 0.1 log Pa·s as Fe³⁺/Fe^TOT increases from 0.0 to 0.44.

Unfortunately, no general viscosity model, which could be used to predict the viscosity of peridotite melts, takes iron oxidation state into account. For instance, the Giordano et al. (2008) model, which uses polynomial interpolative functions to predict the effect of melt composition on viscosity, considers only the total iron concentration. The absence of a liquid viscosity model that includes the effect of Fe³⁺/Fe^TOT is a consequence of the very few datasets that systematically examine how Fe³⁺/Fe^TOT affects melt viscosity. In theory, this prevents an assessment of the effect of Fe³⁺/Fe^TOT on melt viscosity in the context of this work. However, existing viscosity models and structural knowledge on the role of Fe²⁺ and Fe³⁺ in silicate and aluminosilicate glasses and melts can provide clues.

Indeed, as previously presented, a variety of spectroscopic methods attest to the prevailing role of Fe²⁺ as a network modifier cation in silicate melts, similar to Mg²⁺ or to Ca²⁺, whereas Fe³⁺ behaves, at least partially, as a network former cation like Al³⁺ (see for a review of this Le Losq et al., 2021b,; Mysen and Richet, 2019). In general, this similarity arises from their similar ionic radii and charges, where Z/r for ^IVAl³⁺ = 7.7 and for ^IVFe³⁺ = 6.1, while Z/r for ^VIMg²⁺ = 2.78 and ^VIFe²⁺ = 2.6 (Shannon et al., 1976). Therefore, we use Al³⁺ as an analogue for the network former Fe³⁺O₄^5-, while the properties of either Mg²⁺ or Ca²⁺ are presumed to apply to network modifier Fe³⁺ and Fe²⁺, such that Fe³⁺/Fe^TOT variations are equivalent to variations in Al³⁺/(Al³⁺ + MO), with M = Ca or Mg. In this manner, the observed NBO/T variation as a function of Fe³⁺/Fe^TOT is replicated: it varies from 2.45 for fully depolymerised reduced-like melts to 2.26 for oxydised-like melts (values here are uncorrected from the systematic shift between compositional and spectroscopic NBO/T, see Results section and Figure 6).

With these simplifications, the existing parametric model from Giordano et al. (2008) is employed to evaluate melt viscosity at 2000 °C and 1 bar as a function of NBO/T. We further used an extension of the i-Melt machine learning model (Le Losq et al., 2021c), trained to predict melt and glass properties (including viscosity) in the system Na₂O-K₂O-CaO-MgO-Al₂O₃-SiO₂ (Le Losq et al., 2021a). This version of i-Melt allows prediction of melt viscosity on the entire glass-forming domain of the Na₂O-K₂O-CaO-MgO-Al₂O₃-SiO₂ system with a mean test error of 0.4 log Pa·s.

At 2000 °C, a temperature in the range of those inferred for magma oceans (e.g., Elkins-Tanton, 2012), calculated viscosities with both models range between −1.5 and −1.8 log Pa·s (Figure 8). The errors on the predictions from i-Melt were evaluated using MC Dropout (Gal and Ghahramani, 2016), and are lower than ± 0.3 log Pa·s (2σ) in the composition-temperature range of interest (Figure 8). In Figure 8, the NBO/T is recalculated from composition, taking into account that 66% of all Fe³⁺ cations and 94% of all Fe²⁺ cations act as network modifiers. At 2000 °C, the measurements of Dingwell et al. (2004) are extrapolated to give a viscosity of −1.86 log Pa·s. We see thus a small shift between values from the i-Melt and Giordano et al. (2008) models presented in Figure 8 and the measurements of Dingwell et al. (2004). This is expected as the synthetic Fe-free peridotite-like melts are only an approximation of true peridotite melts, owing to the approximation that Fe³⁺O₄⁵⁻ behaves like Al³⁺O₄⁵⁻ in the melt structure, and modifiers Fe²⁺/Fe³⁺ like Ca²⁺ or Mg²⁺. It should also be noted that the composition of Dingwell et al. (2004) is poorer in MgO (∼32 wt%) than our peridotite glasses (∼38 wt%). Nevertheless, the models indicate that small variations in melt NBO/T induced by variations in the cationic ratio T³⁺/M²⁺, with T³⁺ a trivalent network former cation and M²⁺ a divalent network modifier cation, will generate limited viscosity variations at the very high, superliquidus temperatures expected in magma oceans at their surface. Here, at most, we expect variations lower than 0.1 log Pa·s as the melt Fe³⁺/Fe^TOT varies from 0.0 to 0.44 and its compositional NBO/T decreases by ∼0.19 (Figure 8). This is within the previously highlighted range of expected variations when considering the experimental data of Dingwell (1991) on CaFeSi₂O_x melts.

FIGURE 8

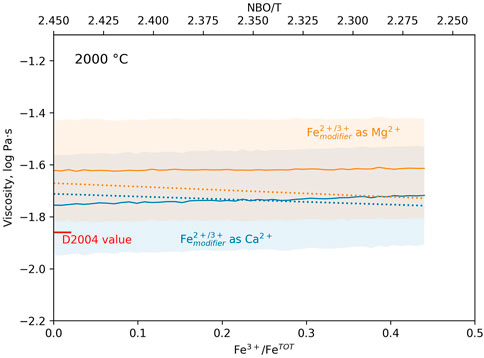
FIGURE 8. Viscosity (log Pa·s) of analogue peridotite melts at 2000 °C as a function of their Fe³⁺/Fe^TOT and NBO/T. Here, network former Fe³⁺O₄⁵⁻ is assumed to behave analogous to Al³⁺ and network modifiers Fe³⁺ and Fe²⁺ as either Mg²⁺ (orange symbols and lines) or Ca²⁺ (blue symbols and lines). NBO/T varies from 2.45 for fully depolymerised reduced melts to 2.26 for oxidised-like melts (values uncorrected from the systematic shift between compositional and spectroscopic NBO/T). Solid lines are i-Melt predictions (see for model details Le Losq et al., 2021c), with errors indicated by the colored areas. Dotted lines are calculations performed with the Giordano et al. (2008) model. The red tick on the left annotated “D2004 value” refers to the viscosity value at 2000 °C determined from the extrapolation of the measurements of Dingwell et al. (2004) with the VFT equation.

Such small variations in viscosity are unlikely to affect fluid dynamical processes. A simple calculation highlights this result. For instance we consider, a magma ocean of thickness = 1,000 km, composed of a silicate melt with constant ρ = 3000 kg m⁻¹ across its thickness, thermal diffusivity κ = 10^–8 m² s⁻¹ (Eriksson et al., 2003) and thermal expansivity α = 10^–4 K⁻¹ (Gottsmann et al., 1999). The temperature gradient over its thickness is taken to be 1000 K. Of course, these values are only meant to be illustrative of those that could typify magma oceans and we neglect here the decrease in viscosity and changes in density with depth, given that our results are applicable only at 1 bar. Nevertheless, given ${\eta }_{silicate}$ = 10^–1.86 Pa·s at 2000 °C, R_a = 2.2 × 10²⁹. A small decrease of 0.1 in ${\eta }_{silicate}$ leads to R_a = 1.8 × 10²⁹. Such variation is negligible, and such high R_a numbers simply indicate a very turbulent system in which viscous forces can be neglected. Naturally, from Eq. 1, only variations in ${\eta }_{silicate}$ of orders of magnitude can significantly influence R_a. In a magma ocean, such large variations in ${\eta }_{silicate}$ may originate from a large temperature gradient as well as extensive crystallization and degassing, which also can drive drastic changes in melt rheology (e.g., see Giordano et al., 2008; Mader et al., 2013 and references cited therein). It is therefore very unlikely that second-order parameters, such as small variations in melt composition and iron oxidation state, play a role in the dynamics of fluid flow in turbulent magma oceans, at least of peridotitic compositions at 1 bar. However, the effect of pressure also appears to be subordinate to that of temperature and crystallinity. Xie et al. (2021) report viscosities that are within uncertainty of one another between 10 and 25 GPa, though they are systematically a factor ∼4 to 5 lower than that determined by Dingwell et al. (2004) at 1 bar. In other terms, and as expected, cooling and crystallization of magma oceans are likely the main factors leading to the death of turbulent, rapid fluid movements in such systems. Nevertheless, owing to diversity of compositions expected in rocky planets orbiting extrasolar systems from that of their host stars (e.g., Unterborn et al., 2020), the required order-of-magnitude variations in viscosity relative to peridotite could arise solely from changes in composition.

5 Conclusion

In this study, we analysed the Raman spectra of glasses with peridotitic composition synthesised at 2173 K and 1 bar, with Fe³⁺/Fe^TOT ranging from 0.01 to 0.44. We find that the peridotite glasses are largely comprised of Q² units, with lower proportions of Q¹ and Q³. The proportion of Q³ units increases at the expense of those of Q¹ and Q² as Fe³⁺/Fe^TOT increases. From these data, we calculate Raman-based NBO/T values as a function of Fe³⁺/Fe^TOT. The change in NBO/T with Fe³⁺/Fe²⁺ in the Raman-based methodology is less pronounced than that expected from compositional calculations that assume all Fe³⁺ cations play a network forming role. This suggests that Fe³⁺ cations act both as network formers and network modifiers in peridotitic silicate melts, confirming the amphoteric behavior of Fe³⁺ observed in aluminosilicate melts (Ottonello et al., 2001; Moretti, 2005; Moretti and Ottonello, 2022). In fact, this behaviour is exaggerated in the present peridotite composition, as roughly two-thirds of the Fe³⁺ cations appear to act as network modifiers, while more than 90% of Fe²⁺ are network modifiers. As a result, changes in melt polymerisation as a function of Fe³⁺/Fe²⁺ ratio are limited, with compositional NBO/T decreasing of ∼0.19 as Fe³⁺/Fe^T increases from ∼0.01 to ∼0.44. Using existing viscosity models and the machine learning model i-Melt, we show that such limited structural variations have an insignificant influence on melt viscosity, but are consistent with experimentally determined estimates of peridotite viscosity. We therefore conclude that any variations in the redox state of the Earth’s magma ocean did not influence its convective vigour, although the variability of compositions among rocky exoplanetary mantles could be sufficiently different from that of peridotite to induce significant changes in Ra.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

CL and PS designed the idea during the 2021 CLEEDI workshop. Starting glass materials and XANES treatment were carried out by PS. CL analysed the glasses by Raman spectroscopy, interpreted the spectra, and produced the first draft of the manuscript. CL and PS contributed to the final manuscript.

Funding

CL acknowledges funding from the Australian Research Council Laureate Fellowship FL130100066 to Prof. Hugh O’Neill (Monash University), from a Chaire d’Excellence and the Data intelligence institute of Paris, IdEX Université de Paris, ANR-18-IDEX-0001. PS thanks the Swiss National Science Foundation (SNSF) via an Ambizione Fellowship (180025), an Eccellenza Professorship (203668) and the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract number MB22.00033, a SERI-funded ERC Starting Grant “2ATMO”. CL thanks R. Moretti (IPGP, France) for discussions about the amphoteric behavior of iron in glasses, and J. Badro (IPGP, France) for suggestions to improve Figure 8. We thank three reviewers that provided constructive comments on the machine learning approach, and encouraged a wider assessment of the literature on spectroscopy and density measurements of ultramafic liquids.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abe, Y. (1997). Thermal and chemical evolution of the terrestrial magma ocean. Phys. Earth Planet. Interiors 100, 27–39. doi:10.1016/s0031-9201(96)03229-3

CrossRef Full Text | Google Scholar

Alderman, O. L. G., Wilding, M. C., Tamalonis, A., Sendelbach, S., Heald, S. M., Benmore, C. J., et al. (2017). Iron K-edge X-ray absorption near-edge structure spectroscopy of aerodynamically levitated silicate melts and glasses. Chem. Geol. 453, 169–185. doi:10.1016/j.chemgeo.2017.01.020

CrossRef Full Text | Google Scholar

Armstrong, K., Frost, D. J., McCammon, C. A., Rubie, D. C., and Boffa Ballaran, T. (2019). Deep magma ocean formation set the oxidation state of Earth’s mantle. Science 365, 903–906. doi:10.1126/science.aax8376

PubMed Abstract | CrossRef Full Text | Google Scholar

Bajgain, S. K., Ashley, A. W., Mookherjee, M., Ghosh, D. B., and Karki, B. B. (2022). Insights into magma ocean dynamics from the transport properties of basaltic melt. Nature Comms. 13 (1), 7590. doi:10.1038/s41467-022-35171-y

CrossRef Full Text | Google Scholar

Bajt, S., Sutton, S. R., and Delaney, J. S. (1994). X-ray microprobe analysis of iron oxidation states in silicates and oxides using X-ray absorption near edge structure (XANES). Geochimica Cosmochimica Acta 58 (23), 5209–5214. doi:10.1016/0016-7037(94)90305-0

CrossRef Full Text | Google Scholar

Berry, A. J., O’Neill, H. St. C., Jayasuriya, K. D., Campbell, S. J., and Foran, G. J. (2003). XANES calibrations for the oxidation state of iron in a silicate glass. Am. Mineralogist 88, 967–977. doi:10.2138/am-2003-0704

CrossRef Full Text | Google Scholar

Brawer, S. A., and White, W. B. (1977). Raman spectroscopic investigation of the structure of silicate glasses (II). Soda-alkaline earth-alumina ternary and quaternary glasses. J. Non-Crystalline Solids 23, 261–278. doi:10.1016/0022-3093(77)90009-6

CrossRef Full Text | Google Scholar

Brawer, S. A., and White, W. B. (1975). Raman spectroscopic investigation of the structure of silicate glasses. I. The binary alkali silicates. J. Chem. Phys. 63, 2421–2432. doi:10.1063/1.431671

CrossRef Full Text | Google Scholar

Canup, R. M. (2004). Dynamics of lunar formation. Annu. Rev. Astronomy Astrophysics 42, 441–475. doi:10.1146/annurev.astro.41.082201.113457

CrossRef Full Text | Google Scholar

Canup, R. M. (2012). Forming a Moon with an earth-like composition via a giant impact. Science 338, 1052–1055. doi:10.1126/science.1226073

PubMed Abstract | CrossRef Full Text | Google Scholar

Canup, R. M., Visscher, C., Salmon, J., and Jr, B. F. (2015). Lunar volatile depletion due to incomplete accretion within an impact-generated disk. Nat. Geosci. 8, 918–921. doi:10.1038/ngeo2574

PubMed Abstract | CrossRef Full Text | Google Scholar

Chevrel, M. O., Giordano, D., Potuzak, M., Courtial, P., and Dingwell, D. B. (2013). Physical properties of CaAl₂Si₂O₈–CaMgSi₂O₆–FeO–Fe₂O₃ melts: Analogues for extra-terrestrial basalt. Chem. Geol. 346, 93–105. doi:10.1016/j.chemgeo.2012.09.004

CrossRef Full Text | Google Scholar

Cochain, B., Neuville, D. R., Henderson, G. S., McCammon, C. A., Pinet, O., and Richet, P. (2012). Effects of the iron content and redox state on the structure of sodium borosilicate glasses: A Raman, mössbauer and boron K-edge XANES spectroscopy study. J. Am. Ceram. Soc. 95, 962–971. doi:10.1111/j.1551-2916.2011.05020.x

CrossRef Full Text | Google Scholar

Cochain, B., Sanloup, C., Leroy, C., and Kono, Y. (2017). Viscosity of mafic magmas at high pressures. Geophys. Res. Lett. 44, 818–826. doi:10.1002/2016GL071600

CrossRef Full Text | Google Scholar

Deguen, R., Landeau, M., and Olson, P. (2014). Turbulent metal–silicate mixing, fragmentation, and equilibration in magma oceans. Earth Planet. Sci. Lett. 391, 274–287. doi:10.1016/j.epsl.2014.02.007

CrossRef Full Text | Google Scholar

Deng, J., Du, Z., Karki, B. B., Ghosh, D. B., and Lee, K. K. M. (2020). A magma ocean origin to divergent redox evolutions of rocky planetary bodies and early atmospheres. Nat. Commun. 11, 2007. doi:10.1038/s41467-020-15757-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Genova, D., Hess, K.-U., Chevrel, M. O., and Dingwell, D. B. (2016). Models for the estimation of Fe³⁺/Fe^tot ratio in terrestrial and extraterrestrial alkali- and iron-rich silicate glasses using Raman spectroscopy. Am. Mineralogist 101, 943–952. doi:10.2138/am-2016-5534ccbyncnd

CrossRef Full Text | Google Scholar

Di Muro, A., Métrich, N., Mercier, M., Giordano, D., Massare, D., and Montagnac, G. (2009). Micro-Raman determination of iron redox state in dry natural glasses: Application to peralkaline rhyolites and basalts. Chem. Geol. 259, 78–88. doi:10.1016/j.chemgeo.2008.08.013

CrossRef Full Text | Google Scholar

Dingwell, D. B., Brearley, M., and Virgo, D. (1988). The dual role of ferric iron in liquid silicates: Effects on density & viscosity. Chem. Geol. 70, 86. doi:10.1016/0009-2541(88)90442-1

CrossRef Full Text | Google Scholar

Dingwell, D. B., Courtial, P., Giordano, D., and Nichols, A. R. L. (2004). Viscosity of peridotite liquid. Earth Planet. Sci. Lett. 226, 127–138. doi:10.1016/j.epsl.2004.07.017

CrossRef Full Text | Google Scholar

Dingwell, D. B. (1991). Redox viscometry of some Fe-bearing silicate melts. Am. Mineralogist 76, 1560–1562.

Google Scholar

Dingwell, D. B. (1989). Shear viscosities of ferrosilicate liquids. Am. Mineralogist 74, 1038–1044.

Google Scholar

Dingwell, D. B., and Virgo, D. (1988). Viscosities of melts in the Na₂O-FeO-Fe₂O₃-SiO₂ system and factors controlling relative viscosities of fully polymerized silicate melts. Geochimica Cosmochimica Acta 52, 395–403. doi:10.1016/0016-7037(88)90095-6

CrossRef Full Text | Google Scholar

Dingwell, D. B., and Virgo, D. (1989). Viscosity-oxidation state relationship for hedenbergitic melt. United States: Carnegie Institution of Washington Year Book, 48–53. 87.

Google Scholar

Drewitt, J. W. E., Jahn, S., Sanloup, C., de Grouchy, C., Garbarino, G., and Hennet, L. (2015). Development of chemical and topological structure in aluminosilicate liquids and glasses at high pressure. J. Phys. Condens. Matter 105103, 105103. doi:10.1088/0953-8984/27/10/105103

PubMed Abstract | CrossRef Full Text | Google Scholar

Drewitt, J. W. E., Sanloup, C., Bytchkov, A., Brassamin, S., and Hennet, L. (2013). Structure of (Fe_xCa_1−xO)_y(SiO₂)_1−y liquids and glasses from high-energy X-ray diffraction: Implications for the structure of natural basaltic magmas. Phys. Rev. B 87, 224201. doi:10.1103/PhysRevB.87.224201

CrossRef Full Text | Google Scholar

Elkins-Tanton, L. T. (2012). Magma Oceans in the inner solar system. Annu. Rev. Earth Planet. Sci. 40, 113–139. doi:10.1146/annurev-earth-042711-105503

CrossRef Full Text | Google Scholar

Eriksson, R., Hayashi, M., and Seetharaman, S. (2003). Thermal diffusivity measurements of liquid silicate melts. Int. J. Thermophys. 24, 785–797. doi:10.1023/a:1024048518617

CrossRef Full Text | Google Scholar

Farges, F., Lefrère, Y., Rossano, S., Berthereau, A., Calas, G., and Brown, G. E. (2004). The effect of redox state on the local structural environment of iron in silicate glasses: A combined XAFS spectroscopy, molecular dynamics, and bond valence study. J. Non-Crystalline Solids 344, 176–188. doi:10.1016/j.jnoncrysol.2004.07.050

CrossRef Full Text | Google Scholar

Farges, F., Rossano, S., Lefrre, Y., Wilke, M., and Brown, G. E. B. (2005). Iron in silicate glasses a systematic analysis of PreEdge, XANES and EXAFS features. Phys. Scr. 957, 957. doi:10.1238/Physica.Topical.115a00957

CrossRef Full Text | Google Scholar

Fincham, C. J. B., and Richardson, F. D. (1954). The behaviour of sulphur in silicate and aluminate melts. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 223, 40–62. doi:10.1098/rspa.1954.0099

CrossRef Full Text | Google Scholar

Furukawa, T., Fox, K. E., and White, W. B. (1981). Raman spectroscopic investigation of the structure of silicate glasses. III. Raman intensities and structural units in sodium silicate glasses. J. Chem. Phys. 75, 3226–3237. doi:10.1063/1.442472

CrossRef Full Text | Google Scholar

Gal, Y., and Ghahramani, Z. (2016). Dropout as a bayesian approximation: Representing model uncertainty in deep learning international conference on machine learning (PMLR), 1050–1059. Available at: http://proceedings.mlr.press/v48/gal16.html (Accessed April 23, 2021).

Google Scholar

Giordano, D., Russell, J. K., and Dingwell, D. B. (2008). Viscosity of magmatic liquids: A model. Earth Planet. Sci. Lett. 271, 123–134. doi:10.1016/j.epsl.2008.03.038

CrossRef Full Text | Google Scholar

Gottsmann, J., Dingwell, D. B., and Gennaro, C. (1999). Thermal expansion of silicate liquids; direct determination using container-based dilatometry. Am. Mineralogist 84, 1176–1180. doi:10.2138/am-1999-7-821

CrossRef Full Text | Google Scholar

Hannoyer, B., Lenglet, M., Dürr, J., and Cortes, R. (1992). Spectroscopic evidence of octahedral iron (III) in soda-lime silicate glasses. J. Non-Crystalline Solids 151, 209–216. doi:10.1016/0022-3093(92)90031-E

CrossRef Full Text | Google Scholar

Herzog, F., and Zakaznova-Herzog, V. P. (2011). Quantitative Raman spectroscopy: Challenges, shortfalls, and solutions - application to calcium silicate glasses. Am. Mineralogist 96, 914–927. doi:10.2138/am.2011.3508

CrossRef Full Text | Google Scholar

Hoffman, M. D., and Gelman, A. (2014). The No-U-turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15, 1593–1623. doi:10.5555/2627435.2638586

CrossRef Full Text | Google Scholar

Huang, D., Murakami, M., Brodholt, J., McCammon, C., and Petitgirard, S. (2022). Structural evolution in a pyrolitic magma ocean under mantle conditions. Earth Planet. Sci. Lett. 584, 117473. doi:10.1016/j.epsl.2022.117473

CrossRef Full Text | Google Scholar

Jackson, W. E., Farges, F., Yeager, M., Mabrouk, P. A., Rossano, S., Waychunas, G. A., et al. (2005). Multi-spectroscopic study of Fe(II) in silicate glasses: Implications for the coordination environment of Fe(II) in silicate melts. Geochimica Cosmochimica Acta 69, 4315–4332. doi:10.1016/j.gca.2005.01.008

CrossRef Full Text | Google Scholar

Jayasuriya, K. D., O’Neill, H. St. C., Berry, A. J., and Campbell, S. J. (2004). A Mössbauer study of the oxidation state of Fe in silicate melts. Am. Mineralogist 89, 1597–1609. doi:10.2138/am-2004-11-1203

CrossRef Full Text | Google Scholar

Kalampounias, A. G., Nasikas, N. K., and Papatheodorou, G. N. (2009). Glass formation and structure in the MgSiO3–Mg2SiO4 pseudobinary system: From degraded networks to ioniclike glasses. J. Chem. Phys. 131, 114513. doi:10.1063/1.3225431

PubMed Abstract | CrossRef Full Text | Google Scholar

Karato, S., and Murthy, R. V. (1997). Core formation and chemical equilibrium in the Earth—I. Physical considerations. Phys. Earth Planet. Interiors 100, 61–79. doi:10.1016/S0031-9201(96)03232-3

CrossRef Full Text | Google Scholar

Knipping, J. L., Behrens, H., Wilke, M., Göttlicher, J., and Stabile, P. (2015). Effect of oxygen fugacity on the coordination and oxidation state of iron in alkali bearing silicate melts. Chem. Geol. 411, 143–154. doi:10.1016/j.chemgeo.2015.07.004

CrossRef Full Text | Google Scholar

Labrosse, S., Hernlund, J. W., and Coltice, N. (2007). A crystallizing dense magma ocean at the base of the Earth’s mantle. Nature 450, 866–869. doi:10.1038/nature06355

PubMed Abstract | CrossRef Full Text | Google Scholar

Landeau, M., Olson, P., Deguen, R., and Hirsh, B. H. (2016). Core merging and stratification following giant impact. Nat. Geosci. 9, 786–789. doi:10.1038/ngeo2808

CrossRef Full Text | Google Scholar

Le Losq, C., Baldoni, B., Valentine, A. P., and Neuville, D. R. (2021a). Modeling the properties of melts along calc-alkaline and alkaline magmatic differentiation trends using deep learning. in.

Google Scholar

Le Losq, C., Berry, A. J., Kendrick, M. A., Neuville, D. R., and O’Neill, H. St. C. (2019). Determination of the oxidation state of iron in Mid-Ocean Ridge basalt glasses by Raman spectroscopy. Am. Mineralogist 104, 1032–1042. doi:10.2138/am-2019-6887

CrossRef Full Text | Google Scholar

Le Losq, C., Cicconi, M. R., and Neuville, D. R. (2021b). “Iron in silicate glasses and melts,” in Magma redox geochemistry (Washington, D.C.: American Geophysical Union), 233–253. doi:10.1002/9781119473206.ch12

CrossRef Full Text | Google Scholar

Le Losq, C., Moretti, R., Oppenheimer, C., Baudelet, F., and Neuville, D. R. (2020). In situ XANES study of the influence of varying temperature and oxygen fugacity on iron oxidation state and coordination in a phonolitic melt. Contrib. Mineral. Petrol 175, 64. doi:10.1007/s00410-020-01701-4

CrossRef Full Text | Google Scholar

Le Losq, C., Mysen, B. O., and Cody, G. D. (2022). Water solution mechanism in calcium aluminosilicate glasses and melts: Insights from in and ex situ Raman and ²⁹Si NMR spectroscopy. Comptes Rendus Géoscience 354, 199–225. doi:10.5802/crgeos.127

CrossRef Full Text | Google Scholar

Le Losq, C., Valentine, A. P., Mysen, B. O., and Neuville, D. R. (2021c). Structure and properties of alkali aluminosilicate glasses and melts: Insights from deep learning. Geochimica Cosmochimica Acta 314, 27–54. doi:10.1016/j.gca.2021.08.023

CrossRef Full Text | Google Scholar

Liebske, C., Behrens, H., Holtz, F., and Lange, R. A. (2003). The influence of pressure and composition on the viscosity of andesitic melts. Geochimica Cosmochimica Acta 67, 473–485. doi:10.1016/S0016-7037(02)01139-0

CrossRef Full Text | Google Scholar

Liebske, C., Schmickler, B., Terasaki, H., Poe, B., Suzuki, A., Funakoshi, K., et al. (2005). Viscosity of peridotite liquid up to 13 GPa: Implications for magma ocean viscosities. Earth Planet. Sci. Lett. 240, 589–604. doi:10.1016/j.epsl.2005.10.004

CrossRef Full Text | Google Scholar

Liu, Q., and Lange, R. A. (2006). The partial molar volume of Fe₂O₃ in alkali silicate melts: Evidence for an average Fe³⁺ coordination number near five. Am. Mineralogist 91 (2-3), 385–393. doi:10.2138/am.2006.1902

CrossRef Full Text | Google Scholar

Mader, H. M., Llewellin, E. W., and Mueller, S. P. (2013). The rheology of two-phase magmas: A review and analysis. J. Volcanol. Geotherm. Res. 257, 135–158. doi:10.1016/j.jvolgeores.2013.02.014

CrossRef Full Text | Google Scholar

Maekawa, H., Maekawa, T., Kawamura, K., and Yokokawa, T. (1991). The structural groups of alkali silicate glasses determined from ²⁹Si MAS-NMR. J. Non-Crystalline Solids 127, 53–64. doi:10.1016/0022-3093(91)90400-Z

CrossRef Full Text | Google Scholar

Magnien, V., Neuville, D. R., Cormier, L., Mysen, B. O., Briois, V., Belin, S., et al. (2004). Kinetics of iron oxidation in silicate melts: A preliminary XANES study. Chem. Geol. 213, 253–263. doi:10.1016/j.chemgeo.2004.08.047

CrossRef Full Text | Google Scholar

Malfait, W. J. (2009). Quantitative Raman spectroscopy: Speciation of cesium silicate glasses. J. Raman Spectrosc. 40, 1895–1901. doi:10.1002/jrs.2338

CrossRef Full Text | Google Scholar

McMillan, P. F. (1984). Structural studies of silicate glasses and melts - applications and limitations of Raman spectroscopy. Am. Mineralogist 69, 622–644.

Google Scholar

McMillan, P. F., Wolf, G. H., and Poe, B. T. (1992). Vibrational spectroscopy of silicate liquids and glasses. Chem. Geol. 96, 351–366. doi:10.1016/0009-2541(92)90064-c

CrossRef Full Text | Google Scholar

Moretti, R., and Ottonello, G. (2022). “Silicate melt thermochemistry and the redox state of magmas,” in Geological melts reviews in mineralogy & geochemistry (Chantilly: Mineralogical Society of America), 339–403.

CrossRef Full Text | Google Scholar

Moretti, R. (2005). Polymerisation, basicity, oxidation state and their role in ionic modelling of silicate melts. Ann. Geophys. 48. doi:10.4401/ag-3221

CrossRef Full Text | Google Scholar

Mysen, B. O. (1995). Experimental, in situ, high-temperature studies of properties and structure of silicate melts relevant to magmatic processes. Eur. J. Mineralogy 7, 745–766. doi:10.1127/ejm/7/4/0745

CrossRef Full Text | Google Scholar

Mysen, B. O., Finger, L. W., Virgo, D., and Seifert, F. A. (1982). Curve-fitting of Raman spectra of silicate glasses. Am. Mineralogist 67, 686–695.

Google Scholar

Mysen, B. O., and Frantz, J. D. (1993). Structure of silicate melts at high temperature: In-situ measurements in the system BaO-SiO₂. Am. Mineralogist 78, 699–709.

Google Scholar

Mysen, B. O. (1996). Haploandesitic melts at magmatic temperatures: In situ, high-temperature structure and properties of melts along the join K₂Si₄O₉-K₂(KAl)₄O₉ to 1236 °C at atmospheric pressure. Geochimica Cosmochimica Acta 60, 3665–3685. doi:10.1016/0016-7037(96)00198-6

CrossRef Full Text | Google Scholar

Mysen, B. O., and Richet, P. (2019). Silicate glasses and melts. 2nd ed. Amsterdam: Elsevier.

Google Scholar

Mysen, B. O., Scarfe, C. M., and Cronin, D. J. (1985a). Viscosity and structure of iron- and aluminum-bearing calcium silicate melts at 1 atm. Am. Mineralogist 70, 487–498.

Google Scholar

Mysen, B. O., Seifert, F., and Virgo, D. (1980). Structure and redox equilibria of iron-bearing silicate melts. Am. Mineralogist 65, 867–884.

Google Scholar

Mysen, B. O. (1999). Structure and properties of magmatic liquids: From haplobasalt to haploandesite. Geochimica Cosmochimica Acta 63, 95–112. doi:10.1016/s0016-7037(98)00273-7

CrossRef Full Text | Google Scholar

Mysen, B. O. (2007). The solution behavior of H₂O in peralkaline aluminosilicate melts at high pressure with implications for properties of hydrous melts. Geochimica Cosmochimica Acta 71, 1820–1834. doi:10.1016/j.gca.2007.01.007

CrossRef Full Text | Google Scholar

Mysen, B. O. (2006). The structural behavior of ferric and ferrous iron in aluminosilicate glass near meta-aluminosilicate joins. Geochimica Cosmochimica Acta 70, 2337–2353. doi:10.1016/j.gca.2006.01.026

CrossRef Full Text | Google Scholar

Mysen, B. O., Virgo, D., Neumann, E.-R., and Seifert, F. A. (1985b). Redox equilibria and the structural states of ferric and ferrous iron in melts in the system CaO-MgO-AI₂O₃-SiO₂-Fe-O: Relationships between redox equilibria, melt structure and liquidus phase equilibria. Am. Mineralogist 70, 317–331.

Google Scholar

Mysen, B. O., Virgo, D., and Seifert, F. A. (1985). Relationships between properties and structure of aluminosilicate melts. Am. Mineralogist 70, 88–105.

Google Scholar

Neal, R. M. (2012). MCMC using Hamiltonian dynamics. arXiv:1206.1901 [physics, stat]. Available at: http://arxiv.org/abs/1206.1901 (Accessed July 24, 2018).

Google Scholar

Nesbitt, H. W., Henderson, G. S., Bancroft, G. M., and Neuville, D. R. (2021). Spectral Resolution and Raman Q³ and Q² cross sections in ∼40 mol% Na₂O glasses. Chem. Geol. 562, 120040. doi:10.1016/j.chemgeo.2020.120040

CrossRef Full Text | Google Scholar

Nesbitt, H. W., O’Shaughnessy, C., Henderson, G. S., Michael Bancroft, G., and Neuville, D. R. (2019). Factors affecting line shapes and intensities of Q³ and Q⁴ Raman bands of Cs silicate glasses. Chem. Geol. 505, 1–11. doi:10.1016/j.chemgeo.2018.12.009

CrossRef Full Text | Google Scholar

Neuville, D. R., de Ligny, D., and Henderson, G. S. (2014). “Advances in Raman spectroscopy applied to earth and material sciences,” in Reviews in mineralogy and geochemistry (Chantilly: Mineralogical Society of America), 509–541.

CrossRef Full Text | Google Scholar

Neuville, D. R. (2006). Viscosity, structure and mixing in (Ca, Na) silicate melts. Chem. Geol. 229, 28–41. doi:10.1016/j.chemgeo.2006.01.008

CrossRef Full Text | Google Scholar

O’Neill, H. St. C., Berry, A. J., McCammon, C. C., Jayasurika, K. D., Campbell, S. J., and Foran, G. (2006). An experimental determination of the effect of pressure on the Fe³+/ΣFe ratio of an anhydrous silicate melt to 3.0 GPa. Am. Mineralogist 91, 404–412. doi:10.2138/am.2005.1929

CrossRef Full Text | Google Scholar

Osipov, A., Osipova, L., and Zainullina, R. (2015). Raman spectroscopy and statistical analysis of the silicate species and group connectivity in cesium silicate glass forming system. Int. J. Spectrosc. 2015, 1–15. doi:10.1155/2015/572840

CrossRef Full Text | Google Scholar

Ottonello, G. (2005). Chemical interactions and configurational disorder in silicate melts. Annals of Geophysics. Available at: http://www.earth-prints.org/handle/2122/924 (Accessed June 27, 2016).

Google Scholar

Ottonello, G., Moretti, R., Marini, L., and Vetuschi Zuccolini, M. (2001). Oxidation state of iron in silicate glasses and melts: A thermochemical model. Chem. Geol. 174, 157–179. doi:10.1016/S0009-2541(00)00314-4

CrossRef Full Text | Google Scholar

Roskosz, M., Toplis, M. J., Neuville, D. R., and Mysen, B. O. (2008). Amorphous materials: Properties, structure, and durability: Quantification of the kinetics of iron oxidation in silicate melts using Raman spectroscopy and assessment of the role of oxygen diffusion. Am. Mineralogist 93, 1749–1759. doi:10.2138/am.2008.2861

CrossRef Full Text | Google Scholar

Rubie, D. C., Nimmo, F., and Melosh, H. J. (2007). “formation of Earth’s core,” in Treatise on geophysics. Editor G. Schubert (Amsterdam: Elsevier), 51–90. doi:10.1016/B978-044452748-6.00140-1

CrossRef Full Text | Google Scholar

Salvatier, J., Wiecki, T. V., and Fonnesbeck, C. (2016). Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2, e55. doi:10.7717/peerj-cs.55

CrossRef Full Text | Google Scholar

Sanloup, C. (2016). Density of magmas at depth. Chem. Geol. 429, 51–59. doi:10.1016/j.chemgeo.2016.03.002

CrossRef Full Text | Google Scholar

Sanloup, C., Drewitt, J. W. E., Crépisson, C., Kono, Y., Park, C., McCammon, C., et al. (2013a). Structure and density of molten fayalite at high pressure. Geochimica Cosmochimica Acta 118, 118–128. doi:10.1016/j.gca.2013.05.012

CrossRef Full Text | Google Scholar

Sanloup, C., Drewitt, J. W. E., Konôpková, Z., Dalladay-Simpson, P., Morton, D. M., Rai, N., et al. (2013b). Structural change in molten basalt at deep mantle conditions. Nature 503, 104–107. doi:10.1038/nature12668

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaefer, L., and Fegley, B. (2004). A thermodynamic model of high temperature lava vaporization on Io. Icarus 169, 216–241. doi:10.1016/j.icarus.2003.08.023

CrossRef Full Text | Google Scholar

Schramm, C. M., de Jong, B. H. W. S., and Parziale, V. E. (1984). Silicon-29 magic angle spinning NMR study on local silicon environments in amorphous and crystalline lithium silicates. J. Am. Chem. Soc. 106, 4396–4402. doi:10.1021/ja00328a018

CrossRef Full Text | Google Scholar

Seifert, F., Mysen, B. O., and Virgo, D. (1982). Three-dimensional network structure of quenched melts (glass) in the systems SiO₂-NaAlO₂, SiO₂-CaAl₂O₄ and SiO₂-MgAl₂O₄. Am. Mineralogist 67, 696–717.

Google Scholar

Sen, S., Maekawa, H., and Papatheodorou, G. N. (2009). Short-range structure of invert glasses along the pseudo-binary join MgSiO₃−Mg₂SiO₄: Results from 29Si and 25Mg MAS NMR spectroscopy. J. Phys. Chem. B 113, 15243–15248. doi:10.1021/jp9079603

PubMed Abstract | CrossRef Full Text | Google Scholar

Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 32, 751–767. doi:10.1107/S0567739476001551

CrossRef Full Text | Google Scholar

Solomatov, V. (2007). “9.04 - magma Oceans and primordial mantle differentiation,” in Treatise on geophysics. Editor G. Schubert (Amsterdam: Elsevier), 91–119. doi:10.1016/B978-044452748-6.00141-3

CrossRef Full Text | Google Scholar

Sossi, P. A., Burnham, A. D., Badro, J., Lanzirotti, A., Newville, M., and O’Neill, H. St. C. (2020). Redox state of Earth’s magma ocean and its Venus-like early atmosphere. Sci. Adv. 6, eabd1387. doi:10.1126/sciadv.abd1387

PubMed Abstract | CrossRef Full Text | Google Scholar

Spice, H., Sanloup, C., Cochain, B., de Grouchy, C., and Kono, Y. (2015). Viscosity of liquid fayalite up to 9 GPa. Geochimica Cosmochimica Acta 148, 219–227. doi:10.1016/j.gca.2014.09.022

CrossRef Full Text | Google Scholar

Spiekermann, G., Steele-MacInnis, M., Kowalski, P. M., Schmidt, C., and Jahn, S. (2013). Vibrational properties of silica species in MgO–SiO₂ glasses obtained from ab initio molecular dynamics. Chem. Geol. 346, 22–33. doi:10.1016/j.chemgeo.2012.08.020

CrossRef Full Text | Google Scholar

Tonks, W. B., and Melosh, H. J. (1993). Magma ocean formation due to giant impacts. J. Geophys. Res. 98, 5319–5333. doi:10.1029/92JE02726

CrossRef Full Text | Google Scholar

Unterborn, C., Schaefer, L., and Krijt, S. (2020). “The composition of rocky planets,” in Planetary Diversity: Rocky planet processes and their observational signatures. Editors E. J. Tasker, C. Unterborn, M. Laneuville, Y. Fujii, S. J. Desch, and H. E. Hartnett (Bristol: IOP Publishing), 5-1–5-52.

CrossRef Full Text | Google Scholar

Virgo, D., Mysen, B. O., Danckwerth, P., and Seifert, F. (1982). Speciation of Fe³⁺ in 1-atm Na₂O-SiO₂-Fe-O melts. Carnegie Institution of Washington Year Book, 349–353.

Google Scholar

Virgo, D., Mysen, B. O., and Kushiro, I. (1980). Anionic constitution of 1-atmosphere silicate melts: Implications for the structure of igneous melts. Science 208, 1371–1373. doi:10.1126/science.208.4450.1371

PubMed Abstract | CrossRef Full Text | Google Scholar

Virgo, D., and Mysen, B. O. (1985). The structural state of iron in oxidized vs. reduced glasses at 1 atm: A ⁵⁷Fe mössbauer study. Phys. Chem. Miner. 12, 65–76. doi:10.1007/BF01046829

CrossRef Full Text | Google Scholar

Wacheul, J.-B., Le Bars, M., Monteux, J., and Aurnou, J. M. (2014). Laboratory experiments on the breakup of liquid metal diapirs. Earth Planet. Sci. Lett. 403, 236–245. doi:10.1016/j.epsl.2014.06.044

CrossRef Full Text | Google Scholar

Wang, Y., Sakamaki, T., Skinner, L. B., Jing, Z., Yu, T., Kono, Y., et al. (2014). Atomistic insight into viscosity and density of silicate melts under pressure. Nat. Commun. 5, 3241. doi:10.1038/ncomms4241

PubMed Abstract | CrossRef Full Text | Google Scholar

Waychunas, G. A., Apted, M. J., and Brown, G. E. (1983). X-Ray K-edge absorption spectra of Fe minerals and model compounds: Near-edge structure. Phys. Chem. Minerals 10 (1), 1–9. doi:10.1007/bf01204319

CrossRef Full Text | Google Scholar

Wilke, M., Farges, F., Petit, P. E., Brown, G. E., and Martin, F. (2001). Oxidation state and coordination of Fe in minerals: An Fe K-XANES spectroscopic study. American Mineralogist 86 (5–6), 714–730. doi:10.2138/am-2001-5-612

CrossRef Full Text | Google Scholar

Wilke, M., Farges, F., Partzsch, G., Thunder, M., Schmidt, C., and Behrens, H. (2007). Speciation of Fe in silicate glasses and melts by in-situ XANES spectroscopy. Am. Mineralogist 92, 44–56. doi:10.2138/am.2007.1976

CrossRef Full Text | Google Scholar

Wilke, M., Partzsch, G. M., Bernhardt, R., and Lattard, D. (2004). Determination of the iron oxidation state in basaltic glasses using XANES at the K-edge. Chem. Geol. 213, 71–87. doi:10.1016/j.chemgeo.2004.08.034

CrossRef Full Text | Google Scholar

Xie, L., Yoneda, A., Katsura, T., Andrault, D., Tange, Y., and Higo, Y. (2021). Direct viscosity measurement of peridotite melt to lower-mantle conditions: A further support for a fractional magma-ocean solidification at the top of the lower mantle. Geophys. Res. Lett. 48, e2021GL094507. doi:10.1029/2021GL094507

CrossRef Full Text | Google Scholar

You, J.-L., Jiang, G.-C., Hou, H.-Y., Chen, H., Wu, Y.-Q., and Xu, K.-D. (2005). Quantum chemistry study on superstructure and Raman spectra of binary sodium silicates. J. Raman Spectrosc. 36, 237–249. doi:10.1002/jrs.1287

CrossRef Full Text | Google Scholar

Zakaznova-Herzog, V. P., Malfait, W. J., Herzog, F., and Halter, W. E. (2007). Quantitative Raman spectroscopy: Principles and application to potassium silicate glasses. J. Non-Crystalline Solids 353, 4015–4028. doi:10.1016/j.jnoncrysol.2007.06.033

CrossRef Full Text | Google Scholar

Zhang, H. L., Cottrell, E., Solheid, P. A., Kelley, K. A., and Hirschmann, M. M. (2018). Determination of Fe³⁺/ΣFe of XANES basaltic glass standards by Mössbauer spectroscopy and its application to the oxidation state of iron in MORB. Chem. Geol. 479, 166–175. doi:10.1016/j.chemgeo.2018.01.006

CrossRef Full Text | Google Scholar

Zhang, H. L., Hirschmann, M. M., Cottrell, E., and Withers, A. C. (2017). Effect of pressure on Fe³⁺/ΣFe ratio in a mafic magma and consequences for magma ocean redox gradients. Geochimica Cosmochimica Acta 204, 83–103. doi:10.1016/j.gca.2017.01.023

CrossRef Full Text | Google Scholar

Zotov, N., Ebbsjö, I., Timpel, D., and Keppler, H. (1999). Calculation of Raman spectra and vibrational properties of silicate glasses: Comparison between Na₂Si₄O₉ and SiO₂ glasses. Phys. Rev. B 60, 6383–6397. doi:10.1103/physrevb.60.6383

CrossRef Full Text | Google Scholar