3D seismic simulation analysis of the Longtoushan Town Basin during the 2014 Ludian earthquake, Yunnan province

On 3 August 2014, a magnitude Ms 6.5 earthquake struck Ludian County, Zhaotong City, Yunnan Province, causing grave losses of life and property in the Longtoushan Town Basin near the fault. In this study, a three-dimensional model of the Longtoushan Town Basin and the velocity structure of the surrounding area, and the Spectral Elements in Elastic Dynamics code, which combines the discontinuous Galerkin technique and the spectral element method (SEM) are used to simulate and study the entire seismic wave propagation process. The results show that due to the variations in the basin geometry and the impedance ratio of the media inside and outside the basin, the seismic waves incident on the basin edge are refracted and diffracted, further prolonging the ground motion holding time within the basin. In the bedrock outside the basin, the velocity peaks are higher at higher elevations; viceversa within the basin, the locally depressed basement produces an obvious amplification effect. The amplitude of the ground motion is not the greatest in the thickest sedimentary layers in the basin, and it is closely related to the degree of undulation at the base of the sedimentary layers, the overburden thickness, and the basin geometry. The peak ground accelerations (PGAs) of approximately 8 m/s² in the east–west (E–W) direction and 3 m/s2 in the north–south (N–S) direction are influenced by the rupture directivity effect (the ruptured surface is the Baogunao–Xiaohe fault that is oriented in the N–W direction). The peak ground velocity with a sedimentary model is 2.6 and 1.6 times that of the non-sedimentary model in the E–W and N–S directions, respectively. The maximum amplification factor for PGA in the E–W direction is 2.8 and that in the N–S direction is approximately 2.3. The results are in agreement with the actual observed seismic station data in terms of the waveforms and peaks, and the intensity distribution map matches the actual damage distribution. This proves the accuracy and rationality of the method used in this study. The results are useful for the seismic zoning of cities, and they can help engineers predict ground motions for future large earthquakes.

1 Introduction

Numerous cities around the world are located in basins, such as Los Angeles Olsen (2000); Komatitsch et al. (2004), Osaka Pitarka et al. (1998), Taipei Lee et al. (2008), Chengdu Yu (2017), and Xi’an Ren et al. (2013). Therefore, the study of basin effects is an active topic of interest for seismologists and engineers. For example, during the 2008 Wenchuan earthquake, a VII degree intensity anomaly zone (with a VI degree surrounding intensity) was observed in the Baoji–Meixian region, which is located at the edge of the Weihe Basin, and a VI degree anomaly zone within a V degree zone was observed in Xi’an in the interior of the basin (Parsons et al., 2008; Li et al., 2016). On 3 August 2014, a magnitude Ms 6.5 earthquake occurred in Ludian County, Zhaotong City, Yunnan Province, with an epicenter at 27.1° N, 103.3° E and a depth of 12 km (according to the China Earthquake Administration). Although the earthquake was not a mega-quake, the Longtoushan Township Basin, Ludian County, which is located near the epicenter, suffered severe damage, with an intensity reaching IX degrees (Zhang Y. et al., 2014; Lin et al., 2020). The earthquake counts 617 deaths, 112 missing people, 3,143 injured, and its direct economic loss was about 3.46 billion dollars (Li et al., 2016). Most of the buildings in Longtoushan Town were seriously damaged or collapsed due to the strong earthquake. The experts analyzing the damage of Longtoushan Town observed obvious differences in the degree of earthquake damage between two adjacent areas (Lin et al., 2020). Thus, the propagation process and distribution pattern of the ground vibrations within the basin under the effect of earthquake need to be systematically researched and analyzed, which helps in the seismic zoning of cities and the seismic design of structures.

For the Ms 6.5 magnitude earthquake in Ludian County, Zhaotong City, Yunnan Province, that occurred on 3 August 2014, Liu (2021) developed a two-dimensional (2D) basin model of the Longtou Mountain present in this region based on borehole and topographic data. They analyzed the site amplification effect under the action of SV waves (a shear wave that is polarized so that its direction of propagation and particle motion occur in a vertical plane) using the explicit finite element method. However, several previous studies have shown that 2D models do not represent the magnitude and duration of ground shaking in three-dimensional (3D) models. Horike et al. (1990) compared the differences in the amplification effect of ground shaking between 3D and 2D basins and found that the 2D model does not represent the magnitude and duration of the ground shaking in the 3D model. Toshinawa and Ohmachi (1992) used a 3D finite element method to simulate the propagation of Love waves in the Kanto Basin, Japan. They determined that the 3D model yields a larger amplitude and longer duration of ground shaking than the 2D model, and the simulation results obtained by the 3D model were closer to the observed record than those obtained by the 2D model. Ohori et al. (1990) compared the differences between a 3D resonance model and one-dimensional (1D) and 2D resonance models and found that the resonance amplification factors and resonance frequencies were greater in the 3D model than those in the 1D and 2D models. In addition, they found that the 3D basin structures have a significant effect on the ground shaking. Compared to the 2D model, the irregular 3D basin comprises the same edge, focusing, and resonance effects as in the 2D basin, and the 3D basin makes the internal propagation of body and surface waves more complex. Therefore, this study performs a 3D ground motion simulation analysis of the Longtoushan Town Basin after the 2014 Ludian earthquake in the Yunnan region.

The main techniques for studying the seismic effects in the basins are analytical methods, ground vibration observation methods, and numerical simulation methods. Analytical methods are only applicable to regularly shaped basins, wherein the media inside and outside the basin are single or layered linear elastic media. The analytical solutions of 2D sedimentary basins under seismic wave incidence have been relatively well studied (Trifunac, 1971; Wong and Trifunac, 1974; Bard and Bouchon, 1980a; 1980b; Todorovska and Lee, 1990; Yuan and Liao, 1995; Paudyal et al., 2012). Since the real site conditions are complex and the topography is often irregular, obtaining an analytical solution to the corresponding problem is difficult, and thus, the problem is usually solved using numerical analysis. The seismic observation method employs a dense seismic record within the basin, which already considers the influence of the media and site conditions within the basin, making the results highly accurate (Frankel, 1993; Wen and Peng, 1998; Cornou et al., 2003a; 2003b). However, this method has several disadvantages. First, it is computation expensive and requires an intensive seismic record of the basin; thus, the current seismic network is only used for some basins in earthquake-prone areas. Second, it requests high-quality seismic data, e.g., the record cannot contain significant ambient background noise. Third, the number of seismic records obtained is limited; therefore, the method is still under development.

The main numerical simulation methods are the finite element method (Bao et al., 1998), the finite difference method (Olsen and Schuster, 1995; Graves et al., 1998; Lee et al., 2008), the boundary element method (Lee, 2013; Semblat et al., 2022; Huang et al., 2022), and the Spectral Element Method (SEM) (Smerzini and Villani, 2012; Liu et al., 2013; Abraham et al., 2016; Vijaya et al., 2020). Finite difference methods are prone to numerical dispersion near large gradients in the wavefield or when the used grid is too coarse. Thus, they do not achieve the same accuracy when imposing free boundary conditions on the surface cells as that in the inner region. Furthermore, they are only applicable to simple geometrical changes and may affect the calculation stability when a deformed grid is used. The finite element method is based on the variational form of the wave equation. It naturally introduces the free boundary conditions and is suitable for describing complex media with arbitrary shapes but usually has significant numerical dispersion properties, with pseudo-waves appearing in higher-order conventional finite elements. The boundary element method is based on the integral expressions for quantities associated with the physical boundaries and can accurately model the propagation of outgoing waves on the boundary. However, it is often restricted to linear and homogeneous problems and may yield solutions that are not unique. SEM, which was introduced by Patera (1984) for computational fluid dynamics, combines the spectral method with the finite unit method, taking advantage of the fast convergence of the spectral method and the flexibility of the finite unit method. SEM can well adapt to complex terrains and can accurately model surface waves. Hence, it has been increasingly used in recent years for simulating the seismic responses in basins.

Lee et al. (2009) used SEM to simulate the strong ground motion in the Taipei Basin and investigated the interaction between mountains and sedimentary basins as well as the effects of the earthquake source location, depth, and rupture processes on the distribution of the ground motion in the basin. Stupazzini et al. (2009) used a high-performance SEM program to simulate the seismic response of a near-fault earthquake in the Glenoble Valley, France. Hu et al. (2011) employed SEM to simulate the topographic effects of the Wenchuan earthquake that occurred on 12 May 2008. Liu et al. (2013) investigated the amplification effect of seismic wave propagation in the Shidian Basin using SEM. Liu et al. (2017) studied the effects of the wave velocity and dip angle of soil layers under the action of strike–slip faults on the seismic amplification effect of sedimentary basins as well as the seismic response of 3D sedimentary basins under the action of point sources. Yu (2017) used high-precision parallel SEM to better understand the seismic effects in the Shidian Basin and Sichuan Basin.

However, this method has some limitations that need to be addressed, such as the complexity of the geometric constraints and dealing with complex 3D non-homogeneous media while keeping the computational cost low. The Politecnico di Milano, Italy, developed the numerical Spectral Elements in Elastic Dynamics (SPEED) code (http://mox.polimi.it/it/progetti/speed). This code combines non-coherent discretization methods, discontinuous Galerkin (DG) techniques, and SEM and can handle non-uniform polynomial distributions (N-Adaptive) and locally varying grid sizes (h-Adaptive). SPEED is a numerical code for simulating both linear and non-linear elastodynamic problems in heterogeneous media based on the Spectral Elements (SE) decomposition technique, allowing for non-conforming meshes through a DG approach (Mazzieri et al., 2013).

In this study, the SPEED code is used to simulate the entire seismic wave propagation process that occurred in the Longtoushan Town Basin during the 2014 Ludian earthquake. This basin is narrow and has a width of approximately 3.1 km from the north to south and a length of 2.8 km from the east to west. We investigate the generation and propagation of the seismic waves and we analysed the differences in the ground motion at different locations in the basin and the effect of the topographic reliefs. The correctness and rationality of the study results are verified by comparing them with the observed data from seismic stations and the observed distribution of the damage to buildings caused by the earthquake.

2 Geological framework

As shown in Figure 1, the epicenter of the 2014 Ludian earthquake was located southwest of the Ludian County, and it was along the Lianfengshan fault in the NE direction and the Zhaotong, Zemuhe, Xiaojiang, Anning, and Yuanmou–Lujuijiang faults in the NS direction. The Zhaotong–Ludian fault begins from the west of Yiliang Niujie in the NE and ends SW of the Niulan River after passing through Zhaotong and Ludian. The total length of the Zhaotong–Ludian fault is about 160 km, the overall strike is 30°, the rake direction is southeast, and the dip is 60°–80°(USGS; Zhang et al., 2014). According to the solution of the main seismic source mechanism, aftershock spatial distribution, regional geological structure, seismic intensity, strong ground motion record, and other data, the seismic fault of this earthquake is determined to be NNW to Baogunao–Xiaohe fault, which is the NW secondary slipping fault that is NE to the Zhaotong–Ludian fault system; all the faults belong to the Xiaojiang fault system (USGS; Zhang Z. G. et al., 2014; Li et al., 2015; Zhao and Sun, 2014; Xu et al., 2014; Li and Li, 2016). The Baogunao–Xiaohe fault is a Holocene fault; no earthquake with M ≥ 5.0 has been recorded in its history, and the largest earthquake recorded of this fault and its major fault system was the Ludian earthquake with Ms 4.4 that occurred on 6 August 1989.

FIGURE 1

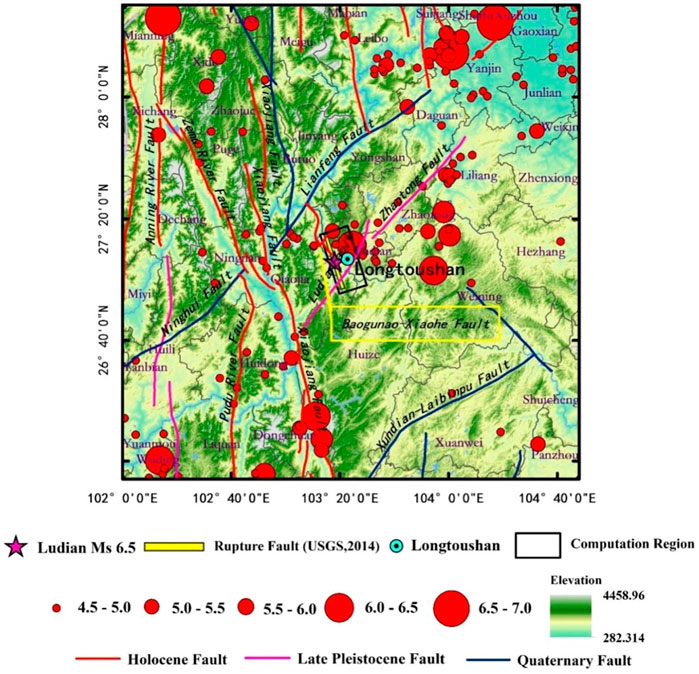
FIGURE 1. Seismogenic structure and historical seismicity around the M6.5 Ludian earthquake. The pink star and the yellow rectangular with black border outline the epicenter and projection of the rupture fault of this earthquake provided by the USGS, respectively. The area within the black rectangular is the study area. Red circles of different sizes represent historical earthquakes of different magnitudes. The red, pink, and blue lines represent Holocene, Late Pleistocene, and Quaternary faults, respectively.

3 Source model of the Ms 6.5 2014 Ludian-Longtoushan Basin earthquake

The coverage area of the present research is shown in detail in Figure 2. The elevation data for the sedimentary layer in the basin were obtained from observed data, including the geological cloud (https://geocloud.cgs.gov.cn/), boreholes in the basin, resistivity profile inversion along the measuring lines (Pang et al., 2016), and a safety evaluation report. The basin model was set to comprise of single depositional layer. The S- and P-wave velocities in the basin were 450 and 814.5 m/s, respectively, and the quality factors Q_S and Q_P were 45 and 82, respectively (Liu et al., 2013). The CRUST1.0 (https://blog.seisman.info/crust1/) model based on the global velocity structure model is used as the calculation parameter in the velocity medium model outside the basin. The model parameters are presented in Table 1.

FIGURE 2

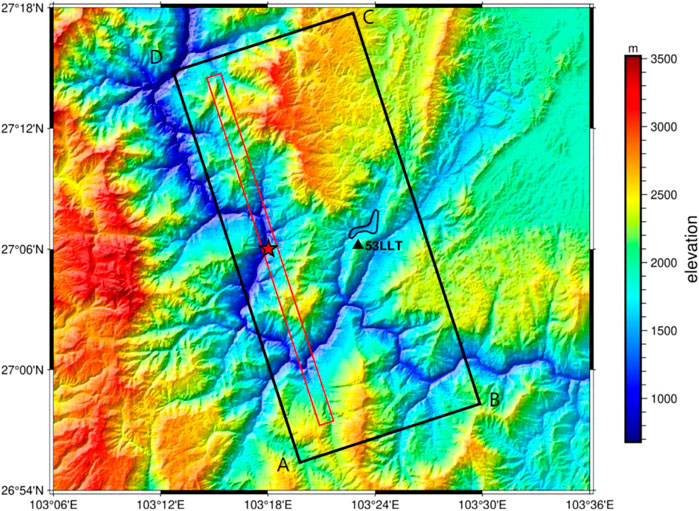
FIGURE 2. Map displaying the source location of the M6.5 Ludian earthquake. The area within the black rectangular outline is the study area. The red rectangular outline is the projection of the rupture fault location of the Ludian earthquake in Yunnan provided by the USGS. The red star denotes the epicenter location provided by the USGS. The black outline denotes the location of the Longtoushan town.

TABLE 1

TABLE 1. Medium parameters used in the simulation.

We simulate the Ms 6.5 earthquake occurred on 3 August 2014 in Ludian County where the source is located on the west side of the basin and at 12 km-depth. The source time function is obtained from the inversion results (Zhang Y. et al., 2014), and the rise time was 0.2 s with a total source duration of about 10.7 s (Figure 3A).

FIGURE 3

FIGURE 3. Source model of the Ms 6.5 2014 Ludian earthquake. (A) Ludian source time function obtained through inversion by Zhang Z. G et al. (2014). (B) Slip distribution of Ludian earthquake obtained by Hao et al. (2014).

Following this earthquake, many researchers utilized different data and methods to invert a series of source rupture models. In this study, Hao’s dislocation model (Hao et al., 2014) is used. It was built based on the near-field ground motion stations, and the rupture process of the earthquake is obtained using the data from this model. Source mechanism solutions are based on the United States Geological Survey (USGS) data (strike, dip, and rake of the nodal plane are 162°, 86°, and 6°, respectively; the second strike, dip, and rake of the nodal plane are 72°, 84°, and 176°, respectively). Herein, the fault style is set as a normal fault. It is 50 km long along the strike direction and 25 km wide along the dip direction. The grid points in the fault profile of the model are taken as the sub-source points and are transformed into second-order spectral element points, and the corresponding seismic moments are applied to each sub-source point. Additionally, the rake is taken to 6°. The epicenter of the earthquake was located at 27.1° N, 103.3° E, and the slip distribution on the fault plane is shown in Figure 3B (Hao et al., 2014).

Figure 3B shows that the fault has a major slip area, which is represented by the red area on the fault plane, with a maximum slip of 26 cm. For the Ludian earthquake, a constant rupture speed of 2.1 km/s is assumed. Then, according to the relative positions of the source and the initial rupture point, the rupture time of each sub-source is defined.

The corresponding slip is assigned to each point according to Figure 3B, and the magnitude of the seismic moment corresponding to each point is obtained according to the shear modulus of the medium for simulating the dislocation of the whole fault. The seismic moment and shear modulus are calculated as follows:

$M=S\bullet G\bullet A$

$G=v_s^2\bullet \rho$

where M (N·m) is the seismic moment, S (m) is the slip, G is the shear modulus of the soil, A (m²) is the control area at each point, vs. (m/s) is the shear wave velocity of the layer, and $\rho$ (kg/m³) is the density of the medium.

4 Calculation method

The open-source spectral element program SPEED (http://mox.polimi.it/it/progetti/speed) is used to simulate the seismic effect of the Ludian earthquake in the Longtoushan Basin. SEM aims to divide the computational range into finite elements and to configure non-uniformly distributed nodes (Legendre–Gauss–Lobatto points, LGL points) on each element. The approximate solution of the element is expressed as the corresponding truncated orthogonal polynomial, and the Galerkin method is used to solve for the approximate global solution. The main difference method or the Newmark predictor calibration is usually adopted as the time integration scheme (Mazzieri et al., 2013).

The model used herein considers the influence of the 3D terrain (Figure 4A). The regional grid size in the basin is set as 80 m, and the regional grid outside the basin is set as 200–500 m (Figure 4B). To ensure the continuity of the deformation, discontinuous contact surfaces are set between soil layers 1 and 2 and between soil layers 2 and 3. As is shown in Figures 4C, D, the number of grids is greatly reduced using this method, which consequently improves the calculation efficiency. This model comprises 312995 units and 347286 nodes. Absorbing boundary conditions are applied on five boundary surfaces, except the ground surface. In each SE, a polynomial degree N = 2 is used, and thus each element contains (N + 1)³ = 27 LGL integration points. According to the accuracy requirement of spectral element method which contains at least five grid points in the shortest wavelength, and the LGL integration points for the elements at the surface of the basin were about 80 m, so the shortest wavelength is hence equal to about 320 m, which is sufficiently small to accurately model the softest sediments within the plain up to a maximum frequency of about 1.125 Hz (Komatitsch and Tromp, 1999).

FIGURE 4

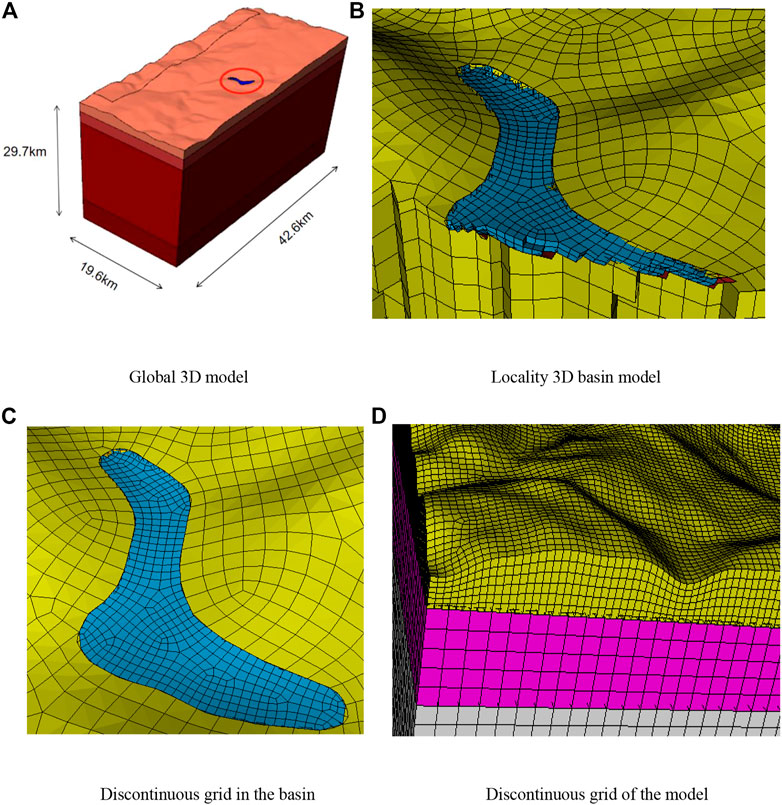
FIGURE 4. 3D computational model of the 2014 M6.5 Ludian–Longtoushan Basin earthquake. (A) Global 3D model. (B) Locality 3D basin model. (C,D) Discontinuous grid in the basin.

The calculation area is divided into five blocks, and the multi-node parallel computing technology based on the Linux system is adopted. The time step is 0.001 s, and the simulation time is 60 s; the total calculation time is about 38 h.

5 Results and discussion

In this section, the calculation results of the wavefield snapshots, time profiles, peak distributions, and amplification coefficients are analyzed to investigate the seismic effects of the Longtoushan Town Basin and its surrounding bedrock sections.

5.1 Wavefield snapshot

A snapshot of the velocity wavefield in the east–west (E–W) direction in the computed area is shown in Figure 5, which displays the propagation of the seismic waves at the surface. At around t = 1–1.7 s, the seismic waves excited by the fault dislocation spread outwards, and the P-waves propagating outwards from the epicenter are roughly elliptical. During this time, the vibrations in the basin are relatively weak, and no significant surface wave generation is observed. At t = 2.4 s, the S-wave reaches the basin. At t = 4.8–6.3 s, the amplitude of the ground shaking within the basin becomes significantly larger than that in the outer bedrock areas due to the presence of low-wave-velocity sedimentary layers. In addition, due to the low wave velocity of the media in the basin, simultaneous arrivals of waves from multiple source points occur in the sedimentary depression region of the Longtoushan Town Basin. They superimpose and interfere in this area, resulting in elevated ground shaking amplitudes and significant delay and bending of the S-wave front. At around t = 7.3–8.7 s, the body wave largely passes through the basin, but most of the fluctuating energy is captured in the basin. At this time, surface waves with large amplitudes are generated and they propagate after the body waves; when they encounter the opposite edge of the basin, some of the surface waves are reflected again into the basin. At around t = 13.5 s, the ground shaking response outside the basin largely dissipates and some residual surface waves remain scattered within the basin, which further prolongs the ground shaking holding time within the basin. This phenomenon indicates that the response time of the seismic waves in the low-velocity basin is greater than that in the surrounding bedrock section, reflecting the strong wake phenomenon of the seismic waves in the low-velocity region.

FIGURE 5

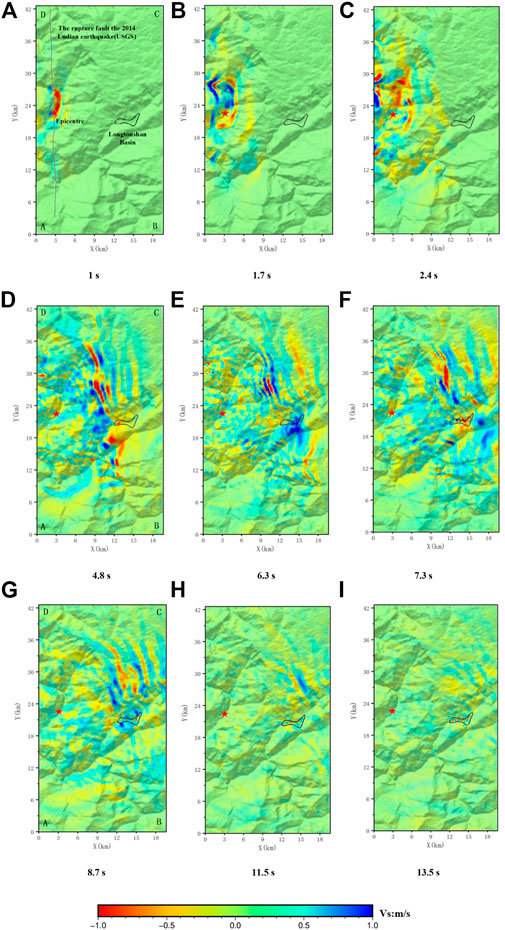
FIGURE 5. Wave field snapshots of east–west components of the surface ground motion. The black outline denotes the basin. The red star and gray line denote the epicenter and rupture fault of this earthquake provided by the USGS, respectively. (A) 1 s; (B) 1.7 s; (C) 2.4 s; (D) 4.8 s; (E) 6.3 s; (F) 7.3 s; (G) 8.7 s; (H) 11.5 s; (I) 13.5 s.

The snapshot of the wave field (Figure 5) shows that because the basin contains sedimentary layer with low wave velocity, the complex seismic waves radiated by the fault during rupture are captured in the basin and are superimposed in certain areas within the basin. This leads to an interference phase length phenomenon, which increases the duration of the seismic waves in the basin. Due to the above phenomenon and the fact that the basin is along the propagation direction of the wave front generated by the fault movement, the ground shaking is stronger in some areas of the basin.

5.2 Time history analysis

Figure 6 displays the outline of Longtoushan Town and six typical profiles. Profiles A–A′, B–B′, C–C′, and F–F′ trend E–W, while profiles D–D′ and E–E’ trend north–south (N–S). Each profile runs through the basin, and for each profile, both the bedrock surface outside the basin and the interior of the basin can be seen. The relief within the Longtoushan Basin is relatively gentle, with surface elevations ranging from 1,550 to 1800 m. In this study, the response pattern of the basin is analyzed under the effect of ground shaking by studying the elevation changes on the profiles and the vibration time range and peak ground velocity (PGV) changes at the selected points on each profile.

FIGURE 6

FIGURE 6. Location of the basin and locations of the selected profiles in the basin.

The topography of the basin floor, the E–W component velocity timescales, and their peak velocities corresponding to the selected points on all six profiles are shown in Figure 7. The amplification of the ground shaking by the basin and the longer duration of the shaking within the basin than that outside the basin are observed for all the profiles; that is, the amplitude of the velocity timescale within the basin is much greater than that outside the basin. In the bedrock section outside the basin, the profiles exhibit some differences. In profiles A–A′ and B–B′, the western part of the basin has lower elevation than the eastern part; thus, the peak bedrock velocity in the west is significantly lower than that in the east. The peak velocities in the bedrock outside the basin range from approximately 15–40 cm/s, and the durations are approximately 10 s. The peak velocities in the soil within the basin range from 40 to 80 cm/s, and durations are approximately 20 s. The six profiles are analyzed in more detail below.

FIGURE 7

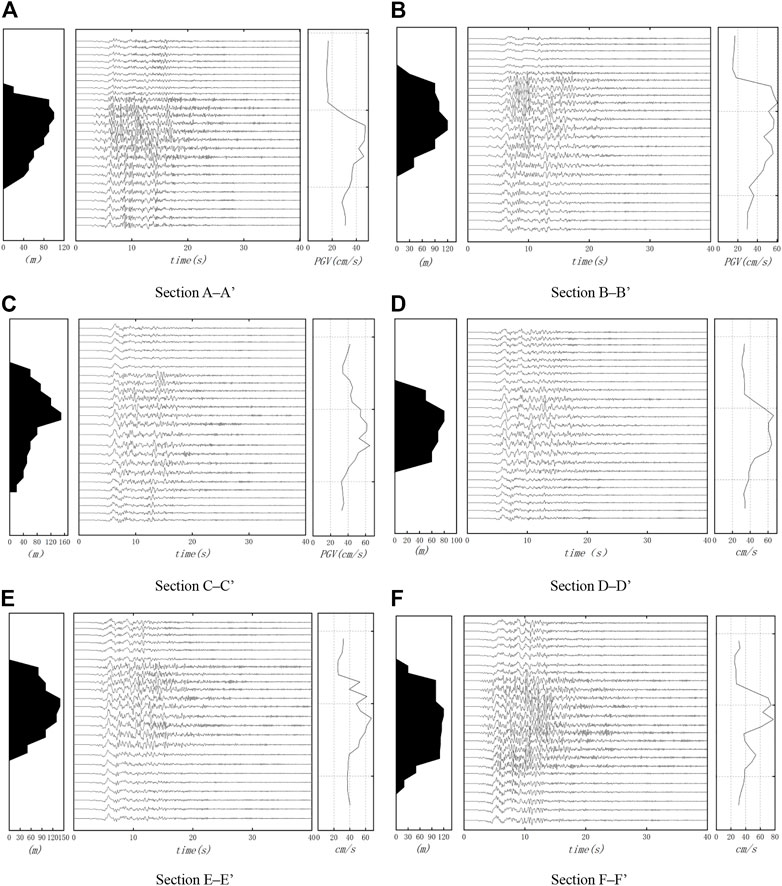
FIGURE 7. Ground motion time history. Thickness of the deposit (left, black area) corresponding to the observation points on sections A–A′ to F–F′, velocity time histories at the observation points (middle), and the PGV at the surface of each section (right). (A) Section A–A’; (B) Section B–B’ (C) Section C–C’; (D) Section D–D’; (E) Section E–E’; (F) Section F–F’.

Profiles A–A′ and B–B′ are located in the northern part of Longtoushan Town, and the surface elevation map shows that the ground surface comprises depressions. In profile A–A′, the maximum thickness of the sediment layer is approximately 150 m; in profile B-B′, it is approximately 200 m. The velocity curves of both profiles have large amplitudes at the location of the lowest point in the depression. In this area, the waveform dramatically changes, and the peak velocity is roughly 2.5 times that of the surrounding bedrock. The peak velocities in profile A–A′ show that in the bedrock section, the peak velocity is small (approximately 20 cm/s) and the amplitude and waveform little vary. After the seismic waves enter the depression, the seismic intensity gradually increases, with a maximum value of 56 cm/s at approximately the center of the depression. Then, the amplitude decreases, and the amplitude of profile A–A′ is slightly smaller than that of profile B–B′. This may be because the thickness of the deposit in profile B–B′ is larger than that in profile A–A′, with more surface wave development, and the waves reflected from the basin are more likely to be superimposed at this location. It is speculated that the depressed substrate converges the seismic waves at a central location, resulting in a more intense seismic response.

Profile C–C′ is located in the deepest part of the Longtoushan Town Basin and cuts diagonally through several important buildings, such as the Longtoushan Township police station, and through the center of the basin, where the sediments are the thickest. Figure 7 shows that the bottom of the depression in profile C–C′ is relatively smooth, and the velocity–time plot shows that the change of the peak velocity is relatively gentle in the profile, with a peak velocity of 60 cm/s. Due to the low wave velocity of the media in the basin, the arrival of the body waves in the basin lags behind that outside the basin. The ground shaking on the profile is similar in the central part but is smaller at the edges, and the amplitude and duration are not very different. Figure 7 also shows that the peak velocity of profile C–C′ is smaller than that of profile F–F′, which is most likely due to the large width-to-thickness ratio in this region. This causes the surface waves to take longer time to propagate to the middle of the basin and makes them difficult to superimpose. Furthermore, the effect of the basin edge is relatively weak in this area. This phenomenon suggests that the response to ground shaking is not necessarily the greatest in the basin areas with thick sedimentary layer and that the magnitude of the response to ground shaking is closely related to the surrounding topography, the overburden thickness, and the basin shape.

Profiles D–D′ and E–E′ are located in the central part of the Longtoushan Town Basin in a narrow zone between mountains (Figure 6). The two profiles are similar in shape, and the sedimentary layer in profile E–E′ is somewhat thicker than that in profile D–D′; thus, the peak velocity of profile D–D′ is slightly larger. The waveforms show that the velocity peaks in both profiles (D–D′, E–E′) are greater than those in profiles A–A′ and B–B′. This is because the two profiles are located between the two boundaries of the basin, with a narrow N–S extent, and the surface waves propagate back and forth within the basin, with significant basin edge effects.

Profile F–F′ is located in the southernmost part of Longtoushan Town, and the variations in the base of the sediment layer in this profile are greater than those in the other profiles. Moreover, the peak velocity of this profile is greater than that of the other five profiles, with a maximum PGV of approximately 80 cm/s. This is probably due to the narrow of the overlying strata in this profile and the complex undulation of the base of the overburden, which leads to a basin-focusing effect. In addition, the profile is located at the edge of the basin and close to the seismogenic fault. The direct body waves and the surface waves propagating within the basin as well as the waves from outside the basin that enter via the edge of the basin overlap, resulting in a strong interference phenomenon, thus significantly amplifying some vibration frequencies and exhibiting the edge effect of the basin.

5.3 PGA distribution

Figure 8 shows the peak ground acceleration (PGA) distribution in three directions, E–W, N–S, and vertical (U–D), for the terrain in and around Longtoushan Town, Ludian County, Yunnan Province, during of the earthquake.

FIGURE 8

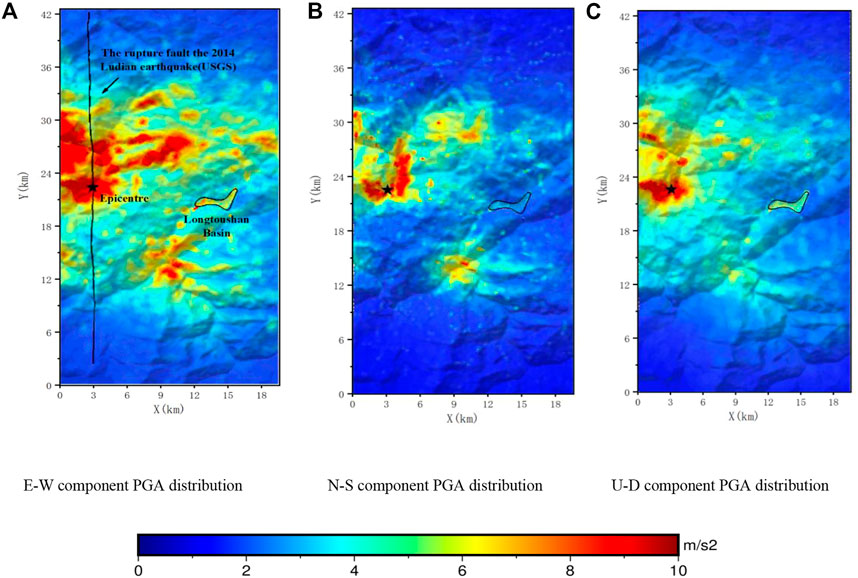
FIGURE 8. PGA distribution of the model. The black star and black line denote the epicenter and rupture fault of this earthquake provided by the USGS, respectively. (A) E-W component PGA distribution. (B) N-S component PGA distribution. (C) U-D component PGA distribution.

Figure 8 shows that the PGA distribution is influenced by the direction of the seismic wave propagation. The PGA distribution is related to the propagation of the wave front in Figure 5, which shows that the wave front passes with larger PGA values are located near the fault surface, within the basin area, and in the hilltop location. The waves within the basin are amplified compared to those in the surrounding bedrock, which is consistent with the observed record.

In the E–W direction, the areas with large PGA values within the basin are concentrated in the southern part of the basin, around profile F–F′, with values of approximately 8 m/s². This is caused by the trapping effect of the depressions on the seismic wave energy and the interference among the seismic waves reflected from the basin boundary in different directions, both of which can cause sustained ground shaking with large magnitudes.

The ground shaking in the basin is less intense in the N–S direction than that in the other two directions, and the overall PGA distribution in the basin exhibits a similar pattern. As shown in Figure 8, the PGA in the part of the basin with the deepest cover (157 m) is approximately 2.1 m/s2, which is smaller than that in the other areas (for example, 110 m in F-F′) of the basin. This is mainly because comparing this area with the other areas, the bottom of the depression is flatter, and the secondary surface waves generated are weaker and do not have a significant focusing effect.

In the U–D direction, the average PGA in the basin is approximately 6 m/s², which is approximately three times that of the surrounding bedrock.

5.4 PGV distribution

The ground motion velocity is related to the kinetic energy of particle vibration and is often used as a physical quantity to measure the ground motion energy Bao et al. (1998). The shear wave impedance between the basin and bedrock determines the amount of incident wave energy that can pass through the basin–bedrock interface, which affects the generation of secondary surface waves in the basin. Figure 9 presents a model containing a sedimentary basin and a model with bedrock only. The distributions of the PGVs E–W, N–S, and U–D components in the calculated area that are obtained via simulation using these two models are used to study the influence of the sedimentary basin in the area affected by seismic activity. The simulations using different models exhibit the same trends of the ground shaking distributions, but the differences in the distribution of the ground shaking in the basin are greater than outside the basin.

FIGURE 9

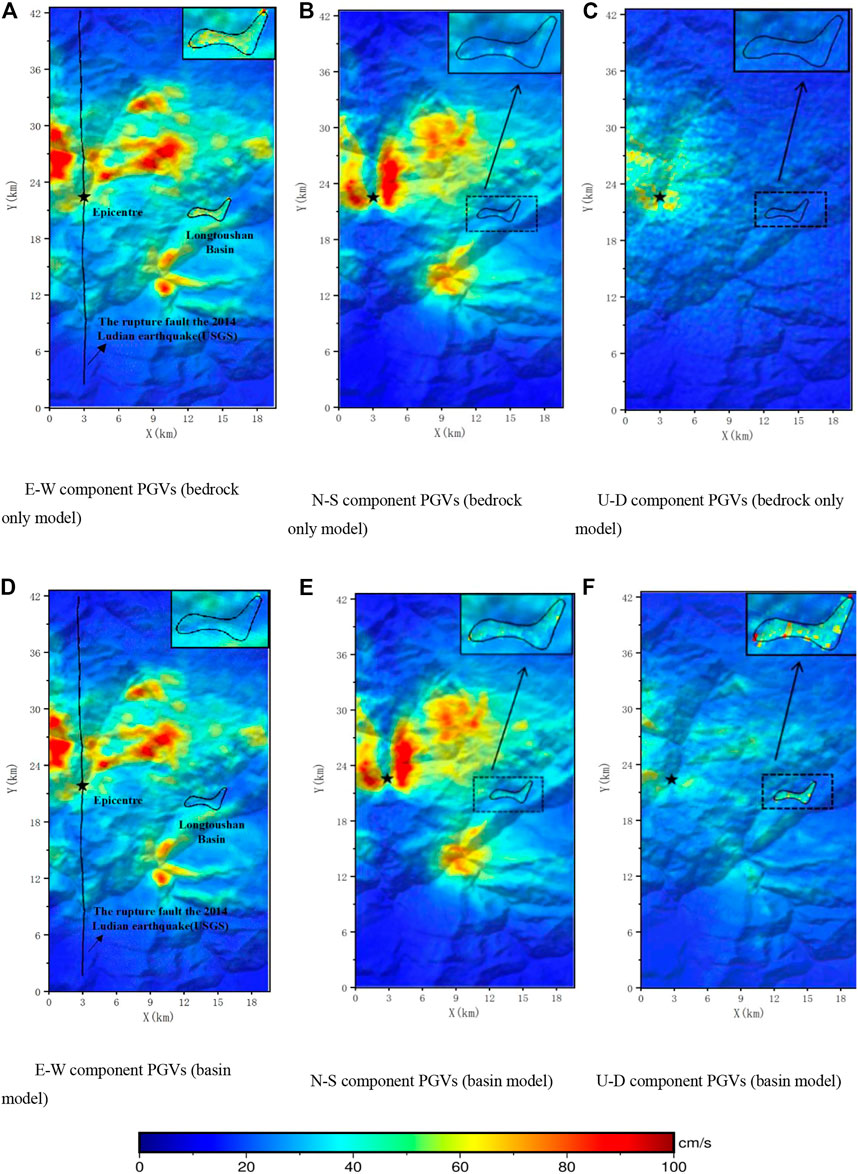
FIGURE 9. PGV (m/s) distribution of E–W, N–S, and U-D components obtained using different models. The black star and black line denote the epicenter and rupture fault of this earthquake provided by the USGS, respectively. (A) E-W component PGVs (bedrock only model). (B) N-S component PGVs (bedrock only model). (C) U-D component PGVs (bedrock only model). (D) E-W component PGVs (basin model). (E) N-S component PGVs (basin model). (F) U-D component PGVs (basin model).

In the E–W direction, the peak velocity is approximately 25 cm/s for the bedrock model and 65 cm/s for the basin model. In the N–S direction, the amplitude of the ground shaking in the basin area is approximately 35 cm/s for the bedrock model and 57 cm/s for the basin model. In the U–D direction, the peak velocity is about 18 cm/s for the bedrock model and about 73 cm/s for the basin model.

The results show that the Longtoushan Town Basin significantly influences the distribution of the ground shaking in the E–W and U–D directions. The N–S component is less influenced by the sedimentary layers than the E–W component. The peaks of the seismograms are also high in some areas at the edge of the basin, reflecting the basin edge effect.

5.5 Magnification factor

In order to reflect the amplification of the sedimentary basin, the amplification factor of the basin is defined as the ratio of the PGA simulated using the model containing the basin to the PGA simulated using the model without the basin. Figure 10 illustrates the distribution of the amplification factors for the three PGA components in the Longtoushan Basin. For the E–W component, the areas with larger amplification factors are mainly located in the deeper areas of the basin and the smaller amplification factors are mainly located at the edge of the basin, and the largest amplification coefficient is 2.8, which is located near profile F–F. For the N–S component, the maximum amplification factor is approximately 2.3, which is located at the edge of the basin. For the U–D component, the maximum amplification factor is 2.18, which is smaller than those of the other two components. The amplification effect of the basin mainly stems from two aspects: the influence of the basin geometry and the influence of the difference in the wave impedances of the media inside and outside the basin.

FIGURE 10

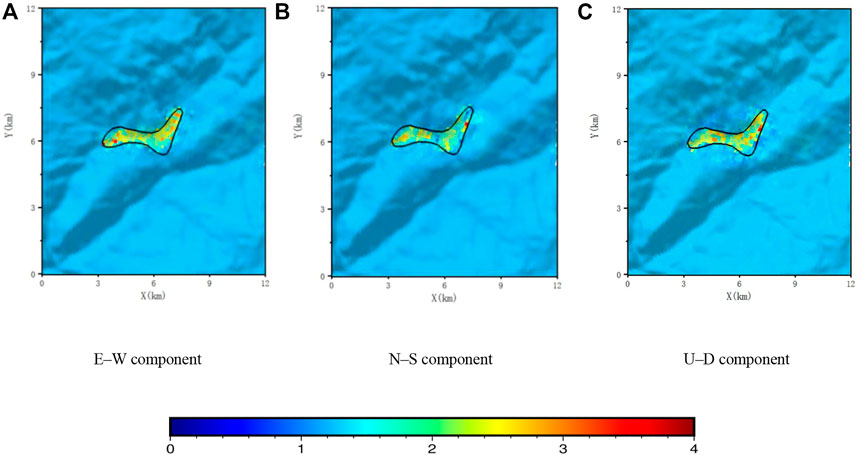
FIGURE 10. Distribution of the amplification factors of PGA (E–W, N–S, and U–D components) in the Longtoushan Town basin model compared with the bedrock site model without the basin. (A) E–W component. (B) N–S component. (C) U–D component.

6 Validation

6.1 Comparison between simulated time history and observed records

During the strong ground Ludian motions in 2014, strong earthquakes were recorded at stations in the China Strong-Motion Networks Center, which provide a reference for validating the correctness of the simulation results. The site records are used for comparison: 53LLT (27.1°N, 103.4°E) is located about 1 km from the basin and is the only station in the calculation range of this study (Figure 2). The calculation accuracy is verified by the acceleration curve and acceleration response spectrum (Figure 11).

FIGURE 11

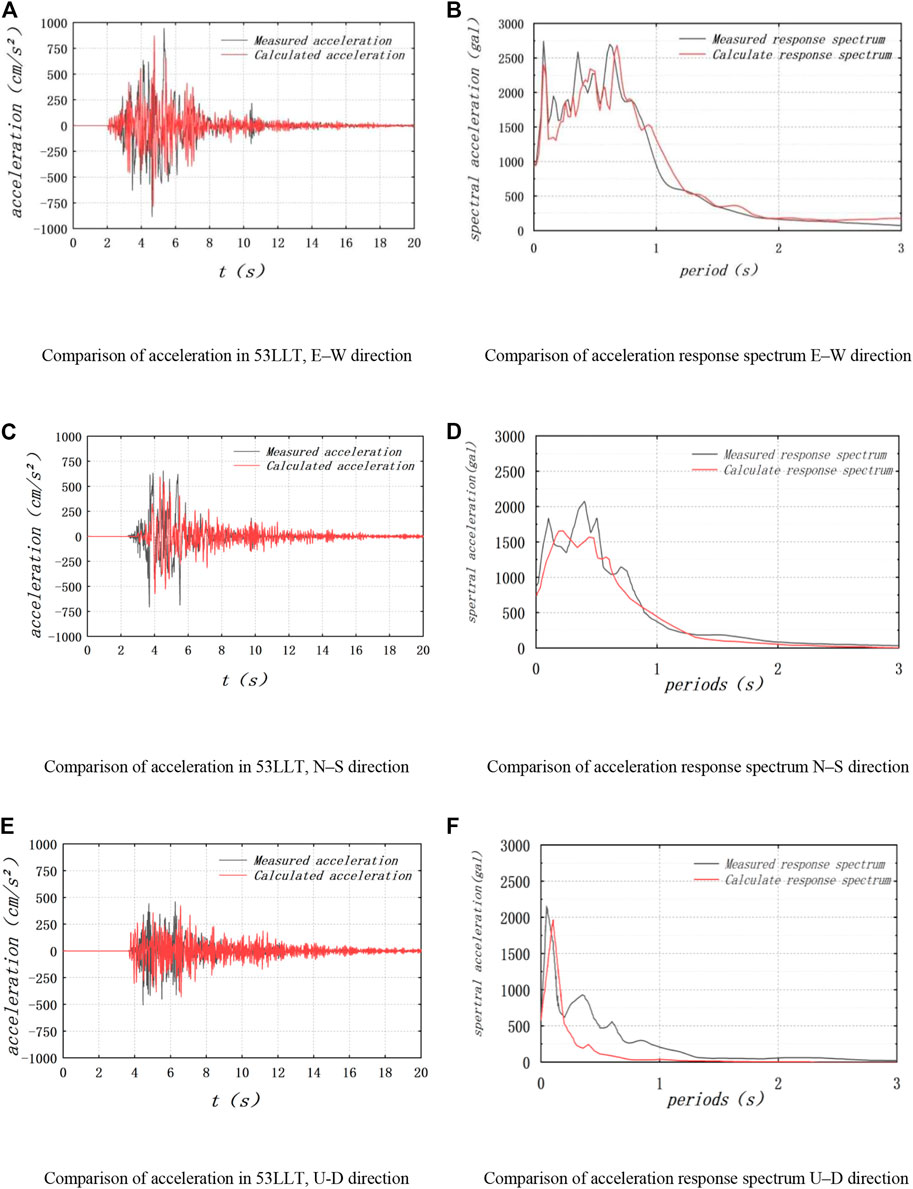
FIGURE 11. Comparison between the simulation and observed records. (A) Comparison of acceleration in 53LLT, E–W direction. (B) Comparison of acceleration response spectrum E–W direction. (C) Comparison of acceleration in 53LLT, N–S direction. (D) Comparison of acceleration response spectrum N–S direction. (E) Comparison of acceleration in 53LLT, U-D direction. (F) Comparison of acceleration response spectrum U–D direction.

Overall, the calculated results are close to the peak values of the observed records. Particularly, the peak value of the simulation results of the three-component is close to that recorded at 53LLT, but the simulation results after 6 s are greater than the observed values.

The acceleration response spectra obtained from accelerations at 53LLT are compared with the simulation results at the corresponding location, as shown in Figures 11B, D, F. In general, the characteristics of the acceleration response spectra of the three-component match the observations for this site reasonably well, especially in the E–W and N–S directions, which validate the applicability of the proposed method in this paper. Figure 11B, D, F shows that the larger values in the response spectrum of 53LLT are concentrated at periods shorter than 1 s. This may be due to the fact that 53LLT is located close to the fault where the ground motion response is more intense, resulting in the pulse phenomenon.

For the rupture process of the earthquake, we considered the complexity of the structures and the geological conditions. For example, the present model uses a constant rupture velocity and sliding angle, but in the rupture zone in the Ludian region, the geological structure and the rupture process of the earthquake source are very complex. Therefore, the difference between the observed results and the simulation results obtained in this study is considered acceptable, and the calculations reflect the validity of the basin model and the rupture of the earthquake source to a certain extent.

In this research, the maximum frequency was about 1.125 Hz; however, the actual strong ground motion caused by earthquakes is often presented as a wide band signal. The reduction of the grid scale to increase the computing frequency will greatly increase the number of computing nodes and make computation difficult. Owing to the computational and knowledge constraints associated with the rupture process and velocity structure at fine spatial scales, the method of this study is difficult to resolve at high frequencies. In the future, wide-band ground motion simulation will be investigated and more scenarios covering a range of magnitudes and source parameters of basins will be computed, which will provide a better understanding of the seismic effect of the basin for detailed hazard assessment. And we will consider the source directivity effects (Wen et al., 2015; Convertito et al., 2016; Vincenzo et al., 2016; Ross et al., 2020; Colavitti et al., 2022) in our future research in more detail below.

6.2 Comparison of post-earthquake damage investigation

Following the work of Lin et al. (2020), we analyzed the seismic damages for 192 buildings in Longtoushan Town (Figure 12A). Based on the remote sensing data and historical news reported before and after the earthquake (Li et al., 2016; Lin et al., 2020), the spatial distribution of the seismic damage to the buildings caused by the Ludian earthquake in 2014 is obtained. Figure 12A shows that the building damage is mainly divided into five grades, among which the buildings with serious damage are mainly distributed on the left side of the figure and buildings with minor damage are mainly distributed on the right side.

FIGURE 12

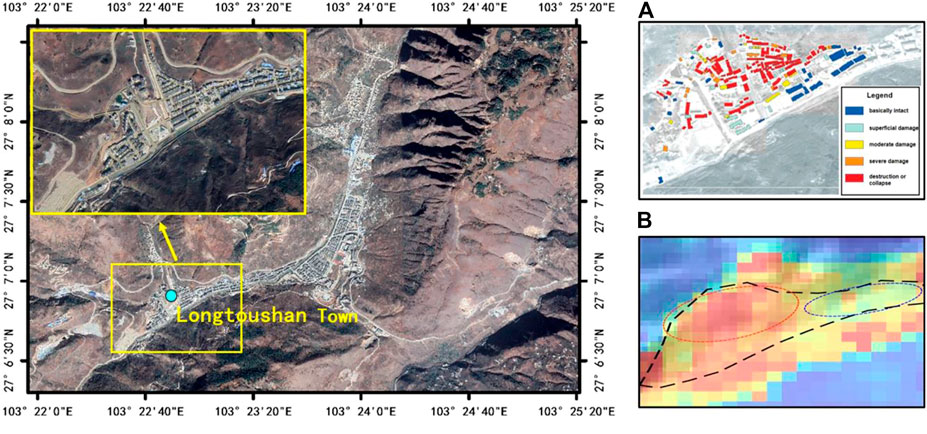
FIGURE 12. Comparison of the actual damage. (A) Spatial distribution of the seismic damage to buildings in Longtoushan Town Lin et al. (2020). (B) Local PGA map of Longtoushan Town, this study. The colour scale is the same as Figure 8.

Figure 12B shows the simulated PGA map, and its scope corresponds to Figure 12A. The black line in Figure 12 represents the general outline of Longtoushan Town. The red and blue ellipses denote the areas with more and less serious damage, respectively. The calculation results are consistent with the actual damage.

7 Conclusion

In this study, a three-dimensional model of the Longtoushan Town Basin and the velocity structure of the surrounding area are used to simulate and study the entire seismic wave propagation process in the basin during the 2014 Ludian earthquake using the Spectral Elements in Elastic Dynamics code, which combines the discontinuous Galerkin technique and the spectral element method (SEM). The simulation results were comprehensively analyzed based on the snapshots of the wave field propagation, surface wave characteristics with different geometric features on the profiles, and the distribution of the peak ground shaking (PGA and PGV) in areas with and without sedimentary layers. Analysis was performed by comparing the data with actual station records and the observed distribution of building damage caused by the earthquake.

Due to the special geometry of the basin and the difference in the impedance ratio between the media inside and outside the basin, the seismic waves incident on the basin’s edge were refracted and diffracted, causing the response time of seismic waves in the low-wave-velocity basin media to be significantly greater than that in the surrounding bedrock, which reflects the generation of large amplitude seismic waves in the low-wave-velocity basin media.

Examination of the elevation changes on each profile, the vibration time histories at the simulated points on the profiles, and the PGV change patterns showed that for the bedrock areas outside the basin, the peak velocities were higher at sites with higher topography and the ground vibration holding times were significantly lower than those inside the basin. Inside the basin, the locally depressed substrates had a focusing effect, which resulted in a more intense seismic response. The ground shaking response was not necessarily the greatest in the thickest sedimentary layers within the basin. The ground shaking amplitude was closely related to the degree of undulation of the base of the sedimentary layers, the overburden thickness, and the basin geometry.

The maximum PGA distribution in the E–W direction was higher than that in the N–S direction. The PGA was approximately 8 m/s² in the E–W direction and approximately 3 m/s² in the N–S direction.

Comparison of the simulation results for the models with and without sedimentary layers showed that for the model with sedimentary layers, PGV was 2.6 times higher in the E–W direction and 1.6 times higher in the N–S direction than that for the model without sedimentary layers. The maximum amplification factor of PGA was 2.8 in the E–W direction, approximately 2.3 in the N–S direction, and approximately 2.18 in the U–D direction, which is smaller than that in the other two directions. The amplification effect of the basin was mainly due to the influence of the basin geometry and the difference in the wave impedances of the media inside and outside the basin.

The acceleration time history and acceleration response spectrum simulated in this study were compared with the actual records for station 53LLT, and the simulated local intensity distribution map of the basin was compared with the spatial distribution of the seismic damage to the building complexes after the 2014 Ludian earthquake. The comparison revealed that the simulated time course was consistent with the records in terms of the waveforms and peaks, and the local intensity distribution cloud map for Longtoushan Town matched the actual damage situation. This proves the accuracy and rationality of the method used in this research.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

CL: Methodology, software, writing and review, investigation; PL: Software, writing (original draft); ZL: Conceptualization, project administration, resources; XY: Conceptualization, validation, resources; YT: Software, validation, writing (review); HZ: Writing (review and editing); ZC: Validation, writing (review).

Funding

This study was supported by the Scientific Research Fund of Institute of Engineering Mechanics, China Earthquake Administration (2019C07), the National Natural Science Foundation of China (grant nos. 52008287, 51878434, and 51968015), Key project of Tianjin Science and Technology 513 Support Plan (19YFZCSN01180) and Key Laboratory of Earthquake Engineering and Engineering Vibration, China Earthquake Administration (2020EEEVL0302).

Acknowledgments

We thank the editors and reviewers for their very helpful comments and detailed suggestions for improving the manuscript. Data for this study are provided by the Institute of Engineering Mechanics, China Earthquake Administration. We thank Professor Lin Xuchuan for giving us the precise positioning of the station.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abraham, J. R., Smerzini, C., Paolucci, R., and Lai, C. G. (2016). Numerical study on basin-edge effects in the seismic response of the Gubbio valley, Central Italy. Bull. Earthq. Eng. 14 (6), 1437–1459. doi:10.1007/s10518-016-9890-y

CrossRef Full Text | Google Scholar

Bao, H., Bielak, J., Ghattas, O., Kallivokas, L. F., O'Hallaron, D. R., Shewchuk, J. R., et al. (1998). Large-scale simulation of elastic wave propagation in heterogeneous media on parallel computers. Comput. Methods Appl. Mech. Engrg. 152, 85–102. doi:10.1016/s0045-7825(97)00183-7

CrossRef Full Text | Google Scholar

Bard, P. Y., and Bouchon, M. (1980a). The seismic response of sediment-filled valleys. Part 1. The case of incidentSHwaves. Bull. Seism. Soc. Am. 70 (4), 1263–1286. doi:10.1785/bssa0700041263

CrossRef Full Text | Google Scholar

Bard, P. Y., and Bouchon, M. (1980b). The seismic response of sediment-filled valleys. Part 2. The case of incidentPandSVwaves. Bull. Seism. Soc. Am. 70 (5), 1921–1941. doi:10.1785/bssa0700051921

CrossRef Full Text | Google Scholar

Colavitti, L., Lanzano, G., Sgobba, S., Pacor, F., and Gallovič, F. (2022). Empirical evidence of frequency-dependent directivity effects from small-to-moderate normal fault earthquakes in Central Italy. J. Geophys. Res. Solid Earth 127, e2021JB023498. doi:10.1029/2021jb023498

CrossRef Full Text | Google Scholar

Convertito, V., Nicola, A. P., and Francesca, D. L. (2016). Investigating source directivity of moderate earthquakes by multiple approach: the 2013 Matese (southern Italy) Mw = 5 event. Geophys. J. Int. 207 (3), 1513–1528. doi:10.1093/gji/ggw360

CrossRef Full Text | Google Scholar

Cornou, C., Bard, P. Y., and Dietrich, M. (2003a). Contribution of dense array analysis to the identification and quantification of basin-Edge-Induced waves, Part I: Methodology. Bull. Seism. Soc. Am. 93 (6), 2604–2623. doi:10.1785/0120020139

CrossRef Full Text | Google Scholar

Cornou, C., Bard, P. Y., and Dietrich, M. (2003b). Contribution of dense array analysis to the identification and quantification of basin-edge-induced waves, Part II: Application to Grenoble basin (French Alps). Bull. Seism. Soc. Am. 93 (6), 2624–2648. doi:10.1785/0120020140

CrossRef Full Text | Google Scholar

Frankel, A. (1993). Three-dimensional simulations of ground motions in the San Bernardino Valley, California, for hypothetical earthquakes on the San Andreas fault. Bull. Seismol. Soc. Am. 83 (4), 1020–1041. doi:10.1785/bssa0830041020

CrossRef Full Text | Google Scholar

Graves, R. W., Pitarka, A., and Somerville, P. G. (1998). Ground-motion amplification in the Santa Monica area: Effects of shallow basin-edge structure. Bull. Seism. Soc. Am. 88 (5), 1224–1242. doi:10.1785/bssa0880051224

CrossRef Full Text | Google Scholar

Hao, J. L., Wang, W. M., and Yao, Z. X. (2014). Preliminary results of inversion of the source rupture process of Yunnan Ludian M6.5 earthquake on August 3, 2014. Beijing: Institute of Geology and Geophysics, China Academy of Sciences.

Google Scholar

Horike, M., Uebayashi, H., and Takeuchi, Y. (1990). Seismic response in three-dimensional sedimentary basin due to plane S wave incidence. J. Phys. Earth 38 (4), 261–284. doi:10.4294/jpe1952.38.261

CrossRef Full Text | Google Scholar

Hu, Y. X., Liu, X. R., Luo, J. H., and L, Z. (2011). Simulation of three-dimensional topographic effects of ground shaking in Wenchuan earthquake zone by spectral element method. J. Lanzhou Univ. Nat. Sci. Ed. 47 (4), 24–32.

Google Scholar

Huang, L., Liu, Z. X., Wu, C., and Liang, J. W. (2022). A three-dimensional indirect boundary integral equation method for the scattering of seismic waves in a poroelastic layered half-space. Eng. Anal. Bound. Elem. 135, 167–181. doi:10.1016/j.enganabound.2021.11.012

CrossRef Full Text | Google Scholar

Komatitsch, D., and Tromp, J. (1999). Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophys. J. Int. 139 (3), 806–822. doi:10.1046/j.1365-246x.1999.00967.x

CrossRef Full Text | Google Scholar

Komatitsch, D., Liu, Q. Y., Tromp, J., Suss, P., Stidham, C., and Shaw, J. H. (2004). Simulations of ground motion in the Los Angeles basin based upon the spectral-element method. Bull. Seismol. Soc. Am. 94 (1), 187–206. doi:10.1785/0120030077

CrossRef Full Text | Google Scholar

Lee, J. (2013). Earthquake site effect modeling in the Granada basin using a 3-D indirect boundary element method. Phys. Chem. Earth 63, 102–115. doi:10.1016/j.pce.2013.03.003

CrossRef Full Text | Google Scholar

Lee, S. J., Chen, H. W., and Huang, B. S. (2008). Simulations of strong ground motion and 3D amplification effect in the Taipei Basin by using a composite grid finite-difference method. Bull. Seismol. Soc. Am. 98 (3), 1229–1242. doi:10.1785/0120060098

CrossRef Full Text | Google Scholar

Lee, S. J., Komatitsch, D., Huang, B. S., and Tromp, J. (2009). Effects of topography on seismic-wave propagation: An example from northern Taiwan. Bull. Seismol. Soc. Am. 99 (1), 314–325. doi:10.1785/0120080020

CrossRef Full Text | Google Scholar

Li, P., Liu, H. S., Bo, J. S., Li, X. B., and Yu, X. H. (2016). Effects of river valley topography on anomalously high intensity in the Hanyuan town during the Wenchuan Ms8.0 earthquake. Chin. J. Geophys. 59 (01), 174–184.

Google Scholar

Li, Y., Chen, X. Z., Chen, L. J., and Guo, X. Y. (2015). Investigation on the rupture process of the Ludian MS6. 5 earthquake sequence on 3 August, 2014 in Yunnan province. Chin. J. Geophys. 58 (9), 3232–3238.

CrossRef Full Text | Google Scholar

Li, Y. Q., and Li, Z. L. (2016). Analysis on casualty caused by the Ludian Yunnan MS 6.5 earthquake in 2014. Earthq. Res. China 4, 787–800.

Google Scholar

Lin, X. C., Liu, X. Y., Hu, R. K., and Zhang, L. X. (2020). Regional damage analysis and resilience evaluation of buildings in the epicenter region of 2014 Ludian Earthquake. J. Seismol. Res. 43 (03), 449–455+601.

Google Scholar

Liu, Q. F. (2021). Study on the basin resonance effect in Longtoushan Town during the 2014 Ludian earthquake. Earthq. Eng. Eng. Dyn. 41 (02), 43–52.

Google Scholar

Liu, Q. F., Yu, Y. Y., and Zhang, X. B. (2013). Study of three-dimensional ground vibrations in the Shidian Basin. Earthq. Eng. Eng. Vib. 33 (4), 54–60.

Google Scholar

Liu, Z. X., Liu, M. Z., and Han, J. B. (2017). Simulation of strong ground shaking spectral elements in near-fault sedimentary basins. World Earthq. Eng. 33 (4), 76–86.

Google Scholar

Mazzieri, I., Stupazzini, M., Guidotti, R., and Smerzini, C. (2013). Speed: SPectral elements in elastodynamics with discontinuous Galerkin: A non-conforming approach for 3D multi-scale problems. Int. J. Numer. Methods Eng. 95 (12), 991–1010. doi:10.1002/nme.4532

CrossRef Full Text | Google Scholar

Ohori, M., Koketsu, K., and Minami, T. (1990). Seismic response analyses of sediment-filled valley due to incident plane waves by three-dimensional Aki-Larner method. Bull. Earthq. Res. Inst., Univ. Tokyo 65, 433–463.

Google Scholar

Olsen, K. B., and Schuster, G. T. (1995). Causes of low frequency ground motion amplification in the salt lake basin: The case of the vertically incident P wave. Geophys. J. Int. 122 (3), 1045–1061. doi:10.1111/j.1365-246x.1995.tb06854.x

CrossRef Full Text | Google Scholar

Olsen, K. B. (2000). Site amplification in the Los Angeles basin from three-dimensional modeling of ground motion. Bull. Seismol. Soc. Am. 90 (6B), S77–S94. doi:10.1785/0120000506

CrossRef Full Text | Google Scholar

Pang, W. D., Yang, R. M., Chen, J. L., Li, Z. G., and Lu, J. G. (2016). High density resistivity exploration method for Ludian MS6.5 earthquake in area of Longtoushan Town in 2014. J. Seismol. Res. 39 (04), 622–629+718.

Google Scholar

Parsons, T., Ji, C., and Kirby, E. (2008). Stress changes from the 2008 Wenchuan earthquake and increased hazard in the Sichuan basin. Nature 454 (7203), 509–510. doi:10.1038/nature07177

PubMed Abstract | CrossRef Full Text | Google Scholar

Patera, A. T. (1984). A spectral element method for fluid dynamics: Laminar flow in a channel expansion. J. Comput. Phys. 54, 468–488. doi:10.1016/0021-9991(84)90128-1

CrossRef Full Text | Google Scholar

Paudyal, Y. R., Yatabe, R., Bhandary, N. P., and Dahal, R. K. (2012). A study of local amplification effect of soil layers on ground motion in the Kathmandu Valley using microtremor analysis. Earthq. Eng. Eng. Vib. 11 (2), 257–268. doi:10.1007/s11803-012-0115-3

CrossRef Full Text | Google Scholar

Pitarka, A., Irikura, K., Iwata, T., and Sekiguchi, H. (1998). Three-dimensional simulation of the near-fault ground motion for the 1995 Hyogo-Ken Nanbu (Kobe), Japan, earthquake. Bull. Seismol. Soc. Am. 88 (2), 428–440. doi:10.1785/bssa0880020428

CrossRef Full Text | Google Scholar

Ren, J., Feng, F. Y., Fu-Yun, W., Jian-Bing, P., Chen, L., Wang-Qiang, D., et al. (2013). Revealed the fine crust structures of Xi’an sag in Weihe basin by deep seismic reflection profile. Chin. J. Geophys. 56 (2), 513–521. doi:10.6038/cjg20130215

CrossRef Full Text | Google Scholar

Ross, Z. E., Trugman, D. T., Azizzadenesheli, K., and Anandkumar, A. (2020). Directivity modes of earthquake populations with unsupervised learning. J. Geophys. Res. Solid Earth 125, e2019JB018299. doi:10.1029/2019jb018299

CrossRef Full Text | Google Scholar

Semblat, J. F., Dangla, P., Kham, M., and Duval, A. (2022). Seismic site effects for shallow and deep alluvial basins: In-depth motion and focusing effect. Soil Dyn. Earthq. Eng. 22, 849–854. doi:10.1016/s0267-7261(02)00107-0

CrossRef Full Text | Google Scholar

Smerzini, C., and Villani, M. (2012). Broadband numerical simulations in complex near-field geological configurations: The case of the 2009 M w 6.3 L’Aquila earthquake. Bull. Seismol. Soc. Am. 102 (6), 2436–2451. doi:10.1785/0120120002

CrossRef Full Text | Google Scholar

Stupazzini, M., Paolucci, R., and Igel, H. (2009). Near-Fault earthquake ground-motion simulation in the grenoble valley by a high-performance spectral element code. Bull. Seismol. Soc. Am. 99 (1), 286–301. doi:10.1785/0120080274

CrossRef Full Text | Google Scholar

Todorovska, M. I., and Lee, V. W. (1990). A note on response of shallow circular valleys to Rayleigh waves: Analytical approach. Earthq. Eng. Eng. Vib. 10 (1), 21–34.

Google Scholar

Toshinawa, T., and Ohmachi, T. (1992). Love-wave propagation in a three-dimensional sedimentary basin. Bull. Seismol. Soc. Am. 82 (4), 1661–1677. doi:10.1785/bssa0820041661

CrossRef Full Text | Google Scholar

Trifunac, M. D. (1971). Surface motion of a semi-cylindrical alluvial valley for incident plane SH waves. Bull. Seismol. Soc. Am. 61 (6), 1755–1770. doi:10.1785/bssa0610061755

CrossRef Full Text | Google Scholar

Vijaya, R., Boominathan, A., and Mazzieri, I. (2020). 3D ground response analysis of simplified Kutch Basin by spectral element method. J. Earthq. Tsunami 14 (01), 2050003. doi:10.1142/s1793431120500037

CrossRef Full Text | Google Scholar

Vincenzo, C., Nicola, A. P., and Francesca, D. L. (2016). Investigating source directivity of moderate earthquakes by multiple approach: The 2013 matese (southern Italy) mw = 5 event. Geophys. J. Int. 207 (3), 1513–1528. doi:10.1093/gji/ggw360

CrossRef Full Text | Google Scholar

Wen, K. L., and Peng, H. Y. (1998). Site effects analysis in the Taipei Basin: Results from TSMIP network data. TAO 9 (4), 691–704.

CrossRef Full Text | Google Scholar

Wen, R. Z., Wang, H. W., and Ren, Y. F. (2015). Rupture directivity from strong-motion recordings of the 2013 lushan aftershocks. Bull. Seismol. Soc. Am. 105 (6), 3068–3082. doi:10.1785/0120150100

CrossRef Full Text | Google Scholar

Wong, H. L., and Trifunac, M. D. (1974). Surface motion of a semi-elliptical alluvial valley for incident plane SH waves. Bull. Seism. Soc. Am. 64 (5), 1389–1408. doi:10.1785/bssa0640051389

CrossRef Full Text | Google Scholar

Xu, X. W., Jiang, G. Y., Yu, G. H., Wu, X. Y., Zhang, J. G., and Li, X. (2014). Discussion on seismogenic fault of the Ludian MS6. 5 earthquake and its tectonic attribution. Chin. J. Geophys. 57 (9), 3060–3068.

Google Scholar

Yu, Y. Y. (2017). Study of seismic effects in three-dimensional sedimentary basins. Int. Seismol. Update (6), 33–35.

Google Scholar

Yuan, X., and Liao, Z. P. (1995). Scattering of plane SH waves by a cylindrical alluvial valley of circulararc cross-section. Earthq. Eng. Struct. Dyn. 24 (10), 1303–1313. doi:10.1002/eqe.4290241002

CrossRef Full Text | Google Scholar

Zhang Y., Y., Xv, L. S., Chen, Y. T., and Li, R. F. (2014). Rupture process of Mw6.1 (Ms6.5) earthquake in ludian, yunnan province on August 3, 2014. Chin. J. Geophys. 57 (9), 3052–3059.

Google Scholar

Zhang, Z. G., Sun, Y. C., Xv, J. K., Zhang, W., and Chen, X. F. (2014). Preliminary simulation of strong ground motion for Ludian, Yunnan earthquake of 3 August 2014, and hazard implication. Chin. J. Geophys. 57 (09), 3038–3041.

Google Scholar

Zhao, X. Y., and Sun, N. (2014). Simultaneous inversion for focal location of Yunnan Ludian M S 6.5 earthquake sequence in 2014 and velocity structure in the source region. J. Seismol. Res. 37 (4), 523–531.

Google Scholar