- 1Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China
- 2Key Laboratory of Earthquake Disaster Mitigation, Ministry of Emergency Management, Harbin, China
The topographic site effect plays a vital role in controlling the characteristics of earthquake ground motions. Due to its complexity, the factors affecting topographic amplification have not been fully identified. In this study, 100 ground motion simulations generated by double-couple point sources in the homogeneous linear elastic half-space are performed based on the 3D (three-dimensional) Spectral Element Method, taking the Menyuan area of Qinghai Province, China as a local testbed site. A relationship between incident direction and the strength of topographic amplification has been observed. The horizontal ground motion is affected by the back-azimuth, which is typically chosen to be the direction from seismic station to seismic source measured clockwise from north. Specifically, the east-west PGA (Peak Ground-motion Acceleration) is significantly amplified when back-azimuth is about
Introduction
The topographic site effect refers to the scattering of seismic waves by topographic irregularities, which generally manifests as the ground motion amplified at the convex features such as hilltops and deamplified at the concave features such as valleys. The interaction between seismic waves and irregular topographic features can be dramatic: a high peak ground acceleration (PGA) of 1.78 g was recorded at the Tarzana hilltop stations during the 1994 Northridge earthquake (Bouchon and Barker, 1996; Ashford and Sitar, 1997); A PGA of 1.25 g recorded by the Pacoima Dam site during the 1971 San Fernando earthquake (Trifunac and Hudson, 1971); For moderate earthquakes, severe damage can also be partially attributed to the scattering effect of topography (e.g., Kang et al. 2019).
Although empirical evidence pointing out the contributions of topography do exist in various seismic scenarios (Hartzell et al., 1994; Harris, 1998; Buech et al., 2010; Hough et al., 2010; Pischiutta et al., 2010; Luo et al., 2014), topographic site effects have received less attention compared with stratigraphic site effects. Topographic site effects are often invoked to explain abnormal ground motion amplitudes in local areas, and its complexity makes the relevant research encounter challenges in reproducing the amplification value accurately. More specifically, the relevant information of the source, propagation path, and engineering site are all covered in the ground motion records. Among these, the site condition includes stratified soil, topography, sedimentary basin structure, etc. To perform quantitative analysis, the contribution of the topography itself needs to be extracted separately from the ground motion records, and the influence of source, stratified soil, and other factors on the topographic amplification value cannot be ignored. Asimaki and Mohammadi (2018) emphasized a non-linear coupling between the amplification effects from surface topography and subsurface stratified soil. The thickness, shear wave velocity, damping ratio, and lateral heterogeneity of the underlying geologic materials all affect the topographic amplification (Assimaki and Gazetas, 2004; Assimaki et al., 2005a; Assimaki et al., 2005b; Bouckovalas and Papadimitriou, 2005; Wang et al., 2019; Luo et al., 2020; Song et al., 2020). The source and propagation path indirectly affect the topographic site effect by determining the azimuth and frequency content of the incoming wavefield, and there are few related studies. Using three-dimensional finite difference methods, Mayoral et al. (2019) indicates that for hill slopes, subduction earthquakes led to deep failure surfaces, whereas normal events to shallow failure surfaces.
At present, there are three kinds of methods to study the topographic site effects: experimental method (e.g., Tucker et al., 1984; Wood and Cox, 2016; Stolte et al., 2017), analytical and semi-analytical method (e.g., Yuan and Liao, 1996; Paolucci, 2002) and numerical simulation methods (e.g., Boore, 1972; Geli et al., 1988; Hartzell et al., 2017). The standard spectral ratio (SSR) method (Borcherdt, 1970) is the spectral ratio of ground motions between the target station and the adjacent reference station. It is widely used in the study of topographic site effects due to its ease of operation and clear physical context, but the reference station needs to be located on the bedrock site and cannot be affected by the adjacent topographic features, which limits the amount of available ground motion data. The Nakamura (HVSR, horizontal-to-vertical spectral ratio) method, which avoids the selection of the reference station by using the horizontal to the vertical spectral ratio of the same station to characterize site effects (Nakamura, 1989). However, the topographic amplification of vertical ground motion reduces the accuracy of the estimation of amplification. Some scholars used microtremors to make up for the lack of ground motion records (e.g., Stolte et al., 2017; La Rocca et al., 2020). Numerical simulations also have helped augment the observational record, but the numerical results are usually smaller than those of experiments (Geli et al., 1988; Lovati et al., 2011). The reason is that the underground shear wave velocity structure and soil layer information are usually unclear, and the accuracy of the elevation data used in the numerical simulation is also limited, which greatly affects the accuracy of the numerical modeling (Moore et al., 2011; Burjánek et al., 2012; Burjánek et al., 2014). However, with the growth in computational capabilities, the development of codes capable of handling complex topographies, and more high-quality near-surface geologic data available, it is becoming easier to directly model ground-motion amplification due to topography. Some studies that consider surface topography has obtained simulation results that are in good agreement with observed ground motions (Magnoni et al., 2013; Galvez et al., 2021; Wang et al., 2021).
In this paper, we first adopt the spectral element method to establish a ground motion synthetic database, and then explore the influence of the incident direction of the incoming seismic wavefield on the topographic amplification; in addition, the correlation between geomorphometric parameters, which commonly used to build the ground-motion models (GMMs), and topographic amplification values have also been analyzed. Finally, we discuss the physical mechanism behind the source-site interaction and make recommendations for considering the topographical site effect in real engineering sites.
Ground-motion synthetic database
A powerful and freely available spectral element software, called SPECFEM3D, is adopted to generate the synthetic ground motion data. The Spectral Element Method (SEM) enjoys the geometrical flexibility of the Finite Element Method and the accuracy of the Pseudo-Spectral Method. High-degree Lagrange interpolants are used to express functions in SEM. Therefore, the accuracy of the simulation can be ensured by adjusting the polynomial degree and the representative element size. The polynomial degree is set to 4 in our study [following Komatitsch et al., 2005; Igel, 2017; Yuan et al., 2021], which means one SEM element per wavelength has been found to be accurate. As a comparison, the spatial element size in some finite difference methods must be smaller than approximately one-tenth to one-eighth of the wavelength, which leads to a great number of elements (e.g., Ma et al., 2021). The SEM allows for systematic diagonalization of the mass matrix, which then allows for easy parallelization.
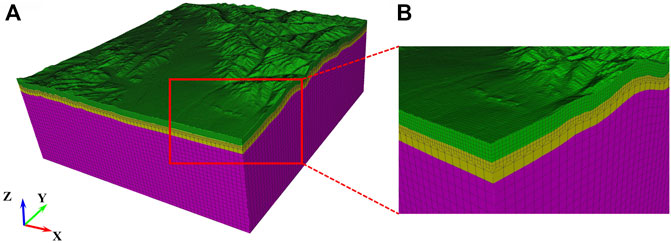
Menyuan area, Qinghai Province, China is located northeast of the Qinghai Tibet Plateau, with a great difference in elevation and the average elevation is 2,866 m. The overall terrain is high in the northwest, low in the southeast, high in the north and south, and low in the middle. The north is adjacent to the Qilian Mountains, and the Datong River Valley in the middle is relatively flat. As shown in Figure 1A, the topography is complex, including ridges, isolated hills, valleys, canyons, and flat surfaces, which cover a large variety of topographic features often present in real cases in which 3D site effects may occur. Therefore, A 3D model with dimensions of
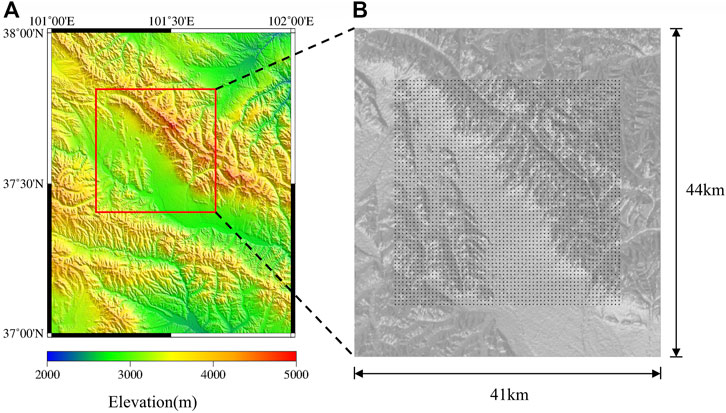
FIGURE 1. (A) Menyuan area elevation map and study region (red box); (B) Locations of the square array of 3,721 virtual receivers (black dots, one station every 500 m).
To isolate topographic site effects from heterogeneities in the subsurface materials, we assume isotropic homogeneous linear elastic half-space with properties given by
100 Mw 4.5 double couple point sources with Gaussian source time function are used as the input of simulations. The focal mechanisms and locations of each source are randomly generated by uniform distribution, and the rise time is obtained by the empirical scaling relations (Somerville et al., 1999). It should be noted that the rupture area of Mw 4.5 is generally about 2–3 km2 (Somerville et al., 1999; Leonard, 2010). The hypocenter depth is limited to above 5 km to ensure the validity of the point source hypothesis. Finding a suitable reference site is not an easy task in the empirical method. But this problem can be easily solved by numerical simulation. An SEM model with a flat ground surface is adopted (the size, medium parameters, and receiver locations of the model are consistent with the previous model) to simulate the reference ground motion. All raw ground motion records in our database need to be filtered by a 4th order Butterworth low-pass filter with a cut-off frequency of 5 Hz before subsequent analysis. Then the three-component ground motion amplification factors of 3,721 receivers can be obtained with the input of each double couple source.
Influence of incident direction on topographic site effects
The amplification factor of PGA,
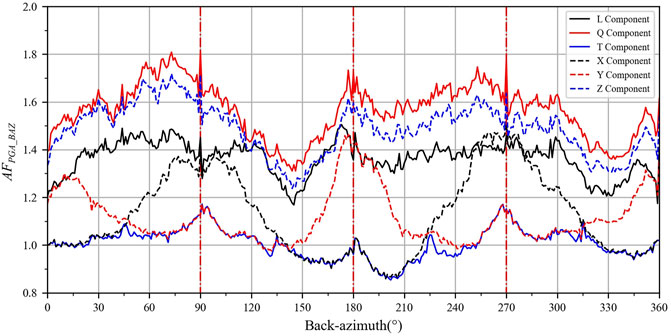
FIGURE 3. The relationship of
For the LQT coordinate system (solid line in Figure 3), the PGA of L and Q components is significantly amplified by the topography, while the
The maximum
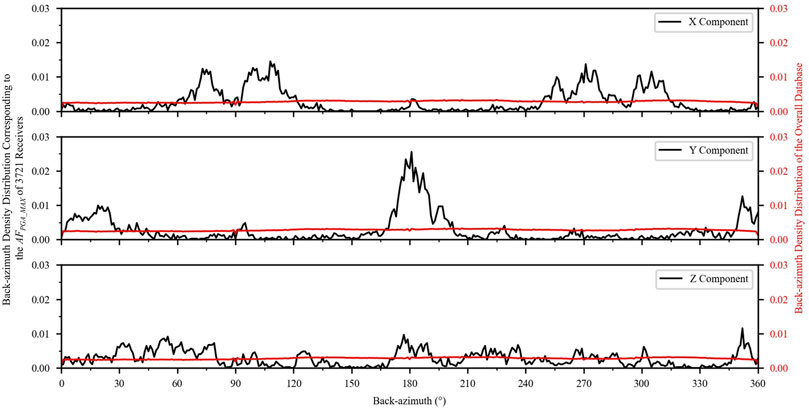
FIGURE 4. The density distribution of back-azimuth. The black solid line represents the density distribution of the back-azimuth corresponding to the
The data set is also divided into 90 subsets based on different dipping angles (taking
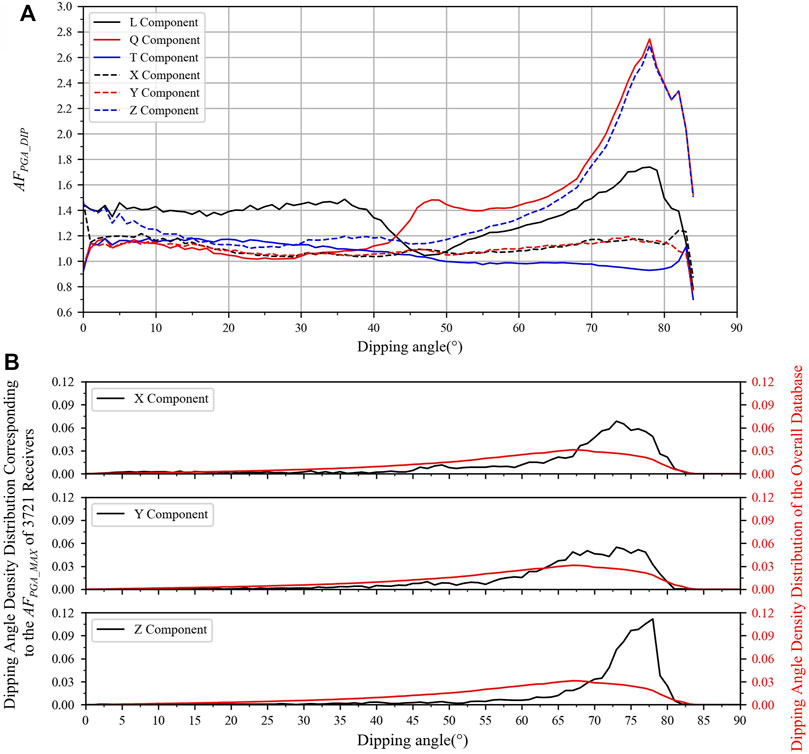
FIGURE 5. The influence of dipping angle on
The dipping angle density distribution of the overall database is mainly concentrated above 45° (red solid line in Figure 5B), which leads to the particle motion of SV wave is mainly projected in the vertical direction, so the
Figure 5B further indicates that the PGA of Z component is strongly amplified when the incident seismic wave is approximately horizontal. For example, 74.5% of the
Our simulation data show that the amplification of P and SV waves is independent of back-azimuth, but correlates with dipping angle. Taking the SV wave as an example, when the dipping angle is smaller than
Figure 6 represents the density distribution of the dipping angle and the incidence angle, where the incidence angle refers to the angle between the incident direction of seismic wave and the normal to the topography surface at the location of the receiver. The incidence angle in this study is also mainly above 45°, and the relationship between PGA amplification factor and dipping angle is similar to that of the incidence angle, so we will not repeat them here.
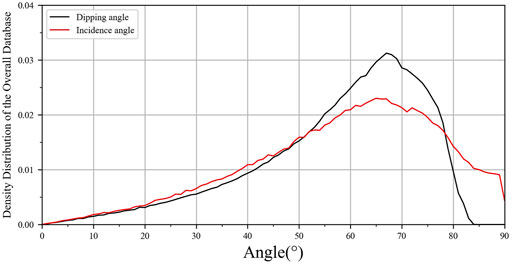
FIGURE 6. Density distribution of dipping angle (black solid line) and incidence angle (red solid line) in the overall database.
Correlation between geomorphometric parameters and topographic site effects
Topographic site effect prediction models based on geomorphometric parameters have been established by previous studies (Maufroy et al., 2015; Zhou et al., 2020). However, due to topographic site effects varying strongly with the stratigraphy and material properties of the underlying geologic material, some researchers believe that topographic site effects cannot be well characterized by studying the effects of ground surface geometry alone (Asimaki and Mohammadi, 2018; Pitarka et al., 2021). Based on the synthetic database, this section studies the correlation between commonly used geomorphometric parameters and topographic amplification to explore whether this correlation can remain stable with different incident directions. The relative elevation and smoothed curvature are initially selected.
Relative elevation (
Referring to
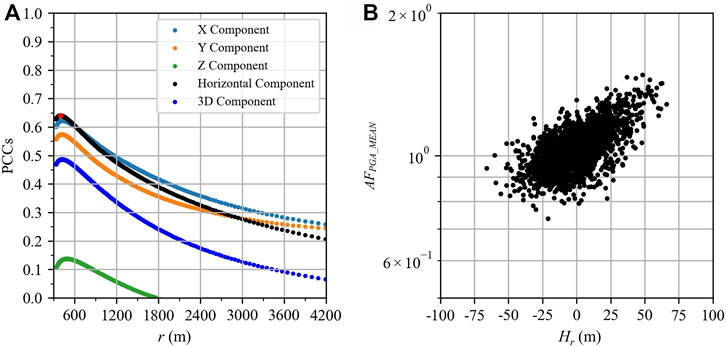
FIGURE 7. Correlation between
It can be observed from Figure 7A that the PCCs of all components increase first and then decrease with
Wang et al. (2018) also studied the correlation between geomorphometric parameters and PGA amplification. They used the vertically incident plane wave as the input ground motion, without considering the variation of incidence angle. After considering the incidence angle, Figure 7 shows that the correlation is found to be weaker than that of Wang et al. (2018). In addition, Figure 7 also indicates that it is hard to determine the
Topographic amplification is frequency-dependent. The ground motion spectral amplification in this study is defined as
We calculate the PCCs between
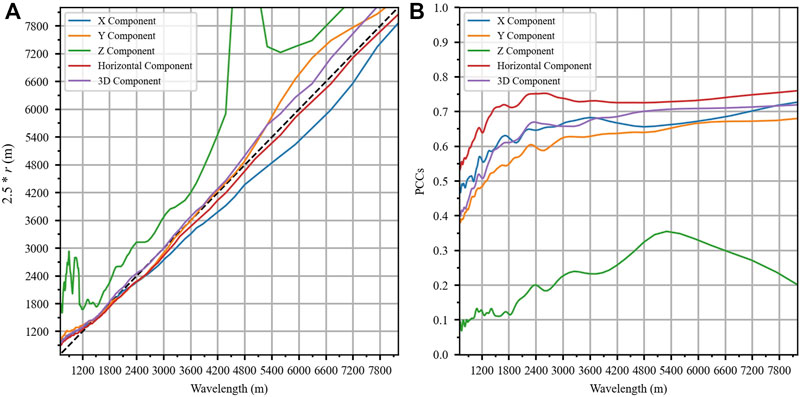
FIGURE 8. The relationship between
By comparing Figure 7A with Figure 8B, we can easily find that
The surface curvature is defined as the second spatial derivative of the elevation map. Following the work of Zevenbergen and Thorne (1987), the Digital Elevation Model (DEM) of the region E should be a rectangular matrix of evenly spaced elevation values with space increment
In which
and
As shown in Table 1, the PCCs between smoothed curvature and
To characterize the spatial correlation between smoothed curvature and ground-motion amplification as a function of frequency, Maufroy et al. (2015) introduced a smoothing operator, which is to convolve matrix
The characteristic length is defined as
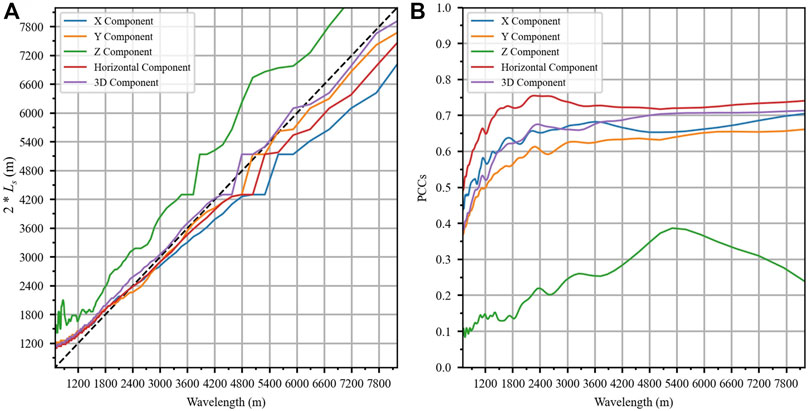
FIGURE 9. The relationship between
Based on the above analysis, it is easy to notice the strong similarity between relative elevation
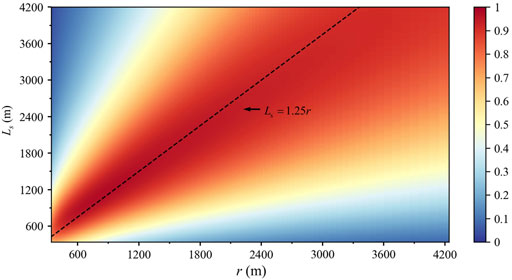
FIGURE 10. Coefficients of determination between relative elevation and smoothed curvature with various
Discussion
The influence of the incident direction of seismic waves on the topographic site effect is revealed in this work based on a large number of 3D numerical simulations, which is useful for us to explain the spatial distribution characteristics of ground motion. However, the applicability of these findings in real earthquake scenarios needs to be discussed.
The homogeneous velocity model introduced in this study leads to some discrepancies between the numerical simulation results and the real earthquake cases, one of which is the difference in dipping angle. In real earthquake scenarios, the shear velocity increase with depth whether it is homogeneous rock or unconsolidated sediments (Kanamori and Schubert, 2015). Based on Snell’s law, when the seismic wave is transmitted from the larger shear velocity medium to the smaller shear velocity medium, the direction of the refracted wave will approach the normal direction. Even if the initial dipping angle is very large, the propagating path of the seismic wave will become approximately vertical in the near-surface after several refractions. Since seismic waves do not refract in the medium with uniform shear velocity (e.g., numerical models used in this work), the dipping angle of seismic waves at the ground surface will be much larger than that in the real world. Based on the discussion of Figure 5 above, the larger dipping angle is part of the reason why the
Numerical simulations and model experiment show that the scattering of body waves to surface waves can be induced by topographic features in homogeneous linear elastic half-space (Gangi and Wesson, 1978; Boore et al., 1981; Ohtsuki and Harumi, 1983; Li and Liao, 2002). We also confirm the existence of converted surface wave based on the spectral element method, see Supplementary Material document for details. The dipping angle may be related to the strength of the generated surface wave. Li and Liao (2002) indicates that the top corner of cliff scatter stronger Rayleigh wave under inclined body waves than vertical body waves and the maximum amplitude of converted Rayleigh wave is about 1.1 times of the free field surface displacement. Assimaki et al. (2005a) demonstrated that all the incident energy with the critical incidence angle (i.e.,
Although numerical simulations alone are not as powerful as simulations used in conjunction with real data, it is currently one of the best ways to understand the mechanisms of topographic site effects. The role of different factors in controlling the highly variable amplification effects is unclear, and the numerical simulation methods are very flexible and can solve these problems to a certain extent. Previous studies have built appropriate models according to the research targets to study the influence of a specific factor on the ground motion (e.g., Lee et al., 2009a; Lee et al., 2009b). It is difficult to explore the influence of back-azimuth on topographic site effect based on real data. The challenges are mainly manifested in two aspects: the first is there are many limitations when selecting a reference station, which is related to the reliability of the topographic amplification factors. The second is that there should be enough historical ground motion records. To ensure the robustness of the conclusion, at least one or two historical earthquakes are required in every
We found that the relative elevation is indeed closely related to the horizontal ground motion amplification, but even for the idealized numerical model used in this paper, this correlation still shows a certain discreteness, which imposes a challenge to the accuracy of the GMM; on the other hand, post-earthquake disaster assessment generally focuses on specific sites that including both muti-layer subsurface structures and topographic features, which imposes a challenge to the applicability of the GMM. Therefore, we plan to classify the topographic features based on the geomorphometric parameters, and then combine it with the site classification (e.g., NEHRP site classification) to evaluate the ground motion amplification level in the real engineering site.
Conclusion
In this paper, we study the influence of back-azimuth and dipping angle on the topographic amplification based on the ground motion synthetic database constructed by the spectral element method. In addition, the correlation between geomorphometric parameters (relative elevation and smooth curvature) and frequency-dependent topographic amplification value is also analyzed. For the isotropic homogeneous numerical model with double couple point sources as the input, the following conclusions can be obtained:
(1) When the dipping angle is smaller than
(2) When the dipping angle is large, the topographic amplification of P wave is more projected on the horizontal components. More specifically, When the back-azimuth angle is around 90° or 270°, the PGA amplification of the X component increases obviously; when the back-azimuth is around 0° or 180°, the PGA amplification of the Y component increases obviously. The PGA amplification of Z component is independent of the back-azimuth and similar to that of SV wave.
(3) The relative elevation and smoothed curvature cover the same information of topography, Considering the algorithmic complexity, relative elevation is recommended as a proxy for topographic site effects.
(4) The correlation of geomorphometric parameters (relative elevation and smoothed curvature) with spectral amplification is stronger than that of geomorphometric parameters with PGA amplification.
(5) The relative elevation and smoothed curvature are both closely related to the horizontal topographic amplification, but independent of that in the vertical component.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
FW implemented the numerical simulations and specifically writing the initial draft. QM determined the research goals and contributed to designing the methodology. DT and QX provided important suggestions for the interpretation of the results and revised the manuscript. All authors contributed to the redaction and final revision of the manuscript.
Funding
This research was partially supported by Scientific Research Fund of Institute of Engineering Mechanics, China Earthquake Administration (Grant No. 2016A03), and National Natural Science Foundation of China (Grant No. U2039209 and 5150082083).
Acknowledgments
We thank NASA’s (National Aeronautics and Space Administration) EOSDIS (Earth Observing System Data and Information System) (https://search.earthdata.nasa.gov) for providing DEM (Digital Elevation Model) data. Some plots were made using Generic Mapping Tools v.5.2.1 and the matplotlib module in Python.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.996389/full#supplementary-material
SUPPLEMENTARY TABLES S1–S2 | Show the coordinate positions of seismic events and stations in the numerical model, respectively.
References
Ashford, S. A., and Sitar, N. (1997). Analysis of topographic amplification of inclined shear waves in a steep coastal bluff. Bull. Seismol. Soc. Am. 87, 692–700. doi:10.1785/BSSA0870030692
Asimaki, D., and Mohammadi, K. (2018). On the complexity of seismic waves trapped in irregular topographies. Soil Dyn. Earthq. Eng. 114, 424–437. doi:10.1016/j.soildyn.2018.07.020
Assimaki, D., Gazetas, G., and Kausel, E. (2005a). Effects of local soil conditions on the topographic aggravation of seismic motion: Parametric investigation and recorded field evidence from the 1999 athens earthquake. Bull. Seismol. Soc. Am. 95, 1059–1089. doi:10.1785/0120040055
Assimaki, D., and Gazetas, G. (2004). Soil and topographic amplification on canyon banks and the 1999 Athens earthquake. J. Earth. Eng. 8, 1–43. doi:10.1142/S1363246904001250
Assimaki, D., Kausel, E., and Gazetas, G. (2005b). Soil-dependent topographic effects: A case study from the 1999 athens earthquake. Earthq. Spectra 21, 929–966. doi:10.1193/1.2068135
Boore, D. M. (1972). A note on the effect of simple topography on seismic SH waves. Bull. Seismol. Soc. Am. 62, 275–284. doi:10.1785/BSSA0620010275
Boore, D. M., Harmsen, S. C., and Harding, S. T. (1981). Wave scattering from a step change in surface topography. Bull. Seismol. Soc. Am. 71, 117–125. doi:10.1785/BSSA0710010117
Borcherdt, R. D. (1970). Effects of local geology on ground motion near San Francisco Bay. Bull. Seismol. Soc. Am. 60, 29–61. doi:10.1785/BSSA0600010029
Bouchon, M., and Barker, J. S. (1996). Seismic response of a hill: The example of Tarzana, California. Bull. Seismol. Soc. Am. 86, 66–72. doi:10.1785/BSSA08601A0066
Bouckovalas, G. D., and Papadimitriou, A. G. (2005). Numerical evaluation of slope topography effects on seismic ground motion. Soil Dyn. Earthq. Eng. 25, 547–558. doi:10.1016/j.soildyn.2004.11.008
Brocher, T. M. (2005). Empirical relations between elastic wavespeeds and density in the earth's crust. Bull. Seismol. Soc. Am. 95, 2081–2092. doi:10.1785/0120050077
Buech, F., Davies, T., and Pettinga, J. (2010). The little red hill seismic experimental study: Topographic effects on ground motion at a bedrock-dominated mountain edifice. Bull. Seismol. Soc. Am. 100, 2219–2229. doi:10.1785/0120090345
Burjánek, J., Edwards, B., and Fäh, D. (2014). Empirical evidence of local seismic effects at sites with pronounced topography: A systematic approach. Geophys. J. Int. 197, 608–619. doi:10.1093/gji/ggu014
Burjánek, J., Moore, J. R., Yugsi Molina, F. X., and Fäh, D. (2012). Instrumental evidence of normal mode rock slope vibration. Geophys. J. Int. 188, 559–569. doi:10.1111/j.1365-246X.2011.05272.x
Ding, H., Yu, Y., and Zheng, Z. (2017). Effects of scarp topography on seismic ground motion under inclined P waves. Rock Soil Mech. 38, 1716–1724+1732. doi:10.16285/j.rsm.2017.06.021
Galvez, P., Petukhin, A., Somerville, P., Ampuero, J. P., Miyakoshi, K., Peter, D., et al. (2021). Multicycle simulation of strike-slip earthquake rupture for use in near-source ground-motion simulations. Bull. Seismol. Soc. Am. 111, 2463–2485. doi:10.1785/0120210104
Gangi, A. F., and Wesson, R. L. (1978). P-wave to Rayleigh-wave conversion coefficients for wedge corners; model experiments. J. Comput. Phys. 29, 370–388. doi:10.1016/0021-9991(78)90140-7
Geli, L., Bard, P.-Y., and Jullien, B. (1988). The effect of topography on earthquake ground motion: A review and new results. Bull. Seismol. Soc. Am. 78, 42–63. doi:10.1785/BSSA0780010042
Gu, L., Ding, H., and Yu, Y. (2017). Effects of scarp topography on seismic ground motion under inclined SV waves. J. Nat. Disast. 26, 39–47. doi:10.13577/j.jnd.2017.0405
Harris, R. A. (1998). Forecasts of the 1989 loma prieta, California, earthquake. Bull. Seismol. Soc. Am. 88, 898–916. doi:10.1785/BSSA0880040898
Hartzell, S. H., Carver, D. L., and King, K. W. (1994). Initial investigation of site and topographic effects at Robinwood Ridge, California. Bull. Seismol. Soc. Am. 84, 1336–1349. doi:10.1785/BSSA0840051336
Hartzell, S., Ramírez-Guzmán, L., Meremonte, M., and Leeds, A. (2017). Ground motion in the presence of complex topography II: Earthquake sources and 3D simulations. Bull. Seismol. Soc. Am. 107, 344–358. doi:10.1785/0120160159
Hough, S. E., Altidor, J. R., Anglade, D., Given, D., Janvier, M. G., Maharrey, J. Z., et al. (2010). Localized damage caused by topographic amplification during the 2010 M 7.0 Haiti earthquake. Nat. Geosci. 3, 778–782. doi:10.1038/ngeo988
Igel, H. (2017). Computational seismology: A practical introduction. Oxford, United Kingdom: Oxford University Press.
Kanamori, H., and Schubert, G. (2015). Treatise on geophysics: Earthquake seismology. Amsterdam, Netherlands: Elsevier Press.
Kang, S., Kim, B., Cho, H., Lee, J., Kim, K., Bae, S., et al. (2019). Ground-motion amplifications in small-size hills: Case study of gokgang-ri, South Korea, during the 2017 ML 5.4 pohang earthquake sequence. Bull. Seismol. Soc. Am. 109, 2626–2643. doi:10.1785/0120190064
Komatitsch, D., Tsuboi, S., Tromp, J., Levander, A., and Nolet, G. (2005). The spectral-element method in seismology. Geoph. Mono. Am. Geoph.Un. 157, 205.
La Rocca, M., Chiappetta, G. D., Gervasi, A., and Festa, R. L. (2020). Non-stability of the noise HVSR at sites near or on topographic heights. Geophys. J. Int. 222, 2162–2171. doi:10.1093/gji/ggaa297
Lee, S.-J., Chan, Y.-C., Komatitsch, D., Huang, B.-S., and Tromp, J. (2009a). Effects of realistic surface topography on seismic ground motion in the Yangminshan region of Taiwan based upon the Spectral-Element Method and LiDAR DTM. Bull. Seismol. Soc. Am. 99, 681–693. doi:10.1785/0120080264
Lee, S.-J., Chen, H.-W., Liu, Q., Komatitsch, D., Huang, B.-S., and Tromp, J. (2008). Three-dimensional simulations of seismic-wave propagation in the Taipei Basin with realistic topography based upon the spectral-element method. Bull. Seismol. Soc. Am. 98, 253–264. doi:10.1785/0120070033
Lee, S.-J., Komatitsch, D., Huang, B.-S., and Tromp, J. (2009b). Effects of topography on seismic-wave propagation: An example from northern Taiwan. Bull. Seismol. Soc. Am. 99, 314–325. doi:10.1785/0120080020
Leonard, M. (2010). Earthquake fault scaling: Self-consistent relating of rupture length, width, average displacement, and moment release. Bull. Seismol. Soc. Am. 100, 1971–1988. doi:10.1785/0120090189
Li, S. Y., and Liao, Z. P. (2002). Wave-type conversion caused by a step topography subjected to inclined seismic body wave. Earthq. Eng. Eng. Vib. 22, 9–15. doi:10.13197/j.eeev.2002.04.002
Lovati, S., Bakavoli, M. K. H., Massa, M., Ferretti, G., Pacor, F., Paolucci, R., et al. (2011). Estimation of topographical effects at Narni ridge (Central Italy): Comparisons between experimental results and numerical modelling. Bull. Earthq. Eng. 9, 1987–2005. doi:10.1007/s10518-011-9315-x
Luo, Y., Del Gaudio, V., Huang, R., Wang, Y., and Wasowski, J. (2014). Evidence of hillslope directional amplification from accelerometer recordings at qiaozhuang (sichuan — China). Eng. Geol. 183, 193–207. doi:10.1016/j.enggeo.2014.10.015
Luo, Y., Fan, X., Huang, R., Wang, Y., Yunus, A. P., and Havenith, H.-B. (2020). Topographic and near-surface stratigraphic amplification of the seismic response of a mountain slope revealed by field monitoring and numerical simulations. Eng. Geol. 271, 105607. doi:10.1016/j.enggeo.2020.105607
Ma, Q., Wang, F., Tao, D., Xie, Q., Liu, H., and Jiang, P. (2021). Topographic site effects of Xishan Park ridge in Zigong city, Sichuan considering epicentral distance. J. Seismol. 25, 1537–1555. doi:10.1007/s10950-021-10048-7
Magnoni, F., Casarotti, E., Michelini, A., Piersanti, A., Komatitsch, D., Peter, D., et al. (2013). Spectral-Element simulations of seismic waves generated by the 2009 L’Aquila earthquake. Bull. Seismol. Soc. Am. 104, 73–94. doi:10.1785/0120130106
Maufroy, E., Cruz-Atienza, V. M., Cotton, F., and Gaffet, S. (2015). Frequency-Scaled curvature as a proxy for topographic site-effect amplification and ground-motion variability. Bull. Seismol. Soc. Am. 105, 354–367. doi:10.1785/0120140089
Mayoral, J. M., De la Rosa, D., and Tepalcapa, S. (2019). Topographic effects during the September 19, 2017 Mexico city earthquake. Soil Dyn. Earthq. Eng. 125, 105732. doi:10.1016/j.soildyn.2019.105732
Moore, J. R., Gischig, V., Burjanek, J., Loew, S., and Fäh, D. (2011). Site effects in unstable rock slopes: Dynamic behavior of the Randa instability (Switzerland). Bull. Seismol. Soc. Am. 101, 3110–3116. doi:10.1785/0120110127
Nakamura, Y. (1989). A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Q. Rep. Railw. Tech. Res. Inst. 30, 25–33.
Ohtsuki, A., and Harumi, K. (1983). Effect of topography and subsurface inhomogeneities on seismic SV waves. Earthq. Eng. Struct. Dyn. 11, 441–462. doi:10.1002/eqe.4290110402
Paolucci, R. (2002). Amplification of earthquake ground motion by steep topographic irregularities. Earthq. Eng. Struct. Dyn. 31, 1831–1853. doi:10.1002/eqe.192
Pischiutta, M., Cultrera, G., Caserta, A., Luzi, L., and Rovelli, A. (2010). Topographic effects on the hill of Nocera Umbra, central Italy. Geophys. J. Int. 182, 977–987. doi:10.1111/j.1365-246X.2010.04654.x
Pitarka, A., Akinci, A., De Gori, P., and Buttinelli, M. (2021). Deterministic 3D ground-motion simulations (0–5 Hz) and surface topography effects of the 30 October 2016 Mw 6.5 Norcia, Italy, earthquake. Bull. Seismol. Soc. Am. 112, 262–286. doi:10.1785/0120210133
Rai, M., Rodriguez-Marek, A., and Yong, A. (2016). An empirical model to predict topographic effects in strong ground motion using California small- to medium-magnitude earthquake database. Earthq. Spectra 32, 1033–1054. doi:10.1193/113014eqs202m
Somerville, P., Irikura, K., Graves, R., Sawada, S., Wald, D., Abrahamson, N., et al. (1999). Characterizing crustal earthquake slip models for the prediction of strong ground motion. Seismol. Res. Lett. 70, 59–80. doi:10.1785/gssrl.70.1.59
Song, J., Gao, Y., and Feng, T. (2020). Influence of interactions between topographic and soil layer amplification on seismic response of sliding mass and slope displacement. Soil Dyn. Earthq. Eng. 129, 105901. doi:10.1016/j.soildyn.2019.105901
Stolte, A. C., Cox, B. R., and Lee, R. C. (2017). An experimental topographic amplification study at Los Alamos National Laboratory using ambient vibrations. Bull. Seismol. Soc. Am. 107, 1386–1401. doi:10.1785/0120160269
Stone, I., Wirth, E. A., and Frankel, A. D. (2022). Topographic response to simulated Mw 6.5–7.0 earthquakes on the seattle fault. Bull. Seismol. Soc. Am. 112, 1436–1462. doi:10.1785/0120210269
Trifunac, M. D., and Hudson, D. E. (1971). Analysis of the Pacoima Dam accelerogram-san Fernando, California, earthquake of 1971. Bull. Seismol. Soc. Am. 61, 1393–1141. doi:10.1785/BSSA0610051393
Tsai, V. C., Bowden, D. C., and Kanamori, H. (2017). Explaining extreme ground motion in Osaka basin during the 2011 Tohoku earthquake. Geophys. Res. Lett. 44, 7239–7244. doi:10.1002/2017GL074120
Tucker, B. E., King, J. L., Hatzfeld, D., and Nersesov, I. L. (1984). Observations of hard-rock site effects. Bull. Seismol. Soc. Am. 74, 121–136. doi:10.1785/BSSA0740010121
Wang, G., Du, C., Huang, D., Jin, F., Roo, R. C. H., and Kwan, J. S. H. (2018). Parametric models for 3D topographic amplification of ground motions considering subsurface soils. Soil Dyn. Earthq. Eng. 115, 41–54. doi:10.1016/j.soildyn.2018.07.018
Wang, L., Wu, Z., Xia, K., Liu, K., Wang, P., Pu, X., et al. (2019). Amplification of thickness and topography of loess deposit on seismic ground motion and its seismic design methods. Soil Dyn. Earthq. Eng. 126, 105090. doi:10.1016/j.soildyn.2018.02.021
Wang, X., Wang, J., Zhang, L., and He, C. (2021). Broadband ground-motion simulations by coupling regional velocity structures with the geophysical information of specific sites. Soil Dyn. Earthq. Eng. 145, 106695. doi:10.1016/j.soildyn.2021.106695
Wood, C. M., and Cox, B. R. (2016). Comparison of field data processing methods for the evaluation of topographic effects. Earthq. Spectra 32, 2127–2147. doi:10.1193/111515eqs170m
Yuan, X., and Liao, Z. (1996). Scattering of plane SH waves by arbitrary circular convex topography. Earthq. Eng. Eng. Vib. 16, 1–13. doi:10.13197/j.eeev.1996.02.001
Yuan, Y. O., Lacasse, M. D., and Liu, F. (2021). Full-wavefield, full-domain deterministic modeling of shallow low-magnitude events for improving regional ground-motion predictions. Bull. Seismol. Soc. Am. 111, 2617–2634. doi:10.1785/0120210031
Zevenbergen, L. W., and Thorne, C. R. (1987). Quantitative analysis of land surface topography. Earth Surf. Process. Landf. 12, 47–56. doi:10.1002/esp.3290120107
Zhou, H., Li, J., and Chen, X. (2020). Establishment of a seismic topographic effect prediction model in the Lushan Ms 7.0 earthquake area. Geophys. J. Int. 221, 273–288. doi:10.1093/gji/ggaa003
Keywords: topographic site effect, spectral element method, back-azimuth, dipping angle, relative elevation, smoothed curvature
Citation: Wang F, Ma Q, Tao D and Xie Q (2023) A numerical study of 3D topographic site effects considering wavefield incident direction and geomorphometric parameters. Front. Earth Sci. 10:996389. doi: 10.3389/feart.2022.996389
Received: 17 July 2022; Accepted: 20 September 2022;
Published: 05 January 2023.
Edited by:
Kun Ji, Hohai University, ChinaReviewed by:
Haiping Ding, Suzhou University of Science and Technology, ChinaZailin Yang, Harbin Engineering University, China
Copyright © 2023 Wang, Ma, Tao and Xie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qiang Ma, bWFxaWFuZ0BpZW0uYWMuY24=
 Fuchen Wang
Fuchen Wang Qiang Ma
Qiang Ma Dongwang Tao
Dongwang Tao Quancai Xie
Quancai Xie