Assessment of earthquake-triggered landslide susceptibility considering coseismic ground deformation

The distance to the surface rupture zone has been commonly regarded as an important influencing factor in the evaluation of earthquake-triggered landslide susceptibility. However, the obvious surface rupture zones usually do not occur in some buried-fault earthquake cases, which means information about the distance to the surface rupture is lacking. In this study, a new influencing factor named coseismic ground deformation was added to remedy this shortcoming. The Mid-Niigata prefecture earthquake was regarded as the study case. To select a more suitable model for generating the landslide susceptibility map, three commonly used models named logistic regression (LR), artificial neural network (ANN), and support vector machine (SVM) were also conducted to assess landslide susceptibility. The performances of these three models were evaluated with the receiver operating characteristic curve. The calculated results showed that the ANN model has the highest area under the curve (AUC) value of 0.82. As the earthquake triggered more landslides in the epicenter area, which makes it more prone to landslides in further earthquakes, the susceptibility analysis at two different mapping scales (the whole study area and the epicenter area) was also applied.

Introduction

Earthquake-triggered landslides are commonly seen in the earthquake disaster chain. The landslides not only bring loss of life and property but also seriously affect the post-earthquake rescue. By summarizing the data of 40 historical earthquake events in the world, Keefer (1984) discovered that the earthquake-triggered landslide was the main reason for the loss of life and property. More than 60 people were killed and nearly 100,000 people were displaced due to the Mid-Niigata earthquake in 2004 (Bandara and Ohtsuka, 2017). In 2008, the Wenchuan earthquake triggered nearly 200,000 landslides, killing about 20,000 people (Xu et al., 2012b). At present, numerous researchers regard susceptibility mapping as an effective way to hazard mitigation and disaster management, and several models have been used to generate landslide susceptibility maps.

At present, one type of commonly used method to evaluate the susceptibility of landslides is the physical-based method. For this type of method, the study area is usually divided into slope units and then LEM or FEM is applied to calculate the safety factor (FS) of each slope unit (Saade et al., 2016). However, the physical mechanism of the landslide is often very complicated, especially for the landslides caused by earthquakes. Due to the difficulty of obtaining enough parameters for slope dynamic analysis, it still is a tough job to assess landslide susceptibility with physical-based models in large-scale areas.

The statistical learning method was another important method for landslide susceptibility assessment. This type of method is based on the assumption that future landslides would easily occur under similar conditions to those of the previous landslides. By analyzing the characteristics of the current landslides, a set of influencing factors is usually selected to implement statistical learning and evaluate the landslide susceptibility map (Nguyen et al., 2019; Zhao et al., 2019; Nsengiyumva and Valentino, 2020; Vojteková and Vojtek, 2020). At present, many statistical learning methods are being used successfully to calculate the landslide susceptibility index (LSI) and generate earthquake-triggered landslide susceptibility maps (Xu et al., 2012a; Pham et al., 2016; Hong et al., 2017; Abeysiriwardana and Gomes, 2022). For example, Yang et al. (2015) established the susceptibility map of seismic landslides for the Lushan earthquake in Sichuan Province with an artificial weighting method. Shrestha and Kang (2019) used a maximum entropy model to produce the landslide susceptibility map of the central region of the Nepal Himalayas. However, the relatively good performance of these methods highly relies on local geo-environment factors and self-features of the methods. For different study areas, the most accurate method is also different. Thus, it is necessary to make comparisons between various methods for selecting a more suitable method which produces a more reliable landslide susceptibility map (Bui et al., 2016).

Gorum et al. (2011) pointed out that the influencing factors of seismic landslides should include seismic correlation parameters, geology parameters, and topography parameters. Ding and Hu (2014) conducted the cluster analysis and the maximum possible classification method to study seismic landslide susceptibility of Beichuan County in the Wenchuan earthquake. Influencing factors which include land-use type, seismic intensity, and annual rainfall were selected to produce a reasonable susceptibility map. Since earthquake-triggered landslides tend to occur frequently near the surface rupture zone (Xu et al., 2012b; Xu, 2014), numerous scholars took the distance to the surface rupture zone as an influencing factor in the evaluation of landslide susceptibility (Xu et al., 2012b; Xu, 2014). However, it is worth noting that some buried-rupture earthquakes often do not have obvious surface rupture zones, and the buried-rupture earthquakes can also trigger abundant landslides (Xu, 2014). The evaluation accuracy of landslide susceptibility for buried-rupture earthquakes is affected by a lack of the factor of the distance to rupture (Regmi et al., 2016). Therefore, it is necessary to improve the accuracy of landslide susceptibility assessment for buried-rupture earthquakes by introducing new influencing factors.

The Mid-Niigata earthquake, which occurred in 2004, has become an important case for studying landslides due to good seismography and a rich collection of seismic landslides. Wang et al. (2007) detected the relationship of landslide occurrence with geological, geomorphological conditions, slope geometry, and earthquake parameters for the Mid-Niigata earthquake. Bandara and Ohtsuka (2017) used the landslide occurrence ratio (LOR) to determine the correlation between the occurrence of earthquake-triggered landslides and geological attributes for the Mid-Niigata earthquake.

In this study, based on GIS technology, three statistical methods and two different scales are evaluated to assess the landslide susceptibility caused by the Mid-Niigata earthquake. First of all, we selected lithology, elevation, slope, slope aspect, surface curvature, distance from the road, and the peak value of earthquake acceleration as the influencing factors to evaluate the susceptibility of seismic landslides in the whole affected zone (large-scale area). For a large-scale area, three different statistical learning methods (Logistic regression (LR), support vector machine (SVM), and artificial neural network (ANN)) are utilized and compared to make reasonable seismic landslide susceptibility maps. As the epicenter area has a higher landslide frequency more prone to earthquake-triggered landslides, the seismic landslide susceptibility in this area is further evaluated. Finally, given the fact of very short surface ruptures, the Mid-Niigata earthquake was regarded as a buried-rupture earthquake (Maruyama et al., 2007). Coseismic ground deformation decomposed from high-resolution DEM is added as an influencing factor to improve the evaluation accuracy of the seismic landslide susceptibility for the epicenter area.

Study site and material

Study site

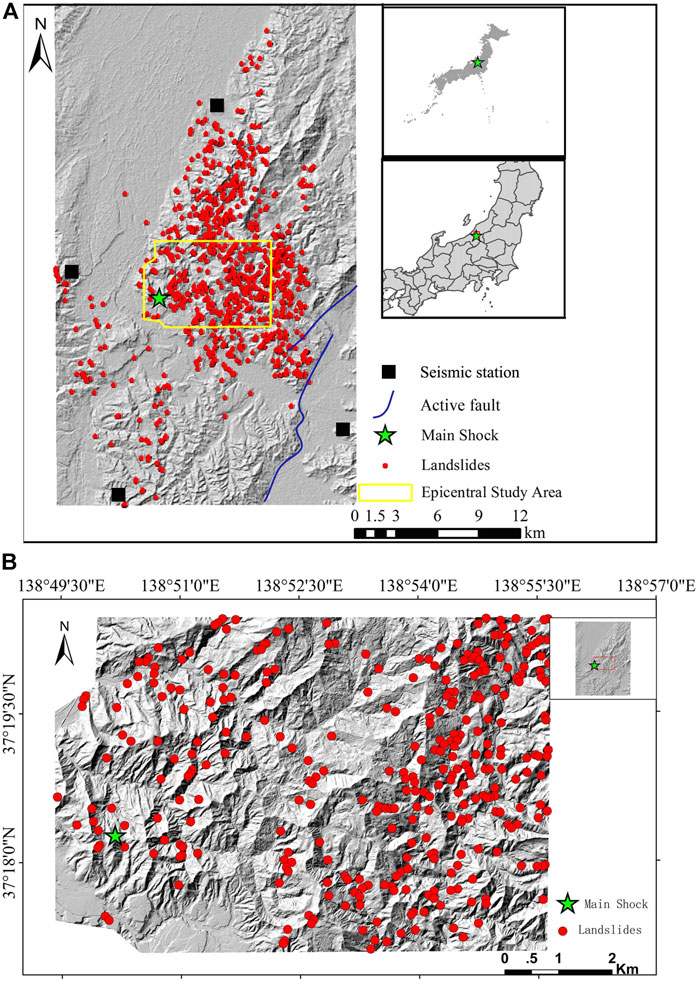
The Mid-Niigata earthquake occurred on 23 October 2004. The Japan Meteorological Agency (JMA) measured the magnitude of the mainshock as 6.8, the epicenter is located at 37°18′16.56″N, 138°50′10.32″E, and the focal depth is about 13.1 km (Chigira and Yagi, 2006; Kokusho et al., 2011). Within 3 days after the mainshock, more than 900 landslides were induced by the earthquake (Chigira and Yagi, 2006; Kokusho et al., 2014). After the earthquake sequences, a very small surface rupture was found along a previously unmapped northern extension fault zone. The length of the surface rupture was about 1 km (Maruyama et al., 2007). The surface slip of the Mid-Niigata earthquake event was also very small (<20 cm of vertical displacement). In addition, the surface rupture zone is also far away from the epicenter zone, where seismic landslides have concentrated distribution (Sato et al., 2005), i.e., the study area of seismic landslide susceptibility did not contain the surface rupture zone. So in this study, we consider that the surface rupture zone has little effect on the formation of seismic landslides and regard the earthquake as a buried-rupture earthquake.

Landslide inventory

In this study, the assessment of seismic landslide susceptibility is performed on two scales, the large area and the epicenter area. As shown in Figure 1, the large-scale area is 22 km wide (east to west) and 40 km long (north to south). The total area of the large-scale area is about 880 km². The epicenter area is 7 km long (north to south) and 9 km wide (west to east). The total area is about 56 km². The epicenter area is located in the bordering area between Nagaoka City and Ojiya City.

FIGURE 1

FIGURE 1. Locations of landslides in the study area: (A) large-scale area; (B) epicenter area.

Many methods have been utilized to set up landslide inventory maps, including satellite image interpretation, aerial photography, field survey, and historical landslide records (Vařilová et al., 2015). In this research, the landslide inventory map was interpreted from satellite image data and then checked by field survey data (Kokusho 2008; Kokusho et al., 2009). As shown in Figure 1A, a total of 957 landslide locations were recorded in the large-scale area, most of which are distributed in the mountainous area around the epicenter area and spread to the northeastern mountainous area. There are also some landslides located in the eastern and southern mountain areas. The landslide inventory map of the epicenter area is also shown in Figure 1B.

Landslide influencing factors

The factors that affect the occurrence of earthquake-triggered landslides usually include geology, topography, hydrology, climate, human activities, and earthquake-related parameters. Based on the availability of data and impacted factors used in previous studies (Reichenbach et al., 2018), seven landslide influencing factors (lithology, elevation, slope, slope aspect, surface curvature, peak ground acceleration, and the distance from the road) were taken into consideration for landslide susceptibility analysis for the large-scale area. In the later analysis in the epicenter area, coseismic ground deformation was added as an influencing factor. The scales of the landslide influencing factors are shown in Table 1.

TABLE 1

TABLE 1. Scales of the landslide-influencing factors.

Lithology directly determines the physical and mechanical properties of the slope, which have a direct impact on slope stability. The lithology maps in the large area and the epicenter area are shown in Figure 2A and Figure 3A. The elevation also affects the occurrence of seismic landslides (Hasegawa et al., 2009). The elevation has been regarded as a key factor determining the gravitational potential energy of the terrain. Elevation also indicates the amplification effect of seismic-induced landslides. The elevation maps of the large-scale area and the epicenter area are shown in Figure 2B and Figure 3B, respectively. The slope angle has a direct impact on slope stability that determines the ratio of the anti-sliding force to sliding force. The slope angle maps of the large-scale area and epicenter area are shown in Figure 3C and Figure 3C, respectively. According to previous studies (Xu et al., 2012a; Pham et al., 2016; Hong et al., 2017), the slope aspect is divided into nine groups. The slope aspect maps of the large study area and the epicenter area are shown in Figure 2D and Figure 3D, respectively, and the P and FL mean the flat area. The surface curvature distributions in the large-scale and epicenter areas are shown in Figure 2E and Figure 3E, respectively.

FIGURE 2

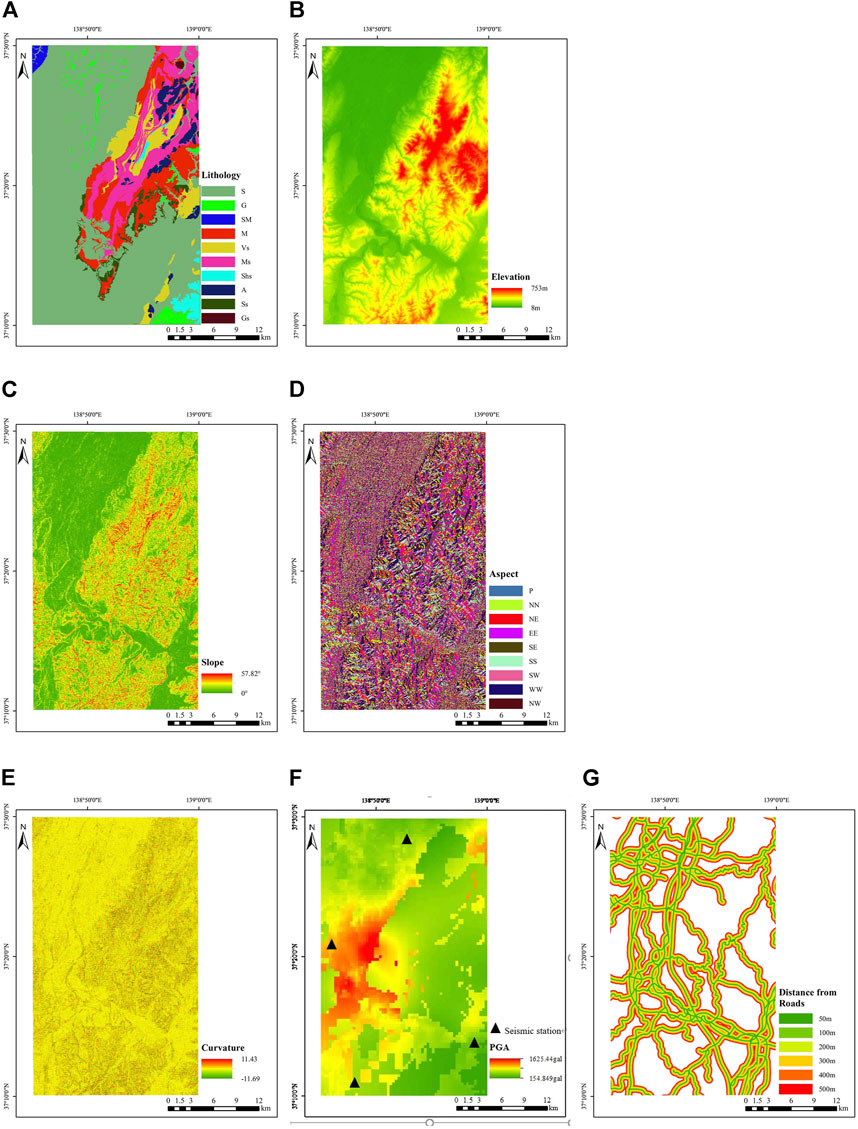
FIGURE 2. Landslide-controlling factors of the large area: (A) lithology; (B) elevation; (C) slope degree; (D) aspect; (E) profile curvature; (F) PGA; and (G) distance to roads.

FIGURE 3

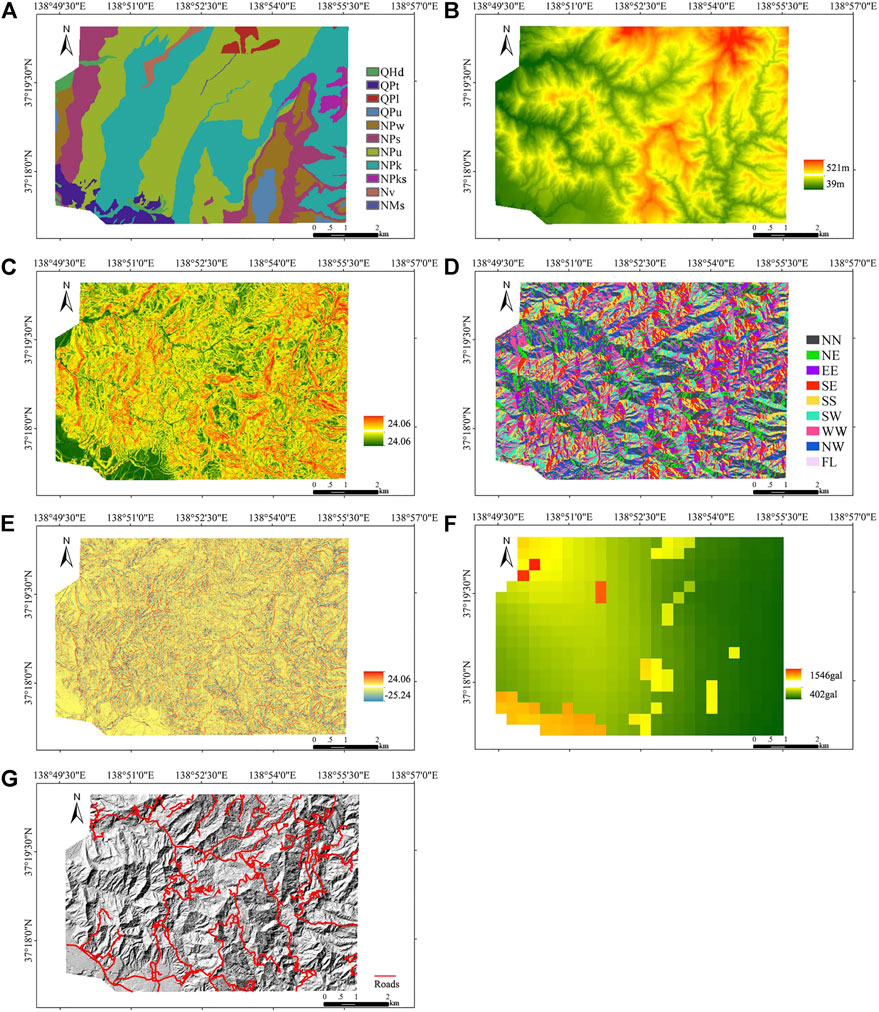
FIGURE 3. Landslide-controlling factors of the epicenter area: (A) lithology; (B) elevation; (C) slope degree; (D) aspect; (E) profile curvature; (F) PGA; and (G) distance to roads.

The peak ground acceleration (PGA) of an earthqauke is the maximum absolute value of the acceleration of the surface soil in the earthquake (Tian et al., 2019; Xu and Xu, 2013; Xu et al., 2013; Li et al., 2013; Xu et al., 2012a,b). The PGA was obtained from inversion analysis based on the K-NET and KiK-net observations. The resolution of PGA data is 350 m. The distribution of peak accelerations in the large-scale area and the epicenter area is shown in Figure 2F and Figure 3F, respectively. Human activities have also greatly impacted the topography features. Road construction not only produced a new steep cutting slope but also caused great disturbance to the original slope. Therefore, the distance to the road is taken into account in the assessment of landslide susceptibility. In this study, the locations of high-grade roads like expressways were interpreted from the satellite image. The distances to the road map were divided into seven classes (0–50, 50–100, 100–200, 200–300, 300–400, 400–500, and >500 m). The distances to road maps of the large-scale area and the epicenter area are shown in Figure 2G and Figure 3G, respectively.

For earthquakes with surface ruptures, previous research studies show that there is a clear connection between landslide distribution and the distance to the rupture zone (Xu et., al 2012b; Xu, 2014), which means the distance to the surface rupture could be used as an influencing factor. However, for buried-rupture earthquakes, as very short or no surface rupture is exposed, it is difficult to establish the relationship between the distribution of landslides and surface rupture. Therefore, it is necessary to introduce new influencing factors to improve the accuracy of landslide susceptibility analysis for buried-rupture earthquakes.

Coseismic ground deformation characterizes the absolute permanent ground deformation before and after the earthquake, and it has been demonstrated that there is a good correlation between landslide distribution and the values of coseismic ground deformation (Chang et al., 2005; Zhao et al., 2014). Therefore, coseismic ground deformation could make up for the disadvantage of losing surface rupture in the assessment of seismic landslide susceptibility to a certain extent. Coseismic ground deformation can be obtained by decomposed high-resolution DEM before and after the earthquake (Zhang et al., 2010; Zhao et al., 2012). Figure 4 shows the description of landform changes in Lagrangian and Eulerian manners. Supposing that a small patch i of the ground surface with one particular node mapped on it is inclined in East-West (x) and North-South (y) directions, Δz_i^e is expressed in terms of the Lagrangian vector {Δx_i^l Δy_i^l Δz_i^l} of the movement of the patch as

${\Delta }_{Z_i}^e=\left\{t_{X,i}{t}_{y,i}1\right\}\cdot {\left\{\Delta X_i^l\Delta y_i^l\Delta Z_i^l\right\}}^T,(1)$

where t_x,i and t_y,i are tangents of the patch plane in the x and y directions, respectively. Taking three adjacent patches, i1, i2, and i3 in a triangle and using the displacement of its center {Δx_i^l Δy_i^l Δz_i^l} as the representative displacement vector of the triangle, the following simultaneous equations are to be satisfied:

$\left\{\begin{array}{l}\Delta {\mathrm{z}}_{i1}^e\\ \Delta {\mathrm{z}}_{i2}^e\\ \Delta {\mathrm{z}}_{i2}^e\end{array}\right\}=\left[\begin{array}{l}{t}_{x,i1}{t}_{x,i1}1\\ t_{x,i1}{t}_{x,i1}1\\ t_{x,i1}{t}_{x,i1}1\end{array}\right]\left\{\begin{array}{l}\Delta x_i^l\\ \Delta x_i^l\\ \Delta x_i^l\end{array}\right\}=T•\left\{\begin{array}{l}\Delta x_i^l\\ \Delta x_i^l\\ \Delta x_i^l\end{array}\right\}.(2)$

FIGURE 4

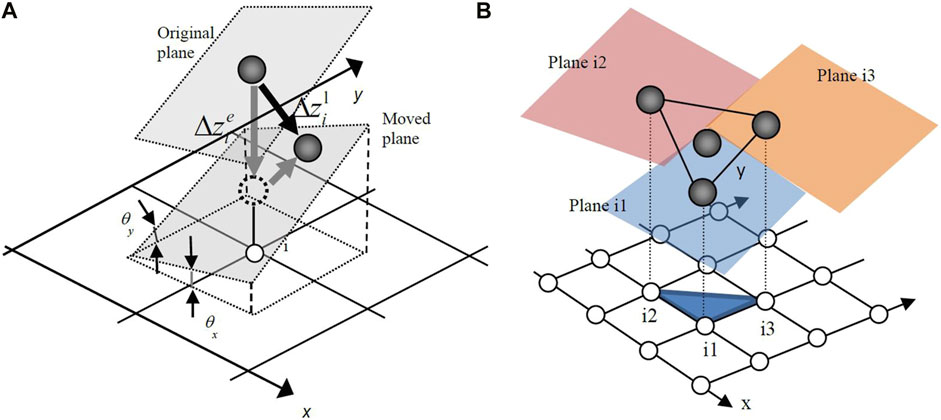
FIGURE 4. Description of landform changes in the Lagrangian and Eurlaian manners: (A) scheme of one point and (B) scheme of three-point (adopted from Zhao et al., 2012).

An assumption that the triangle undergoes a rigid body translation is used in the aforementioned formulation. The inclination of the moving plane (plane i1) is essential for calculating t_x,i and t_y,i. Suppose the equation of the moving plane is expressed as

$z=ax+by+c,(3)$

where a= t_x,i1=tanθ_x,i1 and b= t_y,i1=tanθ_y,i1

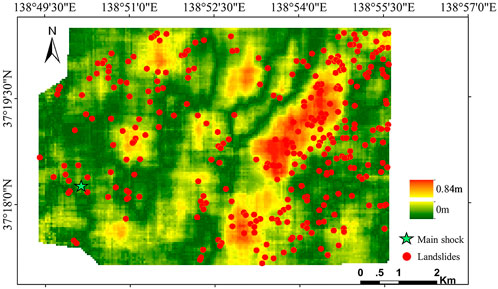
Zhao et al. (2012) provided a more rigorous solution method, including the definition of a nominal plane, the improvement of DEM comparability, and matrix condition test. In this study, we used the method proposed by Zhao et al. (2012) to calculate coseismic ground deformation. It is to be noted that the decomposition algorithm requires high-resolution (2 m) DEM. Thus, coseismic ground deformation is added as an influencing factor for the epicenter area only. The DEMs before the earthquake were derived from aerial photos shot by the Geospatial Information Authority of Japan in 1975 and 1976. Triangulation points prepared for road construction in 1986 were then used to orthogonalize and digitize these photos by Aero Asahi (2004). The standard deviation of the digitized aero photos from the triangulation data is 0.589 and 0.517 m in the horizontal and vertical directions, respectively. The DEMs after the earthquake were prepared by airborne LiDAR scanning conducted by Nakanihon Air Service on 24 Oct 2008, the second day of the mainshock and three major aftershocks. After scanning and post-processing standard courses, calibration courses were performed. The average differences for the x coordinate, y coordinate, and elevation are 0.09, 0.2, and 0.06 m respectively, showing good repeatability of scanning. Both sets of DEMs have a resolution of 2 m×2 m. Since the two sets of DEMs were prepared in different ways, it is not appropriate to directly compare them in the calculation. The contour line derived from the 1975 DEMs is quite smooth while that from the 2004 DEMs is curly and tilted owing to the high spatial frequency components. Therefore, we used smoothed elevations instead of the original ones for the 2004 DEMs by substituting the x and y coordinates of each point into the equation of its nominal plane. Given that three adjacent points undergo a rigid body translation movement, their coseismic deformation can be decomposed by solving simultaneous equations. A cut-off window was selected according to regional geology to obtain the tectonic displacements. The properly defined nominal plane could also fully or partially eliminate terrain changes owing to human activities during the time gap between two sets of DEMs since the size of the smooth window is larger than all man-made changes. In addition, to verify the accuracy of the calculated coseismic ground deformation, the calculated displacements were also compared with those at points of triangulation. In total, 11 available triangulation points buried on roads were used. The compared results showed that the difference between the observed displacement and calculated displacement was small, which demonstrated that the calculated coseismic ground deformation is accurate. Details can also be found in the studies by Konagai et al. (2009) and Zhao et al. (2012). The distribution of coseismic ground deformation in the epicenter area is shown in Figure 5.

FIGURE 5

FIGURE 5. Distribution of coseismic ground deformation in the epicenter area.

The orientation of the computed coseismic ground deformation could be divided into two directions: lateral components and vertical components. Zhao et al. (2012) compared the location of earthquake-triggered landslides with the displacement field of lateral components and vertical components, respectively. The results showed that landslide clusters were found within large lateral deformation regions, while landslides seem to be off where the vertical displacement is large. Therefore, in this study, only lateral deformation is used. Figure 5 also shows the distribution of the absolute value of the lateral ground deformation.

Landslide data preparation

In this study, the numbers of landslide points and non-landslide points are sampled at a ratio of 1:1.2 for the large-scale area. A total of 1,117 non-landslide points’ data were randomly selected in the non-landslide area. Subsequently, 70% of the landslide points and non-landslide points were selected randomly from the landslide inventory map as the training dataset, with the rest as the testing dataset. To obtain optimum results, we randomly selected the sample points (landslides points and non-landslide points) 10 times, respectively. For different selections, the training and testing samples are different, but the numbers of sample points are the same. In the epicenter area, as the used method to calculate coseismic ground deformation needs high-resolution DEM, the whole epicenter area was converted into 2 m pixels. The total number of pixels is 555,324, and the number of seismic landslide pixels is 45,852. Similarly, 70% of the landslide pixels and non-landslide pixels were selected randomly as the training dataset, with the remaining 30% as the testing dataset.

Methodology

Logistic regression

Logistic regression is suitable for describing the relationship between the categorical outcome (landslide or non-landslide) and input variables (landslide-affecting factors). The principle of the LR is to analyze the spatial relationship between the landslide-affecting factors and the occurrence of a landslide. The results of the regression usually can be interpreted as the probability which is constrained in the interval between 0 and 1.

The LR is indicated by an equation of the form

$Y=f\left(P\right)=\ln \left(\frac{P}{1-P}\right)={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdot \cdot \cdot +{\beta }_n{X}_n,(4)$

where Y represents outcome variables (landslide or non-landslide), X = X₁, X₂ … Xn represents input variables, n is the nth landslide-affecting factor, β₀ is the intercept condition, and β₁, β₂ … β _n are the regression coefficients (Tu, 1996).

The SPSS 10.0 was used to conduct the LR analysis to predict the correlation between the occurrence of landslides and landslide-affecting factors. The regression coefficients were then obtained.

The probability of a landslide event (P) can be determined from the following equation:

$P=P\left(Y/X\right)=\frac{e^{{\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdot \cdot \cdot +{\beta }_{n}X}}{1+e^{{\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdot \cdot \cdot +{\beta }_{n}X}}.(5)$

The probability values change from 0 to 1, with 0 indicating a 0% probability of landslide occurrences and one indicating a 100% probability.

Artificial neural networks

An ANN model has many advantages compared with other models (Yi̇lmaz, 2009a). An ANN could process imprecise and fuzzy data without any assumptions. The ANN model with the most frequently used back-propagation BP algorithm (Pradhan and Lee, 2010b) is used in this study.

The model mainly consists of one input layer, several hidden layers, and an output layer. There are usually two stages for using an ANN, the training stage and classifying stage. During the training stage, the hidden and the input layer neurons handle their inputs by a corresponding weight, sum the product, and then deal with the sum using a nonlinear transfer function to generate a result. During the classification period, the ANN predicts a target value by adjusting the weights in accordance with the errors between the actual output values and the target output ones and makes the difference minimum.

In this study, the number of hidden layer nodes is calculated by the following equation (Yi̇lmaz, 2009a):

$N_h=2N_i+1,(6)$

where N_i is the number of input nodes and N_h is the number of hidden nodes.

Then, a three-layer network with one input layer (7 neurons), one hidden layer (15 neurons), and one output layer was used in the large-scale area. In the epicenter area, a three-layer network consisting of one input layer (8 neurons), one hidden layer (17 neurons), and one output layer was utilized. It is important to decide the initial weight range influencing the convergence of the model. In this study, the initial weights were randomly selected from a small range of [-0.25 to 0.25] as proposed by Yi̇lmaz, 2009b. For the hidden layer, the activation function is the hyperbolic tangent, and the activation function is the softmax function for the output layer. We did not use an optimization algorithm for the ANN model.

Support vector machine

The SVM model employs nonlinear transformations of the covariates into a higher dimensional feature space. The two main principles of the SVM are the optimal classification hyperplane and the use of a kernel function (Yao et al., 2008).

The details of a two-class SVM model are described as follows. Given a set of linear separable training vectors x_i (i=1,2 … n) that consist of two categorical outcomes (landslide or non-landslide denoted as y= ±1), the purpose of the SVM is to find an n-dimensional hyperplane differentiating the two categories by the maximum gap.

Mathematically, the gap $\frac{1}{2}{\Vert w\Vert }^2$could be a minimized subject to the following constraints:

$y_i\left(\left(w\cdot x_i\right)+b\right)\ge 1,(7)$

where ||w|| is the norm of the normal of the hyperplane, b is a scalar base, and (·) denotes the scalar product operation. Using the Lagrangian multiplier, the cost function can be defined as

$L=\frac{1}{2}{\Vert w\Vert }^2-{\displaystyle \sum }_{i=1}^n{\lambda }_i\left(y_i\left(\left(w•x\right)+b\right)\right)\ge 1,(8)$

where λ_i is the Lagrangian multiplier. The solution can be obtained by the dual minimization of Eq. (8) with respect to w and b

In this study, the two-class SVM method was used due to its good performance in landslide susceptibility analysis (Yao et al., 2008; Yi̇lmaz, 2010).

Results

Training and validating the statistical models for the large-scale area

In this study, the performances of the three models (LR, ANN, and SVM) for the large-scale area were validated using a receiver operating characteristic (ROC) curve. The area under the curve (AUC) indicates how good the statistical model is. It means the model has perfect performance when the AUC value equals to 1. A higher AUC value indicates better performance of the statistical model.

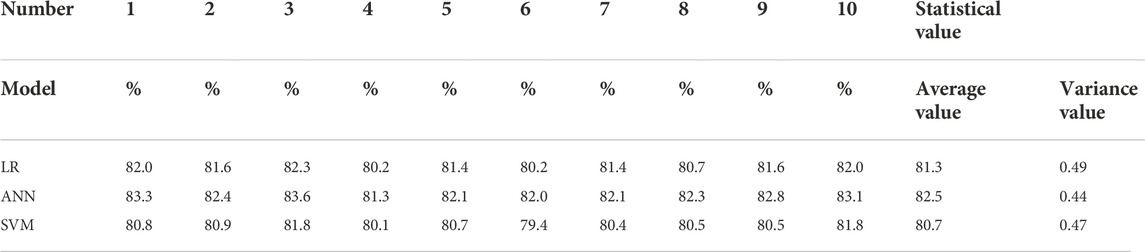
Because each sample dataset is selected randomly, the landslide susceptibility calculated by the same model is not the same. To determine the best model, the models are utilized 10 times for analysis of randomly selected datasets, respectively. For different analyses, the training and testing samples are different. For the same analyses, the training samples and testing samples are the same for all three models. The area under the ROC curve (AUC) of each analysis was compared to explore the difference between the three methods. The results are shown in Table 2.

TABLE 2

TABLE 2. AUC values of different models in the large-scale area.

Table 2 shows that the ANN model performed the best among the three models with the highest AUC value and the accuracy of the SVM model was the worst. Based on the maximum AUC values of 10 simulations, the ANN simulation result was also the best (83.6%). The average value and variance of the ANN model were 82.5 and 0.44%, respectively, which was better than those of the LR and SVM models. It means the robustness of the ANN model is better than that of the LR and SVM models.

Yi̇lmaz (2009a) used three models including frequency ratio (FR), ANN, and LR to generate the landslide susceptibility maps of Kat County (Tokat–Turkey). The result showed that the ANN model performed better than the other models. Yi̇lmaz (2010) utilized four different models, namely, conditional probability (CP), LR, ANN, and SVM models to assess the landslide susceptibility of Koyulhisar (Sivas, Turkey). The results also showed that the performance of the ANN model was the best. Some other research studies also showed that the ANN model performed more accurately than the other models (Gómez and Kavzoglu, 2005; Yesilnacar and Topal 2005). We consider the ANN model performed better than the other models because it has a good global searching ability and can learn the near-optimum solution without the gradient information of error functions. As there are about a total of 2,000 samples in the calibration and validation sets, large numbers of samples in the calibration stage will lead to sufficient training of the model and establish an appropriate structure of the ANN model. So the ANN model performs well on the condition that those large numbers of samples were available. For any algorithm, the quantity and quality of samples have key impacts on the accuracy of the predicted results the algorithm makes.

Development of landslide susceptibility maps for the large-scale area

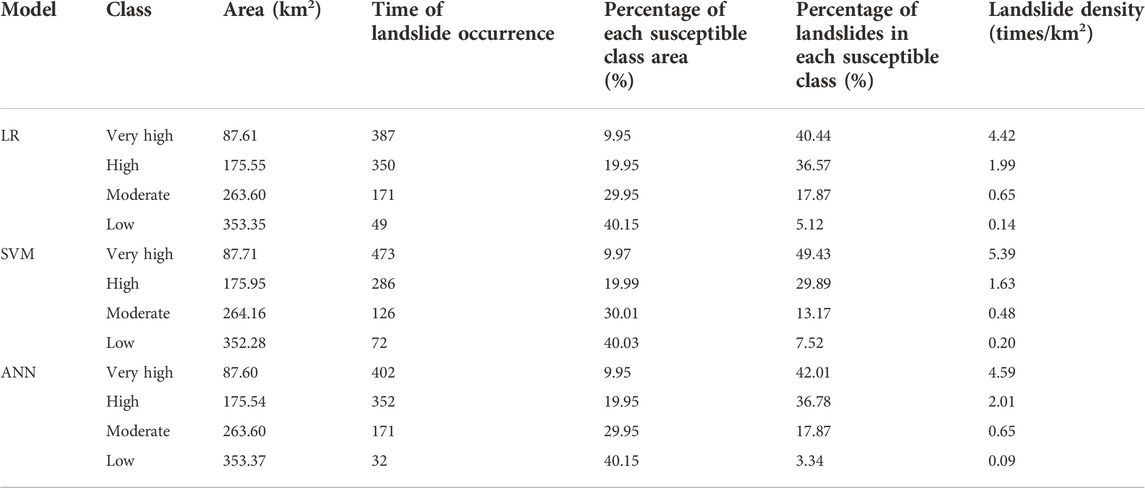
In this study, all three models have been used to calculate the landslide susceptibility index (LSI) and then generate the landslide susceptibility maps. There are several mathematical methods including quantiles, natural breaks, standard deviation, equal intervals, and descending area percentage to be reclassified in the LSI (Ayalew et al., 2004). Among the aforementioned methods, the descending area percentage technique is the most widely used. In this study, the descending area percentage technique was used. The landslide susceptibility maps were constructed into four classes: low (40%), moderate (30%), high (20%), and very high (10%). The landslide density was used to assess the performance of landslide susceptibility maps. The landslide density (LD) is defined as the ratio of the number of landslides and the area of each susceptible class.

The calculated landslide densities by using the three different models are shown in Table 3. It can be observed that all maps present good spatial predictions of landslides as landslide density is ascending from very low to very high class (Yi̇lmaz, 2009b). The results using the ANN model show that the very high class contains 42.01% of the total landslides; however, it only covers 9.95% of the total study area, and the LD of the very high class was 4.59. In comparison, the low classes only contain 3.34% landslides; however, it covers 40.15% area and the LD of the low class was 0.09. This indicates that the ANN model performed well in susceptibility classification as it fits well with the landslide inventories.

TABLE 3

TABLE 3. Distribution of different classes obtained by different methods.

The landslide susceptibility maps of different methods are shown as Figure 6. The analysis results of LR, SVM, and ANN models are very close. The epicenter area is a very high susceptible area, the northeast and the southwest mountain areas are high and very high susceptible areas, respectively, and the northern plains area is distributed with the low susceptible class. The susceptibility map of the ANN model shows that the high susceptible areas and low susceptible areas are more concentrated into blocks, and zonation produced by the SVM and LR are more dispersed. Overall, all three models could generate reasonable landslide susceptibility maps.

FIGURE 6

FIGURE 6. Landslide susceptibility maps using different models for the large area. (A) LR model. (B) SVM model. (C) ANN model.

Model performance validation for the epicenter area

From the landslide susceptibility map of the large-scale area, it is known that the susceptibility level in the epicenter area is generally high. Since it is still too costly to remediate all slopes in the approximately 60 km² area, it is necessary to further evaluate the landslide susceptibility in the epicenter area. It can be seen in Section 4.1 that the ANN model is the most suitable model for landslide susceptibility assessment in this area. Therefore, we only use the ANN model to analyze and evaluate the landslide susceptibility in the epicenter area.

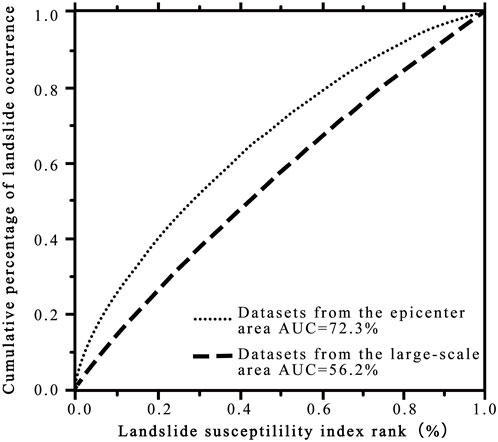
First, to evaluate the significance of landslide susceptibility analysis by considering different scales, the values of the AUC for the epicenter area are calculated in two different conditions. First, we calculate the values of the AUC based on the corresponding calculated LSI of the epicenter area from the large-scale (whole affected area) datasets. Then, the values of the AUC are calculated based on the calculated LSI from the epicenter area datasets. The values of the AUC of the two different conditions are shown in Figure 7. The results show that the AUC is 56.2% based on the calculated LSI from the large-scale datasets, in contrast, the AUC is 72.3% based on the calculated LSI from the epicenter area solely. The results show that it is necessary to assess landslide susceptibility under different scales.

FIGURE 7

FIGURE 7. Analysis of the ROC curve under different scales.

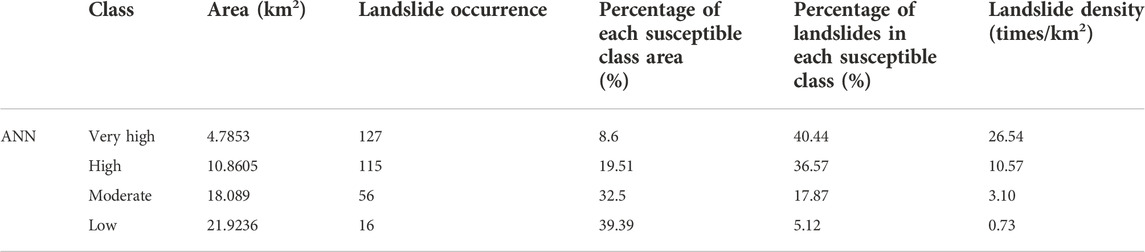
Subsequently, the landslide density and landslide susceptibility map of the epicenter area were obtained as shown in Table 4 and Figure 8. The results show that the very high class contains 40.44% of the total landslides; however, it only covers 8.6% of the epicenter area and the LD of the very high class was 26.54. In comparison, the low classes contain only 5.12% landslides; however, it covers 40.15% area and the LD of the low class was only 0.73. The landslide density increases gradually between the low class and very high class. This indicates that the landslide susceptibility map fits well with the landslide inventories.

TABLE 4

TABLE 4. Distribution of different classes in the epicenter area.

FIGURE 8

FIGURE 8. Landslide susceptibility map of the epicenter area.

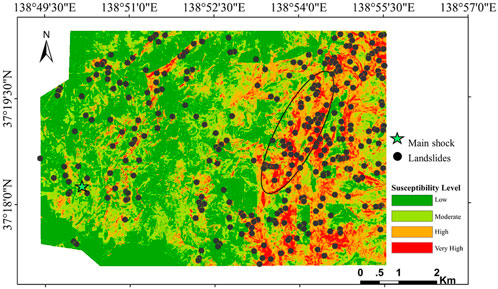
As shown in Figure 8, the very high-class area is mainly distributed along the long axis of the ellipse in the east of the study area, and a large amount of deep-seated landslides occurred in this area. The high-susceptibility area is also distributed in the northwestern area. The occurrence possibility of landslides in the central area and southwest plain area is relatively low. Compared with the epicenter area parts in the landslide susceptibility map of the large-scale area, the landslide susceptibility maps obtained by the epicenter area research have a better discrimination degree, which can meet the key prevention and control requirements in the small area.

Discussion

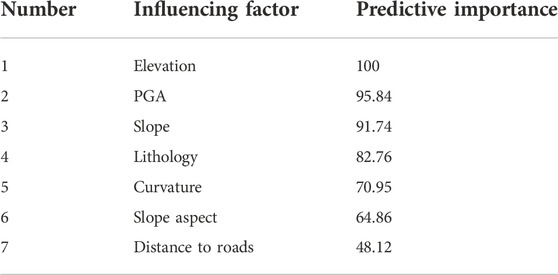
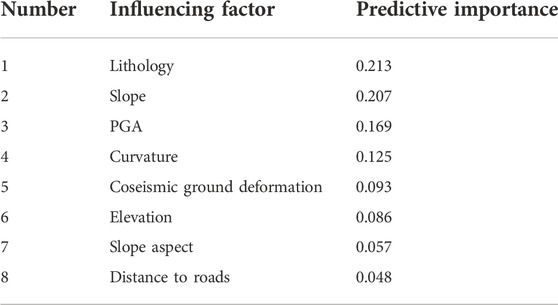
It is important to select suitable influenced factors in landslide susceptibility mapping. The analysis of the predictive importance for the input variables in the large-scale analysis is also conducted. The predictive importance of the input variables in the large-scale analysis is calculated by the variance method. The predictive importance of the influence factors in the large-scale analysis is shown in Table 5.

TABLE 5

TABLE 5. Predictive importance of different influencing factors in the large-scale analysis.

As shown in Table 5, elevation has the greatest impact on the occurrence of earthquake landslides and the impact of other factors is in order of peak earthquake acceleration, slope, lithology, curvature, aspect, and distance from the road. As all values are positive, it means all the selected influencing factors make a positive contribution to the assessment of landslide susceptibility in large-scale analysis.

Influencing factors including lithology, elevation, slope, slope aspect, surface curvature, peak ground acceleration, the distance from the road, and coseismic ground deformation were considered in the small-scale analysis. Since the contribution of these factors to landslide models might be different, it is necessary to quantify the effects of influential factors on the assessment of landslide susceptibility. The analysis of variance method has been utilized to evaluate the predictive capability of these factors in the small-scale analysis. The factors with higher variance values indicate a higher contribution to landslide models and vice versa. The predictive capability of eight landslide-affecting factors is shown in Table 6.

TABLE 6

TABLE 6. Predictive importance of different influencing factors in the epicenter area.

As Table 6 shows, lithology has the greatest impact on the occurrence of earthquake landslides and the impact of other factors is in order of slope, peak earthquake acceleration, curvature, coseismic ground deformation, elevation, aspect, and distance from the road. As all values are positive, it means all the selected influenced factors make a positive contribution to the assessment of landslide susceptibility. Reichenbach et al. (2018) critically reviewed the statistically-based landslide susceptibility assessment literature by systematically searching for and then compiling an extensive database of 565 peer-review articles from 1983 to 2016. The results showed that elevation, aspect, and distance from the road are commonly chosen as influencing factors in the assessment of landslide susceptibility. The importance of coseismic surface deformation is higher than the elevation, aspect, and distance from the road. It means that coseismic ground deformation should be regarded as an important factor in the assessment of landslide susceptibility.

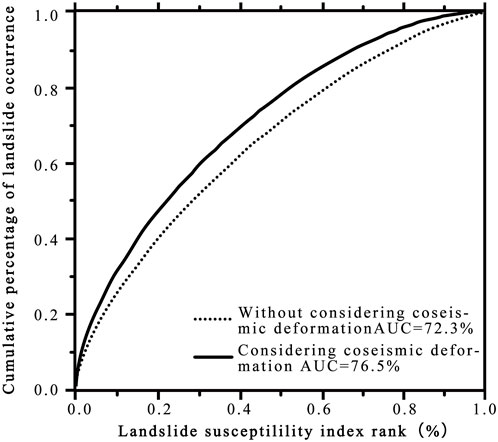
Then, to evaluate the effects of the new factor coseismic ground deformation on the assessment of landslide susceptibility, two different situations are considered. One situation regards coseismic deformation as an influencing factor, whereas the other does not. Figure 9 shows the values of the AUC by considering coseismic surface deformation or not. From Figure 9, it can be seen that the AUC is 72.3% without considering coseismic surface deformation, in contrast, the AUC is 76.5% by considering coseismic surface deformation. It means that coseismic surface deformation has a positive effect on the assessment of landslide susceptibility.

FIGURE 9

FIGURE 9. Analysis of the ROC curve considering coseismic surface deformation or not.

In addition, there are other several advantages to regarding coseismic ground deformation as an important factor in landslide mapping. Coseismic ground deformation will help to reveal hidden subsurface damage. It should be noted that not all deformation will directly lead the landslides. However, the area with large coseismic surface deformation often indicates that the movement of the rock mass may be further developed and the integrity of the rock mass is reduced, which renders slopes prone to landslip in future earthquakes again. Zhao et al. (2012) explored the localized coseismic deformation in Kizawa (a small village), Japan, after the earthquake. The results showed that the calculated coseismic deformation in Kizawa is relatively large but the landslides are sparse. However, after a detailed investigation, it was found that underground structures such as tunnels and wells were severely damaged. The road alignment of the Kizawa tunnel, which was buried 30 m beneath the ground surface, was shifted sideways 1–1.5 m in the east-to-southeast direction. Furthermore, two irrigation wells were dislocated at 30 and 20 m, beneath the ground, respectively. Therefore, it is highly possible that the ground underwent some subsurface damage at locations with large coseismic deformation. Although the deformation did not form landslides at these locations in the 2004 Mid-Niigata earthquake, as there was accumulated deformation within the rock and soil, a landslide will easily occur in the next earthquake event. Therefore, especially in the case of buried-fault earthquakes, coseismic surface deformation can be considered an important influencing factor in the assessment of earthquake landslide susceptibility.

However, it should be noted that some limitations still existed in this study. The spatial resolution of the PGA map in the epicenter area is relatively low. The PGA map of the epicenter area is the result of back-analysis from sparse seismic station data. It is to be noted that the used PGA map is also the highest resolution map that the authors could get and most back-analyses can offer. It also inferred that the low resolution of the PGA map is also the main reason that causes the relatively lower value of the AUC (0.72) in the epicenter area, as the value of the AUC in the large-scale area is 0.82 for the ANN model. However, in other words, the low value of the AUC also demonstrated the urgent demand for introducing new factors to improve the assessment of landslide susceptibility.

Conclusion

In this study, the LR, ANN, and SVM models are applied to generate landslide susceptibility maps based on the 2004 Mid-Niigata earthquake-triggered landslide inventories. A total of seven impact factors, namely, lithology, elevation, slope, aspect, surface curvature, peak acceleration, and the distance from the road are selected as the influenced factors. The ROC curve evaluation results clearly demonstrate that the map obtained from the ANN model performed the best among the three models. The variance of the AUC for randomly selected datasets by the ANN is also the smallest, which means that the ANN model has excellent robustness.

Therefore, the ANN model can be used for the assessment and development of landslide susceptibility maps. Then, the significance of landslide susceptibility analysis considering different scales is also evaluated. The results show that the AUC is 56.2% based on the datasets from the large-scale, in contrast, the AUC is 72.3% based on the datasets from the epicenter area solely. The results show it is necessary to assess landslide susceptibility under different scales. At the same time, we included coseismic ground deformation as the influencing factor for landslide susceptibility in the epicenter area. The AUC increased from 0.723 to 0.765 after considering the newly added factor. The predictive capability of eight landslide-affecting factors also showed that the importance of coseismic surface deformation is higher than the elevation, aspect, and distance from the road. Therefore, for the buried-rupture earthquake, coseismic surface deformation can be considered an important factor to evaluate the susceptibility of landslides.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YZ, ZH, and ZW conceived this research. YZ, JZ, and KK designed the methodology and performed the experiments. YZ and ZW analyzed the results and wrote the manuscript. All authors contributed to the preparation of this manuscript.

Funding

This research was supported financially by the National Natural Science Foundation of China (Grant No. 52178359 and Grant No 51988101), the Fundamental Research Funds for the Central Universities (2019FZJD002) and the Natural Science Foundation of Sichuan Province (Grant No. 2022NSFSC1129).

Acknowledgments

The authors appreciate Fuchu Dai in the Beijing University of Technology for his advice on improving the study.

Conflict of interest

ZH was employed by the company Powerchina Zhongnan Engineering Corp. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abeysiriwardana, H. D., and Gomes, P. I. A. (2022). Integrating vegetation indices and geo-environmental factors in GIS-based landslide-susceptibility mapping: Using logistic regression. J. Mt. Sci. 19, 477–492. doi:10.1007/s11629-021-6988-8

CrossRef Full Text | Google Scholar

Ayalew, L., Yamagishi, H., and Ugawa, N. (2004). Landslide susceptibility mapping using GIS-based weighted linear combination, the case in Tsugawa area of Agano River, Niigata Prefecture, Japan. Landslides 1 (1), 73–81. doi:10.1007/s10346-003-0006-9

CrossRef Full Text | Google Scholar

Bandara, S., and Ohtsuka, S. (2017). Spatial distribution of landslides induced by the 2004 Mid-Niigata prefecture earthquake, Japan. Landslides 14 (6), 1877–1886. doi:10.1007/s10346-017-0819-6

CrossRef Full Text | Google Scholar

Bui, D. T., Nguyen, Q. P., Hoang, N. D., and Klempe, H. (2016). A novel fuzzy K -nearest neighbor inference model with differential evolution for spatial prediction of rainfall-induced shallow landslides in a tropical hilly area using GIS. Landslides 14 (1), 1–17. doi:10.1007/s10346-016-0708-4

CrossRef Full Text | Google Scholar

Chang, K. J., Taboada, A., and Chan, Y. C. (2005). Geological and morphological study of the Jiufengershan landslide triggered by the Chi-Chi Taiwan earthquake. Geomorphology 71 (3), 293–309. doi:10.1016/j.geomorph.2005.02.004

CrossRef Full Text | Google Scholar

Chigira, M., and Yagi, H. (2006). Geological and geomorphological characteristics of landslides triggered by the 2004 Mid Niigta prefecture earthquake in Japan. Eng. Geol. 82 (4), 202–221. doi:10.1016/j.enggeo.2005.10.006

CrossRef Full Text | Google Scholar

Ding, M., and Hu, K. (2014). Susceptibility mapping of landslides in Beichuan County using cluster and MLC methods. Nat. Hazards (Dordr). 70 (1), 755–766. doi:10.1007/s11069-013-0854-0

CrossRef Full Text | Google Scholar

Gómez, H., and Kavzoglu, T. (2005). Assessment of shallow landslide susceptibility using artificial neural networks in Jabonosa river basin, Venezuela. Eng. Geol. 78 (1–2), 11–27. doi:10.1016/j.enggeo.2004.10.004

CrossRef Full Text | Google Scholar

Gorum, T., Fang, X. M., Westen, C. J. V., Huang, R. Q., Xu, Q., Tang, C., et al. (2011). Distribution pattern of earthquake-induced landslides triggered by the 12 May 2008 Wenchuan earthquake. Geomorphology 133 (3–4), 152–167. doi:10.1016/j.geomorph.2010.12.030

CrossRef Full Text | Google Scholar

Hasegawa, S., Dahal, R. K., Nishimura, T., Nonomura, A., and Yamanaka, M. (2009). DEM-based analysis of earthquake-induced shallow landslide susceptibility. Geotech. Geol. Eng. (Dordr). 27 (3), 419–430. doi:10.1007/s10706-008-9242-z

CrossRef Full Text | Google Scholar

Hong, H., Liu, J. Z., Zhu, A. X., Shahabi, H., Pham, B. T., Chen, W., et al. (2017). A novel hybrid integration model using support vector machines and random subspace for weather-triggered landslide susceptibility assessment in the Wuning area (China). Environ. Earth Sci. 76 (19), 652. doi:10.1007/s12665-017-6981-2

CrossRef Full Text | Google Scholar

Keefer, D. K. (1984). Landslides caused by earthquakes. Geol. Soc. Am. Bull. 95 (4), 406. doi:10.1130/0016-7606(1984)95<406:lcbe>2.0.co;2

CrossRef Full Text | Google Scholar

Kokusho, T., Ishizawa, T., and Hara, T. (2009). Slope failures during the 2004 niigataken chetsu earthquake in Japan. Earthquake geotechnical case histories for performance-based design. Balkema: CRC Press, 47–70.

CrossRef Full Text | Google Scholar

Kokusho, T., Ishizawa, T., and Koizumi, K. (2011). Energy approach to seismically induced slope failure and its application to case histories. Eng. Geol. 122 (1-2), 115–128. doi:10.1016/j.enggeo.2011.03.019

CrossRef Full Text | Google Scholar

Kokusho, T., Koyanagi, T., and Yamada, T. (2014). Energy approach to seismically induced slope failure and its application to case histories –Supplement. Eng. Geol. 181, 290–296. doi:10.1016/j.enggeo.2014.08.019

CrossRef Full Text | Google Scholar

Kokusho, T. (2008). Report of the 2004 niigataken chuetsu earthquake slope disaster database. Tokyo: Chuo University. (In Janpanese).

Google Scholar

Konagai, K., Fujita, T., Ikeda, T., and Takatsu, S. (2009). Tectonic deformation buildup in folded mountain terrains in the October 23, 2004, Mid-Niigata earthquake. Soil Dyn. Earthq. Eng. 29, 261–267. doi:10.1016/j.soildyn.2008.01.013

CrossRef Full Text | Google Scholar

Li, W. L., Huang, R. Q., Tang, C., Xu, Q., and Westen, C. V. (2013). Co-Seismic landslide inventory and susceptibility mapping in the 2008 wenchuan earthquake disaster area, China. J. Mt. Sci. 10 (3), 339–354. doi:10.1007/s11629-013-2471-5

CrossRef Full Text | Google Scholar

Maruyama, T., Iemura, K., Azuma, T., Yoshioka, T., Sato, M., and Miyawaki, R. (2007). Paleoseismological evidence for non-characteristic behavior of surface rupture associated with the 2004 Mid-Niigata Prefecture earthquake, central Japan. Tectonophysics 429 (1), 45–60. doi:10.1016/j.tecto.2006.09.008

CrossRef Full Text | Google Scholar

Nguyen, H., Mehrabi, M., Kalantar, B., Moayedi, H., and Abdullahi, M. M. (2019). Potential of hybrid evolutionary approaches for assessment of geo-hazard landslide susceptibility mapping. Geomatics, Nat. Hazards Risk 10, 1667–1693. doi:10.1080/19475705.2019.1607782

CrossRef Full Text | Google Scholar

Nsengiyumva, J. B., and Valentino, R. (2020). Predicting landslide susceptibility and risks using GIS-based machine learning simulations, case of upper Nyabarongo catchment. Geomatics, Nat. Hazards Risk 11, 1250–1277. doi:10.1080/19475705.2020.1785555

CrossRef Full Text | Google Scholar

Pham, B. T., Pradhan, B., Tien Bui, D., Prakash, I., and Dholakia, M. B. (2016). A comparative study of different machine learning methods for landslide susceptibility assessment: A case study of uttarakhand area (India). Environ. Model. Softw. 84, 240–250. doi:10.1016/j.envsoft.2016.07.005

CrossRef Full Text | Google Scholar

Pradhan, B., and Lee, S. (2010a). Landslide susceptibility assessment and factor effect analysis: Backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling. Environ. Model. Softw. 25 (6), 747–759. doi:10.1016/j.envsoft.2009.10.016

CrossRef Full Text | Google Scholar

Pradhan, B., and Lee, S. (2010b). Regional landslide susceptibility analysis using back-propagation neural network model at Cameron Highland, Malaysia. Landslides 7 (1), 13–30. doi:10.1007/s10346-009-0183-2

CrossRef Full Text | Google Scholar

Regmi, A. D., Dhital, M. R., Zhang, J. Q., Su, L, J., and Chen, X. Q. (2016). Landslide susceptibility assessment of the region affected by the 25 April 2015 Gorkha earthquake of Nepal. J. Mt. Sci. 3 (11), 1941–1957. doi:10.1007/s11629-015-3688-2

CrossRef Full Text | Google Scholar

Reichenbach, P., Rossi, M., Malamud, D. B., Mihir, M., and Guzzetti, F. (2018). A review of statistically-based landslide susceptibility models. Earth. Sci. Rev. 180, 60–91. doi:10.1016/j.earscirev.2018.03.001

CrossRef Full Text | Google Scholar

Saade, A., Abou-Jaoude, G., and Wartman, J. (2016). Regional-scale co-seismic landslide assessment using limit equilibrium analysis. Eng. Geol. 204, 53–64. doi:10.1016/j.enggeo.2016.02.004

CrossRef Full Text | Google Scholar

Sato, H. P., Sekiguchi, T., Kojiroi, R., Suzuki, Y., and Iida, M. (2005). Overlaying landslides distribution on the earthquake source, geological and topographical data: The Mid niigata prefecture earthquake in 2004, Japan. Landslides 2 (2), 143–152. doi:10.1007/s10346-005-0053-5

CrossRef Full Text | Google Scholar

Shrestha, S., and Kang, T. S. (2019). Assessment of seismically-induced landslide susceptibility after the 2015 Gorkha earthquake, Nepal. Bull. Eng. Geol. Environ. 78 (3), 1829–1842. doi:10.1007/s10064-017-1191-4

CrossRef Full Text | Google Scholar

Tian, Y. Y., Xu, C., Hong, H. Y., Zhou, Q., and Wang, D. (2019). Mapping earthquake-triggered landslide susceptibility by use of artificial neural network (ANN) models: An example of the 2013 minxian (China) mw 5.9 event. Geomatics, Nat. Hazards Risk 10, 1–25. doi:10.1080/19475705.2018.1487471

CrossRef Full Text | Google Scholar

Tu, J. V. (1996). Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J. Clin. Epidemiol. 49 (11), 1225–1231. doi:10.1016/s0895-4356(96)00002-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Vařilová, Z., Kropáček, J., Zvelebil, J., Šťastný, M., and Vilímek, V. (2015). Reactivation of mass movements in Dessie graben, the example of an active landslide area in the Ethiopian Highlands. Landslides 12 (5), 985–996. doi:10.1007/s10346-015-0613-2

CrossRef Full Text | Google Scholar

Vojteková, J., and Vojtek, M. (2020). Assessment of landslide susceptibility at a local spatial scale applying the multi-criteria analysis and GIS: A case study from Slovakia. Geomatics, Nat. Hazards Risk 11, 131–148. doi:10.1080/19475705.2020.1713233

CrossRef Full Text | Google Scholar

Wang, H. B., Sassa, K., and Xu, W. Y. (2007). Analysis of a spatial distribution of landslides triggered by the 2004 Chuetsu earthquakes of Niigata Prefecture, Japan. Nat. Hazards (Dordr). 41 (1), 43–60. doi:10.1007/s11069-006-9009-x

CrossRef Full Text | Google Scholar

Xu, C., Dai, F., Xu, X., and Yuan, H. L. (2012a). GIS-based support vector machine modeling of earthquake-triggered landslide susceptibility in the Jianjiang River watershed, China. Geomorphol. (Amst). 145–146 (2), 70–80. doi:10.1016/j.geomorph.2011.12.040

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, C. (2014). Do buried-rupture earthquakes trigger less landslides than surface-rupture earthquakes for reverse faults? Geomorphology 216, 53–57. doi:10.1016/j.geomorph.2014.03.029

CrossRef Full Text | Google Scholar

Xu, C., and Xu, X. (2013). Controlling parameter analyses and hazard mapping for earthquake-triggered landslides: An example from a square region in beichuan county, sichuan Province, China. Arab. J. Geosci. 6, 3827–3839. doi:10.1007/s12517-012-0646-y

CrossRef Full Text | Google Scholar

Xu, C., Xu, X., Dai, F., and Saraf, A. K. (2012b). Comparison of different models for susceptibility mapping of earthquake triggered landslides related with the 2008 Wenchuan earthquake in China. Comput. Geosciences 46 (3), 317–329. doi:10.1016/j.cageo.2012.01.002

CrossRef Full Text | Google Scholar

Xu, C., Xu, X., and Yu, G. (2013). Landslides triggered by slipping-fault-generated earthquake on a plateau: An example of the 14 april 2010, ms 7.1, yushu, China earthquake. Landslides 10, 421–431. doi:10.1007/s10346-012-0340-x

CrossRef Full Text | Google Scholar

Yang, Z. H., Lan, H. X., Gao, X., Li, L. P., Meng, Y. S., and Wu, Y. M. (2015). Urgent landslide susceptibility assessment in the 2013 Lushan earthquake-impacted area, Sichuan Province, China. Nat. Hazards (Dordr). 75 (3), 2467–2487. doi:10.1007/s11069-014-1441-8

CrossRef Full Text | Google Scholar

Yao, X., Tham, L. G., and Dai, F. C. (2008). Landslide susceptibility mapping based on support vector machine: A case study on natural slopes of Hong Kong, China. Geomorphology 101 (4), 572–582. doi:10.1016/j.geomorph.2008.02.011

CrossRef Full Text | Google Scholar

Yesilnacar, E., and Topal, T. (2005). Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, hendek region (Turkey). Eng. Geol. 79 (3–4), 251–266. doi:10.1016/j.enggeo.2005.02.002

CrossRef Full Text | Google Scholar

Yi̇lmaz, I. (2009b). A case study from Koyulhisar (Sivas-Turkey) for landslide susceptibility mapping by artificial neural networks. Bull. Eng. Geol. Environ. 68 (3), 297–306. doi:10.1007/s10064-009-0185-2

CrossRef Full Text | Google Scholar

Yi̇lmaz, I. (2010). Comparison of landslide susceptibility mapping methodologies for koyulhisar, Turkey: Conditional probability, logistic regression, artificial neural networks, and support vector machine. Environ. Earth Sci. 61 (4), 821–836. doi:10.1007/s12665-009-0394-9

CrossRef Full Text | Google Scholar

Yi̇lmaz, I. (2009a). Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: A case study from Kat landslides (tokat-Turkey). Comput. Geosciences 35 (6), 1125–1138. doi:10.1016/j.cageo.2008.08.007

CrossRef Full Text | Google Scholar

Zhang, Y. S., Yao, X., Xiong, T. Y., Ma, Y. S., Hu, D. G., Yang, N., et al. (2010). Rapid identification and emergency investigation of surface ruptures and geohazards induced by the m_s 7.1 yushu earthquake. Acta Geol. Sin. Ed. 84 (6), 1315–1327.

Google Scholar

Zhao, Y., and Konagai, K. (2014). Evidence of a hidden landslide slip surface beneath a mountain hamlet. Environ. Earth Sci. 71 (10), 4615–4624. doi:10.1007/s12665-014-3078-z

CrossRef Full Text | Google Scholar

Zhao, Y., Konagai, K., and Fujita, T. (2012). Multi-scale decomposition of Co-seismic deformation from high resolution DEMs: A case study of the 2004 mid-niigata earthquake. Acta Geol. Sin. - Engl. Ed. 86 (4), 1013–1021. doi:10.1111/j.1755-6724.2012.00725.x

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, R., Jiang, Y. J., Liu, H. J., and Wei, Z. L. (2019). GIS-based logistic regression for rainfall-induced landslide susceptibility mapping under different grid sizes in Yueqing, Southeastern Chinaerent grid sizes in Yueqing, Southeastern China. Eng. Geol. 259, 105147. doi:10.1016/j.enggeo.2019.105147

CrossRef Full Text | Google Scholar

APPENDIX TABLE A1 Lithological distribution in the large-scale area.

The lithology data used in this paper are redrawn from the 1: 50,000 geological map of Nagaoka and Ojiya by the Geological Survey of Japan’s Ministry of International Trade and Industry. There are 10 different lithology groups in the large-scale area (Appendix Table A1) and 11 different lithology groups in the epicenter area (Appendix Table A2).

APPENDIX TABLE A2 Lithological distribution in the epicenter area.

The elevation data used in this paper are generated from the 30 m resolution DEM data obtained from the ASTER Global Digital Elevation Model (ASTER GDEM). The slope angle in the study area ranges from 0° to 57.82° for the large area. A 0° slope angle means a flat area. The west part of the large-scale area is an almost flat area, whereas the mountains mainly spread from the NE direction to the SW direction. The influence of the slope aspect on the stability of the slope is multifaceted. Different slope directions have different influences of solar radiation and rainfall on the slopes that control the moisture of the terrain that affects landslide occurrences. Surface curvature determines the pooling and dispersion of surface water and affects the strength and stability of rocks and soils. In addition, there is a strong correlation between soil thickness and surface curvature due to soil sedimentation caused by the water flow. Since the inertia forces generated by earthquakes are important causes of earthquake-triggered landslides, the PGA is generally chosen as the impact factor of landslide susceptibility. It has been acknowledged that the slope stability is affected not only by the PGA of the mainshock but also by that of aftershocks. However, introducing more influencing factors of the same types will also lead to overfitting problems. Therefore, at present, almost all studies only considered the PGA map of mainshock as influencing factors regardless of the effect of aftershocks on the assessment of landslide susceptibility, and the concluded landslide susceptibility mappings were also reliable.