Multi-scale interactive network in the application of DAS seismic data processing

Distributed acoustic sensing (DAS) is regarded as a novel acquisition technology for seismic data. Compared with conventional electrical geophones, DAS has a series of obvious advantages including low-cost, high spatial resolution, good coverage, and strong resistance to the harsh environment. Noise attenuation is an essential step in seismic data processing. However, there are two main difficulties faced by the denoising task of DAS seismic data. On the one hand, some background noise in DAS seismic data, such as optical low-frequency noise, horizontal noise, and fading noise, is unique and not presented in the conventional seismic data; on the other hand, the signal-to-noise ratio (SNR) of DAS seismic data is relatively low. Recently, a convolutional neural network (CNN) has shown superior denoising performance compared to the traditional method. To follow this promising trend, we propose a multi-scale interactive convolutional neural network (MSI-Net) and apply it to denoise the challenging DAS seismic data. Different from most of the existing CNN architecture used in seismic data denoising, the MSI-Net considers both coarse-scale and fine-scale features by improving the inherent serial convolution to multi-scale parallel convolution, which is beneficial to recover detailed information. Moreover, we utilize some connections to achieve the information interaction between different scales, which promotes the flow of information and enables the network to extract more informative multi-scale features from the DAS seismic data. Moreover, both synthetic and real examples demonstrate that the proposed MSI-Net can effectively attenuate a variety of unique DAS background noise and also completely recover the weak signals. Compared with conventional CNN architecture, MSI-Net exhibits better performance in global SNR and local details.

Introduction

In the wake of developments in oil and gas exploration, the quality requirements for seismic data have gradually increased, finding a seismic data processing technology with higher accuracy and resolution is also a difficult problem we must face. Distributed acoustic sensing (DAS) is considered an emerging acquisition technology in seismic exploration. DAS uses changes in the phase information of the scattered optical signal to record the wavefield (Spikes et al., 2019). Compared to conventional electronic geophones, DAS has advantages in acquisition geometry, such as low cost and high-density observations. In recent years, DAS has been applied to vertical seismic profile (VSP) data acquisition (Dong et al., 2022). However, the scattered light signal with weak energy is extremely susceptible to background noise, which negatively affects the quality of the acquired seismic data (Binder et al., 2020). In addition, the in-well acquisition environment also brings new challenges to data processing, and some disturbances are not present in conventional seismic surveys, such as time-varying optical noise and coupling noise (Wang et al., 2021). The seismic data collected in the field is mixed with a wide variety of noise due to the underground geological conditions, collection conditions and environmental factors. Affected by the mixed noise, the quality of the real seismic records decreases, and the signal-to-noise ratio (SNR) and resolution of the data are relatively low, which brings difficulties to subsequent inversion, imaging and interpretation. Improving the SNR and resolution of data is of great significance to the study of underground structures and the exploration of oil, gas and mineral resources.

In seismic data processing, obtaining data with high SNR and resolution is the goal. The noise can interfere with the effective seismic information to cause a low SNR, at the same time, narrowing the effective frequency band of the seismic data and reducing the data resolution. It is a challenging problem to reduce the noise in seismic data while taking into account the resolution. Among the traditional noise reduction methods, Band-pass filtering, Wiener filtering (Mendel, 1977) and F-X deconvolution (Canales, 1984) was used earlier for seismic noise suppression. Several time-frequency attenuation algorithms have also been developed to improve the denoising capability of seismic data, including short-time Fourier transform (Lu and Li, 2013) and time-frequency peak filtering (TFPF) (Wu et al., 2011). In general, the denoising principle of these methods is based on the difference between the reflected signal and the background noise in terms of physical characteristics or frequency components to eliminate complex interference. However, the above methods cannot handle the complex DAS background noise. In addition, multi-scale denoising methods use the features of the sparse decomposition results to construct suitable filters for the purpose to suppress the noise to retain the effective signal, and typical methods include wavelet transform filtering (Mousavi et al., 2016; Anvari et al., 2017), Curvelet transform filtering (Neelamani et al., 2008; Gorszczyk et al., 2014), Shearlet transform filtering (Gan et al., 2015; Chen and Fomel 2018), empirical mode decomposition (EMD) (Bekara and van der Baan, 2009; Amezquita Sanchez et al., 2017) and variational modal decomposition (VMD) (Kesharwani et al., 2021). Unfortunately, when dealing with DAS recordings containing complex noise, researchers have difficulty in obtaining optimal filtering parameters, which leads to noise residuals and loss of amplitude of the effective signal. In addition, many other methods have been widely used in seismic data processing including singular value decomposition (SVD) (Oropeza and Sacchi, 2011), dictionary learning methods (Chen et al., 2016; Yarman et al., 2018; Wang and Ma, 2020), robust principal component analysis (RPCA) (Cheng et al., 2015; Liu et al., 2021), but the application of these methods in DAS data denoising is rarely reported. It is difficult for conventional methods to provide a better processing effect when the DAS data is seriously disturbed by noise, and give consideration to SNR and resolution. Meanwhile, it involves the manual selection of various parameters in data processing for conventional methods introduced above, which greatly increases the running time of the processing work and depends on artificial experience heavily. For the sake of high-precision seismic exploration, more intelligent and faster data processing technology is urgently needed.

In recent years, deep learning methods have become popular solutions to various seismic data processing problems. Deep learning (DL) (Lecun et al., 2015) is considered an important machine learning method that has started to be introduced into seismic data processing. And there are already some successful applications such as seismic data denoising (Chen et al., 2019; Saad and Chen, 2020), arrival picking (Tsai et al., 2018; Yuan et al., 2019; Zhang et al., 2020), fault identification (Wu et al., 2019), lithology prediction (Zhang et al., 2018) and geologic structure classification (Li, 2018). The deep learning algorithm can automatically learn highly complex nonlinear features, and it is applied to the suppression of background noise in pre-stack seismic data to achieve automatic and efficient background noise separation by automatically learning random noise features. Yu et al. (2019) proposed an intelligent CNN-based denoising method, which does not require precise modeling of signal and noise, nor optimization of parameter tuning. Wang and Chen (2019) used a deep CNN framework with residual learning for 2-D post-stack seismic random noise attenuation. Treating seismic signals as time series, Saad and Chen (2020) proposed a deep denoising autoencoder (DDAE) to attenuate seismic random noise. Li et al. (2022) proposed to leverage a deep convolutional neural network (CNN) to achieve seismic image super-resolution and denoising simultaneously. Jiang et al. (2021) proposed an improved convolutional autoencoder (CAE) method to achieve simultaneous reconstruction and denoising of seismic data. Yang et al. (2021) proposed an improved ResNet to achieve seismic random noise attenuation. Wang et al. (2022)) are applied to seismic noise attenuation tasks (Creswell et al., 2017; Wang et al., 2021), and some successful applications on ground record processing have been achieved. Furthermore, transfer learning was introduced into the training of denoising networks to enhance the generalization of the model to process the real records (Li et al., 2022; Sun et al., 2022). Supervised learning-based denoising methods need to label a large number of clean seismic data to fit the network, which will increase labor and computational costs. Therefore, some denoising models based on unsupervised learning or self-supervised learning have been proposed to address the lack of paired data in seismic signal processing (Wang et al., 2022; Yang et al., 2021; Liu et al., 2021; 2022; Qiu et al., 2022). Meanwhile, deep learning-based algorithms have also achieved good results in denoising DAS records (Zhao et al., 2022; Wang et al., 2021). In general, these denoising networks aim to establish a non-linear high-dimensional mapping relationship between noisy records and desired signals. In the training process, we can use training data to strengthen the learned mapping, and the final denoising models are obtained after training and have been proven to be effective in practical application. Notably, unlike conventional methods, the denoising network can be considered a “data-driven” approach to adaptively accomplish complex seismic noise suppression without parameter fine-tuning. If the training data is complete, CNN-based networks can always achieve more advantageous results than conventional methods. However, most of the traditional networks, such as DnCNN (Zhang et al., 2017), are based on single-scale information to extract potential features, which has reduced effectiveness and generalization when dealing with complex seismic data (Zhong et al., 2022). In addition, most existing methods transmit input through a network and reconstruct output at the last layer. Although the characterization learned by this type of network can aggregate local features with the increase of layers, it also has the characteristics of coarse scale, that is, the resolution after reconstruction is not fine enough and some detail features are ignored. As a result, it is difficult to obtain accurate prediction results in the task of seismic data processing, especially when the data is disturbed by strong noise. The stronger noise can lead to a rapid decrease in the sensitivity of the final output characterization space, a decrease in the accuracy of the reconstruction, and even some false seismic events.

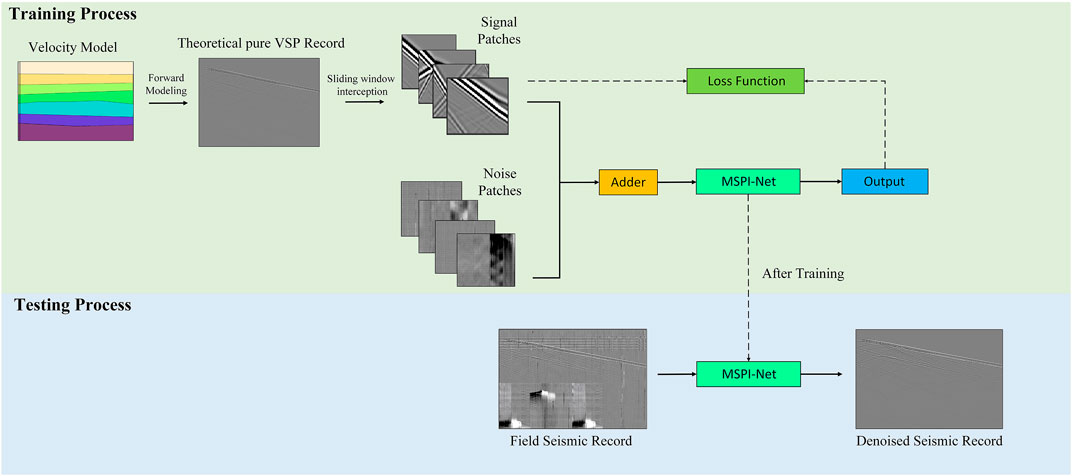
Therefore, there has been an increasing interest in designing efficient denoising networks to improve the processing capability of DAS-VSP data. To solve the above problem, a multi-scale interactive deep convolutional neural network (MSI-Net) is constructed in this paper. The network builds a multi-scale framework by gradually fusing sub-networks on the main network, and repeated information interactions are performed on parallel multi-scale sub-networks to complete the repetitive information fusion between scales, which enhances the generalization ability of the network. The network can learn more abundant multi-scale characterization and reconstruct high-resolution seismic data. The experiment results show that the network can not only suppress noise effectively, but also predict effective signals accurately, it can achieve processing requirements of high SNR and resolution, and greatly reduce false seismic events. We construct a high-quality training dataset containing synthetic signals and actual DAS background noise to train the network. We also process synthetic and field DAS data to check the effectiveness of the proposed network. Compared with traditional denoising methods and recently proposed denoising networks, the proposed method in this paper has advantages in DAS background noise attenuation and weak signal amplitude retention.

Methods

DAS records often contain complex wave fields, including incident down-going waves and reflected up-going waves. The recovery of events in seismic records is very important, however, it is difficult to identify seismic events with the interference of noise, hence noise suppression is necessary. The convolutional neural network can eliminate noise, and also plays an important role in the high-resolution reconstruction of signals. To make the signal recovery more accurate, it is common practice to obtain exact semantic information through down-sampling, and then perform an up-sampling operation to restore high-resolution signal details, such as U-Net (Ronneberger et al., 2015). However, this practice leads to some loss of effective information in the continuous upsampling and downsampling. If the high-resolution transmission is maintained throughout the whole process, such as DnCNN (Zhang et al., 2017), a wider range of perceptions cannot be obtained, and some false events are often generated in the results. In this paper, a wide range of semantic information is obtained through parallel multiple resolution sub-networks and continuous information interaction between different network branches. And the proposed method achieves the purpose of recovering signal details accurately while suppressing noise effectively. To better denoise the actual DAS data, we analyzed the wave fields and complex noise in real DAS data. Then, we constructed a dedicated training set to train the model. The following sections introduce the analysis of wavefield and noise in the DAS record, the construction of the dataset, the structure of the network and the denoising principle.

Analysis of wavefield and noise in DAS-VSP

Figure 1 shows DAS-VSP data acquired from Xinjiang, western China. The horizontal coordinate represents the number of seismic traces and the vertical coordinate represents the time. The time sampling interval of the DAS data shown is 400 $\mu s$ and the spatial sampling interval is 1 m. From the figure, we can observe that the data are heavily contaminated by noise, and the effective signals such as the incident down-going waves (as indicated by the blue line) and reflected up-going waves (as indicated by the yellow line) are almost covered by noise. It can be observed that the types of noise are also complex, such as random noise (as shown in region A), background abnormal interference (as shown in region B), fading noise (as shown in region C), horizontal noise (as shown in region D) and checkerboard noise (as shown in region E) and coupling noise (as shown in region F). The characteristics and causes of these noises are described as follows.

FIGURE 1

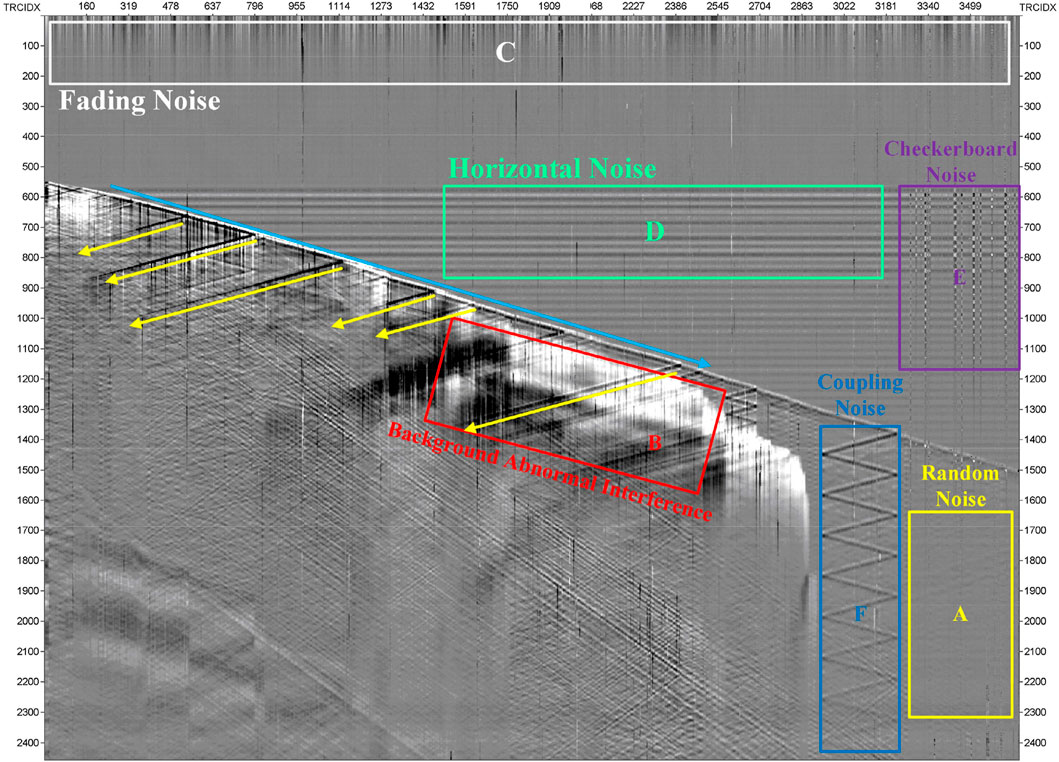
FIGURE 1. DAS VSP data with several common noises. Areas (A–F) are marked with random noise, background abnormal interference, fading noise, horizontal noise, checkerboard noise and coupling noise, respectively.

The random noise is common background noise in DAS-VSP data, with a wide frequency band and strong energy, mainly caused by vibration during data acquisition. The source of noise may come from machine vibration, underground random vibration, current disturbance, etc. Random noise is generally more uniformly distributed and is the main factor affecting the quality of DAS-VSP data.

The abnormal interference with low dominant frequency and very strong energy may be caused by downhole temperature anomalies. The abnormal interference tends to have large areas and high amplitudes in the records. In the presence of abnormal interference, the effective signal is completely covered and the DAS-VSP data quality is seriously affected.

The fading noise is caused by the phase canceling interference of randomly spaced backscattered light. Fading noise is mainly manifested in long periods and high amplitude. In general, the fading noise appears on the uppermost side of the record, less affecting the effective signal below the first arrival wave. It is easy to mix with horizontal noise to generate new types of noise.

The horizontal noise is caused by vibration during optical measurements. Shaking the interrogator box is probably the main trigger. The potential leakage of electronic equipment can also be another cause of horizontal noise. The horizontal noise usually appears as a short horizontal band with essentially the same phase in all traces and decreasing in amplitude over time.

The checkerboard noise is generally generated by a mixture of horizontal noise and fading noise. The checkerboard noise has approximately the same properties as the horizontal noise. For example, both checkerboard noise and horizontal noise have horizontal motion, and the amplitude gradually decays over time. However, checkerboard noise tends to have different phases in different traces. In general, the checkerboard noise is also more distributed before the first arrival.

The coupling noise is mainly caused by the poor coupling of the fiber and the measurement line. It often accompanies the reflected signal and is highly similar to the signal within the local view. Conventional methods are generally more difficult to distinguish between signal and coupled noise. At present, there are three ways to deploy DAS systems in wells. The first one is to permanently fix the fiber outside the casing. It maximizes the coupling between the fiber and the formation, resulting in less coupling noise in the acquired DAS data (Jiang et al., 2016). The second one is to fix the fiber to the tubing and there will still be a small amount of coupling noise. The third one is to use weights to suspend the fiber in the casing. However, the optical fiber is not in close contact with the borehole, which may produce strong coupling noise (Constantinou et al., 2016).

Construction of training set

The purpose of deep learning is to learn the feature, which can obtain hierarchical feature information adaptively through the network, solving the problem of manually designing operators for feature extraction in the past. Dataset is an important basis for deep learning algorithms, and its completeness determines the potential upper limit that the method can touch. In seismic exploration, it is difficult to obtain pure seismic signals. To obtain a more complete and realistic training set, forward modeling is used to construct a pure signal set as shown in Figure 2. For DAS-VSP, to obtain subsurface information, we usually place artificial sources to excite the seismic wave field and place receivers along the longitudinal direction to record the seismic waves. In this paper, the synthetic data are modeled based on the acoustic wave equation in the time domain, as shown in the following equation.

$\frac{{\partial }^{2}u\left(x,y,t\right)}{\partial t^2}=v{\left(x,y\right)}^2\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)+s\left(x,y,t\right)(1)$

where $v$ represents the wave velocity and $u$ represents the acoustic wavefield. $s\left(x,y,t\right)$ denotes the function of the source. $\left(x,y\right)$ denotes the spatial location and $t$ denotes time. We have built 100 velocity models with different stratigraphic configurations. The detailed parameters of the model are shown in Table 1. After preparing the velocity models, the shots of the seismic data corresponding to each velocity model are generated in the numerical simulation of the acoustic wavefield. We solve the acoustic wave equations using a staggered-grid finite-difference method in the time domain. The size of each grid is defined as 10 m × 10 m. As for the observation of each velocity model, we place a source as shown in Figure 2 to simulate the shot gathers. The source is placed at (500, 0) m. The survey line is placed along the vertical direction at $x$= 10 m. The recording geometry consists of 2000 receivers. In Figures 2A,B, we show a representative velocity model and the corresponding generated seismic record. By solving the wave equation, 100 simulated pure seismic records with a size of 2,000 × 2,000 are obtained, which can be used as a part of the pure signal set for network learning. To adapt to the network training, we divide the amplitude-normalized synthetic seismic records into patches with a size of 400 × 400 to obtain the pure signal set $X=\left\{x_1,x_2,\cdots ,x_e\right\}$. Part of the pure signal patch is shown in Figure 2C.

FIGURE 2

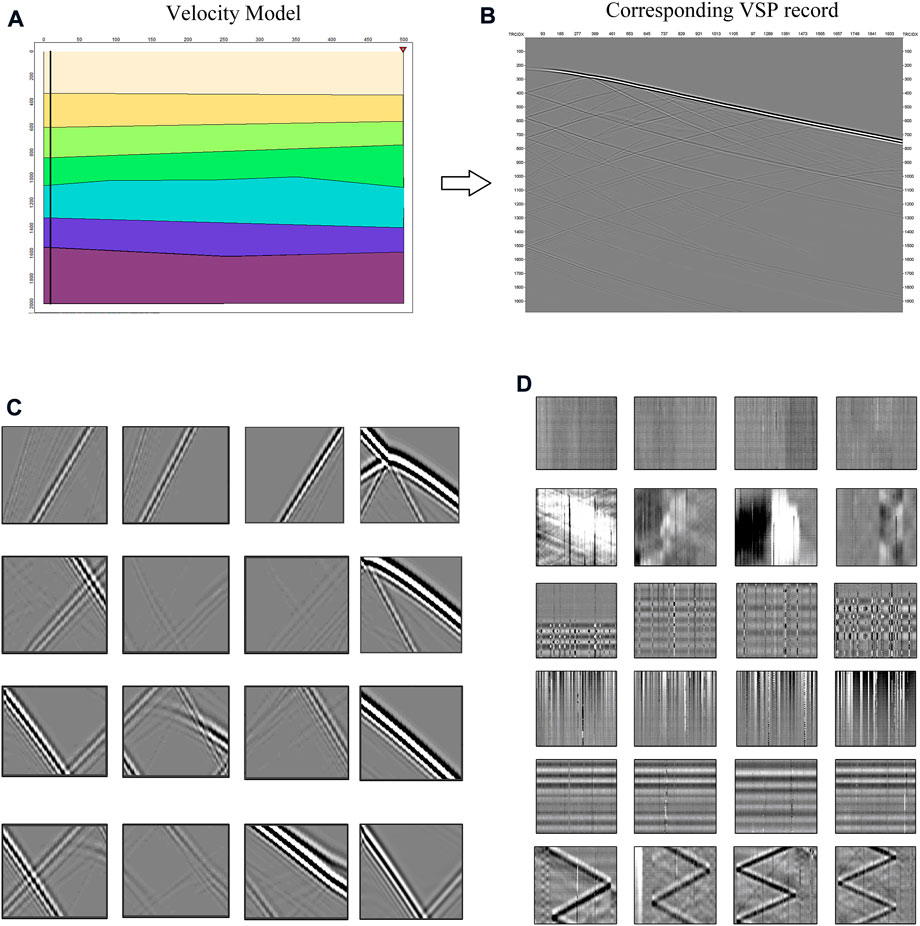
FIGURE 2. Construction of the dataset. (A) The velocity model. (B) The corresponding synthetic DAS-VSP record. (C) Samples of the signal dataset. (D) Samples of the noise dataset. These patches are the random noise, the abnormal interference, the checkerboard noise, the fading noise, the horizontal noise and the coupling noise from top to bottom.

TABLE 1

TABLE 1. The parameters of the forward modeling.

A large amount of noise data is needed to synthesize the noise set. The noise in the training set should be as close as possible to the noise in field seismic data. We have selected various types of noise data collected from the actual DAS records to enrich the noisy set. A complete noise set $N=\left\{n_1,n_2,\cdots ,n_e\right\}$ can be built, and Figure 2D shows a portion of the noise patch. Similarly, the noise data is divided into patches with a size of 400 × 400 and superimposed with the pure signal patches to generate a noisy set $Y=\left\{y_1,y_2,\cdots ,y_g\right\}$.

The structure of network

In the denoising process, the higher the resolution of the local structure, the more conducive to the reduction of the noise, but the rich information brought by the high resolution will also produce misjudgment in processing, resulting in some false seismic events. Therefore, it is also important to grasp the overall structure of data, which requires us to use data at different resolutions. The lower-resolution data components are more conducive to the recovery of the overall signal. It is of great significance to improve the performance of the overall task by analyzing and processing signals at different resolutions. How to design a network with multi-resolution representation is a key issue for us to consider. To make the network achieve multi-scale feature extraction, the model gradually adds sub-networks with low-resolution feature maps in parallel to the main network with high-resolution feature maps to complete the feature fusion between scales. The multi-resolution interactive network shown in Figure 3A is used for noise suppression and high-resolution reconstruction of seismic data. The design idea of the proposed network takes reference from HRNet (Sun et al., 2019). In Figure 3A, the horizontal transfer process represents the representation changes with the increase of processing layers, and the vertical process represents the scale change of the feature maps. The first level (which we called stage 1) shows the main network, and its feature map is maintained at a high-resolution standard. The signal is transmitted through the main network in stage1, and more low-resolution sub-networks are gradually added in parallel in subsequent stages. The resolution of the parallel sub-network in the latter stage is composed of all previous resolutions and a new resolution, that is, in the $n$-th stage, feature processing is performed in sub-networks of $n$ resolutions in parallel. Every time a lower resolution sub-network is added, the resolution is reduced to half, and the corresponding channels are doubled.

FIGURE 3

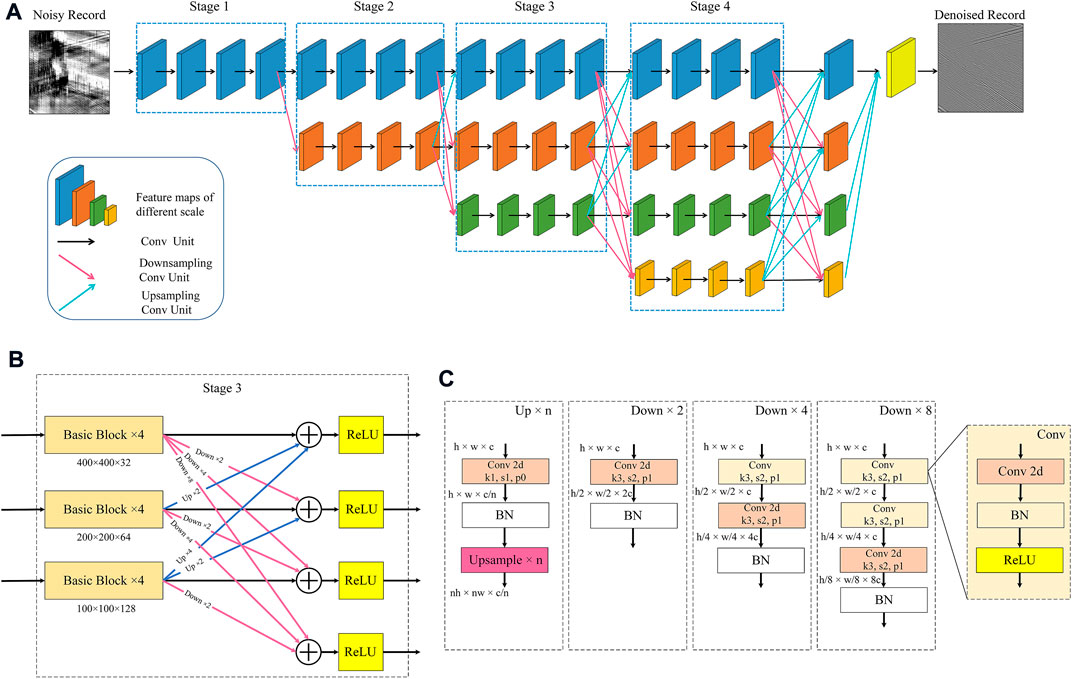
FIGURE 3. The architecture of the proposed network. (A) The architecture of MSI-Net. (B) The structure of a stage (Take the 3-th stage as an example) (C) Detailed structure of each part in Figure 3B.

In addition to analyzing signals in a multi-scale manner, the repeated exchange of information at various resolutions to promote multi-resolution information fusion is also an important reason for the network to maintain high performance. Similarly, it enables the network to maintain the accuracy of high-resolution reconstruction of signals under the blessing of low-resolution features. As shown in Figure 3B, taking a fusion at the 3-th stage as an example, it can be seen that the output of each resolution is related to the inputs at three different resolutions, namely ${\mathrm{R}}_{\tau }\prime =T_{1\to \tau }\left({\mathrm{R}}_1\right)+T_{2\to \tau }\left({\mathrm{R}}_2\right)+T_{3\to \tau }\left({\mathrm{R}}_3\right)$. At the same time, a new output at a lower resolution is produced, that is, ${\mathrm{R}}_4\prime =T_{1\to 4}\left({\mathrm{R}}_1\right)+T_{2\to 4}\left({\mathrm{R}}_2\right)+T_{3\to 4}\left({\mathrm{R}}_3\right)$, where $R_i$ represents the input feature map of different resolutions, $R_i^{\prime }$ represents the output feature map of different resolutions, and $T_{i\to \tau }$ is an operator to process features between different resolutions. The operator is a down-sampling operation from high to low resolution, an up-sampling operation from low to high resolution, and the identity during the same resolution, respectively. In this way, while the parallel convolutional operations move forward synchronously, the network also carries out feature interaction between scales, to realize multi-scale feature fusion and extraction. Among them, the basic block adopts the structure of ResNet (He et al., 2016). The detailed introduction of each module is shown in Figure 3C. The introduction of each functional module can be obtained in Table 2. The designed network consists of four stages, and the feature extraction of each resolution in every stage is completed by four residual convolution operations. With the final integration of the feature maps obtained on each resolution, noise suppression and high-resolution signal reconstruction can be completed.

TABLE 2

TABLE 2. The specific description of the layers or functions.

The denoising principle

In this paper, the DAS-VSP record disturbed by noise can be expressed as:

$y=x+n(2)$

among them, $x$ refers to the potential pure seismic signal and $n$ refers to noise interference. In the proposed structure, the constructed high-resolution reconstruction network aims to learn the end-to-end mapping function between the noisy signal $y$ and the pure signal $x$, and the predicted pure signal can be expressed as:

$\stackrel{\sim }{x}=\mathrm{H}\left(y;\mathrm{\Theta }\right)(3)$

In Equation 3, $\mathrm{H}$ represents the multi-scale interactive reconstruction network, $\Theta =\left\{W,b\right\}$ is the network optimized parameters with weights $W$ and biases $b$.

Figure 4 shows the workflow of the DL-based denoising algorithm. During the training process, we can calculate the error between the network output $\stackrel{\sim }{x}$ and the pure record $x$, and update the network parameters by gradient backpropagation. After several iterations, the error will converge to a small enough value and the network parameters can be determined. In the inference process, given the seismic data, the denoised DAS data can be predicted by the network. In this paper, the $L2$ loss function is used as the cost function to guide the training process of the model, and the equation is given as follows:

$L=\frac{1}{2N}{\displaystyle \sum }_{i=1}^N{\Vert \mathrm{H}\left(y_i;\mathrm{\Theta }\right)-x_i\Vert }_F^2(4)$

where $\mathrm{H}\left(y_i;\Theta \right)$ represents the denoising result of the training sample $y_i$, and $x_i$ represents the pure signal which we called the label, that is, the output we expect from the network. $i$ is the index of the sample and $N$ is the batch size. The gradient descent method is used to minimize the loss function. To improve the reconstruction ability for seismic signals, the network adjusts the weight parameters reversely layer by layer and performs frequent iterative training. Specifically, we use Adam optimizer to optimize the network. More network training parameters can be found in Table 3. After the training, we use the trained network to process the noisy DAS records.

FIGURE 4

FIGURE 4. The flowchart of MSI-Net denoising procedures.

TABLE 3

TABLE 3. The details of training the proposed network.

Results

Experiment settings

Synthetic DAS-VSP data were generated by forward modeling, and a seven-layer 2D geological model is shown in Figure 5. The horizontal coordinates indicate the horizontal distance and the vertical coordinates indicate the depth. The velocities of the P-wave from the top to the bottom are 2,000, 2,250, 2,500, 2,750, 3,000, 3,250, and 3,500 m/s. And the media densities from the top to the bottom are 2,050, 2,100, 2,150, 2,200, 2,250, and 2,300 $kg/m^3$. Next, we set up the acquisition geometry. As shown in Figure 5, the inverted triangle represents the source and the vertical black line represents the measurement line formed by the fiber optic sensor. The time sampling interval is 400 $\mu s$, and the spatial sampling interval is 1 m. By solving the elastic wave equation, we can obtain the synthetic clean DAS -VSP data as shown in Figure 5B, where D1 is the direct wave, R1-R5 are the reflected up-going wave, and D2-D5 are the incident down-going waves. Common noises in DAS, such as random noise (as shown in region A), background anomalous interference (as shown in region B), fading noise (as shown in region C), horizontal noise (as shown in region D), and checkerboard noise (as shown in region E) are added as shown in Figure 5C. Because the generation mechanism of coupling noise is not yet clear, in the simulation experiment, it is not considered to add coupling noise to the simulation DAS record. The remade simulated pure signals and the noise collected together form synthetic noisy records and are used as a test. Figure 5D shows the synthesized noisy DAS-VSP data. We synthesized 10 noise-bearing records as the test set. The effect of the proposed method on the signal reconstruction task is evaluated on the test data set. The data used for testing and the data used for training are independent of each other. Experiments were carried out by the Pytorch framework for network training and testing in the Python environment and deployed on a computer equipped with Inter Xeon CPU E5-2620 and double Nvidia GeForce GTX 1080Ti GPUs. The proposed method is used to process synthetic and field noisy records. Meanwhile, some competitive methods are also used to process records, including the conventional method—band-pass filtering, wavelet transform filtering, weighted nuclear norm minimization (WNNM) and the deep learning common models—DnCNN and U-Net. For the convenience of description, the proposed method in this paper is called MSI-Net.

FIGURE 5

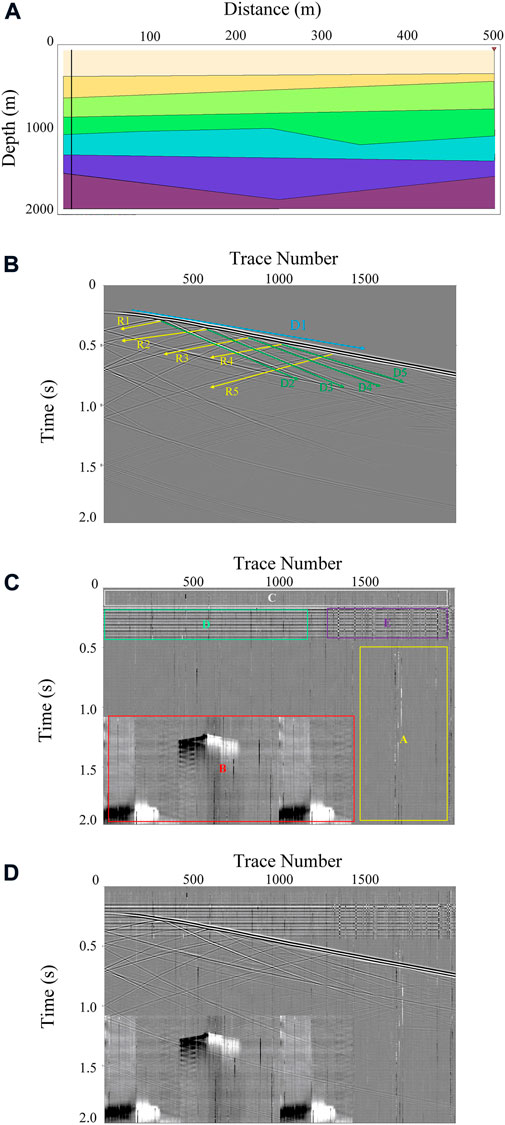
FIGURE 5. Construction of the noisy synthetic DAS-VSP record. (A) The velocity model. (B) The theoretical pure DAS-VSP record. (C) The added field noise. (D)The synthetic noisy record with the SNR of -0.5132 dB.

Synthetic data denoising results

Taking a synthetic DAS-VSP record containing complex noise as an example in Figure 5D, this paper shows the signal reconstruction results and removed noise in Figure 6 of different methods. The SNR of the synthesized noisy record is −0.5132 dB. We can observe that MSI-Net can suppress many common noises at one time, and the denoising process is more efficient and faster. The results are shown in Figures 6K,L, where Figure 6K is the denoising result and Figure 6L is the difference between noisy input and the predicted pure signal, which can also be considered as the noise predicted by the method. From the quantitative analysis, on the whole, the SNR of the results of the three deep learning methods is much higher than that of the traditional methods. In deep learning methods, the SNR of the result of the MSI-Net (19.0062 dB) is the highest, which is higher than that of DnCNN (18.3209 dB) and U-Net (18.4935 dB). From the point of view of signal recovery, all kinds of signals in the wave field are recovered, and the direct wave, reflected up-going wave and incident down-going waves which were originally polluted by noise can be observed, which will be beneficial to the subsequent inversion and imaging. From the point of view of noise suppression, all noises are suppressed. In contrast, the denoising effect of the conventional method for DAS-VSP records does not meet the requirements of seismic exploration. The analysis of the processing results shows that band-pass filtering can only attenuate noise in a defined frequency band in Figure 6A, which not only fails to suppress the noise but also damages the signal. Wavelet transform filtering can only remove a part of random noise, and most of the noise is still retained in the denoised record in Figure 6C. The filtering effect of WNNM is poor, only part of the noise can be removed mechanically, there is still a large amount of noise residue in the record in Figure 6E, and obvious signal leakage can also be observed in the removed noise result in Figure 6F, which is unacceptable for reconstruction. Compared with the three traditional methods, DnCNN, U-Net and MSI-Net have better denoising effects, the noise suppression is more uniform and thorough, and there is no obvious signal leakage in the removed noise results.

FIGURE 6

FIGURE 6. Comparisons for denoising results of different methods. (A–B) The denoising result with the SNR of 1.9371 dB and predicted noise of Band-pass filtering. (C–D) The denoising result with the SNR of 1.0421 dB and predicted noise of Wavelet transform filtering. (E–F) The denoising result with the SNR of 0.5712 dB and predicted noise of WNNM. (G–H) The denoising result with the SNR of 18.3209 dB and predicted noise of DnCNN. (I–J) The denoising result with the SNR of 18.4935 dB and predicted noise of U-Net (K–L) The denoising result with the SNR of 19.0062 dB and predicted noise of MSI-Net.

The comparison results of the three deep learning methods are more focused on the high-resolution reconstruction of the signal structure. For MSI-Net, the idea of multi-scale analysis is adopted, and the suppression effect of noise is better than that of DnCNN (only at a single scale). At the same time, we can see that MSI-Net has the highest resolution in denoised recovery, and the recovery effect of weak signals is better than DnCNN and U-net, which shows that MSI-Net is more suitable for the high-resolution requirements of seismic exploration. We also analyze the signals and differences of various methods in the frequency domain as shown in Figure 7, and mainly expect to observe whether the signals leaked by various methods through the frequency spectrum. From the frequency domain, it can be seen that the traditional method does not recover the signal well. At the same time, there are different degrees of signal leakage in their differences. In contrast, the results of the three deep learning methods are closer to the original record. And it is difficult to see the leakage of the signal in the difference between the three methods. The three deep learning methods are not significantly different in the frequency domain. The comparison of the three kinds of deep learning relies more on quantitative analysis.

FIGURE 7

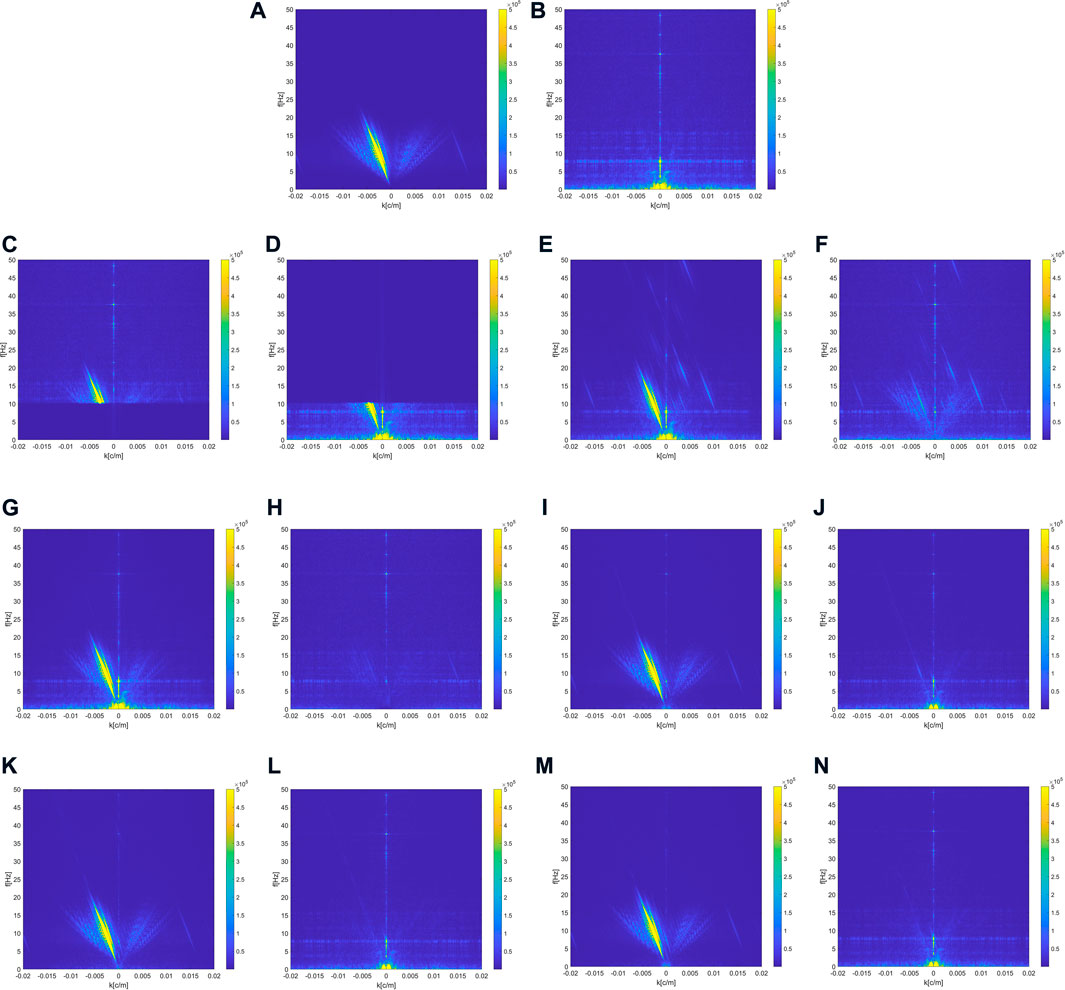
FIGURE 7. F-K domain analysis for the denoising results of different methods. (A,B) F-K spectrum of the pure record and noise data. (C,D) F-K spectra of the denoising results and predicted noise of Band-pass filtering. (E,F) F-K spectra of the denoising results and predicted noise of Wavelet Transform filtering. (G,H) F-K spectra of the denoising results and predicted noise of WNNM. (I,J) F-K spectra of the denoising result and predicted noise of DnCNN (K,L) F-K spectra of the denoising result and predicted noise of U-Net (M,N) F-K spectra of the denoising result and predicted noise of MSI-Net.

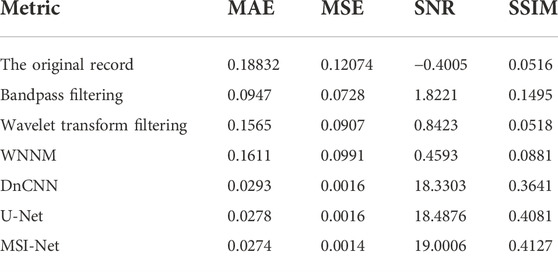
The signal-to-noise ratio (SNR) is one of the important indexes to measure the quality of seismic data, and the improvement of SNR is an important index to evaluate the performance of denoising methods. According to the size of the calculation, SNR can be divided into global SNR and local SNR. Global SNR is usually used to measure the overall quality of seismic data. Besides, mean absolute error (MAE), mean square error (MSE) and structural similarity (SSIM) (Wang et al., 2004) are commonly used measures. In this paper, SNR, MAE, MSE and SSIM are used to quantitatively evaluate several methods.

Generally speaking, higher SNR, SSIM and smaller MAE, MSE represent better denoising results. The denoising results of different methods are shown in Table 4, from which it can be seen that MSI-Net has the highest performance in the evaluation of four indexes. We also realize that the global SNR may not be sensitive to the quality of local data. There may be some cases where the local data quality is poor, but the overall SNR is high, which is unacceptable for DAS records with large differences in global. The local SNR can describe the quality of local seismic data in detail, so it is used to quantitatively analyze the denoising performance of the proposed method. A moving window with a size of 5 × 5 and a step of one is used to segment DAS-VSP data, and the local SNR is calculated in the moving window. The local SNR of the data at $\left(t,x\right)$ can be expressed as

$\mathrm{S}\mathrm{N}\mathrm{R}\left(t,x\right)=10{\log }_{10}\frac{{\sum }_{i=t-\left(w-1\right)/2}^{t+\left(w-1\right)/2}{\sum }_{j=x-\left(w-1\right)/2}^{x+\left(w-1\right)/2}(S(i,j)-\overline{S}(i,j){)}^2}{{\sum }_{i=t-\left(w-1\right)/2}^{t+\left(w-1\right)/2}{\sum }_{j=x-\left(w-1\right)/2}^{x+\left(w-1\right)/2}(Dn(i,j)-\overline{Dn}(i,j){)}^2}(5)$

where $S$is the pure signal and $Dn$is the denoised data. $\overline{S}$and $\overline{Dn}$ is the mean of $S$and $Dn$, respectively. And $w$ is the window length. The local SNR of the result of the MSI-Net and the methods for comparison is shown in Figure 8, where the abscissa is the number of seismic traces, the ordinate is the sampling point and the number in the color bar is the SNR (dB). Figure 8A shows the local SNR of synthetic noisy DAS-VSP data. We can see that the local SNR of areas affected by different noises is low, which is consistent with the actual situation. Figure 8G shows the local SNR of the results processed by the proposed method. It can be seen that the method proposed in this paper has the best performance in improving the local SNR.

TABLE 4

TABLE 4. Performance statistics of different denoising methods on the test sets.

FIGURE 8

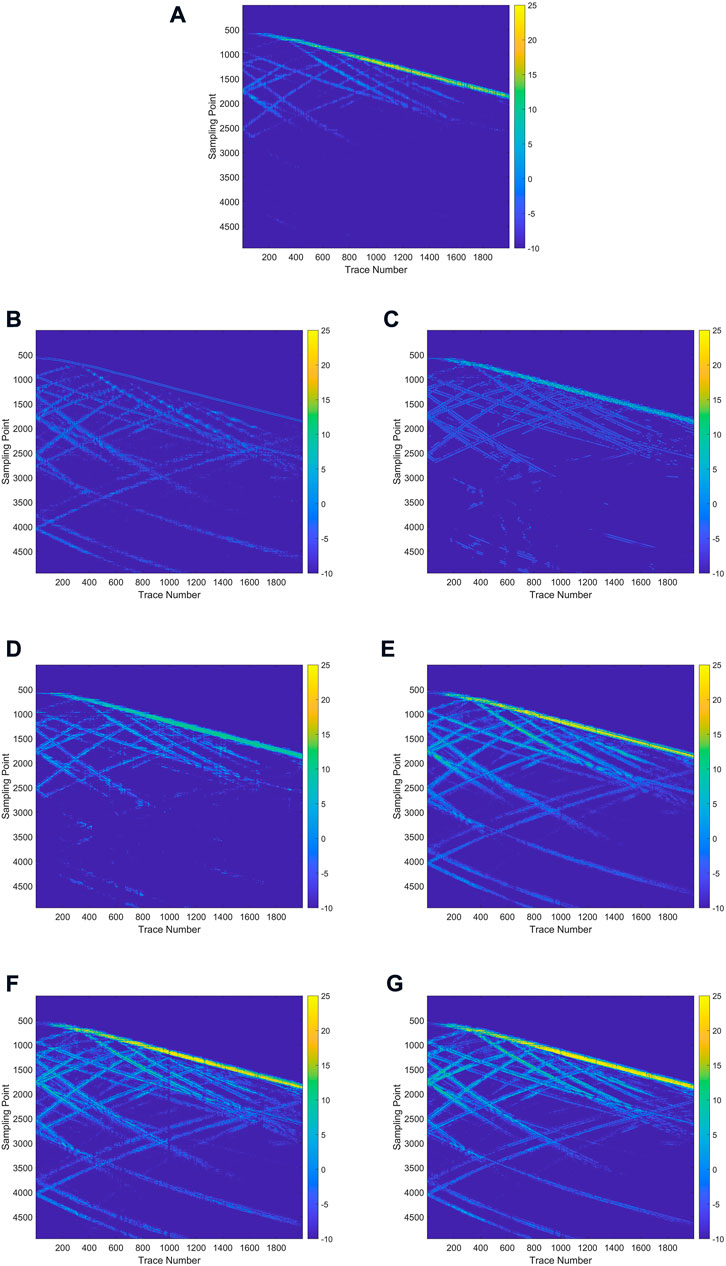
FIGURE 8. Local SNR analysis. (A) Local SNR of the synthetic noisy DAS-VSP data. (B–G) Local SNR of the denoised result of Band-pass filtering, Wavelet transform filtering, WNNM, DnCNN, U-Net, MSI-Net, respectively.

Denoising results of field DAS-VSP data

To verify the practicability and generalization performance of the network, the field DAS-VSP data was processed through the proposed method and other competitive methods. The time sampling interval of the DAS data shown is 400 $\mu s$ and the spatial sampling interval is 1 m. The processing results are shown in Figure 9. From the field seismic records, it can be observed that there is a lot of noise in the records, and the SNR is generally low. Some random noise interferes with the presentation of effective signals seriously and even submerges the seismic events completely. Traditional methods are less effective in denoising the actual records. Band-pass filtering makes a rough distinction between signal and noise, greatly destroying the valid signal in Figure 10A. The reconstructed result of wavelet transform filtering still retains some random noise, and the recovery of the effective signal is also poor in Figure 10B. The suppression effect of WNNM on various kinds of noise is not obvious, and the result after denoising still retains a large number of various kinds of noise in Figure 10C. It can be seen that, compared with the traditional denoising methods, the MSI-Net is effective for signal recovery and noise suppression in actual records. As shown in the blue area in Figure 10F, the reflected up-going wave and the converted wave, which were originally seriously affected by noise, become clearer and more continuous after denoising, which proves that MSI-Net has a good ability to recover the signals in DAS-VSP. As shown in the red area in Figure 10F, the reflected up-going wave with weak energy can hardly be observed under the influence of noise. After being treated by the MSI-Net, it is obviously recovered. Compared with DnCNN and U-Net, the amplified signal leakage of the method proposed in this paper is obviously less. It proves that MSI-Net has a better ability to retain valid signals. This makes the MSI-Net better meet the high amplitude-preserving requirements of DAS-VSP data processing. For the actual records after processing, we also observe that the first arrival of the processed direct wave is discontinuous. The first arrival wave in the original record may be discontinuous due to the poor coupling of the optical fiber during the data acquisition. The neural network not only removes noise but also restores weak signals. This also causes the discontinuity of the first arrivals to be more prominent. This problem can be resolved during acquisition.

FIGURE 9

FIGURE 9. Field DAS-VSP data.

FIGURE 10

FIGURE 10. Comparisons for the denoising results of the field DAS-VSP record. (A–F) The denoising results for Band-pass filtering, Wavelet transform filtering, WNNM, DnCNN, U-Net, and MSI-Net, respectively.

To further illustrate the denoising ability of different methods, we selected a representative local enlargement to evaluate them in detail in Figure 11. Though the interference of random noise can be eliminated basically, the three deep learning methods have different performances in the recovery of signals. Observing the magnified partial processing results, it can be found that the recovered signals recovered by DnCNN shown in Figure 11E are not continuous due to the relatively small receptive field. In DnCNN, the features are only based on single-scale analysis, and the expansion of the receptive field can only depend on the increase of the number of layers, which makes it difficult to expand the receptive field of DnCNN too much.

FIGURE 11

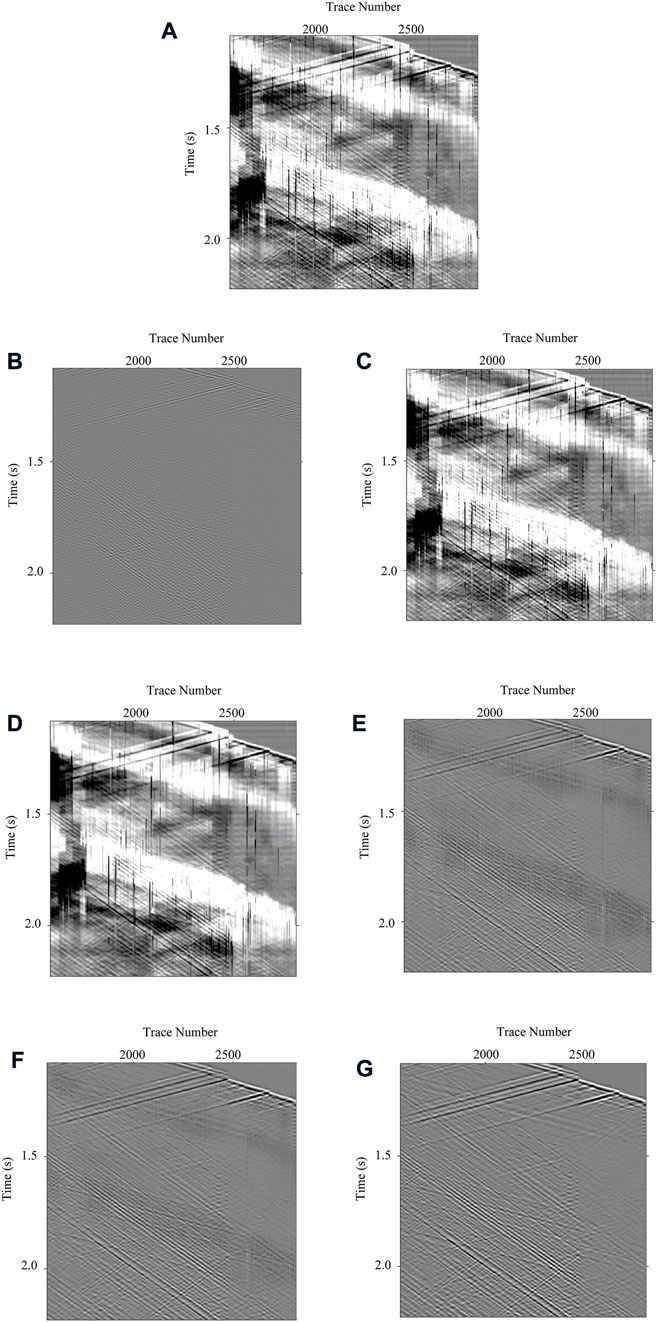
FIGURE 11. Local enlargements for the denoising results of different methods. (A) Local enlargements of the field noisy DAS-VSP data. (B–G) Local enlargements of denoising results by utilizing Band-pass filtering, Wavelet transform filtering, WNNM, DnCNN, U-Net, and MSI-Net, respectively.

The continuity of reconstructed signals by U-Net shown in Figure 11F is relatively better, but some details of the signals are still missing. On the whole, the MSI-Net has more advanced effects on the high-resolution reconstruction of signals, whether in the maintenance of events continuity or the recovery of signal details as shown in Figure 11G. From the local view, the method proposed in this paper is obviously better for signal recovery. Specifically, DnCNN is always maintained in high-resolution representation, so the prediction of the signal may be limited by the local receptive field, which is often vague. U-Net adopts the processing mode of downsampling before upsampling, and its recovery effect for high resolution is not as good as that of MSI-Net. The MSI-Net adopts a multi-scale processing method, and it also frequently uses information exchange among scales, which better fuses multi-scale signals, so it has a better effect on high-resolution restoration.

In addition, the difference between each method is shown in Figure 12. From the difference, we can observe that there is often some residual signal in the results processed by the conventional method. For example, the leakage of the signal can be clearly observed in the difference in the band-pass filtering. In contrast, it can be seen that the signal leakage in the difference between the three deep learning-based methods is very small. Among them, there is basically no signal leakage in the difference between the MSI-Net. It proves that the method proposed in this paper basically does not damage the effective signal.

FIGURE 12

FIGURE 12. Comparisons for the predicted noise of different methods. (A–F) The predicted noise for Band-pass filtering, Wavelet transform filtering, WNNM, DnCNN, U-Net, and MSI-Net, respectively.

The generalization ability is a crucial evaluation criterion for a denoising network in practice applications. The main purpose of training the network is to obtain capture features and learns the laws from the training data. The model should have the generalization ability that can make the trained model perform well when processing different data with a similar pattern. To test the generalization performance of MSI-Net, we utilize MSI-Net to process more records. Figure 13A shows other DAS records that contain various types of noise. It was collected from other wells in the same region as the record shown in Figure 9. Figure 13B shows the result processed by MSI-Net, and Figure 13C shows the difference after denoising. It can be seen that for each DAS record, the effective signal has been completely restored. The MSI-Net can still maintain good performance in the denoising of other records, indicating that our model has a good generalization ability for DAS records. At the same time, the different kinds of noise in the DAS-VSP record were completely predicted. In particular, the trained network can also accurately predict the coupled noise in the record. This is even more important for the high-resolution reconstruction of the DAS record.

FIGURE 13

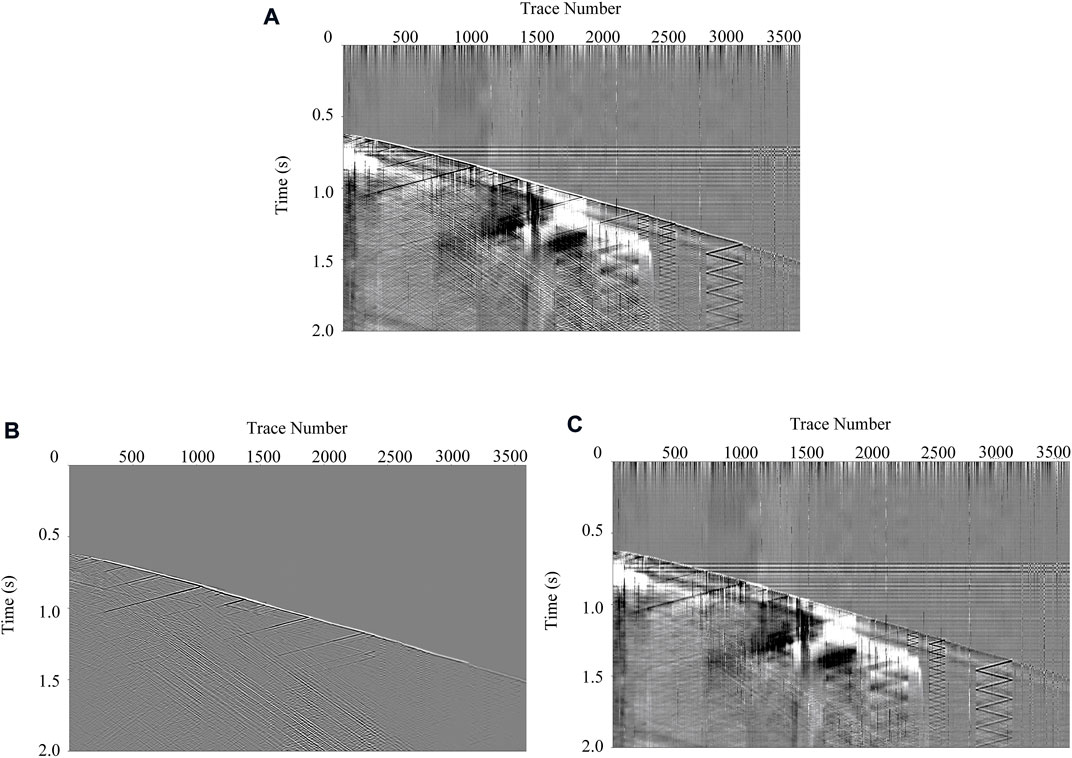
FIGURE 13. The denoising result of another field DAS-VSP record. (A) The new field DAS-VSP data. (B) The denoising results for the proposed method. (C) The predicted noise of the proposed method.

Conclusion

In this paper, we proposed a network for high-resolution reconstruction of DAS-VSP records. With the help of multi-scale feature learning and frequent information interaction between scales, the network can successfully acquire abundant multi-resolution characterizations. The low-resolution information of different scales is used to supplement the high-resolution information at the same time, to realize accurate high-resolution reconstruction. The proposed method achieves an excellent reconstruction effect in processing synthetic and field DAS-VSP records, especially improving the SNR and resolution. Benefiting from multi-scale analysis, the network recovers local details better than previous general network architectures. High-resolution reconstructed records can have positive implications for subsequent imaging. In addition, the multi-scale analysis also inevitably increases the computational cost, so more efficient multi-scale strategies will be explored in the future.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HW (First Author): Conceptualization, Methodology, Software, Investigation, Formal Analysis, Writing—Original Draft; JL (Corresponding Author): Data Curation, Funding Acquisition, Resources, Supervision; DS: Software, Validation; XD (Corresponding Author): Data Curation, Visualization, Investigation; YL (Corresponding Author): Conceptualization, Funding Acquisition, Resources, Supervision, Writing—Review and Editing.

Funding

This work was supported by the National key research and development program of China under Grant 2021YFA0716800 and National Science Foundation of China under Grant 42230805, 42074123. Besides, this work was also supported by Key project of Guangdong Province for Promoting High-quality Economic Development (Marine Economic Development) in 2022: Research and development of key technology and equipment for Marine vibroseis system (GDNRC(2022)29).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amezquita Sanchez, J. P., Chavez Alegria, O., Valtierra Rodriguez, M., Abeyro, Lopez Cruz, Jose, Antonio, Millan Almaraz, J. R., et al. (2017). Detection of ULF geomagnetic anomalies associated to seismic activity using EMD method and fractal dimension theory. IEEE Lat. Am. Trans. 15 (2), 197–205. doi:10.1109/tla.2017.7854612

CrossRef Full Text | Google Scholar

Anvari, R., Siahsar, M. A. N., Gholtashi, S., Roshandel Kahoo, A., and Mohammadi, M. (2017). Seismic random noise attenuation using synchrosqueezed wavelet transform and low-rank signal matrix approximation. IEEE Trans. Geosci. Remote Sens. 55 (11), 6574–6581. doi:10.1109/tgrs.2017.2730228

CrossRef Full Text | Google Scholar

Binder, G., Titov, A., Liu, Y., Simmons, J., Tura, A., Byerley, G., et al. (2020). Modeling the seismic response of individual hydraulic fracturing stages observed in a time-lapse distributed acoustic sensing vertical seismic profiling survey. Geophysics 85 (4), T225–T235. doi:10.1190/geo2019-0819.1

CrossRef Full Text | Google Scholar

Bekara, M., and Van der Baan, M. (2009). “Random and coherent noise attenuation by empirical mode decomposition. Geophysics 74 (5), V89–V98

CrossRef Full Text | Google Scholar

Canales, L. L. (1984). “Random noise reduction,” in 54th Annual International Meeting, SEG, Expanded Abstracts, 525–527.

CrossRef Full Text | Google Scholar

Chen, Y., and Fomel, S. (2018). EMD-seislet transform. Geophysics 83 (1), A27–A32. doi:10.1190/geo2017-0554.1

CrossRef Full Text | Google Scholar

Chen, Y., Jianwei, M., and Fomel, S. (2016). Double-sparsity dictionary for seismic noise attenuation. Geophysics 81 (2), V103–V116. doi:10.1190/geo2014-0525.1

CrossRef Full Text | Google Scholar

Chen, Y., Zhang, M., Bai, M., and Chen, W. (2019). Possible site effects revealed by regional earthquake records in the qaidam basin, China. Seismol. Res. Lett. 90, 280–293. doi:10.1785/0220180095

CrossRef Full Text | Google Scholar

Cheng, J., Chen, K., and Sacchi, M. D. (2015). Application of robust principal component analysis (RPCA) to suppress erratic noise in seismic records, 4646.

Google Scholar

Constantinou, A., Farahani, A., Cuny, T., and Hartog, A. (2016). “Improving DAS acquisition by real-time monitoring of wireline cable coupling”, in Proc. SEG Tech. Program Expanded Abstracts, 5603–5607 10.1190/segam2016-13950092.1

CrossRef Full Text | Google Scholar

Creswell, A., White, T., Dumoulin, V., Arulkumaran, K., Sengupta, B., and Bharath, A. A. (2017). Generative adversarial networks: An overview. IEEE Signal Process. Mag. 35 (1), 53–65. doi:10.1109/msp.2017.2765202

CrossRef Full Text | Google Scholar

Dong, X., Li, Y., Zhong, T., Wu, N., and Wang, H. (2022). Random and coherent noise suppression in DAS-VSP data by using a supervised deep learning method. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi:10.1109/lgrs.2020.3023706

CrossRef Full Text | Google Scholar

Gan, S., Wang, S., Chen, Y., Zhang, Y., and Jin, Z. (2015). Dealiased seismic data interpolation using seislet transform with low-frequency constraint. IEEE Geosci. Remote Sens. Lett. 12 (10), 2150–2154. doi:10.1109/lgrs.2015.2453119

CrossRef Full Text | Google Scholar

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2020). Generative adversarial networks. Communications of the ACM 63 (11), 139–144.

CrossRef Full Text | Google Scholar

Gorszczyk, A., Adamczyk, A., and Malinowski, M. (2014). Application of curvelet denoising to 2D and 3D seismic data; practical considerations. J. Appl. Geophys. 105, 78–94. doi:10.1016/j.jappgeo.2014.03.009

CrossRef Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in 2016 IEEE Conference On Computer Vision And Pattern Recognition (Cvpr), 770. doi:10.1109/CVPR.2016.90

CrossRef Full Text | Google Scholar

Jiang, J., Ren, H., and Zhang, M. (2021). A Convolutional Autoencoder Method for Simultaneous Seismic Data Reconstruction and Denoising. IEEE geoscience and remote sensing letters 19, 1–5.

Google Scholar

Jiang, T., Zhan, G., Hance, T., Sugianto, S., Soulas, S., and Kjos, E. (2016). “Valhall dual-well 3D DAS VSP field trial and imaging for active wells”, in Proc. SEG Tech. Program Expanded Abstracts, 5582–5586 10.1190/segam2016-13871754.1.

CrossRef Full Text | Google Scholar

Kesharwani, A., Aggarwal, V., Singh, S. B. R, R., and Kumar, A. (2021). Marine seismic signal denoising using VMD with Hausdorff distance and wavelet transform. J. Def. Model. Simul. 19 (4). doi:10.1177/15485129211036044

CrossRef Full Text | Google Scholar

Lecun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nat. Lond. 521 (7553), 436–444. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W. (2018). Classifying geological structure elements from seismic images using deep learning. SEG Technical Program, Expanded Abstracts, 4643–4648. doi:10.1190/segam2018-2998036.1

CrossRef Full Text | Google Scholar

Li, J., Wu, X., and Hu, Z. (2022). Deep Learning for Simultaneous Seismic Image Super-Resolution and Denoising. IEEE transactions on geoscience and remote sensing 60, 1–11.

CrossRef Full Text | Google Scholar

Liu, X., Chen, X., Li, J., and Chen, Y. (2021). Nonlocal weighted robust principal component analysis for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 59 (2), 1745–1756. doi:10.1109/tgrs.2020.2996686

CrossRef Full Text | Google Scholar

Liu, D., Deng, Z., Wang, C., Wang, X., and Chen, W. (2022). An Unsupervised Deep Learning Method for Denoising Prestack Random Noise. IEEE geoscience and remote sensing letters 19, 1–5.

CrossRef Full Text | Google Scholar

Lu, W., and Li, F. (2013). Seismic spectral decomposition using deconvolutive short-time Fourier transform spectrogram. Geophysics 78, V43–V51. doi:10.1190/geo2012-0125.1

CrossRef Full Text | Google Scholar

Mendel, J. (1977). White-noise estimators for seismic data processing in oil exploration. IEEE Trans. Autom. Contr. 22 (5), 694–706. doi:10.1109/tac.1977.1101597

CrossRef Full Text | Google Scholar

Mousavi, S. M., Langston, C. A., and Horton, S. P. (2016). Automatic microseismic denoising and onset detection using the synchrosqueezed continuous wavelet transform. Geophysics 81 (4), V341–V355. doi:10.1190/geo2015-0598.1

CrossRef Full Text | Google Scholar

Neelamani, R., Baumstein, A. I., Gillard, D. G., Hadidi, M. T., and Soroka, W. L., (2008). Coherent and random noise attenuation using the curvelet transform. Lead. Edge 27 (2), 240–248. doi:10.1190/1.2840373

CrossRef Full Text | Google Scholar

Oropeza, V., and Sacchi, M. D. (2011). Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis. Geophysics 76 (3), V25–V32. doi:10.1190/1.3552706

CrossRef Full Text | Google Scholar

Qiu, C., Wu, B., Liu, N., Zhu, X., and Ren, H. (2022). Deep Learning Prior Model for Unsupervised Seismic Data Random Noise Attenuation. IEEE geoscience and remote sensing letters 19, 1–5.

CrossRef Full Text | Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net: Convolutional networks for biomedical image segmentation. 234.

Google Scholar

Saad, O., and Chen, Y. (2020). Deep denoising autoencoder for seismic random noise attenuation. Geophysics 85 (4), V367–V376. doi:10.1190/geo2019-0468.1

CrossRef Full Text | Google Scholar

Saad, O. M., Oboue, Yapo Abole Serge Innocent, Bai, M., Samy, L., Yang, L., and Chen, Y. (2021). Self-Attention Deep Image Prior Network for Unsupervised 3-D Seismic Data Enhancement. IEEE transactions on geoscience and remote sensing 60, 1–14.

Google Scholar

Spikes, K. T., Tisato, N., Hess, T. E., and Holt, J. W. (2019). Comparison of geophone and surface-deployed distributed acoustic sensing seismic data. Geophysics 84 (2), A25–A29. doi:10.1190/geo2018-0528.1

CrossRef Full Text | Google Scholar

Sun, K., Xiao, B., Liu, D., and Wang, J. (2019). Deep high-resolution representation learning for human pose estimation, 5686.

Google Scholar

Sun, H., Yang, F., and Ma, J. (2022). Seismic Random Noise Attenuation via Self-Supervised Transfer Learning. IEEE geoscience and remote sensing letters 19, 1–5.

CrossRef Full Text | Google Scholar

Tsai, K. C., Hu, W., Wu, X., Chen, J., and Han, Z. (2018). First-break automatic picking with deep semisupervised learning neural network. SEG Technical Program, Expanded Abstracts, 2181–2185. doi:10.1190/segam2018-2998106.1

CrossRef Full Text | Google Scholar

Wang, F., and Chen, S. (2019). Residual Learning of Deep Convolutional Neural Network for Seismic Random Noise Attenuation. IEEE geoscience and remote sensing letters 16 (8), 1314–1318.

CrossRef Full Text | Google Scholar

Wang, H., Li, Y., and Dong, X. (2021). Generative adversarial network for desert seismic data denoising. IEEE Trans. Geosci. Remote Sens. 59 (8), 7062–7075. doi:10.1109/tgrs.2020.3030692

CrossRef Full Text | Google Scholar

Wang, S., Li, Y., and Zhao, Y. (2022). Attribute-guided target data separation network for DAS VSP data. IEEE Trans. Geosci. Remote Sens. 60, 1–16. doi:10.1109/tgrs.2021.3126022

CrossRef Full Text | Google Scholar

Wang, X., and Ma, J. (2020). Adaptive dictionary learning for blind seismic data denoising. IEEE Geosci. Remote Sens. Lett. 17 (7), 1273–1277. doi:10.1109/lgrs.2019.2941025

CrossRef Full Text | Google Scholar

Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P. (2004). Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 13 (4), 600–612. doi:10.1109/tip.2003.819861

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, N., Li, Y., and Yang, B. (2011). Noise attenuation for 2-D seismic data by radial-trace time-frequency peak filtering. IEEE Geosci. Remote Sens. Lett. 8 (5), 874–878. doi:10.1109/lgrs.2011.2129552

CrossRef Full Text | Google Scholar

Wu, X., Liang, L., Shi, Y., and Fomel, S. (2019). FaultSeg3D: Using synthetic datasets to train an end-to-end convolutional neural network for 3D seismic fault segmentation. Geophysics 84 (3), IM35–IM45. doi:10.1190/geo2018-0646.1

CrossRef Full Text | Google Scholar

Yarman, C. E., Kumar, R., and Rickett, J. (2018). A model-based data-driven dictionary learning for seismic data representation. Geophys. Prospect. 66 (1), 98–123. doi:10.1111/1365-2478.12533

CrossRef Full Text | Google Scholar

Yang, L., Wang, S., Chen, X., Saad, O. M., Chen, W., Oboue, Yapo Abole Serge Innocent, et al. (2021). Unsupervised 3-D Random Noise Attenuation Using Deep Skip Autoencoder. IEEE transactions on geoscience and remote sensing 60, 1–16.

Google Scholar

Yu, S., Ma, J., and Wang, W. (2019). Deep learning for denoising. Geophysics 84 (6), V333–V350. doi:10.1190/geo2018-0668.1

CrossRef Full Text | Google Scholar

Yuan, P., Hu, W., Wu, X., Chen, J., and Van Nguyen, H. (2019). First arrival picking using U-net with lovasz loss and nearest point picking method. SEG Technical Program, Expanded Abstracts, 2624–2628. doi:10.1190/segam2019-3214404.1

CrossRef Full Text | Google Scholar

Zhang, G., Lin, C., and Chen, Y. (2020). Convolutional neural networks for microseismic waveform classification and arrival picking. Geophysics 85 (4), WA227–WA240. doi:10.1190/geo2019-0267.1

CrossRef Full Text | Google Scholar

Zhang, G., Wang, Z., and Chen, Y. (2018). Deep learning for seismic lithology prediction. Geophys. J. Int. 215, 1368–1387. doi:10.1093/gji/ggy34

CrossRef Full Text | Google Scholar

Zhang, K., Zuo, W., Chen, Y., Meng, D., and Zhang, L. (2017). Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 26 (7), 3142–3155. doi:10.1109/tip.2017.2662206

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., Li, Y., and Wu, N. (2022). Distributed acoustic sensing vertical seismic profile data denoiser based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 60, 1–11. doi:10.1109/tgrs.2020.3042202

CrossRef Full Text | Google Scholar

Zhong, T., Cheng, M., Dong, X., and Wu, N. (2022). Seismic random noise attenuation by applying multiscale denoising convolutional neural network. IEEE Trans. Geosci. Remote Sens. 60, 1–13. doi:10.1109/tgrs.2021.3095922

CrossRef Full Text | Google Scholar