Analysis on “three-box” model of stress-strain in frozen soil porous media based on representative macroscopic Volume

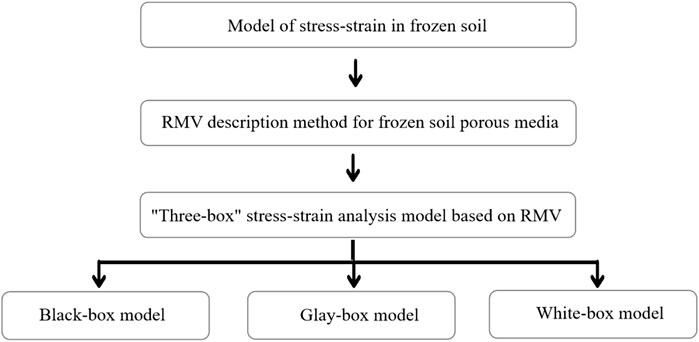
In cold regions, the pore space’s composition and phase state can affect the elastic modulus of the media. During the winter, the freezing conditions in the soil results in the release of water from the pore space, which results in significant changes in the media’s distribution and composition. There are a few weaknesses in the current research with respect to the elastic modulus change example of frozen soil. This paper presents that the Representative Macroscopic Volume (RMV) choice strategy is provided for frozen soil with porosity as a typical condition variable. Under the state of freezing, a “three-box” analytical model for stress-strain calculation of frozen soil porous media is established, namely, the black-box model, the gray-box model, and the white-box model. The relevant equations for calculating elastic modulus are presented based on the proposed “three-box” model and the analysis of the stress conduction process. Results show that the discrepancy between the computed and experimental values of the white-box model is slight, and the elastic modulus of frozen soil calculated by the model established in this paper is consistent with the actual state. It can be deduced that the model established in this paper has practicality and the conclusions of the study are of guiding significance for the application of frozen soil.

1 Introduction

The frozen soil region is rich in natural resources, while many projects in China, such as energy, transportation, communication, water, and oil pipelines, are established in the frozen soil region (Zhang et al., 2015; Che et al., 2019; Ma et al., 2019; Streletskiy et al., 2019). The distribution and form of pore accesses in frozen soil vary, the momentum, energy, and mass transfer processes interact, and couple with each other, and the transfer phenomena and mechanisms are complex and variable (Sweidan et al., 2022; Yu et al., 2021; Fu et al., 2022). Some of the essential characteristics are difficult to obtain precisely (Alzoubi et al., 2019; Chang et al., 2019). Soil is a typical porous medium, and the study of its stress transfer mechanism involves some basic disciplines, such as soil mechanics, solid mechanics, and other disciplines, which is an interdisciplinary cross-science problem (Li et al., 2022a; Li et al., 2022b). The study of stress-strain in frozen soil porous media at home and abroad generally adopts simple experimental methods to analyze the stress-strain in frozen soil (Esmaeili-Falak et al., 2020; Xu et al., 2020; Luo et al., 2018; Zhang D. et al., 2020). There are few reports on the macroscopic level mechanism of stress-strain in frozen soil porous media.

With the development of soil mechanics and frozen soil mechanics, the understanding of soil bodies is getting deeper and deeper (Jiang and Huang, 2016). Soil is a complex multiphase porous medium, and its mechanical properties and equilibrium state are the results of the mutual coupling of the phases in the soil and various environmental effects (Ott et al., 2020; Yan et al., 2022; Guo P. et al., 2021). von Terzaghi (1923) proposed the effective stress principle of saturated soils (Gudehus, 2021), which made soil mechanics independent from general mechanics into an independent discipline and prepared for the improvement of present day soil mechanics (Jiang and Huang, 2018). When using the principle of effective stress, the saturated soil can be equated to a single-phase medium so that the soil can be analyzed for deformation and strength using the method of continuous medium mechanics (Liu E. et al., 2018). However, in practice, the soil body is subjected to stress variables such as the effective stress and other state variables, so considering only the effect of the effective stress is a concise but approximate treatment (Li, 2003; Jiang et al., 2017).

The multiphase pore medium theory (or mixture theory) starts from the first law of thermodynamics and the second law of thermodynamics, takes into account the action of various factors, and after reasonable assumptions and strict derivation, a set of intrinsic constitutive equations describing the properties of the soil can be obtained (Edip et al., 2018; Kjelstrup et al., 2018; He et al., 2021; Oka and Kimoto, 2021). The intrinsic constitutive equations derived from mixture theory are scientifically systematic and rigorous (Guo Z. et al., 2021; Liu and Lai, 2020; Liu et al., 2017; Liu et al., 2020). Hence, it is of good theoretical significance to study and explore the properties of frozen soil based on mixture theory, which has become the theoretical basis for describing the properties of multiphase pore media, including soils (Kefayati et al., 2021; Liu and Wang, 2021; Niu et al., 2022). Among them, Wei (2014) established a theoretical framework for describing the physicochemical properties of unsaturated soils using the composite mixture theory and focused on analyzing the effects of the Donna permeability phenomenon on the suction, effective stress, and chemical potential balance of unsaturated soils.

The frozen soil as a typical multiphase porous medium containing phase change, many scholars have also used the mixture theory to establish a theoretical framework to analyze the properties of frozen soil (Xu et al., 2022; Suh and Sun, 2021; Hu et al., 2021; He et al., 2021). Among them, Liu Y. et al. (2018) built an elastoplastic model of saturated permafrost based on porous media theory, thermodynamics, and elastoplastic mechanics and mathematically analyzed the stress-strain relationship of permafrost.

Ji et al. (2018) considered the connection between soil porosity and powerful pressure and laid out a coupled warm water driven mechanical model depicting the development of single-molecule ice under compelled conditions. The paper then performed a comprehensive analysis of the various effects of exterior stress on the unfrozen earth. It also took into account the separation stress and the equal water stress for ice separation. The results of this study allowed the paper to develop a model of separated ice lens (Zhou et al., 2012). Lai et al. (2014) conducted an laboratorial and numerical research on saturated frozen soil’s coupled water-thermal-force freezing and swelling characteristics. They used the conversation of energy and conservation of mass equations obtained about the porosity and temperature obtained from energy conservation and mass conservation equations to describe the soil freezing swelling and determine the formation of sexual ice lenses using critical porosity.

Because the composition of pore accesses in frozen soil porous media is highly uncertain, the mechanism of action is complex and variable, the influencing factors are difficult to determine, and many problems have not yet been solved (Rouabhi et al., 2018; Ming et al., 2020; Chen et al., 2021). The current analytical methods and research models have certain limitations (Sweidan et al., 2020; Hu et al., 2018; Huang F. et al., 2022). To address the scientific problem of uncertain information and factors that are not easy to quantify in frozen soil-preserving porous media. In this paper, based on the Representative Macroscopic Volume (RMV), a “three-box” stress-strain model for frozen soil porous media is established. The mathematical model for calculating the elastic modulus under different stress-strain models is given, and numerical calculations and simulations are carried out to obtain some meaningful results on the variation of elastic modulus with porosity, pore access distribution variate, and tortuosity.

2 Materials and methods

2.1 Materials

Frozen soil is a kind of noncontinuous four-phase system composed of soil skeleton, water, air and ice (Huang W. et al., 2022; Luo et al., 2022). In the course of forming frozen soil under a certain temperature and pressure, the pore water is converted into pore ice, changing the internal structure of the soil, thus affecting the interaction between the various phase components of the soil, and thus changing the strength of the soil, so the frozen soil has more complicated physical and mechanical characters (Zhang M. et al., 2020). The mechanical properties of the frozen soil are the most important factors that affect its stability. Understanding these factors is very important for the development and construction of frozen soil structures (Yang et al., 2018; Yin et al., 2022).

The elastic modulus serves as a deformation index, and different selection criteria will affect their numerical value, thus changing the deformation distribution law in the calculation of the structures (Huang et al., 2021; Li et al., 2022c). Due to the complex mechanical characters of frozen soil, so the lack of a uniform standard for the measure of the elastic modulus of frozen soil, it is important that the research on this subject is carried out properly as displayed in Figure 1.

FIGURE 1

FIGURE 1. Research roadmap.

2.2 RMV description method for frozen soil porous media

2.2.1 RMV description and characterization method for porous media

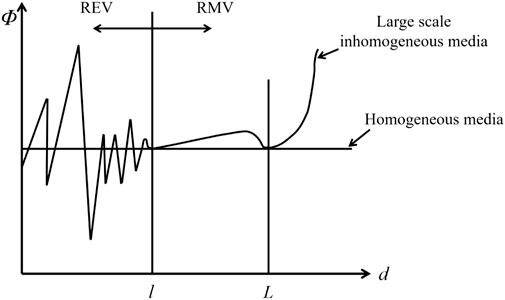
When using the macroscopic approach, in order to build a mathematical model based on the continuous medium theory, the fluid parameters around a point p in the porous medium must be averaged at the macroscopic level, replacing the actual local value with an average value within a specific range, the chosen average range is called the Representative Elementary Volume (REV) (Zhou and Meschke, 2018; Zhao et al., 2021). Nia and Jessen (2015) give a general approach to the selection of the REV. Compared to the size of the entire fluid region, the REV should be in a small range around the point p. The REV should be much larger than a single pore space and contain a sufficient number of pores. In the REV, the variation of the fundamental parameters with spatial coordinates is slight, and the average value tends to the actual value infinitely (Han et al., 2022a; Han et al., 2022b).

In practical problems, the selection of REV is complex and cannot be determined according to the variation law of the measured parameters (Huang et al., 2017). For averaging requirements that are not entirely accurate, the parameters can be averaged at the coarse level, and the control elements can be selected at the coarse level. At present, the academic circle calls the control elements selected by this method the Representative Macroscopic Volume (RMV) (Wang et al., 2020a; Wang et al., 2020b). For the selection of the RMV, the feature-length d, the size of the entire region L, and the size of the macroscopic parameter inhomogeneity l must satisfy $l\le d\le L$, as displayed in Figure 2.

FIGURE 2

FIGURE 2. Relationship between average volume size and porosity$\phi$

2.2.2 RMV description and characterization method based on porosity concept

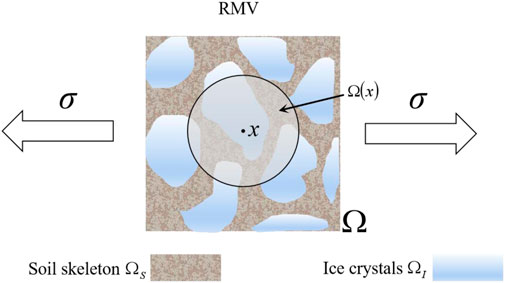
The soil porous media, similar to the general porous media, is composed of the assembly of soil phase elements and the interelement pores. The pores are filled with ice crystals, as a typical soil-ice two phase media, and the porosity is a important concept to describe the composition structure of porous media. Since the elastic modulus of the studied soil porous media is mainly influencing by the composition structure, i.e. the porosity, therefore, this paper takes the porosity as the representative state variable, and proposes the selection method for “three-box” model based on RMV.

The soil porous media can be equalized as a single continuum, and it is assumed that the state variable of any point in the continuous medium is the statistical mean value of corresponding state variable in a certain volume centered on this point, as displayed in Figure 3.

FIGURE 3

FIGURE 3. The medial volume centered on point x in porous media.

If the statistical medial of the state variable obtained by a selected volume is constant, then the continuous function of the center point and coordinates in space can be used to determine the elastic modulus of the soil, that is, this volume is the Representative Macroscopic Volume of corresponding state variable.

As displayed in Figure 3, assuming that the frozen soil has a geometrical zone $\mathrm{\Omega }$ (RMV zone), and it is divided into matrix zone ${\mathrm{\Omega }}_S$, and ice system zone ${\mathrm{\Omega }}_I$, i.e. the soil matrix media and ice media, which can be similar to two continuous media superimposed in space (Xu et al., 2011).

In the event that dot x is a random dot in the mathematical zone $\mathrm{\Omega }$ of unsaturated ice-containing soil, the media zone accepting dot x as the mathematical focus is $\mathrm{\Omega }\left(x\right)$, and in this zone, the mathematical volume is V, and the extensive amount is $E\left(x\right)$.

When the epitaxial quantity in zone ${\mathrm{\Omega }}_n\left(x\right)$ is $E_n\left(x\right)$, $F\left(x\right)$ is the inner parameters (structure, seepage and pressure) in macro scale of the epitaxial quantity of point x.

$\mathrm{\Omega }={\displaystyle \sum }_n{\mathrm{\Omega }}_n,n\in \left\{S,I\right\}(1)$

${\mathrm{\Omega }}_n\left(x\right)=\mathrm{\Omega }\left(x\right)\cap {\mathrm{\Omega }}_n,n\in \left\{S,I\right\}(2)$

$E\left(x\right)={\displaystyle \sum }_n{E}_n\left(x\right)(3)$

$F_n\left(x\right)=\underset{V_0\to V}{\lim }\frac{E_n\left(x\right)}{V_0}(4)$

$F_n\left(x\right)=\underset{y\to x}{\lim }{F}_n\left(y\right),y\in \left\{\mathrm{\Omega }\left(x\right)\right\}(5)$

At the point when the coice of media zone $\mathrm{\Omega }\left(x\right)$ fulfills the two Eqs 4, 5, the comparing V is the RMV of the frozen soil. For this article, the analysis of frozen soil porous media should select the RMV in stress process, and the method is shown above.

2.3 “Three-box” stress-strain analysis model based on RMV

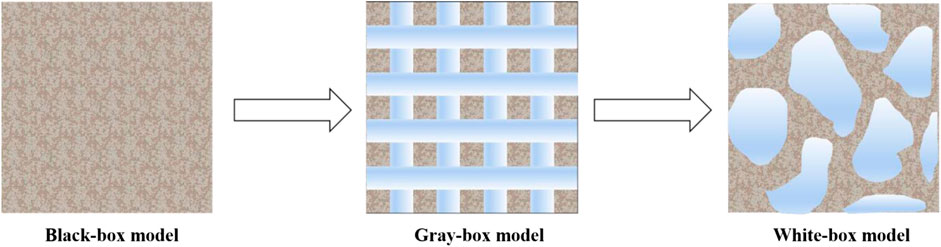
The “three-box” method is widely used in engineering fire analysis. The “three-box” model consists of three basic models: black-box model, gray-box model, and white-box model, which can be chosen according to the different requirements of analysis accuracy: black-box model, white-box model, or gray-box model. The black-box model is used chiefly for rough analysis; the white-box model is used for refined analysis; the gray-box model is between the black-box model and the white-box model and can be used for relatively refined analysis.

Therefore, in this paper, based on RMV, combining the “three-box” analysis method in engineering fire analysis, introducing the assumption of continuous medium, gradually reducing the blackness of the model, increasing the whiteness, and making appropriate simplifications to establish a simple “three-box” analysis model of the stress transfer process, as shown in Figure 4.

FIGURE 4

FIGURE 4. Simplified RMV model of porous media.

With the introduction of the continuous medium assumption, the solid and fluid phases can be treated as a continuum overlapping each other, replacing the real porous medium system (both the porous medium and the pore substance inside the porous medium) with an ideal continuous system. Any property in this continuous medium system (whether it is the property of the porous medium or the property of the substance in it, or the mechanical property of the system) can be described in terms of continuous variables. The internal microstructure and applied conditions of frozen soil porous media are very complex, and there are stochastic factors such as parameter and model inaccuracies in the modeling and simulation calculation process. For frozen soil porous media, this paper proposes a “three-box” stress-strain analysis model based on RMV.

2.4 Black-box description model of RMV in frozen soil porous media

2.4.1 Black-box model definition

The so-called black-box, i.e., the interior of the control element surrounded by the frozen soil RMV, is not “transparent.” This model is suitable for porous media with no or incomplete basic parameters, and only a rough analysis of the frozen soil stress conduction process is possible, which is also called the “original model."

The black-box model is an analytical method that is both simple and can lead to important conclusions, which is the main reason why black-box analysis is widely used. The REV black-box model for frozen soil porous media established in this paper is shown in Figure 5. We consider the frozen soil porous medium as a system surrounded by a “non-transparent” boundary, with the solid line indicating the system boundary and the arrow indicating the output stress.

FIGURE 5

FIGURE 5. RMV-based black-box description model for porous media.

This allows the frozen soil RMV to be considered as a whole without considering the stress transformation between the soil skeleton and solid ice inside the system and only considering the stress conduction process between the whole system and the outside world at the system boundary. The model is mainly used for the rough analysis of the stress conduction process in the frozen soil RMV. When little information is related to the frozen soil porous medium, the black-box model can be used to describe it.

2.4.2 Analysis of stress conduction process in black-box

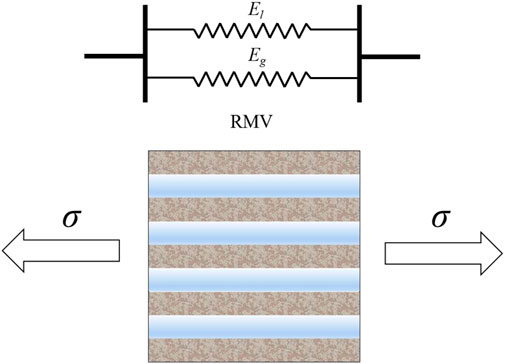
When the stress direction is horizontal to the pore access (parallel), only the porosity $\varphi$ of the fundamental structural parameter of the porous medium is known. According to the theory of mesomechanics of composite materials (Panin et al., 1998) and Reuss (1929) series model, combined with the composition and mechanical characteristics of the frozen soil, the permafrost is regarded as a horizontal isotropic solid medium composed of ice crystals and dry hard solid soil. According to the deformation coordination condition, typical micro-elementary volume of monolayer composites were used as the study subjects, the elastic modulus of the isotropic surface of the frozen soil was deduced respectively as follows, as shown in Figure 6.

FIGURE 6

FIGURE 6. RMV-based parallel model of porous media black-box.

The elastic modulus can be expressed as

$\frac{1}{E_{hb}}=\left(1-\varphi \right)\frac{1}{E_g}+\varphi \frac{1}{E_l}(6)$

Simplify to get

$E_{hb}=\frac{E_g{E}_l}{\varphi E_g+\left(1-\varphi \right)E_l}(7)$

where, $\varphi$ is the frozen soil porosity; E_hb is the effective elastic modulus when the stress direction is parallel to the pore access, MPa; E_g is the elastic modulus of the soil skeleton, MPa; E_l is the elastic modulus of the ice crystals in the pore space, MPa. When the stress direction is perpendicular to the pore access (in series), only the porosity $\varphi$ of the fundamental structural parameter of the porous medium is known, as shown in Figure 7. According to the theory of mesomechanics of composite materials (Panin et al., 1998) and Voigt (1889) parallel model, the elastic modulus can be expressed as

$E_{hc}=\left(1-\varphi \right)E_g+\varphi E_l(8)$

where, E_hc is the effective elastic modulus when the stress direction is perpendicular to the pore access, MPa.

FIGURE 7

FIGURE 7. RMV-based black-box series model of porous media.

2.5 Gray-box description model of RMV in frozen soil porous media

2.5.1 Gray-box model definition

The internal part of control element surrounded by the frozen soil RMV is “transparent” and is called the gray-box model. Compared with the black-box model, the gray-box model has been developed and refined to allow for a refined analysis of the frozen soil stress conduction process and is also referred to as the “development model,” as shown in Figure 8.

FIGURE 8

FIGURE 8. RMV-based gray-box description model for porous media.

The gray-box model studies the stress conduction process inside the frozen soil porous medium while studying the stress conduction between the system and the outside world, which is more comprehensive in describing, characterizing, and analyzing the stress conduction process inside the RMV compared with the black-box model. Furthermore, the gray-box model can be used for a more refined analysis of the frozen soil stress conduction process. When more information related to the frozen soil pore medium is known, the gray-box model can be used for the description.

2.5.2 Analysis of stress conduction process in the gray-box

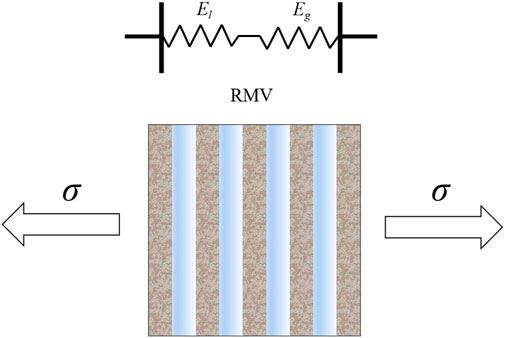
The actual porous media are often non-homogeneous and anisotropic, complicating porous media’s transfer phenomena and coupling mechanism. Therefore, the gray-box model can be approximated by the simultaneous coexistence of the “parallel” and “series” models in the black-box stress-strain model. In this way, the model is further made “transparent” based on the black-box model, the fundamental structural parameter porosity is known, and the pore access distribution variate $\alpha$ are introduced to calculate the elastic modulus based on the gray-box stress-strain model. The pore access distribution variate $\alpha$ defined as

$\alpha =\frac{N_c}{N}\times 100\%(9)$

where, N_c is the entire quantity of pore accesses parallel to the stress direction; N is the entire quantity of RMV pore accesses. Then, the elastic modulus can be expressed as

$E_h=\alpha E_{hc}+\left(1-\alpha \right)E_{hb}(10)$

where E_h is the effective elastic modulus of the porous medium for the gray-box stress-strain model, MPa. Substituting Eq. 7, 8 into Eq. 10 to simplify gives

$E_h=\frac{\left(2\alpha {\varphi }^2-2\alpha \varphi +1\right)E_g{E}_l+\alpha \varphi \left(1-\varphi \right)\left(E_g^2+E_l^2\right)}{\varphi E_g+\left(1-\varphi \right)E_l}(11)$

A dimensionless constant k can be used to represent the elastic modulus of the ice crystals E_l and the elastic modulus of the solid skeleton E_g. i.e.

$E_g=k{E}_l(12)$

Substituting Eq. 12 into Eq. 11 to simplify gives

$E_h=\frac{k\left(2\alpha {\varphi }^2-2\alpha \varphi +1\right)+\alpha \varphi \left(1-\varphi \right)\left(k^2+1\right)}{\varphi \left(k-1\right)+1}{E}_l(13)$

where $0<\varphi <1;0\le \alpha \le 1;k<1$. For the two exceptional cases, $\alpha =0$ and $\alpha =1$, there areWhen $\alpha =0$simplifying Eq. 13, we get

$E_h=\frac{k}{\varphi \left(k-1\right)+1}{E}_l(14)$

When $\alpha =1$, simplifying Eq. 13, the following Eq. can be obtained

$E_h=\frac{k\left(2{\varphi }^2-2\varphi +1\right)+\varphi \left(1-\varphi \right)\left(k^2+1\right)}{\varphi \left(k-1\right)+1}{E}_l(15)$

2.6 White-box description model of RMV in frozen soil porous media

2.6.1 White-box model definition

The white-box model, i.e., the control element surrounded by the frozen soil RMV, is entirely “transparent” inside. This model is suitable for porous media where all basic parameters are known. Compared with the gray-box model, the white-box model is further developed and refined to allow accurate analysis of the frozen soil stress conduction process, also referred to as the “ideal model,” as shown in Figure 9.

FIGURE 9

FIGURE 9. RMV-based white-box description model for porous media.

2.6.2 Analysis of stress conduction process in white-box

It is difficult to measure all the basic parameters of porous media, and it is pretty challenging to analyze the problem using the white-box model. The actual process is that the black-box model gradually evolves into the gray-box model and gradually converges to the white-box model, and the gray-box can gradually correct the mathematical model and experimental tests.

The internal pore accesses are curved in typical porous media, soil and rock. The degree of curvature specifically influences the stress conduction course in porous media. Therefore, the average tortuosity is introduced based on the gray-box stress-strain model. In this way, the model is further made “transparent” based on the gray-box model, and the fundamental structural parameters porosity, pore access distribution variate, and average tortuosity are known. Calculating the elastic modulus based on the white-box stress-strain model is carried out. The tortuosity ${\tau }_i$, defined as

${\tau }_i={\left(\frac{L_{ei}}{L_i}\right)}^2(16)$

where, L_ei is the actual longness of the curved pore access; L_i is the straight-line longness linking the both ends of the curved pore access. Medial tortuosity is defined as

$\tau =\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\tau }_i(17)$

Then, the elastic modulus can be expressed as

$E_b=\tau \cdot E_h=\tau \cdot \frac{\left(2\alpha {\varphi }^2-2\alpha \varphi +1\right)E_g{E}_l+\alpha \varphi \left(1-\varphi \right)\left(E_g^2+E_l^2\right)}{\varphi E_g+\left(1-\varphi \right)E_l}(18)$

where, E_b is the effective elastic modulus of the porous medium for the white-box stress-strain model, MPa. According to the expressions (13), (14), and (15) for the effective elastic modulus of the porous medium of the gray-box model, we can obtain

$E_b=\tau \cdot E_h=\tau \cdot \frac{k\left(2\alpha {\varphi }^2-2\alpha \varphi +1\right)+\alpha \varphi \left(1-\varphi \right)\left(k^2+1\right)}{\varphi \left(k-1\right)+1}{E}_l(19)$

$E_b=\tau \cdot E_h=\tau \cdot \frac{k}{\varphi \left(k-1\right)+1}{E}_l(20)$

$E_b=\tau \cdot E_h=\tau \cdot \frac{k\left(2{\varphi }^2-2\varphi +1\right)+\varphi \left(1-\varphi \right)\left(k^2+1\right)}{\varphi \left(k-1\right)+1}{E}_l(21)$

3 Results of model verification comparison

3.1 Experimental method

The elastic modulus of frozen soil has two methods of determination:

1) $\sigma -\epsilon$ expressed as the slope of the line linking the point on the curve $\epsilon =0.2\%$ corresponding to the strain to the origin of the coordinates.

2) Based on the test data of uniaxial compressive strength, take the ratio of 1/2 of the instantaneous uniaxial compressive strength to its corresponding strain value:

$E=\frac{{\sigma }_s/2}{{\epsilon }_{1/2}}(22)$

where: E is the elastic modulus of the specimen, MPa; ${\sigma }_s$ is the instantaneous uniaxial compressive strength of the specimen, MPa; ${\epsilon }_{1/2}$ is the strain corresponding to half of the instantaneous uniaxial compressive strength value of the specimen, %.

3.2 Experiment verification model

Because method 1) is the Mechanics of Materials (Gere and Timoshenko, 1997) for no obvious yield stage of plastic material to calculate, used to compute the permafrost elastic modulus deviation is larger, and method 2) is the Artificial Frozen Soil Physical Mechanics Performance Test (MT/T 593-2011, 2011) about the description of frozen soil elastic modulus calculation, than method 1) calculated closer to the actual situation, more representative. From a practical point of view, testers prefer the latter method. Therefore, Wang et al. (2008) conducted an experimental research on the compressive strength of sandy soil with different volume ice content (porosity) at a standard atmospheric pressure of 101.325 kPa and a temperature of −8°C by method 2) and calculated the elastic modulus values for different volume ice content (porosity). This experiment and the related data were used to verify the model built in this paper to judge the correctness of this new model. The soil structural physical parameters and the media elastic modulus (Wang et al., 2008) involved in the experiments are displayed in Table 1.

TABLE 1

TABLE 1. Experimental parameters.

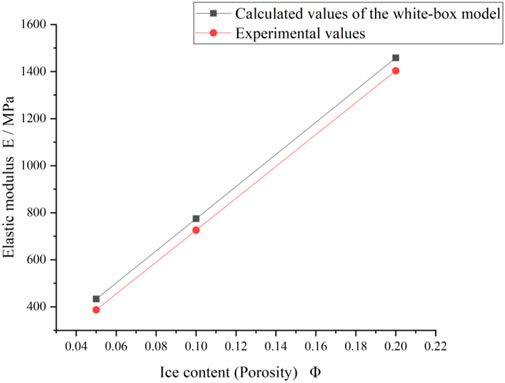
Since the white-box model is the closest stress conduction model to the actual condition among the models developed, the model is used to compare with the experimental data for demonstration, which is displayed in Figure 10. As can be seen from Figure 10, both the experimental and calculated values show an increasing trend as the volumetric ice content (porosity) increases. The calculated values of the white-box model built in this paper showed a most extreme of 11.85% and a base deviation of 3.91% compared with the experimental values. The frozen soil elastic modulus calculated by the model built in this paper agrees with the actual one. In addition, it can be seen from Figure 11 that the test results deviate from the simulated calculations and specifications mainly because of the non-homogeneity of the soil porous media in terms of components and porosity during the test. Meanwhile, the black-box and gray-box models are also verified in this paper, which is like the white-box model and will not be rehashed.

FIGURE 10

FIGURE 10. Relationship between calculated and experimental values of the white-box model.

FIGURE 11

FIGURE 11. Relationship between elastic modulus E and porosity $\phi$ for black-box model.

4 Results of numerical calculation analysis

Based on the “three-box” stress-strain model of porous media established by RMV, the elastic modulus of frozen soil is numerically calculated to analyze the relationship between the distribution of pore accesses, porosity, and elastic modulus of frozen soil porous media. In this paper, saturated frozen sandy soil at −8°C is used for the numerical calculation when most of the pore water has frozen into ice. The relevant parameters are shown in Table 1.

The free water and capillary water content in the fully frozen soil are also minimal, and the frozen soil body accounts for a large proportion of the soil particle skeleton, which is a dry, tough, and dense solid medium, as another part of its filling medium is mainly ice crystals. Therefore, it is reasonable to consider frozen soil as a composite unit composed entirely of soil and ice without considering the influence of unfrozen water. Based on this, frozen soil is considered a transversely isotropic solid medium composed of ice crystals and dry, tough, and dense soil with complete filling and complete adhesion. According to the deformation coordination condition, Typical micro-elementary volume of monolayer composites were used as the study subjects, the elastic modulus of the isotropic surface of the frozen soil was deduced respectively.

4.1 Calculation of elastic modulus based on black-box model

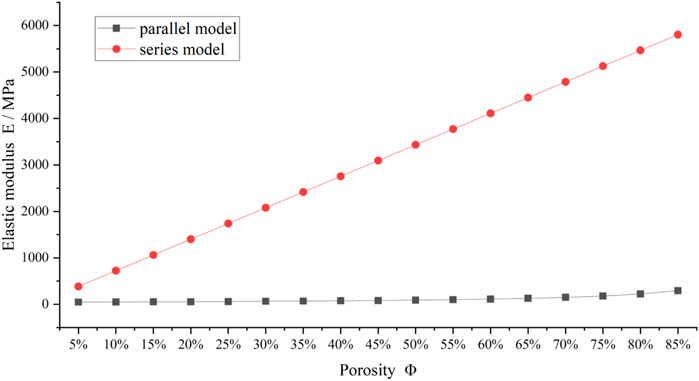
According to Eq. 2, 3, the elastic modulus of the black-box model is calculated numerically. The porosity $\varphi$ of the frozen soil was selected to be 5–85%. The variation of the elastic modulus E with porosity $\varphi$ is shown in Figure 11. From Figure 11, it can be seen that the elastic modulus of both the black-box model in parallel and the black-box model in series increases with the increase of porosity. The elastic modulus of the black-box model in parallel is always more significant than that of the black-box model in series under different porosity, and the difference between them increases with the increase of porosity. The maximum and minimum values of their respective elastic modulus of the black-box stress-strain model in parallel and series are 246.973 MPa, respectively 5419.2 MPa.

The elastic modulus of the series model is greater than that of the parallel model due to the elastic modulus of ice crystals is approximately 148 times larger than that of sandy soil, which is even larger than the elastic modulus of sandy soil. The elastic modulus gradually increments as the porosity increments. It is because when the porosity expands, the ice content of soil grains increases, and the contiguous region among soil grains and solid ice increases, making the frozen soil stronger and the elastic modulus larger.

4.2 Calculation of elastic modulus based on the gray-box model

According to Eq. 8, the elastic modulus of the gray-box model is calculated numerically.

The porosity $\varphi$ of the frozen soil was selected to be 5–85%. The variation of the elastic modulus E with the pore access distribution variate $\alpha$ is displayed in Figure 12. From the data in Figure 12, it can be seen that the elastic modulus of the gray-box model gradually increases, when the pore access distribution variate is certain and the pore rate gradually increases, and the derivative does not change much. The difference between the maximum and minimum values gradually increases. When the porosity is certain, and the pore access distribution variate gradually increases, the gray-box model’s elastic modulus also gradually increases because the larger the pore access distribution variate, the more the number of series accesses in the RMV, the less the number of parallel accesses. The elastic modulus of the parallel model is less than that of the series model, so the elastic modulus increases.

FIGURE 12

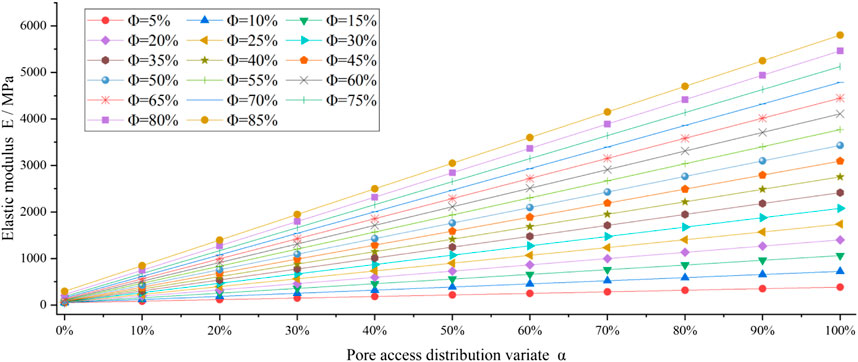
FIGURE 12. Relationship between elastic modulus E and pore access distribution variate $\alpha$ for gray-box model.

4.3 Calculation of elastic modulus based on white-box model

According to Eq. 16, the elastic modulus of the white-box model is calculated numerically.

When the porosity $\varphi$ is 50%, and the pore access distribution variate $\alpha$ are 0–100%, the elastic modulus E changes with the tortuosity $\tau$ as displayed in Figure 13. As can be seen from Figure 13, when the pore access distribution variate is certain, the elastic modulus of the white-box model increments gradually with the gradual increment of the tortuosity, and the disparity among the maximum and minimum values increases gradually. When the tortuosity is certain, the elastic modulus increases gradually when the pore access distribution variate increases gradually.

FIGURE 13

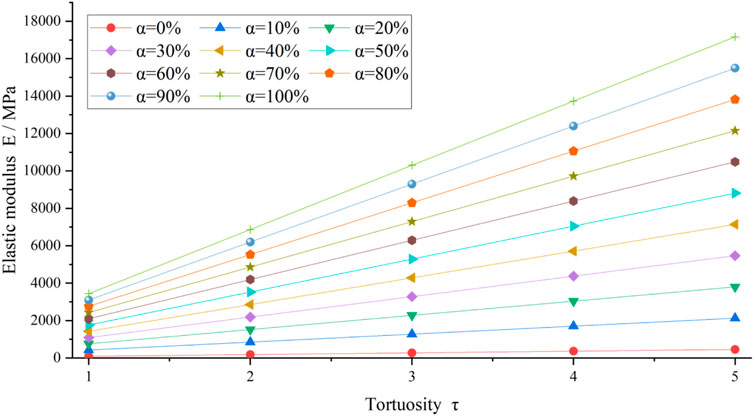
FIGURE 13. Relationship between elastic modulus E and tortuosity $\tau$ of the white-box model with different pore access distribution variate $\alpha$

The pore access distribution variate $\alpha$ was chosen to be 50%, and the elastic modulus E varied with the tortuosity $\tau$ when the porosity $\varphi$ was selected to be 5–85% as displayed in Figure 14. It can be seen from Figure 14 that the elastic modulus of the white-box stress-strain model increments with the increment of the tortuosity when the porosity is certain, and the elastic modulus of the white-box stress conduction model increments with the increment of the porosity when the tortuosity is certain.

FIGURE 14

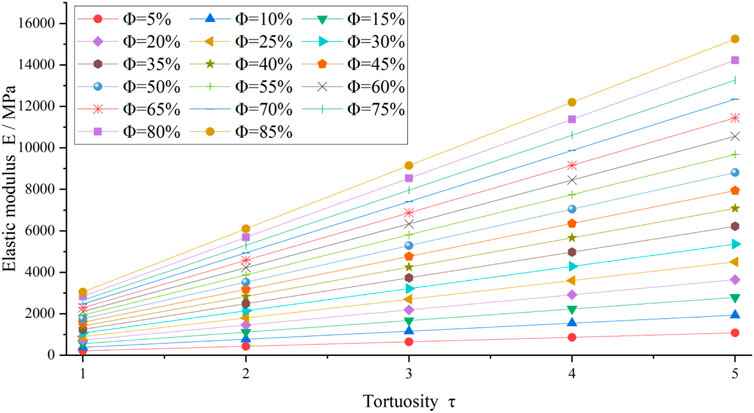
FIGURE 14. Relationship between elastic modulus E and tortuosity $\tau$ for the white-box model with different porosity $\phi$

As can be seen from Figure 13 and Figure 14, when the porosity and pore access distribution variate is certain, the elastic modulus gradually increments with the increment of tortuosity. It is because, within the pore structure, the path through which the stress is conducted becomes more tortuous and can no longer pass smoothly through the pores, and the strength of resistance to deformation increases. Thus, the effective elastic modulus increases at this time.

Based on the black-box and gray-box model, the formula for the elastic modulus of frozen soil porous medium is given, numerical simulations are also performed, and the elastic modulus increases with the increasing porosity. The closer the pore access distribution variate is to 1, the greater the internal elastic modulus of the frozen soil porous medium, and the closer to the ideal white-box model.

Under the black-box model, as the properties of the porosity increases, it is closer to the properties of the ice crystal, and the internal elastic modulus becomes larger. Under the box-model, the influence of porosity on the frozen soil elastic modulus is the same as the black-box model; because the elastic modulus of soil skeleton and ice crystal is quite different, the total elastic modulus is basically curve distributed, and the numerical difference between series elastic modulus and parallel elastic modulus is quite large. For the white-box model, the experimental and numerical analysis show that for the pore-type porous media, with the increase of the pore rate, the fundamental soil skeleton filling is gradually insufficient, and the continuity of the ice crystals gradually increases in space, which leads to the increase of the elastic modulus of the frozen soil.

5 Discussion

In winter, the freezing phenomenon of media such as water within the pores of the porous soil media occurs, and its phase state, constituent, and distribution change, which causes a substantial change in the elastic modulus (Lai et al., 2013). In this paper, in view of the construction and material of frozen soil under freezing conditions, a “three-box” analytical model of stress-strain in frozen soil porous media based on characterization elements is established, the expressions of elastic modulus under different models are derived, and comparative verification and computational analysis are conducted using existing tests.

Assuming that the practical soil porous medium is a continuous medium, the characters are explained and studied based on the constructions of frozen soil using a continuous mathematical method (Prévost, 1980). In order to validate the feasibility of the description and selection method of RMV of frozen soil porous media involving porosity as a typical condition variable. It provides a new direction for developing permafrost resources and studying the build of roadworks in permafrost areas (Tang et al., 2019; Wang et al., 2022). It provides new ideas for investigating and studying the essential characteristics of frozen soil and the law of development and change, as well as the measures to prevent and control frost damage, and further serves for the development and economic construction in cold areas (Lai et al., 2018; Yu et al., 2020). Involving porosity as a delegate state variable.

Albeit the impact of porosity, pore access distribution variate, and tortuosity on the elastic modulus of frozen soil is studied, there are many factors affecting the elastic modulus, which can also be studied from the aspects of saturation and different soil (Ming et al., 2017). In addition, the elastic modulus research of frozen soil is limited by the lack of factors, and we cannot accurately know the change rules beyond the scope of this model. Therefore, the subsequent study can also expand the scope of research factors to get more accurate rules.

Due to the complex structure of frozen soil porous media and its occurrence conditions, it is difficult to accurately describe it, and related mechanistic model research for specific conditions, the adaptability is not strong, “model inaccurate” and “parameter incomplete” become the “bottleneck” problem (Chen et al., 2022). How to describe the structure of frozen soil porous media and analyze the relationship between stress conduction and pore structure needs further study.

The study of permafrost stress conduction model can provide a theoretical basis for the deformation and stability prediction and evaluation of various engineering foundations in permafrost areas, especially those with high ice content (Zhang and Liu, 2018). Therefore, it is of significant meaning to research the physical and mechanical characters of permafrost systematically and deeply (Shen et al., 2018). The “three-box” analysis way given in this paper can study the stress conduction characteristics of permafrost porous medium from coarse to fine, which has some significance for mastering some relevant mechanisms in the mining process of permafrost resources and analyzing the change law of stress conduction process. However, the model proposed in this paper is still stuck at the theoretical level, and it still needs to be applied and analyzed and verified according to the actual production of frozen soil, so as to supplement and improve the built model.

Although this paper examines the elastic modulus change law of frozen soil under different porosity, but there is only a fixed test temperature, and the mechanical characters of frozen soil are greatly influenced by the temperature, which makes the conclusion have certain limitations. Therefore, in the future, frozen soil at different temperatures should be tested indoors, to study the change law of mechanical characters of frozen soil under more variables (Shen et al., 2020; Sun et al., 2020). Therefore, we need to carry out a lot of tests on the frozen soil to further deepen the research, a clearer understanding of the constitutive relationship of the frozen soil under complex stress conditions, the established equation must have high accuracy and practicability (Tounsi et al., 2019; Wang and Zhou, 2018). In this way, we can find the risk factors in the construction in the process of construction, and find a fast and accurate solution according to the test simulation.

6 Conclusion

The analysis and study of stress-strain processes in frozen soil porous media have theoretical connotations and are a robust science for engineering practice. The validity of the model is validated by comparing and analyzing the calculated results of the in being tests and the white-box model. The results show that the discrepancy between the computed and experimental values of the white-box model is slight, and the elastic modulus of frozen soil calculated by the model established in this article is consistent with the veritable situation, so the model established in this paper has practicality.

Under the standard atmospheric pressure of 101.325 KPa and temperature of −8°C, the established black-box model, gray-box model, and white-box model were analyzed by numerical calculation under the condition of sandy soil as an example. It is concluded that the variation law of frozen soil elastic modulus is influenced by the pore size, the soil structural distribution, components, and the degree of pore access curvature, among others, which requires specific analysis in each case.

The elastic modulus of the black-box model increments with the porosity. When the porosity of the gray-box model is certain, the elastic modulus is positively correlated with the pore access distribution variate, and the effect of changing the elastic modulus is greater than the effect of changing the pore access distribution variate. In the white-box model, the elastic modulus still increases with the porosity; with the constant porosity and the porosity of the porous medium, and with the constant porosity, the elastic modulus increases with the pore access variate.

This paper proposes a “three-box” stress-strain model for frozen soil porous media based on RMV, which provides a reference for the study of momentum, energy, and mass transfer characteristics in frozen soil porous media and other porous media, and the conclusions of the study are of guiding significance for the application of frozen soil (Yang et al., 2018; Yin et al., 2022).

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

ZW contributed to the conception of the study; QH: contributed to literature synthesis and wrote the manuscript; ZT, YZ, and JC helped perform the analysis with constructive discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alzoubi, M. A., Zueter, A., Nie-Rouquette, A., and Sasmito, A. P. (2019). Freezing on demand: A new concept for mine safety and energy savings in wet underground mines. Int. J. Min. Sci. Technol. 29, 621–627. doi:10.1016/j.ijmst.2019.06.015

CrossRef Full Text | Google Scholar

Chang, D., Lai, Y., and Zhang, M. (2019). A meso-macroscopic constitutive model of frozen saline sandy soil based on homogenization theory. Int. J. Mech. Sci. 159, 246–259. doi:10.1016/j.ijmecsci.2019.06.002

CrossRef Full Text | Google Scholar

Che, T., Li, X., Liu, S., Li, H., Yang, X., Tan, J., et al. (2019). Integrated hydrometeorological, snow and frozen-ground observations in the alpine region of the Heihe River Basin, China. Earth Syst. Sci. Data 11, 1483–1499. doi:10.5194/essd-11-1483-2019

CrossRef Full Text | Google Scholar

Chen, C., Huang, H., Mo, X., Xue, H., Liu, M., and Chen, H. (2021). Insights into the kinetic processes of solute migration by unidirectional freezing in porous media with micromodel visualization at the pore-scale. Sci. Total Environ. 784, 147178. doi:10.1016/j.scitotenv.2021.147178

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, P., Zhang, H., Yang, G., Guo, Z., and Yang, G. (2022). Thermo-Hydro-mechanical coupling model of unsaturated soil based on modified VG model and numerical analysis. Front. Earth Sci. 1054. doi:10.3389/feart.2022.947335

CrossRef Full Text | Google Scholar

Edip, K., Sesov, V., Butenweg, C., and Bojadieva, J. (2018). Development of coupled numerical model for simulation of multiphase soil. Comput. Geotech. 96, 118–131. doi:10.1016/j.compgeo.2017.08.016

CrossRef Full Text | Google Scholar

Esmaeili-Falak, M., Katebi, H., and Javadi, A. A. (2020). Effect of freezing on stress-strain characteristics of granular and cohesive soils. J. Cold Reg. Eng. 34, 05020001. doi:10.1061/(ASCE)CR.1943-5495.0000205

CrossRef Full Text | Google Scholar

Fu, Z., Wu, Q., Zhang, W., He, H., and Wang, L. (2022). Water migration and segregated ice formation in frozen ground: Current advances and future perspectives. Front. Earth Sci. 10, 826961. doi:10.3389/feart.2022.826961

CrossRef Full Text | Google Scholar

Gere, J. M., and Timoshenko, S. P. (1997). Mechanics of materials. Schenectady, N.Y: Van Nostrand Reinhold Co.

Google Scholar

Gudehus, G. (2021). Implications of the principle of effective stress. Acta Geotech. 16, 1939–1947. doi:10.1007/s11440-020-01068-7

CrossRef Full Text | Google Scholar

Guo, P., Gu, J., Su, Y., Wang, J., and Ding, Z. (2021a). Effect of cyclic wetting–drying on tensile mechanical behavior and microstructure of clay-bearing sandstone. Int. J. Coal Sci. Technol. 8, 956–968. doi:10.21203/rs.3.rs-65369/v2

CrossRef Full Text | Google Scholar

Guo, Z., Shi, Y., Huang, F., Fan, X., and Huang, S. (2021b). Landslide susceptibility zonation method based on C5.0 decision tree and K-means cluster algorithms to improve the efficiency of risk management. Geosci. Front. 12, 101249–101261. doi:10.1016/j.gsf.2021.101249

CrossRef Full Text | Google Scholar

Han, Q., Wang, Z., and Qin, R. (2022a). Thermal conductivity model analysis of unsaturated ice-containing soil. Geofluids 2022, 1–15. doi:10.1155/2022/3717705

CrossRef Full Text | Google Scholar

Han, Q., Wang, Z., Teng, Z., Zhang, Y., Xue, M., and Qin, X. (2022b). Analysis on stress-strain model of unsaturated ice-containing soil. Geofluids 2022, 1–14. doi:10.1155/2022/4294389

CrossRef Full Text | Google Scholar

He, R., Jia, N., Jin, H., Wang, H., and Li, X. (2021). Experimental study on thermal conductivity of organic-rich soils under thawed and frozen states. Geofluids 2022, 1–12. doi:10.1155/2021/7566669

CrossRef Full Text | Google Scholar

Hu, R., Liu, Q., and Xing, Y. (2018). Case study of heat transfer during artificial ground freezing with groundwater flow. Water 10, 1322. doi:10.3390/w10101322

CrossRef Full Text | Google Scholar

Hu, F., Li, Z., Tian, Y., and Hu, R. (2021). Failure patterns and morphological soil–rock interface characteristics of frozen soil–rock mixtures under compression and tension. Appl. Sci. (Basel). 11, 461. doi:10.3390/app11010461

CrossRef Full Text | Google Scholar

Huang, F., Huang, J., Jiang, S., and Zhou, C. (2017). Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng. Geol. 218, 173–186. doi:10.1016/j.enggeo.2017.01.016

CrossRef Full Text | Google Scholar

Huang, F., Tao, S., Chang, Z., Huang, J., Jiang, S. H., Zhu, L., et al. (2021). Efficient and automatic extraction of slope units based on multi-scale segmentation method for landslide assessments. Landslides 18, 3715–3731. doi:10.1007/s10346-021-01756-9

CrossRef Full Text | Google Scholar

Huang, F., Chen, J., Liu, W., Huang, J., Hong, H., and Chen, W. (2022a). Regional rainfall-induced landslide hazard warning based on landslide susceptibility mapping and a critical rainfall threshold. Geomorphol. (Amst). 408, 108236. doi:10.1016/j.geomorph.2022.108236

CrossRef Full Text | Google Scholar

Huang, W., Mao, X., Wu, Q., Zhao, S., and Zhang, J. (2022b). Experimental and analytical investigation on frost heave characteristics of coarse-grained soils under closed and open systems. Front. Earth Sci. (Lausanne). 10, 854586. doi:10.3389/feart.2022.854586

CrossRef Full Text | Google Scholar

Ji, Y., Zhou, G., Zhou, Y., Hall, M. R., Zhao, X., and Mo, P. Q. (2018). A separate-ice based solution for frost heaving-induced pressure during coupled thermal-hydro-mechanical processes in freezing soils. Cold Reg. Sci. Technol. 147, 22–33. doi:10.1016/j.coldregions.2017.12.011

CrossRef Full Text | Google Scholar

Jiang, S. H., and Huang, J. (2016). Efficient slope reliability analysis at low-probability levels in spatially variable soils. Comput. Geotech. 75, 18–27. doi:10.1016/j.compgeo.2016.01.016

CrossRef Full Text | Google Scholar

Jiang, S. H., and Huang, J. (2018). Modeling of non-stationary random field of undrained shear strength of soil for slope reliability analysis. Soils Found. 58, 185–198. doi:10.1016/j.sandf.2017.11.006

CrossRef Full Text | Google Scholar

Jiang, S. H., Huang, J., Yao, C., and Yang, J. H. (2017). Quantitative risk assessment of slope failure in 2-D spatially variable soils by limit equilibrium method. Appl. Math. Model. 47, 710–725. doi:10.1016/j.apm.2017.03.048

CrossRef Full Text | Google Scholar

Kefayati, G., Tolooiyan, A., Bassom, A. P., and Vafai, K. (2021). A mesoscopic model for thermal–solutal problems of power-law fluids through porous media. Phys. Fluids (1994) 33, 033114. doi:10.1063/5.0042526

CrossRef Full Text | Google Scholar

Kjelstrup, S., Bedeaux, D., Hansen, A., Hafskjold, B., and Galteland, O. (2018). Non-isothermal transport of multi-phase fluids in porous media. the entropy production. Front. Phys. 6, 126. doi:10.3389/fphy.2018.00126

CrossRef Full Text | Google Scholar

Lai, Y., Xu, X., Dong, Y., and Li, S. (2013). Present situation and prospect of mechanical research on frozen soils in China. Cold Reg. Sci. Technol. 87, 6–18. doi:10.1016/j.coldregions.2012.12.001

CrossRef Full Text | Google Scholar

Lai, Y., Pei, W., Zhang, M., and Zhou, J. (2014). Study on theory model of hydro-thermal–mechanical interaction process in saturated freezing silty soil. Int. J. Heat. Mass Transf. 78, 805–819. doi:10.1016/j.ijheatmasstransfer.2014.07.035

CrossRef Full Text | Google Scholar

Lai, J., Wang, X., Qiu, J., Zhang, G., Chen, J., Xie, Y., et al. (2018). A state-of-the-art review of sustainable energy based freeze proof technology for cold-region tunnels in China. Renew. Sustain. Energy Rev. 82, 3554–3569. doi:10.1016/j.rser.2017.10.104

CrossRef Full Text | Google Scholar

Li, Q., Geng, J., Song, D., Nie, W., Saffari, P., and Liu, J. (2022a). Automatic recognition of erosion area on the slope of tailings dam using region growing segmentation algorithm. Arab. J. Geosci. 15, 438. doi:10.1007/s12517-022-09746-4

CrossRef Full Text | Google Scholar

Li, Q., Song, D., Yuan, C., and Nie, W. (2022b). An image recognition method for the deformation area of open-pit rock slopes under variable rainfall. Meas. (. Mahwah. N. J) 188, 110544. doi:10.1016/j.measurement.2021.110544

CrossRef Full Text | Google Scholar

Li, X., Li, Q., Hu, Y., Chen, Q., Peng, J., Xie, Y., et al. (2022c). Study on three-dimensional dynamic stability of open-pit high slope under blasting vibration. Lithosphere 2021, 6426550. doi:10.2113/2022/6426550

CrossRef Full Text | Google Scholar

Li, X. S. (2003). Effective stress in unsaturated soil: A microstructural analysis. Geotechnique 53, 273–277. doi:10.1680/geot.53.2.273.37273

CrossRef Full Text | Google Scholar

Liu, E., and Lai, Y. (2020). Thermo-poromechanics-based viscoplastic damage constitutive model for saturated frozen soil. Int. J. Plast. 128, 102683. doi:10.1016/j.ijplas.2020.102683

CrossRef Full Text | Google Scholar

Liu, T., and Wang, M. (2021). Critical REV size of multiphase flow in porous media for upscaling by pore-scale modeling. Transp. Porous Media 144, 111–132. doi:10.1007/s11242-021-01621-2

CrossRef Full Text | Google Scholar

Liu, L. L., Cheng, Y. M., Jiang, S. H., Zhang, S. H., Wang, X. M., and Wu, Z. H. (2017). Effects of spatial autocorrelation structure of permeability on seepage through an embankment on a soil foundation. Comput. Geotech. 87, 62–75. doi:10.1016/j.compgeo.2017.02.007

CrossRef Full Text | Google Scholar

Liu, E., Lai, Y., Wong, H., and Feng, J. (2018a). An elastoplastic model for saturated freezing soils based on thermo-poromechanics. Int. J. Plast. 107, 246–285. doi:10.1016/j.ijplas.2018.04.007

CrossRef Full Text | Google Scholar

Liu, Y., Wei, C. F., Zhao, C. G., Fang, Q., and Li, J. (2018b). Work input for unsaturated soils considering interfacial effects. Int. J. Numer. Anal. Methods Geomech. 42, 1078–1094. doi:10.1002/nag.2784

CrossRef Full Text | Google Scholar

Liu, Y., Liu, E., and Yin, Z. (2020). Constitutive model for tailing soils subjected to freeze–thaw cycles based on meso-mechanics and homogenization theory. Acta Geotech. 15, 2433–2450. doi:10.1007/s11440-020-00937-5

CrossRef Full Text | Google Scholar

Luo, J., Tang, L., Ling, X., and Geng, L. (2018). Experimental and analytical investigation on frost heave characteristics of an unsaturated moderately expansive clay. Cold Reg. Sci. Technol. 155, 343–353. doi:10.1016/j.coldregions.2018.08.023

CrossRef Full Text | Google Scholar

Luo, D., Guo, D., Jin, H., Yang, S., Phillips, M., and Frey, B. (2022). Editorial: Ecological impacts of degrading permafrost. Front. Earth Sci. 10, 967530. doi:10.3389/feart.2022.967530

CrossRef Full Text | Google Scholar

Ma, Q., Zhang, K., Jabro, J. D., Ren, L., and Liu, H. (2019). Freeze–thaw cycles effects on soil physical properties under different degraded conditions in Northeast China. Environ. Earth Sci. 78, 1–12. doi:10.1007/s12665-019-8323-z

CrossRef Full Text | Google Scholar

Ming, F., Chen, L., Li, D., and Wei, X. (2020). Estimation of hydraulic conductivity of saturated frozen soil from the soil freezing characteristic curve. Sci. Total Environ. 698, 134132. doi:10.1016/j.scitotenv.2019.134132

PubMed Abstract | CrossRef Full Text | Google Scholar

Ming, F., Li, D., Zhang, M., and Zhang, Y. (2017). A novel method for estimating the elastic modulus of frozen soil. Cold Reg. Sci. Technol. 141, 1–7. doi:10.1016/j.coldregions.2017.05.005

CrossRef Full Text | Google Scholar

MT/T 593-2011 (2011). Artificial frozen soil physical mechanics performance test. Beijing: Ministry of Emergency Management of the People’s Republic of China.

Google Scholar

Nia, S. F., and Jessen, K. (2015). Theoretical analysis of capillary rise in porous media. Transp. Porous Media. 110, 141–155. doi:10.1007/s11242-015-0562-1

CrossRef Full Text | Google Scholar

Niu, Z., Yang, Z., Luo, Y., Zhang, Y., Xia, D., Zheng, T., et al. (2022). The application of REV-LBM double mesh local refinement algorithm in porous media flow simulation. Geofluids 2022, 1–12. doi:10.1155/2022/1082386

CrossRef Full Text | Google Scholar

Oka, F., and Kimoto, S. (2021). Computational multiphase geomechanics. London, UK: CRC Press.

Google Scholar

Ott, H., Kharrat, A., Borji, M., and Arnold, P. (2020). Fluid-phase topology of complex displacements in porous media. Phys. Rev. Res. 2, 023240. doi:10.1103/physrevresearch.2.023240

CrossRef Full Text | Google Scholar

Panin, V. E., Korotaev, A. D., Makarov, P. V., and Kuznetsov, V. M. (1998). Physical mesomechanics of materials. Russ. Phys. J. 41, 856–884. doi:10.1007/bf02508720

CrossRef Full Text | Google Scholar

Prévost, J. H. (1980). Mechanics of continuous porous media. Int. J. Eng. Sci. 18, 787–800. doi:10.1016/0020-7225(80)90026-9

CrossRef Full Text | Google Scholar

Reuß, A. (1929). Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. Z. Angew. Math. Mech. 9, 49–58. doi:10.1002/zamm.19290090104

CrossRef Full Text | Google Scholar

Rouabhi, A., Jahangir, E., and Tounsi, H. (2018). Modeling heat and mass transfer during ground freezing taking into account the salinity of the saturating fluid. Int. J. Heat. Mass Transf. 120, 523–533. doi:10.1016/j.ijheatmasstransfer.2017.12.065

CrossRef Full Text | Google Scholar

Shen, Y. J., Yang, G. S., Huang, H. W., Rong, T. L., and Jia, H. L. (2018). The impact of environmental temperature change on the interior temperature of quasi-sandstone in cold region: Experiment and numerical simulation. Eng. Geol. 239, 241–253. doi:10.1016/j.enggeo.2018.03.033

CrossRef Full Text | Google Scholar

Shen, Y., Xu, P., Qiu, S., Rao, B., and Yu, B. (2020). A generalized thermal conductivity model for unsaturated porous media with fractal geometry. Int. J. Heat. Mass Transf. 152, 119540. doi:10.1016/j.ijheatmasstransfer.2020.119540

CrossRef Full Text | Google Scholar

Streletskiy, D. A., Suter, L. J., Shiklomanov, N. I., Porfiriev, B. N., and Eliseev, D. O. (2019). Assessment of climate change impacts on buildings, structures and infrastructure in the Russian regions on permafrost. Environ. Res. Lett. 14, 025003. doi:10.1088/1748-9326/aaf5e6

CrossRef Full Text | Google Scholar

Suh, H. S., and Sun, W. C. (2021). Int. J. Numer. Anal. Methods Geomech. 2111, 14983. doi:10.1002/nag.3408

CrossRef Full Text

Sun, Y., Zhai, C., Xu, J., Cong, Y., Qin, L., and Zhao, C. (2020). Characterisation and evolution of the full size range of pores and fractures in rocks under freeze-thaw conditions using nuclear magnetic resonance and three-dimensional X-ray microscopy. Eng. Geol. 271, 105616. doi:10.1016/j.enggeo.2020.105616

CrossRef Full Text | Google Scholar

Sweidan, A. H., Heider, Y., and Markert, B. (2020). A unified water/ice kinematics approach for phase-field thermo-hydro-mechanical modeling of frost action in porous media. Comput. Methods Appl. Mech. Eng. 372, 113358. doi:10.1016/j.cma.2020.113358

CrossRef Full Text | Google Scholar

Sweidan, A. H., Niggemann, K., Heider, Y., Ziegler, M., and Markert, B. (2022). Experimental study and numerical modeling of the thermo-hydro-mechanical processes in soil freezing with different frost penetration directions. Acta Geotech. 17, 231–255. doi:10.1007/s11440-021-01191-z

CrossRef Full Text | Google Scholar

Tang, Y., Xiao, S., and Zhou, J. (2019). Deformation prediction and deformation characteristics of multilayers of mucky clay under artificial freezing condition. Ksce J. Civ. Eng. 23, 1064–1076. doi:10.1007/s12205-019-1599-4

CrossRef Full Text | Google Scholar

Tounsi, H., Rouabhi, A., Tijani, M., and Guérin, F. (2019). Thermo-hydro-mechanical modeling of artificial ground freezing: Application in mining engineering. Rock Mech. Rock Eng. 52, 3889–3907. doi:10.1007/s00603-019-01786-9

CrossRef Full Text | Google Scholar

Voigt, W. (1889). Uber die beziehung zwischen den beiden elastizitiitskonstanten isotroper krper. Ann. Phys. 38, 573–587. doi:10.1002/andp.18892741206

CrossRef Full Text | Google Scholar

von Terzaghi, K. (1923). Die Berechnug der Durchlassigkeit des Tones aus dem Verlauf der hydromechanischen Spannungserscheinungen. Sitzungsber. Akad. Wiss.(Wien). Math.-Naturwiss. Kl. Abt. Iia. 132, 125–138.

Google Scholar

Wang, P., and Zhou, G. (2018). Frost-heaving pressure in geotechnical engineering materials during freezing process. Int. J. Min. Sci. Technol. 28, 287–296. doi:10.1016/j.ijmst.2017.06.003

CrossRef Full Text | Google Scholar

Wang, Z. Z., Mu, S. Y., Niu, Y. H., Chen, L. J., Liu, J., and Li, X. D. (2008). Predictions of elastic constants and strength of transverse isotropic frozen soil. Rock Soil Mech. 29, 475–480. doi:10.16285/j.rsm.2008.s1.009

CrossRef Full Text | Google Scholar

Wang, Q., Hu, Y. P., and Ji, H. H. (2020a). Leakage, heat transfer and thermal deformation analysis method for contacting finger seals based on coupled porous media and real structure models. Proc. Institution Mech. Eng. Part C J. Mech. Eng. Sci. 234, 2077–2093. doi:10.1177/0954406219900219

CrossRef Full Text | Google Scholar

Wang, Q., Hu, Y. P., and Ji, H. H. (2020b). An anisotropic porous media model for leakage analysis of finger seal. Proc. Institution Mech. Eng. Part G J. Aerosp. Eng. 234, 280–292. doi:10.1177/0954410019862080

CrossRef Full Text | Google Scholar

Wang, P., Zhou, Z., Liu, J., Xu, C., Wang, K., Liu, Y., et al. (2022). Application of a new distributed hydrological model based on soil–gravel structure in the Niyang River Basin, Qinghai–Tibet Plateau. Hydrol. Earth Syst. Sci. 2022, 1–35. doi:10.5194/hess-2022-215

CrossRef Full Text | Google Scholar

Wei, C. (2014). A theoretical framework for modeling the chemomechanical behavior of unsaturated soils. Vadose Zone J. 13, vzj2013.07.0132. doi:10.2136/vzj2013.07.0132

CrossRef Full Text | Google Scholar

Xu, X., Lai, Y., Dong, Y., and Qi, J. (2011). Laboratory investigation on strength and deformation characteristics of ice-saturated frozen sandy soil. Cold Reg. Sci. Technol. 69, 98–104. doi:10.1016/j.coldregions.2011.07.005

CrossRef Full Text | Google Scholar

Xu, X., Bai, R., Lai, Y., Zhang, M., and Ren, J. (2020). Work conjugate stress and strain variables for unsaturated frozen soils. J. Hydrol. X. 582, 124537. doi:10.1016/j.jhydrol.2019.124537

CrossRef Full Text | Google Scholar

Xu, X., Zhang, W., and Wang, Y. (2022). Measuring and modeling the dielectric constant of soil during freezing and thawing processes: An application on silty clay. Acta Geotech. 2022, 1–20. doi:10.1007/s11440-022-01487-8

CrossRef Full Text | Google Scholar

Yan, G., Li, Z., Torres, S. A. G., Scheuermann, A., and Li, L. (2022). Transient two-phase flow in porous media: A literature review and engineering application in geotechnics. Geotechnics 2, 32–90. doi:10.3390/geotechnics2010003

CrossRef Full Text | Google Scholar

Yang, H., Shan, R., Zhang, J., Wu, F., and Guo, Z. (2018). Mechanical properties of frozen rock mass with two diagonal intersected fractures. Int. J. Min. Sci. Technol. 28, 631–638. doi:10.1016/j.ijmst.2018.02.005

CrossRef Full Text | Google Scholar

Yin, Q., Andò, E., Viggiani, G., and Sun, W. (2022). Freezing‐induced stiffness and strength anisotropy in freezing clayey soil: Theory, numerical modeling, and experimental validation. Int. J. Numer. Anal. Methods Geomech. 46, 2087–2114. doi:10.1002/nag.3380

CrossRef Full Text | Google Scholar

Yu, W., Zhang, T., Lu, Y., Han, F., Zhou, Y., and Hu, D. (2020). Engineering risk analysis in cold regions: State of the art and perspectives. Cold Reg. Sci. Technol. 171, 102963. doi:10.1016/j.coldregions.2019.102963

CrossRef Full Text | Google Scholar

Yu, L., Zeng, Y., and Su, Z. (2021). STEMMUS-UEB v1. 0.0: Integrated modeling of snowpack and soil water and energy transfer with three complexity levels of soil physical processes. Geosci. Model Dev. 14, 7345–7376. doi:10.5194/gmd-14-7345-2021

CrossRef Full Text | Google Scholar

Zhang, C., and Liu, Z. (2018). Freezing of water confined in porous materials: Role of adsorption and unfreezable threshold. Acta Geotech. 13, 1203–1213. doi:10.1007/s11440-018-0637-6

CrossRef Full Text | Google Scholar

Zhang, C., Wang, L., Du, J., and Tian, Y. (2015). Numerical modelling rock deformation subject to nitrogen cooling to study permeability evolution. Int. J. Coal Sci. Technol. 2, 293–298. doi:10.1007/s40789-015-0084-z

CrossRef Full Text | Google Scholar

Zhang, D., Liu, E., and Huang, J. (2020a). Elastoplastic constitutive model for frozen sands based on framework of homogenization theory. Acta Geotech. 15, 1831–1845. doi:10.1007/s11440-019-00897-5

CrossRef Full Text | Google Scholar

Zhang, M., Zhang, X., Lai, Y., Lu, J., and Wang, C. (2020b). Variations of the temperatures and volumetric unfrozen water contents of fine-grained soils during a freezing–thawing process. Acta Geotech. 15, 595–601. doi:10.1007/s11440-018-0720-z

CrossRef Full Text | Google Scholar

Zhao, L. Y., Lai, Y. M., Shao, J. F., Zhang, W. L., Zhu, Q. Z., and Niu, F. J. (2021). Friction-damage coupled models and macroscopic strength criteria for ice-saturated frozen silt with crack asperity variation by a micromechanical approach. Eng. Geol. 294, 106405. doi:10.1016/j.enggeo.2021.106405

CrossRef Full Text | Google Scholar

Zhou, G., Zhang, Q., Xu, Z., and Zhou, Y. (2012). Infrared radiation method for measuring ice segregation temperature of artificially frozen soils. Int. J. Min. Sci. Technol. 22, 35–40. doi:10.1016/j.ijmst.2011.06.004

CrossRef Full Text | Google Scholar

Zhou, M. M., and Meschke, G. (2018). A multiscale homogenization model for strength predictions of fully and partially frozen soils. Acta Geotech. 13, 175–193. doi:10.1007/s11440-017-0538-0

CrossRef Full Text | Google Scholar