
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 06 January 2023
Sec. Geohazards and Georisks
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.990454
This article is part of the Research Topic Rock Landslide Risk Assessment, Stability Analysis and Monitoring for The Development of Early Warning Systems and Reinforcement Measures View all 24 articles
A landslide of the north open-pit (323N) and the stability and design optimization of the south open-pit (323S) slope in the 323 belts of the Tanjianshan Gold Mine were studied. On 14 September 2020, a large landslide occurred on the east side of 323N, which posed a severe threat to the safety production of the mine. To avoid a similar slide on the south open-pit in the 323S, the limit equilibrium method was used to estimate the stability of the final slope of the designed initially open-pit in the 323N. The results show that the location and scale of the landslide are in good agreement with the three-dimensional laser scanning data. The effectiveness of the limit equilibrium method in slope stability analysis of the Tanjianshan Gold Mine was validated. The stability of the final slope of the initial design of 323S was analyzed. The sensitivity of the safety factor of homogeneous slope and heterogeneous rock slope to the bench face angle (BFA) and the difference of landslide type were compared and studied. When the spatial geometric relationship of rock masses with different lithology is complex, the engineering analogy method is inapplicable to calculation of parameters such as the BFA of heterogeneous rock slope and overall slope angle of the open-pit. The slope safety factor should be checked, and the slope step parameters are warranted to be optimized. The safety and economic benefits of the slope can be improved.
Herein, the term “slope” is used to refer to stacked rock and soil with an inclined or vertical angle. Many projects involve slopes in geotechnical engineering, geological engineering, and other fields. In terms of the causes of slope formation, it is generally divided into artificial slopes and natural slopes (Wu, 2019). In mining engineering, the design of slopes is increasing day by day, and there are two contradictory requirements: steepening the slope to reduce the amount of excavation can save money; the stability of excessively steep slopes becomes worse, which may threaten the safety of life and property (Hoek and Bray, 1977). The design and stability of the open-pit slope need to be explored to achieve the goal of economic optimization on the premise of safety (Cai et al., 2004). There are mainly two kinds of slope stability analysis methods; one is the limit equilibrium method based on the rigid body limit equilibrium theory (Chen, 2003; Duncan, 1996), and the other is the numerical calculation method represented by the finite element method (Duncan, 1996; Griffiths and Lane, 2001; Zhang, 2002; Zheng et al., 2002). The Fellenius method proposed by Petersson in 1916 is the earliest limit equilibrium method (Wu, 2019). Currently, there are more than 10 limit equilibrium slice methods (Zhu et al., 2003), the difference between them lies in the assumption of interslice force and the equilibrium conditions to be satisfied (Zhu et al., 2005). For the general shape sliding surface, both theoretical and engineering analysts believe that the strict slice method must be adopted, that is, the slice meets all the equilibrium conditions (Duncan, 1996), to obtain a more reasonable safety factor. Morgenstern–Price method (Price and Morgenstern, 1967), Spencer’s method (Spencer, 1968), and strict Janbu’s method (Janbu, 1973) are widely used strict slice methods. The solution using the Morgenstern–Price method to calculate the safety factor is quite complex. Although some scholars have proposed various iterative methods for its solution (Chen and Morgenstern, 1983; Zhu et al., 2001), it is still difficult to master. Sarma’s method (Sarma, 1973) is recognized as the most suitable method for rock slopes with steep discontinuities.
There are significant differences between rock mass and rock in metal mine slope engineering. Rock mass refers to the general term of in-situ media containing layers, faults, joints, folds, and other structural characteristics. The rock mass is discontinuous and has heterogeneous engineering properties (Brady and Brown, 2006). The geotechnical types and properties of heterogeneous slopes rock mass may vary greatly over even a short distance (Keefer and Larsen, 2007).
The limit equilibrium method can calculate the slope safety factor with clear physical meaning and the possible failure surface (Duncan, 1996), The slope safety factors calculated by the limit equilibrium method and the finite element method are similar, so it has become the most widely used method in slope stability analysis and is especially welcomed by the engineering community (Zeng and Tian, 2005).
Du Yan and Xie Mowen et al. proposed a possible mechanism for translational landslides, stepwise subsidence, which shows that geological conditions are the fundamental factors underlying translational land-slides (Du et al., 2020). Divya Shaunik and Mahendra Singh proposed a method of calculation for the bearing capacity of foundations on rock slopes intersected by a non-persistent discontinuity (Shaunik and Singh, 2020). A set of building reinforcement and community resilience enhancement methods that can resist slope deformation were proposed to improve the ability of urban areas to cope with slope geological hazards and emergency response (Jiaxing et al., 2022). A new method combining variable selection, the sparrow search algorithm, and a deep extreme-learning machine was proposed to investigate complex rock slope collapse, landslide, and other engineering disasters (Jiang et al., 2022).
Through communication with open-pit slope designers, it is found that the initial design of open-pit slopes in China is still based on an empirical analogy method, and the final slope angle given is an interval, which is not accurate enough. The empirical analogy method is usually accurate for homogeneous slope. In the design of heterogeneous slope, there will be a variety of staggered distribution of rock layers. It is impossible to draw an analogy according to the strength of a certain rock. In the present work, the limit equilibrium method software Rocscience Slide was used to analyze the stability of the final slope of the open-pit initially designed in 323N. The results show that the location and scale of the landslide can well match three-dimensional laser scanning data. The effectiveness of the limit equilibrium method in slope stability analysis of the Tanjianshan Gold Mine was verified. The stability of the final slope of the initial design of 323S was estimated.
A landslide event occurred in 323N during the production process. 323S is about 70 m away from the straight-line distance of 323N. The open-pit slope of 323S is designed by using the engineering analogy method. To avoid similar landslide events, the safety factor calculation and parameter optimization of the initial design of 323S were conducted. The present work covers the slope design process using the observational method or engineering analogy method to determine the final slope angles to study the possible problems, observational method, and engineering analogy method relies on determining parameters such as the coefficient of a rock mass slope angle can determine the final stability and angle of repose, it is generally believed rock strength is higher, the greater the final slope angles can be, that is to say, the when final slope angle is smaller so the safety factor is larger. The landslide of 323N shows that the empirical method to determine the final slope angle has some shortcomings. When the spatial geometric relationship of rock masses with different lithology is complex, the engineering analogy method does not apply to calculating parameters such as the bench face angle (BFA) of heterogeneous rock slope and overall slope angle of an open-pit. The slope safety factor should be checked, and the slope step parameters should be optimized. The safety and economic benefits of the slope can be improved.
The Tanjianshan Gold Mine is located in Dachaidan Town, Haixi Mongolian and Tibetan Autonomous Prefecture, Qinghai Province (Figure 1). Geographical coordinates: 94°23′22″–94°34′2″ east longitude; 38°13′00″∼38°22′ 51″ north latitude; transportation in the mining area is relatively convenient.
As shown in Figure 2, there are currently four ore blocks in the Tanjianshan Gold Mine: the Qinglonggou North ore block, Qinglonggou South ore block (QLGS), 323N and 323S from north to south. The four ore blocks will form independent mining units. In this paper, 323N and 323S open-pits with a minimum straight-line distance of 70 m are taken as research objects. Geological conditions of them are basically the same. The engineering analogy method is applied to the mining design of 323. The mining design of 323S refers to the slope instability problem that occurs in the mining process of 323N, and the slope parameters are optimized.
The main faults in the mining area strike NW-SE, incline to SW, and dip at 60°. It has little influence on slope stability.
The rocks exposed in the mining area mainly include dolomite marble, phyllite, meta sandstone, schist, etc. Except for the relatively low hardness of phyllite, others are relatively hard. Generally, complete rock masses demonstrate good stability.
Figure 3A indicates that fissures and joints are not well developed, and the degree of fragmentation is low. As can be seen from Figure 3B, only rocks and ores near the fold axis and the fault zone are broken, and fissures, cleavages and schistosity are developed. The rock mass shows good stability, and the rock mass in the compressed schistosity zone formed by local tectonism has poor stability.

FIGURE 3. On-site photographs showing rock strata at the open slope site. (A) joints are not well developed. (B) only rocks and ores near the fold axis and the fault zone are broken.
The geomorphic type of the mining area shows that the borehole reveals that the mining area is not a high-pressure area. In-situ stress arises mainly from self-weight vertical stress. Modern tectonic stress has little effect on the stability of the slope.
The mining area has a typical continental plateau climate and belongs to the inland arid climate area. This area has an average annual precipitation of less than 100 mm and small water volume in the open-pit, which mainly stems from atmospheric precipitation. Groundwater has little effect on slope stability.
In 2015, relevant staff of University of Science and Technology Beijing conducted on-site rock samples (core diameters were all 61 mm). A total of 66 specimens were tested. Except for two specimens that were damaged in the process of core cutting and grinding, the remaining 64 specimens were all involved in the test. The test items included uniaxial compressive strength test of rock, uniaxial compressive deformation test of rock, tensile strength test of rock, and shear test of structural plane of rock. The physico-mechanical parameters of the rock were obtained.
Hoek mentioned in the technical description of RocNews in 2012 that the blasting disturbance coefficient D reflects the impact of blasting and slope movement on rock mass strength (Hoek, 2012). When determining the value of disturbance coefficient D, factors such as blasting scale and bench height of open-pit mine should be considered. When mining the open-pit slope, the conventional blasting coefficient is taken as 1.0, for mechanical excavation it is set to 0.7, and in controlled blasting it is set to between 0.8 and 0.9 (herein we use D = 1.0). Based on the rock mechanics experiment, this paper obtains the rock mechanics parameters according to the rock strength calculation method proposed by Hoek (Table 1).
According to the proportion of different lithology in the 2# section, the strength of different lithology is taken from the basis of the weighted average. The average value is obtained as the rock mass strength of the whole slope. At this time, it is considered that the slope is homogeneous rock mass, and the safety factor is calculated and compared with that of an equivalent heterogeneous slope.
323N comprises 45 ore bodies, and the mining objects are the M6 to M44 ore bodies. It is distributed in the NNW trending mineralized zone, which is about 650 m long and 135 m wide. The control elevation is 3,314–3,555 m, the depth is generally 30–151 m, and the burial depth of individual ore bodies is more than 187 m. The ore body trend is NNW-SSE, inclining to NE and nearly vertical. The average thickness of the ore body is 1 m to several meters, and the maximum thickness is 13.68 m. The gold grade in the ore body is generally 1.00–6.00 g/t.
According to the engineering geological and hydrogeological conditions, combined with the factors such as slope height and service life, the final slope of the open-pit was designed using the engineering analogy method with reference to the relevant slope data of the Jinlonggou open-pit boundary of the adjacent mining area of the mine. The open-pit mining is shown in Figure 4, and the parameters of the open-pit are listed in Table 2.
A landslide event occurred in 323N During the production process, on 14 September 2020, a landslide mass some 215.48 m long, 65.32 m wide, 49 m high (elevation 3,489–3,538 m) and 63,650 m3 in volume slipped. The mine regularly uses three-dimensional laser scanning to measure and record the open-pit slope. The slope shapes before and after the landslide are shown in Figure 5. Figure 5A shows the slope before the landslide, Figure 5B displays the slope after the landslide, and Figure 5C exhibits the slope shape after the landslide mass is cleared and the slope is expanded. The landslide classification proposed by Varnes is more detailed and comprehensive. The system of landslide classification devised by the late D.J. Varnes has become the most widely used system (Varnes, 1958; Varnes, 1978; Cruden and Varnes, 1996). Hungr et al. (2014) proposed an update to this in 2014, The primary recommendation is to modify the definition of landslide-forming materials, to provide compatibility with accepted geotechnical and geological terminology of rocks and soils. According to the shape of the landslide and rock type, the slide is of the rock rotational slide-type, with an arc sliding surface. Due to the strength of the rock mass being lower than the design expectation, as the mining depth and slope height increase, the strength of rock mass is insufficient to maintain the stability of slopes.
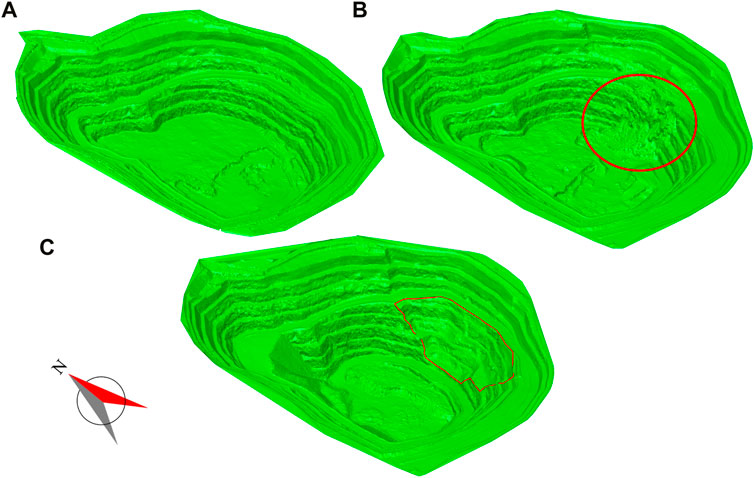
FIGURE 5. Three-dimensional laser scanning model. (A) Before the landslide, (B) After the landslide, (C) After the landslide rock is cleared.
The profile analysis of the landslide area is shown in Figures 6, 7.
The safety factor of the slope calculated by using Janbu’s method is 0.867, and the landslide mass is shown in Figure 7, which is similar to the actual location of the landslide mass. The safety factor of the open-pit slope in the initial design of 323N is too low, leading to a landslide. The results show that the location and scale of the landslide are in good agreement with the three-dimensional laser scanning data. The effectiveness of the limit equilibrium method in slope stability analysis of the Tanjianshan Gold Mine was verified. When analyzing the final slope stability of 323N, the safety factor, landslide location and landslide scale of the slope can be assessed by using a limit equilibrium slice method.
323S comprises 16 ore bodies, which are II-M1–II-M12 and III-M1–III-M4, respectively. The main ore body is II-M1, which occurs at an elevation of 3,300–3,513 m. The quaternary covers the surface, and the burial depth exceeds 35 m. The strike of the ore body is 169°–206°, the overall dip is northeast, and the dip angle is 55°–90°. The average thickness of the ore body is 7.00 m, and the average grade is 7.21 g/t.
According to the engineering geological and hydrogeological conditions, combined with the factors such as slope height and service life, the final slope of the open-pit was designed by using the engineering analogy method with reference to the relevant slope data of the 323N open-pit (a straight-line distance of about 70 m). The open-pit mining is shown in Figure 4, and the parameters of the open-pit are listed in Table 2.
According to Chinese National Standard GB51016-2014 Technical code for non-coal open-pit mines slope engineering, the slope of 323S is more than 160 m high, and the landslide may cause casualties and direct economic losses of more than 1 million yuan and potential economic losses of more than 10 million yuan. The hazard level of the slope is level I, the corresponding safety level is level I, and the load combination includes self-weight, blasting vibration force and groundwater. The load combination in the non-production period is self-weight and groundwater. By checking the relevant table, the design safety factor is determined to be 1.2–1.25. For conservatism, the design safety factor is not less than 1.25. The initial design slope is taken as the initial state, and its factor of safety (FOS) is calculated. If FOS is below 1.25, the BFA is reduced to obtain a larger safety factor, and the road width, sweeping platform width and safety platform width remain unchanged. The elements of the open-pit slope are shown in Figure 8. After the initial design is determined, the slope stability is optimized by reducing and changing the BFA to improve the slope safety factor.
The profile of the open-pit is shown in Figure 9. According to the three-dimensional geological model of lithologic data provided by the mine, the profile shown in Figure 10 is obtained.
The slope can be divided into two parts during the calculation, as shown in Figure 11. This research calculated the safety factors of the left and right slopes, constantly modified the slope parameters (BFA and final slope angle) and calculated the safety factor. Simplified Bishop method, GLE/Morgenstern-Price method, Janbu’s method, modified Janbu’s method, ordinary slice method/Fellenius method, Spencer’s method, Lowe-Karafiath method, etc., were used for calculations. Due to the different calculation principles of different methods, the calculated FOS is slightly different. To ensure safety, the minimum value of FOS in different calculation methods was selected as the result.
As illustrated in Figure 12A, the safety factor of the slope is 0.982, and the arc line in the figure is the landslide line with a safety factor of less than 1.25. (a) Initial design slope; (b) The BFA at the landslide (the part with FOS less than 1.25) is modified from 65° to 55°, and the safety factor is 0.944, mainly because the fracture zone has been exposed after modification; (c) The BFA at the landslide (the part with FOS less than 1.25) BFA is adjusted from 55° to 50°; (d) The BFA at the landslide (the part with FOS less than 1.25) is changed from 50° to 49°. The safety factor is 1.295, which meets the requirements. The BFA of benches at the fracture zone and fault is 49°, the BFA of benches above and below the fracture zone is 55°, and the BFA of other benches is 60°. The BFA of Quaternary steps is 55°. The final slope angle is 38°.
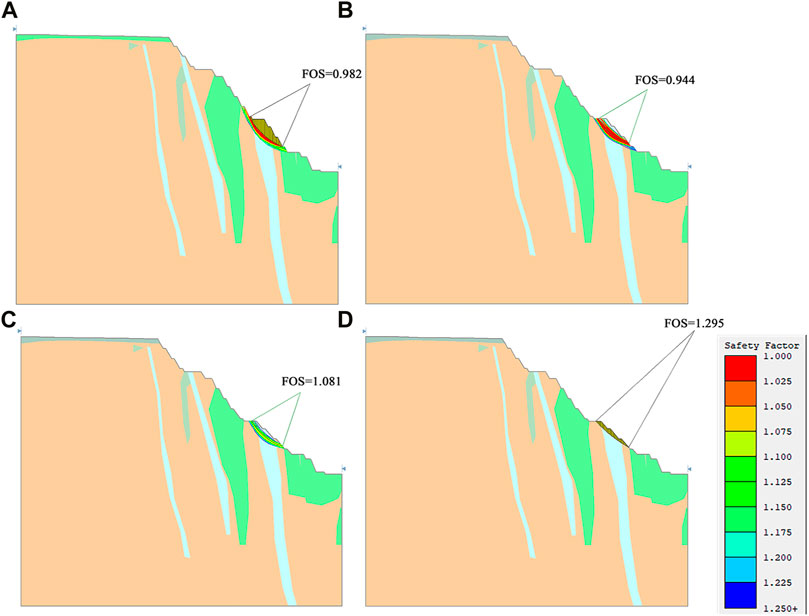
FIGURE 12. Calculation process of the slope FOS of 1# profile-left. (A) Initial design slope, (B) The BFA is modified from 65° to 55°, (C) The BFA is modified from 55° to 50°, (D) The BFA is modified from 50° to 49°.
As shown in Figure 13A, the safety factor of the slope is 1.135 and 0.982. (a) Initial design slope; (b) Modifying the BFA at the landslide (the part with FOS less than 1.25) from 65° to 60°; (c) Adjusting the BFA at the landslide (the part with FOS less than 1.25) from 60° to 55°, the landslide is located at the faults; (d) The BFA of benches at the faults is modified to 49°. The landslide is located at the fracture zone and four adjacent benches at the lower part; (e) The BFA of benches at the fracture zone is modified to 49°. The BFA of four adjacent benches at the lower part of the fracture zone is changed to be 50°; (f)The BFA of four adjacent benches at the lower part of the fracture zone is modified to be 49°; (g) The BFA of benches at the fracture zone is modified to 48°; (h) The BFA of benches at the fracture zone is modified to 45°; (i) The BFA of benches at the fracture zone is modified to 43°; (j) The BFA of benches at the fracture zone is modified to 42°; (k) The BFA of benches at the fracture zone is modified to 41°, the safety factor is 1.394, which meets the requirements. The BFA of benches at the fracture zone and fault is 41°, the BFA of four adjacent benches at the lower part of the fracture zone is 49°, and the BFA of other benches is 60–65°. The BFA of Quaternary steps is 55°. The final slope angle is 35°.
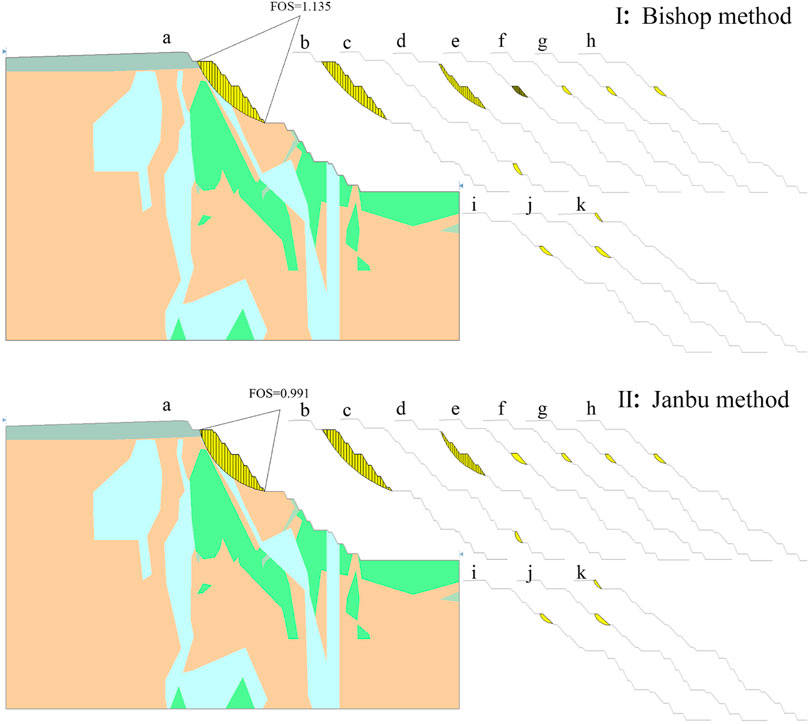
FIGURE 13. Calculation process of the slope FOS of 1# profile-left by Bishop and Janbu method. (A) Initial design slope, (B–K) The BFA was gradually reduced to optimize the slope parameters.
Curves I–VI shown in Figure 15 correspond to Figures 13, 14 respectively. Figure 15 and Table 3 indicate that the I–VI curve corresponds to the change of the slope FOS in Figures 13, 14, respectively. As shown in Figure 14, the strength of rock mass is shown to affect the shape of slope landslides. When the strength of the homogeneous slope is low, it is generally only a local landslide, ranging from a few meters to tens of meters, covering several steps. When a homogeneous slope is subjected to a high strength, the landslide is the landslide of the whole slope. Comparing Figure 13 and Figure14, heterogeneous slopes generally show landslides in weak rock mass or faults, that is, local landslides.
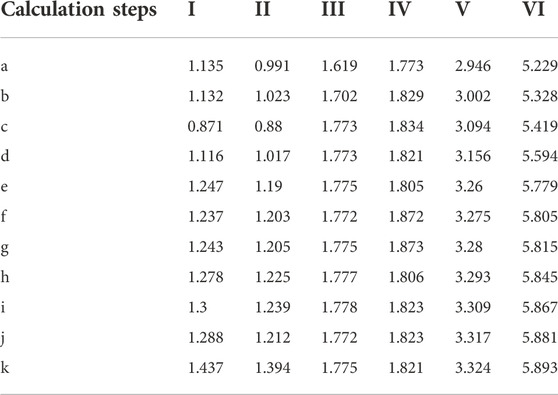
TABLE 3. Details of the data plotted Figure 15.
As shown in Figure 15, for heterogeneous slopes, the FOS did not increase monotonically with the decrease of BFA during the optimization process. Targeted reduction of step slope angle in areas with small safety factors can improve the FOS of the slope. From the curve of the homogeneous slope, the optimization after step C does not affect the FOS of the homogeneous slope; because the metal open-pit mine does not comprise a homogeneous single lithology, it is not appropriate to use the homogeneous slope to calculate the FOS and design the final slope. When compared with other mines, the lithology and rock mass strength are often compared, and the occurrence form of rock and slope form and the relationship between them are more ignored. The slope safety factor obtained in this way is often inappropriate. For example, the initial design of 323S refers to the design of 323N exposed slope, which is only 70 m away and has been adjusted according to the landslide event. The safety factor of the 323S initial design is still less than 1.
The two open-pit slopes of the Tanjianshan Gold Mine as the research object of this paper, are heterogeneous, and the following conclusions are drawn:
1) The engineering analogy method is adopted to design the final slope of the open-pit in the 323N and 323S. There are three types of the safety factors of the slope: ① If the safety factor is greater than the requirements of the relevant specifications, the final slope angle will be smaller, the stripped rock engineering work will be increased, and the mining efficiency and enterprise economic benefits will be reduced; ② Meeting the requirements of the safety factor of relevant specifications; ③ If the safety factor is less than the requirements of the safety factor of relevant specifications, which needs to be avoided, the risk of a landslide on the slope will occur, which is not conducive to the safety and stability of the mine;
2) When the same rock mass exists in the open-pit slope with the same slope parameters in different forms, its safety factor is different. The fault/fracture zone herein has different forms, and whether it is exposed or not will greatly affect the safety factor of the slope;
3) Generally, reducing the BFA of the slope will increase the safety factor of the slope when reducing the final slope angle, however, the study found that the safety factor does not increase linearly with the decrease of step slope angle, and sometimes the safety factor will decrease as the step slope angle decreases;
4) Generally speaking, when using the traditional engineering analogy method to design the final slope of the open-pit, the limit equilibrium method or numerical simulation method should be used to evaluate the stability of the slope, check the safety factor, and optimize the slope parameters after the initial design is completed.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Investigation, XZ and YZ; methodology, XZ and YZ. Writing—original draft preparation, YZ and WY; Writing—review and editing, YZ and WY; data curation, XZ and WY. All authors have read, and agreed upon the published version of the manuscript.
This work was supported by a project of the NSFC Shandong United Fund (U1806208) and the Key Projects of National Natural Science Foundation of China (52130403), the Fundamental Research Funds for the Central Universities (N2001033 and N2101022) and the Opening Project of State Key Laboratory of Nickel and Cobalt Re-sources Comprehensive Utilization.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Brady, B. H., and Brown, E. T. (2006). Rock mechanics: For underground mining. Berlin: Springer science & business media.
Cai, M., Qiao, L., Li, C., and Wng, J. (2004). Stability analysis and design optimization of High and Steep Slope in deep concave open-pit Mine. Journal of University of Science and Technology Beijing 26(05), 6. doi:10.13374/j.issn1001-053x.2004.05.004
Chen, Z., and Morgenstern, N. R. (1983). Extensions to the generalized method of slices for stability analysis. Can. Geotech. J. 20 (1), 104–119. doi:10.1139/t83-010
Chen, Z. (2003). Soil slope stability analysis: Theory, methods and program. Beijing: China Water Power Press.
Cruden, D. M., and Varnes, D. J. (1996). “Landslide types and processes,” in Landslides-investigation and mitigation. National research council transportation research board special report 247. Editors K. A. Turner, and R. L. Schuster (Washington, DC: National Academy Press).
Du, Y., Xie, M., and Jia, J. (2020). Stepped settlement: A possible mechanism for translational landslides. Catena 187, 104365. doi:10.1016/j.catena.2019.104365
Duncan, J. M. (1996). State of the art: Limit equilibrium and finite-element analysis of slopes. J. Geotech. Engrg. 123 (7), 577–596. doi:10.1061/(asce)0733-9410(1996)122:7(577)
Griffiths, D. V., and Lane, P. A. (2001). Slope stability analysis by finite elements. Géotechnique 51 (7), 653–654. doi:10.1680/geot.1999.49.3.387
Hoek, E. (2012). “Blast damage factor D,” in Technical note for RocNews, 1–7. February 2, 2012, Winter 2012 Issue, RocScience (2012). Available at: http://www.rocscience.com/assets/files/uploads/8584.pdf
Hoek, E., and Bray, J. (1977). Rock slope engineering. Revised Second Edition. London: Institute of Mining & Metallurgy.
Hungr, O., Leroueil, S., and Picarelli, L. (2014). The Varnes classification of landslide types, an update. Landslides 11 (2), 167–194. doi:10.1007/s10346-013-0436-y
Janbu, N. (1973). Slope stability computations. New Jersey, United States: John Wiley and Sons. Incorporated.
Jiang, S., Liu, H., Lian, M., Lu, C., Zhang, S., Li, J., et al. (2022). Multi-source information fusion and displacement prediction of rock slope based on variable selection and SSA-DELM model. Front. Environ. Sci. 982069.
Jiaxing, Z., Fei, L., Jin-an, W., Anqi, G., and Chengyuan, H. (2022). Stability control of slopes in open-pit mines and resilience methods for disaster prevention in urban areas: A case study of fushun west open pit mine. Front. Earth Sci. (Lausanne). 10879387. doi:10.3389/feart.2022.879387
Keefer, D. K., and Larsen, M. C. (2007). Assessing landslide hazards. Science 316 (5828), 1136–1138. doi:10.1126/science.1143308
Price, V. E., and Morgenstern, N. R. (1967). The analysis of stability of general slip surface. Geotechnique 15 (3), 393–394.
Sarma, S. K. (1973). Stability analysis of embankments and slopes. Géotechnique 23 (3), 423–433. doi:10.1680/geot.1973.23.3.423
Shaunik, D., and Singh, M. (2020). Bearing capacity of foundations on rock slopes intersected by non-persistent discontinuity. Int. J. Min. Sci. Technol. 30 (5), 669–674. doi:10.1016/j.ijmst.2020.03.018
Spencer &, E. (1968). A method of analysis of the stability of embankments assuming parallel inter-slice forces. Géotechnique 18 (3), 384–386. doi:10.1680/geot.1968.18.3.384
Varnes, D. J. (1958). “Landslide types and processes,” in Landslides and engineering practice, 24: 20–47. State of California: National Research Council (U.S.). Highway Research Board Reprinted.
Varnes, D. J. (1978). Slope movement types and processes. In: in Editor Schuster RL., and RJ. Krizek. (eds) Landslides, analysis and control, special report 176: Transportation research boardNational Academy of SciencesWashington, DC, 11–33.
Zeng, Y., and Tian, W. (2005). Slope stability analysis by combining FEM with equilibrium method. Journal of Rock Mechanics and Engineering 24 (S2), 5355–5359.
Zhang, J. (2002). Finite element simulation and stability evaluation of slope excavation. Journal of Rock Mechanics and Engineering 21 (06), 843–847. doi:10.3321/j.issn:1000-6915.2002.06.016
Zheng, H., Li, C., Li, Z., and Ge, X. (2002). Finite element method for solving safety factor. Journal of Geotechnical Engineering. (05), 626–628. doi:10.3321/j.issn:1000-6915.2002.06.016
Zhu, D., Li, Z., Huang, M., and Qian, Q. (2005). Modification to three well-known methods if slope stability analysis. Journal of Rock Mechanics and Engineering. 24 (02), 183–194. doi:10.3321/j.issn:1000-6915.2005.02.001
Zhu, D. Y., Lee, C. F., and Jiang, H. D. (2003). Generalised framework of limit equilibrium methods for slope stability analysis. Géotechnique 53 (4), 377–395. doi:10.1680/geot.53.4.377.37322
Keywords: open-pit mine, slope, heterogeneous, metal mine, safety factor
Citation: Zhao X, Zhao Y and Yu W (2023) The safety factor of a heterogeneous slope in an open-pit metal mine: A case study from the Tanjianshan gold mine. Front. Earth Sci. 10:990454. doi: 10.3389/feart.2022.990454
Received: 10 July 2022; Accepted: 07 September 2022;
Published: 06 January 2023.
Edited by:
Yan Du, University of Science and Technology Beijing, ChinaReviewed by:
Yanlin Zhao, Hunan University of Science and Technology, ChinaCopyright © 2023 Zhao, Zhao and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yifan Zhao, enlmX25ldUAxMjYuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.