A comparison study of face stability between the entering and exiting a shallow-buried tunnel with a front slope

Worldwide, it is a great challenge to tunnel in portal section, where excessive deformation, cracking, or even collapse often occurs during the construction process. This paper presents a comparison study of face stability between entering and exiting a shallow-buried tunnel with a front slope. Firstly, the theoretical solutions of support pressure σ_T and safety coefficient FS of the excavation face considering surface slope are derived by upper-bound limit analysis method. Secondly, for different slope angles, buried depth and surrounding rocks of the exit and entrance sections, the σ_T and FS are obtained. The results show that when the burial depth of the tunnel crown h remain constant, the σ_T increased first and then decreased while the FS increased gradually, and both become steady when the slope angle α arrive at a certain value. In addition, the thicker the h is, the smaller the certain value α is. When the h and α remain constant, the loose area in front of the excavate face will decreased apparently with the increase of the internal friction angle φ, thus the σ_T will decrease and FS will increase. Moreover, the σ_T decreased linearly with the increase of cohesion c and unit weigh γ of surrounding rock, while the FS is the opposite. Compared with the entrance section, the construction risk at the exit section is greater.

1 Introduction

The tunnel portal section is often affected by unfavorable terrain and geological conditions such as shallow burial depth, unsymmetrical loading and broken surrounding rocks, resulting in various damages such as excessive deformation, cracking, or even collapse during the construction process (Ye et al., 2012; Liu et al., 2015). Currently, there have been a large number of studies and reports on tunnel portal section, covering various aspects such as pre-reinforcement technology (Coulter and Martin, 2006; Xiao et al., 2016; Yang et al., 2019), slope and face stability (Adam et al., 2014; Lei et al., 2015; Yuan et al., 2020; Zhou et al., 2021; Li et al., 2022), excavation methods and support (Miura, 2003; Yang et al., 2021), damage and treatment (Kontogianni et al., 2004; Yang et al., 2019; Cui et al., 2021), and others (He and Kusiak, 2017; Li et al., 2021a; Li et al., 2021b). However, the existing literatures has mainly focus on the condition of entering the tunnel, while relatively few studies have been carried out on the exit section. Actually, the occurrence of all kinds of damage in the tunnel exit section is not uncommon, such as the Pingzhai Tunnel of Xiamen—Chengdu Highway, due to shallow burial and low quality of surrounding rock, collapse occurred during exiting process. Firstly, a circular collapse about 50 cm appeared on the surface (Figure 1), and the collapse gradually increased with the further excavation. The distortion of primary support, breakage of pipe roof and collapse of slope in the tunnel exit section of Wafanggou Tunnel of Shangzhou - Manchuanguan Highway (Li, 2009). Li and Yang (2016) used a 3D numerical model to simulate the excavation of Pingzhai Tunnel portal, the result showed that the stress and deformation of surrounding rock are different between entering and exiting the portal using the same excavation method.

FIGURE 1

FIGURE 1. Collapse during exiting the Pingzhai Tunnel (western China).

Limit analysis method or limit equilibrium method is often used in the theoretical analysis of tunnel excavation face stability. In 1987, Broms and Bennermark, (1967) firstly put forward the concept of stability factor N of tunnel face in undrained clay stratum and suggested that n < 6 should be taken as the condition for the excavation face to remain stable. In the following decades, this method has been widely used and improved. For instance, Anagnostou and Perazzelli (2013) and Wu et al. (2015) proposed formulas for calculating the limit support pressure considering the arching effect in soil, respectively. Liang et al. (2017) changed the failure area of the square wedge body in front of excavation face into the spiral body, and deduced the calculation model considering excavation footage. Leca and Dormieux (1990) proposed a failure criterion for the tunnel face in the general case of a cohesive and friction soil, and provided charts to allow a bracketed estimate of the required retaining pressure. Based on the Leca’s model, Mollon et al. (2009) and Zhang et al. (2015) proposed the failure modes composing of multiple rigid truncated cones, and obtained the upper-bound solution for the face stability through optimization, respectively. Zhao et al. (2017) obtained the optimal upper limit solution for support pressure by using the sequential quadratic programming method. The above mentioned literatures are mainly carried out under the condition that the surface is horizontal. However, the tunnel portal section is usually shallow buried, hence the effect of surface slope should not be ignored.

In this paper, the tunnel portal with a front slope, which is one of the most typical portal types, is taken to investigate the difference between entering and exiting the tunnel. As shown in Figure 2, the covering depth of this tunnel on the left and right sides is almost the same, and therefore no obviously unsymmetrical loading is formed. However, the covering depth gradually increases along the tunnel axis to form a front slope with a dip direction parallel to the tunnel axis. The construction of this tunnel portal section, i.e., excavation at the foot of the front slope, will easily lead to the instability of slope and surrounding rock. Firstly, the theoretical solutions of support pressure σ_T and safety coefficient FS of the excavation face considering surface slope are derived by upper-bound limit analysis method. Then the face stability under entering and exiting conditions is systematically compared through calculation the σ_T and FS of different burial depth, surrounding rock parameters and the slope angles. The conclusion can serve as references for the excavation and support of similar engineering.

FIGURE 2

FIGURE 2. A typical front slope tunnel portal.

2 Limit analysis of the tunnel face stability

2.1 Failure mode

Since such tunnel portal is symmetrically distributed along the center line, a two-dimensional model can be used for simplified analysis. The assumed failure mode of tunnel face is shown in Figure 3, AB is the excavation face; BF is the sliding surface on the top of the vault; AF is the sliding surface on the lower part of the bottom vault. According to the research results of Chambon and Corté (1994) and Takano et al. (2010), it is assumed that the loose area in front of the face is in the shape of a logarithmic spiral, i.e. AF in Figure 3 is a logarithmic spiral curve (O is the center point), and the equation is

$R=R_0\exp \left[\left(\theta -{\theta }_0\right)\tan \phi \right](1)$

FIGURE 3

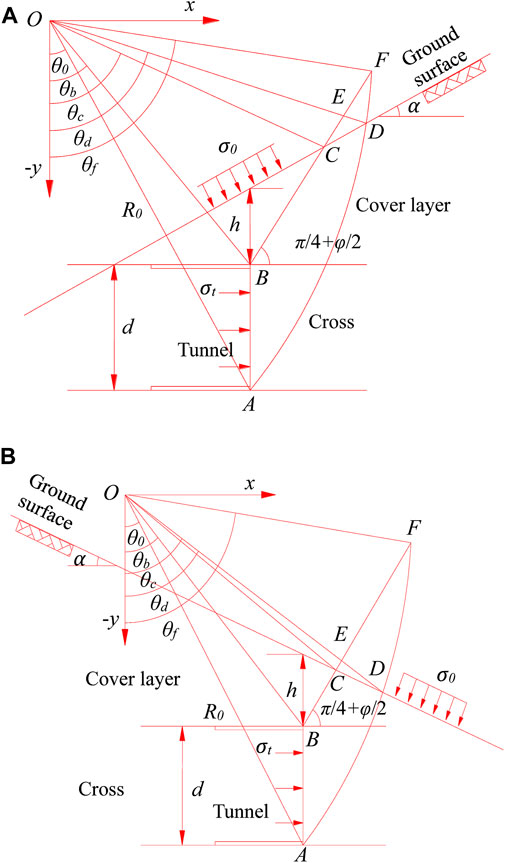
FIGURE 3. The failure model of tunnel face at portal section: (A) entrance section; (B) exit section.

The included angle between AF and the horizontal plane at the tunnel bottom surface, the included angle between BF and the horizontal plane, and the included angle between OA and the–y axial are all (π/4+φ/2) (Chambon and Corté, 1994; Takano et al., 2010).

2.2. Geometry parameter

As shown in Figure 3, the equations for BF and the ground surface CD are

${\text{y}}_{BF}=\tan \left(\pi /4+\phi /2\right)\cdot x+d-R_0\left[\cos {\theta }_0+\tan \left(\pi /4+\phi /2\right)\sin {\theta }_0\right](2)$

${\text{y}}_{CD}=\tan \alpha \cdot x+d+h-R_0\left(\cos {\theta }_0+\tan \alpha \sin {\theta }_0\right)(3)$

The coordinates of points A (x_A and y_A), B (x_B and y_B), C (x_C and y_C), D (x_D and y_D) and F (x_F and y_F) can be easily obtained by combining the above (Eqs. 1–3), and the values are as follows respectively:

$x_A=R_0\sin {\theta }_0,y_A=-R_0\cos {\theta }_0(4)$

$x_B=R_0\sin {\theta }_0,y_B=-R_0\cos {\theta }_0+d(5)$

$\{\begin{array}{c}{x}_C=R_0\sin {\theta }_0+h/\left[\tan \left(\pi /4+\phi /2\right)-\tan \alpha \right]\\ y_C=\tan \alpha \cdot x_C+d+h-R_0\left[\cos {\theta }_0+\tan \alpha \sin {\theta }_0\right]\end{array}(6)$

$\{\begin{array}{l}{x}_D=R_{OD}\cdot \sin {\theta }_d\\ y_D=-R_{OD}\cdot \cos {\theta }_d\\ R_{OD}=R_0\exp \left[\left({\theta }_0-{\theta }_d\right)\tan \phi \right]\cdot \tan \alpha \cdot \left(R_0\sin {\theta }_0-R_{OD}\sin {\theta }_c\right)\\ +R_0\cos {\theta }_0-d-h-R_{OD}\cos {\theta }_d\end{array}(7)$

$\{\begin{array}{l}{x}_F=R_{OF}\cdot \sin {\theta }_f\\ y_F=-R_{OF}\cdot \cos {\theta }_f\\ R_{OF}=R_0\exp \left[\left({\theta }_0-{\theta }_f\right)\tan \phi \right]\cdot \tan \left(\pi /4+\phi /2\right)\cdot \left(R_0\sin {\theta }_0-R_{OF}\sin {\theta }_f\right)\\ +R_0\cos {\theta }_0-d-R_{OF}\cos {\theta }_f\end{array}(8)$

From Eqs 4–8, the length R_OD, R_OF, L_OB, L_OC, L_BC, L_CD and L_BF can be obtained.

2.3 External load power

When the rigid slider ABCD rotates around the center of rotation O (i.e., the origin of coordinates), the sliding surfaces AD and BC are velocity discontinuity surfaces. The power of the external work done by ABCD due to its own weight can be obtained by adding the power algebraic of the external work done by the blocks OAB, OBC, OCD, and OAD. The specific expression of the power done by each block due to its own weight is as follows:

$W_{OAB}=\frac{1}{3}\gamma {\left(R_0\sin {\theta }_0\right)}^{2}d\omega (9)$

$W_{OBC}=\frac{1}{3}\gamma L_{OB}{L}_{BC}\sin \left({\theta }_b+\frac{\pi }{4}-\frac{\phi }{2}\right)\times \left[R_0\sin {\theta }_0+L_{BC}\cos \left(\frac{\pi }{4}+\frac{\phi }{2}\right)\right]\omega (10)$

$W_{OCD}=\frac{1}{3}\gamma L_{OC}{R}_{OD}\sin \left({\theta }_d-{\theta }_c\right)\times \left[L_{OC}\sin {\theta }_c+L_{CD}\cos \alpha \right]\omega (11)$

$W_{OAD}={\displaystyle {\int }_{{\theta }_0}^{{\theta }_d}\frac{\gamma R^2}{2}}\cdot \frac{2}{3}R\sin \theta \cdot \omega \text{d}\theta =\frac{R_0^3\omega }{3\left(1+9{\tan }^2\phi \right)}\cdot \left[\begin{array}{l}\left(\cos {\theta }_0+3\tan \phi \sin {\theta }_0\right)\\ -\left(\cos {\theta }_d+3\tan \phi \sin {\theta }_d\right)\\ \times \exp \left[3\left({\theta }_0-{\theta }_d\right)\tan \phi \right]\end{array}\right](12)$

As shown in Figure 3A, for the entrance section, the power of the external work done by ABCD due to its own weight is

$W_G=W_{OAD}-W_{OAB}-W_{OBC}-W_{OCD}(13)$

and Eq. 13 is also applicable for the exit section when (π/2+α) > θc (as shown in Figure 3B, the corresponding α of the exit is a negative value). For the exit section when (π/2+α)<θc, the power of external work done by ABCD due to its own weight is

$W_G=W_{OAD}-W_{OAB}-W_{OBC}+W_{OCD}(14)$

When the intersection F between AF and BF is located inside the slope, the power of the external work done by the rigid slider ABF due to its own weight can be obtained by algebraically adding the external work power done by OAB, OAF, and OBF

$W_{OAF}=\frac{R_0^3\omega }{3\left(1+9{\tan }^2\phi \right)}\left[\begin{array}{l}\left(\cos {\theta }_0+3\tan \phi \sin {\theta }_0\right)\\ -\left(\cos {\theta }_f+3\tan \phi \cos {\theta }_f\right)\\ \times \exp \left[3\left({\theta }_0-{\theta }_f\right)\tan \phi \right]\end{array}\right](15)$

$W_{OBF}=\frac{1}{3}\gamma L_{OB}{L}_{BF}\sin \left({\theta }_b+\frac{\pi }{4}-\frac{\phi }{2}\right)\times \left[R_0\sin {\theta }_0+L_{BF}\cos \left(\frac{\pi }{4}+\frac{\phi }{2}\right)\right]\omega (16)$

When the slider ABF is located inside the slope, the power of external work done due to its own weight is as follows:

$W_G=W_{OAF}-W_{OAB}-W_{OBF}(17)$

The power W₀ and W_T of the external work done by the surface overload σ₀ and the supporting pressure σ_T on the tunnel excavation surface is as follows respectively:

$W_0=\frac{2}{3}{\sigma }_0{L}_{CD}\cos \alpha \left[L_{OC}\cos {\theta }_d+L_{CD}\cos \alpha \right]\omega (18)$

$W_T={\sigma }_{T}d\left(R_0\cos {\theta }_0-\frac{d}{2}\right)\omega (19)$

2.4 Internal energy dissipation

According to the upper-bound theorem of limit analysis, the internal energy dissipation on the section between different speeds is calculated. The energy dissipation of the failure mode shown in Figure 3 includes the energy consumption on AD and BC on the top of the vault. The calculation formula is as follows:

$D_{AD}={\displaystyle {\int }_{{\theta }_0}^{{\theta }_d}\frac{cR}{\cos \phi }\cdot }R\cos \phi \cdot \omega \text{d}\theta =\frac{c{R}_0^2\omega }{2\tan \phi }\left\{1-\exp \left[2\left({\theta }_0-{\theta }_d\right)\tan \phi \right]\right\}(20)$

$D_{BC}=c{L}_{BC}{L}_{OB}\sin \left({\theta }_b+\frac{\pi }{4}-\frac{\alpha }{2}\right)\cos \phi \cdot \omega (21)$

Then, the total internal energy dissipation on the sliding surface is

$D=D_{AD}+D_{BC}(22)$

When the intersection F between AF and BF is located inside the slope, the total internal energy dissipation on the sliding surface is

$D=D_{BF}+D_{AF}=\frac{c{R}_0^2\omega }{2\tan \phi }\left\{1-\exp \left[2\left({\theta }_0-{\theta }_f\right)\tan \phi \right]\right\}+c{L}_{OF}{L}_{OB}\sin \left({\theta }_b+\frac{\pi }{4}-\frac{\alpha }{2}\right)\cos \phi \cdot \omega (23)$

2.5 Calculation and verification

According to the virtual work principle in the limit analysis theory, the external load power is equal to the internal energy dissipation power, i.e. D = W_G+W₀+W_T, and the objective function of the limit support pressure σ_T of the tunnel excavation face is obtained as follows:

${\sigma }_T=\frac{D-W_G-W_0}{d\left(R_0\cos {\theta }_0-0.5d\right)\cdot \omega }(24)$

The strength reduction method was adopted to obtain the safety coefficient FS of the tunnel face

$FS=\frac{c}{c^{\prime }}=\frac{\tan \left(\phi \right)}{\tan \left({\phi }^{\prime }\right)}(25)$

where c and φ are the cohesion and friction angle of the surrounding rocks, respectively. And c’ and φ′ are the reduction parameters of the cohesion and friction angle for the failure of the excavation face, respectively. Substituting Eq. 25 into Eq. 24 so as to make sure σ_T of the tunnel face is equal to 0, and then FS of the tunnel face can be obtained.

Calculations of σ_T at given parameter values (c = 7 kPa, φ=17°, γ =18 kN/m³, D=10 m, σ₀ =0 kPa) are carried out and comparisons with others are conducted. Graphically, the calculation results are depicted in Figure 4. It can be seen that the calculation results in this paper are very close to those in the existing literatures, which are 6.2 and 6.5% lower than those of Mollon et al. (2009) and Zhao et al. (2017), respectively, but are 11.9% higher than those of Leca and Dormieux. (1990). When c/d is greater than 0.6, the loose area is located inside the slope, and σ_T of the face is constant, which is consistent with the actual situation. Through the above comparison and analysis, the rationality and correctness of the calculation method in this paper are verified.

FIGURE 4

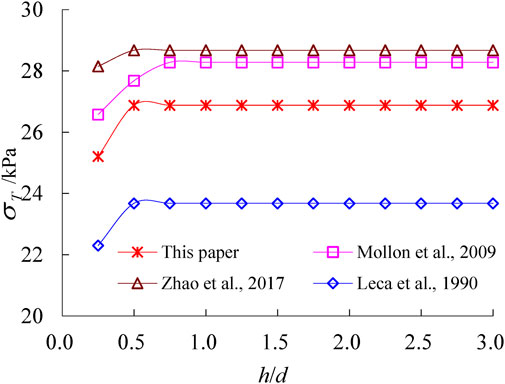
FIGURE 4. Calculated limit support pressure σ_T at given parameters (c = 7 kPa, φ=17°, γ =18 kN/m³, D=10 m, σ₀ =0 kPa).

3 Comparison in entering and exiting

The slope at the tunnel entrance and exit sections is indicated by α (a positive value representing the slope of the ground surface at the tunnel entrance section or a negative value representing the slope of the ground surface at the tunnel exit section). In order to analyze the influence of the surface slope at the tunnel entrance and exit sections on the stability of the tunnel surface, the following parameters are taken: D =10 m, h =4 m, γ =18 kN/m³, c =7 kPa and φ=17°. When analyzing the influence of a certain factor on the stability of the tunnel face, other parameters shall remain unchanged.

3.1 Different burial depth

The relationships between the σ_T and FS of the tunnel face and the slope of the ground under the condition of different burial depth of the tunnel crown h are shown in Figure 5.

FIGURE 5

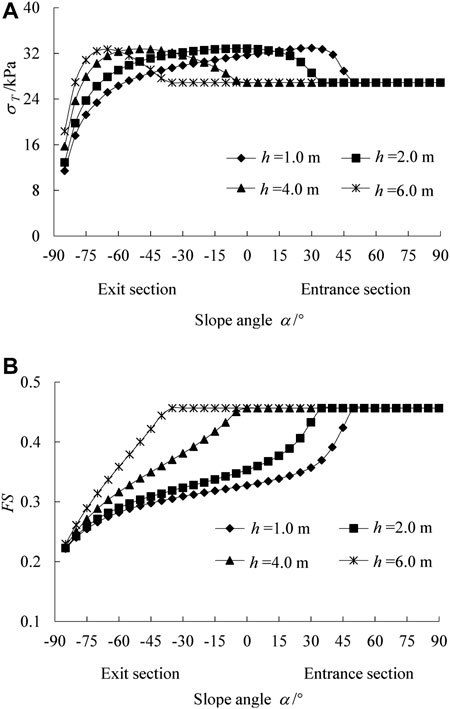
FIGURE 5. Limit support pressure σ_T and safety coefficient FS changing with slope angle α and burial depth h (A) σ_T; (B) FS.

Figure 5A shows under the same h, with the increase of α, the σ_T of the face increases first, and then decreases to a certain value, and eventually goes steady. When the σ_T is constant, the loose area in front of the face will be all inside the slope, and the loose area no longer extends upward due to the arching effect of the surrounding rock, so the increase of h will not lead to the increase of σ_T. When the α is small, the loose area will shrink, thus the required σ_T will decrease; With the increase of α and the loose area, the increase of external load power will decrease gradually, while the increase of internal energy dissipation on the sliding surface is approximately a constant value (Figure 3), thus causing σ_T increasing first and then decreasing. In addition, it is easy to understand that the larger the h is, the smaller the corresponding α when reaching the maximum value and the constant value, and the change of h has no influence on the maximum value and the constant value of σ_T.

Figure 5B shows when h is the same, the FS of the face increases gradually with the increase of the surface slope until the loose area is completely inside the slope; when the α remains a small value, the larger the h is, the larger the corresponding FS is. When α = −70° and H = 1.0 m, the corresponding FS and σ_T are the smallest; when α = −15° and H = 1.0 m, the corresponding FS is the largest, but the σ_T is the largest.

According to the above results, the stability of the tunnel face at the exit section is lower than that at the entrance section. When the loose area is completely located inside slope, the stability of the excavation face are the highest.

3.2 Strength parameters of different surrounding rocks

3.2.1 Internal friction angle φ

When the internal friction angle φ of the surrounding rock is different, the relationship between the σ_T and FS of the tunnel face and the surface slope α is shown in Figure 6.

FIGURE 6

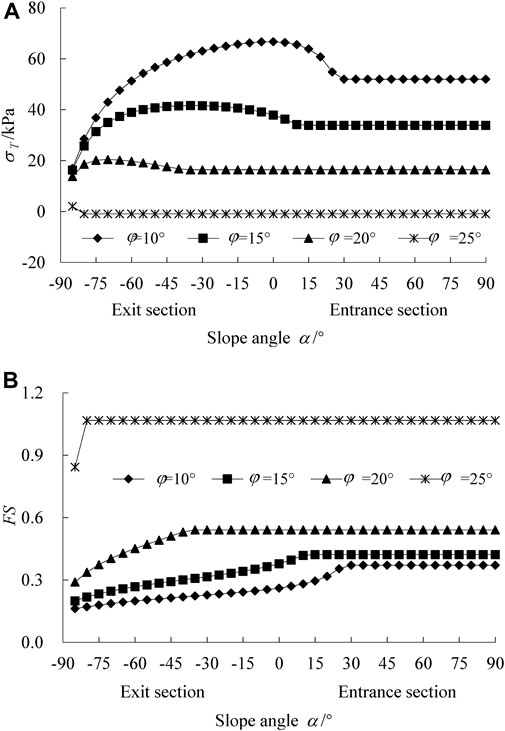
FIGURE 6. Limit support pressure σ_T and safety coefficient FS changing with slope angle α and internal friction angle φ: (A) σ_T; (B) FS.

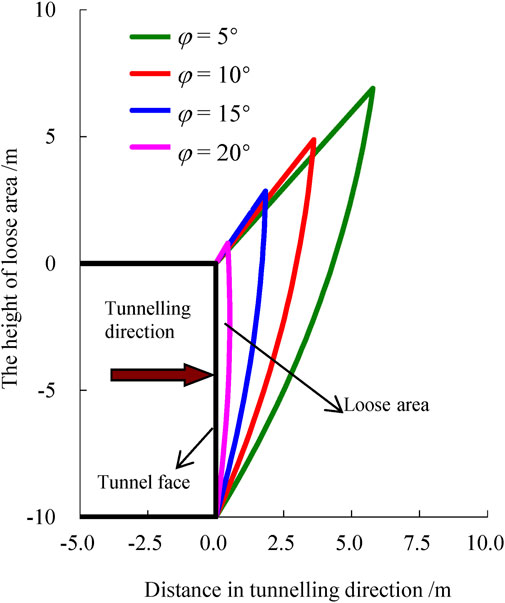
It can be seen that when h is constant and φ is small, the σ_T of the face increases with the increase of α and then decreases, and finally tends to be constant; FS of the face gradually increases with the increase of α, and finally reaches a constant value; the larger the φ is, the smaller the α is when σ_T and FS reach constant values. When the α is large, σ_T and FS of the face are both constant; when α is constant, the larger the φ is, the smaller the corresponding σ_T is, and the larger the FS is. The main reason is that the increase of φ makes the loose area in front of the face decrease significantly, resulting in a significant reduction of external load power, as shown in Figure 7. And when the σ_T and FS are constant, it means that the loose area of the surrounding rock is completely located inside the slope, and the loose area is no longer developed upward due to the arching effect of the surrounding rock.

FIGURE 7

FIGURE 7. The effect of internal friction angle φ on the loose area.

3.2.2 Cohesion c

Under different cohesion c, the relationship between the σ_T and FS of the tunnel face and the surface slope α is shown in Figure 8. When α is constant, the σ_T decrease linearly with the increase of c, while FS increase linearly with the increase of c.

FIGURE 8

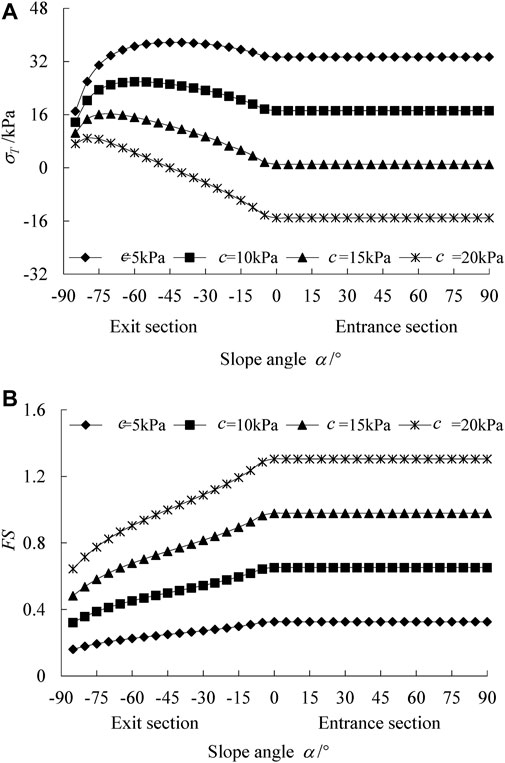
FIGURE 8. Limit support pressure σ_T and safety coefficient FS changing with slope angle and soli cohesion: (A) σ_T; (B) FS.

When the surface is horizontal (i.e., α = 0°), the change law of c and φ corresponding to different FS are shown in Figure 9. The values of other parameters are as follows: d =10 m, h = 10 m, and γ = 20 kN/m³. It can be seen that c and φ can significantly affect the FS. When the FS of the face is constant, the required c decreases gradually with the increase of the φ, and the decreasing amplitude increases gradually. The larger the φ is, the smaller the difference in c required to meet the requirements of different stability factors of the excavation face is.

FIGURE 9

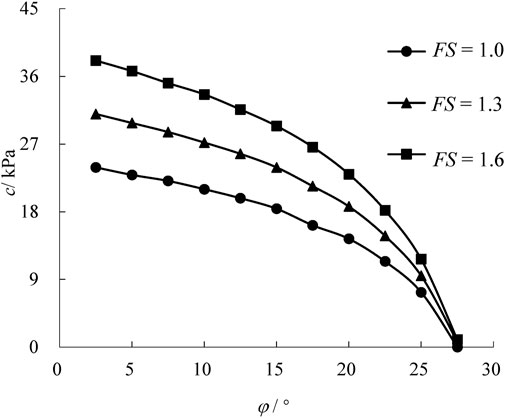
FIGURE 9. Change law of cohesion c and internal friction angle φ of the surrounding rock corresponding to different safety coefficients FS (α =10°, d =10 m, h = 10 m, and γ = 20 kN/m³).

3.3 Unit weight of the surrounding rock γ

Under the condition of different unit weight γ of surrounding rocks, the relationship between σ_T and FS of the tunnel face and α is shown in Figure 10. It can be seen that when the α is the same, the σ_T and FS of the tunnel face decrease and increase linearly with the increase of γ, respectively.

FIGURE 10

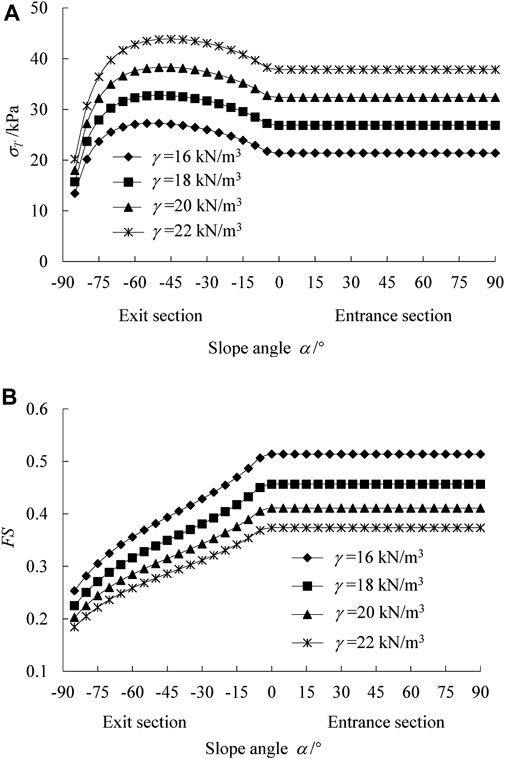
FIGURE 10. Limit support pressure σ_T and safety coefficient FS changing with slope angle and unit weight of surrounding rock: (A) σ_T; (B) FS.

4 Conclusions and perspectives

Based on the upper-bound theorem of limit analysis, a calculation method to quantitatively analyze the limit support pressure σ_T and safety coefficient FS of the tunnel face is put forward. Compared with the existing literature results, the correctness and effectiveness of this method adopted in this paper are verified. By using such method, the calculation of the σ_T and FS of the tunnel face under the conditions of different surface slopes α at the tunnel entrance and exit sections is carried out. The following conclusions are drawn:

1) The σ_T of the tunnel face increases first and then decreases with the increase of α and finally reaches a constant value; the FS increases gradually with the increase of α, and goes steady when α increases to a certain value.

2) When α is small, the FS of the tunnel face gradually increases with the increase of the burial depth of the tunnel crown h; when the loose area in front of the excavation is completely located inside the slope, the loose area no longer develops upward due to the arching effect, so when the slope increases by a certain amount, the σ_T and FS of the tunnel face are no longer affected by the change of h.

3) The cohesion c and internal friction angle φ of the surrounding rock can significantly affect the σ_T and FS of the face. The increase of φ will obviously reduce the loose area in front of the face and will significantly improve the face stability; when the α is constant, the σ_T and FS of the face increase linearly with the increase of c and unit weight of the surrounding rock γ. The larger the φ is, the smaller the difference in c required to meet the requirements of different safety coefficients of the excavation face is.

4) For shallow buried tunnel, the FS of exiting is relatively low compared with that of entering. Therefore, more attention should be paid during the excavation of exiting the tunnel.

5) Research results show that the face stability between entering and exiting excavation is different for the shallow-buried tunnel with a front slope, which can serve as references for the excavation and support of this portal. Further research can be carried out for other types of tunnel portals, such as the shallowly buried and asymmetrically loaded tunnel portal.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XZL: resources, data curation, project; investigation. XLL Calculation: Theoretical methods; validation. CY: writing-original draft preparation; editing; project.

Funding

This work is supported by the National Natural Science Foundation of China (No. 42177132); Natural Science Foundation of Hubei Province (Nos. 2021CFA090 and 2021CFB536); the Open Fund of Key Laboratory of Geological Hazards on Three Gorges Reservoir Area (China Three Gorges University), Ministry of Education (2015KDZ04).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

FS, safety coefficient; R, polar radius of the logarithmic spiral curve (m); R₀, length of OA (m); R_OD, length of OD (m); R_OF, length of OF (m); L_OB, length of OB (m); L_OC, length of OC (m); L_BC, length of BC (m); L_CD, length of CD (m); L_BF, length of BF (m); θ, polar angle of the logarithmic spiral curve (°); θ₀, included angle between OA and –y axial (°); θ_b, included angle between OB and –y axial (°); θ_c, included angle between OC and –y axial (°); θ_d, included angle between OD and –y axial (°); θ_f, included angle between OF and –y axial (°); h, burial depth of the tunnel crown (m); d, tunnel height (m); α, included angle between ground surface and the horizontal plane (°), it is positive at the entrance and negative at the exit; γ, unit weight (kN/m³); c, cohesion (kPa); φ, internal friction angle (°); σ_T, support pressure distributed on the excavation surface (kPa); σ₀, additional pressure acting on the surface (kPa); ω, rotational angular velocity.

References

Adam, D., Markiewicz, R., and Brunner, M. (2014). Block-in-matrix structure and creeping slope: Tunneling in hard soil and/or weak rock. Geotech. Geol. Eng. (Dordr). 32 (6), 1467–1476. doi:10.1007/s10706-012-9591-5

CrossRef Full Text | Google Scholar

Anagnostou, G., and Perazzelli, P. (2013). The stability of a tunnel face with a free span and a non-uniform support. Geotechnik 36 (1), 40–50. doi:10.1002/gete.201200014

CrossRef Full Text | Google Scholar

Broms, B. B., and Bennermark, H. (1967). Stability of clay at vertical opening. J. Soil Mech. Found. Div. 93 (1), 71–94. doi:10.1061/jsfeaq.0000946

CrossRef Full Text | Google Scholar

Chambon, P., and Corté, J. F. (1994). Shallow tunnels in cohesionless soil: Stability of tunnel face. J. Geotech. Engrg. 120 (7), 1148–1165. doi:10.1061/(asce)0733-9410(1994)120:7(1148)

CrossRef Full Text | Google Scholar

Coulter, S., and Martin, C. D. (2006). Effect of jet-grouting on surface settlements above the Aeschertunnel, Switzerland. Tunn. Undergr. Space Technol. 21 (5), 542–553. doi:10.1016/j.tust.2005.07.005

CrossRef Full Text | Google Scholar

Cui, S., Pei, X., Jiang, Y., Wang, G., Fan, X., Yang, Q., et al. (2021). Liquefaction within a bedding fault: Understanding the initiation and movement of the Daguangbao landslide triggered by the 2008 Wenchuan Earthquake (Ms = 8.0). Eng. Geol. 295, 106455. doi:10.1016/j.enggeo.2021.106455

CrossRef Full Text | Google Scholar

He, Y., and Kusiak, A. (2017). Performance assessment of wind turbines: Data-derived quantitative metrics. IEEE Trans. Sustain. Energy 9 (1), 65–73. doi:10.1109/tste.2017.2715061

CrossRef Full Text | Google Scholar

Kontogianni, V., Tzortzis, A., and Stiros, S. (2004). Deformation and failure of the tymfristos tunnel, Greece. J. Geotech. Geoenviron. Eng. 130, 1004–1013. doi:10.1061/(asce)1090-0241(2004)130:10(1004)

CrossRef Full Text | Google Scholar

Leca, E., and Dormieux, L. (1990). Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material. Geotechnique 40 (4), 581–606. doi:10.1680/geot.1990.40.4.581

CrossRef Full Text | Google Scholar

Lei, M. F., Peng, L. M., and Shi, C. H. (2015). Model test to investigate the failure mechanisms and lining stress characteristics of shallow buried tunnels under unsymmetrical loading. Tunn. Undergr. Space Technol. 46, 64–75. doi:10.1016/j.tust.2014.11.003

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D., and Cheng, Q. (2021a). Short-term nacelle orientation forecasting using bilinear transformation and ICEEMDAN framework. Front. Energy Res. 9, 780928. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. (2021b). Monitoring and identifying wind turbine generator bearing faults using deep belief network and EWMA control charts. Front. Energy Res. 9, 799039. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Li, H., He, Y., Xu, Q., Deng, j., Li, W., and Wei, Y. (2022). Detection and segmentation of loess landslides via satellite images: A two-phase framework. Landslides 19, 673–686. doi:10.1007/s10346-021-01789-0

CrossRef Full Text | Google Scholar

Li, J. M., and Yang, C. (2016). Impact of excavation sequence from inside on surrounding rock stability at the portal of a shallow and unsymmetrically loaded tunnel. Electron. J. Geotechnical Eng. 21 (13), 4739–4749.

Google Scholar

Li, T. J. (2009). Cause analysis of tunnel initial support deformation and the treatment. Highw. Auto Appl. 4 (3), 197–199. (in Chinese). doi:10.3969/j.issn.1671-2668.2009.03.063

CrossRef Full Text | Google Scholar

Liang, Q., Yang, X. L., and Chen, X. (2017). Limit equilibrium analysis of round length in tunnel excavation. J. South China Univ. Technol. Nat. Sci. Ed. 45 (5), 123–119. (in Chinese). doi:10.3969/j.issn.1000-565X.2017.05.016

CrossRef Full Text | Google Scholar

Liu, X. J., Yang, C., and Yu, J. (2015). The influence of moisture content on the time-dependent characteristics of rock material and its application to the construction of a tunnel portal. Adv. Mater. Sci. Eng. 2015, 1–13. doi:10.1155/2015/725162

CrossRef Full Text | Google Scholar

Miura, K. (2003). Design and construction of mountain tunnels in Japan. Tunn. Undergr. Space Technol. 18, 115–126. doi:10.1016/s0886-7798(03)00038-5

CrossRef Full Text | Google Scholar

Mollon, G., Dias, D., and Soubra, A. H. (2009). Probabilistic analysis and design of circular tunnels against face stability. Int. J. Geomech. 9 (6), 237–249. doi:10.1061/(asce)1532-3641(2009)9:6(237)

CrossRef Full Text | Google Scholar

Takano, D., Otani, J., Fukushige, S., and Natagani, H. (2010). Investigation of interaction behavior between soil and face bolts using X-ray CT. Adv. X-ray Tomogr. Geomaterials 26 (4), 389–395. doi:10.1002/9780470612187.ch41

CrossRef Full Text | Google Scholar

Wu, J., Liao, S. M., and Shi, Z. H. (2015). Workface stability of shield tunnel considering arching effect. J. Tongji Univ. Nat. Sci. 43 (2), 213–220. (in Chinese). doi:10.11908/j.issn.0253-374x.2015.02.008

CrossRef Full Text | Google Scholar

Xiao, J. Z., Dai, F. C., Wei, Y. Q., Xing, Y. C., Cai, H., and Xu, C. (2016). Analysis of mechanical behavior in a pipe roof during excavation of a shallow bias tunnel in loose deposits. Environ. Earth Sci. 75 (4), 293. doi:10.1007/s12665-015-5176-y

CrossRef Full Text | Google Scholar

Yang, C., Chen, Y. H., Guo, Z., and Wang, R. H. (2021). Surface settlement control in the excavation of a shallow intersection between a double-arched tunnel and a connection. Tunn. Int. J. Geomechanics 24 (4), 04021035. doi:10.1061/(ASCE)GM.1943-5622.0001983

CrossRef Full Text | Google Scholar

Yang, C., Chen, Y. H., Huang, D., and Wang, L. H. (2019). Arching effect between the pipes of a pipe umbrella support system in a shallow-buried tunnel. KSCE J. Civ. Eng. 23 (12), 5215–5225. doi:10.1007/s12205-019-5197-2

CrossRef Full Text | Google Scholar

Yang, C., Hu, Z. X., Huang, D., and Guo, F. (2019). Failure mechanism of primary support for a shallow and asymmetrically loaded tunnel portal and treatment measures. J. Perform. Constr. Facil. 34, 0001385. doi:10.1061/(ASCE)CF.1943-5509.0001385

CrossRef Full Text | Google Scholar

Ye, F., He, C., Wang, S. M., and Zhang, J. L. (2012). Landscape design of mountain highway tunnel portals in China. Tunn. Undergr. Space Technol. 29, 52–68. doi:10.1016/j.tust.2012.01.001

CrossRef Full Text | Google Scholar

Yuan, B. X., Sun, M., Xiong, L., Luo, Q. Z., Pradhan, S. P., and Li, H. Z. (2020). Investigation of 3D deformation of transparent soil around a laterally loaded pile based on a hydraulic gradient model test. J. Build. Eng. 28 (3), 101024. doi:10.1016/j.jobe.2019.101024

CrossRef Full Text | Google Scholar

Zhang, C., Han, K., and Zhang, D. (2015). Face stability analysis of shallow circular tunnels in cohesive–frictional soils. Tunn. Undergr. Space Technol. 50, 345–357. doi:10.1016/j.tust.2015.08.007

CrossRef Full Text | Google Scholar

Zhao, L., Li, D., Li, L., Feng, Y., Cheng, X., and Luo, W. (2017). Three-dimensional stability analysis of a longitudinally inclined shallow tunnel face. Comput. Geotechnics 87, 32–48. doi:10.1016/j.compgeo.2017.01.015

CrossRef Full Text | Google Scholar

Zhou, J., Wei, J., Yang, T., Zhang, P., Liu, F., and Chen, J. (2021). Seepage channel development in the crown pillar: Insights from induced microseismicity. Int. J. Rock Mech. Min. Sci. 145, 104851. doi:10.1016/j.ijrmms.2021.104851

CrossRef Full Text | Google Scholar