Synthesis of field and satellite data to elucidate recent mass balance of five ice rises in Dronning Maud Land, Antarctica

We investigated mass balance changes over five ice rises in the last few decades near Fimbul and Nivl ice shelves in central Dronning Maud Land. We use the Input-Output Method constrained using field-based geophysical measurements conducted during the austral summers of 2012–14 over three ice rises near the Fimbul Ice Shelf. Further, we use satellite altimetry data (ICESat, ICESat-2, and CryoSat-2) to estimate geodetic mass balance over all five ice rises in recent decades. Both field- and satellite-based estimates show that until 2010, three out of five ice rises were thickening (0.4–0.2 m_ieq a⁻¹) while two were close to balance. However, over the last decade, the ice rises thickening previously started to thin (−0.2–−0.6 m_ieq a⁻¹) while the other two remained close to balance. Much of this variability is likely associated with regional surface mass balance trends, with each ice rise exhibiting its characteristics depending on its local glaciological settings.

1 Introduction

About three-quarters of the Antarctic Ice Sheet drains into ice shelves, which regulate the position of the grounding zone and the ice flux through it, eventually affecting the Antarctic contributions to the sea-level rise (Dupont and Alley, 2005). In addition to the embayment confining an ice shelf, local grounded areas within it can significantly influence its buttressing potential on the grounded ice sheet (Fürst et al., 2016). Due to compressive stresses, ice upstream of ice rises and rumples provide greater buttressing, resulting in thicker ice. While, downstream, due to tensile stresses, the ice can be thinner and subject to crevasses. The large shearing around ice rises can lead to fractures within the ice shelves, promoting future calving (Borstad et al., 2013). Conversely, the local ice flow of ice rises is influenced by the ice shelf flow around them.

The ice flow of an ice rise can range from outwardly radiating streamlines originating from the summit of a dome-shaped ice rise to near-parallel streamlines over an ice rise with a distinct ridge (e.g., Matsuoka et al., 2015). The mass input to an ice rise is limited to the net surface mass balance (SMB) over the ice rise, typically showing an upwind-downwind pattern with larger SMB on the upwind side (King, 2004; Drews et al., 2013; Drews et al., 2015; Goel et al., 2017; Kausch et al., 2020). This pattern results from orographic precipitation over these features, with the final SMB pattern subject to many factors, including the size and morphology of the ice rise relative to the prevailing winds and the distance from the source of precipitation (Lenaerts et al., 2014). The ice-flow field and SMB over an ice rise are interconnected with the morphology of the ice rise and the surrounding ice shelf flow regime. As a result, the mass balance of ice rises could indicate past and ongoing changes in local and regional climate and ice-dynamical processes (Bindschadler et al., 1989; Goel et al., 2017).

The 33 ice rises scattered along the coast of Dronning Maud Land (DML, Figure 1) play an important role in the region’s dynamics and stability. Out of these ice rises, only four show distinct surface features (double, near-parallel lineations) indicative of long-term stability, thus implying ongoing ice-dynamical changes over most ice rises in this region (Goel et al., 2020). Over the recent decades, the central part of the DML coast has shown an increase in mass balance, from net mass loss (−27.5 ± 4.5 Gt a⁻¹) in 2009 to mass gains (63.4 ± 9.65 Gt a⁻¹) in 2017 (Schröder et al., 2019). These mass gains are most likely attributable to several extreme snowfall anomalies observed during this period (Boening et al., 2012; Lenaerts et al., 2013; Rignot et al., 2019). Furthermore, over the last two decades (2002–2020), mass balance changes in DML were found to be strongly correlated with SMB (Diener et al., 2021). Studies focusing exclusively on the ice shelves for the 2007–2017 period also show an overall thickening (3.9 m over these 11 years) over the ice shelves in DML, with significant local variability (Hogg et al., 2020; Smith et al., 2020). Even though they are exposed to similar regional oceanic and atmospheric forcings, complex interactions between ice shelves, ice rises, and the ice sheet with varied response periods can lead to different local mass balance over ice rises. Ice-flow modelling has been used over several ice rises to constrain their ice flow history and mass balance over centennial and millennial timescales (Kingslake et al., 2014; Drews et al., 2015; Goel et al., 2018), but determining short-term mass balance over ice rises has remained a challenge.

FIGURE 1

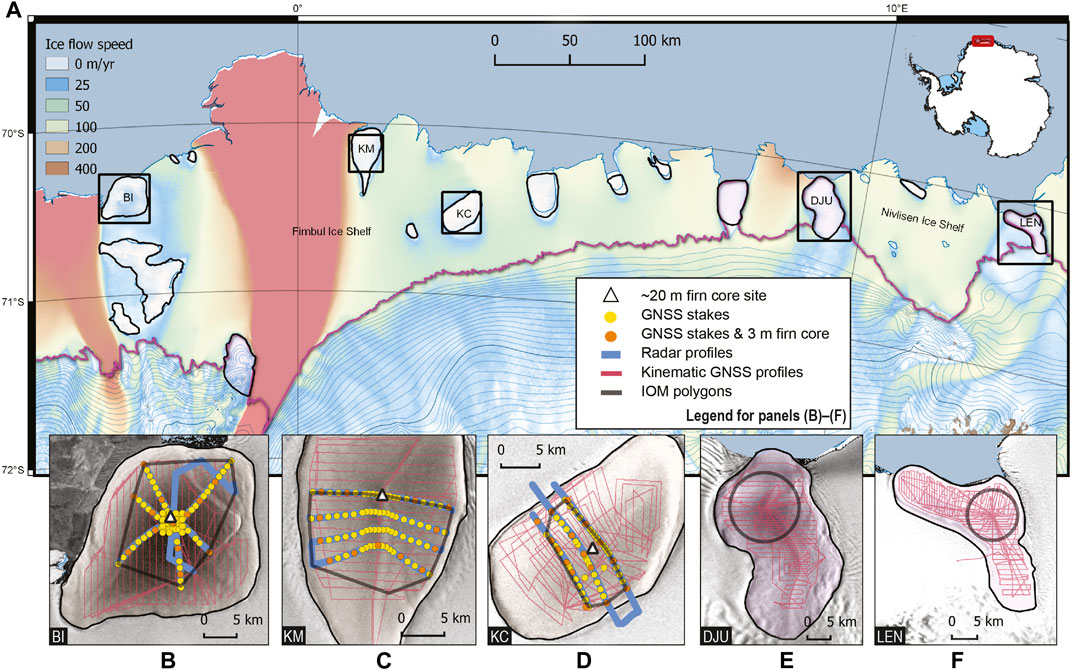
FIGURE 1. Ice rises in central Dronning Maud Land. Panel (A) shows ice rises outlined in black (Matsuoka et al., 2015) over a flow speed map (Rignot et al., 2011). The grounding zone of the ice sheet is illustrated in thick pink (Bindschadler et al., 2011). Inset shows the coverage of this map. Black boxes show the extent of sub-panels (B–F) of ice rises investigated in this study. Acronyms stand for BI: Blåskimen Island, KM: Kupol Moskovskij, KC: Kupol Ciolkovskogo, DJU: Djupranen, and LEN: Leningradkollen. Panels (B–F) show close-up views of ice rises and the various field data collected and discussed in this study. The background of these panels is Radarsat-1 satellite imagery (Jezek et al., 2002). Maps are projected to the Antarctic Polar Stereographic view (EPSG: 3031) using Quantarctica (Matsuoka et al., 2021).

In many ways, ice rises are miniature versions of ice sheets. Thus, methods for estimating ice sheet mass balance might also be applicable over ice rises. Three main methods are used to quantify the recent mass balance of ice sheets: the Input-Output Method (IOM), geodetic method (satellite altimetry), and satellite gravimetry. Ice rises are too small to be resolved by satellite gravimetry, so we focus on the first two in this study. The IOM is another version of the “mass conservation” or “mass continuity” method commonly used for alpine glaciers (e.g., Hubbard et al., 2000; Berthier and Vincent, 2012; Vincent et al., 2016; Bisset et al., 2020; van Tricht et al., 2021; Miles et al., 2021). Over ice sheets, IOM comprises dividing the ice body into smaller sections and calculating the total of all incoming and outgoing mass fluxes (e.g., Rignot and Kanagaratnam, 2006; Conway and Rasmussen, 2009; Zwally and Giovinetto, 2011; Andersen et al., 2015; Shepherd et al., 2018). This approach is data intensive and requires extensive field-based measurements. Alternatively, in the geodetic method, changes in ice volume are estimated through repeat elevation measurements from satellite altimeters (Moholdt et al., 2014; Zwally et al., 2015; Morris et al., 2020; Smith et al., 2020). These volume changes are then converted to mass changes making informed approximations for material density. Both these methods are applicable for estimating ice rise mass balance.

This study examines the mass balance changes over five ice rises within 600 km distance along the coast in the central DML region over the last few decades. These ice rises are in similar coastal settings but have varying glaciological characteristics. Our main research questions are: Are these ice rises thickening or thinning? Which driving forces determine the spatial and temporal variability of mass balance changes over these ice rises? To answer these questions, we determine the glaciological settings of these ice rises and estimate their present mass balance using both field-based IOM and altimetry-based geodetic method. We present a synthesis of the findings and discuss the drivers of mass balance changes over ice rises and the emerging picture of the dynamics of this coastal region.

2 Study area

We studied three ice rises in the Fimbul Ice Shelf and two ice rises in the adjacent Nivl Ice Shelf, both in DML (Figure 1). The three ice rises in Fimbul are all isles and were selected because of their distinct glaciological settings within the ice shelf. Blåskimen Island (BI) is located west of the fast-flowing outlet of the Jutulstraumen Glacier, while Kupol Ciolkovskogo (KC) and Kupol Moskovskij (KM) are located to the east. BI and KM terminate into calving fronts to the open ocean and have shear margins of fast-flowing glacier outlets to one of their sides. For example, the ice shelf on the western side of KM is four times faster than on the eastern side. On the contrary, KC is surrounded by a slowly flowing part of the ice shelf. In terms of size and shape, BI (area: 650 km²) is the largest of the three and shaped like a dome with a ridge-like feature extending from its summit towards the southwest. KM (508 km²) and KC (450 km²) are smaller ice rises with prominent ridges. The ridge on KM extends from a narrow tail in the south to a rounded front in the north, while KC is more uniformly elongated with its ridge in a northeast-southwest direction.

Towards the east, we investigated two promontories, Djupranen (DJU) and Leningradkollen (LEN), which form the lateral ends of the Nivl Ice Shelf. DJU (731 km²) has a ridge extending from the ice sheet to a saddle before rising into a seaward ice dome. LEN (375 km²) has a similar but smaller ridge extending from the ice sheet and a saddle, but the seaward dome has another ridge extending west, making the topography more complicated than the other ice rises.

3 Data and methods

We used field-based measurements to estimate the present mass balance of BI, KM, and KC. Moreover, we analyzed satellite altimetry data for all five ice rises to investigate temporal changes in mass balance.

3.1 Field measurements

Field measurements on BI, KM, and KC were made during the austral summers of 2012–2013 and 2013–2014. The measurements included kinematic and static GNSS surveys, shallow- and deep-sounding radar profiling, as well as firn coring and borehole temperature measurements. The locations of these measurements are shown in Figures 1B–D. The data collected over BI were reported by Goel et al. (2017). The measurements and data analysis on KM and KC were consistent with Goel et al. (2017) and are briefly summarized below.

To map their surface topography, kinematic GNSS surveys were carried out in grid pattern with profiles covering 770 km (BI), 620 km (KM), and 630 km (KC) of total distance. We used six Trimble dual-phase receivers; four were installed as rovers on snowmobiles moving at about ∼15 km h⁻¹, while the other two were installed as base stations near each of the ice-rise summits. This resulted in an elevation measurement at every ∼4 m along a profile, with typical spacing of 1–2 km between two adjacent profiles in a grid. For the field-based mass balance estimation, the resulting heights above the WGS84 ellipsoid were converted to heights above local sea level by subtracting geoid heights (BI = 15 m, KM = 16 m, KC = 16 m) from the GOCE gravity product (https://earth.esa.int/web/guest/data-access/browse-data-products/-/article/goce-gravity-fields-5777). Kinematic GNSS measurements on DJU and LEN were made similarly over 910 km (DJU) and 909 km (LEN) as reported by Pratap et al. (2021). These kinematic data were then bilinearly interpolated to create digital elevation models (DEMs) of the ice rises at 200 m resolution.

Aluminum stakes (3-m-long, hollow type) were installed at numerous locations over BI (90 stakes), KM (80 stakes), and KC (56 stakes) to determine local ice flow and SMB. These locations were chosen along the steepest descent paths after the kinematic GNSS data were preliminarily analyzed onsite. The position of each stake was determined by static GNSS measurement over 20-min-long periods along with the tape measurements of the stake height above the surface. These measurements were repeated the following year to obtain the lateral displacement of the stakes and the height of snow deposited around the stake over this period.

Three firn cores of ∼20 m in length were obtained from each of the ice divides of the three Fimbul ice rises to determine decadal SMB. The cores from BI, KM, and KC were dated back to the years 1996, 1995, and 1958, respectively, by counting annual cycles of oxygen isotopes and identifying volcanic horizons using non-sea-salt sulphate data (Vega et al., 2016). In addition, several 3-m-long shallow cores were obtained across these ice rises (13 over BI, 14 over KM, and 16 over KC) to determine the spatial variability of near-surface density. Measurements of their length, diameter, and weight were carried out on-site, after which the cores were discarded.

Radar surveys were made using two different ice-penetrating radar setups: An in-house radar system with resistively loaded dipole antennas at 2 MHz (deep-sounding) and a GSSI/SIR3000 radar with a 400 MHz (shallow-sounding) antenna. These surveys were aimed to determine bed elevations and englacial ice stratigraphy. These radar profiles were made along the steepest-descent paths going across the ice divides determined using the kinematic GNSS data. Both radar surveys were collected with snowmobiles moving at 8–10 km h⁻¹ and towing the antennas. The radar positions were determined using kinematic GNSS attached to the snowmobiles. The measurements resulted in an average radar-trace spacing of ∼5 m for the deep-sounding radar and ∼0.25 m for the shallow-sounding radar. Post-processing included a dewow filter, an Ormsby band-pass filter, and depth-variable gain functions (Goel et al., 2017). To calculate ice thickness, we assumed a radio-wave propagation speed of 169 m μs⁻¹ and added a firn correction term of 4–7 m to account for faster propagation in the firn. The correction was estimated using a steady-state firn density model (Herron and Langway, 2010) constrained using density data from firn cores and, the relation for estimating propagation speed by Kovacs et al. (1995).

We have two sources of SMB estimates: stake-height changes and shallow radar reflector depths constrained by firn core dating and densities. SMB derived from stake-height data has fewer uncertainties but is limited to stake locations and represents only one specific year. SMB derived from radar reflector depths dated by firn cores is continuous along survey profiles and represents several decades but is prone to larger uncertainties (See Discussion).

3.2 In-situ mass balance from input-output method

We derived the mass balance for the three Fimbul ice rises using the field-based Input-Output Method (IOM). For dividing the ice rises into ice-thickness columns, we used two different setups: 1) polygon and 2) grid setup. In the polygon setup, the ice rise is divided into polygonal columns, with the position of the polygon’s vertex decided based on the availability of stake-derived flow speed data (Figures 2G–I). In the grid setup, the ice rise is divided into a uniform grid of squares of 200-m-long sides in polar stereographic projection (EPSG:3031). For each polygon or grid cell, the total mass flux coming in or out is calculated. At the surface, the net SMB inside the polygon is the only input. We assume that no mass exchange takes place at the bed, and that it is frozen. This is based on radar and ice-flow modeling evidence for BI (Goel et al., 2018), and the same diagnosis framework applied for KM and KC suggests frozen beds (BI = −8.4°C; KM = −10.5°C; KC = −11.5°C). For the polygon setup with the ice-flow velocity data at each corner, we derived the mass ($m$) going in or out of the vertical face as:

$\mathit{m}=\mathit{\gamma }{\mathit{v}}_{\mathit{s}}\mathit{A}\mathit{\rho }(1)$

Where $\rho$ is the depth-averaged ice density, $A$ is the area of the vertical face, $v_s$ the surface flow velocity, and $\gamma$ is the ratio of the depth-averaged flow speed to the surface flow speed. For the grid setup, we used bilinear interpolation to make grids from ice flow measured at stakes, ice thickness measured along radar profiles, and SMB ($M_{SMB}$) derived from stake heights or radar profiles. For a local rectangular coordinate x and y, the mass balance ($M_{MB}$) for each grid cell is then estimated from the continuity equation as:

${\mathit{M}}_{\mathit{M}\mathit{B}}=\frac{\partial \mathit{h}}{\partial \mathit{t}}={\mathit{M}}_{\mathit{S}\mathit{M}\mathit{B}}+\mathit{\gamma }\left(\frac{\partial \mathit{u}}{\partial \mathit{x}}+\frac{\partial \mathit{v}}{\partial \mathit{y}}\right)\mathit{h}+\mathit{\gamma }\left(\mathit{u}\frac{\partial \mathit{h}}{\partial \mathit{x}}+\mathit{v}\frac{\partial \mathit{h}}{\partial \mathit{y}}\right)(2)$

FIGURE 2

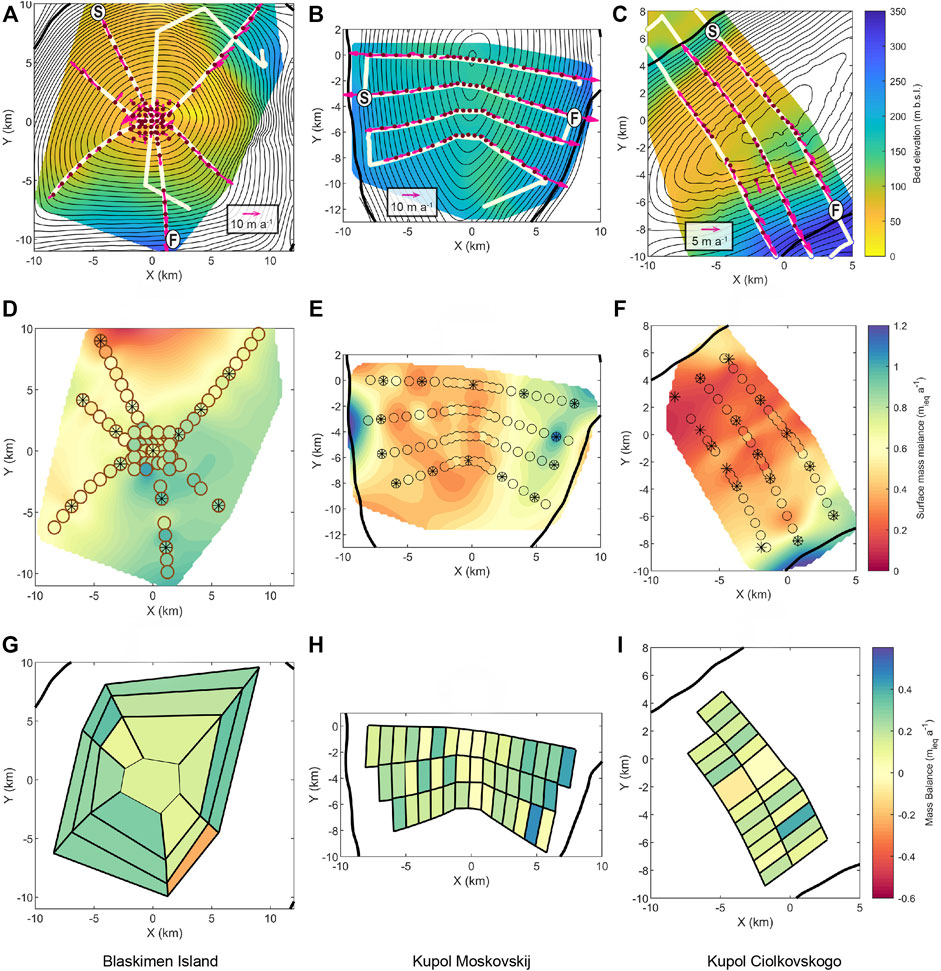
FIGURE 2. Glaciological settings and mass balance over ice rises in the Fimbul region. Panels in each column show the data and results from Blåskimen Island (BI, left), Kupol Moskovskij (KM, center), and Kupol Ciolkovskogo (KC, right). Data from Blåskimen Island (A, D, and G) have been published in Goel et al., 2017. Panels in the first row (A–C) show the surface elevation contours (10 m) derived by GNSS surveys (Figures 1B–D) together with bed topography derived from radar surveys along the white curves. Radargrams connecting the starting (S) and finishing (F) places are shown in Figure 3. Blue dots show the location of installed stakes, while pink arrows show the ice-flow vectors measured with these stakes. Panels in the second row (D–F) show SMB derived at stake positions and interpolated map using these data. Circles show the stake position and estimated SMB. Circles with ‘*’ inside show the stakes where we have surface density measurements as well. Note that the same colorbar is used for all three panels, despite the large variations of ice-rise mean SMB. Panels in the third row (G–I) show the mass balance estimated using polygon setup with a γ value of 0.8 (Eqs 1, 2). For these estimates, we used stake-derived SMB between 2013 and 2014 for BI, 2012–2013 for KM, and 2012–2013 for KC.

Here $u$ and $v$ are velocity components in the $x$ and $y$ directions, h is the variable for ice thickness, and $\gamma$ is assumed isotropic in both directions. In the end, mass-balance values derived for the grid setup are averaged within each polygon used for the polygon setup. This lets us compare the two setups and removes the finer noise inherent to the small grid size of the grid setup.

Considering the characteristic of ice flow between the ice divide to ice rise margins, it is safe to assume that $\gamma$ values lie between 0.7 and 0.9 (see Section 4.2.1 in Goel et al., 2017). Thus, for the two IOM setups, we obtain mass balance estimates for this range of $\gamma$, leading to an ensemble. Each mass balance estimate represents the period of input SMB and assumes no change in ice-flow speeds over this period. The latter assumption might not be true for an ice rise that responds to ongoing forcings. However, accounting for potential velocity changes would either require periodic field measurements of these parameters over the given period or realistic ice flow model simulations, both of which are beyond the scope of this study. In this paper, we use meter ice equivalent per year (m_ieq a⁻¹) as the unit for mass balance.

3.3 Geodetic mass balance from GNSS and satellite altimetry

We used NASA’s ICESat and ICESat-2 laser altimeters and ESA’s CryoSat-2 radar altimeter to derive geodetic mass balance over the ice rises for 3–10 year periods.

The ICESat (Ice, Cloud, and land Elevation Satellite) and ICESat-2 satellites are space-based laser altimeters with temporal coverage between 2003 and 2010, and 2018 to the present, respectively (Schutz et al., 2005; Smith et al., 2020). ICESat’s laser had a ∼65 m footprint on the surface with a measurement every 172 m along the track. ICESat-2 has a finer footprint of ∼14.5 m and a much higher along-track sampling with a measurement every 0.7 m. In addition, ICESat-2 has three pairs of beams, resulting in a much denser spatial coverage and allowing for cross-track slope estimation within each beam pair. Both the satellites have repeat orbit periods of ∼91 days, offering 2–4 repeat passes over a year. Since the ground tracks of the two satellites are different, we compare ICESat/ICESat–2 measurements with our GNSS-based DEMs to obtain elevation changes for periods before and after our field survey. To calculate the elevation change, we subtract the ICESat point measurement from the respective DEM elevation (bilinearly interpolated with reference to the WGS84 ellipsoid) and divide it by the time difference between the two measurements. To compare with IOM results and avoid steeply sloping regions over the ice rises, we limit this analysis to the region within the outermost polygons for KM, KC, and BI (black polygons in Figures 1B–D) from the IOM method. For DJU and LEN, we defined circular regions of radius 7.5 km and 5 km, centered around their summits for this analysis (Figures 1E,F).

The CryoSat-2 is a radar altimeter (Ku band) aimed toward cryospheric applications. Unlike a laser altimeter, a radar altimeter has a footprint several kilometers wide. The returning backscatter starts from the point on the surface closest to the satellite (point of closest approach; POCA), increasing as more of the surface is illuminated before trailing off. Also, unlike a laser altimeter, the radar pulse can penetrate several meters into snow and firn, potentially resulting in a penetration bias between the glacier surface and retrieved elevation. We applied a leading-edge maximum slope retracker and swath processor (Gray et al., 2013, 2015) to the interferometric mode data allowing retrieval of a geolocated elevation estimate at the POCA and other geolocated elevations along the whole swath across the track. The swath method can provide up to two orders of magnitude more elevation estimates than the conventional POCA (Gourmelen et al., 2018). Over the ice rises, we used Baseline-D data with coverage from 2011 to 2019, with approximately one pass each month. Spatially, we estimate elevation changes over the area of these ice rises as used for ICESat/ICESat-2 and IOM.

With its dense spatial and temporal coverage, the CryoSat-2 dataset allows us to compute elevation changes over our area and period of interest without any additional data. This circumvents the potential issue of a CryoSat-2 penetration bias with respect to the surface elevations from GNSS and ICESat/ICESat-2. To estimate elevation changes from CryoSat-2 we first filter all the POCA and swath points for quality and then compute the elevation change rate on a square-grid basis generated using a least-squares plane fit (Morris et al., 2020). This results in a map of elevation change rates at the prescribed 1 km resolution. To resolve temporal changes, we split the 9-year dataset into three 3-year-long periods and calculated separate elevation change rates for each period.

Elevation measurements from ICESat and ICESat-2 are accurate to within a few decimeters over typical surface slopes of ice rises (Moholdt et al., 2010; Brunt et al., 2019). The DEMs generated using GNSS data have intrinsic elevation accuracies of: BI = 0.02 ± 0.32 m, KM = −0.02 ± 0.11 m, KC = 0.00 ± 0.30 m, DJU = −0.03 ± 0.46 m and LEN = −0.03 ± 0.55 m, related to bilinear interpolation between GNSS tracks (Goel et al., 2017). Additional cm-scale biases may arise from antenna height measurements and geophysical impacts on the GNSS data. However, since we compare elevation measurements spaced over 5–10 years, these biases have a small impact if the elevation change rates are significant. Comparatively, in the case of CryoSat-2 measurements, the biases associated with the instrument can be higher due to the penetration of the signal into the surface and coarser spatial resolution. We expect the bias to be stable within ∼0.5 m based on GNSS–CryoSat-2 comparisons on the Austafonna ice cap (Morris et al., 2021). However, over ice rises, since the snowpack is generally cold and stable, it is reasonable to assume that radar backscattering properties and potential penetration biases are constant year-to-year and thus have only a small impact on the derived elevation change rates. Moreover, our approach of using a least-squares plane-fit algorithm to multiyear CryoSat-2 POCA and swath points was found to provide robust estimates of elevation change rates in regions with significant seasonal variability in near-surface properties (Morris et al., 2021). Neither ICESat–GNSS comparison, nor the intra–CryoSat-2 comparison approach is superior to the other, but together they give us a good picture of the elevation changes over the ice rises.

For both methods, the measured elevation changes can result from pure ice-dynamical changes within the ice rises or changes in surface processes (e.g., precipitation, densification, erosion etc.). In the latter case, the elevation change should account for the near-surface density to estimate the geodetic mass balance. Evaluating the firn-core data over the ice rises, we find the average surface density up to 3 m of depth varies within 450–500 kg m³, which is approximately half the density of ice. As both surface-based and deeper ice-dynamical changes are plausible, it results in a ∼50% uncertainty range for the geodetic mass balance estimates. In most cases, this uncertainty is far greater than the uncertainty from other sources of uncertainty in our geodetic mass balance estimates. We thus ignore other sources of uncertainty except if estimated elevation changes are close to zero, in which case, we introduce a minimum error bound of 0.05 m_ieq a⁻¹ considering the different biases discussed above.

4 Results

4.1 Topography and ice-flow

The surface topography of the three ice rises in the Fimbul Ice Shelf is presented in Figures 2A–C, and also the transect along with three radar profiles (Figures 3G–I). Among the ice rises in the Fimbul area, BI is the highest, elevated by ∼360 m above the surrounding ice shelf (Figure 2A). KM and KC, on the other hand, are similarly elevated by ∼230 m above the surrounding ice shelf (Figures 2B,C). Subtracting the radar-measured ice thickness from the GNSS measured surface elevation reveals that all ice rises are grounded on a bed much lower than the current sea level. Overall, BI is grounded ∼100 m below the sea level, similar to KC (∼80 m.b.s.l), while KM sits on the ground much below (∼200 m b.s.l) (Figures 2A–C), with rather smooth beds underneath the summit regions. Some areas towards the edge of the ice rises show steep slopes, e.g., on KC in the region south of the summit, the bed slopes steeply falling by ∼220 m over a distance of ∼4 km. This feature also corresponds to the sharp change in the surface elevation at the same location and faster ice flow over the downstream steeper surface. BI also has a similar slope change towards the northeast corner (Figure 2A), and its surface impression is visible in the satellite imagery (Figure 1B).

FIGURE 3

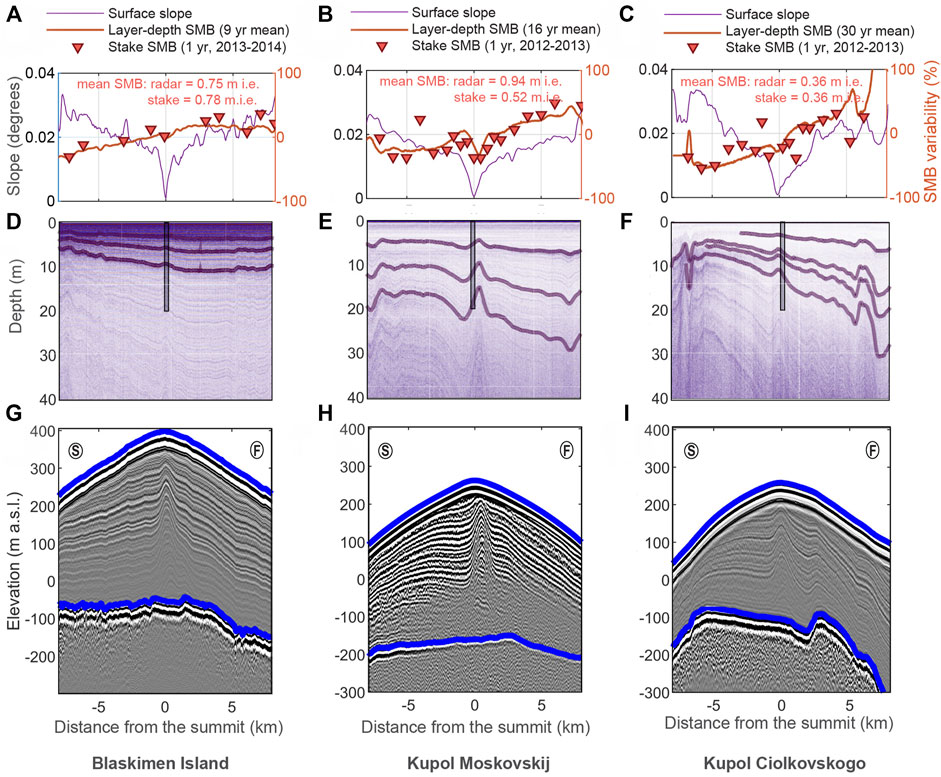
FIGURE 3. Surface mass balance and shallow and deep sounding radargrams over ice rises in the Fimbul region. Subpanels in each column show the data and results from Blåskimen Island, Kupol Moskovskij, and Kupol Ciolkovskogo, respectively. Data from Blåskimen Island (A, D, and G) have been published earlier (Goel et al., 2017). Panels in the first row (A–C) show surface slope profiles across the ice rises, as well as spatial patterns of radar-measured and stake-measured SMB normalized by respective means. Panels in the second row (D–F) show radargrams obtained from shallow-sounding radar with the tracked reflectors and position of firn-core used to date radar reflectors. Panels in the third row (G–I) show radargrams obtained using deep-sounding radar showing the surface and bed topography as well as the englacial structures.

Stake-measured surface flow speed patterns over the three ice rises are, as expected, governed by the surface topography, with the measured flow vectors oriented along the local descent path on the surface (Figures 2A–C). Typically, the ice in the vicinity of the summit and ridge flows very slowly (<2 m a⁻¹). This flow increases moving away from the summit/ridge with a maximum speed of 7–15 m a⁻¹ towards the ice rise margin. All three ice rises show a slight asymmetry with higher surface flow speeds on the upwind slope. This imbalance is the strongest on KC (15 m a⁻¹ on the upwind side vs 7 m a⁻¹ on the downwind side at ∼7 km from the summit) and the weakest (12–10 m a⁻¹) on KM.

4.2 Surface density and surface mass balance

The 3-m-long cores obtained at 14 sites over BI show that the surface density in the top 3 m varies by ±2.5% among these sites, with a mean value of 453 kg m⁻³. Over KM, measured surface density through firn cores varies by ∼±7% over 14 sites, with a mean value of 488 kg m⁻³. For KC, measured surface density through firn cores varies by ±2.5% over 18 sites, with a mean value of 468 kg m⁻³. Although these observed spatial variabilities are close to the density uncertainty estimated at BI (about ±3%, Goel et al., 2017), all ice rises show the highest density near the margin of the ice rises and the lowest density near the summit.

These surface density measurements were used together with stake heights to derive single-year SMB in 2012–2013 (KM and KC) and 2013–2014 (BI) (Figures 2D–F and Figures 3A–C). The resulting estimates show an average SMB of 0.78 m_ieq a⁻¹ for BI for the 2013–2014 period, 0.52 m_ieq a⁻¹ for KM (2012–2013), and 0.36 m_ieq a⁻¹ for KC (2012–2013). All three ice rises show higher SMB on the upwind side than the downwind side. This contrast is the strongest on KC and weakest on BI, as seen along profiles across the divide in Figures 3A–C. Denser stake measurements near the summit can capture an anomalous low in SMB near the ice divide for KM and KC. These features are associated with a flatter surface near the divide. Although the surface is similarly flat near the dome of BI, anomalously low SMB is not observed there despite the similarly high density of the stakes.

Multi-year-averaged SMB is derived from the shallow radar reflectors dated using the firn cores near the summits (Vega et al., 2016). BI’s deepest continuous dated radar reflector detected with shallow-sounding radar shows a spatially averaged SMB of 0.81 m_ieq a⁻¹ for the 2005–2014 period (Figure 3D). For KM, even though the tracked reflector is deeper, it goes back to only ∼16 years (1998–2014), with an average SMB of 0.92 m_ieq a⁻¹ (Figure 3E). For KC, the deepest reflector is dated to 30 years before the survey (1984–2013) due to its lower SMB of 0.36 m_ieq a⁻¹ (Figure 3F). Spatial patterns of the stake-measured single-year SMB and radar-measured multiyear SMB match very well (Figures 3A–C).

Using the uncertainty estimate procedure developed for BI based on the error propagation scheme (Goel et al., 2017), we estimate a ±12% uncertainty in the SMB derived using dated radar reflectors. This estimate includes uncertainty in the 1) reflector depths (±10 cm), 2) age of the reflectors (±1 year), 3) surface density (±2.5–7%), and the density-depth model used to fit the observations (±3%). For SMB derived using the stake method, the overall uncertainty comes to be ±6%, accounting for errors in measuring stake height and surface density. We exclude the possibility of the stakes sinking under their weight due to high observed surface densities.

4.3 Mass balance

IOM mass balance estimates are presented in Figures 2G–I, whereas satellite data coverage for geodetic mass balance estimates are presented in Figure 4 and corresponding results are presented in Supplementary Figures S1–S5. These estimates are compared and summarized Figures 5, 6.

FIGURE 4

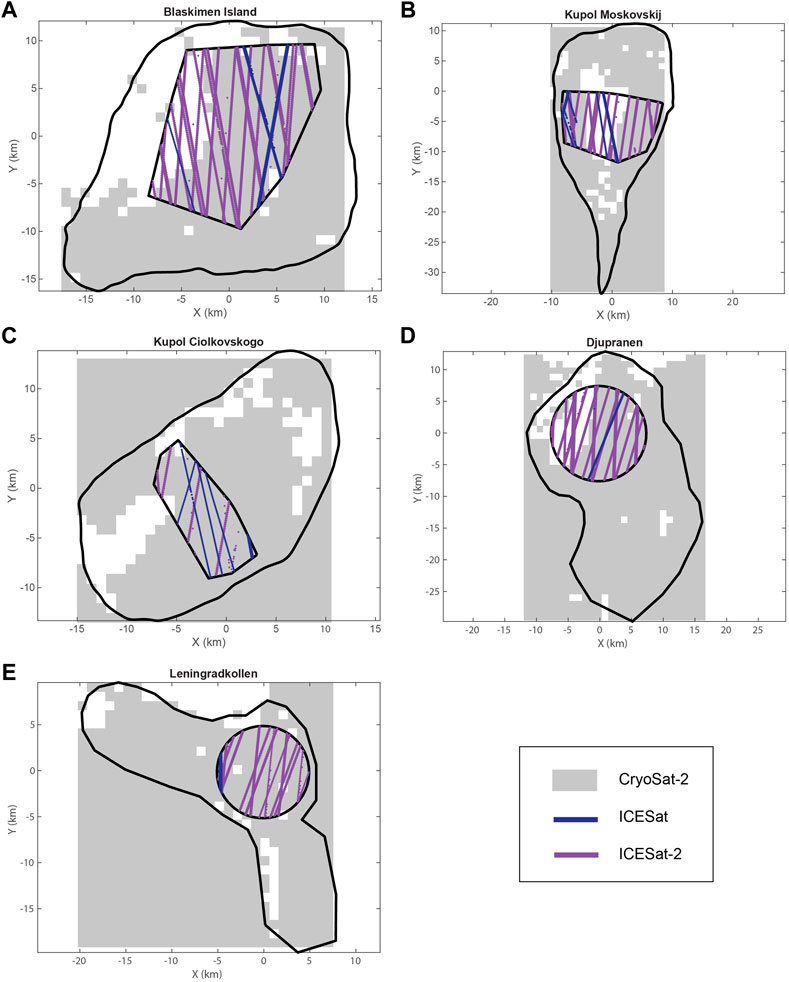
FIGURE 4. Altimetry data coverage over ice rises. Blåskimen Island (A), Kupol Moskovskij (B), Kupol Ciolkovskogo (C), Djupranen (D) and Leningradkollen (E). Coverage of ICESat (blue), ICESat-2 (Purple), and CryoSat-2 grid after removing noisy and low confidence data. In this study, we only consider the data inside each of the polygons (and circles) used for mass balance estimation. These altimetry data are summarized in Supplementary Figures S1–S5.

FIGURE 5

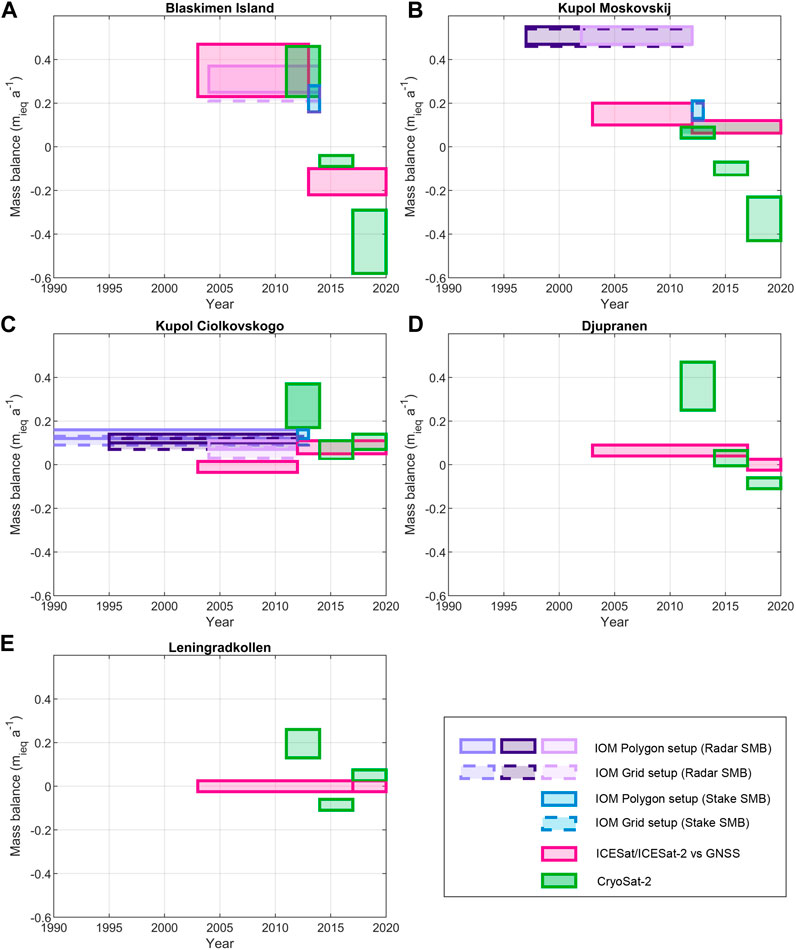
FIGURE 5. An overview of mass balance estimates over ice rises Blåskimen Island (A), Kupol Moskovskij (B), Kupol Ciolkovskogo (C), Djupranen (D) and Leningradkollen (E). Each box represents the time interval (width) and the uncertainty (height) of the estimates. The polygon and grid IOM setups use the same data but differ in methodology and are shown as continuous and dashed boxes, respectively. As discussed in the paper, we suspect that the IOM estimate using radar-derived SMB for KM is erroneous.

FIGURE 6

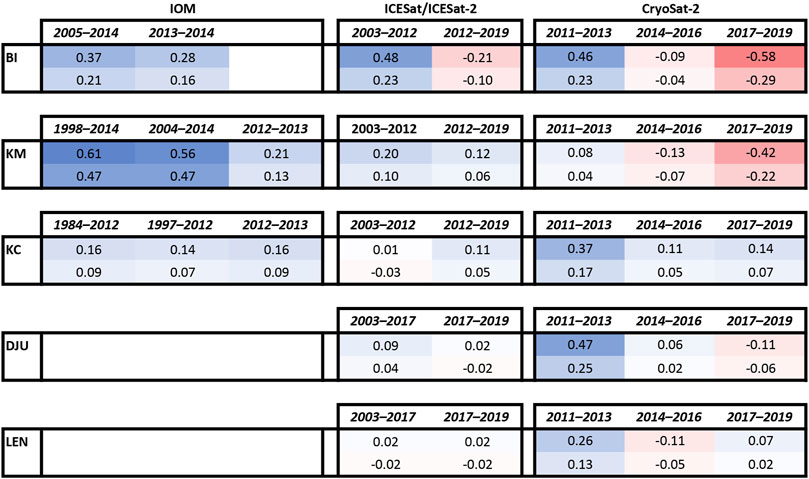
FIGURE 6. An overview diagram of mass balance estimates showing their maximum and minimum values for different time periods in units of m_ieq a⁻¹. The color used varies on a red-white-blue colormap varying from −0.6–0.6 m_ieq a⁻¹. For values near zero we introduce a minimum error bound of 0.05 m_ieq a⁻¹. All values are rounded to 2 decimal places.

4.3.1 Input-output method

Observational and modeling results cannot precisely constrain the γ value concerning depth-averaged ice velocity (Eqs 1, 2). As the beds of the ice rises are frozen, we assume a single $\gamma$ value can represent depth profiles of the horizontal ice flow speeds. Under this assumption, the estimated mass balance varies with the $\gamma$ value linearly, but the spatial pattern stays unchanged. We use $\gamma$ values ranging from 0.7 to 0.9. This $\gamma$ range causes 15%–33% uncertainty in these estimates. Other sources of uncertainty, such as measurement errors, are much less than this range, so we do not consider them. The polygon and grid IOM setups use the same input data and adopt different interpolation methods to do the same analysis. Mass balance derived using the grid setup and averaged over the polygons is highly consistent with the polygon setup’s mass balance. Overall, the results from the two setups differed by 0.01–0.04 m_ieq a⁻¹ for the three ice rises. In Figures 2G–I, we present results for polygon-setup for the $\gamma$ of 0.8 using stake-derived SMB as input.

Spatially, BI has six slopes with three polygons each, around the summit polygon. All but one polygon shows thickening. Even with the upwind-downwind SMB contrast, the mass fluxes are balanced such that we do not see any distinct patterns in the net mass balance. Over KM, there are three rows of polygons going across the ice divide. The polygons of the northern and central rows show a slight upwind-downwind contrast with higher values on the upwind side. Near the ice divide, polygons along the ice divide are near balance for all three rows. This near-balance estimate could be a result of the anomalously low SMB observed near the divide as well as the divergent mass flow over both slopes. Over KC, the polygons are arranged in two rows going across the ice divide. Like KM, the polygons at the divide are close to balance. However, unlike KM, we do not see any contrast between the slopes. Surface flow speed across KC shows the most marked contrast (Flow speeds of stakes close to 150 m a.s.l. contour; upwind: 6, 7, 6, and 7 m a⁻¹; downwind stakes: 3, 3, 5, and 4 m a⁻¹) with faster flow speed on the upwind side with high SMB. The faster outflow likely balances the higher SMB on this side.

For BI, with input stake-derived SMB for 2013–2014, the mean mass balance ranged between 0.16 and 0.28 m a⁻¹ for $\gamma$ ranging from 0.7 to 0.9 for both polygon and grid setups (Figures 5A, 6). With input radar-derived SMB estimate for the 2005–2014 period, the mean mass balance ranged between 0.21 and 0.37 m_ieq a⁻¹. For KM, with input stake-derived SMB for 2012–2013, the mean mass balance ranged between 0.13 and 0.21 m_ieq a⁻¹ (Figure 5B). With the input radar-derived SMB estimate for the 1998–2014 period, the mean mass balance ranged between 0.47 and 0.61 m_ieq a⁻¹. For the shorter SMB period 2004–2014, the results stay very similar. For KC, input stake-derived SMB for 2012–2013, the mean mass balance ranged between 0.09 and 0.16 m_ieq a⁻¹ (Figure 5C). With the input SMB estimate for the 1984–2013 period, the mean mass balance ranged between 0.09 and 0.16 m_ieq a⁻¹. While for the shorter 1997–2013 period, mass balance ranges between 0.07 and 0.14 m_ieq a⁻¹.

4.3.2 Geodetic method

By comparing ICESat measurements in 2003 (see Figure 4 for track locations) to GNSS-based DEM elevations in 2012, we find significant thickening over BI. If this is caused by the thickening of pure ice (e.g., slowing ice flow), the ice-equivalent mass balance would be 0.48 m_ieq a⁻¹ (See Supplementary Figures S1–S5). If the elevation change is caused by the thickening of near-surface firn (e.g., increasing SMB), the measured elevation change can be converted to ice equivalent mass using firn density that we measured to 3 m. Thus, for pure SMB changes considering the measured firn density of 453 kg m⁻³, the mass balance of BI comes to 0.23 m_ieq a⁻¹. Hereafter, we consider the two values as upper and lower bounds of mass balance, stated as 0.48–0.23 m_ieq a⁻¹. Moreover, for values close to zero we add a minimum error bound of 0.05 m_ieq a⁻¹ around it. Despite thickening from 2003 to 2012 over BI, a comparison of the GNSS elevations in 2012 and ICESat-2 elevations in 2019 show that BI has thinned at a rate of −0.21–−0.10 m_ieq a⁻¹. Similarly, we find KM thickening by ∼0.20–0.10 m_ieq a⁻¹ for the 2003–2012 period and sustaining thickening at a slightly lower rate of 0.12–0.06 m_ieq a⁻¹ for the 2012–2019 period. We find KC to be near balance (0.01–−0.03 m_ieq a⁻¹) for the 2003–12 period and slightly thickening (0.11–0.05 m_ieq a⁻¹) between 2012 and 2019. Further east around Nivl Ice Shelf, for the period 2003–2017 between ICESat and GNSS measurements, we find DJU slightly thickening (0.09–0.04 m_ieq a⁻¹) and LEN in balance (0.02–−0.02 m_ieq a⁻¹). These results do not change much over the period 2017–2019, with both DJU and LEN near balance (0.02–−0.02 m_ieq a⁻¹).

Comparing CryoSat-2 elevations for three consecutive 3-year-long periods between 2011 and 2019, we find BI to switch from strongly thickening (0.46–0.23 m_ieq a⁻¹) for 2011–2013 to slightly thinning (−0.09–−0.04 m_ieq a⁻¹) for 2014–2016 and strongly thinning (−0.58–−0.29 m_ieq a⁻¹) for 2017–2019 (Figure 5). KM and DJU show a similar decreasing trend over these three periods. Mass balance estimated for KC and LEN over different periods cluster near balance show a less significant trend than those observed on the other ice rises.

5 Discussion

5.1 Glaciological settings

The three Fimbul ice rises are within about 100 km of each other. They share several glaciological characteristics, but they also differ in several aspects. The similarities in their settings could be attributed to more regional characteristics such as bed formations, regional atmospheric processes, and ice-shelf dynamics. While on the other hand, the differences highlight the more local characteristics.

Starting with the bed, all three Fimbul ice rises are grounded 100–200 m below the sea level, and the beds below the summit/divide area are smooth and flat compared to the bed under promontories at landward locations in this region (Goel et al., 2020). The bed elevation within 2 km from the divide of the three Fimbul ice rises varies only 6%–12%, thus providing little topographic control on their divide positions. This aspect of bed topography is also similar to the Nivl ice rises (see Figure 6 of Goel et al., 2020 for bed topography of the two Nivl ice rises). However, the bed is not smooth all over, with the surface of BI and KC showing steeply sloping local features away from the divide, whose origins are associated with rough bed topography. In terms of shape and size, these ice rises differ significantly. BI is mostly domed-shaped with a minor ridge, while KM and KC have more prominent ridges. These differences in shape are primarily controlled by the overall shape and dimensions of the elevated bed currently under the ice rises.

At Fimbul, wind during precipitation events is oriented in a primarily easterly to the northeasterly direction, while katabatic winds responsible for wind erosion and redistribution are aligned in a mostly southeasterly direction. These winds together result in the observed SMB distribution. Out of the similarly elevated ice rises KM and KC, KM has a higher mean SMB. This difference is a likely result of varying proximity of the ice rises to the moisture sources. Interestingly, the observed SMB contrast between upwind and downwind slopes of all three Fimbul ice rises is strongest on KC. Being closer to the ice sheet’s grounding zone, KC presumably experiences stronger katabatic winds, which might cause an increase in wind erosion and thus, a stronger contrast. Over to Nivl, both DJU and LEN are located at the calving front, but DJU has higher SMB and stronger SMB contrast than LEN (Pratap et al., 2021). This could be attributed to a weaker orographic effect on LEN, with its surface being the least elevated (174 m a.s.l) among all five ice rises.

5.2 Comparison of mass balance estimates

While stake-derived SMB provides a reliable estimate between two repeated measurements, radar-derived SMB can provide for longer periods at a higher spatial resolution. For BI and KC, the magnitude and spatial pattern of stake- and radar-derived SMB match well (Figures 3A–C). In the case of KM, while the spatial pattern of both stake- and radar-derived estimates match well, the radar-derived estimate is nearly twice in magnitude. As a result, the IOM mass balance estimated using these two estimates significantly differs in their magnitudes (Figure 5B). There are two probable causes of the observed mismatches. First, the stake-derived SMB could have been an anomalous year with a lower SMB than the typical SMB for the ice rise. This is possible as annual SMB estimated from the firn-core retrieved from the summit of KM shows significant yearly variations in SMB (Vega et al., 2016), and it is possible to have single-year SMB to be half of the long-term mean (Supplementary Figure S6). Second, firn-core dating could be in error. We argue that the latter is more likely because the IOM mass balance estimated using stake-derived SMB (0.13–0.21 m_ieq a⁻¹ for 2013–2014) is much closer to the geodetic mass balance estimated using altimetry data around these periods (0.12–0.06 m_ieq a⁻¹ for the 2012–2019 and 0.08–0.04 m_ieq a⁻¹ for 2011–2013). Moreover, preliminary ice-flow modeling results show that the model can replicate the observed surface flow speeds using the stake-derived SMB, while radar-derived SMB estimates require a strongly positive mass balance with a large rate of thickening (∼1 m_ieq a⁻¹) to reproduce observed surface flow speeds.

Broadly, the geodetic mass balance results agree with the IOM results. All three ice rises in the Fimbul region had been thickening, but recently the thickening switched to thinning for BI and KM (Figure 5). KC, on the other hand, continues to thicken but at a rate close to balance. The agreement between these mass balance estimates using two different methods increases our confidence in the geodetic mass balance estimates for DJU and LEN, for which we do not have IOM estimates. DJU shows a similar switch from thickening to thinning as observed for Fimbul ice rises, while LEN has been close to balance. The discrepancies observed between these estimates are likely a result of differences in the time of measurements of the satellites and the time span of the estimate, especially considering the temporal variability of SMB is in the region. Next, we discuss the possible limitations in our methodology which might explain the observed discrepancies.

5.3 Current limitations to estimate mass balance of ice rises

The mass balance estimates of this study are limited to the areas inside selected polygons that do not extend to the grounding zones of these ice rises. This sampling bias was unavoidable due to safety constraints during fieldwork; However, careful consideration was given to their shape and size so that they are still representative of the overall mass balance of the ice rises. The polygons are shaped to be near symmetric around the summit/ice divides of the ice rises to capture possibly variable mass balance caused by large SMB variations between the slopes. Also, they are large enough to sample not only the summit regions but also most of the flank sites. Dome (or ridge) specific ice dynamics appear within a few ice thicknesses of the summit/ice-divide to lateral directions (Martín et al., 2009). Ice thicknesses at the summit of BI, KM and KC range between 400 and 600 m and the extent of the polygons over an ice rise are typically extend ∼30 times of the ice thickness from the summit/ice divide. Moreover, on comparing elevation changes observed over the polygons to whole ice rise areas, we find very similar temporal trends between the periods, with the latter varying from polygon-wide estimates by standard deviations of 0.04 m_ieq a⁻¹(BI), 0.1 m_ieq a⁻¹(KM), 0.09 m_ieq a⁻¹ (KC), 0.04 m_ieq a⁻¹ (DJU) and 0.05 m_ieq a⁻¹ (LEN), for individual ice rises (See Supplementary Table S1).

As can be seen in Figure 4, in the geodetic method, the coverage of the different datasets over the ice rises can differ. ICESat being the oldest sensor in our comparison, has few passes over the polygons, with LEN having the least. ICESat-2 data does not have this limitation due to its significantly denser spatial coverage. CryoSat-2 data also has good coverage due to the utilization of both POCA and swath points, except BI where the distribution is skewed towards south-eastern side and thus might be biased due to the upwind-downwind SMB contrast.

For IOM, we assume no changes in flow speed over the period of the mass balance estimate. Changes in ice thickness can lead to changes in the surface slope, thus resulting in changes in driving stresses which ultimately contribute to changes in ice fluxes. Constraining these changes would require repeat measurements of ice flow speed, which are not available. However, repeat measurements are the strength of satellite altimetry. With the advent of high-resolution sensors like ICESat-2 and CryoSat-2, it is now possible to make repeat elevation measurements all over the continent. ICESat-2, specifically with its short repeat pass time, can be used in conjunction with firn densification and SMB models to segregate height changes based on the sources such as precipitation, firn compaction, or ice-dynamic-driven height changes (e.g., Smith et al., 2022 preprint, The Cryosphere Discussions). There is also a potential to measure volume scattering observed with CryoSat-2 data to estimate yearly snowpack thickness in areas exposed to surface melting and refreezing (Morris et al., 2021). These developments suggest satellite altimetry is likely the key to obtaining mass balance trends over ice rises across the margins of the Antarctic Ice Sheet. Field-based observations will still remain crucial for validation and process understanding.

5.4 Forces driving mass-balance changes

SMB in coastal DML is highly variable as episodic extreme precipitation events are responsible for more than 80%–90% of the variance of the annual precipitation, depositing ∼50% of the annual precipitation in just 20–30 days (Turner et al., 2019). On ice rises, these changes are further amplified due to the orographic effect. Reanalysis data from ERA5 shows these large annual variations in total precipitation, but with no significant trend for the last 3 decades over Fimbul and Nivl regions (Hersbach et al., 2020, Figure 7). Nonetheless, total precipitation shows a decreasing trend (Fimbul: 0.014 m_weq a⁻¹, r² = 0.41; Nivl: slope = 0.025 m_weq a⁻¹, r² = 0.61) from 2011 onward. This recent trend in total precipitation matches well with our mass balance estimates for BI, KM, and DJU, which show gradual switching from strongly thickening in the past to thinning over the last decade However, for KC and LEN, this trend is not as clear. This is because the mean SMB over these ice rises is smaller, and so are the resulting variations in mass balance, which are closer to the uncertainty in our estimates. Yet, it seems clear that SMB closely influences intra-annual changes in the mass balance of ice rises. Thus, factors influencing SMB variability, i.e., orographic effect, proximity to moisture source, prominence of precipitation events etc., are critical to understanding ice rise response to changing climate.

FIGURE 7

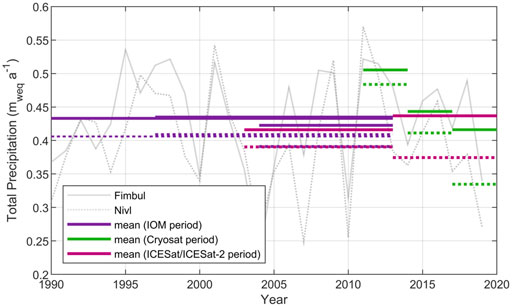
FIGURE 7. Annual precipitation reanalysis data from ERA5 averaged over Fimbul and Nivl regions (Hersbach et al., 2020). Solid and dotted gray curves show annual precipitation for Fimbul and Nivl regions, respectively. The data are averaged temporally for different time periods used for IOM, CryoSat-2 and ICESat/ICEsat-2 geodetic mass balance estimates, solid lines for Fimbul and dashed lines for Nivl.

The mass outflux through the margins of the ice rise is regulated by the thickness of the ice shelf at the margins and the ice-shelf flow speed. The thickness at the grounding zone controls the total mass flux exiting the ice rise and is related to the bed topography and the ice-shelf thickness. The relation of ice-flow speed to the buttressing experienced at the margins of an ice rise is complex as it depends on the shape and orientation of the ice rise relative to the ice shelf and other grounded bodies. Significant changes in either ice-shelf margin thickness or ice shelf flow speed could thus affect the mass balance of an ice rise. The Fimbul Ice Shelf has been thickening for the past 25 years (1992–2017) at a rate of 0.3 ± 0.15 m a⁻¹ and even more strongly by 0.6 ± 0.03 m a⁻¹ in 2010–2017 (Hogg et al., 2020; Zhang et al., 2020). This increase in annual thickness amounts to less than 0.1% of the ice-shelf thickness, insignificant in terms of its direct effect on ice fluxes at the ice-rice margins. However, changes in thickness could result in changes in driving stress and, thus, the ice flow speed. Flow speed change data over slowly moving ice shelves can be unreliable. But even in the fast-flowing Jutulstraumen glacier outlet over the 2012–2018 period, flow speed shows no trends with year-to-year fluctuations varying by less than 5% (0–40 m a⁻¹) of the annual speed, according to the data generated using auto-RIFT (Gardner et al., 2018) and provided by the NASA MEaSUREs ITS_LIVE project (Gardner et al., 2019). In recent decades, no significant changes have been reported in the ice shelves around the ice rises in this study.

Overall, as we see no significant ice-dynamical changes around the margins of these ice rises, the observed mass balance changes are dominated mainly by the SMB changes in the region. Goel et al. (2018) showed that long-term (millennial) changes over BI have largely been controlled by the long-term SMB changes in the region. This suggests that even on longer timescales, the adjacent Fimbul Ice Shelf has remained stable. Considering the role ice rises play in the dynamics of the Antarctic coast and their strong relation to SMB, it again shows how connected the ice dynamics is to the climate of the region.

6 Conclusion

We investigated the characteristics and ongoing changes over five ice rises in the central DML region. We find that the three ice rises in the Fimbul Ice Shelf are grounded well below sea level, with smooth beds under their summit/divide regions. The SMB over these ice rises shows an upwind-downwind contrast with corresponding high-low SMB, typical for ice rises, although with varying strength. Moreover, the ice rises closer to the open ocean have higher overall SMB, likely due to proximity to the moisture source, while less elevated ice rises show lower SMB due to a weaker orographic effect. Mass balance estimates using the field-based IOM and using satellite altimetry data match reasonably well. Kupol Ciolkovskogo and Leningradkollen remain close to balance, with no distinct trend. Blåskimen Island, Kupol Moskovskij, and Djupranen show strong thickening prior to year ∼2012, switching to thinning afterwards. This decreasing trend in mass balance overlaps with the decreasing SMB in these regions, which suggests SMB is the key influence behind the observed mass balance changes. This similarity in mass balance across the ice rises further suggests a similar origin of the observed trend. Unlike ice-dynamical changes around the ice rises, SMB changes can happen over larger regions over short timespans and thus are the key influence on the mass balance of ice rises. The recent advances in satellite altimetry with higher spatial and temporal resolutions will allow us to compare even seasonal elevation changes over these ice rises and further unravel the role of SMB in influencing their mass balance. The field-based IOM technique, although resource intensive, will remain a good source of determining the mass balance history of an ice rise if the ice core data is available as a constraint.

Data availability statement

The GNSS and derived digital elevation models for ice rises in the Fimbul area are available at: https://doi.org/10.21334/npolar.2018.b951f760. The shallow and deep-sounding radar data for ice rises in Fimbul area are available at https://doi.org/10.21334/npolar.2016.925d72c7 and https://doi.org/10.21334/npolar.2016.e12eb5f5. Access to GNSS data from DJU and LEN is described in Pratap et al. (2021). Firn core data from ice rises in Fimbul area and their availability are described in Vega et al. (2016).

Author contributions

VG and KM conceived this study. VG and KM conducted fieldwork, and VG led the overall data analysis. GM helped with ICESat and ICESat-2 data analysis. AM applied swath-based processing to the CryoSat-2 data and aided with its further analysis. VG led data interpretations and manuscript preparation through discussion with all co-authors.

Funding

This is a contribution to the India-Norway MADICE project supported by the Ministry of Earth Sciences, India (Grant No. MoES/Indo-Nor/PS-3/2015) and the Research Council of Norway (Grant No. 248780). Field data from the three ice rises in the Fimbul Ice Shelf were obtained with the IceRises project funded by the Norwegian Antarctic Research Expeditions (NARE) and the Center for Ice Climate and Ecosystems (ICE) of the Norwegian Polar Institute.

Acknowledgments

We thank NASA/NSIDC and European Space Agency for making the ICESat/ICESat-2 and CryoSat-2 data publicly available. Joel Brown developed the GPR processing workflow, which VG adopted. IceRises field campaigns were supported by Troll Station of NARE and SANAE Station of the South African National Antarctic Programs, as well as Joel Brown, Peter Leopold, Ørjan Karlsen, Kjetil Bakkland, and Harvey Goodwin. MADICE field campaigns were supported by Maitri Station. Bhanu Pratap and Katrin Lindback contributed to the field data collection. We are grateful to the leader of MADICE in India, Thamban Meloth and the NCPOR and NPI logistics personnel. Figure 1 was prepared using Quantarctica (https://www.npolar.no/quantarctica). We thank the scientific editor and the two reviewers for their constructive comments, which improved the manuscript significantly. This is NCPOR contribution no. J-42/2022-23.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.975606/full#supplementary-material

References

Andersen, M. L., Stenseng, L., Skourup, H., Colgan, W., Khan, S. A., Kristensen, S. S., et al. (2015). Basin-scale partitioning of Greenland ice sheet mass balance components (2007–2011). Earth Planet. Sci. Lett. 409, 89–95. doi:10.1016/j.epsl.2014.10.015

CrossRef Full Text | Google Scholar

Berthier, E., and Vincent, C. (2012). Relative contribution of surface mass-balance and ice-flux changes to the accelerated thinning of Mer de Glace, French Alps, over1979-2008. J. Glaciol. 58, 501–512. doi:10.3189/2012JoG11J083

CrossRef Full Text | Google Scholar

Bindschadler, R. A., Roberts, E. P., and MacAyeal, D. R. (1989). Distribution of net mass balance in the vicinity of crary ice rise, Antarctica. J. Glaciol. 35, 370–377. doi:10.3189/S0022143000009291

CrossRef Full Text | Google Scholar

Bindschadler, R., Choi, H., Wichlacz, A., Bingham, R., Bohlander, J., Brunt, K., et al. (2011). Getting around Antarctica: New high-resolution mappings of the grounded and freely-floating boundaries of the Antarctic ice sheet created for the International Polar Year. Cryosphere 5, 569–588. doi:10.5194/tc-5-569-2011

CrossRef Full Text | Google Scholar

Bisset, R. R., Dehecq, A., Goldberg, D. N., Huss, M., Bingham, R. G., and Gourmelen, N. (2020). Reversed surface-mass-balance gradients on himalayan debris-covered glaciers inferred from remote sensing. Remote Sens. (Basel). 12, 1563. doi:10.3390/rs12101563

CrossRef Full Text | Google Scholar

Boening, C., Lebsock, M., Landerer, F., and Stephens, G. (2012). Snowfall-driven mass change on the East Antarctic ice sheet. Geophys. Res. Lett. 39, L21501. doi:10.1029/2012gl053316

CrossRef Full Text | Google Scholar

Borstad, C. P., Rignot, E., Mouginot, J., and Schodlok, M. P. (2013). Creep deformation and buttressing capacity of damaged ice shelves: Theory and application to larsen C ice shelf. Cryosphere 7, 1931–1947. doi:10.5194/tc-7-1931-2013

CrossRef Full Text | Google Scholar

Brunt, K. M., Neumann, T. A., and Smith, B. E. (2019). Assessment of ICESat-2 ice sheet surface heights, based on comparisons over the interior of the antarctic ice sheet. Geophys. Res. Lett. 46, 13072–13078. doi:10.1029/2019GL084886

CrossRef Full Text | Google Scholar

Conway, H., and Rasmussen, L. A. (2009). Recent thinning and migration of the western divide, central west Antarctica. Geophys. Res. Lett. 36, L12502. doi:10.1029/2009GL038072

CrossRef Full Text | Google Scholar

Diener, T., Sasgen, I., Agosta, C., Fürst, J. J., Braun, M. H., Konrad, H., et al. (2021). Acceleration of dynamic ice loss in Antarctica from satellite gravimetry. Front. Earth Sci. 9, 20. doi:10.3389/feart.2021.741789

CrossRef Full Text | Google Scholar

Drews, R., Martín, C., Steinhage, D., and Eisen, O. (2013). Characterizing the glaciological conditions at halvfarryggen ice dome, dronning Maud land, Antarctica. J. Glaciol. 59, 9–20. doi:10.3189/2013JoG12J134

CrossRef Full Text | Google Scholar

Drews, R., Matsuoka, K., Martín, C., Callens, D., Bergeot, N., and Pattyn, F. (2015). Evolution of derwael ice rise in dronning Maud land, Antarctica, over the last millennia. J. Geophys. Res. Earth Surf. 120, 564–579. doi:10.1002/2014JF003246

CrossRef Full Text | Google Scholar

Dupont, T. K., and Alley, R. B. (2005). Assessment of the importance of ice-shelf buttressing to ice-sheet flow. Geophys. Res. Lett. 32. doi:10.1029/2004GL022024

CrossRef Full Text | Google Scholar

Fürst, J. J., Durand, G., Gillet-Chaulet, F., Tavard, L., Rankl, M., Braun, M., et al. (2016). The safety band of Antarctic ice shelves. Nat. Clim. Chang. 6, 479–482. doi:10.1038/nclimate2912

CrossRef Full Text | Google Scholar

Gardner, A. S., Moholdt, G., Scambos, T., Fahnstock, M., Ligtenberg, S., van den Broeke, M., et al. (2018). Increased West Antarctic and unchanged East Antarctic ice discharge over the last 7 years. Cryosphere 12, 521–547. doi:10.5194/tc-12-521-2018

CrossRef Full Text | Google Scholar

Gardner, A. S., Fahnestock, M. A., and Scambos, T. A. (2019). MEaSUREs ITS_LIVE landsat image-pair glacier and ice sheet surface velocities: Version 1. Data Archived at National Snow and Ice Data Center. doi:10.5067/IMR9D3PEI28U

CrossRef Full Text | Google Scholar

Goel, V., Brown, J., and Matsuoka, K. (2017). Glaciological settings and recent mass balance of blåskimen Island in dronning Maud land, Antarctica. Cryosphere 11, 2883–2896. doi:10.5194/tc-11-2883-2017

CrossRef Full Text | Google Scholar

Goel, V., Martín, C., and Matsuoka, K. (2018). Ice-rise stratigraphy reveals changes in surface mass balance over the last millennia in Dronning Maud Land. J. Glaciol. 64, 932–942. doi:10.1017/jog.2018.81

CrossRef Full Text | Google Scholar

Goel, V., Matsuoka, K., Berger, C. D., Lee, I., Dall, J., and Forsberg, R. (2020). Characteristics of ice rises and ice rumples in dronning Maud land and enderby land, Antarctica. J. Glaciol. 66, 1064–1078. –15. doi:10.1017/jog.2020.77

CrossRef Full Text | Google Scholar

Gourmelen, N., Escorihuela, M. J., Shepherd, A., Foresta, L., Muir, A., Garcia-Mondéjar, A., et al. (2018). CryoSat-2 swath interferometric altimetry for mapping ice elevation and elevation change. Adv. Space Res. 62, 1226–1242. doi:10.1016/j.asr.2017.11.014

CrossRef Full Text | Google Scholar

Gray, L., Burgess, D., Copland, L., Cullen, R., Galin, N., Hawley, R., et al. (2013). Interferometric swath processing of Cryosat data for glacial ice topography. Cryosphere 7, 1857–1867. doi:10.5194/tc-7-1857-2013

CrossRef Full Text | Google Scholar

Gray, L., Burgess, D., Copland, L., Demuth, M. N., Dunse, T., Langley, K., et al. (2015). CryoSat-2 delivers monthly and inter-annual surface elevation change for Arctic ice caps. Cryosphere 9, 1895–1913. doi:10.5194/tc-9-1895-2015

CrossRef Full Text | Google Scholar

Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., et al. (2020). The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049. doi:10.1002/qj.3803

CrossRef Full Text | Google Scholar

Hogg, A. E., Gilbert, L., Shepherd, A., Muir, A. S., and McMillan, M. (2020). Extending the record of Antarctic ice shelf thickness change, from 1992 to 2017. Adv. Space Res. 68, 724–731. doi:10.1016/j.asr.2020.05.030

CrossRef Full Text | Google Scholar

Herron, M. M., and Langway, C. C. (1980). Firn Densification: An Empirical Model. J. Glaciol. 25, 373–385. doi:10.3189/S0022143000015239

CrossRef Full Text | Google Scholar

Hubbard, A., Willis, I., Sharp, M., Mair, D., Nienow, P., Hubbard, B., et al. (2000). Glacier mass-balance determination by remote sensing and high-resolution modelling. J. Glaciol. 46, 491–498. doi:10.3189/172756500781833016

CrossRef Full Text | Google Scholar

Kausch, T., Lhermitte, S., Lenaerts, J. T. M., Wever, N., Inoue, M., Pattyn, F., et al. (2020). Impact of coastal east antarctic ice rises on surface mass balance: Insights from observations and modeling. Cryosphere 14, 3367–3380. doi:10.5194/tc-14-3367-2020

CrossRef Full Text | Google Scholar

King, J. C. (2004). Wind-borne redistribution of snow across an Antarctic ice rise. J. Geophys. Res. 109, D11104. doi:10.1029/2003JD004361

CrossRef Full Text | Google Scholar

Kingslake, J., Hindmarsh, R. C. A., Aðalgeirsdóttir, G., Conway, H., Corr, H. F. J., Gillet-Chaulet, F., et al. (2014). Full-depth englacial vertical ice sheet velocities measured using phase-sensitive radar. J. Geophys. Res. Earth Surf. 119, 2604–2618. doi:10.1002/2014JF003275

CrossRef Full Text | Google Scholar

Kovacs, A., Gow, A. J., and Morey, R. M. (1995). The in-situ dielectric constant of polar firn revisited. Cold Reg. Sci. Technol. 23, 245–256. doi:10.1016/0165-232X(94)00016-Q

CrossRef Full Text | Google Scholar

Lenaerts, J. T. M., Brown, J., Van Den Broeke, M. R., Matsuoka, K., Drews, R., Callens, D., et al. (2014). High variability of climate and surface mass balance induced by Antarctic ice rises. J. Glaciol. 60, 1101–1110. doi:10.3189/2014JoG14J040

CrossRef Full Text | Google Scholar

Lenaerts, J. T. M., van Meijgaard, E., van den Broeke, M. R., Ligtenberg, S. R. M., Horwath, M., and Isaksson, E. (2013). Recent snowfall anomalies in Dronning Maud Land, East Antarctica, in a historical and future climate perspective. Geophys. Res. Lett. 40, 2684–2688. doi:10.1002/grl.50559

CrossRef Full Text | Google Scholar

Martín, C., Gudmundsson, G. H., Pritchard, H. D., and Gagliardini, O. (2009). On the effects of anisotropic rheology on ice flow, internal structure, and the age-depth relationship at ice divides. J. Geophys. Res. 114, F04001. doi:10.1029/2008JF001204

CrossRef Full Text | Google Scholar

Matsuoka, K., Hindmarsh, R. C. A., Moholdt, G., Bentley, M. J., Pritchard, H. D., Brown, J., et al. (2015). Antarctic ice rises and rumples: Their properties and significance for ice-sheet dynamics and evolution. Earth. Sci. Rev. 150, 724–745. doi:10.1016/j.earscirev.2015.09.004

CrossRef Full Text | Google Scholar

Matsuoka, K., Skoglund, A., Roth, G., de Pomereu, J., Griffiths, H., Headland, R., et al. (2021). Quantarctica, an integrated mapping environment for Antarctica, the Southern Ocean, and sub-Antarctic islands. Environ. Model. Softw. 140, 105015. doi:10.1016/j.envsoft.2021.105015

CrossRef Full Text | Google Scholar

Miles, E., McCarthy, M., Dehecq, A., Kneib, M., Fugger, S., and Pellicciotti, F. (2021). Health and sustainability of glaciers in High Mountain Asia. Nat Commun 12, 2868. doi:10.1038/s41467-021-23073-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Moholdt, G., Hagen, J. O., Eiken, T., and Schuler, T. V. (2010). Geometric changes and mass balance of the Austfonna ice cap, Svalbard. Cryosphere 4, 21–34. doi:10.5194/tc-4-21-2010

CrossRef Full Text | Google Scholar

Moholdt, G., Padman, L., and Fricker, H. A. (2014). Basal mass budget of Ross and Filchner-Ronne ice shelves, Antarctica, derived from Lagrangian analysis of ICESat altimetry. JGR. Earth Surf. 119, 2361–2380. doi:10.1002/2014JF003171

CrossRef Full Text | Google Scholar

Morris, A., Moholdt, G., Gray, L., Schuler, T. V., and Eiken, T. (2021). CryoSat-2 interferometric mode calibration and validation: A case study from the austfonna ice cap, svalbard. Remote Sens. Environ. 269, 112805. doi:10.1016/j.rse.2021.112805

CrossRef Full Text | Google Scholar

Morris, A., Moholdt, G., and Gray, L. (2020). Spread of svalbard glacier mass loss to barents sea margins revealed by CryoSat-2. J. Geophys. Res. Earth Surf. 125, e2019JF005357. doi:10.1029/2019JF005357

CrossRef Full Text | Google Scholar

Pratap, B., Dey, R., Matsuoka, K., Moholdt, G., Lindbäck, K., Goel, V., et al. (2021). Three-decade spatial patterns in surface mass balance of the nivlisen ice shelf, central dronning Maud land, east Antarctica. J. Glaciol. 68, 174–186. doi:10.1017/jog.2021.93

CrossRef Full Text | Google Scholar

Rignot, E., and Kanagaratnam, P. (2006). Changes in the velocity structure of the Greenland ice sheet. Science 311, 986–990. doi:10.1126/science.1121381

PubMed Abstract | CrossRef Full Text | Google Scholar

Rignot, E., Mouginot, J., and Scheuchl, B. (2011). Ice Flow of the Antarctic Ice Sheet. Science 333, 1427–1430. doi:10.1126/science.1208336

PubMed Abstract | CrossRef Full Text | Google Scholar

Rignot, E., Mouginot, J., Scheuchl, B., van den Broeke, M., van Wessem, M. J., and Morlighem, M. (2019). Four decades of antarctic ice sheet mass balance from 1979–2017. Proc. Natl. Acad. Sci. U. S. A. 116, 1095–1103. doi:10.1073/pnas.1812883116

PubMed Abstract | CrossRef Full Text | Google Scholar

Schröder, L., Horwath, M., Dietrich, R., Helm, V., van den Broeke, M. R., and Ligtenberg, S. R. M. (2019). Four decades of Antarctic surface elevation changes from multi-mission satellite altimetry. Cryosphere 13, 427–449. doi:10.5194/tc-13-427-2019

CrossRef Full Text | Google Scholar

Schutz, B. E., Zwally, H. J., Shuman, C. A., Hancock, D., and DiMarzio, J. P. (2005). Overview of the ICESat mission. Geophys. Res. Lett. 32, L21S01. doi:10.1029/2005GL024009

CrossRef Full Text | Google Scholar

Shepherd, A., Ivins, E., Rignot, E., Smith, B., van den Broeke, M., Velicogna, I., et al. (2018). Mass balance of the antarctic ice sheet from 1992 to 2017. Nature 558, 219–222. doi:10.1038/s41586-018-0179-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, B., Fricker, H. A., Gardner, A. S., Medley, B., Nilsson, J., Paolo, F. S., et al. (2020). Pervasive ice sheet mass loss reflects competing ocean and atmosphere processes. Science 368, 1239–1242. doi:10.1126/science.aaz5845

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, B. E., Medley, B., Fettweis, X., Sutterley, T., Alexander, P., Porter, D., et al. (2022). Evaluating greenland surface-mass-balance and firn-densification data using ICESat-2 altimetry, cryosphere discuss. (Accessed October 22, 2022). doi:10.5194/tc-2022-44

CrossRef Full Text | Google Scholar

Turner, J., Phillips, T., Thamban, M., Rahaman, W., Marshall, G. J., Wille, J. D., et al. (2019). The dominant role of extreme precipitation events in antarctic snowfall variability. Geophys. Res. Lett. 46, 3502–3511. doi:10.1029/2018GL081517

CrossRef Full Text | Google Scholar

Van Tricht, L., Huybrechts, P., Van Breedam, J., Vanhulle, A., Van Oost, K., and Zekollari, H. (2021). Estimating surface mass balance patterns from unoccupied aerial vehicle measurements in the ablation area of the Morteratsch–Pers glacier complex (Switzerland). Cryosphere 15, 4445–4464. doi:10.5194/tc-15-4445-2021

CrossRef Full Text | Google Scholar

Vega, C. P., Schlosser, E., Divine, D. V., Kohler, J., Martma, T., Eichler, A., et al. (2016). Surface mass balance and water stable isotopes derived from firn cores on three ice rises, Fimbul Ice Shelf, Antarctica. Cryosphere 10, 2763–2777. doi:10.5194/tc-10-2763-2016

CrossRef Full Text | Google Scholar

Vincent, C., Wagnon, P., Shea, J. M., Immerzeel, W. W., Kraaijenbrink, P., Shrestha, D., et al. (2016). Reduced melt on debris-covered glaciers: Investigations from changri NupGlacier, Nepal. Cryosphere 10, 1845–1858. doi:10.5194/tc-10-1845-2016

CrossRef Full Text | Google Scholar

Zhang, B., Liu, J., Wang, Z., Liu, T., and Yang, Q. (2020). Antarctic ice-shelf thickness changes from CryoSat-2 SARIn mode measurements: Assessment and comparison with IceBridge and ICESat. J. Earth Syst. Sci. 129, 127. doi:10.1007/s12040-020-01392-2

CrossRef Full Text | Google Scholar

Zwally, H. J., and Giovinetto, M. B. (2011). Overview and assessment of antarctic ice-sheet mass balance estimates: 1992–2009. Surv. Geophys. 32, 351–376. doi:10.1007/s10712-011-9123-5

CrossRef Full Text | Google Scholar

Zwally, H. J., Li, J., Robbins, J. W., Saba, J. L., Yi, D., and Brenner, A. C. (2015). Mass gains of the Antarctic ice sheet exceed losses. J. Glaciol. 61, 1019–1036. doi:10.3189/2015JoG15J071

CrossRef Full Text | Google Scholar