How the climate shapes stalagmites—A comparative study of model and speleothem at the Sofular Cave, Northern Turkey

Understanding how stalagmites grow under changing climate conditions is of great significance for their application as a paleoclimate archive. In this study, we present a shape modeling approach to stalagmite growth by combining three existing models accounting for climate variables, karst water chemistry, and speleothem deposition. The combined model requires only four input parameters: calcium concentration of the water drop, drip interval, cave temperature, and cave carbon dioxide ($\mathrm{C}{\mathrm{O}}_2$) concentration. Using the output of the coupled atmosphere–ocean–land surface model MPI-ESM1.2 and the CaveCalc model for speleothem chemistry, we simulated stalagmite growth at Sofular Cave, Northern Turkey, (in the last 25 kyr) and compared the results to those of the existing So-1 stalagmite from the same cave. This approach allows simulating, completely independent of measured boundary conditions, a stalagmite geometry that follows the trend of the experimental data for the growth rate, with input parameters within the respective error ranges. When testing the sensitivity of the individual model parameters, the model suggests that the stalagmite radius mainly depends on the drip interval, whereas the growth rate is driven by the calcium concentration of the water drop. The model is also capable of showing some basic phenomena, like a decrease in growth rate (as observed in the real stalagmite), as CO₂ concentration in the cave increases. The coupling of input parameters for the model to climate models represents the first attempt to understand an important climate archive in its shape and isotope content and opens the possibility for a new inverse approach to paleoclimate variables and model constraints.

1 Introduction

Stalagmites are potential archives for paleoclimatology because they grow in a protected environment for 10³–10⁵ years and record changes in climatic conditions both within the cave and above the cave, such as precipitation, temperature, and vegetation, through modifications of their shape and isotopic composition (Fairchild et al., 2006; Götrük et al., 2011). While isotopic proxies measured in the carbonate and fluid inclusions from sampled stalagmite material are standard tools in reconstructing paleo-climate signals (Fleitmann et al., 2003), the geometrical information of the shape of a stalagmite has received less attention. First, efforts have been undertaken considering the theoretical growth models by Dreybrodt (1999). These early models have been used to discuss changes in climatic forcing, such as temperature changes, changes in precipitation and in carbon dioxide concentration, and the growth geometries of stalagmites (Kaufmann, 2003). Later, these climate variables have been recovered from both synthetic and real stalagmite geometries by formal inversion (Kaufmann and Dreybrodt, 2004). However, difficulties in extracting climate information from stalagmite shapes arise from the overlaying soil and karst which affects soil $\mathrm{C}{\mathrm{O}}_2$ supply and infiltration patterns, ultimately feeding the drip water and chemical composition. But, the great benefit of extracting climate information from the shape is the ease to recover growth rates and shapes from real-world stalagmites by simple measurements.

Hence, we attempt to couple models of stalagmite growth, climate, and infiltration that permit a fully independent prediction of the growth of stalagmites. We test our coupling for a particularly well-studied speleothem from the Sofular cave in Turkey, for which most classical proxies have been measured, including the growth history of the speleothem. The applied models have a tremendous degree of freedom in a large number of poorly constrained variables; hence, we attempt to simulate a real-world speleothem throughout the last glacial termination (Berger, 1978), for which an Earth System model (ESM) supplies strong changes in soil activity, precipitation, and local temperature. Our results strongly suggest that the combination of the different model outputs might permit sufficient constraints to derive important conclusions for future work concerning speleothem growth and shapes.

2 Methods

2.1 Sofular Cave and stalagmite So-1

Sofular Cave is located in Northern Turkey, less than 10 km from the coast of the Black Sea at 41°25’N and 31°56’E (Figure 1). It is situated on the northern foothills of the Akçakoca Mountain range, a part of the North Anatolian Mountain chain in Turkey (Laumanns and Kaufmann, 1988; Götrük et al., 2011), and developed in the lower cretaceous limestone (Tüysüz, 1999). The vegetation above is dense and consists mainly of deciduous trees (oak, beech, and elms) and shrubs. The soil above the Sofular Cave is thin, with an estimated maximum depth of approximately 30 cm. The highly fissured bedrock above the cave is around 40 m thick, which suggests a fast response (days to weeks) of travel time for precipitation to the drip site in the cave (Badertscher et al., 2014). As a reference stalagmite, we mainly work with the So-1 stalagmite, recovered in August 2005. It is candle-shaped, 1.70 m high, and started growing at around 50.3 kyr BP (Fleitmann et al., 2009). Because most of the growth processes took place in the last 25 kyr (1.35 m out of 1.7 m), we focus on this time interval. It contains the main growth process, and changes in growth rates can be investigated. As the exact sampling position has not been recorded, we discuss the influence of the possible locations in the cave.

FIGURE 1

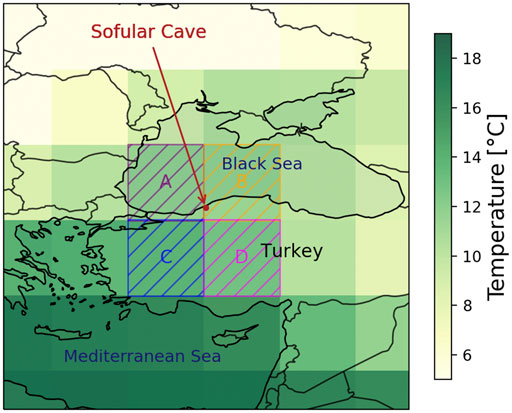
FIGURE 1. Location of Sofular Cave in Turkey, and four cells of the ESM model (A–D). Colors represent modeling surface temperatures from the ESM run for the present day.

To verify the output of our shape model, the resulting age/depth plot of the simulation is compared with measured growth data taken at the apex of the stalagmite. There are many different publications about the precise measurement of the age profile, not just for the So-1 but also for the So-2 stalagmite (Fleitmann et al., 2009; Therre, 2020). For further investigation, the actual shape of the simulated and real-world stalagmite is compared (Figure 2). Both stalagmites have recorded favorable growth conditions and periods, where no growth was happening. Generally, the climatic conditions during the Last Glacial Maximum (LGM) were less favorable for stalagmite growth when compared to the last 10 kyr. As the So-1 stalagmite grows continuously for the interested time interval, it is chosen as a further reference.

FIGURE 2

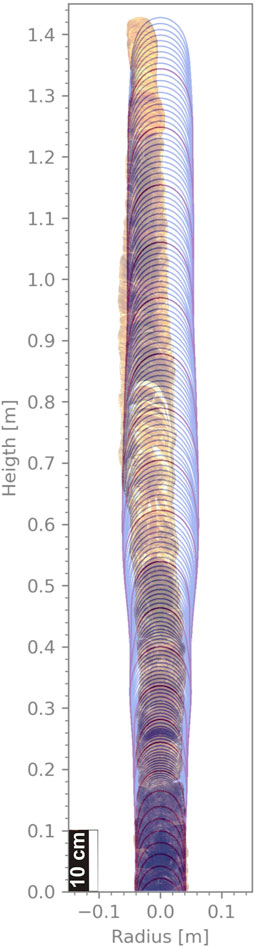
FIGURE 2. So-1 stalagmite and FLOW modeled stalagmite superimposed for comparison. Shapes of the simulation are redrawn every 100 years by blue lines, whereas purple lines indicate 1,000 years steps.

2.2 Earth system model MPI–ESM and climate output

We use climate variables from a transient deglaciation experiment performed with the Max Planck Institute for Meteorology Earth System Model (MPI-ESM), version 1.2 (Mauritsen et al., 2019), in spatial resolution T31GR30 (Meccia and Mikolajewicz, 2018), corresponding to roughly 3.75° in latitude and longitude at the equator. The model includes a full representation of the terrestrial carbon cycle.

After a spin-up at constant 26 ka BP boundary conditions, the model experiment covers the time period from 26 ka BP to the present day. We prescribed orbital forcing from Berger (1978) and greenhouse gases from Köhler et al. (2017). Furthermore, we prescribed ice-sheet extent from the GLAC-1D ice sheet reconstruction (Tarasov et al., 2012; Briggs et al., 2014; Ivanovic et al., 2016). Ice-sheet extent, as well as bathymetry and topography (Meccia & Mikolajewicz, 2018), and river routing (Riddick et al., 2018) were continuously updated at ten-year intervals throughout the deglaciation.

From this experiment, we used the near-surface air temperature and precipitation fields, obtained as means over 100 years, to drive our model. Furthermore, we used the soil carbon content and heterotrophic respiration from the decomposition of litter detritus and soil organic matter by microorganisms.

2.3 Parameterization to the soil CO₂

To calculate soil $\mathrm{C}{\mathrm{O}}_2$ concentrations c_soil from soil respiration, we use an existing simplistic soil respiration model (Cerling, 1984; Quade et al., 1989; Cerling et al., 1991). Assuming diffusive transport of $\mathrm{C}{\mathrm{O}}_2$ in soils, we use the transient diffusion equation with a depth-dependent $\mathrm{C}{\mathrm{O}}_2$ production rate Q(z),

$\frac{\partial c_{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}}{\partial t}=D\frac{{\partial }^{\mathit{2}}{c}_{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}}{\partial z^{\mathit{2}}}+Q\left(z\right)[1]$

With time t and depth z, but for steady-state conditions (dc_soil/dt=0). The diffusion coefficient for $\mathrm{C}{\mathrm{O}}_2$ in soils, D = 0.144 cm²/s, is adopted from Cerling et al. (1991). We further assume an exponential decrease of $\mathrm{C}{\mathrm{O}}_2$ production with a characteristic depth z*. Integrating Q(z) overall soil layers results in the soil respiration R_s, which was obtained as a function of time from MPI-ESM:

$R_s=\int Q\left(z\right)dz=\int Q_{\mathit{0}}{e}^{-z/z^{*}}dz[2]$

With the boundary conditions $\underset{z\to \infty }{\mathit{lim}}\frac{\partial c_{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}}{\partial z}\left(z\right)=\mathit{0}$ and $c_{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}\left(z=\mathit{0}\right)=c_{\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{o}}$, the steady-state solution of Eq. 1 is as follows:

$c_{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}\left(z\right)=\frac{z^{*}}{D}{R}_{\mathrm{s}}\left(\mathit{1}-e^{-z/z^{*}}\right)+c_{\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{o}}.[3]$

In this study, we chose a characteristic depth of z* = 30 cm, which is commonly taken as the boundary between the topsoil and subsoil layers (Hiederer and Koechy, 2011). Additionally, studies at Sofular Cave suggested a maximum soil depth between 30 and 50 cm (Rudzka et al., 2011; Badertscher et al., 2014), which further supports our chosen value for z*. In this layer, the majority of $\mathrm{C}{\mathrm{O}}_2$ production is expected to take place. To calculate a mean $\mathrm{C}{\mathrm{O}}_2$ concentration, the resulting $\mathrm{C}{\mathrm{O}}_2$ concentration profile c_soil (z) is averaged from the surface to a depth of 100 cm. The atmospheric $\mathrm{C}{\mathrm{O}}_2$ concentration $c_{\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{o}}$, as a function of time, is taken from Köhler et al. (2017).

2.4 Soil and epikarst model CaveCalc

The chemical and physical processes in the soil and the karst above the cave are modeled using CaveCalc, a numerical model for speleothem chemistry and isotopes (Owen et al., 2018). The chemistry in CaveCalc is calculated with the program PHREEQC (Parkhurst and Appelo, 2013), a program simulating aqueous geochemistry. A CaveCalc run involves two PHREEQC-based steps: an equilibration step for a reference volume of water with a predefined soil gas and a subsequent step equilibrating the same water with limestone. This simulates $\mathrm{C}{\mathrm{O}}_2$ uptake of percolating water in the soil and limestone dissolution. The water equilibrated with limestone represents the drip water from which the speleothem is precipitated. From the CaveCalc output, the Ca²⁺ concentration in the drip water, ${\mathrm{C}\mathrm{a}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}$, can be extracted and used as an input for the shape model. To obtain ${\mathrm{C}\mathrm{a}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}$ time series, CaveCalc was separately run for each time step with a variable soil $\mathrm{C}{\mathrm{O}}_2$ concentration as described earlier.

2.5 Shape model for stalagmite growth

The shape model contains the three existing parameterizations (FLOW, EXP, and GAUSS) of stalagmite growth and allows a mixing process for the latter two. For exhaustive descriptions of those models, the reader is referred to the respective first publication (Dreybrodt, 1999; Kaufmann, 2003; Romanov et al., 2008). The underlying geometry model to describe the surface of the stalagmite with a polygon is explained by Kaufmann (2003). Here, we just state the results.

$F_{\mathit{0}}=\alpha \cdot \left(c_{\mathrm{i}\mathrm{n}}-c_{\mathrm{a}\mathrm{p}\mathrm{p}}\right)[4]$

We can separate the shape model into two parts (FLOW and EXP/GAUSS). We start with the FLOW equations by stating the underlying initial deposition rate F [${\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{m}}^{-3}{\mathrm{s}}^{-1}$]:

The index 0 refers to the position of the deposition rate and indicates that we look at the apex of the stalagmite. $\alpha$ is the kinetic constant [$\mathrm{m}{\mathrm{s}}^{-1}$], $c_{\mathrm{i}\mathrm{n}}$ is the actual calcium concentration of the water drop [${\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{m}}^{-3}$], and $c_{\mathrm{a}\mathrm{p}\mathrm{p}}$ is the apparent equilibrium calcium concentration of water in the cave [${\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{m}}^{-3}$] computed as a function of temperature T [°C] and $\mathrm{C}{\mathrm{O}}_2$ pressure [atm] in the cave (Busenberg and Plummer, 1985; Dreybrodt, 1988). $\alpha$ depends on the film thickness $\delta$ [m] of the water film on top of the stalagmite and on temperature T [°C] (Dreybrodt, 1988; Baker et al., 1998), Supplementary Figure S1. The formula implies that the calcium concentration at the apex is always equal to $c_{\mathrm{i}\mathrm{n}}$. This equation leads to the equilibrium radius:

$R_{\mathrm{e}\mathrm{q}}=\sqrt{\frac{V_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}}{\pi \cdot \alpha \cdot \tau }}.[5]$

Here, $V_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}$ [m³] stands for the volume of the water drop and is set to $V_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}$ = 0.1 ${\mathrm{c}\mathrm{m}}^3$ (Dreybrodt, 1988) and $\tau$ is the drip interval [$\mathrm{s}$]. The decrease in the deposition rate along the horizontal profile is described by the following formula (Dreybrodt and Romanov, 2008), where the index i ∈ [$\mathit{0},\mathrm{n}$] describes the points from the center outward:

$F_{i+\mathit{1}}=F_{\mathit{0}}\cdot \left(\mathit{1}-\mathit{2}\cdot \frac{R_i\cdot \Delta l_i}{R_{\mathrm{e}\mathrm{q}}^{\mathit{2}}}\right)[6]$

with $R_i$ as the distance of the point i from the apex and $\Delta l_i$ as the distance between two points of the polygon. For the second approach (EXP and GAUSS), the average deposition rate over the time $\tau$ between two drops is considered. The initial deposition rate is described by

$F_{\mathit{0}}^{\mathrm{a}\mathrm{v}}=\frac{\delta \cdot \left(c_{\mathrm{i}\mathrm{n}}-c_{\mathrm{a}\mathrm{p}\mathrm{p}}\right)}{\tau }\cdot \left(\mathit{1}-e^{-\frac{\alpha \cdot \tau }{\delta }}\right)[7]$

The model is applied for the film thickness values $\delta$ of 0.01 $\mathrm{c}\mathrm{m}$, 0.0075 $\mathrm{c}\mathrm{m}$, and 0.005 $\mathrm{c}\mathrm{m}$, as these are realistic values, and the approximation for $\alpha$ to be independent of $\delta$ is legitimate (Crul, 1973; Dreybrodt, 1999). This leads to an equilibrium radius of

$R_{\mathrm{e}\mathrm{q}}^{\mathrm{a}\mathrm{v}}=\sqrt{\frac{V_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}}{\pi \cdot \delta \cdot \left(\mathit{1}-e^{-\frac{\alpha \cdot \tau }{\delta }}\right)}}.[8]$

Through this approach, two different descriptions of the decrease in deposition rate along the horizontal profile are possible: The exponential relationship (referred to as “EXP”) is described by

$F_i=F_{\mathit{0}}\cdot \exp \left(-\frac{{\sum }_i{l}_i}{R_{\mathit{0}}^{\mathrm{a}\mathrm{v}}}\right).[9]$

The Gaussian distribution (referred to as “GAUSS”) has the same functional assumptions as the EXP but assumes a Gaussian relationship for the square of the distance (variance) over the mean radius:

$F_i=F_{\mathit{0}}\cdot \exp \left(-\frac{\pi \cdot {\sum }_i{l}_i}{{{\mathit{4}\cdot R}_{\mathit{0}}^{a\mathrm{v}}}^{\mathit{2}}}\right).[10]$

These methods also allow a mixing process between the water drop and the solution on top of the stalagmite according to Mühlinghaus et al. (2007). $\Phi$ describes the percentage of excess calcium of the drop mixing with the solution layer and ranges therefore from 0 to 1. Iterating the mixing process for many drops, the universal mixing factor $\lambda$ follows according to Mühlinghaus et al. (2007):

$\lambda =\frac{\Phi }{\mathit{1}-\left(\mathit{1}-\Phi \right)\cdot e^{-\frac{\alpha \cdot \tau }{\delta }}}[11]$

$\lambda$ describes the memory of the mixing processes and can reach values of up to 0.2 for very large drip intervals.

Also, this changes Eqs.7,8 to

$F_{\mathit{0},\mathrm{m}\mathrm{i}\mathrm{x}}^{\mathrm{a}\mathrm{v}}=\lambda \cdot F_{\mathit{0}}^{\mathrm{a}\mathrm{v}}[12]$

$R_{\mathrm{m}\mathrm{i}\mathrm{x}}^{\mathrm{a}\mathrm{v}}=R_{\mathrm{e}\mathrm{q}}^{\mathrm{a}\mathrm{v}}\cdot \sqrt{\frac{\mathit{1}}{\lambda }}.[13]$

2.6 Free parameters and fixed constraints

We start with a naive approach and use the simulated output of the MPI-ESM. For the temperature in the cave, we use the surface temperatures from the four box units around the Sofular location, without weighting any of the boxes as being more important than others (Supplementary Figures S2, S3). The resulting temperature corresponds to the arithmetic mean of the four boxes:

$T_{\mathrm{c}\mathrm{a}\mathrm{v}\mathrm{e}}=T_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$

To estimate the drip interval is very difficult. Hence, we here follow a very simplistic parameterization in the absence of any information about past drip intervals. We assume an artificially chosen lowest drip interval of 25 s and expect this number to dramatically increase with decreasing precipitation. We have chosen to couple the drip interval $\tau$ to the precipitation, supposing the maximum precipitation leads to the lowest drip interval of 25 s due to high infiltration. The maximum corresponds to the highest value of the time series. Lower precipitation leads to longer drip intervals; hence, the difference between maximum precipitation and actual precipitation is important. Here, we scale $\tau$ according to precipitation following Eq. 14:

$\tau =\gamma \left[\max \left(Precip\right)-Precip\right]+\mathit{25}[14]$

(Supplementary Figure S4) It should be noted that the resulting drip interval time series is completely artificial and has no real physical correspondence as it just scales the drip interval to fit the shape of the So-1 stalagmite based on all other time series. The factor γ converts the units (mm/year) into seconds; hence, [γ] = 1s year/mm.

The $\mathrm{C}{\mathrm{O}}_2$ concentration in the cave is set equal to the atmospheric $\mathrm{C}{\mathrm{O}}_2$ concentration [(Köhler et al., 2017); Supplementary Figure S5].

The $\mathrm{C}{\mathrm{a}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}$ concentration is calculated through CaveCalc (Supplementary Figure S6).

3 Results

We now use the FLOW model and the standard parameter values derived to simulate the So-1 stalagmite. The age/depth plot in Figure 3A reveals that the calculated values with $T_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ do result in a simulated stalagmite, which is too small in its vertical extension. Hence, in contrast to our initial assumption, we now weigh the continental higher temperature as moderately more important than the mean using Eq. 15. This results in only slight adjustments of the growth as can be seen in Figure 3B.

FIGURE 3

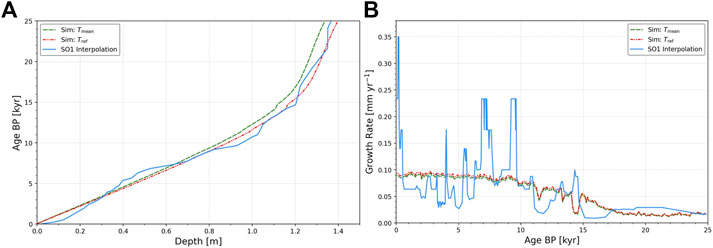
FIGURE 3. Age/depth (A) and growth rate/depth (B) plot for the naive approach, the best fit, and the experimental data. Solid lines represent a linear interpolation to construct the age through stable oxygen isotopes which follow the U/Th dates (Badertscher et al., 2011).

The resulting stalagmite shape using this modified temperature $T_{\mathrm{r}\mathrm{e}\mathrm{f}}$ (see Eq. 15) is shown in Figure 4. It shows small variations in the radius, which are visible due to the exaggerated scale of the x-axis, indicating different growth conditions. The lower part of the simulated stalagmite is an equilibrium state, as we let the model run for 25 kyr with the earliest climatic input data and then started plotting. As the So-1 stalagmite actually grows for 50 kyr, it is reasonable to start with equilibrium conditions for growth.

FIGURE 4

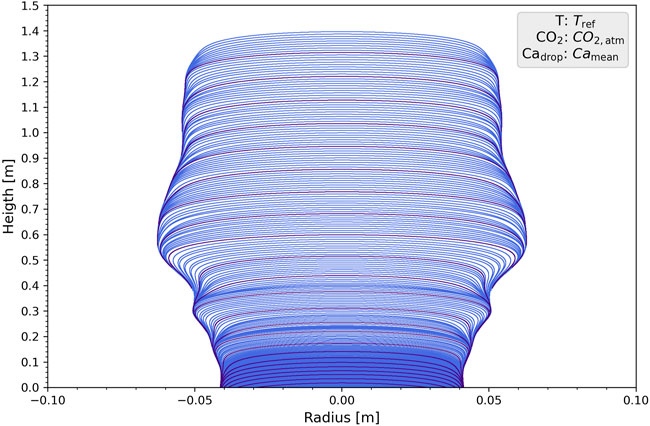
FIGURE 4. Simulated stalagmite with the FLOW model. Stalagmite starts growing in equilibrium, and the temperature is modified to achieve the best fit in the depth/age plot. Shapes of the simulation are redrawn every 100 years by the blue lines, whereas the purple lines indicate 1,000 years steps.

To obtain a better fit, we modify the temperature function according to

$T_{\mathrm{r}\mathrm{e}\mathrm{f}}=\mathit{0.65}\cdot T_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}+\mathit{0.35}\cdot T_{\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}}[15]$

With this parameterization, we reduce the amplitude of the temporal variation of the cave temperature (damping) and compensate by a static shift. $T_{\mathrm{r}\mathrm{e}\mathrm{f}}$ is identified as the reference temperature for the best model output (see age-depth plot in Figure 3A). This seems plausible considering the special location of the Sofular cave in the mountains near the Black Sea and that the ESM generated quite different values for the four grid boxes around Sofular, as shown in Supplementary Figure S3. Therefore, the resulting stalagmite in Figure 4 uses the modified temperature data.

This will be the reference stalagmite for all further investigations in this study, which is also superimposed on the real shape in Figure 2. Through modification of growth conditions, the resulting stalagmite agrees with the age/depth plot quite well (see Figure 3A). It is important to mention that the simulated data only follow the mean trends of the growth rate with smaller values during the glacial and increasing values during the interglacial. The model is, however, not capable of reproducing fluctuations of the growth around the mean. This is demonstrated in a growth rate versus time plot (see Figure 3B), for which the observed data show strong temporal variability around the mean with fluctuations of up to an order of magnitude, while the model predicts rather smooth growth, except for a short growth decline during the Bölling/Allerod warming around 14.5 kyr ago.

3.1 Comparing different shape model approaches

The modeled stalagmite radius mainly depends on the drip interval $\tau$ and on the temperature T, which influences $\alpha$. We now compare the predicted shape of the stalagmite, using three different parameterizations: the Gaussian (GAUSS), exponential (EXP), and flow (FLOW) approach (Romanov et al., 2008). By comparing the tip of the So-1 stalagmite with the model prediction, the degree of realism of the different shape models can be tested (see Supplementary Figure S7). The EXP model drops off too fast when compared to the real-world So-1 stalagmite. The GAUSS model, on the other hand, slightly overestimates the radius. The FLOW model achieves a reasonably good fit.

There are two additional arguments in favor of picking the FLOW model: first, the growth rate of the FLOW model is independent of the unconstrained, freely chosen drip interval τ, as described by Eq. 4. Here, the growth rates predicted by the FLOW model correspond better to the real growth rate derived from U/Th dating (Fleitmann et al., 2009). Second, the equations of the FLOW model are faster in reaching an equilibrium status (Romanov et al., 2008). This means that changes in the input parameters are reflected more quickly in the shape of the stalagmite. Given the correct prediction of speleothem height and shape of the tip, we opt here to use only the FLOW model for further discussion of the sensitivity and influence of several unknown parameters on the growth and shape of the simulated So-1. In Figure 2, the results of the stalagmite shape from a FLOW model run are placed over the photo of the So-1 stalagmite. The photo is cropped to show the growth of the last 25 kyr, according to U/Th dating (Fleitmann et al., 2009). There are some large deviations: first, the modeled radius becomes far too large. The model predicts a bigger radius at the tip, but the real stalagmite does not confirm this prediction. Obviously, the description of the relation between precipitation and drip interval by Eq. 14 is only a rough approximation. Additionally, Figure 2 shows that the peaks of the simulation and the real So-1 stalagmite do not match in their horizontal position. The So-1 stalagmite has some variations in the apex to the left and right, which probably results from small changes in the drip locations or other external effects (Rajendran et al., 2015).

4 Discussion

In the following text, we will discuss in more detail the role of different responses of the shape model with respect to the key variables. We again use the MPI-ESM1.2 and CaveCalc model output to avoid multiple dependencies of model coupling. We are fully aware that the total coupled uncertainty of the three interacting models with numerous estimated parameters and transfer functions implies a largely unexplored and possible systematic source of error in shape prediction. Here, we want to discuss the response and partial sensitivity of the shape model to its input and a few interesting predictions resulting from it. As the full discussion of testing the general applicability of such an approach would need a larger set of environments and test speleothems, it is yet beyond the scope of this work. Therefore, we focus as stated on the key drivers and the resulting implications and investigate the role of the input parameters.

4.1 Cave temperature

Temperature plays a significant role in the shape of the stalagmite, with a reduction in the temperature resulting in less growth, whereas an increase in temperature enhances the growth (Kaufmann, 2003). This is illustrated in Supplementary Figure S8 and results from the temperature-dependent calculation of the apparent calcium concentration inside the cave $c_{\mathrm{a}\mathrm{p}\mathrm{p}}$ and the temperature-sensitive calcite precipitation expressed through the factor $\alpha$. For a constant temperature, expressed through the mean value of the timeseries ($T=\overline{T_{\mathrm{r}\mathrm{e}\mathrm{f}}}$), the growth is reduced. Consequently, higher temperature ($T=T_{\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}}$) enhances stalagmite growth and lower temperature reduces it. Additionally, a lower temperature results in a larger equilibrium radius, but this effect is rather insignificant.

4.2 Drip interval $\mathit{\tau }$

Since the modeled age over depth is independent of the drip interval, we must evaluate the radius, here the equilibrium radius, to identify the effect of drip rates. Supplementary Figure S9 shows the simulated equilibrium radius/age graphs for different drip intervals. According to Eq. 5, lowering the drip interval results in a larger radius. The more interesting case is the situation of an even higher interval. As demonstrated, the radius does not vary a lot after a certain threshold is passed, which has already been discussed in Kaufmann (2003) and Romanov et al. (2008). It stays rather constant at a low value. Therefore, the model suggests that a regular diameter of stalagmites can be the result of a constant drip interval or alternatively a very long one (here more than 100 s), in accordance with results from Romanov et al. (2008). The model also confirms results from Miorandi et al. (2010), as the drip interval converted to a drip rate is below 0.3l day⁻¹ and the result is a candle-shaped stalagmite. By taking the mean value of the drip interval estimated from the precipitation data, the graph shows a clear increase of the equilibrium radius some 15 kyr ago, which highlights the influence of temperature for $\alpha$. Thus, temperature becomes visible only when the drip interval is constant over time. Consequently, it becomes clear that in our simulations, the drip interval is the key driver for the radius compared to the impact of temperature. This observation is most interesting if the drip interval responds to precipitation changes as we have presumed here, which is, given the complexity of infiltration and flow, not necessarily the case. In a more constrained environment or knowing the equilibrium radius well could thus help construct time series of drip intervals.

4.3 Carbon dioxide concentration

The age/depth graphs for different air $\mathrm{C}{\mathrm{O}}_2$ concentrations in the cave are shown in Supplementary Figure S10. Lowering the cave $\mathrm{C}{\mathrm{O}}_2$ concentration results in more growth, as expected from the enhanced gradient. But, this situation is purely theoretical as the atmospheric $\mathrm{C}{\mathrm{O}}_2$ concentration in our approximations is already at the lowest possible limit for $\mathrm{C}{\mathrm{O}}_2$ concentration inside a cave, which reflects a well-ventilated atmospheric cave. More realistic are higher $\mathrm{C}{\mathrm{O}}_2$ concentrations in the cave, and we would need to adjust other model parameters to keep the speleothem as close as possible to its predicted shape. Interestingly, when keeping $\mathrm{C}{\mathrm{O}}_2$ concentrations constant through time, thus ignoring known atmospheric changes as recorded in ice-cores, we obtain larger growth rates. So again, the model indicates that lower $\mathrm{C}{\mathrm{O}}_2$ concentrations enhance the growth more than large ones reducing it. Furthermore, Supplementary Figure S10 shows a growth hiatus after 14–15 kyr for the graph with the high $\mathrm{C}{\mathrm{O}}_2$ concentration. If we reconsider Eq. 4, it becomes clear that for high growth rates, the stalagmite needs a large difference between the calcium concentration of the water drop and the apparent equilibrium calcium concentration. As an increase in the $\mathrm{C}{\mathrm{O}}_2$ concentration increases the apparent calcium concentration (Supplementary Figure S11), the absence of growth for the So-2 stalagmite after 21 kyr could consequently result from a locally high $\mathrm{C}{\mathrm{O}}_2$ concentration, which inhibits precipitation.

4.4 Calcium concentration

By increasing the ${\mathrm{C}\mathrm{a}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}$ concentration, the difference in the apparent calcium concentration gets larger and subsequently the growth rate increases. As illustrated in Supplementary Figure S12, the stalagmite has twice the height after an increase in the ${\mathrm{C}\mathrm{a}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}$ concentration of around 30% (see Supplementary Figure S6 for the calcium values). This shows that the modeled system is highly sensitive to the calcium concentration as expected. The mean calcium concentration indicates that the changes in the growth rate mainly arise from variations in the ${\mathrm{C}\mathrm{a}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}$ concentration because the resulting graph is nearly linear. In general, the calcium concentration of the water drop calculated with CaveCalc is rather low compared to the results of Baker et al., 2016. However, the calculated values are comparable to measurements from the Clamouse Cave, France. There are several reasons common to both caves that may explain the low calcium concentration. As for the Clamouse Cave, the studied Sofular Cave has a Mediterranean climate, which comes with less abundant vegetation, compared to mid-latitude maritime or continental climates. In addition, the soil is very fine, which limits CO₂ production and thus dissolved calcium in the groundwater (Genty et al., 2001; Badertscher et al., 2014).

4.5 Mixing factor

To investigate the influence of the mixing factor between the water drops, which means the renewal rate of the chemical composition of the precipitating film, we need to use the Gauss model as the flow model does not allow mixing by definition. As the stalagmite resulting from the Gauss model is shorter, we need different settings for the temperature to approximate the So-1 interpolation graph with a mixing factor of 1. It should be noted that the used temperature is still between $T_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ and $T_{\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}}$. Overall, similar behavior is observed for a decreasing ${\mathrm{C}\mathrm{a}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}$ concentration or increasing $\mathrm{C}{\mathrm{O}}_2$ concentration. Decreasing the mixing factor, which means that the solution on top of the stalagmite is less dependent on the new water drop, reduces the growth rate (see Supplementary Figure S13). Apart from inhibiting the growth with a low mixing factor, which means a slow renewal rate of the chemical film composition, a low mixing factor also increases the equilibrium radius in the Gauss model (see Supplementary Figure S14).

4.6 Coupling of input parameters

While the impacts of calcium concentration, mixing factor, and cave air $\mathrm{C}{\mathrm{O}}_2$ are mostly linear, a combination of those with temperature and calcium concentration is not necessarily linear. We explore this aspect briefly in the Supplementary Material (see Supplementary Figure S15) to resolve the shape if we consider one out of four parameters or a pair of parameters time-invariant. Keeping temperature and calcium concentration constant yields an interesting observation since the growth is reduced in the first 15 kyr but enhanced in the last 10 kyr. Overall, the effects cancel out each other. The coupling between the mixing factor and the drip interval provides further insights into the model. It is observed that if the drip interval passes a certain threshold, there are no variations in the radius anymore and the equilibrium radius is small. This can be coupled with the discovery that the mixing factor increases the equilibrium radius. Consequently, if there is a high drip interval and a mixing factor of around 0.1, the stalagmite can have a fairly regular radius of reasonable size (see Supplementary Figure S14).

4.7 Location of the stalagmite in the cave

Taking all these aspects together, one consequence becomes clear: the position of stalagmite inside the cave may impact the shape of the stalagmite because temperature and $\mathrm{C}{\mathrm{O}}_2$ concentration variations in the cave will have a significant effect on the shape. While temperature mostly varies by 1–2°C (Genty et al., 2006), which would result in a difference of height of only 15–20 cm considering a period of 25 kyr, the $\mathrm{C}{\mathrm{O}}_2$ concentration in a cave varies over a much larger range, from atmospheric conditions to values as high as a few thousand ppm (which equals a few 1 × ${\mathit{10}}^{-\mathit{3}}$ atm) (Baldini, 2010; Breeker et al., 2012). Assuming temperature to vary little compared to one order of magnitude variation in $\mathrm{C}{\mathrm{O}}_2$, the cave can be considered isothermal. The height of the speleothem is sensitive to adding $\mathrm{C}{\mathrm{O}}_2$ to the cave air. There is an exponential-like decrease in height which reaches zero at around 1.3 × ${\mathit{10}}^{-\mathit{3}}$ atm (see Supplementary Figure S16). Figure 5 illustrates the differences between stalagmites which grow at different positions in the cave, still forced by the same climate model output and CaveCalc chemistry. The two stalagmites with higher $\mathrm{C}{\mathrm{O}}_2$ concentration do not start growing in an equilibrium condition because there is no growth for the first few kyr; therefore, the bottom parts of the modeled stalagmites are less reliable. As demonstrated, the shape model predicts that under these ideal scenarios, stalagmites growing under similar conditions are smaller, the farther the stalagmite is inside the cave or in a less ventilated place. This results from the increase in $\mathrm{C}{\mathrm{O}}_2$ with the distance to the cave entrances or point of ventilation (Breeker et al., 2012). It should be noted that the model coupling is tuned to provide the best fit to the So-1 shape as a first example. We are well-aware of the large uncertainty in the used parameter space, but our last result highlights the importance of local climatology.

FIGURE 5

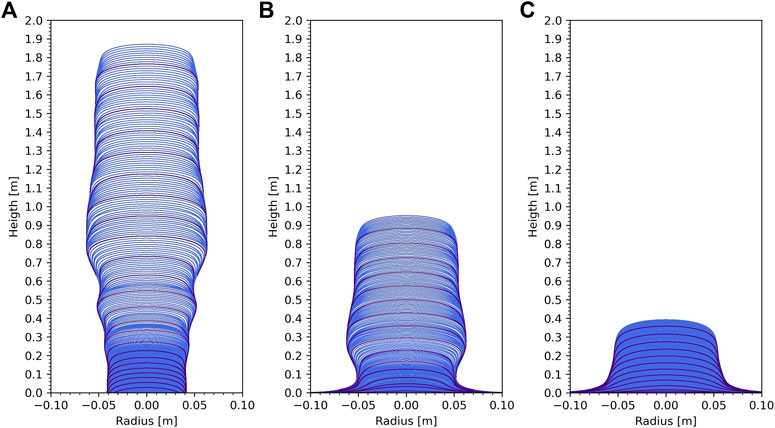
FIGURE 5. Stalagmite at different $\mathrm{C}{\mathrm{O}}_2$ concentrations. For (A), the atmospheric $\mathrm{C}{\mathrm{O}}_2$ concentration was used (Supplementary Figure S5); for (B), 3 × ${10}^{-3}$ atm was added; and for (C) 7 × ${10}^{-3}$ atm. It should be noted that here the upper limit of the ${\mathrm{C}\mathrm{a}}_{\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}}$ value from Supplementary Figure S7 is used because, otherwise, the stalagmite will stop growing if approximately 500 × ${10}^{-6}$ atm is passed.

5 Conclusion

We have demonstrated the sensitivity of speleothem growth to climatic conditions by combining algorithms to describe the equilibrium radius and the growth rate of a numerically generated stalagmite shape driven by an Earth-system model and a drip-water chemistry model. As a test case, we used the So-1 stalagmite from the Sofular Cave in Northern Turkey. The presented shape model (Romanov et al., 2008) only needs four input parameters to simulate the stalagmite: cave temperature, calcium concentration of the water drop, drip interval, and $\mathrm{C}{\mathrm{O}}_2$ concentration within the cave. To determine these values, we use modeled data from the climate model MPI-ESMI1.2 and ice core data (Köhler et al., 2017). Additionally, we use CaveCalc, a numerical model for speleothem chemistry and isotopes (Owen et al., 2018), to calculate the chemical reactions in the soil and rock above the cave. For the stalagmite geometry, we used three different methods, whose main difference is the decrease in growth as the distance to the apex increases. We were able to simulate a stalagmite, which follows the trend of the observed So-1 stalagmite data for the growth rate, using the input parameters inside the respective error ranges. Real-world growth variations with periods smaller than 5 kyr are not visible. Furthermore, the effects of the individual parameters were tested. Here, we investigated not only the influence of higher and lower values but also the benefit of taking time series instead of constant values. The model suggests that the radius predominantly depends on the drip interval and just slightly upon temperature. Our model already includes many features and can be used to investigate several questions concerning the growth and shape of stalagmites. It opens the possibility to simulate a shape that roughly agrees with the real-world stalagmite. Consequently, the short answer to the question if a simulated stalagmite can look like a real-world stalagmite has to be “possibly” at this point. Even though the model does not perfectly reproduce the actual sample in all aspects, we can conclude that our approach bears great potential for future studies on the influence of climate parameters on stalagmite shape.

Data availability statement

The python code is published on GitHub under the following link: https://github.com/niklas1347/Stalagmite-Simulation-Shape-Model.git.

Author contributions

NM: conceptualization, methodology, software, writing—original draft, and visualization. AH: methodology and software. TK: resources, data curation, and writing—review and editing. ST: writing—review and editing and supervision. GK: writing—review and editing and methodology. NF: conceptualization, writing—review and editing, supervision, and project administration.

Funding

This research has been supported by the DFG (Grant Nos. FR1341/4-1 and FR1341/4-2). TK. is funded by the project PalMod of the German Federal Ministry of Education and Research (BMBF), Research for Sustainability initiative FONA (Grant No. 01LP1921A). For the publication fee, we acknowledge financial support by Deutsche Forschungsgemeinschaft within the funding program “Open Access Publikationskosten” as well as by Heidelberg University.

Acknowledgments

The authors would like to thank Dominik Fleitmann for providing valuable information in form of high-resolution images of the stalagmite. We are also very grateful to anonymous reviewers for their constructive feedback, which has contributed substantially to the quality of our manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.969211/full#supplementary-material

References

Badertscher, S., Borsato, A., Frisia, S., Cheng, H., Edwards, R., Tuysuz, O., et al. (2014). Speleothems as sensitive recorders of volcanic eruptions – The bronze age minoan eruption recorded in a stalagmite from Turkey. Earth Planet. Sci. Lett. 392, 58–66. doi:10.1016/j.epsl.2014.01.041

CrossRef Full Text | Google Scholar

Badertscher, S., Fleitmann, D., Cheng, H., Edwards, R. L., Gokturk, O. M., Zumbuhl, A., et al. (2011). Pleistocene water intrusions from the mediterranean and caspian seas into the Black Sea. Nat. Geosci. 4 (4), 236–239. doi:10.1038/ngeo1106

CrossRef Full Text | Google Scholar

Baker, A., Flemons, I., Andersen, M. S., Coleborn, K., and Treble, P. C. (2016). What determines the calcium concentration of speleothem-forming drip waters? Glob. Planet. Change 143, 152–161. doi:10.1016/j.gloplacha.2016.06.001

CrossRef Full Text | Google Scholar

Baker, A., Genty, D., Dreybrodt, W., Barnes, W. L., Mockler, N. J., and Grapes, J. (1998). Testing theoretically predicted stalagmite growth rate with recent annually laminated samples: Implications for past stalagmite deposition. Geochimica Cosmochimica Acta 62 (3), 393–404. doi:10.1016/S0016-7037(97)00343-8

CrossRef Full Text | Google Scholar

Baldini, J. U. L. (2010). Cave atmosphere controls on stalagmite growth rate and palaeoclimate records. Geol. Soc. Lond. Spec. Publ. 336 (1), 283–294. doi:10.1144/SP336.15

CrossRef Full Text | Google Scholar

Berger, A. L. (1978). Long-Term variations of daily insolation and quaternary climatic changes. J. Atmos. Sci. 35 (12), 2362–2367. doi:10.1175/1520-0469(1978)035<2362:LTVODI>2.0.CO;2

CrossRef Full Text | Google Scholar

Breeker, D. O., Payne, A. E., Quade, J., Banner, J. L., Ball, C. E., Meyer, K. W., et al. (2012). The sources and sinks of CO2 in caves under mixed woodland and grassland vegetation. Geochim. Cosmochim. Acta 96, 230–246. doi:10.1016/j.gca.2012.08.023

CrossRef Full Text | Google Scholar

Briggs, R. D., Pollard, D., and Tarasov, L. (2014). A data-constrained large ensemble analysis of Antarctic evolution since the Eemian. Quat. Sci. Rev. 103, 91–115. doi:10.1016/j.quascirev.2014.09.003

CrossRef Full Text | Google Scholar

Busenberg, E., and Plummer, L. N. (1985). Kinetic and thermodynamic factors controlling the distribution of SO32− and Na+ in calcites and selected arag- onites. Geochimica Cosmochimica Acta 49 (3), 713–725. doi:10.1016/0016-7037(85)90166-8

CrossRef Full Text | Google Scholar

Cerling, T. E., Solomon, D. K., Quade, J., and Bowman, J. R. (1991). On the isotopic composition of carbon in soil carbon dioxide. Geochimica Cosmochimica Acta 55 (11), 3403–3405. doi:10.1016/0016-7037(91)90498-T

CrossRef Full Text | Google Scholar

Cerling, T. E. (1984). The stable isotopic composition of modern soil carbonate and its relationship to climate. Earth Planet. Sci. Lett. 71 (2), 229–240. doi:10.1016/0012-821X(84)90089-X

CrossRef Full Text | Google Scholar

Crul, R. L. (1973). Minimum diameter stalagmites. Bull. Natl. Speleological Soc. 35 (1), 1–9.

Google Scholar

Dreybrodt, W. (1999). Chemical kinetics, speleothem growth and climate. Boreas 28 (3), 347–356. doi:10.1111/j.1502-3885.1999.tb00224.x

CrossRef Full Text | Google Scholar

Dreybrodt, W. (1988). Processes in karst systems: Physics, chemistry, and geology. s.l. Berlin Heidelberg: Springer.

Google Scholar

Dreybrodt, W., and Romanov, D. (2008). Regular stalagmites: The theory behind their shape. Acta Carsologica 37 (2-3). doi:10.3986/ac.v37i2-3.145

CrossRef Full Text | Google Scholar

Fairchild, I. J., Frisia, S., Borsato, A., and Tooth, A. F. (2006). “Speleothems,” in Geochemical sediments and landscapes.

Google Scholar

Fleitmann, D., Burns, S. J., Neff, U., Mangini, A., and Matter, A. (2003). Changing moisture sources over the last 330, 000 years in Northern Oman from fluid-inclusion evidence in speleothems. Quat. Res. 60 (2), 223–232. doi:10.1016/S0033-5894(03)00086-3

CrossRef Full Text | Google Scholar

Fleitmann, D., Cheng, H., Badertscher, S., Edwards, R. L., Mudelsee, M., Gokturk, O. M., et al. (2009). Timing and climatic impact of Greenland interstadials recorded in stalagmites from northern Turkey. Geophys. Res. Lett. 36, L19707. doi:10.1029/2009GL040050

CrossRef Full Text | Google Scholar

Genty, D., Baker, A., and Vokal, B. (2001). Intra- and inter-annual growth rate of modern stalagmites. Chem. Geol. 176 (1-4), 191–212. doi:10.1016/s0009-2541(00)00399-5

CrossRef Full Text | Google Scholar

Genty, D., Blamart, D., Ghaleb, B., Plagnes, V., Causse, C., Bakalowicz, M., et al. (2006). Timing and dynamics of the last deglaciation from European and North African δ13C stalagmite profiles—Comparison with Chinese and south hemisphere stalagmites. Quat. Sci. Rev. 25 (17-18), 2118–2142. doi:10.1016/j.quascirev.2006.01.030

CrossRef Full Text | Google Scholar

Götrük, O. M., Fleitmann, D., Badertscher, S., Cheng, H., Edwards, R., Leuenberger, M., et al. (2011). Climate on the southern Black Sea coast during the holocene: Implications from the sofular cave record. Quat. Sci. Rev. 30 (19-20), 2433–2445. doi:10.1016/j.quascirev.2011.05.007

CrossRef Full Text | Google Scholar

Hiederer, R., and Koechy, M. (2011). Global soil organic carbon estimates and the harmonized world soil database. Luxembourg: Publications Office of the European Union, 79. EUR 25225 EN. doi:10.2788/13267

CrossRef Full Text | Google Scholar

Ivanovic, R. F., Gregoire, L. J., Kageyama, M., Roche, D. M., Valdes, P. J., Burke, A., et al. (2016). Transient climate simulations of the deglaciation 21–9 thousand years before present (version 1) – PMIP4 Core experiment design and boundary conditions. Geosci. Model Dev. 9 (7), 2563–2587. doi:10.5194/gmd-9-2563-2016

CrossRef Full Text | Google Scholar

Kaufmann, G., and Dreybrodt, W. (2004). Stalagmite growth and palaeo-climate: An inverse approach. Earth Planet. Sci. Lett. 224 (3-4), 529–545. doi:10.1016/j.epsl.2004.05.020

CrossRef Full Text | Google Scholar

Kaufmann, G. (2003). Stalagmite growth and palaeo-climate: The numerical perspective. Earth Planet. Sci. Lett. 214 (1-2), 251–266. doi:10.1016/S0012-821X(03)00369-8

CrossRef Full Text | Google Scholar

Köhler, P., Nehrbass-Ahles, C., Schmitt, J., Stocker, T. F., and Fischer, H. (2017). A 156 kyr smoothed history of the atmospheric greenhouse gases CO&lt;sub&gt;2&lt;/sub&gt;, CH&lt;sub&gt;4&lt;/sub&gt;, and N&lt;sub&gt;2&lt;/sub&gt;O and their radiative forcing. Earth Syst. Sci. Data 9 (1), 363–387. doi:10.5194/essd-9-363-2017

CrossRef Full Text | Google Scholar

Laumanns, M., and Kaufmann, G. (1988). Drei höhlen der Region zonguldak, schwarzes meer, türkey. Verband dt. Höhlen- Karstforscher 34 (4), 110–112.

Google Scholar

Mauritsen, T., Bader, J., Becker, T., Behrens, J., Bittner, M., Brokopf, R., et al. (2019). Developments in the MPI-M earth system model version 1.2 (MPI-ESM1.2) and its response to increasing CO2. J. Adv. Model. Earth Syst. 11 (4), 998–1038. doi:10.1029/2018MS001400

PubMed Abstract | CrossRef Full Text | Google Scholar

Meccia, V. L., and Mikolajewicz, U. (2018). Interactive ocean bathymetry and coastlines for simulating the last deglaciation with the Max Planck Institute earth system model (MPI-ESM-v1.2). Geosci. Model Dev. 11 (11), 4677–4692. doi:10.5194/gmd-11-4677-2018

CrossRef Full Text | Google Scholar

Miorandi, R., Borsato, A., Frisia, S., Fairchild, I. J., and Richter, D. K. (2010). Epikarst hydrology and implications for stalagmite capture of climate changes at grotta di Ernesto (NE Italy): Results from long-term monitoring. Hydrol. Process. 24 (21), 3101–3114. doi:10.1002/hyp.7744

CrossRef Full Text | Google Scholar

Mühlinghaus, C., Scholz, D., and Manginni, A. (2007). Modelling stalagmite growth and δ13C as a function of drip interval and temperature. Geochimica Cosmochimica Acta 71 (11), 2780–2790. doi:10.1016/j.gca.2007.03.018

CrossRef Full Text | Google Scholar

Owen, R., Day, C. C., and Henderson, G. M. (2018). CaveCalc: A new model for speleothem chemistry & isotopes. Comput. Geosci. 119, 115–122. doi:10.1016/j.cageo.2018.06.011

CrossRef Full Text | Google Scholar

Parkhurst, D. L., and Appelo, C. A. J. (2013). “Description of input and examples for PHREEQC version 3—a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations,” in Modeling techniques (Denver, CO: U.S. Geological Survey). Available at: https://pubs.usgs.gov/tm/06/a43/.

Google Scholar

Quade, J., Cerling, T. E., and Bowman, J. R. (1989). Systematic variations in the carbon and oxygen isotopic composition of pedogenic carbonate along elevation transects in the southern Great Basin. GSA Bulettin 101 (4), 464–475. doi:10.1130/0016-7606(1989)101<0464:SVITCA>2.3.CO;2

CrossRef Full Text | Google Scholar

Rajendran, C. P., Sanwal, J., Morell, K. D., Sandiford, M., Kotlia, B. S., Hellstrom, J., et al. (2015). Stalagmite growth perturbations from the Kumaun Himalaya as potential earthquake recorders. J. Seismol. 20 (2), 579–594. doi:10.1007/s10950-015-9545-5

CrossRef Full Text | Google Scholar

Riddick, T., Brovkin, V., Hagemann, S., and Mikolajewicz, U. (2018). Dynamic hydrological discharge modelling for coupled climate model simulations of the last glacial cycle: The MPI-DynamicHD model version 3.0. Geosci. Model Dev. 11 (10), 4291–4316. doi:10.5194/gmd-11-4291-2018

CrossRef Full Text | Google Scholar

Romanov, D., Kaufmann, G., and Dreybrodt, W. (2008). Modeling stalagmite growth by first principles of chemistry and physics of calcite precipitation. Geochimica Cosmochimica Acta 72 (2), 423–437. doi:10.1016/j.gca.2007.09.038

CrossRef Full Text | Google Scholar

Rudzka, D., McDermott, F., Baldini, L., Fleitmann, D., Moreno, A., and Stoll, H. (2011). The coupled δ13C-radiocarbon systematics of three Late Glacial/early Holocene speleothems; insights into soil and cave processes at climatic transitions. Geochimica Cosmochimica Acta 75 (15), 4321–4339. doi:10.1016/j.gca.2011.05.022

CrossRef Full Text | Google Scholar

Tarasov, L., Dyke, A. S., Neal, R. M., and Peltier, W. R. (2012). A data-calibrated distribution of deglacial chronologies for the North American ice complex from glaciological modeling. Earth Planet. Sci. Lett. 315-316, 30–40. doi:10.1016/j.epsl.2011.09.010

CrossRef Full Text | Google Scholar

Therre, S., 2020. Radiocarbon in stalagmites: Indicator of climate variability and key to atmospheric radiocarbon reconstruction. doi:10.11588/heidok.00028743

CrossRef Full Text | Google Scholar

Tüysüz, O. (1999). Geology of the cretaceous sedimentary basins of the western pontides. Geol. J. 34 (1-2), 75–93. doi:10.1002/(sici)1099-1034(199901/06)34:1/2<75::aid-gj815>3.0.co;2-s

CrossRef Full Text | Google Scholar