Influence mechanism of confining pressure on the hydraulic aperture based on the fracture deformation constitutive law

The confining pressure induces the deformation of fractures with seepage through the fracture. The seepage characteristics can reflect the deformation of the hydraulic aperture. We propose theoretical models to describe the mechanism by which the confining pressure influences the hydraulic aperture based on the fracture deformation constitutive law models of Goodman, Bandis, Sun, and Rong. Hydromechanical testing data were used to validate the four types of proposed models. The experiment results reveal the confining pressure and hydraulic aperture model based on Sun’s exponential model describes the mechanism the best. The maximum hydraulic aperture closure deformation and initial hydraulic aperture go through a growth phase with a decreasing rate, and then, they enter a stability phase when the flow rate increases to 7 ml/min, while the normal stiffness of the fracture decreases to a certain value and then tends to a stable value. Flow rate decreases as confining pressure increases in a nonlinear progression, which is described by Sun’s exponential model well. We further found that in laboratory tests at various temperatures and in field tests, the confining pressure’s influence on the hydraulic aperture is highly consistent with the model based on Sun’s model. The model developed in this study describes the mechanism by which the confining pressure influences the hydraulic aperture, and it is meaningful to rock seepage engineering with in situ stress changes at different temperatures.

Introduction

Fractures are the key to fluid flow, transport, and heat transfer inside natural rock masses with distinct apertures due to the complex in situ stress (confining pressure), and knowledge of these fracture apertures plays an irreplaceable role in the seepage through fractures in many subsurface engineering applications, including seawater intrusion (Sebben et al., 2015), geothermal energy exploitation (Wang et al., 2021b; Li et al., 2022), Water–Silt Inrush Hazard (Ma et al., 2022a) and urban drainage systems (García et al., 2015; Ma et al., 2022b). However, previous research has focused on the relationship between the hydraulic aperture and in situ stress, and there are no theoretical models for predicting the change in the hydraulic aperture under in situ stress. It is meaningful to study the hydraulic aperture based on fracture deformation for performance assessment and optimization design in tunnels, urban underground railways, and many other underground spaces (Zhao et al., 2021).

To characterize the hydraulic aperture, the finite difference method was used to solve the lubrication equation, and the calculated results were displayed as a function of the ratio of the mean mechanical aperture to the standard deviation of the roughness distribution. The third power of the ratio of the hydraulic aperture to the average mechanical aperture is related to the ratio of the standard deviation of the mechanical aperture to the average mechanical aperture (Zimmerman and Bodvarsson, 1996). The ratio of the hydraulic aperture to the average mechanical aperture is not constant, and it can be expressed as an exponential relationship with the standard deviation of the average mechanical aperture (Renshaw, 1995). In tests conducted on gradient samples, the mean mechanical aperture was calculated and found to be considerably broader than the hydraulic aperture (Chen et al., 2000). In rock engineering applications, as one parameter used to estimate the fracture aperture, the hydraulic aperture was used in field hydraulic tests (Li et al., 2013; Cao et al., 2016). It is widely accepted that the hydraulic aperture is relevant to the fracture geometry and is meaningful to the accurate measurement of the hydraulic aperture and the permeability of the fractured rock. Affected by the measurement methods and characterization parameters of the fracture morphology used (Sun et al., 2020), the measurement accuracy of the fracture geometry is difficult in rock engineering.

Previous research has shown that the confining pressure has a non-negligible influence on the permeability and hydraulic aperture, which is affected by the ambient conditions, such as the temperature (Watanabe et al., 2017; Hopp et al., 2019), confining pressure (Chen et al., 2016; Shu et al., 2020), hydraulic pressure (Zhao et al., 2019) and dynamic disturbance (Du et al., 2019; Huang et al., 2022). However, the temperature has less impact on the change in the permeability at higher confining pressures (Ding et al., 2016). Moreover, transient pulse test results have shown that the roughness is no longer critical to the permeability when the confining pressure is greater than a certain value (Zhao et al., 2017). As an irreplaceable parameter affecting the permeability, only the experimental regularity of the confining pressure has been summarized. For the permeability reduction of fractured rocks, the technique of filling fractures with grout was proposed, and the stress-induced changes in the permeability of the infilled fractures were investigated (Zhou et al., 2020). Owing to the construction of buildings and the excavation of underground spaces, the distribution of the stress field in the original rock mass is changed (Chen et al., 2022; Yang et al., 2022). The change in the stress field distribution will inevitably lead to changes in the geometric parameters of the fracture in the rock mass, which will contribute to the change in the permeability of the fracture in the rock mass (Wang et al., 2021a; Ma et al., 2021). The change in the permeability of the rock mass will directly give rise to changes in the stability of the rock mass and the buildings on it. There is not even a reasonable theoretical model that describes the change in the hydraulic aperture under confining pressure.

By reviewing the discussion above, the mechanism of confining pressure on hydraulic aperture required further research. In this study, we investigated how the confining pressure affects the hydraulic aperture based on the fracture deformation constitutive law and how the flow rate is controlled by the confining pressure. Hydromechanical tests were conducted under different confining pressures (P_c=10–38 MPa) with a constant flow rate or seepage pressure. The results of this study enhance our understanding of the interaction between the seepage and the surrounding rock under different in situ stress conditions and offer guidance for rock engineering projects.

Model of hydraulic aperture and confining pressure

We studied the mechanism by which the confining pressure influences the hydraulic aperture (Figure 1). The artificial fracture specimens from a shale block, which was taken from Changning. Figure 1B expresses the fracture of the sample, which is produced by cutting along the diameter. There are conclusions that different lithology has a certain effect on permeability and non-Darcy flow coefficient of water flow in fractured rock (Ma et al., 2013), while the lithology was not focused in this manuscript. For incompressible steady-state fluid flow through a single fracture, the Navier-Stokes equation based on Newton’s second law was used:

$\rho \left[\frac{\partial \mathbf{u}}{\partial \mathrm{t}}+\left(\mathbf{u}\cdot \nabla \right)\mathbf{u}\right]=-\nabla P+\mu {\nabla }^2\mathbf{u}+\mathbf{F}(1)$

where u is the flow velocity; ρ is the fluid density; ▽P is the fluid pressure gradient; µ is the dynamic viscosity coefficient; and F is the body force vector.

FIGURE 1

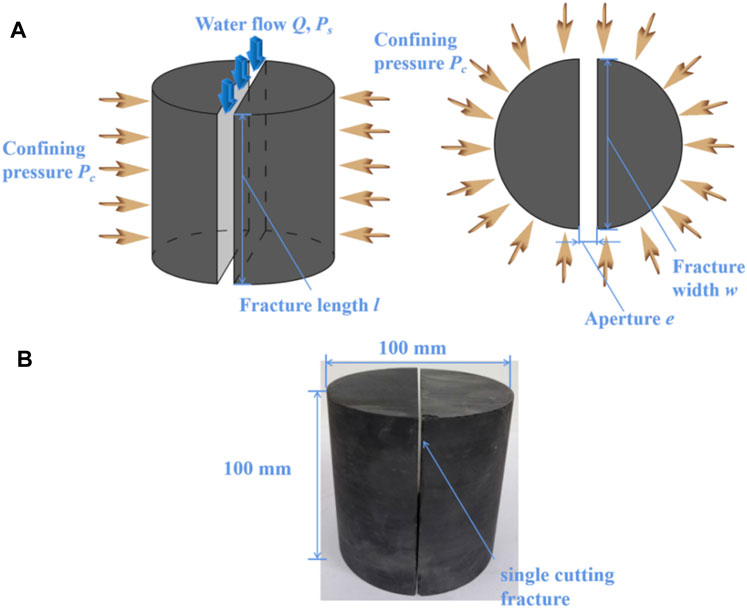
FIGURE 1. (A) Theoretical model of the confining pressure and hydraulic aperture (P_c−e_h) based on the fracture deformation constitutive law. (B) A shale sample is cut by a single fracture. The shale block was polished and cut in half along its diameter.

The inertial forces are negligible compared to the viscous forces. Thus, the N-S equation reduces to the Stokes equation, and the cubic law is obtained based on the assumption that the single fracture consists of two smooth parallel plates. The cubic law is as follows (Witherspoon et al., 1980):

$Q=-\frac{k{A}_h}{\mu }\nabla P=-\frac{w{e}_h^3}{12\mu }\nabla P(2)$

where Q is the discharge; k is the intrinsic permeability; A_h is the cross-sectional area; w is the fracture width; and e_h is the hydraulic aperture. The hydraulic aperture e_h can be calculated from the cubic law (Watanabe et al., 2008; Quinn et al., 2020) as follows:

$e_h^3=\frac{Q}{\raisebox{1ex}{$P_s$}\!\left/ \!\raisebox{-1ex}{$l$}\right.}\frac{12\mu }{w}(3)$

I. Goodman proposed the hyperbolic model of the fracture deformation constitutive law (Goodman, 1974):

$\Delta V_f=V_m-V_m{P}_i\frac{1}{P_c}(4)$

$\Delta V_f=e_h^i-e_h(5)$

where $\Delta V_f$ is the fracture closure deformation; $V_m$ is the maximum hydraulic aperture closure deformation; $P_i$ is the initial confining pressure; $P_c$ is the confining pressure; and $e_h^i$ is the initial hydraulic aperture. By combining Eqs 4, 5, the hydraulic aperture can be expressed as

$e_h=e_h^i-V_m+V_m{P}_i\frac{1}{P_c}(6)$

By combining Eqs 3, 6, under a constant seepage pressure P_s, the flow rate Q can be expressed as

$Q=\frac{P_{s}w}{12\mu l}{\left(e_h^i-V_m+V_m{P}_i\frac{1}{P_c}\right)}^3(7)$

II. Eq. 4 can be replaced by the hyperbolic model proposed by Bandis (Bandis et al., 1983):

$\Delta V_f=\frac{P_c{V}_m}{P_c+K_{ni}{V}_m}(8)$

where $K_{ni}$ is the initial normal stiffness of the fracture. The hydraulic aperture and flow rate, respectively, can be written as

$e_h=e_h^i-\frac{P_c{V}_m}{K_{ni}{V}_m+P_c}(9)$

$Q=\frac{P_{s}w}{12\mu l}{\left(e_h^i-\frac{P_c{V}_m}{K_{ni}{V}_m+P_c}\right)}^3(10)$

III. Sun proposed the exponential model (Sun and Lin, 1983):

$\Delta V_f=V_m-V_m\exp \left(-P_c/K_n\right)(11)$

where $K_n$ is the normal stiffness of the fracture. The hydraulic aperture and flow rate, respectively, can be written as

$e_h=e_h^i-V_m+V_m\exp \left(-\raisebox{1ex}{$P_c$}\!\left/ \!\raisebox{-1ex}{$K_n$}\right.\right)(12)$

$Q=\frac{P_{s}w}{12\mu l}{\left(e_h^i-V_m+V_m\exp \left(-\raisebox{1ex}{$P_c$}\!\left/ \!\raisebox{-1ex}{$K_n$}\right.\right)\right)}^3(13)$

IV. Rong proposed the g−λ model (Rong et al., 2012):

$\Delta V_f=V_m-V_m{\left(\frac{\lambda P_c}{K_{ni}{V}_m}+1\right)}^{-\frac{1}{\lambda }}(14)$

where $\lambda$ is a parameter associated with the fracture weathering, roughness, fluctuation degree, the matching of fracture surface and strength of the wall of the rock fracture. The hydraulic aperture and flow rate, respectively, can be written as

$e_h=e_h^i-V_m+V_m{\left(\frac{\lambda P_c}{K_{ni}{V}_m}+1\right)}^{-\frac{1}{\lambda }}(15)$

$Q=\frac{P_{s}w}{12\mu l}{\left[e_h^i-V_m+V_m{\left(\frac{\lambda P_c}{K_{ni}{V}_m}+1\right)}^{-\frac{1}{\lambda }}\right]}^3(16)$

In this theoretical model, the hydraulic aperture is used to characterize the aperture of the fracture, and the fracture deformation constitutive law is used to describe the effect of the confining pressure on the hydraulic aperture. This model gives the theoretical expression for the confining pressure P_c and the hydraulic aperture e_h related to the interaction between the flowing fluid and the surrounding rock. It provides a quantitative framework for investigating the evolution of the seepage characteristics with confining pressure.

Experimental methodology

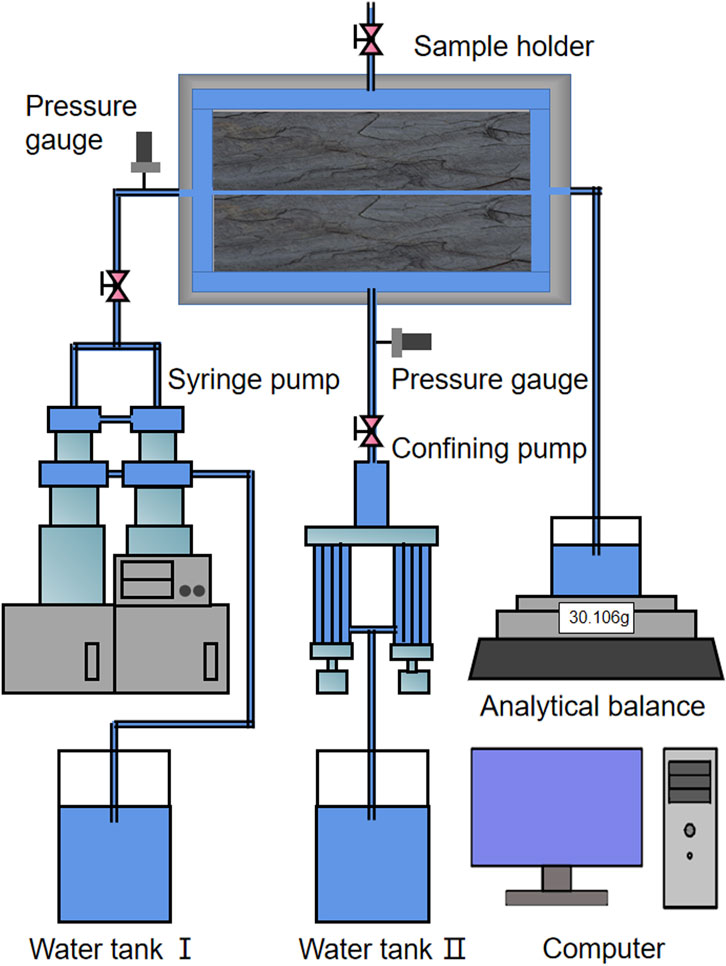
The above models show the mechanism by which the confining pressure P_c influences the hydraulic aperture e_h based on the fracture deformation constitutive law (fracture deformation constitutive law models of Goodman, Bandis, Sun, and Rong), and the relevant equations are proposed. To further validate the equations relating P_c to e_h or Q, we conducted hydromechanical tests on a shale sample cut by a single fracture (100 mm in width and 100 mm in length; Figure 1B) in the laboratory. The tests were performed using a device consisting of a confining pump (2J-X plunger metering pump), a syringe pump (ISCO 65D), pressure gauges, and a sample holder. The hydromechanical tests were conducted at a constant flow rate Q (2–14 ml/min) under confining pressure P_c (10–28 MPa), and at a constant seepage pressure P_s (400–2000 kPa) under confining pressure P_c (20–38 MPa).

The fluid mechanic’s test was carried out using laboratory instruments (Figure 2). The fluid mechanic’s experiment processes are as follows:

(1) The prefabricated single fracture rock sample was put into the holder. After placing the rock sample, connect the high-pressure pump, ring pressure pump and holder with capillary iron pipes to combine the fluid mechanic’s experimental system.

(2) The ring pressure pump was controlled by the computer to inject water into the ring pressure cavity of the holder, which is connected with water. After the confining pressure required for the experiment is reached, the water flow was injected into the holder through the high-pressure pump.

(3) Set up the flow required in the experiment. After the seepage flow was stable, measure the corresponding seepage pressure, record the data, and then apply the next-level seepage flow. Every level of seepage flow was constant.

(4) After recording the osmotic pressure under different seepage flow rates corresponding to the set confining pressure, gradually increase the confining pressure to the next confining pressure, repeat the previous step (3), and measure the seepage pressure under different flow rates.

FIGURE 2

FIGURE 2. Experimental equipment diagram.

Results and discussion

Relationship between the confining pressure P_c and hydraulic aperture e_h

The seepage pressure data for the hydromechanical tests under different confining pressures with a constant flow rate were precisely captured and recorded. Subsequently, the hydraulic aperture e_h was determined using Eq. 3.

Figure 3 shows the recorded confining pressure P_c and hydraulic aperture e_h of the shale sample cut by a single fracture for different flow rates Q. The curves of the hydraulic aperture versus confining pressure (e_h−P_c) illustrate that the four kinds of fracture deformation constitutive models (Goodman model, Bandis model, Sun model, and Rong model) apply to the relationship between the hydraulic aperture e_h and the confining pressure P_c (10–28 MPa) at different constant flow rates Q. The fitting curve and correlation coefficient R² was obtained for the curves in Figure 3. The hydraulic aperture decreases as the confining pressure continuously increases, and the rate of decrease of the curve becomes smooth after 16 MPa, indicating that the change in the hydraulic aperture with confining pressure is nonlinear when the confining pressure is greater than a certain value. The correlation coefficients R² of the Goodman model, Bandis model, Sun model, and Rong model are 0.9506–0.9706, 0.9484–0.9722, 0.9803–0.9926, and 0.8947–0.9769, respectively. A comparison of these four fitting curves revealed that the Sun model fits the test results better than the others.

FIGURE 3

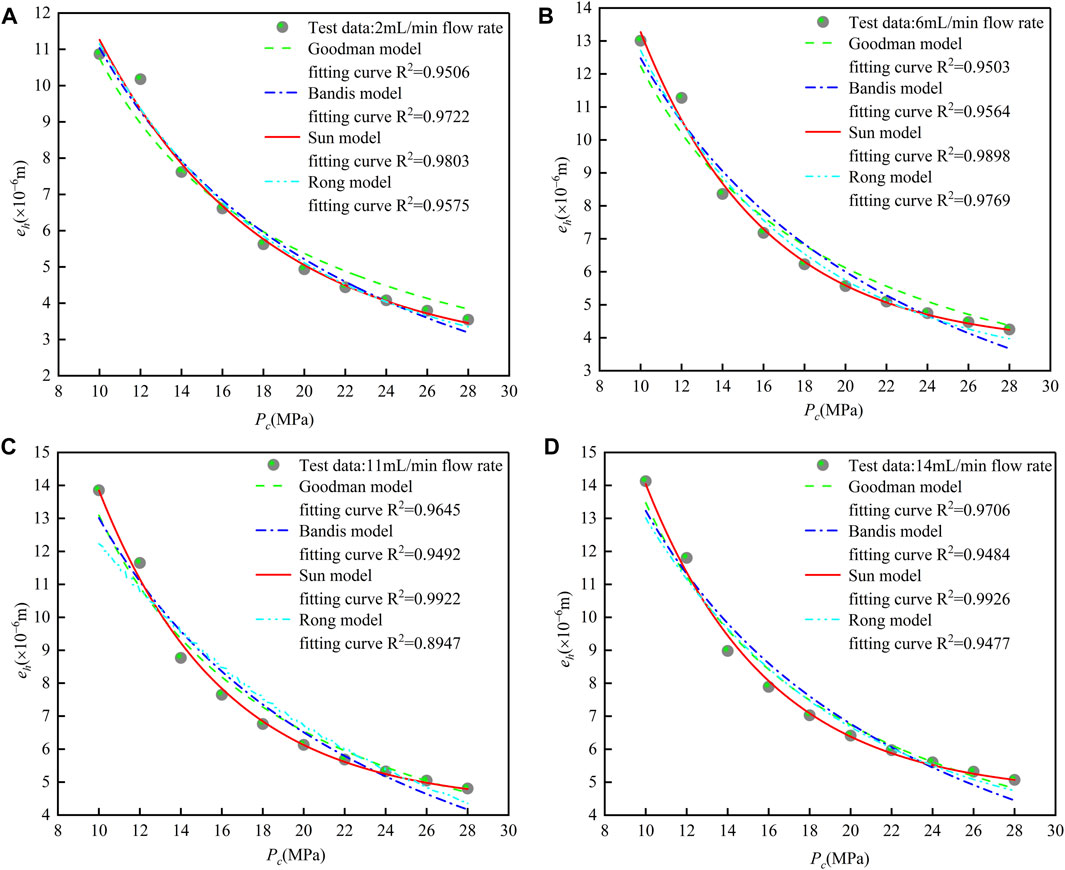
FIGURE 3. Variations in the hydraulic aperture (e_h) with increasing confining pressure (P_c). (A) Shale sample with a single fracture, Q=2 ml/min. (B) Shale sample with a single fracture, Q = 6 ml/min. (C) Shale sample with a single fracture, Q = 11 ml/min. (D) Shale sample with a single fracture, Q = 14 ml/min. The solid line is the fitting curve for the Sun model, the dashed line is the fitting curve for the Goodman model, the dotted-dashed line is the fitting curve for the Bandis model, and the dashed-dotted-dotted line is the fitting curve for the Rong model. The discrete symbols are measurement points from the hydromechanical tests with different flow rates.

Here, we provide a quantitative analysis of the confining pressure and hydraulic aperture based on four fracture deformation constitutive law models (Goodman model in Eq. 4; Bandis model in Eq. 8; Sun model in Eq. 11; Rong model in Eq. 14), and relevant equations for the relationship between the confining pressure and hydraulic aperture are proposed (Eqs 6, 9, 12, 15).

Based on the relatively close regression effect of the Sun model, a series of related parameters were taken into consideration (Figure 4), including the maximum hydraulic aperture closure deformation V_m, initial hydraulic aperture e_hⁱ, and normal stiffness of the fracture K_n. Calculation value of V_m, e_hⁱ and K_n were obtained from the fitting results in Figure 3. V_m and e_hⁱ go through a growth phase with a decreasing rate, and then, they enter a stability phase when Q increases to 7 ml/min. V_m and e_hⁱ are 50 and 54 μm in the stable phase, respectively. There is a decline phase with a decreasing rate for the change in K_n with Q. It similarly enters a stable phase, and the stable K_n is 6 MPa/μm when the flow rate increases to 7 ml/min. As the flow rate increases, $V_m$ and $e_h^i$ increase to certain values and then tend to stable values, and $K_n$ decreases to a certain value and then tends to a stable value. The correlation coefficient R² describes the fitting results of the Sun model of the fracture deformation constitutive law (Figure 3), and the fitting result increases significantly when the flow rate is less than a certain value. It is reasonable that insufficient water flow may lead to a deviation in the course of the experiment and inaccuracy of the cubic law in this model and the hydromechanical tests.

FIGURE 4

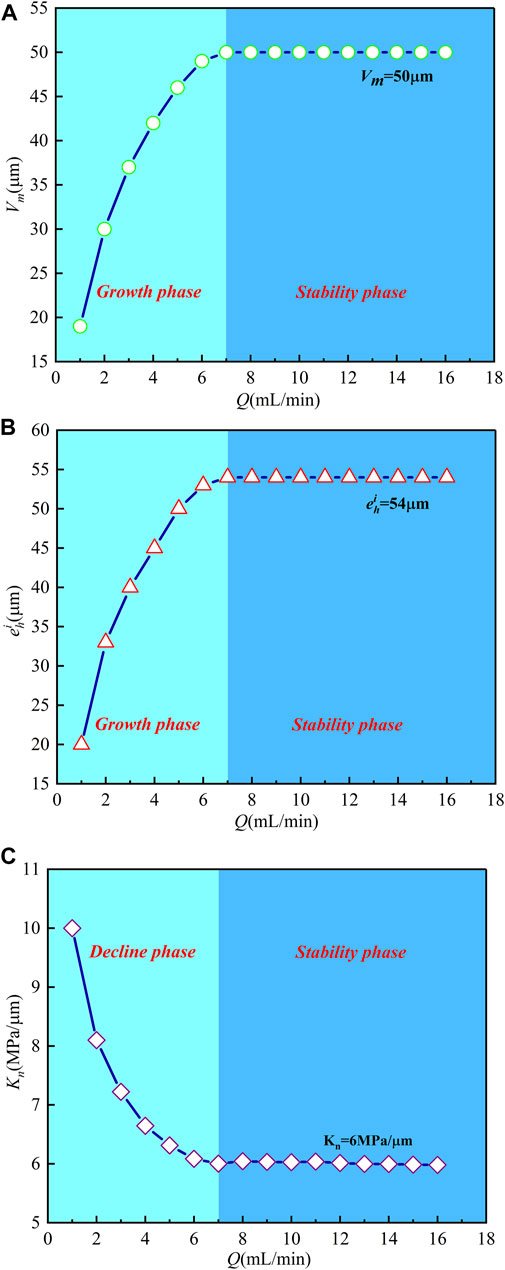
FIGURE 4. Regression results for the Sun model of the fracture deformation constitutive law. (A) Maximum hydraulic aperture closure deformation V_m and flow rate Q, (B) initial hydraulic aperture e_hⁱ and flow rate Q, and (C) normal stiffness of the fracture K_n and flow rate Q.

Relationship between the confining pressure P_c and flow rate Q

To explore the relationship between the flow rate Q and confining pressure P_c based on the fracture deformation constitutive law, we obtained a series of hydromechanical test data under various confining pressures at constant seepage pressures P_s (400, 1,000, 1,600, and 2,000 kPa). As for the different models of the fracture deformation constitutive law (Eqs 7, 10, 13, 16), constant seepage pressure is a prerequisite to obtaining the direct relationship between Q and P_c. The changes in Q under various P_c are shown in Figure 5, and the relevant models of the fracture deformation constitutive law were used to fit the hydromechanical test data.

FIGURE 5

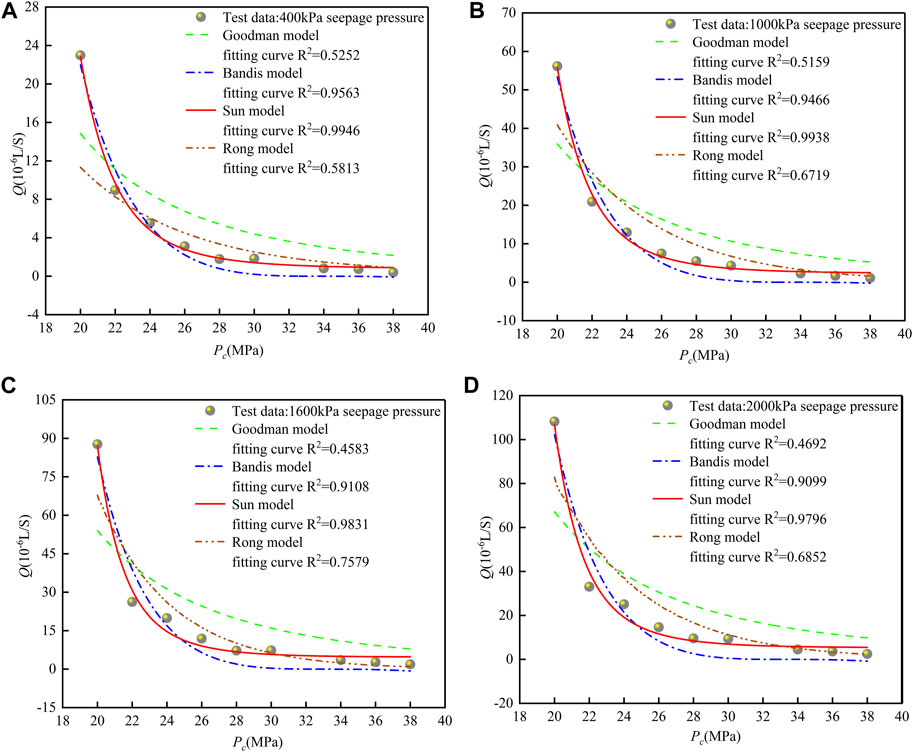
FIGURE 5. Variations in the flow rate (Q) with the confining pressure (P_c). (A) P_s = 400 kPa, (B) P_s = 1,000 kPa, (C) P_s = 1,600 kPa, and (D) P_s = 2,000 kPa. The solid line is the fitting curve for the Sun model, the dashed line is the fitting curve for the Goodman model, the dotted-dashed line is the fitting curve for the Bandis model, and the dashed-dotted-dotted line is the fitting curve for the Rong model. The discrete symbols are measurement points from the hydromechanical tests with different flow rates.

Figure 5 is a plot of the flow rate Q versus the confining pressure P_c based on the four proposed models of the fracture deformation constitutive law, and a series of hydromechanical test data were obtained under various confining pressures P_c (20–38 MPa) at different constant seepage pressures P_s. The Sun model can effectively describe the relationship between Q and P_c based on the constitutive law. Figure 5 shows that Q decreases as P_c increases in a nonlinear progression. It was found that Sun’s exponential model describes the fracture deformation characterized by the hydraulic aperture and affected by the confining pressure for a wide range of applications. Determination of the relationship between the flow rate and confining pressure based on the fracture deformation constitutive law has theoretical value and can be used to calculate the seepage parameters in rock engineering projects with widespread and variable in situ stress conditions.

Evaluation of the relationship between e_h and P_c based on Sun’s model, laboratory tests at various temperatures, and field tests

We evaluated the theoretical model using laboratory tests conducted at various temperatures (Shu et al., 2020) and field tests (Witherspoon et al., 1979). The above research results (Figure 5) show that the model for the relationship between the hydraulic aperture and the confining pressure based on Sun’s model of the fracture deformation constitutive law (Eq. (12)) most effectively fits the results, and the series of related parameters ($V_m$, $e_h^i$, and $K_n$) are all reasonable. Thus, the theoretical model based on Sun’s model was used to evaluate the relationship between e_h and P_c, and the correlation coefficients R² are listed in Figure 6.

FIGURE 6

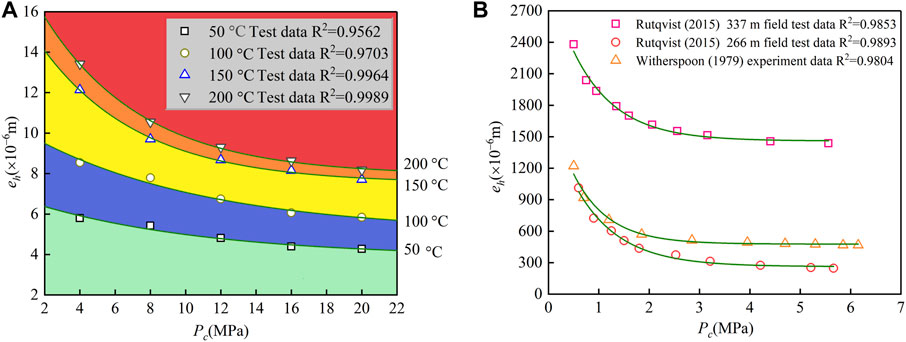
FIGURE 6. Evaluation of the proposed model for the relationship between the hydraulic aperture and the confining pressure based on Sun’s model of the fracture deformation constitutive law. (A) Hydraulic aperture and confining pressure test data for various temperatures. The green area represents the part where the temperature is less than 50°C, the blue area represents the part where the temperature is greater than 50°C and less than 100°C, and the yellow area represents the part where the temperature is greater than 100°C and less than 150°C, the orange area represents the part where the temperature is greater than 150°C and less than 200°C, and the orange area represents the part where the temperature is greater than 200°C. (B) The field test data for the hydraulic aperture and confining pressure for fractures at depths of 266 and 227 m, and the test data from an ultra-large core experiment. The solid line is the fitting curve for the Sun model, and the discrete symbols are the test data.

The proposed model for the relationship between the hydraulic aperture and the confining pressure based on Sun’s model of the fracture deformation constitutive law was used to fit the experimental data obtained at various temperatures and the field test data. The results indicate that under various temperature conditions (Figure 6A) and field conditions (Figure 6B), this model can predict the influence of the confining pressure on the hydraulic aperture well. This model is meaningful to rock engineering applications under various in situ temperature conditions and coupling conditions.

Conclusion

In this study, we investigated the mechanism by which the confining pressure influences the hydraulic aperture based on the fracture deformation constitutive law using a combination of hydromechanical tests and a theoretical model, and regression analysis was performed on the test data using the proposed model. The main conclusion of this study are as follows.

(1) Four types of models for the relationship between the hydraulic aperture or flow rate and the confining pressure were obtained, and the hydromechanical tests were performed under different confining pressures.

(2) The fitting results of the hydromechanical test data show that the proposed model based on Sun’s model of the fracture deformation constitutive law describes the relationship between the confining pressure, hydraulic aperture, and flow rate the best.

(3) In this study, the hydraulic aperture and confining pressure model based on Sun’s model of the fracture deformation constitutive law was evaluated using laboratory tests conducted at various temperatures and field tests.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

PF, HM, and JQ contributed to conception and design of the study. QL organized the database. JW performed the statistical analysis. PF wrote the first draft of the manuscript. PF, JW, and HM wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 41831289, 41772250, and 41877191).

Acknowledgments

The authors also thank the reviewers for their helpful comments and suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bandis, S. C., Lumsden, A. C., and Barton, N. R. (1983). Fundamentals of rock joint deformation. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 20 (6), 249–268. doi:10.1016/0148-9062(83)90595-8

CrossRef Full Text | Google Scholar

Cao, Y. B., Feng, X. T., Yan, E. C., Chen, G., Lü, F. F., Ji, H. B., et al. (2016). Calculation method and distribution characteristics of fracture hydraulic aperture from field experiments in fractured granite area. Rock Mech. Rock Eng. 49 (5), 1629–1647. doi:10.1007/s00603-015-0881-0

CrossRef Full Text | Google Scholar

Catalli, F., Meier, M. A., and Wiemer, S. (2013). The role of Coulomb stress changes for injection-induced seismicity: The Basel enhanced geothermal system. Geophys. Res. Lett. 40 (1), 72–77. doi:10.1029/2012GL054147

CrossRef Full Text | Google Scholar

Chen, J., Jiang, D., Ren, S., and Yang, C. (2016). Comparison of the characteristics of rock salt exposed to loading and unloading of confining pressures. Acta Geotech. 11 (1), 221–230. doi:10.1007/s11440-015-0369-9

CrossRef Full Text | Google Scholar

Chen, Y., Lin, H., Xie, S., Ding, X., He, D., Yong, W., et al. (2022). Effect of joint microcharacteristics on macroshear behavior of single-bolted rock joints by the numerical modelling with PFC. Environ. Earth Sci. 81, 276. doi:10.1007/s12665-022-10411-y

CrossRef Full Text | Google Scholar

Chen, Z., Narayan, S. P., Yang, Z., and Rahman, S. S. (2000). An experimental investigation of hydraulic behaviour of fractures and joints in granitic rock. Int. J. Rock Mech. Min. Sci. 37 (7), 1061–1071. doi:10.1016/S1365-1609(00)00039-3

CrossRef Full Text | Google Scholar

Ding, Q. L., Ju, F., Song, S. B., Yu, B. Y., and Ma, D. (2016). An experimental study of fractured sandstone permeability after high-temperature treatment under different confining pressures. J. Nat. Gas Sci. Eng. 34, 55–63. doi:10.1016/j.jngse.2016.06.034

CrossRef Full Text | Google Scholar

Du, H., Song, D., Chen, Z., and Guo, Z. (2019). Experimental study of the influence of structural planes on the mechanical properties of sandstone specimens under cyclic dynamic disturbance. Energy Sci. Eng. 8, 4043–4063. doi:10.1002/ese3.794

CrossRef Full Text | Google Scholar

Fu, G., Butler, D., Khu, S. T., and Sun, S. A. (2011). Imprecise probabilistic evaluation of sewer flooding in urban drainage systems using random set theory. Water Resour. Res. 47 (2). doi:10.1029/2009WR008944

CrossRef Full Text | Google Scholar

García, L., Barreiro-Gomez, J., Escobar, E., Téllez, D., Quijano, N., and Ocampo-Martínez, C. (2015). Modeling and real-time control of urban drainage systems: A review. Adv. Water Resour. 85, 120–132. doi:10.1016/j.advwatres.2015.08.007

CrossRef Full Text | Google Scholar

Goodman, R. E. (1974). The mechanical properties of joints. Proceedings of the third congress of the International Society for Rock Mechanics,21 1–7. Denver, Colorado

Google Scholar

Hopp, C., Sewell, S., Mroczek, S., Savage, M., and Townend, J. (2019). Seismic response to injection well stimulation in a high-temperature, high-permeability reservoir. Geochem. Geophys. Geosyst. 20 (6), 2848–2871. doi:10.1029/2019GC008243

CrossRef Full Text | Google Scholar

Huang, J., Liu, X. L., Song, D. Q., Zhao, J., Wang, E. Z., and Zhang, J. M. (2022). Laboratory-scale investigation of response characteristics of liquid-filled rock joints with different joint inclinations under dynamic loading. J. Rock Mech. Geotechnical Eng. 14 (2), 396–406. doi:10.1016/j.jrmge.2021.08.014

CrossRef Full Text | Google Scholar

Jiménez-Martínez, J., Porter, M. L., Hyman, J. D., Carey, J. W., and Viswanathan, H. S. (2016). Mixing in a three-phase system: Enhanced production of oil-wet reservoirs by CO2 injection. Geophys. Res. Lett. 43 (1), 196–205. doi:10.1002/2015GL066787

CrossRef Full Text | Google Scholar

Li, L., Meng, Q., Wang, S., Li, G., and Tang, C. (2013). A numerical investigation of the hydraulic fracturing behaviour of conglomerate in Glutenite formation. Acta Geotech. 8 (6), 597–618. doi:10.1007/s11440-013-0209-8

CrossRef Full Text | Google Scholar

Li, Q., Ma, D., Zhang, Y., Liu, Y., and Ma, Y. (2022). Insights into controlling factors of pore structure and hydraulic properties of broken rock mass in a geothermal reservoir. Lithosphere 2022, 387382. doi:10.2113/2022/3887832

CrossRef Full Text | Google Scholar

Ma, D., Duan, H., Zhang, J., Liu, X., and Li, Z. (2022a). Numerical simulation of water–silt Inrush hazard of fault rock: A three-phase flow model. Rock Mech. Rock Eng. 55, 5163–5182. doi:10.1007/s00603-022-02878-9

CrossRef Full Text | Google Scholar

Ma, D., Duan, H., and Zhang, J. (2022b). Solid grain migration on hydraulic properties of fault rocks in underground mining tunnel: Radial seepage experiments and verification of permeability prediction. Tunn. Undergr. Space Technol. 126, 104525. doi:10.1016/j.tust.2022.104525

CrossRef Full Text | Google Scholar

Ma, D., Miao, X. X., Chen, Z. Q., and Mao, X. B. (2013). Experimental investigation of seepage properties of fractured rocks under different confining pressures. Rock Mech. Rock Eng. 46 (5), 1135–1144. doi:10.1007/s00603-012-0329-8

CrossRef Full Text | Google Scholar

Ma, H., Wang, J., Qian, J., Tan, X., Chen, L., Deng, Y., et al. (2021). Two-dimensional SPH analysis of seepage with water injection process for different crack morphologies. KSCE J. Civ. Eng. 25 (5), 1909–1917. doi:10.1007/s12205-021-1202-7

CrossRef Full Text | Google Scholar

Parisio, F., and Yoshioka, K. (2020). Modeling fluid reinjection into an enhanced geothermal system. Geophys. Res. Lett. 47 (19), e2020GL089886. doi:10.1029/2020GL089886

CrossRef Full Text | Google Scholar

Quinn, P. M., Cherry, J. A., and Parker, B. L. (2020). Relationship between the critical Reynolds number and aperture for flow through single fractures: Evidence from published laboratory studies. J. Hydrology 581, 124384. doi:10.1016/j.jhydrol.2019.124384

CrossRef Full Text | Google Scholar

Renshaw, C. E. (1995). On the relationship between mechanical and hydraulic apertures in rough-walled fractures. J. Geophys. Res. 100 (B12), 24629–24636. doi:10.1029/95JB02159

CrossRef Full Text | Google Scholar

Rong, G., Huang, K., Zhou, C., Wang, X., and Peng, J. (2012). A new constitutive law for the nonlinear normal deformation of rock joints under normal load. Sci. China Technol. Sci. 55 (2), 555–567. doi:10.1007/s11431-011-4654-z

CrossRef Full Text | Google Scholar

Sebben, M. L., Werner, A. D., and Graf, T. (2015). Seawater intrusion in fractured coastal aquifers: A preliminary numerical investigation using a fractured henry problem. Adv. water Resour. 85, 93–108. doi:10.1016/j.advwatres.2015.09.013

CrossRef Full Text | Google Scholar

Shu, B., Zhu, R., Elsworth, D., Dick, J., Zhang, S., Tan, J., et al. (2020). Effect of temperature and confining pressure on the evolution of hydraulic and heat transfer properties of geothermal fracture in granite. Appl. Energy 272, 115290. doi:10.1016/j.apenergy.2020.115290

CrossRef Full Text | Google Scholar

Sun, G. Z., and Lin, W. Z. (1983). The compresstional deformation law of rockmass structure surface and a constitutive equation of rockmass elastic deformation. Chin. J. Geol. 2, 81–87. (In Chinese).

Google Scholar

Sun, Z., Wang, L., Zhou, J. Q., and Wang, C. (2020). A new method for determining the hydraulic aperture of rough rock fractures using the support vector regression. Eng. Geol. 271, 105618. doi:10.1016/j.enggeo.2020.105618

CrossRef Full Text | Google Scholar

Wang, J., Ma, H., Qian, J., Feng, P., Tan, X., and Ma, L. (2021a). Experimental and theoretical study on the seepage mechanism characteristics coupling with confining pressure. Eng. Geol. 291, 106224, 106224. doi:10.1016/j.enggeo.2021.106224

CrossRef Full Text | Google Scholar

Wang, Y., de Hoop, S., Voskov, D., Bruhn, D., and Bertotti, G. (2021b). Modeling of multiphase mass and heat transfer in fractured high-enthalpy geothermal systems with advanced discrete fracture methodology. Adv. Water Resour. 154, 103985. doi:10.1016/j.advwatres.2021.103985

CrossRef Full Text | Google Scholar

Ward, D. S., Buss, D. R., Mercer, J. W., and Hughes, S. S. (1987). Evaluation of a groundwater corrective action at the Chem-Dyne hazardous waste site using a telescopic mesh refinement modeling approach. Water Resour. Res. 23 (4), 603–617. doi:10.1029/WR023i004p00603

CrossRef Full Text | Google Scholar

Watanabe, N., Egawa, M., Sakaguchi, K., Ishibashi, T., and Tsuchiya, N. (2017). Hydraulic fracturing and permeability enhancement in granite from subcritical/brittle to supercritical/ductile conditions. Geophys. Res. Lett. 44 (11), 5468–5475. doi:10.1002/2017GL073898

CrossRef Full Text | Google Scholar

Watanabe, N., Hirano, N., and Tsuchiya, N. (2008). Determination of aperture structure and fluid flow in a rock fracture by high-resolution numerical modeling on the basis of a flow-through experiment under confining pressure. Water Resour. Res. 44 (6). doi:10.1029/2006WR005411

CrossRef Full Text | Google Scholar

Witherspoon, P. A., Amick, C. H., Gale, J. E., and Iwai, K. (1979). Observations of a potential size-effect in experimental determination of the hydraulic properties of fractures. Water Resour. Res. 15 (5), 1142–1146. doi:10.1029/WR015i005p01142

CrossRef Full Text | Google Scholar

Witherspoon, P. A., Wang, J. S., Iwai, K., and Gale, J. E. (1980). Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 16 (6), 1016–1024. doi:10.1029/WR016i006p01016

CrossRef Full Text | Google Scholar

Yang, H., Lin, H., Chen, Y., Wang, Y., Zhao, Y., Yong, W., et al. (2022). Influence of wing crack propagation on the failure process and strength of fractured specimens. Bull. Eng. Geol. Environ. 81, 71. doi:10.1007/s10064-021-02550-6

CrossRef Full Text | Google Scholar

Zhang, B., Wang, S., Diao, M., Fu, J., Xie, M., Shi, J., et al. (2019). Microbial community responses to vanadium distributions in mining geological environments and bioremediation assessment. J. Geophys. Res. Biogeosci. 124 (3), 601–615. doi:10.1029/2018JG004670

CrossRef Full Text | Google Scholar

Zhao, Y., Liu, Q., Zhang, C., Liao, J., Lin, H., and Wang, Y. (2021). Coupled seepage-damage effect in fractured rock masses: Model development and a case study. Int. J. Rock Mech. Min. Sci. 144, 104822. doi:10.1016/j.ijrmms.2021.104822

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, Y., Wang, W., Tang, L., Liu, Q., and Chen, G. (2019). Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mech. 101, 59–66. doi:10.1016/j.tafmec.2019.01.026

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, L., Wang, W., Tang, J., Lin, H., and Wan, W. (2017). Transient pulse test and morphological analysis of single rock fractures. Int. J. Rock Mech. Min. Sci. 91, 139–154. doi:10.1016/j.ijrmms.2016.11.016

CrossRef Full Text | Google Scholar

Zhou, D., Zhao, Z., Li, B., Chen, Y., and Ding, W. (2020). Permeability evolution of grout infilled fractures subjected to triaxial compression with low confining pressure. Tunn. Undergr. Space Technol. 104, 103539. doi:10.1016/j.tust.2020.103539

CrossRef Full Text | Google Scholar

Zimmerman, R. W., and Bodvarsson, G. S. (1996). Hydraulic conductivity of rock fractures. Transp. Porous Media 23 (1), 1–30. doi:10.1007/BF00145263

CrossRef Full Text | Google Scholar

Nomenclature

Latin alphabet

A_h cross-sectional area

e_h hydraulic aperture

e_hⁱ initial hydraulic aperture

F body force vector

k intrinsic permeability

K_n normal stiffness of the fracture

K_nⁱ initial normal stiffness of the fracture

P_c confining pressure

P_i initial confining pressure

P_s seepage pressure

∇P fluid pressure gradient

Q flow rate

R² Correlation coefficient

u flow velocity

V_m maximum hydraulic aperture closure deformation

w fracture width

ΔV_f fracture closure deformation

λ Parameter

µ dynamic viscosity coefficient

ρ fluid density