A possible characteristic of foreshocks derived from the evaluation of loading/unloading induced by earth tides

The detection of the potential of a larger event immediately after a moderate earthquake is a quite difficult problem. In this work, we devised an approach to determine whether an earthquake is a foreshock to a larger mainshock by evaluating loading/unloading states. This is done by calculating the Coulomb failure stress (CFS) change induced by Earth tides along the tectonically preferred slip direction on the seismogenic fault surface of each of the candidates. The technique is based on the load/unload response ratio (LURR) method, but the determination of the sliding direction of CFS is different, which is derived from the moderate earthquake that has just occurred rather than the assumption from the regional stress setting. Using the approach, we tested since the year 2000 the M_s ≥ 4.0 foreshocks of the M_s ≥ 6.0 earthquakes on the Chinese mainland, and also the earthquake swarms where no subsequent larger mainshocks were expected in the previous 10 years. The former mostly occurred in the loading process, while the latter arose more frequently in a random process. The marked difference indicates that the occurrence of earthquakes during loading may imply the critical state of the seismogenic faults, and the derived stress is more likely to trigger a larger event than that of the earthquakes that occurred during unloading.

Highlights

1. A new approach to detect characteristics of foreshocks is devised, which is based on the LURR method but more applicable.

2. The evaluation of loading/unloading induced by Earth tides may be a feasible way to identify foreshocks.

3. By establishing the Red-Yellow-Green signal model, this approach may be applied to the real-time evaluation of earthquake potential.

Introduction

On average, more than 100 earthquakes of magnitude 6.0 and above occur in the world annually, of which about 15% have foreshocks (Reasenberg 1999; Marzocchi and Zhuang, 2011). The existence of foreshocks may provide an opportunity for the prediction of the upcoming larger mainshocks. Unfortunately, the method to identify foreshocks has not been found yet. On 6 April 2009, an earthquake of magnitude 6.3 hits L'Aquila, Italy, which killed more than 300 people (Jordan et al., 2011). Prior to the mainshock, two moderate earthquakes of magnitude 4.3 and 4.0 occurred within 50 km of the epicenter on March 30 and 5 April 2009, respectively. These two earthquakes, however, were not regarded as the foreshocks to the subsequent mainshock. China is also a very active area of seismicity, in which the foreshocks are often observed. For example, before the M_s 6.4 Yangbi mainshock on 21 May 2021 (Beijing time), four moderate earthquakes of M_s > 4.0 occurred successively in the epicentral area since May 18. Although China has carried out foreshock identification immediately after these earthquakes, the final rupture of Yangbi was not alarmed via its foreshocks.

It is difficult to perform foreshock identification because the candidates far outnumbered the foreshocks (Jones and Molnar, 1979). Agnew and Jones (1991) developed the Empirical Foreshock Probability (EFP) model, but the prediction efficiency of this method is often discounted due to the uncertainty of background seismicity (Michael, 2011). The model of Epidemic Type Aftershock Sequence (ETAS) is believed to be a feasible method for foreshock identification (Marzocchi and Zhuang, 2011). Unfortunately, it is hard to distinguish foreshocks, mainshocks, and aftershocks with the tiny probability gain. There also are attempts focusing on the alarm-based earthquake predictions (Zechar and Jordan, 2008), such as the Pattern Informatics (PI) (Rundle et al., 2002), Reverse Tracking Precursor (RTP) (shebalin et al., 2006), Region-Time-Length (RTL) (Sobolev, 2001) as well as the b value resulted from the Gutenberg Richter law (Gerstenberger et al., 2005), Accelerate Moment Release (AMR) based on the concept of the critical point (Bowman et al., 1998) and seismic velocity ratio derived from the change of rock properties (Scholz et al., 1973). However, the large warning areas and high false alarms prevent these methods to be used as tools for foreshock identification.

In recent years, some researchers have found that tidal stress has a great influence on the occurrence of earthquakes (Cochran et al., 2004). Based on this thought, Yin et al. (1995) set the parameter of load/unload response ratio (LURR) to evaluate the potential of future large earthquakes. They concluded that the LURR derived from the difference between responses during the loading and unloading phases induced by Earth tides could be adopted to reveal the criticality of the crustal system. When the LURR is low, the system is in a stable state; and when the LURR is high, the system is close to failure. Since the LURR is calculated by using the Benioff strains of earthquakes within certain temporal and special windows, the loading/unloading states of some marked foreshocks that release more Benioff strains should have a greater influence on the change of LURR (Yin et al., 2008). This may provide an opportunity for the identification of foreshocks as well as the evaluation of the criticality of the ensuing larger mainshocks.

In this study, we attempt to refine the LURR method to assess the potential of a future large earthquake by substituting the calculation of the ratio between Benioff strains of earthquakes during the loading and unloading processes with the evaluation of the loading/unloading states of the earthquakes of magnitude 4.0 and above. To show the validity of this method, the M_s ≥ 4.0 foreshocks of 16 earthquakes of magnitude 6.0 and above on the Chinese mainland since 2000 were chosen as the examples. In addition, we examined the loading/unloading states of some earthquake swarms which were not followed by larger mainshocks subsequently.

Methods

The load/unload response ratio (LURR) method (Yin et al., 2000) has been widely used in earthquake prediction. In this study, by analyzing the loading/unloading state of each moderate earthquake that has occurred, we apply this technique to identify foreshocks. The methodology of this approach is based on the traditional LURR method. Therefore, we first make a brief review of the LURR method and then describe the strategy of foreshock identification and related algorithm on this basis.

The LURR method

The occurrence of a large earthquake can be regarded as a sudden rupture in the upper crust due to the accumulation of tectonic stress (Allmann and Shearer, 2009). The LURR method is set to detect the potential of future large earthquakes by determining the stress state of source media (Yin et al., 2000).

Generally, the stress in the Earth’s crust mainly includes the tectonic and tide ones, and the tidal stress is far smaller than tectonic stress. The LURR is defined as:

$Y=\frac{X_{+}}{X_{-}},(1)$

where “+” and “-” indicate the loading/unloading states, and X is expressed as:

$X=\underset{\mathrm{\Delta }P\to 0}{\lim }\frac{\mathrm{\Delta }R}{\mathrm{\Delta }P},(2)$

in which R and P represent the response and load of a rock medium, respectively (Figure 1, Yin et al., 2000).

FIGURE 1

FIGURE 1. The variation of LURR with rock constitutive curve.

When the stress level is low, the response to loading is the same as that of the unloading, and LURR = 1.0. Whereas when tectonic stress exceeds the linear elastic stage, the responses to the loading and unloading should become quite different, and LURR >1.0.

In seismic data testing, the LURR is usually defined as:

$Y=\frac{{\left({{\displaystyle \sum }}_{i=1}^{N_{+}}{B}_i\right)}_{+}}{{\left({{\displaystyle \sum }}_{i=1}^{N_{-}}{B}_i\right)}_{-}},(3)$

where Bi is the Benioff strain of the ith earthquakes within certain time-space windows (Yu et al., 2006), and N₊ or N_- denote respectively the numbers of earthquakes during the loading and unloading processes.

The LURR and foreshocks

In previous studies, quite a lot of cases have shown that anomalous high LURR peaks could be found, days to months, before the occurrence of a large earthquake (Yin et al., 2000; Yu et al., 2006, 2020). The results indicate that earthquakes can be modulated by tidal stress only when seismogenic faults are critically loaded (Yu et al., 2006). The reason lies in that if the system is in a linear elastic state, small stress disturbances (tidal stress) are difficult to trigger fractures, and if the system reaches the yield or dilatant stage, any small stress disturbance may cause fractures. Meanwhile, the results also indicate that earthquakes tend to occur during the tide-induced loading rather than the unloading. This can be approved by the observations of the Kaiser effect (Li and Nordlund, 1993). When rock is subjected to the cyclic load, more cracks are created during the loading process. On the other hand, the foreshocks and their mainshock should result from the same process of stress accumulation because they occur in the same neighborhoods and during the same periods. In this sense, foreshocks are more likely to be modulated by tide-induced loading. Determination of the loading/unloading states of the foreshocks, the criticality of the seismogenic faults, and the potential of the ensuing larger events may be obtained.

Loading/unloading evaluation

The earthquake is a kind of dislocation along the fault surface. This type of fracture is usually caused by the effective shear stress (Byerlee, 1978). The Coulomb failure stress (CFS) should be adopted to identify the loading and unloading processes, and the failure of rock is decided by the Coulomb failure criterion (Jaeger et al., 2007).

The CFS on a fault plane can be expressed by using the synthetic-effective shear stress:

$\overrightarrow{\tau }={\overrightarrow{\tau }}^T+{\overrightarrow{\tau }}^t,(4)$

where, ${\overrightarrow{\tau }}^T$ and ${\overrightarrow{\tau }}^t$ represent respectively the tectonic-induced and tide-induced effective shear stresses, and $\overrightarrow{\mathrm{\tau }}$ is the synthetic effective shear stress in the tectonically preferred slip direction.

Previous studies have found that tectonic stress is 100–1000 times of tidal stress (Emter, 1997), while the time scale of the tectonic stress change is more than 10,000 times of amplitude of tidal stress (Vidali et al., 1998). Although tidal stress is much less than tectonic stress, the change rate of tidal stress far outweighs that of tectonic stress. From Eq. 4, we can approximately get:

$\mathit{\Delta }\overrightarrow{\tau }\approx {\overrightarrow{\tau }}^t.(5)$

The change of CFS can then be expressed by the projection of tide-effective shear stress in the direction of tectonic-effective shear stress. In practice, the direction of tectonic-effective shear stress is usually the same as the tectonically preferred slip direction on a seismogenic fault surface. Thus, we have:

$\mathrm{\Delta }CFS\approx {\overrightarrow{\text{τ}}}^t\cdot \frac{\overrightarrow{\text{u}}}{\left|\overrightarrow{\text{u}}\right|},(6)$

where, $\overline{u}$ is the slip vector on a seismogenic fault surface.

When the directions of tide-induced and tectonic-induced effective shear stresses are the same, the tidal stress can be considered as the loading, and when they are in the opposite direction, it can be regarded as the unloading. Specifically, when the angle between the tide-induced and tectonic-induced effective shear stresses is greater than π/2, it is in the unloading process; and when θ < π/2, loading (Figure 2).

FIGURE 2

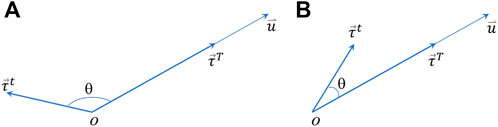
FIGURE 2. Relationship between the tectonic-induced and tide-induced effective shear stresses in the tectonically preferred slip direction. (A): Tidal stress is in the unloading process, (B): Tidal stress plays the loading role.

If the rate of Coulomb failure stress change is taken into consideration, the parameter for determination of the loading and unloading stages can be defined as:

$p=\frac{d}{dt}(\text{Δ}{\overrightarrow{\text{τ}}}^t\cdot \frac{\overrightarrow{\text{u}}}{\left|\overrightarrow{\text{u}}\right|}).(7)$

When p > 0, it is loading, and when p < 0, unloading.

Calculation of tidal stress

The tide-induced stress can be solved by using the methodology given by Yin et al. (2000), in which the elastic deformation in the crust is expressed by six differential equations of the first order (Dziewonski and Anderson, 1981). By combining with the tidal generating potential induced by a celestial body, the components of stress tensor at any location on the Earth sphere can be obtained. Adopting the Runge-Kutta method, the tidal stress components on any arbitrary section can then be derived numerically (Melchior, 1978). The detailed solutions as well as the boundary conditions and some physical parameters, such as the average density and radius of Earth, mean acceleration of gravity, have been listed in Yu et al. (2020). The software adopted to calculate tidal stress is provided by professor Yin (Yin et al., 2000, 2008). The code has been applied to test earthquakes on the Chinese mainland in our previous studies (Yu and Zhu, 2010; Yu et al., 2015).

Application to foreshocks

As a retrospective study, we firstly applied this approach to the two marked foreshocks of the M_s 6.3 L'Aquila, Italy mainshock on 6 April 2009 (Figure 3A). The earthquake catalogs were retrieved from the USGS website. The focal mechanism of the mainshock which was used to determine the direction of CFS was from the Global CMT Catalog, and the internal friction coefficient is 0.4. Figure 3B shows the loading/unloading states of the two foreshocks within 50 km of the mainshock. They all occurred in the tide-induced loading process.

FIGURE 3

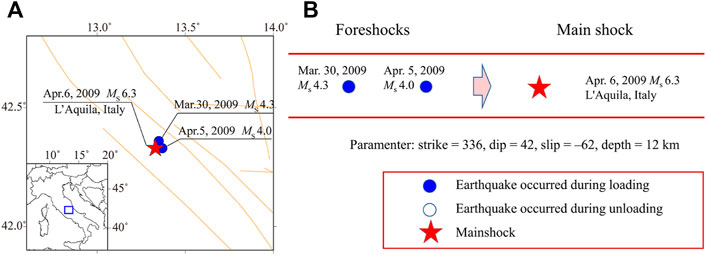
FIGURE 3. The loading/unloading analysis of the foreshocks of the 2009 M_s 6.3 L'Aquila, Italy earthquake. (A): The location of the foreshocks and mainshock. (B): The loading/unloading states of the foreshocks. The gray and dark lines denote the active faults and national borders, respectively. The star represents the mainshock, and the loading and unloading states of the foreshocks are indicated by the solid and hollow circles.

We then tested the foreshocks of the M_s ≥ 6.0 earthquakes on the Chinese mainland since 2000 (Figure 4A). The earthquakes of magnitude 4.0 (M_s-2, Rundle et al., 2002) and above occurred within 20 km from the epicenter and 2 months before a mainshock were regarded as the foreshocks. The earthquake catalogs were retrieved from the China earthquake networks Center (CENC). Their source models were listed in Table 1, which were from the China Earthquake Administration (CEA), Global CMT Catalog and Li et al. (2021). The internal friction coefficient for the calculation of CFS is also 0.4.

FIGURE 4

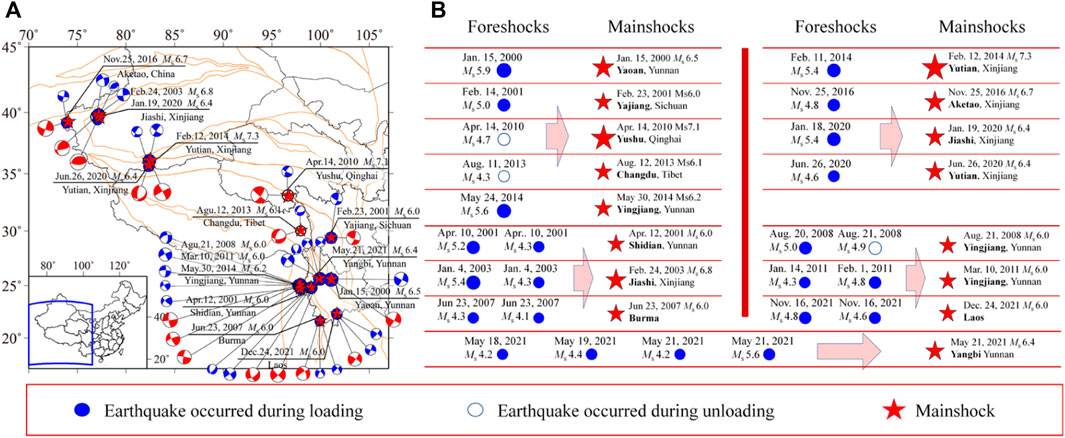
FIGURE 4. The loading/unloading analysis of the foreshocks of the M_s ≥ 6.0 earthquakes on the Chinese mainland since 2000. All the descriptions in (A,B) are the same as for Figure 2 except the dark lines in (A) indicate the provincial borders. The focal mechanisms of the foreshocks and mainshocks are also shown in the figure.

TABLE 1

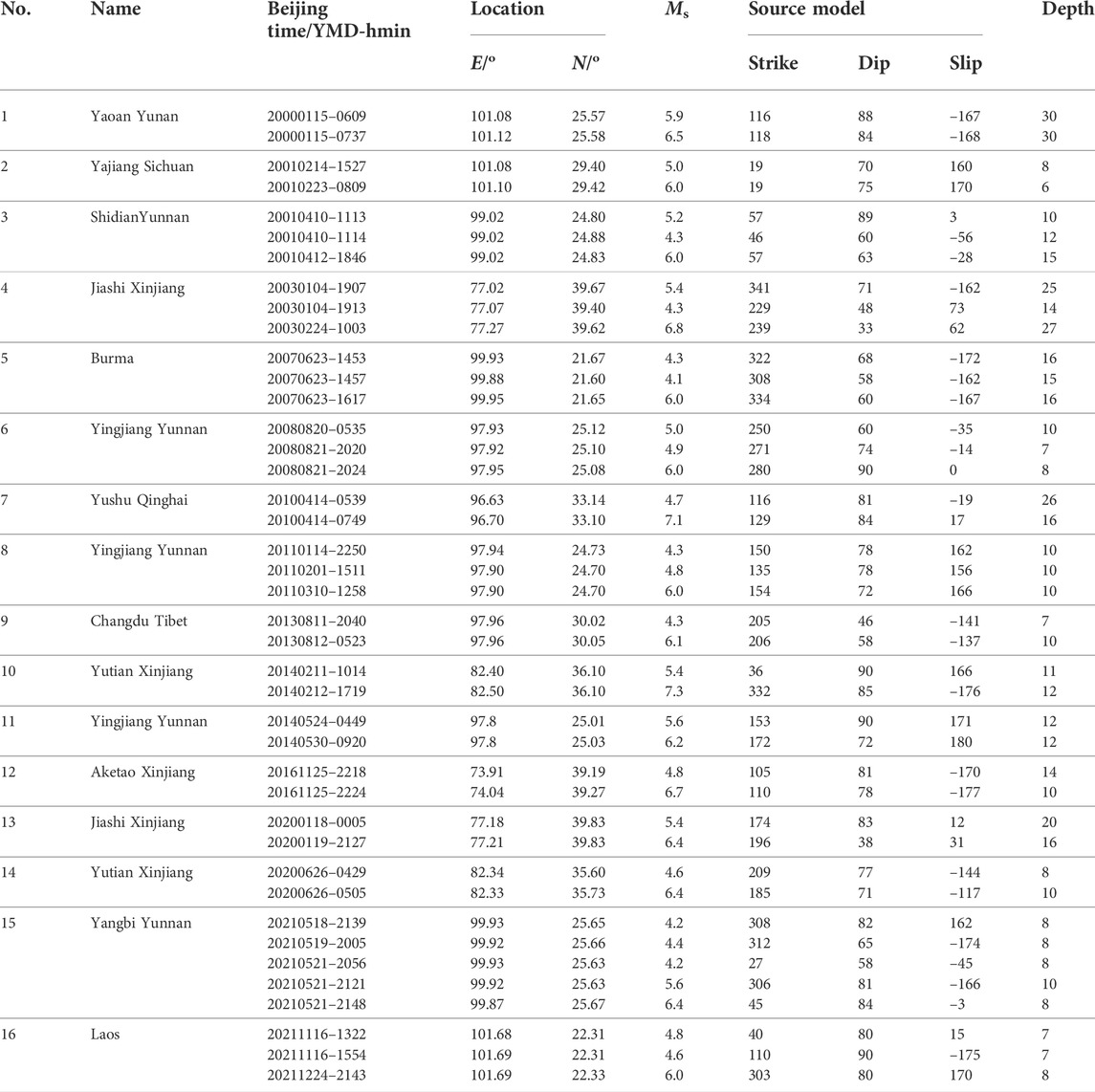
TABLE 1. Detailed source models of the M_s ≥ 6.0 mainshocks and their foreshocks on the Chinese mainland since 2000.

Although the mainshock and foreshock occurred in the same neighborhoods, the seismogenic fault of the mainshock may be quite different from that of the foreshocks. For example, the source model of the largest foreshock of the 2021 M_s 6.4 Yangbi earthquake is believed to be orthogonal to that of the mainshock (Lei et al., 2020). It should be more suitable to calculate the loading/unloading states of foreshocks by using its focal mechanism solution. More importantly, before a large earthquake, we cannot get the focal mechanism solution of the mainshock, directly. On the other hand, we have displayed the focal mechanism solutions of the foreshocks and mainshocks in Figure 4A. The ruptures of the earthquakes are consistent with the regional active tectonics, mainly the strike-slip and thrust faults. Thus, we calculate the CFS based on the focal mechanism solution of each of the foreshocks. Figure 4B displays the loading/unloading states of the foreshocks.

It is clear that most of the foreshocks occurred in the loading process induced by Earth tides. There are 16 mainshocks in Figure 4, of which 9 cases have a single foreshock, 6 times have two foreshocks, and one examples has four foreshocks, i.e., the 2021 M_s 6.4 Yangbi earthquake. In the nine examples with one foreshock, the proportion of foreshocks that occurred in the loading stage is 7/9, except for the two earthquakes in the Yushu, Qinghai with magnitude of 7.1, and Changdu, Tibet with magnitude of 6.1 occurred during the unloading process. The monitoring ability in these two areas is weak, and the quality of data may be suffered. Moreover, in the 7 cases with multiple foreshocks, 15 of the 16 foreshocks were in the loading process. We also noticed that most of the mainshocks such as the 2001 Shidian, 2007 Burma, 2011 Yingjiang, 2021 Yangbi and Laos earthquakes, foreshocks occurred in the loading process consecutively. Especially for the 2021 Yangbi M_s 6.4 earthquake, the four foreshocks all fell in the tidal-induced loading process.

Earthquake swarm tests

To make a more rigorous comparison, we further calculate the loading/unloading states of earthquakes in the swarms where no ensuing larger mainshock (M_s ≥ 6.0) were expected. We define that a swarm contains more than two earthquakes of M_s 4.0–5.5 within 1 month, and the distance between them is less than 20 km. We adopted the earthquakes that occurred on the Chinese mainland in the past 10 years as the targets.

Figure 5A displays the earthquake swarms selected for the loading/unloading analysis, which are distributed in the Xinjiang, Tibet, Qinghai, and Yunnan provinces. Although the earthquake swarms occurred at the most active areas of seismicity on the Chinese mainland, some of them are very close to the Tibet geothermal belt (Jiang et al., 2016). The location looks different from the spatial distribution of foreshocks and mainshocks displayed in Figure 4A which are in the Sichuan, Yunnan, and Xinjiang provinces, with almost no records in Tibet. If the geothermal fluids are involved, these moderate earthquakes might be influenced by tidal normal stress rather than shear stress and CFS (Lei et al., 2021). The 2013 Nima, 2016 Shigatse, and 2020 Bomi earthquake swarms, mainly the normal faults (Figure 5A), are possibly this case. Therefore, these earthquakes were excluded from the statistics.

FIGURE 5

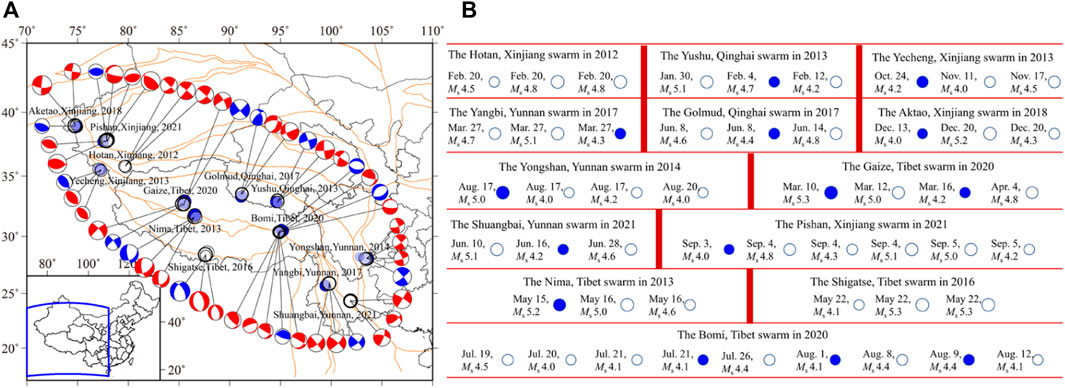
FIGURE 5. The loading/unloading analysis of the earthquakes in the selected swarms on the Chinese mainland in the past 5 years. All the descriptions in (A,B) are the same as for Figure 3 except the foreshocks were replaced by the earthquake swarms. The focal mechanisms of the earthquakes are also shown in the figure.

Figure 5B indicates the loading/unloading states of the earthquakes in the swarms. The slip direction for the calculation of CFS is derived from the focal mechanism solution of each of the earthquakes. The detailed source models of these earthquakes were from the CEA and are listed in Table 2. Unlike the results shown in Figure 4B, most of the earthquakes, in this case, not occurred during the loading process. Statistically, the proportion of earthquakes during loading is no more than 30%, moreover, no earthquakes occurred consecutively during loading.

TABLE 2

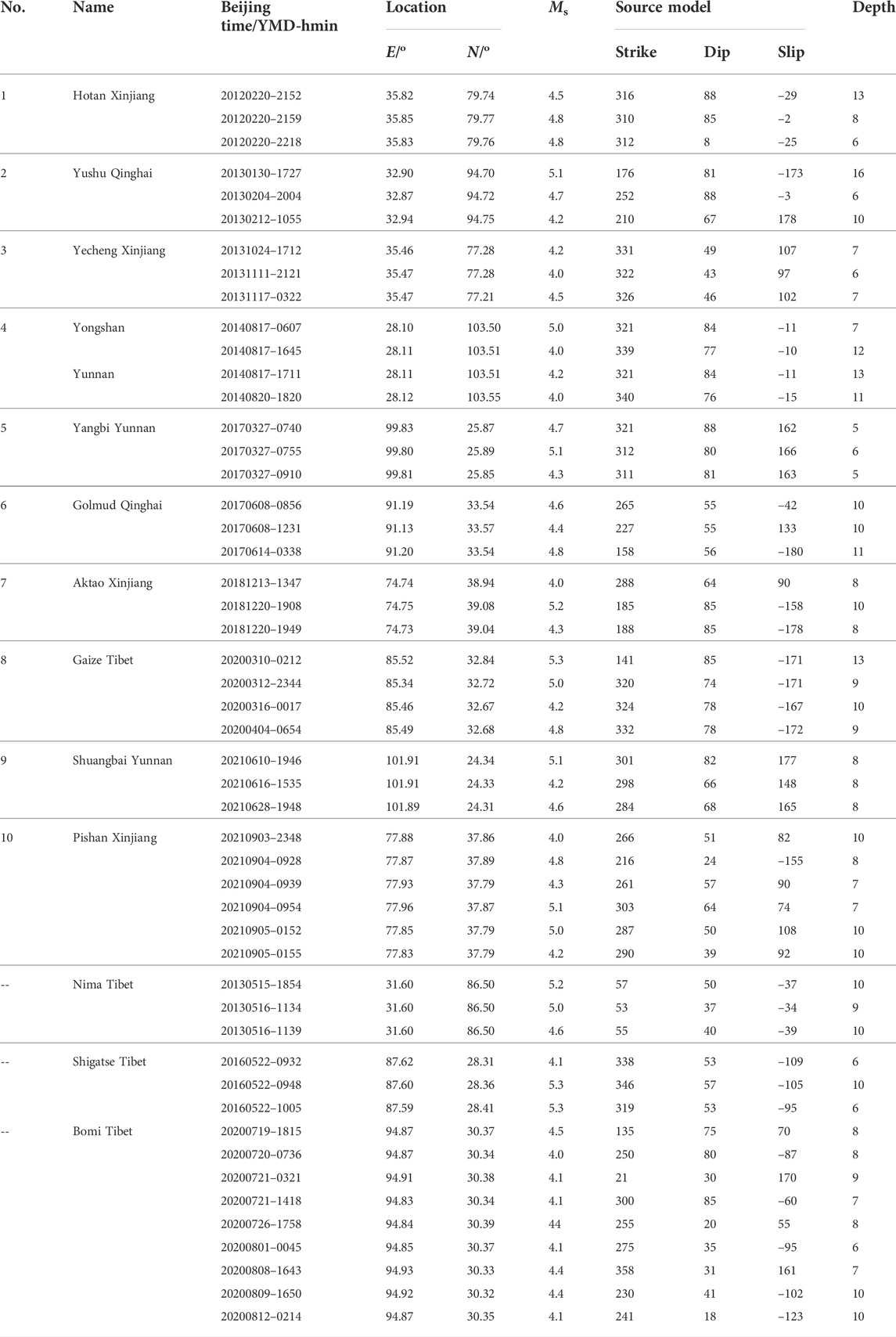
TABLE 2. The source models of the earthquakes in the selected swarms on the Chinese mainland in the past 5 years --: The earthquakes were not included in the statistics.

The fact that most of the foreshocks occurred in the loading process may reveal the criticality of seismogenic faults (Figure 4B). Due to the high tectonic stress accumulation, any tiny increase of the CFS along the tectonically preferred direction may trigger earthquakes. This should be a precondition to determine whether an earthquake is a foreshock to a larger mainshock. However, for the earthquakes where no ensuing larger mainshocks were expected (Figure 5B), even though most of them occurred in the unloading process, there still were events during loading. Thus, in practice using the approach, it might be difficult to evaluate the potential of an ensuing larger earthquake when just a single earthquake is detected during loading. The cases, with two or more moderate earthquakes that all occurred during loading, are more likely to be identified as the foreshocks to a larger event.

R-score analysis

To clearly show the prediction efficiency of the loading/unloading approach, we apply the R-score technique to test the results listed in Figures 4, 5. The R-score is defined as (Yu et al., 2022):

$R=\frac{N_H}{N_T}-\frac{N_F}{N_P},(8)$

where N_H and N_T denote respectively numbers of hit and all mainshocks within the prediction window of 2 months. N_F and N_P are numbers of false alarms and all predictions.

This definition is the same as one of the possible “loss functions” derived from the Molchan error diagram (Molchan, 1991):

$L=1-\tau -\phi ,(9)$

in which the rate of false and missed alarms are denoted by the τ and φ, respectively.

Adopting respectively the results in Figures 4, 5 as the proxies to depict the rate of hit mainshocks and false alarms made by the Loading/unloading approach on the Chinese Mainland, we can calculate the R-score with Eq. 8.

Firstly, we take the loading/unloading state of every single earthquake as the statistical object. If there are multiple foreshocks, the one nearest to the mainshock is selected. We can get N_H=13, N_T=16 (Figure 4), and N_F=10, N_P=35 (Figure 5). The corresponding R-score is 0.53. Note that when an earthquake occurs during unloading, it can be excluded from the foreshocks with a probability of more than 81% (13/16).

On the other hand, if foreshocks occurring during tidal loading and unloading were regarded as a random process, this selection would represent a probability (P_r) of 50% in the loading process. Thus, we can get the probability gain of 3% by using the following equation:

$P_g=R-P_r.(10)$

Moreover, we take two earthquakes that occurred during loading consecutively as the statistical object. Then, we have N_H=6, N_T=7, N_F=0, N_P=10, and R=0.85. In this case, the P_r is 0.25, and the probability gain reaches 60%. The significant level is uncommon and would indicate an effective prediction of future mainshocks. More earthquakes are not applicable, because very few earthquakes have more than two foreshocks of magnitude 4.0 and above (Figure 4).

It should be pointed out that our method seems to show some probability gain of foreshock identification; however, the robustness is unclear because just limited data are available for this analysis. Due to insufficient observations, it is difficult to obtain focal mechanism solutions for moderate earthquakes in the earlier years. Nevertheless, the example we used in this study is representative, and the corresponding results may provide a feasible scheme for the identification of foreshocks.

Discussions

The approach presented in this paper is based on the LURR method proposed by Yin et al. (1995). Compared with the traditional application of LURR, however, does show some noticeable advantages.

(1) In the traditional LURR practices, at least one cycle of data is needed to evaluate the difference between the responses during the loading and unloading phases. To reduce strong fluctuation in the LURR time series, the time window for calculating LURR usually contains multiple loading and unloading cycles to ensure a sufficient number of earthquakes. However, in our approach, we do not need to consider the size of the calculation time window but just for some moderate earthquakes. The applicability of the LURR method is therefore improved.

(2) In the calculation of CFS, the direction of tectonic-induced effective shear stress should be preset. This is usually obtained by assuming that the direction of tectonic-induced effective shear stress is consistent with the tectonically preferred slip direction on the fault plane of the subsequent mainshock. However, this priori information is hard to be presented before the mainshock. In addition, the local influence factors, such as the tide-induced migrations of deep fluids and fault weakening may also impact CFS calculation. The uncertainty of stress direction reduces greatly the accuracy of the LURR. In our approach, the problems can easily be solved by adopting the focal mechanism of foreshocks to determine the direction of tectonic shear stress.

The larger events are tended to be triggered by the earthquakes that occur during loading. Zhuang et al. (2019) have indicated that earthquakes are created by continuous accumulation of tectonic stress in the crust and the stress increment imposed by previous earthquakes may trigger offspring, i.e., the stress perturbation of an earthquake is straightforward for fault instability. However, this process is not only controlled by the regional tectonic stress level but also modulated by the loading and unloading state of tide-induced stress. Similar to tidal stress, this stress perturbation is difficult to create earthquakes by itself. It works only when the tectonic stress is high. If the stress perturbation is superimposed on the tidal loading, the triggering of fault instability should be enhanced. That is, the effective shear stress derived from the earthquakes that occurred during loading is relatively higher, which would be easier to trigger an ensuing larger event.

Knowing the unique characteristics of the loading/unloading approach, we may use that for evaluation of the potential of an ensuing larger event immediately after the moderate earthquakes. In China, the focal mechanism solutions for earthquakes of magnitude 4.0 and above can be produced within 20 min, which makes the research possible. Similar to the studies of Gulia and Wiemer (2019), we define three-alarm status which can be represented by the colors green, yellow and red (Figure 6). When an earthquake occurs in the unloading process, little possibility of a larger mainshock is expected (less than 19%), i.e., it is safe and the color is green. When the earthquake is detected in the loading process, it is difficult to identify the potential of a larger event (the probability gain is just 3%), and the corresponding color is yellow. When multiple moderate or strong earthquakes are observed in a short period and a small area, all occurring in the tidal loading period, it is worthy of attention, and the color is set as red. There is a higher risk of a larger mainshock within a timeframe of 2 months (mostly within a week). We suggest observation of two earthquakes that occur during the loading phases, the probability gain is about 60%.

FIGURE 6

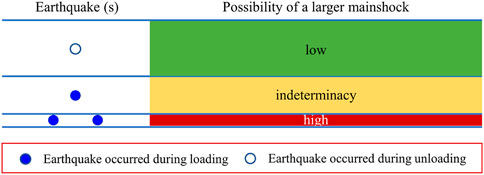
FIGURE 6. The Red-Yellow-Green signal model of foreshock identification. Green represents the earthquake that occurred in the unloading process, and the possibility of a larger mainshock is very low; yellow means just a single earthquake that occurred during loading, which is hard to determine; Red: The possibility of a larger mainshock is high.

Finally, according to the study of Lei et al. (2021), seismic activity in geothermally active regions might be more susceptible to tidal modulation. The foreshocks are more likely to occur when deep fluids play a role, and thus fluids may improve the short-term predictability of large earthquakes by tidal normal stress rather than shear stress. We conducted an interesting test. If the CFS was replaced by the normal stress to calculate tide-induced loading and unloading, the 2013 M_s 6.1 Changdu, Tibet earthquake, which is a normal fracture and close to the Tibet geothermal belt (Jiang et al., 2016), should occur during loading, rather than the unloading in Figure 4. However, such enhancement is not so good for the strike-slip and thrust earthquakes. In this study, because most earthquakes are the strike-slip and thrust faults (Figures 4A, 5A), the loading/unloading state is still calculated by using the CFS. Nevertheless, this strategy should be a potential way to augment the prediction efficiency of the current technique.

Conclusion

By analyzing the loading/unloading states of the moderate earthquakes (M_s ≥ 4.0), we may have a chance to determine whether they are the foreshocks to a larger event. This new technique underlines the basically physical framework of the LURR method, but it is more applicable. The calculation does not need any priori information related to the regional stress setting. If the time, location, and focal mechanism of a moderate earthquake are known, this approach can be applied to the practical assessment of the potential of its ensuing larger event. The earthquakes that occurred during the unloading process are easy to be excluded from the foreshocks, while the earthquakes that occurred during loading might be significant for detecting subsequent larger events, especially the situations with multiple moderate or strong earthquakes. The results, which are derived from the statistics of earthquake cases on the Chinese mainland over the years, are general and representative. Through the statistically and practically feasible model of the Red-Yellow-Green signals, we may apply this method to the real-time evaluation of seismic hazards.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://data.mendeley.com/datasets/sgsxdp26xk/1.

Author contributions

HY, JL, and RY wrote the main article text, HY prepared Figures 5, 6, YM, CY, BZ, and YM prepared Figures 1–4, SL, ZY, MH, HT, and ZZ prepared Tables 1 and 2. All authors reviewed this article.

Funding

This work has been supported by the Earthquake Joint Funds of NSFC (Grant No. U2039205), the National Key Research and Development Project of China (Grant No. 2018YFE0109700), and the Major Science and Technology Projects of Qinghai Province (2019-ZJ-A10).

Acknowledgments

We are very grateful to the constructive suggestions and comments made by ProfessorHaitao Wang.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agnew, D. C., and Jones, L. M. (1991). Prediction probabilities from foreshocks. J. Geophys. Res. 96, 11959. doi:10.1029/91jb00191

CrossRef Full Text | Google Scholar

Allmann, B. P., and Shearer, P. M. (2009). Global variations of stress drop for moderate to large earthquakes. J. Geophys. Res. 114, B01310. doi:10.1029/2008jb005821

CrossRef Full Text | Google Scholar

Bowman, D. D., Ouillon, G., Sammis, C. G., Sornette, A., and Sornette, D. (1998). An observational test of the critical earthquake concept. J. Geophys. Res. 103, 24359–24372. doi:10.1029/98jb00792

CrossRef Full Text | Google Scholar

Byerlee, J. D. (1978). Friction of rocks. Pure Appl. Geophys. 116, 615–626. doi:10.1007/bf00876528

CrossRef Full Text | Google Scholar

Cochran, E. S., Vidale, J. E., and Tanaka, S. (2004). Earth tides can trigger shallow thrust fault earthquakes. Science 306, 1164–1166. doi:10.1126/science.1103961

PubMed Abstract | CrossRef Full Text | Google Scholar

Dziewonski, A. M., and Anderson, D. L. (1981). Preliminary reference earth model. Phys. Earth Planet. Inter. 25, 297–356.

CrossRef Full Text | Google Scholar

Emter, D. (1997). “Tidal triggering of earthquakes and volcanic events,” in Tidal phenomena. Editor H. Wilhem, W. Zürn, and H. G. Wenzel (Springer), 293–309.

Google Scholar

Gerstenberger, M. C., Wiemer, S., Jones, L. M., and Reasengerg, P. A. (2005). Real-time forecasts of tomorrow's earthquakes in California. Nature 435, 328–331. doi:10.1038/nature03622

PubMed Abstract | CrossRef Full Text | Google Scholar

Gulia, L., and Wiemer, S. (2019). Real-time discrimination of earthquake foreshocks and aftershocks. Nature 574, 193–199. doi:10.1038/s41586-019-1606-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaeger, J. C., Cook, N. G. W., and Zimmerman, R. W. (2007). Fundamentals of rock mechanics. 4th Ed. Oxford, United Kingdom: Blackwell Publishing, 90–100.

Google Scholar

Jiang, G. Z., Gao, P., and Rao, S. (2016). Compilation of heat flow data in the continental area of China (4^th edition). Chin. J. Geophys. 59 (8), 2892–2910. (In Chinese).

Google Scholar

Jones, L. M., and Molnar, P. (1979). Some characteristics of foreshocks and their possible relationship to earthquake prediction and premonitory slip on faults. J. Geophys. Res. 84 (B7), 3596–3608. doi:10.1029/jb084ib07p03596

CrossRef Full Text | Google Scholar

Jordan, T. H., Chen, Y. T., Gasparini, P., Madariaga, R. M., Main, I., Marzocchi, W., et al. Operational earthquake forecasting state of knowledge and guidelines for utilization, report by the international commission on earthquake forecasting for civil protection, released by the department of civil protection, Rome, Italy, on 2011.

Google Scholar

Lei, X. L., Sun, J. B., and Su, J. R. (2020). Fluid-driven seismicity in relatively stable continental regions: Insights from the February 3rd, 2020 M_S 5.1 Qingbaijiang isolated earthquake. Earthq. Res. Adv. 1, 100007. doi:10.1016/j.eqrea.2021.100007

CrossRef Full Text | Google Scholar

Lei, X., Wang, Z., and Ma, S. (2021). A preliminary study on the characteristics and mechanism of the May 2021 M_s 6.4 Yangbi earthquake sequence, Yunnan, China. Acta Seismol. Sin. 43 (3), 1–24.

Google Scholar

Li, C., and Nordlund, E. (1993). Experimental verification of the Kaiser effect in rocks. Rock Mech. Rock Eng. 26 (4), 333–351. doi:10.1007/bf01027116

CrossRef Full Text | Google Scholar

Li, Q., Li, C., Tan, K., Lu, X., and Zuo, X. (2021). Slip model of the 2020 Yutian (northwestern Tibetan Plateau) earthquake derived from joint inversion of InSAR and teleseismic data. Earth Space Sci. 8, e2020EA001409. doi:10.1029/2020ea001409

CrossRef Full Text | Google Scholar

Marzocchi, W., and Zhuang, J. (2011). Statistics between mainshocks and foreshocks in Italy and Southern California. Geophys. Res. Lett. 38, L09310. doi:10.1029/2011gl047165

CrossRef Full Text | Google Scholar

Melchior, P. (1978). The tide of the planet earth. New York, NY, USA: Pergamon Press.

Google Scholar

Michael, A. J. (2011). Fundamental questions of earthquake statistics, source behavior, and the estimation of earthquake probabilities from possible foreshocks. Bull. Seismol. Soc. Am. 102, 2547–2562. doi:10.1785/0120090184

CrossRef Full Text | Google Scholar

Molchan, G. M. (1991). Structure of optimal strategies in Earth-quake prediction. Tectonophysics 193, 267–276. doi:10.1016/0040-1951(91)90336-q

CrossRef Full Text | Google Scholar

Reasenberg, P. A. (1999). Foreshock occurrence rates before large earthquakes worldwide. Pure Appl. Geophys. 155, 355–379. doi:10.1007/s000240050269

CrossRef Full Text | Google Scholar

Rundle, J. B., Tiampo, K. F., Klein, W., and Martins, J. S. S. (2002). Self-organization in leaky threshold systems: The influence of near-mean field dynamics and its implications for earthquakes, neurobiology, and forecasting. Proc. Natl. Acad. Sci. U. S. A. 99, 2514–2521. doi:10.1073/pnas.012581899

PubMed Abstract | CrossRef Full Text | Google Scholar

Scholz, C. H., Sykes, L. R., and Aggarwal, Y. P. (1973). Earthquake prediction: A physical basis. Science 181, 803–810. doi:10.1126/science.181.4102.803

PubMed Abstract | CrossRef Full Text | Google Scholar

Shebalin, P., Keilis-Borok, V., Gabrielov, A., Zaliapin, I., and Turcotte, D. (2006). Short-term earthquake prediction by reverse analysis of lithosphere dynamics. Tectonophysics 413, 63–75. doi:10.1016/j.tecto.2005.10.033

CrossRef Full Text | Google Scholar

Sobolev, G. (2001). The examples of earthquake preparation in Kamchatka and Japan. Tectonophysics 338, 269–279. doi:10.1016/s0040-1951(01)00082-8

CrossRef Full Text | Google Scholar

Vidali, J. E., Agnew, D. C., Johnston, M. J. S., and Oppenheimer, D. H. (1998). Absence of earthquake correlation with Earth tides: An indication of high preseismic fault stress rate. J. Geophys. Res. 103, 24567–24572. doi:10.1029/98jb00594

CrossRef Full Text | Google Scholar

Yin, X. C., Chen, X. Z., Song, Z. P., and Yin, C. (1995). A new approach to earthquake Prediction–the Load/Unload Response Ratio (LURR) theory. Pure Appl. Geophys. 145, 701–715. doi:10.1007/bf00879596

CrossRef Full Text | Google Scholar

Yin, X. C., Wang, Y. C., Peng, K., Bai, Y. L., Wang, H., Yin, X. F., et al. (2000). Development of a new approach to earthquake prediction: Load/Unload Response Ratio (LURR) theory. Pure Appl. Geophys. 157, 2365–2383. doi:10.1007/pl00001088

CrossRef Full Text | Google Scholar

Yin, X. C., Zhang, L. P., Zhang, Y. X., Peng, K. Y., Wang, H. T., Song, Z. P., et al. (2008). The newest developments of load-unload response ratio (LURR). Pure Appl. Geophys. 165, 711–722. doi:10.1007/s00024-008-0314-z

CrossRef Full Text | Google Scholar

Yu, H., Yuan, Z., Yu, C., Zhang, X., Gao, R., Chang, Y., et al. (2022). The medium-to-short-term earthquake predictions in China and their evaluations based on the R-score. Seismol. Res. Lett. 93, 840–852. doi:10.1785/0220210081

CrossRef Full Text | Google Scholar

Yu, H. Z., Shen, Z. K., Wan, Y. G., Zhu, Q. Y., and Yin, X. C. (2006). Increasing critical sensitivity of the Load/Unload Response Ratio before large earthquakes with identified stress accumulation pattern. Tectonophysics 428, 87–94. doi:10.1016/j.tecto.2006.09.006

CrossRef Full Text | Google Scholar

Yu, H. Z., Yu, C., Ma, Z., Zhang, X. T., Zhang, H., Yao, Q., et al. (2020). Temporal and spatial evolution of load/unload response ratio before the M7.0 jiuzhaigou earthquake of aug. 8, 2017 in sichuan province. Pure Appl. Geophys. 177, 321–331. doi:10.1007/s00024-019-02101-x

CrossRef Full Text | Google Scholar

Yu, H. Z., and Zhu, Q. Y. A. (2010). Probabilistic approach for earthquake potential evaluation based on the load/unload response ratio method. Concurr. Comput.: Pract. Exp. 22, 1520–1533.

Google Scholar

Yu, H. Z., Zhou, F. R., Cheng, J., and Wan, Y. G. (2015). The sensitivity of load/unload response ratio and critical region selection before large earthquakes. Pure Appl. Geophys. 172, 173–183.

CrossRef Full Text | Google Scholar

Zechar, J. D., and Jordan, T. H. (2008). Testing alarm-based earthquake predictions. Geophys. J. Int. 172, 715–724. doi:10.1111/j.1365-246x.2007.03676.x

CrossRef Full Text | Google Scholar

Zhuang, J., Murru, M., Falcone, G., and Guo, Y. (2019). An extensive study of clustering features of seismicity in Italy from 2005 to 2016. Geophys. J. Int. 216, 302–318. doi:10.1093/gji/ggy428

CrossRef Full Text | Google Scholar