Mw ≥ 5 aftershocks of the 2008 Sichuan earthquake: Analysis of temporal variation of Omori Law p-value

Strong to great earthquakes considerably weaken the structural strength of the subsurface strata and civil constructions. The occurrence of Mw ≥ 5 aftershocks further contributes to the loss of human lives and damage to property. Therefore, the estimate of the duration of such aftershocks occurring near a metropolitan area is of major concern. In a previous study (Gupta et al., 2008), aftershocks for the destructive Sichuan earthquake, China (12 May 2008 Mw 7.9) for 23 days were used to estimate p-value and it was proposed that the M ≥ 5 aftershocks may continue for 7 months. In the present study, we analyze aftershock activity of Mw≥ 5 for 2-year duration within an area of 300 km radius from the epicenter, using modified Omori Law, which is well-known for analyzing aftershock rate and duration. We compare our results with the duration of aftershocks estimated using the exponential scaling law for the M ≥ 5 aftershock duration for major to great Himalayan earthquakes. Our analysis suggests that a high p-value (>1) indicates a slow decay of aftershocks as observed. As the p-value changes with time, the estimates of the duration of the occurrence of aftershocks of M ≥ 5 may change. Using a dynamic approach, the data of the first 100 days has been used in this study and the duration of occurrence of Mw ≥ 5 earthquakes is estimated to be ∼300 days, which is found to be true. Our analysis suggests that the temporal variation of the p-value from the onset of the mainshock and the slope of its variation are the key elements in comprehending the duration of the occurrence of the aftershocks of a certain magnitude. We infer that a high p-value (p>1) after the main earthquake, indicates a longer duration of larger aftershocks, which has been found in the case of the Sichuan earthquake. The p-value decreases with time, however, an intermittent increase in the p-value could be an indicator of an increased chance for the occurrence of a higher magnitude aftershock. The proposed dynamic approach to estimating temporal p-values may help in forecasting the occurrence of stronger aftershocks more effectively. We believe that this is the first time, where the temporal variation of p-values is estimated and related to the occurrence of aftershocks.

Introduction

Earthquakes of magnitude ≥7 are commonly followed by M ≥ 5 aftershocks, which are capable of damaging civil constructions and cause injuries and even claim human lives (Hough and Jones, 1997; Di Sarno, 2013). Therefore, understanding the aftershock pattern is of paramount interest for minimizing the damage. The characteristics of the foreshock and aftershock sequence associated with an earthquake depend on the properties of the subsurface materials/fault and the magnitude of the main event (Mogi, 1962; Kisslinger and Jones, 1991; Utsu et al., 1995). Seismologists have been using the modified Omori Law for modeling the aftershock sequence duration and probability of occurrence of different magnitude events in a sequence (Omori, 1894; Utsu, 1961; Utsu et al., 1995). According to Utsu (1961), the modified Omori Law for the number of aftershocks for unit time interval t, after the main event, can be written as:

$n\left(t\right)=K{\left(t+c\right)}^{-p}.(1)$

Here K, c, p are the constants. The p and c values are the sensitive parameters characterizing the individual mainshock and aftershock sequence in the analysis (Utsu, 1961; Utsu, 1969). Physically c denotes the small fraction of time delay. Utsu et al., (1995) have analyzed more than 200 earthquakes from the published literature and suggested 0.01 t to 1.00 t as the lower and upper boundaries of c and 0.6 to 2.5 as a reasonable range of p-value.

Eq. 1 can be written as follows for the cumulative number of earthquakes until a time t after the mainshock:

$\mathit{N}\left(\mathit{t}\right)=\frac{\mathrm{K}\left\{{\mathit{c}}^{\mathit{1}-\mathit{p}}-{\left(\mathit{t}+\mathit{c}\right)}^{1-\mathit{p}}\right\}}{\mathit{p}-1}\left(\mathit{p}\ne 1\right).$(2a)

When p > 1 N(t) reaches a constant level given by

${\mathit{N}}_{\infty }=\frac{\mathit{K}}{\left\{\left(\mathit{p}-1\right){\mathit{c}}^{\mathit{1}-\mathit{p}}\right\}}\left(\mathit{a}\mathit{s}\mathit{t}\to \infty \right),$(2b)

and for p ≤ 1 $N_{\infty }\to \infty \left(ast\to \infty \right)$.

Several studies have demonstrated a satisfactory prediction of aftershocks from the modified Omori Law. However, most of the studies use the p-value estimated from the first few days of data and assume the aftershock process as a static process. In reality, the aftershock activity is non-linear and hence is dynamic as the structural strength or heterogeneity of the subsurface rock material changes with time in the zones affected by major earthquakes. Therefore, we attempt here to analyze the p-value and its temporal variation to unveil its relationship with the aftershock activity of the 2008 Sichuan earthquake.

Earthquake data used in this study

We have downloaded the earthquake catalog data from International Seismological Centre (ISC) for the 12 May 2008 Mw 7.9 Sichuan earthquake, China, that occurred at 06:28:02 UTC. Figure 1 depicts the location of the epicenter of the Sichuan earthquake and the distribution of Mw 4 and larger earthquakes that have occurred till May 2010 within a radius of 300 km of the epicenter of the Sichuan earthquake. The Sichuan earthquake is located on the northeast-trending Longmenshan fault bordering the Tibetan Plateau on the west and the Sichuan Basin on the east. The tectonics of the earthquake fault zone has been addressed by Burchfiel et al., (1995). A shallow oblique reverse faulting on the northwestern margin of the Sichuan Basin is apparently responsible for several killer earthquakes that occurred on the northwestern margin of the Sichuan Basin during the past century (Figure 2). The M 7.5 Dixie earthquake of 25 August 1933 is one of the strongest earthquakes that claimed more than 9,300 human lives preceding the 12 May 2008 Sichuan earthquake (Figure 2). The other Mw ∼ 7 in the vicinty of Sichuan earthquake include 24 May 1923 Renda earthquake claiming 4800 human lives; 28 May 1948 Litang earthquake claiming 800 human lives; 23 September 1955 Yuzha earthquake claiming 730 human lives and the 6 February 1973 Luhuo earthquake claiming 2200 human lives. The Sichuan earthquake killed more than 95,000 people (Gupta et al., 2008; Hayes et al., 2017). Kobayashi et al., (2009) have made use of SAR image matching to address the locations and types of ruptures caused by the 2008 Sichuan earthquake.

FIGURE 1

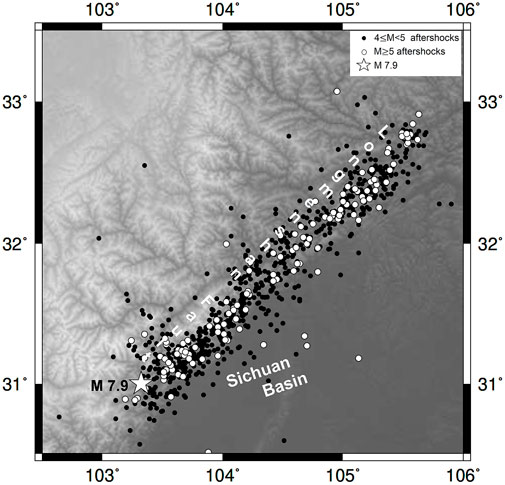
FIGURE 1. Location of the 12 May 2008 Mw 7.9 Sichuan earthquake (white color star) and M ≥ 5 earthquakes (white filled dots), and 4 ≤ Mw < 5 (black filled dots) till May 2010.

FIGURE 2

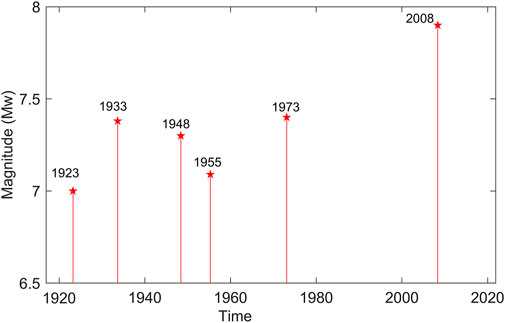
FIGURE 2. Earthquakes of Mw ≥ 7.0 that occurred within a 300 km radius of the epicenter of the 12 May 2008 Sichuan earthquake of Mw 7.9 since 1920.

Methodology and analyses

For over a century now, Omori’s relation $\mathrm{n}\left(\mathrm{t}\right)=K{\left(t+c\right)}^{-1}$ and later modified to $\mathrm{n}\left(\mathrm{t}\right)=K{\left(t+c\right)}^{-\mathrm{p}}$ have been used to study the aftershocks (Utsu et al., 1995). The use has been continued till date to estimate the aftershock duration. Studies in the last 5 decades or so have shown that Omori’s relations generally provide a good estimate of the temporal variation of the aftershock activity. The “p” value differs from one earthquake sequence to another. However, for the first time, we are presenting a temporal variation of the p-value from the day of the earthquake to a finite duration of 1800 days to understand its relationship with the aftershock duration. The p-value can be estimated using the modified Omori Law using the number of aftershocks observed within a unit time interval t after the main event as

$p=\frac{\log \left(n\left(t\right)/K\right)}{\log \left(t+c\right)},(3)$

where n(t), K, and c are the same as mentioned earlier for Eq. 1. We use the catalog data in discrete time intervals beginning from the event time to the multiples of 1-day time steps to compute the p-value time series. The first value of the p will be computed using the data of the catalog spanning 1 day from the time of earthquake and the last p-value in the time series is obtained from the complete catalog used in the study.

We have estimated the p-value using the modified Omori Law for the cumulative number of aftershocks of Mw ≥ 5.0 for periods starting from day one to 1800 days that occurred within 300 km of the epicenter of the Sichuan earthquake. Figure 3 shows the temporal distribution of aftershocks and p-value estimates. It may be noted in this figure that the initial p-value was high being 1.17. In the first hundred days, it drops to 1.05 associated with a drop in Mw ≥ 5 events. After a rise, the p-value again drops to 1.05 after completion of ∼300 days. From around the 300th day to the ∼400th day there are no Mw ≥ 5 events.

FIGURE 3

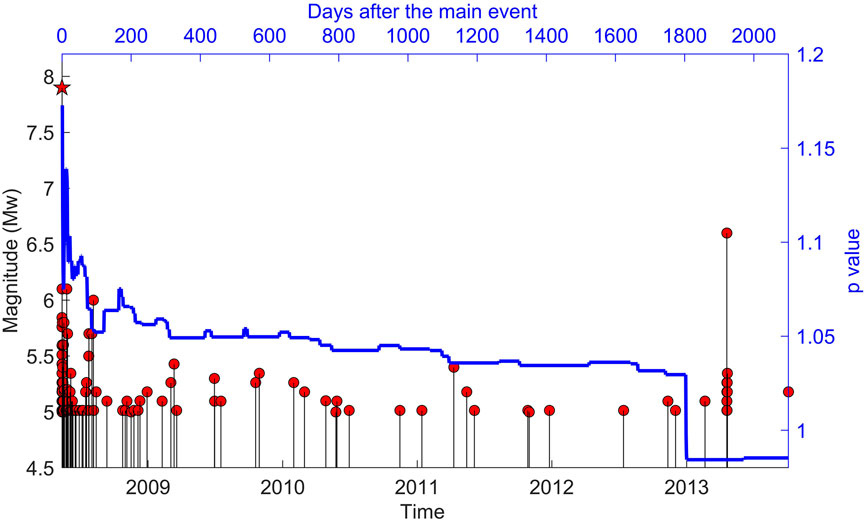
FIGURE 3. Mw ≥ 5.0 earthquakes and the temporal p-value variation within the 300 km radius of the 12 May 2008 Sichuan earthquake.

Compared to the Muzafarbad earthquake of 2005, the p-values noticed for the Sichuan earthquake are high as well as the Sichuan earthquake had a larger number of aftershocks (Gupta and Rekapalli, 2022). The number of aftershocks is high and the decay of aftershocks is slow for the Sichuan earthquake.

The following is inferred through a comparison of the temporal variation of p-values with the seismicity:

(i) The p-value shows a peak value within the first 2 days after the main event following a sharp fall.

(ii) The initial p-value >1 with a slow decay indicates a longer duration of aftershocks (p-values are throughout over 1.0)

(iii) An intermittent increase in p-value following the main event increases the possibility of the occurrence of larger magnitude earthquakes and a longer duration of aftershocks.

Figure 4 shows the observed and predicted cumulative number of earthquakes. Figure 5 depicts earthquakes of Mw 4 and larger for the period 12 May 2008 through 12 May 2022 that occurred within 300 km radius of the 2008 Sichuan earthquake. Significant events of Mw ∼ 6.8 occurred in 2013 (20 April 2013), 2017 (08 August 2017) and 2022 (05 September 2022). As shown by the dotted black lines in Figure 5, it appears that there are cycles of occurrence of Mw ∼ 7 earthquakes at an interval of 5 years within a 300 km radius of the 2008 Sichuan earthquake epicenter. It may be noted in Figure 3 that there was a drop in Mw ≥ 5 earthquakes after ∼100 days of the 12 May 2008 Sichuan earthquake. In Figure 4 cumulative number of the aftershocks of Mw ≥ 5 is plotted (red curve) as well as the cumulative number of the Mw ≥ 5 aftershocks computed using the data of the first 100 days of Mw ≥ aftershocks based on modified Omori’s Law.

FIGURE 4

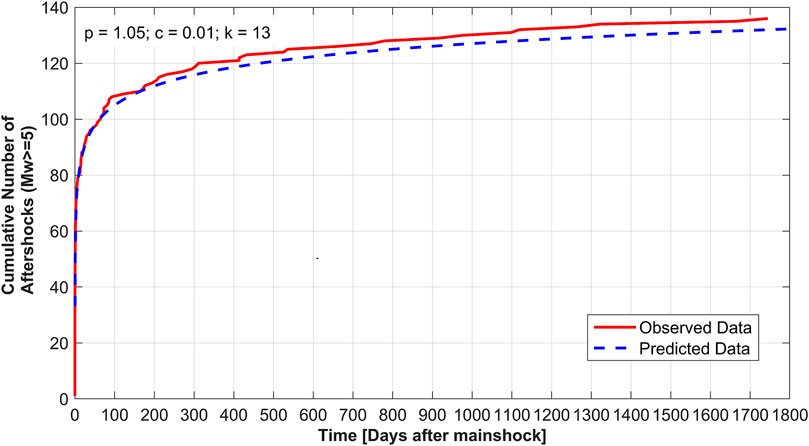
FIGURE 4. The cumulative number of Mw ≥ 5 aftershocks observed and predicted. The red line shows the cumulative number of observed earthquakes and the blue dashed line shows the aftershocks predicted using the modified Omori Law using the aftershock data of the first 100 days. The p, c and k values obtained from the first 100 days of aftershock data of Mw≥ 5 are shown in the figure.

FIGURE 5

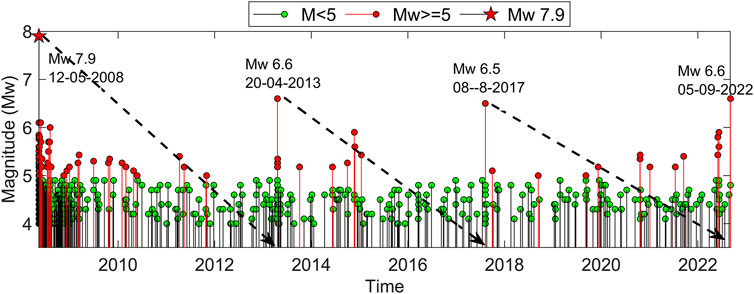
FIGURE 5. Earthquakes of 4<Mw< 5 (green filled dots) and Mw ≥ 5 (red filled dots) occurring within the 300 km radius of the 2008 Sichuan earthquakes for the period 12 May 2008 through 05 September 2022. After the Sichuan earthquake, earthquakes of Mw ∼ 6.5 occurred at an interval of ∼4–5 years, the latest being of Mw 6.5 on 5th September 2022.

From the above Table 1, it is inferred that the number of the aftershocks of Mw ≥ 5 fell to 2 every hundred days after 300 days and finally 1 every hundred days. A new cycle began with the occurrence of the Mw 6.7 earthquake on 20 April 2013 (Figure 5). It is further noted in Figure 4 that the cumulative number of aftershocks forecasted using Omori’s modified law for the first 100 days matches quite well with the actual occurrence of Mw ≥ 5 earthquakes for the following 1800 days. A change in the slope of the theoretical curve is noticeable in Figure 4 after 100 days. So, in hindsight it can be stated that using the data of the aftershocks for the first 100 days, it could be forecasted that Mw≥ 5 aftershocks would continue for 300 days. A drop in the number of aftershocks after 300 days is clearly visible in Figure 3.

TABLE 1

TABLE 1. Time distribution of the Mw ≥ 5 earthqaukes observed after the 12 May 2008 Sichuan earthquake for 1800 days with in 300 km radius of the main event.

Davidsen et al., (2015) have also indicated that the p-value decreases with increasing M. In general, smaller p-values and the slope of the observed data being lower than predicted is an indication that aftershocks of significant magnitudes may occur (Utsu et al., 1995). We can notice a similar situation for the M ≥ 5 predicted and observed curves in Figure 4. As the p-value, computations using 2-year data in a single window show some hints on the duration of the aftershocks, but we cannot understand its temporal variation and its link with aftershock duration and rate. Therefore, we have obtained the p-value using the expanding window method with 1 day step from the 2nd day to 740 days following the main event.

Discussions and conclusions

Omori’s “p-value” estimations have been extensively used to study the aftershock sequences. In an important article Utsu et al., (1995), summarized the use of Omori relation to study the decay of the aftershocks. They observed that the modified Omori relation generally provides useful information on the temporal variation of aftershocks. They further observed that there is no systematic dependence of the p-value on the magnitude of the main shock. Usually, the p-value varies from 0.9 to 1.5 (Utsu et al., 1995). inferred that this variability is related to the tectonic condition of the earthquake source zone, including structural heterogeneity, temperature and stress. However, it is not clear as to which of these factors influences the p-value most. In an interesting study Shcherbakov et al., (2004), observed that the earthquake aftershock sequences normally satisfy three important scaling relations, namely the Gutenberg-Richter’s frequency-magnitude relation, Bath’s law for the difference in the magnitude of the main shock and its largest aftershock, and the modified Omori’s law for the temporal decay of the aftershock activity. Shcherbakov et al., (2004) developed a generalized Omori’s law for temporal decay of the aftershocks. It is observed that several factors, specific to an earthquake source, influence the temporal decay of the aftershocks. They further observed that “c” as originally stipulated to be a constant, is not so, but depends on the magnitude of the main shock as well as the cut-off value of the lower magnitude earthquakes. They tested the modified Omori’s Law for aftershock sequences in California, United States and found it to be satisfactory. Nanjo et al., (2007) investigated the decay of aftershocks for four recent Japanese earthquakes. One of their main conclusion is that the “c” heavily depends on the aftershock dynamics. An estimate of the spatio-temporal distribution of the Mw ≥ 5 aftershocks of a strong earthquake is an important aspect in minimizing the loss as they cause severe damage to the structures previously weakened by the mainshock. Here, we present the analysis of the aftershock sequence of the Mw 7.9 Sichuan earthquake that occurred on 12 May 2008 using the modified Omori Law for aftershock decay. The p-value temporal changes obtained from the 2-years seismicity data after the event in a 300 km radius around the main event indicate that variations are associated with the aftershock rate and magnitude. The estimated p-value given by Gupta et al., (2008) from the first 23 days data, immediately after the event, is comparatively low (p=0.87). This may be due to the non-availability of the complete data within 23 days of the occurrence of the earthquake. The analysis of the temporal variation in p-value suggests that the rate of the aftershocks depends on the slope of the p-value time series. As the p-value is not constant over time, the estimates of aftershock number and temporal durations estimated using the data of the first few days may not be a valid approach for forecasting. The past studies also pointed out that the p-value has no scaling with either the magnitude of the mainshock or the cutoff magnitude Mc (Kisslinger and Jones, 1991; Utsu et al., 1995). Despite several attempts, no clear conclusion on the functional dependency and sensitivity of the p-value on structural heterogeneity, stress and temperature in the crust is available (MOGI, 1962; Kisslinger and Jones, 1991; Utsu et al., 1995). In a recent study (Gupta and Rekapalli, 2022), deduced a relationship of M ≥ 5 aftershock duration with the magnitude of the Himalayan earthquakes. This relation shows a direct exponential scaling of aftershock duration with the magnitude of the main shock. According to the relationship developed by them, the M ≥ 5 aftershock duration of the Sichuan earthquake amounts to ∼780 days. Compared to Omori’s aftershock law, the recent exponential relationship deduced for the Himalayan region has a scaling with the magnitude besides being controlled by the regional tectonics/fault settings.

Considering the relationship of p-value with aftershock activity from the 2-years data, we noticed the temporal variation of p-values after the earthquake. These changes have been compared with the aftershock rate and magnitude to derive relations for future aftershock forecasts. Interestingly, our analysis revealed that the slope of rising and falling p-values is the main indicator for the aftershock duration and magnitude. If the p-value rises and decays very sharply after the mainshock, there would be no -strong aftershocks in the sequence. We have noticed a high p-value (>1) after the Sichuan earthquake which shows very slow decay (nearly 100 days) of aftershocks followed by a slow recovery indicating the longer aftershock activity with the occurrence of Mw ≥ 5 earthquakes. This study reveals that the duration of occurrence of Mw ≥ 5 earthquakes, as estimated from the p-value of the first 100 days of Mw ≥ 5 aftershocks is 300 days. In the first 100 days there were 110 Mw ≥ 5 aftershocks; in the next hundred days 5; and 4 in the subsequent hundred days. After 300 days, only 2 or 1 Mw ≥ 5 aftershocks occurred per 100 days. It has been also noted that earthquakes of Mw ∼ 6.7 occur every 4/5 years within a 300 km radius of the Sichuan earthquake, followed by an enhanced number of Mw 5 aftershocks.

The present study provides an approach to estimating temporal changes in p-value and forms the basis to estimate the duration of occurrence of damaging Mw ≥ 5 earthquakes. In the case of the Sichuan earthquake data of the first 100 days provided a good estimate of the enhanced occurrence of Mw ≥ 5 aftershocks for 300 days, after which the seismic activity fell to a background level of occurrence of 1 or 2 Mw ≥ 5 earthquakes every 100 days. We hope that the combined analysis of the dynamical/temporal estimates of the p-value as well as the exponential law of Gupta and Rekapalli, (2022) may be useful in forecasting aftershock activity more effectively (Nyffenegger and Frohlich, 1998; Tosi et al., 2010).

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://earthquake.usgs.gov/earthquakes/search/.

Author contributions

Both the authors contributed equally to the planning of the research problem, analysis and manuscript preparation.

Acknowledgments

The authors thank the Director, CSIR-NGRI, Hyderabad for his permission to publish this work. Harsh K. Gupta also thanks the National Academy of Sciences (NASI), India for Platinum Jubilee Fellowship. Council of Scientific and Industrial Research-National Geophysical Research Institute (CSIR-NGRI) reference number of the article is NGRI/Lib/2022/Pub-94.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Burchfiel, B. C., Zhiliang, C., Yupinc, L., and Royden, L. H. (1995). Tectonics of the Longmen Shan and adjacent regions, central China. Int. Geol. Rev 37 (8), 661–735. doi:10.1080/00206819509465424

CrossRef Full Text | Google Scholar

Davidsen, J., Gu, C., and Baiesi, M. (2015). Generalized Omori-Utsu law for aftershock sequences in southern California. Geophys. J. Int 201 (2), 965–978. doi:10.1093/gji/ggv061

CrossRef Full Text | Google Scholar

Di Sarno, L. (2013). Effects of multiple earthquakes on inelastic structural response. Eng. Struct 56, 673–681. doi:10.1016/j.engstruct.2013.05.041

CrossRef Full Text | Google Scholar

Gupta, H. K., Rao, N. P., Shashidhar, D., and Mallika, K. (2008). The disastrous M 7.9 sichuan earthquake of 12 may 2008. J. Geol. Soc. India 72 (3), 325–330.

Google Scholar

Gupta, H. K., and Rekapalli, R. (2022). A short note on the aftershock duration of strong to major himalayan earthquakes. J. Geol. Soc. India 98 (5), 611–614. doi:10.1007/s12594-022-2034-x

CrossRef Full Text | Google Scholar

Hayes, G. P., Meyers, E. K., Dewey, J. W., Briggs, R. W., Earle, P. S., Benz, H. M., et al. (2017). Tectonic summaries of magnitude 7 and greater earthquakes from 2000 to 2015. Geol. Surv. Open-File Rep. 2016 1192, 148. doi:10.3133/ofr20161192

CrossRef Full Text | Google Scholar

Hough, S. E., and Jones, L. M. (1997). Aftershocks: Are they earthquakes or afterthoughts?. Eos Trans. AGU 78 (45), 505–508. doi:10.1029/97eo00306

CrossRef Full Text | Google Scholar

Kisslinger, C., and Jones, L. M. (1991). Properties of aftershock sequences in southern California. J. Geophys. Res 96, 947–958. doi:10.1029/91jb0120

CrossRef Full Text | Google Scholar

Kobayashi, T., Takada, Y., Furuya, M., and Murakami, M. (2009). Locations and types of ruptures involved in the 2008 Sichuan earthquake inferred from SAR image matching. Geophys. Res. Lett 36 (7), 1–5. doi:10.1029/2008gl036907

CrossRef Full Text | Google Scholar

Mogi, K. (1962). On the time distribution of aftershocks accompanying the recent major earthquakes in and near Japan. Bull. Earthq. Res. Inst. Univ. Tokyo 40, 107–124.

Google Scholar

Nanjo, K. Z., Enescu, B., Shcherbakov, R., Turcotte, D. L., Iwata, T., and Ogata, Y. (2007). Decay of aftershock activity for Japanese earthquakes. J. Geophys. Res. Solid Earth 112 (8), 1–12. doi:10.1029/2006jb004754

CrossRef Full Text | Google Scholar

Nyffenegger, P., and Frohlich, C. (1998). Recommendations for determining p-values for aflershock sequences and catalogs. Bull. Seismol. Soc. Am. 88 (5), 1144–1154.

Google Scholar

Omori, F. (1894). On the after-shocks of earthquakes. J. Coll. Sci., Imperial University of Tokyo 7, 111–200.

Google Scholar

Shcherbakov, R., Turcotte, D. L., and Rundle, J. B. (2004). A generalized Omori's law for earthquake aftershock decay. Geophys. Res. Lett 31 (11), 1–5. doi:10.1029/2004gl019808

CrossRef Full Text | Google Scholar

Tosi, P., De Rubeis, V., and Sbarra, P. (2010). Stacked analysis of earthquake sequences: Statistical space-time definition of clustering and Omori law behavior. Synchronization Triggering Fract. Earthq. Process 1, 323–337. doi:10.1007/978-3-642-12300-9_19

CrossRef Full Text | Google Scholar

Utsu, T. (1961). A statistical study of the occurrence of aftershocks. Geophys. Mag 30, 521–605.

Google Scholar

Utsu, T. (1969). Aftershocks and earthquake statistics (1): Some parameters which characterize an aftershock sequence and their interrelations. J. Fac. Sci., Hokkaido University. Ser. 7, Geophys 3 (3), 129–195.

Google Scholar

Utsu, T., Ogata, Y., Ritsuko, S., and Matsu-ura, (1995). The centenary of the Omori formula for a decay law of aftershock activity. J. Phys. Earth 43, 1–33. doi:10.4294/jpe1952.43.1

CrossRef Full Text | Google Scholar