Assessment of probability of failure on rainfall-induced shallow landslides at slope scale using a physical-based model and fuzzy point estimate method

Shallow hillslope failure caused by rainfall is characterized by complex soil hydrology and mechanical behavior. It is important to understand the hydraulic behavior of hillslopes and quantify the effect of the uncertainty of mechanical parameters on hillslope stability for forewarning and hillslope management. Intra-hole deformation and displacement were record for the hillslope of the Babaoliao collapse site in the Chiayi County, as a case study. The fuzzy point estimation method and physical-based model were combined with the local factor of safety (LFS) theory to calculate the internal local factor of safety of the hillslope. A reliability analysis was then performed to determine the failure probability at different depths. Historical rainfall events were used to validate the model and predict the development of the failure probability for different rainfall patterns with the same warning rainfall. The results revealed that the failure probability model could effectively predict the area of hillslope instability and its changes over time and space. Different rainfall patterns affected the infiltration flux, leading to the difference in hillslope failure time. The delayed rainfall pattern had a significant impact on the time of slope instability, and shallow collapse was most likely to occur earlier. This study can be used as a reference for developing future hillslope warnings.

Highlights

Uncertainty propagation is handled through physical-based model

Fuzzy method can respond to the uncertainties inherent in practical landslide

The proposed framework was applied to practical hillslope to verify its feasibility

Introduction

Landslides are geomorphic processes occurring globally in areas with hillslopes, covering different climatic zones and soil materials, and can potentially result in environmental and economic loss (Tiranti and Cremonini 2019). Rainfall is the most common landslide trigger (Iverson 2000). When rainfall infiltrates into the unsaturated soil of a hillslope, the increased water content of the soil leads to a loss of matric suction and an increase in soil weight (Lacerda 2007; Godt et al., 2009; Augusto Filho and Fernandes 2019), leading to hillslope instability and failure. Usually, rainfall-induced hillslope failure occurs preferentially at shallow depths. In contrast, a single high-intensity rainfall event may cause rapid and deep failure, while slow and deep hillslope failure requires long hydrological processes (Sidle and Bogaard 2016). The internal hydrological processes, timing, and location of failures caused by rainfall on hillslopes remain a complex and ongoing research problem. Bogaard and Greco (2016) defined the hydrological processes that trigger hillslope failure as landslide hydrology and noted that storage and flux measurements are essential for understanding and quantifying landslide failure. The evolution of transient unsaturated groundwater flow and local stress can be considered based on physical models to effectively describe rainfall-induced internal hydrological and mechanical changes and failure mechanisms of hillslopes (Zhang J. et al., 2018).

As the physical model can combine hydrological and mechanical mechanisms, it can describe the internal hydrological and mechanical changes and the failure mechanisms of hillslopes caused by transient rainfall. Moreover, the model has a high predictive capability for quantifying the effects of various parameters on the hillslope stability (Corominas et al., 2014). Common hillslope stability analysis usually based on limit equilibrium analysis (e.g., Fellenius, 1936; Janbu, 1954; Bishop, 1955; Morgentern and Price, 1965) or shear strength reduction techniques (Matsui and San 1992; Dawson et al., 1999; Cai and Ugai 2004; Cheng et al., 2007). In addition, research on developed constitutive models that consider soil stress state variables, such as suction stress (Lu and Likos 2006; Lu 2020) and thermal and chemical processes (Nuth and Laloui 2008; Zhang et al., 2012; Bai et al., 2019; Bai et al., 2021), has gradually become prevalent. However, using a single stability index (factor of safety, Fs) for the hillslope makes it challenging to describe the spatiotemporal evolution of the hillslope unstable surface. Recently, Lu et al. (2012) proposed the local factor of safety (LFS) theory. Based on the Mohr-Coulomb failure criterion, the finite element method was used to solve the transient variably saturated flow and stress state, thereby analyzing the local safety factor of each position inside the hillslope. This method can capture the evolution of the stress state and failure surface with rainfall infiltration without the prior condition of the potential failure surface, thereby overcoming the challenges of limit equilibrium analysis. This method has also been applied to study the evolution of hillslope failure surfaces caused by changes in water content dynamics (Moradi et al., 2018) and the change in infiltration characteristics on embankment stability over time and space (Hinds et al., 2019). However, because the physical model relies on an extensive database of in situ or laboratory parameters, the quality and quantity of the database are major issues in this analysis, indicating that the model is susceptible to uncertainties arising from measurement errors, spatial variability, and incomplete data (Phoon and Kulhawy 1999). The geotechnical parameters of hillslope material, such as cohesion and friction angle, are inherently heterogeneous in space and these data are often limited in acquisition (Baecher and Christian 2005). The uncertainty of the input model parameters is the main factor that causes the deviation of the hillslope stability analysis results from reality (Burton et al., 1998).

Probabilistic analysis has been widely applied to quantify the uncertainty in hillslope stability analysis (El-Ramly et al., 2002; Griffiths and Fenton 2004; Xiao et al., 2017; Zhang L. et al., 2018; Li et al., 2020). As physical-based slope stability analysis is highly dependent on reliable estimates of soil parameters, the reliability of slopes for soil variables has been increasingly investigated (Jiang et al., 2014; Liu et al., 2019; Johari & Fooladi 2020). However, Nawari and Liang (2000) and Giasi et al. (2003) suggested that probability analysis requires a sufficient number of reliable observations to construct a reasonable probability density function. In addition, the uncertainty of the parameters may be non-stochastic (Juang et al., 1998; Nawari and Liang 2000). When data are limited and insufficient to define the probability density function, fuzzy set theory based on cognitive origin seems to be more suitable for analyzing the uncertainty of geotechnical parameters (Luo et al., 2011; Beer et al., 2013). In some case, this theory has been applied to hillslope stability analysis (Dodagoudar and Venkatachalam 2000; Park et al., 2012; Gong et al., 2014; Xu et al., 2014; Park et al., 2017, 2019; Zhou et al., 2019; Habibagahi et al., 2021).

In this study, by combining the fuzzy theory and hydraulic coupling model to quantify the uncertainty of mechanical parameters (cohesion and internal friction angle), we evaluated the internal hydrological and mechanical processes of hillslopes under rainfall conditions, the two-dimensional spatial distribution of hillslope stability and failure probability, and the impact and evolution of different rainfall patterns on the failure surface using the existing hillslope as an example.

Study methods

The fuzzy theory was used to establish the dependence functions of the soil mechanics parameters, namely cohesion and internal friction angle. The fuzzy point estimation method combined with the finite element analysis model HYDRUS2D and the Slope Cube Module effectively described the changes in the soil hydraulic behavior of the unsaturated layer affected by rainfall infiltration. HYDRUS 2D is a hydrological model that is widely used to simulate the movement of soil water (Bufon et al., 2012; Dabach et al., 2013; Kanda et al., 2020), heat (Wang et al., 2013; Nakhaei and Šimůnek, 2014), and solute (Pang et al., 2000) in variably saturated soils. The Slope Cube Module is a supplemental package of HYDRUS 2D to simulate the transient fields of soil suction, suction stress, and local factor of safety (LFS). Finally, the failure probability was calculated using reliability analysis. The hydraulic analysis process is illustrated in Figure 1, and each method is explained as follows.

FIGURE 1

FIGURE 1. Flowchart of one way coupled hydro-mechanical calculation in this study.

Hydrological model

The two-dimensional HYDRUS2D seepage control equation is a transient unsaturated layer seepage control equation developed by Šimůnek et al. (2008) based on Richards’ equation (Richards 1931).

$\frac{\partial \theta \left(h\right)}{\partial t}=\nabla \cdot K\left(h\right)\nabla H+W(1)$

where t denotes the time [T]; $W$, the source or sink [T⁻¹]; $H$, the total head [L]; $K\left(h\right)$, the hydraulic conductivity function (HCF) [LT⁻¹]; and $\theta \left(h\right)$, the volumetric water content [L³L⁻³]. Soil water characteristic curve (SWCC) links the relationships between matric suction and volumetric water content, and is of great importance for exploring the hydraulic and mechanical behavior of unsaturated soils. In this study, the SWCC model proposed by van Genuchten (1980) and the HCF proposed by Mualem (1976) were used to describe the water retention capacity and hydraulic conductivity coefficients of unsaturated soil, as shown in Eqs 2, 3:

$\theta \left(h\right)={\theta }_r+\frac{{\theta }_s-{\theta }_r}{{\left[1+{\left(\alpha \left|h\right|\right)}^n\right]}^{1-\frac{1}{n}}}(2)$

$K\left(h\right)=K_s\frac{{\left\{1-{\left(\alpha \left|h\right|\right)}^{n-1}{\left[1+{\left(\alpha \left|h\right|\right)}^n\right]}^{\frac{1}{n}}-1\right\}}^2}{{\left\{1+{\left[\alpha \left|h\right|\right]}^n\right\}}^{\frac{1}{2}-\frac{1}{2n}}}(3)$

where ${\theta }_s$ denotes the saturated soil water content [L³L⁻³]; ${\theta }_r$, the residual soil water content [L³L⁻³]; $h$, the pressure head [L]; $\alpha$ [1/L] and $n$ [-], the fitted parameters of SWCC [-]; and$K$, the saturated hydraulic conductivity [LT⁻¹].

Stress-strain deformation model

The Hillslope Cube Module adopts the two-dimensional finite element code FEM2D (Reddy 1985) to solve the stress distribution at each point within the hillslope based on the momentum balance. The method is based on plane stress linear elasticity to simulate the stress change caused by the change in transient unit weight, and applies suction stress in the computation of effective stress and displacement. The control equation is expressed as follows:

$\nabla \cdot \left(\mathrm{\sigma }\right)+\gamma b=0(4)$

where $\sigma$ denotes the three independent stress variables (i.e., ${\sigma }_{xx}$, ${\sigma }_{yy}$, ${\sigma }_{xy}$) [ML⁻¹T⁻²]; $\gamma$, the bulk unit weight of the hillslope soil material [ML⁻²T⁻²]; and $b$, the unit vector of body forces [-]. Therefore, the elastic modulus $E=\sigma /\epsilon$ [ML⁻¹T⁻²] and Poisson’s ratio $\nu$ [-] can be used to solve the stress and displacement.

The unified effective stress developed and validated by Lu and Likos (2004,2006), and Lu et al. (2010) was adopted.

${\mathrm{\sigma }}^{\prime }=\mathrm{\sigma }-u_a-{\mathrm{\sigma }}^s(5)$

where $u_a$ is the pore-air pressure [ML⁻¹T⁻²] and ${\sigma }^s$ is the suction stress [ML⁻¹T⁻²], representing all the physical and chemical mechanisms that can occur between soil particles, expressed as follows:

${\mathrm{\sigma }}^s=-{\mathrm{\sigma }}_c=-\mathrm{\sigma }{}_{cap}-{\mathrm{\sigma }}_{pc}-S\left(u_a-u_w\right)(6)$

where ${\sigma }_c$ is the Born repulsive force [ML⁻¹T⁻²]; ${\sigma }_{cap}$, the capillary force [ML⁻¹T⁻²]; ${\sigma }_{pc}$, the combination of van der Waals attractive force and electric double-layer force [ML⁻¹T⁻²]; S, the soil saturation [-]; and $\left(u_a-u_w\right)$, the matric suction [ML⁻¹T⁻²], where $u_w$ is the pore-water pressure [ML⁻¹T⁻²]. The matric suction, capillary, van der Waals, and electric double-layer force of the soil balance each other out with the Born repulsive force, but the effects of van der Waals and electric double-layer force can be neglected as the grain size of the soil increases. Lu et al. (2010) used thermodynamic theory to consider suction as the energy stored in a unit soil as each stress component of soil can be expressed as a function of matric suction, saturation, and water content, and since soil suction is mainly controlled by soil water content. The suction stress characteristic curve can be estimated from the same set of parameters from the SWCC model. The formula can be expressed as follows:

${\mathrm{\sigma }}^s=-\left(u_a-u_w\right)u_a-u_w\le 0$

${\mathrm{\sigma }}^s=-\frac{\left(u_a-u_w\right)}{{\left\{1+{\left[\alpha \left(u_a-u_w\right)\right]}^n\right\}}^{\left(n-1\right)/\mathrm{n}}}{u}_a-u_w>0(7)$

Hillslope stability model

The LFS theory developed by Lu et al. (2012) was used to assess the internal stability of the hillslopes. The LFS is based on the Mohr-Coulomb failure criterion and represents the process of changing the soil stress state toward the direction of failure owing to rainfall infiltration. LFS is defined as the ratio of shear strength to shear stress at any point inside the slope, as follows:

$LFS=\frac{{\tau }^{*}}{\tau }=\frac{\cos {\varphi }^{\prime }}{{\mathrm{\sigma }}_{II}^{\prime }}\left(c^{\prime }+{\mathrm{\sigma }}_I^{\prime }\tan {\varphi }^{\prime }\right)(8)$

where ${\tau }^{*}$ is the shear strength, also known as potential Coulomb stress [ML⁻¹T⁻²]; $\tau$, the shear stress, also known as current Coulomb stress [ML⁻¹T⁻²];$c^{\prime }$, effective cohesion [ML⁻¹T⁻²]; and${\varphi }^{\prime }$, the effective internal friction angle [°]. ${\sigma }_I^{\prime }$ [ML⁻¹T⁻²] and ${\sigma }_{II}^{\prime }$ [ML⁻¹T⁻²] are the positions of the center and radius of the Mohr circle in two dimensions and can be expressed as follows:

${\mathrm{\sigma }}_I=\frac{{\sigma }_1^{\prime }+{\mathrm{\sigma }}_3^{\prime }}{2}=\frac{{\mathrm{\sigma }}_1+{\mathrm{\sigma }}_3}{2}-{\mathrm{\sigma }}^s{\mathrm{\sigma }}_{II}=\frac{{\mathrm{\sigma }}_1^{\prime }+{\mathrm{\sigma }}_3^{\prime }}{2}=\frac{{\mathrm{\sigma }}_1-{\mathrm{\sigma }}_3}{2}-{\mathrm{\sigma }}^s(9)$

Substituting Eq. 9 into Eq. 8, LFS can be expressed as follows:

$LFS=\frac{\cos {\varphi }^{\prime }}{{\mathrm{\sigma }}_1-{\mathrm{\sigma }}_3}\left[2c^{\prime }+\left({\mathrm{\sigma }}_1+{\mathrm{\sigma }}_3-2{\mathrm{\sigma }}^s\right)\tan {\varphi }^{\prime }\right](10)$

This study calculated the suction stress by combining the water content, matric suction, and total stress changes. The LFS was then calculated using the unified effective stress based on suction stress. This linear theory-based computational mechanics framework solves the stresses and displacements of statically admissible fields, regardless of the complex elastoplastic theory. The redistribution of pressure or displacement caused by a hillslope failure is defined by the static allowable stress field as that satisfies the equilibrium differential equation (Malvern 1969). Therefore, an LFS of less than one indicates the location of potential hillslope failure (Lu et al., 2012), which can be used to indicate the location of potential failure areas. This model and finite element analysis can be used to analyze the stability of soil elements at different locations or depths of the hillslope affected by changes in water content or suction stress, overcoming the challenges of conventional hillslope stability analysis.

Fuzzy set theory

The traditional set rationality defines whether an element $\mathrm{x}$ belongs to set $\mathrm{A}$, and its characteristic function is expressed as follows:

${\mu }_A\left(\mathrm{x}\right)=\{\begin{array}{l}1,\mathrm{x}\in \mathrm{A}\\ 0,\mathrm{x}\notin \mathrm{A}\end{array}(11)$

When $\mathrm{x}$ belongs to $\mathrm{A}$,${\mu }_A\left(\mathrm{x}\right)=1$; when $\mathrm{x}$ does not belong to $\mathrm{A}$, ${\mu }_A\left(\mathrm{x}\right)=0$. There are only two cases of 0–1. Zadeh (1965) proposed the fuzzy theory to represent the uncertainty and fuzzy phenomenon, also known as the fuzzy set theory. The characteristic function is extended into a continuous value function ${\mu }_A\left(\mathrm{x}\right)$ in the interval [0,1], called the membership function. The value of the membership function indicates the degree to which element $\mathrm{x}$ belongs to set $\mathrm{A}$. The most significant difference between a fuzzy set and a traditional set is that a traditional set has only a unique characteristic function. In contrast, a fuzzy set has an infinite number of membership functions to represent. Common membership functions include a triangular shape, trapezoid shape, Gaussian shape, S function, and Z function. Triangular and trapezoid functions are less computationally intensive and highly adoptable (Dodagoudar and Venkatachalam 2000). Fuzzy theory is also known as fuzzy set theory, and the fuzzy number is a special case of fuzzy set, its characteristic is that the shape of the membership function is unimodal, and at least one degree of membership is 1. If there is no specific assumption (under the condition of lack of data), the fuzzy number can be assumed to be a triangle, expressed as $TFN\left[a,m,b\right]$, including upper bound (a), lower bound (b), and peak value (m). In general, the peak value is usually estimated from the average of the available data (Luo et al., 2011). This study used cohesion and internal friction angle as analysis variables. We used the mean value of cohesion and friction angle from the laboratory test as the peak value of their fuzzy numbers. Upper and lower bounds were determined using an estimated approach of the standard deviation of uncertain parameters. Therefore, the triangular fuzzy number of cohesion and friction angle can be expressed as follows:

$x_c=TFN\left[m_c-k{\mathrm{\sigma }}_c,m_c,m_c+k{\mathrm{\sigma }}_c\right]x_{\varphi }=TFN\left[m_{\varphi }-k{\mathrm{\sigma }}_{\varphi },m_{\varphi },m_{\varphi }+k{\mathrm{\sigma }}_{\varphi }\right](12)$

The value of k depends on the actual conditions of the hillslope project and ranges from 0.5 to 3. When the value of k is larger, the distribution of the mechanical parameters is larger and the selected parameter is less reliable, and vice versa. Luo et al. (2011) and Park et al. (2017) considered it reasonable to estimate the upper and lower bounds using the mean value of ± 2$\sigma$. Therefore, the value of k in this study was considered to be 2 $cv$ is the coefficient of variation, which indicates the degree of parameter variation ($cv=\sigma /\mu$):$cv$of cohesion is 25–30%, and that of the internal friction angle is 10–20% (Phoon & Kulhawy 1999; Hsiao et al., 2008; Park et al., 2013).

The fuzzy point estimation method combines the fuzzy vertex and the point estimation methods. The fuzzy vertex method was proposed by Dong and Shah (1987) and is based on $\alpha$- intercept set and interval analysis to obtain the vertex combinations of variables and replace the membership functions as input variables. Thus, there are vertex combinations for N membership functions as the input variables$2^N$. Rosenblueth (1975) proposed a point estimation method to evaluate the uncertainty parameters of a performance function. Two points estimate the mean and standard deviation of the performance function, and the upper bounds of the variables obtained through $\alpha$- intercept set are $\left(c_{-}^{{\alpha }_i},c_{+}^{{\alpha }_i}\right)$ and $\left({\varphi }_{-}^{{\alpha }_i},{\varphi }_{+}^{{\alpha }_i}\right)$, respectively. In this study, the $\alpha$- intercept set took nine membership degrees from 0.1 to 0.9 to reduce the dispersion of the analysis results. Each $\alpha$- intercept set can cut out a range of two points and obtain four sets of vertex combinations, and four sets of output values were obtained through simulation $\left(LF{S}_{--},LF{S}_{-+},LF{S}_{+-},LF{S}_{++}\right)$. When considering the difference in the contribution of each $\alpha$- intercept set to the results, this study used the concept of fuzzy weighted average, and the mean and standard deviation of the fuzzy weighted factor of safety is expressed as follows.

$E\left[LFS\right]=\frac{{\sum }_{i=1}^M{\alpha }_{i}LF{S}_{{\alpha }_i}}{{\sum }_{i=1}^M{\alpha }_i}(13)$

${\mathrm{\sigma }}_{LFS}=\sqrt{E\left[LF{S}^2\right]-{\left(E\left[LFS\right]\right)}^2}(14)$

$M$is the number of $\alpha$- intercept sets. The failure probability is obtained from the reliability index. Assuming that the factor of safety is normally distributed, the reliability index is a standard normal distribution. The reliability index$\beta$ and failure probability ($P_f$) are expressed as follows:

$\beta =\frac{E\left[LFS\right]-1}{{\mathrm{\sigma }}_{LFS}}(15)$

$P_f=1-\mathrm{\Phi }\left(\beta \right)=\mathrm{\Phi }\left(-\beta \right)(16)$

Study site

Background of the study site

Located at the collapse site of Babaoliao in the Dongxing Village, Zhongpu Township, Chiayi County, the topography of the study site is low-altitude hilly terrain with elevations ranging from 420–580 m. The slopes of the area are Grade 5 and Grade 6 (slope >40°), and the slope direction decreases from north to south, followed by southeast, southwest, and west. The rocks belong to the western piedmont belt geological area, and the exposed strata are of Miocene to Pleistocene age. As shown in Figure 2, the regional geological unit contained the main stratum of the collapse site—the beak layer (Niaotsui Formation, Nt), with a lithology of muddy sandstone, sandy shale, and thick sandstone. The Yunshuichi Formation (Yh) was first exposed and was composed to shale, sandy shale, and mudstone on the west side of the collapse site. The Liuchungchi Formation (Lu), with silt-layered shales, sandy shales, or interbedded muddy sandstones, is exposed on the west side of the collapse site. Tangenshan sandstone (Tn), located on the eastern side of the collapse site, is dominated by thickly bedded gray to massive mudstone sandstone, occasionally interbedded with sandstone or thin shale. The Changchikeng Formation (Cc) is dominated by greenish-grey fine-grained sandstone, muddy sandstone, and thick grey sand shale, commonly interbedded with mound-like laminations. In the geological structure, the Liuchungchi Fault passes through the southern side of the collapsed area, while the Chukou and Lunhou Faults are the main fault structures in the area. The collapse site was mainly located on the back-slope axis (anticline axis) and its eastern flank slope. The northeastern portion of the collapse site presents a localized oblique structure. This complex geological condition is one factor contributing to the higher collapse potential of the area. Since the formation of the collapse site in November 2011, the landslide area has continued to expand owing to heavy rains and typhoons, and there are signs of continuous sliding. The potential collapse area is 11.31 ha, with a risk of shallow collapse and deep sliding. Systematic surveys have been conducted since 2017. To date, the collapse site has undergone integrated analysis such as field surveys, geophysical/chemical investigations, sampling and analysis, observation system construction, UAV interpretation, and application models. Related observations are ongoing, and the investigation strategy is being revised in response to spatiotemporal changes to clarify the sliding mechanism of the potential landslide and formulate countermeasures (Branch, 2018).

FIGURE 2

FIGURE 2. Schematic diagram of geology and geological structure in Babaoliao area.

Hydrogeological assessment

The internal factor of the Babaoliao collapse mechanism was regional geological fragmentation, and the external triggering factor was mainly rainfall. When rainfall infiltrates into shallow soil or generates fracture -advantageous water flow on the sliding surface, it may cause hillslope instability. Therefore, we conducted soil sampling and indoor test analysis on the collapse site to understand the internal hydraulic behavior of hillslope soils due to rainfall and its effect on stability. The test items included the general physical property test of soil (unit weight, porosity ratio, specific gravity, and saturation), general physical property test of rock (water content, porosity, durability, unit weight, and specific gravity), triaxial water permeability test of soil, pressure cooker test of soil, and direct shear test of rock. The tests were performed by the geotechnical engineering test laboratory of Sinotech Engineering Consultants with TAF certification. The hydro-mechanical properties of geological materials are listed in Table 1 and reported in detail in SWCB (2018). The results and parameters of the tests were used as references for subsequent conceptual modeling of the collapse site. The soil composition of the fine particles was mainly fine sand to powder soil, whereas the coarse particles with relatively high content are mainly medium sand. The results of the soil permeability test showed that the permeability values ranged from 1.64×10⁻⁷–8.99×10^–6 cm/s at 20°C under different compression pressure. The test results showed that the unit weight of the rock sample was 2.37–2.69 t/m³, water content was 1.9–8.7%, specific gravity was 2.68–2.73, porosity was 0.08–0.19, and water absorption rate was 2.7–12.8%.

TABLE 1

TABLE 1. Hydraulic and mechanical parameters of three geological materials.

Conceptual modeling of hillslopes

This study used the section from BH05-CI to BH-02 on the upper slope of the disaster-prone area at the Babaoliao collapse site as an example. The soil thickness of this section ranges from 3.8 to 7.2 m, and the rock plate is muddy sandstone. On-site surveys have shown that the surface soil has undergone erosion caused by rainfall events, forming several eroded pits and trenches, and is prone to disasters such as rock chippings. BH-05CI established an automatic observation record of in-hole deformation in July 2018, and obvious deformation was observed during the rainfall period from 08/23/2018 to 08/24/2018. This study adopted a rainfall event (hereafter referred to as the 0823 rainfall event) for subsequent numerical simulations. In this study, the geological conceptual model from BH05-CI to BH-02 was first established based on the results of previous field surveys and tests, as shown in Figure 3, and the actual elevation of the slope before the rainfall event was used for the surface elevation. According to the experimental parameters of the test (Table 1), we adopted the best-fitting SWCC, HCF, and estimated SSCC through Eq. 7, as shown in Figure 4.

FIGURE 3

FIGURE 3. Conceptual model of slope geometry and boundary conditions.

FIGURE 4

FIGURE 4. Hydraulic properties of materials (A) SWCC (B) SSCC (C) HCF.

Stratification was used as the mesh refinement unit in this study. The soil layer was set to 0.8 m, and the weathered rock debris layer was 1.6 m. The farther the grid distance from the set stratification, the larger the size, and the system automatically optimizes the target grid size to 5.6 m; that is, the grid distribution to the target grid size stops. The overall grid was divided into 2,453 nodes and 5,032 elements. The hydrological boundary is the atmospheric boundary on the slope, seepage surface boundary on the slope below BH-02, constant head boundary on the right side, time-varying head boundary on the left side, and zero-flow boundary at the bottom. The mechanical boundary is the free displacement boundary on the slope, the zero-displacement boundary in the x-direction on the left and right sides, and the zero-displacement boundary in the z-direction at the bottom. The simulation of the 0823 rainfall events included the complete rainfall events. To include the complete rainfall event, the simulation time used in this study was 60 h, and the iterative convergence conditions are 0.001 water content tolerance and 0.01 m pressure head tolerance. The simulation results showed that the root mean square error of water level was ∼0.35 m, and the coefficient of determination R² was ∼0.95 at the BH05-CI, as shown in Figure 5, indicating the reasonableness of the model.

FIGURE 5

FIGURE 5. Validation of simulated value against observed values at BH05-CI.

Establishment of cohesion and internal friction angle fuzzy numbers

In this study, the cohesion force and internal friction angle were considered triangular fuzzy numbers, and the values in Table 1 were considered the mean values. The maximum coefficient of variation was used to establish the triangular fuzzy numbers, which were 30% of the cohesion coefficient of variation and 20% of the internal friction angle coefficient of variation. The top sets of cohesion and internal friction angle were obtained by intercepting nine affiliations from 0.1 to 0.9. A total of 36 input variables were obtained, as listed in Table 2. After the model calculation, 36 sets of output variables were obtained, subsequently, the hillslope failure probability was obtained by calculating Eqs 13–15.

TABLE 2

TABLE 2. The value of cohesion and friction angle of three geological materials in this study.

Results and discussion

Analysis of failure probability of historical rainfall events

This study used the 0823 rainfall event as the analysis period. We obtained different combinations of parameters with varying degrees of affiliation through the intercept set without considering the correlation between cohesion and angle of internal friction. We considered an observation point at a depth of 1 m for BH-05CI and the 48th hour of rainfall as an example. The results show that the reliability index increased as the degree of affiliation increased. The average local safety coefficient at this location varied from [1.064, 1.075] to [0.217, 2.278], as shown in Figure 6. The fuzzy weighted average local safety factor considering the degree of membership was 1.073. The change in the fuzzy weighted average local safety factor over time is shown in Figure 7. According to the rainfall data, continuous heavy rainfall began at the 15th hour. The BH-05CI observation deformation records in the wellbore show that the position started to deform by 0.54 mm at the 23rd hour, the deformation increased by more than 1 mm per hour, and the maximum deformation was 25.04 mm at the 32nd hour. Therefore, the LFS (LFS = 1.258) at the 23rd hour was considered a critical value in this study. The change in the failure rate of this observation point with time showed that the LFS decreased with the increase in cumulative rainfall, and the failure rate increased with it. The failure rates were 50% at the 23rd hour, 90% at the 48th hour, and 94% at the 60th hour. The spatial distribution of the failure rate was mainly concentrated around BH-05CI, indicating that the unstable area of the slope extended from the surface to the bottom as the rainfall infiltration increased. A failure rate of 50% was used as an indicator of instability. The instability depth was ∼1.5 m at the 23rd hour, 1.8 m at the 48th hour, and 2 m at the 60th hour. As shown in Figure 8, the areas with a failure rate of over 50% were consistent with the interface of elevation loss, indicating that the model can predict the area of slope instability and its change over time and space.

FIGURE 6

FIGURE 6. Variation of average LFS, reliability index with the degree of membership.

FIGURE 7

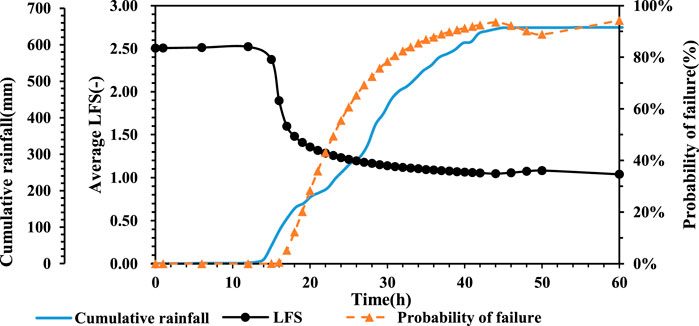
FIGURE 7. Temporal variation in accumulation rainfall, fuzzy weighted average LFS and probability of failure at observation point.

FIGURE 8

FIGURE 8. Distribution of probability of failure at 23, 48, and 60 h at the top of slope.

Analysis of rainfall pattern failure probability

In this study, regarding the warning management benchmark of Babaoliao, the cumulative rainfall of the yellow warning in the area was 200 mm, and the average rainfall intensity was 20 mm/h (SWCB, 2018). Therefore, in this study, four rainfall patterns were designed based on the principle of 24-h cumulative rainfall of 200 mm, namely, uniform, delayed, normal, and advanced rainfall patterns (Rahimi et al., 2011), as shown in Figure 9, to investigate the effect of different rainfall patterns on the hydraulic behavior and stability of the hillslope.

FIGURE 9

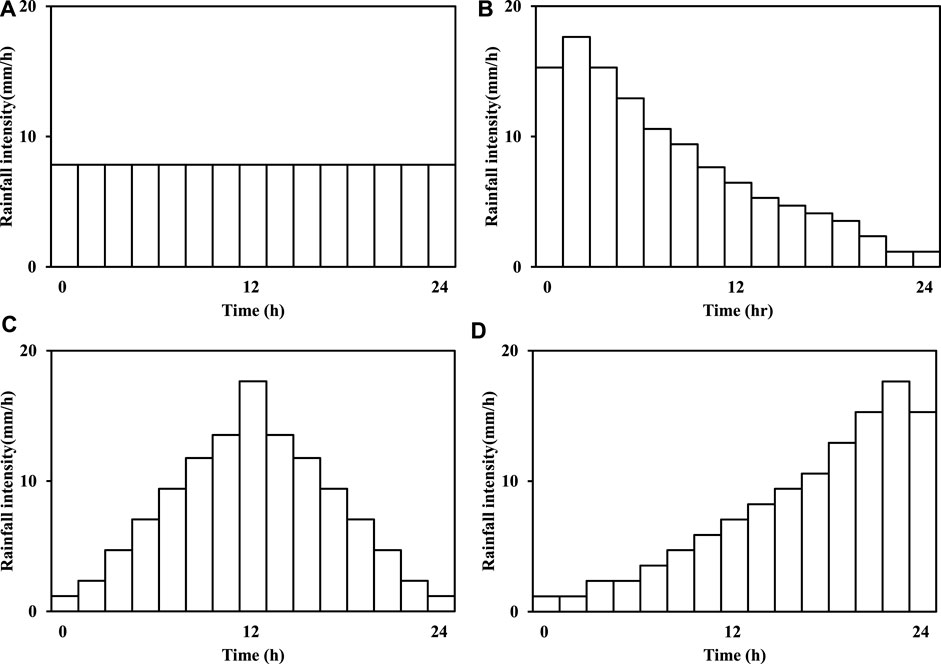
FIGURE 9. Four rainfall patterns with the same accumulated rainfall, 200 mm: (A) uniform rainfall pattern, (B) delayed rainfall pattern, (C) normal rainfall pattern, (D) advanced rainfall pattern.

This study first analyzed the cumulative runoff and infiltration flux of the atmospheric boundary at the surface of the slope under four rainfall patterns. Surface runoff analysis showed that the retrogressive rain pattern was third in rainfall time owing to the strong initial rainfall intensity. Surface runoff occurs in hours, and surface runoff occurred at the latest in the progressive rain pattern of ∼ the 14th hour, as shown in Figure 10A. The cumulative infiltration flux shows that the overall cumulative infiltration flux of the delayed rainfall pattern was higher than that of the other rainfall patterns in each time period, as shown in Figure 10B. This study evaluated the changes in the volumetric water content of the surface soil with depth in different time periods under four rainfall conditions on the BH-05CI vertical profile. The delayed rainfall pattern caused the soil surface to reach saturation in a short time (the sixth hour as an example). Furthermore, the wet zone had a deep advancing depth, and the water content response depth was ∼2 m. Advanced rainfall patterns had little initial and accumulated rainfall intensity, so the water content response depth was ∼0.7 m, and the surface layer was saturated. As shown in Figure 11A, at the 12th hour, the water content reaction states of the homogeneous and normal types were similar. After the 24th hour, the surface layer reached a saturated state, and the depth of the saturation zone was ∼0.7 m. The water content response changed below the saturation zone in the order of delayed rainfall pattern> uniform rainfall pattern> normal rainfall pattern> advanced rainfall pattern. The soil water content was affected by the rainfall pattern and accumulated rainfall. In the process of rainfall infiltration, rainfall intensity affected the development of the shallow saturation profile, revealing the important influence of vertical seepage on shallow hydrological responses. Chinkulkijniwat et al. (2016) conducted experiments to evaluate the hydrological response of different shallow slope and showed similar findings. The slope soil was unstable owing to rainfall infiltration, which was affected by the change and distribution of soil water content. The analysis of the probability of failure shows that in the sixth hour, except for the advanced rainfall pattern, other rainfall patterns caused instability of the surface soil. Along with the vertically downward direction of the saturation zone, the instability range also developed in the deep soil, as shown in Figure 11B; in the 24th hour, the location with a 100% probability of failure was ∼1 m below the surface.

FIGURE 10

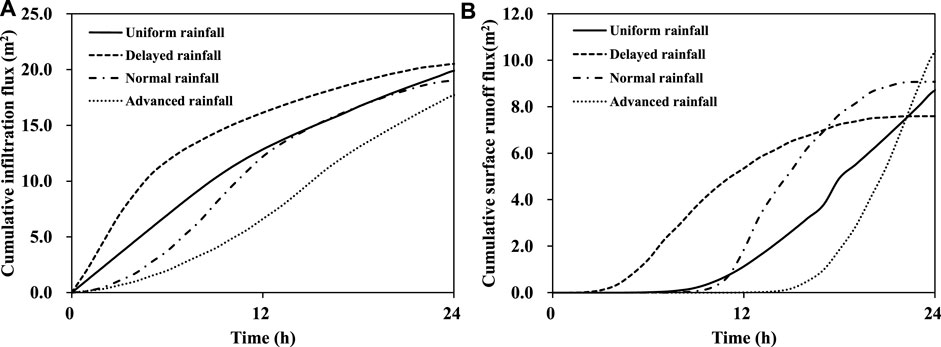
FIGURE 10. Result of flux analysis on atmospheric boundary condition under four rainfall pattern(A)cumulative infiltration flux and (B) cumulative surface runoff flux.

FIGURE 11

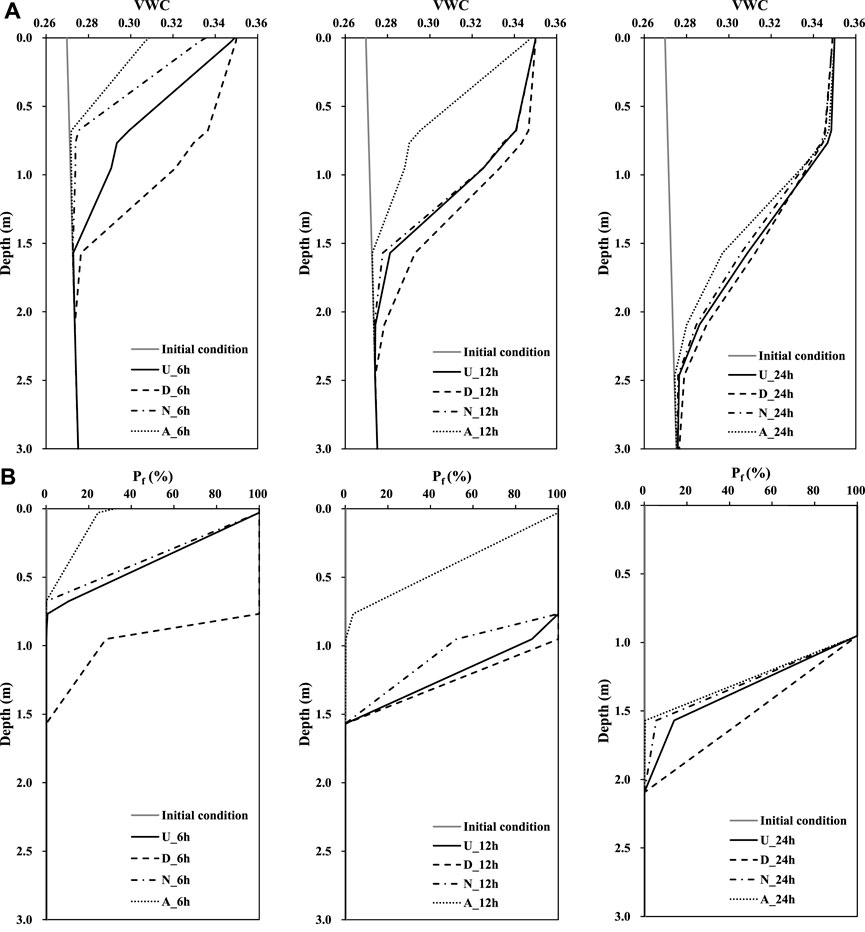
FIGURE 11. Result of (A) volumetric water content and (B) probability of failure change with depth at 6, 12 and 24 h (U: Uniform rainfall pattern; D: Delayed rainfall pattern; N: Normal rainfall pattern; A: Advanced rainfall pattern).

Under the four rainfall conditions, the spatial variability of the hillslope failure probability was affected by the boundary flux and hillslope topography, as shown in Figure 12. The spatial distribution of the failure probability of 50% was presented at the end of the rainfall time (24th hour) as the basis of analysis, which showed that different rainfall patterns would lead to different degrees of development of the unstable area for the same cumulative rainfall of 200 mm. At the end of the rainfall event, the delayed rainfall pattern had the largest instability area, followed by the uniform and normal types. In contrast, the advancing rain type had the smallest instability area. The variation in stability over time was evaluated at the observation point of BH-05CI at a depth of 1 m. When considering the time variability, this study considered the observation point at a depth of 1 m at BH-05CI as an example to evaluate the changes in stability over time under the four different rainfall patterns, as shown in Figure 13. The average local safety factor of the delayed rainfall pattern had a large decreasing slope, reaching a failure probability of 100% in the third hour, followed by a uniform rainfall pattern at the sixth hour, a normal rainfall pattern at the ninth hour, and an advanced rainfall pattern at the 13th hour. This shows that even if the accumulated rainfall over 24-h was 200 mm, depending on the rainfall intensity, the overall infiltration flux of the slope changes dynamically, affecting the time of slope instability. Among them, the delayed rainfall pattern significantly impacted on the time of slope instability, and shallow collapse was most likely to occur earlier. Rahimi et al. (2011) showed that the delayed rainfall pattern occurred earlier and exhibited similar results. It should be noted that this study only considered the effects of different rainfall patterns on the boundary fluxes, slope hydraulic behavior, and stability for the same 24-h rainfall. When the rainfall is of the long-delay, high-intensity continuous type, deeper slope failure may occur after the shallow collapse, which is not included in the scope of this study. The type and scale of slope failure are controlled by slope hydraulic behavior, geomaterial properties, and slope structure. Shallow failures are usually the priority soil-sand hazards caused by rainfall, indicating the importance of evaluating shallow soil hydraulic behavior and failure mechanisms.

FIGURE 12

FIGURE 12. Distribution of 50% probability of failure at 24 h at the top of slope.

FIGURE 13

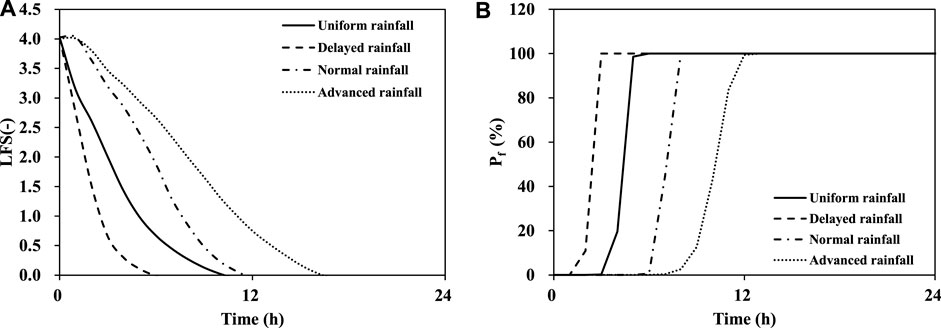
FIGURE 13. Result of (A) slope stability analysis and (B) probability of failure under four rainfall patterns.

Conclusion

This study considered uncertainties in the mechanical parameters. The fuzzy theory was combined with the hydraulic coupling model and the LFS theory was used to evaluate the LFS at different depths of the shallow slope. Reliability analysis was then used to calculate the failure rate of the slope at different depths. To verify the rationality of the analytical model, this study used a case study of the Babaoliao hillslope, which has a record of in-hole deformation and observed displacements, to simulate the 0823 rainfall event, analyze of the simulation results, calculate the failure probability, and compare the instability range.

The observation of 1 m underground displacement in BH-05CI, and the time of the beginning of displacement after the 23rd h was used as the benchmark. The local safety factor at this time was regarded as the critical value (LFS = 1.258), and the underground factor was calculated—the change in the probability of failure with time. The results showed that the failure rate was 50% at the 23rd hour, 90% at the 48th hour, and 94% at the 60th hour. Spatial analysis showed that the change in the failure rate was mainly concentrated around BH-05CI, and the relative instability area is consistent with the elevation loss interface, indicating that the model could effectively describe the development and distribution of the slope instability area with in situ observation data.

We evaluated the effect of different rainfall patterns on hillslope stability concerning yellow alert rainfall (24-h cumulative rainfall of 200 mm), which is the benchmark value of the Babaoliao alert management. The results showed that the boundary flux controls the overall infiltration of water into the slope and affects the change in soil water content, which in turn causes slope instability. Delayed rainfall causes early slope instability, therefore, special attention should be paid to this type of rainfall pattern. According to the occurrence sequence of soil-sand disasters, shallow landslides and soil-rock flows are usually the priority soil-sand disasters. They are influenced by the internal hydraulic behavior of the slope, the characteristics of the geological material, and the structure that controls the type and scale of slope failure, indicating that shallow failure is one of the precursors of large-scale collapse. Therefore, evaluating the hydraulic behavior and failure mechanisms of shallow soils is crucial.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Material preparation, investigation, data collection and curation were performed by C-CK, N-CC, and K-CC. Conceptualization, data analysis, visualization and the original draft was performed by Y-SY. Supervision and Writing-reviewing and editing was performed by H-FY. All authors commented on previous versions of the manuscript and approved the final manuscript.

Conflict of interest

C-CK and N-CC were employed by the company Sinotech Engineering Consultants, Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Augusto Filho, O., and Fernandes, M. A. (2019). Landslide analysis of unsaturated soil slopes based on rainfall and matric suction data. Bull. Eng. Geol. Environ. 78 (6), 4167–4185. doi:10.1007/s10064-018-1392-5

CrossRef Full Text | Google Scholar

Baecher, G. B., and Christian, J. T. (2005). Reliability and statistics in geotechnical engineering. John Wiley & Sons.

Google Scholar

Bai, B., Yang, G. C., Li, T., and Yang, G. S. (2019). A thermodynamic constitutive model with temperature effect based on particle rearrangement for geomaterials. Mech. Mat. 139, 103180. doi:10.1016/j.mechmat.2019.103180

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Cai, G., Hu, W., and Yang, G. (2021). Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotech. 137, 104272. doi:10.1016/j.compgeo.2021.104272

CrossRef Full Text | Google Scholar

Beer, M., Zhang, Y., Quek, S. T., and Phoon, K. K. (2013). Reliability analysis with scarce information: Comparing alternative approaches in a geotechnical engineering context. Struct. Saf. 41, 1–10. doi:10.1016/j.strusafe.2012.10.003

CrossRef Full Text | Google Scholar

Bishop, A. W. (1955). The use of the slip circle in the stability analysis of slopes. Géotechnique 5 (1), 7–17. doi:10.1680/geot.1955.5.1.7

CrossRef Full Text | Google Scholar

Bogaard, T. A., and Greco, R. (2016). Landslide hydrology: From hydrology to pore pressure. WIREs Water 3 (3), 439–459. doi:10.1002/wat2.1126

CrossRef Full Text | Google Scholar

Branch, N. (2018), Large-scale collapse investigation and monitoring plan in the Babaoliao area - evaluation and correlation of key factors of multi-scale sliding signs in collapse (in Chinese)). Soil and water conservation bureau council of agriculture. Executive Yuan.

Google Scholar

Bufon, V. B., Lascano, R. J., Bednarz, C., Booker, J. D., and Gitz, D. C. (2012). Soil water content on drip irrigated cotton: Comparison of measured and simulated values obtained with the hydrus 2-D model. Irrig. Sci. 30 (4), 259–273. doi:10.1007/s00271-011-0279-z

CrossRef Full Text | Google Scholar

Burton, A., Arkell, T. J., and Bathurst, J. (1998). Field variability of landslide model parameters. Environ. Geol. 35 (2-3), 100–114. doi:10.1007/s002540050297

CrossRef Full Text | Google Scholar

Cai, F., and Ugai, K. (2004). Numerical analysis of rainfall effects on slope stability. Int. J. Geomech. 4 (2), 69–78. doi:10.1061/(asce)1532-3641(2004)4:2(69)

CrossRef Full Text | Google Scholar

Cheng, Y. M., Lansivaara, T., and Wei, W. (2007). Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods. Comput. Geotech. 34 (3), 137–150. doi:10.1016/j.compgeo.2006.10.011

CrossRef Full Text | Google Scholar

Chinkulkijniwat, A., Yubonchit, S., Horpibulsuk, S., Jothityangkoon, C., Jeeptaku, C., and Arulrajah, A. (2016). Hydrological responses and stability analysis of shallow slopes with cohesionless soil subjected to continuous rainfall. Can. Geotech. J. 53 (12), 2001–2013. doi:10.1139/cgj-2016-0143

CrossRef Full Text | Google Scholar

Corominas, J., van Westen, C., Frattini, P., Cascini, L., Malet, J. P., Fotopoulou, S., et al. (2014). Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 73 (2), 209–263. doi:10.1007/s10064-013-0538-8

CrossRef Full Text | Google Scholar

Dabach, S., Lazarovitch, N., Šimůnek, J., and Shani, U. (2013). Numerical investigation of irrigation scheduling based on soil water status. Irrig. Sci. 31 (1), 27–36. doi:10.1007/s00271-011-0289-x

CrossRef Full Text | Google Scholar

Dawson, E., Roth, W., and Drescher, A. (1999). Slope stability analysis by strength reduction. Geotechnique 49 (6), 835–840. doi:10.1680/geot.1999.49.6.835

CrossRef Full Text | Google Scholar

Dodagoudar, G., and Venkatachalam, G. (2000). Reliability analysis of slopes using fuzzy sets theory. Comput. Geotech. 27 (2), 101–115. doi:10.1016/S0266-352X(00)00009-4

CrossRef Full Text | Google Scholar

Dong, W., and Shah, H. C. (1987). Vertex method for computing functions of fuzzy variables. Fuzzy Sets Syst. 24 (1), 65–78. doi:10.1016/0165-0114(87)90114-X

CrossRef Full Text | Google Scholar

El-Ramly, H., Morgenstern, N., and Cruden, D. (2002). Probabilistic slope stability analysis for practice. Can. Geotech. J. 39 (3), 665–683. doi:10.1139/t02-034

CrossRef Full Text | Google Scholar

Fellenius, W. (1936). Paper presented at the transactions, Calculation of stability of earth dam. Washington, DC. 2nd Congress Large Dams.

Google Scholar

Giasi, C., Masi, P., and Cherubini, C. (2003). Probabilistic and fuzzy reliability analysis of a sample slope near Aliano. Eng. Geol. 67 (3-4), 391–402. doi:10.1016/S0013-7952(02)00222-3

CrossRef Full Text | Google Scholar

Godt, J. W., Baum, R. L., and Lu, N. (2009). Landsliding in partially saturated materials. Geophys. Res. Lett. 36 (2). doi:10.1029/2008GL035996

CrossRef Full Text | Google Scholar

Gong, W., Wang, L., Khoshnevisan, S., Juang, C. H., Huang, H., and Zhang, J. (2014). Robust geotechnical design of Earth slopes using fuzzy sets. J. Geotech. Geoenviron. Eng. 141 (1), 04014084. doi:10.1061/(ASCE)GT.1943-5606.0001196

CrossRef Full Text | Google Scholar

Griffiths, D., and Fenton, G. A. (2004). Probabilistic slope stability analysis by finite elements. J. Geotech. Geoenviron. Eng. 130 (5), 507–518. doi:10.1061/(asce)1090-0241(2004)130:5(507)

CrossRef Full Text | Google Scholar

Habibagahi, G., Shahgholian, R., and Sahraeian, S. M. S. (2021). Stochastic analysis of rock slope stability: Application of fuzzy sets theory. Iran. J. Sci. Technol. Trans. Civ. Eng. 45, 851–863. doi:10.1007/s40996-020-00525-3

CrossRef Full Text | Google Scholar

Hinds, E., Lu, N., Mirus, B., and Wayllace, A. (2019). Effects of infiltration characteristics on spatial-temporal evolution of stability of an interstate highway embankment. J. Geotech. Geoenviron. Eng. 145 (9), 05019008. doi:10.1061/(ASCE)GT.1943-5606.0002127

CrossRef Full Text | Google Scholar

Hsiao, E. C., Schuster, M., Juang, C. H., and Kung, G. T. (2008). Reliability analysis and updating of excavation-induced ground settlement for building serviceability assessment. J. Geotech. Geoenviron. Eng. 134 (10), 1448–1458. doi:10.1061/(asce)1090-0241(2008)134:10(1448)

CrossRef Full Text | Google Scholar

Iverson, R. M. (2000). Landslide triggering by rain infiltration. Water Resour. Res. 36 (7), 1897–1910. doi:10.1029/2000WR900090

CrossRef Full Text | Google Scholar

Janbu, N. (1954). “Application of composite slip surface for stability analysis,” in Paper presented at the Proceedings of European Conference on Stability of Earth Slopes (Sweden.

Google Scholar

Jiang, S. H., Li, D. Q., Zhang, L. M., and Zhou, C. B. (2014). Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method. Eng. Geol. 168, 120–128. doi:10.1016/j.enggeo.2013.11.006

CrossRef Full Text | Google Scholar

Juang, C., Jhi, Y.-Y., and Lee, D.-H. (1998). Stability analysis of existing slopes considering uncertainty. Eng. Geol. 49 (2), 111–122. doi:10.1016/S0013-7952(97)00078-1

CrossRef Full Text | Google Scholar

Kanda, E. K., Senzanje, A., and Mabhaudhi, T. (2020). Soil water dynamics under Moistube irrigation. Phys. Chem. Earth Parts A/B/C 115, 102836. doi:10.1016/j.pce.2020.102836

CrossRef Full Text | Google Scholar

Lacerda, W. A. (2007). Landslide initiation in saprolite and colluvium in southern Brazil: Field and laboratory observations. Geomorphology 87 (3), 104–119. doi:10.1016/j.geomorph.2006.03.037

CrossRef Full Text | Google Scholar

Li, T., Liu, G., Wang, C., Wang, X., and Li, Y. (2020). The probability and sensitivity analysis of slope stability under seepage based on reliability theory. Geotech. Geol. Eng. 38, 3469–3479. doi:10.1007/s10706-020-01226-4

CrossRef Full Text | Google Scholar

Liu, L., Zhang, S., Cheng, Y.-M., and Liang, L. (2019). Advanced reliability analysis of slopes in spatially variable soils using multivariate adaptive regression splines. Geosci. Front. 10 (2), 671–682. doi:10.1016/j.gsf.2018.03.013

CrossRef Full Text | Google Scholar

Lu, N., Godt, J. W., and Wu, D. T. (2010). A closed‐form equation for effective stress in unsaturated soil. Water Resour. Res. 46 (5). doi:10.1029/2009WR008646

CrossRef Full Text | Google Scholar

Lu, N., and Likos, W. J. (2006). Suction stress characteristic curve for unsaturated soil. J. Geotech. Geoenviron. Eng. 132 (2), 131–142. doi:10.1061/(asce)1090-0241(2006)132:2(131)

CrossRef Full Text | Google Scholar

Lu, N., and Likos, W. J. (2004). Unsaturated soil mechanics. Wiley.

Google Scholar

Lu, N., Şener Kaya, B., Wayllace, A., and Godt, J. W. (2012). Analysis of rainfall‐induced slope instability using a field of local factor of safety. Water Resour. Res. 48 (9), 2012WR011830. doi:10.1029/2012WR011830

CrossRef Full Text | Google Scholar

Lu, N. (2020). Unsaturated soil mechanics: Fundamental challenges, breakthroughs, and opportunities. J. Geotech. Geoenviron. Eng. 146 (5), 02520001. doi:10.1061/(ASCE)GT.1943-5606.0002233

CrossRef Full Text | Google Scholar

Luo, Z., Atamturktur, S., Juang, C. H., Huang, H., and Lin, P. S. (2011). Probability of serviceability failure in a braced excavation in a spatially random field: Fuzzy finite element approach. Comput. Geotech. 38 (8), 1031–1040. doi:10.1016/j.compgeo.2011.07.009

CrossRef Full Text | Google Scholar

Malvern, L. E. (1969). Introduction to the mechanics of a continuous medium.

Google Scholar

Matsui, T., and San, K.-C. (1992). Finite element slope stability analysis by shear strength reduction technique. Soils Found. 32 (1), 59–70. doi:10.3208/sandf1972.32.59

CrossRef Full Text | Google Scholar

Moradi, S., Huisman, J., Class, H., and Vereecken, H. (2018). The effect of bedrock topography on timing and location of landslide initiation using the local factor of safety concept. Water 10 (10), 1290. doi:10.3390/w10101290

CrossRef Full Text | Google Scholar

Morgentern, N., and Price, V. (1965). The analysis of stability of general slip surface. Geotechnique 15 (1), 79–93.

Google Scholar

Mualem, Y. (1976). A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 12 (3), 513–522. doi:10.1029/WR012i003p00513

CrossRef Full Text | Google Scholar

Nakhaei, M., and Šimůnek, J. (2014). Parameter estimation of soil hydraulic and thermal property functions for unsaturated porous media using the HYDRUS-2D code. J. Hydrol. Hydromech. 62 (1), 7–15. doi:10.2478/johh-2014-0008

CrossRef Full Text | Google Scholar

Nawari, N., and Liang, R. (2000). Fuzzy-based approach for determination of characteristic values of measured geotechnical parameters. Can. Geotech. J. 37 (5), 1131–1140. doi:10.1139/t00-025

CrossRef Full Text | Google Scholar

Nuth, M., and Laloui, L. (2008). Effective stress concept in unsaturated soils: Clarification and validation of a unified framework. Int. J. Numer. Anal. Methods Geomech. 32 (7), 771–801. doi:10.1002/nag.645

CrossRef Full Text | Google Scholar

Pang, L., Close, M. E., Watt, J. P., and Vincent, K. W. (2000). Simulation of picloram, atrazine, and simazine leaching through two New Zealand soils and into groundwater using HYDRUS-2D. J. Contam. Hydrol. 44 (1), 19–46. doi:10.1016/S0169-7722(00)00091-7

CrossRef Full Text | Google Scholar

Park, H. J., Jang, J. Y., and Lee, J. H. (2017). Physically based susceptibility assessment of rainfall-induced shallow landslides using a fuzzy point estimate method. Remote Sens. (Basel). 9 (5), 487. doi:10.3390/rs9050487

CrossRef Full Text | Google Scholar

Park, H. J., Jang, J. Y., and Lee, J. H. (2019). Assessment of rainfall-induced landslide susceptibility at the regional scale using a physically based model and fuzzy-based Monte Carlo simulation. Landslides 16 (4), 695–713. doi:10.1007/s10346-018-01125-z

CrossRef Full Text | Google Scholar

Park, H. J., Lee, J. H., and Woo, I. (2013). Assessment of rainfall-induced shallow landslide susceptibility using a GIS-based probabilistic approach. Eng. Geol. 161, 1–15. doi:10.1016/j.enggeo.2013.04.011

CrossRef Full Text | Google Scholar

Park, H. J., Um, J.-G., Woo, I., and Kim, J. W. (2012). Application of fuzzy set theory to evaluate the probability of failure in rock slopes. Eng. Geol. 125, 92–101. doi:10.1016/j.enggeo.2011.11.008

CrossRef Full Text | Google Scholar

Phoon, K. K., and Kulhawy, F. H. (1999). Characterization of geotechnical variability. Can. Geotech. J. 36 (4), 612–624. doi:10.1139/t99-038

CrossRef Full Text | Google Scholar

Rahimi, A., Rahardjo, H., and Leong, E. C. (2011). Effect of antecedent rainfall patterns on rainfall-induced slope failure. J. Geotech. Geoenviron. Eng. 137 (5), 483–491. doi:10.1061/(ASCE)GT.1943-5606.0000451

CrossRef Full Text | Google Scholar

Reddy, J. N. (1985). An introduction to the finite element method, 2. New York: McGraw-Hill.

Google Scholar

Richards, L. A. (1931). Capillary conduction of liquids through porous mediums. Physics 1 (5), 318–333. doi:10.1063/1.1745010

CrossRef Full Text | Google Scholar

Rosenblueth, E. (1975). Point estimates for probability moments. Proc. Natl. Acad. Sci. U. S. A. 72 (10), 3812–3814. doi:10.1073/pnas.72.10.3812

PubMed Abstract | CrossRef Full Text | Google Scholar

Sidle, R. C., and Bogaard, T. A. (2016). Dynamic Earth system and ecological controls of rainfall-initiated landslides. Earth. Sci. Rev. 159, 275–291. doi:10.1016/j.earscirev.2016.05.013

CrossRef Full Text | Google Scholar

Šimůnek, J., van Genuchten, M. T., and Šejna, M. (2008). Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose zone J. 7 (2), 587–600. doi:10.2136/vzj2007.0077

CrossRef Full Text | Google Scholar

Tiranti, D., and Cremonini, R. (2019). Editorial: Landslide hazard in a changing environment. Front. Earth Sci. 7, 3. doi:10.3389/feart.2019.00003

CrossRef Full Text | Google Scholar

van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44 (5), 892–898. doi:10.2136/sssaj1980.03615995004400050002x

CrossRef Full Text | Google Scholar

Wang, J., Gong, S., Xu, D., Juan, S., and Mu, J. (2013). Numerical simulations and validation of water flow and heat transport in a subsurface drip irrigation system using HYDRUS‐2D. Irrig. Drain. 62 (1), 97–106. doi:10.1002/ird.1699

CrossRef Full Text | Google Scholar

Xiao, T., Li, D. Q., Cao, Z. J., and Tang, X. S. (2017). Full probabilistic design of slopes in spatially variable soils using simplified reliability analysis method. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 11 (1), 146–159. doi:10.1080/17499518.2016.1250279

CrossRef Full Text | Google Scholar

Xu, C., Wang, L., Tien, Y. M., Chen, J.-M., and Juang, C. H. (2014). Robust design of rock slopes with multiple failure modes: Modeling uncertainty of estimated parameter statistics with fuzzy number. Environ. Earth Sci. 72 (8), 2957–2969. doi:10.1007/s12665-014-3201-1

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Inf. Control 8 (3), 338–353. doi:10.1016/S0019-9958(65)90241-X

CrossRef Full Text | Google Scholar

Zhang, J., Li, J., and Lin, H. (2018). Models and influencing factors of the delay phenomenon for rainfall on slope stability. Eur. J. Environ. Civ. Eng. 22 (1), 122–136. doi:10.1080/19648189.2016.1179682

CrossRef Full Text | Google Scholar

Zhang, L., Li, J., Li, X., Zhang, J., and Zhu, H. (2018). Rainfall-induced soil slope failure: Stability analysis and probabilistic assessment. Boca Raton, USA: CRC Press.

Google Scholar

Zhang, S., Leng, W., Zhang, F., and Xiong, Y. (2012). A simple thermo-elastoplastic model for geomaterials. Int. J. Plast. 34, 93–113. doi:10.1016/j.ijplas.2012.01.011

CrossRef Full Text | Google Scholar

Zhou, X., Li, J., Liu, Z., and Tang, Y. (2019). Analysis of slope stability with imprecise soil properties using uncertain sets. Math. Probl. Eng. 2019, 1–9. doi:10.1155/2019/1062347

CrossRef Full Text | Google Scholar