Investigating metallic cores using experiments on the physical properties of liquid iron alloys

An outstanding goal in planetary science is to understand how terrestrial cores evolved to have the compositions, thermal properties, and magnetic fields observed today. To achieve that aim requires the integration of datasets from space missions with laboratory experiments conducted at high pressures and temperatures. Over the past decade, technological advances have enhanced the capability to conduct in situ measurements of physical properties on samples that are analogs to planetary cores. These challenging experiments utilize large-volume presses that optimize control of pressure and temperature, and diamond-anvil cells to reach the highest pressures. In particular, the current experimental datasets of density, compressional velocity, viscosity, and thermal conductivity of iron alloys are most relevant to the core conditions of small terrestrial planets and moons. Here we review the physical properties of iron alloys measured in the laboratory at conditions relevant to the cores of Mars, the Moon, and Mercury. We discuss how these properties inform models of core composition, as well as thermal and magnetic evolution of their cores. Experimental geochemistry (in particular, metal-silicate partitioning experiments) provides additional insights into the nature and abundance of light elements within cores, as well as crystallization processes. Emphasis is placed on the Martian core to discuss the effect of chemistry on core evolution.

Introduction

Investigating the cores of terrestrial planets and moons provides fundamental knowledge regarding their present-day structure, origin, and evolution. Understanding the chemical and physical properties of metallic cores contributes to the revision or elaboration of paradigms for the global structure, differentiation, dynamics, and thermal history of terrestrial bodies. These properties govern large-scale dynamics and phase changes, such as the generation of a magnetic field, mantle convection, as well as surface activity through volcanism and tectonics (e.g., Breuer et al., 2021) and thus are the keystone for understanding the processes that have shaped planetary interiors and evolution.

Field measurements provide the critical framework for a unified knowledge of a present-day core. On Earth, geophysical properties, especially seismic velocities, have constrained the size of the metallic core and are used to interrogate its interior with ever-increasing precision. These observations have been combined with laboratory measurements and theoretical investigations to describe core structure and composition (e.g., Dziewonski and Anderson, 1981; Li and Fei, 2014 and references therein; Badro et al., 2015; Tateno et al., 2018; Hirose et al., 2021 and references therein). In comparison, the dataset of direct field measurements for other terrestrial planets and moons is meager. Despite their limitations, existing field observations of the Moon, Mars, and Mercury can be used to place useful constraints on their cores, and thus, expand our general understanding of terrestrial bodies. These constraints are obtained using global measurements--such as the moment of inertia, mass, and tidal response--as well as in situ seismic experiments, including the Apollo Passive Seismic Experiment (Moon) and the Insight SEIS experiment (Mars). These space data sometimes confirm and further our models and hypotheses about planetary cores, and sometimes challenge them. The exploration of Mars offers an example for both cases: the Insight data suggest a core size of 1830 km in radius (Stähler et al., 2021), in agreement with previous estimates using the moment of inertia and the tidal Love number (Rivoldini et al., 2011) or by inverting for a range of physical and chemical properties (Khan et al., 2018). The SEIS experiment did not measure seismic velocities in the Martian core, but the combination of seismic observations in the mantle with laboratory studies suggests low density and low compressional wave velocity estimates for the core (Stähler et al., 2021) that are difficult to explain with our current knowledge of metallic cores. These results question our understanding of the Martian core and its present-day chemistry, and more generally, of the formation and evolution of terrestrial cores.

Maximizing the scientific return from field measurements requires their comparison and integration with other datasets. As an example, the combination of field observations and samples returned from Lunar missions (especially Luna, Apollo, Clementine, and Lunar Prospector) with experimental, geochemical, and theoretical studies significantly advanced our understanding of lunar crust formation and mantle melting processes (e.g., Jolliff et al., 2006). Likewise, regarding metallic cores, the integration of field measurements with laboratory experiments on relevant compositions is key to successful interpretation, which also aids in planning future space exploration missions (Breuer et al., 2021). Among the fundamental questions that can be addressed by combining field and laboratory experiments is the current physical state of the core, which depends primarily on its temperature and composition. A solid vs partially or fully molten present-day core will provide different benchmarks in planetary cooling models and result in contrasting evolutionary pathways (e.g., Breuer et al., 2015 and references therein).

Several independent field observations provide information about the state of a core. First, the measurement of tidal deformation of a terrestrial body can imply the presence (or absence) of a liquid phase in the core. Second, seismic measurements are critical for identifying the presence and extent of a liquid phase, given that shear waves do not propagate in the liquid. Third, the presence of a magnetic field generated by core convection indicates the motion of an electrically conducting liquid. However, taken alone, these field data are not sufficient to uniquely define core chemistry or the degree of core crystallization. The most straightforward approach to access this information is the comparison of core temperature estimates that match the field observations with the phase diagram of iron alloys, the latter being constrained from phase equilibria experiments under pressure and temperature.

Such a comparison is illustrated in Figure 1 for the Martian, Lunar, and Hermean cores. The present-day pressure-temperature conditions of these three cores overlap with most iron alloy melting curves, suggesting that the cores are at least partly molten, especially if they contain elements that lower the solidus temperature (such as S, Si, O, C, H). Partly or fully molten cores are consistent with the existing field observations [e.g., Weber et al., 2011 (Moon); Stähler et al., 2021 (Mars); Hauck et al., 2013 (Mercury)], and the presence of some light elements (LEs) is in agreement with predictions from iron meteorite chemistry and geochemical studies (e.g., Wasson and Kallemeyn, 1988; Jarosewich, 1990). However, the nature, abundances, and distribution of light elements in these metallic cores is still poorly understood, and the details of the mantle-core differentiation process that partitioned these elements between the core and mantle also remains elusive. More generally, the effect of light elements on core evolution is not well known and requires a detailed understanding of the physical properties of iron alloys. To that end, laboratory experiments on iron and its alloys under controlled pressure, temperature, and redox conditions are once again required.

FIGURE 1

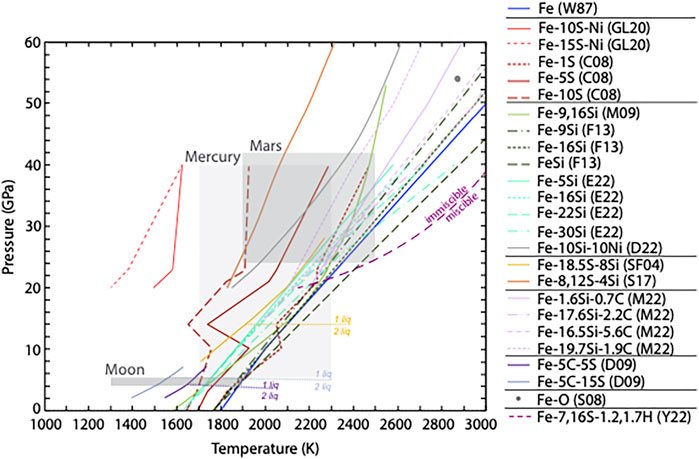
FIGURE 1. A compilation of melting curves of iron and iron alloys from experimental studies. Compositions in the legend indicate the wt% of light elements. Horizontal dotted lines correspond to immiscibility fields (1 liquid vs 2 liquids) in the molten state. Shaded areas indicate the present-day pressure and temperature conditions of the core of Mars, the Moon, and Mercury. Details of the melting data may be found in the following references: W87, Williams et al., 1987; GL20, Gilfoy and Li, 2020; C08, Chen et al., 2008; M09, Miller and thesis, 2009; F13, Fischer et al., 2013; E22, Edmund et al., 2022; D22, Dobrosavljevic et al., 2022; SF04, Sanloup and Fei, 2004; S17, Sakairi et al., 2017; M22: Miozzi et al., 2022; D09: Dasgupta et al., 2009; S08, Seagle et al., 2008; Y22, Yokoo et al., 2022.

Alloying agents, including light elements, affect the crystallization of a metallic core, as well as the way the liquid convects and releases heat through time (e.g., Davies and Pommier, 2018; Hemingway and Driscoll, 2021, for Mars). To understand their influence on planet-scale properties, such as the generation and sustainability of a magnetic field, it is essential to measure the physical properties of liquid iron alloys. These experimental results can then be used to develop physical models of the core as a function of composition, pressure, and temperature. Among the physical properties, density and seismic velocities (including compressional wave velocity, Vp, and shear wave velocity, Vs) are both measured in the field and in the laboratory, and are sensitive to chemistry (e.g., Terasaki et al., 2019). Both properties are therefore particularly relevant to investigate the present-day composition of cores. This first-order constraint on core properties can be complemented by other physical properties measured in the laboratory, i.e., viscosity and thermal conductivity. These transport properties provide information about melt mobility and heat transport, which are fundamental to understand core dynamics and cooling, respectively.

In this study, we review four physical properties of iron alloys in the molten state: seismic velocity, density, viscosity, and thermal conductivity. These experimental measurements at temperature and pressure conditions relevant to the cores of Mars, the Moon, and Mercury, provide fundamental data for understanding liquid cores. Because of the small size of these planetary bodies, the crystallized solid inner core (if any) would be iron with a face-centered cubic structure (fcc-Fe). Therefore, we also summarize density and velocity for fcc-Fe and fcc-FeNi alloy. Laboratory measurements are compared with the currently available physical properties of these cores, from direct measurements and modeling, to define the compositions that satisfy the observational data. Possible “candidates” for core chemistry are discussed together with the input from geochemistry, especially metal-silicate partitioning experiments. Finally, cooling models of terrestrial cores, the role of crystallization in the redistribution of light elements within the core, and the generation of a magnetic field are discussed.

Available observational constraints

The physical properties considered in this section are density and seismic velocities, given that they are measured both in the field and in laboratory experiments on core analogs. Density profiles across Mars, the Moon, and Mercury, and when available, compressional wave velocity (Vp) and shear wave velocity (Vs.) profiles are presented in Figure 2.

FIGURE 2

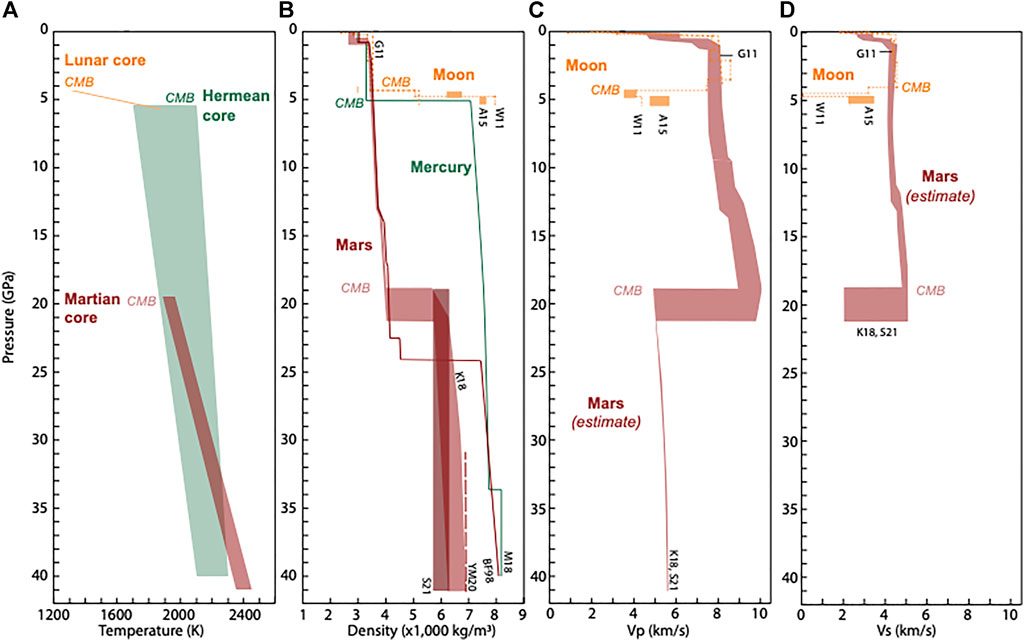
FIGURE 2. Temperature (A), density (B), Vp (C) and Vs. (D) profiles across Mars, the Moon, and Mercury. Density profiles are from Khan et al., 2018 (K18), Bertka and Fei, 1998 (BF98) (Mars); Weber et al., 2011 (W11) and Garcia et al., 2011 (G11) (orange dashed lines), and Antonangeli et al., 2015 (A15; orange rectangles) (Moon); Margot et al., 2018 (Mercury). Mars mean core density from Yoshizaki and McDonough, 2020 (YM20) and Stähler et al., 2021 (S21) is also shown. Seismic velocities are from Stähler et al., 2021, Khan et al., 2018 (Mars), Weber et al., 2011, Garcia et al., 2011, and Antonangeli et al., 2015 (Moon). For each terrestrial body, CMB refers to core-mantle boundary.

Core size and temperature

Geodetic constraints such as the moment of inertia and libration, and when available, seismic measurements, provide information on the core size of Mars, the Moon, and Mercury. In contrast, temperature estimates across the core are not immediately obtained from field observations, and strongly depend on assumptions regarding the composition and structure of the planet or moon. Thermal profiles are difficult to estimate directly, and they are very important to determine given the fundamental control exerted by temperature on the physical properties of planetary cores. The temperature profiles of the different cores are based on thermodynamic modeling, mainly utilizing physical properties of liquid iron alloys, as well as mantle properties. For example, Bertka and Fei (1997) considered a thermal profile representative of hot conditions and under thermodynamic equilibrium to estimate temperatures across the Martian core. Khan et al. (2018) considered cold and hot areotherms (from Bertka and Fei, 1997; Verhoeven et al., 2005) to model temperature in the mantle, and then compared computed core compositions with phase diagrams to estimate the temperature of the core. It is important to note that assumptions used to determine temperature profiles prevents unequivocal determination of internal structure (Khan et al., 2018). However, relating physical, chemical and petrological data can provide important constraints about the thermal structure of planetary bodies (e.g., Kuskov and Kronrod, 2009).

The Martian core covers a pressure range of about 24–40 GPa, representing ∼24% of the planet’s mass (e.g., Bertka and Fei, 1998). By comparison, the Earth’s core encompasses ∼32% of its mass. Based on inversions from geophysical data and assumptions on core chemistry, the estimated potential temperature across the Martian core (aerotherm) varies from 1,900 to 2,500 K (Khan et al., 2018). The Lunar core represents only ∼2% of its mass, spanning a limited pressure range of about 4.5–5.5 GPa (e.g., Garcia et al., 2011). A small lunar core is consistent with the giant impact hypothesis (e.g., Righter, 2002), which posits that the Moon formed from hot and mostly rocky debris after a Mars-sized object impacted the early Earth. The proposed temperature estimates across the Lunar core (selenotherm) range from 1,300 to 1,900 K (e.g., Wieczorek, 2006). In contrast, the core of Mercury encompasses ∼75% of the planet’s present mass. The origin of such a large core remains debated. One hypothesis (exogenous) posits that successive impacts have been responsible for collisional stripping of the silicate portion of the planet, which was initially much larger than its current size (Benz et al., 1988; Chau et al., 2018). Another hypothesis (endogenous) suggests that Mercury’s high metal content was instead inherited from nebular condensation processes (Weidenschilling, 1978). The present-day core-mantle boundary of Mercury is located between 5 and 6 GPa, and pressure across the core increases up to 40 GPa (Margot et al., 2018). Temperature is thought to vary from 1700 to 2300 K across the core (hermeotherm; Dumberry and Rivoldini, 2015; Knibbe and van Westrenen, 2018), but might be higher depending on composition (e.g., Edmund et al., 2022).

Core density and seismic velocities

Given that no seismic waves have been recorded at core depth in Mars, Insight’s seismic and geodetic data for the mantle have been used to construct models of the density and seismic velocity in the Martian core (Stähler et al., 2021). The preferred mean core density increases with depth from 5,700 to 6,300 kg/m³, which is low compared to previous estimates (e.g., >7,500 kg/m³ (Bertka and Fei, 1998); 6,000–6,900 kg/m³ (Khan et al., 2018)) (Figure 2). Preferred core velocity models have Vp values varying from 4.7 to 5.8 km/s (similar to Khan et al., 2018), whereas the Vs. profile could not be obtained. Stähler et al. (2021) support the idea of a liquid core, based on the argument that core-reflected wave (ScS) energy was detected, which would not be possible with a solid core. Tidal measurements from Mars Global Surveyor also suggest a liquid core (Yoder et al., 2003). An entirely liquid core has been argued on the basis of a short-lived early Martian core dynamo and the measured low melting temperature of plausible core materials (Fei and Bertka, 2005).

NASA’s Apollo seismic data have rarely identified seismic waves at Lunar core depth, which makes seismic profiles across the core difficult to obtain. However, by reanalyzing the seismic data from the Apollo Passive Seismic Experiment and combining them with other geophysical observations, Weber et al. (2011) obtained density and seismic models of the Lunar interior consistent with a partially molten lowermost mantle, a liquid outer core, and a solid inner core (Figure 2). A density of 5,000 kg/m³ was obtained for the outer core, and this value increased up to 8,000 kg/m³ in the inner core. The presence of a molten outer core is consistent with non-seismic observations, such as the moment of inertia and the tidal response (Love numbers). However, these seismic data have also been interpreted differently, supporting the absence of a solid inner core (e.g., Very Preliminary Reference Moon Model, Garcia et al., 2011). In the VPRMM, the Lunar core density is about 5,200 kg/m³ throughout the core. Density and sound velocity estimates from Weber et al. (2011) for the inner core have also been revised by Antonangeli et al. (2015) (Figure 2), based on the argument that the Vs and Vp values from Weber et al. (2011) are significantly lower than that of pure iron or any plausible alloys. In the preferred model by Antonangeli et al. (2015), the outer core has a density of 6,500–7,000 kg/m³ and Vp values of 3.5–5 km/s, while the inner core density is 7,600–7,800 kg/m³, with Vp values of 4.75–5.7 km/s and Vs values of 2.2–3.45 km/s.

Current observational constraints of Mercury’s interior come from Earth-based observations as well as NASA’s Mariner 10 and MESSENGER orbiters. These data will likely be complemented by new observations from two orbiters of the ongoing ESA-JAXA Bepi-Colombo mission. In the absence of any seismological observations, the available field observations that inform us about Mercury’s interior come from the planet’s rotation, gravity field, spin state, tidal response, magnetic field, and surface geology. Following the MESSENGER mission, Margot et al. (2018) proposed a Preliminary Reference Mercury Model that provides a size and density profile of Mercury’s core consistent with the planet’s mass, radius, and moment of inertia. The liquid outer core density estimate varies from ∼6,800 to 7,500 kg/m³, and the density of a potential solid inner core increases up to 8,215 kg/m³ (Figure 2). However, the presence of a solid inner core remains to be confirmed; its presence has not been detected unambiguously using field measurements (Hauck et al., 2013; Margot et al., 2018). Recently, Lark et al. (2022) showed that Mercury’s outer shell moment of inertia requires a dense core, consistent with an Fe-Si alloy containing 3–9 wt% Si, and a solid inner core with a radius up to 1,200 km.

Laboratory measurements of physical properties

In-situ measurement of the physical properties of liquid alloys is particularly challenging. The measurements considered in this study come mostly from experiments performed in large-volume presses (LVPs), namely multi-anvil press, Paris–Edinburgh (P-E) press, and piston-cylinder apparatuses, because 1) they cover the pressure and temperature ranges of the planetary cores considered; 2) sample volumes in these experiments are large enough (>1 mm³) to characterize the physical properties; and 3) pressure and temperature in LVPs are very well controlled. One exception regards the thermal conductivity database, which consists of experiments at 1 atm. In addition, a few experiments performed in diamond-anvil cells are included in the dataset of density and velocity measurements because they were performed at pressure and temperature conditions relevant to the cores considered in this study (e.g., Antonangeli et al., 2015; Kawaguchi et al., 2017). Viscosity experiments on liquid iron alloys performed at atmospheric pressure and high temperature have been added to the dataset (Vatolin et al., 1962; Vostryakov et al., 1964; Nakanishi et al., 1967; Barmin et al., 1970), because of the limited set of viscosity measurements conducted under pressure. All experiments are performed under static or quasi-static conditions.

Most physical properties are measured at synchrotron facilities, where the sample size and phase transformations are measured in situ and monitored in real time during the experiment. The different high-pressure techniques used for the measurement of physical properties have been reviewed elsewhere (e.g., Sherman and Stadtmuller, 1987; Miletich, 2005), and only a general description of these techniques is presented here. The density of iron and iron alloys can be measured at synchrotron facilities using an X-ray absorption method (Sanloup et al., 2000). The relationship between the brightness of incident and transmitted X-rays is obtained from radiographic imaging of the sample and provides density (e.g., Terasaki et al., 2010; Shimoyama et al., 2013). Techniques have also been developed to retrieve density of liquid alloys by in-situ X-ray diffuse scattering (Kuwayama et al., 2020) and by the sink-float method (Balog et al., 2003).

Compressional and shear sound velocities can be obtained from ultrasonic measurements conducted at synchrotron facilities (Jing et al., 2014). In these experiments, an alumina buffer rod in contact with the iron or iron alloy sample is used to propagate elastic waves and define the sample position. The waves are then reflected and converted into electrical signals by a transducer, and these signals are captured by an oscilloscope. Nuclear resonant inelastic X-ray scattering (NRIXS) has also been used to obtain Vs and Vp of solid FeHx (no data available in the molten state) (Mao et al., 2004). This technique uses the Mössbauer-active isotope ⁵⁷Fe to determine the Fe partial phonon density of states, and ultimately determine the compressional and shear velocities when combined with an equation of state of the alloy. Inelastic X-ray scattering (IXS) is also used to determine compressional sound velocities from measurements of the phonon dispersion of the material at high pressures and temperatures (e.g., Badro et al., 2007; Nakajima et al., 2015).

The viscosity of molten iron and alloys is measured using the falling or floating sphere viscometry technique at synchrotron facilities. A microsphere is placed either near the top of the sample for a falling sphere experiment (e.g., Terasaki et al., 2006) or near the bottom for a floating sphere experiment (e.g., Zhu et al., 2022). At the target pressure, the sample is rapidly heated to a temperature above the liquidus temperature of the sample, to ensure that the sample is fully molten and the sphere can fall or float freely, depending on the density contrast between the sphere and the molten alloy. The movement of the sphere is recorded by a high-speed X-ray camera, and the viscosity of the sample is calculated using the Stokes’ equation with correction factors for the effect of the wall and end of the sample container.

Thermal conductivity is challenging to measure at extreme pressure and temperature conditions (Williams, 2018). There is a lack of measurements on molten iron alloys in large-volume presses, and most experiments have been conducted at 1 atm (e.g., Toulokian et al., 1970; Watanabe et al., 2019). A common technique consists of the electromagnetic levitation of a droplet sample, which is heated periodically (Watanabe et al., 2019). A static magnetic field is applied to the sample by a superconducting magnet to suppress surface oscillation and convection in the droplet. The phase lag between the modulated laser heating and the variation of temperature provides the thermal conductivity. Other 1-atm techniques are summarized by Assael et al. (2017). One way to avoid difficulties inherent to the measurement of thermal properties is to perform electrical experiments and apply the Wiedemann-Franz law that relates electrical and thermal conductivities.

$\text{k}=\text{L}\times \text{T}\times \sigma (1)$

k is the thermal conductivity (W/(mK)) generated by thermal transport by electrons, T is the temperature (K), σ is the electrical conductivity (S/m), and L is the Lorenz number (ideally 2.445 × 10^–8 W $\Omega .$K⁻²). Among the steady-state methods used to measure electrical conductivity of iron and its alloys, the four-wire method is common in large-volume presses (e.g., Pommier and Leinenweber, 2018; Yin et al., 2019; Berrada et al., 2021). Other methods to measure the electrical properties of alloys in steady state consist of the voltmeter direct reading, direct-current bridge methods, the van der Pauw method, and the galvanometer amplifier method (e.g., Ho et al., 1983 and refs. therein). However, the accuracy of the Wiedemann-Franz law deteriorates for iron alloys due to the decoupling of heat transport from charge transport caused by inelastic electron-electron scattering (Williams, 2018). Using the ideal Lorenz number with this approach has been found to underestimate the thermal conductivity by 15%–30% (Williams, 2018; Pommier, 2020).

Physical properties of liquid core analogs from laboratory experiments

Density and compressional velocity of liquid Fe and its alloys

Static high-pressure and high-temperature experiments have provided density and compressional velocity (Vp) of pure liquid iron and iron alloys at conditions relevant to the core of Mars, the Moon, and Mercury (Figures 3, 4).

FIGURE 3

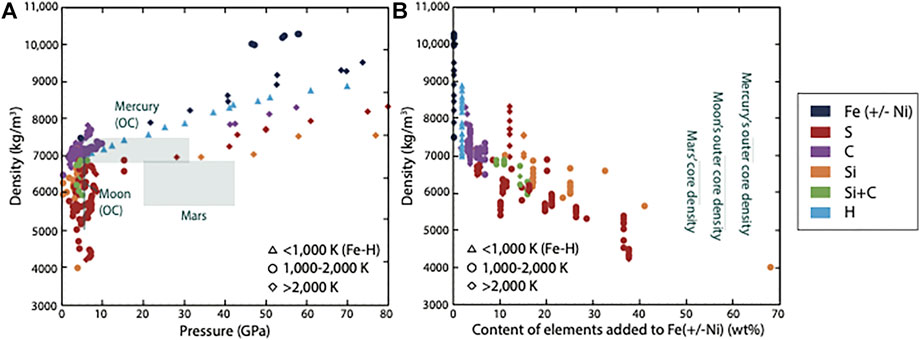
FIGURE 3. Density of liquid iron and iron alloys from previous experimental studies as a function of pressure (A), and content of elements added to Fe or Fe+Ni (B) for different temperatures. The core conditions of Mars (5,700–6,900 kg/m³), the Moon (5,000–7,000 kg/m³), and Mercury are indicated with shaded areas, and values depending on the studies considered (see text for details). Data source: Chen et al., 2014; Knibbe et al., 2021; Kuwayama et al., 2020; Lee et al., 2015; Mao et al., 2004 (solid); Morard et al., 2013, 2014, 2017; Nishida et al., 2008, 2011; Sanloup et al., 2000, 2004, 2011; Shibazaki et al., 2012 (solid); Shimoyama et al., 2013, 2016; Tateyama et al., 2011; Terasaki et al., 2010, 2019; Urakawa et al., 2018; Xu et al., 2021; Zhu et al., 2021.

FIGURE 4

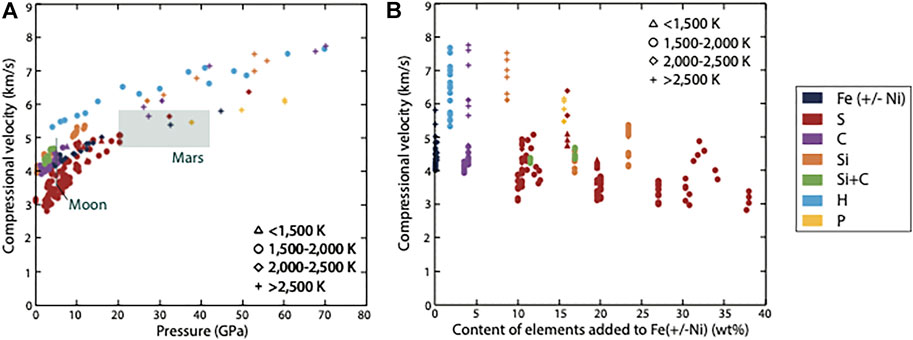
FIGURE 4. Compressional (P-wave) velocity of liquid iron and iron alloys from previous experimental studies as a function of pressure (A) and content of elements added to Fe or Fe+Ni (B) for different temperatures. Vp estimates for the core of Mars and the Moon are indicated with shaded areas. For Fe-H alloys, data only exist in the solid state, and therefore the bulk sound velocity is shown (see text for details). Data source: Jing et al., 2014; Kawaguchi et al., 2017; Kinoshita et al., 2020; Knibbe et al., 2021; Kuwabara et al., 2016; Kuwayama et al., 2020; Mao et al., 2004 (solid); Nakajima et al., 2015, 2020; Nasch et al., 1997; Nishida et al., 2016, 2020; Shibazaki et al., 2012 (solid); Terasaki et al., 2019.

The density of liquid iron alloys increases with increasing pressure (Figure 3A). The effect of pressure has been systematically investigated for Fe-S (e.g., Sanloup et al., 2000; Balog et al., 2003; Chen et al., 2014), Fe-C (e.g., Terasaki et al., 2010; Sanloup et al., 2011), Fe-Ni-C (Zhu et al., 2021), and Fe-Si (e.g., Sanloup et al., 2004) liquids (Supplementary Table S1). Because it is difficult to directly measure the density of Fe-H liquid in the large-volume press, no density data for Fe-H liquid are available to date, but density measurements of iron hydride are useful for evaluating the effect of hydrogen on alloy density (e.g., Shibazaki et al., 2012). In these studies, the alloy chemistry and temperature were fixed while measurements were performed at different pressures. One exception is the study of Tateyama et al. (2011), who did not observe any effect of pressure on the density of Fe-Si liquid over 3–4.5 GPa using the sink-float method.

Isolating the effect of temperature on the density of iron alloys is difficult to assess because most studies varied pressure and/or composition in addition to changing temperature. The density measurements by Shimoyama et al. (2013) on an Fe-C alloy containing 3.5 wt% C cover a temperature range of 1,500–2,200 K and showed a systematic decrease in density as temperature increases. For instance, at 2 +/−0.1 GPa, density decreases by 4% over the 1,700–2,100 K temperature range, and the same decrease was measured at 4.2 +/−0.25 GPa. Our compilation of density measurements (Figure 3B) indicates that increasing the content of light elements decreases density. However, this effect is not linear with the content of alloying agent. For example, the density measurements of Fe-C liquids for three compositions, 3.5, 5.7, and 6.7 wt% C, by Shimoyama et al. (2013), Sanloup et al. (2011), and Terasaki et al. (2010), respectively, cannot be easily interpolated as a function of the C content. The origin of high densities measured at pressures between 5.6 and 6.8 GPa by Shimoyama et al. (2013) is not well understood. All liquid density measurements by the X-ray absorption method are limited to pressures below 10 GPa. Very few density data were collected by in situ X-ray diffraction using laser-heated diamond anvil cell on Fe-C liquid alloys at higher pressure (from 41 to 57 GPa; Morard et al., 2017). These density values, extracted from the minimization of the oscillation in the short distance of the radial distribution function, typically have large uncertainties.

The density measurements of liquid Fe-S cover a large compositional range with up to 38 wt% S (Figure 3B). A large dataset (Supplementary Table S1) is available for modeling liquid density as a function of pressure, temperature, and composition. Interestingly, nonideal mixing behavior has been reported for Fe–S liquid. Liquid structure measurements can also provide additional information; for example, Shibazaki and Kono (2018) showed that the addition of a small amount of S does not affect the structure of liquid iron. As a consequence, density alone may not be sufficient to detect the presence of a small amount of light elements in the molten part of metallic cores.

Most compressional velocity (Vp) measurements under pressure have been conducted on pure Fe and Fe-S liquids, though recent work has also considered Fe-Si and Fe-C alloys. As illustrated in Figure 4A and Supplementary Table S2, Vp increases with increasing pressure. At high temperature (>2,000 K), the compressional velocity of pure iron tends to decrease with increasing temperature. Alloying Ni to Fe reduces Vp, and the velocity of Fe-Ni liquids is not sensitive to temperature (Kuwabara et al., 2016). In contrast, the Vp values of Fe-Ni-C and Fe-C alloys are temperature dependent. Adding carbon to iron (Kuwabara et al., 2016; Shimoyama et al., 2016) and increasing pressure (Nakajima et al., 2015; Kuwabara et al., 2016) tends to increase the velocity of C-bearing alloys. In S-bearing alloys, experiments indicate that the effect of temperature depends on the amount of S as well as pressure: at pressures <3 GPa, the Vp of Fe-Ni-S alloys containing 16.9 wt% S (Terasaki et al., 2019) and 27 wt% S (Jing et al., 2014) is not sensitive to temperature, contrasting with the temperature dependence observed for Fe-Ni-S liquids containing ∼10 wt% S under pressure (Terasaki et al., 2019) and at 1 atm (Nasch et al., 1997). At pressures >3 GPa, no clear temperature dependence is observed for Fe-S alloys, independent of their sulfur content (Jing et al., 2014; Terasaki et al., 2019; Nishida et al., 2020), and a small dependence of Vp to pressure was measured for S-bearing alloys. A small effect of temperature on the velocity of Fe-Ni-Si liquids (16.9–23.4 wt% Si) was measured by Terasaki et al. (2019). The measured effect of pressure on Vp of Si-bearing alloys corresponds to an increase of ∼1–1.5 km/s (Terasaki et al., 2019; Nakajima et al., 2020), and the effect of Si content on Vp is unclear from the current dataset. Adding Si and C to Fe does not seem to affect Vp significantly (Knibbe et al., 2021), though further work is needed (Figure 4B).

The velocity of Fe-H alloys is not well constrained due to experimental challenges with measuring the properties of Fe-H liquids. Given the absence of Vp and density data for molten H-bearing alloys, we used experimental studies on solid Fe-H samples at room temperature (Mao et al., 2004; Shibazaki et al., 2012) to evaluate the effect of hydrogen on Vp and density. The best way to estimate the Vp of Fe-H liquid is through the bulk sound velocity because the compressional wave velocity is identical to the bulk sound velocity for liquid. Huang et al. (2018) measured the bulk sound velocity for Fe-11.8 wt% S liquid by shock compression, compared with the calculated bulk sound velocities for both solid and liquid alloy based on equation of state data. The results show that the bulk sound velocity of the solid phase is comparable to that of the liquid alloy, and therefore it can be a good approximation in the absence of direct measurements of Vp of the liquid phase. We calculated the bulk sound velocity (Vc) of Fe-H alloy at room temperature from the Vp and Vs values determined by Shibazaki et al. (2012) and Mao et al. (2004) using

$V_c^2=\left(V_p^2-\frac{4}{3}{V}_s^2\right)(2)$

The bulk sound velocity of the Fe-H liquid would be about 2% higher than the room-temperature values based on the values recently determined for Fe and Fe-Si alloy (Huang et al., 2022). Finally, the dataset for Fe-P alloys is currently limited to one study that identified a decrease in Vp of ∼0.5 km/s when pressure increases from 40 to 60 GPa and temperature from 2,450 to 2,800 K (Kinoshita et al., 2020).

Density and compressional velocity are related under pressure (Williamson and Adams, 1923; Birch, 1952). Considering an isotropic medium, the relationship between seismic velocity and density provides information about the compressibility of the liquid alloy through the following equation (Williamson and Adams, 1923)

$V_p^2\left(P,T\right)=\frac{K_S\left(P,T\right)}{\rho \left(P,T\right)}(3)$

with Vp being the compressional velocity, ρ the density, and K_s the adiabatic bulk modulus (or incompressibility), all of which depend on pressure (P) and temperature (T). Very few studies measured simultaneously the density and Vp of molten iron and iron alloys at the pressure conditions considered in this study (Shibazaki et al., 2012; Shimoyama et al., 2016; Terasaki et al., 2019). The resulting velocity-density relationship is shown in Figure 5. Although a general trend is visible for all systems, with Vp increasing with increasing density, each iron alloy has its own behavior. For the Fe-H system, we plotted the bulk sound velocity for comparison. The Fe-C liquid shows the lowest compressional velocity at the same density, indicating that incorporation of C in the core may substantially reduce the velocity.

FIGURE 5

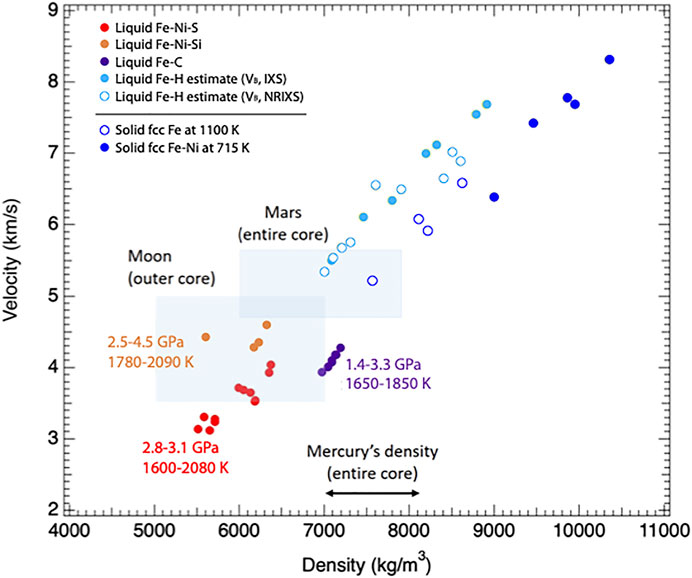
FIGURE 5. Compressional velocity-density relationship of liquid iron alloys from experiments, and comparison with solid fcc iron. Both properties were measured as part of the same studies. Data for Fe-H are from studies on solids (not liquids) at room temperature by Mao et al. (2004) (orange) and Shibazaki et al. (2012) (yellow), and the bulk sound velocity (V_B) data were plotted here (see text for details). Data for liquid Fe-Ni-S and liquid Fe-Ni-Si are from Terasaki et al. (2019), and data for liquid Fe-C are from Shimoyama et al. (2016). The velocity-density relations for solid fcc-Fe (Antonangeli et al., 2015) and fcc-FeNi alloy (Kantor et al., 2007) are shown for comparison (in light and dark blue). The entire dataset covers a pressure range of 6–70 GPa and a temperature range of 1,600–2,090 K. The shaded areas indicate velocity and density values for the present-day outer core of the Moon and the core of Mars.

Liquid structure measurements have indicated that incompressibility decreases with increasing amount of sulfur in S-rich iron alloys (>∼20 at% S; Sanloup et al., 2004; Shibazaki and Kono, 2018), while the structure of the alloy is not strongly affected at lower S contents. Si and C do not affect significantly the local structure of liquid iron (Shibazaki and Kono, 2018), although a structural change in a liquid Fe-C alloy at ∼5 GPa has been reported by Shibazaki et al. (2015). The incorporation of Si in liquid Fe shortens the nearest (r1) and second (r2) neighbor distances, while incorporation of C and small amount of S expands these distances. A small effect of H on the local structure of liquid iron has also been observed (Katayama et al., 2010). These behaviors are the result of the different incorporation mechanisms of light elements into liquid iron: substitutional incorporation of Si, and interstitial incorporation of C, H, and S (Katayama et al., 2010; Shibazaki and Kono, 2018), though theoretical studies showed that S can change its behavior under pressure (Posner and Steinle-Neumann, 2019). Understanding the effect of light element content on the liquid structure and incorporation mechanisms requires further investigation.

Viscosity and thermal conductivity of liquid Fe and its alloys

The viscosity of iron and alloys determined experimentally is presented in Figure 6 and Supplementary Table S3. Because of technical difficulties related to the falling/floating sphere viscometry technique, most experiments have been performed at low pressure (<7 GPa), with only a few experiments performed at higher pressure (up to 16.1 GPa; Terasaki et al., 2006). No clear pressure-dependence on the viscosity of pure iron and alloys is observed over the 1 atm-16 GPa pressure range. In contrast, increasing temperature decreases viscosity (Figure 6A). The effect of temperature on viscosity has been well characterized at 1 atm for Fe-C liquids by Vatolin et al. (1962), who observed that the viscosity of Fe-4.2 wt% C liquid decreases by 61% over 1,543–1,823 K. At defined pressure and temperature, the amount of alloying agent has a nonlinear effect on viscosity (Figure 6B). At 1 atm, the viscosity of Fe-P liquids decreases with increasing phosphorus content up to 12 wt%, then increases sharply up to 20 wt% P and decreases at higher contents (Vostryakov et al., 1964). The same study showed that the viscosity of Fe-S liquid slightly decreases with increasing S content up to 20 wt%, and then slightly increases at higher S content (up to 36.5 wt%). The viscosity of alloys at fixed high pressure and temperature conditions has not been investigated systematically. However, some studies observed a significant effect of sulfur content on viscosity. For instance, Kono et al. (2015) showed that at 1–6 GPa and 2,073 K, the viscosity of liquid FeS is 31%–42% lower than that of pure iron. The viscosity of iron alloys as a function of pressure or light element content is complex and strongly depends on local ordering of atoms. In the Fe-S system, it has been suggested that at low pressure, moderate S contents break the ordering in Fe liquid, and that increasing pressure improves atom order (e.g., Kono et al., 2015).

FIGURE 6

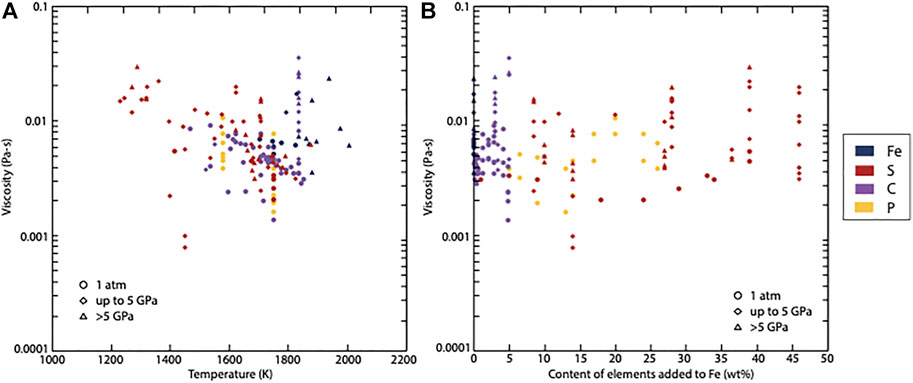
FIGURE 6. Viscosity of liquid iron and iron alloys from previous experimental studies as a function of temperature (A) and content of elements added to Fe (B). Data source: Barmin et al., 1970; Dobson et al., 2000; Funakoshi, 2010; Kono et al., 2015; Rutter et al., 2002; Secco et al., 2002; Terasaki et al., 2001, 2002, 2006; Urakawa et al., 2001; Vatolin et al., 1962; Vostryakov et al., 1964.

It is not clear from liquid structure measurements on pure iron whether a structural change exists (Sanloup et al., 2000; Shen et al., 2004) and affects viscosity (Terasaki et al., 2002; Kono et al., 2015). Similarly, a structural transition has been reported for Fe-(Ni)-C (Shibazaki et al., 2015; Lai et al., 2017), but its effect on viscosity (and density) is not fully resolved (Terasaki et al., 2006; Sanloup et al., 2011; Shimoyama et al., 2013; Zhu et al., 2022). The correlation between structure and viscosity of molten iron alloys remains to be explored at pressure and temperature conditions relevant to planetary cores.

As mentioned above, thermal conductivity measurements under pressure and temperature are challenging, and this physical property can be considered the most difficult to characterize (Williams, 2018). The experimental dataset on molten iron alloys therefore focuses on measurements at 1 atm, and on pure Fe and Fe-Ni alloys. The effect of light elements (or more generally, impurities) on thermal conductivity remains to be explored, both at 1 atm and under pressure. Available measurements are presented in Figure 7A. A very weak dependence of thermal conductivity to temperature is observed. Only three Fe-Ni alloys (X_Fe=0.8, 0.6, and 0.2) show a slight increase in thermal conductivity with increasing temperature (Watanabe et al., 2019). The effect of Ni on thermal conductivity is unclear, though Ni-rich alloys tend to be more conductive than Ni-poor alloys and pure iron. The effect of nickel on thermal conductivity from electrical experiments at 4.5 and 8 GPa suggests that Ni does not influence significantly the temperature-dependence of conductivity of Fe-S alloys, but it affects the pressure dependence (Pommier, 2020). Another example of thermal conductivity estimates from electrical conductivity measurements is shown in Figure 7B for Fe-S-O alloys at 10 GPa (Pommier et al., 2020a). Estimates are obtained using the Wiedemann-Franz law and applying a correction of 20%. The effect of temperature and of composition on thermal conductivity is higher than at 1 atm, and direct thermal conductivity measurements under pressure are required to further understand the effect of these parameters on the thermal properties of iron and iron alloys. Important input is also provided by theoretical and structural studies of iron alloys. For example, Figure 7B suggests that adding oxygen decreases thermal conductivity. This has been predicted by first-principles simulations (de Koker et al., 2012; Wagle et al., 2019), based on the observation that oxygen atoms occupy interstitial sites in the alloy, which shortens distances between Fe and O atoms and decreases charge transport efficiency.

FIGURE 7

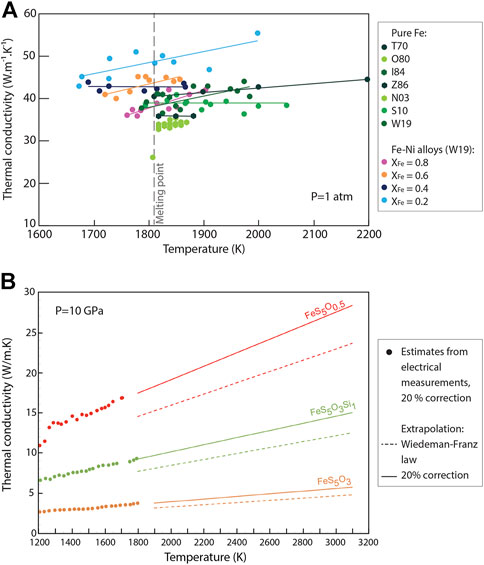
FIGURE 7. Thermal conductivity of iron and iron alloys from previous experimental studies. (A) Measurements at atmospheric pressure. Studies from Touloukian et al., 1970 (T70); Ostrovskii et al., 1980 (O80); Ilinykh et al., 1984 (I84); Zinovyev et al., 1986 (Z86); Nishi et al., 2003 (N03); Sugie et al., 2010 (S10); Watanabe et al., 2019 (W19). Ilinykh et al., 1984 measured thermal diffusivity, and the corresponding conductivity is from Assael et al. (2017). The lines are a guide for the eye. The dashed line corresponds to the melting temperature of pure iron. (B) Thermal conductivity estimates for Fe-S-O alloys estimated from electrical measurements at 10 GPa (after Pommier et al., 2020a). Estimates account for a 20% correction on the values obtained using the Wiedemann-Franz law.

A couple of attempts have been made to measure viscosity and electrical conductivity simultaneously in iron alloys (Vostryakov et al., 1964; Pommier et al., 2020b), and the relationship between the self-diffusion of Fe and S (that control viscosity) and the mean free path of electrons (that is proportional to the electrical conductivity) remains to be explored. Both transport properties are thermally activated, and a linear correlation has been observed between electrical and viscosity at high temperature for Fe-S melts (Pommier et al., 2020b).

Assessment of core composition

Taken separately, density and velocity are unlikely to constrain core composition, because several alloys present comparable density or comparable velocity values at defined pressure and temperature (Figures 3, 4). However, Figure 5 suggests different Vp-density relations in liquid iron-light element compositions. Other previous studies observed distinct Vp-density trends in solid iron alloys with different light element compositions (e.g., Sakamaki et al., 2016, and references therein). Although uncertainties in the Vp and density observations in planetary cores are large, joint Vp-density laboratory measurements have the potential to clarify light element compositions. Further work on liquid alloys is needed to explore these relationships in compositions relevant to metallic cores, especially in ternary systems.

Another input from the laboratory, consisting of metal-silicate experiments, needs to be accounted for together with physical measurements in order to identify the most plausible core compositions. Results from partitioning experiments considered in this study are listed in Supplementary Tables S4–S6 and Figure 8. The compositions from these experiments are listed in molar fraction.

FIGURE 8

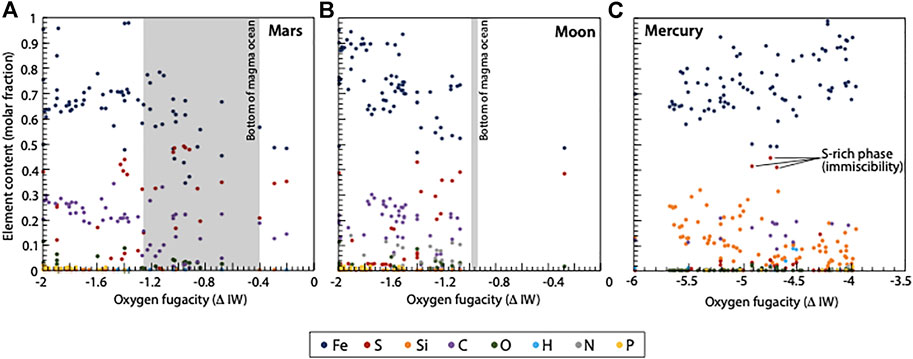
FIGURE 8. Composition of the metallic phase part of silicate-metal partitioning experiments as a function of the estimated oxygen fugacity (relative to the iron–wüstite buffer (ΔIW)). Experiments were selected for each core according to the conditions listed in Table 1. (A) Results from experiments relevant to the Martian core; (B) Results from experiments relevant to the Lunar core; (C) Results from experiments relevant to the Hermean core. All partitioning data come from studies listed in Supplementary Supplementary Tables S4–S6.

As previously pointed out for the Earth’s core (Poirier, 1994), there are three major requirements for candidate light elements in a metallic core. First, they must be sufficiently abundant in the building blocks of the planet or moon. Chondritic meteorites are considered a fundamental reference for the bulk composition of terrestrial planets. Among them, CI chondrites have the most primitive composition with the abundance of non-volatile elements matching closely with that of the solar photosphere (Anders and Ebihara, 1982). Chemical analyses of chondritic meteorites have indicated that significant amounts of light elements can be present (e.g., Braukmüller et al., 2018). In addition, iron meteorites, that possibly formed in the core of their parent asteroids contain alloying agents, such as S, C, P, and H (e.g., Jarosewich, 1990).

Second, candidate elements must be siderophile at the pressure, temperature, and redox conditions of the early formation of the core. Here, the simple and convenient assumption is made that metal-silicate equilibration occurs at the base of a whole-mantle magma ocean, which is likely a simplification in most cases (e.g., Solomatov, 2000; Wood et al., 2006). Using laboratory experiments, Righter and Drake (1996) calculated the depth of a Martian magma ocean and found that it was likely located at 6–9 GPa, 1900–2000 K, and with a relative oxygen fugacity of ΔIW=[−0.40; −1.25]. The bottom of the Lunar magma ocean is estimated to be at 3.5 GPa, 2,200 K and ΔIW=−1 (Righter and Drake, 1996). Given the uncertainty on Mercury’s formation scenario and no chemical analyses of known Mercury meteorites, the conditions of the magma ocean are difficult to assess and the pressure at the bottom of the magma ocean is not known. In the case of the endogenous hypothesis, this pressure should be less than the present-day core-mantle boundary (CMB) (i.e., <∼5 GPa), while in the case of the exogenous hypothesis, this pressure can be >5 GPa. Petrological models have suggested a CMB pressure of ∼10 GPa after magma ocean crystallization and prior to overturn (Brown and Elkins-Tanton, 2009), and we use this pressure estimate below. Temperature and redox conditions are not well defined, but chemical analyses at Mercury’s surface imply highly reducing conditions (with ΔIW∼[−7; −3]; McCubbin et al., 2012; Zolotov et al., 2013; Righter et al., 2016).

Third, the solubility of candidate elements should remain high at the present-day core conditions. Knowledge of the solubility comes principally from metal-silicate partitioning experiments, which consist of equilibrating a silicate phase (mantle analog) with a metal phase (core analog) under controlled pressure, temperature, and redox conditions. Quantitative analyses are then performed on the retrieved sample in order to understand the partitioning of relevant elements between mantle and core. Given the abundance of silicate-metal partitioning experiments in the literature, we selected experiments that match strictly the conditions at the bottom of the magma oceans listed above and the conditions of the present-day cores (see Table 1).

TABLE 1

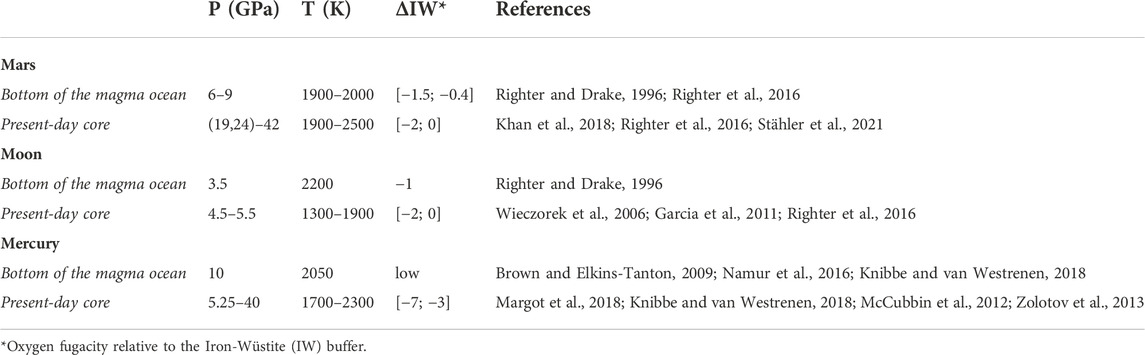
TABLE 1. Pressure, temperature, and redox conditions considered for the bottom of the magma ocean and presented-day core of Mars, the Moon, and Mercury.

Additional information about core composition can be obtained from volatility trends. These trends result from plotting the abundances of elements in the silicate portion of the terrestrial body relative to the chondritic reference (CI chondrite, representing the building blocks) as a function of the temperature at which 50% of the element would condense from a gas of solar composition (Lodders, 2003; Wood et al., 2019). This plot helps identify the distribution within the planet or moon of elements that can influence the physical properties of the core (e.g., Hirose et al., 2021). Due to the lack of compositional data for Mercury’s silicate mantle, no volatility trend has been proposed for this planet yet. However, volatility trends exist for Mars and the Moon and will be discussed further below (Figure 9). Although the volatility trend has been used to place constraints on the amount of some elements in the core by estimating their missing mass relative to their abundance in the chondritic reference (e.g., sulfur in the Earth’s core; Dreibus and Palme, 1996), the information provided is mostly qualitative because the depletion of light elements in the silicate portion could reflect not only loss to the core, but also loss to the atmosphere through volatility, or meteorite alteration and weathering (e.g., Braukmüller et al., 2018).

FIGURE 9

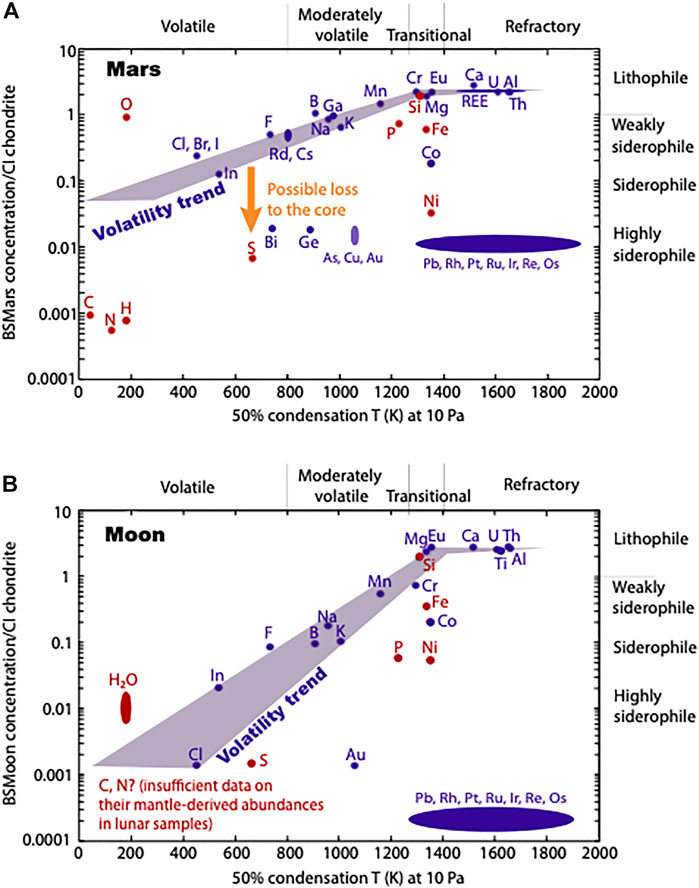
FIGURE 9. Volatility trends for Mars (A) and the Moon (B) showing the concentration of elements in bulk silicate Mars (BSMars) and bulk silicate Moon (BSMoon) relative to CI chondrite. Data for Mars are from Yoshizaki and McDonough, 2020, and data for the Moon are from Hauri et al., 2015. 50% condensation T values at 10 GPa are from Lodders, 2003.

Mars

The Vp estimates in Stähler et al. (2021) derive from models that are based on experimentally determined equations of state of Fe-S alloys and, therefore, are not from direct field measurements. The density values of the Martian core based on field observations and petrological modeling (from 5,700 up to 8,100 kg/m³, Figure 2) are significantly lower than the density of pure iron (Figure 3) and are consistent with the presence of light elements. It is worth noting that the current experimental density database does not reproduce the density range suggested by Stähler et al., 2021 (5,700–6,300 kg/m³). Despite a lack of experimental data at the pressure conditions of the Martian core, the current database shows that neither sulfur, hydrogen nor carbon decrease sufficiently the density of Fe to match this estimate, even if they are present in substantial amounts. However, laboratory data are consistent with the higher core density estimates from previous studies (from 6,000 and up to 8,100 kg/m³; Bertka and Fei, 1998; Khan et al., 2018).

The density estimates for Mars from these three studies were obtained using different approaches or parameters. Bertka and Fei (1998) calculated the density profile of Mars using an experimentally determined modal mineralogy for a model mantle (equation-of-state modeling) and the moment of inertia available at the time. Their model assumed an SNC composition, an Fe-S core composition, a crustal density of 3.0 g/cm³ and a crust thickness of 50 km. Khan et al. (2018) inverted the tidal response, mean mass, and moment of inertia for chemical composition, thermal state, and interior structure. Different mantle compositions were considered, laboratory studies were used to model mantle dissipation, and the core composition was assumed to be in the Fe-S system. Stähler et al. (2021) adopted a geophysical approach and inverted the most recent differential seismic and geodetic data from Insight in the form of the Love number, mean density, and mean moment of inertia for mantle P and S-wave velocity and density, epicentral distance for all considered events, and radius and mean density of the core. Six Martian compositions were considered, and the equation of state of the core was modeled assuming that the liquid alloy is an ideal solution with liquid Fe, liquid FeS, liquid FeO, FeH, and Fe₃C as end-members. It is unclear how the difference in the density estimates of Stähler et al. (2021) and the estimates of the other two studies can be explained. Comparing the different assumptions (especially, on the thermal state of the core) for each model and discussing the lack of clarity in some of these models is out of the scope of the present study.

Density estimates by Bertka and Fei (1998) and Khan et al. (2018) are in the same range as the measured density of Fe-S and Fe-Si alloys at relevant conditions (Figure 3), and the Vp estimates overlap with velocity measurements on Fe-S and Fe-P (Figure 4). Silicon is not expected to be present in significant amounts in the Martian core, because the redox conditions (Table 1) are not sufficiently reduced or temperature sufficiently high for Si to partition into the metallic phase (e.g., Wade and Wood, 2005). This is illustrated by the partitioning experiments compiled in Figure 8A and Supplementary Table S4. These experiments suggest that phosphorus is a minor element in the core (Chabot and Agee, 2003; Siebert et al., 2011), and therefore, is unlikely to influence the physical properties of the Martian core. Figure 8A shows that S can be a major element in the metal phase (e.g., Chabot et al., 2005; Li et al., 2016; Tsuno et al., 2018), though its content in the Martian core is debated, and estimates vary from 3.5 to >25 wt% (e.g., Yoshizaki and McDonough, 2020, and references therein). C and O can also be incorporated into the metallic phase at conditions relevant to core formation at the bottom of a magma ocean. For instance, experiments by Tsuno et al. (2018) performed at 6 GPa show a Fe-S-C-O metal phase composition with 0.8–15 at% C and 0.5–4 at% O. Some studies excluded carbon as a candidate due to the lack of C fractionation in SNC meteorites (e.g., Yoshizaki and McDonough, 2020). Density measurements on Fe-C liquids at 27–42 GPa and 2,160–2,850 K by Nakajima et al. (2015) agree with the upper range of Vp values for the Martian core. Further density and velocity measurements on Fe-C liquids are needed at conditions relevant to the Martian core so that a comparison with field estimates can be made.

The volatility trend (Figure 9A) supports a Si-poor core and indicates that S could be abundant, with the possible addition of small amounts of H and N. Very few experiments at the pressure and fO₂ conditions relevant to the Martian core have studied the partitioning of H and N. Results by Clesi et al. (2018) (5–20 GPa and ΔIW from −3.75 to −0.20) suggest that H is unlikely to be stored in the core. However, the partitioning coefficients from their study differ from earlier studies in the LVP as well as more recent DAC studies and ab initio calculations (e.g., Li et al., 2020; Tagawa et al., 2021), and it is possible that hydrogen was lost during decompression of the experiments by Clesi et al. (2018). Regarding nitrogen, results by Grewal et al. (2021) (3 GPa and ΔIW from −8.30 to −1.91) indicate that substantial amounts of this element (up to several wt% N) can be stored in the core if it undergoes instantaneous accretion.

Recently, Yoshizaki and McDonough (2020) and Stähler et al. (2021) proposed two different Martian core compositions that consider S and O as the major elements: an Fe-Ni core with 6.6 wt% S, 5.2 wt% O and 0.9 wt% H, and with 10–15 wt% S, <5 wt% O, and <1 wt% H and C, respectively. Both estimates are based on models that adjust the amount of alloying agent in the core by varying the FeO content in the mantle and fit the mass, bulk density, and moment of inertia. Our compilation of experimental physical and chemical data is in agreement with S and O being the major elements in the core. However, the comparison between laboratory and field-based estimates is limited by the field observations and the fact that experiments have been performed almost exclusively on binary systems. Density and velocity measurements on complex systems (in particular, in the Fe-S-O (-C) system) are needed to further explore the Martian core, because different elements do not affect the structural and physical properties of metallic liquids in the same way. Theoretical computations highlight that O and C are incorporated through a quasi-interstitial mechanism, while the behavior of S varies from quasi-interstitial to substitutional, depending on pressure (Posner and Steinle-Neumann, 2019). The competing effects of these elements can affect the physical properties of iron alloys.

Moon

Core density estimates of the Lunar core vary from 5,000 to 7,000 kg/m³ and compressional velocity values are low (<4 km/s; Figure 2). The available laboratory experiments suggest that these density and velocity values can be reproduced by several molten alloys, especially in the Fe-S, Fe-C, and Fe-Si systems (Figures 3, 4). As previously observed (Garcia et al., 2019), silicate-metal partitioning data at the conditions of the bottom of the Lunar magma ocean and present-day core (Supplementary Table S5 and Figure 8B) suggest that a significant amount of Si in the Lunar core is unlikely, and that both S and C can be expected to be major elements. Assuming a core composition in the Fe-FeS system, Antonangeli et al. (2015) estimated the total amount of sulfur in the core to be ∼3–6 wt%, using the Apollo field data and mass balance between a sulfur-bearing liquid outer core (10–20 at% S, i.e., 6–11 wt% S) and a pure iron solid inner core. In the case of an Fe-C core, a larger density and higher temperature (40–80 K) compared to an Fe-S core should be expected (Shimoyama et al., 2016), implying that an Fe-C core should be smaller than an Fe-S core in order to satisfy the Lunar mean moment of inertia.

The volatility trend (Figure 9B) is consistent with a Si-poor, S-bearing core. In addition, partitioning experiments show that nitrogen and oxygen could be stored in the Lunar core in substantial amounts (Figure 8B). However, no information about carbon and nitrogen can be retrieved from the volatility trend, due to the lack of data on the abundance of these two elements in Lunar samples (Hauri et al., 2015). Malavergne et al. (2019) observed that small amounts of carbon can be stored in metallic iron at P-T-fO₂ conditions relevant to the Lunar core. Small amounts of phosphorus (<3 at%) might have been incorporated into the core during differentiation, and it is unlikely that such small amounts would affect significantly the bulk physical properties of the Lunar core.

The solubilities of S, C, N, and O in metallic iron at Lunar core conditions are not independent from each other. For instance, at 4.5 GPa, 2,073 K, and ΔIW varying from –1.2 to –0.7, the partitioning of N to the metal phase increases slightly from pure alloy to an alloy with 16 wt% S and decreases for an alloy containing >20 wt% S (Grewal et al., 2019). Partitioning experiments at 3 GPa and 1673 K by Li et al. (2015) show that the effect of S on the solubility of C in Fe–Ni–S melt is negligible, and that the addition of Si to the melt will significantly decrease the C content (from 5.6 to 1.8 wt% C). The complex interplay between elements makes it difficult to place quantitative constraints on core chemistry, because most experiments are not performed in a system containing S, C, N, and O. However, some experiments by Grewal et al. (2019) at 3 and 4.5 GPa, 1,873–2,073 K, and for ΔIW from −2 to −1, contain the four major elements expected in the Lunar core (S, C, N and O). Chemical analyses of the metal phase from these experiments provided the following ranges of light elements contents: 0.04–39 at% S, 0.5–19 at% C, 1.8–10 at% N, and 0.5–3.7 at% O.

Mercury

The core density profile by Margot et al. (2018) (Figure 2) is consistent with density measurements on several core compositions. In particular, the outermost core density values are comparable to that measured for Fe-C, Fe-Si and Fe-S alloys (Figure 3). Si, C, and a small amount of S are stable at Mercury’s core conditions. The highly reduced state of Mercury results in oxygen staying in the silicate phase. Partitioning studies at the conditions of the bottom of the magma ocean and of the present-day core (Supplementary Table S6) show that both Si and C could have been added to the core in significant amounts (Figure 8C), and that C is more siderophile than S. For instance, chemical analyses of the Fe-Si-C (-S) metallic phase in experiments at 3–8 GPa, ΔIW = [−6; −4.5] have provided Si ranges of 4–13 at%, C ranges of 11–21 at% and S ranges of 0.8–3.5 at% (Li et al., 2016). However, interactions between C and S are complex, and under certain conditions (such as accretion from S-rich (>30 wt% S) materials), C could have been expelled from the core (Li et al., 2016). Other interactions between alloying agents likely influence the core composition of Mercury. For example, the presence of silicon limits the presence of other elements, such as nitrogen. It has been shown that the solubility of N in a highly reduced core is largely controlled by Si, where increasing the Si content decreases N solubility (Grewal et al., 2019).

Partitioning experiments highlight that only small amounts of sulfur could be stored in the core (<5 at%) at highly reduced conditions (Figure 8C; Namur et al., 2016). A few experiments (e.g., Corgne et al., 2008a; Grewal et al., 2019) observed immiscibility in the metal phase, with a S-rich liquid (>40 at. %S) coexisting with a S-poor liquid (<4 at% S). Immiscibility in a multi-component system would lead to a layered structure of the core that involves a sulfide layer in the outer portion of the core and a S-poor underlying core (e.g., Malavergne et al., 2010). An FeS layer at the top of the core has been proposed (Hauck et al., 2013), and its insulating properties might contribute to explain the low magnetic field (Pommier et al., 2019). However, the origin, thickness, and physical properties of this sulfide layer is debated.

Like for any other planet, the exact composition of Mercury’s core is not known, but previous studies have suggested an Fe-Ni-Si(+/−S, C) chemistry, with a Si content up 25 wt% (Hauck et al., 2013; Chabot et al., 2014; Margot et al., 2018; Nittler et al., 2018; Vander Kaaden et al., 2020) and a low S content (<1.5 wt%; Namur et al., 2016; Cartier et al., 2020). Carbon is abundant in Mercury’s crust (e.g., Charlier and Namur, 2019), which could be compatible with a C-saturated core (Vander Kaaden et al., 2020), although carbon partitioning into the core might have been limited (Keppler and Golabek, 2019). Studies of C solubility in Mercury’s core reveal that the addition of Ni, Si and S decreases the partitioning of carbon to the metallic phase (e.g., Dasgupta et al., 2013; Kim et al., 2014; Vander Kaaden et al., 2020). Depending on the composition of the building blocks (EH or CB chondrites), Vander Kaaden et al. (2020) obtained a preferred core composition consisting of 1–25 wt% Si and S and C amounts of less than 5 wt% each. Our compilation of density measurements (Figure 3) suggests that the presence of 25 wt% Si in the core is unlikely, because it would lead to density values significantly lower than estimates from Margot et al. (2018). The current density dataset is consistent with lower Si contents, up to ∼15 wt%.

Mercury possibly contains a solid inner core (e.g., Margot et al., 2018; Charlier and Namur, 2019). The partitioning of light elements between the liquid outer core and solid inner core would produce a density jump at the inner core boundary. Partitioning experiments have shown that Si strongly partitions into the solid phase in the Fe-Si-S system (Tao and Fei, 2021). A crystallized Si-bearing inner core would be stable in the face-centered cubic phase field of iron at low Si contents and in the body-centered cubic phase at Si contents >6 wt% (Edmund et al., 2022). The density and velocity of these relevant phases can be used to model the core profiles (Kantor et al., 2007; Antonangeli et al., 2015), and the melting relations are essential for identifying the inner-core boundary along with core temperature models (Tao and Fei, 2021).

Effect of light elements on core dynamics

Convection in a planetary core is typically generated either by thermal buoyancy, driven by cooling the core faster than heat can conduct through it, or by compositional buoyancy, driven by a phase change within the core. Ultimately, both processes are driven by cooling of the core by the mantle, so it is heat transfer through the mantle that determines how much energy is available to drive core flows and magnetic field generation. On the core side, the thermal conductivity determines the amount of heat that can be transported through the core in the absence of fluid motion. If the core-mantle boundary (CMB) heat flow exceeds the conductive limit of the core (i.e., the maximum amount of heat the core fluid can conduct before becoming buoyant), then the remaining heat will be transported by convection. If the core temperature profile intersects a material phase boundary then a phase change will occur, such as solidification, which will release latent heat, gravitational heat, and compositionally buoyant liquid, if the residual fluid is more or less dense than the background fluid. Although thermal buoyancy requires a CMB heat flow in excess of the conductive limit to drive flow, compositional buoyancy does not have an analogous conductive limit to overcome in a well-mixed core, and therefore the compositionally buoyant fluid will drive flow as the phase change occurs. However, in a core that is thermally stratified (i.e., the CMB heat flow is less than the conductive limit), compositional buoyancy must still overcome the thermal stratification to drive fluid motion.

Complexity increases if the system is immiscible, which has been observed for several iron alloys under pressure. Immiscibility results in the coexistence of two compositionally distinct metallic liquids at specific pressure and temperature. For instance, in the Fe-Si-S system, an immiscible zone where S-rich and S-poor liquids coexist is present up to 4 GPa and 2,200 K and closes at higher pressures (Morard and Katsura, 2010). In the Fe-S-C system, immiscibility has been observed up to at least 5 GPa for alloys containing 15 wt% S and 5 wt% C (Dasgupta et al., 2009). Corgne et al. (2008b) observed that two immiscible liquid alloys coexist to about 5.5 GPa in Fe-Ni-S-C-O system, with one liquid being enriched in S and the other enriched in C. Immiscibility has also been reported in Fe-Si-O (Arveson et al., 2019) and Fe-S-H (Yokoo et al., 2022). Another type of immiscibility (where two light elements combine and exsolve) has been suggested for Fe-Mg-O (Badro et al., 2015) and Fe-Si-O (Hirose et al., 2017) alloys. If a planetary core is fully or partially molten at pressures lower than the closure of these immiscibility zones, then immiscibility could induce stratification (e.g., Dasgupta et al., 2009). This closure occurs at pressures that are relevant to the Lunar core (<5.5 GPa) but too low for the cores of Mars and Mercury, although it has been suggested that immiscibility can be present at higher pressure in the Fe-S ± C ± O system (Dasgupta et al., 2009). The presence of immiscible core layers will likely mute the rigor of convection, potentially limiting the convection to occurring within each layer separately. The presence of an immiscible and stably stratified electrically conductive fluid layer at the top of the core could cause magnetic attenuation (or shielding), which is expected to filter out small scale magnetic field features (Christensen and Wicht, 2008).

The core material properties that are critical to its dynamics, such as viscosity (Figure 6), thermal conductivity (Figure 7), the melting curve (Figures 1, 10), and the adiabatic gradient, are all sensitive to the composition of the core fluid. In fact, some properties vary so much with composition that the style of convection can change from planet to planet. This is illustrated in Figure 11, which compares the liquidus and adiabatic gradients for Mercury, the Moon, Mars, and Earth. The parameters used in this figure are listed in Table 2. Cores with adiabatic gradients steeper than their liquidus gradients will solidify at the top of the core in a “top-down” regime, while the reverse results in a “bottom-up” solidification regime. In Earth’s Fe-rich core, the adiabatic gradient is shallower than the melting curve so that the alloy solidifies from the center of the core outwards. In contrast, the Martian core is expected to contain enough sulfur to make the melting curve shallower than the adiabat, which implies that solidification occurs from the top down. In this case, given that the solid species is denser than the residual liquid, the solid is expected to “snow” down, either re-melting at some depth or accumulating a solid “snow layer” at the base of the core. In the former case, re-melting of the iron snow can produce a convection cycle analogous to thermal cooling, and can potentially drive a dynamo (Olson et al., 2017; Davies and Pommier, 2018; Hemingway and Driscoll, 2021). Whether the iron snow re-melts as it falls depends on the size of the snow particles and how the core adiabatic slope compares to the snow melting curve. The “top-down” solidification could also add complication in determining the first liquidus phase as in the Fe-Si system where other liquidus phases exist at low pressure. Figure 11 also demonstrates that the relatively large uncertainties in these material properties prevent a definitive conclusion for the core solidification regimes of Mercury, Mars, and the Moon. One caveat about Figure 11 is that these gradients are taken at the CMB for each planet. In reality, the adiabat and liquidus vary differently enough with depth to change their solidification regime.

FIGURE 10

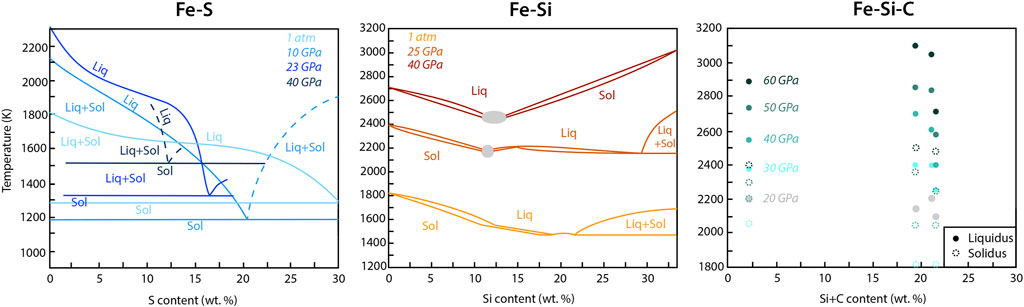
FIGURE 10. Phase diagrams for three iron alloys (Fe-S, Fe-Si, and Fe-Si-C) under pressure and temperature. Data for the Fe-S system are from Waldner and Pelton (2005) (1bar), Chen et al. (2008) (10 GPa), and Stewart et al. (2007) (23 and 40 GPa), data for the Fe-Si system are from Edmund et al. (2022), and data for the Fe-Si-C system are from Miozzi et al. (2022).

FIGURE 11

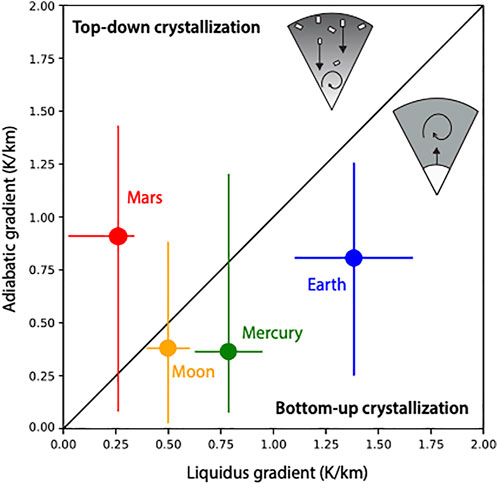
FIGURE 11. Comparison of the core solidification regimes of Mercury, Mars, the Moon, and Earth. Cores with adiabatic gradients steeper than the core liquidus solidify at the top of the core in a “top-down” style, potentially generating “iron snow”. Cores with liquidus gradients steeper than the adiabat solidify at the base of the core in a “bottom-up” style. The adiabatic gradient is dT/dr_ad=αgT_CMB/c_p. Vertical error bars reflect the range of plausible values, horizonal error bars are assumed to be 20% of the nominal value. The two greyscale sketches represent cross-section of the core in each regime, with solids in white and liquid in grey. The parameters used in this figure are listed in Table 2.

TABLE 2

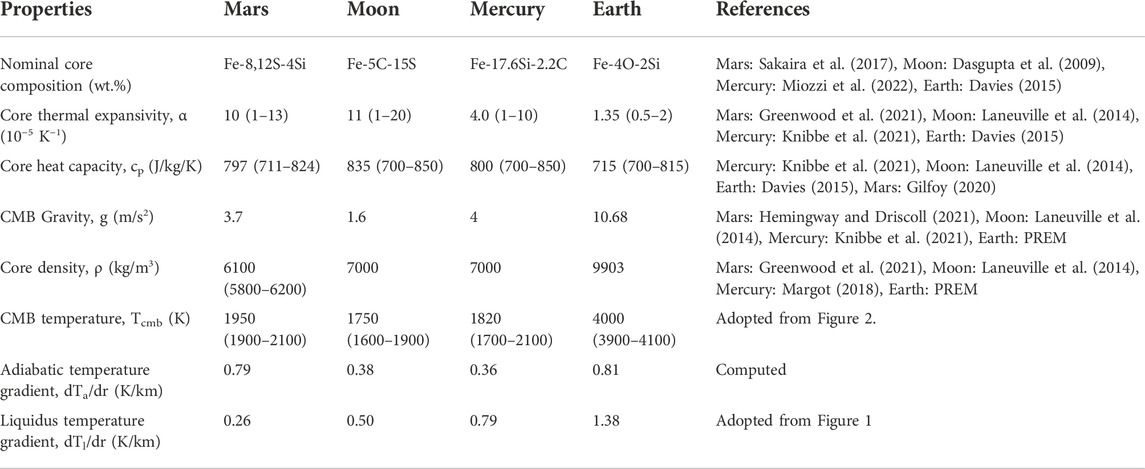
TABLE 2. Material properties of Mars, Moon, Mercury, and Earth used in Figures 11, 12. CMB is core-mantle boundary. PREM is the Preliminary Reference Earth Model of Dziewonski and Anderson (1981).

The maintenance of a core-generated dynamo is also sensitive to the transport properties of the core. The Wiedemann-Franz law in Eq. 1 implies that as the core becomes better at conducting heat it also becomes a better conductor of electrical currents. This has an interesting implication for dynamos: at low thermal/electrical conductivity, the core is likely thermally convecting but does not generate strong enough currents to maintain a magnetic field against decay, while at high thermal/electrical conductivity, thermal convection becomes more difficult, inhibiting magnetic induction. These two “conductivity limits” imply that a peak magnetic induction rate occurs at moderate thermal/electrical conductivities (Driscoll and Du, 2019). Figure 12 shows the application of this theory to Mars where Eq. 1 has been used to convert thermal to electrical conductivity. Adopting a core thermal conductivity of 30 W/m/K, and with a temperature-dependence from Figure 7B for FeS₅O_0.5, implies that the electrical conductivity has increased slightly as the Martian core has cooled (red curve in Figure 12). We have assumed the present-day Martian core heat flow is 5% of the surface heat flow estimate of 2.73 TW (Parro et al., 2017) to ensure it is thermally stratified (filled circle). According to this model, the electrical conductivity of the hot early Martian core was low enough to allow for thermal convection until T_CMB∼2,100 K, at which point thermal convection is predicted to have stopped, and the dynamo to cease. Present-day estimates for the state of the Martian core place it in the “no dynamo” region, with the possibility of the dynamo turning back on in the future as the core begins to solidify around T_CMB∼1,600 K (also see Greenwood et al., 2021; Hemingway and Driscoll, 2021). Although the regimes in Figure 12 are helpful in understanding the evolution of the Martian core, it does not reflect the uncertainties in these parameters, which could change our perceived evolution of the Martian core significantly. Application of this model to the other planets could provide insight into their core evolution and material properties but is outside the scope of this review.

FIGURE 12

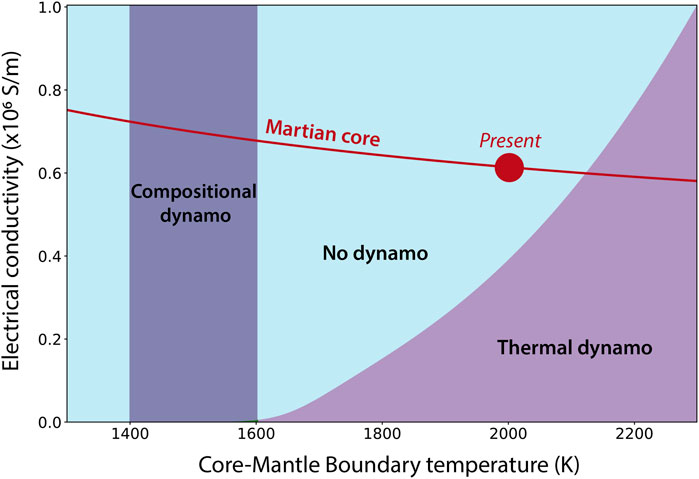
FIGURE 12. Martian dynamo regimes in electrical conductivity - temperature space. The model of Driscoll and Du (2019) is applied to Mars, with the upper conductivity limit for thermal convection (grey curve) from their Equation 13, assuming k_LM=5 W/m/K, α=2.5 × 10⁻⁵ K⁻¹, g=3.721 m/s² ρ_LM=3,550 kg/m³, c_m=798 J/kg/K, and ν_ref=1.1749 × 10¹⁰ m²/s. The nominal present-day Martian core state is assumed to be T_CMB=2,000 K, thermal conductivity k=30 W/m/K, corresponding to electrical conductivity σ=6.14 × 10⁵ S/m (red circle). The central core solidification temperature from Figure 1 for Fe-10S (Chen et al., 2008) is extrapolated along a core adiabat to the core-mantle boundary (CMB) to estimate T_CMB at which core solidification begins, ∼1,600 K, and full core solidification occurs, ∼1,400 K (blue region).

Lastly, the viscosity of the core liquid plays an important role in the dynamics and, therefore, morphology of any core-generated magnetic field. Higher (lower) viscosity will tend to produce flows with longer (shorter) characteristic length scales and time scales (Schwaiger et al., 2021). Typically, magnetic fields generated by dynamos with longer characteristic length and time scales tend to be more dipolar and have low secular variation, and those with shorter characteristic length and times tend to be more multi-polar and have higher secular variation (Driscoll and Olson, 2009). In cores that have a stratified layer at the top, the viscosity influences how far convective flows can penetrate the layer, potentially thinning it out by entraining the stratified fluid. The viscosity of the core fluid can also influence the efficiency of core-mantle equilibration during core formation (Deguen et al., 2014).

Perspectives

Addressing fundamental scientific questions about core formation and evolution requires exceptionally precise and sensitive instrumentation and techniques, both in the laboratory and in the field. In the absence of laboratory and field measurements, inferences about the structure and composition of metallic cores are challenging and are strongly model dependent. Significant technological advances have occurred in the laboratory setting and will likely continue to improve our understanding of planets and moons in the Solar System as well as terrestrial exoplanets and exomoons. For example, experiments in large-volume presses at synchrotron facilities provide excellent constraints on pressure and temperature while allowing the measurement of physical properties.

The investigation of complex (ternary, quaternary) iron alloy systems is an important direction for future experimental work. This review underlines that the dataset of physical properties for binary systems is becoming substantial, despite limited measurements at some specific pressures and temperatures (for instance, measurements of any properties above 10 GPa are scarce, and very few compressional data exist above 2,000 K in the considered pressure range). In contrast, the exploration of ternary iron alloys that represent relevant core analogs, such as Fe-S-C, Fe-S-Si, or Fe-S-O, is only emerging in the laboratory, and the same observation can be made for numerical studies (Posner and Steinle-Neumann, 2019). Multi-component efforts have been focused on pressures relevant to the Earth’s core, but very little is understood at pressures relevant to Mars-sized or Moon-sized bodies, particularly in the pressure range of 10–40 GPa. This limitation applies to the physical properties of iron alloys as well as their phase diagram. The effect of nickel on these properties also remains to be explored.

Constraining the heat flow during core cooling requires the determination of thermal conductivity of iron alloys. It implies facing the challenge of direct measurements of thermal conductivity in large-volume presses, as well as determining the electrical-thermal conductivity relationship for iron alloys. Recent advances have shown successful thermal conductivity measurements in the multi-anvil for perovskite materials (Manthilake et al., 2020). More generally, exploring the relationship between the physical properties of iron alloys requires the combination of different measurements as part of single experiment, ideally at beamline facilities where the structure of the sample can be monitored while under pressure and temperature.

The synergy between core crystallization parameterized models and laboratory experiments would also benefit from dynamic studies. The physical properties of iron alloys are measured as part of static experiments, where thermodynamic equilibrium is achieved. However, non-equilibrium reactions likely influence core cooling regimes. Comparing static and dynamic studies is needed, so that core crystallization can be explored under both equilibrium and non-equilibrium conditions. Our ability to understand the physical properties of iron alloys, from the atomic level to the scale of a core, will provide the necessary knowledge to interpret space measurements and observations from ongoing and future missions, and thus, to understand terrestrial planets and moons in our Solar System and beyond.

Author contributions

AP led the study, compiled the data, made the figures, and wrote the first draft of the manuscript. PD contributed to the dynamics section, helped with Figures 11, 12, and edited the manuscript. YF helped with Figure 5, calculated the velocities of Fe-H alloys, and edited the manuscript. MW contributed to shape the content of the manuscript with AP, discussed the data, and edited the manuscript.

Funding

AP acknowledges support from NSF-NERC Grant 1832462.

Acknowledgments

We thank the Guest Editors for their invitation to contribute to this Special Issue, and Guest Editor Bin Chen for his editorial work. AP thanks Francesca Miozzi and Eric Edmund for their help with compiling the Mars data for Figure 8 and for discussion, and Christopher Davies, Tilio Rivoldini, and Bernard Charlier for discussions. The authors are grateful to Carnegie-EPL librarians M.A. O’Donnell and Shaun Hardy for their help with the literature. We thank three reviewers for their comments that improved the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.956971/full#supplementary-material

References

Anders, E., and Ebihara, M. (1982). Solar-system abundances of the elements. Geochim. Cosmochim. Acta 46, 2363–2380. doi:10.1016/0016-7037(82)90208-3

CrossRef Full Text | Google Scholar

Antonangeli, D., Morard, G., Schmerr, N. C., Komabayashi, T., Krisch, M., Fiquet, G., et al. (2015). Toward a mineral physics reference model for the Moon’s core. Proc. Natl. Acad. Sci. U. S. A. 112 (13), 3916–3919. doi:10.1073/pnas.1417490112

PubMed Abstract | CrossRef Full Text | Google Scholar

Assael, M. J., Chatzimichailidis, A., Antoniadis, K. D., Wakeham, W. A., Huber, M. L., and Fukuyama, H. (2017). Reference correlations for the thermal conductivity of liquid copper, gallium, indium, iron, lead, nickel and tin. High. Temp. High. Press. 46 (6), 391–416.

PubMed Abstract | Google Scholar

Badro, J., Brodholt, J. P., Piet, H., Siebert, J., and Ryerson, F. J. (2015). Core formation and core composition from coupled geochemical and geophysical constraints. Proc. Natl. Acad. Sci. U. S. A. 112 (40), 12310–12314. doi:10.1073/pnas.1505672112

PubMed Abstract | CrossRef Full Text | Google Scholar

Badro, J., Fiquet, G., Guyot, F., Gregoryanz, E., Occelli, F., Antonangeli, D., et al. (2007). Effect of light elements on the sound velocities in solid iron: Implications for the composition of Earth's core. Earth Planet. Sci. Lett. 254, 233–238. doi:10.1016/j.epsl.2006.11.025

CrossRef Full Text | Google Scholar

Balog, P. S., Secco, R. A., Rubie, D. C., and Frost, D. J. (2003). Equation of state of liquid Fe-10 wt % S:Implications for the metallic cores of planetary bodies. J. Geophys. Res. 108, B22124. doi:10.1029/2001JB001646

CrossRef Full Text | Google Scholar

Barmin, L. N., Estin, O. A., and Dobrovinskii, I. E. (1970). Application of theory of regular solutions to isotherms of viscosity and molar volume in binary sulphide melts. Russ. J. Phys. Chem. USSR. 44, 1450–1453.

Google Scholar

Benz, W., Slattery, W. L., and Cameron, A. G. W. (1988). Collisional stripping of Mercury's mantle. Icarus 74 (3), 516–528. doi:10.1016/0019-1035(88)90118-2

CrossRef Full Text | Google Scholar

Berrada, M., Secco, R. A., and Yong, W. (2021). Adiabatic heat flow in Mercury’s core from electrical resistivity measurements of liquid Fe-8.5 wt%Si to 24 GPa. Earth Planet. Sci. Lett. 568, 117053. doi:10.1016/j.epsl.2021.117053

CrossRef Full Text | Google Scholar

Bertka, C. M., and Fei, Y. (1998). Density profile of an SNC model Martian interior and the moment-of-inertia factor of Mars. Earth Planet. Sci. Lett. 157, 79–88. doi:10.1016/S0012-821X(98).00030-2

CrossRef Full Text | Google Scholar

Bertka, C. M., and Fei, Y. (1997). Mineralogy of the Martian interior up to core-mantle boundary pressures. J. Geophys. Res. 102 (B3), 5251–5264.

CrossRef Full Text | Google Scholar

Bouhifd, M. A., Andrault, D., Bolfan-Casanova, N., Hammouda, T., and Devidal, J. L. (2013). Metal silicate partitioning of Pb and U: Effects of metal composition and oxygen fugacity. Geochim. Cosmochim. Acta 114, 13–28. doi:10.1016/j.gca.2013.03.034

CrossRef Full Text | Google Scholar

Bouhifd, M. A., and Jephcoat, A. P. (2011). Convergence of Ni and Co metal–silicate partition coefficients in the deep magmaocean and coupled silicon–oxygen solubility in iron melts at high pressures. Earth Planet. Sci. Lett. 307, 341–348. doi:10.1016/j.epsl.2011.05.006

CrossRef Full Text | Google Scholar

Boujibar, A., Habermann, M., Righter, K., Ross, D. K., Pando, K., Righter, M., et al. (2019). U, Th, and K partitioning between metal, silicate, and sulfide and implications for Mercury's structure, volatile content, and radioactive heat production. Am. Mineral. 104, 1221–1237. doi:10.2138/am-2019-7000

CrossRef Full Text | Google Scholar

Braukmuller, N., Wombacher, F., Hezel, D. C., Escoube, R., and Munker, C. (2018). The chemical composition of carbonaceous chondrites: Implications for volatile element depletion, complementarity and alteration. Geochim. Cosmochim. Acta 239, 17–48. doi:10.1016/j.gca.2018.07.023

CrossRef Full Text | Google Scholar

Breuer, D., Rueckriemen, T., and Spohn, T. (2015). Iron snow, crystal floats, and inner-core growth: Modes of core solidification and implications for dynamos in terrestrial planets and moons. Prog. Earth Planet. Sci. 2 (1), 39–26. doi:10.1186/s40645-015-0069-y

CrossRef Full Text | Google Scholar

Breuer, D., Spohn, T., van Hoolst, T., van Westrenen, W., Stanley, S., and Rambaux, N. (2021). Interiors of earth-like planets and satellites of the solar system. Surv. Geophys. 43, 177–226. doi:10.1007/s10712-021-09677-x

CrossRef Full Text | Google Scholar

Brown, S. M., and Elkins-Tanton, L. T. (2009). Compositions of Mercury's earliest crust from magma ocean models. Earth Planet. Sci. Lett. 286 (3-4), 446–455. doi:10.1016/j.epsl.2009.07.010

CrossRef Full Text | Google Scholar

Cartier, C., Namur, O., Nittler, L. R., Weider, S. Z., Crapster-Pregont, E., Vorburgerf, A., et al. (2020). No FeS layer in mercury? Evidence from Ti/Al measured by MESSENGER. Earth Planet. Sci. Lett. 534 (116), 116108. doi:10.1016/j.epsl.2020.116108

CrossRef Full Text | Google Scholar

Chabot, N., Draper, D. S., and Agee, C. B. (2005). Conditions of core formation in the earth: Constraints from nickel and cobalt partitioning. Geochim. Cosmochim. Acta 69 (8), 2141–2151. doi:10.1016/j.gca.2004.10.019

CrossRef Full Text | Google Scholar

Chabot, N. L., and Agee, C. B. (2003). core formation in the earth and moon: New experimental constraints from V, Cr, and Mn. Geochim. Cosmochim. Acta 67, 2077–2091. doi:10.1016/s0016-7037(02)01272-3

CrossRef Full Text | Google Scholar

Chabot, N. L., Wollack, E. A., Klima, R. L., and Minitti, M. E. (2014). Experimental constraints on Mercury's core composition. Earth Planet. Sci. Lett. 390, 199–208. doi:10.1016/j.epsl.2014.01.004

CrossRef Full Text | Google Scholar

Charlier, B., and Namur, O. (2019). The origin and differentiation of planet mercury. Elements 15, 9–14. doi:10.2138/gselements.15.1.9

CrossRef Full Text | Google Scholar

Chau, A., Reinhardt, C., Helled, R., and Stadel, J. (2018). Forming mercury by giant impacts. Astrophys. J. 865 (1), 35. doi:10.3847/1538-4357/aad8b0

CrossRef Full Text | Google Scholar

Chen, B., Li, J., and Hauck, S. A. (2008). Non-ideal liquidus curve in the Fe-S system and Mercury’s snowing core. Geophys. Res. Lett. 35, L07201. doi:10.1029/2008gl033311

CrossRef Full Text | Google Scholar

Chen, J., Yu, T., Huang, S., Girard, J., and Liu, X. (2014). Compressibility of liquid FeS measured using X-ray radiograph imaging. Phys. Earth Planet. Interiors 228, 294–299. doi:10.1016/j.pepi.2013.12.012

CrossRef Full Text | Google Scholar

Chi, H., Dasgupta, R., Duncan, M. S., and Shimizu, N. (2014). Partitioning of carbon between Fe-rich alloy melt and silicate melt in a magma ocean – implications for the abundance and origin of volatiles in Earth, Mars, and the moon. Geochim. Cosmochim. Acta 139, 447–471. doi:10.1016/j.gca.2014.04.046

CrossRef Full Text | Google Scholar

Chidester, B. A., Rahman, Z., Righter, K., and Campbell, A. J. (2017). Metal–silicate partitioning of U: Implications for the heat budget of the core and evidence for reduced U in the mantle. Geochim. Cosmochim. Acta 199, 1–12. doi:10.1016/j.gca.2016.11.035

CrossRef Full Text | Google Scholar

Christensen, U. R., and Wicht, J. (2008). Models of magnetic field generation in partly stable planetary cores: Applications to Mercury and Saturn. Icarus 196 (1), 16–34. doi:10.1016/j.icarus.2008.02.013

CrossRef Full Text | Google Scholar

Clesi, V., Bouhifd, M. A., Bolfan-Casanova, N., Manthilake, G., Fabbrizio, A., and Andrault, D. (2016). Effect of H₂O on metal–silicate partitioning of Ni, Co, V, Cr, Mn and Fe: Implications for the oxidation state of the Earth and Mars. Geochim. Cosmochim. Acta 192, 97–121. doi:10.1016/j.gca.2016.07.029

CrossRef Full Text | Google Scholar

Clesi, V., Bouhifd, M. A., Bolfan-Casanova, N., Manthilake, G., Schiavi, F., Raepsaet, C., et al. (2018). Low hydrogen contents in the cores of terrestrial planets. Sci. Adv. 4, e1701876. doi:10.1126/sciadv.1701876

PubMed Abstract | CrossRef Full Text | Google Scholar

Corgne, A., Keshav, S., Wood, B. J., McDonough, W. F., and Fei, Y. (2008a). Metal–silicate partitioning and constraints on core composition and oxygen fugacity during Earth accretion. Geochim. Cosmochim. Acta 72, 574–589. doi:10.1016/j.gca.2007.10.006

CrossRef Full Text | Google Scholar

Corgne, A., Wood, B. J., and Fei, Y. (2008b). C- and S-rich molten alloy immiscibility and core formation of planetesimals. Geochim. Cosmochim. Acta 72, 2409–2416. doi:10.1016/j.gca.2008.03.001

CrossRef Full Text | Google Scholar

Dalou, C., Hirschmann, M. M., von der Handt, A., Mosenfelder, J., and Armstrong, L. S. (2017). Nitrogen and carbon fractionation during core–mantle differentiation at shallow depth. Earth Planet. Sci. Lett. 458, 141–151. doi:10.1016/j.epsl.2016.10.026

CrossRef Full Text | Google Scholar

Dasgupta, R., Buono, A., Whelan, G., and Walker, D. (2009). High-pressure melting relations in Fe–C–S systems: Implications for formation, evolution, and structure of metallic cores in planetary bodies. Geochim. Cosmochim. Acta 73, 6678–6691. doi:10.1016/j.gca.2009.08.001

CrossRef Full Text | Google Scholar

Dasgupta, R., Chi, H., Shimizu, N., Buono, A. S., and Walker, D. (2013). Carbon solution and partitioning between metallic and silicate melts in a shallow magma ocean: Implications for the origin and distribution of terrestrial carbon. Geochim. Cosmochim. Acta 102, 191–212. doi:10.1016/j.gca.2012.10.011

CrossRef Full Text | Google Scholar

Davies, C. J., and Pommier, A. (2018). Iron snow in the Martian core? Earth Planet. Sci. Lett. 481, 189–200. doi:10.1016/j.epsl.2017.10.026

CrossRef Full Text | Google Scholar

De Koker, N., Steinle-Neumannn, G., and Vlcek, V. (2012). Electrical resistivity and thermal conductivity of liquid Fe alloys at high P and T, and heat flux in Earth’s core. Proc. Natl. Acad. Sci. U. S. A. 109 (11), 4070–4073. doi:10.1073/pnas.1111841109

PubMed Abstract | CrossRef Full Text | Google Scholar

Deguen, R., Landeau, M., and Olson, P. (2014). Turbulent metal–silicate mixing, fragmentation, and equilibration in magma oceans. Earth Planet. Sci. Lett. 391, 274–287. doi:10.1016/j.epsl.2014.02.007

CrossRef Full Text | Google Scholar

Dobrosavljevic, V. V., Zhang, D., Sturhahn, W., Zhao, J., Toellner, T. S., Chariton, S., et al. (2022). Melting and phase relations of Fe-Ni-Si determined by a multi-technique approach. Earth Planet. Sci. Lett. 584, 117358. doi:10.1016/j.epsl.2021.117358

CrossRef Full Text | Google Scholar

Dobson, D. P., Crichton, W. A., Vocadlo, L., Jones, A. P., Wang, Y., Uchida, T., et al. (2000). In situ measurement of viscosity of liquids in the Fe-FeS system at high pressures and temperatures. Am. Mineral. 85, 1838–1842. doi:10.2138/am-2000-11-1231

CrossRef Full Text | Google Scholar

Dreibus, G., and Palme, H. (1996). Cosmochemical constraints on the sulfur content in the Earth’s core. Geochim. Cosmochim. Acta 60, 1125–1130. doi:10.1016/0016-7037(96)00028-2

CrossRef Full Text | Google Scholar

Driscoll, P. E., and Du, Z. (2019). Geodynamo conductivity limits. Geophys. Res. Lett. 46, 7982–7989. doi:10.1029/2019GL082915

CrossRef Full Text | Google Scholar

Driscoll, P. E., and Olson, P. (2009). Polarity reversals in geodynamo models with core evolution. Earth Planet. Sci. Lett. 282, 24–33. doi:10.1016/j.epsl.2009.02.017

CrossRef Full Text | Google Scholar

Dumberry, M., and Rivoldini, A. (2015). Mercury’s inner core size and core-crystallization regime. Icarus 248, 254–268. doi:10.1016/j.icarus.2014.10.038

CrossRef Full Text | Google Scholar

Dziewonski, A. M., and Anderson, D. L. (1981). Preliminary reference Earth model. Phys. Earth Planet. Interiors 25, 297–356. doi:10.1016/0031-9201(81)90046-7

CrossRef Full Text | Google Scholar

Edmund, E., Morard, G., Baron, M. A., Rivoldini, A., Yokoo, S., Boccato, S., et al. (2022). The Fe-FeSi phase diagram at Mercury’s core conditions. Nat. Commun. 13, 387. doi:10.1038/s41467-022-27991-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Fei, Y., and Bertka, C. M. (2005). The interior of Mars. Science 308, 1120–1121. doi:10.1126/science.1110531

PubMed Abstract | CrossRef Full Text | Google Scholar

Fichtner, C. E., Schmidt, M. W., Liebske, C., Bouvier, A.-S., and Baumgartner, L. P. (2021). Carbon partitioning between metal and silicate melts during Earth accretion. Earth Planet. Sci. Lett. 554, 116659. doi:10.1016/j.epsl.2020.116659

CrossRef Full Text | Google Scholar

Fischer, R. A., Campbell, A. J., Reaman, D. M., Miller, N. A., Heinz, D. L., Dera, P., et al. (2013). Phase relations in the Fe–FeSi system at high pressures and temperatures. Earth Planet. Sci. Lett. 373, 54–64. doi:10.1016/j.epsl.2013.04.035

CrossRef Full Text | Google Scholar

Fischer, R. A., Nakajima, Y., Campbell, A. J., Frost, D. J., Harries, D., Langenhorst, F., et al. (2015). High pressure metal–silicate partitioning of Ni, Co, V, Cr, Si, and O. Geochim. Cosmochim. Acta 167, 177–194. doi:10.1016/j.gca.2015.06.026

CrossRef Full Text | Google Scholar

Funakoshi, K.-i. (2010). In-situ viscosity measurements of liquid Fe–S alloys at high pressures. High. Press. Res. 30 (1), 60–64. doi:10.1080/08957951003616356

CrossRef Full Text | Google Scholar

Garcia, R. F., Gagnepain-Beyneix, J., Chevrot, S., and Lognonné, P. (2011). Very preliminary reference Moon model. Phys. Earth Planet. Interiors 188, 96–113. doi:10.1016/j.pepi.2011.06.015

CrossRef Full Text | Google Scholar

Garcia, R. F., Khan, A., Drilleau, M., Margerin, L., Kawamura, T., Sun, D., et al. (2019). Lunar seismology: An update on interior structure models. Space Sci. Rev. 215 (8), 50–6308. doi:10.1007/s11214-019-0613-y

CrossRef Full Text | Google Scholar

Gilfoy, F., and Li, J. (2020). Thermal state and solidification regime of the Martian core: Insights from the melting behavior of FeNi-S at 20 GPa. Earth Planet. Sci. Lett. 541, 116285. doi:10.1016/j.epsl.2020.116285

CrossRef Full Text | Google Scholar

Greenwood, S., Davies, C. J., and Pommier, A. (2021). Influence of thermal stratification on the structure and evolution of the Martian core. Geophys. Res. Lett. 48, e2021GL095198. doi:10.1029/2021GL095198

CrossRef Full Text | Google Scholar

Grewal, D. S., Dasgupta, R., and Aithala, S. (2021). The effect of carbon concentration on its core-mantle partitioning behavior in inner Solar System rocky bodies. Earth Planet. Sci. Lett. 571, 117090. doi:10.1016/j.epsl.2021.117090

CrossRef Full Text | Google Scholar

Grewal, D. S., Dasgupta, R., Holmes, A. K., Costin, G., Li, Y., and Tsuno, K. (2019). The fate of nitrogen during core-mantle separation on Earth. Geochim. Cosmochim. Acta 251, 87–115. doi:10.1016/j.gca.2019.02.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Hauck, S. A., Margot, J. L., Solomon, S. C., Phillips, R. J., Johnson, C. L., Lemoine, F. G., et al. (2013). The curious case of Mercury's internal structure. J. Geophys. Res. Planets 118 (6), 1204–1220. doi:10.1002/jgre.20091

CrossRef Full Text | Google Scholar

Hauri, E. H., Saal, A. E., Rutherford, M. J., and Van Orman, J. A. (2015). Water in the Moon’s interior: Truth and consequences. Earth Planet. Sci. Lett. 409, 252–264. doi:10.1016/j.epsl.2014.10.053

CrossRef Full Text | Google Scholar

Hemingway, D. J., and Driscoll, P. E. (2021). History and future of the Martian dynamo and implications of a hypothetical solid inner core. JGR. Planets 126 (4), e2020JE006663. doi:10.1029/2020je006663

CrossRef Full Text | Google Scholar

Hirose, K., Wood, B., and Vocadlo, L. (2021). Light elements in the Earth’s core. Nat. Rev. Earth Environ. 2, 645–658. doi:10.1038/s43017-021-00203-6

CrossRef Full Text | Google Scholar

Hirose, K., Morard, G., Sinmyo, R., Umemoto, K., Hernlund, J., Helffrich, G., et al. (2017). Crystallization of silicon dioxide and compositional evolution of the Earth's core. Nature, 543. doi:10.1038/nature21367

PubMed Abstract | CrossRef Full Text | Google Scholar

Ho, C. Y., Ackerman, M. W., Wu, K. Y., Oh, S. G., and Havill, T. N. (1975). Thermal conductivity of ten selected binary alloy systems. In CINDAS-TPRC report 30. Washington, DC: National Bureau of Standards, U.S. Department of Commerce. Office of Standard Reference Data.

Google Scholar

Ho, C. Y., Ackerman, M. W., Wu, K. Y., Havill, T., Bogaard, R., Matula, R., et al. (1983). Electrical resistivity of ten selected binary alloy systems. J. Phys. Chem. Ref. Data 12, 183–322.

CrossRef Full Text | Google Scholar

Huang, H., Fan, L., Liu, X., Xu, F., Wu, Y., Yang, G., et al. (2022). Inner core composition paradox revealed by sound velocities of Fe and Fe-Si alloy. Nat. Commun. 13, 616. doi:10.1038/s41467-022-28255-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, H., Leng, C., Wang, Q., Yang, G., Hu, X., Wu, Y., et al. (2018). Measurements of sound velocity of liquid Fe-11.8 wt % S up to 211.4 GPa and 6, 150 K. J. Geophys. Res. Solid Earth 123, 4730–4739. doi:10.1029/2017JB015269

CrossRef Full Text | Google Scholar

Ilinykh, S. A., Taluts, S. G., Zinovyev, V. E., and Bautin, S. P. (1984). Izmerenie temperaturoprovodnosti v rezhime subsekundnogo nagreva. Zhelezo vblizi tochki plavleniya [Measurement of thermal diffusivity in the second heating mode, the soup. Iron near the melting point]. High. Temp. (USSR) 22, 709–714.

Google Scholar

Ito, E., Morooka, K., Ujike, O., and Katsura, T. (1995). Reactions between molten iron and silicate melts at high pressure: Implications for the chemical evolution of Earth’s core. J. Geophys. Res. 100, 5901–5910. doi:10.1029/94jb02645

CrossRef Full Text | Google Scholar

Jackson, C. R. M., Bennett, N. R., Du, Z., Cottrell, E., and Fei, Y. (2018). Early episodes of high-pressure core formation preserved in plume mantle. Nature 553, 491–495. doi:10.1038/nature25446

PubMed Abstract | CrossRef Full Text | Google Scholar

Jarosewich, E. (1990). Chemical analyses of meteorites: A compilation of stony and iron meteorite analyses. Meteoritics 25, 323–337. doi:10.1111/j.1945-5100.1990.tb00717.x

CrossRef Full Text | Google Scholar

Jing, Z., Wang, Y., Kono, Y., Yu, T., Sakamaki, T., Park, C., et al. (2014). Sound velocity of Fe–S liquids at high pressure: Implications for the Moon’s molten outer core. Earth Planet. Sci. Lett. 396, 78–87. doi:10.1016/j.epsl.2014.04.015

CrossRef Full Text | Google Scholar

Jolliff, B. L., Wieczorek, M. A., Shearer, C. K., and Neal, C. R. (2006). New views of the Moon, Vol. 60. Chantilly, VA: Mineralogical Society of America.

Google Scholar

Kantor, A. P., Kantor, I. Y., Kurnosov, A. V., Kuznetsov, A. Y., Dubrovinskaia, N. A., Krisch, M., et al. (2007). Sound wave velocities of fcc Fe–Ni alloy at high pressure and temperature by mean of inelastic X-ray scattering. Phys. Earth Planet. Interiors 164, 83–89. doi:10.1016/j.pepi.2007.06.006

CrossRef Full Text | Google Scholar

Kawaguchi, S. I., Nakajima, Y., Hirose, K., Komabayashi, T., Ozawa, H., Tateno, S., et al. (2017). Sound velocity of liquid Fe-Ni-S at high pressure. J. Geophys. Res. Solid Earth 122, 3624–3634. doi:10.1002/2016JB013609

CrossRef Full Text | Google Scholar

Keppler, H., and Golabek, G. (2019). Graphite floatation on a magma ocean and the fate of carbon during core formation. Geochem. Persp. Let. 11, 12–17. doi:10.7185/geochemlet.1918

CrossRef Full Text | Google Scholar

Khan, A., Liebske, C., Rozel, A., Rivoldini, A., Nimmo, F., Connolly, J., et al. (2018). A geophysical perspective on the bulk composition of Mars. J. Geophys. Res. Planets 123 (2), 575–611. doi:10.1002/2017je005371

CrossRef Full Text | Google Scholar

Kim, D.-H., Paek, M.-K., Kim, T.-J., Won, S.-Y., and Pak, J.-J. (2014). Carbon solubility in liquid iron containing V, Mo, and Ni. Mat. Trans. 55, 610–615. doi:10.2320/matertrans.m2013392

CrossRef Full Text | Google Scholar

Kinoshita, D., Nakajima, Y., Kuwayama, Y., Hirose, K., Iwamoto, A., Ishikawa, D., et al. (2020). Sound velocity of liquid Fe–P at high pressure. Phys. Status Solidi B 257, 2000171. doi:10.1002/pssb.202000171

CrossRef Full Text | Google Scholar

Knibbe, J. S., Rivoldini, A., Luginbuhl, S. M., Namur, O., Charlier, B., Mezouar, M., et al. (2021). Mercury's interior structure constrained by density and P-wave velocity measurements of liquid Fe-Si-C alloys. J. Geophys. Res. Planets 126, e2020JE006651. doi:10.1029/2020JE006651

CrossRef Full Text | Google Scholar

Knibbe, J. S., and van Westrenen, W. (2018). The thermal evolution of Mercury's Fe–Si core. Earth Planet. Sci. Lett. 482, 147–159. doi:10.1016/j.epsl.2017.11.006

CrossRef Full Text | Google Scholar

Kono, Y., Kenney-Benson, C., Shibazaki, Y., Park, C., Shen, G., and Wang, Y. (2015). High-pressure viscosity of liquid Fe and FeS revisited by falling sphere viscometry using ultrafast X-ray imaging. Phys. Earth Planet. Interiors 241, 57–64. doi:10.1016/j.pepi.2015.02.006

CrossRef Full Text | Google Scholar

Kuskov, O. L., and Kronrod, V. A. (2009). Geochemical constraints on the model of the composition and thermal conditions of the Moon according to seismic data. Izv. Phys. Solid Earth 45, 753–768. doi:10.1134/S1069351309090043

CrossRef Full Text | Google Scholar

Kuwabara, S., Terasaki, H., Nishida, K., Shimoyama, Y., Takubo, Y., Higo, Y., et al. (2016). Sound velocity and elastic properties of Fe–Ni and Fe–Ni–C liquids at high pressure. Phys. Chem. Miner. 43, 229–236. doi:10.1007/s00269-015-0789-y

CrossRef Full Text | Google Scholar

Kuwayama, Y., Morard, G., Nakajima, Y., Hirose, K., Baron, A. Q. R., Kawaguchi, S. I., et al. (2020). Equation of state of liquid iron under extreme conditions. Phys. Rev. Lett. 124, 165701. doi:10.1103/physrevlett.124.165701

PubMed Abstract | CrossRef Full Text | Google Scholar

Lai, X., Chen, B., Wang, J., Kono, Y., and Zhu, F. (2017). Polyamorphic transformations in Fe-Ni-C liquids: Implications for chemical evolution of terrestrial planets. J. Geophys. Res. Solid Earth 122, 9745–9754. doi:10.1002/2017JB014835

CrossRef Full Text | Google Scholar

Lark, L. H., Parman, S., Huber, C., Parmentier, E. M., and Head, J. W. (2022). Sulfides in Mercury's mantle: Implications for Mercury's interior as interpreted from moment of inertia. Geophys. Res. Lett. 49. doi:10.1029/2021GL096713

CrossRef Full Text | Google Scholar

Li, J., and Agee, C. B. (2001). The effect of pressure, temperature, oxygen fugacity and composition on partitioning of nickel and cobalt between liquid Fe-Ni-S alloy and liquid silicate: Implications for the Earth’s core formation. Geochim. Cosmochim. Acta 65, 1821–1832. doi:10.1016/s0016-7037(00)00613-x

CrossRef Full Text | Google Scholar

Li, J., and Fei, Y. (2014). Experimental constraints on core composition. Treatise geochem. 3, 527–557. doi:10.1016/B978-0-08-095975-7.00214-X

CrossRef Full Text | Google Scholar

Li, Y., Dasgupta, R., Tsuno, K., Monteleone, B., and Shimizu, N. (2016). Carbon and sulfur budget of the silicate Earth explained by accretion of differentiated planetary embryos. Nat. Geosci. 9, 781–785. doi:10.1038/ngeo2801

CrossRef Full Text | Google Scholar

Li, Y., Dasgupta, R., and Tsuno, K. (2015). The effects of sulfur, silicon, water, and oxygen fugacity on carbon solubility and partitioning in Fe-rich alloy and silicate melt systems at 3 GPa and 1600°C: Implications for core-mantle differentiation and degassing of magma oceans and reduced planetary mantles. Earth Planet. Sci. Lett. 415, 54–66. doi:10.1016/j.epsl.2015.01.017

CrossRef Full Text | Google Scholar

Li, Y., Vocadlo, L., Sun, T., and Brodholt, J. P. (2020). The Earth's core as a reservoir of water. Nat. Geosci. 13, 453–458. doi:10.1038/s41561-020-0578-1

CrossRef Full Text | Google Scholar

Lodders, K. (2003). Solar System abundances and condensation temperatures of the elements. Astrophys. J. 591, 1220–1247. doi:10.1086/375492

CrossRef Full Text | Google Scholar

Malavergne, V., Toplis, M., Berthet, S., and Jones, J. (2010). Highly reducing conditions during core formation on Mercury: Implications for internal structure and the origin of a magnetic field. Icarus 206, 199–209. doi:10.1016/j.icarus.2009.09.001

CrossRef Full Text | Google Scholar

Malavergne, V., Bureau, H., Raepsaet, C., Gaillard, F., Poncet, M., Surblé, S., et al. (2019). Experimental constraints on the fate of H and C during planetary core-mantle differentiation. Implications for the Earth. Icarus 321, 473–485. doi:10.1016/j.icarus.2018.11.027

CrossRef Full Text | Google Scholar

Mann, U., Frost, D. J., and Rubie, D. C. (2009). Evidence for high pressure core–mantle differentiation from the metal–silicate partitioning of lithophile and weakly-siderophile elements. Geochim. Cosmochim. Acta 73, 7360–7386. doi:10.1016/j.gca.2009.08.006

CrossRef Full Text | Google Scholar

Manthilake, M. A. G. M., de Koker, N., and Frost, D. J. (2020). Thermal conductivity of CaGeO₃ perovskite at high pressure. Geophys. Res. Lett. 38, L08301. doi:10.1029/2011GL046882

CrossRef Full Text | Google Scholar

Mao, W., Sturhahn, W., Heinz, D., Mao, H., Shu, J., and Hemley, R. (2004). Nuclear resonant X-ray scattering of iron hydride at high pressure. Geophys. Res. Lett. 31, L15618. doi:10.1029/2004gl020541

CrossRef Full Text | Google Scholar

Margot, J.-L., Hauck, S. A., Mazarico, E., Padovan, S., and Peale, S. J. (2018). “Mercury’s internal structure,” in Mercury – the view after MESSENGER. Editors S. C. Solomon, B. J. Anderson, and L. R. Nittler (Cambridge, UK: CUP).

Google Scholar

McCubbin, F. M., Riner, M. A., Vander Kaaden, K. E., and Burkemper, L. K. (2012). Is Mercury a volatile-rich planet? Geophys. Res. Lett. 39, L09202. doi:10.1029/2012gl051711

CrossRef Full Text | Google Scholar

Miletich, R. (2005). Mineral behaviour at extreme conditions. EMU Notes Mineralogy 7, 488. Etvs University Press.

Google Scholar

Miller, N. A., and thesis, M. S. (2009). Melting and phase relations in iron–silicon alloys with applications to the Earth’s core. College Park: University of Maryland.

Google Scholar

Miozzi, F., Morard, G., Antonangeli, D., Baron, M. A., Pakhomova, A., Clark, A. N., et al. (2022). The Fe-Si-C system at extreme P-T conditions: A possible core crystallization pathway for reduced planets. Geochim. Cosmochim. Acta 322, 129–142. doi:10.1016/j.gca.2022.01.013

CrossRef Full Text | Google Scholar

Morard, G., Andrault, D., Antonangeli, D., Nakajima, Y., Auzende, A. L., Boulard, E., et al. (2017). Fe–FeO and Fe–Fe₃C melting relations at Earth's core-mantle boundary conditions: Implications for a volatile-rich or oxygen-rich core. Earth Planet. Sci. Lett. 473, 94–103. doi:10.1016/j.epsl.2017.05.024

CrossRef Full Text | Google Scholar

Morard, G., Garbarino, G., Antonangeli, D., Andrault, D., Guignot, N., Siebert, J., et al. (2014). Density measurements and structural properties of liquid and amorphous metals under high pressure. High. Press. Res. 34, 9–21. doi:10.1080/08957959.2013.860137

CrossRef Full Text | Google Scholar

Morard, G., and Katsura, T. (2010). Pressure–temperature cartography of Fe–S–Si immiscible system. Geochim. Cosmochim. Acta 74, 3659–3667. doi:10.1016/j.gca.2010.03.025

CrossRef Full Text | Google Scholar

Morard, G., Siebert, J., Andrault, D., Guignot, N., Garbarino, G., Guyot, F., et al. (2013). The Earth's core composition from high pressure density measurements of liquid iron alloys. Earth Planet. Sci. Lett. 373, 169–178. doi:10.1016/j.epsl.2013.04.040

CrossRef Full Text | Google Scholar

Nakajima, Y., Imada, S., Hirose, K., Komabayashi, T., Ozawa, H., Tateno, S., et al. (2015). Carbon-depleted outer core revealed by sound velocity measurements of liquid iron-carbon alloy. Nat. Commun. 6, 8942. doi:10.1038/ncomms9942

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakajima, Y., Kawaguchi, S. I., Hirose, K., Tateno, S., Kuwayama, Y., Sinmyo, R., et al. (2020). Silicon-depleted present-day Earth's outer core revealed by sound velocity measurements of liquid Fe-Si alloy. J. Geophys. Res. Solid Earth 125, e2020JB019399. doi:10.1029/2020JB019399

CrossRef Full Text | Google Scholar

Nakanishi, K., Sato, T., and Shiraishi, Y. (1967). On the viscosity of molten iron and its dilute binary alloys of aluminum, silicon, and oxygen. J. Jpn. Inst. Metals Mater. 37, 881–887. doi:10.2320/jinstmet1952.31.7_881

CrossRef Full Text | Google Scholar

Namur, O., Charlier, B., Holtz, F., Cartier, C., and McCammon, C. (2016). Sulfur solubility in reduced mafic silicate melts: Implications for the speciation and distribution of sulfur on mercury. Earth Planet. Sci. Lett. 448, 102–114. doi:10.1016/j.epsl.2016.05.024

CrossRef Full Text | Google Scholar

Nasch, P. M., Manghnani, M. H., and Secco, R. A. (1997). Anomalous behavior of sound velocity and attenuation in liquid Fe–Ni–S. Science 277, 219–221. doi:10.1126/science.277.5323.219

CrossRef Full Text | Google Scholar

Nishi, T., Shibata, H., Waseda, Y., and Ohta, H. (2003). Thermal conductivities of molten iron, cobalt, and nickel by laser flash method. Metall. Mat. Trans. A 34, 2801–2807. doi:10.1007/s11661-003-0181-2

CrossRef Full Text | Google Scholar

Nishida, K., Ohtani, E., Urakawa, S., Suzuki, A., Sakamaki, T., Terasaki, H., et al. (2011). Density measurement of liquid FeS at high pressures using synchrotron X-ray absorption. Am. Mineral. 96, 864–868. doi:10.2138/am.2011.3616

CrossRef Full Text | Google Scholar

Nishida, K., Shibazaki, Y., Terasaki, H., Higo, Y., Suzuki, A., Funamori, N., et al. (2020). Effect of sulfur on sound velocity of liquid iron under Martian core conditions. Nat. Commun. 11:1954 | doi:10.1038/s41467-020-15755-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishida, K., Suzuki, A., Terasaki, H., Shibazaki, Y., Higo, Y., Kuwabara, S., et al. (2016). Towards a consensus on the pressure and composition dependence of sound velocity in the liquid Fe–S system. Phys. Earth Planet. Interiors 257, 230–239. doi:10.1016/j.pepi.2016.06.009

CrossRef Full Text | Google Scholar

Nishida, K., Terasaki, H., Ohtani, E., and Suzuki, A. (2008). The effect of sulfur content on density of the liquid Fe–S at high pressure. Phys. Chem. Min. 35, 417–423. doi:10.1007/s00269-008-0236-4

CrossRef Full Text | Google Scholar

Nittler, L. R., Chabot, N. L., Grove, T. L., and Peplowski, P. N. (2018). “The chemical composition of mercury,” in Mercury – the view after MESSENGER. Editors S. C. Solomon, B. J. Anderson, and L. R. Nittler (Cambridge, UK: CUP).

CrossRef Full Text | Google Scholar

Olson, P., Landeau, M., and Hirsh, B. H. (2017). Laboratory experiments on rain-driven convection: Implications for planetary dynamos. Earth Planet. Sci. Lett. 457, 403–411. doi:10.1016/j.epsl.2016.10.015

CrossRef Full Text | Google Scholar

Ostrovskii, O. I., Ermachenkov, V. A., Popov, V. M., Grigoryan, V. A., and Kogan, L. B. (1980). Thermophysical properties of liquid iron, cobalt, and nickel. Russ. J. Phys. Chem. 54, 739–741.

Google Scholar

Parro, L. M., Jiménez-Díaz, A., Mansilla, F., and Ruiz, J. (2017). Present-day heat flow model of mars. Sci. Rep. 7 (1), 45629–9. doi:10.1038/srep45629

PubMed Abstract | CrossRef Full Text | Google Scholar

Poirier, J. P. (1994). Light elements in the earth's outer core: A critical review. Phys. Earth Planet. Interiors 85 (3–4), 319–337. doi:10.1016/0031-9201(94)90120-1

CrossRef Full Text | Google Scholar

Pommier, A., Davies, C. J., and Zhang, R. (2020a). A joint experimental-modeling investigation of the effect of light elements on dynamos in small planets and moons. J. Geophys. Res. Planets 125, e2020JE006492. doi:10.1029/2020JE006492

CrossRef Full Text | Google Scholar

Pommier, A. (2020). Experimental investigation of the effect of nickel on the electrical resistivity of Fe-Ni and Fe-Ni-S alloys under pressure. Am. Mineral. 105, 1069–1077. doi:10.2138/am-2020-7301

CrossRef Full Text | Google Scholar

Pommier, A., and Leinenweber, K. D. (2018). Electrical cell assembly for reproducible conductivity experiments in the multi-anvil. Am. Mineral. 103 (8), 1298–1305. doi:10.2138/am-2018-6448

CrossRef Full Text | Google Scholar

Pommier, A. K., Leinenweber, T., and Tran, (2019). Mercury's thermal evolution controlled by an insulating liquid outermost core?. Earth Planet. Sci. Lett. 517, 125–134.

CrossRef Full Text | Google Scholar

Pommier, A., Leinenweber, K., Pirotte, H., Yu, T., and Wang, Y. (2020b). In situ electrical resistivity and viscosity measurements of iron alloys under pressure using synchrotron X-ray radiography. High. Press. Res. 41, 1–13. doi:10.1080/08957959.2020.1865343

CrossRef Full Text | Google Scholar

Posner, E. S., and Steinle-Neumann, G. (2019). Mass transport and structural properties of binary liquid iron alloys at high pressure. Geochem. Geophys. Geosyst. 20, 3556–3568. doi:10.1029/2019GC008393

CrossRef Full Text | Google Scholar

Ricolleau, A., Fei, Y., Corgne, A., Siebert, J., and Badro, J. (2011). Oxygen and silicon contents of Earth’s core from high pressure metal–silicate partitioning experiments. Earth Planet. Sci. Lett. 310, 409–421. doi:10.1016/j.epsl.2011.08.004

CrossRef Full Text | Google Scholar

Righter, K. (2002). Does the moon have a metallic core? Constraints from giant impact modeling and siderophile elements. Icarus 158, 1–13. doi:10.1006/icar.2002.6859

CrossRef Full Text | Google Scholar

Righter, K., and Drake, M. J. (1996). core formation in Earth’s moon, mars, and vesta. Icarus 124, 513–529. doi:10.1006/icar.1996.0227

CrossRef Full Text | Google Scholar

Righter, K., Sutton, S. R., Danielson, L., Pando, K., and Newville, M. (2016). Redox variations in the inner Solar System with new constraints from vanadium XANES in spinels. Am. Mineral. 101 (9-10), 1928–1942. doi:10.2138/am-2016-5638

CrossRef Full Text | Google Scholar

Rivoldini, A., Van Hoolst, T., Verhoeven, O., Mocquet, A., and Dehant, V. (2011). Geodesy constraints on the interior structure and composition of Mars. Icarus 213 (2), 451–472. doi:10.1016/j.icarus.2011.03.024

CrossRef Full Text | Google Scholar

Rose-Weston, L., Brenan, J. M., Fei, Y., Secco, R. A., and Frost, D. J. (2009). Effect of pressure, temperature, and oxygen fugacity on the metal-silicate partitioning of Te, Se, and S: Implications for earth differentiation. Geochim. Cosmochim. Acta 73, 4598–4615. doi:10.1016/j.gca.2009.04.028

CrossRef Full Text | Google Scholar

Rutter, M. D., Secco, R. A., Uchida, T., Hongjian, L., Wang, Y., Rivers, M. L., et al. (2002). Towards evaluating the viscosity of the Earth’s outer core: An experimental high pressure study of liquid Fe-S (8.5 wt.% S). Geophys. Res. Lett. 29 (8), 58-1–58-4. doi:10.1029/2001GL014392

CrossRef Full Text | Google Scholar

Sakairi, T., Ohtani, E., Kamada, S., Sakai, T., Sakamaki, T., and Hirao, N. (2017). Melting relations in the Fe–S–Si system at high pressure and temperature: Implications for the planetary core. Prog. Earth Planet. Sci. 4 (10). doi:10.1186/s40645-017-0125-x

CrossRef Full Text | Google Scholar

Sakamaki, T., Ohtani, E., Fukui, H., Kamada, S., Takahashi, S., Sakairi, 1 T., et al. (2016). Constraints on Earth’s inner core composition inferred from measurements of the sound velocity of hcp-iron in extreme conditions. Sci. Adv. 2, e1500802. doi:10.1126/sciadv.1500802

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanloup, C., and Fei, Y. (2004). Closure of the Fe-S-Si liquid miscibility gap at high pressure. Phys. Earth Planet. Interiors 147, 57–65. doi:10.1016/j.pepi.2004.06.008

CrossRef Full Text | Google Scholar

Sanloup, C., Fiquet, G., Gregoryanz, E., Morard, G., and Mezouar, M. (2004). Effect of Si on liquid Fe compressibility: Implications for sound velocity in core materials. Geophys. Res. Lett. 31, L07604. doi:10.1029/2004GL019526

CrossRef Full Text | Google Scholar

Sanloup, C., Guyot, F., Gillet, P., Fiquet, G., Hemley, R. J., Mezouar, M., et al. (2000). Structural changes in liquid Fe at high pressures and high temperatures from Synchrotron X-ray Diffraction. Europhys. Lett. 52 (2), 151–157. doi:10.1209/epl/i2000-00417-3

CrossRef Full Text | Google Scholar

Sanloup, C., Guyot, F., Gillet, P., Fiquet, G., Mezouar, M., and Martinez, I. (2000). Density measurements of liquid Fe–S alloys at high-pressure. Geophys. Res. Lett. 27, 811–814. doi:10.1029/1999GL008431

CrossRef Full Text | Google Scholar

Sanloup, C., van Westrenen, W., Dasgupta, R., Maynard-Casely, H., and Perrillat, J.-P. (2011). Compressibility change in iron-rich melt and implications for core formation models. Earth Planet. Sci. Lett. 306 (1–2), 118–122. doi:10.1016/j.epsl.2011.03.039

CrossRef Full Text | Google Scholar

Schwaiger, T., Gastine, T., and Aubert, J. (2021). Relating force balances and flow length scales in geodynamo simulations. Geophys. J. Int. 224 (3), 1890–1904. doi:10.1093/gji/ggaa545

CrossRef Full Text | Google Scholar

Seagle, C. T., Heinz, D. L., Campbell, A. J., Prakapenka, V. B., and Wanless, S. T. (2008). Melting and thermal expansion in the Fe–FeO system at high pressure. Earth Planet. Sci. Lett. 265, 655–665. doi:10.1016/j.epsl.2007.11.004

CrossRef Full Text | Google Scholar

Secco, R., Rutter, M., Balog, S., Liu, H., Rubie, D., Uchida, T., et al. (2002). Viscosity and density of Fe–S liquids at high pressures. J. Phys. Condens. Matter 14 (44), 11325–11330. doi:10.1088/0953-8984/14/44/476

CrossRef Full Text | Google Scholar

Shen, G., Prakapenka, V., Rivers, M. L., and Sutton, S. R. (2004). Structure of liquid iron at pressures up to 58 GPa. Phys. Rev. Lett. 92 (18), 185701. doi:10.1103/PhysRevLett.92.185701

PubMed Abstract | CrossRef Full Text | Google Scholar

Sherman, W. F., and Stadtmuller, A. A. (1987). Experimental techniques in high-pressure research. John Wiley & Sons, 471. 6.

Google Scholar

Shibazaki, Y., and Kono, Y. (2018). Effect of silicon, carbon, and sulfur on structure of liquid iron and implications for structure-property relations in liquid iron light element alloys. J. Geophys. Res. Solid Earth 123, 4697–4706. doi:10.1029/2018JB015456

CrossRef Full Text | Google Scholar

Shibazaki, Y., Kono, Y., and Fei, Y. (2015). Microscopic structural change in a liquid Fe-C alloy of ∼5 GPa. Geophys. Res. Lett. 42, 5236–5242. doi:10.1002/2015GL064271

CrossRef Full Text | Google Scholar

Shibazaki, Y., Ohtani, E., Fukui, H., Sakai, T., Kamada, S., Ishikawa, D., et al. (2012). Sound velocity measurements in dhcp-FeH up to 70 GPa with inelastic X-ray scattering: Implications for the composition of the Earth’s core. Earth Planet. Sci. Lett. 313314, 79–85. doi:10.1016/j.epsl.2011.11.002–

CrossRef Full Text | Google Scholar

Shimoyama, Y., Terasaki, H., Ohtani, E., Urakawa, S., Takubo, Y., Nishida, K., et al. (2013). Density of Fe-3.5 wt% C liquid at high pressure and temperature and the effect of carbon on the density of the molten iron. Phys. Earth Planet. Interiors 224, 77–82. doi:10.1016/j.pepi.2013.08.003

CrossRef Full Text | Google Scholar

Shimoyama, Y., Terasaki, H., Urakawa, S., Takubo, Y., Kuwabara, S., Kishimoto, S., et al. (2016). Thermoelastic properties of liquid Fe-C revealed by sound velocity and density measurements at high pressure. J. Geophys. Res. Solid Earth 121 (11), 7984–7995. doi:10.1002/2016JB012968

CrossRef Full Text | Google Scholar

Siebert, J., Corgne, A., and Ryerson, F. J. (2011). Systematics of metal-silicate partitioning for many siderophile elements applied to Earth's core formation. Geochim. Cosmochim. Acta 75, 1451–1489.

CrossRef Full Text | Google Scholar

Solomatov, V. S. (2000). “Fluid dynamics of a terrestrial magma ocean,” in Origin of the Earth and moon. Editors R. Canup, and K. Righter (Tucson, Arizona: Univ. of Arizona Press), 323–338.

CrossRef Full Text | Google Scholar

Stähler, S. C., Khan, A., Banerdt, W. B., Lognonné, P., Giardini, D., Ceylan, S., et al. (2021). Seismic detection of the Martian core. Science 373 (6553), 443–448. doi:10.1126/science.abi7730

PubMed Abstract | CrossRef Full Text | Google Scholar

Steenstra, E. S., Berndt, J., Klemme, S., Fei, Y., and van Westernen, W. (2020a). A possible high-temperature origin of the Moon and its geochemical consequences. Earth Planet. Sci. Lett. 538, 116222. doi:10.1016/j.epsl.2020.116222

CrossRef Full Text | Google Scholar

Steenstra, E. S., Seegers, A. X., Putter, R., Berndt, J., Klemme, S., Matveev, S., et al. (2020b). Metal-silicate partitioning systematics of siderophile elements at reducing conditions: A new experimental database. Icarus 335, 113391. doi:10.1016/j.icarus.2019.113391

CrossRef Full Text | Google Scholar

Stewart, A. J., Schmidt, M. W., van Westrenen, W., and Liebske, C. (2007). Mars: A new core-crystallization regime. Science 316, 1323–1325. doi:10.1126/science.1140549

PubMed Abstract | CrossRef Full Text | Google Scholar

Sugie, K., Kobotake, H., Fukuyama, H., Baba, Y., Sugioka, K.-i., and Tsukada, T. (2010). Development of thermophysical property measurement for liquid Fe using noncontact laser modulation calorimetry. Tetsu-to-Hagané 96 (12), 673–682. doi:10.2355/tetsutohagane.96.673

CrossRef Full Text | Google Scholar

Tagawa, S., Sakamoto, N., Hirose, K., Yokoo, S., Hernlund, J., Ohishi, Y., et al. (2021). Experimental evidence for hydrogen incorporation into Earth's core. Nat. Commun. 12, 2588. doi:10.1038/s41467-021-22035-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Tao, R., and Fei, Y. (2021). High-pressure experimental constraints of partitioning behavior of Si and S at the Mercury’s inner core boundary. Earth Planet. Sci. Lett. 562, 116849. doi:10.1016/j.epsl.2021.116849

CrossRef Full Text | Google Scholar

Tateno, S., Hirose, K., Sinmyo, R., Morard, G., Hirao, N., and Ohishi, Y. (2018). Melting experiments on Fe-Si-S alloys to core pressures: Silicon in the core? Am. Mineral. 103, 742–748. doi:10.2138/am-2018-6299

CrossRef Full Text | Google Scholar

Tateyama, R., Ohtani, E., Terasaki, H., Nishida, K., Shibazaki, Y., Suzuki, A., et al. (2011). Density measurements of liquid Fe-Si alloys at high pressure using the sink-float method. Phys. Chem. Miner. 38 (10), 801–807. doi:10.1007/s00269-011-0452-1

CrossRef Full Text | Google Scholar

Terasaki, H., Kato, T., Urakawa, S., Funakoshi, K.-i., Suzuki, A., Okada, T., et al. (2001). The effect of temperature, pressure, and sulfur content on viscosity of the Fe-FeS melt. Earth Planet. Sci. Lett. 190, 93–101. doi:10.1016/s0012-821x(01)00374-0

CrossRef Full Text | Google Scholar

Terasaki, H., Kato, T., Urakawa, S., Funakoshi, K., Sato, K., Suzuki, A., et al. (2002). Viscosity change and structural transition of Molten Fe at 5 GPa. Geophys. Res. Lett. 29 (8), 68-1–68-3. doi:10.1029/2001GL014321

CrossRef Full Text | Google Scholar

Terasaki, H., Nishida, K., Shibazaki, Y., Sakamaki, T., Suzuki, A., Ohtani, E., et al. (2010). Density measurements of Fe₃C liquid using X-ray absorption image up to 10 GPa and effect of light elements on compressibility of liquid iron. J. Geophys. Res. 115 (B6), B06207. doi:10.1029/2009jb006905

CrossRef Full Text | Google Scholar

Terasaki, H., Rivoldini, A., Shimoyama, Y., Nishida, K., Urakawa, S., Maki, M., et al. (2019). Pressure and composition effects on sound velocity and density of core-forming liquids: Implication to core compositions of terrestrial planets. J. Geophys. Res. Planets 124, 2272–2293. doi:10.1029/2019JE005936

CrossRef Full Text | Google Scholar

Terasaki, H., Suzuki, A., Ohtani, E., Nishida, K., Sakamaki, T., and Funakoshi, K. (2006). Effect of pressure on the viscosity of Fe-S and Fe-C liquids up to 16 GPa. Geophys. Res. Lett. 33, L22307. doi:10.1029/2006GL027147

CrossRef Full Text | Google Scholar

Touloukian, Y. S., Powell, R. W., Ho, C. Y., and Klemens, P. G. (1970). “Thermophysical properties of matter,” in Thermal conductivity, metallic elements and alloys. Editors Y. S. Touloukian, and C. Y. Ho (New York: IFI/Plenum), 1.

Google Scholar

Tsuno, K., Grewal, D. S., and Dasgupta, R. (2018). Core-mantle fractionation of carbon in Earth and Mars: The effects of sulfur. Geochim. Cosmochim. Acta 238, 477–495. doi:10.1016/j.gca.2018.07.010

CrossRef Full Text | Google Scholar

Urakawa, S., Kamuro, R., Suzuki, A., and Kikegawa, T. (2018). Phase relationships of the system Fe-Ni-S and structure of the high-pressure phase of (Fe_1−xNi_x)₃S₂. Phys. Earth Planet. Interiors 277, 30–37. doi:10.1016/j.pepi.2018.01.007

CrossRef Full Text | Google Scholar

Urakawa, S., Terasaki, H., Funakoshi, K., Kato, T., and Suzuki, A. (2001). Radiographic study on the viscosity of the Fe-FeS melts at the pressure of 5 to 7 GPa. Am. Mineral. 86 (4), 578–582. doi:10.2138/am-2001-0420

CrossRef Full Text | Google Scholar

Vander Kaaden, K. E., McCubbin, F. M., Turner, A. A., and Ross, D. K. (2020). Constraints on the abundances of carbon and silicon in Mercury's core from experiments in the Fe-Si-C system. JGR. Planets 125, e2019JE006239. doi:10.1029/2019JE006239

CrossRef Full Text | Google Scholar

Vatolin, N. V., Vostryakov, A. A., and Yesin, O. A. (1962). Viscosity of molten ferrocarbon alloys. Phys. Met. Metallogr. 15 (2), 53–58.

Google Scholar

Verhoeven, O., Rivoldini, A., Vacher, P., Mocquet, A., Choblet, G., Menvielle, M., et al. (2005). Interior structure of terrestrial planets: Modeling Mars’ mantle and its electromagnetic, geodetic, and seismic properties. J. Geophys. Res. 110, E04009. doi:10.1029/2004JE002271

CrossRef Full Text | Google Scholar

Vogel, A. K., Jennings, E. S., Laurenz, V., Rubie, D. C., and Frost, D. J. (2018). The dependence of metal-silicate partitioning of moderately volatile elements on oxygen fugacity and Si contents of Fe metal: Implications for their valence states in silicate liquids. Geochim. Cosmochim. Acta 237, 275–293. doi:10.1016/j.gca.2018.06.022

CrossRef Full Text | Google Scholar

Vostryakov, A. A., Vatolin, N. A., and Yasin, O. A. (1964). Viscosity and electrical resistivity of molten alloys of iron with phosphorous and sulphur. Fiz. Metal. Metalloved. 18, 476–477.

Google Scholar

Wade, J., and Wood, B. J. (2005). Core formation and the oxidation state of the Earth. Earth Planet. Sci. Lett. 236, 78–95. doi:10.1016/j.epsl.2005.05.017

CrossRef Full Text | Google Scholar

Wagle, F., Steinle-Neumann, G., and de Koker, N. (2019). Resistivity saturation in liquid iron–light-element alloys at conditions of planetary cores from first principles computations. Comptes Rendus Geosci. 351 (2–3), 154–162. doi:10.1016/j.crte.2018.05.002

CrossRef Full Text | Google Scholar

Waldner, P., and Pelton, A. D. (2005). Thermodynamic modeling of the Fe-S system. J. Phase Equilibria Diffus. 26, 23–38. doi:10.1361/15477030522455

CrossRef Full Text | Google Scholar

Wasson, J. T., and Kallemeyn, G. W. (1988). Compositions of chondrites. Philos. Trans. Roy. Soc. Lond. A Math. Phys. Eng. Sci. 325, 535–544. doi:10.1098/rsta.1988.0066

CrossRef Full Text | Google Scholar

Watanabe, M., Adachi, M., Uchikoshi, M., and Fukuyama, H. (2019). Thermal conductivities of Fe-Ni melts measured by non-contact laser modulation calorimetry. Metall. Mat. Trans. A 50 (7), 3295–3300. doi:10.1007/s11661-019-05250-9

CrossRef Full Text | Google Scholar

Weber, R. C., Lin, P.-Y., Garnero, E. J., Williams, Q., and Lognonné, P. (2011). Seismic detection of the lunar core. Science 331 (6015), 309–312. doi:10.1126/science.1199375

PubMed Abstract | CrossRef Full Text | Google Scholar

Weidenschilling, S. J. (1978). Iron/silicate fractionation and the origin of mercury. Icarus 35, 99–111. doi:10.1016/0019-1035(78)90064-7

CrossRef Full Text | Google Scholar

Wieczorek, M. A. (2006). The constitution and structure of the lunar interior. Rev. Mineral. Geochem. 60, 221–364. doi:10.2138/rmg.2006.60.3

CrossRef Full Text | Google Scholar

Williams, Q., Jeanloz, R., Bass, J., Svendsen, B., and Ahrens, T. J. (1987). The melting curve of iron to 250 gigapascals: A constraint on the temperature at earth's center. Science 236 (4798), 181–182. doi:10.1126/science.236.4798.181

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, Q. (2018). The thermal conductivity of Earth’s core: A key geophysical parameter’s constraints and uncertainties. Annu. Rev. Earth Planet. Sci. 46, 47–66. doi:10.1146/annurev-earth-082517-010154

CrossRef Full Text | Google Scholar

Wood, B. J., Smythe, D. J., and Harrison, T. (2019). The condensation temperatures of the elements: A reappraisal. Am. Mineral. 104, 844–856. doi:10.2138/am-2019-6852ccby

CrossRef Full Text | Google Scholar

Wood, B. J., Walter, M. J., and Wade, J. (2006). Accretion of the Earth and segregation of its core. Nature 441, 825–833. doi:10.1038/nature04763

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, F., Morard, G., Guignot, N., Rivoldini, A., Manthilake, G., Chantel, J., et al. (2021). Thermal expansion of liquid Fe-S alloy at high pressure. Earth Planet. Sci. Lett. 563, 116884. doi:10.1016/j.epsl.2021.116884

CrossRef Full Text | Google Scholar

Yin, Y., Zhai, K., Zhang, B., and Zhai, S. (2019). Electrical resistivity of iron phosphides at high-pressure and high-temperature conditions with implications for lunar core's thermal conductivity. J. Geophys. Res. Solid Earth 124, 5544–5556. doi:10.1029/2018JB017157

CrossRef Full Text | Google Scholar

Yoder, C. F., Konopliv, A. S., Yuan, D. N., Standish, E. M., and Folkner, W. M. (2003). Fluid core size of mars from detection of the solar tide. Science 300, 299–303. doi:10.1126/science.1079645

PubMed Abstract | CrossRef Full Text | Google Scholar

Yokoo, S., Hirose, K., Tagawa, S., Morard, G., and Ohishi, Y. (2022). Stratification in planetary cores by liquid immiscibility in Fe-S-H. Nat. Commun. 13, 644. doi:10.1038/s41467-022-28274-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoshizaki, T., and McDonough, W. F. (2020). The composition of Mars. Geochim. Cosmochim. Acta 273, 137–162. doi:10.1016/j.gca.2020.01.011

CrossRef Full Text | Google Scholar

Zhu, F., Lai, X., Wang, J., Amulele, G., Kono, Y., Shen, G., et al. (2021). Density of Fe-Ni-C liquids at high pressures and implications for liquid cores of Earth and the Moon. J. Geophys. Res. Solid Earth 126, e2020JB021089. doi:10.1029/2020JB021089

CrossRef Full Text | Google Scholar

Zhu, F., Lai, X., Wang, J., Williams, Q., Liu, J., Kono, Y., et al. (2022). Viscosity of Fe-Ni-C liquids up to core pressures and implications for dynamics of planetary cores. Geophys. Res. Lett. 49, e2021GL095991. https://doi. org/10.1029/2021GL095991.

CrossRef Full Text | Google Scholar

Zinovyev, V. Y., Polev, V. F., Taluts, S. G., Zinovyeva, G. P., and Ilinykh, S. A. (1986). Diffusivity and thermal conductivity of 3d-transition metals in solid and liquid states. Phys. Metall. Metallogr. 61, 85–92.

Google Scholar

Zolotov, M. Y., Sprague, A. L., Hauck, S. A., Nittler, L. R., Solomon, S. C., and Weider, S. Z. (2013). The redox state, FeO content, and origin of sulfur-rich magmas on Mercury. J. Geophys. Res. Planets 118, 138–146. doi:10.1029/2012je004274

CrossRef Full Text | Google Scholar