Thermo-Hydro-Mechanical Coupling Model of Unsaturated Soil Based on Modified VG Model and Numerical Analysis

A modified VG model considering both pore ratio and temperature effect is constructed. Based on the wet-thermal elasticity theory and mixture theory, coupled thermo-hydro-mechanical (THM) equations for moisture migration, heat transfer, and deformation in unsaturated soil are derived. The numerical implementation of the coupled theory was implemented by secondary development in the finite element platform. The validity of the established theoretical equation was verified by comparing it with the experimental data. Then the THM coupling response characteristics and internal mechanism of axisymmetric soil samples were numerically analyzed. Study shows that the water in unsaturated soil migrates from high-temperature zone to low-temperature zone under temperature load, and the permeability will change during the process of moisture absorption and dehydration. Particular attention should pay to the reasonable determination of the parameters in the modified VG model for the warming and cooling process of different measurement points during the numerical calculation. The higher the heat source temperature, the greater the saturation at the specific measurement point of the soil sample at thermal stability. The lower the heat source temperature, the shorter the time required for the saturation to stabilize at the specific measuring point. The volumetric strain of unsaturated soil results from a combination of wet expansion and thermal expansion, which is dominated by wet expansion near the heat source and mainly by thermal expansion far from the heat source. The change of the total displacement with time is dominated by the z-direction displacement, and its change trend along the radial direction is similar to that in the r-direction. The peak of the total displacement curve keeps moving backward with time.

Introduction

The THM multiphysics coupling process in unsaturated soil plays a significant role in engineering geology or environmental engineering (Hu et al., 2021). It has crucial applications in many areas, such as deep underground resource mining, geothermal resource development, nuclear waste disposal, and so on (Fu et al., 2020; Bai et al., 2021a; Bai et al., 2021b; Zhou et al., 2022). The theoretical model and numerical solution techniques for the THM coupling describing the characteristics of seepage, heat transfer, and mechanical behavior of unsaturated soils have become an important research content.

The research history of the THM coupling problem of unsaturated soil is relatively tortuous. The physical field develops from two fields to multiple fields, the influencing factors are considered from single to multiple, and the theoretical model is established from simple to complex. Booker (Booker and Savvidou, 1984) and Savvidou (Savvidou and Booker, 2010) theoretically solved the THM coupling problem using the mathematical transformation, and provided an analytical solution under the effect of point and cylindrical heat sources. Ghorbani et al. (2016) developed a theoretical model to completely describe the hydro-mechanical coupling phenomenon in non-saturation soil under static or dynamic loads, and verified the correctness of the established model through case analysis. Chen et al. (2009) established a theoretical model of the THM coupling problem in the three-phase system, and then the numerical analysis was performed based on the developed 3-D computer code THYME3D. Li et al. (2016) developed a mathematical model describing the THM coupling process by considering the three transport behaviors of convection, molecular diffusion, and mechanical escape of pollutants in unsaturated soil, and applied it to the simulation of an engineering clay barrier system. Akrouch et al. (2016) studied the heat exchange efficiency and hydrothermal coupling response characteristics of the heat source columns, and gave a calculation formula to quickly evaluate the heat exchange efficiency of heat source columns under different saturation levels. Recently, based on the theory of particle thermo-dynamics, Bai et al. (2021c) developed a new multi-field coupling theory considering the rearrangement of soil particles in the deformation process describing the microscopic changes of unsaturated soil particles under different loads. The soil-water characteristic curve (SWCC) is an effective mean of describing the hydraulic characteristics of unsaturated soil. It has been widely accepted in the theoretical derivation of the THM coupling problem by the numerous above scholars. However, the SWCC is difficult to obtain accurately due to multiple factors, resulting in incomplete numerical calculation and theoretical analysis.

Tarantinod (Tarantino, 2015) investigated the water-retention behavior of unsaturated soil across a wide scope of void ratios and then confirmed how void ratios affect the SWCC of unsaturated soil. Ghavam-Nasiri et al. (2019), Gallipoli et al. (2003), and Azizi et al. (2017) also analyzed the influence of void ratio on SWCC in different ways. The study reveals that the hydraulic properties can be more effectively described through establishing an SWCC that considers the pore ratio effect. In addition, temperature, as the main factor affecting the SWCC, has also been proved by many experiments. For example, Liu et al. (2002) conducted experimental research using an improved negative pressure soil tensiometer, indicating that temperature impacts the water potential of unsaturated soil. Cao et al. (2021) tested the SWCC of unsaturated soil under different heat loads and densities conditions using a filter paper-based method, and obtained the changing profile of SWCC. Romero et al. (2001), Jacinto et al. (2009), and Villar and Lloret, (2004) carried out numerical experiments to study the effect of temperature on the moisture redistribution in seepage processes, and modified the classical SWCC considering the temperature effect to improve calculation accuracy. It is clear that the void ratio and temperature have a significant impact on the SWCC. However, it is rare to introduce the above two main factors simultaneously when modifying and optimizing the unsaturated SWCC.

Based on the classical VG model, this paper develops a modified VG model that takes the pore ratio and temperature effect into account. The THM coupling equation of unsaturated soil, which describes the moisture migration, heat transfer, and mechanical response in unsaturated soil, is derived based on the wet-thermal elasticity theory. The second developed COMSOL numerical platform was used to calculate the indoor tests to verify the constructed theoretical model. Then the coupled THM response characteristics of unsaturated soil was analyzed.

Modified VG Model

van Genuchten, (1980) proposed a smooth and closed three-parameter mathematical model in 1980 to fit the SWCC. The expression is as follows:

$S_{ew}=\frac{S_w-S_r}{S_s-S_r}={\left[\frac{1}{1+{\left(\alpha H_{\text{c}}\right)}^n}\right]}^m(1)$

$m=1-\frac{1}{n}(2)$

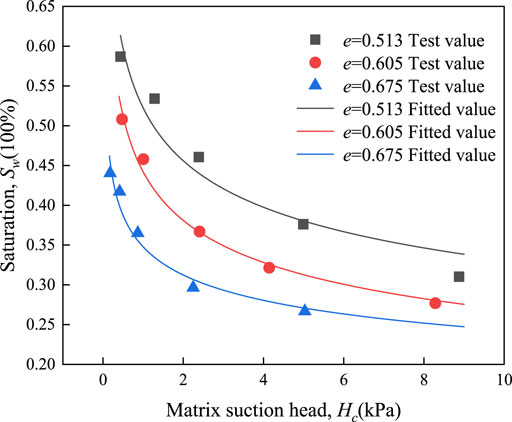
where α, n, and m are fitting parameters; S_ew is the effective saturation; S_r is the residual saturation; S_w is the pore water saturation; S_s is the maximum saturation; H_c is matrix suction head; According to the work of Zhang et al. (2020), the SWCC fitting test of unsaturated soil was carried out based on Eq. 1. It can be observed from Figure 1 that the void ratio significantly affects the SWCC of unsaturated soil, and the increase in the void ratio causes the SWCC to shift. In addition, the SWCC curves for different pore ratios were plotted by fitting calculations using the experimental data (as shown in Figure 2).

FIGURE 1

FIGURE 1. Fitted SWCC with different void ratios.

FIGURE 2

FIGURE 2. SWCC with different void ratio.

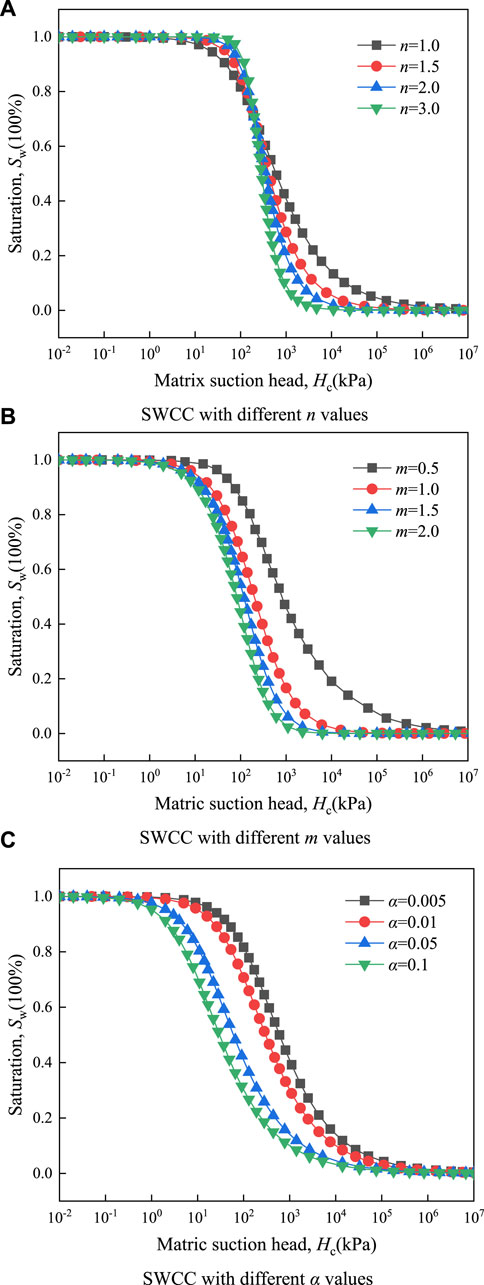
The effects of the three parameters α, n, and m on the shape variation of the VG model are given in Figure 3. According to Figure 3A, it can be seen the change of n causes SWCC to rotate around the turning point, and the change of m mainly affects the change of SWCC in the high suction region from Figure 3B. Comparing Figure 3C with Figure 2, it can be seen that there is a high similarity in the morphological changes of SWCC caused by the change of parameter α and pore ratio. In addition, according to the test of Tarantino, (2015), the relationship between void ratio and matrix suction approximately is a power function. Therefore, the correction considering the pore ratio effect on the classical VG model can start from the parameter α to introduce a correction term in the form of a power function. As opposed to establishing a connection between the parameters m and n (as shown in Eq. 2), the SWCC fitted by treating the parameters as independent variables agrees well with test data (Lu and Likos, 2004). The modified VG model considering the effect of void ratio is as follows:

$S_{ew}={\left[\frac{1}{1+{\left({\alpha }_m{e}^b{H}_{\text{c}}\right)}^{n_m}}\right]}^{m_m}(3)$

where e is void ratio; α_m, n_m, and m_m are the fitting parameters of the modified VG model; b is the new proposed fitting parameter.

FIGURE 3

FIGURE 3. SWCC of unsaturated soil with different parameter values.

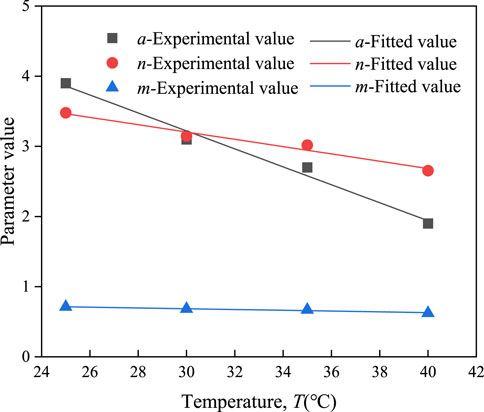
In numerical analysis, the influence of temperature on the VG model is generally reflected by fitting parameters α, n, and m (Romero et al., 2001; Jacinto et al., 2009). Qiao et al. (2019) tested the VG fitting parameters of unsaturated soil at different temperatures based on experiments. The fitting calculations indicated that fitting parameters decrease linearly with the temperature increas (as illustrated in Figure 4). Therefore, it is assumed that the modified VG model parameters α_m, n_m, and m_m are linearly related to temperature:

$\begin{array}{l}{\alpha }_m={\alpha }_0+{\lambda }_{\alpha }\left(T-T_0\right)\\ n_m=n_0+{\lambda }_n\left(T-T_0\right)\\ m_m=m_0+{\lambda }_m\left(T-T_0\right)\end{array}\}(4)$

FIGURE 4

FIGURE 4. Changes in VG model parameters of unsaturated soil at different temperatures.

where T is temperature; α₀, n₀, and m₀ are fitting parameters at the reference temperature T₀; λ_α, λ_n, and λ_m are the fitting parameters of the modified VG model. Then the modified VG model considering the effects of temperature and void ratio can be obtained from Eqs 3, 4 as follows:

$S_{ew}={\{\frac{1}{1+{\left[\left({\alpha }_0+{\lambda }_{\alpha }T-{\lambda }_{\alpha }{T}_0\right)e^b{H}_{\text{c}}\right]}^{n_0+{\lambda }_n\left(T-T_0\right)}}\}}^{m_0+{\lambda }_m\left(T-T_0\right)}(5)$

$H_c=\frac{P_c}{{\rho }_{w}g}(6)$

where P_c (P_c = P_g-P_w) is matrix suction; P_w and P_g are pore water and pore gas pressure, respectively; ρ_w is pore water density; g is the acceleration of gravity.

THM Coupling Model

Seepage Differential Equation

Unsaturated soil is a three-phase multi-component porous material made up of pore water, pore gas, and solid particles. According to the mixture theory (Malakpoor et al., 2007), The mass conservation law of each phase is as follows:

$\frac{\partial }{\partial t}\left({\varphi }_i{\rho }_i\right)+\nabla \cdot \left({\varphi }_i{\rho }_i{\mathit{v}}_i\right)=0(7)$

where ϕ_i, ρ_i, and v_i represent the volume fraction, density, and velocity of each component; The subscript i can be replaced by w, g, and s, representing pore water, pore gas, and solid particles, respectively. The volume fraction of each component is as follows:

$\begin{array}{l}{\varphi }_w=n{S}_w\\ {\varphi }_g=n{S}_g\\ {\varphi }_s=1-n\end{array}\}(8)$

where n is porosity; S_g is the saturation of pore gas, and S_g = 1-S_w. When pore water is incompressible and the gravity effect is considered, the velocity v of each phase in unsaturated soil has the following relationship (Rutqvist et al., 2001; Bai et al., 2020a):

${\varphi }_w\cdot \left({\mathit{v}}_w-{\mathit{v}}_s\right)=-\frac{K{K}_{rw}}{{\mu }_w}\cdot \left(\nabla P_w+{\rho }_{w}g\cdot \nabla z\right)={\mathit{u}}_w(9)$

${\varphi }_g\cdot \left({\mathit{v}}_g-{\mathit{v}}_s\right)=-\frac{K{K}_{rg}}{{\mu }_g}\cdot \left(\nabla P_g+{\rho }_{g}g\cdot \nabla z\right)={\mathit{u}}_g(10)$

where K is permeability; K_rw and K_rg are the relative permeability of pore water and pore gas, respectively; μ_w and μ_g are the viscosity coefficients of pore water and pore gas, respectively; u_w and u_g are the average relative velocity of pore water and pore gas in the cross section of porous media, respectively. In addition, there are the following relationships (Qin, 2010):

$\nabla {\mathit{v}}_s=\frac{D{\epsilon }_v}{Dt}\approx \frac{\partial {\epsilon }_v}{\partial t}(11)$

where ε_v is volumetric strain. After the formula (11) is introduced into the mass conservation equation of solid particles, it can be calculated (Guo, 2018):

$\frac{\partial n}{\partial t}=\frac{1-n}{{\rho }_{\text{s}}}\frac{\partial {\rho }_{\text{s}}}{\partial t}+\left(1-n\right)\frac{\partial {\epsilon }_v}{\partial t}(12)$

Based on Eqs 8–12, the seepage differential equation of pore water for unsaturated soil can be obtained as follows:

$\begin{array}{l}n{\rho }_w(C_P\frac{\partial P_w}{\partial t}-C_P\frac{\partial P_g}{\partial t}-C_T\frac{\partial T}{\partial t})={\rho }_w{S}_w\left(\frac{\partial {\epsilon }_v}{\partial t}+\frac{n}{{\rho }_w}\frac{\partial {\rho }_w}{\partial t}+\frac{1-n}{{\rho }_s}\frac{\partial {\rho }_s}{\partial t}\right)\\ -\nabla \cdot \left[{\rho }_w\frac{K{K}_{rw}}{{\mu }_w}\cdot \left(\nabla P_w+{\rho }_{w}g\cdot \nabla z\right)\right]\end{array}(13)$

The seepage differential equation of pore gas is:

$\begin{array}{l}n{\rho }_g(C_P\frac{\partial P_g}{\partial t}-C_P\frac{\partial P_w}{\partial t}+C_T\frac{\partial T}{\partial t})={\rho }_g{S}_g\left(\frac{\partial {\epsilon }_v}{\partial t}+\frac{n}{{\rho }_g}\frac{\partial {\rho }_g}{\partial t}+\frac{1-n}{{\rho }_s}\frac{\partial {\rho }_s}{\partial t}\right)\\ -\nabla \cdot \left[{\rho }_g\frac{K{K}_{rg}}{{\mu }_g}\cdot \left(\nabla P_g+{\rho }_{g}g\cdot \nabla z\right)\right]\end{array}(14)$

where C_p and C_T are water-holding coefficients under capillary action and temperature action, respectively, which are two critical parameters of the seepage differential equation. They reflect the two driving effects in the seepage process and are determined by the SWCC (Guo and Bai, 2018). The following expressions can be obtained based on the modified VG model:

$C_P=\frac{\partial S_w}{\partial P_c}=\frac{-{\alpha }_m{m}_m{n}_m{e}^b}{{\rho }_{w}g}{S}_{ew}^{\frac{m_m+1}{m_m}}{\left(S_{ew}^{-\frac{1}{m_m}}-1\right)}^{\frac{n_m-1}{n_m}}\left(S_s-S_r\right)(15)$

$\begin{array}{l}{C}_T=\frac{\partial S_w}{\partial T}=\{S_{ew}{\lambda }_m\ln \left(S_{ew}^{-\frac{1}{m_m}}\right)+\frac{m_m{n}_m{\lambda }_{\alpha }}{{\alpha }_m}{S}_{ew}^{\frac{m_m+1}{m_m}}\left(S_{ew}^{-\frac{1}{m_m}}-1\right)\\ -S_{ew}^{\frac{m_m+1}{m_m}}\left[\frac{m_m{\lambda }_n}{n_m}\left(S_{ew}^{-\frac{1}{m_m}}-1\right)\ln \left(S_{ew}^{-\frac{1}{m_m}}-1\right)\right]\}\left(S_s-S_r\right)\end{array}(16)$

Heat Transfer Differential Equation

When ignoring the influence of soil particle displacement on heat transfer, the energy conservation equation can write as (Rutqvist et al., 2001; Bai et al., 2017; Bai et al., 2022):

$\begin{array}{l}\nabla \cdot \left[h_{w}n{S}_w{\rho }_w\cdot {\mathit{v}}_w+h_{g}n{S}_g{\rho }_g\cdot {\mathit{v}}_g+h_s(1-n){\rho }_s\cdot {\mathit{v}}_s\right]+\left(n{S}_w{P}_w\nabla \cdot {\mathit{v}}_w+n{S}_g{P}_g\nabla \cdot {\mathit{v}}_g\right)\\ +\frac{\partial }{\partial t}\left[n{S}_w{\rho }_w{e}_w+n{S}_g{\rho }_g{e}_g+(1-n){\rho }_s{e}_s\right]+(1-n)3K_m\left({\beta }_{T}T+{\beta }_M{S}_w\right)\frac{\partial {\epsilon }_v}{\partial t}+\nabla \cdot (k_t\cdot T)=Q\end{array}(17)$

where K_m is the bulk modulus of soil particles; e_w, e_g and e_s are the internal energy per unit mass of pore water, pore gas and solid particles, respectively; β_T and β_M are the linear thermal expansion coefficient and linear moisture expansion coefficient of soil particles, respectively; h_w, h_g and h_s are the heat content per unit mass of pore water, pore gas and solid particles, respectively; k_t is the overall thermal conductivity; Q is the total heat source strength. The first item in Eq. 17 is the energy differential per unit time between entering and leaving; The second item is the energy caused by the fluid pressure change (Nowacki, 1970; Busch and Schade, 1976); The third item is the internal energy change rate in unsaturated soil; The fourth term is the change rate of reversible elastic energy due to strain of solid particles (Nowacki, 1970; Bear and Bachmat, 1990); The fifth item is the heat conduction term. The internal energy constitutive equation can be expressed as (Guo, 2018; Bai et al., 2020b):

$\frac{\partial e_i}{\partial t}=c_{vi}\frac{\partial T}{\partial t}+\left(T-T_0\right)\frac{\partial c_{vi}}{\partial t}(18)$

$\frac{\partial h_i}{\partial t}=c_{pi}\frac{\partial T}{\partial t}+\left(T-T_0\right)\frac{\partial c_{pi}}{\partial t}(19)$

where e_i is the internal energy per unit mass; h_i is the heat content per unit mass; c_vi and c_pi are constant volume and constant pressure specific heat, respectively. The subscript i can be replaced by w, g, and s, representing pore water, pore gas, and solid particles, respectively. By substituting Eqs 9–12, 18, 19 into Eq. 17, the heat transfer differential equation can be obtained as follows:

$\begin{array}{l}{\displaystyle \sum _{i=s,w,g}\left[{\varphi }_i{\rho }_i\left(T-T_0\right)\frac{\partial c_{vi}}{\partial t}\right]}+{\displaystyle \sum _{i=s,w,g}\left[\left({\varphi }_i{\rho }_i{c}_{vi}\right)\frac{\partial T}{\partial t}+e_i\frac{\partial }{\partial t}\left({\varphi }_i{\rho }_i\right)\right]}\\ +{\displaystyle \sum _{i=w,g}\left(c_{pi}{\rho }_i\cdot {\mathit{u}}_i\right)\cdot \nabla T}+\nabla \cdot \left(k_t\cdot \nabla T\right)=Q-\left(1-n\right)3K_m\left({\beta }_{T}T+{\beta }_M{S}_w\right)\frac{\partial {\epsilon }_v}{\partial t}\\ -{\displaystyle \sum _{i=w,g}\left[h_s\left(1-n\right){\rho }_s-h_i{\varphi }_i{\rho }_i-{\varphi }_i{\rho }_i{P}_i\right]\frac{\partial {\epsilon }_v}{\partial t}}-{\displaystyle \sum _{i=w,g}\left[{\varphi }_i{P}_i\nabla \cdot \left(\frac{{\mathit{u}}_i}{{\varphi }_i}\right)+\left(T-T_0\right)\nabla \cdot \left(c_{pi}{\rho }_i\cdot {\mathit{u}}_i\right)\right]}\end{array}(20)$

As a key thermodynamic parameter for numerical calculation, the overall thermal conductivity can be expressed as (Côté and Konrad, 2005):

$k_t=k_s\left(1-n\right)+k_w{\theta }_w+k_g\left(n-{\theta }_w\right)(21)$

Where k_s, k_w, and k_g are thermal conductivity of solid phase, liquid phase, and gas phase respectively; θ_w is volumetric water content.

Principal Equation

According to the equivalent stress principle of unsaturated soil developed by Zienkiewicz et al. (1990), (Zienkiewicz et al., 1990), and Bear and Bachmat. (1990) and the effective stress increment equation developed by Rutqvist et al. (2001), the total stress in unsaturated soil is:

$\mathit{\sigma }=\mathit{D}:\left(\epsilon -{\epsilon }_T-{\epsilon }_S-{\epsilon }_P\right)-{\alpha }_B\overline{P}\mathit{I}(22)$

where σ is the total stress; ε is total strain of solid skeleton; D and I are the tangential stiffness matrix and the unit matrix, respectively.‾P is weighted average pore pressure; α_B is the Biot coefficient; ε_P, ε_T, and ε_S are respectively the solid skeleton strains caused by pore pressure, temperature, and humidity, which are given by the following formula (Bai and Li, 2013; Bai et al., 2014; Fu et al., 2017; Guo, 2018):

$\begin{array}{l}{\epsilon }_T={\beta }_T\left(T-T_0\right)\\ {\epsilon }_P=-\frac{\overline{P}-{\overline{P}}_0}{3K_m}\\ {\epsilon }_S={\beta }_M\left(S_w-S_{w0}\right)\end{array}\}(23)$

Then the stress-strain relationship in unsaturated soil is:

$\mathit{\sigma }=\mathit{D}:\epsilon -3K_m{\beta }_T\left(T-T_0\right)\mathit{I}-{\alpha }_B\overline{P}\mathit{I}-\left(1-{\alpha }_B\right){\overline{P}}_0\mathit{I}-3K_m{\beta }_M\left(S_w-S_{w0}\right)\mathit{I}(24)$

Numerical Verification and Coupling Response Characteristics

Physical Model and Parameters

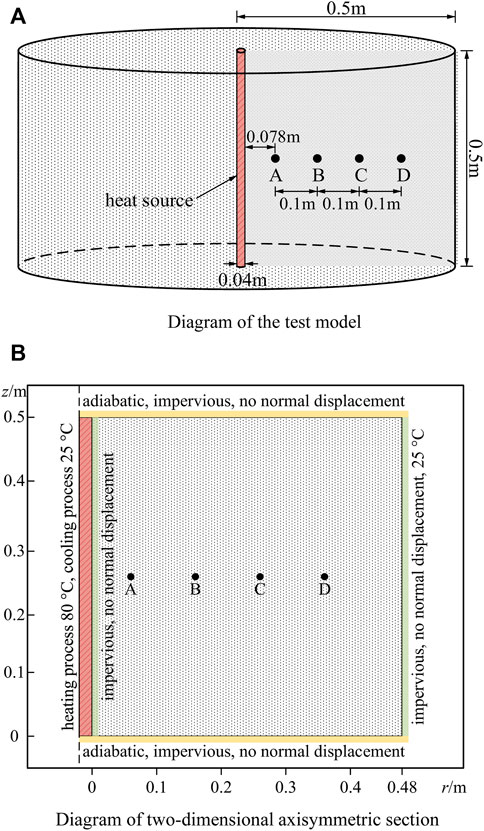
To verify the reliability of the THM coupling theory constructed in this work, the numerical calculation was carried out based on the indoor test of unsaturated clay in the literature (Bai et al., 2020b), and the THM coupling response characteristics were analyzed. The physical model used in the calculation conforms to the axisymmetric (as given in Figure 5). The radius of the outer cylindrical surface of the sample is 0.5 m, and the height is 0.5 m; The radius of the heat source column is 0.02 m, and the height is 0.5 m. The symmetry axis of the heat source column coincides with the soil column. The four measuring points A, B, C, and D for temperature and moisture content were arranged sequentially outward from r = 0.078 m with a spacing of 0.1 m. The normal displacement of all boundaries of the hollow axisymmetric soil column (including the upper and lower base surfaces, inner and outer cylindrical surfaces) is zero. The soil under the action of the heat source is a closed system (no material exchange with the external environment). During the test, the top and bottom surfaces of the soil were adiabatic, and the outer cylindrical surface remained constant at 25°C. The initial temperature and initial volumetric water content of soil samples are 25°C and 19.6%, respectively. The temperature of the heat source rises to 80°C in a short time and remains constant for 5 days (a heating process), then falls to 25°C in a short time and lasts for 3 days (a cooling process).

FIGURE 5

FIGURE 5. Diagram of the calculation model.

According to the relevant literature (Mualem, 1976; van Genuchten, 1980; Thomas and Vauclin, 1986; Guo, 2018), the parameters of the modified VG model are calculated as given in Table 1, 2 shows the parameters of the physical properties of the soil samples used in the experiments. Other state variables are calculated using a nonlinear relationship with temperature (Eckert & Rg, 1972; Vargaftik, 1975; Chen et al., 1999). Based on COMSOL numerical analysis platform, the corresponding program is compiled to model the THM coupling process in unsaturated soil. The seepage differential equation of gas adopts the Darcy seepage interface, the seepage differential equation of water and principal equation adopts porous elastic interface, and the energy equation adopts porous medium heat transfer interface. Due to the difference between the theoretical model and the built-in physical field equation in the COMSOL Multiphysics platform, the above physical field interfaces are secondarily developed by modifying the underlying equation to realize the numerical modeling of THM coupling theory.

TABLE 1

TABLE 1. Modified VG model parameters.

TABLE 2

TABLE 2. Physical parameters of soil sample.

Model Validation and Analysis

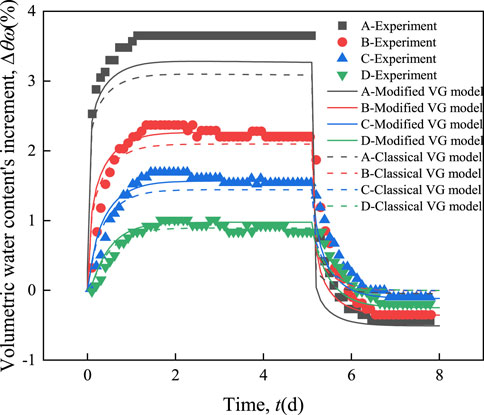
Figure 6 compares the numerical solution and the measured value of volumetric water content increment at different measuring points. The numerical results of measuring point A are lower than the measured data, and the numerical solutions of points B, C, and D are in close consistency with the experimental data. However, all simulation results are generally consistent with the variation trend of the volumetric water content incremental of the experimental data. Compared with the classical VG model, the numerical solution of the THM coupling equations using the modified VG model is in good agreement with the experimental data.

FIGURE 6

FIGURE 6. Comparison of volumetric moisture content increment test value and numerical solution.

Numerical simulation experiments show that the calculation results of volumetric water content increment in soil columns agree well with the experiment by changing the modified VG model parameters when simulating the corresponding cooling process of each measuring point. The specific approach is that the α₀ values of A, B, C, and D are 1.631, 1.623, 1.606, and 1.614, respectively. The volumetric water content of each measuring point grows continually during the heating phase of the soil sample (a hygroscopic process), and it gradually declines during the cooling process (a dehydration process). Because the SWCC of unsaturated soil during the moisture hygroscopic-dehydration process are different, i.e., the parameters of the modified VG model are different during the heating and cooling process of soil samples, and this difference must be fully considered in the numerical calculation process. In addition, it is found that the parameters of the modified VG model vary significantly when the distance between the measuring point and the heat source is different, and the closer to the heat source, the greater the difference in the model parameters.

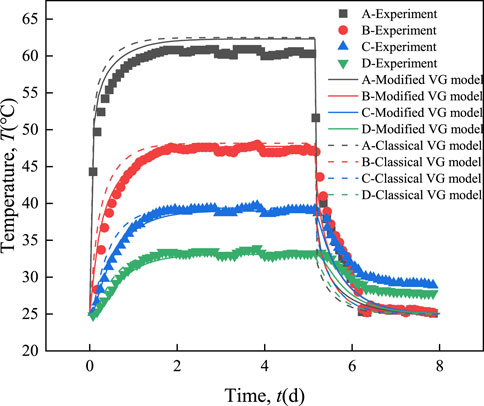
Figure 7 shows the comparison between the numerical results of temperature at different measuring points and the experimental values. It can be observed from Figure 7 that the calculation results of temperature at different points in all numerical calculations (both the modified VG model and the classical VG model) agree well with the experimental results. Overall, the calculated results of the temperature evolution of each measuring point during the heating process agree better with the experimental results than the cooling process. The deviation between the calculation results and the experimental results during the cooling process is significant, but the changing trend is consistent.

FIGURE 7

FIGURE 7. Comparison of temperature test value and numerical solution.

To quantify the difference between the predicted value of the theoretical model and the measured data, average relative error (AVRE) was used to evaluate the model’s performance. The closer the AVRE value was to 1, the better the numerical simulation was. As can be seen from Table 3, compared with the classical VG model, the AVRE values of the numerical solution (including the volumetric water content and temperature during the heating and cooling processes) under the modified VG model are all closer to 1, indicating that the numerical simulation is better. In addition, the simulation values of temperature and volumetric water content during the heating and cooling of soil samples were compared, and the AVRE was calculated. The results show that the AVRE values of the heating process are closer to 1, indicating that the calculation accuracy in the process is higher than that in the cooling process. By comparing the AVRE values of temperature and moisture content under two kinds of SWCC models, it is found that the accuracy difference of temperature numerical solution is relatively small, indicating that the selection of the SWCC model has little effect on the heat transfer process.

TABLE 3

TABLE 3. AVRE of the different model.

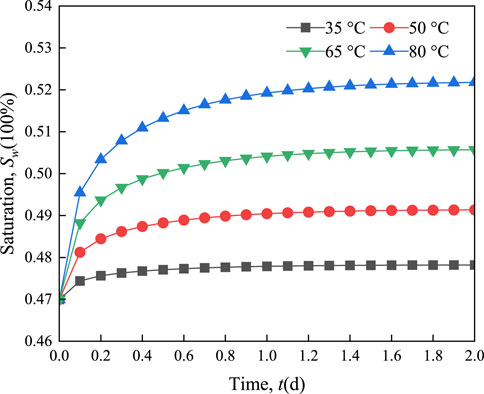
Figure 8 shows the saturation variation of measuring point B with time during the heating process of soil samples under different heat source temperatures. The temperature in unsaturated soil increases gradually under the continuous action of the heat source, which makes the water migrate from the high-temperature area to the low-temperature area, leading to a gradual increase in the saturation of point B. The increased rate of saturation of measuring point B is first fast and then slow. In addition, the slope of the saturation curve at the initial stage of temperature increase is greater under higher temperature of heat sources. The higher the heat source temperature, the greater the slope of the saturation curve at the initial stage of the temperature increase. In the numerical calculation, the initial temperature of the soil sample is 25°C, and the set heat source temperatures are 35°C→50°C→65°C→80°C, respectively. Correspondingly, the time when the saturation of point B reaches a stable state is 0.2, 0.9, 1.3, and, and 2 days, respectively. It is known that the smaller the temperature difference between the initial temperature of the soil sample and the heat source, the faster the saturation of the soil sample reaches a stable state.

FIGURE 8

FIGURE 8. Variation of saturation at B point with time under different heat source temperatures.

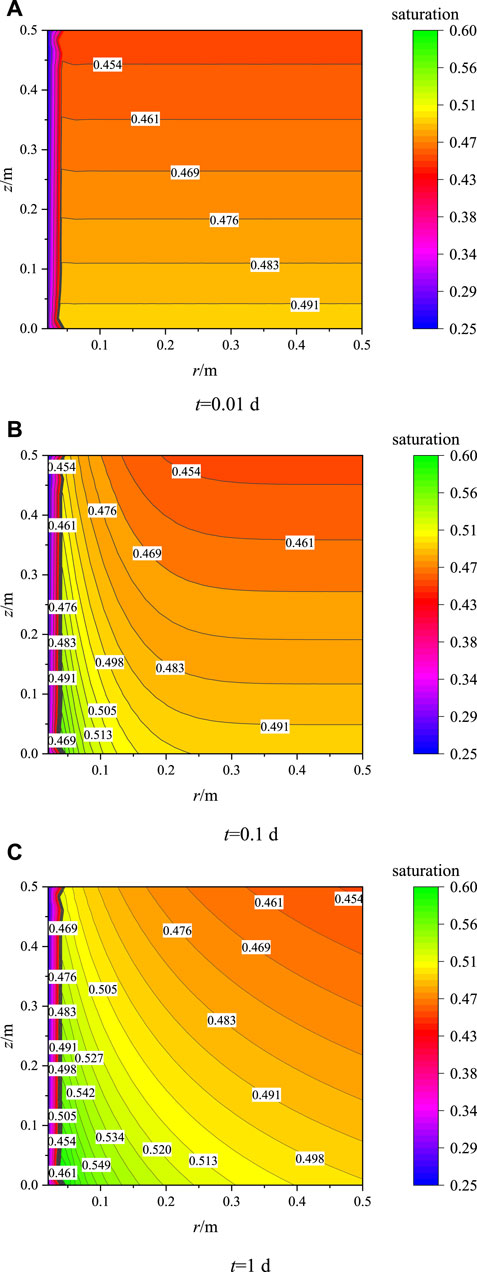
Figure 9 shows the saturation contours of the symmetric plane at 0.01, 0.1, and 1 day during the heating process. It can be seen that in the initial stage (t = 0.01 days), the vertical distribution of soil saturation is slightly uneven due to the gravity effect in the range of r > 0.04 m. Still, there is no significant change relative to the initial saturation. When t = 0.1 day, the pore water moves outward from the vicinity of the heat source under the effect of the temperature gradient. The saturation of the soil sample in the left lower range (0.04 m < r < 0.35 m) increases gradually, showing a gradual decrease from the left lower to the right upper. When t = 1 day, the area where the saturation of the soil sample increases further expands, while the saturation near the heat source (r < 0.04 m) is still small.

FIGURE 9

FIGURE 9. Variation of saturation with time on the symmetric plane.

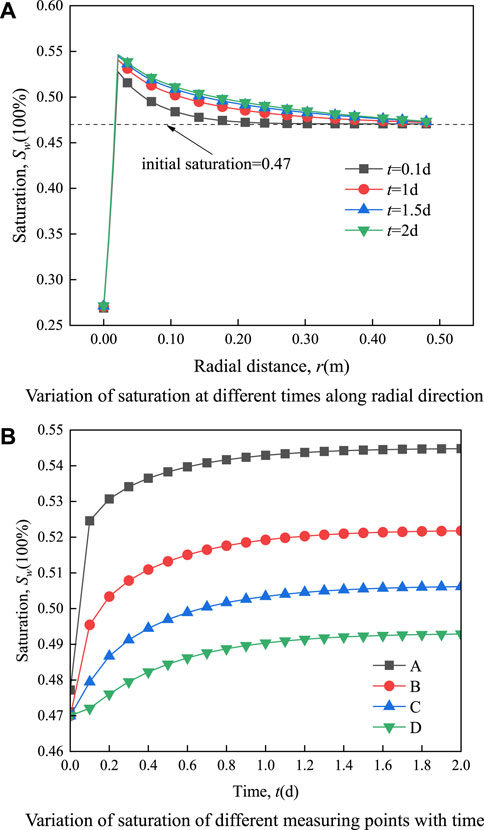
Figure 10A shows the distribution profile of saturation along the radial direction at z = 0.25 m at different times (namely, 0.1, 1, 1.5, and , 2 days) in the heating process of soil samples. It can be seen that the saturation curve moves upward with time, indicating that the saturation increases with time. When t = 1.5 days and t = 2 days, the saturation curve basically coincides, meaning that the soil saturation reaches a stable state when t = 2 days. In addition, the saturation curves generally show an accelerated rise followed by a slow decline, and the slope and the amplitude of change in the rising phase are larger. This phenomenon indicates that the saturation changes rapidly near the heat source, and reaches the maximum saturation at r = 0.02 m. The slope of the saturation curve becomes smaller as the radial distance increases in the descending section of the saturation curve. That is, the farther away from the heat source, the smaller the change of saturation along the radial direction, and the influence of the heat source on saturation becomes weaker with the increase of distance.

FIGURE 10

FIGURE 10. Variation of saturation at height z = 0.25 m.

Figure 10B shows the saturation variation of different measuring points with time during the heating process. It can be seen that the variation of saturation with time is similar to that of volumetric water content increment (as shown in Figure 6) with time. The saturation growth rate of measuring points A, B, C, and D showed the characteristics of first large and then small. The saturation of each measurement point to reach steady state was 0.544, 0.521, 0.506, and 0.492, and the increments of saturation were 0.074, 0.051, 0.036, and 0.022, respectively. It shows that the closer to the heat source, the greater the saturation increment during the heating process.

Figure 11 shows the radial distribution of volumetric strain at z = 0.25 m at different times during the heating process of soil samples. The overall trend of the volumetric strain curve is highly consistent with the variation of saturation in the radial direction, and the maximum values of volumetric strain and saturation are in roughly the same position. The temperature gradient causes the pore water to migrate outwards and accumulates near the heat source to form a local high moisture content region. The wet swelling causes the volumetric strain of the soil in this region to increase gradually, and accordingly, volumetric strain reaches the maximum at the position of maximum saturation. In addition, the variation amplitude of volumetric strain in the decline stage is much larger than that of saturation, which is the combined effect of temperature and boundary constraints. The volumetric strain near the outer boundary of the soil column is negative, primarily passive compression deformation, and the volumetric strain in the middle of the soil is positive, primarily active expansion deformation.

FIGURE 11

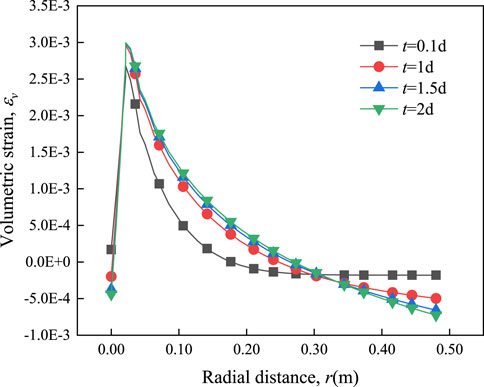
FIGURE 11. Variation law of volumetric strain with radial distance at different times at height z = 0.25 m.

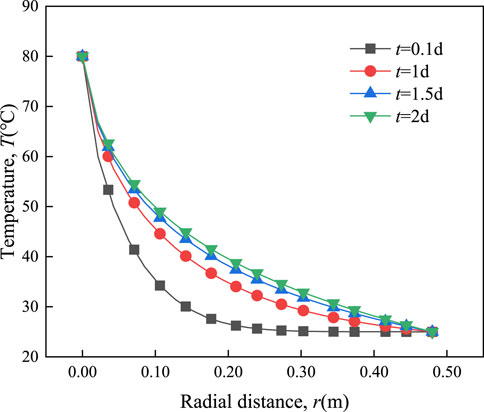
Figure 12 shows the distribution profile of temperature along the radial direction at different times during the heating process of soil samples. With the increase of time, the temperature gradually increases along the radial direction and reaches the thermal stability state approximately at t = 2 days. In addition, the temperature gradient near the heat source during heat transfer decreases gradually with time. However, the temperature gradient away from the heat source increases gradually with time under the first type of thermal boundary. The comparison shows a certain similarity between the changes in temperature and volumetric strain along the radial direction in the region r > 0.3 m (That is, both are nearly straight at t = 0.1 day, while both curves at the remaining three times have a certain slope). The thermal expansion caused by the temperature difference in the region far from the heat source is the main factor driving the soil volumetric strain.

FIGURE 12

FIGURE 12. Variation of temperature with radial distance at different times at height z = 0.25 m.

Figures 13A–C show the radial distribution of total displacement, r-direction displacement, and z-direction displacement corresponding to four time points (0.1, 1, 1.5, and 2 days) in the heating process. It can be observed from Figure 13 that the total displacement increases first and then decreases along the radial direction, and decreases with time, which has the same variation profile with the displacement in the r-direction. The z-direction displacement is negative (the direction is opposite to the z coordinate direction), and the absolute value of the displacement increases along the radial direction and decreases with time. Because the absolute value of z-direction displacement is much larger than that in r-direction, the total displacement is mainly dominated by z-direction displacement. By comparing Figures 13A,B, it can be observed that the variation trend of the total displacement curve is similar to that of the r-direction displacement, and the peak points on the two displacements curves move outward with time.

FIGURE 13

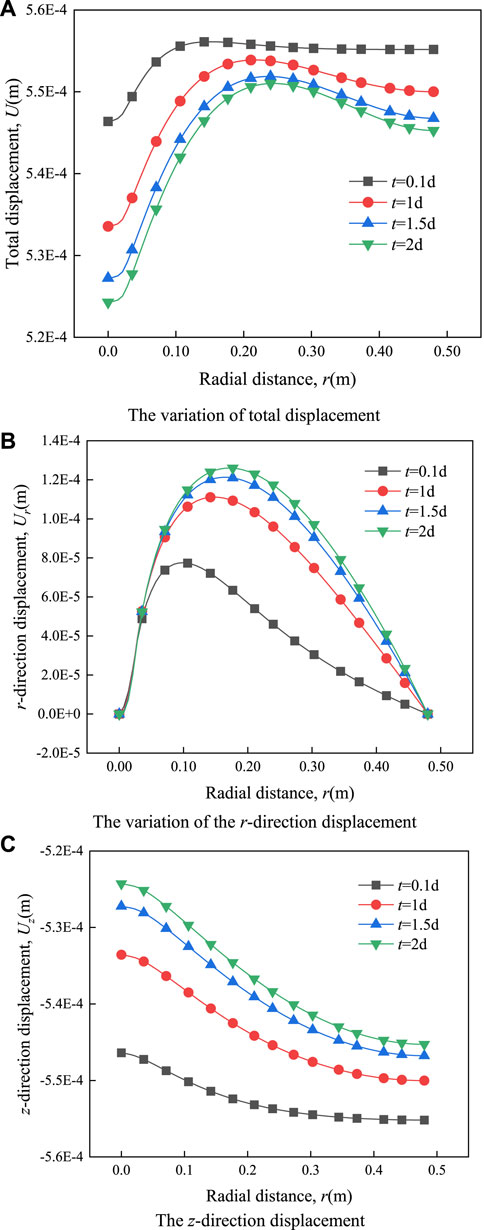
FIGURE 13. The variation law of the displacement with radial distance at different times at height z = 0.25 m.

Conclusion

A modified VG model considering both void ratio and temperature effect is proposed. The THM coupling theoretical model of unsaturated soil is given based on the wet-thermal elasticity theory and mixture theory. The numericalization of the theoretical model is realized by the secondary development of COMSOL Multiphysics. The validity of the theoretical model equation is verified using the indoor test data. Finally, the thermal-hydro-mechanical coupling response characteristics are analyzed. The main conclusions are as follows.

(1) Moisture in axisymmetric soil samples migrates from high-temperature region to low-temperature region under the action of the heat source, and its dynamic redistribution causes the change of soil permeability. Accordingly, the reasonable determination of the modified VG model parameters should be paid attention to in the numerical calculation. The analysis shows that the modified VG model parameters of the heating process of four measuring points can take the same value, while the values of the model parameters are different in the cooling process.

(2) The temperature of the heat source directly affects the change of the saturation of the measuring point. The higher the temperature of the heat source, the greater the saturation of the specific position when the soil is thermally stable. However, the change of the soil saturation can be stabilized faster under the lower temperature heat source. Under the same temperature of the heat source, the growth rate of saturation decreases with time, and the bottom saturation of unsaturated soil is greater than the top saturation under gravity. The saturation near the heat source is low.

(3) The volumetric strain of unsaturated soil results from the combined action of wet expansion and thermal expansion, which is dominated by moisture expansion near the heat source, and is mainly dominated by thermal expansion far away from the heat source. The volumetric strain near the outer boundary of the soil column is negative, primarily passive deformation, and the volumetric strain in the middle of the soil is positive, primarily active expansion deformation. The change of the total displacement of soil with time is dominated by the z-direction displacement, and its change trend along the radial direction is similar to that in the r-direction. The peak value of the total displacement curve moves outward with time.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

PC; methodology. HZ, GY, ZG, and GY; investigation and research.

Funding

National Natural Science Foundation of China (518026); General Project of Scientific Research Program of Beijing Education Commission (KM201910016003); Pyramid Talent Training Project of BUCEA (JDYC20200325); Graduate innovation project of BUCEA (PG2021045).

Conflict of Interest

Author ZG was employed by China Construction Civil Engineering Co., Ltd, China

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akrouch, G. A., Sánchez, M., and Briaud, J.-L. (2016). An Experimental, Analytical and Numerical Study on the Thermal Efficiency of Energy Piles in Unsaturated Soils. Comput. Geotechnics 71, 207–220. doi:10.1016/j.compgeo.2015.08.009

CrossRef Full Text | Google Scholar

Azizi, A., Jommi, C., and Musso, G. (2017). A Water Retention Model Accounting for the Hysteresis Induced by Hydraulic and Mechanical Wetting-Drying Cycles. Comput. Geotechnics 87, 86–98. doi:10.1016/j.compgeo.2017.02.003

CrossRef Full Text | Google Scholar

Bai, B., Guo, L., and Han, S. (2014). Pore Pressure and Consolidation of Saturated Silty Clay Induced by Progressively Heating/cooling. Mech. Mater. 75, 84–94. doi:10.1016/j.mechmat.2014.04.005

CrossRef Full Text | Google Scholar

Bai, B., and Li, T. (2013). Irreversible Consolidation Problem of a Saturated Porothermoelastic Spherical Body with a Spherical Cavity. Appl. Math. Model. 37 (4), 1973–1982. doi:10.1016/j.apm.2012.05.003

CrossRef Full Text | Google Scholar

Bai, B., Long, F., Rao, D., and Xu, T. (2017). The Effect of Temperature on the Seepage Transport of Suspended Particles in a Porous Medium. Hydrol. Process. 31 (2), 382–393. doi:10.1002/hyp.11034

CrossRef Full Text | Google Scholar

Bai, B., Nie, Q. k., Zhang, Y. k., Wang, X. l., and Hu, W. (2020). Cotransport of Heavy Metals and SiO2 Particles at Different Temperatures by Seepage. J. Hydrology 597, 125771. doi:10.1016/j.jhydrol.2020.125771

CrossRef Full Text | Google Scholar

Bai, B., Wang, Y., Rao, D., and Bai, F. (2022). The Effective Thermal Conductivity of Unsaturated Porous Media Deduced by Pore-Scale SPH Simulation. Front. Earth Sci.. doi:10.3389/feart.2022.943853

CrossRef Full Text | Google Scholar

Bai, B., Xu, T., Nie, Q., and Li, P. (2020). Temperature-driven Migration of Heavy Metal Pb2+ along with Moisture Movement in Unsaturated Soils. Int. J. Heat Mass Transf. 153, 119573. doi:10.1016/j.ijheatmasstransfer.2020.119573

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Cai, G., Hu, W., and Yang, G. (2021). Coupled Thermo-Hydro-Mechanical Mechanism in View of the Soil Particle Rearrangement of Granular Thermodynamics. Comput. Geotechnics 137 (8), 104272. doi:10.1016/j.compgeo.2021.104272

CrossRef Full Text | Google Scholar

Bai, X.-D., Cheng, W.-C., and Li, G. (2021). A Comparative Study of Different Machine Learning Algorithms in Predicting EPB Shield Behaviour: a Case Study at the Xi'an Metro, China. Acta Geotech. 16, 4061–4080. doi:10.1007/s11440-021-01383-7

CrossRef Full Text | Google Scholar

Bai, X.-D., Cheng, W.-C., Sheil, B. B., and Li, G. (2021). Pipejacking Clogging Detection in Soft Alluvial Deposits Using Machine Learning Algorithms. Tunn. Undergr. Space Technol. 113, 103908. doi:10.1016/j.tust.2021.103908

CrossRef Full Text | Google Scholar

Bear, J., and Bachmat, Y. (1990). Introduction to Modeling of Transport Phenomena in Porous Media. theory & Appl. Transp. porous media 117, 517–526. doi:10.1007/978-94-009-1926-6

CrossRef Full Text | Google Scholar

Booker, J. R., and Savvidou, C. (1984). Consolidation Around a Spherical Heat Source. Int. J. Solids Struct. 20, 1079–1090. doi:10.1016/0020-7683(84)90091-x

CrossRef Full Text | Google Scholar

Busch, G., and Schade, H. (1976). Transport Phenomena. Lect. solid state Phys. 21 (2), 351–404. doi:10.1016/b978-0-08-016894-4.50016-4

CrossRef Full Text | Google Scholar

Cao, B., Tian, Y., Gui, R., and Liu, Y. (2021). Experimental Study on the Effect of Key Factors on the Soil-Water Characteristic Curves of Fine-Grained Tailings. Front. Environ. Sci. 9, 710986. doi:10.3389/fenvs.2021.710986

CrossRef Full Text | Google Scholar

Chen, J., Hopmans, J. W., and Grismer, M. E. (1999). Parameter Estimation of Two-Fluid Capillary Pressure-Saturation and Permeability Functions. Adv. Water Resour. 22 (5), 479–493. doi:10.1016/s0309-1708(98)00025-6

CrossRef Full Text | Google Scholar

Chen, Y., Zhou, C., and Jing, L. (2009). Modeling Coupled THM Processes of Geological Porous Media with Multiphase Flow: Theory and Validation against Laboratory and Field Scale Experiments. Comput. Geotechnics 36 (8), 1308–1329. doi:10.1016/j.compgeo.2009.06.001

CrossRef Full Text | Google Scholar

Côté, J., and Konrad, J.-M. (2005). A Generalized Thermal Conductivity Model for Soils and Construction Materials. Can. Geotech. J. 42 (2), 443–458. doi:10.1139/t04-106

CrossRef Full Text | Google Scholar

Eckert & Rg, E. (1972). Analysis of Heat and Mass Transfer. New York: Hemisphere Publishing.

Google Scholar

Fu, X., Sheng, Q., Li, G., Zhang, Z., Zhou, Y., and Du, Y. (2020). Analysis of Landslide Stability under Seismic Action and Subsequent Rainfall: a Case Study on the Ganjiazhai Giant Landslide along the Zhaotong-Qiaojia Road during the 2014 Ludian Earthquake, Yunnan, China. Bull. Eng. Geol. Environ. 79 (10), 5229–5248. doi:10.1007/s10064-020-01890-z

CrossRef Full Text | Google Scholar

Fu, X., Sheng, Q., Zhang, Y., Chen, J., Zhang, S., and Zhang, Z. (2017). Computation of the Safety Factor for Slope Stability Using Discontinuous Deformation Analysis and the Vector Sum Method. Comput. Geotechnics 92, 68–76. doi:10.1016/j.compgeo.2017.07.026

CrossRef Full Text | Google Scholar

Gallipoli, D., Wheeler, S. J., and Karstunen, M. (2003). Modelling the Variation of Degree of Saturation in a Deformable Unsaturated Soil. Géotechnique 53 (1), 105–112. doi:10.1680/geot.2003.53.1.105

CrossRef Full Text | Google Scholar

Ghavam-Nasiri, A., El-Zein, A., Airey, D., and Rowe, R. K. (2019). Water Retention of Geosynthetics Clay Liners: Dependence on Void Ratio and Temperature. Geotext. Geomembranes 47 (2), 255–268. doi:10.1016/j.geotexmem.2018.12.014

CrossRef Full Text | Google Scholar

Ghorbani, J., Nazem, M., and Carter, J. P. (2016). Numerical Modelling of Multiphase Flow in Unsaturated Deforming Porous Media. Comput. Geotechnics 71, 195–206. doi:10.1016/j.compgeo.2015.09.011

CrossRef Full Text | Google Scholar

Guo, Z. (2018). The Hydro-Thermal Effect and Transport Characteristics of Contaminants Inporous Media. Beijing: Beijing Jiaotong University.

Google Scholar

Guo, Z., and Bai, B. (2018). Effect of Saturation on Thermo-Hydro-Mechanical Coupled Responses in Porous Media. Chin. J. Geotechnical Eng. 40 (06), 1021–1028. doi:10.11779/CJGE201806007

CrossRef Full Text | Google Scholar

Hu, W., Cheng, W.-C., Wen, S., and Mizanur Rahman, M. (2021). Effects of Chemical Contamination on Microscale Structural Characteristics of Intact Loess and Resultant Macroscale Mechanical Properties. CATENA 203, 105361. doi:10.1016/j.catena.2021.105361

CrossRef Full Text | Google Scholar

Jacinto, A., Villar, M., Gomezespina, R., and Ledesma, A. (2009). Adaptation of the Van Genuchten Expression to the Effects of Temperature and Density for Compacted Bentonites. Appl. Clay Sci. 42, 575–582. doi:10.1016/j.clay.2008.04.001

CrossRef Full Text | Google Scholar

Li, X., Du, Y., Duan, Q., and Ju, J. W. (2016). Thermodynamic Framework for Damage-Healing-Plasticity of Granular Materials and Net Damage Variable. Int. J. Damage Mech. 25 (2), 153–177. doi:10.1177/1056789515576042

CrossRef Full Text | Google Scholar

Liu, S., Wang, G., Zhu, J., Ma, A., and Xu, A. (2002). Improvement and Application on Soil Tension Meter with Negative-Pressure Mercury. Acta Agric. Boreali-occidentalis Sin. 11 (2), 29–33. doi:10.7606/j.issn.1004-1389.2002.2.008

CrossRef Full Text | Google Scholar

Lu, N., and Likos, W. J. (2004). Unsaturated Soil Mechanics. John Wiley & Sons.

Google Scholar

Malakpoor, K., Kaasschieter, E. F., and Huyghe, J. M. (2007). Mathematical Modelling and Numerical Solution of Swelling of Cartilaginous Tissues. Part I: Modelling of Incompressible Charged Porous Media. Esaim M2an 41 (4), 661–678. doi:10.1051/m2an:2007036

CrossRef Full Text | Google Scholar

Mualem, Y. (1976). A New Model for Predicting the Hydraulic Conductivity of Unsaturated Porous Media. Water Resour. Res. 12 (3), 513–522. doi:10.1029/wr012i003p00513

CrossRef Full Text | Google Scholar

Nowacki, W. (1970). Problems of Thermoelasticity. Prog. Aerosp. Sci. 10, 1–63. doi:10.1016/0376-0421(70)90003-5

CrossRef Full Text | Google Scholar

Qiao, X., Ma, S., Pan, G., and Liu, G. (2019). Effects of Temperature Change on the Soil Water Characteristic Curve and a Prediction Model for the Mu Us Bottomland, Northern China. Water 11 (6), 1235. doi:10.3390/w11061235

CrossRef Full Text | Google Scholar

Qin, B. (2010). Thermal-Water-Mechanical Coupling Analysis Model of Unsaturated Soil Based on Mixture Theory I. Appl. Math. Mech. 31 (12), 1476–1488. doi:10.1007/s10483-010-1384-6

CrossRef Full Text | Google Scholar

Romero, E., Gens, A., and Lloret, A. (2001). Temperature Effects on the Hydraulic Behaviour of an Unsaturated Clay. Geotechnical Geol. Eng. 19, 311–332. doi:10.1007/978-94-015-9775-3_5

CrossRef Full Text | Google Scholar

Rutqvist, J., Börgesson, L., Chijimatsu, M., Kobayashi, A., Jing, L., Nguyen, T. S., et al. (2001). Thermohydromechanics of Partially Saturated Geological Media: Governing Equations and Formulation of Four Finite Element Models. Int. J. Rock Mech. Min. Sci. 38 (1), 105–127. doi:10.1016/s1365-1609(00)00068-x

CrossRef Full Text | Google Scholar

Savvidou, C., and Booker, J. R. (2010). Consolidation Around a Heat Source Buried Deep in a Porous Thermoelastic Medium with Anisotropic Flow Properties. Int. J. Numer. Anal. Methods Geomechanics 13 (1), 75–90. doi:10.1002/nag.1610130107

CrossRef Full Text | Google Scholar

Tarantino, A. (2015). A Water Retention Model for Deformable Soils. Géotechnique 59 (9), 751–762. doi:10.1680/geot.7.00118

CrossRef Full Text | Google Scholar

Thomas, H. R., and Vauclin, M. (1986). Experimental and Numerical Analysis of Two-phase Infiltration in a Partially Saturated Soil. Transp. Porous Media 1 (1), 27–55. doi:10.1007/BF01036524

CrossRef Full Text | Google Scholar

van Genuchten, M. T. (1980). A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 44 (5), 892–898. doi:10.2136/sssaj1980.03615995004400050002x

CrossRef Full Text | Google Scholar

Vargaftik, N. B. (1975). Tables of Thermophysical Properties of Liquids and Gases. New York: Hemisphere Publishing.

Google Scholar

Villar, M. V., and Lloret, A. (2004). Influence of Temperature on the Hydro-Mechanical Behaviour of a Compacted Bentonite. Appl. Clay Sci. 26, 337–350. doi:10.1016/j.clay.2003.12.026

CrossRef Full Text | Google Scholar

Zhang, H., Li, H., and Li, C. (2020). Temperature Effect of Soil-Water on Characteristic Curve of Aeolian Sand Subgrade Soil. China J. Highw. Transp. 33 (07), 42–49. doi:10.19721/j.cnki.1001-7372.2020.07.004

CrossRef Full Text | Google Scholar

Zhou, Y., Sheng, Q., Li, N., and Fu, X. (2022). The Dynamic Mechanical Properties of a Hard Rock under True Triaxial Damage-Controlled Dynamic Cyclic Loading with Different Loading Rates: A Case Study. Rock Mech. Rock Eng. 55 (4), 2471–2492. doi:10.1007/s00603-021-02756-w

CrossRef Full Text | Google Scholar

Zienkiewicz, O. C., Chan, A., Pastor, M., and Shiomi, D. (1990). Static and Dynamic Behaviour of Soils: A Rational Approach to Quantitative Solutions. I Fully Saturated Problems. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci. 429, 285–309. doi:10.1098/rspa.1990.0061

CrossRef Full Text | Google Scholar