An empirical model for the travel distance prediction of deflection-type rock avalanches in the wenchuan earthquake area

Travel distance is a significant indicator for evaluating the mobility of rock avalanches and is usually used to identify the approximate delineation of potentially endangered regions. The deflection-type rock avalanche is a typical laterally confined rock avalanche and is characterized by obvious changes in the travel path. In this study, we selected deflection-type rock avalanches that occurred in the Wenchuan earthquake area as the research object and statistically analyzed 54 rock avalanches collected from the literature. Multiple linear regression of the logarithm of the ratio of slope height to travel distance (h/L) versus the logarithm of other parameters was developed to obtain a best-fit empirical model for the travel distance prediction of deflection-type rock avalanches. The validity of the proposed empirical model was verified by the satisfactory agreement between observations and predictions. Moreover, the sensitivity of local topographic parameters on the mobility of deflection-type rock avalanches is also discussed using regression analysis.

1 Introduction

Rock avalanches are extremely rapid mass flows following the fragmentation of large rockslides or rockfalls (Hungr et al., 2014; Knapp and Krautblater, 2020; Mitchell et al., 2020). In the recent 2 decades, numerous typical rock avalanches have struck the southwestern mountain area of China, such as Touzhai rock avalanches (Yang et al., 2017), Guanling landslide (Kang et al., 2017), Chenjiaba landslide (Huang et al., 2017), Jiweishan landslide (Ge et al., 2019), Zhongbao landslide (Chen et al., 2021), etc., Due to their extremely high mobility (Ge et al., 2020a; Lin et al., 2022), they can travel unexpectedly long distances along different topographies (Hsu 1975; Ge et al., 2019), which always cause huge destructiveness to local residents and property in mountainous regions (Mitchell et al., 2019; Liu et al., 2021a).

The term “Fahrböschung” was first proposed by Heim (1932) in Elm landslide survey, and was used to measure the mobility of rock avalanches. A previous study revealed the inverse relationship between the Fahrböschung values and volumes of rock avalanches (Strom et al., 2019; Mitchell et al., 2020). Thus, large rock avalanches are considered more mobile (Liu et al., 2021a). The travel distance, also called the runout distance, is another significant consideration for evaluating the mobility of rock avalanches. Since the famous Elm landslide event in 1881, the rapid long-travel distance rock avalanche harvest attention to continuously increasing interest from the scientists (e.g., Hsu 1975; Hungr and Evans 2004), which motivates further study to better estimate the mobility of these events. Moreover, travel distance is usually used to identify the rough delineation of potentially endangered regions (Hattanji and Moriwaki 2009). Therefore, it also has significance in the risk assessment of rock avalanches.

Previous studies have revealed that the mobility of rock avalanches is strongly affected by the local topography (Ge et al., 2020b; Liu et al., 2021a). The local topography along the travel path of rock avalanches mainly includes three basic confinement types: laterally confined, unconfined and frontally confined (Strom et al., 2019), also called valley, open and blocked topography (Zhang and Yin 2013). Laterally confined rock avalanches often move down a narrow or broad valley due to the constraint of the valley slopes of lateral mountains (Liu et al., 2021a), and their travel path usually undergoes obvious changes. The deflection angle, also known as impact angle (Ge et al., 2020b), is defined as the acute angle between the initial motion direction of the rock avalanches and the valley extension direction in the horizontal plan (Figure 1), which is used to describe the change in the travel path (Fan et al., 2015). According to the size of the deflection angle, the laterally confined rock avalanches can be further divided into two types, that is, deflection-type and channelized rock avalanches. The Wenjia gully rock avalanches triggered by the Wenchuan earthquake are striking examples of deflection-type rock avalanches. It underwent multiple changes in its travel path (Tang et al., 2012; Kang et al., 2021) and caused more than 50 people to lose their lives (Zhang et al., 2013, 2016). However, the effects of various topographical parameters on the mobility of deflection-type rock avalanches are still unclear at present.

FIGURE 1

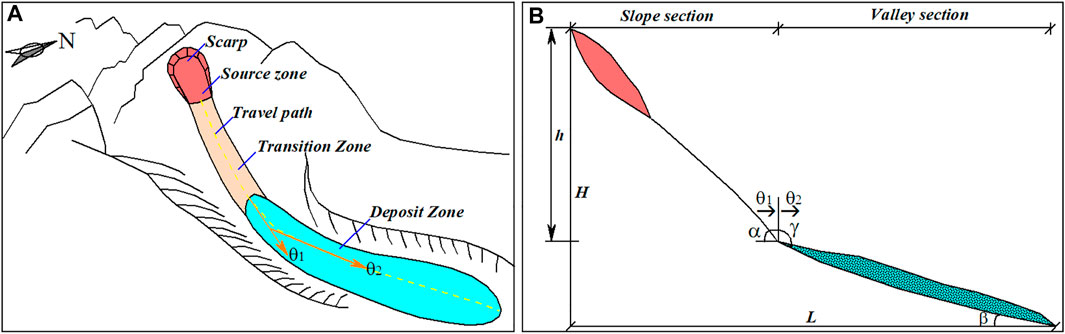
FIGURE 1. (A) Plane sketch of the deflected-type rock avalanches (θ₁ is refers to the initial motion direction of the rock avalanches, and θ₂ is refers to the valley extension direction); (B) Schematic diagram of local topography longitudinal section along the direction of motion path showing the main local topographic parameters of the deflection-type rock avalanches consist of the slope angle (α), channel angle (β), slope height (h), deflection angle (θ), slope transition angle (γ) and fall height (H).

Although the Wenchuan earthquake was over 10 years ago, it provided enormous amount of unstable slope for the post-earthquake hazards, such as the rainfall-induced Sanxicun landslide (Gao et al., 2017) and Xinmo rock avalanches (Huang et al., 2019) that severely threaten dwellings and infrastructures (Ding and Hu 2014). Therefore, the post-earthquake effect is still significant (Fan et al., 2018). Rock avalanches are the most common type of geological disasters in this region. Accordingly, the construction of a prediction model for the travel distance of rock avalanches is meaningful for the risk assessment of rock avalanches in this region (Zhan et al., 2017). Generally, travel distance prediction for rock avalanches is a complicated issue due to the great diversity in travel path materials (Liu et al., 2021a) and geotechnical parameters of mass flows (Qiu et al., 2018). The empirical prediction model, which avoids the usage of uncertain and highly variable parameters, provides a practical method (Qiu et al., 2018). Therefore, it has been widely applied to preliminary assessments of the travel distance of rock avalanches (e.g., Guo et al., 2014; Zhan et al., 2017; Strom et al., 2019; Mitchell et al., 2020). In the present study, the deflection-type rock avalanche was selected as the research object. A multiple linear regression model of the logarithm of h/L versus the logarithm of other parameters was developed to obtain a best-fit empirical model for the travel distance prediction of deflection-type rock avalanches, which provides a useful tool for the preliminary prediction of the potential threat range of such rock avalanches in the Wenchuan earthquake area. In addition, the effects of local topography on the mobility of deflection-type rock avalanches are further discussed.

2 Rock avalanche database

The Tibetan Plateau, located at the junction of Indian and Asian plates, has undergone long–term and complex tectonic activities since the late Mesozoic (Zhang et al., 2022). Longmen Shan Mountain (LMS) Orogenic Zone belongs to southeastern region of the Tibetan Plateau, and is one of the most intense areas in mainland China on crustal deformation characterized by frequent large earthquakes (Wang et al., 2014). Rock slides and collapses are the main types of earthquake disasters in LMS Orogenic Zone, and each strong earthquake usually causes massive rockslides and collapses in this region. For example, the tectonic uplift caused by the Wenchuan earthquake changed the slope gradient instantly (Li et al., 2014) and triggered more than 60,000 rock slides over an elliptical area of approximately 44,000 km² along the fault rupture zone (Liu et al., 2021b), which directly led to approximately 20,000 deaths.

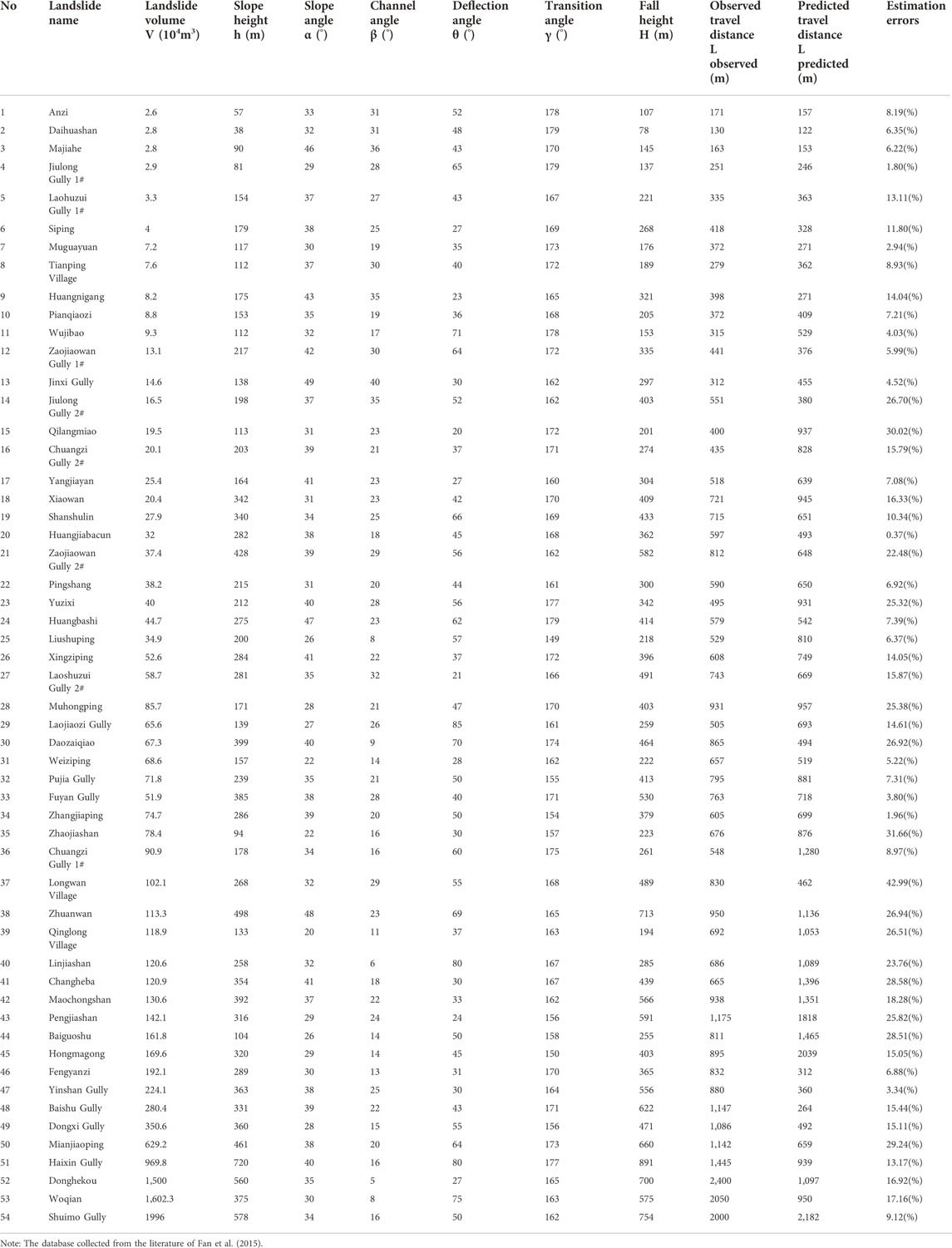
The co-seismic landslides triggered by Wenchuan earthquake provides a rich database for landslide statistical analysis. Therefore, we compile three databases of rock avalanches in this study (see Tables 1, 2, 3). The collected data is associated with the Wenchuan earthquake area. As shown in Figure 2, the rock avalanches listed in the databases are distributed on the surface rupture zone with northeast-trending between the Sichuan Basin and the Tibetan Plateau. Database one consists of 22 rock avalanches collected from the literature (Table 1). It was used to validate the general applicability of the empirical model proposed in this paper in travel distance prediction. Database two consists of 54 deflected-type rock avalanches (Table 2). The volumes of these rock avalanches ranged from 2.6 to 1996 × 10⁴ m³, with travel distances between 0.13 and 2.40 km (Table 2). Deflected-type rock avalanches were used to develop an empirical model for travel distance prediction. In addition, as shown in Table 3, database three consisting of 10 deflected-type rock avalanches was applied to verify the validity of the presented model. The data in database three were collected based on remote sensing interpretation and field investigation on Subaohe river Basins, Beichuan county in the Wenchuan earthquake area (see inset of Figure 2).

TABLE 1

TABLE 1. The database of laterally confined rock avalanches.

TABLE 2

TABLE 2. Data of various parameters of deflected-type rock avalanches.

TABLE 3

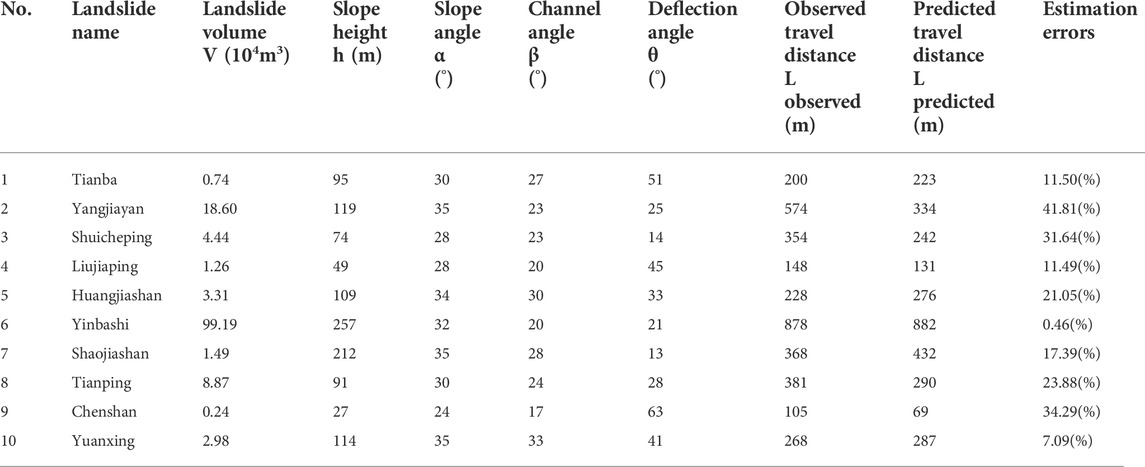
TABLE 3. Database of deflection-type rock avalanches used for applicability verification of the improved empirical model.

FIGURE 2

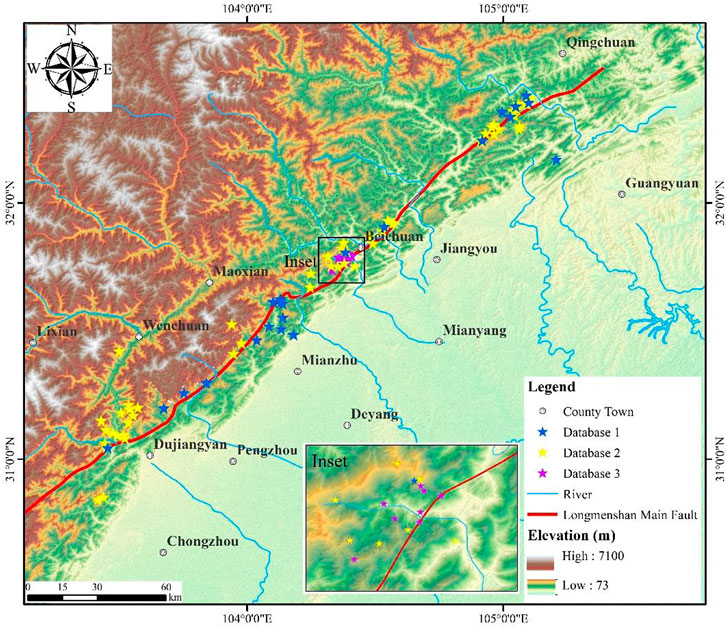
FIGURE 2. The locations of rock avalanches in the Wenchuan earthquake area collected in three databases.

3 Method

3.1 Relevant parameters

The local morphology of a deflection-type rock avalanche can be divided into two sections consisting of slope and valley sections (Figure 1A). The terms and notations of the deflection-type rock avalanches are shown in Figure 1B. The slope angle (denoted as α) refers to the average inclination from the slope toe to the top of the scarp (Qiu et al., 2018). The channel angle (denoted as β) refers to the average inclination of the sectional valley (Zhan et al., 2017). The topographic relief change between slope and valley is defined as the slope transition angle (denoted as γ) (Guo et al., 2014). The fall height (denoted as H) is the vertical distance from the top of the scarp to the front end of the deposit (Basharat et al., 2015). The slope height (denoted as h) refers to the vertical distance from the top of the scarp to the slope toe. The symbol θ₁ is used to represent the initial motion direction of the rock avalanches, whereas the symbol θ₂ is used to represent the valley extension direction. The deflection angle (denoted as θ) is the acute angle between θ₁ and θ₂ (Fan et al., 2015). Therefore, the main local topographic parameters of the deflection-type rock avalanches consist of the slope angle (α), channel angle (β), slope height (h), deflection angle (θ), slope transition angle (γ) and fall height (H).

3.2 Empirical model

Empirical-statistical methods have been used as common tools to study the mobility of rock avalanches (Zhan et al., 2017). In reference to existed study (e.g., Heim 1932; Hsu 1975; Qiu et al., 2018; Zheng et al., 2018), although there are many empirical models available for travel distance prediction of rock avalanches, they can be summarized into just three categories, as shown in Eqs 1, 2, 3. However, Eqs 1, 2 only describe the simple statistical relationships between mobility parameters and landslide volume, while Eq. 3-1 proposed by Zheng et al. (2018) and Eq. 3-2 proposed in this paper have much more physical significance. Therefore, Eq. 3 was selected as the empirical model for travel distance prediction.

$L\left(V\right)={\lambda }_0{V}^{{\lambda }_1},(1)$

$\frac{H}{L}\left(V\right)={\gamma }_0{V}^{{\gamma }_1},(2)$

$L\left(VH\right)={\eta }_0{\left(VH\right)}^{0.25},$(3-1)

$\frac{H}{L}\left(V\right)={\chi }_0{\left(V^{1/3}{H}^{-1}\right)}^{{\chi }_1},$(3-2)

where the L is the indicator variable, H is the fall height, V is the landslide volume, and λ₀, λ₁, γ₀, γ₁, η₀, χ₀ and χ₁ are the corresponding regression coefficients.

The mobility of rock avalanches is affected by several influential factors (Guo et al., 2014). Hence, some scholars have aimed to introduce more quantifiable influential factors in empirical models to improve the prediction accuracy of travel distance (e.g., Finlay et al., 1999; Guo et al., 2014; Zhan et al., 2017; Qiu et al., 2018). The local topography is an important factor influencing the mobility of rock avalanches (Liu et al., 2021a). Therefore, after introducing the main topographic parameters in Eq. 3-1 and Eq. 3-2, the empirical model can be expressed as Eq. 4. The linear regression model on the logarithmic transform of the variables was conducted under the assumption of linear association, in which logarithmic transformation of the variables is equivalent to a power law consistent with the existing research (Mitchell et al., 2020).

$\mathit{log}L={\beta }_0+{\beta }_1\mathit{log}{\left(VH\right)}^{0.25}+{\beta }_2\mathit{log}{C}_1+{\beta }_3\mathit{log}{C}_2+...+{\beta }_{n+1}\mathit{log}{C}_n+\epsilon ,$(4-1)

$\mathit{log}\left(\frac{H}{L}\right)={\beta }_0+{\beta }_1\mathit{log}\left(V^{1/3}{H}^{-1}\right)+{\beta }_2\mathit{log}{C}_1+{\beta }_3\mathit{log}{C}_2+...+{\beta }_{n+1}\mathit{log}{C}_n+\epsilon ,$(4-2)

where log is the logarithm of 10, L is the travel distance, H is the fall height, V is the landslide volume, C_i (i = 1, 2, 3..., n + 1) are the indicator variables of topographical parameters, β_i (i = 1, 2, 3..., n + 1) are the regression coefficients and ε is the residual error, which is assumed to be normally distributed with zero mean (Mitchell et al., 2020).

As shown in Eqs 5, 6, the mean absolute percentage error, hereinafter referred to as $MAPE$ (Armstrong and Collopy 1992), and the Theil inequality coefficient, hereinafter referred to as $TIC$ (Leuthold 1975), can be used to evaluate the prediction accuracy of the empirical model for the travel distance prediction of deflected-type rock avalanches.

$\mathit{M}\mathit{A}\mathit{P}\mathit{E}=\frac{1}{\mathrm{n}}{\displaystyle \sum }_1^n\left|\frac{p_i-A_i}{A_i}\right|,(5)$

$TIC=\frac{\sqrt{1/\mathrm{n}{\displaystyle \sum }_1^n{\left(p_i-A_i\right)}^2}}{\sqrt{1/\mathrm{n}{\displaystyle \sum }_1^n{p}_i^2}+\sqrt{1/\mathrm{n}{\displaystyle \sum }_1^n{A}_i^2}},(6)$

where p_i and A_i refer to predictions and actual observations of travel distance, respectively. A smaller MAPE or TIC value indicates that the empirical models are more accurate in predicting the travel distance of rock avalanches (Qiu et al., 2018).

4 Results and validation

4.1 General applicability validation

The parameters of 22 rock avalanches listed in the test database one consist of landslide volume (V), fall height (H), slope angle (α) and channel angle (β). Therefore, the slope angle (α) and channel angle (β) were considered in Eq. 4. Based on the multivariate regression method, the best-fit regression equation for travel distance prediction was derived from the dataset of Table 1 (see Eq. 7).

$L=e^{2.312}{\left(\mathit{tan}\alpha {)}^{-0.308}(\mathit{tan}\beta \right)}^{-0.817}{\left(VH\right)}^{0.25},$(7-1)

$\frac{H}{L}=e^{0.1247}{\left(\mathit{tan}\alpha {)}^{0.5211}(\mathit{tan}\beta \right)}^{0.4017}{\left(V^{1/3}{H}^{-1}\right)}^{-0.0184}.$(7-2)

The regression results show that correlation coefficients are 0.39 and 0.77 for Eq. 7-1 and Eq. 7-2. Meanwhile, the p value of Eq. 7-2 is 0.013 and is less than that of Eq. 7-1, which indicates that the overall regression of Eq. 7-2 satisfies higher statistical significance level. In addition, the residual plots illustrate normality, constant variance and absence of trends in the residuals (Figure 3), which shows that the selection of Eq. 7-2 as empirical prediction model for travel distance is more reasonable. To further validate Eq. 7-2, we list the estimation errors ($\left|L_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}}-L_{\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}\right|/L_{\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}\times 100\%$) of 22 rock avalanches in Table 1. Most of the estimation errors are less than 10%, which indicates that the travel distance of most rock avalanches is predicted accurately. Therefore, the empirical model (Eq. 4-2) has good applicability in travel distance prediction for rock avalanches.

FIGURE 3

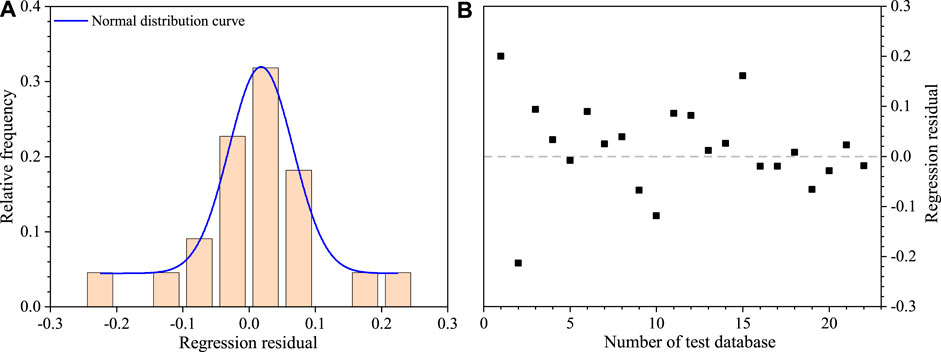
FIGURE 3. The regression analysis results of Eq. 7-2 based on the test database of 22 channelized rock avalanches: (A) Histogram of the relative frequency of the log(H/L) regression residuals. (B) Plot of regression residuals of log(H/L).

4.2 Travel distance prediction for the deflection-type rock avalanches

For the travel distance prediction of deflected-type rock avalanches, four characteristic parameters of local topography, including α, β, θ and γ, were considered in the empirical model (Eq. 4-2), and the best-fit multivariate regression model (Eq. 8) was obtained based on the regression analysis of the database of deflection-type rock avalanches, which is as follows:

$\frac{H}{L}=e^{0.1839}{\left(\mathit{tan}\alpha \right)}^{0.6181}{\left(\mathit{tan}\beta \right)}^{0.2586}{\left(\mathit{tan}\theta \right)}^{0.0318}{\left(\mathit{sin}\gamma \right)}^{0.0063}{\left(V^{1/3}{H}^{-1}\right)}^{-0.0480}.(8)$

The histogram of relative frequency (Figure 4A) shows that log(H/L) regression residuals approximately fit a normal distribution, which supports the normality assumption. The plot of residuals shows an absence of trends (Figure 4B), indicating the independence in residuals and its homogeneity of variance (Liu et al., 2021a). Moreover, the p value (0.0062) of the significance test of Eq. 8 is less than 0.05, indicating that the regression relationship is statistically significant at a 95% confidence level. The regression results indicate that the best-fit multivariate regression model (Eq. 8) has a high correlation coefficient (R²=0.93) and a strong statistical significance level.

FIGURE 4

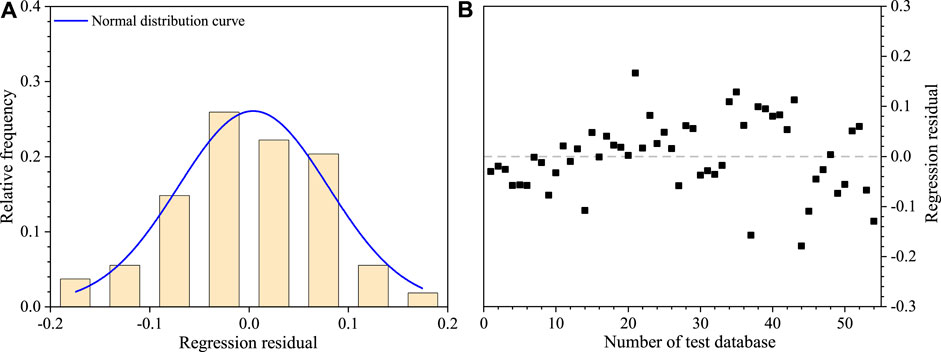
FIGURE 4. The regression analysis results of Eq. 8 based on the database of 54 deflected-type rock avalanches: (A) Histogram of the relative frequency of the log(H/L) regression residuals. (B) Plot of regression residuals of log(H/L).

However, some uncertain parameters were included in the empirical model, resulting in limitations in its practical engineering application. For example, the fall height H is an uncertain parameter before the occurrence of rock avalanches. Some scholars have introduced the height of the source area (h') or slope height (h) to replace the fall height (H) in empirical models (e.g., Zhan et al., 2017; Fan et al., 2015). However, the slope height (h) has much more physical significance because it implies the preimpact potential energy of rock avalanches (Guo et al., 2014). In addition, the channel angle (β) is closely related to the slope angle (α) and slope transition angle (γ). Therefore, the slope height (h), landslide volume (V), slope angle (α), slope transition angle (γ) and deflection angle (θ) were considered in the improved empirical model (see Eq. 9). Eventually, the best-fit regression equation was derived from the dataset of Table 2, as shown in Eq. 9:

$h/L=e0.1621{\left(\mathit{tan}\alpha \right)}^{0.6958}{{\left(\tan \theta \right)}^{0.0727}\left(\sin \gamma \right)}^{0.0865}{\left(V^{1/3}{h}^{-1}\right)}^{-0.1206}(9)$

The adjusted coefficient of determination R² is relatively high, with a value of 0.7, which indicates a good correlation between h/L and the landslide volume, slope height and the three characteristic parameters of local topography. This high R² indicates the small scatter in the data points about the regression line. In addition, the histogram of relative frequency (Figure 5A) shows that the regression residuals of log h/L also follow an approximate normal distribution. Meanwhile, the plot of residuals (Figure 5B) demonstrates the independence in residuals and homogeneity of variance. The p value (0.036) of the significance test for Eq. 9 is less than 0.05, indicating that this improved empirical model is also statistically significant at a 95% confidence level.

FIGURE 5

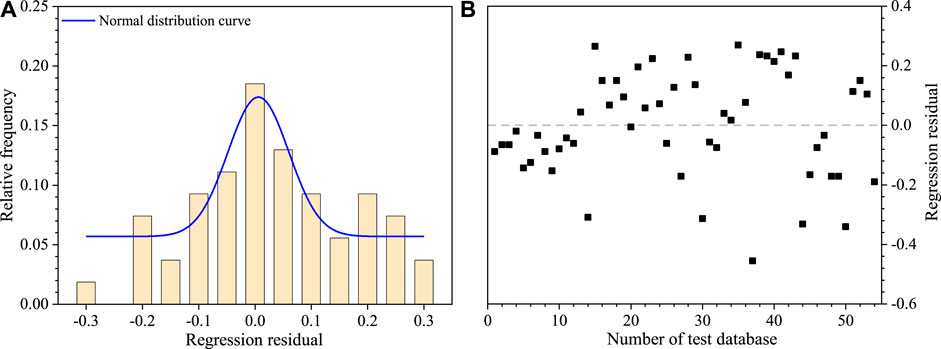
FIGURE 5. The regression analysis results of Eq. 9 based on the database of 54 deflected-type rock avalanches: (A) Histogram of the relative frequency of the log(h/L) regression residuals. (B) Plot of regression residuals of log(h/L).

4.3 Applicability validation

The agreement between predictions and observations is usually used to evaluate the prediction accuracy of the empirical model (Qiu et al., 2018). Figure 6A compares the predicted travel distances estimated by Eq. 9 with the observed avalanches of 54 deflected-type rock avalanches. The predicted values of the samples are close to the observed values (Figure 6A). The estimation error results show that Eq. 9 has an average error of < 20% (Table 2). The self-verification results suggest that Eq. 9 is valid for most deflection-type rock avalanches (Figure 6A). The database of Table 3 is used to further discuss the validity of Eq. 9. The compared results between the observed and predicted travel distances of 10 deflected-type rock avalanches are depicted in Figure 6B. The analysis results of the estimation error show that the maximum error is 41.81%, the minimum error is 0.46% and the average error is approximately 20% (Table 3). Based on this, it can be determined that the improved empirical model (Eq. 9) achieves an acceptable prediction accuracy for the travel distance of deflected-type rock avalanches in the Wenchuan earthquake area.

FIGURE 6

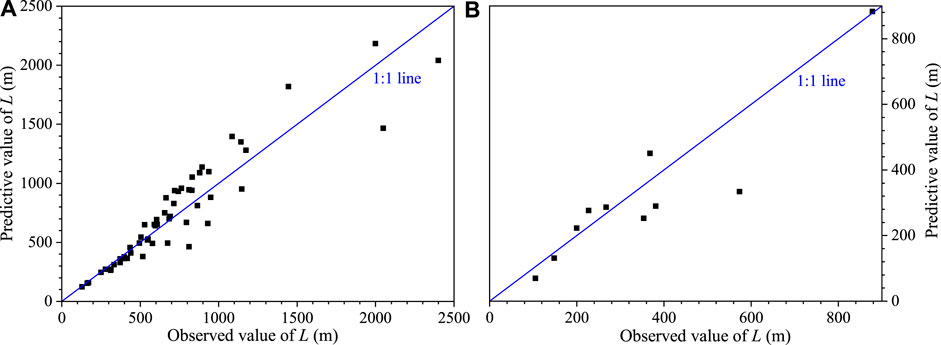
FIGURE 6. The comparison between the observed and predicted travel distances for Eq. 9: (A) Comparison results of 54 deflected-type rock avalanches; (B) comparison results of an independent validation dataset of 10 deflected-type rock avalanches.

5 Discussion

The H/L ratio is commonly used to study the mobility of rock avalanches in previous study (e.g., Qiu et al., 2018; Liu et al., 2021a). Many studies have shown a negative correlation between the H/L ratio and the landslide volume, although the slope and intercept of its regressive relationship are varied (e.g., Hattanji and Moriwaki 2009; Qiu et al., 2018; Strom et al., 2019; Mitchell et al., 2020). In this study, we propose an alternative parameter, the h/L ratio, and the regression analysis results show that the h/L ratio decreases with an increasing landslide volume (V), suggesting the h/L ratio also can be used to evaluate the mobility of rock avalanches. Compared to H/L ratio, the h/L ratio is preferable as a measure of the travel distance prediction of rock avalanches due to the higher coefficient of determination of h. In addition, the simple linear regression of the logarithm of the h/L ratio plotted against the logarithm of V^1/3/h also show a negative correlation, but the very low coefficient of determination R² (0.26) indicates that the simple linear regression is weak (Figure 7A). This finding may primarily be attributed to neglecting the effects of other influence factors, such as local topographic parameters, etc., As shown in Eq. 9, the multiple linear regression of the logarithm of h/L versus the logarithm of other parameters consisting of slope height (h), landslide volume (V), slope angle (α), deflection angle (θ) and slope transition angle (γ) has a high correlation coefficient (R²=0.7) and strong statistical significance level. It can be concluded that the local topography plays an important role in the mobility of rock avalanches. Therefore, more consideration should be given to the influence of local topographic parameters in the empirical model for the travel distance prediction of deflection-type rock avalanches.

FIGURE 7

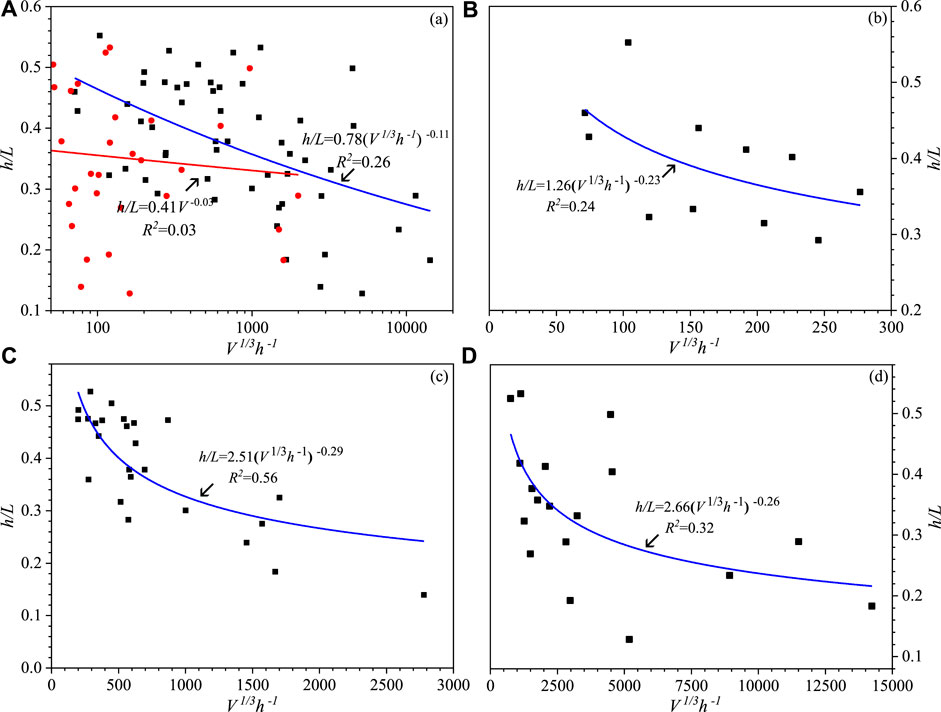
FIGURE 7. Simple linear regression of the logarithm of the h/L ratio predicted from the logarithm of V^1/3/h or V without consideration of the local topography: (A) Regardless of the volume effect; (B) large-scale rock avalanches; (C) medium-scale rock avalanches; (D) small-scale rock avalanches.

In previous study, the effects of local topography on rock avalanches’ mobility have been constantly focus of attention by some authors who explored the variability in behaviour between the rock avalanches events of different local topography categories (e.g., Zhang and Yin, 2013; Liu et al., 2021a). However, the focus of this paper is the sensitivity analysis of different local topographic parameters to rock avalanches’ mobility for a certain confinement type. Therefore, another three best-fit regression models, in which only two local topographic parameters are considered, were derived from the dataset of 54 deflected-type rock avalanches (Table 4). A comparison shows that the correlation coefficients for these three regression models are 0.52, 0.68, 0.67 respectively, which both lower than that of Eq. 9. This means that the travel distance predicted using three independent topographic variables performs better than the travel distance predicted using two independent variables. Additionally, MAPE and TIC values can directly reflect the effect of various topographic parameters on the mobility of deflected-type rock avalanches. The results show that the MAPE and TIC values calculated by Eq. 12 are the lowest, followed by the MAPE and TIC values calculated by Eq. 11. The MAPE and TIC values calculated by Eq. 10 are the highest. The results suggest that the prediction accuracy decreases in turn for Eqs 10–12. Hence, according to the MAPE and TIC values, it can be inferred that the order of sensitivity of the three independent topographic parameters on the mobility of deflected-type rock avalanches is as follows from large to small successively: α > θ > γ. This indicate that the slope angle (α) is predominant in the travel distance, which is reverse to the channelized rock avalanches. Previous study shows the slope angle (α) does not have a significant correlation with travel distance, whereas the channel angle (β) plays the dominating role in the travel distance of channelized rock avalanches (Zhan et al., 2017). Moreover, the sensitivity analysis results indicate that the mobility of deflected-type rock avalanches is also strongly dependent on the deflection angle (θ), which is different from channelized rock avalanches.

TABLE 4

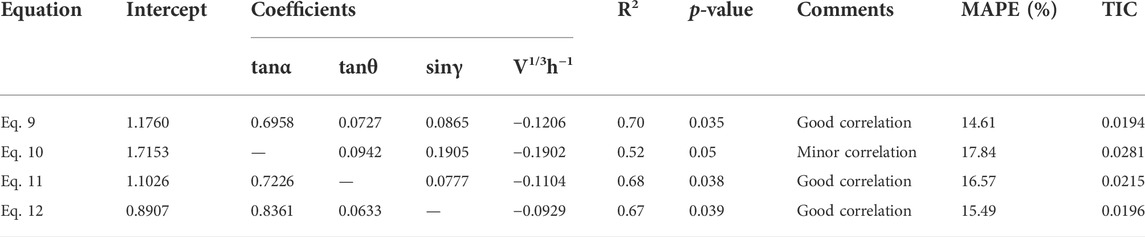
TABLE 4. Comparison of the regression results for different empirical models using different independent topographic variables.

The positive correlation between travel distance and landslide volume of rock avalanches has been discussed in previous study (e.g., Budetta and De Riso 2004; Guo et al., 2014), and the predominant effects of landslide volume on mobility of rock avalanches was stressed. In this study, 54 deflected-type rock avalanches were divided into three categories, including large-scale (V >100 × 10⁴ m³), medium-scale (10 × 10⁴ ≤ V ≤ 100 × 10⁴ m³) and small-scale (V <10 × 10⁴ m³) rock avalanches according to the landslide volume. The results show a lower significance level and correlation coefficients of the simple linear regressions of the logarithm of h/L versus the logarithm of V^1/3/h for rock avalanches with different scales (Figures 7B–D). This indicate that the simple linear regressions between the logarithm of h/L ratio and logarithm of V^1/3/h is rather weak. However, the multiple linear regression models in which the local topographic parameters were considered (Eqs. 13–15) have higher significance levels and correlation coefficients (Table 5). The correlation coefficients in sequence from large to small corresponds to the regression models of small-, medium- and large-scale rock avalanches. In addition, the calculation results of MAPE and TIC show that the prediction accuracy from large to small corresponds to Eqs 13–15 (Table 5). This result suggests that the effect of local topography on the mobility of rock avalanches gradually decreases with increasing landslide scale. Therefore, we suggest that more quantifiable influential factors should be introduced in the empirical model to improve the prediction accuracy of large-scale deflection-type rock avalanches.

TABLE 5

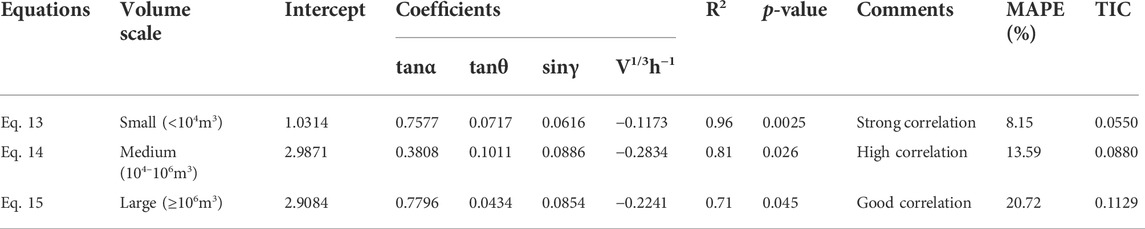
TABLE 5. The multiple linear regression results for deflection-type rock avalanches with different landslide scales.

Empirical models as a practical tool to estimate travel distance can be introduced in the GIS operation platform, which can provide a preliminary delineation of potentially endangered regions of potential rock avalanche (Mergili et al., 2015). This puts forward higher requirements for the accuracy of the prediction models. Although we have verified the validity of the presented empirical model (see Eq. 9) for travel distance prediction of deflected-type rock avalanches triggered by earthquake, there are also some limitations or constraints. On the one hand, the effects of numerous factors, such as ground water, substrate material, stratum lithology, etc., on travel distance were not considered in empirical model. Previous studies have revealed that these factors have a significant impact on the mobility of rock avalanches (e.g., Corominas 1996; Sassa et al., 2004; Guo et al., 2014). For example, due to extensive distribution of groundwater (Zhang et al., 2021), it provides hydrological conditions for the seismic liquefaction of the base material on the movement path, which contributes to the long-distance movement of rock avalanches. Therefore, it deserves more attention that how to quantify these relevant influence factors and incorporate them into the empirical model for travel distance prediction in the future study. On the other hand, in this paper, our database is limited to 54 deflected-type rock avalanches with only seven quantifiable parameters, which might result in wide dispersion and a low coefficient of correlation in some empirical models. Therefore, the next phase of the research focus on a much larger rock avalanche database creation with more quantifiable influential factors, which is conducive to further improve the prediction accuracy of the empirical model.

6 Conclusion

In this study, a database consisting of 54 deflection-type rock avalanches triggered by the Wenchuan earthquake was compiled to obtain a best-fitting empirical model for travel distance prediction. The results indicated that the multiple linear regression of the logarithm of h/L versus the logarithm of other multivariable parameters consisting of slope height (h), landslide volume (V), slope angle (α), deflection angle (θ) and slope transition angle (γ) had a high correlation coefficient and strong statistical significance level. The validity of the proposed empirical model was verified by an independent validation database consisting of 10 deflected-type rock avalanches in the same area. One of the greatest advantages of this empirical model is that all parameters can be quantifiable and obtained before a landslide occurs; thus, this model might be practically applicable in the Wenchuan earthquake area. The results also suggested that the influence of the slope angle (α) on the mobility of rock avalanches was greater than that of the deflection angle (θ) and slope transition angle (γ). However, the influence of local topography on the mobility of large-scale rock avalanches was less than that of small- and medium-scale rock avalanches.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ZP: Supervision; Project administration; Writing- reviewing and editing. HY: Methodology; Investigation; Writing-original draft preparation. ZH: Investigation; Data-gathering. JL: Investigation; Drafting. XX: Investigation; Data-gathering.

Acknowledgments

We sincerely thank anonymous reviewers for their constructive and valuable suggestions, which help improving this manuscript substantially.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Armstrong, J. S., and Collopy, F. (1992). Error measures for generalizing about forecasting methods: Empirical comparisons. Int. J. Forecast 8, 69–80. doi:10.1016/0169-2070(92)90008-W

CrossRef Full Text | Google Scholar

Basharat, M., and Rohn, J. (2015). Effects of volume on travel distance of mass movements triggered by the 2005 Kashmir earthquake, in the Northeast Himalayas of Pakistan. Nat. Hazards 77, 273–292. doi:10.1007/s11069-015-1590-4

CrossRef Full Text | Google Scholar

Budetta, P., and De, Riso. R. (2004). The mobility of some debris flows in pyroclastic deposits of the northwestern Campanian region (southern Italy). Bull. Eng. Geol. Environ. 63 (4), 293–302. doi:10.1007/s10064-004-0244-7

CrossRef Full Text | Google Scholar

Chen, L. C., Yang, H. Q., Song, K. L., Huang, W., Ren, X. H., and Xu, H. (2021). Failure mechanisms and characteristics of the Zhongbao landslide at liujing village, wulong, China. Landslides 18, 1445–1457. doi:10.1007/s10346-020-01594-1

CrossRef Full Text | Google Scholar

Corominas, J. (1996). The angle of reach as a mobility index for small and larger landslides. Can. Geotech. J. 33, 260–271. doi:10.1139/t96-005

CrossRef Full Text | Google Scholar

Ding, M. T., and Hu, K. H. (2014). Susceptibility mapping of landslides in Beichuan County using cluster and MLC methods. Nat. Hazards 70, 755–776. doi:10.1007/s11069-013-0854-0

CrossRef Full Text | Google Scholar

Fan, X. M., Hsein, J. C., Janusz, W., Huan, R. Q., Xu, Q., Gianvito, S., et al. (2018). What we have learned from the 2008 wenchuan earthquake and its aftermath: A decade of research and challenges. Eng. Geol. 241, 25–32. doi:10.1016/j.enggeo.2018.05.004

CrossRef Full Text | Google Scholar

Fan, X. Y., Leng, X. Y., and Duan, X. D. (2015). Influence of terrain factor on movement distances of toe-type and turning-type landslides triggered by earthquake. Chin. J. Rock Soil Mech. 36, 1380–1388. doi:10.16285/j.rsm.2015.05.021

CrossRef Full Text | Google Scholar

Finlay, P. J., Mostyn, G. R., and Fell, R. (1999). Landslide risk assessment: Prediction of travel distance. Can. Geotech. J. 36, 556–562. doi:10.1139/cgj-36-3-556

CrossRef Full Text | Google Scholar

Gao, Y., Yin, Y. P., Li, B., Feng, Z., Wang, W. P., and Zhang, N., (2017). Characteristics and numerical runout modeling of the heavy rainfall-induced catastrophic landslide–debris flow at sanxicun, dujiangyan, china, following the wenchuan Ms 8.0 earthquake. Landslides 14 (4), 1361–1374. doi:10.1007/s10346-016-0793-4

CrossRef Full Text | Google Scholar

Ge, Y. F., Tang, H. M., Eldin, M. A. M. Ez., Chen, H. Z., Zhong, P., and Zhang, L., (2019). Deposit characteristics of the Jiweishan rapid long-runout landslide based on field investigation and numerical modeling. Bull. Eng. Geol. Environ. 78 (6), 4383. doi:10.1007/s10064-018-1422-3

CrossRef Full Text | Google Scholar

Ge, Y. F., Zhou, T., Tang, H. M., and Lin, Z. S. (2020a). Influence of the impact angle on the motion and deposition of granular flows. Eng. Geol. 275, 105746. doi:10.1016/j.enggeo.2020.105746

CrossRef Full Text | Google Scholar

Ge, Y. F., Zhou, T., Tang, H. M., and Lin, Z. S. (2020b). Influence of the impact angle on the motion and deposition of granular flows. Eng. Geol 275, 105746. doi:10.1016/j.enggeo.2020.105746

CrossRef Full Text | Google Scholar

Guo, D., Hamada, M., He, C., Wang, Y., and Zou, Y. (2014). An empirical model for landslide travel distance prediction in Wenchuan earthquake area. Landslides 11 (2), 281–291. doi:10.1007/s10346-013-0444-y

CrossRef Full Text | Google Scholar

Hattanji, T., and Moriwaki, H. (2009). Morphometric analysis of relic landslides using detailed landslide distribution maps: Implications for forecasting travel distance of future landslides. Geomorphology 103 (3), 447–454. doi:10.1016/j.geomorph.2008.07.009

CrossRef Full Text | Google Scholar

Heim, A. (1932). Landslides and human lives. Vancouver, BC, Canada: Bitech Publishers. 0-921095-06-6.

Google Scholar

Hsu, K. J. (1975). Catastrophic debris streams (sturzstroms) generated by rockfalls. Geol. Soc. Am. Bull. 86, 1292–2140. doi:10.1130/0016-7606(1975)86<129:CDSSGB>2.0.1

CrossRef Full Text | Google Scholar

Huang, D., Li, Y. Q., Song, Y. X., Xu, Q., and Pei, X. J. (2019). Insights into the catastrophic xinmo rock avalanche in maoxian county, China: Combined effects of historical earthquakes and landslide amplification. Eng. Geol. 258, 105158. doi:10.1016/j.enggeo.2019.105158

CrossRef Full Text | Google Scholar

Huang, T., Ding, M. T., Tao, S., Tian, S. J., and Yang, J. T. (2017). Numerical simulation of a high-speed landslide in Chenjiaba, Beichuan, China. J. Mt. Sci. 14 (11), 2137–2149. doi:10.1007/s11629-017-4516-7

CrossRef Full Text | Google Scholar

Hungr, O., and Evans, S. G. (2004). Entrainment of debris in rock avalanches: An analysis of a long run-out mechanism. Geol. Soc. Am. Bull. 116 (9–10), 1240–1252. doi:10.1130/B25362.1

CrossRef Full Text | Google Scholar

Hungr, O., Leroueil, S., and Picarelli, L. (2014). The Varnes classification of landslide types, an update. Landslides 11, 167–194. doi:10.1007/s10346-013-0436-y

CrossRef Full Text | Google Scholar

Kang, C., Ren, D. X., Gao, X. F., Han, C. T., and Wang, Y. X. (2021). Study of kinematic characteristics of a rock avalanche and subsequent erosion process due to a debris flow in Wenjia gully, Sichuan, China. Nat. Hazards 106, 937–964. doi:10.1007/s11069-021-04501-6

CrossRef Full Text | Google Scholar

Kang, Y., Zhao, C. Y., Zhang, Q., Lu, Z., and Li, B. (2017). Application of InSAR techniques to an analysis of the guanling landslide. Remote. Sens. 9 (10), 1046. doi:10.3390/rs9101046

CrossRef Full Text | Google Scholar

Knapp, S., and Krautblatter, M. (2020). Conceptual framework of energy dissipation during Disintegration in rock avalanches. Front. Earth Sci. 8, 263. doi:10.3389/feart.2020.00263

CrossRef Full Text | Google Scholar

Leuthold, R. M. (1975). On the use of Theil's inequality coefficients. Am. J. Agric. Econ. 57, 344–346. doi:10.2307/1238512

CrossRef Full Text | Google Scholar

Li, Y., Zhou, R. J., Zhao, G. H., Li, H. B., Su, D. C., and Ding, H. R., (2014). Tectonic uplift and landslides triggered by the wenchuan earthquake and constraints on orogenic growth: A case study from hongchun gully, longmen mountains, sichuan, China. Quatern. Int. 349 (28), 142–152. doi:10.1016/j.quaint.2014.05.005

CrossRef Full Text | Google Scholar

Liu, H. W., Zhao, X. Y., and Xiao, D. (2021a2021). Effects of local topography on the mobility of rock avalanches: A statistical analysis based on 36 cases from south-western China. Eng. Geol. 294, 106351. doi:10.1016/j.enggeo.2021.10635

CrossRef Full Text | Google Scholar

Liu, H. X., Qiu, T., and Xu, Q. (2021b). Dynamic acceleration response of a rock slope with a horizontal weak interlayer in shaking table tests. PLoS ONE 16 (4), e0250418. doi:10.1371/journal.pone.0250418

PubMed Abstract | CrossRef Full Text | Google Scholar

Mergili, M., Krenn, J., and Chu, H-J. (2015). r.randomwalk v1, a multi-functional conceptual tool for mass movement routing. Geosci. Model Dev. 8, 4027–4043. doi:10.5194/gmd-8-4027-2015

CrossRef Full Text | Google Scholar

Mitchell, A., McDougall, S., Nolde, N., BrideauWhittall, M. A. J., and Aaron, J. B. (2020). Rock avalanche runout prediction using stochastic analysis of a regional dataset. Landslides 17, 777–792. doi:10.1007/s10346-019-01331-3

CrossRef Full Text | Google Scholar

Qiu, H. J., Cui, P., Hu, S., Regmi, A. D., Wang, X. G., and Yang, D. D. (2018). Developing empirical relationships to predict loess slide travel distances: A case study on the loess plateau in China. B. Eng. Geol. Environ. 77, 1299–1309. doi:10.1007/s10064-018-1328-0

CrossRef Full Text | Google Scholar

Sassa, K., Wang, G. H., Fukuoka, H., Wang, F. W., Ochiai, T., and Sugiyama, M. (2004). Landslide risk evaluation and hazard zoning for rapid and long-travel landslides in urban development areas. Landslides 1, 221–235. doi:10.1007/s10346-004-0028-y

CrossRef Full Text | Google Scholar

Strom, A. L., Li, L., and Lan, H. (2019). Rock avalanche mobility: Optimal characterization and the effects of confinement. Landslides 16, 1437–1452. doi:10.1007/s10346-019-01181-z

CrossRef Full Text | Google Scholar

Tang, C., van Asch, T. W. J., Chang, M., Chen, G. Q., Zhao, X. H., and Huang, X. C. (2012). Catastrophic debris flows on 13 august 2010 in the qingping area, southwestern China: The combined effects of a strong earthquake and subsequent rainstorms. Geomorphol 139–140, 559–576. doi:10.1016/j.geomorph.2011.12.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Ran, Y. K., Li, Y. B., Gomez, F., and Chen, L. C. (2014). Southwest China is on the southeastern edge of the Tibetan Plateau and is characterised by complex geological structures. Tectonophysics 628, 206–217. doi:10.1016/j.tecto.2014.04.040

CrossRef Full Text | Google Scholar

Yang, J. Q., Xu, Z. M., Zhang, R., Chen, J. P., Ren, Z., and Luo, R. Z., (2017). Formation and evolution of Emeishan basalt saprolite in vadose zones of Touzhai landslide source Rockmass. J. Mt. Sci. 14 (6), 1174–1184. doi:10.1007/s11629-016-4169-y

CrossRef Full Text | Google Scholar

Zhan, W. W., Fan, X. M., Huang, R. Q., Pei, X. J., Xu, Q., and Li, W. L. (2017). Empirical prediction for travel distance of channelized rock avalanches in the Wenchuan earthquake area. Nat. Hazards Earth Syst. Sci. 17, 833–844. doi:10.5194/nhess-17-833-2017

CrossRef Full Text | Google Scholar

Zhang, M., Yin, Y., and McSaveney, M. (2016). Dynamics of the 2008 earthquake-triggered wenjiagou creek rock avalanche, qingping, sichuan, China. Eng. Geol. 200, 75–87. doi:10.1016/j.enggeo.2015.12.008

CrossRef Full Text | Google Scholar

Zhang, M., and Yin, Y. P. (2013). Dynamics, mobility-controlling factors and transport mechanisms of rapid long-runout rock avalanches in China. Eng. Geol. 167, 37–58. doi:10.1016/j.enggeo.2013.10.010

CrossRef Full Text | Google Scholar

Zhang, Y. H., Dai, Y. S., Wang, Y., Huang, X., Xiao, Y., and Pei, Q. M. (2021). Hydrochemistry, quality and potential health risk appraisal of nitrate enriched groundwater in the Nanchong area, southwestern China. Sci. Total Environ. 784, 147186. doi:10.1016/j.scitotenv.2021.147186

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y. H., Yao, R. W., Wang, Y., Duo, J., and Cao, H. W. (2022). Zircon U−Pb and sericite Ar−Ar geochronology, geochemistry and S−Pb−Hf isotopes of the Zebuxia Pb−Zn deposit, Tibet, southwestern China. Ore Geol. Rev. 148, 104999. doi:10.1016/j.oregeorev.2022.104999

CrossRef Full Text | Google Scholar

Zheng, G., Xu, Q., and Peng, S. Q. (2018). Chute experiments of the long-runout distance of rock avalanche (in Chinese). Rock Soil Mech. 40 (12), 1–10. doi:10.16285/j.rsm.2018.1827

CrossRef Full Text | Google Scholar