Time-Varying Effect of Ductile Flexural Toppling Failure on Antidip Layered Rock Slope

Ductile flexural toppling failure is a common form of toppling failure, and it is the product of long-term geological history and shows the characteristics of long-term deformation and progressive failure. The creep characteristics of rock mass have been seldom considered in the current research on toppling, especially interlayer creep of rock layers in the process of toppling. Based on the thought of deformation stability analysis, the flexural toppling failure was divided into the following four stages: start-up, rapid deformation, transient stability, and long-term creep stages. Combined with mechanical analysis, the developmental conditions of the start-up, transient stability, and long-term creep development stages are discussed respectively. Finally, several cases were selected to analyze the stage and the stability of the toppling deformation body, as well as to verify the rationality of the mechanical analysis condition. Study results show that the start-up conditions meet Equation 2, the rock layer inclination and slope angle is $\mathrm{0}\mathrm{.5}\pi -\phi$ in the transient stability stage, and that angle is the infinite $\mathrm{0}\mathrm{.5}\pi$ in the long-term creep stage. Other external forces (such as water pressure) will intensify the development of ductile flexural toppling failure, so that the angle between the toppled bedding surface and the slope surface increases. It is of great significance to analyze the development stage of the ductile flexural toppling, comprehensively analyze and evaluate the stability of the ductile flexural toppling, reasonably develop and utilize its self-stability ability, and set up support measures.

Highlights

1. Based on the thought of deformation stability analysis, we divided flexural toppling failure into four stages.

2. The developmental conditions of the start-up, transient stability, and long-term creep development stages are discussed respectively using mechanical analysis.

3. Several cases were selected to verify the rationality of the developmental conditions.

4. This study is of great significance for comprehensively analyzing the development stage and evaluating the stability of the ductile flexural toppling.

Introduction

Toppling failure of antidip layered rock slope, as a typical slope failure, has been reported in an increasing number of situations with the construction of mines, highways, hydropower stations, and so on (Cruden and Hu 1994; Tamrakar et al., 2002; Huang 2007; Liu et al., 2016; Zhang et al., 2018; Cai et al., 2019; Ning et al., 2019; Zhu et al., 2020). Goodman (2013) summarized the developments in the research of toppling deformation and concluded that toppling generally occurs in foundations, tunnels, and underground chambers or on a small scale in any rocky landscape where frost, creep, or water forces are active.

According to the characteristics of deformation and scale of toppled slopes, the following two types of failure mechanisms associated with toppling were proposed by Nichol et al. (2002) and Huang and Li (2017): a ductile flexural toppling mechanism and a brittle toppling mechanism, as described by Goodman (2013). Brittle toppling is generally developed in hard layered rock mass, mainly characterized by “fold and break” of the rock plate, rigid rotational structural deformation, and small-scale instability in the shallow of a slope. Furthermore, ductile flexural toppling often occurs in a thin layer of soft rock mass over a long time and at a considerable depth, and the slope deformation is mainly characterized by “bent but not broken.” The deformation essence is mainly the gravity creep deformation of rock strata in the long geological history, and its development depth can reach tens or even hundreds of meters.

Toppling failure has been found in many locations, and new topples continue to be discovered and observed (Wang et al., 1992; Huang 2007; Zhang et al., 2015; Xie et al., 2018; Xia et al., 2019; Tu et al., 2020; Zhao et al., 2021). In particular, in mountain and gorge regions, this type of toppling failure has a large toppling development depth more than 100 m and has been observed in several notable locations: the left bank slope of Jinping-I Hydropower Station (>200 m), the Yinshuigou deformable slope at Xiaowan Hydropower Station (>200 m), the slope of Miaowei Hydropower Station (>200 m), the right abutment slope of Huangdeng Hydropower Station (>150 m), the right bank slope of Wulonglong Hydropower Station (>130 m), and the left bank slope of Longtan Hydropower Station (>200 m). Such large-scale toppling will eventually and possibly develop into a giant landslide, posing threats to the project. Huang (2007), Huang (2008), and Huang and Li (2017) proposed the concept of three-stage development of surface regeneration, long-term time-dependent deformation, and progressive failure of high slope based on the above studies.

Previous studies on toppling failure mainly focus on the mechanical theory research based on the mechanics of brittle materials, stability analysis at a certain moment, or study on the deformation failure mechanism based on physical tests and numerical tests. Aydan and Kawamoto (1992), Adhikary et al. (1997), and Adhikary and Dyskin (2007) established the toppling mechanics model of cantilever beam by applying the limit equilibrium theory, assuming that the interlayer force is the concentrated force and considering the self-weight of rock strata, and they verified it through the physical test. Amini et al. (2009), Amini et al. (2012), Amini et al. (2017), Amini et al. (2018) combined the GB method with the method of Aydan to introduce a solution for the analysis of block flexure toppling failure, secondary toppling failure, and they proposed an efficient method for analysis of the toppling based on compatibility principles governing the behavior of a cantilever beams. Liu et al. (2009) proposed the transfer coefficient method to analyze the stability of the toppling deformation body, and they analyzed the stability or designed the support scheme by calculating the residual sliding force of the slope foot block.

The existing studies of toppling fracture depth concentrate on the first toppling depth, since the actual field phenomenon is the product of multi-toppling, and there are several toppling interfaces or discontinuities. After the first toppling, the shape of the progressive failure of the second or multiple toppling illustrates the characteristics of flexural toppling. The studies indicate that the flexural toppling has notably the characteristics of time-dependent deformation and progressive failure. The creep characteristics of rock mass are seldom considered in the current studies of toppling, especially interlayer creep of rock layers in the process of toppling. Xiao and Wang (1991) and Wang et al. (1992) studied the creep mechanism of bending toppling of the toppled slope on the left bank of Longtan Hydropower Station. Pang et al. (2016) introduced a rheological model to consider creep characteristics of rock mass in the analysis of toppling fracture depth. Whereas, the creep contribution rate of rock mass is seldom for the flexural toppling, which is mainly due to the interlaminar dislocation and shear creep. Therefore, based on the start-up condition of toppling, a method for the analysis of bending toppling stage considering interlaminar shear creep is proposed in this study. From the perspective of time-dependent deformation and progressive failure, the mechanical conditions and stage characteristics of slope morphology were analyzed, and they further studied the deformation characteristics under the action of external forces (water pressure). It is important to understand the relationship between the development stage and the development state of the deformed body. According to the thought of deformation stability, the creep model of interlayers can be better and actually used to analyze the development process of ductile flexural toppling deformation.

Mechanical Conditions of the Process of Ductile Flexural Toppling

The ductile flexural toppling is based on the following assumptions. 1) The toppling can occur when the bedding surface is steeper and the slope angle is larger. 2) The thickness of the rock layer is infinitesimal relative to the scale of the whole slope, which can be regarded as a thin slab with little stiffness. 3) The unbalanced force on thin rock slab drives the bending and toppling of rock slabs, and the weight of that is negligible relative to the value of the stress field. 4) The maximum principal stress appears in the slope surface approximately parallel to the slope surface.

The bending and toppling deformation of antidip layered rock mass can be divided into translational displacement and rotational displacement. This study only deals with the rotational displacement. Considering the complexity of stress change and adjustment in the process of bending toppling, the deformation state at instantaneous termination is only considered in the analysis. The process of bending toppling occurs as follow: the start-up, rapid deformation, transient stability, and long-term toppling creep stage. The mechanical conditions at each stage are briefly described in the following:

Start-Up Condition

Goodman and Bray (1976) believed that the occurrence of flexural toppling needs to meet the requirements of interlayer dislocation, and the bending tensile stress of rock slab exceeds its tensile strength. This approach ignored the cohesion between layers and only considered the relationship between the slope angle, the inclination angle of the rock slab, and the internal friction angle, and the kinematic conditions for the toppling of the rock slab were obtained (Figure 1):

$\left(\mathit{180}\mathrm{-}\alpha \mathrm{-}\beta \right)\le \left(\mathrm{90-}\phi \right)\mathrm{,}\text{simplified to}\mathit{\beta }\ge \left(90\mathrm{-}\alpha \right)+\phi ,(1)$

where σ is parallel to the slope surface, β is the angle between the bedding plane and the horizontal plane, φ is the internal friction angle of the bedding plane, and α is the angle between the slope surface and the horizontal plane.

FIGURE 1

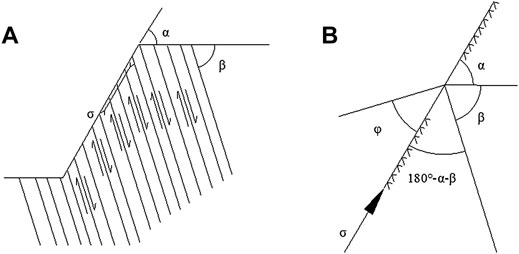
FIGURE 1. Kinematic conditions for flexural slip preceding toppling: (A) directions of stress and slip directions in rock slope; (B) condition for interlayer slip.

Due to the neglect of cohesion between layers, the calculation results are safer. Therefore, a comprehensive internal friction angle can be adopted to comprehensively analyze the start-up conditions of interlayer dislocation considering cohesion.

$\beta \ge \left(\mathit{90}\mathrm{-}\alpha \right)+{\phi }_e,(2)$

where φ_e is the comprehensive angle of internal friction.

Transient Stability

Based on the assumption of basic conditions, an element is selected from a part of a rock slab in the slope (Figure 2), plane a is the bedding surface, and plane b is the virtual surface. Assume that the internal friction angle of the bedding surface is φ, and cohesion is c, taking the center point O of the microelement zone as the rotation center point. The moment condition for the suspension of the rotation of the element is M_r ≥ M_t, i. e,

$\mathrm{0}\mathrm{.5}b\cdot a\cdot \left[{\tau }_r+\left({\tau }_r+\mathrm{\Delta }\tau \right)\right]\ge \mathrm{0}\mathrm{.5}a\cdot b\cdot \left[{\tau }_t+\left({\tau }_t+\mathrm{\Delta }\tau \right)\right].(3)$

FIGURE 2

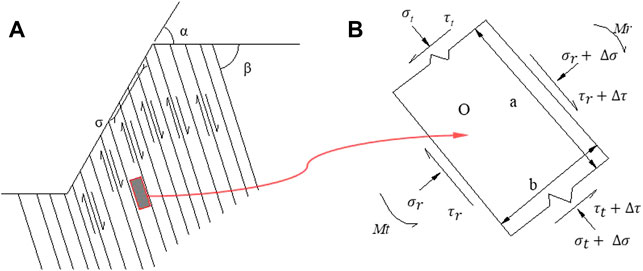
FIGURE 2. Force system on elements of bending and toppling deformation slope: (A) toppling model; (B) elements.

Because of ${\tau }_r+\left({\tau }_r+\mathrm{\Delta }\tau \right)\le {\sigma }_r\cdot \mathit{tan}\phi +c+\left({\sigma }_r+\mathrm{\Delta }\sigma \right)\cdot \mathit{tan}\phi +c$ Then,

${\tau }_t\le {\sigma }_r\cdot \mathit{tan}\phi +c.(4)$

When the rotation is terminated, the stress reaches the equilibrium state and is in the transient stable state.

When the rotation of the rock slab terminates, the stress of the rock slab that reaches the equilibrium state and then it gets into the transient stable state. Thus,

$\begin{array}{l}{\tau }_r={\tau }_t\\ {\tau }_r\le {\sigma }_r\cdot \mathit{tan}\phi +c.\end{array}(5)$

The toppling bending deformation of layered rock mass is mainly realized by the relative shear displacement between layers. The accumulated shear displacement and the rotation of rock slabs present the overall bending and the toppling deformation of slope.

Using the graphic method of the Coulomb–Mohr strength theory, the stress, corresponding to the shaded region in Figure 3A, does not satisfy the condition of transient stability. Assuming that V is the angle between the normal of the bedding surface and σ₁, the instability interval can be expressed as upper bound V₁ and lower bound V₂.

$\begin{array}{l}\mathit{sin}\omega =\frac{{\sigma }_1+{\sigma }_3+2c \mathit{tan}\phi }{{\sigma }_1-{\sigma }_3}\cdot \mathit{sin}\phi \\ 2V_1=\omega +\phi 2V_2=\pi -\omega +\phi \text{, then}\end{array}$

$V_1=\mathrm{0}\mathrm{.5}\left[\phi +{\mathit{sin}}^{-1}\left(\frac{{\sigma }_1+{\sigma }_3+2c \mathit{cot}\phi }{{\sigma }_1-{\sigma }_3}\cdot \mathit{sin}\phi \right)\right],(6)$

$V_2=\mathrm{0}\mathrm{.5}\left[\pi +\phi -{\mathit{sin}}^{-1}\left(\frac{{\sigma }_1+{\sigma }_3+2c \mathit{cot}\phi }{{\sigma }_1-{\sigma }_3}\cdot \mathit{sin}\phi \right)\right],(7)$

where V∈[$V_1\mathrm{,}{V}_2$], the rock slab will toppled and bended.

FIGURE 3

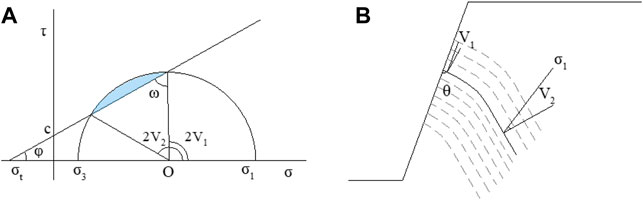
FIGURE 3. Coulomb–Mohr diagram of the toppling condition of rock slab. (A) Coulomb–mohr diagram of toppling condition; (B) toppling form.

During the process of toppling, the angle V between the normal of bedding surface and ${\sigma }_1$ gradually increases, and the angle θ between the bedding surface and the slope surface decreases. The conditions for toppling can be expressed by V:

$V=V_1=\mathrm{0}\mathrm{.5}\left[\phi +{\mathit{sin}}^{-1}\left(\frac{{\sigma }_1+{\sigma }_3+2c \mathit{cot}\phi }{{\sigma }_1-{\sigma }_3}\cdot \mathit{sin}\phi \right)\right].(8)$

Assuming that the stress distribution in the slope is continuous, the ductile flexural toppling deformation shape is approximately continuous as well. Finite element method can be used to determine the slope stress distribution, and the experiments were used to determine the internal friction angle of the bedding surface. Then, the profile of flexural toppling shape can be calculated and ascertained. The stress field obtained at the slope surface is as follows: ${\sigma }_1$ is parallel to the slope surface, and ${\sigma }_3$ approaches 0:

$V_0=\mathrm{0}\mathrm{.5}\left[\phi +{\mathit{sin}}^{-1}\left(\left(1+2c\frac{\mathit{cot}\phi }{{\sigma }_1}\right)\mathit{sin}\phi \right)\right].(9)$

Assuming θ is the angle between bedding plane and slope surface, then

$\theta =\mathrm{0}\mathrm{.5}\pi -V_0=\mathrm{0}\mathrm{.5}\pi -\mathrm{0}\mathrm{.5}\left[\phi +{\mathit{sin}}^{-1}\left(\left(1+2c\frac{\mathit{cot}\phi }{{\sigma }_1}\right)\mathit{sin}\phi \right)\right].(10)$

Considering weathering or other external forces, the bedding surface opens and separates, c tends to 0, and it is concluded that

$V_0=\phi \theta =\mathrm{0}\mathrm{.5}\pi -\phi .(11)$

To sum up, with respect to the antidip layered slope transformed by weathering or external forces, the angle θ at the slope surface is no more than $\mathrm{0}\mathrm{.5}\pi -\phi$, toppling deformation will occur. For the slope of original rock mass, θ may be <$\mathrm{0}\mathrm{.5}\pi -\phi$, and then Equation 11 can be regarded as an intuitive criterion for whether the start-up occurrence of flexural toppling in antidip weathered rock mass.

Time-Varying on Interlaminar Shear Creep

The shear stress on the bedding surface meets ${\tau }_t=\mathrm{0}\mathrm{.5}\cdot \left({\sigma }_1-{\sigma }_3\right)\cdot \mathit{sin}2V$ at transient stability state, and the shear stress will cause rock slab shear creep along the bedding plane and further toppling. Interlaminar shear dislocation creep property was expressed by ${\tau }_r=\eta \cdot \dot{\epsilon }$ reported by Sun and Zhang (1985); among them, the $\eta$ and $\epsilon$ are for viscous coefficient and the shear strain of the bedding surface, respectively.

By combining the above two formulas, we can obtain:

$\eta \cdot d\epsilon =0.5\cdot \left({\sigma }_1-{\sigma }_3\right)\cdot \mathit{sin}2V\cdot dt\epsilon .(12)$

When the toppled deformation occurs slightly, we can obtain Equation 13 from Figure 4:

$d\epsilon =-dV,(13)$

where dV is the increment of toppled angle of bedding surface of rock slab,

$\mathrm{then,}dt=-\frac{\eta }{{\sigma }_1-{\sigma }_3}\cdot \frac{d2V}{\mathit{sin}2V}.(14)$

FIGURE 4

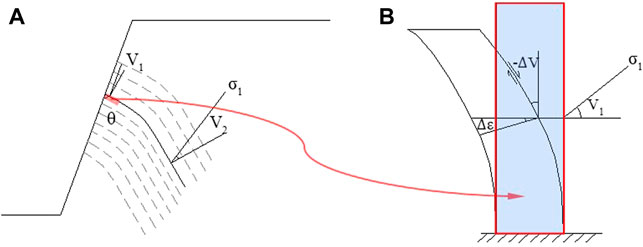
FIGURE 4. Model for shear creep of bedding surface. (A) Toppling element of shear creep; (B) stress-strain state.

We integrate both sides to get

${\displaystyle {\int }_0^{t}dt=-\frac{\eta }{{\sigma }_1-{\sigma }_3}}\cdot {\displaystyle {\int }_{V_1}^V\frac{d2V}{\mathit{sin}2V}},(15)$

$\mathrm{that is,}V={\mathit{tan}}^{-1}\left(\mathit{tan}{V}_1\cdot e^{-\frac{{\sigma }_1-{\sigma }_3}{\eta }\cdot t}\right),(16)$

V₁ can be obtained from Equation 6. Then,

$0\le V\le V_{1}t\in [0,\infty ),(17)$

where $t=0,$ $V=V_1$, $t\to \infty$, and $V\to 0_{\mathrm{o}}$.

At the slope surface, the cohesion

$c \cong 0,{\sigma }_3\cong 0\text{, }\mathit{then}V=\mathit{ta}{\mathit{n}}^{-1}\left(\mathit{tan}{V}_1\cdot e^{-\frac{{\sigma }_1}{\eta }\cdot t}\right),(18)$

according to Equation 18:

$0\le V\le \phi ,\mathrm{0}\mathrm{.5}\pi -\phi \le \theta \le \mathrm{0}\mathrm{.5}\pi t\in [0,\infty ),(19)$

where $t=0,$ $0\le V\le \phi$, $0.5\pi -\phi \le \theta \le 0.5\pi$; $t\to \infty$, $V\to 0,$ $\theta \to 0.5\pi$.

When there is water, the water pressure will cause the rock slab to be further toppled and developed, according to the effective stress principle. Then, the angle $V_1$ between the major stress and the normal of the bedding surface becomes $V_1^{\prime }$:

$V_1^{\prime }=\mathrm{0}\mathrm{.5}\cdot \left[\phi +\mathit{si}{\mathit{n}}^{-1}\left(\frac{{\sigma }_1+{\sigma }_3+2c \mathit{cot}\phi -2\mu }{{\sigma }_1-{\sigma }_3}\cdot \mathit{sin}\phi \right)\right]\le V_1.(20)$

Cases Validation and Discussion

Several typical toppling deformation cases were analyzed by using the mechanical model corresponding to the toppling deformation stage, and the following conclusions were obtained. The details information of typical toppled slopes are shown in Table 1.

TABLE 1

TABLE 1. Some examples of toppling deformation and failure.

Because case 1 has been toppled and destroyed, it must meet the requirements of β ≥ (90―α) + φ. With the relevant information of the formula substituted, it can be obtained that 45°≥ (90° -80°) +24°=34°. The current state the toppled slope is 45°≤ (90° -50°) +24°=64°, indicating that the start-up condition is not satisfied at this time. Judging by the transient stability condition, $\theta =\mathrm{0}\mathrm{.5}\pi -\phi$ =90°–24°=66°, and the angle between the bedding surface and the slope surface is 180°-45°–50°=85° > 66°, which indicates that the transient stability state has passed. Now the time effect of creep was still endured and has not reached the final state of long-term creep by using formula θ_∞=90°>85°.

Similarly, the toppled deformation states of other cases can be judged by the information from Table 1. As for case 9, the initial start-up condition is 40°≤ (90°–60°) +19°=49°, which does not meet the start-up condition formula. Judging from the transient stability condition, $\theta =\mathrm{0}\mathrm{.5}\pi -\phi$ =90°–19°=71°, the angle between the untoppled bedding surface and the slope surface is 180°-60°–40°=80°>71°, indicating that the initial state of the untoppled layers is in the creep stage. The angle of toppled bedding surface and the slope surface was 180°-32°–40°=108°>θ_∞=90°, which indicated that the state of the toppled slope exceeds the final time-varying state, and the toppled angle reaches 18° caused by the long-term cumulative creep and external forces. This example illustrates that interlaminar creep plays a significant role in ductile flexural toppling.

According to the analysis results of typical toppled slopes (Figure 5), the angle θ between the slope surface and bedding surface is summarized in Figure 6A. When the toppling deformation is stable, the angle θ is relatively close to 0.5π. This study investigated the toppling slopes near the Miaowei Hydropower Station, and the investigation results indicate that the angle θ between the toppling layers plane and slope surface is mostly about 0.5π (as shown in Figure 6B), when the toppling rock layer is stable. In some cases, the angle θ near the slope surface increased due to slope structure and other external forces. The similar results were reported by Wu (1997), who investigated the cutting slope along the Yangpingguan–Yanzibian section of the Baocheng railway, and found that several ductile flexural toppling slopes induced by rainfall occur in this region, and the angle θ was close to 90° or >90°. Those cases illustrate the water pressure stress intensified flexural toppling deformation.

FIGURE 5

FIGURE 5. Cases from bank slope on the Miaowei Hydropower Station.

FIGURE 6

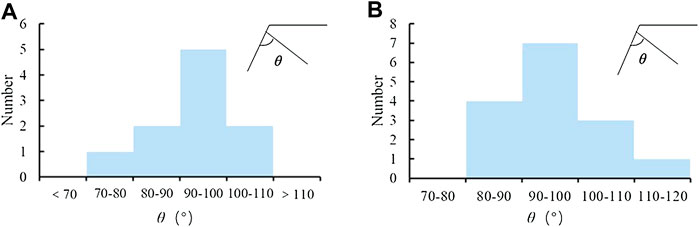
FIGURE 6. Cases of flexural toppling deformation: (A) cases from typical example; (B) cases from bank slope on the Miaowei Hydropower Station.

Conclusion

Ductile flexural toppling is a product of long-term geological evolution history. Considering its progressive failure characteristics, the development process of ductile flexural toppling takes place as follows: the initial start-up stage, rapid development stage, transient stability stage and long-term toppling creep stage.

1) The start-up condition of ductile flexural toppling satisfies Equation 2, which ignores the cohesion between rock strata, and the calculated result is safer. Therefore, a comprehensive internal friction angle can be used to comprehensively analyze the start-up condition of interlayer dislocation with considering cohesion. Under the condition of transient stability, the angle of V₁ between the normal of bedding surface and σ₁ is determined by Equation 6, and θ between the bedding surface and the slope surface is determined by Equation 10 at the final stage of the ductile flexural toppling, where the angle between the toppled bedding surface and the slope surface is $\theta =\mathrm{0}\mathrm{.5}\pi -\phi$.

2) Slip and shear creep occurs between the layers in the transient stability state, thus causing the whole bending and toppling creep deformation of deformation. The angle of V at any time can be determined by Equation 16 and the angle of the slope surface determined by Equation 18. The final state of angle V, considering interlaminar shear creep, is perpendicular to σ₁. That is, the toppled bedding surface is perpendicular to the slope surface.

3) The water pressure can decrease the deformation and stability angle V of the transient stability state and aggravate the toppling of the rock slab. The angle θ of partial toppling deformation bodies between the bedding surface and the slope surface may be >0.5π due to disturbances of other external forces. Various typical cases were statistically analyzed, and the mechanical conditions during the development of ductile flexural toppling deformation were comprehensively analyzed from the start-up stage, over the transient stage, to the long-term creep stage.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author Contributions

JC, DZ, and NJ conceived and designed the paper. JC and DZ analyzed the mechanical model; NJ analyzed and interpreted the data; JC wrote the paper, DZ, JW, XZ, and DL revised the paper.

Funding

The study is financially supported by the National Key R&D Program of China (2018YFC1504905), the Opening Fund of State Key Laboratory of Geohazard Prevention and Geoenvironment Protection (Chengdu University of Technology, SKLGP 2022K004), and the National Natural Science Foundation of China (41907250,41772317). The Opening Fund of State Key Laboratory of Geohazard Prevention and Geoenvironment Protection (Chengdu University of Technology, SKLGP 2022K004) pays for open access publication fees.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Special thanks go to the expertise comments from the reviewers and editors for improving the manuscript.

References

Adhikary, D. P., Dyskin, A. V., Jewell, R. J., and Stewart, D. P. (1997). A Study of the Mechanism of Flexural Toppling Failure of Rock Slopes. Rock Mech. Rock Engng 30 (2), 75–93. doi:10.1007/BF01020126

CrossRef Full Text | Google Scholar

Adhikary, D. P., and Dyskin, A. V. (2007). Modelling of Progressive and Instantaneous Failures of Foliated Rock Slopes. Rock Mech. Rock Engng. 40 (4), 349–362. doi:10.1007/s00603-006-0085-8

CrossRef Full Text | Google Scholar

Amini, M., Ardestani, A., and Khosravi, M. H. (2017). Stability Analysis of Slide-Toe-Toppling Failure. Eng. Geol. 228, 82–96. doi:10.1016/j.enggeo.2017.07.008

CrossRef Full Text | Google Scholar

Amini, M., Majdi, A., and Aydan, Ö. (2009). Stability Analysis and the Stabilisation of Flexural Toppling Failure. Rock Mech. Rock Eng. 42, 751–782. doi:10.1007/s00603-008-0020-2

CrossRef Full Text | Google Scholar

Amini, M., Majdi, A., and Veshadi, M. A. (2012). Stability Analysis of Rock Slopes against Block-Flexure Toppling Failure. Rock Mech. Rock Eng. 45, 519–532. doi:10.1007/s00603-012-0220-7

CrossRef Full Text | Google Scholar

Amini, M., Sarfaraz, H., and Esmaeili, K. (2018). Stability Analysis of Slopes with a Potential of Slide-Head-Toppling Failure. Int. J. Rock Mech. Min. Sci. 112, 108–121. doi:10.1016/j.ijrmms.2018.09.008

CrossRef Full Text | Google Scholar

Aydan, O., and Kawamoto, T. (1992). The Stability of Slopes and Underground Openings against Flexural Toppling and Their Stabilisation. Rock Mech. Rock Engng 25 (3), 143–165. doi:10.1007/BF01019709

CrossRef Full Text | Google Scholar

Cai, J.-C., Ju, N.-P., Huang, R.-Q., Zheng, D., Zhao, W.-H., Li, L.-Q., et al. (2019). Mechanism of Toppling and Deformation in Hard Rock Slope: a Case of Bank Slope of Hydropower Station, Qinghai Province, China. J. Mt. Sci. 16, 924–934. doi:10.1007/s11629-018-5096-x

CrossRef Full Text | Google Scholar

Cruden, D. M., and Hu, X.-Q. (1994). Topples on Underdip Slopes in the Highwood Pass, Alberta, Canada. Q. J. Eng. Geol. Hydrogeology 27, 57–68. doi:10.1144/GSL.QJEGH.1994.027.P1.08

CrossRef Full Text | Google Scholar

Goodman, R. E., and Bray, J. W. (1976). “Toppling of Rock Slopes,” in Rock Engineering for Foundations & Slopes (Boulder, CO: ASCE), 201–234.

Google Scholar

Goodman, R. E. (2013). “Toppling - - A Fundamental Failure Mode in Discontinuous Materials --- Description and Analysis,” in 2013 Congress on Stability and Performance of Slopes and Embankments III, Geo-Congress 2013 (San Diego, United States: Geotechnical Special Publication. ASCE), 2348–2378. doi:10.1061/9780784412787.227

CrossRef Full Text | Google Scholar

Huang, R. Q. (2008). Geodynamic Process and Stability Control of High Rock Slope Development. Chin. J. Rock Mech. Eng. 27 (08), 1525–1544. doi:10.3321/j.issn:1000-6915.2008.08.002

CrossRef Full Text | Google Scholar

Huang, R. Q. (2007). Large-scale Landslides and Their Sliding Mechanisms in China since the 20th Century. Chin. J. Rock Mech. Eng. 26, 433–454. doi:10.3321/j.issn:1000-6915.2007.03.001

CrossRef Full Text | Google Scholar

Huang, R. Q., and Li, Y. S. (2017). Yan M the Implication and Evaluation of Toppling Failure in Engineering Geology Practice. J. Eng. Geol. 25 (05), 1165–1181. doi:10.13544/j.cnki.jeg.2017.05.001

CrossRef Full Text | Google Scholar

Liu, C. H., Jaksa, M. B., and Meyers, A. G. (2009). A Transfer Coefficient Method for Rock Slope Toppling. Can. Geotech. J. 46 (1), 1–9. doi:10.1139/t08-094

CrossRef Full Text | Google Scholar

Liu, M., Liu, F.-Z., Huang, R.-Q., and Pei, X.-J. (2016). Deep-seated Large-Scale Toppling Failure in Metamorphic Rocks: a Case Study of the Erguxi Slope in Southwest China. J. Mt. Sci. 13, 2094–2110. doi:10.1007/s11629-015-3803-4

CrossRef Full Text | Google Scholar

Nichol, S. L., Hungr, O., and Evans, S. G. (2002). Large-scale Brittle and Ductile Toppling of Rock Slopes. Can. Geotech. J. 39 (4), 773788–788. doi:10.1139/t02-027

CrossRef Full Text | Google Scholar

Ning, Y., Zhang, G., Tang, H., Shen, W., and Shen, P. (2019). Process Analysis of Toppling Failure on Anti-dip Rock Slopes under Seismic Load in Southwest China. Rock Mech. Rock Eng. 52, 4439–4455. doi:10.1007/s00603-019-01855-z

CrossRef Full Text | Google Scholar

Pang, B., Zheng, D., and Huang, P. (2016). Geological Model Analysis on the Depth of Toppling Deformation in the Anti-dip Rock Slopes. Sci. Technol. Eng. 16 (18), 129–134. 1671-1815( 2016) 018-0129-06. doi:10.3969/j.issn.1671-1815.2016.18.023

CrossRef Full Text | Google Scholar

Sun, G. Z., and Zhang, W. B. (1985). A Common Rock Structure-Board Crack Structure and its Mechanical Model. J. Eng. Geol. 28 (3), 275–282.

Google Scholar

Tamrakar, N. K., Yokota, S., and Osaka, O. (2002). A Toppled Structure with Sliding in the Siwalik Hills, Midwestern Nepal. Eng. Geol. 64, 339–350. doi:10.1016/S0013-7952(01)00095-3

CrossRef Full Text | Google Scholar

Tu, G., Deng, H., Shang, Q., Zhang, Y., and Luo, X. (2020). Deep-Seated Large-Scale Toppling Failure: A Case Study of the Lancang Slope in Southwest China. Rock Mech. Rock Eng. 53, 3417–3432. doi:10.1007/s00603-020-02132-0

CrossRef Full Text | Google Scholar

Wang, S. J., Xiao, Y., and Du, Y. L. (1992). The Mechanism of Bending Creep of Bedded Rockmass in the Slope on the Left Bank of Longtan Dam Site in Hongshui River, Guangxi, China. Chin. J. Geol. S1, 342–352.

Google Scholar

Wu, F. Q. (1997). Theoretical Analysis of Bending and Toppling Deformation in Slopes of Mica-Quartz Schist. J. Eng. Geol. 5 (04), 19–24.

Google Scholar

Xia, M., Ren, G. M., Li, T. B., Cai, M., Yang, T. J., and Wan, Z. L. (2019). Complex Rock Slope Deformation at Laxiwa Hydropower Station, China: Background, Characterization, and Mechanism. Bull. Eng. Geol. Environ. 78, 3323–3336. doi:10.1007/s10064-018-1371-x

CrossRef Full Text | Google Scholar

Xiao, Y., and Wang, S. J. (1991). Flexural Failure of Rockmass in Slopes. Chin. J. Rock Mech. Eng. 10 (04), 331–338.

Google Scholar

Xie, L., Yan, E., Wang, J., Lu, G., and Yu, G. (2018). Study on Evolutionary Characteristics of Toppling Deformation of Reverse-Dip Layered Rock Slope Based on Surface Displacement Monitoring Data. Environ. Earth Sci. 77 (4), 156. doi:10.1007/s12665-018-7352-3

CrossRef Full Text | Google Scholar

Zhang, G., Wang, F., Zhang, H., Tang, H., Li, X., and Zhong, Y. (2018). New Stability Calculation Method for Rock Slopes Subject to Flexural Toppling Failure. Int. J. Rock Mech. Min. Sci. 106, 319–328. doi:10.1016/j.ijrmms.2018.04.016

CrossRef Full Text | Google Scholar

Zhang, Z., Liu, G., Wu, S., Tang, H., Wang, T., Li, G., et al. (2015). Rock Slope Deformation Mechanism in the Cihaxia Hydropower Station, Northwest China. Bull. Eng. Geol. Environ. 74 (3), 943–958. doi:10.1007/s10064-014-0672-y

CrossRef Full Text | Google Scholar

Zhao, W., Zhang, C., and Ju, N. (2021). Identification and Zonation of Deep-Seated Toppling Deformation in a Metamorphic Rock Slope. Bull. Eng. Geol. Environ. 80, 1981–1997. doi:10.1007/s10064-020-02027-y

CrossRef Full Text | Google Scholar

Zhu, C., He, M., Karakus, M., Cui, X., and Tao, Z. (2020). Investigating Toppling Failure Mechanism of Anti-dip Layered Slope Due to Excavation by Physical Modelling. Rock Mech. Rock Eng. 53 (11), 5029–5050. doi:10.1007/s00603-020-02207-y

CrossRef Full Text | Google Scholar