
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 07 July 2022
Sec. Geohazards and Georisks
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.941070
This article is part of the Research Topic Advances in Modeling, Assessment, and Prevention of Geotechnical and Geological Disasters View all 44 articles
The dynamic response of twin circular unlined tunnels is studied by indirect boundary integral equation method (IBIEM). The twin tunnels are assumed to lie in an unbounded elastic space subjected to blasting P waves. The influence of incident angle on the distribution of DSCF around the twin tunnels is analyzed. Besides, the influences of normalized wave number αa and normalized distance d* (ratio of spacing distance to tunnel radius) on the reference DSCF, that is, the peak DSCF for different incident angles with an assurance rate of 95%, are discussed. Results show that 1) the IBIEM is a high-precision method analyzing the DSCF around twin circular unlined tunnels induced by blasting P waves; 2) the incident angle θ0, αa, and d* all have significant influences on the distribution of DSCF; 3) for a constant d*, the peak DSCF around the right tunnel is slightly greater than the left one; 4) the reference DSCF decreases exponentially with the increasing of αa or d*, and the corresponding fitting functions are proposed.
In recent years, underground tunnels have been widely developed due to transportation problems induced by the dramatic growth of population (Li et al., 2017; Zhang et al., 2021). In many populous cities, twin tunnels are increasingly constructed to improve transportation capacity (Alielahi and Adampira, 2016). When the drilling and blasting method is adopted, blasting waves will impose a potential danger on the adjacent existing tunnels (Xia et al., 2013; Zhou et al., 2016; Dang et al., 2018; Xue et al., 2019; Peng et al., 2021). Evaluating the dynamic response and proposing a safety criterion of the existing tunnels subjected to blasting waves are of the utmost importance.
In the past years, extensive studies have been carried out in evaluating the dynamic response of underground tunnels caused by incident waves. These studies mainly focus on the dynamic response of the rock or the lining of a single tunnel. Yi et al. (2008) studied the dynamic response of an arch-with-vertical-wall lining, and concluded that the incidence angle of incident waves has a significant influence on the critical vibration velocity. Furthermore, Yi et al. (2016) discussed the dynamic response of a circular lined tunnel with an imperfectly bonded interface under plane P waves, and found that the interface stiffness has a great influence on the distribution of dynamic stress concentration factors (DSCF) of the tunnel. Pao and Mow (1973) investigated the dynamic stress concentration of lined and unlined circular tunnels subjected to plane P and S waves numerically. Lu et al. (2019a), Lu et al. (2019b), and Lu et al. (2021) studied the DSCF and peak particle velocity of a circular tunnel subjected to cylindrical P waves theoretically. Wang et al. (2014) studied the dynamic responses of the tunnel at various depths in double-layer rocks by finite element method. Li et al. (2018) firstly proposed the theoretical formula to evaluate the DSCF around a circular opening subjected to blasting wave and studied the dynamic response of deep-buried tunnels under triangular blasting loads. Liu et al. (2011) and Chen et al. (2012) discussed the dynamic response of a rock tunnel subjected to harmonic P, S, and R waves by numerical simulation method. Xu et al. (2014) investigated the effects of incident frequency, incident angle, and rock conditions on a circular lining tunnel subjected to incident plane P waves. Zhang et al. (2022) explored the stresses and vibrations of a single circular tunnel under the incidence of cylindrical P waves and proposed the PPV criterion. Qiu et al. (2022) studied the blasting dynamic behavior of deep buried tunnels and discussed their safety. Zlatanović et al. (2021) and Yuan et al. (2020) explored the influence of new structures on the dynamic responses of existing tunnels subjected to different incident waves. Although the study on different factors influencing dynamic response of underground tunnels subjected to incident waves has made great progress, the quantitative relationship between different factors and dynamic response of tunnels subjected to incident waves is very limited.
In this article, the dynamic response of twin circular unlined tunnels subjected to blasting P waves is studied by indirect boundary integral equation method (IBIEM). The influence of the incident angle on DSCF of the twin tunnels is analyzed. Furthermore, the influences of normalized wave number and normalized distance (ratio of spacing distance to tunnel radius) on the reference DSCF, that is, the peak DSCF for different incident angles with an assurance rate of 95%, are discussed. The fitting functions determining the reference DSCF are proposed.
Assume two circular unlined tunnels with a distance d lie in an unbounded space, centering at O1 and O2, respectively. The radii are denoted by a1 on the left side and a2 on the right side. A right-handed Cartesian coordinate system O1xy is established, as shown in Figure 1. The virtual sources are represented by S1 and S2 with less radii b1 and b2 to simulate the outgoing waves and avoid singularity on the tunnel boundaries. The displacement potential function of incident P wave can be expressed as:
where
Let φ denote the linear sum of the potentials of the incident and diffracted P waves, ψ denote the linear sum of the potential of the incident and diffracted S wave, then
where M and N are the numbers of virtual sources in the left and right tunnels,
The diffracted waves generated by the i-th virtual source can be expressed in terms of 0-th Hankel functions as:
where Ri is the distance between an arbitrary point in the surrounding rock and the i-th virtual source, defined by
According to the relations between stress and displacement, the stress can be expressed as:
Then substituting Eqs 1–4 into Eq. 5, the displacements and stresses can be written as follows:
The stress components in Cartesian coordinate system can be transformed to those in polar coordinate system by the following equations.
The traction-free boundary conditions are given by
Substituting Eqs 6a–6e and 7 into Eq. 8, the boundary conditions can be rewritten in the matrix form.
where H is the Green’s influence matrix, A is the undermined coefficients representing the source density, and S is the vector of stresses induced by the incident wave.
In general, Eq. 9 is overdetermined, and only the approximate solution can be obtained by the least square method.
The relative error is always determined as follows:
where
DSCF is an important parameter to evaluate structural stability (Fan et al., 2019; Ming et al., 2019; Jang et al., 2020; Li et al., 2020), which is defined as follows:
where σ0 is the stress intensity of the incident wave in the direction of propagation, defined by σ0=μβ2φ0, μ is the shear modulus.
In order to get some general results, we need to define the following dimensionless parameter: the normalized distance as d*=d/a, where a is the maximum of a1 and a2. αa is another quite important index, generally called the dimensionless wave number, which equals 2π times the ratio of a to the wave length of the incident wave.
In order to determine the calculation accuracy, we choose the case of d*=4 for analysis. Table 1 shows the relative errors determined by Eq. 11 for different θ0 when αa = 0.1 and 2. The numbers of source points and observation points are generally different and the previous is less.
It is found that the relative error decreases with the increasing numbers of source and observation points. When the numbers of source and observation points equal to 60 and 80, the maximum relative errors are 1.014 × 10−4 for αa = 0.1 and 1.542 × 10−3 for αa = 2, which are sufficiently accurate. When the numbers of source and observation points equal to 80 and 100, the maximum relative errors are 2.433 × 10−8 for αa = 0.1 and 2.328 × 10−6 for αa = 2, which become far smaller. Therefore, we believe that 80 source points and 100 observation points are suitable in the following analysis.
The distribution of DSCF around the twin tunnels under different αa and θ0 is shown in Figure 2, where d* = 4.
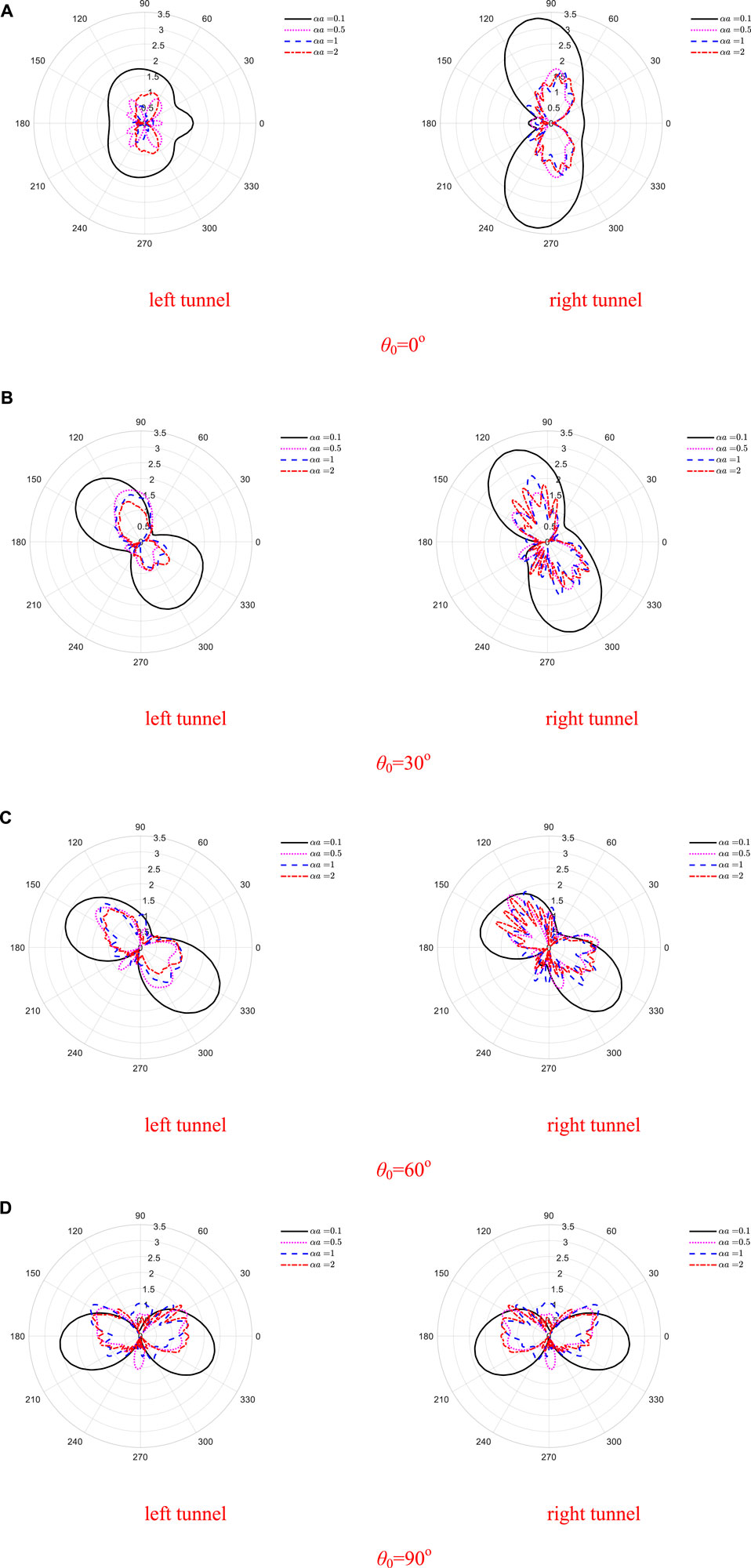
FIGURE 2. Distribution of DSCF around twin tunnels. (A) θ0 = 0°; (B) θ0 = 30°; (C) θ0 = 60°; (D) θ0 = 90°.
The DSCF of the tunnels is approximately symmetrically distributed about the incident direction for αa = 0.1, and it becomes more complex with the increase of αa. It is obvious that the distribution of DSCF around the twin tunnels changes obviously with the variation of θ0. For the left tunnel, the peak DSCF around the left tunnel at θ0 = 0° is smaller than that at others for a fixed αa. For the right tunnel, the peak DSCF around the right tunnel occurs at θ0 = 0° for αa = 0.1, while at others for αa = 0.5, 1, and 2. This suggests that the incident angle θ0 of blasting P waves has a significant influence on the distribution of DSCF.
For a fixed θ0, the peak DSCF at αa = 0.1 is obviously greater than other cases, but the values at αa = 0.5, 1, and 2 do not change apparently, which indicates that the peak DSCF decreases quickly at first, then varies slower and slower, eventually tends to a steady value.
Although the left tunnel is located at the incident side, the DSCF of the right tunnel is larger under the same αa, which may result from that the left tunnel deflects and focuses stress on, just like a convex lens.
According to the above analysis, the DSCF of tunnels changes with θ0. In a practical project, θ0 may be unknown and the upper bound of DSCF for different θ0 has a critical reference value for engineers. Figure 3 and Figure 4 show the variation of the reference DSCF (i.e., 95% of peak DSCF values are less than the given value) with αa and d* ,respectively.
It is found from Figure 3 that the peak DSCF around the left tunnel is more discrete than the right tunnel and its decreasing rate with αa for θ0 = 0o is obviously greater. The discreteness reduces with the increasing value of d*. By using the least square method, we found the variation of the reference DSCF can be well fitted exponential functions. According to the fitting functions, the attenuation of peak DSCF around the left tunnel is faster than the right tunnel for a same d*.
The summation of fitting functions in Figure 3 is listed in Table 2.
It is observed from Figure 4 that the peak DSCF for the left tunnel fluctuates obviously at αa = 0.1, the variation tendency becomes clearer at αa = 1 and 2. Besides, the smallest DSCF occurs at θ0 = 90° for αa =0.1 while at θ0 = 0° for αa = 1 and 2. For the right tunnel, the peak DSCF shows a wave-like change at αa = 0.1. When αa = 1 and 2, the variation trends of DSCF with d* are similar, the peak value of DSCF occurs at θ0 = 30° or 45°. Compared with the left tunnel, the distribution of peak DSCF of the right tunnel is more concentrated.
It is also found that the variation of the reference DSCF can be well fitted exponential functions. According to the fitting functions, the attenuation of peak DSCF around the right tunnel is faster for a constant αa while slower for a constant d* compared with that around the left tunnel.
The summation of fitting functions in Figure 4 is listed in Table 3.
Based on the above analysis, the attenuation of the reference DSCF with αa or d* can be well expressed by exponential functions. Considering the joint impact of αa and d*, the DSCF changing with both αa and d* of the twin tunnels is shown in Figure 5.
The fitting surfaces for both tunnels are expressed in Eq. 13.
It is found that the fitting function can well reflect the previous results and αa has a greater influence on DSCF than d*. Eq. 13 can be proposed as the reference function and engineers can quickly obtain the critical value to prevent damage to such underground structures.
In this article, the dynamic response of twin circular unlined tunnels in an unbounded space subjected to blasting P waves is studied. According to the research results, the following conclusions can be obtained:
(1) The DSCF around twin circular unlined tunnels subjected to blasting P waves is calculated by indirect boundary integral equation method, which is of high precision.
(2) The incident angle θ0, normalized wave number αa, and normalized distance d* all have a significant influence on the distribution of DSCF around the twin tunnels.
(3) For a constant d*, the peak DSCF around the right tunnel is slightly greater than the left one.
(4) The reference DSCF decreases exponentially with the increase of αa or d*, and the corresponding fitting functions are proposed. Compared with d*, the influence of αa is more distinct.
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.
Conceptualization: SL, YY; Methodology: SL and YJ; Formal analysis and investigation: JS, SL, and ZZ; Draft preparation: SL and LJ.
The study was sponsored by the Hubei Provincial Natural Science Foundation (Grant No. 2019CFB224), Hubei Provincial Department of Education (Grant No. Q20191308), and Open Research Fund of Hubei Key Laboratory of Blasting Engineering (Grant No. HKLBEF202011).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Alielahi, H., and Adampira, M. (2016). Effect of Twin-Parallel Tunnels on Seismic Ground Response Due to Vertically In-Plane Waves. Int. J. Rock Mech. Min. Sci. 85, 67–83. doi:10.1016/j.ijrmms.2016.03.010
Chen, C.-H., Wang, T.-T., Jeng, F.-S., and Huang, T.-H. (2012). Mechanisms Causing Seismic Damage of Tunnels at Different Depths. Tunn. Undergr. Space Technol. 28 (1), 31–40. doi:10.1016/j.tust.2011.09.001
Dang, V. K., Dias, D., Do, N. A., and Vo, T. H. (2018). Impact of Blasting at Tunnel Face on an Existing Adjacent Tunnel [J]. Int. J. GEOMATE 15 (47), 22–31. doi:10.21660/2018.47.04640
Fan, Z., Zhang, J., and Xu, H. (2019). Theoretical Study of the Dynamic Response of a Circular Lined Tunnel with an Imperfect Interface Subjected to Incident SV-Waves. Comput. Geotechnics 110, 308–318. doi:10.1016/j.compgeo.2019.02.026
Jang, P., Ri, Y., Ri, S., Pang, C., and Ok, C. (2020). Scattering of SH Wave by a Semi-Circle Inclusion Embedded in Bi-material Half Space Surface. J. Mech. 36 (4), 497–506. doi:10.1017/jmech.2019.72
Li, S., Liu, B., Xu, X., Nie, L., Liu, Z., Song, J., et al. (2017). An Overview of Ahead Geological Prospecting in Tunneling. Tunn. Undergr. Space Technol. 63, 69–94. doi:10.1016/j.tust.2016.12.011
Li, X., Li, C., Cao, W., and Tao, M. (2018). Dynamic Stress Concentration and Energy Evolution of Deep-Buried Tunnels under Blasting Loads. Int. J. Rock Mech. Min. Sci. 104, 131–146. doi:10.1016/j.ijrmms.2018.02.018
Li, Z., Tao, M., Du, K., Cao, W., and Wu, C. (2020). Dynamic Stress State Around Shallow-Buried Cavity under Transient P Wave Loads in Different Conditions. Tunn. Undergr. space Technol. 97, 103228. doi:10.1016/j.tust.2019.103228
Liu, Z., Liang, J., and Zhang, H. (2011). Scattering of Rayleigh Wave by a Lined Tunnel in Elastic Half-Space [J]. Chin. J. Rock Mech. Eng. 30 (8), 1627–1637. (in Chinese).
Lu, S., Zhou, C., Zhang, Z., Ji, L., and Jiang, N. (2021). Theoretical Study on Dynamic Responses of an Unlined Circular Tunnel Subjected to Blasting P-Waves. J. Mech. 37, 242–252. doi:10.1093/jom/ufaa029
Lu, S., Zhou, C., Zhang, Z., and Jiang, N. (2019a). Dynamic Stress Concentration of Surrounding Rock of a Circular Tunnel Subjected to Blasting Cylindrical P-Waves. Geotech. Geol. Eng. 37, 2363–2371. doi:10.1007/s10706-018-00761-5
Lu, S., Zhou, C., Zhang, Z., and Jiang, N. (2019b). Particle Velocity Response of Surrounding Rock of a Circular Tunnel Subjected to Cylindrical P-Waves. Tunn. Undergr. Space Technol. 83, 393–400. doi:10.1016/j.tust.2018.09.020
Ming, T., Li, Z., Cao, W., Li, X., and Wu, C. (2019). Stress Redistribution of Dynamic Loading Incident with Arbitrary Waveform through a Circular Cavity[J]. Int. J. Numer. Anal. Methods Geomechanics 43 (6), 1279–1299. doi:10.3303/CET1655006
Pao, Y. H., and Mow, C. C. (1973). The Diffraction of Elastic Waves and Dynamic Stress Concentrations [M]. New York: Crane, Russak & Company Inc.
Peng, Y., Liu, G., Wu, L., Zuo, Q., Liu, Y., and Zhang, C. (2021). Comparative Study on Tunnel Blast-Induced Vibration for the Underground Cavern Group [J]. Environ. Earth Sci. 80 (2), 100–111. doi:10.1007/s12665-020-09362-z
Qiu, J., Liu, K., and Li, X., (2022). Influence of Blasting Disturbance on Dynamic Response and Safety of Deep Tunnels [J]. Geomechanics Geophys. Geo-Energy Geo-Resources 8, 1–17. doi:10.1007/s40948-021-00308-8
Wang, T.-T., Hsu, J.-T., Chen, C.-H., and Huang, T.-H. (2014). Response of a Tunnel in Double-Layer Rocks Subjected to Harmonic P- and S-Waves. Int. J. Rock Mech. Min. Sci. 70, 435–443. doi:10.1016/j.ijrmms.2014.06.002
Xia, X., Li, H. B., Li, J. C., Liu, B., and Yu, C. (2013). A Case Study on Rock Damage Prediction and Control Method for Underground Tunnels Subjected to Adjacent Excavation Blasting. Tunn. Undergr. Space Technol. 35, 1–7. doi:10.1016/j.tust.2012.11.010
Xu, H., Li, T. B., Xu, J., and Wang, L. J. (2014). Dynamic Response of Underground Circular Lining Tunnels Subjected to Incident P Waves[J]. Math. Problems Eng. 2014, 297424. doi:10.1155/2014/297424
Xue, F., Xia, C., Li, G., Jin, B., He, Y., and Fu, Y. (2019). Safety Threshold Determination for Blasting Vibration of the Lining in Existing Tunnels under Adjacent Tunnel Blasting. Adv. Civ. Eng. 2019 (3), 1–10. doi:10.1155/2019/8303420
Yi, C., Lu, W., Zhang, J., and Zhang, A. P. (2008). Study on Critical Failure Vibration Velocity of Arch with Vertical Wall Lining Subjected to Blasting Vibration[J]. Rock Soil Mech. 29 (8), 2203–2208. (in Chinese). doi:10.3969/j.issn.1000-7598.2008.08.034
Yi, C. P., Lu, W. b., Zhang, P., Johansson, D., and Nyberg, U. (2016). Effect of Imperfect Interface on the Dynamic Response of a Circular Lined Tunnel Impacted by Plane P-Waves. Tunn. Undergr. Space Technol. 51, 68–74. doi:10.1016/j.tust.2015.10.011
Yuan, Z., Cai, Y., Sun, H., Shi, L., and Pan, L. (2020). The Influence of a Neighboring Tunnel on the Critical Velocity of a Three-Dimensional Tunnel-Soil System [J]. Int. J. Solids Struct. 212, 23–45.doi:10.1016/j.ijsolstr.2020.11.026
Zhang, P., Cai, J., Zong, F., He, Y., and Wang, Q. (2021). Dynamic Response Analysis of Underground Double-Line Tunnel under Surface Blasting. Shock Vib. 2021 (2), 1–13. doi:10.1155/2021/9226615
Zhang, Z., Jia, J., Lu, S., and Dong, Q. (2022). Dynamic Response and Safety Criterion of Surrounding Rock of a Circular Tunnel Subjected to Cylindrical P-Waves [J]. Arabian J. Geosciences 15, 1–7. doi:10.1007/s12517-022-10091-9
Zhou, Y., Wang, S. L., and Wang, J. (2016). Vibration Response of an Existing Tunnel to Adjacent Blasting Construction [J]. Chem. Eng. Trans. 55, 31–36. doi:10.1002/nag.2897
Keywords: dynamic response, blasting wave, twin circular tunnel, dynamic stress concentration factor, indirect boundary integral equation method
Citation: Lu S, Yao Y, Jia Y, Sun J, Ji L and Zhang Z (2022) Dynamic Response of Twin Circular Unlined Tunnels Subjected to Blasting P Waves. Front. Earth Sci. 10:941070. doi: 10.3389/feart.2022.941070
Received: 11 May 2022; Accepted: 27 May 2022;
Published: 07 July 2022.
Edited by:
Xiaodong Fu, Institute of Rock and Soil Mechanics (CAS), ChinaReviewed by:
Yaxiong Peng, Hunan University of Science and Technology, ChinaCopyright © 2022 Lu, Yao, Jia, Sun, Ji and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yingkang Yao, c2hhbnhpeWFvQGpodW4uZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.