Analysis on the Shear Stress Propagation Mechanism in the Rock Reinforcement System

Rock reinforcement is significant in maintaining the stability of excavated structures, such as tunnels and underground roadways. However, shear failure in the rock reinforcement system, especially the shear failure at the rock reinforcement bolt surface, induces a threat to the rock reinforcement system. To reveal the shear stress (SS) propagation mechanism in the rock reinforcement system, this article conducted a literature review. First, the investigation approaches that were used by previous researchers to study the SS propagation were summarized. The advantages and disadvantages of experimental tests, analytical simulation, and numerical simulation were compared and analyzed. Then, the SS propagation process in the rock reinforcement system was presented. Two typical SS propagation modes were explained. More attention was given to the SS propagation mode in which the maximum SS propagates from the external end of rock reinforcement bolts to the internal end of rock reinforcement bolts. After that, a discussion section was given. In the discussion section, the significance of the SS propagation was further emphasized. Moreover, the limitations in the analytical simulation and numerical simulation were indicated. It is concluded that when studying the SS propagation mechanism of rock reinforcement bolts, combining experimental tests, analytical simulation, and numerical simulation is a better choice. This study is beneficial for revealing the SS propagation mechanism of the rock reinforcement system.

Introduction

In rock mechanics, failure of rock masses is commonly encountered (Wang et al., 2021a). This is because fractures distribute non-uniformly in rock masses (Nikolenko et al., 2021; Yang et al., 2021). Moreover, experiment work proves that rock masses which are full of fractures are quite low in strength (Gao et al., 2021).

This is more prominent when the rock masses are subjected to manual excavations (Zhang et al., 2021). For example, in civil engineering and mining engineering, excavation activities are performed to create tunnels, chambers, or roadways (Chen et al., 2022). These tunnels and roadways will be later used in serving transportation and ventilation (Yao et al., 2020).

It is ensured that this manual excavation disturbs the initial stability of rock masses (Wu et al., 2018). Moreover, due to manual excavations, stress concentration occurs in rock masses (Chen et al., 2020; Zhang et al., 2022). Consequently, fractures are likely to develop in rock masses (Zhang et al., 2020a; Chen et al., 2021a; Yang et al., 2022). This further weakens the rock mass strength.

To guarantee the safety of the rock mass excavation, rock reinforcement bolts are commonly used (Li et al., 2021a; Wang et al., 2021b; Chang et al., 2021). Experimental work proves that rock reinforcement bolts can combine the jointed rock mass. Moreover, once rock masses converge, shear deformation will occur in the grout column. Consequently, stress can be transferred in the rock reinforcement system (Thompson et al., 2012).

During the loading process, the shear stress (SS) propagation plays a significant role (Wang et al., 2020a). Therefore, proper understanding of the SS propagation mechanism in the rock reinforcement system is quite significant.

This article aims at revealing the SS propagation mechanism in the rock reinforcement system. To realize this purpose, a literature review was conducted. This study is beneficial to propose new reinforcement approaches to prevent rock mass failure.

Previous Study on the SS Propagation

Investigation Approaches

To study the SS propagation mechanism in the rock reinforcement system, previous researchers adopted various approaches. Generally, investigation approaches can be classified into three different types: experimental tests (Marian et al., 2021), analytical simulation (Liu et al., 2017; Li et al., 2021b), and numerical simulation (Chen et al., 2021a).

Experimental tests should be the most credible one. Specifically, strain gauges are adhered on the bolt surface (Wang et al., 2019). Then, this instrumented bolt is installed in a rock block. Grout is used to bond the bolt with the rock block (Chen et al., 2021b; Yu et al., 2021). After full curing, the bolt is pulled out. During testing, tensile force distribution along with the bolt can be measured. Then, Eq. 1 is adopted to simply calculate the SS at the bolt surface (Aoki et al., 2003).

$\tau =\frac{D_{b}E\left({\epsilon }_1-{\epsilon }_2\right)}{4\mathrm{\Delta }L},(1)$

where τ is SS at the bolt surface, D_b is the bolt diameter, E is the elastic modulus of the bolt, ε is the tensile strain of the bolt, and ΔL is the spacing between two adjacent strain gauges.

This approach has been used by a number of researchers (Wang et al., 2020b). However, a shortcoming is that the attached strain gauges are likely to be stripped from the bolt surface. To solve this issue, Chekired and Benmokrane (Chekired et al., 1997) developed the tension measuring device. This device can be mounted on the bolt to measure the strain distribution. Additionally, Martin and Pakalnis (Martin et al., 2008) proposed replacing the central wire in the cable bolt with a modified wire. Specifically, along with this modified wire, strain gauges were attached.

In addition, analytical simulation is an efficient approach to study the SS propagation mechanism (Chen et al., 2021c). Specifically, although the bolt may have a long length, the infinitesimal method can be used to analyze the SS at the bolt surface, as shown in Eq. 2 (Ma et al., 2019):

$\tau =\frac{D_b}{4}\frac{d{\sigma }_b\left(x\right)}{dx},(2)$

where dσ_b(x) is the increment of the tensile stress in the bolt.

Then, it is assumed that the bolt surface has the same mechanical property (Zou and Zhang, 2019). A bond-slip equation can be used to depict the relationship between the SS at the bolt surface and the slip (Zhang et al., 2020b). By incorporating the bond-slip equation into Eq. 2, analytical equations can be developed.

This analytical approach was initially proposed by Farmer (Farmer, 1975). However, at that period, the decoupling behavior was not considered. Later, this analytical method was adopted by others (Zhu et al., 2021). Aydan and Ichikawa (Aydan et al., 1985) made a significant improvement on analytical simulation. Their innovation is that the classic trilinear equation was proposed to describe the slip behavior of the bolt surface. Based on the trilinear equation, the bolt surface encountered the elastic, softening, and decoupling behavior. Therefore, the coupling and decoupling behavior of the bolt surface can be simulated.

Moreover, the trilinear equation may be simplified into the bilinear equation to evaluate the SS propagation of the bolt surface (Cai et al., 2004). The main difference between the bilinear equation and the trilinear equation is that there is no linear softening behavior in the bilinear equation.

In recent years, numerical simulation has become more popular in rock reinforcement analysis. It is because numerical simulation is powerful in establishing and calculating complicated structures (Mohamed et al., 2020). As for the rock reinforcement analysis, more research was focused on using the structure element, such as the cable or pile. There is a significant difference between the cable and pile. Specifically, the cable only considers the longitudinal performance of rock reinforcement bolts. In contrast, the pile can analyze both the longitudinal performance and the lateral performance of rock reinforcement bolts.

The advantage is that numerical elements have already been created by commercial companies. Therefore, users can conveniently adopt the structure element to simulate different rock reinforcement cases. In contrast, the shortcoming is that the original constitutive equation may not truly reflect the proper behavior of the rock reinforcement system. For example, in the structure element of the cable, the bolt surface is assumed to deform following an elastic perfectly plastic equation, as shown in Eq. 3 (Nemcik et al., 2014).

$\{\begin{array}{l}\tau =k_g\delta \left(\delta \le {\delta }_p\right)\\ \tau ={\tau }_p\left(\delta >{\delta }_p\right)\end{array},(3)$

where k_g is the shear stiffness of the grout column, δ is the slip of the bolt surface, δ_p is the slip of the bolt surface when the peak strength reaches, and τ_p is the peak strength of the bolt surface.

It neglects the post-failure behavior of the bolt surface. Therefore, it cannot truly simulate the loading performance of bolts without modification.

Nevertheless, the commercial software usually reserves the secondary development interface. For example, for the structure element of the cable, the Itasca Company prepared a number of FISH functions (Chen et al., 2021d). For the structure element of the pile, the Itasca Company created the TABLE function (Chen and Li, 2022). Therefore, users can use these FISH functions or TABLE function to modify the original rock reinforcement elements. For example, Figure 1 shows the comparison between the original pile and the revised pile. Apparently, with the original pile, at the end of the SS propagation process, the SS at the full bolt surface equaled the peak strength. This overestimated the loading capacity of bolts. In contrast, with the modified pile, there was always a non-uniform SS distribution at the bolt surface. This was more consistent with the experimental test results. Consequently, it saw a wide application of the commercial numerical tools in the rock reinforcement analysis (Shang et al., 2018).

FIGURE 1

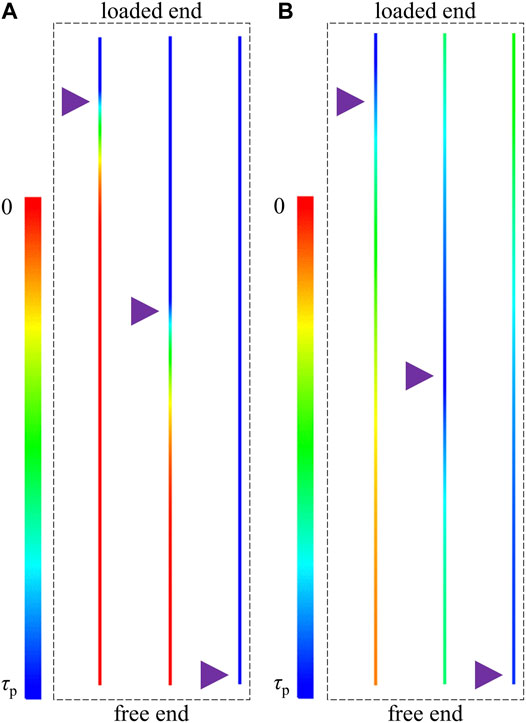
FIGURE 1. Comparison between the structure element of pile in analyzing the SS propagation process: (A) The original pile and (B) the revised pile.

SS Propagation Mechanism

Based on the previous research, it is accepted that the SS at the bolt surface may have a uniform distribution if the anchor length was short enough (Blanco Martín et al., 2010). Benmokrane and Chennouf (Benmokrane et al., 1995) indicated that when the anchor length is less than four times the bolt diameter, the SS can be treated equal. Based on this concept, Eq. 4 was used to calculate the SS at the bolt surface (Ma et al., 2013):

$\tau =\frac{F}{\pi D_{b}L},(4)$

where F is the pulling force and L is the anchor length.

It should be noted that Eq. 4 is valid when the anchor length is constant during the pulling process. Nevertheless, it is more common to encounter the scenario where the anchor length decreases gradually. Then, Eq. 5 can be used to calculate the SS (Ma et al., 2013).

$\tau =\frac{F}{\pi D_b\left(L-u_b\right)},(5)$

where u_b is the pulling displacement.

More importantly, rock reinforcement bolts usually have a long length (Cao et al., 2013). In this case, after the bolt is subjected to tensile loading, a non-uniform SS distribution occurs. For the laboratory monotonous loading condition, the bolt usually has two ends. One is embedded in the rock block, and it is called the internal end. By contrast, the other one is left outside and it is called the external end. Since there is a non-uniform SS distribution, SS propagation between the two ends of the bolts generates.

Some research indicated that the maximum SS under each loading level was likely to occur around the same position (Teymen and Kılıç, 2018). Moreover, that position was close to the borehole collar.

In contrast, it is more common to see that during the initial load process, the SS at the borehole collar increased gradually. With the loading increasing, the SS at the borehole collar increased to the peak strength. Then, it started dropping. More interestingly, the maximum SS moved toward the internal end direction. This SS propagation ended when the SS at the internal end of the bolt reached the peak strength.

As a validation of this SS propagation concept, Rong and Zhu (Rong et al., 2004) conducted laboratory pull-out tests on bolts. Strain gauges were attached on the bolt surface to record the tensile force distribution. Later, Ma and Nemcik (Ma et al., 2013) analyzed these experimental data. Eq. 1 was used to calculate the SS at the bolt surface. The analysis results showed that at the initial loading grade, the SS at the borehole collar increased gradually. However, after a certain loading level, the SS at the borehole collar reached the peak strength. With the loading level further increasing, the maximum SS propagated gradually toward the external end. This analysis result was consistent with the above SS propagation concept. Therefore, the experimental work and the corresponding data analysis proved the reliability of the SS propagation concept.

Additionally, the analytical simulation and numerical simulation can better reflect the SS propagation process. Ren and Yang (Ren et al., 2010) used the classic trilinear equation to depict the slip behavior of the bolt surface. They analyzed the SS propagation process at the bolt surface. The results showed that the maximum SS at the bolt surface propagated from the external end to the internal end. Moreover, although each point at the bolt surface experienced the elastic, softening, and decoupling behavior, the full bolt surface underwent five different grades. They were the elasticity, elasticity-weakening, elasticity-weakening-decoupling, weakening-decoupling, and decoupling grades. Later, Blanco Martín and Tijani (Blanco Martín et al., 2013) indicated that when the trilinear equation was used to depict the slip behavior of the bolt surface, the full bolt surface may undergo a pure softening grade.

It should be mentioned that when different bond-slip equations are used, the full bolt surface may undergo different grades. For example, Chen and Liu (Chen et al., 2021e) indicated that when a bilinear equation was used to depict the slip behavior of the bolt surface, the full bolt surface only experienced three grades: the elastic grade, elastic-decoupling grade, and decoupling grade.

Although different bond-slip equations can be used, the SS propagation mechanism was consistent. Specifically, the maximum SS at the bolt surface consistently propagated from the external end to the internal end, as shown in Figure 2.

FIGURE 2

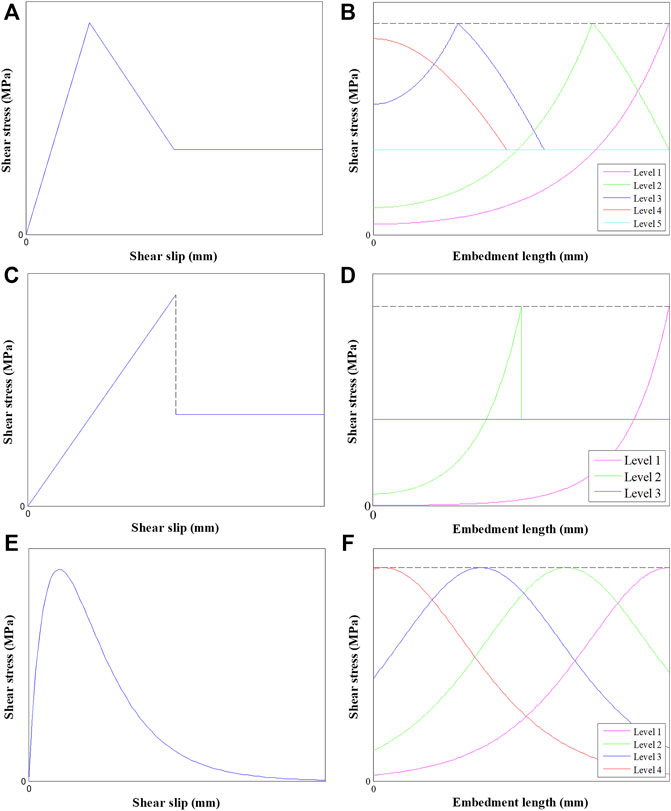
FIGURE 2. SS propagation process: (A) Trilinear equation, (B) the corresponding SS propagation process, (C) bilinear equation, (D) the corresponding SS propagation process, (E) non-linear equation, and (F) the corresponding SS propagation process.

This finding was also confirmed with the numerical simulation. Nemcik and Ma (Nemcik et al., 2014) modified the original structure element in FLAC2D and simulated the SS propagation process at the bolt surface. A non-linear bond-slip equation was used. The results showed that each point at the bolt surface obeyed the same non-linear bond-slip equation. With the loading level increasing, the maximum SS at the bolt surface propagated toward the internal end. This finding was consistent with the others (Nie et al., 2018).

Discussion

The SS at the bolt surface plays a significant role in determining the loading capacity of bolts (Wu et al., 2019). Under the static loading condition, the loading capacity of the bolts equals the sum of the shear force at the bolt surface (Ho et al., 2019). Since the SS at the bolt surface can be calculated directly with the shear force at the bolt surface, as shown in Eq. 6, there is a close relationship between the SS at the bolt surface and the loading capacity of the bolts (Zuo et al., 2019).

$\tau =\frac{F_s}{A_s},(6)$

where F_s is the shear force at the bolt surface and A_s is the contact area between the bolt and the grout column.

Therefore, it is valuable to understand the SS propagation mechanism of bolts. To realize this purpose, previous researchers used various approaches. It is believed that the experimental approach is more credible. This is because compared with the experimental approach, the analytical simulation and numerical simulation usually relied on a number of assumptions (Yokota et al., 2019). Whether those assumptions are reasonable is doubted. In the analytical simulation, it is usually assumed that the bolt, grout column, and surrounding rock masses deform elastically. In fact, in experimental tests, failure of the rock masses may occur because of the radial dilation at the bolt surface. Therefore, under this scenario, the analytical simulation which assumes that only slip failure occurs at the bolt surface may not be trustable.

Similarly, in the numerical simulation, rock masses are simulated with different elastoplastic equations. Among kinds of equations, the Mohr–Coulomb equation is more commonly used. This equation is relatively simpler and its input parameters can be acquired directly from experimental tests. However, it cannot properly simulate the post-failure behavior of rock masses. Specifically, after the peak, the strain softening behavior and residual behavior of rock masses cannot be properly simulated. In this case, the interaction between the numerical rock mass and bolts cannot be the same as in the reality. This is also the reason why the numerical simulation work should be calibrated and compared with experimental results.

Nevertheless, this is not to deny the significance of analytical simulation and numerical simulation. In fact, these two approaches are more effective for researchers to understand the SS propagation mechanism of bolts. Therefore, it is suggested that combining the experimental tests, analytical simulation, and numerical simulation is a better choice for studying the SS propagation mechanism of bolts.

Conclusion

This article conducted a literature review on the SS propagation mechanism of rock reinforcement bolts. The previous investigation approaches were summarized. It is concluded that previous researchers usually used experimental tests, analytical simulation, and numerical simulation. Among those approaches, the experimental approach is more widely used. The experimental test results are also more likely to be accepted by others. By contrast, the analytical approach had more degree of freedom. With this approach, researchers can use different bond-slip equations to depict the slip behavior of the bolt surface. As for the numerical simulation, it is convenient for users since the original constitutive equation has already been created by the developer. Moreover, developers usually reserve the secondary development interface for users to modify the original constitutive equations.

As for the SS propagation mechanism, it is more commonly agreed that during the pulling process of bolts, the SS at the borehole collar firstly increased. With the loading level increasing, the SS at the borehole collar gradually reaches the peak strength. Then, with the further increasing of the loading level, the maximum SS starts propagating toward the internal end. This phenomenon was consistently observed in experimental tests, analytical simulation, and numerical simulation.

Author Contributions

Writing: JC, HL, SZ, HZ, and CZ; conceptualization: JZ and DL.

Funding

The National Natural Science Foundation of China (52034009, 51904302, 52174093, and 52104155), Open Fund of State Key Laboratory of Water Resource Protection and Utilization in Coal Mining (Grant No. WPUKFJJ 2019-08), Yue Qi Distinguished Scholar Project (800015Z1179), and the Beijing Municipal Natural Science Foundation (8212032).

Conflict of Interest

HL is employed by the company China National Coal Group Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aoki, T., Shibata, K., Nakahara, F., Maeno, Y., Kawano, R., and Obara, Y. (2003). “Pull Tests of Long-Embedded Cablebolts,” in Proccedings of Conference Pull tests of long-embedded cablebolts, Gauteng, South Africa, September 08 2003, 45–48.

Google Scholar

Aydan, O., Ichikawa, Y., and Kawamoto, K. (1985). Load Bearing Capacity and Stress Distributions In/along Rockbolts with Inelastic Behaviour of Interfaces, Proccedings of Conference Load bearing capacity and stress distributions in/along rockbolts with inelastic behaviour of interfaces, Nagoya, 1281–1292.

Google Scholar

Benmokrane, B., Chennouf, A., and Mitri, H. S. (1995). Laboratory Evaluation of Cement-Based Grouts and Grouted Rock Anchors. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 32, 633–642. doi:10.1016/0148-9062(95)00021-8

CrossRef Full Text | Google Scholar

Blanco Martín, L., Tijani, M., and Hadj-Hassen, F. (2010). A New Analytical Solution to the Mechanical Behaviour of Fully Grouted Rockbolts Subjected to Pull-Out Tests. Constr. Build. Mater. 25, 1–18. doi:10.1016/j.conbuildmat.2010.07.011

CrossRef Full Text | Google Scholar

Blanco Martín, L., Tijani, M., Hadj-Hassen, F., and Noiret, A. (2013). Assessment of the Bolt-Grout Interface Behaviour of Fully Grouted Rockbolts from Laboratory Experiments under Axial Loads. Int. J. Rock Mech. Min. Sci. 63, 50–61. doi:10.1016/j.ijrmms.2013.06.007

CrossRef Full Text | Google Scholar

Cai, Y., Esaki, T., and Jiang, Y. (2004). A Rock Bolt and Rock Mass Interaction Model. Int. J. Rock Mech. Min. Sci. 41, 1055–1067. doi:10.1016/j.ijrmms.2004.04.005

CrossRef Full Text | Google Scholar

Cao, C., Jan, N., Ren, T., and Naj, A. (2013). A Study of Rock Bolting Failure Modes. Int. J. Min. Sci. Technol. 23, 79–88. doi:10.1016/j.ijmst.2013.01.012

CrossRef Full Text | Google Scholar

Chang, J., He, K., Pang, D., Li, D., Li, C., and Sun, B. (2021). Influence of Anchorage Length and Pretension on the Working Resistance of Rock Bolt Based on its Tensile Characteristics. Int. J. Coal Sci. Technol. 8, 1384–1399. doi:10.1007/s40789-021-00459-9

CrossRef Full Text | Google Scholar

Chekired, M., Benmokrane, B., and Mitri, H. S. (1997). Laboratory Evaluation of a New Cable Bolt Tension Measuring Device. Int. J. Rock Mech. Min. Sci. 34, 1–13. doi:10.1016/s1365-1609(97)00076-2

CrossRef Full Text | Google Scholar

Chen, Y., Teng, J., Bin Sadiq, R. A., and Zhang, K. (2020). Experimental Study of Bolt-Anchoring Mechanism for Bedded Rock Mass. Int. J. Geomech. 20, 1–12. doi:10.1061/(asce)gm.1943-5622.0001561

CrossRef Full Text | Google Scholar

Chen, Y., Zuo, J., Liu, D., Li, Y., and Wang, Z. (2021). Experimental and Numerical Study of Coal-Rock Bimaterial Composite Bodies under Triaxial Compression. Int. J. Coal Sci. Technol. 8, 908–924. 1-17. doi:10.1007/s40789-021-00409-5

CrossRef Full Text | Google Scholar

Chen, J., Hagan, P. C., and Saydam, S. (2021). An Experimental Study of the Specimen Geometry Effect on the Axial Performance of Cement-Based Grouts. Constr. Build. Mater. 310, 125167. doi:10.1016/j.conbuildmat.2021.125167

CrossRef Full Text | Google Scholar

Chen, J., Zhao, Y., Zhao, H., Zhang, J., Zhang, C., and Li, D. (2021). Analytic Study on the Force Transfer of Full Encapsulating Rockbolts Subjected to Tensile Force. Int. J. Appl. Mech. 13, 1–13. doi:10.1142/s1758825121500976

CrossRef Full Text | Google Scholar

Chen, J., Zhao, H., He, F., Zhang, J., and Tao, K. (2021). Studying the Performance of Fully Encapsulated Rock Bolts with Modified Structural Elements. Int. J. Coal Sci. Technol. 8, 64–76. doi:10.1007/s40789-020-00388-z

CrossRef Full Text | Google Scholar

Chen, J., Liu, P., Zhao, H., Zhang, C., and Zhang, J. (2021). Analytical Studying the Axial Performance of Fully Encapsulated Rock Bolts. Eng. Fail. Anal. 128, 1–16. doi:10.1016/j.engfailanal.2021.105580

CrossRef Full Text | Google Scholar

Chen, J., and Li, D. (2022). Numerical Simulation of Fully Encapsulated Rock Bolts with a Tri-linear Constitutive Relation. Tunn. Undergr. Space Technol. 120, 1–13. doi:10.1016/j.tust.2021.104265

CrossRef Full Text | Google Scholar

Chen, J., Liu, P., Liu, L., Zeng, B., Zhao, H., Zhang, C., et al. (2022). Anchorage Performance of a Modified Cable Anchor Subjected to Different Joint Opening Conditions. Constr. Build. Mater. 336, 1–12. doi:10.1016/j.conbuildmat.2022.127558

CrossRef Full Text | Google Scholar

Farmer, I. W. (1975). Stress Distribution along a Resin Grouted Rock Anchor. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 12, 347–351. doi:10.1016/0148-9062(75)90168-0

CrossRef Full Text | Google Scholar

Gao, H., Wang, Q., Jiang, B., Zhang, P., Jiang, Z., and Wang, Y. (2021). Relationship between Rock Uniaxial Compressive Strength and Digital Core Drilling Parameters and its Forecast Method. Int. J. Coal Sci. Technol. 8, 605–613. doi:10.1007/s40789-020-00383-4

CrossRef Full Text | Google Scholar

Ho, D.-A., Bost, M., and Rajot, J.-P. (2019). Numerical Study of the Bolt-Grout Interface for Fully Grouted Rockbolt under Different Confining Conditions. Int. J. Rock Mech. Min. Sci. 119, 168–179. doi:10.1016/j.ijrmms.2019.04.017

CrossRef Full Text | Google Scholar

Li, D., Cai, M., and Masoumi, H. (2021). A Constitutive Model for Modified Cable Bolts Exhibiting Cone Shaped Failure Mode. Int. J. Rock Mech. Min. Sci. 145, 104855. doi:10.1016/j.ijrmms.2021.104855

CrossRef Full Text | Google Scholar

Li, D., Li, Y., Chen, J., and Masoumi, H. (2021). An Analytical Model for Axial Performance of Rock Bolts under Constant Confining Pressure Based on Continuously Yielding Criterion. Tunn. Undergr. Space Technol. 113, 103955. doi:10.1016/j.tust.2021.103955

CrossRef Full Text | Google Scholar

Liu, J., Yang, H., Wen, H., and Zhou, X. (2017). Analytical Model for the Load Transmission Law of Rock Bolt Subjected to Open and Sliding Joint Displacements. Int. J. Rock Mech. Min. Sci. 100, 1–9. doi:10.1016/j.ijrmms.2017.01.018

CrossRef Full Text | Google Scholar

Ma, S., Nemcik, J., and Aziz, N. (2013). An Analytical Model of Fully Grouted Rock Bolts Subjected to Tensile Load. Constr. Build. Mater. 49, 519–526. doi:10.1016/j.conbuildmat.2013.08.084

CrossRef Full Text | Google Scholar

Ma, H.-C., Tan, X.-H., Qian, J.-Z., and Hou, X.-L. (2019). Theoretical Analysis of Anchorage Mechanism for Rock Bolt Including Local Stripping Bolt. Int. J. Rock Mech. Min. Sci. 122, 104080. doi:10.1016/j.ijrmms.2019.104080

CrossRef Full Text | Google Scholar

Marian, W., Krzysztof, K., Jacek, N., Marcin, S., and Wioleta, B. (2021). An Exsitu Underground Coal Gasification Experiment with a Siderite Interlayer: Course of the Process. Int. J. Coal Sci. Technol. 8, 1447–1460. doi:10.1007/s40789-021-00456-y

CrossRef Full Text | Google Scholar

Martin, L., Pakalnis, R., and Milne, D. (2008). Determination of Physical Properties of Cable Bolts in Cement Grout Pull Tests Using Instrumented King Wires. Spokane: National Institute for Occupational Safety and Health Spokane, 1–8.

Google Scholar

Mohamed, K., Rashed, G., and Radakovic-Guzina, Z. (2020). Loading Characteristics of Mechanical Rib Bolts Determined through Testing and Numerical Modeling. Int. J. Min. Sci. Technol. 30, 17–24. doi:10.1016/j.ijmst.2019.12.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Nemcik, J., Ma, S., Aziz, N., Ren, T., and Geng, X. (2014). Numerical Modelling of Failure Propagation in Fully Grouted Rock Bolts Subjected to Tensile Load. Int. J. Rock Mech. Min. Sci. 71, 293–300. doi:10.1016/j.ijrmms.2014.07.007

CrossRef Full Text | Google Scholar

Nie, W., Zhao, Z. Y., Ma, S. Q., and Guo, W. (2018). Effects of Joints on the Reinforced Rock Units of Fully-Grouted Rockbolts. Tunn. Undergr. Space Technol. 71, 15–26. doi:10.1016/j.tust.2017.07.005

CrossRef Full Text | Google Scholar

Nikolenko, P. V., Epshtein, S. A., Shkuratnik, V. L., and Anufrenkova, P. S. (2021). Experimental Study of Coal Fracture Dynamics under the Influence of Cyclic Freezing-Thawing Using Shear Elastic Waves. Int. J. Coal Sci. Technol. 8, 562–574. doi:10.1007/s40789-020-00352-x

CrossRef Full Text | Google Scholar

Ren, F. F., Yang, Z. J., Chen, J. F., and Chen, W. W. (2010). An Analytical Analysis of the Full-Range Behaviour of Grouted Rockbolts Based on a Tri-linear Bond-Slip Model. Constr. Build. Mater. 24, 361–370. doi:10.1016/j.conbuildmat.2009.08.021

CrossRef Full Text | Google Scholar

Rong, G., Zhu, H., and Zhou, C. (2004). Testing Study on Working Mechanism of Fully Grouted Bolts of Thread Steel and Smooth Steel. Chin. J. Rock Mech. Eng. 23, 469–475. (In Chinese). doi:10.3321/j.issn:1000-6915.2004.03.021

CrossRef Full Text | Google Scholar

Shang, J., Yokota, Y., Zhao, Z., and Dang, W. (2018). DEM Simulation of Mortar-Bolt Interface Behaviour Subjected to Shearing. Constr. Build. Mater. 185, 120-137. doi:10.1016/j.conbuildmat.2018.07.044

CrossRef Full Text | Google Scholar

Teymen, A., and Kılıç, A. (2018). Effect of Grout Strength on the Stress Distribution (Tensile) of Fully-Grouted Rockbolts. Tunn. Undergr. Space Technol. 77, 280–287. doi:10.1016/j.tust.2018.04.022

CrossRef Full Text | Google Scholar

Thompson, A. G., Villaescusa, E., and Windsor, C. R. (2012). Ground Support Terminology and Classification: An Update. Geotech. Geol. Eng. 30, 553–580. doi:10.1007/s10706-012-9495-4

CrossRef Full Text | Google Scholar

Wang, S., Xiao, H. G., Zou, Z. S., Cao, C., Wang, Y. H., and Wang, Z. L. (2019). Mechanical Performances of Transverse Rib Bar during Pull-Out Test. Int. J. Appl. Mech. 11, 1–15. doi:10.1142/s1758825119500480

CrossRef Full Text | Google Scholar

Wang, S., Wang, Z., Gong, J., Wang, Y., and Huang, Q. (2020). Coupling Effect Analysis of Tension and Reverse Torque during Axial Tensile Test of Anchor Cable. Dynaii 95, 288–293. doi:10.6036/9603

CrossRef Full Text | Google Scholar

Wang, S. R., Wang, Y. H., Gong, J., Wang, Z. L., Huang, Q. X., and Kong, F. L. (2020). Failure Mechanism and Constitutive Relation for an Anchorage Segment of an Anchor Cable under Pull-Out Loading. Acta Mech. 231, 3305–3317. doi:10.1007/s00707-020-02717-4

CrossRef Full Text | Google Scholar

Wang, Z., Wang, T., Wu, S., and Hao, Y. (2021). Investigation of Microcracking Behaviors in Brittle Rock Using Polygonal Grain‐based Distinct Method. Int. J. Numer. Anal. Methods Geomechanics 45, 1871–1899. doi:10.1002/nag.3246

CrossRef Full Text | Google Scholar

Wang, S., Wang, Y., Wang, Z., Gong, J., and Li, C. (2021). Anchoring Performances Analysis of Tension-Torsion Grouted Anchor under Free and Non-free Rotating Conditions. Dynaii 96, 166–172. doi:10.6036/9985

CrossRef Full Text | Google Scholar

Wu, S., Chen, H., Lamei Ramandi, H., Hagan, P. C., Hebblewhite, B., Crosky, A., et al. (2018). Investigation of Cable Bolts for Stress Corrosion Cracking Failure. Constr. Build. Mater. 187, 1224–1231. doi:10.1016/j.conbuildmat.2018.08.066

CrossRef Full Text | Google Scholar

Wu, S., Ramandi, H. L., Chen, H., Crosky, A., Hagan, P., and Saydam, S. (2019). Mineralogically Influenced Stress Corrosion Cracking of Rockbolts and Cable Bolts in Underground Mines. Int. J. Rock Mech. Min. Sci. 119, 109–116. doi:10.1016/j.ijrmms.2019.04.011

CrossRef Full Text | Google Scholar

Yang, H., Krause, M., and Renner, J. (2021). Determination of Fracture Toughness of Mode I Fractures from Three-point Bending Tests at Elevated Confining Pressures. Rock Mech. Rock Eng. 54, 5295–5317. doi:10.1007/s00603-021-02432-z

CrossRef Full Text | Google Scholar

Yang, H., Renner, J., Brackmann, L., and Röttger, A. (2022). Normal Indentation of Rock Specimens with a Blunt Tool: Role of Specimen Size and Indenter Geometry. Rock Mech. Rock Eng. 55, 2027–2047. doi:10.1007/s00603-021-02732-4

CrossRef Full Text | Google Scholar

Yao, H., Wang, H., Li, Y., and Jin, L. (2020). Three-dimensional Spatial and Temporal Distributions of Dust in Roadway Tunneling. Int. J. Coal Sci. Technol. 7, 88–96. doi:10.1007/s40789-020-00302-7

CrossRef Full Text | Google Scholar

Yokota, Y., Zhao, Z., Nie, W., Date, K., Iwano, K., and Okada, Y. (2019). Experimental and Numerical Study on the Interface Behaviour between the Rock Bolt and Bond Material. Rock Mech. Rock Eng. 52, 869–879. doi:10.1007/s00603-018-1629-4

CrossRef Full Text | Google Scholar

Yu, H., Jia, H., Liu, S., Liu, Z., and Li, B. (2021). Macro and Micro Grouting Process and the Influence Mechanism of Cracks in Soft Coal Seam. Int. J. Coal Sci. Technol. 8, 969–982. doi:10.1007/s40789-020-00404-2

CrossRef Full Text | Google Scholar

Zhang, Z., Deng, M., Bai, J., Yu, X., Wu, Q., and Jiang, L. (2020). Strain Energy Evolution and Conversion under Triaxial Unloading Confining Pressure Tests Due to Gob-Side Entry Retained. Int. J. Rock Mech. Min. Sci. 126, 1–10. doi:10.1016/j.ijrmms.2019.104184

CrossRef Full Text | Google Scholar

Zhang, W., Huang, L., and Juang, C. H. (2020). An Analytical Model for Estimating the Force and Displacement of Fully Grouted Rock Bolts. Comput. Geotechnics 117, 1–10. doi:10.1016/j.compgeo.2019.103222

CrossRef Full Text | Google Scholar

Zhang, Z., Deng, M., Bai, J., Yan, S., and Yu, X. (2021). Stability Control of Gob-Side Entry Retained under the Gob with Close Distance Coal Seams. Int. J. Min. Sci. Technol. 31, 321–332. doi:10.1016/j.ijmst.2020.11.002

CrossRef Full Text | Google Scholar

Zhang, C., Zhao, Y., Han, P., and Bai, Q. (2022). Coal Pillar Failure Analysis and Instability Evaluation Methods: A Short Review and Prospect. Eng. Fail. Anal. 138, 1–19. doi:10.1016/j.engfailanal.2022.106344

CrossRef Full Text | Google Scholar

Zhu, S., Chen, C., Mao, F., and Cai, H. (2021). Application of Disturbed State Concept for Load-Transfer Modeling of Recoverable Anchors in Layer Soils. Comput. Geotechnics 137, 1–16. doi:10.1016/j.compgeo.2021.104292

CrossRef Full Text | Google Scholar

Zou, J., and Zhang, P. (2019). Analytical Model of Fully Grouted Bolts in Pull-Out Tests and In Situ Rock Masses. Int. J. Rock Mech. Min. Sci. 113, 278–294. doi:10.1016/j.ijrmms.2018.11.015

CrossRef Full Text | Google Scholar

Zuo, J.-p., Wen, J.-h., Li, Y.-d., Sun, Y.-j., Wang, J.-t., Jiang, Y.-q., et al. (2019). Investigation on the Interaction Mechanism and Failure Behavior between Bolt and Rock-like Mass. Tunn. Undergr. Space Technol. 93, 103070. doi:10.1016/j.tust.2019.103070

CrossRef Full Text | Google Scholar