- 1School of Civil Engineering, Chongqing Three Gorges University, Chongqing, China
- 2School of Civil Engineering, Chongqing University of Arts and Sciences Chongqing, Chongqing, China
- 3School of Civil Engineering, Chongqing University, Chongqing, China
Ground surface settlement under subway tunnel construction is one of the main sources of urban ground surface settlement, which may threaten the safety of existing buildings. Therefore, it is necessary to study the influence of subway tunnel construction on the safety and stability of surface subsidence. In the current study, the ground settlement originating from the operation of a tunnel-boring machine (TBM) while excavating a double-line tunnel that underpasses existing buildings is studied. To this end, numerical simulations were carried out and experimental data were analyzed. The boring parameters for the underpass interval section were derived by simulating the construction process and analyzing the TBM parameters in a real project. Then, the influence of thrust force, grouting pressure, and frictional force was considered on the surface settlement. For spatial locations between the existing buildings and the tunnel in the underpass area, the width of the ground surface settlement caused by different excavation sequences of the TBM two-line tunnel was analyzed. The obtained results demonstrate that the performed calculations are consistent with the monitoring data. It is found that the width and depth of the ground surface settlement trough are affected by the distance between the existing buildings and the TBM construction tunnel. However, the settlement location is independent of the excavated sequence but depends on the location of the TBM tunnel and the existing building.
1 Introduction
With rapid development of urbanization and continuous promotion of urban rail transportation, the surface settlement caused by metro tunnel construction has attracted the attention of many scholars worldwide. Although the development, design, and manufacturing techniques of tunnel boring machines (TBMs) have continually improved and the excavating technology has improved rapidly in the past few decades, the ground surface settlement caused by TBM excavation may damage the existing buildings (Li et al., 2021). In order to resolve this enormous problem, it is of significant importance to study the surface settlement. In this regard, numerous numerical and experimental investigations have been carried out to study the ground surface settlement caused by TBM tunnel excavation (Zhang et al., 2002; Dias and Kastnher, 2013). In the field experiment, Huang and Zhang (2001) studied the ground subsidence caused by different construction stages. Yu et al. (2014) carried out experiments and demonstrated that the ground surface settlement is mainly concentrated at the stage when the boring machine approaches the monitoring section and the shield tail detaches from the monitoring section. Moreover, Jin et al. (2018) studied eighteen tunnels to analyze the deformation characteristics of the ground surface in depth. Moreover, Chen et al. (2012) performed numerical simulations and studied the influence of construction on the ground surface settlement under different arrangements of multiple tunnels. Meanwhile, the surface settlement characteristics were analyzed using empirical expressions and the superposition principle. Wang et al. (2013) considered the effects of grouting pressure and palm surface thrust force and studied the ground surface settlement caused by boring machines in the construction of metro tunnels. Comodromos et al. (2014) and Qiu et al. (2017) studied the influence of ground surface settlement caused by TBM tunnel excavation and analyzed the interaction between the ground and existing structures. Finally, an improved method was proposed to predict the ground surface settlement in double-line tunnels. Yin et al. (2018) demonstrated that the settlement of the overlying soil of the tunnel is mainly affected by the existing structures and showed that grouting is an effective method to control the ground surface settlement caused by the excavation gap. Feng and Yu (2019) showed that excavating the tunnel has a remarkable effect on the surface deformation of the tunnel after excavation. It is worth noting that this deformation may lead to uneven ground surface settlement after the completion of double-line tunnel boring.
In order to study surface settlement laws, it is necessary to investigate the surface settlement trough. The peck expression has simple calculations, and the calculated curve is consistent with the experimental data (Peck, 1969; Fang et al., 2021). However, it is a challenge to obtain the parameter of the width of the settlement trough. Han and Li. (2007) showed that the settlement trough is related to the burial depth of the tunnel and the stratum conditions. Moreover, Wei (2009) showed that the width of the settlement trough is also affected by the diameter of the tunnel and proposed an expression to calculate the width of the settlement trough. Based on the peck formula and the superposition principle, Liu et al. (2006), Ma (2008), Chen et al. (2014), and Lu et al. (2019) studied the surface settlement caused by the double-line tunnel and deeply analyzed the width of the settlement trough caused by the left- and right-line tunnels (Fattah et al., 2011a; Al-Damluji et al., 2011; Fattah et al., 2011b; Fattah et al., 2012; Fattah et al., 2013; Fattah et al., 2015).
The performed literature survey indicates that there is limited knowledge about ground surface settlement caused by different excavation sequences of TBM double-line tunnels that underpass existing buildings. More specifically, the effects of TBM boring parameters and the existing buildings on surface settlement troughs and maximum settlement values under composite rock stratum conditions have rarely been investigated so far. Aiming at resolving this shortcoming, Chongqing Metro Line 9 was selected as the research object of the current study. The influence of different parameters, including the underpass interval, TBM boring parameters, different excavation sequences, and the spatial distance between the existing building and the tunnel, was studied. The main objective of the present study is to predict the ground settlement of an underpass interval section during the construction of the TBM double-line tunnel using experimental data and numerical simulation.
2 Project
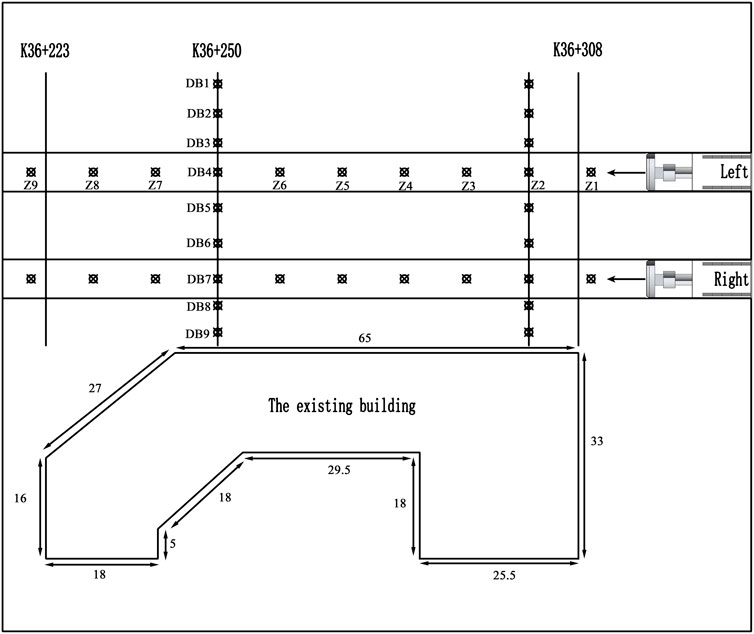
The interval section between Congyan Temple Station (CTS) and Central Park East Station (CPES) in Chongqing Metro Line 9 was selected as the research object. The studied area (hereafter called Zhongcong Tunnel) is located in Yubei District, Chongqing, and is under construction using the TBM excavation method. The left line is 1952.037 m long and expands from K38 + 137.5 to K36 + 185.463. Furthermore, the right line is 1959.037 m long and expands from K38 + 144.5 to K36 + 185.463. The interval of the tunnel is 85 m long and underpasses existing buildings from K36 + 308 to k36 + 223. The geological structure in the interval main is composite strata, which is mainly composed of the Jurassic System Middle and Lower Artesian Well Group sandy mudstone, sandstone, and a 25-m overburden layer. The tunnel diameter is 6.6 m, the distance between the left and the right line is 10.5 m, and the existing building is 7.5 m above the right side of the right line. The location of the Zhongcong Tunnel in Chongqing Metro Line 9 and the underpass existing building is shown in Figure 1.
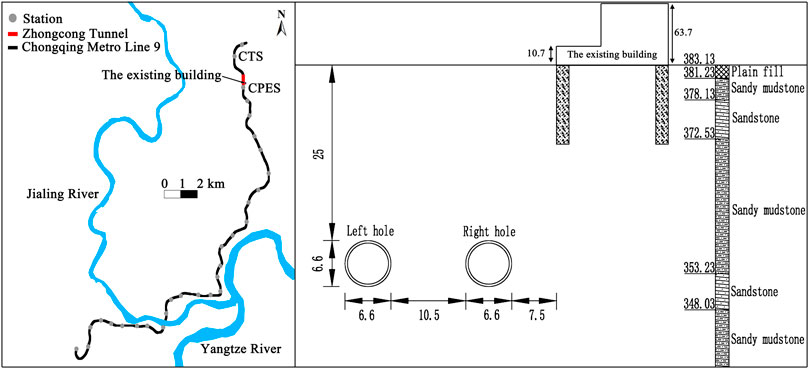
FIGURE 1. Location of the Zhongcong Tunnel in Chongqing Metro Line 9, and the profile map of the underpass existing building.
Figure 2 shows the layout of monitoring points in the interval that underpass the existing buildings. A transverse monitoring section is placed every 50 m, and a ground surface settlement monitoring point is placed every 10 m along the tunnel axis. These monitoring points are directly found above the tunnel between the left and right lines.
3 Calculation of shield frictional force and palm surface thrust force
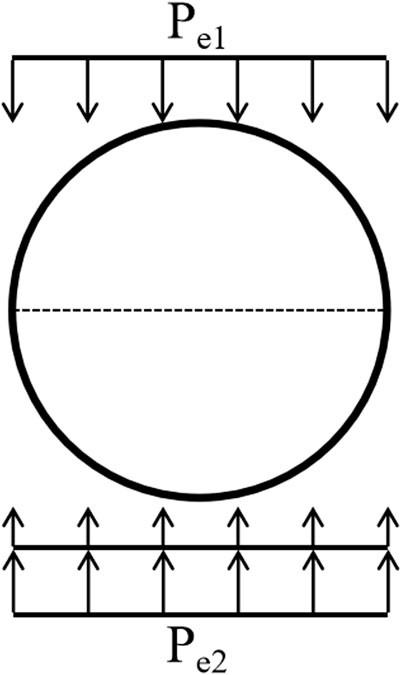
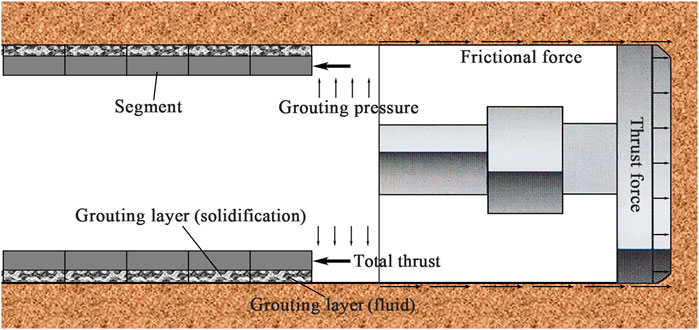
3.1 Frictional force between the shield and the surrounding rock
To calculate the frictional force between the shield and the surrounding rock using the frictional force expression (Shi et al., 2009) and experimental data, the frictional force between the TBM shield sides was divided into upper and lower parts. In the upper part, the frictional force was calculated by multiplying the friction factor µ by the positive soil pressure at the tunnel top, whereas in the lower part, the frictional force was calculated by multiplying the friction factor µ by summing the positive soil pressure at the tunnel top and the weight of the shield mainframe. The schematic of friction calculation is presented in Figure 3, where Pe1 and Pe2 denote the pressure on the upper and lower shields, respectively. These parameters can be calculated using the following equations:
where K0=1-sin
Therefore, the frictional force between the shield shell and the surrounding rock during TBM boring can be obtained from the following expressions:
where Ff is the total frictional force between the shield and the surrounding rock; fs and fx are the frictional force between the upper and lower parts of the shield, respectively;
3.2 The thrust force of the palm surface
In the current study, the total thrust force was divided into four parts, namely, the frictional force Ff, the thrust force FN on the tunnel face, the frictional force FS between the shield tail and the segment, and other force FL originating from the traction force of the rear supporting equipment and the change of direction resistance (Guan, 2008). This classification can be expressed as follows:
Studies (Guan, 2008) show that the sum of the frictional and thrust forces in the tunnel face is 95–99% of the total thrust. Consequently, Eq. 7 can be simplified in the form below:
4 TBM tunneling parameters
Figure 4 shows the distributions of the TBM total thrust, grouting pressure, and volume against the excavating distance. It is observed that the total thrust in the left line (i.e., 5900 kN–11,200 kN) is slightly larger than that of the right line (i.e., 5500 kN–10,200 kN). Meanwhile, the range of the grouting pressure in the left line is 0.18–0.30 MPa, while that of the right line is 0.28–0.33 MPa. It was found that the grouting pressure in the right line is significantly larger than that in the left line, and the simultaneous grouting volume in the two lines varies in the range of 4–5 m3.
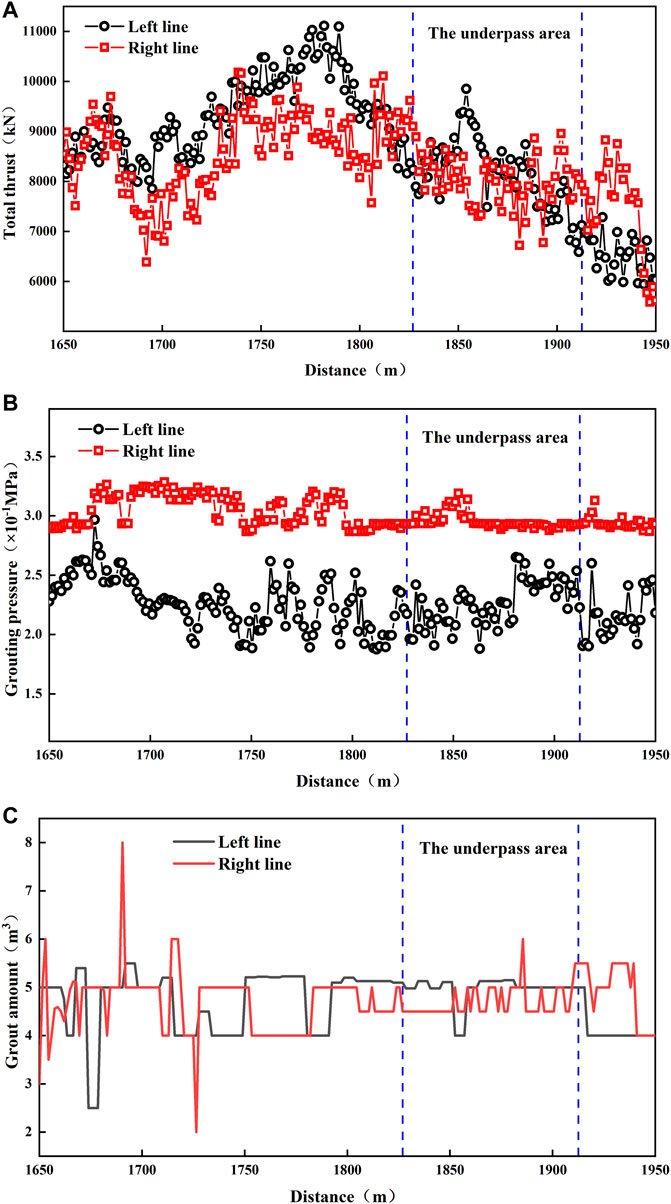
FIGURE 4. TBM tunneling parameters in underpass existing buildings: (A) total thrust; (B) grouting pressure; (C) grout volume.
5 Numerical simulation for underpass existing buildings
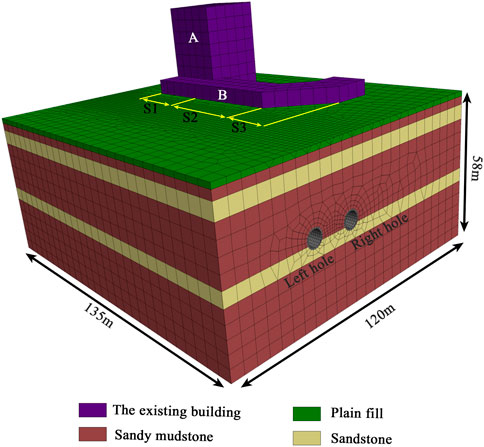
5.1 Calculating models
In order to reduce the influence of boundary effects on the results, the axial and lateral directions are set to 135 and 120 m, respectively. The upper part is assumed at the ground level, while the lower part is set to 26.4 m, which is four times the excavating diameter. Accordingly, the dimensions of the three-dimensional computing model are 120 m × 135 m × 58 m. The boundary conditions are horizontal constraint around the model, vertical constraint into the bottom, and the ground surface being free (Zhang et al., 2022). Figure 5 shows the established model and the imposed boundary conditions.
5.2 Simulating the tunnel boring machine working in the tunnel
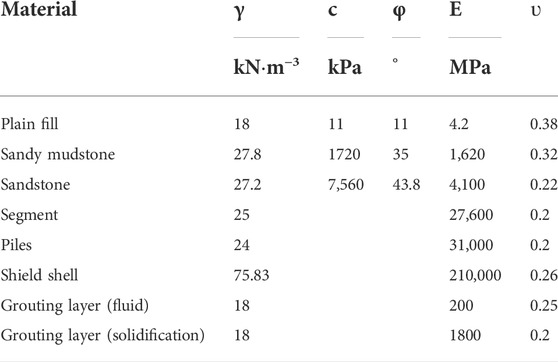
In this section, the shield shell, grouting layer, and the TBM segment are assumed as elastic materials (Yin et al., 2018; Lai et al., 2021). The equivalent load substitution method (He et al., 2008) was used to simulate the existing buildings. In this regard, the structural unit in FLAC3D software was used to simulate the foundation piles in the building, while the Mohr–Coulomb constitutive model was used in the rock and soil layer. The physical and mechanical parameters of strata and materials are presented in Table 1. Moreover, the stiffness transfer method was used to simulate the dynamic construction process of TBM. The thrust load in the construction face, frictional force, grouting pressure, and total thrust was applied to the palm surface, rock surface, shield shell surface, and shield tail, respectively. According to the mechanical parameters of the Zhongcong tunnel, the total thrust is 8,500 kN, and the grouting pressure in the left and right lines is 0.25 MPa and 0.3 MPa, respectively. Based on Eqs. 4, 5, 7, the upper shield shell, the frictional force in the lower part, and the thrust in the palm surface are 1980 kN, 2,220 kN, and 4,300 kN, respectively. The simulation process is shown in Figure 6.
5.3 Validation of the model
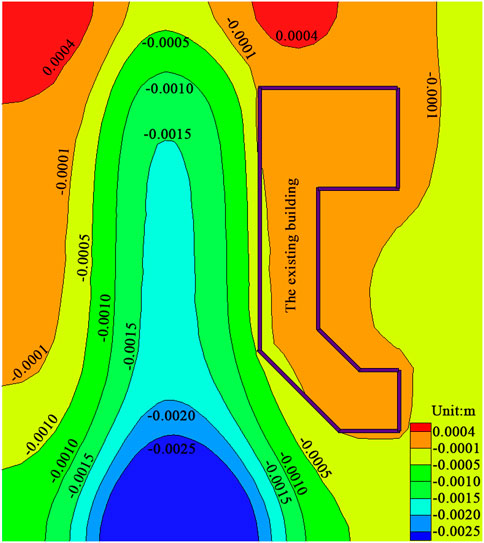
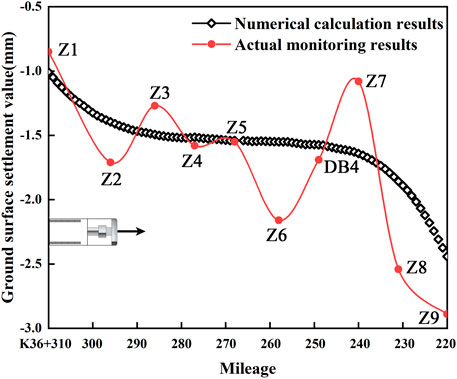
Figure 7 shows the vertical deformation contour of rock strata after excavation in a double-line tunnel. Figure 8 illustrates the vertical ground deformation contour in the underpass area. It is found that the ground surface settlement in the underpass area is remarkably affected by the existing buildings. Meanwhile, the subsidence width and depth significantly increase with the tunnel distance that underpasses the existing buildings. Figures 9, 10 show monitoring results, indicating that the actual value of the ground surface settlement is slightly greater than that of the calculated results. This may be attributed to the rock anisotropicity, while the rock is assumed to be isotropic strata in the established model. Accordingly, an error inevitably occurs in the numerical simulation. However, the monitoring data and the calculated results are consistent, thereby verifying the calculations.
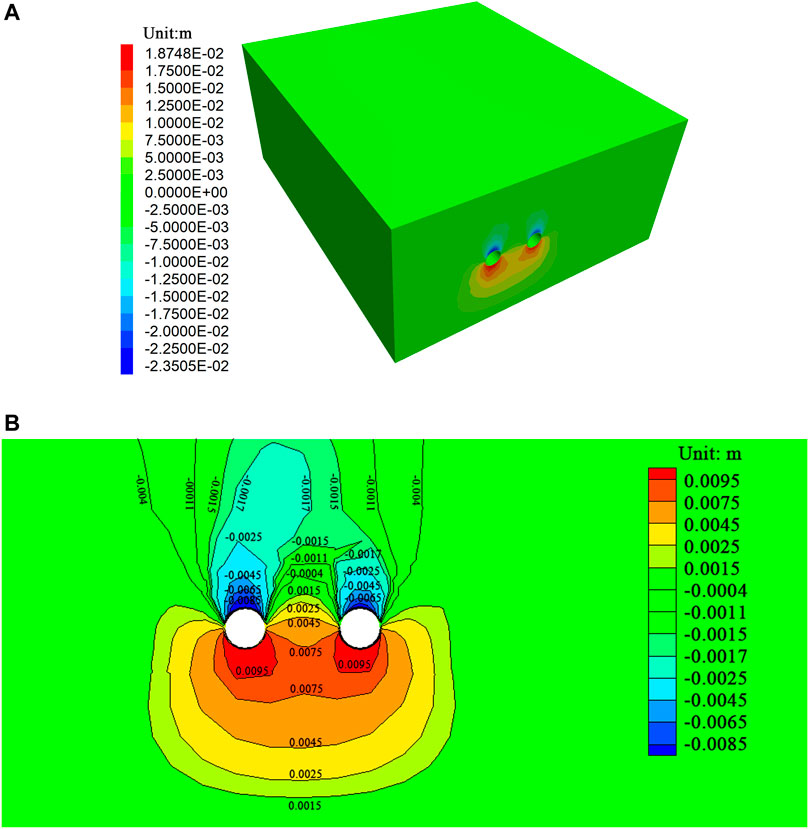
FIGURE 7. Vertical deformation contour of rock strata in the double-line tunnel boring. (A) Settlement nephogram of the surrounding rock. (B) Settlement nephograms at K36 + 250.
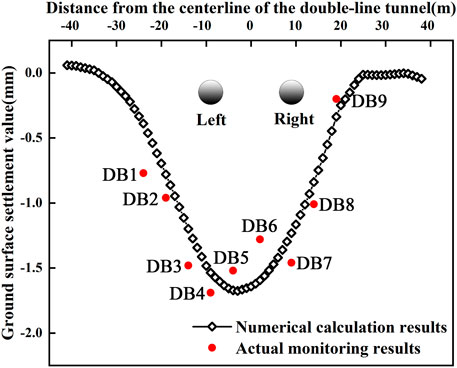
FIGURE 10. Cross-sectional ground surface settlement after the completion of the double-line tunnel boring (K36 + 250).
5.4 Ground surface settlement results in different excavating sequences
TBM excavating sequences can be mainly divided into three working conditions: working condition 1, wherein the right line begins to excavate after completion of excavation in the left tunnel; working condition 2, wherein the left line begins to excavate after completion of excavation in the right tunnel; working condition 3, wherein the double-line tunnels in the left and right lines work simultaneously. It is worth noting that working condition 1 was used in the Zhongcong tunnel.
5.4.1 Calculated results for the cross-section of the ground surface settlement
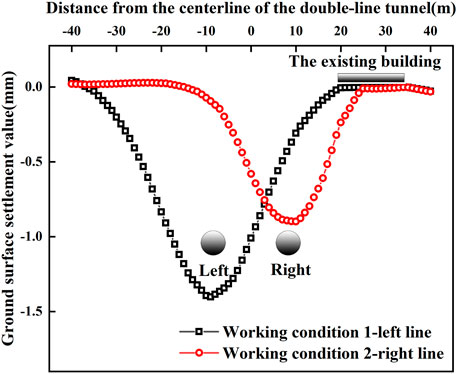
Figure 11 shows the obtained results on the cross-section of the ground surface settlement at K36 + 250 under working conditions 1 and 2. It is observed that the maximum settlement location always is the upper part of the tunnel axis. Furthermore, it is found that the maximum settlement value caused by the right line is significantly smaller, and the settlement value of the ground surface caused by the right line is 64% of the left line. Similarly, the width of the settlement trough in the right line is significantly smaller than that of the left line. This is because the right line is closer to the existing buildings and is more severely affected by the existing buildings. Lu et al. (2019) showed that the diameter, burial depth, and stratum conditions of the left and right line tunnels in the same cross-section are the same, so the width of the settlement trough and the maximum settlement value caused by the left and right lines can be considered to be the same. However, the influence of existing buildings was not considered in the study by Lu et al. (2019). Therefore, the present study is expected to provide a reference for the study of surface settlement caused by TBM double-line tunnels underpass existing buildings.
Figure 12 shows the obtained results of the cross-section of ground surface settlement at K36+250 for different working conditions after completion of excavation in left and right lines. It is found that the location at the extreme point for subsidence is the same, while the ground settlement under working conditions 1 and 2 has some deviations. More specifically, the maximum value in working condition 2 is 2.6% larger than that in working condition 1. Meanwhile, it is found that the subsidence width in working condition 3 is about 1.2 times larger than that in working conditions 1 and two. This may be attributed to the disturbance effect on each other in the simultaneous excavation of the left and right lines. After completion of excavation in the left line, the ground settlement at K36 + 250 points in the working condition 1 is 1.227 mm, which accounts for 73.2% of the completion of this double-line construction. Moreover, the ground settlement in working condition 2 after completion of excavation in the right line is 0.307 mm, which accounts for 17.8% of the completion of this double-line construction.
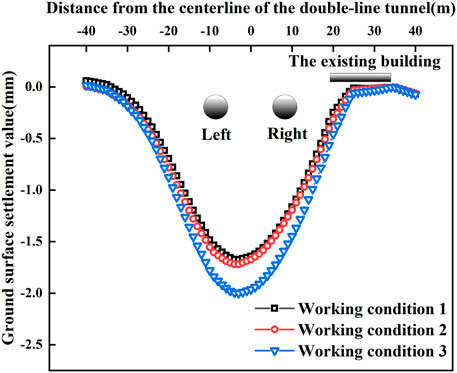
FIGURE 12. Ground surface settlement in cross-section after the completion of double-line construction (K36 + 250).
5.4.2 Results in the vertical section of the ground surface settlement
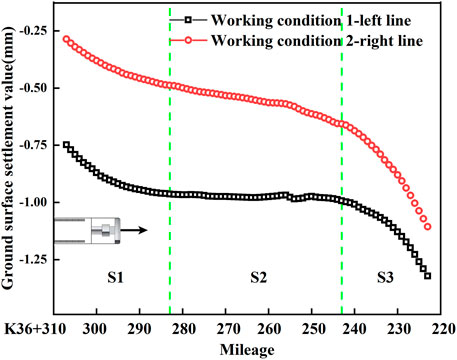
Figure 13 shows the ground settlement at the centerline in two tunnels under working conditions 1 and two. Figure 14 shows the ground settlement at the centerline in the two tunnels after completion of excavation in three working conditions. S1 is the interval section of the TBM tunnel that underpasses existing buildings A and B, and S2 is the interval section of the parallel tunnel that underpasses building B. It is found that the ground settlement curves caused by TBM construction at three working conditions are affected by the existing buildings on right. The S1 interval section absorbed the deformation caused by excavation, so the TBM disturbance decreases on theground surface. In the S3 interval section, the distance between the existing buildings and the tunnel gradually increases, and the ground settlement increases rapidly.
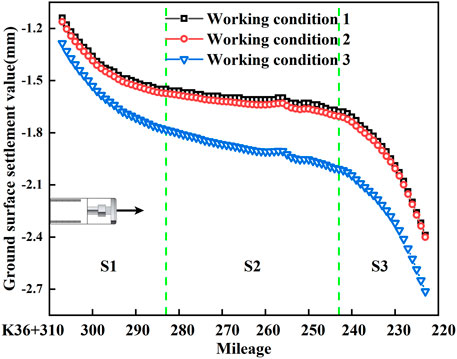
FIGURE 14. Ground settlement at the centerline in the two tunnels after the excavation in three working conditions. S1 ∼ S3 are the three interval sections that underpass the existing buildings.
6 Conclusion
In the current study, the Zhongcong tunnel in Chongqing Metro Line 9 was selected as the research object, and the ground settlement was studied using numerical and field real-time monitoring methods. Based on the obtained results, the main conclusions can be summarized as follows:
1) The influence degree of the existing buildings is related to the distance between the building and the tunnel. The smaller the distance, the greater the influence degree, and the smaller the width of this surface settlement trough. As the distance between the building and the tunnel gradually increases, the ground settlement increases rapidly. The present study is expected to provide a reference for the study of surface settlement caused by TBM double-line tunnels underpass existing buildings.
2) There are remarkable differences in the ground surface settlement under simultaneous excavation and excavation by steps. More specifically, the maximum ground settlement under simultaneous excavation is about 1.2 times larger than that of excavation by steps.
3) The location of the maximum ground settlement is independent of the excavation sequence, but its value is affected by the location of the TBM tunnel and existing buildings.
4) When excavating a single-line tunnel, the maximum settlement occurs above the tunnel axis, while the maximum settlement in three working conditions occurs between the centerline of tunnels and the left axis, which is away from the existing buildings.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
Each author has contributed to the present manuscript. TR, HZ, YG, YT, and QL conceived and designed the experiments; TR performed the experiments and analyzed the experimental data. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Chongqing, China (cstc2021jcyj-msxmX0354), the Key Project of Science and Technology of Chongqing Municipal Education Commission (KJZD-K202201304), the Scientific Innovation Project of Chongqing Graduate (CYS21491), and the Open Fund for Master of Civil Engineering in Chongqing Three Gorges University (TMSL20TS08) for financial support.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Al–Damluji, O. F. S., Fattah, M. Y., and Al-Adthami, R. A. J. (2011). Analysis of soil media containing cavities or tunnels by the boundary element method. Alhosn Univ. J. Eng. Appl. Sci. 3 (2), 27–49.
Chen, S., Gui, M., and Yang, M. (2012). Applicability of the principle of superposition in estimating ground surface settlement of twin- and quadruple-tube tunnels. Tunn. Undergr. Space Technol. 28, 135–149. doi:10.1016/j.tust.2011.10.005
Chen, C., Zhao, C., Wei, G., and Ding, Z. (2014). Prediction of soil settlement induced by double-line shield tunnel based on peck formula. Rock Soil Mech. 35 (8), 2 212–2 218. doi:10.16285/j.rsm.2014.08.024
Comodromos, E. M., Papadopoulou, M. C., and Konstantinidis, G. K. (2014). Numerical assessment of subsidence and adjacent building movements induced by TBM-EPB tunneling. J. Geotech. Geoenviron. Eng. 140 (11), 04014061. doi:10.1061/(ASCE)GT.1943-5606.0001166
Dias, D., and Kastnher, R. (2013). Movements caused by the excavation of tunnels using face pressurized shields - analysis of monitoring and numerical modeling results. Eng. Geol. 152 (1), 17–25. doi:10.1016/j.enggeo.2012.10.002
Fang, Q., Du, J., Wang, Z., and Liu, X. (2021). Model experimental study on stratum deformation of shield tunnelling in sand. China J. Highw. Transp. 34 (05), 135–143+214. doi:10.19721/j.cnki.1001-7372.2021.05.013
Fattah, M. Y., Shlash, K. T., and Salim, N. M. (2011a). settlement trough due to tunneling in cohesive ground. Indian Geotechnical J. 41 (2), 64–75.
Fattah, M. Y., Shlash, K. T., and Salim, N. M. (2011b). Effect of reduced ko zone on time dependent analysis of tunnels. Adv. Civ. Eng. 2011, 12. doi:10.1155/2011/963502
Fattah, M. Y., Shlash, K. T., and al-Soud, M. S. (2012). Boundary element analysis of a lined tunnel problem. ije. 25 (2), 89–97. doi:10.5829/idosi.ije.2012.25.02b.02
Fattah, M. Y., Shlash, K. T., and Salim, N. M. (2013). Prediction of settlement trough induced by tunneling in cohesive ground. Acta Geotech. 8, 167–179. doi:10.1007/s11440-012-0169-4
Fattah, M. Y., Hamood, M. J., and Dawood, S. H. (2015). Dynamic response of a lined tunnel with transmitting boundaries. Earthquakes Struct. 8 (1), 275–304. doi:10.12989/eas.2015.8.1.275
Feng, H., and Yu, R. (2019). Numerical analysis of influence of double - line tunnel shield tunneling on ground surface settlement. J. Railw. Eng. Soc. 36 (03), 78–83. doi:10.3969/j.issn.1006-2106.2019.03.014
Guan, H. (2008). “Study on the calculat ing models of key parameters & mechanical behavior of the EPB shield machine,” Doctoral Dissertation (Sichuan, China: Southwest Jiaotong University).
Han, X., and Li, N. (2007). Comparative analysis of strata prediction models for ground movement induced by tunnel construction. Chin. J. Rock Mech. Eng. 26 (3), 594–600. doi:10.3321/j.issn:1000-6915.2007.03.022
He, M., Le, G., Liu, J., Wang, M., and Zhang, D. (2008). “Study of the affection of foundation settlement by spacing adjustment between tunnels and high building,” in Proceedings of the 2nd national environmental geotechnical engineering and geo-synthetic materials technology symposium(2). Editor D. Wang (Changsha, China: Hunan University Magazines), 110–114.
Huang, H., and Zhang, D. (2001). Shield tunnelling induced surface settlement and in-situ monitoring. Chin. J. Rock Mech. Eng. S1, 1814–1820. doi:10.3321/j.issn:1000-6915.2001.z1.046
Jin, D., Yuan, D., Li, X., and Zheng, H. (2018). Analysis of the settlement of an existing tunnel induced by shield tunneling underneath. Tunn. Undergr. Space Technol. 81, 209–220. doi:10.1016/j.tust.2018.06.035
Lai, H. P., Wang, T. T., Zhang, L. J., Yuan, Y., and Luo, W. (2021). Construction control of shield tunneling underneath existing metro tunnel considering friction between shield shell and soil. Tunn. Constr. 41 (5), 729. doi:10.3973/j.issn.2096-4498.2021.05.005
Li, J., Li, G., Zhang, K., Pei, Z., and Zhao, S. (2021). Cu-loaded Brushite bone cements with good antibacterial activity and operability. J. Biomed. Mat. Res. B Appl. Biomater. 41 (6), 877–889. doi:10.1002/jbm.b.34752
Liu, B., Tao, L., Ding, C., Li, H., Pan, Q., and Gao, X. (2006). Prediction for ground subsidence induced by subway double tube tunneling. J. China Univ. Min. Technol. 35 (3), 356–361. doi:10.3321/j.issn:1000-1964.2006.03.014
Lu, J., Yao, A., Zheng, X., Zhang, J., and Tian, T. (2019). Study on the law and computational method of ground surface settlement induced by double-line tunnel excavation. Chin. J. Rock Mech. Eng. 38, 3735–3747. doi:10.13722/j.cnki.jrme.2019.0630
Ma, K. (2008). “Research on the ground settlement caused by the shield construction and the protection of the adjacent building,” Doctoral Dissertation (Hubei, China: Huazhong University of Science and Technology).
Peck, R. (1969). Deep excavations and tunnelling in soft ground. Proc. 7th Int. Conf. SMFE, 226–290.
Qiu, M., Yang, G., Wu, Z., Jiang, A., and Lin, Y. (2017). Distribution laws of surface settlement induced by shield construction of twin-tube metro tunnels. Mod. Tunn. Technol. 54 (02), 96–105. doi:10.13807/j.cnki.mtt.2017.02.014
Shi, C., Peng, L., and Lei, M. (2009). Study of time-space united calculating method of stratum deformation caused by shield tunnel excavation. Rock Soil Mech. 30 (08), 2379–2384. doi:10.3969/j.issn.1000-7598.2009.08.032
Wang, F., Miao, L., and Li, C. (2013). Numerical analysis of shield tunnel settlement considering construction process. Chin. J. Rock Mech. Eng. 32 (S1), 2907–2914. doi:10.3969/j.issn.1000-6915.2013.z1.043
Wei, G. (2009). Study on calculation for width parameter of surface settlement trough induced by shield tunnel. Ind. Constr. 39 (12), 74–79. doi:10.13201/j.gyjz2009.12.004
Yin, M., Jiang, H., Jiang, Y., Sun, Z., and Wu, Q. (2018). Effect of the excavation clearance of an under-crossing shield tunnel on existing shield tunnels. Tunn. Undergr. Space Technol. 78, 245–258. doi:10.1016/j.tust.2018.04.034
Yu, X., Ren, H., and Hu, X. (2014). Analysis of the disturbance to surrounding soils during shield driving for the hangzhou metro line 1 project. Mod. Tunn. Technol. 51 (5), 166–173. doi:10.13807/j.cnki.mtt.2014.05.026
Zhang, Y., Ying, Z., and Xu, Y. (2002). Analysis on three-dimensional ground surface deformation due to shield tunnel. Chin. J. Rock Mech. Eng. 21 (03), 388–392. doi:10.3321/j.issn:1000-6915.2002.03.019
Keywords: double-line tunnel, TBM, excavating parameters, underpass existing buildings, ground surface settlement
Citation: Ren T, Zhang H, Guo Y, Tang Y and Li Q (2022) Numerical simulation of ground surface settlement of underpass building in tunnel boring machine double-line tunnels. Front. Earth Sci. 10:937524. doi: 10.3389/feart.2022.937524
Received: 06 May 2022; Accepted: 09 August 2022;
Published: 05 September 2022.
Edited by:
Fanyu Zhang, Lanzhou University, ChinaReviewed by:
Mohammed Y. Fattah, University of Technology, IraqNenad Milorad Vusovic, University of Belgrade, Serbia
Copyright © 2022 Ren, Zhang, Guo, Tang and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hailong Zhang, emhhbmdobEBjcXd1LmVkdS5jbg==
 Ting Ren
Ting Ren Hailong Zhang
Hailong Zhang Yuancheng Guo1
Yuancheng Guo1