Law of Nuclide Migration in Clayey Rocks considering Diffusion and Fluid Transport

A core concern in the research on deep geological disposal of high-level radioactive waste is the migration of radionuclides in geological bodies. Most studies on radionuclide migration consider the role of only the rock fissures without incorporating the influence of the rock matrix. In this paper, the rock mass for geological disposal of high-level radioactive waste is regarded as a fissure-pore medium. Considering the influences of radionuclide diffusion and fluid transport on radionuclide migration in the process of disposal, the governing equation of radionuclide migration and evolution in the pore-fissure medium is established. The numerical scheme of the governing equation is given based on the mixed finite volume method (FVM), using our program solution module written in C++. On this basis, the numerical test model with fissures was developed, which analyzed the radionuclide migration law in clayey rocks under various fissure and rock matrix diffusion coefficients and hydraulic conductivities. The simulation results are compared with finite element method results, revealing the superiority of the mixed FVM method in solving problems of radionuclide migration in discontinuous geological bodies containing hiatuses, mutations, and fissures. The study provides a theoretical basis for evaluating the safety, feasibility, and suitability of geological disposal repositories for high-level radioactive waste in terms of radionuclide migration.

1 Introduction

During the operation and closure of geological repositories for high-level radioactive waste, the stored nuclear waste continuously releases radionuclides with long half-lives, strong radioactivity, and high toxicity (IAEA, 2010; Cho et al., 2012; Wu, 2017). The design life of a geological repository for high-level radioactive waste is typically tens of thousands of years. On such a long time scale, the artificial engineering barriers, e.g., nuclear waste packaging, buffer layers, and surrounding rocks and linings, are likely to experience damage and failure. Coupled with geological structuring, radionuclides may leak and migrate to surrounding rocks and the biosphere of the repository (Martin et al., 2009; Grupa et al., 2017). Once the radionuclides enter the ecosystem, they can cause irreversible radioactive damage and possibly threaten the lives of humans and other organisms (Labib and Harris, 2015; L’Annunziata, 2016; Ahmad et al., 2019). Therefore, one core challenge in the safety evaluation of radioactive waste disposal is to quantitatively evaluate the migration law of radionuclides with underground water and other carriers.

With low permeability, strong retardation to radionuclide migration, and self-sealing properties, clayey rocks are considered reasonable geological barriers for high-level radioactive waste disposal (Yu et al., 2018; 2021). Countries like Switzerland, France, and Belgium have selected clayey rock as a candidate for geological disposal repositories of high-level radioactive waste. They conducted significant research and development on clayey rock site screening and feature evaluation and built underground clayey rock laboratories (Van Marcke et al., 2010; Jacops et al., 2015; Bossart et al., 2017; Leupin et al., 2017; Wigger et al., 2018).

The clayey rock surface, which generally exhibits electronegativity, is prone to adsorb cations with strong electrophilicity. Nuclides with weak electrophilicity and anionic nuclides do not tend to be adsorbed on the clay surface, and their diffusion is relatively fast (Van Loon et al., 2007). For radionuclides with strong radioactivity, high toxicity, and long half-lives, the question arises of whether multiple barriers can effectively prevent them from migrating to the biosphere during a long process of geological disposal. Van Loon et al. (2005) studied the diffusion behavior of some key elements (e.g., tritiated water (HTO), Cl⁻, Na⁺) in clayey rocks, e.g., Opalinus Clay, using the diffusion cell method and obtained many migration parameters. In another study, Leupin et al. (2017) presented the research results of the Mont Terri Laboratory about material migration in Opalinus Clay in the last 20 years, which provided valuable data for the safety evaluation of underground laboratories and disposal repositories in Switzerland. Additionally, Jacops et al. (2015; 2017) studied the diffusion coefficients of dissolved gas and HTO in Boom clayey rocks by the diffusion cell method, providing a useful experimental basis for the construction of disposal repositories in Belgium. Bazer-Bach et al. (2006) provided evidence of a kinetically limited slight retention of iodide in Callovo-Oxfordian argillites at low total iodine concentration through batch experiments. Further research by Altmann et al. (2012) addressed the migration and diffusion of radionuclides from clayey rocks in the geological nuclear waste repository to the biosphere. These data of diffusion-driven transfer in strata revealed extreme differences in the measurements or simulated behaviors of various radionuclides, which were mainly due to the varying effects of halogen elements on diffusion and adsorption. Some progress has been made in the study of radionuclide migration laws in clayey rocks. However, radionuclide migration is time-consuming and slow in transformation, so some mechanisms and laws require further investigations for a better understanding.

After lengthy diagenesis and tectonic movement, the clayey rock mass inevitably contains many pores and micro-fissures, and the deep geological disposal repository for radioactive waste depends on just this geological body. Conventionally, the migration mechanisms of nuclides in fissured rocks focus on diffusion, convection, adsorption, and retardation, without considering the influence of pores. In fact, pores, comprising a typical non-connecting factor, form the fissure-pore permeability channel together with fissures. Fissure fillings and rock matrixes with various hydraulic properties are often encountered in the geological disposal of radioactive waste. When the permeability of the filling is better than that of the rock matrix, the network composed of random fissures will form dominant water channels and control the overall seepage field and radionuclide migration of the geological body. When the hydraulic conductivity of the filling is lower than that of the rock matrix, the fissure network will form an obstacle into shielding seepage. Under this circumstance, the rock matrix where the pores are located controls the overall seepage field, and the filling becomes a low-permeability barrier, hindering the migration of radionuclides in the geological body.

Conventional fissure medium models only consider the mechanical and seepage characteristics of fissures, ignoring the role of the rock matrix. In most cases, the fissure surface aperture of the fissured rock mass is relatively large, maintaining good water conductivity, and the fillings contain mostly rock and soil materials with good permeability, e.g., weathered sediments. The water conductivity of the fissure is better than that of the rock matrix (Zhang et al., 2012; Tran et al., 2021), so the role of the rock mass can be neglected in the numerical model. However, when studying the geological disposal of high-level radioactive waste, the influence of the rock matrix cannot be ignored in the simulation, and the numerical method for the fissure-pore medium becomes necessary. The main difference between this method and conventional porous medium methods is that the former considers the fissure–fissure and fissure–rock matrix flow exchanges in numerical discretization.

Currently, fluid migration simulation in fissure-pore media is mostly based on the finite volume method (FVM) or its improved versions. Among the various versions, the cell-centered FVM (CFVM) is the most widely used (Nordbotten, 2014), in which two major approaches have been formed: embedded discrete fissure model (EDFM) (Tene et al., 2017) and discrete fissure model (DFM) (Mohammad and Abbas, 2003). They adopt different mesh generation methods and discretization methods and have their respective advantages and disadvantages. Specifically, EDFM adopts an orthogonally structured mesh generation, whereas DFM uses a more complex non-structured triangular mesh. The mesh of EDFM enables weak mesh dependence, which saves time and energy in mesh processing. However, because it uses the transfer function to simulate the flow exchange between the fissure and rock matrix, its accuracy is lower than that of the DFM method. The DFM method uses a more accurate conforming mesh and addresses the flow exchange problem through the pressure gradient of nodes and cells. It takes the fissure surface as the constraint boundary of meshing and calls the constrained Delaunay algorithm to realize a non-structured mesh generation (Mustapha, 2014). The DFM method is applicable to both CFVM (Nordbotten, 2014) and nodal-based FVM (NFVM) (Amaziane et al., 2009). To the best of the author’s knowledge, however, publications on radionuclide migration analysis have rarely used the mixed FVM.

In this paper, the evolution of radionuclide migration in the fissure-pore medium is systematically studied by the mixed FVM. The numerical discretization steps and program module are introduced, with the program solution module independently written in C++ to analyze the diffusion, fluid migration, and decay of radionuclides in clayey rocks and their migration under adsorption and retardation of the rock matrix. This study can provide a theoretical basis for evaluating the safety, feasibility, and suitability of geological disposal repositories for high-level radioactive waste in terms of radionuclides migration.

2 Radionuclide Migration Law Considering Diffusion

2.1 Theory of Radionuclide Migration Considering Diffusion

Similar to the governing equations of heat conduction and fluid migration, the migration of nuclides in the rock matrix is governed by mass conservation and satisfies a hyperbolic partial differential equation (PDE):

$\frac{\partial C}{\partial t}+\nabla \cdot \mathbf{F}=f(1)$

where $C$ is the concentration, $\mathbf{F}$ is the flow function, and $f$ is the source function, which are all functions of time $t$ and the spatial coordinate $x$.

The flow $\mathbf{J}$ of the diffusion material in the medium is calculated by Fick’s first law:

$\mathbf{J}=-\mathbf{D}\nabla C(2)$

where $\mathbf{D}$ is the diffusion coefficient, which is a second-order tensor whose anisotropy and evolution with concentration can be considered. Its form by components is

$\{\begin{array}{c}{J}_x=-D_x\frac{\partial C}{\partial X}\\ J_y=-D_y\frac{\partial C}{\partial Y}\end{array}(3)$

where $J_x$ and $J_y$ are the diffusion material flows in $x$ and $y$ direction, respectively; $D_x$ and $D_y$ are the diffusion coefficients in $x$ and $y$ direction, respectively, varying with the concentration; and $\frac{\partial C}{\partial X}$ and $\frac{\partial C}{\partial Y}$ are the concentration gradients in $x$ and $y$ direction, respectively.

Substituting Eq. 2 into Eq. 1 Obtains

$\frac{\partial C}{\partial t}-\nabla \cdot \left(\mathbf{D}\nabla C\right)=f(4)$

Equation 4 is the governing equation of radionuclide migration considering only diffusion, which is applicable to the diffusion of nuclides without decay or with a research time scale significantly smaller than the nuclide half-life, without considering fluid migration and adsorption of the fissure-pore medium.

The initial boundary values of the PDE system need to be given at the boundary $\mathrm{\Gamma }$, whole domain $\mathrm{\Omega }$, and time period $T$ to make the problem well-posed

$\{\begin{array}{c}C=\overline{C}withinboundaryandtime\\ \mathbf{J}=\overline{\mathbf{J}}withinboundaryandtime\\ f\left(\mathbf{J}\right)=\overline{f}\left(\mathbf{J}\right)withinwholedomainandtime\end{array}(5)$

where $T$ defines the overall duration of the diffusion process and $\left[0,t_n\right]\in T$. The iterative time step is advanced through time discretization by $t^{n+1}=\mathrm{\Delta }t+t^n$. Eqs 3, 4 and the initial boundary condition (5) constitute the basic equations of radionuclide migration considering only diffusion.

When accounting for the influence of natural pores, the pores can be set to be filled or not. When the pores are filled, the filling material can be given various diffusion properties with the option to define as a special fissure or matrix in the numerical processing. When the pores are not filled, the boundary can be treated as a special internal boundary, for which only the corresponding conditions need to be added to the solution.

2.2 Numerical Scheme

According to the basic principle of the FVM method, Eq. 4 is integrated within the whole spatial domain $\mathrm{\Omega }$ and time $\left[t_n,t_n+\mathrm{\Delta }t\right]$:

${\displaystyle {\int }_{\mathrm{\Delta }t}{\displaystyle {\int }_{\mathrm{\Omega }}\frac{\partial C}{\partial t}}}dVdt+{\displaystyle {\int }_{\mathrm{\Delta }t}{\displaystyle {\int }_{\mathrm{\Omega }}-\nabla \cdot \left(\mathbf{D}\nabla C\right)}}dVdt={\displaystyle {\int }_{\mathrm{\Delta }t}{\displaystyle {\int }_{\mathrm{\Omega }}{Q}_C}}dVdt(6)$

where $\frac{\partial C}{\partial t}$ is the time term. When discretizing the time item, the choice of implicit or explicit iteration should be made. Implicit iteration exhibits a high accuracy but involves a complex iterative process, which is prone to errors in the numerical implementation. Explicit iteration, though having a slightly lower accuracy, exhibits high algorithm stability and presents an easy numerical solution process. Therefore, this paper adopts the scheme of explicit iteration to approximate Eq. 6:

${\displaystyle {\int }_{\mathrm{\Omega }}\frac{C^{n+1}-C^n}{\mathrm{\Delta }t}}dV+{{\displaystyle {\int }_{\mathrm{\Omega }}-\nabla \cdot \left(\mathbf{D}\nabla C\right)}}^{n}dV={\displaystyle {\int }_{\mathrm{\Omega }}{Q}_C^n}dV(7)$

The first term on the left side of Eq. 7 represents the time discretization, the second term is the diffusion, and the right-hand side is the source-sink term. Considering model establishment and mesh generation, the total number of cells in the region is denoted as $n^{all}$, and Eq. 7 is discretized spatially to form a semi-discrete scheme:

${\displaystyle \sum _{i=1}^{n^{all}}{\displaystyle {\int }_{{\mathrm{\Omega }}_i^{ele}}\frac{C^{n+1}-C^n}{\mathrm{\Delta }t}}dV}+{\displaystyle \sum _{i=1}^{n^{all}}{{\displaystyle {\int }_{{\mathrm{\Omega }}_i^{ele}}-\nabla \cdot \left(\mathbf{D}\nabla C\right)}}^{n}dV}={\displaystyle \sum _{i=1}^{n^{all}}{\displaystyle {\int }_{{\mathrm{\Omega }}_i^{ele}}{Q}_C^n}dV}(8)$

where ${\displaystyle \sum _{i=1}^{n^{all}}{\displaystyle {\int }_{{\mathrm{\Omega }}_i^{ele}}dV}}$ sums the integrals of each cell and ${\mathrm{\Omega }}_i^{ele}$ represents a fissure or rock matrix cell.

Eq. 8 is applicable to radionuclide migration in the fissure-pore medium considering diffusion. To transform the semi-discrete scheme of Eq. 8 into a fully discrete one, the field variable is interpolated to find a solution $C$. In this paper, the piecewise interpolation function of the finite element is used for the interpolation of variables at arbitrary points.

The CFVM has a piecewise-continuous interpolation function and, therefore, is regarded as a special finite element method (FEM). The numerical solution aims to solve the governing equation and the unknown concentration field variable $C$ under the initial boundary values. In this paper, the trial function in the sense of the finite element is adopted, and the shape function of the Galerkin finite element $\zeta$ enables the interpolation approximation of the concentration field variable:

$C={\displaystyle \sum _{i=1}^{n^{all}}{\zeta }_i{C}_i}(9)$

Therefore, the concentration at any point in the domain can be solved by Eq. 9. The shape function $\zeta$ of the Galerkin finite element is as follows:

${\zeta }_i=\{\begin{array}{c}1Celli\\ 0Cellj\end{array}(10)$

The shape of the piecewise interpolation function $\zeta$ represented by Eq. 10 is piecewise-continuous in terms of cells. Owing to the characteristics of the CFVM, the concentration remains constant within cell $i$ and abruptly changes on its boundary with the adjacent cell $j$. This method can describe the step-change in concentration field between the fissure and rock matrix cells, which is different from the continuous, differentiable boundary in conventional FVM. If $\zeta$ is classified as a special finite element shape function, the mixed FVM can be regarded as a special discontinuous finite element scheme.

Substituting Eq. 9 for the field variable to be solved in Eq. 8, transforming the volume integral of the diffusion term into a surface integral through the Gauss’s formula, and considering the spatial discretization, the fully discrete scheme of the mixed FVM for radionuclide migration simulation in the fissure-pore medium considering only diffusion can be obtained as

$\frac{V_i{\zeta }_i}{\mathrm{\Delta }t}\left(C_i^{n+1}-C_i^n\right)+{\displaystyle \sum _{\ast =j,k,m}^{n_i^{neig}}{\mathbf{J}}_{i\ast }^n{A}_{i\ast }}=Q_C^n{V}_i(11)$

where $n_i^{neig}$ represents the number of adjacent cells for $\text{Cell}$ $i$. For triangular meshes, the adjacent cells of any non-boundary cell $i$ are $j$, $k$, and $m$, whereas the adjacent cells of a boundary cell are $j$ and $k$, or only $j$. The volume of Cell $i$ is $V_i$ (area in a two-dimensional problem); $\mathrm{\Delta }t$ is the iterative time step, and the time is updated at each step by $t^{n+1}=t^n+\mathrm{\Delta }t$; ${\zeta }_i$ is the interpolation function defined in Eq. 10; ${\mathbf{J}}_{i\ast }$ is the diffusion vector between $i$ and ∗. The second item in the above formula is refined to

${\displaystyle \sum _{\ast =j,k,m}^{n_i^{neig}}{\mathbf{J}}_{i\ast }^n{A}_{i\ast }}={\displaystyle \sum _{\ast =j,k,m}^{n_i^{neig}}{\left[{\mathrm{\Lambda }}_{i\ast }^C\left({\zeta }_i{C}_i-{\zeta }_{\ast }{C}_{\ast }\right)\right]}^n}(12)$

where ${\mathrm{\Lambda }}_{i\ast }^C$ is the concentration transfer coefficient that considers the diffusion between two adjacent cells. Following the treatment in numerical heat transfer theory and computational fluid dynamics considering the diffusion interaction between two adjacent cells, ${\mathrm{\Lambda }}_{i\ast }^C$ takes the harmonic average between the two adjacent cells in Eq. 9:

${\mathrm{\Lambda }}_{i\ast }^C=\frac{{\mathrm{\Lambda }}_i^C{\mathrm{\Lambda }}_{\ast }^C}{{\mathrm{\Lambda }}_i^C+{\mathrm{\Lambda }}_{\ast }^C}(13)$

where ${\mathrm{\Lambda }}_i^C$ represents the diffusion coefficient between $i$, and ∗ and is calculated by

${\mathrm{\Lambda }}_i^C=\frac{A_{i\ast }D}{D_{i\ast }}(14)$

where $D_{i\ast }$ is the distance from $i$ to the common-side surface (common side in a two-dimensional problem) of ∗, and $D$ is the diffusion coefficient.

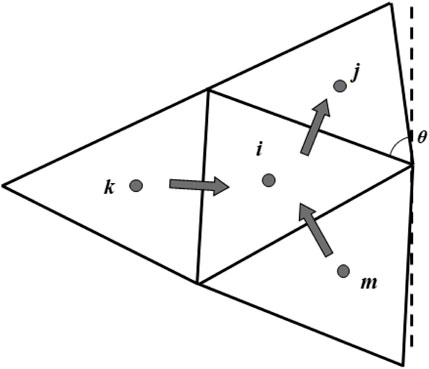
Figure 1 displays a possible case of flow exchange. Taking the flow transport between $i$ and $j$ as an example, the straight line $l_{ij}$ is the common side between $i$ and $j$, the length is denoted as $\mathrm{\Delta }{A}_{ij}$, and the angle between $l_{ij}$ and the vertical line is $\theta$. Combined with Eq. 3, the following holds:

$\{\begin{array}{c}{Q}_{Cx}=-D_x\left(\mathrm{\Delta }{A}_{ij}\cos \theta \right)\frac{\mathrm{\Delta }C\cos \theta }{D_{ij}}\\ Q_{Cy}=-D_y\left(\mathrm{\Delta }{A}_{ij}\sin \theta \right)\frac{\mathrm{\Delta }C\sin \theta }{D_{ij}}\end{array}(15)$

where $Q_{Cx}$ represents the amount of material transferred in $x$ direction and $Q_{Cy}$ indicates the amount of material transferred in $y$ direction. The total amount of transferred material is $Q_C$ by summing the two:

$Q_C=Q_{Cx}+Q_{Cy}=-\mathrm{\Delta }{A}_{ij}\frac{\mathrm{\Delta }C}{D_{ij}}\left(D_x{\cos }^2\theta +D_{y}si{n}^2\theta \right)(16)$

FIGURE 1

FIGURE 1. Flow exchange.

Comparing Eqs 12, 14, 16, the comprehensive diffusion coefficient $D$ is obtained as

$D=D_x{\cos }^2\theta +D_y{\sin }^2\theta (17)$

The concentration transfer coefficient ${\mathrm{\Lambda }}_i^C$ in Eq. 12 in anisotropic cases is rewritten as

${\mathrm{\Lambda }}_i^C=\frac{\mathrm{\Delta }{A}_{i\ast }\left(D_x{\cos }^2\theta +D_{y}si{n}^2\theta \right)}{D_{i\ast }}(18)$

Equation 17 degenerates into a case of isotropy when $D_x=D_y$. The values of ${\cos }^2\theta$ and ${\sin }^2\theta$ are greater than or equal to zero, indicating that the concentration transfer coefficient ${\mathrm{\Lambda }}_i^C$ in Eq. 17 is not affected by the inflow or outflow direction of the upwind scheme. Additionally, this means ${\mathrm{\Lambda }}_i^C$ is only determined by the position of the common side, which is a universal case. In the numerical simulation, the position of the common side is determined by its two ends. Since the coordinates of these two ends are known, the corresponding angle $\theta$ can be easily obtained.

2.3 Program Implementation

The numerical discretization method for simulating radionuclide migration in the fissure-pore medium by mixed FVM considering only diffusion is thoroughly described in the previous sections. The key challenge of numerical implementation is the use of explicit iteration to handle the time term in the governing equation and the diffusion material flow exchange between the fissure and rock mass. This section introduces the radionuclide migration simulation program. The main modules of numerical simulation for the fissure-pore medium are the following: (1) pre-processing (the generation of fissure and matrix cells using the ABAQUS pre-processing module), (2) the assembly of the diffusion and migration governing equations (based on mixed FVM), (3) iterative calculation in time steps, and (4) post-processing (using Paraview).

The heterogeneous diffusion coefficient can be considered in the simulation of radionuclide migration by assigning various diffusion coefficients to the fissure and rock matrix cells. Anisotropic diffusion coefficients ($D_x\ne D_y$) of a homogeneous material can also be considered, which can automatically degenerate into isotropic diffusion when $D_x=D_y$. The radionuclide migration simulation program was independently developed with C++. The physical essence of this process is material transport, the most prominent feature of which is time dependence, as reflected by the time term $\frac{\partial C}{\partial t}$ in Eq. 6. Because of this time correlation, an iterative method is used to solve the transportation process, and explicit iteration is adopted here. First, the amount of material diffusion is solved based on the concentration at the end of the previous iteration, followed by the solution of the concentration increment. In other words, the concentration at the end of the current iteration is obtained, which is then used as the initial concentration of the next iteration.

2.4 Example Analysis

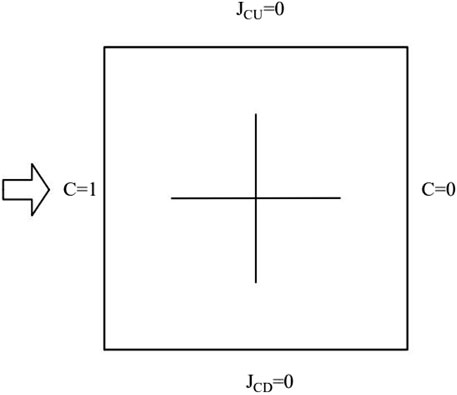
This section explains how our developed mixed FVM program was analyzed through the numerical test model of clayey rocks with orthogonal fissures, as displayed in Figure 2. The model was a square with a side length of 9 m, in the middle of which were two orthogonal fissures. Each fissure was 5 m long and 0.1 m wide. The left boundary of the model was where the nuclides were injected, so the concentration was maintained at $C$ = 1 mol/m³. The right boundary was set as the nuclide output position, and the concentration was maintained at $C$ = 0 mol/m³. At the other boundaries, the material flow conditions were set to $J_{CU}=J_{CD}=0$.

FIGURE 2

FIGURE 2. Fissure-pore medium model with orthogonal fissures.

Various studies have been conducted to obtain the diffusion coefficient for the migration of radionuclides through the host rock. Meeussen et al. (2017) estimated the pore diffusion coefficient of Boom Clay, which was in the range of 5.7 × 10^–12 to 8.5 × 10^–9 m²/s. When setting the arbitrary test values for the compartments’ waste and host rock (Boom Clay) radionuclides used in the benchmark calculations, Grupa et al. (2017) chose 2.0 × 10^–10 m²/s for the diffusion coefficient. Based on diffusion experiments, Bucur et al. (2000) found that the diffusion coefficient of main radionuclide CS-137 and \Co-60 ranged from 9.89 × 10⁻⁹–6.5 × 10^–8 m²/s and 7.59 × 10⁻⁹–4.94 × 10^–8 m²/s, respectively, in red clay with a higher montmorillonite content.

Here, we chose $D_m=D_{mx}=D_{my}=5\times {10}^{-10}$ m²/s as the diffusion coefficient for the clayey rock matrix. To study the influence of fissures on the migration and diffusion of ions or nuclides, three conditions were assumed for the diffusion coefficient in fissures: Condition A ($D_f/D_m=1\times 100$, i.e., $D_f=5\times {10}^{-8}$ m²/s, where $D_f$ is the nuclide diffusion coefficient in fissures), Condition B ($D_f/D_m=1$, i.e., $D_f=5\times {10}^{-10}$ m²/s), and Condition C ($D_f/D_m=0.01$, i.e., $D_f=5\times {10}^{-12}$ m²/s). The concentration of injected nuclides was 1 mol/m³.

The mixed FVM adopted a total of 1670 triangular cells, and 441 DC2D4 cells were used in ABAQUS. The mass diffusion (transient) analysis step was used for the calculation, the total time was set to 1.5763 × 10¹⁰ s (500 years), and the initial and maximum time increment step was set to 3.1536 × 10⁷ s (1 year). The simulation results of the mixed FVM method were visualized through the open-source software Paraview, and the ABAQUS simulation results were displayed through the ABAQUS/CAE post-processing module, as presented in Figures 3–5. ABAQUS allowed the “Monitor” function for dynamic monitoring in the calculation. When the time interval of each ABAQUS step in the implicit iterative calculation was 3.1536 × 10⁷ s (1 year), convergence was possible. Considering the boundary conditions, internal concentration field distribution, and the concentration change of each time increment step, the time increment $\mathrm{\Delta }t$ of the mixed FVM program was configured to 3.1536 × 10⁵ s, which achieved adequate calculation accuracy of each time increment step (the 2-norm of all cell residuals ${\Vert {\mathbf{R}}^n\Vert }_2\le 1\times {10}^{-5}$, defined below) and maintained a sufficient calculation efficiency.

FIGURE 3

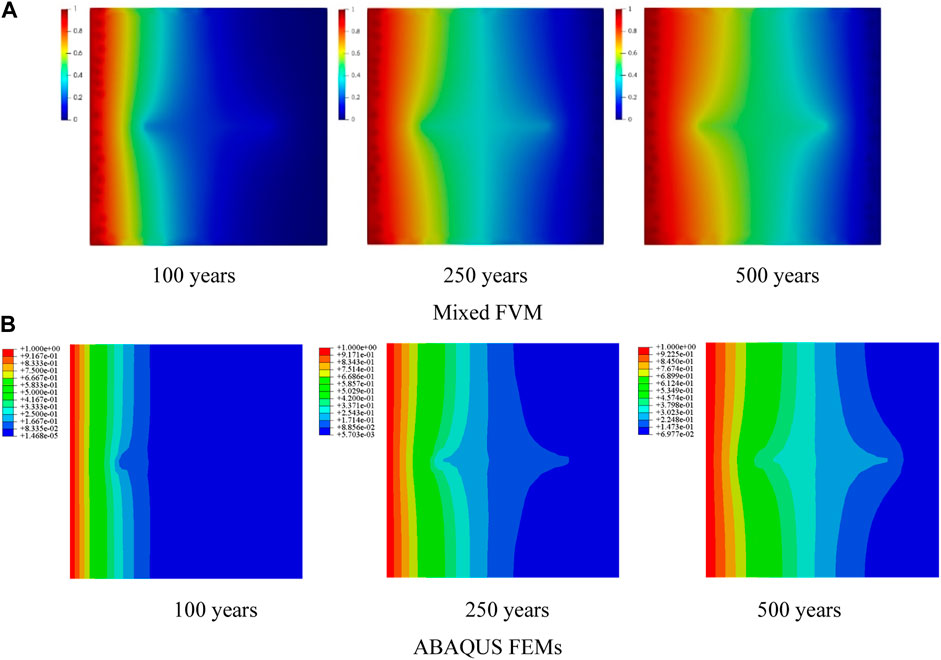
FIGURE 3. Comparison of the mixed FVM and ABAQUS FEMs under Condition A ($D_f/D_m=100$). (A) Mixed FVM. (B) ABAQUS FEMs.

FIGURE 4

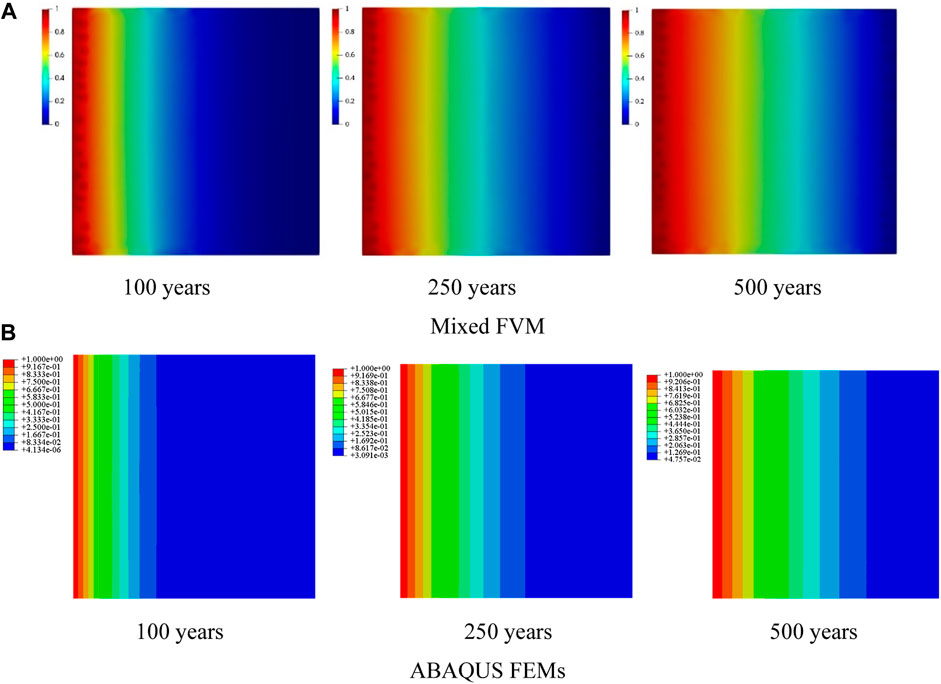
FIGURE 4. Comparison of the mixed FVM and ABAQUS FEMs under Condition B ($D_f/D_m=1$). (A) Mixed FVM. (B) ABAQUS FEMs.

FIGURE 5

FIGURE 5. Comparison of the mixed FVM and ABAQUS FEMs under Condition C ($D_f/D_m=0.01$). (A) Mixed FVM. (B) ABAQUS FEMs.

The residual of each time step is defined as

${\mathbf{R}}^n=\left[\begin{array}{cc}{\mathbf{R}}_m^n& {\mathbf{R}}_f^n\end{array}\right](19)$

where ${\mathbf{R}}_m^n$ represents the vector composed of rock matrix cell residuals in the nth time iteration step and ${\mathbf{R}}_f^n$ represents the vector composed of rock fissure cell residuals in the nth time iteration step.

For a single rock matrix cell $i$, the residual $R_{mi}^n$ in the nth time iteration step is defined as

$R_{mi}^n=\frac{V_i{\zeta }_i}{\mathrm{\Delta }t}\left(C_i^{n+1}-C_i^n\right)+{\displaystyle \sum _{\ast =j,k,m}^{n_i^{neig}}{\left[{\mathrm{\Lambda }}_{i\ast }^C\left({\zeta }_i{C}_i-{\zeta }_{\ast }{C}_{\ast }\right)\right]}^{n+1}}-Q_C^{n+1}{V}_i(20)$

In addition, for a single rock fissure cell $i$, the residual $R_{fi}^n$ in the nth time iteration step can be defined as

$R_{mi}^n=\frac{\mathrm{\Delta }{L}_i\mathrm{\Delta }{a}_i{\zeta }_i}{\mathrm{\Delta }t}\left(C_i^{n+1}-C_i^n\right)+{\displaystyle \sum _{\ast =j,k,m}^{n_i^{neig}}{\left[{\mathrm{\Lambda }}_{i\ast }^C\left({\zeta }_i{C}_i-{\zeta }_{\ast }{C}_{\ast }\right)\right]}^{n+1}}-Q_C^{n+1}\mathrm{\Delta }{L}_i\mathrm{\Delta }{a}_i(21)$

where $\mathrm{\Delta }{L}_i$ is the length of fissure $i$ and $\mathrm{\Delta }{a}_i$ is the width of fissure $i$. Therefore, the rationality of the time increment $\mathrm{\Delta }t$ choice in the mixed FVM program could be examined by the 2-norm ${\Vert {\mathbf{R}}^n\Vert }_2$ of residuals.

The numerical test results revealed that the nuclide concentration distributions in the matrix calculated by mixed FVM and ABAQUS were roughly the same, though a large difference was present around the fissures:

(a) For $D_f/D_m=100$ (Figure 3), the diffusion coefficient of nuclides in the fissure was two orders of magnitude larger than that in the matrix, so the fissure was equivalent to a dominant diffusion channel. Between 100 and 250 years, nuclides rapidly diffused and accumulated along the fissures, which also altered the concentration field of the matrix around the fissures. The matrix nuclide concentration distribution calculated by mixed FVM exhibited obvious step-changes near the fissures. The results of the FEM showed that the concentration distribution near the fissures was relatively continuous, with some extensions and bends at the left and right tips of the orthogonal fissures, which did not fully reflect the influence of fissures on nuclide diffusion in the matrix.

(b) For $D_f/D_m=1$ (Figure 4), the diffusion coefficient of the fissure was equivalent to that of the matrix. From the perspective of nuclide diffusion, the influences of fissure and matrix on diffusion were essentially the same. From the beginning of diffusion to 500 years afterward, the nuclide gradually diffused horizontally, and the fissures could be regarded as a part of the matrix, which had little impact on nuclide diffusion. In this case, the calculation results of the mixed FVM and FEMs were consistent, indicating the applicability of mixed FVM in simulating the diffusion behavior of ions or nuclides in continuous media.

(c) For $D_f/D_m=0.01$ (Figure 5), the diffusion coefficient of the fissure was two orders of magnitude smaller than that of the matrix, so the fissure was equivalent to a diffusion barrier. When the radionuclides diffused to the vertical fissure, the diffusion rate decreased because of the low diffusion coefficient. The radionuclides continued to gather near the fissure, and the concentration was higher than that of the matrix on the upper and lower sides. Blocked by the fissure, the diffusion area of nuclides in the matrix under this condition was smaller than that under Conditions A and B at 500 years. According to the results of FVM, a step-change in nuclide concentration was evident on both sides of the vertical fissure. The results calculated by the FEM revealed a considerable change only in the middle of the vertical fissure, which could still be regarded as a continuous change.

3 Radionuclide Migration Law Considering Fluid Transport

3.1 Theory of Radionuclide Migration Considering Fluid Transport

The migration of nuclides in underground rocks is often accompanied by the migration of groundwater, so the convection term needs to be added to the governing equation:

$\frac{\partial C}{\partial t}+\nabla \cdot \mathbf{F}+\nabla \cdot \left(\mathbf{u}C\right)=f(22)$

The third term on the left side of Eq. 22 can be equivalent to:

$\nabla \cdot \left(\mathbf{u}C\right)=C\cdot \nabla \mathbf{u}+\mathbf{u}\cdot \nabla C(23)$

In a stable flow field, assuming that the fluid is incompressible and the divergence of fluid velocity is zero. That is to say $C\cdot \nabla \mathbf{u}=0$ Eq. 22 can be transformed:

$\frac{\partial C}{\partial t}+\nabla \cdot \mathbf{F}+\mathbf{u}\cdot \nabla C=f(24)$

where $\mathbf{u}$ is the fluid velocity. Groundwater is dominated by seepage, so $\mathbf{u}$ can be obtained from Darcy’s Law:

$\mathbf{u}=K\nabla H(25)$

where $K$ is the hydraulic conductivity and $H$ is the head. Considering the influences of anisotropy and temperature on the hydraulic conductivity, Eq. 25 can be rewritten as

$\{\begin{array}{c}{u}_x=-K_x\frac{\partial H}{\partial x}\\ u_y=-K_y\frac{\partial H}{\partial y}\end{array}(26)$

where $u_x$ and $u_y$ are the penetration rates in $x$ and $y$ directions, respectively; $K_x$ and $K_y$ are the hydraulic conductivities in $x$ and $y$ directions, respectively, which are related to temperature; and $\frac{\partial H}{\partial x}$ and $\frac{\partial H}{\partial y}$ are the hydraulic gradients in $x$ and $y$ directions, respectively. Substituting Eq. 26 into the convection term in Eq. 24 yields

$\mathbf{u}\cdot \nabla C=u_x\frac{\partial C}{\partial x}+u_y\frac{\partial C}{\partial y}=-K_x\frac{\partial H}{\partial x}\frac{\partial C}{\partial x}-K_y\frac{\partial H}{\partial y}\frac{\partial C}{\partial y}(27)$

Equation 24 is the convection term of the governing equation considering fluid transport. Otherwise, the boundary conditions and the scheme accounting for the influence of pores are consistent with those introduced in Section 2.1 Eq. 24 can describe the diffusion and migration of nuclides under fluid transport without decay or with a research time scale much smaller than the nuclide half-life, such as the migration of nuclides in rock matrixes containing groundwater, in the atmosphere (Ge et al., 2021), and with the ocean current in coastal areas (Li et al., 2020).

3.2 Numerical Scheme

According to the basic principle of FVM, Eq. 24 is integrated over the whole spatial domain $\mathrm{\Omega }$ and time $\left[t_n,t_n+\mathrm{\Delta }t\right]$:

${\displaystyle {\int }_{\mathrm{\Delta }t}{\displaystyle {\int }_{\mathrm{\Omega }}\frac{\partial C}{\partial t}}}dVdt+{\displaystyle {\int }_{\mathrm{\Delta }t}{\displaystyle {\int }_{\mathrm{\Omega }}-\nabla \cdot \left(\mathbf{D}\nabla C\right)}}dVdt+{\displaystyle {\int }_{\mathrm{\Delta }t}{\displaystyle {\int }_{\mathrm{\Omega }}\mathbf{u}\cdot \nabla C}}dVdt={\displaystyle {\int }_{\mathrm{\Delta }t}{\displaystyle {\int }_{\mathrm{\Omega }}{Q}_C}}dVdt(28)$

The time term of Eq. 28 is discretized numerically. From Section 2.4, the explicit iteration algorithm is relatively simple and easy to implement. This highly efficient calculation achieves accuracy without solving the equations in each time increment step. Therefore, this section also adopts explicit iteration to approximate Eq. 28:

${\displaystyle {\int }_{\mathrm{\Omega }}\frac{C^{n+1}-C^n}{\mathrm{\Delta }t}}dV+{{\displaystyle {\int }_{\mathrm{\Omega }}-\nabla \cdot \left(\mathbf{D}\nabla C\right)}}^{n}dV+{{\displaystyle {\int }_{\mathrm{\Omega }}\mathbf{u}\cdot \nabla C}}^{n}dV={\displaystyle {\int }_{\mathrm{\Omega }}{Q}_C^n}dV(29)$

The first term on the left side of Eq. 29 is the time-discrete term, the second term represents diffusion, the third term is convection, and the right-hand side is the source-sink term. Considering model establishment and mesh generation (the total number of cells is $n^{all}$), Eq. 29 is discretized in the spatial domain to form a semi-discrete scheme:

${\displaystyle \sum _{i=1}^{n^{all}}{\displaystyle {\int }_{{\mathrm{\Omega }}_i^{ele}}\frac{C^{n+1}-C^n}{\mathrm{\Delta }t}}dV}+{\displaystyle \sum _{i=1}^{n^{all}}{{\displaystyle {\int }_{{\mathrm{\Omega }}_i^{ele}}-\nabla \cdot \left(\mathbf{D}\nabla C\right)}}^{n}dV}+{\displaystyle \sum _{i=1}^{n^{all}}{{\displaystyle {\int }_{{\mathrm{\Omega }}_i^{ele}}\mathbf{u}\cdot \nabla C}}^{n}dV}={\displaystyle \sum _{i=1}^{n^{all}}{\displaystyle {\int }_{{\mathrm{\Omega }}_i^{ele}}{Q}_C^n}dV}(30)$

The shape function $\zeta$ of Eq. 10 of the Galerkin finite element is used to interpolate and approximate the concentration field variable $C$, and the volume integral of the diffusion term is transformed into a surface integral by Gauss’s formula. The semi-discrete scheme in Eq. 30 is transformed by integration to a fully discrete scheme of mixed FVM for radionuclide migration simulation in the fissure-pore medium considering fluid transport:

$\frac{V_i{\zeta }_i}{\mathrm{\Delta }t}\left(C_i^{n+1}-C_i^n\right)+{\displaystyle \sum _{\ast =j,k,m}^{n_i^{neig}}{\left[{\mathrm{\Lambda }}_{i\ast }^C\left({\zeta }_i{C}_i-{\zeta }_{\ast }{C}_{\ast }\right)\right]}^n}+{\displaystyle \sum _{\ast =j,k,m}^{n_i^{neig}}{\left[\frac{u_x\left({\zeta }_{\ast }{C}_{\ast }-{\zeta }_i{C}_i\right)\cos \theta }{{\mathrm{\Lambda }}_{i\ast }^D}+\frac{u_y\left({\zeta }_{\ast }{C}_{\ast }-{\zeta }_i{C}_i\right)\sin \theta }{{\mathrm{\Lambda }}_{i\ast }^D}\right]}^n}{V}_i=Q_C^n{V}_i(31)$

where ${\mathrm{\Lambda }}_{i\ast }^D$ represents the harmonic average of the distances between $i$ and its adjacent cells, as expressed by

$\frac{1}{{\mathrm{\Lambda }}_{i\ast }^D}=\frac{\frac{1}{D_{i\ast }}\frac{1}{D_{\ast i}}}{\frac{1}{D_{i\ast }}+\frac{1}{D_{\ast i}}}(32)$

The penetration rates $u_x$ and $u_y$ in $x$ and $y$ directions, respectively, can be expressed as follows, based on previous discussions:

$\{\begin{array}{c}{u}_x=-\frac{{\mathrm{\Lambda }}_{i\ast }^H\cos \theta }{A_{i\ast }}\left({\xi }_{\ast }{H}_{\ast }-{\xi }_i{H}_i\right)\\ u_y=-\frac{{\mathrm{\Lambda }}_{i\ast }^H\sin \theta }{A_{i\ast }}\left({\xi }_{\ast }{H}_{\ast }-{\xi }_i{H}_i\right)\end{array}(33)$

The residual of each time iteration step can be defined as:

${\mathbf{R}}^n=\left[\begin{array}{cc}{\mathbf{R}}_m^n& {\mathbf{R}}_f^n\end{array}\right](34)$

For a single rock matrix cell $i$, the residual $R_{mi}^n$ in the nth time iteration can be defined as

$\begin{array}{l}{R}_{mi}^n=\frac{V_i{\zeta }_i}{\mathrm{\Delta }t}\left(C_i^{n+1}-C_i^n\right)+{\displaystyle \sum _{\ast =j,k,m}^{n_i^{neig}}{\left[{\mathrm{\Lambda }}_{i\ast }^C\left({\zeta }_i{C}_i-{\zeta }_{\ast }{C}_{\ast }\right)\right]}^{n+1}+}\\ {\displaystyle \sum _{\ast =j,k,m}^{n_i^{neig}}{\left[\frac{u_x\left({\zeta }_{\ast }{C}_{\ast }-{\zeta }_i{C}_i\right)\cos \theta }{{\mathrm{\Lambda }}_{i\ast }^D}+\frac{u_y\left({\zeta }_{\ast }{C}_{\ast }-{\zeta }_i{C}_i\right)\sin \theta }{{\mathrm{\Lambda }}_{i\ast }^D}\right]}^{n+1}}{V}_i-Q_C^{n+1}{V}_i\end{array}(35)$

For a single rock fissure cell $i$, the residual $R_{fi}^n$ in the nth time iteration step can be defined as:

$\begin{array}{l}{R}_{mi}^n=\frac{\mathrm{\Delta }{L}_i\mathrm{\Delta }{a}_i{\zeta }_i}{\mathrm{\Delta }t}\left(C_i^{n+1}-C_i^n\right)+{\displaystyle \sum _{\ast =j,k,m}^{n_i^{neig}}{\left[{\mathrm{\Lambda }}_{i\ast }^C\left({\zeta }_i{C}_i-{\zeta }_{\ast }{C}_{\ast }\right)\right]}^{n+1}}\\ +{\displaystyle \sum _{\ast =j,k}^{n_i^{neig,matrix}}{\left[\frac{u_x\left({\zeta }_{\ast }{C}_{\ast }-{\zeta }_i{C}_i\right)\cos \theta }{{\mathrm{\Lambda }}_{i\ast }^D}+\frac{u_y\left({\zeta }_{\ast }{C}_{\ast }-{\zeta }_i{C}_i\right)\sin \theta }{{\mathrm{\Lambda }}_{i\ast }^D}\right]}^{n+1}}\mathrm{\Delta }{L}_i\mathrm{\Delta }{a}_i\\ +{\displaystyle \sum _{\ast =j,k,m,n}^{n_i^{neig,frature}}\frac{u{\left({\zeta }_{\ast }{C}_{\ast }-{\zeta }_i{C}_i\right)}^{n+1}}{{\mathrm{\Lambda }}_{i\ast }^D}}\mathrm{\Delta }{L}_i\mathrm{\Delta }{a}_i-Q_C^{n+1}\mathrm{\Delta }{L}_i\mathrm{\Delta }{a}_i\end{array}(36)$

where $\mathrm{\Delta }{L}_i$ is the length of the fissure $i$ and $\mathrm{\Delta }{a}_i$ is the width of $i$. Therefore, the rationality of the time increment $\mathrm{\Delta }t$ choice in the self-made mixed FVM program can be verified using the 2-norm ${\Vert {\mathbf{R}}^n\Vert }_2$ of residuals.

3.3 Program Implementation

The numerical discretization methods for simulating radionuclide migration in the fissure-pore medium by mixed FVM considering diffusion and fluid transport have been introduced in the previous sections. This section discusses the simulation program. The radionuclide migration simulation program module was independently developed in C++. When accounting for the effect of the seepage field, the time scale of the seepage pressure is extremely small compared to that of radionuclide migration because it propagates in the form of a pressure wave. Therefore, in the numerical solution, the two activities can be separated by sequential decoupling. In other words, the distribution of osmotic pressure can be solved first, and then the distribution of the concentration field under fluid transport can be solved by the convection term in the governing equation.

The main modules of fissure-pore medium simulation are (1) pre-processing (fissure and matrix cells are divided using the ABAQUS pre-processing module), (2) the assembly and solution of the seepage governing equation matrix (based on mixed FVM), (3) the assembly of the diffusion and migration governing equation matrix (based on mixed FVM, considering the influence of the seepage field), (4) iteration in time steps, and (5) post-processing (using Paraview). The fissure-pore medium modeling and cell division in pre-processing are conducted in the ABAQUS pre-processing module. The radionuclide migration simulation program in this section can account for cases of homogeneous or heterogeneous properties, isotropic or anisotropic diffusion, and permeability. Each cell in the fissure and rock matrix is assigned with diffusion and hydraulic conductivities corresponding to the required research condition. The physical essence of this process is material transport, the most prominent features of which are time and flow dependencies, as reflected by the time term $\frac{\partial C}{\partial t}$ and convection term $u\cdot \nabla C$ in Eq. 24. The simulation program first solves the time-independent flow field distribution and then solves the time-dependent transport process by explicit iteration.

3.4 Example Analysis

3.4.1 Validation of the Mixed FVM Program

Our mixed FVM program was analyzed through the numerical test model of a clayey rock with two vertical fissures, as displayed in Figure 6, and validated with the calculation results of Yan et al. (2020). The model was a square with a side length of 0.1 m. The length of both fissures was 0.02 m, and the width was 0.002 m. The left boundary of the model was set as the nuclide injection position, where the concentration was maintained at $C$ = 1 mol/m³. The right boundary was set as the nuclide output position, and the concentration was kept at $C$ = 0 mol/m³. The other boundary material flows were set to $J_{CU}=J_{CD}=0$. The head boundary conditions were set as $H_L=1$ m, $H_R=0$ m. The left boundary of the model was set as the fluid injection position, and the right boundary was set as the fluid outflow position. The other boundary material flows were configured as $q_{HU}=q_{HD}=0$. The diffusion coefficient of nuclides in the rock matrix was $D_m=9\times {10}^{-11}$ m²/s; the fissure was of the diffusion insulation type, and the diffusion coefficient was $D_f=9\times {10}^{-14}$ m²/s. The hydraulic conductivity of the rock matrix was $K_m=9\times {10}^{-11}$ m/s; the fissure was of the seepage-insulation type, and the hydraulic conductivity was $K_f=9\times {10}^{-14}$ m/s.

FIGURE 6

FIGURE 6. Fissure-pore medium model with two vertical fissures.

The mixed FVM adopted 1261 triangular cells, and the total time was set to 1.728 × 10⁷ s (200 days). The time increment $\mathrm{\Delta }t$ of the mixed FVM program was set to 1.728 s, considering the boundary conditions, the internal concentration field distribution, and the concentration change in each time increment step. This choice achieved sufficient calculation efficiency and accuracy of each time increment step (2-norm of all cell residuals ${{\displaystyle \sum \Vert R\Vert }}_2\le 1\times {10}^{-5}$). The simulation results of the mixed FVM method were visualized through Paraview, as shown in Figure 7 with the calculation results of Yan et al. (2020).

FIGURE 7

FIGURE 7. Comparison of the mixed FVM and FEMs.(A) Mixed FVM (B) FEMs (Yan et al., 2020)

The numerical results revealed that the radionuclides moved from left to right under the influence of diffusion and fluid transport, and the concentration field distributions calculated by the two methods were roughly the same, which indicated the accuracy and effectiveness of the mixed FVM program. Because the fissure had diffusion- and seepage-insulation properties, the fissure hindered the migration of materials and affected the concentration field distribution in the whole region. Especially on both sides of the fissure, a step-change in the concentration field was present. To enhance the finite element calculation results, Yan et al. (2020) hollowed the fissure part. Using the mixed FVM, however, the step-change in concentration could be observed clearly without subsequent treatment. Therefore, the mixed FVM more effectively describes discontinuous media involving hiatuses, mutations, and fissures.

3.4.2 Effect of Hydraulic Conductivity on Radionuclide Migration

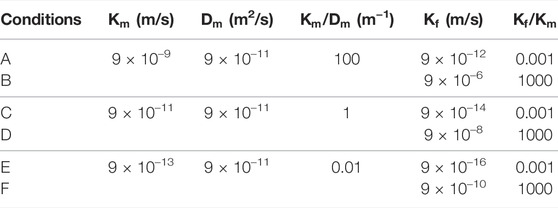
For the model shown in Figure 6, the mixed FVM method adopted triangular cells to study the influence of rock matrix and fissure permeability on radionuclide migration. The diffusion and hydraulic conductivities used in the simulation are displayed in Table 1. The total time was set to 1.728 × 10⁸ s (2,000 days), and the other parameters and boundary conditions were the same as those in Section 3.4.1.

TABLE 1

TABLE 1. Parameter settings.

By comparing the distribution patterns of radionuclide migration concentration under various conditions as in Figure 8, the following conclusions could be drawn:

(a) Under Conditions A and B in Figures 8A,B, where $K_m/D_m={10}^2$ m⁻¹, fluid transport played a major role in radionuclide migration. Nuclides diffused and migrated rapidly along the direction of water flow. For Condition A, the hydraulic conductivity of the fissure was far smaller than that of the matrix, and, clearly, the fissure blocked fluid seepage and nuclide diffusion. For Condition B, the hydraulic conductivity of the fissure was far greater than that of the matrix, so the fissure was the dominant channel of seepage though still blocked nuclide diffusion. The nuclide concentration distributions on the fifth day revealed the blocking effect of fissures on radionuclide migration. Nuclide migration near the fissure and rock matrix interface was affected by both fluid transport and diffusion. Figure 9 displays the distribution pattern of water pressure on the fifth day under Conditions A and B. Under Condition A, the water pressure changed because of the fissure, and the fluid transport near the fissure weakened, blocking radionuclide migration. Under Condition B in Figure 9B, because the fissure could channel water, the water pressure distribution was relatively uniform. Although the fissure acted as a barrier of nuclide diffusion, the nuclide managed to pass smoothly via fluid transport; therefore, the distribution of the nuclide concentration field in the rock matrix behind the fissure was different from that under Condition A. As a result, the time for the full coverage of nuclides under Condition A was longer than that under Condition B.

(b) Under Conditions C and D in Figures 8C,D, where $K_m/D_m=1$ m⁻¹, the influences of fluid transport and diffusion on radionuclide migration were comparable. As the hydraulic conductivities of matrix and fissure were both considerably reduced, the nuclide migration rates under Conditions C and D were significantly lower than that under Conditions A and B, respectively. The fissures under Conditions C and D hindered fluid seepage and nuclide diffusion. When the final stable state was reached, the areas of high nuclide concentration were significantly reduced, and the influences of flow field on concentration field distribution were less, as compared to those of Conditions A and B, respectively. Radionuclide migration rates under Conditions C and D were similar, revealing that when effects of transport and diffusion were comparable, the hydraulic conductivity difference between the vertical fissure and the rock matrix had little impact on the radionuclide migration rate under the studied time scale.

(c) Under Conditions E and F in Figures 8E,F, where $K_m/D_m={10}^{-2}$ m⁻¹, the effect of diffusion was dominant in radionuclide migration, and the fluid transport weakened. In the process of radionuclide migration to the right, the migration rates under Conditions E and F were slower than that under Conditions C and D, respectively, and the fissure hindered fluid seepage and nuclide diffusion. When the final stable state was reached, the areas of high nuclide concentration under Conditions E and F were smaller, manifesting smaller influences of the flow fields on the concentration field distributions, when compared to those under Conditions C and D. The nuclide diffusion rates of Conditions E and F were roughly the same, indicating that when the diffusion effect dominated, the hydraulic conductivity difference between the vertical fissure and the rock matrix had little impact on the radionuclide migration rate.

FIGURE 8

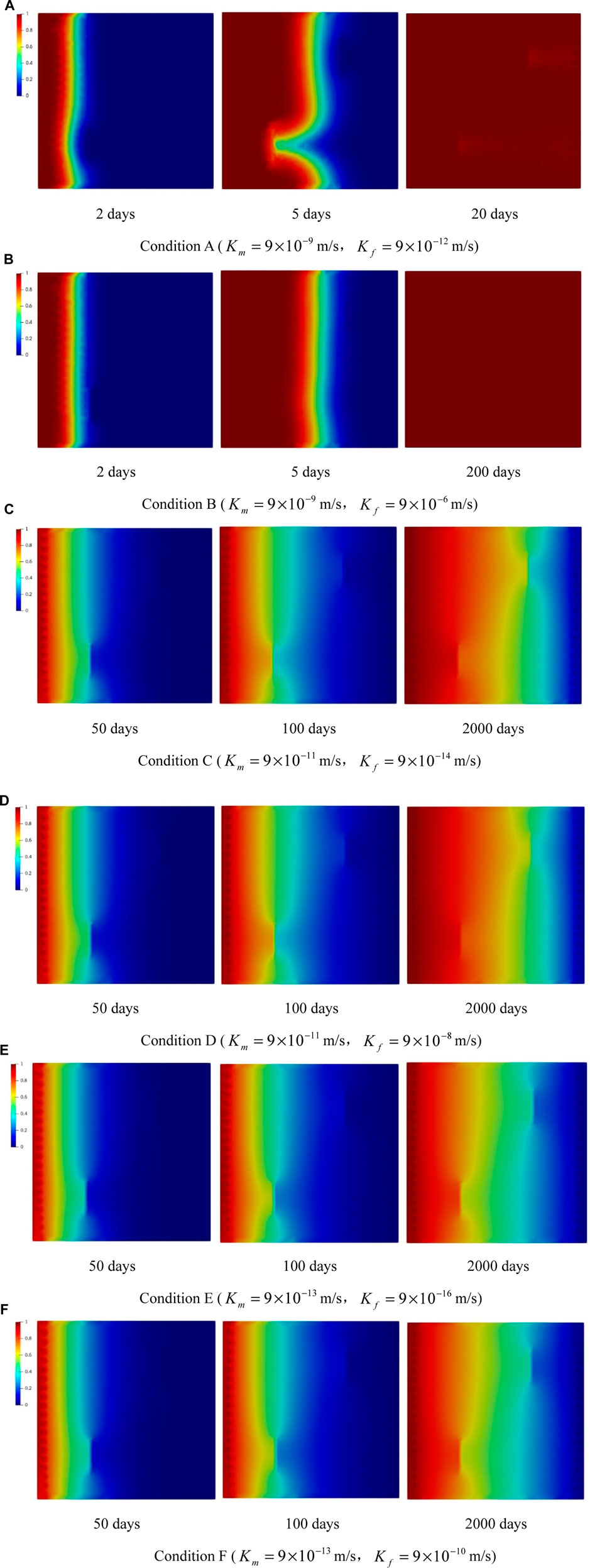
FIGURE 8. (Continued). Distribution pattern of radionuclide migration concentration under various conditions. (A) Condition A ($K_m=9\times {10}^{-9}$ m/s, $K_f=9\times {10}^{-12}$ m/s). (B) Condition B ($K_m=9\times {10}^{-9}$ m/s, $K_f=9\times {10}^{-6}$ m/s). (C) Condition C ($K_m=9\times {10}^{-11}$ m/s, $K_f=9\times {10}^{-14}$ m/s). (D) Condition D ($K_m=9\times {10}^{-11}$ m/s, $K_f=9\times {10}^{-8}$ m/s). (E) Condition E ($K_m=9\times {10}^{-13}$ m/s, $K_f=9\times {10}^{-16}$ m/s) (F) Condition F ($K_m=9\times {10}^{-13}$ m/s, $K_f=9\times {10}^{-10}$ m/s).

FIGURE 9

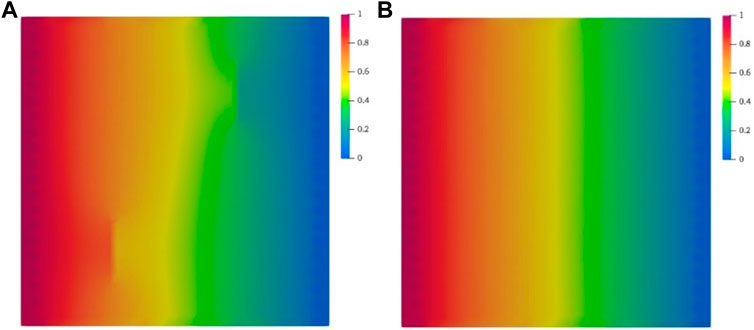
FIGURE 9. Distribution pattern of water pressure under Conditions A and B. (A) Condition A, (B) Condition B.

4 Conclusion

In this paper, the rock mass around the geological disposal repository for high-level radioactive waste was regarded as a fissure-pore medium to determine the influences of nuclide diffusion and fluid transport on radionuclide migration in the rock mass during high-level radioactive waste disposal. The governing equation of radionuclide migration and evolution in the pore-fissure medium is established. The corresponding numerical scheme is given based on the mixed FVM method, using our program solution module written in C++. On this basis, a numerical test model containing fissures was established to analyze the nuclide migration process in the clayey rock under various fissure and rock matrix diffusion conditions. The comparison of the effects of the rock matrix and fissure hydraulic conductivities on radionuclide migration yielded the following conclusions. When fluid transport dominated in radionuclide migration, the radionuclide migration rate was high, and the distribution of concentration field in the migration process was greatly affected by the permeability difference between the fissure and the rock matrix. When the fluid transport and diffusion effects were comparable or when the diffusion played a major role, the radionuclide migration rate decreased. Additionally, the permeability difference between the fissure and the rock matrix had little impact on concentration field distribution in the process of diffusion migration. The comparison between the mixed FVM and the finite element methods using ABAQUS revealed significant advantages of the mixed FVM method in describing discontinuous media involving hiatuses, mutations, and fissures. By changing the parameters such as diffusion and hydraulic conductivities, the method can be applied in the study of radionuclide migration laws in other geological bodies with high-level radioactive waste. This study will provide an important scientific basis for the failure analysis of the geological disposal of HLW.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

HY: Conceptualization, Investigation, Formal analysis, Supervision, Funding acquisition, Writing–original draft, Writing–review and editing. CL: Investigation, Data curation, Formal analysis, Writing–original draft, Writing–review and editing. WC: Conceptualization, Project administration, Funding acquisition, Writing–original draft, Writing–review and editing. LW: Resources, Writing–original draft, Writing. HoL: Supervision–review and editing. HaL: Funding acquisition, Writing–original draft, Writing–review and editing.

Funding

The financial support of the National Natural Science Foundation of China (No. 51979266, 51879258, and 51974203) is greatly acknowledged.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Appreciations are extended to Sweetland K and Yu Y, who have given valuable suggestions and worked hard on improving the English of this article.

References

Ahmad, A. Y., Al-Ghouti, M. A., AlSadigAbu-Dieyeh, I. M., and Abu-Dieyeh, M. (2019). Vertical Distribution and Radiological Risk Assessment of 137Cs and Natural Radionuclides in Soil Samples. Sci. Rep. 9, 12196. doi:10.1038/s41598-019-48500-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Altmann, S., Tournassat, C., Goutelard, F., Parneix, J.-C., Gimmi, T., and Maes, N. (2012). Diffusion-driven Transport in Clayrock Formations. Appl. Geochem. 27 (2), 463–478. doi:10.1016/j.apgeochem.2011.09.015

CrossRef Full Text | Google Scholar

Amaziane, B., Bergam, A., El Ossmani, M., and Mghazli, Z. (2009). A Posterioriestimators for Vertex Centred Finite Volume Discretization of a Convection-Diffusion-Reaction Equation Arising in Flow in Porous Media. Int. J. Numer. Meth. Fluids 59 (3), 259–284. doi:10.1002/fld.1456

CrossRef Full Text | Google Scholar

Bazer-Bachi, F., Tevissen, E., Descostes, M., Grenut, B., Meier, P., Simonnot, M. O., et al. (2006). Characterization of Iodide Retention on Callovo-Oxfordian Argillites and its Influence on Iodide Migration 31(10-14), 517–522. doi:10.1016/j.pce.2006.04.015

CrossRef Full Text | Google Scholar

Bossart, P., Bernier, F., Birkholzer, J., Bruggeman, C., Connolly, P., Dewonck, S., et al. (2017). Mont Terri Rock Laboratory, 20 Years of Research: Introduction, Site Characteristics and Overview of Experiments. Swiss. J. Geosci. 110, 3–22. doi:10.1007/s00015-016-0236-1

CrossRef Full Text | Google Scholar

Bucur, C., and Popa, A. (2000). Diffusion Coefficients of Critical Radionuclides from Radioactive Waste in Geological MediumWM’00 Conferencrsene, C., and Olteanu, M. Tucson, AZ. February 27 – March 2, 2000.

Google Scholar

Cho, W.-J., Lee, J.-O., and Choi, H.-J. (2012). Radionuclide Migration through an Unsaturated Clay Buffer under Thermal and Hydraulic Gradients for a Nuclear Waste Repository. Ann. Nucl. Energy 50, 71–81. doi:10.1016/j.anucene.2012.07.010

CrossRef Full Text | Google Scholar

Ge, B. Z., Lu, Q. Q., Chen, X. S., and Wang, Z. F. (2021). A Review of the Numerical Simulations of the Atmospheric Dispersion of Radionuclides[J]. Acta Sci. Circumstantiae 41 (5), 1599–1609.

Google Scholar

Grupa, J.,B., Meeussen, J. C. L., Rosca-Bocancea, E., Buhmann, D., Laggiard, E., and Wildenborg, A. F. B. (2017). Migration of Radionuclides in Boom Clay PA Model 'Clay'. Report. Vlissingen, Netherlands: OPERA-PU-NRG7212.

Google Scholar

IAEA (2010). Production of Long Lived Parent Radionuclides for Generators: 68Ge, 82Sr, 90Sr and 188W. IAEA Radioisotopes and Radiopharmaceuticals Series No. 2. Vienna, Austria: International Atomic Energy Agency VIENNA.

Google Scholar

Jacops, E., Aertsens, M., Maes, N., Bruggeman, C., Krooss, B. M., Amann-Hildenbrand, A., et al. (2017). Interplay of Molecular Size and Pore Network Geometry on the Diffusion of Dissolved Gases and HTO in Boom Clay. Appl. Geochem. 76, 182–195. doi:10.1016/j.apgeochem.2016.11.022

CrossRef Full Text | Google Scholar

Jacops, E., Wouters, K., Volckaert, G., Moors, H., Maes, N., Bruggeman, C., et al. (2015). Measuring the Effective Diffusion Coefficient of Dissolved Hydrogen in Saturated Boom Clay. Appl. Geochem. 61, 175–184. doi:10.1016/j.apgeochem.2015.05.022

CrossRef Full Text | Google Scholar

Labib, A., and Harris, M. J. (2015). Learning How to Learn from Failures: The Fukushima Nuclear Disaster. Eng. Fail. Anal. 47, 117–128. doi:10.1016/j.engfailanal.2014.10.002

CrossRef Full Text | Google Scholar

L’Annunziata, M. F. (2016). RaddioactivityIntroduction and History, from the Quantum to Quarks. Second Edition. B.VElsevier. 978-0-444-63489-4.

Google Scholar

Leupin, O. X., Van Loon, L. R., Gimmi, T., Wersin, P., and Soler, J. M. (2017). Exploring Diffusion and Sorption Processes at the Mont Terri Rock Laboratory (Switzerland): Lessons Learned from 20 Years of Field Research. Swiss. J. Geosci. 110 (1), 391–403. doi:10.1007/s00015-016-0254-z

CrossRef Full Text | Google Scholar

Li, Z. C., Zhou, T., Si, G. C., and Zhang, B. Y. (2020). Study on Radionuclide Migration Path and Concentration Distribution in Coastal Waters of Haiyang Nuclear Power Plant in Winter and Summer[J]. Nucl. Power Eng. 41 (4), 135–140.

Google Scholar

Martin, O., Nilsson, K.-F., and Jakšić, N. (2009). Numerical Simulation of Plastic Collapse of Copper-Cast Iron Canister for Spent Nuclear Fuel. Eng. Fail. Anal. 16 (1), 225–241. doi:10.1016/j.engfailanal.2008.03.005

CrossRef Full Text | Google Scholar

Meeussen, J., Rosca-Bocancea, E., Schröder, T., Koenen, M., Valega Mackenzie, F., Maes, N., et al. (2017). Model Representation of Radionuclide Diffusion in Boom Clay. Vlissingen, Netherlands: OPERA-PU-NRG6131.

Google Scholar

Mohammad, K. F., and Abbas, F. (2003). Numerical Simulation of Water Injection in Fractured Media Using the Discrete-Fracture Model and the Galerkin Method. SPE Reserv. Eval. Eng. 6 (2), 117–126.

Google Scholar

Mustapha, H. (2014). A Gabriel-Delaunay Triangulation of 2D Complex Fractured Media for Multiphase Flow Simulations. Comput. Geosci. 18, 989–1008. doi:10.1007/s10596-014-9440-0

CrossRef Full Text | Google Scholar

Nordbotten, J. M. (2014). Cell‐centered Finite Volume Discretizations for Deformable Porous Media. Int. J. Numer. Meth. Engng 100 (6), 399–418. doi:10.1002/nme.4734

CrossRef Full Text | Google Scholar

Tene, M., Bosma, S. B. M., Kobaisi, M. S. A., and Hajibeygi, H. (2017). Projection-based Embedded Discrete Fracture Model (pEDFM) [J]. Adv. Water. Resour. 105, 205–216.

Google Scholar

Tran, E., Zavrin, M., Kersting, A. B., Klein-BenDavid, O., Teutsch, N., and Weisbrod, N. (2021). Colloid-facilitated Transport of 238Pu, 233U and 137Cs through Fractured Chalk: Laboratory Experiments, Modelling, and Implications for Nuclear Waste Disposal. Sci. Total Environ. 757, 143818. doi:10.1016/j.scitotenv.2020.143818

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Loon, L. R., Glaus, M. A., and Müller, W. (2007). Anion Exclusion Effects in Compacted Bentonites: Towards a Better Understanding of Anion Diffusion. Appl. Geochem. 22 (11), 2536–2552. doi:10.1016/j.apgeochem.2007.07.008

CrossRef Full Text | Google Scholar

Van Loon, L. R., Müller, W., and Iijima, K. (2005). Activation Energies of the Self-Diffusion of HTO, 22Na+ and 36Cl− in a Highly Compacted Argillaceous Rock (Opalinus Clay). Appl. Geochem. 20 (5), 961–972. doi:10.1016/j.apgeochem.2004.10.007

CrossRef Full Text | Google Scholar

Van Marcke, P., and Bastiaens, W. (2010). Excavation Induced Fractures in a Plastic Clay Formation: Observations at the HADES URF. J. Struct. Geol. 32 (11), 1677–1684. doi:10.1016/j.jsg.2010.01.010

CrossRef Full Text | Google Scholar

Wigger, C., Kennell-Morrison, L., Jensen, M., Glaus, M., and Van Loon, L. (2018). A Comparative Anion Diffusion Study on Different Argillaceous, Low Permeability Sedimentary Rocks with Various Pore Waters. Appl. Geochem. 92, 157–165. doi:10.1016/j.apgeochem.2018.02.009

CrossRef Full Text | Google Scholar

Wu, Y. F. (2017). Evaluation of Transport Properties of Radionuclides in Clay Materials. Delft, Netherlands: Delft University of Technology. Master thesis.

Google Scholar

Yan, H. X., Sedighi, M., and Jivkov, A. P. (2020). Peridynamics Modelling of Coupled Water Flow and Chemical Transport in Unsaturated Porous Media[J]. J. Hydrol. 591, 1–16. doi:10.1016/j.jhydrol.2020.125648

CrossRef Full Text | Google Scholar

Yu, H., Chen, W., Gong, Z., Tan, X., and Yang, D. (2018). Loading-unloading Behavior of a Clayey Rock under Thermo-Hydro-Mechanical Conditions. Int. J. Rock Mech. Min. Sci. 148, 104966. doi:10.1016/j.ijrmms.2021.104966

CrossRef Full Text | Google Scholar

Yu, H., Lu, C., Chen, W., and Li, H. (2021). Permeability Changes in Fractured Tamusu Mudstone in the Context of Radioactive Waste Disposal. Bull. Eng. Geol. Environ. 80, 7945–7957. doi:10.1007/s10064-021-02445-6

CrossRef Full Text | Google Scholar

Zhang, W., Tang, X., Weisbrod, N., and Guan, Z. (2012). A Review of Colloid Transport in Fractured Rocks. J. Mt. Sci. 9 (6), 770–787. doi:10.1007/s11629-012-2443-1

CrossRef Full Text | Google Scholar