Overriding Lithospheric Strength Affects Continental Collisional Mode Selection and Subduction Transference: Implications for the Greater India–Asia Convergent System

The India–Asia collision, starting from 55 ± 5 Ma, leads to the formation of the Himalayas and Tibetan Plateau with great gravity potential energy and large forces acting on the surrounding blocks. However, the subduction transference/jump does not occur in the southern Indian continental margin or the northern Indian oceanic plate as supposed to happen repeatedly during the preceding Tethys evolution. Instead, the continental collision and orogeny continues until present day. The total amount of convergence during the India–Asia collision has been estimated to be ∼2,900–4,000 km and needs to be accommodated by shortening/extrusion of the Tibetan plate and/or subduction of the Greater Indian plate, which is a challenging issue. In order to study the collision mode selection, deformation partition, and continental mass conservation, we integrate the reconstruction-based convergence rate of the India–Asia collision into a large-scale thermomechanical numerical model and systematically investigate the effects of overriding Tibetan lithospheric strength and the amount of convergence. The model results indicate that the absence of subduction transference during the India–Asia collision may be attributed to strain localization and shortening of the rheologically weak Tibetan plate. In case of the India–Asia collision for ∼50 Myr with a total convergence of ∼2,900 km, the model with the intermediately weak Tibetan plate could reconcile the general deformation partition and continental mass balance of the Himalayan–Tibetan system. However, the longer period of India–Asia collision for ∼55 Myr leads to significant shortening of the overriding plate that is not consistent with the Tibetan observations, in which case an oceanic basin may be required for the Greater Indian continent.

Introduction

The evolution of the Tethyan system has been a long-lived global geodynamic process since the early Paleozoic, which includes multiple Wilson’s cycles of continental breakup, drifting, collision, and accretion, as well as the subduction initiation (SI) in the neighboring oceanic plate, i.e., subduction transference or subduction jump (Zhong and Li, 2020; and references therein). In summary, there are mainly three periods of continental terranes splitting from the Gondwana super-continent, drifting northward and finally accreted to the Eurasian continent, including the Galatian terrane, Cimmerian terranes, and Indian continent (Stampfli et al., 2013; Torsvik and Cocks, 2013; Wan et al., 2019; Zhu et al., 2021). The collision between Galatia and Eurasia induced subduction transferring into the Paleo-Tethyan Oceanic plate (Stampfli et al., 2013). Subsequently, the collision between Cimmeria with Eurasia closed the Paleo-Tethyan Ocean, leading to the SI of Neo-Tethyan Oceanic plate (Stampfli and Borel, 2002; Wan et al., 2019; Zhong and Li, 2020). Finally, when the Indian continent collided with Eurasia at about 55 ± 5 Ma, the continuous convergence created the most spectacular orogenic belt on the Earth, i.e., the Himalayan orogen and the Tibetan Plateau (Figure 1). However, the southern Indian continental margin and northern Indian oceanic plate have shown no signs of SI until today, which is a puzzling issue and widely debated with several mechanisms being proposed, including the resistance from the triangular shape of southern Indian continental margin, the relatively old ocean-continent transition zone with great resistance, and the continuous shortening of the overriding Tibetan Plateau (Stern, 2004; Stern and Gerya, 2018; Cloetingh et al., 1989; Zhong and Li, 2020). In a recent study by Zhong and Li (2022), systematic 3D numerical models revealed that the wedge-shaped southern Indian continental margin without proper weakness hinders its subduction initiation after the long-term India–Asia collision. In that study, the shortening and uplift of a narrowed and simplified Tibetan plate, due to the spatial resolution limit of 3D model (Zhong and Li, 2022), does not affect the subduction transference. In this study, we further investigate this issue by applying comparable spatial and temporal scales of the Tibetan Plateau, as well as the reconstruction-based, realistic convergence rate of the India–Asia collision.

FIGURE 1

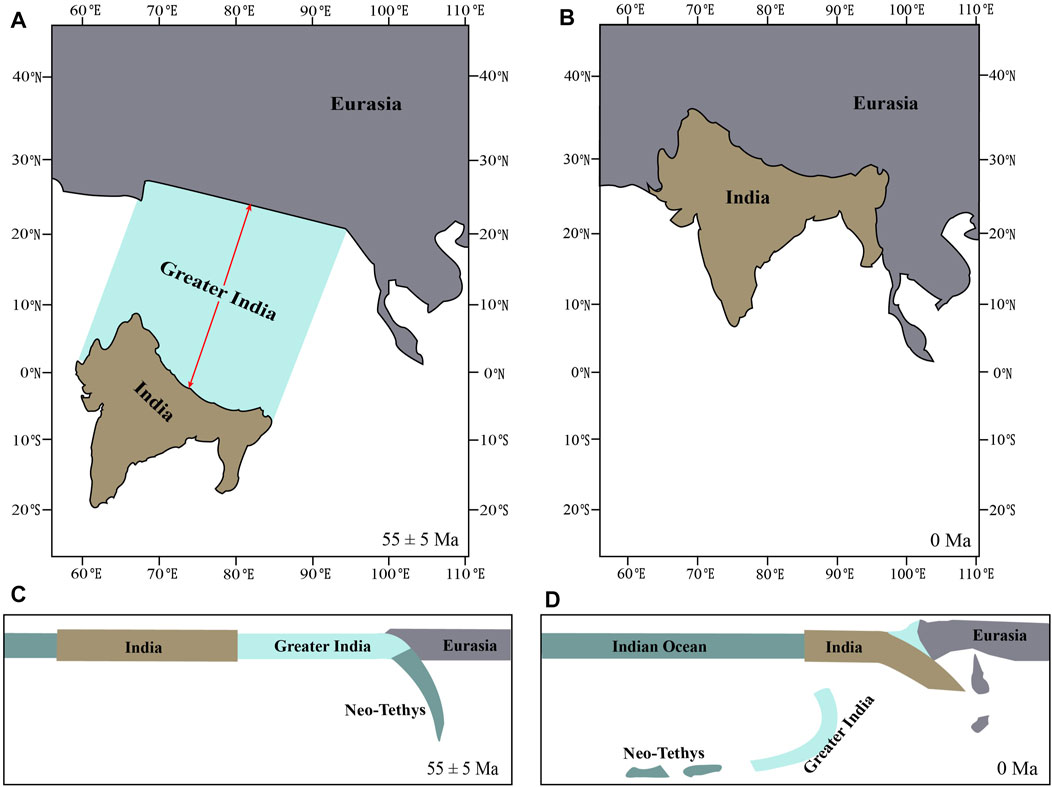
FIGURE 1. Tectonic background and corresponding profiles of the Indo-Eurasian system at the initial collision (A,C) and present-day Tibetan plateau(B,D) (Yi et al., 2011; Ingalls et al., 2016; Wang et al., 2019; van Hinsbergen et al., 2019; Meng et al., 2019, 2020; Parsons et al., 2020).

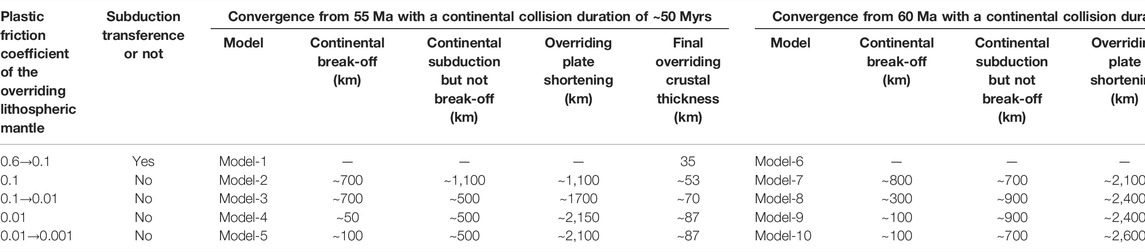
Due to the absence of collision-induced subduction transference, the continuous India–Asia convergence needs be accommodated by the shortening of the Tibetan Plateau and/or the subduction of the Greater Indian plate. The long-lasting India–Asia collision began with a relatively high convergent rate of ∼14 cm/yr at ∼55 Ma, and then it gradually decreases to ∼4 cm/yr at the present (Lee and Lawver, 1995; Müller et al., 2008; Molnar and Stock, 2009; Copley et al., 2010; van Hinsbergen et al., 2011). With such reconstructions, the total amount of convergence since 55 ± 5 Ma will be ∼2,900–4,000 km, which needs to be consumed by the Tibetan Plateau and the Indian plate (Molnar and stock, 2009; Copley at al., 2010; van Hinsbergen et al., 2011; van Hinsbergen et al., 2012; van Hinsbergen et al., 2019; Zhou and Su, 2019). Several mechanisms have been suggested for the accommodation of convergence by the Tibetan Plateau, including crustal shortening, lateral extrusion of the Indo–China block, the lower crustal flow, and surface erosion (Tapponnier et al., 1982; Gan et al., 2007; Replumaz et al., 2010; Yakovlev and Clark, 2014; Ingalls et al., 2016; Cui et al., 2021). The amount of Tibetan shortening has been widely estimated. However, the results vary significantly. The shortening of the Tibetan Plateau interior, i.e., from the Indus-Yalung suture zone in the south to the Kunlun Mountains in the north, is estimated to be about 1,100 ± 50 km (van Hinsbergen et al., 2019), which may have a large variation from 500 km (Yakovlev and Clark, 2014) to 1,700 km (Sun et al., 2012). For the northeastern Tibetan Plateau, the shortening may be about 500–600 km (e.g., Yin and Harrison, 2000). Consequently, there is still ∼1,200–2,400 km left to be accommodated by the lower plate, i.e., the Greater India. Two types of models have been proposed for the consumption of the Greater Indian plate. In the first type of models, the Greater India is entirely composed of continental material. The upper part of the Greater Indian crust is detached and accumulated in the Himalayan orogeny during continental collision, whereas the lower part is subducted and recycled into the mantle. The deep subduction of such a long continental slab is a great challenge for this type of models (Ding et al., 2017; Meng et al., 2019, 2020). However, a recent study proposed that the phase-transition-induced densification of deeply subducted felsic crust below 170 km drives the continuous subduction of continental slab, i.e. Self-driven Continental Deep Subduction model (Wang et al., 2022). The other type of models assumes an oceanic basin within the Greater India, for example, the Greater Indian Oceanic Basin model (van Hinsbergen et al., 2012, 2019) or the Intra-Oceanic Arc model (Aitchison et al., 2007; Gibbons et al., 2015; Kapp and DeCelles, 2019; Martin et al., 2020). The oceanic plate within the Greater India can easily subduct and accommodate a large amount of convergence without any geodynamic difficulties in these models. However, the major problem is the lack of geological evidence for this period of oceanic subduction (Najman et al., 2010; Aitchison and Ali, 2012; Wu et al., 2014; Hu et al., 2016; Ding et al., 2017; and reference therein). In addition, the continuously decreasing convergence rate since ∼55 Ma is difficult to be reconciled with the subduction of such an oceanic plate.

In this study, we aim to investigate the deformation partition and mass conservation during the long-lasting collision of the Greater India and Eurasia continent, if no oceanic basin is present within the Greater India. Notably, the models with the Greater Indian Oceanic Basin are not investigated in the current models, which require to be examined in further studies. In the previous numerical models, a constant convergent rate is generally applied to investigate the continental collision process (e.g., Kelly et al., 2016; Li et al., 2016; Liu et al., 2021). However, the northward convergent rate of the India–Asia collision has been changing significantly over time (Lee and Lawver, 1995; Müller et al., 2008; Molnar and Stock, 2009; Copley et al., 2010; van Hinsbergen et al., 2011), which may strongly affect the deformation partition and mass conservation. Consequently, a large-scale thermomechanical numerical model is integrated with the reconstruction-based plate convergence rate of the India–Asia collision, to investigate the dynamics of Himalayan and Tibetan orogeny, with paying special attention on two key issues: 1) why the continued India–Asia collision for >50 Myr does not lead to subduction transference to the present-day Indian Ocean and 2) if without an oceanic basin in the Greater India, how to reconcile the general deformation partition and mass conservation of the Greater India–Asia collision?

Numerical Model Setup

The numerical models are conducted with the code I2VIS (Gerya, 2010). The extended numerical methodologies and specific parameters (i.e. governing equations, rheological flow laws, phase transitions, hydration, and partial melting) are shown in the supporting information and following Li et al. (2019).

Initial Material and Thermal Configurations

The initial model is configured in a two-dimensional box with a spatial scale of 8,000 × 1,400 km, as shown in Figure 2A. The horizontal spatial resolution of the model domain is 10 km. In the vertical direction, the spatial resolution is 1 km from 0 to 200 km depth and gradually changing to 10 km downward. The total number of grids is 800 × 350. Within the model box, four plates are configured, including the spreading oceanic plate (1,500 km in length), the drifting continental plate (2,000 km in length), the subducting oceanic plate (500 km horizontally and ∼800 km subducted), and the overriding continental plate (∼3,800 km in length).

FIGURE 2

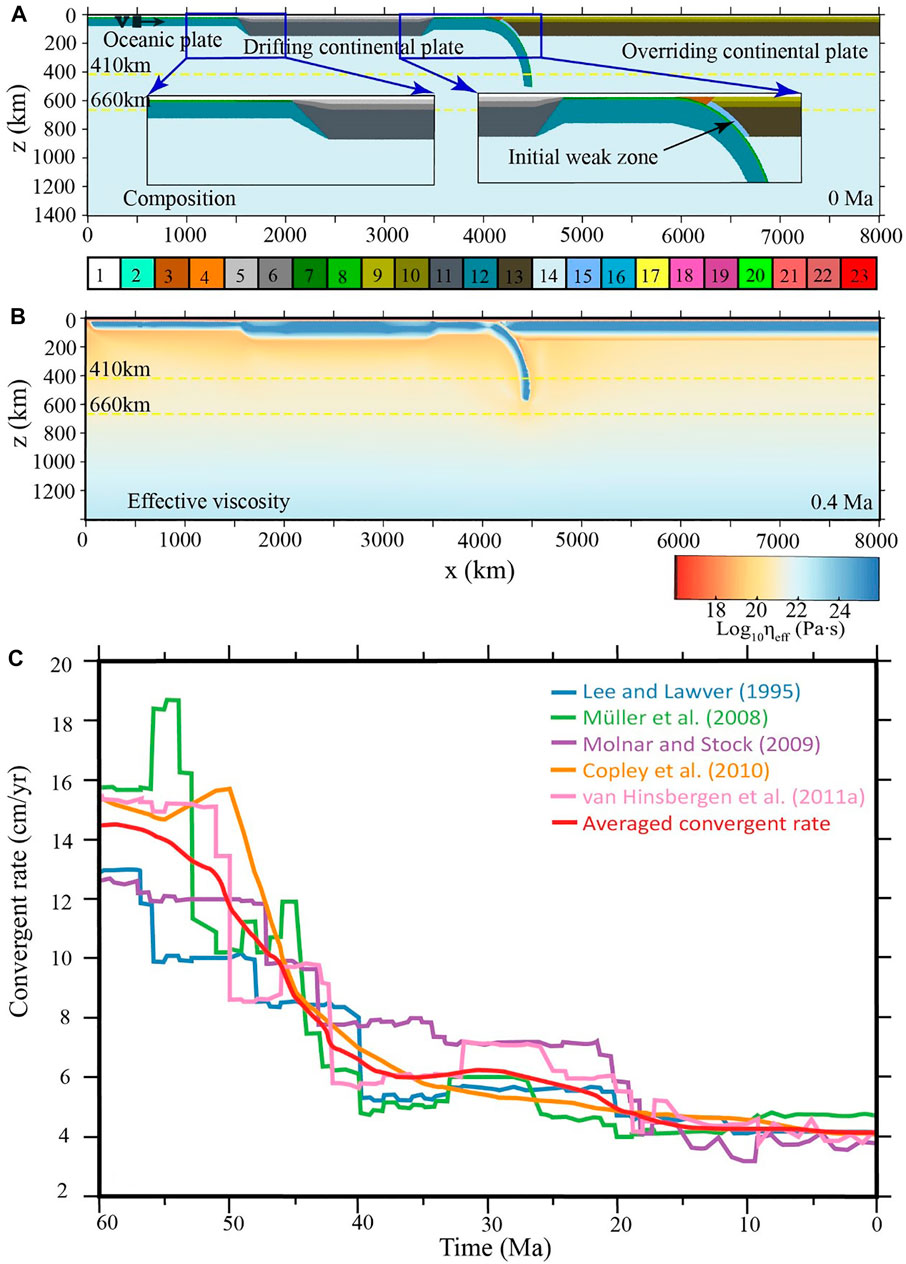
FIGURE 2. Initial model configuration and boundary convergent rate. (A) Composition field with colorbar shown at the bottom: 1, stick air; 2, seawater; 3,4, sediments; 5,6, drifting continental upper and lower crust, respectively; 7,8, oceanic upper and lower crust, respectively; 9,10, overriding continental upper and lower crust, respectively; 11, drifting continental lithospheric mantle; 12, oceanic lithospheric mantle; 13, overriding continental lithospheric mantle, 14, asthenosphere, 15, hydrated mantle; 16, serpentinized mantle; 17, partially molten sediments; 18, partially molten drifting continental upper crust; 19, partially molten drifting continental lower crust; 20, partially molten oceanic crust; 21, partially molten overriding continental upper crust; 22, partially molten overriding continental lower crust; and 23, partially molten mantle. (B) Effective viscosity field with the colorbar shown at the bottom. The yellow dotted lines indicate the 410 and 660 km discontinuities, with the Clapeyron slopes of phase transitions of +3 and −1 MPa/K, respectively. (C) The time-dependent velocity of the India–Asia convergence since 60 Ma, according to the previous plate reconstruction studies (Lee and Lawver, 1995; Müller et al., 2008; Molnar and Stock, 2009; Copley et al., 2010; van Hinsbergen et al., 2011). The red line shows the averaged convergence rate of the five reconstructions, which is further applied in the numerical model as a boundary condition as shown by a black rectangle and arrow in (A).

The oceanic lithosphere consists of a 3 km-thick upper crust, a 5 km-thick lower crust, and a lithospheric mantle with its thickness controlled by the age of the oceanic plate. The initial age of the spreading oceanic plate is set to be 30 Myr, with the corresponding lithospheric thickness of about 60 km (Turcotte and Schubert, 2002). On the other hand, the age of the horizontal section of the subducting oceanic plate is set to be 60 Myr, with the corresponding lithospheric thickness of about 86 km (Turcotte and Schubert, 2002). The age of the subducted oceanic plate is gradually changing from 60 Myr on the top to 30 Myr at the bottom, representing the slab heating during subduction. The continental lithosphere consists of an upper crust of 15 km, a lower crust of 20 km, and a lithosphere mantle of 105 km. An initial weak zone is set between the subducting oceanic plate and the overriding continental plate, which denotes a weak subduction channel. The top of the model is covered with a “sticky air” layer of 10 km (above the continental plate) or 12 km (above the oceanic plate), to simulate the free surface allowing crustal deformation (Schmeling et al., 2008). Detailed material properties of rocks are shown in Supplementary Tables S1, S2 in the supporting information.

For the initial temperature field of the model, the continental lithosphere is configured with a constant geothermal gradient of about 9.6 K/km, which indicates a temperature of ∼1623 K at the bottom of the lithosphere. On the other hand, the half-space cooling model is applied for the oceanic lithosphere (Turcotte and Schubert, 2002). The “sticky air” layer has a constant temperature of 273 K and the sublithospheric mantle has an initial thermal gradient of 0.5 K/km. For the thermal boundary conditions, the upper and lower boundaries have constant temperatures of 273 and 2248 K, respectively. The left and right boundaries are adiabatic with no horizontal heat flux.

Kinematic Boundary Conditions

The free-slip condition is applied for all the four boundaries. Plate convergence is driven by an internal pushing velocity as indicated in Figure 2A. In order to study the specific case of the India–Asia collision, we have compiled its convergent rate based on five independent studies of plate reconstructions and obtained an averaged time-dependent velocity evolution since 60 Ma, as shown in Figure 2C (Lee and Lawver, 1995; Müller et al., 2008; Molnar and Stock, 2009; Copley et al., 2010; van Hinsbergen et al., 2011). The averaged convergent rate (i.e. red line in Figure 2C, from either 55 and 60 Ma) is further implemented into the numerical model as an internal boundary condition as shown by the black rectangle and arrow in Figure 2A. The velocity patch is fixed in and moving with the spreading oceanic plate during convergence.

Model Results

The exact time of the initial India–Asia continental collision is still in debate. However, it is generally accepted to be at about 55 ± 5 Ma, i.e. between 60 and 50 Ma (Klootwijk et al., 1992; Molnar et al., 1993; Tapponnier et al., 2001; Wang et al., 2014; Ding et al., 2016; Hu et al., 2016; Ingalls et al., 2016; Zheng and Wu, 2018). In the current model, there is a horizontal section of the oceanic lithosphere with a length of 500 km between the drifting continental plate and overriding continental plate (Figure 2A). With a high convergence rate of >10 cm/yr before 50 Ma (Figure 2C), the subduction and consumption of this oceanic section will be within 5 Myr.

In this study, two groups of models are conducted, with applying reconstruction-based convergence rate from either 55 or 60 Ma (Figure 2C), which indicate the onset of collision at about 50 or 55 Ma, correspondingly. In each group of models, the effects of rheological strength of the overriding continental lithospheric mantle are systematically studied with the model results shown in Figures 3–12. It should be noted that the overriding Tibetan lithosphere has undergone multiple stages of ocean subduction and terrane accretion before the India–Asia collision. Thus, the Tibetan lithospheric mantle could be significantly weakened by the accompanying fluid/melt activities, which may strongly affect the final collision dynamics (Molnar et al., 1993; Li et al., 2016, 2021; Huangfu et al., 2019). In this study, the weakness of the Tibetan plate is represented by a lower plastic friction coefficient of the overriding lithospheric mantle.

FIGURE 3

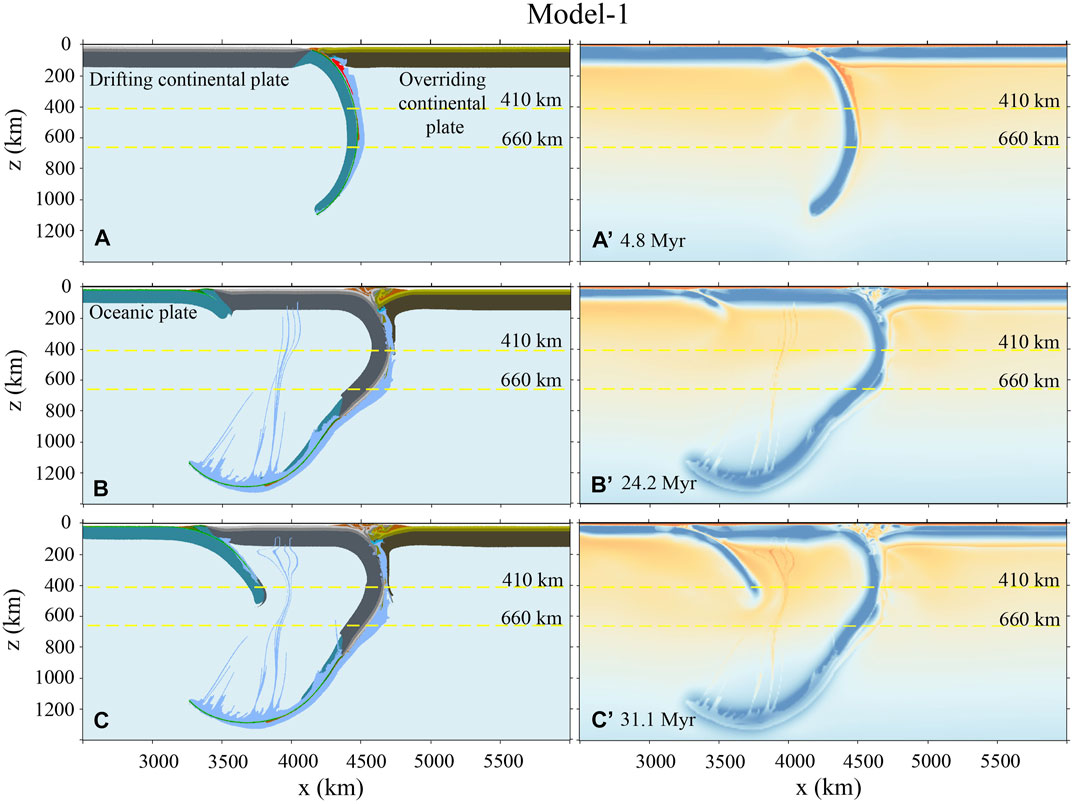
FIGURE 3. Model-1 evolution with a strong overriding plate. The reconstruction-based convergence rate is applied from 55 Ma (Figure 2C). The plastic friction coefficient of the overriding lithospheric mantle is initially $\lambda ·\text{sin}\left(\phi \right)=$ 0.6 and will decrease linearly to 0.1 with the accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information), which is the same as that of the underthrusting Indian lithospheric mantle. (A–C) The composition field evolution with the corresponding colorbar is shown in Figure 2A. (A’–C’) The effective viscosity evolution with the corresponding colorbar is shown in Figure 2B.

Numerical Models With India–Asia Convergence From 55 Ma

In this group of models, the plate subduction and collision is pushed by the reconstruction-based India–Asia convergence rate from 55 Ma (Figure 2C). With such a time-dependent convergence rate, a total amount of about 3,600 km will be achieved when the model runs for the whole 55 Myr. The Indian Continent is generally considered as a pre-Cambrian craton, which has a rheologically strong lithosphere (Replumaz et al., 2014; Jain et al., 2020). However, the overriding Tibetan lithosphere could be weakened before the final collision with the Indian Continent. In order to study the effects of overriding lithospheric strength on the continental collision mode selection and deformation partition, a series of models with variable rheological strength of overriding lithospheric mantle have been conducted.

In Model-1, the overriding continental plate is rheologically strong. The plastic friction coefficient of its lithospheric mantle is the same as the underthrusting Indian lithosphere, which was initially $\lambda ·\text{sin}\left(\phi \right)=$ 0.6 and will decrease linearly to 0.1 with the accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). In this model, the continental collision occurs after convergence for ∼4.8 Myr (Figure 3A). Subsequently, the drifting continental plate subducts following the preceding oceanic lithosphere, with the continental upper crust detached and accumulated in the orogeny (Figure 3B). The resistance builds gradually during the subduction of less dense continental plate, which contributes to the formation of a new subduction zone in the neighboring oceanic plate (Figures 3B,C). It indicates that the collision-induced subduction transference favors the strong overriding plates rheologically, which leads to the strain localization in the neighboring passive margin.

In Model-2, the plastic friction coefficient of the overriding lithospheric mantle decreased to 0.1 and does not depend on the plastic strain anymore. The collision between the drifting and overriding continental plates occurs similarly at about 4.8 Myr after the initial model convergence (Figure 4A). Then, the drifting continental plate subducts to a depth of ∼660 km at 16.3 Myr, following the sinking oceanic lithosphere (Figure 4B). At about 35 Myr, the slab break-off occurs in the subducted continental lithosphere, with the lower section sinking into the mantle and the upper section rolling back (Figure 4C). During the continuous continental subduction and collision, the overriding continental lithosphere is shortened due to its relative weakness (Figures 4C,D). Finally, the total convergence of ∼2,900 km is achieved after the initial collision (i.e. after ∼4.8 Myr) in this model, which is accommodated by overriding plate shortening of ∼1,200 km, continental slab break-off of ∼700 km, and continental subduction without break-off of ∼1,000 km, respectively. As a result, the thickness of the overriding continental crust increases from 35 km to an average value of ∼50 km, with its time-dependent evolution shown in Supplementary Figure S1 of the supporting information.

FIGURE 4

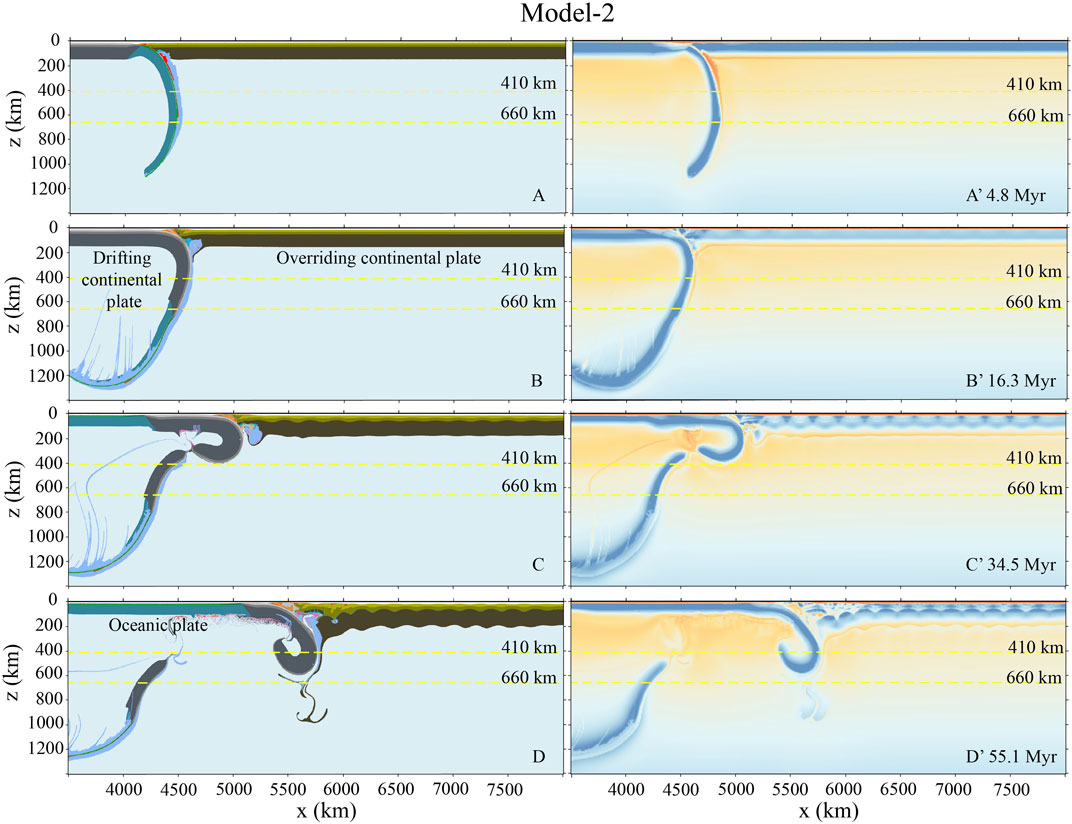
FIGURE 4. Model-2 evolution with a decreased and uniform plastic friction coefficient of the overriding lithospheric mantle of $\lambda ·\text{sin}\left(\phi \right)=$ 0.1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). All the other parameters are identical to Model-1 (Figure 3). (A–D) The composition field evolution with the corresponding colorbar is shown in Figure 2A. (A’–D’) The effective viscosity evolution with the corresponding colorbar is shown in Figure 2B.

In Model-3, the plastic friction coefficient of the overriding lithospheric mantle is decreased to $\lambda ·\text{sin}\left(\phi \right)=$ 0.1 initially and further to 0.01 with accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). After the continental collision at ∼4.9 Myr, the drifting continental plate subducts following the preceding oceanic plate (Figures 5A,B). At ∼25 Myr, the slab break-off occurs in the subducted drifting continental plate, with the oceanic slab and a section of the subducted continental slab detached and sinking into the subjacent mantle. Under the continuous loading of convergence, the drifting continental plate underthrusts the overriding continental plate and drives significant shortening of the latter (Figure 5C). Finally, the delamination of the overriding lithospheric mantle is predicted at the latest stage of model evolution (Figure 5D). The total convergence of ∼2,900 km is achieved after the initial collision (i.e., after ∼4.9 Myr) in this model. The lower (Greater Indian) plate accommodates ∼1,200 km, including ∼500 km of the underthrusting continental plate and ∼700 km of the detached continental plate. The residual convergence of ∼1700 km is accommodated by the shortening of the overriding continental plate. As a result, the thickness of the overriding continental crust increases from 35 km to an average value of ∼64 km, with its time-dependent evolution shown in Supplementary Figure S1 of the supporting information.

FIGURE 5

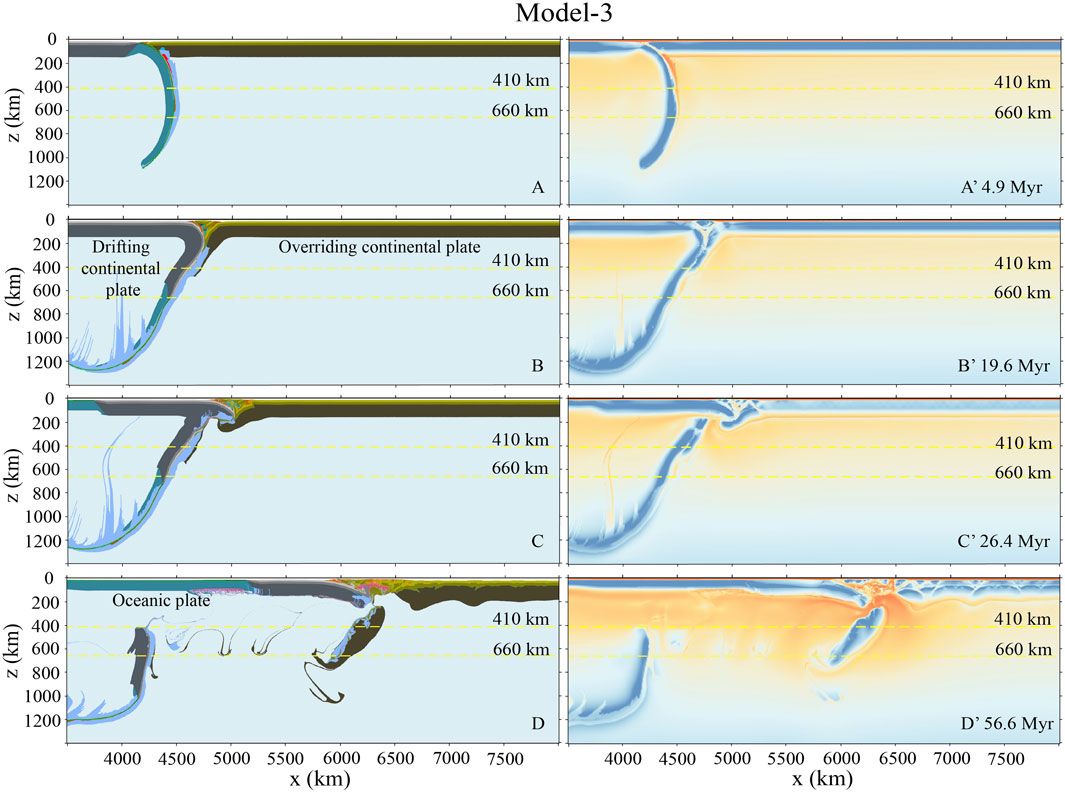
FIGURE 5. Model-3 evolution with a further decreased plastic friction coefficient of the overriding lithospheric mantle, which is initially $\lambda ·\text{sin}\left(\phi \right)=$ 0.1 and will decrease linearly to 0.01 with the accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). All the other parameters are identical to Model-2 (Figure 4). (A–D) The composition field evolution with the corresponding colorbar is shown in Figure 2A. (A’–D’) The effective viscosity evolution with the corresponding colorbar is shown in Figure 2B.

In Model-4, the plastic friction coefficient of the overriding lithospheric mantle is further decreased to 0.01 and does not depend on the plastic strain anymore. With such a greatly weakened overriding lithosphere, the collision occurs a bit later (at ∼5.9 Myr) than the previous cases (Figures 3–5), due to the shortening of the overriding plate during the oceanic subduction stage (Figure 6A). After the continental collision happens, the convergence-induced strain mostly localizes in the overriding plate, whereas the amount of continental subduction is limited. At ∼10 Myr after the initial collision, the slab break-off occurs, during which a short continental slab of ∼50 km is detached with the preceding oceanic slab (Figure 6B). Afterward, the overriding plate accommodates most of the convergence with lithospheric thickening and delamination (Figures 6C,D). In addition, the drifting continental plate underthrusts beneath the thickened overriding crust after the detachment of the lithospheric mantle (Figures 6C,D). Finally, the total convergence of the two continents after the collision is ∼2,700 km. The overriding plate accommodates the majority of convergence with ∼2,150 km, while the drifting continental plate absorbs the residual amount of convergence by detachment (∼50 km) and subduction (∼500 km) (Table 1). As the model evolved to ∼55 Myr, the thickened overriding crust reached an averaged value of ∼87 km, with its time-dependent evolution shown in Supplementary Figure S1 of the supporting information.

FIGURE 6

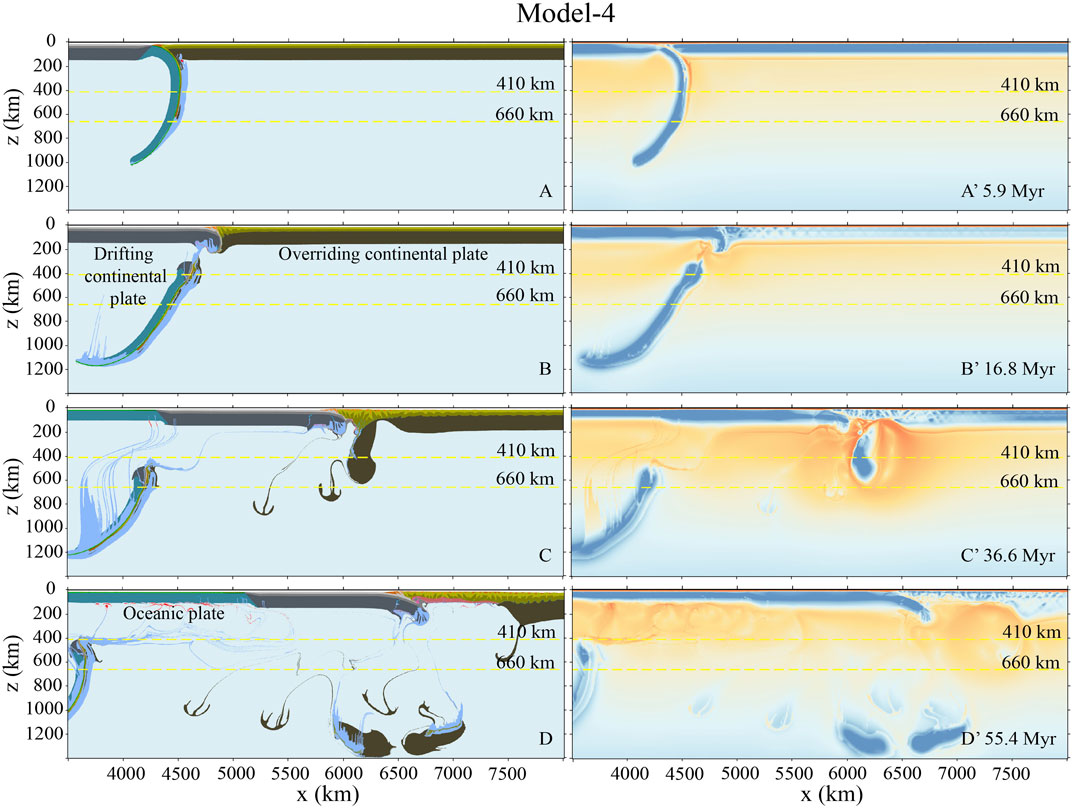
FIGURE 6. Model-4 evolution with a further decreased and uniform plastic friction coefficient of the overriding lithospheric mantle of $\lambda ·\text{sin}\left(\phi \right)=$ 0.01 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). All the other parameters are identical to Model-3 (Figure 5). (A–D) The composition field evolution with the corresponding colorbar is shown in Figure 2A. (A’–D’) The effective viscosity evolution with the corresponding colorbar is shown in Figure 2B.

TABLE 1

TABLE 1. Summary of model parameters and results.

In Model-5, with the weakest overriding plate, the plastic friction coefficient is decreased to $\lambda ·\text{sin}\left(\phi \right)=$ 0.01 initially and further to 0.001 with the accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). The general evolution of this model is similar to Model-4 (Figure 6), with most of the convergence accommodated by the shortening of the overriding plate (Figure 7). The slab break-off occurs at ∼20 Myr, when a short continental plate of ∼100 km and the preceding oceanic slab detaches sinking into mantle (Figure 7B). In this model, the small-scaled delamination happens at the bottom of the overriding plate repeatedly during continuous convergence, because of the significantly weakened overriding lithospheric mantle (Figures 7C,D). When the model evolves to the end at ∼55 Ma, the overriding lithospheric mantle is almost completely delaminated. The thickness of the crust reaches ∼87 km, with its time-dependent evolution as shown in Supplementary Figure S1 of the supporting information. The total convergence after the initial collision in this model is ∼2,700 km, of which the drifting continental lithosphere takes up ∼600 km including ∼100 km for break-off and ∼500 km for subduction without break-off. The residual convergence of ∼2,100 km is absorbed by the shortening and delamination of the overriding plate (Table 1).

FIGURE 7

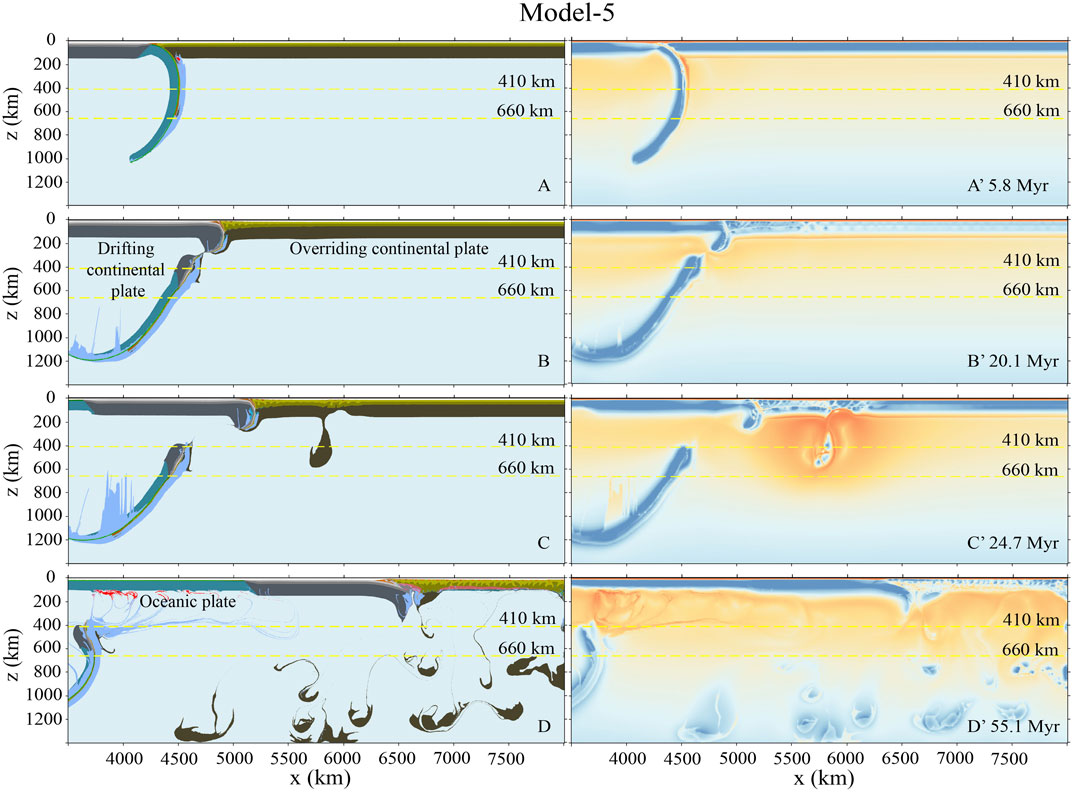
FIGURE 7. Model-5 evolution with weakest overriding plate. The plastic friction coefficient of the overriding lithospheric mantle is initially $\lambda ·\text{sin}\left(\phi \right)=$ 0.01 and will decrease linearly to 0.001 with accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). All the other parameters are identical to Model-4 (Figure 6). (A–D) The composition field evolution with the corresponding colorbar is shown in Figure 2A. (A’–D’) The effective viscosity evolution with the corresponding colorbar is shown in Figure 2B.

Numerical Models With India–Asia Convergence From 60 Ma

In the previous models, the plate reconstruction-based India–Asia convergence rate (Figure 2C) is implemented from 55 Ma. In the order for comparison, another group of models are conducted with the convergence rate from 60 Ma (Figure 2C). All the other parameters are identical to the previous group of models.

In Model-6 (Figure 8), the rheological strength of all the plates are identical to Model-1 (Figure 3), in which the plastic friction coefficient of the strong overriding lithospheric mantle is initially $\lambda ·\text{sin}\left(\phi \right)=$ 0.6 and will decrease linearly to 0.1 with the accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). The general model evolution of the current model is similar to Model-1, with collision-induced subduction transference (c.f. Figures 3, 8). With a higher convergence rate, the subduction initiation occurs at about 10 Myr after the continental collision (Figure 8), whereas it is about 20 Myr in Model-1 with a slower convergence (Figure 3).

FIGURE 8

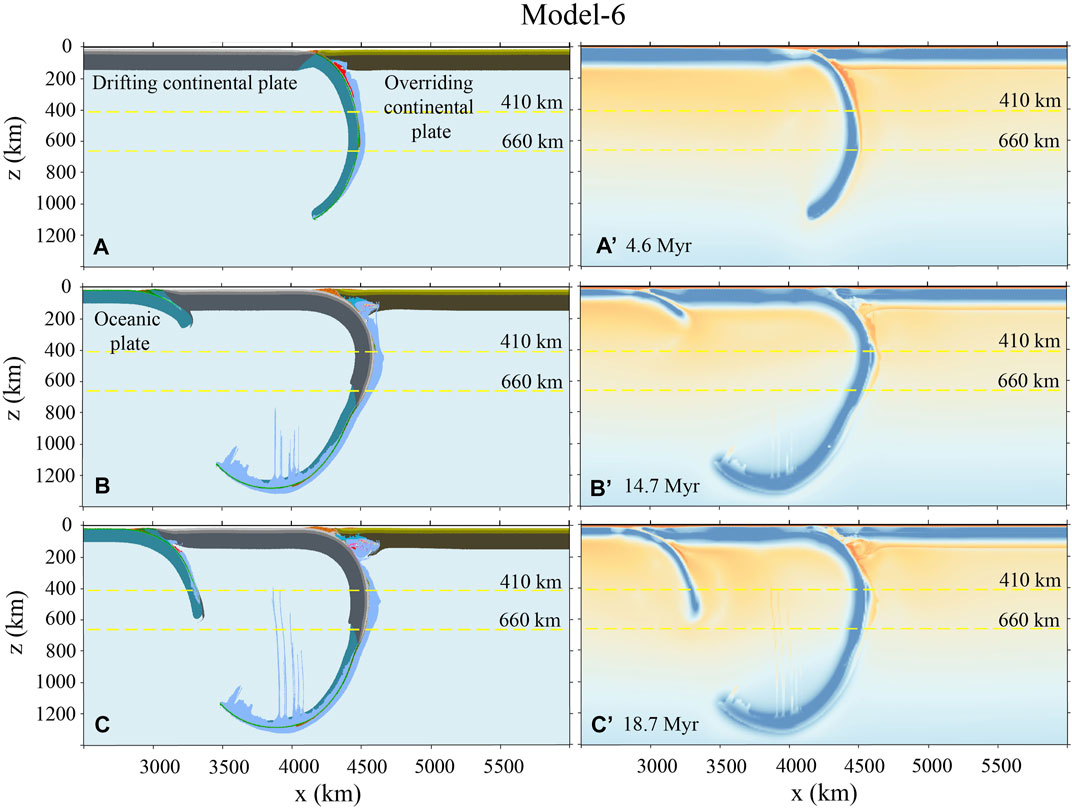
FIGURE 8. Model-6 evolution with a strong overriding plate. The reconstruction-based convergence rate is applied from 60 Ma (Figure 2C). The plastic friction coefficient of overriding lithospheric mantle is initially $\lambda ·\text{sin}\left(\phi \right)=$ 0.6 and will decrease linearly to 0.1 with the accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information), which is the same as that of the underthrusting Indian lithospheric mantle. (A–C) The composition field evolution with the corresponding colorbar is shown in Figure 2A. (A’–C’) The effective viscosity evolution with the corresponding colorbar is shown in Figure 2B.

In Model-7 (Figure 9), the plastic friction coefficient of the overriding lithospheric mantle is extensively reduced to 0.1, similar to Model-2 (Figure 4). The continental collision starts at about 4.7 Myr (Figure 9A). Then, the drifting continental plate subducts beneath the overriding plate following the preceding oceanic slab (Figure 9B). The slab break-off occurs at ∼17 Myr, with a long portion of subducted continental slab detached (Figure 9C). After the slab break-off, the strain localization changes from the subducting plate to the relatively weak overriding plate. The latter is extensively thickened accompanying lithospheric delamination (Figure 9D), which is similar to those in Liu et al. (2021). In this model, the total convergence after the initial collision (i.e. after ∼4.7 Myr) is ∼3,600 km. The lower plate takes up ∼1,500 km of convergence, including ∼800 km of the detached continental plate and ∼700 km of the underthrusting continental plate. The convergence absorbed by the overriding continental plate is ∼2,100 km, with the crust thickening from 35 km to an average value of 82 km (Table 1). The time-dependent evolution of the overriding crustal thickness is shown in Supplementary Figure S2 of the supporting information.

FIGURE 9

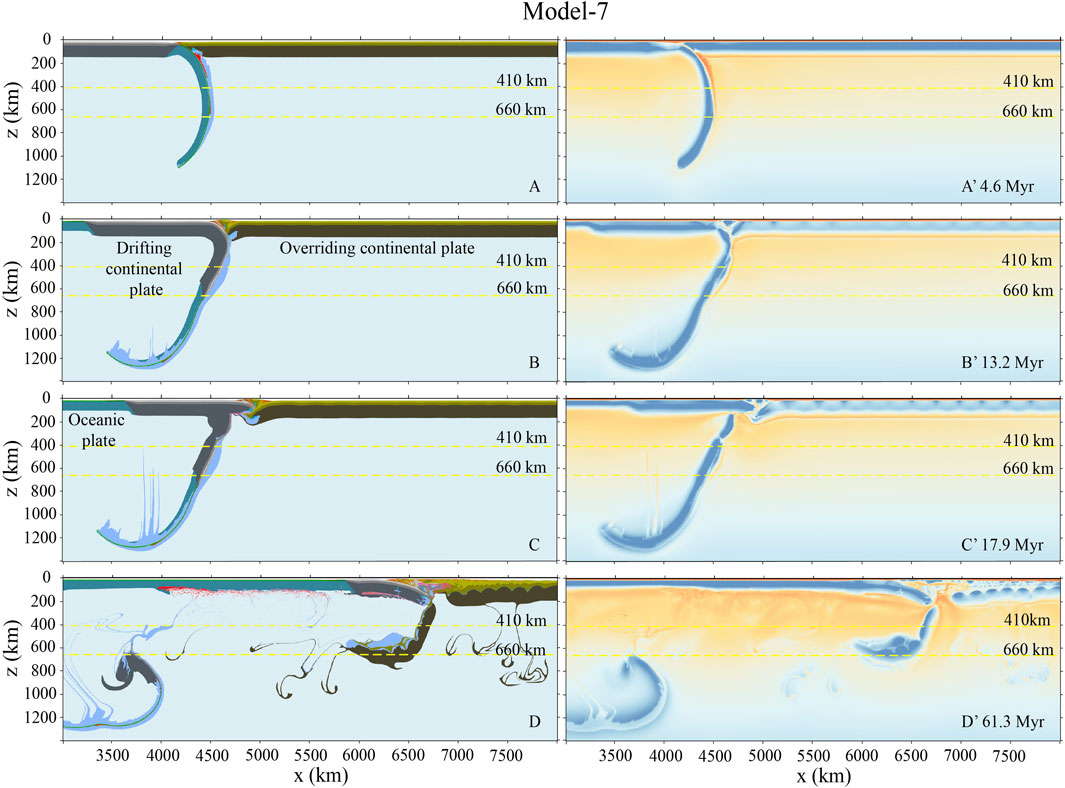
FIGURE 9. Model-7 evolution with a decreased and uniform plastic friction coefficient of the overriding lithospheric mantle of $\lambda ·\text{sin}\left(\phi \right)=$ 0.1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). All the other parameters are identical to Model-6 (Figure 8). (A–D) The composition field evolution with the corresponding colorbar shown in Figure 2A. (A’–D’) The effective viscosity evolution with the corresponding colorbar is shown in Figure 2B.

In Model-8, the plastic friction coefficient of the overriding lithospheric mantle is decreased to $\lambda ·\text{sin}\left(\phi \right)=$ 0.1 initially and further to 0.01 with the accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). In this model, the drifting continental plate also subducts following the subducted oceanic slab, with the slab break-off occurring at ∼17 Myr (Figure 10C). However, the detached continental slab is much shorter than that of Model-7 in Figure 9. Afterward, the drifting continental plate underthrusts slightly beneath the overriding continental lithosphere. Large amount of convergence is accommodated by the shortening of overriding lithosphere, which leads to the extensive delamination of the overriding lithospheric mantle (Figure 10D). The total convergence after the initial collision is about 3,600 km in this model, of which ∼2,400 km is accommodated by the shortening of the overriding plate. Consequently, the final thickness of the overriding crust increases to an average value of ∼100 km, with the time-dependent evolution as shown in Supplementary Figure S2. The remaining convergence is accommodated by the detached continental plate (∼800 km) and the underthrusting continental plate (∼700 km), respectively (Table 1).

FIGURE 10

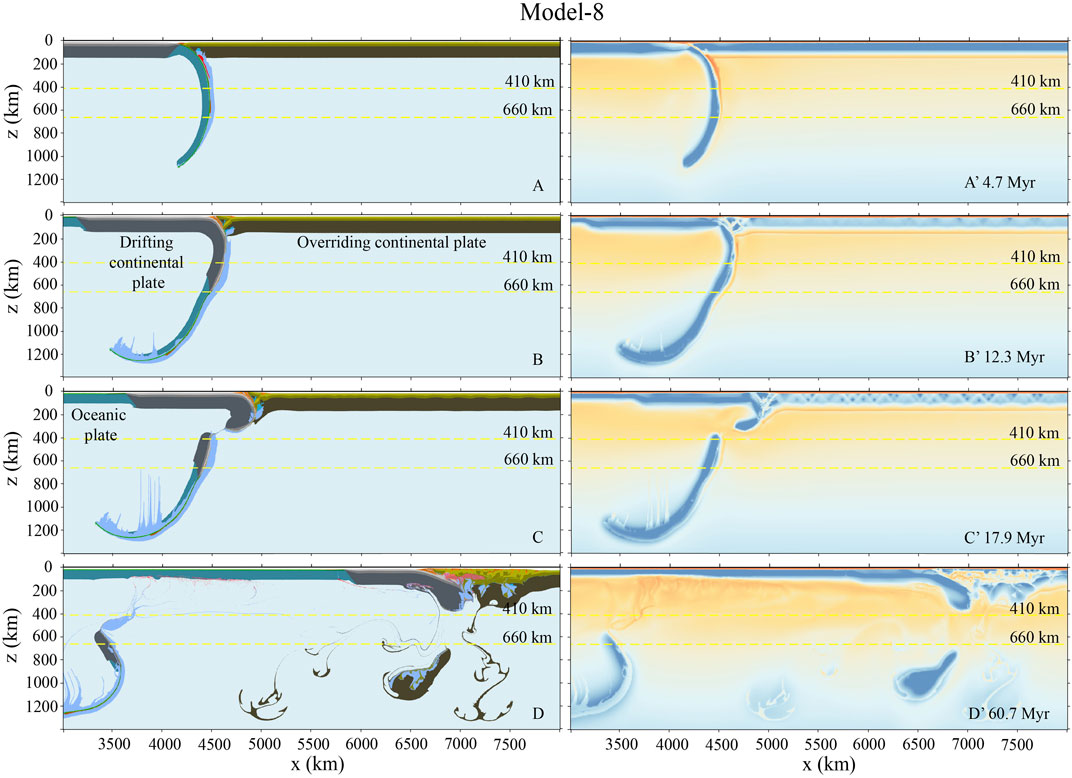
FIGURE 10. Model-8 evolution with a further decreased plastic friction coefficient of the overriding lithospheric mantle, which is initially $\lambda ·\text{sin}\left(\phi \right)=$ 0.1 and will decrease linearly to 0.01 with the accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). All the other parameters are identical to Model-7 (Figure 9). (A–D) The composition field evolution with the corresponding colorbar is shown in Figure 2A. (A’–D’) The effective viscosity evolution with the corresponding colorbar is shown in Figure 2B.

In Model-9, the overriding plate is very weak. The plastic friction coefficient of the lithospheric mantle is implemented as $\lambda ·\text{sin}\left(\phi \right)=$ 0.01 (Figure 11). In this model, the continental subduction is limited, with slab break-off occurring very early at ∼11 Myr (Figure 11B). Then, the $$ convergence is mainly accommodated by the shortening of overriding continental plate and the multiple stages of lithospheric delamination (Figures 11C,D). When the overriding lithospheric mantle mostly delaminates, the drifting plate starts underthrusting again beneath the greatly thickened overriding crust. Finally, the thickness of the overriding crust increases to an averaged value of ∼104 km, with the time-dependent evolution is shown in Supplementary Figure S2 of the supporting information. The amount of convergence after the initial collision is about 3,400 km throughout the evolution of model, most of which (∼2,400 km) is accommodated by the shortening of the overriding plate (Table 1).

FIGURE 11

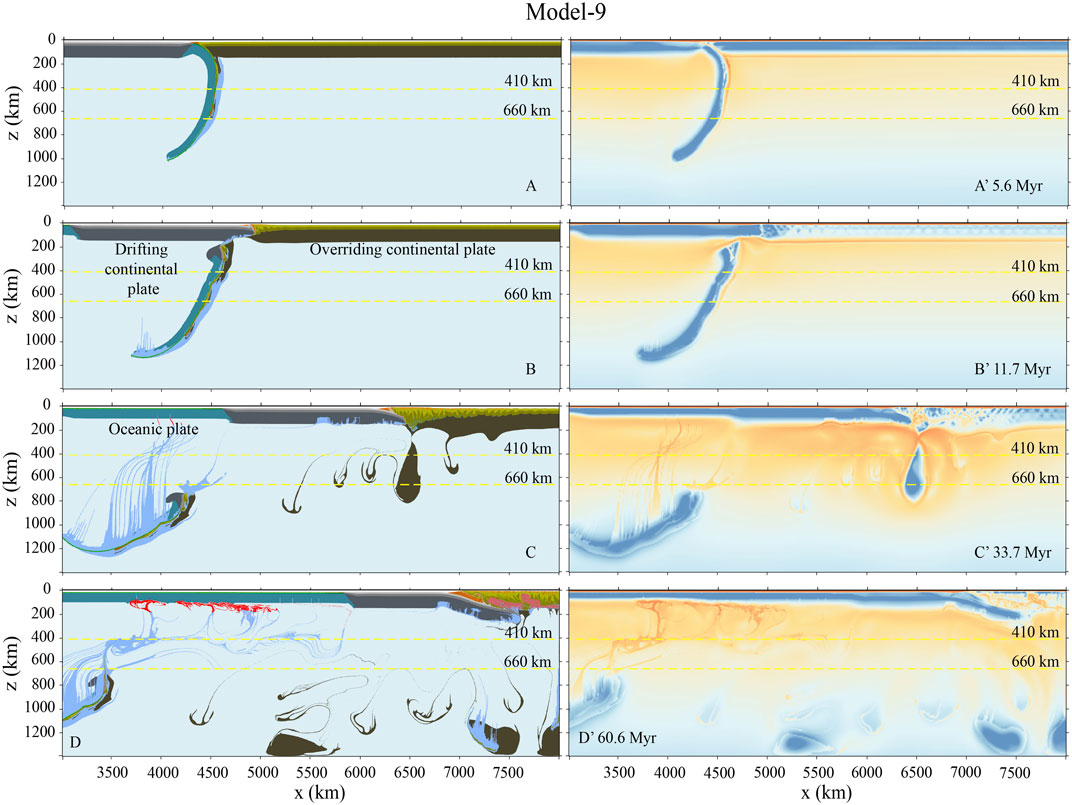
FIGURE 11. Model-9 evolution with a further decreased and uniform plastic friction coefficient of the overriding lithospheric mantle of $\lambda ·\text{sin}\left(\phi \right)=$ 0.01 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). All the other parameters are identical to Model-8 (Figure 10). (A–D) The composition field evolution with the corresponding colorbar is shown in Figure 2A. (A’–D’) The effective viscosity evolution with the corresponding colorbar is shown in Figure 2B.

In Model-10, the overriding lithospheric mantle is the weakest among all models, with plastic friction coefficient of $\lambda ·\text{sin}\left(\phi \right)=$ 0.01 initially and further to 0.001 with the accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). The model evolution is generally consistent with that of Model-9 (Figure 11), with plate convergence mostly accommodated by the shortening of the overriding plate, due to its great weakness. In this model, the lithospheric delamination occurs more frequently with many small blocks of thickened lithospheric mantle detached repeatedly (Figures 12C,D). Finally, the average thickness of the overriding crust increases to ∼127 km, with the time-dependent evolutions shown in Supplementary Figure S2 of the supporting information. The total amount of convergence after the initial collision is about 3,400 km, which is mostly absorbed by the overriding plate. The shortening of the overriding plate accommodates an even large amount of convergence of ∼2,600 km, whereas the subducting continental plate only consumes about 800 km (Table 1).

FIGURE 12

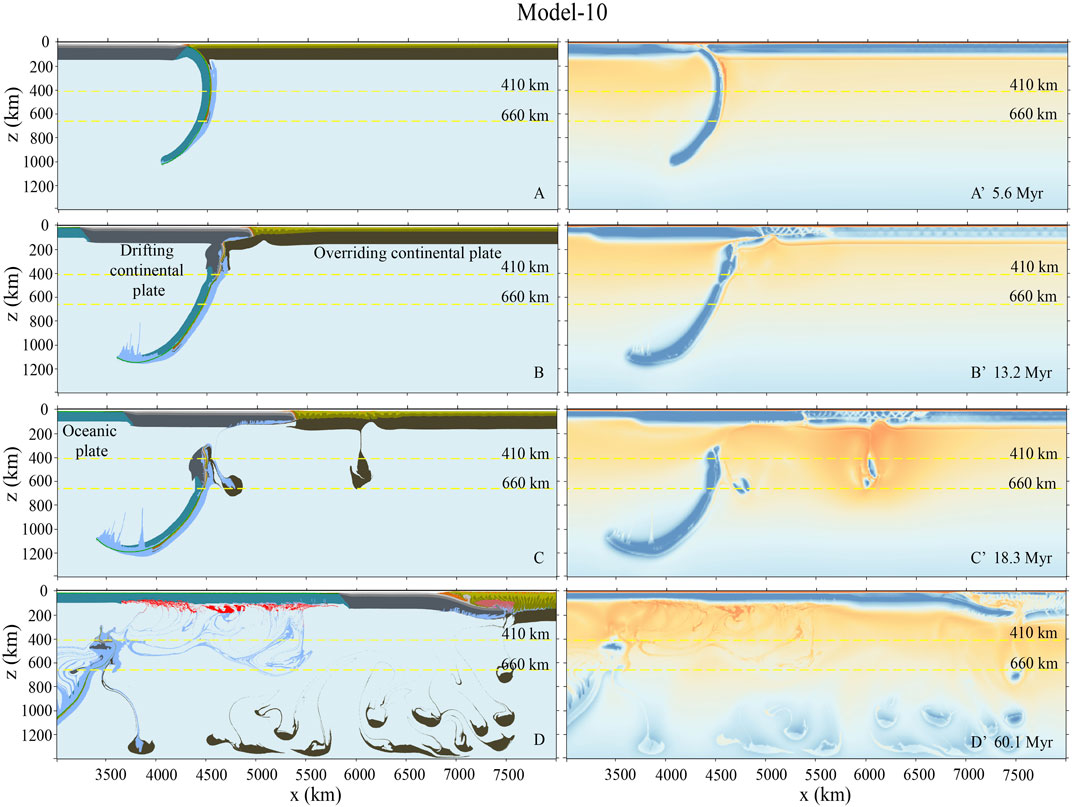
FIGURE 12. Model-10 evolution with the weakest overriding plate. The plastic friction coefficient of the overriding lithospheric mantle is initially $\lambda ·\text{sin}\left(\phi \right)=$ 0.01 and will decrease linearly to 0.001 with accumulated plastic strain to ε_plas = 1 (Supplementary Table S2 and Supplementary Equation S11 in the supporting information). All the other parameters are identical to Model-9 (Figure 11). (A–D) The composition field evolution with the corresponding colorbar is shown in Figure 2A. (A’–D’) The effective viscosity evolution with the corresponding colorbar is shown in Figure 2B.

Summary of Model Results

Based on the numerical models, three continental collision modes are identified (Figure 13), including collision-induced subduction transference (Model-1 and Model-6), continuous continental deep subduction (Model-2, Model-3, Model-7, and Model-8), and overriding plate shortening and delamination (Model-4, Model-5, Model-9, and Model-10). Since the drifting (Indian) continental plate is generally considered to be strong, the collision mode selection is mainly dependent on the rheological strength of the overriding continental plate. When the overriding lithosphere is strong, the continuous convergence after collision leads to the subduction of positively buoyant continental lithosphere. The resulting resistance contributes to the subduction transference to the neighboring oceanic plate, as shown in Figure 13A. When the rheological strength of the overriding plate is reduced, it will accommodate a significant amount of strain during collision. Consequently, the continental subduction rate will be reduced, which will lead to continental crustal detachment and exhumation as well as the heating of sinking continental plate. Thus, the resistant force from continental subduction will be decreased, and the continental deep subduction is favored rather than the subduction transference (Figure 13B). The deeply subducted continental slab will finally break-off and sink into the deeper mantle. When the overriding plate is very weak, the drifting continental plate subducts following the oceanic slab and breaks off earlier at a shallow depth (∼200–400 km) (Figure 13C). After that, most of the convergence will be absorbed by the gradual shortening of the overriding continental plate, which further contributes to lithospheric delamination and crustal thickening (Figure 13C). In addition, when the overriding continental plate is strong (0.6–0.1), the horizontal movement of the drifting continental plate is blocked. Therefore, the drifting continental plate tends to subduct following the oceanic slab. The continuous subduction hinders slab break-off (Figure 13A). In contrast, with the weak overriding continental plate, the drifting continental plate tends to move horizontally rather than subduction. Then, a strong extension is resulted between the horizontal plate and the subducted slab. Thus, the slab break-off is preferred (Figures 13B,C).

FIGURE 13

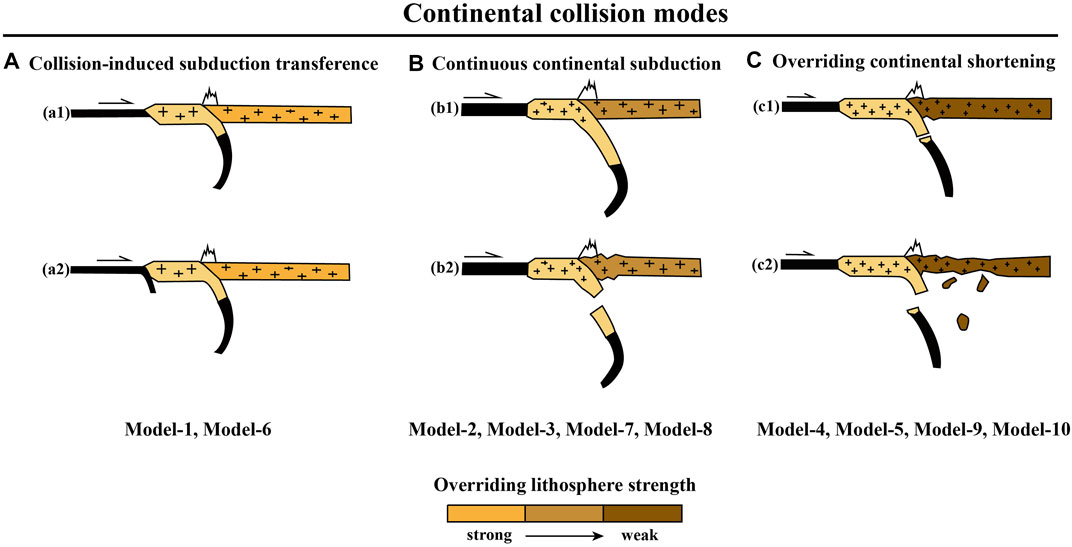
FIGURE 13. Three collision modes dependent on the rheological strength of the overriding lithosphere. (A) Collision-induced subduction transference with a strong overriding plate. (B) Continuous continental deep subduction with intermediate strength of the overriding plate. (C) Overriding lithospheric shortening and delamination with a weak overriding plate.

The different model evolution times (55 and 60 Myr) lead to contrasting amounts of convergence accommodated by the lower and upper plates, which result in different overriding crustal thicknesses (Table 1). However, the general continental collision mode selection is consistent, depending on the rheological strength of the overriding lithosphere (Figure 13).

Discussion

Mechanism for the Absence of Subduction Transference During India–Asia Collision

It is generally considered that the collision of Galatian and Cimmerian terranes with Eurasia leads to SI of the Paleo-Tethyan and Neo-Tethyan Oceanic plates, respectively (Stampfli and Borel, 2002; Stampfli et al., 2013; Wan et al., 2019; Zhong and Li, 2020). However, the collision between the Indian and Eurasian plates does not result in subduction transference to the Indian Ocean, even after the long-time collision of >50 Myr. Instead, the continuous convergence leads to the extensive shortening and delamination of the Tibetan lithosphere.

The absence of subduction transference during the India–Asia collision is an important and controversial problem. The current model results indicate that the strong overriding plate favors subduction transference to the neighboring oceanic plate after the continental collision for 10–20 Myr (Figures 3, 8). In contrast, the rheological weakness of the overriding Tibetan plate before India–Asia collision may accommodate a major part of continental convergence and thus prevent the strain localization in the neighboring oceanic plate. Consequently, the subduction transference will be prohibited.

In the natural India–Asia collision system, the overriding Tibetan plateau is composed of several terranes, including Lhasa, Qiangtang, Songpan-Ganzi, Qaidam, and Qilian terranes from south to north, which have been accreted to the Eurasian Continent before the final Indian collision (Replumaz and Tapponnier, 2003). Each accretion process is following the oceanic subduction with a wide spread magmatism, as evidenced by the magmatic rocks in the Lhasa and Qiangtang terranes (Hsü et al., 1995; Li et al., 2009; Zhu et al., 2011, 2013). Based on the complex formation and evolution of the overriding Tibetan plate, its lithospheric mantle could be rheologically weaker than that of the normal cratonic lithosphere, although the absolute weakness is hard to constrain.

Finally, we propose that the weakness of the overriding Tibetan plate before India–Asia collision plays an important role in prohibiting subduction transference, which thus explains the lack of SI at the southern Indian continental margin and northern Indian oceanic plate.

Deformation Partition and Continental Mass Balance During India–Asia Collision

The continental mass conservation during the India–Asia collision is also a challenging and controversial topic. Previous evaluations and estimations suggest that there is a large amount of deficit mass in the crustal mass of the Greater Indian and Tibetan plates during the long-lasting continental collision (Capitanio et al., 2010; Replumaz et al., 2010; Yakovlev and Clark, 2014; Ingalls et al., 2016). In order to solve this problem, different type of models with assuming an oceanic basin within the Greater India has been proposed (e.g., van Hinsbergen et al., 2012, 2019). The oceanic basin subduction is applied in the model to reconcile the conservation of continental crustal mass. However, there is no geological evidence for this period of oceanic subduction (Najman et al., 2010; Aitchison and Ali, 2012; Wu et al., 2014; Hu et al., 2016; Ding et al., 2017). On the other hand, the exact time of collision has not been well-constrained. The plate reconstructions suggested an extremely high convergence rate of ∼14 cm/yr between the Indian and Asian continents at ∼60–50 Ma. Thus, the uncertainty in the time of initial collision for 5 Myr may lead to a deviation of 700 km in total convergence.

In the current numerical models with the India–Asia convergence from 55 Ma, i.e., continental collision for 50 Myr, the total convergence between India and Eurasia is about 2,700–2,900 km after the collision. A large portion of convergence (i.e., ∼1,600 ± 500 km) is accommodated by the shortening of the overriding Tibetan plate, while the other portion of ∼1,175 ± 625 km is consumed by the subduction and break-off of the drifting continental plate (Table 1). In the natural India–Asia collision system, the shortening of the overriding plate, including the northeastern portion/margin of the Tibetan plateau, may be about 1,600–1700 km (Peltzer and Tapponnier, 1988; Wang 1997; Yin and Harrison, 2000; Yin et al., 2002; Fang et al., 2007; van Hinsbergen et al., 2019). Thus, the total amount of shortening is consistent with the model (e.g., Model-3) with intermediate rheological strength of the Tibetan lithosphere (Table 1). In this case of Model-3, the Greater Indian plate accommodates ∼1,200 km, including ∼700 km of the detached continental slab and ∼500 km of the subducted but not detached continental slab (Figure 5). It indicates that the convergence-induced deformation partition and continental mass balance can be generally reconciled with continental collision for 50 Myr, i.e. the model convergence from 55 Ma with oceanic subduction in the first ∼5 Myr.

In another case with the India–Asia convergence from 60 Ma, i.e. continental collision for ∼55 Myr, the amount of convergence after collision between the two continental plates is about 3,400–3,600 km. The shortening of the overriding plate has to be >2,000 km (Table 1), which is too large to be comparable with the observations (Peltzer and Tapponnier, 1988; Wang 1997; Yin and Harrison, 2000; Yin et al., 2002; Fang et al., 2007; van Hinsbergen et al., 2019). In addition, the resulting overriding crustal thickness is from 82 to 127 km, which is also larger than that of the present-day Tibetan Plateau (Replumaz et al., 2010; Yakovlev and Clark, 2014). Thus, in order to accommodate the excess shortening of the overriding continental plate (∼1,000 km) in this case, other models are required, e.g., the Greater Indian Oceanic Basin model or the Self-driven Continental Deep Subduction model, which needs to be examined in the future study.

Conclusion

In this study, the reconstruction-based India–Asia convergence rate is integrated with a large-scale thermomechanical numerical model, in order to study the dynamics of continental collision mode selection and the conditions for collision-induced subduction transference, as well as the deformation partition and continental mass balance during the India–Asia collision. The main conclusions are shown below:

(1) Three collision modes are identified with variable rheological strength of the overriding plate: collision-induced subduction transference, continuous continental subduction, and overriding plate shortening and delamination.

(2) The collision between the rheologically strong continental plates favors subduction transference to the neighboring oceanic plate. In contrast, the strain localization in the weak overriding plate hinders subduction transference.

(3) If the overriding plate is too weak, it will accommodate most of the convergence, leading to extensive lithospheric thickening and repeated delamination, which is difficult for reconciling the crustal thickness of the present-day Tibetan Plateau.

(4) In case of India–Asia collision for ∼50 Myr, the model with the intermediately weak overriding Tibetan plate may reconcile the general deformation partition and continental mass balance of the Himalayan–Tibetan system, without the requirement of an oceanic basin in the Greater India.

(5) The longer period of India–Asia collision for ≥55 Myr leads to significant shortening of the overriding plate that is hard to be comparable with the present-day Tibetan Plateau. The models with a Greater Indian Oceanic Basin or Self-driven Continental Deep Subduction may be required to solve the problem, which need further examinations.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://doi.org/10.5281/zenodo.5814796.

Author Contributions

Z-HL conceived the study. QL and XZ designed the numerical models. QL ran the models. All authors contributed to the data analysis, discussion, and writing the manuscript.

Funding

This work was supported by the NSFC Tethys project (91855208), the Strategic Priority Research Program (B) of Chinese Academy of Sciences (XDB42000000), and the Fundamental Research Funds for the Central Universities.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Numerical simulations were run with the clusters of the National Supercomputer Center in Guangzhou (Tianhe-II).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.919174/full#supplementary-material

References

Aitchison, J. C., and Ali, J. R. (2012). India-Asia Collision Timing. Proc. Natl. Acad. Sci. U. S. A. 109 (40), E2645. doi:10.1073/pnas.1207859109

CrossRef Full Text | Google Scholar

Aitchison, J. C., Ali, J. R., and Davis, A. M. (2007). When and where Did India and Asia Collide? J. Geophys. Res. 112, B05423. doi:10.1029/2006jb004706

CrossRef Full Text | Google Scholar

Capitanio, F. A., Morra, G., Goes, S., Weinberg, R. F., and Moresi, L. (2010). India-Asia Convergence Driven by the Subduction of the Greater Indian Continent. Nat. Geosci. 3 (2), 136–139. doi:10.1038/ngeo725

CrossRef Full Text | Google Scholar

Cloetingh, S., Wortel, R., and Vlaar, N. J. (1989). On the Initiation of Subduction Zones. Pageoph 129 (1-2), 7–25. doi:10.1007/bf00874622

CrossRef Full Text | Google Scholar

Copley, A., Avouac, J. P., and Royer, J. Y. (2010). India-Asia Collision and the Cenozoic Slowdown of the Indian Plate: Implications for the Forces Driving Plate Motions. J. Geophys. Res. 115, B03410. doi:10.1029/2009jb006634

CrossRef Full Text | Google Scholar

Cui, Q., Li, Z.-H., and Liu, M. (2021). Crustal Thickening versus Lateral Extrusion during India-Asia Continental Collision: 3-D Thermo-Mechanical Modeling. Tectonophysics 818, 229081. doi:10.1016/j.tecto.2021.229081

CrossRef Full Text | Google Scholar

Ding, H., Zhang, Z., Dong, X., Tian, Z., Xiang, H., Mu, H., et al. (2016). Early Eocene (C. 50 Ma) Collision of the Indian and Asian Continents: Constraints from the North Himalayan Metamorphic Rocks, Southeastern Tibet. Earth Planet. Sci. Lett. 435, 64–73. doi:10.1016/j.epsl.2015.12.006

CrossRef Full Text | Google Scholar

Ding, L., Maksatbek, S., Cai, F., Wang, H., Song, P., Ji, W., et al. (2017). Processes of Initial Collision and Suturing between India and Asia. Sci. China Earth Sci. 60 (4), 635–651. doi:10.1007/s11430-016-5244-x

CrossRef Full Text | Google Scholar

Fang, X., Zhang, W., Meng, Q., Gao, J., Wang, X., King, J., et al. (2007). High-resolution Magnetostratigraphy of the Neogene Huaitoutala Section in the Eastern Qaidam Basin on the NE Tibetan Plateau, Qinghai Province, China and its Implication on Tectonic Uplift of the NE Tibetan Plateau. Earth Planet. Sci. Lett. 258 (1-2), 293–306. doi:10.1016/j.epsl.2007.03.042

CrossRef Full Text | Google Scholar

Gan, W., Zhang, P., Shen, Z. K., Niu, Z., Wang, M., Wan, Y., et al. (2007). Present-Day Crustal Motion within the Tibetan Plateau Inferred from GPS Measurements. J. Geophys. Res. 112, B08416. doi:10.1029/2005jb004120

CrossRef Full Text | Google Scholar

Gerya, T. V. (2010). Introduction to Numerical Geodynamic Modelling. Cambridge: Cambridge University Press.

Gibbons, A. D., Zahirovic, S., Müller, R. D., Whittaker, J. M., and Yatheesh, V. (2015). A Tectonic Model Reconciling Evidence for the Collisions between India, Eurasia and Intra-oceanic Arcs of the Central-Eastern Tethys. Gondwana Res. 28 (2), 451–492. doi:10.1016/j.gr.2015.01.001

CrossRef Full Text | Google Scholar

Hsü, K. J., Guitang, P., and Sengör, A. M. C. (1995). Tectonic Evolution of the Tibetan Plateau: A Working Hypothesis Based on the Archipelago Model of Orogenesis. Int. Geol. Rev. 37 (6), 473–508. doi:10.1080/00206819509465414

CrossRef Full Text | Google Scholar

Hu, X., Garzanti, E., Wang, J., Huang, W., An, W., and Webb, A. (2016). The Timing of India-Asia Collision Onset - Facts, Theories, Controversies. Earth-Sci. Rev. 160, 264–299. doi:10.1016/j.earscirev.2016.07.014

CrossRef Full Text | Google Scholar

Huangfu, P., Li, Z.-H., Fan, W., Zhang, K.-J., and Shi, Y. (2019). Continental Lithospheric-Scale Subduction versus Crustal-Scale Underthrusting in the Collision Zone: Numerical Modeling. Tectonophysics 757, 68–87. doi:10.1016/j.tecto.2019.03.007

CrossRef Full Text | Google Scholar

Ingalls, M., Rowley, D. B., Currie, B., and Colman, A. S. (2016). Large-scale Subduction of Continental Crust Implied by India-Asia Mass-Balance Calculation. Nat. Geosci. 9 (11), 848–853. doi:10.1038/ngeo2806

CrossRef Full Text | Google Scholar

Jain, A. K., Banerjee, D. M., and Kale, V. S. (2020). Tectonics of the Indian Subcontinent: An Introduction. Cham, Switzerland: Springer. doi:10.1007/978-3-030-42845-7_1

CrossRef Full Text | Google Scholar

Kapp, P., and DeCelles, P. G. (2019). Mesozoic-Cenozoic Geological Evolution of the Himalayan-Tibetan Orogen and Working Tectonic Hypotheses. Am. J. Sci. 319 (3), 159–254. doi:10.2475/03.2019.01

CrossRef Full Text | Google Scholar

Kelly, S., Butler, J. P., and Beaumont, C. (2016). Continental Collision with a Sandwiched Accreted Terrane: Insights into Himalayan–Tibetan Lithospheric Mantle Tectonics? Earth Planet. Sci. Lett. 455, 176–195. doi:10.1016/j.epsl.2016.08.039

CrossRef Full Text | Google Scholar

Klootwijk, C. T., Gee, J. S., Peirce, J. W., Smith, G. M., and McFadden, P. L. (1992). An Early India-Asia Contact: Paleomagnetic Constraints from Ninetyeast Ridge, ODP Leg 121. Geol 20 (5), 395. doi:10.1130/0091-7613(1992)020<0395:aeiacp>2.3.co;2

CrossRef Full Text | Google Scholar

Lee, T. Y., and Lawver, L. A. (1995). Cenozoic Plate Reconstruction of Southeast Asia. Tectonophysics 251 (1-4), 85–138. doi:10.1016/0040-1951(95)00023-2

CrossRef Full Text | Google Scholar

Li, H., Xu, Z., Yang, J., Cai, Z., Chen, S., and Tang, Z. (2009). Records of Indosinian Orogenesis in Lhasa Terrane, Tibet. J. Earth Sci. 20 (2), 348–363. doi:10.1007/s12583-009-0029-9

CrossRef Full Text | Google Scholar

Li, Z.-H., Liu, M., and Gerya, T. (2016). Lithosphere Delamination in Continental Collisional Orogens: A Systematic Numerical Study. J. Geophys. Res. Solid Earth 121 (7), 5186–5211. doi:10.1002/2016jb013106

CrossRef Full Text | Google Scholar

Li, Z.-H., Gerya, T., and Connolly, J. A. D. (2019). Variability of Subducting Slab Morphologies in the Mantle Transition Zone: Insight from Petrological‐thermomechanical Modeling. Earth-Sci. Rev. 196, 102874. doi:10.1016/j.earscirev.2019.05.018

CrossRef Full Text | Google Scholar

Li, Z. H., Cui, Q., Zhong, X., Liu, M. Q., Wang, Y., and Huangfu, P. (2021). Numerical Modeling of Continental Dynamics: Questions, Progress and Perspectives. Acta Geol. Sin. 95, 238–258. doi:10.1111/1755-6724.14832

CrossRef Full Text | Google Scholar

Liu, L., Liu, L., and Xu, Y. G. (2021). Intermittent Post-Paleocene Continental Collision in South Asia. Geophys. Res. Lett. 48, e2021GL094531. doi:10.1029/2021gl094531

CrossRef Full Text | Google Scholar

Martin, C. R., Jagoutz, O., Upadhyay, R., Royden, L. H., Eddy, M. P., Bailey, E., et al. (2020). Paleocene Latitude of the Kohistan-Ladakh Arc Indicates Multistage India-Eurasia Collision. Proc. Natl. Acad. Sci. U.S.A. 117 (47), 29487–29494. doi:10.1073/pnas.2009039117

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, J., Gilder, S. A., Wang, C., Coe, R. S., Tan, X., Zhao, X., et al. (2019). Defining the Limits of Greater India. Geophys. Res. Lett. 46 (8), 4182–4191. doi:10.1029/2019gl082119

CrossRef Full Text | Google Scholar

Meng, J., Gilder, S. A., Li, Y., Wang, C., and Liu, T. (2020). Expanse of Greater India in the Late Cretaceous. Earth Planet. Sci. Lett. 542, 116330. doi:10.1016/j.epsl.2020.116330

CrossRef Full Text | Google Scholar

Molnar, P., and Stock, J. M. (2009). Slowing of India's Convergence with Eurasia since 20 Ma and its Implications for Tibetan Mantle Dynamics. Tectonics 28 (3), TC3001. doi:10.1029/2008tc002271

CrossRef Full Text | Google Scholar

Molnar, P., England, P., and Martinod, J. (1993). Mantle Dynamics, Uplift of the Tibetan Plateau, and the Indian Monsoon. Rev. Geophys. 31 (4), 357–396. doi:10.1029/93rg02030

CrossRef Full Text | Google Scholar

Müller, R. D., Sdrolias, M., Gaina, C., and Roest, W. R. (2008). Age, Spreading Rates, and Spreading Asymmetry of the World's Ocean Crust. Geochem. Geophys. Geosyst. 9, Q04006. doi:10.1029/2007GC001743

CrossRef Full Text | Google Scholar

Najman, Y., Appel, E., Boudagher-Fadel, M., Bown, P., Carter, A., Garzanti, E., et al. (2010). Timing of India-Asia Collision: Geological, Biostratigraphic, and Palaeomagnetic Constraints. J. Geophys. Res. 115, B12416. doi:10.1029/2010jb007673

CrossRef Full Text | Google Scholar

Parsons, A. J., Hosseini, K., Palin, R., and Sigloch, K. (2020). Geological, Geophysical and Plate Kinematic Constraints for Models of the India-Asia Collision and the Post-Triassic Central Tethys Oceans. Earth-Sci. Rev. 208, 103084. doi:10.1016/j.earscirev.2020.103084

CrossRef Full Text | Google Scholar

Peltzer, G., and Tapponnier, P. (1988). Formation and Evolution of Strike-Slip Faults, Rifts, and Basins during the India-Asia Collision: An Experimental Approach. J. Geophys. Res. 93 (B12), 15085–15117. doi:10.1029/jb093ib12p15085

CrossRef Full Text | Google Scholar

Replumaz, A., and Tapponnier, P. (2003). Reconstruction of the Deformed Collision Zone Between India and Asia by Backward Motion of Lithospheric Blocks. J. Geophys. Res. Solid Earth 108 (B6), 2285. doi:10.1029/2001jb000661

CrossRef Full Text | Google Scholar

Replumaz, A., Negredo, A. M., Guillot, S., der Beek, P. V., and Villaseñor, A. (2010). Crustal Mass Budget and Recycling during the India/Asia Collision. Tectonophysics 492 (1-4), 99–107. doi:10.1016/j.tecto.2010.05.023

CrossRef Full Text | Google Scholar

Replumaz, A., Capitanio, F. A., Guillot, S., Negredo, A. M., and Villaseñor, A. (2014). The Coupling of Indian Subduction and Asian Continental Tectonics. Gondwana Res. 26 (2), 608–626. doi:10.1016/j.gr.2014.04.003

CrossRef Full Text | Google Scholar

Schmeling, H., Babeyko, A. Y., Enns, A., Faccenna, C., Funiciello, F., Gerya, T., et al. (2008). A Benchmark Comparison of Spontaneous Subduction Models—Towards a Free Surface. Phys. Earth Planet. Inter. 171 (1-4), 198–223. doi:10.1016/j.pepi.2008.06.028

CrossRef Full Text | Google Scholar

Stampfli, G. M., and Borel, G. D. (2002). A Plate Tectonic Model for the Paleozoic and Mesozoic Constrained by Dynamic Plate Boundaries and Restored Synthetic Oceanic Isochrons. Earth Planet. Sci. Lett. 196 (1-2), 17–33. doi:10.1016/s0012-821x(01)00588-x

CrossRef Full Text | Google Scholar

Stampfli, G. M., Hochard, C., Vérard, C., Wilhem, C., and vonRaumer, J. (2013). The Formation of Pangea. Tectonophysics 593, 1–19. doi:10.1016/j.tecto.2013.02.037

CrossRef Full Text | Google Scholar

Stern, R. J., and Gerya, T. (2018). Subduction Initiation in Nature and Models: A Review. Tectonophysics 746, 173–198. doi:10.1016/j.tecto.2017.10.014

CrossRef Full Text | Google Scholar

Stern, R. J. (2004). Subduction Initiation: Spontaneous and Induced. Earth Planet. Sci. Lett. 226 (3-4), 275–292. doi:10.1016/s0012-821x(04)00498-4

CrossRef Full Text | Google Scholar

Sun, Z., Pei, J., Li, H., Xu, W., Jiang, W., ZhuWang, Z. X., et al. (2012). Palaeomagnetism of Late Cretaceous Sediments from Southern Tibet: Evidence for the Consistent Palaeolatitudes of the Southern Margin of Eurasia Prior to the Collision with India. Gondwana Res. 21 (1), 53–63. doi:10.1016/j.gr.2011.08.003

CrossRef Full Text | Google Scholar

Tapponnier, P., Peltzer, G., Le Dain, A. Y., Armijo, R., and Cobbold, P. (1982). Propagating Extrusion Tectonics in Asia: New Insights from Simple Experiments with Plasticine. Geology 10 (12), 611. doi:10.1130/0091-7613(1982)10<611:petian>2.0.co;2

CrossRef Full Text | Google Scholar

Tapponnier, P., Zhiqin, X., Roger, F., Meyer, B., Arnaud, N., Wittlinger, G., et al. (2001). Oblique Stepwise Rise and Growth of the Tibet Plateau. Science 294, 1671–1677. doi:10.1126/science.105978

PubMed Abstract | CrossRef Full Text | Google Scholar

Torsvik, T. H., and Cocks, L. R. M. (2013). Gondwana from Top to Base in Space and Time. Gondwana Res. 24 (3-4), 999–1030. doi:10.1016/j.gr.2013.06.012

CrossRef Full Text | Google Scholar

Turcotte, D. L., and Schubert, G. (2002). Geodynamics. 2nd ed. New York: Cambridge Univ. Press, 456.

Google Scholar

van Hinsbergen, D. J. J., Steinberger, B., Doubrovine, P. V., and Gassmöller, R. (2011). Acceleration and Deceleration of India-Asia Convergence since the Cretaceous: Roles of Mantle Plumes and Continental Collision. J. Geophys. Res. 116, B06101. doi:10.1029/2010jb008051

CrossRef Full Text | Google Scholar

van Hinsbergen, D. J. J., Lippert, P. C., Dupont-Nivet, G., McQuarrie, N., Doubrovine, P. V., Spakman, W., et al. (2012). Greater India Basin Hypothesis and a Two-Stage Cenozoic Collision between India and Asia. Proc. Natl. Acad. Sci. U.S.A. 109 (20), 7659–7664. doi:10.1073/pnas.1117262109

PubMed Abstract | CrossRef Full Text | Google Scholar

van Hinsbergen, D. J. J., Lippert, P. C., Li, S., Huang, W., Advokaat, E. L., and Spakman, W. (2019). Reconstructing Greater India: Paleogeographic, Kinematic, and Geodynamic Perspectives. Tectonophysics 760, 69–94. doi:10.1016/j.tecto.2018.04.006

CrossRef Full Text | Google Scholar

Wan, B., Wu, F., Chen, L., Zhao, L., Liang, X., Xiao, W., et al. (2019). Cyclical One-Way Continental Rupture-Drift in the Tethyan Evolution: Subduction-Driven Plate Tectonics. Sci. China Earth Sci. 62, 2005–2016. doi:10.1007/s11430-019-9393-4

CrossRef Full Text | Google Scholar

Wang, C., Dai, J., Zhao, X., Li, Y., Graham, S. A., He, D., et al. (2014). Outward-growth of the Tibetan Plateau during the Cenozoic: A Review. Tectonophysics 621, 1–43. doi:10.1016/j.tecto.2014.01.036

CrossRef Full Text | Google Scholar

Wang, H. Q., Ding, L., Cai, F. L., Sun, Y. L., Li, S., Yue, Y. H., et al. (2019). The Latest Jurassic Protoliths of the Sangsang Mafic Schists in Southern Tibet: Implications for the Spatial Extent of Greater India. Gondwana Res. 79, 248–262. doi:10.1016/j.gr.2019.10.008

CrossRef Full Text | Google Scholar

Wang, E. (1997). Displacement and Timing along the Northern Strand of the Altyn Tagh Fault Zone, Northern Tibet. Earth Planet. Sci. Lett. 150 (1-2), 55–64. doi:10.1016/s0012-821x(97)00085-x

CrossRef Full Text | Google Scholar

Wu, F.-Y., Ji, W.-Q., Wang, J.-G., Liu, C.-Z., Chung, S.-L., and Clift, P. D. (2014). Zircon U-Pb and Hf Isotopic Constraints on the Onset Time of India-Asia Collision. Am. J. Sci. 314 (2), 548–579. doi:10.2475/02.2014.04

CrossRef Full Text | Google Scholar

Yakovlev, P. V., and Clark, M. K. (2014). Conservation and Redistribution of Crust during the Indo-Asian Collision. Tectonics 33 (6), 1016–1027. doi:10.1002/2013tc003469

CrossRef Full Text | Google Scholar

Yi, Z., Huang, B., Chen, J., Chen, L., and Wang, H. (2011). Paleomagnetism of Early Paleogene Marine Sediments in Southern Tibet, China: Implications to Onset of the India Asia Collision and Size of Greater India. Earth Planet. Sci. Lett. 309, 153–165. doi:10.1016/j.epsl.2011.07.001

CrossRef Full Text | Google Scholar

Yin, A., and Harrison, T. M. (2000). Geologic Evolution of the Himalayan-Tibetan Orogen. Annu. Rev. Earth Planet. Sci. 28 (1), 211–280. doi:10.1146/annurev.earth.28.1.211

CrossRef Full Text | Google Scholar

Yin, A., Rumelhart, P. E., Butler, R., Cowgill, E., Harrison, T. M., Foster, D. A., et al. (2002). Tectonic History of the Altyn Tagh Fault System in Northern Tibet Inferred from Cenozoic Sedimentation. Geol. Soc. Am. Bull. 114 (10), 1257–1295. doi:10.1130/0016-7606(2002)114<1257:thotat>2.0.co;2

CrossRef Full Text | Google Scholar

Zhang, L., Wang, Y., and Li, Z.-H. (2022). Where Is the Missing Felsic Crust of Greater Indian Continent? Commun. Earth Environ. doi:10.21203/rs.3.rs-227521/v1

CrossRef Full Text | Google Scholar

Zheng, Y., and Wu, F. (2018). The Timing of Continental Collision between India and Asia. Sci. Bull. 63 (24), 1649–1654. doi:10.1016/j.scib.2018.11.022

CrossRef Full Text | Google Scholar

Zhong, X. Y., and Li, Z. H. (2020). Subduction Initiation during Collision‐induced Subduction Transference: Numerical Modeling and Implications for the Tethyan Evolution. J. Geophys. Res. Solid Earth 125 (2), e2019JB019288. doi:10.1029/2019jb019288

CrossRef Full Text | Google Scholar

Zhong, X., and Li, Z. H. (2022). Wedge‐Shaped Southern Indian Continental Margin Without Proper Weakness Hinders Subduction Initiation. Geochem. Geophys. Geosyst. 23, e2021GC009998. doi:10.1029/2021GC009998

CrossRef Full Text | Google Scholar

Zhou, J., and Su, H. (2019). Site and Timing of Substantial India‐Asia Collision Inferred from Crustal Volume Budget. Tectonics 38, 2275–2290. doi:10.1029/2018tc005412

CrossRef Full Text | Google Scholar

Zhu, D. C., Zhao, Z. D., Niu, Y., Mo, X. X., Chung, S. L., Hou, Z. Q., et al. (2011). The Lhasa Terrane: Record of a Microcontinent and its Histories of Drift and Growth. Earth Planet. Sci. Lett. 301 (1-2), 241–255. doi:10.1016/j.epsl.2010.11.005

CrossRef Full Text | Google Scholar

Zhu, D.-C., Zhao, Z.-D., Niu, Y., Dilek, Y., Hou, Z.-Q., and Mo, X.-X. (2013). The Origin and Pre-Cenozoic Evolution of the Tibetan Plateau. Gondwana Res. 23 (4), 1429–1454. doi:10.1016/j.gr.2012.02.002

CrossRef Full Text | Google Scholar

Zhu, R., Zhao, P., and Zhao, L. (2021). Tectonic Evolution and Geodynamics of the Neo-Tethys Ocean. Sci. China Earth Sci. 65, 1–24. doi:10.1007/s11430-021-9845-7

CrossRef Full Text | Google Scholar