- Center for High Pressure Science and Technology Advanced Research, Beijing, China
The weak x-ray scattering of hydrogen (H) has brought major challenges to the characterization of superionic transitions in high-pressure ice, hydrides, and hydroxides. Combining first-principles molecular dynamics and simulated nuclear magnetic resonance (NMR) spectroscopy, we investigated the behavior of the hydroxyl bonding and structural transitions in the hydrous FeO2H between 300 and 2750 K and up to 130 GPa. Evidence show that an intermediate plastic state with regional H diffusion and anharmonic O-H vibration exists in between the ordinary solid and the superionic phase. The intermediate state features asymmetric hydrogen bonds and anharmonic vibrations, which are readily distinguished from the high-temperature superionic phase. Our work shows NMR is a more sensitive probe to detect H diffusion in superionic solids even in the extreme conditions of Earth’s deep interiors.
Introduction
A substantial portion of H in the Universe may diffuse like a liquid in superionic phases (Cavazzoni et al., 1999; Liu et al., 2020; Cong Liu et al., 2019; Millot et al., 2019; Millot et al., 2018). For example, superionic ice is predicted to be a dominant component of giant icy planets like Uranus and Neptune (Cavazzoni et al., 1999). Superionic hydrous mineral phases are also found to be stable in Earth’s deep lower mantle (Hou et al., 2021; Hu and Mao, 2021). The superionization is signified by the exceptionally high H diffusion rate and soaring ionic conductivity as the H atom moves freely in the host lattice and generates protonic currents. Although the conception of H in the superionic phase is postulated theoretically in the 1980s (Demontis et al., 1988), its optical properties, structural transition, and electrical conductivity are only determined by experiments very recently (Millot et al., 2019; Millot et al., 2018; Zhuang et al., 2022a). Properties like the evolution of H bonding, core-electron interaction, and chemical environments under high pressure-temperature (P-T) conditions are still inconclusive.
The major challenge to study the superionic phase is the experimental probe. Traditional x-ray probes, such as x-ray diffraction (XRD) have been employed as routine tools in characterizing structures under pressure (Mao et al., 2016). However, H is the lightest element, which scatters a very limited amount of x-ray. Even synchrotron-based XRD is unable to measure H motion but only the solid crystalline lattice in the superionic phase (Millot et al., 2018). In short, the behavior of H, particularly as a function of temperature, is still difficult to be described by experiments. Pioneering works used shock compression and optical measurements to detect the onset of superionic ice, but the P-T points have to follow the shock Hugoniot curve (Coppari et al., 2021; Millot et al., 2019). It is also possible to conduct electrical conductivity measurement and laser heating in a diamond anvil cell (Zhuang et al., 2022b) to mark the superionic transition. However, factors like external electrical field and temperature gradient make such analysis much more challenging than other systems (Futera et al., 2020; Hou et al., 2021).
Nuclear magnetic resonance (NMR) spectroscopy is a versatile means to study the structural environments of solids and liquids (Harris, 2004). Owing to the invention of the electromagnetic Lenz lens, it is possible to refine the NMR resonator in a modified diamond anvil cell (Meier et al., 2017; Meier et al., 2021). One important advantage of NMR is that it detects the chemical environments of H with much higher accuracy than XRD (Chen et al., 2020). Also, first-principles calculations can obtain reliable NMR parameters, which are predictable to phase transitions relating to H (Holmes et al., 2017; Meier et al., 2019). For example, Meier et al. 2019 investigated the hydrogen interactions of FeH up to 202 GPa using NMR and revealed the formation of a caged H framework around Fe atoms. Both their calculation and experiments showed that the phase transition induced by H motion can be distinguished by chemical shielding in different structures.
Goethite, or α-FeO2H, is a key component of the banded iron formations (Bekker et al., 2010), and it exhibits a set of structural phase transitions in Earth’s deep interiors (Lu and Chen, 2018; Thompson et al., 2020). FeOOH is thus a potential carrier of water throughout the mantle (Zhuang et al., 2022a). The pyrite-type FeO2H is stable at subduction slabs P-T conditions at 1800 km depth or deeper (Hu and Liu, 2021). Under warmer geothermal conditions, for example, at 81 GPa and 2100 K, a recent study has shown FeO2H decomposes to mixed valence iron oxides and oxygen-rich fluids (Huang and Hu, 2022; Koemets et al., 2021a). The chemical stability of FeO2H may extend to deeper regions above the core-mantle boundary by incorporating Mg (Hu et al., 2021) or inertia elements like He or Xe into the pyrite-type lattice (Peng et al., 2020; Zhang et al., 2018). At the lowermost mantle, the phase transition and crystal chemistry of FeO2H are crucial to the interaction between the mantle and the core and may contribute to the light element budget in the outer core (Mao et al., 2017; Nishi et al., 2017). It is, therefore, necessary to study the high P-T structural transformation of FeO2H at relevant lower mantle conditions.
In this work, we focused on the temperature-induced transition of pyrite-type FeO2H (Hu et al., 2016; Nishi et al., 2017), which is found to enter the conductive superionic phase at above 80 GPa and ∼1800 K (Hou et al., 2021; Hu and Mao, 2021). The temperature resolved NMR spectra and their corresponding structures are calculated by first-principles calculation and molecular dynamics (MD). Prior to the superionic state, FeO2H exhibits an intermediate phase with broadened NMR peak and anharmonic motion and regional diffusion of H. The hierarchical changes of NMR peaks can be used to precisely locate the transition boundaries of the superionic phase in the experiment.
Computational Methods
Although H in the hydrous FeO2H is reported to be nonstoichiometric (Hu et al., 2017; Tang et al., 2021), we considered the full occupation of H in this work to simplify the structural model. The previous spectroscopic experiment also reported that the presence of H has a minor effect on the crystal chemistry of the system of FeO2-FeO2H (Liu et al., 2019). Our system consisted of 32 FeO2H units in a 2 × 2 × 2 supercell. The simulations are based on density functional theory in the PBE approximation (Perdew et al., 1996). We used the projector augmented wave (PAW) method (Kresse and Joubert, 1999) as implemented in Vienna’s ab initio simulation package (Kresse and Furthmüller, 1996). The core radii are Fe: 1.302 Å (3s23p2), O: 0.741 Å (2s22p4), and H: 0.370 Å (1s1). The basis-set energy cutoff is set as 700 eV, which is found sufficient to converge the total energy and pressure to within 5 meV/atom and ±0.5 GPa. Born–Oppenhiemer molecular dynamics calculations are performed in the canonical ensemble using the Nose–Hoover thermostat (Hoover, 1985) and allowed to run for 20–30 picoseconds (ps) with 1-femtosecond (fs) time step. Since H is extremely mobile under high P-T conditions, we also run the test at 0.5 fs with longer trajectories at selected conditions. The structural features obtained from shorter MD timestep are consistent with the one using 1 fs MD timestep. We, therefore, used 1 fs timestep throughout the simulation. The Brillouin zone is sampled only at the Gamma point for MD simulation. It generally takes 5 ps to heat the system to the target temperature. After reaching the temperature, we adjusted lattice parameters to ensure that the stress is pseudo-hydrostatic along all axes, and the system is equilibrated at desired pressures (with ±2 GPa uncertainty). Thermal equilibrium between ions and electrons is judged by the Mermin functional (Mermin, 1965). The adjusting process takes another 5–10 ps. After fully equilibrated, the last 10 ps run is used for data production.
NMR shielding is calculated by using the gauge including the projector augmented wave method (Bonhomme et al., 2012; Pickard and Mauri, 2001). Increased cut-off energy of 900 eV and a k-point spacing of 0.3 Å−1 are used. A denser k-point mesh with a spacing of 0.15 Å−1 is also tested, but it does not generate qualitative different results. In our simulation, we extracted snapshots from an MD trajectory and average NMR shielding from those configurations (Dumez and Pickard, 2009). The snapshots are taken every 200 fs, corresponding to a total number of 50 configurations from the production run. The relatively longer spacing between snapshots is used to ensure they are time uncorrelated (Allen and Tildesley, 1987).
Temperature-Resolved First-Principles MD
Following our previous work (Hou et al., 2021), we conducted high P-T first-principles MD at 70, 100, and 130 GPa, and temperatures up to 2750 K. We first monitored the mean-squared displacements of Fe, O, and H atoms, which have been commonly used to determine the solid-superionic transition. Similar to our previous work, the phase boundary between the ordered solid and the superionic phase followed a positive dP/dT slope, and H atoms exhibited cross-boundary diffusion when temperatures are above 2000 K (Hou et al., 2021). For the superionic state, we took snapshots along the trajectory which clearly showed the crystal lattice of superionic FeO2H is filled with fast-moving protons (Figure 1). The chemical shift δ, which is related to the isotropic NMR shielding σiso by an arbitrary reference σref: was derived at each temperature:
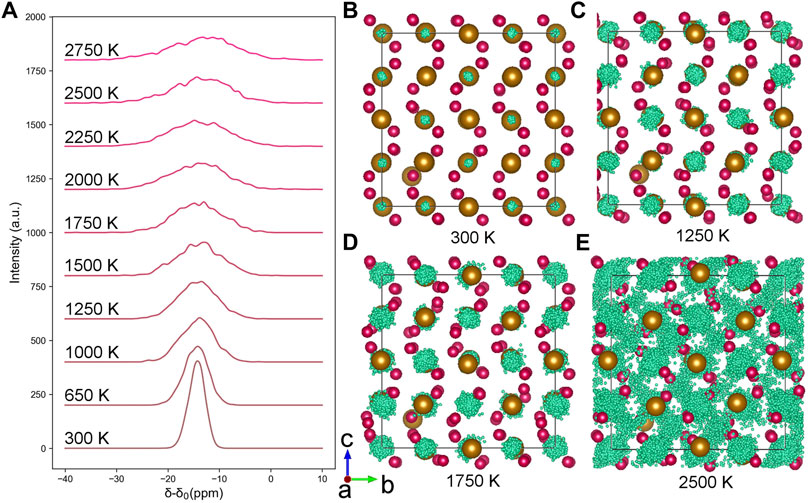
FIGURE 1. Evolution of NMR spectroscopy and their corresponding structures. (A). Calculated NMR spectroscopy at 100 GPa and up to 2750 K. (B–E) Selected structures at 300, 1250, 1750, and 2,500 K. Hydrogen diffusion increases substantially at higher temperatures.
In contrast to the superionic transition determined from H diffusion, the shape of the NMR peak is substantially broadened at much higher temperatures. For example, the full width at half maximum at 1000 K, 100 GPa increased by a factor of four compared to the one at 300 K (Figures 1A, 2). This is approximately 1,000 K before it enters the previous known superionic state (Hou et al., 2021). It is worth noting that at three individual pressures of 70, 100, and 130 GPa, such temperature-induced broadening all occurred between 650 and 1,000 K (Figure 2), and the transition turns out to be insensitive to a pressure similar to ice (Bove et al., 2013). From the Clausius–Clapeyron relation, the sharp slope dP/dT = ΔS/ΔV indicated that the transition induces negligible volume change, which is the signature of a second-order phase transition. Within the P-T regions of this work, they formed a nearly horizontal boundary between 650 and 1,000 K. Below this temperature all the H atoms are symmetrically bonded with two O atoms. Such a symmetric bond corresponds to the single, sharp NMR peak. When the center of the peak is almost unchanged as the temperature is raised to 1,000 K and above, the broadened NMR peak is regarded as an assembly of multiple split peaks with comparable chemical shielding. The shape of the broad peak is similar to that found in glass (Youngman, 2018), suggesting the type of H bonding has become variant.
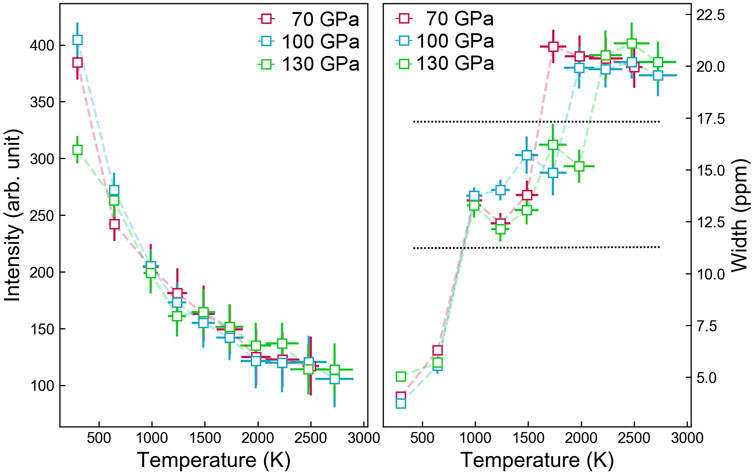
FIGURE 2. Trace of H chemical shift under pressure and temperature. The left and right panels are the intensity and width of the NMR peak of FeO2H, respectively. The hierarchical changes in peak width are due to the temperature response of the O-H-O hydrogen bond, which evolves from symmetric to asymmetric bonding and eventually to the breakdown.
Local Environment of H
We are then motivated to construct the local chemical environment of H in variable temperatures. Angular distribution of O-H-O is a direct probe to study the evolution of H bonds with temperature. In the case of symmetric H bonding, the angle formed by O-H-O bonds should be 180°. However, H bonds in FeO2H connect two FeO6 polyhedra and thus are inevitably affected by the crystal field. At 100 GPa and 300 K (Figures 3A, D), peak values are centered around 170°, which is a little bit off the ideal 180°. In a quasi-harmonic model, the thermal vibration of atoms caused the distribution of angles to follow the normal distribution (Figure 3D). The normal distribution is valid until the temperature raised above 1,000 K, where the second peak of angular distribution occurred around 110° (Figure 3C). This means the vibration of the O-H bond is no longer described by the classic harmonic vibration model. When H atoms gain enough kinetic energy to overcome the harmonic potential well, they are still constrained by neighboring O atoms and move regionally in an anharmonic potential well (Figures 1C, 4). Unlike the superionic state in which H atoms perform cross-boundary diffusion, this intermediate state can be regarded as an anharmonic state or plastic state described by the motion of protonic H freely moving around their center of mass. This plastic state has been well documented in helium ammonia compounds under high pressure and high temperature (Liu et al., 2020).
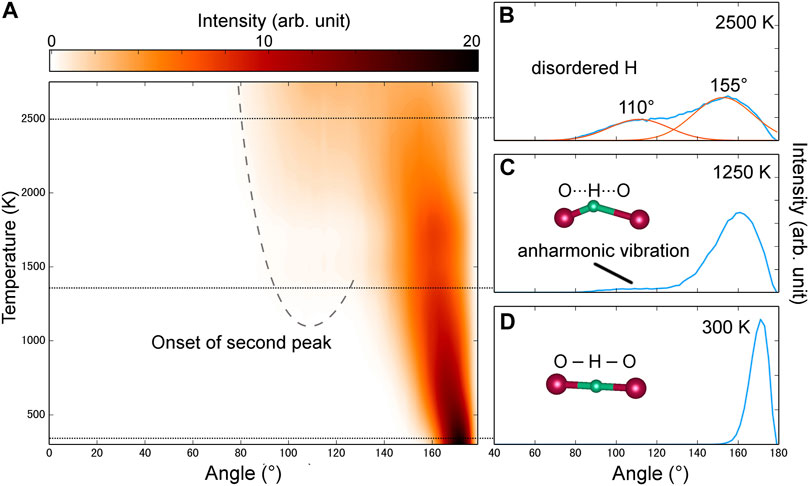
FIGURE 3. Angular distribution of O-H-O bonding at 100 GPa and various temperatures. (A) Interpolated contour. High-intensity distributions are generally in darker colors. We observed an increased number of angles fell around 105° in the anharmonic solid and the superionic state. (B–D) Selected angular distribution spectroscopy at 2,500, 1250, and 300 K, respectively. In b, the angular distribution is fitted to Gaussian functions with R = 0.99. The fitted Gaussian is located at 110° and 155°. Inset figures are schematic representation of hydrogen bonding at different angles.
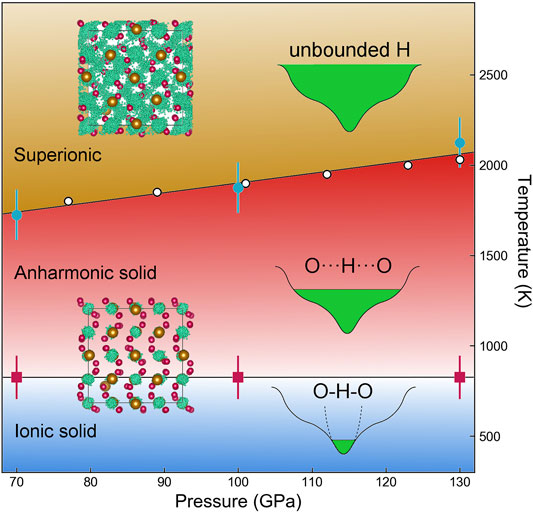
FIGURE 4. Phase diagram of FeO2H on the basis of the motion of hydrogen bond. Open circles are based on the mean-square displacement of H in our previous work (Hou et al., 2021). Solid squares are on the basis of the NMR peak width.
The peak near 110° in the angular distribution continues to grow and becomes significant in the superionic state. It is worth pointing out that we set a threshold of 2.0 Å in O-H bond length for searching H bonding, which is usually large enough for a compressed system. Considering the interstitial O···O distance is ∼2.1 Å at 100 GPa and 2,500 K, the cutoff angle in the searching radar is ∼60°. We can possibly trace the motion of H in the superionic phase by fitting the angular distribution into two Gaussian peaks, which are located at 110° and 155°, respectively (Figure 3B). In a system with rapidly moving H, very few protons are concentrated at the free-standing sites of the lattice, which had small O-H-O angles (e.g. <90°) and non-interacted O-H bonds. However, they preferred to stay in the original space in between two FeO6 polyhedra while moving to neighboring sites by hopping. In this scenario, the H atom is still weakly interacted with at least one O atom.
Discussion and Conclusion
Routine high-pressure probes like XRD and electrical conductivity measurement can identify the onset of the superionic state caused by H diffusion. However, they fail to directly detect the local chemical environment of H, which is critical in describing the high P-T phase transitions. Neutron scattering would be an alternative approach; however, it is too expensive to conduct neutron experiments at the sensitive pressure of the aforementioned superionic phases (Hattori et al., 2019). In short, for its high sensitivity, NMR spectroscopy would be a perfect tool for measuring the H site and describing H motion under high-pressure conditions.
Our simulation is performed on the stoichiometric system of FeO2H, in which H takes full occupation. This is an approximation to the experimental observation that H becomes highly mobile under high-temperature conditions (Tang et al., 2021). In laboratory experiments, the content of H is reported to be fully stoichiometric (Nishi et al., 2017), nearly stoichiometric (Yuan et al., 2018), or partially dehydrated (Koemets et al., 2021b), depending on the P-V and sample conditions (e.g., coating and pressure medium). The variant H contents have become a signature of dense hydrous materials which modulate the mineral structural transition and local redox condition. For example, the superionic transition temperature of FeO2H is lowered (e.g., by ∼150 K at 100 GPa) after losing a portion of H (Hou et al., 2021). Such nonstoichiometry is likely to have similar effects on the transition boundary of the plastic state. The onset temperature of the plastic state might be lower than our prediction in the experiment.
Our computational work has not only verified the superionic transition previously determined by experiment but also identified a harmonic to plastic state transition in hydrous FeO2H. The results are consistent with Raman spectroscopy (Hou et al., 2021), which shows hydroxyl mode softening even at ambient temperature and high pressure. While superionic transition in FeO2H and probably other hydroxides usually occur at high temperatures, they may have precursor structures with fragile H bonding. The transition from ordered solid, via plastic state to the superionic phase, is in line with the archetypal ice water. Compared with plastic ice (Bove et al., 2013), hydrous minerals like FeO2H may also feature higher shear viscosity under moderate heating. Our simulation suggested the set of transitions is readily captured by the change in the NMR spectrum. The use of NMR spectroscopy will be more sensitive than x-ray probes in characterizing potential superionic materials. We proposed the plastic and superionic phase transition would be a universal phenomenon in the high-pressure ice, hydrides, and hydroxides.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author Contributions
QH conceived the project and carried out the theoretical simulation. QH and MT performed the data analysis and wrote the manuscript.
Funding
This work was supported by NSFC Grant no. 42150101. QH was supported by a Tencent Xplorer Prize (XPLORER-2020-1013).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bekker, A., Slack, J. F., Planavsky, N., Krapez, B., Hofmann, A., Konhauser, K. O., et al. (2010). Iron Formation: The Sedimentary Product of a Complex Interplay Among Mantle, Tectonic, Oceanic, and Biospheric Processes. Econ. Geol. 105, 467–508. doi:10.2113/gsecongeo.105.3.467
Bonhomme, C., Gervais, C., Babonneau, F., Coelho, C., Pourpoint, F., Azaïs, T., et al. (2012). First-Principles Calculation of NMR Parameters Using the Gauge Including Projector Augmented Wave Method: A Chemist's Point of View. Chem. Rev. 112, 5733–5779. doi:10.1021/cr300108a
Bove, L. E., Klotz, S., Strässle, T., Koza, M., Teixeira, J., and Saitta, A. M. (2013). Translational and Rotational Diffusion in Water in the Gigapascal Range. Phys. Rev. Lett. 111, 185901. doi:10.1103/physrevlett.111.185901
Cavazzoni, C., Chiarotti, G. L., Scandolo, S., Tosatti, E., Bernasconi, M., and Parrinello, M. (1999). Superionic and Metallic States of Water and Ammonia at Giant Planet Conditions. Science 283, 44–46. doi:10.1126/science.283.5398.44
Chen, D., Gao, W., and Jiang, Q. (2020). Distinguishing the Structures of High-Pressure Hydrides with Nuclear Magnetic Resonance Spectroscopy. J. Phys. Chem. Lett. 11, 9439–9445. doi:10.1021/acs.jpclett.0c02657
Cong Liu, C., Gao, H., Wang, Y., Needs, R. J., Pickard, C. J., Sun, J., et al. (2019). Multiple Superionic States in Helium-Water Compounds. Nat. Phys. 15, 1065–1070. doi:10.1038/s41567-019-0568-7
Coppari, F., Smith, R. F., Wang, J., Millot, M., Kim, D., Rygg, J. R., et al. (2021). Implications of the Iron Oxide Phase Transition on the Interiors of Rocky Exoplanets. Nat. Geosci. 14, 121–126. doi:10.1038/s41561-020-00684-y
Demontis, P., LeSar, R., and Klein, M. L. (1988). New High-Pressure Phases of Ice. Phys. Rev. Lett. 60, 2284–2287. doi:10.1103/physrevlett.60.2284
Dumez, J.-N., and Pickard, C. J. (2009). Calculation of NMR Chemical Shifts in Organic Solids: Accounting for Motional Effects. J. Chem. Phys. 130, 104701. doi:10.1063/1.3081630
Futera, Z., Tse, J. S., and English, N. J. (2020). Possibility of Realizing Superionic Ice VII in External Electric Fields of Planetary Bodies. Sci. Adv. 6, eaaz2915. doi:10.1126/sciadv.aaz2915
Harris, R. K. (2004). NMR Crystallography: the Use of Chemical Shifts. Solid State Sci. 6, 1025–1037. doi:10.1016/j.solidstatesciences.2004.03.040
Hattori, T., Sano-Furukawa, A., Machida, S., Abe, J., Funakoshi, K., Arima, H., et al. (2019). Development of a Technique for High Pressure Neutron Diffraction at 40 GPa with a Paris-Edinburgh Press. High Press. Res. 39, 417–425. doi:10.1080/08957959.2019.1624745
Holmes, S. T., Iuliucci, R. J., Mueller, K. T., and Dybowski, C. (2017). Semi-empirical Refinements of Crystal Structures Using 17O Quadrupolar-Coupling Tensors. J. Chem. Phys. 146, 064201. doi:10.1063/1.4975170
Hoover, W. G. (1985). Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 31, 1695–1697. doi:10.1103/physreva.31.1695
Hou, M., He, Y., Jang, B. G., Sun, S., Zhuang, Y., Deng, L., et al. (2021). Superionic Iron Oxide-Hydroxide in Earth's Deep Mantle. Nat. Geosci. 14, 174–178. doi:10.1038/s41561-021-00696-2
Hu, Q., Kim, D. Y., Yang, W., Yang, L., Meng, Y., Zhang, L., et al. (2016). FeO2 and FeOOH under Deep Lower-Mantle Conditions and Earth's Oxygen-Hydrogen Cycles. Nature 534, 241–244. doi:10.1038/nature18018
Hu, Q., Kim, D. Y., Liu, J., Meng, Y., Yang, L., Zhang, D., et al. (2017). Dehydrogenation of Goethite in Earth's Deep Lower Mantle. Proc. Natl. Acad. Sci. U.S.A. 114, 1498–1501. doi:10.1073/pnas.1620644114
Hu, Q., Liu, J., Chen, J., Yan, B., Meng, Y., Prakapenka, V. B., et al. (2021). Mineralogy of the Deep Lower Mantle in the Presence of H2O. Natl. Sci. Rev. 8, nwaa098. doi:10.1093/nsr/nwaa098
Hu, Q., and Liu, J. (2021). Deep Mantle Hydrogen in the Pyrite-type FeO2-FeO2H System. Geosci. Front. 12, 975–981. doi:10.1016/j.gsf.2020.04.006
Hu, Q., and Mao, H.-k. (2021). Role of Hydrogen and Proton Transportation in Earth's Deep Mantle. Matter Radiat. Extrem. 6, 068101. doi:10.1063/5.0069643
Huang, S., and Hu, Q. (2022). Medium-range Structure Motifs of Complex Iron Oxides. J. Appl. Phys. 131, 070902. doi:10.1063/5.0082503
Jin Liu, J., Hu, Q., Bi, W., Yang, L., Xiao, Y., Chow, P., et al. (2019). Altered Chemistry of Oxygen and Iron under Deep Earth Conditions. Nat. Commun. 10, 153. doi:10.1038/s41467-018-08071-3
Koemets, E., Fedotenko, T., Khandarkhaeva, S., Bykov, M., Bykova, E., Thielmann, M., et al. (2021a). Chemical Stability of FeOOH at High Pressure and Temperature, and Oxygen Recycling in Early Earth History**. Eur. J. Inorg. Chem. 2021, 3048–3053. doi:10.1002/ejic.202100274
Koemets, E., Leonov, I., Bykov, M., Bykova, E., Chariton, S., Aprilis, G., et al. (2021b). Revealing the Complex Nature of Bonding in the Binary High-Pressure Compound FeO2. Phys. Rev. Lett. 126, 106001. doi:10.1103/physrevlett.126.106001
Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169
Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/physrevb.59.1758
Liu, C., Gao, H., Hermann, A., Wang, Y., Miao, M., Pickard, C. J., et al. (2020). Plastic and Superionic Helium Ammonia Compounds under High Pressure and High Temperature. Phys. Rev. X 10, 021007. doi:10.1103/physrevx.10.021007
Lu, C., and Chen, C. (2018). High-pressure Evolution of Crystal Bonding Structures and Properties of FeOOH. J. Phys. Chem. Lett. 9, 2181–2185. doi:10.1021/acs.jpclett.8b00947
Mao, H.-K., Chen, B., Chen, J., Li, K., Lin, J.-F., Yang, W., et al. (2016). Recent Advances in High-Pressure Science and Technology. Matter Radiat. Extrem. 1, 59–75. doi:10.1016/j.mre.2016.01.005
Mao, H.-K., Hu, Q., Yang, L., Liu, J., Kim, D. Y., Meng, Y., et al. (2017). When Water Meets Iron at Earth's Core-Mantle Boundary. Natl. Sci. Rev. 4, 870–878. doi:10.1093/nsr/nwx109
Meier, T., Wang, N., Mager, D., Korvink, J. G., Petitgirard, S., and Dubrovinsky, L. (2017). Magnetic Flux Tailoring through Lenz Lenses for Ultrasmall Samples: A New Pathway to High-Pressure Nuclear Magnetic Resonance. Sci. Adv. 3, eaao5242. doi:10.1126/sciadv.aao5242
Meier, T., Aslandukova, A., Trybel, F., Laniel, D., Ishii, T., Khandarkhaeva, S., et al. (2021). In Situ High-Pressure Nuclear Magnetic Resonance Crystallography in One and Two Dimensions. Matter Radiat. Extrem. 6, 068042. doi:10.1063/5.0065879
Meier, T., Trybel, F., Khandarkhaeva, S., Steinle-Neumann, G., Chariton, S., Fedotenko, T., et al. (2019). Pressure-induced Hydrogen-Hydrogen Interaction in Metallic FeH Revealed by NMR. Phys. Rev. X 9, 031008. doi:10.1103/physrevx.9.031008
Mermin, N. D. (1965). Thermal Properties of the Inhomogeneous Electron Gas. Phys. Rev. 137, A1441–A1443. doi:10.1103/physrev.137.a1441
Millot, M., Hamel, S., Rygg, J. R., Celliers, P. M., Collins, G. W., Coppari, F., et al. (2018). Experimental Evidence for Superionic Water Ice Using Shock Compression. Nat. Phys. 14, 297–302. doi:10.1038/s41567-017-0017-4
Millot, M., Coppari, F., Rygg, J. R., Correa Barrios, A., Hamel, S., Swift, D. C., et al. (2019). Nanosecond X-Ray Diffraction of Shock-Compressed Superionic Water Ice. Nature 569, 251–255. doi:10.1038/s41586-019-1114-6
Nishi, M., Kuwayama, Y., Tsuchiya, J., and Tsuchiya, T. (2017). The Pyrite-type High-Pressure Form of FeOOH. Nature 547, 205–208. doi:10.1038/nature22823
Peng, F., Song, X., Liu, C., Li, Q., Miao, M., Chen, C., et al. (2020). Xenon Iron Oxides Predicted as Potential Xe Hosts in Earth's Lower Mantle. Nat. Commun. 11, 5227. doi:10.1038/s41467-020-19107-y
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865
Pickard, C. J., and Mauri, F. (2001). All-electron Magnetic Response with Pseudopotentials: NMR Chemical Shifts. Phys. Rev. B 63, 245101. doi:10.1103/physrevb.63.245101
Tang, R., Liu, J., Kim, D. Y., Mao, H.-k., Hu, Q., Yang, B., et al. (2021). Chemistry and P-V-T Equation of State of FeO2Hx at the Base of Earth’s Lower Mantle and Their Geophysical Implications. Sci. Bull. 66, 1954–1958. doi:10.1016/j.scib.2021.05.010
Thompson, E. C., Davis, A. H., Brauser, N. M., Liu, Z., Prakapenka, V. B., and Campbell, A. J. (2020). Phase Transitions in ε-FeOOH at High Pressure and Ambient Temperature. Am. Mineral. 105, 1769–1777. doi:10.2138/am-2020-7468
Youngman, R. (2018). NMR Spectroscopy in Glass Science: A Review of the Elements. Materials 11, 476. doi:10.3390/ma11040476
Yuan, L., Ohtani, E., Ikuta, D., Kamada, S., Tsuchiya, J., Naohisa, H., et al. (2018). Chemical Reactions between Fe and H 2 O up to Megabar Pressures and Implications for Water Storage in the Earth's Mantle and Core. Geophys. Res. Lett. 45, 1330–1338. doi:10.1002/2017gl075720
Zhang, J., Lv, J., Li, H., Feng, X., Lu, C., Redfern, S. A. T., et al. (2018). Rare Helium-Bearing Compound FeO2He Stabilized at Deep-Earth Conditions. Phys. Rev. Lett. 121, 255703. doi:10.1103/physrevlett.121.255703
Zhuang, Y., Li, J., Lu, W., Yang, X., Du, Z., and Hu, Q. (2022a). High Temperature Melting Curve of Basaltic Glass by Laser Flash Heating. Chin. Phys. Lett. 39, 020701. doi:10.1088/0256-307x/39/2/020701
Keywords: hydrous mineral, superionic phase, plastic state, nuclear magnetic resonance spectroscopy, iron oxy-hydroxide
Citation: Hu Q and Tang M (2022) Tracing the Anharmonicity and Superionic Phase Transition of Hydrous FeO2H. Front. Earth Sci. 10:913122. doi: 10.3389/feart.2022.913122
Received: 05 April 2022; Accepted: 02 May 2022;
Published: 06 June 2022.
Edited by:
Baohua Zhang, Zhejiang University, ChinaReviewed by:
Zhicheng Jing, Southern University of Science and Technology, ChinaDawei Fan, Institute of Geochemistry (CAS), China
Copyright © 2022 Hu and Tang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qingyang Hu, cWluZ3lhbmcuaHVASHBzdGFyLmFjLmNu
 Qingyang Hu
Qingyang Hu Mingxue Tang
Mingxue Tang