Quantitative Precipitation Estimation Model Integrating Meteorological and Geographical Factors at Multiple Spatial Scales

Heavy precipitation tends to cause mountain torrents, urban waterlogging and other disasters. It poses a serious threat to people’s life and property safety. Therefore, real-time quantitative precipitation estimation is especially important to keep track of precipitation changes and reduce negative impacts. However, high-resolution and high-accuracy quantitative precipitation estimation is a challenging task due to the complex spatial and temporal variability of microphysics in precipitation processes. Previous studies have focused only on small-scale radar reflectivity factors above rain gauges and did not pay enough attention to the contribution of covariates to model performance. Meteorological and geographical factors play an important role in rain process, so these factors are taken into account during our research. In this study, a quantitative precipitation estimation model that can employ multi-scale radar reflectivity factors and fuse meteorological and geographical factors is proposed to further improve precipitation accuracy. In addition, we propose the muti-scale self-attention (MS-SA) module that can further utilize information at multiple spatial scales to improve the accurate precipitation estimation. The proposed model reduced the root mean square error of precipitation estimation by 83.8% compared to the conventional Z-R relationship that correlates the rainfall and radar reflectivity factors, $\text{i}.\text{e}., Z=a{R}^b$, and by 43.7, 24.6, and 22.7% compared to the back propagation neural network (BPNN), convolutional neural network (CNN), and convolutional neural network with the addition of meteorological factors and geographical factors as covariates in the proposed model, respectively. Therefore, we can conclude that multi-scale radar reflectivity factors fused with meteorological and geographical factors can produce more accurate precipitation estimation.

Introduction

Rainfall is a fundamental part of the natural water cycle and is necessary for the continuation of all life in nature. In recent years, as global warming has intensified, the atmosphere contains higher levels of water vapor and the frequency and intensity of heavy precipitation events have increased significantly (Groisman et al., 2005; Cremonini and Tiranti, 2018; Giang, 2021; Zhao et al., 2021). This inevitably leads to natural disasters such as floods and has many indirect negative effects on human social activities such as transportation and agriculture (Iwashima and Yamamoto, 1993; Ramos et al., 2005; Sun and Huang, 2011; Lee et al., 2014; Wu J. et al., 2020; Paxton et al., 2021). Therefore, quantitative precipitation estimation (QPE) based on weather radar with high spatial and temporal resolution can be of great help for decision makers to make timely and correct decisions with great reference value, which in turn also plays an important role in mitigating urban flash floods and warning extreme weather (Morin and Gabella, 2007; Germann et al., 2009; Chen and Chandrasekar, 2015; Gou et al., 2018; Lu et al., 2019). Real-time and high-precision QPE is also continuously studied by meteorologists as an important topic (Sadeghi et al., 2019; Wu H. et al., 2020). Rain gauges are a direct means of measuring rainfall and their measurements are often used in QPE as a label for the ground truth value at a fixed location. However, rain gauge networks suffer from low spatial density, uneven distribution, inconsistent historical recording periods, and high costs in the task of measuring the depth of precipitation in a certain area (Fan et al., 2021). Therefore, rainfall measurements in a certain region based only on rain gauges are not spatially representative. Weather radar, as an indirect means of measuring rainfall, is commonly used to observe the spatial structure characteristics of microscopic particles in the high-dimensional space of precipitation and rainfall fields. Furthermore, in the business of Radar Quantitative Precipitation Estimation (RQPE), weather radar has the advantages of high spatial and temporal resolution, wide geographical coverage, and real-time data transmission (Berne and Krajewski, 2013; Tian et al., 2020). It should be noted that its performance depends on the physical model of the raindrop size distribution and the relationship established by the radar parameters and the physical model. Thus, due to the above-mentioned advantages of radar, and the nature of the spatial distribution of the radar network, it is able to count and model extreme weather and the natural hazards it causes on both spatial and temporal scales. This compensates for the deficiencies of the rain gauge network (Yang et al., 2004; Delrieu et al., 2009; Germann et al., 2009). However, estimating precipitation by radar is a complex process, which is mainly caused by the complex spatiotemporal motion and variation of microscopic particles in the precipitation process, as well as the poor measurement accuracy due to multiple error sources in the radar measurement process (Berne and Krajewski, 2013; Chen et al., 2019). The traditional quantitative precipitation estimation (QPE) algorithm uses the relationship between weather radar echo intensity and rainfall intensity, i.e., the Z-R relationship where Z is the radar echo intensity, R is the rainfall intensity, to invert the rainfall amount of a rainfall field (Legates, 2000; Rosenfeld and Ulbrich, 2003; Barros and Prat, 2009). The empirical coefficients $a$ and $b$ in the Z-R relationship are influenced by many environmental factors, such as weather conditions, geography, etc. It is fundamentally influenced by the spectral characteristics of raindrop size. Therefore, the range and environment to which a fixed Z-R relationship can be adapted is greatly limited. The same Z-R relationship can produce great errors in different areas, especially in mountainous areas and under strong convective weather. Previous studies have mainly focused on increasing the accuracy of the Z-R relationship and trying to break out of this dilemma. Alfieri et al. (2010) considered the Z-R relationship to be closely related to time and they improved it to be constantly updated with time. Specially, they took all available Z-R relationship pairs for each time step to correct the parameters and then adjusted the power law equation to convert the radar reflectivity factor measurements into rainfall rates. Wu et al. (2018) suggested that the echo top height can reflect the stage of storm development and the intensity of precipitation system. Therefore, a new dynamic Z-R relationship for RQPE was established using echo top-height classification, and better performance was obtained in comparison experiments with different seasonal precipitation events. However, although previous studies have considered the effects of independent time and space on the Z-R relationship and calibrated it, or dynamically adjusted the empirical coefficients $a, b$ by grouping reflectivity and precipitation, none of them have addressed the essential problem of the Z-R relationship. The Z-R relationship, as an ideal model that is difficult to satisfy, cannot capture the spatial and temporal variability in the rainfall process well, and because of the Z-R relationship generally operates on independent lattice points and does not take into account the spatial correlation between regions. It is difficult to meet the demand of the meteorological community for high-quality QPE. All these dilemmas have been solved in our study, and the model proposed in our study can be more adaptable to the complex geographical and climatic environments. In addition, our model can provide more accurate precipitation estimation than the Z-R relationship and its derivative methods.

The rapid development of machine learning, especially deep learning in recent years has advanced the research of QPE in the meteorological community (Teschl et al., 2006; Gagne et al., 2014; Kühnlein et al., 2014; Sorooshian et al., 2016; Beusch et al., 2018; Chen et al., 2020; Min et al., 2020; Zhang et al., 2020; Wu et al., 2021). In the era of big data, machine learning has great potential for parsing the underlying patterns of huge data without assuming any physical relationships. And deep learning, with the powerful learning ability of deep neural networks for complex nonlinear relationships in nature, has broadened the applicable field of machine learning and realized numerous applications. In addition, deep neural networks have powerful adaptive and fault-tolerant capabilities. Therefore, the deep neural network is a new option for improving the accuracy of QPE (Wu et al., 2021). Shin et al. (2019) evaluated the applicability of random forests, stochastic gradient augmentation models, and extreme learning machine methods to QPE and used multivariate combinations as inputs. The results show that the approach based on machine learning performs better than the model with Z-R relationship and resolves the time lag between the radar data and ground observations, and the accuracy is improved by an appropriate combination of multiple input variables. The overall performance of their proposed three models is 8.18 mm/h, 8.38 mm/h, 7.91 mm/h for root mean square error (RMSE) values, respectively. Sivasubramaniam et al. (2018) developed a nonparametric prediction model, the K-nearest neighbor regression estimator, and demonstrated that the inclusion of air temperature as an additional covariate for model significantly improved prediction results in cold air with an improvement of 15% in RMSE compared to radar precipitation rate as a single predictor in model. Chen et al. (2019) designed a two-stage neural network for estimating precipitation intensity and inversion of satellite radar profiles, respectively. They demonstrated that the machine learning approach can better detect changes in precipitation microphysical processes. Moreover, Chen et al. (2020) also proposed a data fusion framework based on a multilayer perceptron model with machine learning. The results indicate that the machine learning model is more flexible and can fuse multiple data sources. In addition, the data fusion framework can better capture precipitation intensity. However, although the previous studies used covariate or multiple data sources fusion models proved the validity, they considered only in one dimensional space and did not use two-dimensional data. In other words, they ignored the role of the spatial structure of variables on rainfall estimation during the rainfall process.

In addition to using traditional machine learning methods, Sadeghi et al. (2020) used a U-Net convolutional architecture with infrared information and geographic information as input to verify that adding latitude and longitude information to infrared information can improve real-time precipitation estimation. Then, for RMSE, mean absolute error (MAE) and correlation coefficient (CC), their models were more accurate in summer (winter) than the comparison model, i.e., PERSIANN-CCS (Hong et al., 2007), by 20% (10%), 21% (16%) and 140% (38%), respectively. Wu H. et al. (2020) analyzed the advantages and disadvantages of rainfall gauges and satellite products in rainfall operations. Moreover, they used deep learning methods to model the spatial and temporal correlations of these two sensors. Their CNN-LSTM model provides more accurate rainfall estimates. Specifically, their model outperformed the comparative models (CNN, LSTM, and MLP) with a 17.0 and 14.0% reduction in RMSE and MAE, respectively, and an increase in correlation coefficient from 0.66 to 0.72. It demonstrates the importance of capturing the spatiotemporal correlation of precipitation. A multi-model, multi-task precipitation estimation depth model was proposed by Moraux et al. (2019). The model uses an encoder-decoder as the main framework, and combines multiple modalities and multiple scales in a multitasking manner to suppress the respective errors and improve accuracy. More specifically, it estimates precipitation amount with a MAE of 0.605 mm/h and a RMSE of 1.625 mm/h for instantaneous rates. Furthermore, Moraux et al. (2021) also investigated combining different precipitation measurement modes to improve the accuracy of QPE. They combined well the inputs of three modes, rainfall gauge, radar and infrared satellite imagery, on the basis of the original model and obtained the best accuracy. The results show that RMSE decreases to 1.488 mm/h for rainfall estimates. Then, they demonstrate that building deep learning methods on basis of traditional methods is highly promising in the field of meteorology. Previous deep learning-based approaches have demonstrated the effectiveness of deep learning models in rainfall estimation operations. In addition, multiple sources of two-dimensional data were widely adopted as model inputs. However, considering that the input features can intermingle with information unrelated to rainfall, their model lacks the ability to adaptively adjust the proportion of weights to the features. In our study, we achieve a non-uniform distribution of weights and combine multi-scale information through a multi-scale self-attention module.

Previous studies have focused only on radar reflectivity factors at small-scales, while rainfall is the result of the interaction of complex weather systems at multiple scales (Zhang M. et al., 2021). Inspired by this, we believe that large scale radar reflectivity factors can also provide valid information for rainfall estimation, so we adopt multi-scale rainfall field information as the observations for the model, i.e., covering different ranges of rainfall fields centered on the rainfall collection points. In addition, although previous studies have used additional inputs as covariates, such as temperature (Sivasubramaniam et al., 2018). However, they ignored the influence of the spatial structural characteristics of the covariates on rainfall, so we used meteorological and geographic factors in two dimensions as covariates to establish their association with rainfall at the spatial scale. Finally, we also designed a multi-scale self-attention module, which helps our model to focus on factors that contribute to rainfall estimation and suppress noise. To the best of our knowledge, this has not been considered in previous studies, and our study demonstrates the effectiveness of this module. However, the process of this study also has some shortcomings. Since the radar detection process is affected by ground clutter, biological clutter, etc., the preprocessing scheme used in this study may not completely eliminate the influence of clutter, and this problem will be gradually improved in future studies.

In summary, a multi-scale neural network is built in this study to improve the accuracy of QPE by employing rain gauge and weather radar, with rain gauge data as labels, high spatial and temporal resolution radar data as the main input, and meteorological factors and elevation as covariates. The more accurate the quantitative rainfall estimates are, the better they can help meteorologists in their deeper study of weather systems and assist relevant managers in making more precise and timely warnings to minimize damage caused by natural disasters. The structure of this paper is presented as follows. “DATA AND METHODOLOGY” describes the data areas sampled and the detailed processing of the data set, as well as our specific scheme design, design ideas, evaluation metrics and information criteria. The “RESULTS” section discusses our experimental results and conclusions. Finally, we summarize our work in “CONCLUSION” section.

Data and Methodology

Data and Preprocessing

The data were obtained from the Shijiazhuang Meteorological Station Z9311 Doppler Weather Radar and 17 National Weather Stations (NWSs) from June to September 2017 to 2019. The Shijiazhuang domain spans two geomorphic units, the North China Plain and the Taihang Mountains, with a complex topography of elevated terrain in the west and flat terrain in the east. The climate is characterized by an uneven spatial and temporal distribution of rainfall, with significant seasonal and regional differences in the trend of precipitation, and a rainy season mostly in summer. The Doppler Weather Radar completes a body sweep every 6 min to obtain the radar reflectivity factors and the corresponding latitude and longitude for nine different elevation angles in all directions, with a volumetric sweep of VCP21. The NWSs record minute-by-minute meteorological elements, including barometric pressure, temperature, humidity, rainfall and other data. The study area was taken from longitude 113.5°–115.5° and latitude 37.0°–39.0°. The study area and NWSs are shown in Figure 1.

FIGURE 1

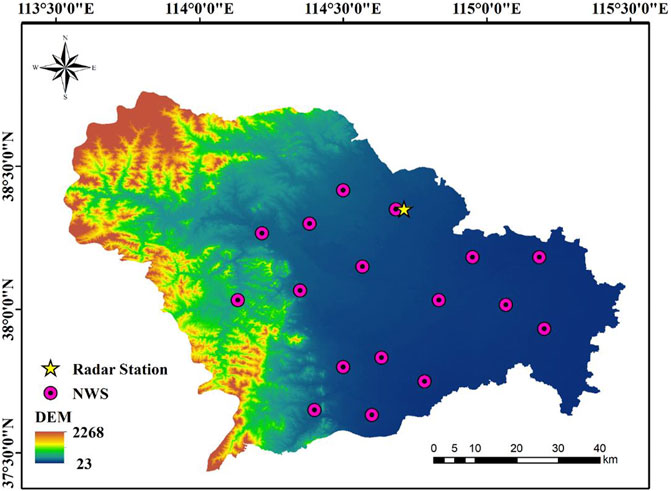
FIGURE 1. Elevation map of Shijiazhuang city. The map shows the distribution of radar stations (yellow pentagons) and 17 NWSs (pink circles) and the extent of our study area.

This study is an estimation of precipitation with radar reflectivity factors as the main input and meteorological and geographical factors as covariates, where temperature e and humidity are used for meteorological factors and elevation is used for geographical factors. Since the radar detection process is influenced by clutter and the radar reflectivity factors of a single elevation angle cannot completely express the real situation of cloud masses in a certain range, we use combined reflectivity. Furthermore, as the radar reflectivity factors of low elevation angles are more closely related to the precipitation, the combined reflectivity factors with maximum radar reflectivity factors of 0.49°, 1.40°, and 2.38° elevation angles are considered. In addition, we calculate the average reflectivity intensity of all radar echo images and sort them from smallest to largest, take the average reflectivity intensity of the smallest 0.1% number of radar echo images as background noise, and denoise the remaining radar echo images to some extent. The radar reflectivity factors need to be matched with the precipitation amount. Considering the delay of precipitation, the sum of the precipitation amount 6 min after the current moment is taken as the rainfall label of this moment. According to the first law of geography (Wasko et al., 2013), the correlation between the neighboring grids and the grid to be estimated decays with increasing distance, so the spatial matching of the radar reflectivity factors and precipitation is performed based on the latitude and longitude of the NWSs, and the grid points closest to the NWSs are selected as the center of the reflectivity. Specifically, considering that the radar reflectivity factors closer to the NWSs are more correlated with the precipitation values and the completeness of rainfall field information at long distances, multi-scale information is fed into our network.

Finally, as shown in Figure 2, the radar reflectivity factors centered at the NWSs in the ranges of 50 km, 25 km, 12.5 km are taken as the input radar reflectivity factors. The spatial resolution of the radar reflectivity factors is 0.005°, i.e., the grid points are 0.5 km away from each other, and the temporal resolution is 6 min. For the meteorological factors used in this study, temperature and humidity are used as covariates. Considering that the temporal resolution of the radar reflectivity factors is 6 min, while the temporal resolution of the meteorological elements is 1 min. Therefore, a temporal matching operation is performed on both data by taking the average of the meteorological factors for a total of 6 min above and below the current moment as the value of the current moment. Specifically, the meteorological factors in the range are interpolated according to the spherical model using Ordinary Kriging interpolation based on the meteorological factor data from the NWSs, and then temporally and spatially matched with the radar reflectivity factors, which are jointly used as inputs. The detail process of Kriging is as follows (Oliver and Webster, 1990):

$\begin{array}{c}E={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\lambda }_{i}z\left(x_i\right)\end{array}(1)$

where $E$ is the estimation of meteorological factors in certain areas, ${\lambda }_i$ is the proportion of weights for each sampling point and $z\left(x_i\right)$ is the data of the real meteorological factors recorded at the sampling sites. The sampling sites in this experiment are NWSs.

FIGURE 2

FIGURE 2. The graph of the weather station in the figure represents the NWS, and the three red triangles represent the boundaries of the sampling ranges for the small-scale input, the medium-scale input, and the large-scale input. The sampling area is a rectangular area centered on the NWS at a horizontal resolution of 0.005°.

Geographical and topographical factors are constant influencing factors of rainfall (Liu et al., 2018; Sadeghi et al., 2020; Sønderby et al., 2020). Therefore, according to the digit elevation model of Shijiazhuang city, the elevation values in grid form are obtained according to the spatial resolution of 0.005°, and then the spatial matching operation is performed to cut multi-scale with the NWSs as the center.

To evaluate the model more accurately, we divided the data set into a training set and a test set in a ratio of 8:2. The training set is used to help the model fit the relationship between the radar reflectivity factors and precipitation, and the test set is used to verify their relationship. For the partitioning of the dataset, random partitioning will lead to an uneven spatial and temporal distribution of the dataset. Therefore, the data set is classified according to the latitude and longitude coordinates of the NWSs and the month. Finally, they are randomly divided into training and test sets in the ratio of 8:2.

Methodology

Baseline Model

Traditional methods usually rely on converting the radar reflectivity factors to rainfall through a nonlinear relationship between the radar echo intensity and rainfall intensity (Z-R relationship). Models based on the Z-R relationship are also widely used in QPE models. The specific equation for the Z-R relationship is:

$\begin{array}{c}Z=\mathrm{a}{R}^b\end{array}(2)$

where $Z$ is the radar echo intensity, $R$ is the rainfall intensity, and $a$ and $b$ are the empirical coefficients. The Z-R relationship is mainly influenced by the spectral characteristics of the rainfall. In addition, the Z-R relationship is influenced by many factors such as geography, meteorological conditions, and hydrology. Parameters $a$ and $b$ will be adjusted to suit different conditions according to these factors (Tian et al., 2020).

Therefore, according to the equation of the relationship between radar reflectivity factor and its physical quantity $dBZ=10\text{lg}Z$, the Z-R relationship is rewritten as:

$\begin{array}{c}\mathrm{l}\mathrm{g}R=\frac{1}{10b}dBZ-\frac{1}{b}\mathrm{l}\mathrm{g}a\end{array}(3)$

Then, we fit the values of the parameters $a$, $b$ using a linear regression model. Finally, the value of $a$ takes the value of 1.91 and the value of $b$ takes the value of 0.578.

Model Architecture

It is well known that precipitation is a complex process, which is closely related to meteorological factors and influenced by geographical factors. Therefore, only considering the radar reflectivity factors cannot accurately fit the relationship with precipitation intensity, and the inclusion of covariates is particularly important. In this study, meteorological factors (temperature and humidity) and geographical factors (elevation) are mainly used as covariates. In addition, an attention mechanism among multiple scales is introduced in this study. With this mechanism, the module not only focuses on the most relevant influences near the site, but also takes into account the spatial variability on a large scale to produce more accurate estimation.

In contrast to the single-scale input of the model in previous studies, our model called MS-FCVNet uses a multi-scale input centered on NWSs. In detail, small-scale images have a small sensory field, focusing on the variation in details of rainfall fields around the station. Large-scale images have a wide range of sensory fields, focusing on the overall spatial structure of weather conditions. And Medium-scale images mainly play a transitional effect, linking the spatial information of large scale and small scale, and providing the necessary spatial change information. In terms of model structure, the model includes Hybrid Dilated Convolution (HDC), pooling layer, fully connected layer, and multi-scale self-attention modules (MS-SA). The model structure is shown in Figure 3, and the details of the modules and their specific functions will be explained in detail below.

FIGURE 3

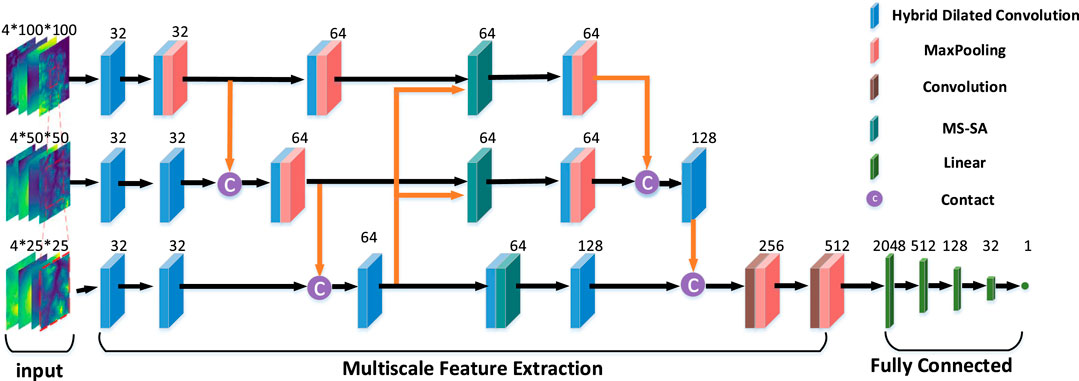
FIGURE 3. The MS-FCVNet model receives information input from three scales, undergoes multi-scale feature extraction and fusion, and finally outputs the predicted values through a fully connected layer.

Hybrid Dilated Convolution

HDC consists of a number of dilated convolutions (Wang et al., 2018a). Dilated convolution mainly involves adding empty holes, i.e., zero pixels, to the feature mapping of the convolution kernel for the purpose of expanding the receptive field. Ordinary convolution generally achieves the purpose of expanding the receptive field by adding a pooling layer, which leads to the loss of detailed information. Compared to ordinary convolution, dilated convolution can improve the resolution of the sampled image without increasing the number of parameters to achieve dense feature extraction in deep CNNs. For an ordinary convolution kernel of size $K$, the corresponding dilated convolution kernel size is $K+\left(K-1\right)\ast (R-1)$, where $R$ is the dilation rate when we sample the feature map. Taking the two-dimensional dilated convolution as an example, the process can be expressed as the following equation:

$\begin{array}{c}\{\begin{array}{c}{\text{f}}_{i,j}^{\left[l\right]}={\displaystyle \sum }_{m=0}^{S-1}{\displaystyle \sum }_{n=0}^{S-1}{w}_{m,n}^{\left[l\right]}{x}_{(m-S//2)\ast r+i,(n-S//2)\ast r+j}^{\left[l-1\right]}+b^{\left[l\right]}\\ x_{i,j}^{\left[l\right]}=g\left(f_{i,j}^{\left[l\right]}\right)\end{array}\end{array}(4)$

where $\text{f}$ is the feature points extracted from the convolution kernel after the convolution operation, $S$ is the length of the convolution kernel, and $w$ is the weight of the convolution kernel. $x$ is the position of the sampled points, $b$ is the bias, and $g$ is the activation function. However, simply stacking the dilated convolutions will lead to a grid effect, i.e., the pixel points on the sampled final feature map will view the information of the original feature map in the form of a grid. This will lead to discontinuities in local information, weakening spatial correlation and not conducive to capturing the spatial information of the image. Therefore, HDC is used to build the network in this study. Specifically, different dilation rates are used for several phase-consecutive dilation convolution kernels in HDC. The main purpose is to compensate for the holes caused by a series of convolutions, so that the pixel points of the sampled feature map can sample a complete region of the original feature map. For a number of $N$ convolution layers, the convolution kernel size of each layer is $K$, and its void rate is $[r1,r2,\mathrm{...},rn]$, and its maximum dilation rate needs to satisfy the following equation:

$\begin{array}{c}{M}_i=\max \left[M_{i+1}-2r_i,M_{i+1}-2\left(M_{i+1}-r_i\right),r_i\right]\end{array}(5)$

where $r_i$ is the dilation rate of layer $i$ and $M_i$ is the maximum dilation rate of layer $i$. With HDC, it can achieve a wider field of perception without losing local information and capture more global information. Figure 4 shows the specific configuration of our HDC, where we take 1, 3, and 5 as consecutive dilation rates.

FIGURE 4

FIGURE 4. HDC with expansion rates of 1, 3, and 5.

Multi-Scale Self-Attention Modules

In our study, we consider that the large-scale radar reflectivity factors will contain more complete meteorological information, such as the overall condition of the cloud mass and the meteorological conditions near the site will be much more important compared to the distant ones. To balance the consideration of large-scale images and small-scale images centered on the site, we design the MS-SA. Its model structure is shown in Figure 5.

FIGURE 5

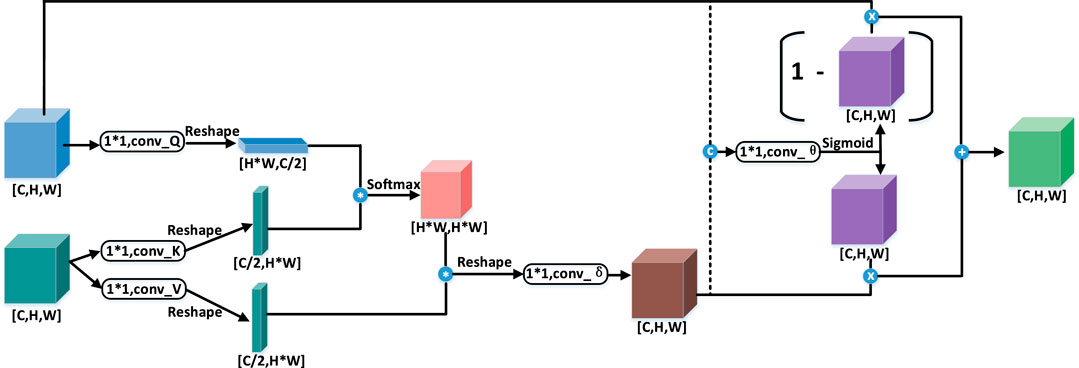
FIGURE 5. The model receives inputs at two different scales and undergoes different convolution operations to generate the Query block, Key block and Value block, respectively. The weighted feature maps are generated by the Query and Key modules, and then multiplied with the Value module to generate the attention-passed feature maps. Finally, the final feature map is generated by mask branching.

The design of MS-SA is based on the non-local block module. The essence of the non-local block module is to capture the global spatio-temporal characteristics for each pixel point on the image, assign different weights, and finally aggregate them at each location to enrich the spatio-temporal characteristics (Wang et al., 2018b). The input is $x_i$, $i \in S^{m\ast n}$. $S^{m\ast n}$ is the set of all pixel points in the image, if the input is spatio-temporal sequence then $i \in S^{t\ast m\ast n}$. The default input in this paper is the image. $conv\_K$, $conv\_Q$, $conv\_V$ are three different feature mappings, and we use 1*1 convolution operation to implement them in the model. The result of the input after $conv\_K$, $conv\_Q$, i.e., the Key module and Query module are multiplied to get the global pixel similarity score between any two pixels in the global pixel, which is expressed as $f_{i,j}={(W_Q\ast x_i)}^T\ast (W_k\ast x_j)$. The expression can be simplified as $f_{ }=Q^T\ast K$. The similarity score is then transformed into the weight score of the global information for each pixel point by the softmax function. The output of each location is represented by $z_i$, which is the weighted sum of the global information.

$\begin{array}{c}{z}_i=W_z\left(\frac{1}{C\left(x\right)}{\displaystyle \sum }_{j=1}^{m\ast n}{f}_{i,j}\ast V\left(x_j\right)\right)+x_i\end{array}(6)$

$i$ is the index of the input and output points, $j$ is the index of the global sampling points, $C\left(x\right)$ is the normalization factor, and $W_z$ is the weight fraction of the global location with respect to location $i$. $V$ is also a mapping operation on the input, i.e., the Value module, and multiplying the two results is the input of each location after non-equal distribution of weights. The addition of the input as the residual term in the formula can make the non-local block module more stable.

To take full advantage of the multi-scale input of the model, MS-SA receives two inputs, i.e., a small-scale feature map $x_M$ and a large-scale feature map $x_L$. The small-scale feature map with feature mapping $conv\_Q$ is used as the Query module, and the large-scale feature map with feature mapping $conv\_K$ and $conv\_V$ is used as the Key and Value modules. Multiplying the Query module and Key module is the $x_M$ and $x_L$ pixel-by-pixel similarity scoring matrix $G_{i,j}={(W_Q\ast {\left(x_M\right)}_i)}^T\ast (W_K\ast {\left(x_L\right)}_j)$. Each row of the similarity matrix is the similarity score of each position of $x_M$ relative to all positions of $x_L$, and each column of the matrix is each position of $x_M$. After the softmax function, the elements in $x_L$ that are similar to $x_M$ will be given higher weights. These elements, after a series of previous convolution operations, will gather more spatial information that is not originally available in the small-scale relative to the elements of $x_M$, especially the edge positions. It can also be interpreted as allowing the small-scale range near the site to learn the spatial information of the wider region and gather in the center. It not only takes into account the spatial information of the larger area but also emphasizes the key information of the small area near the site. As Figure 6 shows the evaluation process of similarity between multiple scales, the spatial information of the central region of the large-scale image has higher similarity with the spatial information of the small-scale image compared with the spatial information of the remaining location regions in the large-scale image. This is because the small-scale image is cropped from the central region of the large-scale image. The feature map processed by the multi-scale attention mechanism not only takes into account the spatial information of large regions but also emphasizes the key information of small regions near the site. The output of each position is represented by $z_i$, which is the result of a preliminary fusion of small-scale and large-scale information:

$\begin{array}{c}{z}_i=W_z\left(\frac{1}{C\left(x\right)}{\displaystyle \sum }_{j=1}^{m\ast n}{G}_{i,j}\ast V\left({\left(x_L\right)}_j\right)\right)\end{array}(7)$

FIGURE 6

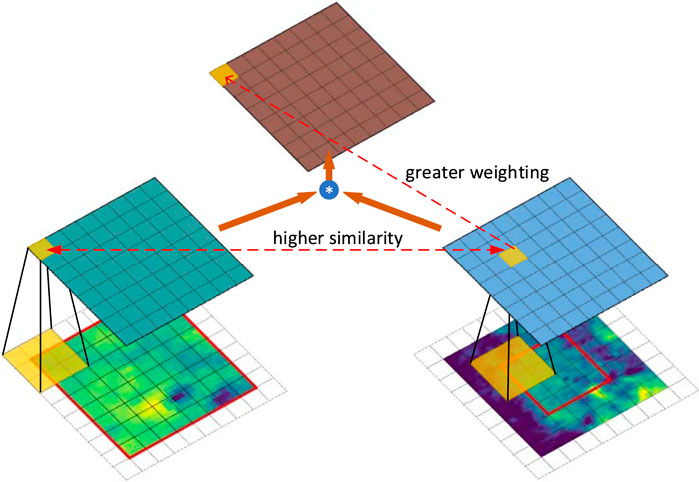
FIGURE 6. The center region of the large-scale image (right) is convolved with respect to the upper left corner region of the small-scale image (left) and the upper left corner region of the small-scale image for similarity scoring. Since the small-scale image is cropped from the large-scale image, the same parts are given more weight in the similarity evaluation by the attention mechanism.

To make the module more stable, the inputs are often connected at the end of the model as a shortcut. However, since there are features on an image that are beneficial for precipitation estimation and features that are not useful for precipitation estimation, a simple summation does not effectively utilize the features that are beneficial for precipitation estimation. Therefore, the model needs to have the ability to adaptively assign weights to each location. To solve this problem, we design a feature fusion module as a mask branch. Combining the input $x_M$ and the output $z$ in the channel direction after aggregating large-scale spatial information, learning spatial information by convolution operation, then feature mapping and adjusting the number of channels by convolution $conv\_\theta$ with a convolution kernel size of 1, and finally activation by sigmoid function to be used as the assigned weights $\zeta$.

$\begin{array}{c}{R}_i=\zeta \ast z_i+\left(1-\zeta \right)\ast {\left(x_M\right)}_i\end{array}(8)$

Fully Connected Layer

The role of the fully-connected layer is to map the distributed high-level features extracted by the model to the target space. Each element of each layer in the fully connected layer is associated with all elements of the previous layer and has a strong fitting capability. The final layer of the fully connected layer outputs the predicted rainfall estimates.

Pooling Layer

The pooling layer mainly plays the role of reducing the dimensionality of the input feature vectors in this study. Pooling is divided into average pooling and maximum pooling, and we use maximum pooling.

$\begin{array}{c}{y}_{i,j}^{\left[l+1\right]}=\underset{1\le \mathrm{m}\le \mathrm{f},1\le \mathrm{n}\le \mathrm{f}}{\text{max}}\left(x_{m,n}^{\left[l\right]}\right)\end{array}(9)$

$m$, $n$ are the coordinates of the pixel points of the convolution kernel, $x$ is the position of the sampled points in the $lth$ layer, and $y$ is the result of the feature extraction in the $(l+1)th$ layer.

Loss Function

In the training process, the loss function we use is a weighted combination of mean square error (MSE) and mean absolute error (MAE). The specific reason is that in experiments, MSE is usually used as the loss function because MSE can better reflect the error between the true and predicted values. However, in QPE, anomalous values are inevitably generated due to strong convective weather and the influence of clutter. In addition to this, there is the problem of skewed distribution of rainfall data. If a single MSE is used as a loss function, it will cause the model to trend towards underestimating the evaluation of rainfall in heavy rainfall situations, as well as paying more attention to the anomalous values. The specific equation is:

$\begin{array}{c}Loss=a\ast MSE+b\ast MAE\end{array}(10)$

where $a$, $b$ are the weight parameters of $MSE$ and $MAE$. After a series of experiments, we take the case where $a$ is 1 and $b$ is 10 to achieve the best training effect. In addition to this, during the training process, we use the gradient descent method to update the errors and get the optimal results based on the analysis of the experimental results in the time and space dimensions. Finally, the model has a learning rate of 0.0001, a batch size of 8, a training epoch of 100, and an optimization algorithm using Adam.

Evaluation Metrics

$\begin{array}{c}RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{\mathrm{i}=1}^N{\left(G_{\mathrm{i}}-R_i\right)}^2}}\end{array}(11)$

$\begin{array}{c}MAE=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|G_i-R_i\right|}\end{array}(12)$

$\begin{array}{c}CC=\frac{{{\displaystyle \sum }}_{i=1}^N\left(G_i-{\overline{G}}_i\right)\left(R_i-{\overline{R}}_i\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^N{\left(G_i-{\overline{G}}_i\right)}^2}\sqrt{{{\displaystyle \sum }}_{i=1}^N{\left(R_i-{\overline{R}}_i\right)}^2}}\end{array}(13)$

where $N$ is the number of samples in the dataset, $G$ is the ground truth value, and $R$ is the model estimation. ${\overline{G}}_{ }$ is the mean of the ground truth value and ${\overline{R}}_{ }$ is the mean of the model estimation. The goal of our study is to make the larger the $CC$ value, the smaller the values of $RMSE$ and $MAE$, which represent the excellence of the model.

Information Criteria

In addition, Since we will compare different models with different input variables and parameters in the RESULTS section, we use the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) (Akaike, 1974; Burnham and Anderson, 2016; Kuha, 2016) which are typically penalized likelihood criteria used to compare non-nested models and can be used to measure the complexity and fit of individual models.

AIC is defined as:

$\begin{array}{c}\text{AIC}=-2\ln \mathrm{ℒ}+2k\end{array}(14)$

where $\mathrm{ℒ}$ is the maximum likelihood of the model and $k$ is the number of parameters required to fit the model to the nonlinear relationship.

BIC is defined as:

$\begin{array}{c}\mathrm{BIC}=-2\mathrm{lnℒ}+k\ln N\end{array}(15)$

where the parameters $\mathrm{ℒ}$ and $k$ are defined in the same way as in the above equation. The parameter $N$ is the number of samples used for the fit.

The AIC mainly depends on the accuracy of the first model and the number of parameters of the second model. When the number of parameters of the models used for comparison is similar, the higher the accuracy of the model, the lower the AIC value. When the difference in the accuracy of the models used for comparison is small, the simpler the model structure is, the lower the AIC value is. Therefore, the lower the AIC, the better the model performance. BIC additionally takes into account the sample size.

Results

In this study, to show the superiority of MS-FCVNet, we compare it with the baseline model (Z-R model), the BPNN network (Rongrui and Chandrasekar, 1997), the CNN (1) network (Tian et al., 2020), and the CNN (2) network. It is worth noting that CNN (1) and CNN (2) have the same network structure, the only difference between them is the input to the network. We only use radar reflectivity factors as input for CNN (1). In contrast, we not only use single radar reflectivity factors as input, but also multivariate inputs for CNN (2). In detail, it takes the radar reflectivity factors as the main variable and temperature, humidity and elevation as covariates, in order to make the inputs of the models used for comparison closer to MS-FCVNet and to make the differences in the experimental results more dependent on the enhancement brought by our model structure itself.

Figure 7 shows the distribution of the predicted values of the models relative to the ground truth value. The horizontal axis of each graph is the ground truth value and the vertical axis is the estimated rainfall value predicted by the model. The more accurate the model predicts, the more the dots in the graph are clustered on the $y=x$ axis. Figure 7A shows the distribution of the predicted values of the Z-R relationship. It is obvious that the distribution is very scattered, so it expresses that the predicted values of Z-R relationship differs significantly from the ground truth value and the traditional method does not fit the relationship between radar reflectivity factors and rainfall well compared to the deep learning method. Among the deep learning methods, as shown in Figure 7B, the distribution of the estimation predicted by BPNN performed more concentration compared to Z-R relationship, which proves the effectiveness of deep learning in fitting the radar reflectivity factors to the rainfall. In contrast, Figures 7C,D display that the performance of the BPNN is slightly less than that of the two CNN networks, which shows that rainfall has a strong spatial correlation, and the CNN captures this spatial structure that is ignored by the BPNN. For both CNN networks, Figure 7D reveals that the CNN (2) network that adds temperature, humidity and elevation as covariates gives more accurate rainfall values than CNN (1) which simply uses the radar reflectivity factors as input, indicating the correlation between rainfall and meteorological and geographic environments. Finally, Figure 7E shows that our proposed model can predict the rainfull that are more concentrated and closer to the $y=x$ axis, i.e., closer to the ground truth value than other models and proves the superiority of our model.

FIGURE 7

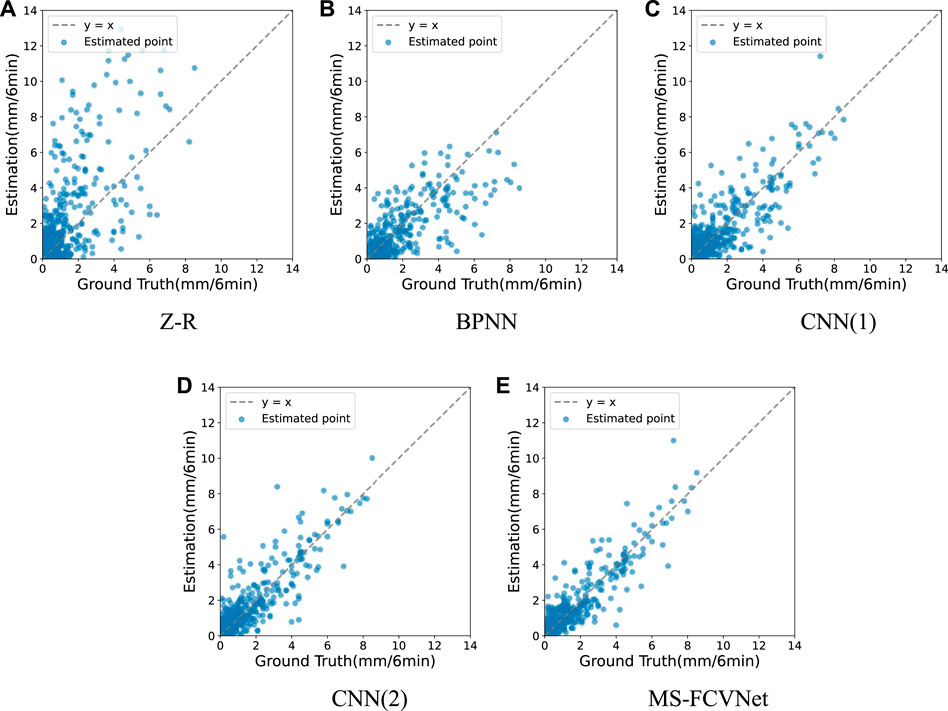
FIGURE 7. Distribution of model (A) Z-R relationship, (B) BPNN, (C) CNN (1), (D) CNN (2) and (E) MS-FCVNet estimation in the test set relative to the ground truth value.

Table 1 shows the comparison of the Z-R, BPNN, CNN (1), CNN (2) and MS-FCVNet under the same evaluation metrics and information criteria. The first column of the table is the names of models. The second to the fifth columns of the table are the inputs to the model, which are the radar reflectivity factors, temperature, humidity, and elevation, respectively. The sixth column shows the selection of MS-SA moudle. The last five columns are the evaluation metrics RMSE, MAE, CC and information criteria AIC, BIC. Their specific meanings have been discussed in Evaluation Metrics Chapter and Information Criteria Chapter respectively. Lower RMSE, MAE values and higher CC values represent better performance of the model. The lower the AIC,BIC, the better the model can balance model complexity and accuracy. The experimental results show that the RMSE and MAE values of Z-R are higher and the CC values are lower, indicating that the fixed Z-R are more restricted and the predicted values are more different from the ground truth value. Considering that deep neural networks and simple linear regression, i.e., the computational process of Z-R relationship, are not comparable in terms of the number of parameters, the AIC, BIC of the Z-R relationship is not considered. The RMSE and MAE values of BPNN are lower than those of Z-R relationship, indicating that the estimation values of BPNN are closer to the ground truth and more concentrated in distribution. In addition, the CC values of BPNN are higher than the Z-R relationship, indicating that the predicted values of BPNN are more correlated with the rainfall. However, compared to the result of the CNN networks which shown in the 4th and 5th rows of the table, the performance of the BPNN is lower than the CNN networks. CNN can capture the spatial information of rainfall fields that BPNN cannot learn and the results demonstrate the influence of spatial correlation in the rainfall process on rainfall estimation and the correctness of using two-dimensional data input in our model. Comparing CNN (1) and CNN (2) networks, CNN (2), i.e., CNN network with covariates, has lower RMSE, MAE and higher CC than CNN (1). It indicates that the rainfall estimates of CNN network with covariates are more accurate and the necessity of the covariates during the precipitation estimation. The focus is on the ablation experiments of MS-FCVNet, i.e., rows 6th to 21st of Table 1. We consider the individual and combined cases of covariate inputs to the model and the changes brought by the addition of MS-SA to the network. Rows 6th to 9th in the table indicate the performance of the model is improved when adding temperature, humidity, and elevation as covariates alone, which is consistent with the findings of other researchers (Shu et al., 2007; Zhang Y. et al., 2021), indicating the relevance of meteorological factors, geographic factors, and precipitation. As shown in rows 10th to 13th of Table 1, when the combination of temperature, humidity and elevation were entered as covariates, the model performed better in some pairings than when they were added separately. It demonstrates that the interconnection of meteorological and geographical factors had an enhancing effect on the correct estimation of the model by adverse or noisy factors of rainfall. Row 14th of the table demonstrates that our model with the addition of the MS-SA module, there is a deterioration in the performance of our model with the radar reflectivity factors alone as an input compared to the model without the addition of the MS-SA module. This may be because, in the absence of covariate constraints, more features with less correlation with precipitation are extracted from the large-scale radar reflectivity factors. And the MS-SA module condenses the features extracted at large-scales into small-scales, which leads the model to focus on more features that are not conducive to precipitation estimation and has a bad effect on the estimation of rainfall. In contrast, the pairing with the MS-SA module produced better performance when meteorological factors were available as covariates. When elevation alone is added as a covariate, as shown in row 17th, the model performance is worse than that without the MS-SA module. The possible reason is that the addition of elevation makes the model more sensitive to areas with complex terrain, such as near stations in the southwestern region of Shijiazhuang, while the aggregation characteristics of the MS-SA module would make the model more insensitive to precipitation characteristics in flat terrain in the eastern region, and without the meteorological factors, the model will be even less effective. Figure 8 shows the comparison of RMSE values, MAE values and CC values for the model with and without MS-SA, using only geography as a fixed covariate. We selected the three most southwestern sites 53693, 53698, 53795 and the three most northeastern sites 53699, 54621, 54701 for comparison experiments to test our conjecture. Figure 8A shows the lower RMSE values of the model with MS-SA added in the more complex topography in the southwest, and the lower RMSE values of the model without MS-SA in the plain area in the northeast. We can find that with the inclusion of the MS-SA module, the maximum overestimation of precipitation estimation by the model can be reduced in regions with complex topography, and the minimum underestimation of precipitation estimation can be mitigated. It is shown in Figure 8B that the inclusion of the MS-SA module in the model reduces the overall degree of error for areas with complex topography. From Figure 8C, it can be understood that model which includes the MS-SA module usually correlate with the true value of rainfall to a greater extent than the model without the MS-SA module. This is consistent with our hypothesis. Compared with Z-R relations, BPNN, CNN (1) and CNN (2), our model performs best with temperature, humidity, and elevation as covariates and with the addition of the MS-SA module. In addition, the RMSE is reduced by 8.42%, the MAE is reduced by 8.63%, and the CC is improved by 3.41% compared to the case without the inclusion of any covariates as well as the MS-SA module. According to the comparison of AIC and BIC of all compared models, it can be found that the AIC and BIC values of CNN (1) and CNN (2) are lower than those of BPNN, which indicates that BPNN stacking too many fully connected layers sacrifices the complexity of the model, but does not improve the accuracy too much. In addition, although our model performs well under most combination of input variables and MS-SA modules relative to the normal CNN networks, i.e., CNN (1),CNN (2) under other evaluation metrics, it sacrifices too much model complexity, which leads to high AIC,BIC. Finally, only the MS-FCVNet with the addition of temperature, humidity, and elevation as covariates and MS-SA has lower AIC, BIC than the other comparison models, indicating that our final model sacrifices model complexity but brings greater accuracy improvement. It is worth mentioning that the performance improvement of MS-FCVNet over the CNN model with the inclusion of meteorological factors and geographical factors is significant, which demonstrates the superiority of our model structure.

TABLE 1

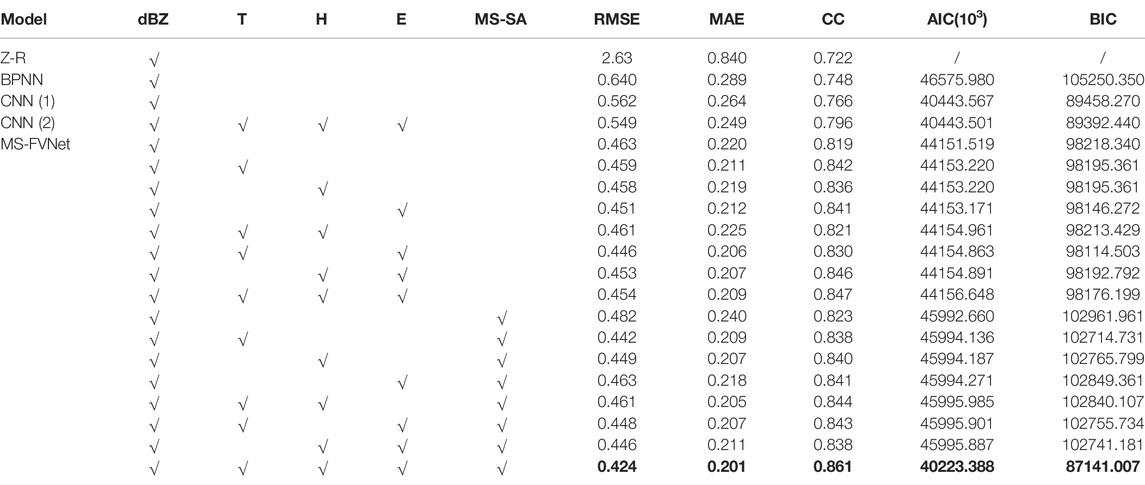
TABLE 1. The scores of Z-R, BPNN, CNN (1), CNN (2) and MS-FCVNet under evaluation metrics RMSE, MAE, CC at the 6-minute scale and information criteria AIC, BIC. The bold text is the optimal level of the evaluation index.

FIGURE 8

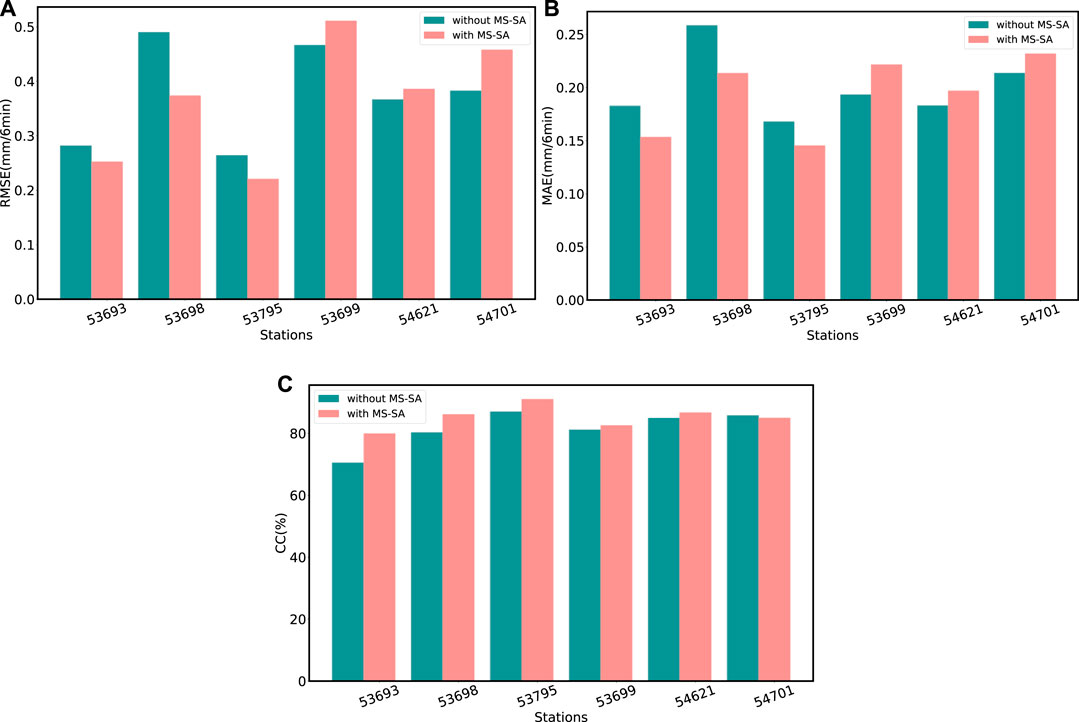
FIGURE 8. Model incorporation of elevation and MS-SA modules for (A) RMSE scores, (B) MAE scores (C) CC scores at the southwestern Shijiazhuang NWSs 53693, 53698, 53795 and the northeastern NWSs 53699, 54621, 54701.

Figure 9 shows the performance of MS-FCVNet and the comparison model at 17 NWSs, 6-min scales, respectively. The horizontal axis of Figure 9 represents the 17 NWSs, and the vertical axis shows the three evaluation metrics RMSE, MAE, and CC. Considering that the coefficients $a,b$ in the Z-R relation have a small adaptation range and are influenced by geographic environment and weather conditions, we use different empirical coefficients $a,b$ for the experiments located at 17 NWSs. From Figure 9A, we can see that the RMSE of Z-R relationship is less stable and has larger errors compared to other machine learning and deep learning algorithms. The BPNN, although better than the Z-R relationship in RMSE evaluation, still generally performs worse than the CNN network that can capture the spatial structure features on each NWS. The RMSE values of CNN (1) and CNN (2) networks have unbalanced performance levels across sites. MS-FCVNet performs optimally on each NWS with a stable RMSE values between 0.1 mm/6 min and 0.8 mm/6 min, which shows that MS-FCVNet overestimates and underestimates the rainfall to a much lesser extent than the other methods. Figure 9B shows the evaluation of MAE values for each model at each station, which is generally consistent with the results of RMSE values. The MAE values of MS-FCVNet are stable between 0.1 mm/6 min and 0.4 mm/6 min. Although the MAE values are high at station 53680, they are still lower than the other methods at this station, indicating that MS-FCVNet is lower than the other methods in terms of overall error. Figure 9C shows the performance of the model in terms of correlation coefficient. The CC values of MS-FCVNet ranges from 74 to 93%, and although there are some fluctuations in the evaluation of the CC at each station, it is still generally better than other methods, indicating the strong correlation between the estimated value of MS-FCVNet and the real value of precipitation.

FIGURE 9

FIGURE 9. MS-FCVNet scores for (A) RMSE, (B) MAE, (C) CC at 17 NWSs.

The performance of the model in strong convective weather is also an indicator that many studies have focused on (Zhang et al., 2020). Figure 10 shows the time series line plot of the model and the true rainfall values for the NWS during a period of heavy rainfall on 12 August 2018. The horizontal coordinate is time and the vertical coordinate is the estimated and true rainfall of the model. Both the Z-R relationship and the BPNN have severe overestimated and underestimated performance in the time series. The Z-R relationship produces a positive deviation of 10 mm/6 min in the rainfall prediction at 13:00 on 12 August 2018, which severely overestimates the rainfall value, indicating the inaccuracy of the Z-R relationship in prediction during heavy rainfall. The rainfall estimate of BPNN reaches a negative deviation of 3.2 mm/6 min at the 13:00 moment on 12 August 2018, and differs significantly from the true value at all other moments, with an average deviation of 0.63 mm/6 min. The overestimation and underestimation of rainfall values predicted by the CNN (1) network are smaller than those of the Z-R relationship and the BPNN, but the bias values are still higher than those of the CNN (2) network at most moments, which demonstrates the effectiveness of the model’s inclusion of covariates in reducing the bias values. The rainfall estimates of the MS-FCVNet network are close to those of the CNN (2) network. Although there are overestimates and underestimates, but overall, the estimation of MS-FCVNet are closer to the true values than the CNN network. Specifically, the positive deviation of our model’s predicted values relative to the true rainfall values does not exceed 0.19 mm/6 min and the negative deviation does not exceed 0.25 mm/6 min.

FIGURE 10

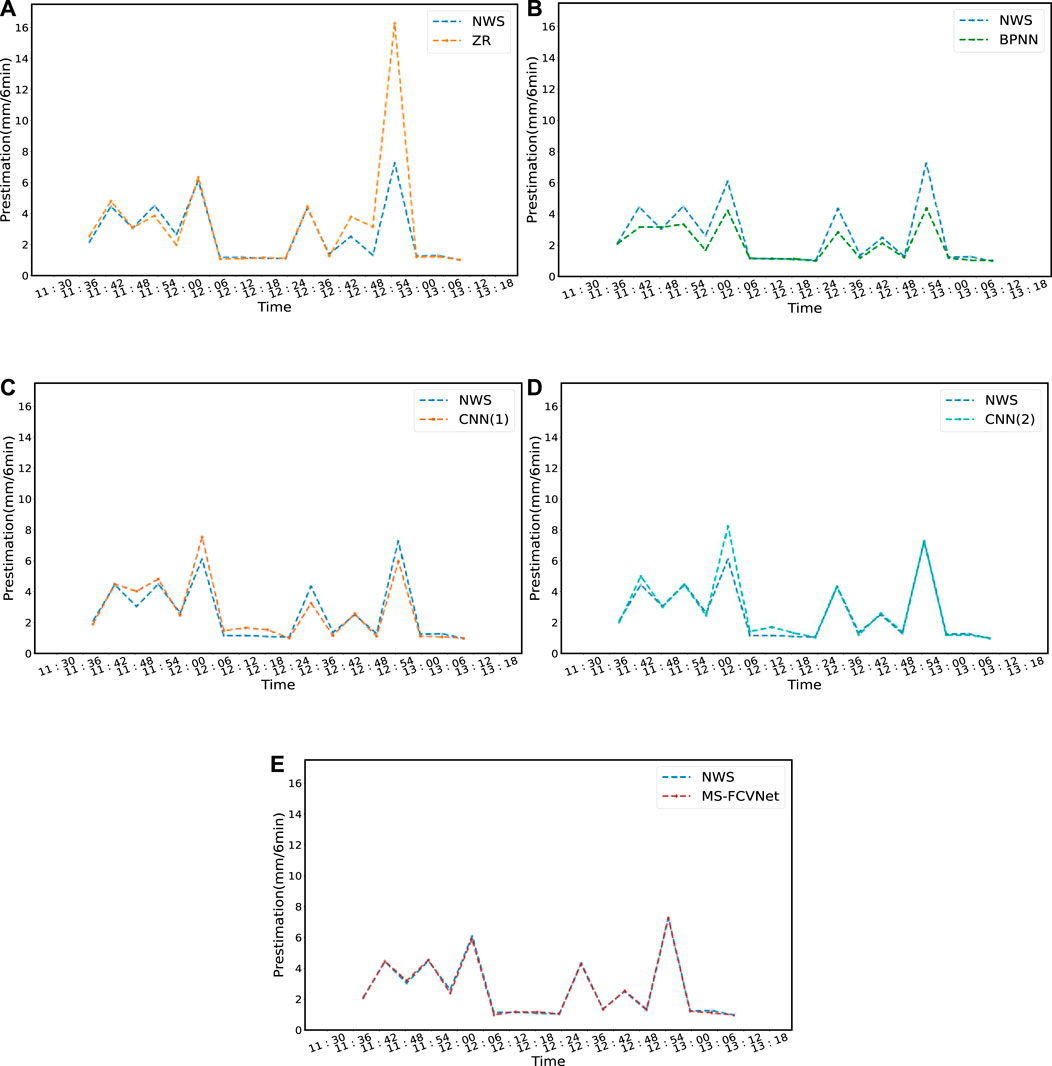
FIGURE 10. Estimated values of models (A) Z-R relationship, (B) BPNN, (C) CNN (1), (D) CNN (2), (E) MS-FCVNet versus ground truth for the rainfall period from 11:30 to 13:18 on 12 August 2018.

Conclusion

In this study, we use deep learning techniques to demonstrate the effectiveness of multi-scale radar reflectivity factors, as well as meteorological and geographic factors as covariates in QPE. In addition, we developed an MS-SA module for better combining factors that favor precipitation estimation in the multi-scale, with some suppression of unfavorable factors. In particular, we have the following innovations and conclusion:

Multi-scale deep learning networks are able to make accurate prediction of rainfall. Compared with deep learning networks with single-scale inputs, the large-scale feature maps in multi-scale can learn the complete rainfall field information over a wide region that also have an impact on rainfall gauges, and in addition, the small-scale feature maps can learn spatial information with stronger correlation with precipitation near the rainfall gauges. Therefore, multi-scale inputs can provide more accurate predictions for QPE.

Temperature, humidity, and elevation as covariates can improve the QPE accuracy. Precipitation is a complex process, and there are many factors affecting precipitation, including meteorological and geographic factors. In addition, the spatial correlation of meteorological and geographic factors is considered to strengthen the spatial modeling capability of the model. In this study, two-dimensional meteorological and geographical factors were used as covariates to capture their spatial characteristics, and the validity was experimentally demonstrated.

The multi-scale self-attentive module MS-SA is a new module we propose to better integrate factors that favor precipitation estimation in different scales and suppress irrelevant factors. It also can integrate covariates with radar reflectivity to constrain each other, reduce errors and make more accurate precipitation estimation. The experimental results further demonstrate the importance of multi-scale integration.

The experimental results show that MS-FCVNet has a RMSE of 0.424 mm per 6 min for precipitation estimation, which is the best performance among Z-R, BPNN, CNN with only radar reflectivity factors as input and CNN with covariates involved, and maintains good performance in different geographical locations as well as time series.

The method proposed in this paper, especially the MS-SA module, is not lightweight enough and requires higher computational effort than the general method, which is also a future research direction. However, in general, our proposed model offers the possibility of more accurate estimation for QPE in operations.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

KS designed the experiments and performed the experiment. LZ and YF prepared the data. SC and LY guide the experiment. WT led the writing of the manuscript. All authors discussed the analysis and results and contributed to the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China (Grant number 42175157 and 41875027), the National Key Research and Development Program of China (Grant number 2021YFE0116900) and the Shijiazhuang Meteorological Bureau (Grant No. SJZQXJHT 2019-45).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors acknowledge Shijiazhuang City for providing Doppler radar data and weather station data.

References

Akaike, H. (1974). A New Look at the Statistical Model Identification. IEEE Trans. Autom. Contr. 19 (6), 716–723. doi:10.1109/tac.1974.1100705

CrossRef Full Text | Google Scholar

Alfieri, L., Claps, P., and Laio, F. (2010). Time-dependent Z-R Relationships for Estimating Rainfall Fields from Radar Measurements. Nat. Hazards Earth Syst. Sci. 10 (1), 149–158. doi:10.5194/nhess-10-149-2010

CrossRef Full Text | Google Scholar

Barros, A. P., and Prat, O. P. (2009). Exploring the Transient Behavior of Z–R Relationships: Implications for Radar Rainfall Estimation. J. Appl. Meteorol. Climatol. 48 (10), 2127–2143. doi:10.1175/2009jamc2165.1

CrossRef Full Text | Google Scholar

Berne, A., and Krajewski, W. F. (2013). Radar for Hydrology: Unfulfilled Promise or Unrecognized Potential? Adv. Water Resour. 51, 357–366. doi:10.1016/j.advwatres.2012.05.005

CrossRef Full Text | Google Scholar

Beusch, L., Foresti, L., Gabella, M., and Hamann, U. (2018). Satellite-Based Rainfall Retrieval: From Generalized Linear Models to Artificial Neural Networks. Remote Sens. 10 (6), 939. doi:10.3390/rs10060939

CrossRef Full Text | Google Scholar

Burnham, K. P., and Anderson, D. R. (2016). Multimodel Inference. Sociol. Methods Res. 33 (2), 261–304. doi:10.1177/0049124104268644

CrossRef Full Text | Google Scholar

Chen, H., Chandrasekar, V., Cifelli, R., and Xie, P. (2020). A Machine Learning System for Precipitation Estimation Using Satellite and Ground Radar Network Observations. IEEE Trans. Geosci. Remote Sens. 58 (2), 982–994. doi:10.1109/tgrs.2019.2942280

CrossRef Full Text | Google Scholar

Chen, H., Chandrasekar, V., Tan, H., and Cifelli, R. (2019). Rainfall Estimation from Ground Radar and TRMM Precipitation Radar Using Hybrid Deep Neural Networks. Geophys. Res. Lett. 46 (17-18), 10669–10678. doi:10.1029/2019gl084771

CrossRef Full Text | Google Scholar

Chen, H., and Chandrasekar, V. (2015). The Quantitative Precipitation Estimation System for Dallas–Fort Worth (DFW) Urban Remote Sensing Network. J. Hydrol. 531, 259–271. doi:10.1016/j.jhydrol.2015.05.040

CrossRef Full Text | Google Scholar

Cremonini, R., and Tiranti, D. (2018). The Weather Radar Observations Applied to Shallow Landslides Prediction: A Case Study from North-Western Italy. Front. Earth Sci. 6. doi:10.3389/feart.2018.00134

CrossRef Full Text | Google Scholar

Delrieu, G., Braud, I., Berne, A., Borga, M., Boudevillain, B., Fabry, F., et al. (2009). Weather Radar and Hydrology. Adv. Water Resour. 32 (7), 969–974. doi:10.1016/j.advwatres.2009.03.006

CrossRef Full Text | Google Scholar

Fan, Z., Li, W., Jiang, Q., Sun, W., Wen, J., and Gao, J. (2021). A Comparative Study of Four Merging Approaches for Regional Precipitation Estimation. IEEE Access 9, 33625–33637. doi:10.1109/access.2021.3057057

CrossRef Full Text | Google Scholar

Gagne, D. J., McGovern, A., and Xue, M. (2014). Machine Learning Enhancement of Storm-Scale Ensemble Probabilistic Quantitative Precipitation Forecasts. Weather Forecast. 29 (4), 1024–1043. doi:10.1175/waf-d-13-00108.1

CrossRef Full Text | Google Scholar

Germann, U., Berenguer, M., Sempere-Torres, D., and Zappa, M. (2009). REAL-Ensemble Radar Precipitation Estimation for Hydrology in a Mountainous Region. Q.J.R. Meteorol. Soc. 135 (639), 445–456. doi:10.1002/qj.375

CrossRef Full Text | Google Scholar

Giang, P. Q. (2021). Prediction of the Variability of Changes in the Intensity and Frequency of Climate Change Reinforced Multi-Day Extreme Precipitation in the North-Central Vietnam Using General Circulation Models and Generalized Extreme Value Distribution Method. Front. Earth Sci. 8. doi:10.3389/feart.2020.601666

CrossRef Full Text | Google Scholar

Gou, Y., Ma, Y., Chen, H., and Wen, Y. (2018). Radar-derived Quantitative Precipitation Estimation in Complex Terrain over the Eastern Tibetan Plateau. Atmos. Res. 203, 286–297. doi:10.1016/j.atmosres.2017.12.017

CrossRef Full Text | Google Scholar

Groisman, P. Y., Knight, R. W., Easterling, D. R., Karl, T. R., Hegerl, G. C., and Razuvaev, V. N. (2005). Trends in Intense Precipitation in the Climate Record. J. Clim. 18 (9), 1326–1350. doi:10.1175/jcli3339.1

CrossRef Full Text | Google Scholar

Hong, Y., Gochis, D., Cheng, J.-t., Hsu, K.-l., and Sorooshian, S. (2007). Evaluation of PERSIANN-CCS Rainfall Measurement Using the NAME Event Rain Gauge Network. J. Hydrometeorol. 8 (3), 469–482. doi:10.1175/jhm574.1

CrossRef Full Text | Google Scholar

Iwashima, T., and Yamamoto, R. (1993). NOTES AND CORRESPONDENCE : A Statistical Analysis of the Extreme Events : Long-Term Trend of Heavy Daily Precipitation. J. Meteorol. Soc. Jpn. 71 (5), 637–640. doi:10.2151/jmsj1965.71.5_637

CrossRef Full Text | Google Scholar

Kuha, J. (2016). AIC and BIC. Sociol. Methods Res. 33 (2), 188–229. doi:10.1177/0049124103262065

CrossRef Full Text | Google Scholar

Kühnlein, M., Appelhans, T., Thies, B., and Nauß, T. (2014). Precipitation Estimates from MSG SEVIRI Daytime, Nighttime, and Twilight Data with Random Forests. J. Appl. Meteorol. Climatol. 53 (11), 2457–2480. doi:10.1175/jamc-d-14-0082.1

CrossRef Full Text | Google Scholar

Lee, T., Shin, J., Park, T., and Lee, D. (2014). Basin Rotation Method for Analyzing the Directional Influence of Moving Storms on Basin Response. Stoch. Environ. Res. Risk Assess. 29 (1), 251–263. doi:10.1007/s00477-014-0870-y

CrossRef Full Text | Google Scholar

Legates, D. (2000). Real-Time Calibration of Radar Precipitation Estimates. Prof. Geogr. 52 (2), 235–246. doi:10.1111/0033-0124.00221

CrossRef Full Text | Google Scholar

Liu, W., Zhang, Q., Fu, Z., Chen, X., and Li, H. (2018). Analysis and Estimation of Geographical and Topographic Influencing Factors for Precipitation Distribution over Complex Terrains: A Case of the Northeast Slope of the Qinghai–Tibet Plateau. Atmosphere 9 (9), 349. doi:10.3390/atmos9090349

CrossRef Full Text | Google Scholar

Lu, Y., Jiang, S., Ren, L., Zhang, L., Wang, M., Liu, R., et al. (2019). Spatial and Temporal Variability in Precipitation Concentration over Mainland China, 1961–2017. Water 11 (5), 881. doi:10.3390/w11050881

CrossRef Full Text | Google Scholar

Min, X., Ma, Z., Xu, J., He, K., Wang, Z., Huang, Q., et al. (2020). Spatially Downscaling IMERG at Daily Scale Using Machine Learning Approaches Over Zhejiang, Southeastern China. Front. Earth Sci. 8. doi:10.3389/feart.2020.00146

CrossRef Full Text | Google Scholar

Moraux, A., Dewitte, S., Cornelis, B., and Munteanu, A. (2021). A Deep Learning Multimodal Method for Precipitation Estimation. Remote Sens. 13 (16), 3278. doi:10.3390/rs13163278

CrossRef Full Text | Google Scholar

Moraux, A., Dewitte, S., Cornelis, B., and Munteanu, A. (2019). Deep Learning for Precipitation Estimation from Satellite and Rain Gauges Measurements. Remote Sens. 11 (21), 2463. doi:10.3390/rs11212463

CrossRef Full Text | Google Scholar

Morin, E., and Gabella, M. (2007). Radar-Based Quantitative Precipitation Estimation over Mediterranean and Dry Climate Regimes. J. Geophys. Res. 112 (D20). doi:10.1029/2006jd008206

CrossRef Full Text | Google Scholar

Oliver, M. A., and Webster, R. (1990). Kriging: a Method of Interpolation for Geographical Information Systems. Int. J. Geogr. Inf. Syst. 4 (3), 313–332. doi:10.1080/02693799008941549

CrossRef Full Text | Google Scholar

Paxton, A., Schoof, J. T., Ford, T. W., and Remo, J. W. F. (2021). Extreme Precipitation in the Great Lakes Region: Trend Estimation and Relation with Large-Scale Circulation and Humidity. Front. Water 3. doi:10.3389/frwa.2021.782847

CrossRef Full Text | Google Scholar

Ramos, M. H., Creutin, J.-D., and Leblois, E. (2005). Visualization of Storm Severity. J. Hydrol. 315 (1-4), 295–307. doi:10.1016/j.jhydrol.2005.04.007

CrossRef Full Text | Google Scholar

Rongrui, X., and Chandrasekar, V. (1997). Development of a Neural Network Based Algorithm for Rainfall Estimation from Radar Observations. IEEE Trans. Geosci. Remote Sens. 35 (1), 160–171. doi:10.1109/36.551944

CrossRef Full Text | Google Scholar

Rosenfeld, D., and Ulbrich, C. W. (2003). Cloud Microphysical Properties, Processes, and Rainfall Estimation Opportunities. Radar Atmos. Sci. A Collect. Essays Honor David Atlas, Meteorol. Monogr. 30, 237–258. doi:10.1007/978-1-878220-36-3_10

CrossRef Full Text | Google Scholar

Sadeghi, M., Asanjan, A. A., Faridzad, M., Nguyen, P., Hsu, K., Sorooshian, S., et al. (2019). PERSIANN-CNN: Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks–Convolutional Neural Networks. J. Hydrometeorol. 20 (12), 2273–2289. doi:10.1175/jhm-d-19-0110.1

CrossRef Full Text | Google Scholar

Sadeghi, M., Nguyen, P., Hsu, K., and Sorooshian, S. (2020). Improving Near Real-Time Precipitation Estimation Using a U-Net Convolutional Neural Network and Geographical Information. Environ. Model. Softw. 134, 104856. doi:10.1016/j.envsoft.2020.104856

CrossRef Full Text | Google Scholar

Shin, J.-Y., Ro, Y., Cha, J.-W., Kim, K.-R., and Ha, J.-C. (2019). Assessing the Applicability of Random Forest, Stochastic Gradient Boosted Model, and Extreme Learning Machine Methods to the Quantitative Precipitation Estimation of the Radar Data: A Case Study to Gwangdeoksan Radar, South Korea, in 2018. Adv. Meteorol. 2019, 1–17. doi:10.1155/2019/6542410

CrossRef Full Text | Google Scholar

Shu, S.-J., Wang, Y., and Xiong, A.-Y. (2007). Estimation and Analysis for Geographic and Orographic Influences on Precipitation Distribution in China. Chin. J. Geophys. 50 (6), 1482–1493. doi:10.1002/cjg2.1168

CrossRef Full Text | Google Scholar

Sivasubramaniam, K., Sharma, A., and Alfredsen, K. (2018). Estimating Radar Precipitation in Cold Climates: the Role of Air Temperature within a Non-parametric Framework. Hydrol. Earth Syst. Sci. 22 (12), 6533–6546. doi:10.5194/hess-22-6533-2018

CrossRef Full Text | Google Scholar

Sønderby, C. K., Espeholt, L., Heek, J., Dehghani, M., Oliver, A., Salimans, T., et al. (2020). Metnet: A Neural Weather Model for Precipitation Forecasting. ArXiv, abs/2003.12140.

Google Scholar

Sorooshian, S., Hsu, K., Gao, X., Tao, Y., and Ihler, A. (2016). A Deep Neural Network Modeling Framework to Reduce Bias in Satellite Precipitation Products. J. Hydrometeorol. 17 (3), 931–945. doi:10.1175/jhm-d-15-0075.1

CrossRef Full Text | Google Scholar

Sun, W., and Huang, Y. (2011). Global Warming over the Period 1961-2008 Did Not Increase High-Temperature Stress but Did Reduce Low-Temperature Stress in Irrigated Rice across China. Agric. For. Meteorol. 151 (9), 1193–1201. doi:10.1016/j.agrformet.2011.04.009

CrossRef Full Text | Google Scholar

Teschl, R., Randeu, W. L., and Teschl, F. (2006). “Weather Radar Estimates of Rainfall Adjusted to Rain Gauge Measurements Using Neural Networks,” in The 2006 IEEE international joint conference on neural network proceedings. doi:10.1109/IJCNN.2006.247242

CrossRef Full Text | Google Scholar

Tian, W., Yi, L., Liu, W., Huang, W., Ma, G., and Zhang, Y. (2020). Ground Radar Precipitation Estimation with Deep Learning Approaches in Meteorological Private Cloud. J. Cloud Comp. 9 (1). doi:10.1186/s13677-020-00167-w

CrossRef Full Text | Google Scholar

Wang, P., Chen, P., Ye, Y., Ding, L., and Cottrell, G. (2018a). “Understanding Convolution for Semantic Segmentation,” in IEEE Winter Conference on Applications of Computer Vision (WACV), 1451–1460. doi:10.1109/wacv.2018.00163

CrossRef Full Text | Google Scholar

Wang, X., Girshick, R., Gupta, A., and He, K. (2018b). “Non-Local_Neural_Networks,” in IEEE/CVF Conference on Computer Vision and Pattern Recognition, 7794–7803. doi:10.1109/CVPR.2018.00813

CrossRef Full Text | Google Scholar

Wasko, C., Sharma, A., and Rasmussen, P. (2013). Improved Spatial Prediction: A Combinatorial Approach. Water Resour. Res. 49 (7), 3927–3935. doi:10.1002/wrcr.20290

CrossRef Full Text | Google Scholar

Wu, H., Yang, Q., Liu, J., and Wang, G. (2020a). A Spatiotemporal Deep Fusion Model for Merging Satellite and Gauge Precipitation in China. J. Hydrol. 584, 124664. doi:10.1016/j.jhydrol.2020.124664

CrossRef Full Text | Google Scholar

Wu, J., Han, Z., Xu, Y., Zhou, B., and Gao, X. (2020b). Changes in Extreme Climate Events in China under 1.5 °C–4 °C Global Warming Targets: Projections Using an Ensemble of Regional Climate Model Simulations. J. Geophys. Res. Atmos. 125 (2), 106. doi:10.1029/2019jd031057

CrossRef Full Text | Google Scholar

Wu, W., Zou, H., Shan, J., and Wu, S. (2018). A Dynamical Z-R Relationship for Precipitation Estimation Based on Radar Echo-Top Height Classification. Adv. Meteorol. 2018, 1–11. doi:10.1155/2018/8202031

CrossRef Full Text | Google Scholar

Wu, Y., Tang, Y., Yang, X., Zhang, W., and Zhang, G. (2021). Graph Convolutional Regression Networks for Quantitative Precipitation Estimation. IEEE Geosci. Remote Sens. Lett. 18 (7), 1124–1128. doi:10.1109/lgrs.2020.2994087

CrossRef Full Text | Google Scholar

Yang, D., Koike, T., and Tanizawa, H. (2004). Application of a Distributed Hydrological Model and Weather Radar Observations for Flood Management in the Upper Tone River of Japan. Hydrol. Process. 18 (16), 3119–3132. doi:10.1002/hyp.5752

CrossRef Full Text | Google Scholar

Zhang, C., Wang, H., Zeng, J., Ma, L., and Guan, L. (2020). Short-Term Dynamic Radar Quantitative Precipitation Estimation Based on Wavelet Transform and Support Vector Machine. J. Meteorol. Res. 34 (2), 413–426. doi:10.1007/s13351-020-9036-7

CrossRef Full Text | Google Scholar

Zhang, M., Li, W., Bi, X., Zong, L., Zhang, Y., and Yang, Y. (2021a). Synergistic Modulations of Large-Scale Synoptic Patterns and Local-Scale Urbanization Effects on Summer Rainfall in South China. Front. Clim. 3. doi:10.3389/fclim.2021.771772

CrossRef Full Text | Google Scholar

Zhang, Y., Chen, S., Tian, W., and Chen, S. (2021b). Radar Reflectivity and Meteorological Factors Merging‐Based Precipitation Estimation Neural Network. Earth Space Sci. 8 (10). doi:10.1029/2021ea001811

CrossRef Full Text | Google Scholar

Zhao, R., Chen, B., and Xu, X. (2021). Intensified Moisture Sources of Heavy Precipitation Events Contributed to Interannual Trend in Precipitation Over the Three-Rivers-Headwater Region in China. Front. Earth Sci. 9. doi:10.3389/feart.2021.674037

CrossRef Full Text | Google Scholar