Ground Motion Time History Simulation for Seismic Response History Analysis

In the seismic design and analysis of important structures, ground motion time histories are generally required as the input for the conduction of seismic response history analysis. Taking a selected spectrum as the target, the approaches for generating spectral compatible time histories based on artificial or synthetic ground motion and real recorded earthquake ground motion, respectively, are commonly used and discussed in this review. The pure artificial approaches have relative higher effectiveness and computational efficiency, while the approaches by adjusting the real records could simulate the nonstationary in both time domain and frequency domain.

Introduction

With the rapid development of water conservancy and hydropower projects in China, large-scale hydropower projects have been constructed in southwestern China. Once an earthquake strikes, the collapse of large hydropower projects and related projects will lead to immeasurable consequences. Therefore, the seismic safety evaluation of major engineering structures is crucial. The methods that can be used for seismic safety evaluation and analysis mainly include pseudo-static method, response spectrum method and seismic response history analysis method (SRHA). Both the pseudo-static method and the response spectrum method cannot fully simulate the response of the structure in the earthquake process, and cannot reflect the effect of vibration duration. SRHA makes up for the shortcomings of the above methods and becomes an important means of seismic response analysis of important engineering structures (Cheng et al., 2021). The seismic design codes of major engineering structures require that the SRHA excited by seismic time histories be carried out in the design, so as to more accurately grasp the dynamic response characteristics of the structure. In SRHA, it is extremely important to reasonably determine the seismic ground motion input. Ground motion input is not only the premise of engineering seismic safety evaluation, but also the primary problem to be solved for engineering seismic safety. Seismic response time history analysis is the main time history analysis method for seismic design verification and seismic identification of major engineering systems, structures, and components.

At present, there are usually three main methods to obtain seismic time history input: 1) Linear scaling of real ground motion records; 2) Spectral compatible pure artificial (or synthetic) time histories; 3) Spectral compatible time histories based on real records. However, considering the limited number and geographical distribution of strong earthquakes recorded in history, there are few earthquake records that can be directly used for construction sites in engineering practice. And therefore, the artificial (or synthetic) ground motion and the adjusted ground motion based on real records are investigated by scholars. This paper aims to summarize and comment on the research methods proposed by domestic and foreign scholars and adopted by national norms in recent years, hoping to be beneficial to the follow-up research.

Spectral Compatible Pure Artificial Time History

Random vibration theory are generally used in the generation of artificial ground motion to simulate the non-stationary characteristics of ground motion, and the synthesized ground motion is usually composed of sinusoidal function as the basis function. Jennings et al. (1968) first systematically introduced the synthesis method of time history. Firstly, a stationary random process was generated, and the user-specified envelope function is multiplied by the random process to obtain a non-stationary random process. Furtherly, the non-stationary random process was continuously iteratively adjusted in the frequency domain until the acceptable matching precision with the target spectrum was achieved. Levy and Wilkinson (1975) used the external envelope function of real ground motion to simulate some non-stationary characteristics of real ground motion. Preumont (1980) and Preumont (1984) used the probability model to generate the energy spectral density of the equivalent stationary Gaussian process with the same maximum response expectation as the target design spectrum. In this series of methods, Fourier series was used to represent the acceleration time history of ground motion. Based on the random vibration theory, the design ground motion time history matching with the target spectrum is generated, and various envelope functions or shape functions are used to simulate the non-stationary characteristics of real ground motion records.

The artificial synthetic ground motion time history can also be obtained from the source models considering the propagation path and site effect. Beresnev and Atkinson (1997) and Beresnev and Atkinson (1998) assumed a ${\omega }^2$ spectrum and specified the duration length and attenuation model, so that it propagated to the specified observation point. The program can generate ground motions under hard rock site conditions and obtain ground motions with frequency-dependent site method coefficients. Boore (2003) simulated ground motion by combining the parametric or functional description function of amplitude spectrum of ground motion with the random phase spectrum related to earthquake magnitude and epicentral distance. Giaralis and Spanos (2009) obtained simulated non-stationary seismic motions by using the stochastic dynamic method based on wavelet technology. Zeng et al. (1994) used the composite source model of the convolution of the synthetic Green’s function to simulate the seismic generation process of complex geological rupture. However, due to the uncertainty of source parameters of historical earthquakes, the generated ground motion has high sensitivity.

The actual recorded ground motions are quite complex, which are affected by source characteristics, rupture process, source propagation path and local site conditions. Although it is convenient to describe ground motion with a small amount of parameters, such representation for earthquake ground motion are incomplete. Since there are not enough real ground motion records available in many regions of the world, many scholars have devoted themselves to the study of adjusting the design spectrum of real ground motion records matching targets.

Spectral Compatible Time History Based on Real Records

Domestic and foreign scholars have proposed a variety of methods to obtain seismic design ground motion by matching with design response spectrum of real seismic records, including the methods based on time-frequency domain transform and inverse transform, the methods based on time domain superposition of adjustment function, and the methods based on components decomposition.

Methods Based on Time-Frequency Domain Transform and Inverse Transform

Fourier transform and wavelet transform are the most commonly used time-frequency domain transform to adjust natural ground motion in the frequency domain. The Fourier transform method (Tsai, 1972) is to apply the suppression filter or overlay the corresponding sine wave in the time domain at the specific frequency where the response spectrum is higher or lower than the target response spectrum value to achieve the purpose of adjusting the response spectrum. Mukherjee and Gupta (2002) and Kaveh and Mahdavi (2016) introduced wavelet transform to transform seismic records into frequency domain, and adjusted the amplitude of different frequency domain components, which can retain the local time-frequency characteristics of the original earthquake. However, the method of adjusting ground motion time history in frequency domain cannot well describe the instantaneous characteristics of ground motion time history.

Methods Based on Superposition of Adjustment Functions

In the method of superposition correction function in time domain, the earliest Kaul (1978) continuously adjusted the local amplitude at a certain time in time domain to improve the fitting accuracy of response spectrum and target spectrum. Abrahamson (1992) used tapered chord wavelet function to locally adjust the time history of ground motion in time domain, but the addition of this wavelet function requires reference to baseline correction method to eliminate the introduced offset. Hancock et al. (2006) solved the time-history shift by using improved sine wavelet function. In order to improve the effectiveness and computational efficiency of the matching process, Al Atik and Abrahamson (2010) put forward an improved tapered cosine wavelet function $w{}_m\left(t\right)$,

$w_m\left(t\right)=\cos \left[{\mathrm{\Omega }}_m\left(t-t_m+\mathrm{\Delta }{t}_m\right)\right]e^{-{\left(\frac{t-t_m+\mathrm{\Delta }{t}_m}{{\gamma }_m}\right)}^2}(1)$

$\begin{array}{ccc}\mathrm{\Delta }{t}_m=\frac{1}{{\mathrm{\Omega }}_m}{\tan }^{-1}\left(\frac{\sqrt{1-{\beta }_m^2}}{{\beta }_m}\right),& {\mathrm{\Omega }}_m={\omega }_m\sqrt{1-{\beta }_m^2},& {\gamma }_m=\frac{6.508}{{\mathrm{\Omega }}_m^{0.93}}\end{array}(2)$

where $t_m-\Delta t_m$ is the peak occurrence time of wavelet, ${\gamma }_m$ is a frequency dependent coefficient for adjusting duration of wavelet, which can generate time history matching with the target spectrum, and improve the computational efficiency, stability and effectiveness of adjustment, as shown in Figure 1.

FIGURE 1

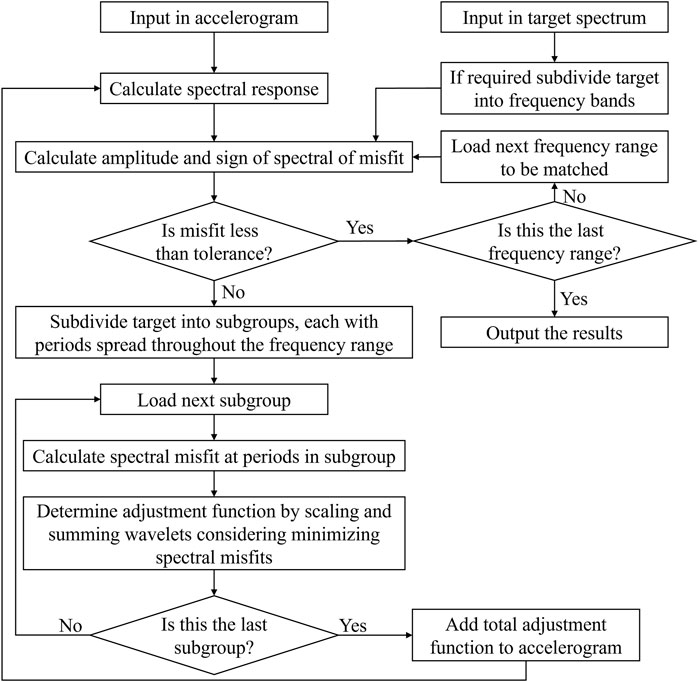
FIGURE 1. General flowchart for wavelet-based spectrum matching (Hancock et al., 2006).

The wavelet-based spectrum matching method has the advantage of high efficiency and less changing of the original earthquake ground motion. However, the time-domain superposition adjustment function often needs to shift the frequency-domain information to the time-domain, sometimes making the time-domain information pulse, resulting in ground motion distortion; each iteration is only for a specific damping or frequency, which is easy to affect the fitting accuracy of damping or frequency, and the matching process often has the “waterbag effect”.

Methods Based on Components Decomposition

Compared with the superposition of irrelevant adjustment functions on ground motion, the spectral characteristics of natural ground motion can be less disturbed by adjusting the frequency component of ground motion itself. Ni et al. (2011), Ni et al. (2013) and Li et al. (2016) used Hilbert-Huang transform (HHT) to decompose the initial ground motion into a set of modal functions with non-overlapping frequency bands, and adjusted the amplitude of each modal function to match the target spectrum by optimization procedures. Amiri et al. (2009) introduced the wavelet packet method to decompose the ground motion into a high-frequency non-overlapping wavelet packet coefficient matrix, and proposed a fast and stable convergence matching method.

Li et al. (2017) introduced the eigenfunction of a six-order eigenproblem as basis to expand earthquake ground motion. Yang et al. (2019) and Yang et al. (2021) proposed an iterative procedure based on eigenfunction expansion by considering the influence on the response spectrum $S_m$ from all other frequency components by

$S_m={\left|{\ddot{u}}_m\left(t\right)\right|}_{\max }={\left|{\displaystyle \sum _{n=N_{\min }}^{N_{\max }}{a}_n\left(-{\omega }_m^2{h}_m\ast {\ddot{\phi }}_n\right)}\right|}_{\max }(3)$

in which $h_m=e^{-\zeta {\omega }_{m}t}\frac{\sin {\omega }_{m}t}{{\omega }_m}$, ${\ddot{\phi }}_n\left(t\right)$ is the basis function. Numerical examples showed a tighter matching with the target spectrum and relative less variability in structural response compared to wavelet-based method.

Novel Methods Combining Intelligent Optimization Algorithms

The process of spectrum matching can also be seen as an optimization problem to find the most matching time history with the target design spectrum. With the rapid improvement of computer hardware level, a variety of intelligent optimization algorithms are also booming, including neural network (Amiri and Bagheri, 2008; Ghaffarzadeh et al., 2013; Izadi and Mohammadi, 2016), particle swarm optimization (PSO) (Amiri et al., 2012; Fakhrmoosavy et al., 2018), genetic algorithm (Naeim et al., 2004), stochastic neural network (Lin and Ghaboussi, 2001; Rajabi and Amiri, 2020) and so on, which are widely used in ground motion simulation in earthquake engineering. Rajasekaran et al. (2006) proposed five neural network models to generate artificial ground motions and response spectra for sites with less real ground motion records using wavelet transform and principal component analysis. Amiri et al. (2012) proposed a method by using PSO algorithm to optimize the network weights, using wavelet packet transform technology for multi-layer feedforward neural network method to generate near-field artificial ground motion acceleration time history matching with the target spectrum, the flowchart of which is shown in Figure 2.

FIGURE 2

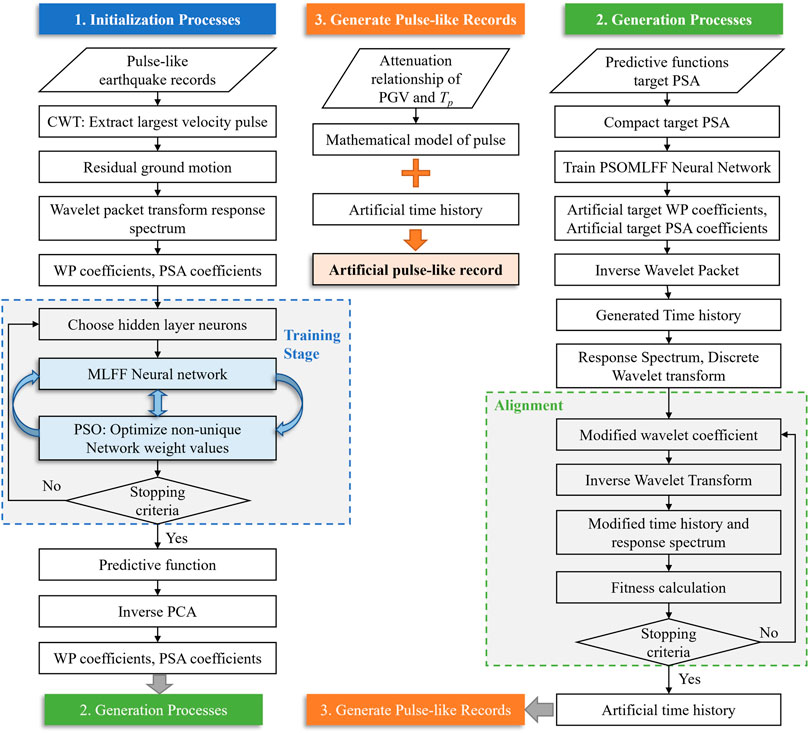
FIGURE 2. Flowchart for the method using PSO-based neural network (Amiri et al., 2012).

The utilization of intelligent algorithm is able to effectively capture the important properties of real accelerograms such as pulse period, energy, amplitude, and frequency content of ground motions and generate ground motions compatible with different design spectra if appropriate training data are provided.

Conclusion

Seismic ground motion is a key input in the seismic response history analysis for crucial engineering structures, systems and components. With the enrich of earthquake records database, conducting structural time history analysis based on real records has become an inevitable trend. With the development of analytical methods and computation level, various approaches with high computational efficiency, matching accuracy and complex computation theory come out. In view of the current research status, the authors believe that the following research needs to be further strengthened:

(1) For the seismic analysis of crucial structures or hydropower stations with components or equipment, it is important to provide seismic ground motion time histories that are compatible with the target spectra with different damping ratio.

(2) More factors could be involved as evaluation index for simulating ground motion in SRHA, including performance-based index of structural response, structural characteristics, etc.

(3) Although the existing methods are capable of generating time histories matching well with the spectra, the simulation of ground motion nonstationary is not reasonably solved yet. The application of intelligent algorithms on the ground motion simulation is promising if the database is sufficient.

Author Contributions

LY was responsible for writing the draft. ZF collected and organized the research literature. DW contributed agreed upon the review objectives, discussion and review.

Funding

The research was financially supported by the Scientific Research Fund of Institute of Engineering Mechanics, China Earthquake Administration (2021D14), the Natural Science Foundation of Jiangsu Province (BK20210476), and the Fundamental Research Funds for the Central Universities (JUSRP121056).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abrahamson, N. A. (1992). Non-Stationary Spectral Matching. Seismol. Res. Lett. 63 (1), 30.

Google Scholar

Al Atik, L., and Abrahamson, N. (2010). An Improved Method for Nonstationary Spectral Matching. Earthq. Spectra 26 (3), 601–617. doi:10.1193/1.3459159

CrossRef Full Text | Google Scholar

Amiri, G. G., and Bagheri, A. (2008). Application of Wavelet Multiresolution Analysis and Artificial Intelligence for Generation of Artificial Earthquake Accelerograms. Struct. Eng. Mech. 28 (2), 153–166. doi:10.12989/sem.2008.28.2.153

CrossRef Full Text | Google Scholar

Amiri, G. G., Bagheri, A., and Razaghi, S. A. S. (2009). Generation of Multiple Earthquake Accelerograms Compatible with Spectrum via the Wavelet Packet Transform and Stochastic Neural Networks. J. Earthq. Eng. 13 (7), 899–915. doi:10.1080/13632460802687728

CrossRef Full Text | Google Scholar

Amiri, G. G., Rad, A. A., Aghajari, S., and Hazaveh, N. K. (2012). Generation of Near-Field Artificial Ground Motions Compatible with Median-Predicted Spectra Using PSO-Based Neural Network and Wavelet Analysis. Computer‐Aided Civ. Infrastructure Eng. 27 (9), 711–730. doi:10.1111/j.1467-8667.2012.00783.x

CrossRef Full Text | Google Scholar

Beresnev, I. A., and Atkinson, G. M. (1998). FINSIM--a FORTRAN Program for Simulating Stochastic Acceleration Time Histories from Finite Faults. Seismol. Res. Lett. 69 (1), 27–32. doi:10.1785/gssrl.69.1.27

CrossRef Full Text | Google Scholar

Beresnev, I. A., and Atkinson, G. M. (1997). Modeling Finite-Fault Radiation from the ωn Spectrum. Bull. Seismol. Soc. Am. 87 (1), 67–84.

Google Scholar

Boore, D. M. (2003). Simulation of Ground Motion Using the Stochastic Method. Pure Appl. Geophys. 160 (3-4), 635–676. doi:10.1007/PL00012553

CrossRef Full Text | Google Scholar

Cheng, H., Wang, D.-S., Li, H.-N., Zou, Y., and Zhu, K.-N. (2021). Investigation on Ultimate Lateral Displacements of Coastal Bridge Piers with Different Corrosion Levels along Height. J. Bridge Eng. 26 (4), 04021015. doi:10.1061/(ASCE)BE.1943-5592.0001696

CrossRef Full Text | Google Scholar

Fakhrmoosavy, S. H., Setayeshi, S., and Sharifi, A. (2018). An Intelligent Method for Generating Artificial Earthquake Records Based on Hybrid PSO-Parallel Brain Emotional Learning Inspired Model. Eng. Comput. 34 (3), 449–463. doi:10.1007/s00366-017-0551-9

CrossRef Full Text | Google Scholar

Ghaffarzadeh, H., Izadi, M. M., and Talebian, N. (2013). Neural Network-Based Generation of Artificial Spatially Variable Earthquakes Ground Motions. Earthquakes Struct. 4 (5), 509–525. doi:10.12989/eas.2013.4.5.509

CrossRef Full Text | Google Scholar

Giaralis, A., and Spanos, P. D. (2009). Wavelet-based Response Spectrum Compatible Synthesis of Accelerograms-Eurocode Application (EC8). Soil Dyn. Earthq. Eng. 29 (1), 219–235. doi:10.1016/j.soildyn.2007.12.002

CrossRef Full Text | Google Scholar

Hancock, J., Watson-Lamprey, J., Abrahamson, N. A., Bommer, J. J., Markatis, A., McCoyh, E., et al. (2006). An Improved Method of Matching Response Spectra of Recorded Earthquake Ground Motion Using Wavelets. J. Earthq. Eng. 10 (Suppl. 001), 67–89. doi:10.1080/13632460609350629

CrossRef Full Text | Google Scholar

Izadi, M. M., and Mohammadi, M. (2016). Simulation of Spectrum-Correspondent Accelerogram by Using Artificial Neural Networks. J. Vibroeng 18 (3), 1617–1630. doi:10.21595/jve.2016.16623

CrossRef Full Text | Google Scholar

Jennings, P. C., Housner, G. W., and Tsai, N. C. (1968). Simulated Earthquake Motions. Pasadena, California: Calfornia Institute of Technology.

Google Scholar

Kaul, M. K. (1978). Spectrum-Consistent Time-History Generation. J. Engrg. Mech. Div. 104 (4), 781–788. doi:10.1243/03093247V13423110.1061/jmcea3.0002379

CrossRef Full Text | Google Scholar

Kaveh, A., and Mahdavi, V. R. (2016). A New Method for Modification of Ground Motions Using Wavelet Transform and Enhanced Colliding Bodies Optimization. Appl. Soft Comput. 47, 357–369. doi:10.1016/j.asoc.2016.06.021

CrossRef Full Text | Google Scholar

Levy, S., and Wilkinson, J. (1975). Generation of Artificial Time-Histories, Rich in All Frequencies, from Given Response Spectra. Nucl. Eng. Des. 38 (2), 241–251. doi:10.1016/0029-5493(76)90099-6

CrossRef Full Text | Google Scholar

Li, B., Ly, B. L., Xie, W. C., and Pandey, M. D. (2017). Generating Spectrum‐Compatible Time Histories Using Eigenfunctions. Bull. Seismol. Soc. Am. 107 (3), 1512–1525. doi:10.1785/0120160206

CrossRef Full Text | Google Scholar

Li, B., Xie, W.-C., and Pandey, M. D. (2016). Generate Tri-directional Spectra-Compatible Time Histories Using HHT Method. Nucl. Eng. Des. 308, 73–85. doi:10.1016/j.nucengdes.2016.08.009

CrossRef Full Text | Google Scholar

Lin, C.-C. J., and Ghaboussi, J. (2001). Generating Multiple Spectrum Compatible Accelerograms Using Stochastic Neural Networks. Earthq. Engng. Struct. Dyn. 30 (7), 1021–1042. doi:10.1002/eqe.50

CrossRef Full Text | Google Scholar

Mukherjee, S., and Gupta, V. K. (2002). Wavelet-Based Generation of Spectrum-Compatible Time-Histories. Soil Dyn. Earthq. Eng. 22, 799–804. doi:10.1016/S0267-7261(02)00101-X

CrossRef Full Text | Google Scholar

Naeim, F., Alimoradi, A., and Pezeshk, S. (2004). Selection and Scaling of Ground Motion Time Histories for Structural Design Using Genetic Algorithms. Earthq. Spectra 20 (2), 413–426. doi:10.1193/1.1719028

CrossRef Full Text | Google Scholar

Ni, S.-H., Xie, W.-C., and Pandey, M. D. (2013). Generation of Spectrum-Compatible Earthquake Ground Motions Considering Intrinsic Spectral Variability Using Hilbert-Huang Transform. Struct. Saf. 42, 45–53. doi:10.1016/j.strusafe.2013.01.008

CrossRef Full Text | Google Scholar

Ni, S.-H., Xie, W.-C., and Pandey, M. D. (2011). Tri-directional Spectrum-Compatible Earthquake Time-Histories for Nuclear Energy Facilities. Nucl. Eng. Des. 241, 2732–2743. doi:10.1016/j.nucengdes.2011.06.014

CrossRef Full Text | Google Scholar

Preumont, A. (1980). A Method for the Generation of Artificial Earthquake Accelerograms. Nucl. Eng. Des. 59 (2), 357–368. doi:10.1016/0029-5493(80)90205-8

CrossRef Full Text | Google Scholar

Preumont, A. (1984). The Generation of Spectrum Compatible Accelerograms for the Design of Nuclear Power Plants. Earthq. Engng. Struct. Dyn. 12 (4), 481–497. doi:10.1002/eqe.4290120405

CrossRef Full Text | Google Scholar

Rajabi, E., and Amiri, G. G. (2020). Generation of Critical Aftershocks Using Stochastic Neural Networks and Wavelet Packet Transform. J. Vib. Control 26 (5-6), 331–351. doi:10.1177/1077546319879536

CrossRef Full Text | Google Scholar

Rajasekaran, S., Latha, V., and Lee, S. C. (2006). Generation of Artificial Earthquake Motion Records Using Wavelets and Principal Component Analysis. J. Earthq. Eng. 10 (5), 665–691. doi:10.1080/13632460609350614

CrossRef Full Text | Google Scholar

Tsai, N.-C. (1972). Spectrum-Compatible Motions for Design Purposes. J. Engrg. Mech. Div. 98 (2), 345–356. doi:10.1061/jmcea3.0001587

CrossRef Full Text | Google Scholar

Yang, L., Xie, W. C., Xu, W., Ly, B.-L., Wang, H., and Meng, Q. (2021). Directional Components of a Seismic Design Accelerogram. J. Earthq. Eng., 1–19. doi:10.1080/13632469.2021.1881657

CrossRef Full Text | Google Scholar

Yang, L., Xie, W. C., Xu, W., and Ly, B. L. (2019). Generating Drift‐Free, Consistent, and Perfectly Spectrum‐Compatible Time Histories. Bull. Seismol. Soc. Am. 109 (5), 1674–1690. doi:10.1785/0120190005

CrossRef Full Text | Google Scholar

Zeng, Y., Anderson, J. G., and Yu, G. (1994). A Composite Source Model for Computing Realistic Synthetic Strong Ground Motions. Geophys. Res. Lett. 21 (8), 725–728. doi:10.1029/94GL00367

CrossRef Full Text | Google Scholar