S-Wave Attenuation Variation and its Impact on Ground Motion Amplitudes During 2016–2017 Central Italy Earthquake Sequence

A very energetic seismic sequence struck the central Apennines, Italy, in 2016–2017, with a series of damaging earthquakes, three of them with moment magnitudes M ≥ 5.9, and five of them with M ≥ 5.0, occurred over a few months between 24 August 2016, and late 2017. Several studies explained the phenomenon of a cascading earthquake sequence with fluid movements that provoked the rupture of different parts of the fault segments at different times and locations (e.g., Miller, Nature, 2004, 427, 724–727; Gabrielli, Frontiers in Earth Science, section Structural Geology and Tectonics, 2022; Malagnini, Frontiers in Earth Science, section Solid Earth Geophysics, 2022). In this study, we investigated the variation of crustal S-wave attenuation in terms of the frequency-dependent quality factor Q(f) before and after the main events (including the Amatrice, Visso, and Norcia sub-sequences, hereafter, AVN, and periods before and after the AVN multi-mainshock sequence). The spectral characteristics of regional attenuation in the central Apennines, as well as of the earthquake sources of the AVN sequence, are derived through regression analysis using a large set of seismograms; Q(f) is modeled, together with the bilinear geometrical spreading, g(r), using a widely used tool, namely, random vibration theory, RVT (Cartwright and Longuet-Higgins, 1956). The primary objective of this effort was to examine how the variability of crustal anelastic attenuation would impact the earthquake-induced ground motions. The latter is quantified in terms of peak ground accelerations (PGAs), peak ground velocities (PGVs), and pseudo spectral accelerations (PSAs) at 0.3 and 2 s . Here, we showed that the main events of the AVN sequence strongly affect crustal S-wave attenuation, including its frequency dependence. However, the effects of 1/Q(f) fluctuations on earthquake-induced ground motions are small and have a negligible impact on the seismic hazard.

1 Introduction

The central Apennines is one of Italy’s most seismically active areas, with a long history of earthquakes which have strongly influenced seismic hazard and risk-related studies in Italy (Akinci et al., 2009). The recent sequences that occurred between 2009 and 2017 caused widespread building collapses due to the closeness of the causative fault to heavily populated urban areas, and to the elevated vulnerability of old edifices in cobblestone. In the 5 months following the 24 August 2016 Amatrice earthquake, nine seismic events with magnitude M > 5.0 occurred in the area. The most significant event of the sequence (M6.3) occurred in the vicinity of the town of Norcia and was preceded, 4 days earlier, by an M5.9 foreshock near Visso. The long sequence provided us with a massive set of seismological data (three events with magnitude larger than 5.9, up to a maximum magnitude of 6.3, see Malagnini and Munafò (2018), and http://eqinfo.eas.slu.edu/Eq. c/Eq. c_mt/MECH.IT/). The highest PGA values (∼0.8 g for the M6.3 Norcia and M6.0 Amatrice earthquakes) were recorded in the near-source area, and were the largest ever documented during an Italian earthquake. The attenuation characteristics of the crust have always been thought to play a significant role in refining seismic hazards for the study area (Lombardi et al., 2005; Akinci et al., 2009).

Several studies in the central Apennines demonstrated the effect of fluid migration along with relatively high-permeability faults, and the possible occurrence of earthquake, including triggered ones, due to an increased pore-pressure from the diffusion of over-pressured fluids (Miller et al., 2004; Lucente et al., 2010; Malagnini et al., 2012; ; Chiarabba et al., 2020; Akinci et al., 2020; Gabrielli et al., 2022; Malagnini et al., 2022).

It has long been understood that seismic attenuation has the potential to be a relevant source of information about the Earth’s interior. It is an important parameter that could greatly improve our understanding of subsurface processes, integrating the seismic velocity and conceding more detailed outcomes (Jackson and Anderson, 1970; Cormier 2011). Attenuation of seismic waves is strongly affected by rock permeability, pore fluids, and saturation levels (Winker and Nur, 1982; Malagnini et al., 2019; Gabrielli et al., 2022; Malagnini et al., 2022). Elevated seismic attenuation is usually observed at active faults in the brittle crust (Rietbrock, 2001).

Malagnini et al. (2022) investigated the seismic attenuation variation as a function of time and frequency before, during, and after the central Apennines seismic sequence of 2016–2017; they concluded that it is the variations in crustal rock’s permeability that drive the observed changes in seismic attenuation. Following Muir-Wood and King (1993), they hypothesized that the coseismic stress drop of a normal-faulting earthquake causes a sudden closure of such cracks, which translates into a sudden decrease in permeability and seismic attenuation. However, Malagnini et al. (2022) did not assess the ground motion parameters induced by the mainshocks of the sequence, parameterizing the seismic wave attenuation, earthquake source, as well as the distortions introduced by subsurface heterogeneities at the recording sites.

Gabrielli et al. (2022) attempted separating scattering and absorption contributions to the total attenuation of coda waves and provided images of their spatial (2D) and temporal variations in different frequency bands during the AVN seismic sequence. Their coda attenuation tomography demonstrated an evident variation between the pre-sequence and the sequence time windows, before and after the three mainshocks of the AVN sequence.

Here, we investigated the anelastic attenuation of S-wave, expressed in terms of a frequency-dependent seismic quality factor Q(f). We also intend to better understand the attenuation characteristics of the crust, and to explore its variability as a function of frequency and time during the central 2016–2017 earthquake sequence. Our main objective was to examine the sensitivity of peak ground acceleration (PGA), peak ground velocity (PGV), and pseudo spectral accelerations (PSAs) at 0.3 and 2 s to the temporal variability of crustal attenuation.

Here, we separated crustal attenuation from source excitation and site response; we performed that by exploiting the theoretical framework of random vibration theory (RVT, see Cartwright and Longuet-Higgins, 1956; Malagnini et al., 2019; Malagnini et al., 2022), which allows using the peak values of narrowband-filtered time histories, instead of the noisier Fourier amplitudes (details in Malagnini and Dreger, 2016). We investigated the events registered between 1 January 2016, and 29 March 2018. We modeled the empirical propagation and excitation terms related to frequency-dependent quality factor, a geometric spreading function, a stress drop parameter, and an operator to account for site effects during the sequence (coseismic and post-seismic periods). For this purpose, we considered velocity seismograms recorded before and after the three main events (including the mainshocks), corresponding to different time windows. Regressions were carried out using large amounts of waveforms from the study area, from earthquakes with magnitudes ranging between M2.0 and M6.3.

First of all, we obtained the scaling relationships for high-frequency ground motion throughout the inversion technique that has been introduced by Raoof et al. (1999). This approach is widely and successfully used for regionalized ground motion studies in many parts of the world (Morasca et al., 2006; Akinci et al., 2006; Malagnini et al., 2007; Malagnini et al., 2011; D’Amico et al., 2012; Akinci et al., 2013; Akinci et al., 2014; D’Amico et al., 2018). Second, the regional attenuation and source scaling were parameterized to describe the observed ground motions as a function of distance, frequency, and seismic moment (or moment magnitude).

A simple grid-search was adopted to perform in order to optimize the attenuation parameters in our scaling model. The earthquake-induced ground motions for the M6.3 Norcia earthquake are obtained by a stochastic finite-fault simulation approach based on dynamic corner frequencies (Motazedian and Atkinson 2005; Boore 2009), which makes use of the parameters obtained here, describing frequency-dependent attenuation, source excitation, and site responses. Finally, comparing simulations and actual recordings, we show the variability of seismic ground motion, and consequently of seismic hazard, in the study region.

2 Dataset

We used weak- and strong-motion data from central Italy (Italy), including the AVN seismic sequence (2.0 ≤ M ≤ 6.3). We selected the focal depths and the hypocentral distances of the events with similar locations from those shallower than 20 km and shorter than 100 km, respectively, distributed along an 80 km long NW-SE-oriented fault system. Almost all the focal mechanisms dominated by normal faulting agree with the extensional tectonic regime in the central Apennines (Zhong et al., 2018; Buttinelli et al., 2021). The dataset contains 1,445 selected events and more than 20,000 recordings between 1 January 2016 and 29 March 2018. This dataset covers more than 2 years of recorded seismicity, including the AVN sequence where three M ≥ 5.9 events occurred over a few months between August 24 and 30 October 2016 (Chiaraluce et al., 2017).

The locations of selected events (dots) and the seismic stations (triangles) are shown in Figure 1A. The distribution of seismicity is indicated with different colors corresponding to the time frames according to the following event start and end dates. These dates during the sequence (24 August 2016–30 January 2017) are selected before and after main events to have a similar time window, approximately a month, at each phase and to have a sufficient number of earthquakes to analyze. However, for the pre- and after sequences (after the Capitignano sequence), we selected events recorded in eight and 2 months, since the frequency of earthquake occurrence decreases over time. Hereinafter, we presented the selected phases in detail.

• January 1 through 23 August 2016: 87 events with M > 3.2 (hereafter phase-I, pre-sequence).

• August 24 through 25 September 2016 (the M6 Amatrice sequence): 130 events with 3.0 ≤ M ≤ 6.0 including the Amatrice mainshock of 24 August 2016, at 1:36:32 UTC (hereafter phase-II, the Amatrice sequence).

• September 30 through 29 October 2016 (the M5.9 Visso sequence): 98 events with 3.0 ≤ M ≤ 5.9 including the Visso mainshock of October 26 at 19:18:08 UTC (hereafter phase-III, the Visso sequence).

• October 30 through 29 November 2016 (the Norcia M6.3 sequence): 339 events with 3.0 ≤ M ≤ 6.33 including the Norcia mainshock of October 30 at 06:40:18 UTC (hereafter phase-IV, the Norcia sequence).

FIGURE 1

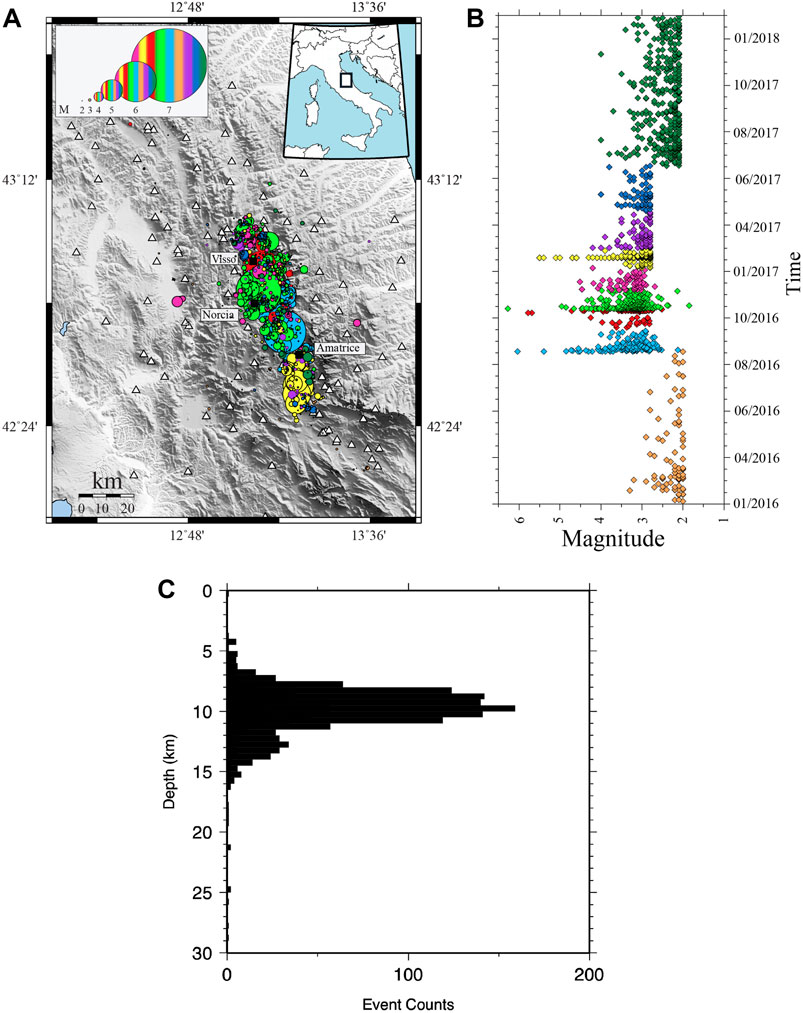
FIGURE 1. (A) Map shows the seismicity distribution in the central Apennines area, earthquakes are shown as colored dots as a function of the time period, where the size of the circle represents the magnitude of the quake. Black squares indicate the main cities in the area, white triangles represent the seismic stations belonging to the National Accelerometric Network (RAN) and the National INGV Seismic Network (RSN). (B) We divided the sequence into nine phases as given in Table 1. (C) Focal depth of the selected events.

• 29 November 2016 through 1 January 2017: 67 events with 3.0 ≤ M ≤ 4.7 (hereafter phase-V).

• 1 January 2017 through 30 January 2017: 176 events recorded with 3.0 ≤ M ≤ 5.5 (hereafter phase-VI, the Capitignano sequence).

• 3 February 2017 through 30 March 2017: 83 events recorded with 3.0 ≤ M ≤ 4.7 (hereafter phase-VII).

• April 1, 2017 through 10 June 2017: 71 events with magnitudes 3.0 ≤ M ≤ 4.0 (hereafter phase-VIII).

• 11 June 2017 through 29 March 2018: 408 events with 2.0 ≤ M ≤ 4.0 (hereafter phase-IX).

Figure 1B shows the event distributions over the nine time windows, each of them presented with a different color. It should be noted that the minimum magnitude in the various periods is variable, that is, M3.0 during the period of the sequence and M2.0 before and after the sequence. The number of events belonging to different time phases is given in Table 1, together with the maximum magnitude registered in each time period. Figure 1C shows the distribution of the focal depths in our dataset, all within 15 km. We gathered seismograms registered by both the accelerometric stations of the Italian strong-motion network (RAN Rete Accelerometrica Nazionale) and the 24-bit broadband weak-motion seismological stations of the Digital Seismic Network run by the Istituto Nazionale di Geofisica e Vulcanologia (INGV). Strong- and weak-motion recordings were downloaded from the ITACA (ITalian ACcelerometric Archive) website or from the European Strong Motion, ESM database, and from the European Integrated Data Archive (EIDA) repository, respectively.

TABLE 1

TABLE 1. S-wave attenuation values obtained in this study as a function of selected time phases and related information.

3 Method and Data Analysis

Our method has been widely and successfully used to determine crustal attenuation, source-, and site-related parameters from recorded seismograms (Akinci et al., 2014; Malagnini and Dreger, 2016; Munafò et al., 2016; Malagnini et al., 2019). These studies demonstrated that the observed seismic attenuation varies significantly from region to region. Regression results can be utilized for estimating earthquake-induced ground motions (i.e., peak acceleration and peak velocity), given a moment magnitude and a hypocentral distance. Rather than regressing Fourier amplitudes, our technique maximizes the signal-to-noise ratio (SNR) by analyzing peak values of narrow bandpass–filtered time histories. Our method is based on a tool called random vibration theory (RVT), developed by Cartwright and Longuet-Higgins (1956). A suitable set of constraints is used for decoupling the attenuation parameters from source and site terms, and for producing a smooth attenuation function; see Malagnini and Dreger (2016) for details.

First of all, we visually examined all the seismograms and picked the P and S arrival times for quality control. For each phase described earlier, peak ground velocities were measured in selected narrow frequency bands from 0.5 to 22.5 Hz; in each time window and for each central frequency, peak values were subsequently regressed to obtain a frequency-dependent attenuation function, a set of excitation terms, and of site responses. The 16 narrow frequency bands were centered at a set of frequencies f_c = 0.5, 0.75, 1.25, 1.75, 2.50, 3.50, 5.0, 6.5, 8.5, 10.50, 12.50, 14.50, 16.50, 18.50, 20.50, and 22.5 Hz; the bandwidth around each central frequency went from $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.f_c$ to $\sqrt{2}{f}_c$; filters were causal eight-pole Butterworth, high-pass and low-pass, respectively.

The peak values of the S-waves from the ith source, recorded at the jth site, at a hypocentral distance r and around a central frequency f_c , are measured on the filtered waveforms, a_peak(r_ij, f_c), and can be defined as A_ij (f_c, r)=log₁₀[a_peak(r, f_c)]. RVT allowing the use of the convolution theorem over peak values (instead of Fourier amplitudes) in our measurements were cast in a matrix form at each frequency band.

$A_{\text{ij}}\left(f_{\text{c}}\text{, r}\right)\mathrm{=}{\text{SRC}}_{\text{i}}\left(f_{\text{c}}\text{,}{r}_{f\text{ix}}\right)\mathrm{+}\text{Path}\left(f_{\text{c}}\text{,}r\text{,}{r}_{f\text{ix}}\right)\mathrm{+}{\text{Site}}_j\left(f_{\text{c}}\right).(1)$

The reference distance r_fix is chosen within the range of observed distances. In order to stabilize inversions in Eq. 1 and to bring a physical meaning to source and site terms, two constraints are applied; Path(r = r_fix)=0 at any f_c, and ΣSite_j (f_c)=0. It is important to note that the Site_j (f_c) term in Eq. 1 indicates the ith individual component of the ground motion. So the horizontal source spectrum is relative to the reference distance r_fix, and to the average network site.

We arbitrarily chose a reference distance r_fix = 40 km. Such a hypocentral distance is chosen to be well inside the range of examined distances: it should be far from the source so that errors in source depth do not significantly alter hypocentral distances, and not so far to be in the range of supercritical reflections from the Moho. Furthermore, a smoothing constraint was implemented to the propagation term Path (f_c, r, r_fix), establishing a condition of minimum roughness with a null second derivative.

The crustal path term is described in terms of a piece-wise linear continuous function (in loglog).

$\text{Path}\left(f_{\text{c}}\text{,}r\text{,}{r}_{f\text{ix}}\right)={\displaystyle {\sum }_{n=1}^{Nnodes}{L}_{n}Pat{h}_n}(2)$

L_n (r) is a linear interpolation function, n is the nodes for the distance segments, and Path_n is the value of the attenuation term at the hypocentral distance of the n-th node. We regularly sampled the dataset over a logarithm scale, choosing a regular length for each node.

Finally, regressions were performed over the selected central frequencies using an L1-norm inversion, as Bartels and Conn (1980) reported. The results are presented individually for all terms being SRC_i (f_c, r_fix), Path (f_c, r, r_fix), and Site_j (f_c) (Eq. 1). The effective signal duration is determined from a time window, including the 5% and 75% of seismic energy following the S-wave arrival. The effective time duration is an important parameter for the ground-motion prediction. It can play an essential role for earthquake damage potential and engineering purposes, notably in evaluating liquefaction and the inelastic deformation, as well as the energy dissipation of the short-period buildings (Bommer and Martinez-Pereira 1999).

4 Ground Motion Modeling and Parameterizations

In order to quantify the regression results concerning the geometrical spreading, the frequency-dependent Q(f), the source scaling, and the site effects, each term in Eq. 1 is modeled using RVT and/or stochastic time-domain simulations (Boore, 1983; Boore and Joyner, 1997). Following RVT, the peak value of the narrow bandpass–filtered seismograms is used instead of the Fourier amplitude included in the same frequency band. The narrow band-pass filters are needed to make the seismograms somewhat “stationary” as prescribed by RVT, yet they cannot be too narrow in order to allow the existence of meaningful peaks.

Clearly, the use of peak values maximizes the signal-to-noise ratios of our results. Moreover, knowing the effective duration of ground motion within a specified bandwidth near a specific center frequency, RVT allows the application of the convolution theorem to peak values. Together with the Parseval’s equality, we can switch between time and frequency domains and write the matrix form for the linear inversion of the peak values (Eq. 1). In brief, given a stationary, random time history of length T, RVT enables a measure of its peak value following a_peak ≈ ξa_RMS, where a_RMS is the root mean square value of the time history calculated in the time window starting at the onset of S-waves, and having a duration T. The parameter ξ can be calculated from the spectral moments of the time history. The band-pass filtering procedure delivers non-zero Fourier amplitudes only between the two-corner frequencies ($\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.f_c$ and $\sqrt{2}{f}_c$), and the following equation holds (Malagnini and Dreger, 2016):

$a_{RMS}\left(f_i\right)=\sqrt{\frac{{\displaystyle \underset{0}{\overset{T}{\int }}{a}^2\left(t,f_i\right)dt}}{T}=}\sqrt{\frac{{\displaystyle \underset{f_{1i}}{\overset{f_{2i}}{\int }}{\widehat{a}}^2\left(f\right)df}}{T}}.(3)$

In our study, we assume that the filtered seismogram is different from zero between the S-wave arrival time (elapsed time t = 0), and an elapsed time t = T. In turn, the effective duration of the ground motion (T) is estimated for each seismogram and for each central frequency. In other words, we have an effective duration which is a function of the central frequency and of the hypocentral distance: $T=T\left(f_c,r\right)$. Finally, once we develop an attenuation/excitation model for the region under investigation, as well as an effective duration function, RVT can be applied to estimate peak values as a function of earthquake size and hypocentral distance, such as, peak accelerations and velocities, and/or response spectra (see for details Malagnini and Dreger, 2016; Lavrentiadis et al., 2021).

4.1 Attenuation Parameters

We modeled the empirically-based attenuation term (Path_emp(r, r_fix, f_c)) by specifying both the crustal anelastic attenuation, represented by the quality factor Q(f) = Q_o(f/ f_ref)ⁿ, and the geometrical spreading g(r). The latter is modeled as a piecewise continuous function of the hypocentral distance (r). The role of the reference frequency f_ref=1.0 Hz is just to keep the non-dimensional nature of the attenuation parameter.

${\text{Path}}_{\text{theo}}\left(r\text{, }{r}_{f\text{ix}}\text{,}f\text{c}\right)\mathrm{=}\text{log}10\left[\left(g\left(r\right)\text{/}g\left(r_{f\text{ix}}\right)\right)\left(\mathit{\text{exp}}\mathrm{-}\pi f\left(r-r_{f\text{ix}}\right)\text{/}\beta Q\left(f\right)\right)\right].(4)$

Equation 4 reveals the effects of frequency-dependent geometrical spreading and anelastic attenuation, relying, for each frequency, on the average velocity structure along the propagation pathway and rock’s physical properties (Aki, 1980). It should be noted that the theoretical attenuation term described in (Eq. 4) is also normalized to zero at the reference distance r_fix.

Figure 2 presents the regressed empirical attenuation peak velocity amplitudes (colored curves), and the theoretical attenuation curves (black curves) obtained from the RVT-based modeling. The results are relative to the nine time windows that correspond to the nine phases described earlier (prior to, and during the sequence). The L2 norm grid search through the parameter space of the geometrical spreading g(r) and the quality factor Q(f) (the 1-Hz attenuation parameter Q_o and the exponent n defining its frequency dependence) gives us the optimal theoretical attenuation models (Path_theo(r, r_fix, f_c)), defined by minimizing the RMS-value of the residuals in each phase of the sequence. For this purpose, we used the observed durations as a function of distance and frequency (Supplementary Figure S1). The residual between the inverted attenuation curves, Path_emp (r, r_fix, f_k) (Figure 2 colored lines) and for the theoretical model curves, Path_theo (r, r_fix, f_k) (Figure 2 black lines) were calculated to determine our preferred ground-motion propagation model for each of the nine subsets as:

$\mathit{RMSE}\mathrm{=}\sqrt{\frac{{{\displaystyle \sum }}_{k,i}{\left(Pat{h}_{emp}\left(r,r_{fix},f_k\right)-Pat{h}_{theo}\left(r,r_{fix},f_k\right)\right)}^2}{{{\displaystyle \sum }}_{k,i}\sigma \left(f_k\right)}},(5)$

where σ (f_k) values are these emerging from the regression results; f_k = 0.5, 0.75, … and 22.5 Hz; values of i are 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 km. Finally, we obtained the solution with the minimum RMSE at all chosen time windows.

FIGURE 2

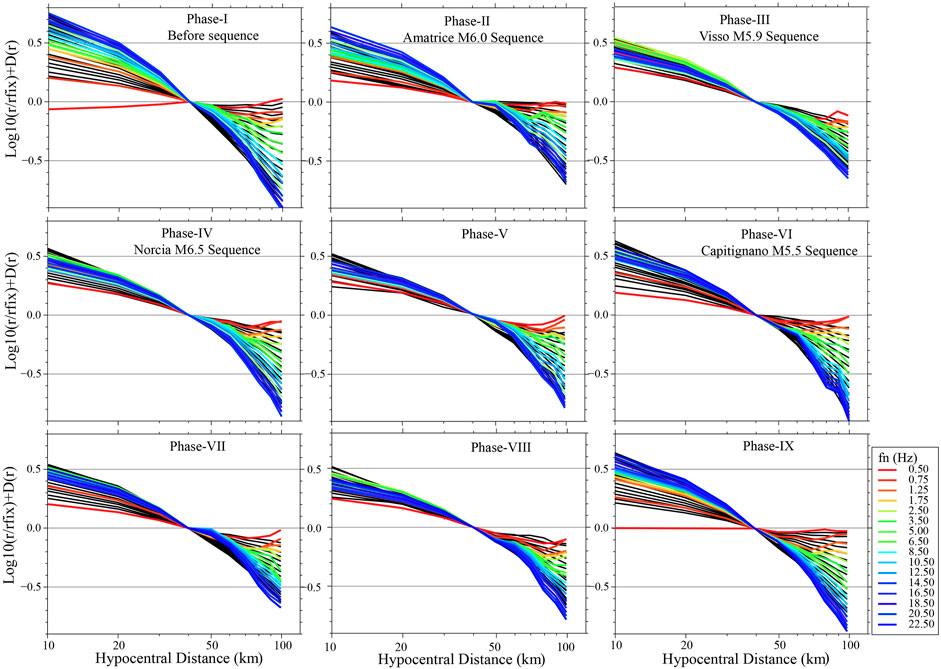
FIGURE 2. Empirical regional attenuation, Path_emp (r, r_fix, f_k) curves experienced by the narrow-band filtered amplitudes of the ground motion, at the 16 central frequencies of 0.5, 0.75, 1.25, 1.75, 2.50, 3.50, 5.0, 6.5, 8.5, 10.50, 12.50, 14.50, 16.50, 18.50, 20.50, and 22.5 Hz that are shown by colored lines at each selected time periods. Black lines in the background are obtained with the attenuation model, Path_theo (r, r_fix, f_k). All lines are normalized by a 1/r decay (the horizontal dashed lines represent the 1/r decay). The reference hypocentral distance is 40 km.

We allowed the quality factor, Q(f) to vary between 20 and 200 and the frequency dependence coefficient, n between 0.2 and 1.5, and the exponent α of the geometrical spreading, g(r)=r^−α, to vary between 0.3 and 1.2 for distance before and after the r_fix = 40 km in terms Path_theo (r, r_fix, f_k) (Eq. 4) using merged datasets. Using the dataset before the sequence, optimum results were obtained for Q(f)=75f^0.6, g(r)=r^−1.1 for distances between 5 and 40 km, and g(r)∼r^−0.5 for distances greater than 40 km. For shorter distances, r^−1.1 describes body-wave crustal propagation, whereas for distances beyond 40 km, g(r)∼r^−0.5 describes the propagation of a wavefield dominated by surface waves. These coefficients are very close to those calculated in the central Apennines by Malagnini et al. (2011). The optimal functional form g(r) obtained pre-sequence was fixed in all the grid searches performed on the subsequent phases, and only the parameters Q_o and n were altered. Figure 3 presents the residuals calculated varying Q_o, n, and geometrical spreading coefficient, g(r), in the nine subsets of data, from 1 January 2016 to 29 March 2018, where the best-fit values are indicated. The best-fit attenuation parameters are presented in Table 1 and Figure 4. Errors are estimated using the F distribution at the 90 percent confidence level. We consider the solutions with normalized residuals (concerning the minimum value) are smaller than 1.3–1.5 from the misfit values in Figure 3 (for details Mayeda et al., 1992; Del Pezzo and Bianco, 2010).

FIGURE 3

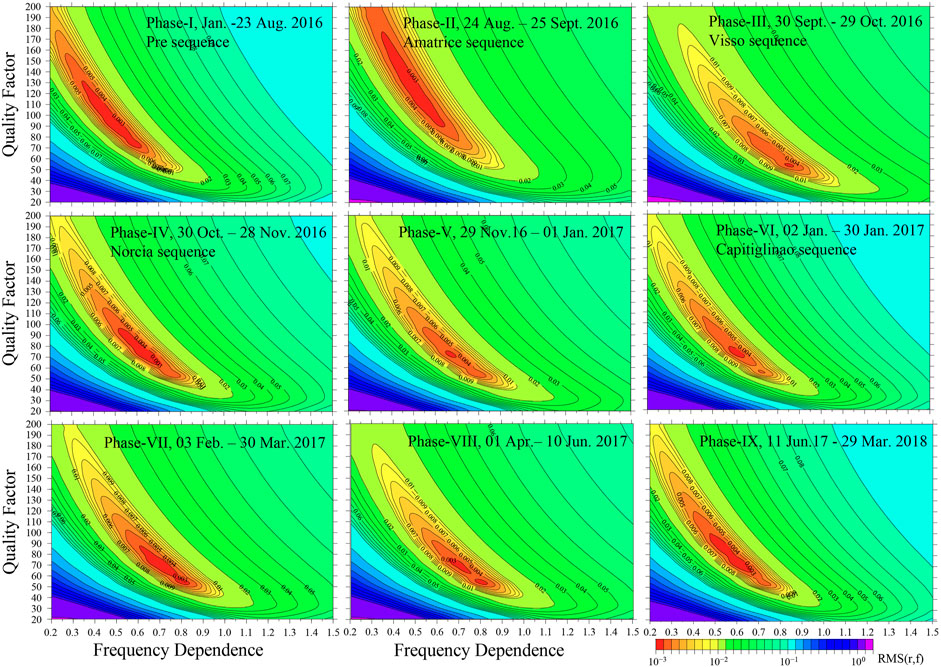
FIGURE 3. Residuals (rms(dist)) obtained from comparing empirical log10(Path_emp(r, r_fix, f_c)) and theoretical log10(Path_theo(r, r_fix, f_c)) of the horizontal components, plotted as a function of Q₀ and n.

FIGURE 4

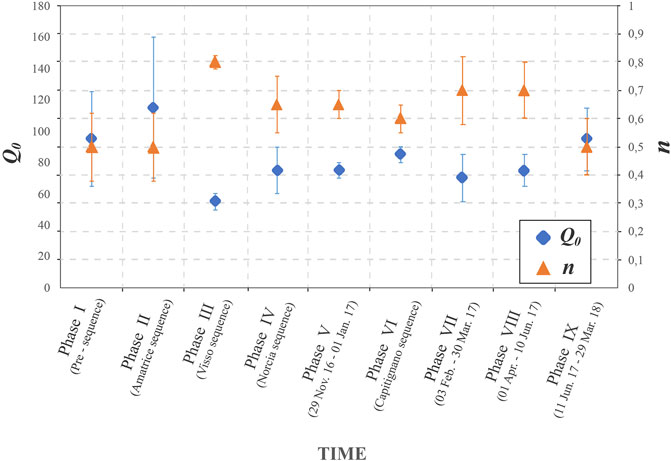
FIGURE 4. Frequency-dependent Q as Q(f) = Q₀ (f/f_ref)ⁿ , f_ref = 1 Hz. The Q₀ (blue dots) and the frequency dependence of the attenuation, n (orange triangles) and their standard errors as a function of nine time phases include Amatrice, Visso, and Norcia earthquake sequences (for the details see Table 1).

4.2 Source and Site Parameters

The seismic sources of our dataset are modeled following the Brune’s (1970), Brune (1971) single-corner frequency spectral model, with the static stress parameter that is a function of the earthquake’s magnitude following the equation:

$\text{SRC}\left(f_{\text{c}},r_{f\text{ix}}\right)={\mathit{log}}_{10}\left[s\left(f,M\right)V\left(f\right)g\left(r_{\text{fix}}\right)\mathit{exp}\left[\mathit{-}\left(\pi f_{\text{c}}{r}_{\text{fix}}\right)\mathrm{/}\left(\beta Q\left(f\right)\right)\right]\mathit{exp}\left(\mathit{-}\pi f{k}_{\mathrm{eff}}\right)\right],(6)$

where s(f, M) = R_ΘΦFN M_o 4πρβ³ (2πf )S(f ) is the Fourier velocity spectra, R_ΘΦ is the average radiation pattern, 0.55, F is the free-surface amplifications, 2.0, and N = 0.707 is the partition of energy into two horizontal recorded components (Boore and Boatwright 1984). S(f) is basically the single corner frequency Brune crack model with corner frequency, f₀ = 0.491(Δσ_BruneM_o)^1/3, Δσ_Brune is the stress-drop parameter in units of Pa, and M₀ is the seismic moment. The parameter ρ is the crustal average density and β is the shear wave velocity at the source of 3.5 km/s.

The term exp(−πfκ_eff) is a simplified version of the more correct functional form: <V(f) exp(−πfκ₀)>_avg, where V(f) represents the site amplification relative to hard rock. The term κ_eff presents the average high-frequency attenuation in the very shallow crust directly beneath each site associated with the parameter κ₀ and the frequency-dependent site amplification, (f) (Boore, 1983; Anderson and Hough, 1984; Boore and Joyner, 1997). Supplementary Figure S2 presents the site terms from the regression on horizontal filtered peak amplitudes. Because the constraint: ΣSite_j (f_c) = 0 was employed to the horizontal component site terms at the stations, we may render the excitation terms that present the average site of the network, 40 km away from the hypocenter. The site term is averaged over all the stations since the constraints adopted for the regression present an average value inferred from the network sites. As a result, the average effect of all the network sites is mapped on the source term (and this is why the average network site effect is included in Eq. 6). Since the site terms continue to trade-off with the observed excitation terms (as seen in Eq. 6), they do not have a functional utility in the existing form, although to look at the behavior of all the individual site terms allows the detection of instrument- or digital amplification-related malfunctions. For the definition of predictive relationships for the ground motion, the most useful site descriptions are represented by the generic site models by Boore and Joyner (1997).

The inverted excitation terms determined by the regression analysis are presented in Figure 5 (black curves) for each M > 5.5 earthquakes in the database. Theoretical (RVT) curves using the Brune spectral model are presented in the same figure (colored curves) at a distance r_fix = 40 km, including the effects of propagation to reference distance due to geometrical spreading and frequency-dependent attenuation parameter. In order to fit the theoretical excitations to the empirical ones, we used a stress drop parameter and the generic rock site amplification factor (the term V(f)exp(−πfκ_eff) in Eq. 6).

FIGURE 5

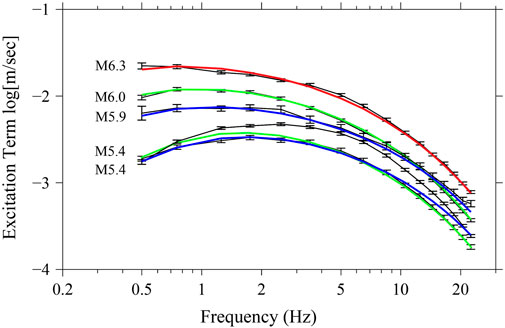
FIGURE 5. Empirical (black) and theoretical (colored) excitation spectra at 40 km distance obtained for the peak of the filtered amplitudes derived from RVT synthetics in the frequency range from 0.5 to 22.5 Hz. The green, blue, and red lines show the predicted excitation terms obtained by using Eq. 6, at the moment magnitudes corresponding to those calculated for the plotted events M6.0 and M5.4 with Q(f)=115 ± 45f ^0.50±0.12, events M5.9 and M5.4 with Q(f) = 55 ± 5f^{0.8 ± 0.025}, and M6.3 Norcia earthquake with Q(f)=70 ± 15f ^0.65±0.1, respectively.

The optimized attenuation parameters for each phase were used to determine the source-related parameters from the best visual fit between inverted and theoretical excitation spectra. The fit for the earthquakes, excellent at all frequencies, is obtained from the following values of the Brune stress drop: Δσ = 15 and 20 MPa for magnitudes M6.0 and M6.3, respectively. Our modeling effort indicates a clear trend for the stress parameter, which steadily increases with magnitude. This behavior together with the retrieved stress drops is in agreement with those obtained by Malagnini and Munafò (2018).

The high-frequency parameter κ_eff is estimated as κ_eff = 0.035 s by fitting the high-frequency part of the spectra of small earthquakes since it is independent of the earthquake size. The soil site category NEHRP B/C boundary site condition with V_s30 of 760 ms⁻¹ is used as the representative generic rock site type amplification in the study area to model the SRC (f_c, r_fix ), excitation terms. Finally, we employed this path and source scaling parameters to estimate a series of ground motion parameters in the study region.

5 Results

5.1 Temporal Variability of Averaged Seismic Attenuation

Our results (Table 1 and Figure 4) provide homogeneous estimates of averaged S-wave quality factor Q(f) for each of the nine selected time windows, showing that the seismic attenuation was not constant over time during the earthquake sequence.

Before the sequence (phase-I, between 1 January 2016 and 23 August 2016), the attenuation term is modeled using a frequency-dependent quality factor, Q(f) = 95 ± 30f ^{0.5 ± 0.12}, together with the geometrical spreading defined by the following bilinear relationship: g(r)=r^−1.1, for r ≤ 40 km and r^−0.5 for distances larger than 40 km.

During the 2016–2017 earthquake sequence, we observed some fluctuations in the attenuation and frequency dependence over the time windows. The attenuation of seismic waves decreases while its frequency dependence increases: Q(f) = 115 ± 45f ^{0.50 ± 0.12} in phase-II (from the 24^th August Amatrice earthquake, M6.0 until the 25^th September 2016, just before the Visso earthquake).

In phase-III (from the 30^th September, Visso earthquake, M5.9 until the 29^th October 2016 just before the Norcia earthquake), both the attenuation parameter and its frequency dependence change: Q(f ) = 55 ± 5f ^{0.80 ± 0.025}. This behavior is evident in Figure 2, where all attenuation curves for the different frequency ranges of S-wave decrease with distance similarly, presenting a high-frequency dependence of attenuation.

In the phase-IV from the 30^th October, Norcia earthquake, M6.3 until the 28^th November 2016, the attenuation parameter Q_o increases, whereas its frequency dependence decreases slightly, Q(f ) = 75 ± 15f ^{0.65 ± 0.12}.

During the phases V, VI, VII, and VIII from the end of November 2016 until the 11^th June 2017, we retrieved similar attenuation values to the previous one as in the fourth one, being Q(f )=75f ^0.65 with slight fluctuations on the Q(f ) and its degree of the frequency dependence. This latest variation in attenuation is quite different from those observed during the Amatrice, Visso, Norcia sequence, suggesting that the major events strongly influenced the attenuation parameters. Finally, from June 2017 to the end of March 2018, we determined Q(f ) = 95 ± 20f ^{0.5 ± 0.1}, similar to the one obtained for the phase-I.

5.2 Investigating the Effects of Seismic Attenuation on Ground Motion Parameters

Utilizing the S-wave seismic attenuation and the source scaling, together with the duration of the ground motions revealed in this study, we produced high-frequency synthetic seismograms. To evaluate the impact of the variation of the seismic attenuation on the ground motion in the central Apennines, we analyzed several ground motion parameters, PGA, PGV, and two PSAs at 0.3 and 2 s for the M6.3, Norcia earthquake of 30 October 2016, as being the largest earthquake occurred during the seismic sequence and probably the best-recorded large earthquake in Italy. The attenuation parameters, together with the source and site-related parameters (Table 2) obtained for the phases II, III, and IV, correspond to Amatrice, Visso, and Norcia earthquake sequences and are introduced for the ground motion simulations through a finite fault stochastic method as given in the Supplementary Appendix A (Motazedian and Atkinson, 2005; Boore, 2009). In this way, we demonstrated the relative implication of this parameter to the ground motion parameters (PGA, PGV, and PSA at 0.3 and 2 s).

TABLE 2

TABLE 2. Model parameters for the finite-fault simulation of the 30 October 2016, M6.3 Norcia Italy earthquake.

5.2.1 Comparisons Between Observed and Simulated Ground Motions

In this section, we compared the simulated accelerations and velocities with the 30 October 2016 Norcia earthquake’s observed ground motions registered by numerous digital stations of temporary and permanent seismic networks expanded shortly after the Amatrice earthquake. We used ground motions recorded at 98 stations located on different site conditions, classified as A, B, C, and D, in accordance with the NTC18 norms. The generic site amplification curves were accounted for in the simulations from different soil classes prescribed by the Italian NTC18 seismic design code: site class-A, -B, -C, and -D following Pischiutta et al. (2021a), Pischiutta et al. (2021b) (Table 2). Figure 6 shows the comparison of the PGAs, and PGVs, PSA at 0.3 and 2 s of the simulated ground motions using three different attenuation parameters with those of the records observed during the M6.3 Norcia earthquake and the reference GMM model (dashed lines) is adopted from Bindi et al. (2011) for three different types of site classes following the Eurocode8, EC8, (CEN 2003).

FIGURE 6

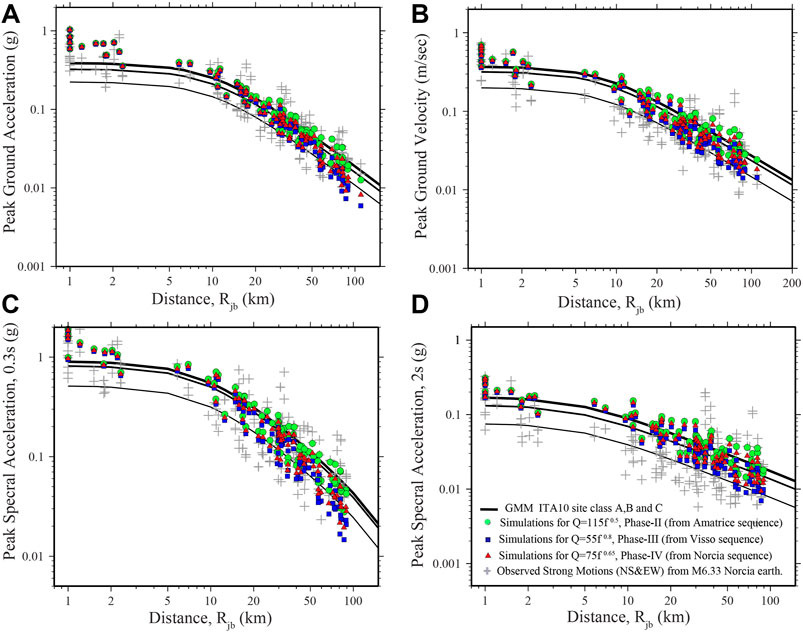
FIGURE 6. (A) Predictions of peak ground acceleration (PGA) for the Norcia mainshock (M6.3) (colored symbols) and comparison with the observed data (gray crosses). Solid black lines refer to Bindi et al. (2011) for sites, A, B, and C classes. Simulation are generated using 1) three different attenuation parameters; Q(f)=105f^0.5 hase-II, from the Amatrice earthquake sequence; Q(f)=55f^0.8 phase-III, from the Visso earthquake sequence; Q(f)=75f^0.65 phase-IV, from the Norcia earthquake sequence and, and 2) geometrical spreading coefficient g(r)=1.0, R < 40 km and g(r)=0.5 for R > 40 km, 3) a stress drop parameter Δσ = 20 MPa and 4 ) κ₀ = 0.025s, 0.035s and 0.045s for sites, A, B, and C classes (B,C,D) same as in frame (a) but for peak ground velocity (PGV), pseudo spectral accelerations at 0.3 and 2 s.

In general, we observed a good compromise between the observed data from the strong-motion recordings and the simulated ground motions from three different attenuation functions, up to a distance of 90 km. The compatibility between observed and predicted data remains the same also at shorter distances, even if the near-field results are governed mainly by source effects, such as directivity. On the other hand, intermediate and longer distances are governed by the path effects such as the frequency-dependent quality factor Q(f) and its frequency dependence. The estimated high-frequency ground motion parameters decay faster (blue squares in Figure 6) during the Visso sequence with Q(f) = 55 ± 5f^{0.80 ± 0.025} compared to those estimated from the Amatrice (green circles) and Norcia (red triangles) sequence attenuation functions, both being less frequency-dependent, Q(f) = 115 ± 45f^{0.50 ± 0.12} and Q(f) = 75 ± 15f^{0.65 ± 0.12} , respectively. This trend is more evident in the case of the PSA at 0.3s, where high-frequency ground motions attenuate quickly as a function of distance compared to PSA at 2s.

Nevertheless, Figure 6 quickly notes that the observed peak ground motions are more scattered than the simulations. This indicates that our simulations cannot capture the total variability of 3-D wave propagation effects (impedance gradients, source radiation pattern, trapped waves, etc.,) through a high-frequency stochastic simulation approach. The observed discrepancy between the recorded (much scattered) and the simulated ground motions (less varied) may also be caused by the insufficient representation of soil amplification factors taken into account in our study (Ojeda et al., 2021; Pitarka et al., 2021).

5.2.2 Residuals Between Observed and Simulated Ground Motions

To get an insight into attenuation variability on the simulated ground motions, we calculated residuals R_jos between observed and simulated values at each distance R_jb, related to station j as R_jos = ln (Y_jobs/Y_jsim), where Y_jobs is the observed ground motion parameter, and Y_jsim is derived from simulations at each station’s distance. We calculated the average values (μ) and standard deviations (σ) from the residuals. The residuals between observed and simulated ground motion parameters, PGA and PGV, as a function of distance, are plotted in Figure 7 for three different site classes (A, B, and C, given with different colors). The residuals of the spectral acceleration parameters at 0.3 and 2 s are presented in Supplementary Figure S3. We observed that, for most stations, the residuals vary between –0.5 and 0.5. The most considerable variation of the R_osj ratio, with increasing residuals, is observed at larger distances, R_jb > 50 km. This deviation becomes evident at high frequencies (PSA at 0.3 s) since the frequency dependence of three attenuation parameters is quite peculiar. The histograms in Figure 8 clearly demonstrate the impact of variation of the attenuation on ground motion parameters; it is very little where the σ is almost invariant around 0.19–0.21 in the case of PGA, while it is 0.21-0-23 for PGV. The median values for the PGA are −0.06, 0.04, and 0.0 for three periods (phases II, III, and IV). The best fit between observed and simulated was captured at phase IV (Norcia sequence), resulting in μ=0.0 and a small σ value. Similarly, we obtained small σ and μ for all of the ground motion parameters, where we used the attenuation function of the Norcia sequence for our simulations. The largest standard deviation and median values determined in the case of the spectral acceleration at 2 s may be caused by the limitations of our approach of the high-frequency stochastic finite-fault approach implemented in this study, which could not wholly capture the longer period effects. In fact, such effects mainly caused by the 3D earth structure cannot be thoroughly simulated with stochastic techniques (Pitarka et al., 2021).

FIGURE 7

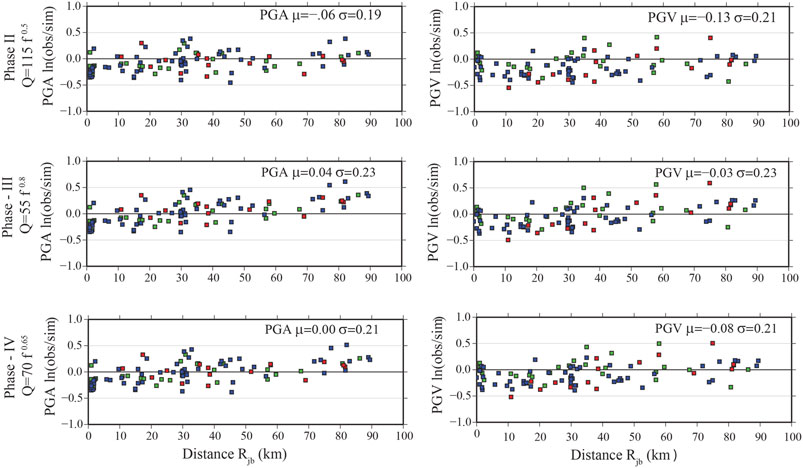
FIGURE 7. Residuals between ground motion parameters observed on data recordings and simulated time-series for the M6.3 Norcia earthquake as a function of distance for three attenuation functions: peak ground acceleration (PGA) and peak ground velocity (PGV).

FIGURE 8

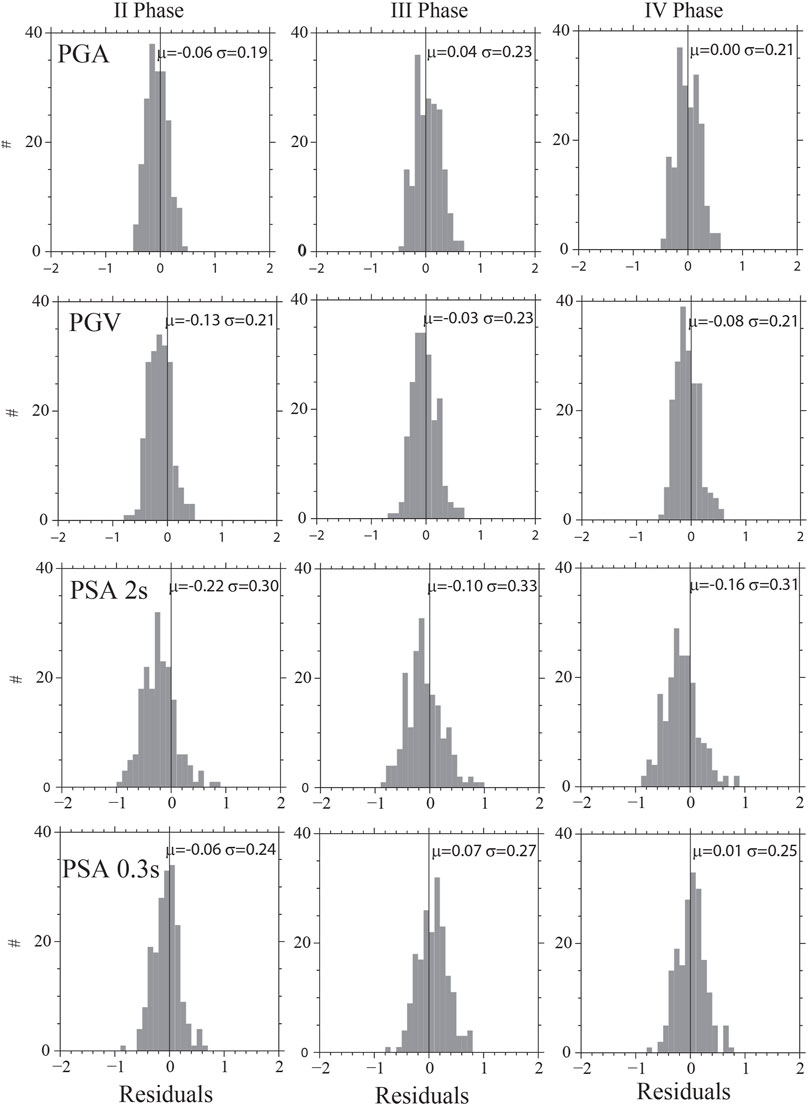
FIGURE 8. Residuals (observed-predicted) of PGA, PGV, and PSA at 0.3 and 2 s calculated for the M6.3 Norcia earthquake. To predict the earthquake-induced ground motion, we used attenuation parameters obtained using the dataset belonging to phases II, III, and IV of the seismic sequence based on a stochastic finite-fault dynamic corner frequency method.

6 Discussion and Concluding Remarks

We carried out a regression analysis to separate path, source, and site effects in different time windows during the 2016–2017 AVN seismic sequence in the central Apennines. The frequency-dependent attenuation parameters and the geometrical spreading function are calculated using a grid-search over a thousand combinations of the attenuation parameters. We found that the crustal attenuation and its frequency dependence are affected by transients induced by the main events and quantify the impact of the seismic wave attenuation variability on the ground-motion hazard in the study region.

In general, we observed that the quality factor (Q_o) is changing between 55 ± 5 and 115 ± 45, and its frequency dependence (n) varies from 0.50 ± 0.025 to 0.80 ± 0.12 over different periods, including Amatrice, Visso, and Norcia earthquake sequences.

Our modeling also indicates a clear trend for the stress-drop parameter, ∆σ, which constantly increases for increasing magnitude being 20 and 15 MPa for M6.3 and M6.0, respectively. These spectral parameters are used to explore the impact of attenuation variability on the seismic hazard through stochastic finite-fault simulations and compared against the observed ground motions for the 2016 Norcia main-shock.

The residuals calculated between the observed and simulated PGA’s and PGV’s for distances up to 100 km offer a quantitative assessment of the effects of the attenuation variability on the earthquake-induced ground motion parameters. When compared to the observed data, our simulations indicate that both the mean values and the standard deviations of PGA, PGV, and PSA at 0.3 and 2 s do not show substantial variations and oscillate slightly over the three time windows (σ = 0.19–0.21, μ = 0.13–0.04) while Q (f ) = Q_o(f/f_ref)ⁿ strongly vary over time, both in amplitude and in frequency dependence. The reason that we observed slight variations on the ground motion parameters for the three different time windows during the AVN earthquake sequence including the Amatrice, Visso, and Norcia main events, is that the attenuation parameter Q(f) does not vary significantly, and provides similar values with the low-end parameter Q_o = 55, which is associated with a high frequency dependence (n = 0.8) and the high-end parameter Q_o = 115, which is associated with a low-frequency dependence (n = 0.45). This variation of attenuation is determined over several time windows as the average values for the study region and may indicate the randomness of the natural phenomenon presented in the stochastic uncertainties. However, the attenuation parameter may present a spatial variation in the studied area and may have a different impact on ground motion variation, which we did not investigate.

The main goal of this study was related to practical purposes for investigating the seismic attenuation variations in the ground motion analysis. In the end, we decided to briefly comment on the temporal variation of attenuation and possible connection with inferred material properties and/or physical states of a medium even if it is out of the scope of this study (e.g., temperature, stress, and water saturation). In fact, it is generally affirmed that bulk permeability and fluid content modulate the seismic attenuation in rocks (Winker and Nur, 1982; Malagnini and Parsons, 2020; Malagnini et al., 2022). When rock permeability reduces due to crack closure, seismic attenuation decreases (Toksӧz et al., 1979). Finally, it is the fault zones that may exhibit high seismic attenuation due to a massive volume of fracturing and fluid content (Ma et al., 2020; Gabrielli et al., 2022; Ma et al., 2022).

For example, Chun et al. (2004) have noted variations in P wave attenuation within a fault region following the 1989 M7.0 Loma Prieta earthquake. This change was interpreted as being generated by coseismic and postseismic variations in permeability and fluid saturation along the fault. Previous studies in the Parkfield area reported a temporal change in attenuation associated with the 2004 M6.0 Parkfield earthquake. Attenuation increased immediately after the earthquake and then slowly decreased over several years (Allmann and Shearer, 2007; Chun et al., 2010; Kelly et al., 2013; Malagnini et al., 2022). Furthermore, numerous studies in the central Apennines investigated the impact of fluid migration along with faults network and the likely earthquake occurrence, triggering seismicity and seismic wave attenuation variations due to increased pore-pressure from the diffusion of over-pressured fluids (Miller et al., 2004; Lucente et al., 2010; Malagnini et al., 2012; Chiarabba et al., 2020; Akinci et al., 2020; Gabrielli et al., 2022; Malagnini et al., 2022).

The attenuation characteristics observed in the present study agree with those remarked in different regions worldwide. For example, high seismic attenuation is observed during the Visso sequence (phase-III), possibly due to increased fracture density and fluid flow across the seismogenic zones. Moreover, in this period, the frequency dependence of attenuation also increased, being ∼ f ^0.8, with that of the previous ∼ f ^0.5. This change could be linked to the fluid saturation and distribution during earthquake sequence since the transformation of energy into heat in solid is relatively independent of frequency while it is proportional to frequency in fluids as demonstrated by Toksӧz et al. (1979) and Tisato and Quintal, (2013) and Tisato and Quintal, (2014).

Our results may provide a valuable framework for understanding the physical parameters that define crustal wave propagation and their impact on the amplitudes of the ground motions observed during the earthquake sequence in Central Italy. We remark that the main events of the sequence strongly influence the crustal S-wave attenuation and frequency dependence, while their effect on the induced ground motion is minimal.

Data Availability Statement

Publicly available datasets were analyzed in this study. These data can be found here: Seismic waveforms were retrieved from the European Integrated Data Archive (EIDA) repository at ORFEUS—EIDA (orfeus-eu.org) and from the Italian Accelerometric Archive at http://itaca.mi.ingv.it (last accessed June 2016). Many of the plots were generated using the Generic Mapping Tools, version 4.2.1 (www.soest.hawaii.edu/gmt, last accessed December 2008; Wessel and Smith, 1998).

Author Contributions

AA, IM, and LM worked together for this manuscript. LM, IM, and AA collected and preprocessed the recordings. AA performed the regression analysis to detect the propagation path attenuation and the source spectra and calculated stochastic simulations for the M6.3 Norcia 2016 earthquake. AA and IM prepared the figures. All authors participated to drafting this article.

Funding

This work has been partially carried out in the framework of the project Pianeta Dinamico/2020–2021 supported by Ministero dell’Istruzione, dell’Università e della Ricerca (MIUR).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.903955/full#supplementary-material

References

Aki, K. (1980). Attenuation of Shear Waves in the Lithosphere for Frequencies from 0.05 to 25 Hz. Phys. Earth Planet. Interiors 21, 50–60. doi:10.1016/0031-9201(80)90019-9

CrossRef Full Text | Google Scholar

Akinci, A., D’Amico, S., Malagnini, L., and Mercuri, A. (2013). Scaling Earthquake Ground Motions in Western Anatolia, Turkey. Phys. Chem. Earth, Parts A/B/C 63, 124–135. doi:10.1016/j.pce.2013.04.013

CrossRef Full Text | Google Scholar

Akinci, A., Galadini, F., Pantosti, D., Petersen, M., Malagnini, L., and Perkins, D. (2009). Effect of Time Dependence on Probabilistic Seismic-Hazard Maps and Deaggregation for the Central Apennines, Italy. Bull. Seismol. Soc. Am. 99, 585–610. doi:10.1785/0120080053

CrossRef Full Text | Google Scholar

Akinci, A., Malagnini, L., Herrmann, R. B., Gok, R., and Sørensen, M. B. (2006). Ground Motion Scaling in the Marmara Region, Turkey. Geophys. J. Int. 166, 635–651. doi:10.1111/j.1365-246x.2006.02971.x

CrossRef Full Text | Google Scholar

Akinci, A., Malagnini, L., Herrmann, R. B., and Kalafat, D. (2014). High-frequency Attenuation in the Lake Van Region, Eastern Turkey. Bull. Seismol. Soc. Am. 104, 1400–1409. doi:10.1785/0120130102

CrossRef Full Text | Google Scholar

Akinci, A., Pezzo, E. D., and Malagnini, L. (2020). Intrinsic and Scattering Seismic Wave Attenuation in the Central Apennines (Italy). Phys. Earth Planet. Interiors 303 (303), 106498. doi:10.1016/j.pepi.2020.106498

CrossRef Full Text | Google Scholar

Allmann, B. P., and Shearer, P. M. (2007). Spatial and Temporal Stress Drop Variations in Small Earthquakes Near Parkfield, California. J. Geophys. Res. 112, 1–17. (B04305). doi:10.1029/2006JB004395

CrossRef Full Text | Google Scholar

Anderson, J. G., and Hough, S. R. (1984). A Model for the Shape of the Fourier Amplitude Spectrum of Acceleration at High Frequencies. Bull. Seism. Soc. Am. 74 (5), 1969–1993.

Google Scholar

Bartels, R. H., and Conn, A. R. (1980). Linearly Constrained Discrete I 1 Problems. ACM Trans. Math. Softw. 6, 594–608. doi:10.1145/355921.355930

CrossRef Full Text | Google Scholar

Beresnev, I. A., and Atkinson, G. M. (1998). FINSIM--a FORTRAN Program for Simulating Stochastic Acceleration Time Histories from Finite Faults. Seismol. Res. Lett. 69, 27–32. doi:10.1785/gssrl.69.1.27

CrossRef Full Text | Google Scholar

Bindi, D., Pacor, F., Luzi, L., Puglia, R., Massa, M., Ameri, G., et al. (2011). Ground Motion Prediction Equations Derived from the Italian Strong Motion Database. Bull. Earthq. Eng. 9 (6), 1899–1920. doi:10.1007/s10518-011-9313-z

CrossRef Full Text | Google Scholar

Bommer, J. J., and Martínez-pereira, A. (1999). The Effective Duration of Earthquake Strong Motion. J. Earthq. Eng. 3, 127–172. doi:10.1080/13632469909350343

CrossRef Full Text | Google Scholar

Boore, D. M., and Boatwright, J. (1984). Average Body-Wave Radiation Coefficients. Bull. Seismol. Soc. Am. 74, 1615–1621. doi:10.1785/bssa0740051615

CrossRef Full Text | Google Scholar

Boore, D. M. (2009). Comparing Stochastic Point-Source and Finite-Source Ground-Motion Simulations: SMSIM and EXSIM. Bull. Seismol. Soc. Am. 99, 3202–3216. doi:10.1785/0120090056

CrossRef Full Text | Google Scholar

Boore, D. M., and Joyner, W. B. (1997). Site Amplifications for Generic Rock Sites. Bull. Seism. Soc. Am. 87, 327–341. doi:10.1785/bssa0870020327

CrossRef Full Text | Google Scholar

Boore, D. M. (2003). Simulation of Ground Motion Using the Stochastic Method. Pure Appl. Geophys. 160, 635–676. doi:10.1007/pl00012553

CrossRef Full Text | Google Scholar

Boore, D. M. (1983). Stochastic Simulation of High-Frequency Ground Motions Based on Seismological Models of the Radiated Spectra. Bull. Seismol. Soc. Am. 73, 1865–1894.

Google Scholar

Brune, J. N. (1971). Correction. J. Geophys. Res. 76, 5002.

Google Scholar

Brune, J. N. (1970). Tectonic Stress and the Spectra of Seismic Shear Waves from Earthquakes. J. Geophys. Res. 75, 4997–5009. doi:10.1029/jb075i026p04997

CrossRef Full Text | Google Scholar

Buttinelli, M., Petracchini, L., Maesano, F. E., D'Ambrogi, C., Scrocca, D., Marino, M., et al. (2021). The Impact of Structural Complexity, Fault Segmentation, and Reactivation on Seismotectonics: Constraints from the Upper Crust of the 2016-2017 Central Italy Seismic Sequence Area. Tectonophysics 810, 228861. doi:10.1016/j.tecto.2021.228861

CrossRef Full Text | Google Scholar

Cartwright, D. E., and Longuet-Higgins, M. S. (1956). The Statistical Distribution of the Maxima of a Random Function. Proc. R. Soc. Lond. A237, 212–232.

Google Scholar

CEN (2003). (pr) EN 1998-1-Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee Standardization: Brussels. Draft No 6, Doc CEN/TC247/SC8/N335, January 2003.

Google Scholar

Chiarabba, C., Buttinelli, M., Cattaneo, M., and De Gori, P. (2020). Earthquakes Driven by Fluid Overpressure: The Apennines Normal Faulting System Case. Tectonics 39. doi:10.1029/2019TC006014

CrossRef Full Text | Google Scholar

Chiaraluce, L., Di Stefano, R., Tinti, E., Scognamiglio, L., Michele, M., Casarotti, E., et al. (2017). The 2016 Central Italy Seismic Sequence: A First Look at the Mainshocks, Aftershocks, and Source Models. Seismol. Res. Lett. 88 (3), 757–771. doi:10.1785/0220160221

CrossRef Full Text | Google Scholar

Chun, K.-Y., Henderson, G. A., and Liu, J. (2004). Temporal Changes inPwave Attenuation in the Loma Prieta Rupture Zone. J. Geophys. Res. 109, B0231715. doi:10.1029/2003JB002498

CrossRef Full Text | Google Scholar

Chun, K.-Y., Yuan, Q.-Y., and Henderson, G. A. (2010). Precursory Rise of P-Wave Attenuation before the 2004 Parkfield Earthquake. Bull. Seismol. Soc. Am. 100 (2), 509–521. doi:10.1785/0120090104

CrossRef Full Text | Google Scholar

Cormier, V. F. (2011). “Seismic, Viscoelastic Attenuation,” in Encyclopedia of Solid Earth Geophysics. Encyclopedia of Earth Sciences Series. Editor H. K. Gupta (Dordrecht: Springer), 1279–1290. doi:10.1007/978-90-481-8702-7_55

CrossRef Full Text | Google Scholar

D'Amico, S., Akinci, A., and Pischiutta, M. (2018). High-frequency Ground-Motion Parameters from Weak-Motion Data in the Sicily Channel and Surrounding Regions. Geophys. J. Int. 214, 148–163. doi:10.1093/gji/ggy107

CrossRef Full Text | Google Scholar

D’Amico, S., Akinci, A., and Malagnini, L. (2012). Predictions of High Frequency Ground-Motion in Taiwan Based on Weak-Motion Data. Geophys. J. Int. 189, 611–628. doi:10.1111/j.1365-246X.2012.05367.x

CrossRef Full Text | Google Scholar

Del Pezzo, E., and Bianco, F. (2010). Two-layer Earth Model Corrections to the MLTWA Estimates of Intrinsic- and Scattering-Attenuation Obtained in a Uniform Half-Space. Geophys. J. Int. 182, 949–955. doi:10.1111/j.1365-246X.2010.04648.x

CrossRef Full Text | Google Scholar

Gabrielli, S., Akinci, A., Ventura, G., Napolitano, F., Del Pezzo, E., and De Siena, L. (2022). Fast-Changes in Seismic Attenuation of the Upper Crust Due to Fracturing and Fluid Migration: the 2016-2017 Central Italy Seismic Sequence. Front. Earth Sci. Sect. Struct. Geol. Tect. 10, 1–18. doi:10.3389/feart.2022.909698

CrossRef Full Text | Google Scholar

Jackson, D. D., and Anderson, D. L. (1970). Physical Mechanisms of Seismic-Wave Attenuation. Rev. Geophys. 8, 1–63. doi:10.1029/rg008i001p00001

CrossRef Full Text | Google Scholar

Kelly, C. M., Rietbrock, A., Faulkner, D. R., and Nadeau, R. M. (2013). Temporal Changes in Attenuation Associated with the 2004 M6.0 Parkfield Earthquake. J. Geophys. Res. Solid Earth 118, 630–645. doi:10.1002/jgrb.50088

CrossRef Full Text | Google Scholar

Lavrentiadis, G., Abrahamson, N. A., and Kuehn, N. M. (2021). A Non-ergodic Effective Amplitude Ground-Motion Model for California. Bull. Earthq. Eng., 1573–1456. doi:10.1007/s10518-021-01206-w

CrossRef Full Text | Google Scholar

Lombardi, A. M., Akinci, A., Malagnini, L., and Mueller, C. H. (2005). Uncertainty Analysis for Seismic Hazard in Northern and Central Italy. Ann. Geophys. 48, 853–865. doi:10.4401/ag-3239

CrossRef Full Text | Google Scholar

Ma, R., Ba, J., CarcioneCarcione, J. M., and Lebedev, M. (2022). PP-Wave Scattering by Randomly Distributed Aligned Cracks in Fractal Media. Geophys. J. Int. 229 (2), 900–914. doi:10.1093/gji/ggab450

CrossRef Full Text | Google Scholar

Ma, R., Ba, J., Lebedev, M., Gurevich, B., and Sun, Y. (2020). Effect of Pore Fluid on Ultrasonic S-Wave Attenuation in Partially Saturated Tight Rocks. Int. J. Rock Mech. Min. Sci. 147, 104910. doi:10.1016/j.ijrmms.2021

CrossRef Full Text | Google Scholar

Malagnini, L., Akinci, A., Mayeda, K., Munafo', I., Herrmann, R. B., and Mercuri, A. (2011). Characterization of Earthquake-Induced Ground Motion from the L’Aquila Seismic Sequence of 2009, Italy. Geophys. J. Int. 184 (1), 325–337. doi:10.1111/j.1365-246x.2010.04837.x

CrossRef Full Text | Google Scholar

Malagnini, L., Dreger, D. S., Bürgmann, R., Munafò, I., and Sebastiani, G. (2019). Modulation of Seismic Attenuation at Parkfield, before and after the 2004 M 6 Earthquake. J. Geophys. Res. Solid Earth 124, 5836–5853. doi:10.1029/2019JB017372

CrossRef Full Text | Google Scholar

Malagnini, L., and Dreger, D. S. (2016). Generalized Free-Surface Effect and Random Vibration Theory: a New Tool for Computing Moment Magnitudes of Small Earthquakes Using Borehole Data. Geophys. J. Int. 206, 103–113. doi:10.1093/gji/ggw113

CrossRef Full Text | Google Scholar

Malagnini, L., Lucente, F. P., De Gori, P., Akinci, A., and Munafo', I. (2012). Control of Pore Fluid Pressure Diffusion on Fault Failure Mode: Insights from the 2009 L’Aquila Seismic Sequence. J. Geophys. Res. 117, 1–15. doi:10.1029/2011JB008911

CrossRef Full Text | Google Scholar

Malagnini, L., Mayeda, K., Uhrhammer, R., Akinci, A., and Herrmann, R. B. (2007). A Regional Ground-Motion Excitation/Attenuation Model for the San Francisco Region. Bull. Seismol. Soc. Am. 97 (3), 843–862. doi:10.1785/0120060101

CrossRef Full Text | Google Scholar

Malagnini, L., and Munafò, I. (2018). On the Relationship between M_L and M_w in a Broad Range: An Example from the Apennines, Italy. Bull. Seism. Soc. Am. 108, 1018–1024. doi:10.1785/0120170303

CrossRef Full Text | Google Scholar

Malagnini, L., Parsons, T., Munafò, I., Mancini, S., Segou, M., and Geist, E. (2022). Crustal Permeability Changes Observed from Seismic Attenuation: Impacts on Multi-Mainshock Sequences. Front. Earth Sci. Sect. Solid Earth Geophys. (under review). doi:10.1002/essoar.10507597.1

CrossRef Full Text | Google Scholar

Malagnini, L., and Parsons, T. (2020). Seismic Attenuation Monitoring of a Critically Stressed San Andreas Fault. Geophys. Res. Lett. 47, 1–11. doi:10.1029/2020GL089201

CrossRef Full Text | Google Scholar

Mayeda, K., Koyanagi, S., Hoshiba, M., Aki, K., and Zeng, Y. (1992). A Comparative Study of Scattering, Intrinsic, and Coda Q⁻¹ for Hawaii, Long Valley, and Central California between 1.5 and 15.0 Hz. J. Geophys. Res. 97, 6643–6659. doi:10.1029/91jb03094

CrossRef Full Text | Google Scholar

Miller, S. A., Collettini, C., Chiaraluce, L., Cocco, M., Barchi, M., and Kaus, B. J. P. (2004). Aftershocks Driven by a High-Pressure CO2 Source at Depth. Nature 427, 724–727. doi:10.1038/nature02251

PubMed Abstract | CrossRef Full Text | Google Scholar

Morasca, P., Malagnini, L., Akinci, A., Spallarossa, D., and Herrmann, R. B. (2006). Ground-Motion Scaling in the Western Alps. J. Seismol. 10, 315–333. doi:10.1007/s10950-006-9019-X

CrossRef Full Text | Google Scholar

Motazedian, D., and Atkinson, G. M. (2005). Stochastic Finite-Fault Modeling Based on a Dynamic Corner Frequency. Bull. Seismol. Soc. Am. 95, 995–1010. doi:10.1785/0120030207

CrossRef Full Text | Google Scholar

Muir-Wood, R., and King, G. C. P. (1993). Hydrological Signatures of Earthquake Strain. J. Geophys. Res. 98 (B12), 22035–22068. doi:10.1029/93jb02219

CrossRef Full Text | Google Scholar

Munafò, I., Malagnini, L., and Chiaraluce, L. (2016). On the Relationship betweenMwandMLfor Small Earthquakes. Bull. Seismol. Soc. Am. 106, 2402–2408. doi:10.1785/0120160130

CrossRef Full Text | Google Scholar

Ojeda, J., Akinci, A., Tinti, E., Arriola, S., and Ruiz, S. (2021). Hybrid Broadband Strong-Motion Simulation to Investigate the Near-Source Characteristics of the M 6.5, 30 October 2016 Norcia, Italy Earthquake. Soil Dyn. Earthq. Eng. 149, 106866. doi:10.1016/j.soildyn.2021.106866

CrossRef Full Text | Google Scholar

Pio Lucente, F., De Gori, P., Margheriti, L., Piccinini, D., Di Bona, M., Chiarabba, C., et al. (2010). Temporal Variation of Seismic Velocity and Anisotropy before the 2009 MW6.3 L’Aquila Earthquake, Italy. Geology 38, 1015–1018. doi:10.1130/g31463.1

CrossRef Full Text | Google Scholar

Pischiutta, M., Akinci, A., Tinti, E., and Herrero, A. (2020a). Broad-band Ground-Motion Simulation of 2016 Amatrice Earthquake, Central Italy. Geophys. J. Int. 224, 1753–1779. doi:10.1093/gji/ggaa412

CrossRef Full Text | Google Scholar

Pischiutta, M., Akinci, A., Tinti, E., and Herrero, A. (2021b). Erratum: Broad-Band Ground-Motion Simulation of 2016 Amatrice Earthquake, Central Italy. Geophys. J. Int. 226 (3), 1695. doi:10.1093/gji/ggab163

CrossRef Full Text | Google Scholar

Pitarka, A., Akinci, A., De Gori, P., and Buttinelli, M. (2021). Deterministic 3D Ground-Motion Simulations (0–5 Hz) and Surface Topography Effects of the 30 October 2016 Mw 6.5 Norcia, Italy, Earthquake. Bull. Seism. Soc. Am. 112 (1), 262–286. doi:10.1785/0120210133

CrossRef Full Text | Google Scholar

Raoof, M., Herrmann, R. B., and Malagnini, L. (1999). Attenuation and Excitation of Three-Component Ground Motion in Southern California. Bull. Seism. Soc. Am. 89, 888–902. doi:10.1785/bssa0890040888

CrossRef Full Text | Google Scholar

Rietbrock, A. (2001). P Wave Attenuation Structure in the Fault Area of the 1995 Kobe Earthquake. J. Geophys. Res. 106, 4141–4154. doi:10.1029/2000jb900234

CrossRef Full Text | Google Scholar

Scognamiglio, L., Tinti, E., Casarotti, E., Pucci, S., Villani, F., and Cocco, M. (2018). Complex Fault Geometry and Rupture Dynamics of the Mw 6.5, 30 October 2016, Central Italy Earthquake. J. Geophys. Res. 123 (4), 2943–2964.

CrossRef Full Text | Google Scholar

Tisato, N., and Quintal, B. (2014). Laboratory Measurements of Seismic Attenuation in Sandstone: Strain versus Fluid Saturation Effects. Geophysics 79, WB9–WB14. doi:10.1190/GEO2013-0419.1

CrossRef Full Text | Google Scholar

Tisato, N., and Quintal, B. (2013). Measurements of Seismic Attenuation and Transient Fluid Pressure in Partially Saturated Berea Sandstone: Evidence of Fluid Flow on the Mesoscopic Scale. Geophys. J. Int. 195, 342–351. doi:10.1093/gji/ggt259

CrossRef Full Text | Google Scholar

Toksӧz, M. N., Johnston, D. H., and Timur, A. (1979). Attenuation of Seismic Waves in Dry and Saturated Rocks: I. Laboratory Measurements. Geophysics 44, 681–690. doi:10.1190/1.1440969

CrossRef Full Text | Google Scholar

Wessel, P., and Smith, W. H. F. (1998). New, Improved Version of Generic Mapping Tools Released. Eos Trans. AGU 79 (47), 579. doi:10.1029/98EO00426

CrossRef Full Text | Google Scholar

Winkler, K. W., and Nur, A. (1982). Seismic Attenuation: Effects of Pore Fluids and Frictional-Sliding. Geophysics 47, 1–15. doi:10.1190/1.1441276

CrossRef Full Text | Google Scholar

Zhong, S., Xu, C., Yi, L., and Li, Y. (2018). Focal Mechanisms of the 2016 Central Italy Earthquake Sequence Inferred from High-Rate GPS and Broadband Seismic Waveforms. Remote Sens. 10 (4), 512. doi:10.3390/rs10040512

CrossRef Full Text | Google Scholar