
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 15 July 2022
Sec. Hydrosphere
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.902226
 David F. Hill1,2*
David F. Hill1,2* Christina Aragon1
Christina Aragon1In late spring of 1992, Christopher McCandless crossed the Teklanika River, west of Healy, Alaska (United States). His summer has been well documented both in the book and the movie ‘Into the Wild.’ In early summer of 1992, he attempted to cross back over the river, but was stopped by high waters and he died later that summer. This paper investigates the hydrologic conditions of the Teklanika River watershed. We consider both climatological conditions and also conditions during the summer of 1992. We run process-based snowpack and runoff models in order to estimate the river hydrograph at the point of Mr. McCandless’ attempted crossing. Our results demonstrate that the Teklanika river is very flashy during the summer, responding rapidly to strong episodic rainfall events. The main snowmelt signal occurred in mid-to-late May, after Mr. McCandless’ first crossing and before his second attempt. The specific day of his attempted re-crossing corresponded to a large runoff event, driven by rainfall. We conclude that Mr. McCandless had unfortunate timing and that, had he tried to cross a day or two earlier or later, the outcome may have been different. This paper is also an opportunity to explore the hydrologic compromises that must be made when trying to study ungauged, or poorly gauged, areas. There is a spectrum of choices regarding input datasets and methodological simplifications and the correct location on that spectrum will depend on the particular watershed the objectives and expectations of the study.
On 18 June 2020, Bus 142 was airlifted (Figure 1) from the wilderness west of Healy, Alaska (United States). The bus, which was used for employee housing during road construction efforts, was abandoned in 1961. After decades in obscurity, the bus became famous upon the publication of ‘Into the Wild’ (Krakauer, 1997) and the subsequent movie of the same title. That book tells the story of Christopher McCandless, who spent the summer of 1992 in the Alaskan wilderness, using the bus as a basecamp. He crossed the Teklanika River from east to west on April 28. After 10 weeks in the wilderness, Mr. McCandless attempted to re-cross the river from west to east on July 5. He encountered impassable conditions and died in August of 1992 due to malnourishment. A recent article (Krakauer et al., 2015) concluded that consumption of H alpinum (wild potato) seeds contributed to his death.

FIGURE 1. Bus 142 being airlifted by the Alaska Army National Guard; 18 June 2020. Source: Wikimedia Commons.
The legacy of Mr. McCandless is a polarizing one, with some parties appreciative of his sense of adventure and others disapproving of his lack of planning and resourcefulness. For example, viable crossing points (a roadway bridge and a cable-car across the river) upstream and downstream were marked on maps available at that time. Visits to the site of Bus 142 were common in the decades following Mr. McCandless’ summer there and multiple drownings in the Teklanika River contributed to the decision to remove the bus.
This article first reviews the basic fluid dynamics associated with crossing a river. The goal for doing this is to provide some general context and guidelines for how the difficulty of crossing a river scales with the volumetric flowrate, or discharge. Next, this article performs an analysis of the hydrology of the Teklanika watershed. This is done by investigating the limited stream gauge data in the vicinity and climatological normals of temperature and precipitation in the area. Additionally, a process-based modeling study of the precipitation, snowmelt, and runoff for the basin for the summers of 1991 and 1992 is carried out. The goal of these efforts is to answer several questions. Was there anything anomalous about the summer of 1992 in terms of temperatures or precipitation? Was the increase in flow that prevented Mr. McCandless from re-crossing the river a summer-long increase due to high-elevation snow and glacial melt? Or, was it a short-lived pulse due to rainfall? In short, this article seeks to add a coda to the story of 1992 by identifying whether or not Mr. McCandless was truly ‘stuck in the wild,’ or simply the victim of unfortunate timing.
Specific statistics on river drownings due to attempted crossings are difficult to obtain. Some studies of mountain fatalities (Faulhaber et al., 2020; Zürcher et al., 2020) focus more on ‘climbing’ accidents, while others (Farstad and Luttrell, 2020) focus on drownings associated with watercraft (kayaing, rafting). One thorough analysis (Heggie and Amundson, 2009) of search and rescue callouts (SAR) in United States national parks separated boating incidents from ‘swimming’ incidents (21 and 6% of SAR incidents, respectively) but swimming is not exactly the same as river crossing. One useful study (Peden et al., 2016) of 10 years of Australian river drownings (n = 770) breaks out fatalities by cause and the ‘swept away’ (n = 23) category represents 3% of the loss of life.
From a fluid dynamics perspective, what matters most initially when crossing a river is the Reynolds number (Re) of the flow, the numerator of which is the product of the flow speed (V) and characteristic length scale (D), which could be taken to be the diameter of your leg. If that number is fairly low, there may be a pattern of alternating swirls downstream, known as a vortex street. As Re increases, the flow becomes more chaotic, or turbulent, and it separates as it passes your legs, creating large wakes downstream. This flow separation produces large drag forces which scale with V2.
What causes a river’s speed to increase? Simply put, more water flowing downhill, or volume discharge Q. Essentially, the hydraulic patterns (distributions of water elevation and velocity) are functions of the hydrology (water volumes). Natural rivers, with irregular cross sections, will have complicated patterns of velocity, but it is useful here to consider the idealized case of a wide rectangular channel. In this case, the Manning equations for velocity and discharge are
In these equations α is a conversion factor that accounts for the system of units (British vs. metric), n is a roughness parameter, y is the depth of the flow, b is the width of the flow, and S0 is the streamwise slope of the river bed. Combining these equations shows that V depends on Q2/5. Thus, doubling the flowrate increases the speed by 30% and increasing the flow by a factor of 10 increases the speed by a factor of two and a half.
Fast-moving water is not the full story of wading a river, however. After all, a swift current that is only ankle or shin deep may be trivial to cross. As the flowrate in a river increases, not only does the speed increase, but the water elevation, or stage, also increases to accommodate the greater volume passing by. If we solve (2) for y, we see that it depends on Q3/5. So, if the flowrate doubles, the stage goes up by 50%. If the flowrate goes up by a factor of 10, the stage quadruples.
This increase in stage matters for two reasons. First, drag forces of water flowing past an object depend on the ‘frontal area’ of the object. If you are knee deep in a flowing river, that frontal area is a rectangular area equal to the width of your calf multiplied by the distance from your knee to the ground. And, multiply this by two, assuming you have both legs in the water. So, as the depth increases, this frontal area increases, and so does the drag. Reducing this frontal area will reduce the drag, so turning your body sideways to the river’s current can make it easier to cross. And, there is the secondary benefit of allowing you to get into a strong stance to resist the flow.
To provide just one sample calculation, consider a person 50 cm wide, who is standing in 1 m of water and facing the current, with legs together. Assuming a drag coefficient of 1.5, which is suitable for an elliptical cross section, with its minor axis parallel to the current, the force due to a current of 1 m per second is roughly 375 N, or 80 pounds. Many people might be able to resist that, but a doubling of the current to 2 m per second would quadruple this force to over 300 pounds.
The second reason that an increase in stage matters has to do with buoyancy and friction (Figure 2). The object on the left has its weight (W) perfectly balanced by the upward force (N) from the ground. Due to friction between the object and the ground, there is a maximum friction force Ff that is proportional to N. As long as the drag force Fd is less than this friction force, the object will stay put. At right, the object is now partially submerged. The key difference here is the balance of forces in the vertical direction. The weight is now countered by the sum of a buoyancy force (Fb) and a smaller upward force (N) from the ground. Since N is reduced, the maximum frictional force is also reduced, meaning it takes much less drag force to dislodge the object.
In every way, therefore, increases in flowrate stack the odds against attempts to cross a river. The increases in flowrate raise the stage of the river and increase its speed, both of which increase the drag forces experienced by a person wading across. And, increases in stage submerge a greater portion of the person’s body, which reduce the ability to resist the drag. Drag forces vary linearly with fluid density and water is 1,000 times more dense than air. Anyone who has been buffeted around by strong wind gusts during a storm should recognize that even modest flows of water, combined with uncertain footing or slippery rocks, can quickly make a river crossing impossible.
The Teklanika river (Figure 3) has its headwaters at the toe of the Cantwell Glacier, just east of Mount Pendleton in the Alaska Range in Denali National Park. This stretch of the Range, which spans east to west from the Denali Massif to the Hayes Range is fantastically straight, as if drawn with a ruler. It is cut on its western side by the Muldrow Glacier, spilling off of the northeastern flanks of Denali itself. It is breached near its middle by the Nenana River, which parallels Highway 3 (Parks Highway), on its way north through the town of Healy. Rivers on the south aspect of this wall of peaks are short lived, quickly gathering into the Chulitna River, as it heads south towards Cook Inlet. Rivers draining the north aspect have much longer paths to take. The two main forks (Figure 4) of the Toklat, the Teklanika, and Sanctuary River all gather up individual drainages like capillaries into veins as they spill down wide glacial valleys. Once they leave the Alaska Range behind, gradients ease and currents slow.
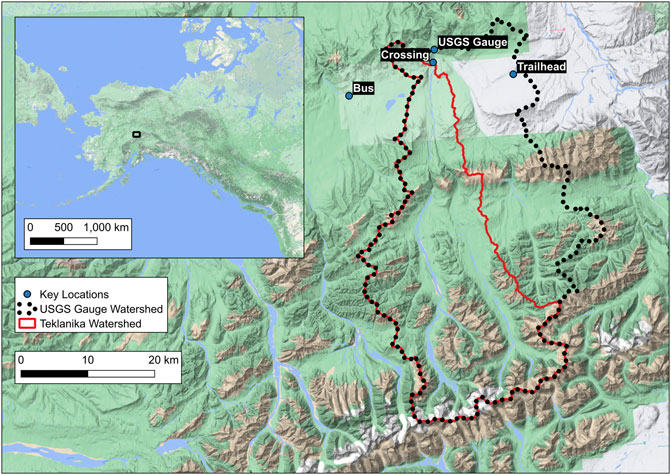
FIGURE 3. Overview (inset) and closeup view of the Teklanika River watershed in south-central Alaska.
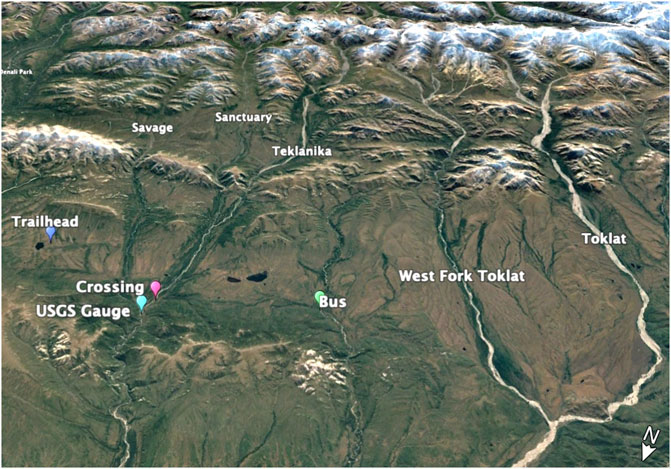
FIGURE 4. View looking south at the Teklanika watershed and other river basins draining the north side of the Alaska Range.
The Teklanika itself flows from its headwaters to Cathedral Mountain, which it skirts on its eastern flanks before passing the Denali Park Road and a National Park Service campground on its eastern bank. Further north, the river passes through a tight gorge west of Mt. Wright and then gathers up Sanctuary River. The Teklanika next joins up with the Savage river just after the crossing of the Stampede Trail. Further north, as it passes Comma Lake, the Teklanika slows dramatically and changes from a heavily braided river to a highly sinuous river with bends that double back on themselves amid countless remnant oxbows. Eventually the Teklanika joins up with the Nenana River and then the Tanana River, before joining the Yukon river on its journey to the Chukchi Sea.
Both Figures 3 and 4 show various points of interest. The Stampede Trail trailhead near Eightmile Lake is where Mr. McCandless was dropped off in late April of 1992. The trail, which amounts to a much deteriorated road from the 1960s, first crosses the Savage River before crossing the Teklanika River. The former location of Bus 142 is shown, in addition to the location of a historic (1964–1974) United States Geological Survey river gauging location (Site 15518350). Figure 3 also shows two watersheds. The ‘USGS’ watershed is the land draining to the gauge location and has an area of about 1,250 km2. The ‘Teklanika’ watershed is the land draining to the intersection of the Stampede Trail and the Teklanika River and this has an area of 800 km2, or 64% that of the USGS watershed. The Teklanika watershed ranges in elevation from about 500 to 2,200 m, with an average elevation of 1,100 m.
Alaska is a challenging state, in terms of long-term gauging datasets. Remote terrain, harsh conditions, and sheer scale mean that many basins are not gauged with the same coverage as those in the conterminous United States. As noted above, the USGS maintained a gauge on the Teklanika River (15518350) for the water years 1965 through 1974. A brief summary of the flow data are provided by The Mangi Environmental Group (2005) and there is also a study (Schalk, 2005) that uses these limited data to estimate flood return periods.
Figure 5 shows hydrographs, or plots of daily river flows, from the 10 years of available USGS data. The gray shaded area spans the minimum and maximum values for each day of the year, and the black line shows the average value over the period of record. The irregular nature of the black line is due to averaging over only 10 years, which is a relatively short period, and also to the fact that the river is quite flashy in nature. The blue line shows a smoothed version of this, which is a better representation of a much longer-term average. From the hydrograph, it is clear that cold winter temperatures keep flows very low. A strong increase in flows is observed from mid-April through October, which is due to a combination of snowmelt and precipitation patterns. These summer flows are about 10 times greater than the winter flows. Over the period of record the average river flow at the gauge was 19.3 m3s−1, which amounts to a runoff depth of 486 mm. The average of the highest flow seen each year over this period was 240 m3 s−1. Finally, the standard deviation, which is a measure of the variability or ‘flashiness’ of the flow, was 29 m3s−1.
Relevant and recent discussion of the hydrology of Alaska rivers is provided by Curran and Biles (2021). They categorize rivers into three broad classes, based upon the timing of peak flow and also the main drivers of flow. Rain-dominated watersheds (category 1) tend to have peaks both in May and October. Snow dominated watersheds (category 2) see peak flows in May/June and often a second peak in September or October. Finally, high-elevation melt watersheds (category 3) see a broad peak that spans summer months and is due to high-elevation snow melt and also ice-melt from glacier surfaces. Curran and Biles (2021) go on to subdivide (A, B, C, etc.) these classes based upon finer-scale details of the timing and magnitudes of hydrographs within each category. A complete inventory of the gauges studied is provided in an accompanying data release and the Teklanika watershed (draining to the USGS gauge) is classified as 3B.
Streamflow is the byproduct of many physical processes. Precipitation, snowmelt, infiltration of water into the soil, evaporation, and other complex processes partition and direct water both in space and in time. The two most significant drivers of streamflow are the patterns of precipitation and temperature. The Scenarios Network for Alaska and Arctic Planning (SNAP) project distributes gridded monthly time series, downscaled to a spatial resolution of 771 m, based on the Climate Research Unit (Harris et al., 2014) (CRU; Version 3.1) datasets. Figure 6 shows the variation in the mean annual precipitation (1980–2009) for much of Alaska, and also for the Teklanika watershed. Coastal Alaska is one of the wettest places on Earth, with the coastal mountain ranges receiving in excess of 8,000 mm of precipitation. Interior Alaska is much drier, and the Teklanika watershed receives between 400 and 800 mm of precipitation per year, with a spatial average of 580 mm. The USGS watershed averaged 550 mm of precipitation over the 1980–2009 period and 573 mm over the 1965–1974 period. This works out to a runoff ratio of 84%, based on the gauge data described above. This is consistent with previous studies (Beamer et al., 2016) in Alaska which looked at sublimation and evaporative fluxes that remove water from a watershed before it is able to run off.
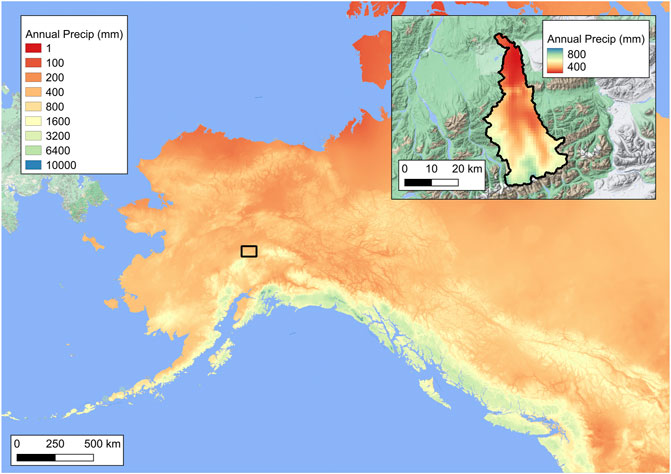
FIGURE 6. Mean annual precipitation for Alaska and (inset) the Teklanika watershed for the period 1980–2009.
The seasonal variations of mean monthly temperature and precipitation, averaged over the Teklanika watershed, are shown in Figure 7. The precipitation data show the presence of strong summer rains, and the mean annual precipitation averaged over the watershed is 580 mm for the 1980–2009 period and 600 mm for the 1965–1974 period. If these precipitation volumes ran off uniformly over the year, they would correspond to streamflows of 14.7 and 15.2 m3s−1 for the two time periods. These are less than the average flow of 19.3 m3s−1 at the USGS Gauge since that gauge captures the Savage River as well. If we apply simple area-scaling to the USGS data, the average river flow of the Teklanika watershed for the 1965–1974 period is estimated to be about 12.4 m3s−1. Finally, note that the temperature data are nearly in phase (slightly ahead) with the precipitation data and show above-freezing temperatures from April through September.
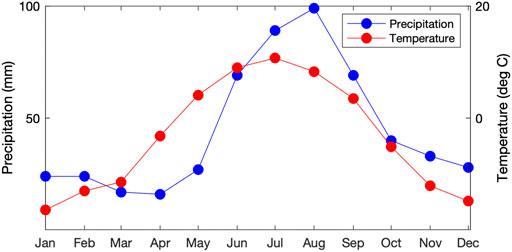
FIGURE 7. Climatologies of mean monthly precipitation and mean monthly temperature averaged over the Teklanika watershed for the period 1980–2009.
In order to model snowpack processes and runoff across the Teklanika watershed, we used a collection of process-based models that have been used widely in high-latitude locations dominated by snow and ice, including Alaska (Beamer et al., 2016, 2017; Crumley et al., 2019, 2021). Only a brief summary is presented here, with readers directed to the original citations for additional details.
MicroMet (Liston and Elder, 2006b) is first used to interpolate weather data (either from discrete stations, or gridded re-analysis cells), including temperature, precipitation, relative humidity, and wind speed and direction, to the high resolution grid used for the model. Following interpolation, individual adjustments are made to each variable. These are done using known relationships between weather variables and topography. Solar and longwave radiation are calculated with sub-models, based on temperature, humidity, and topographic aspect and slope.
Next, SnowModel (Liston and Elder, 2006a) is used to evolve the snowpack over time. This is done using an energy-balance approach rather than relying on statistical approaches or proxy methods such as temperature index equations. Processes in SnowModel include, among others, accumulation of snow precipitation, wind transport of snow, sublimation, and snowpack ripening and melt. SnowModel does not contain glacier dynamics, but it does model the melt of glacier ice after the seasonal snowpack has melted away. In this sense, it is an appropriate model for capturing the hydrologic response of a glaciated environment for a given year.
Finally, HydroFlow (Liston and Mernild, 2012; Mernild and Liston, 2012) was used to route rainfall, snowmelt, and ice-melt across the landscape. It does this through solution of coupled equations for fast-response and slow-response flow and it produces a time series of streamflow at all model grid cells.
Evapotranspiration (ET) was estimated in the following way. First, recall from the gauge data that the runoff ratio for the Teklanika watershed was 84%. Next, we analyzed the MODIS MOD16A2GF.061 dataset (Mu et al., 2011), which is an 8-day composite, 500 m resolution product based on the Penman-Monteith (Monteith, 1965) equation. The MODIS data showed that the annual variation of ET was essentially Gaussian, with a peak at the beginning of July. For the Teklanika watershed, the annual average ET from the MODIS data was about 350 mm. Compared to the precipitation input from the SNAP dataset, this would produce a runoff ratio of only 40% instead of the observed 84%. Therefore, our approach was to preserve both the runoff ratio suggested by the gauge data and the seasonal variation of water abstraction by ET suggested by the MODIS data. To do this, 16% of the annual precipitation volume for our model runs was fit to a Gaussian curve and subsequently removed as ET during the runoff modeling.
Figure 8 shows the model domain used in this study. Both the Teklanika watershed and the USGS watershed are shown for reference, but following results will focus on the former.
The model framework described above requires elevation, land cover, and weather data. The elevation data were obtained (US Geological Survey, 2020) from the 1/3rd arc-second Digital Elevation Model (DEM), which is part of the USGS National Map 3DEP Data Collection. Land cover data were obtained from the 2011 Alaska National Land Cover Database (NLDC) (Homer et al., 2015). These datasets are shown in Figures 9A,B. One of the landcover classifications is permanent snow/ice and Figure 9C shows the ice (glacier) cover in the southwest corner of the Teklanika watershed. The ice cover from the NLCD dataset differs significantly from the Randolph Glacier Inventory (Version 6) (RGI Consortium, 2017), and Figure 9D shows the ice mask representing the union of those datasets. The RGI is generally regarded as a superior product, as it is based on manual inspection and digitization while the NLCD is based on automated processing. The NLCD dataset shows 8.6 km2 of glacier cover in the Teklanika watershed, and the RGI dataset shows 20 km2. Model simulations were carried out with both ice masks, in order to determine the sensitivity of the summer runoff to the glacier cover.
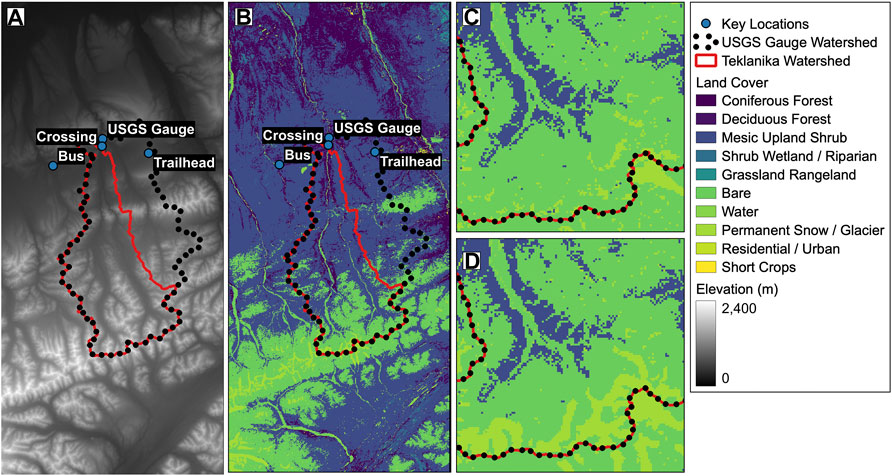
FIGURE 9. Model domain elevation model (A) and land cover classifications (B). Zoomed in views of the southwest corner of the Teklanika watershed land cover are shown in (C) for the NLCD dataset and (D) for the RGI dataset.
For an additional point of context, a portion of the 1951 USGS 1:250000 scale quadrangle for Healy, Alaska is shown in Figure 10. This map indicates fairly comparable glacier cover at the headwaters of the Teklanika, but much more glacier cover at the headwaters of Sanctuary River, which joins the Teklanika upstream of the Stampede crossing. Digitizing the glacier areas of this historic map reveals a cover of 31.6 km2. Note that the Savage River basin has no glacier cover in any of these datasets.
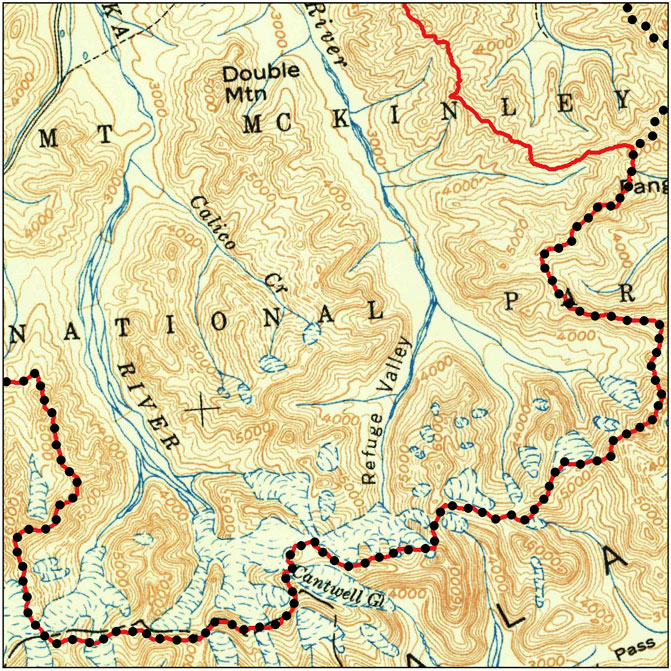
FIGURE 10. A portion of the 1951 USGS 1:250000 quadrangle for Healy, Alaska. The field of view is zoomed in on the upper reaches of the Teklanika watershed.
Finally, weather forcing data were obtained from the Climate Forecast System (CFS) reanalysis product (Saha et al., 2010) which has a 6-h temporal resolution and a spatial resolution of approximately 40 km. As noted above, MicroMet distributes data, either from in-situ stations or from reanalysis grid cell centers, to the high-resolution model grid.
Direct calibration of the Teklanika watershed is complicated by the fact that the period for which streamflow is available does not overlap with the period of record of the CFS reanalysis product. Therefore, for this study, model parameters were selected based on previous comparable studies (Beamer et al., 2016, 2017; Crumley et al., 2019, 2021) in Alaska. Calibration for those studies was based on glacier mass balance data, streamflow data, and snow telemetry data. One of the calibration sites was the Gulkana Glacier, providing some representation to the processes of the eastern Alaska Range.
With these parameters, a model simulation was carried out from 1 October 1990 through 30 September 1992. The model time step was 6 hours, but model output was saved at a daily time step. Note that this model time step is too coarse to adequately capture the diurnal variations in streamflow that are observed in some Alaskan rivers. The model spatial resolution was set at 100 m.
Since runoff starts off largely with the interactions between precipitation and temperature, Figure 11 shows the daily precipitation and temperature, averaged over the Teklanika watershed, for the 1992 water year. The total precipitation for the year is 681 mm. This is consistent with the monthly precipitation grids of Hill et al. (2015) that showed that water year 1992 had about 20% more precipitation than average. A wetter than normal year will certainly contribute to increased streamflow, but the more important question is how the precipitation for that year was distributed over time and how quickly the temperatures for that year melted out the snowpack. Note that the mean daily temperature rises above freezing in mid-May, and drops back below freezing in mid-September. Also, the precipitation time-series shows numerous significant events from the start of June through September. When compared to the previous year, temperatures in summer 1992 rose above freezing much later (1 month) and much more steeply, and summer rains were much more intense.
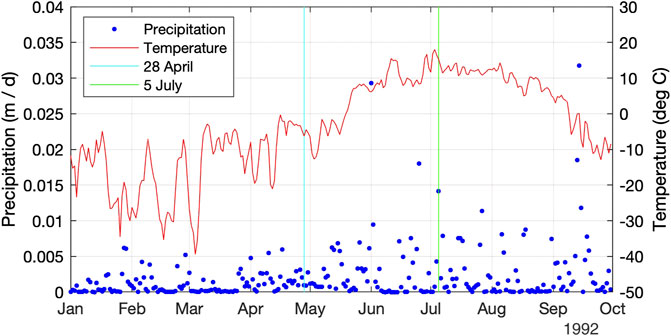
FIGURE 11. Daily precipitation (water equivalent) and temperature, averaged over the Teklanika watershed, for the 1992 water year.
The results for snow cover in the model domain show that October storms quickly blanket the entire domain and depths steadily accumulate throughout winter and early spring. After mid-May (Figure 12), the snow quickly retreats to only the highest elevations in the domain, and by mid-September 1992, snow has returned over much of the area. The average (averaged over the Teklanika watershed) depth of snow water equivalent (SWE) is shown in Figure 13. What is remarkable about this figure is that in just 14 days, starting on May 17, the average SWE drops from 22 to 2 cm. This is due to the steeply rising temperatures seen in Figure 11.
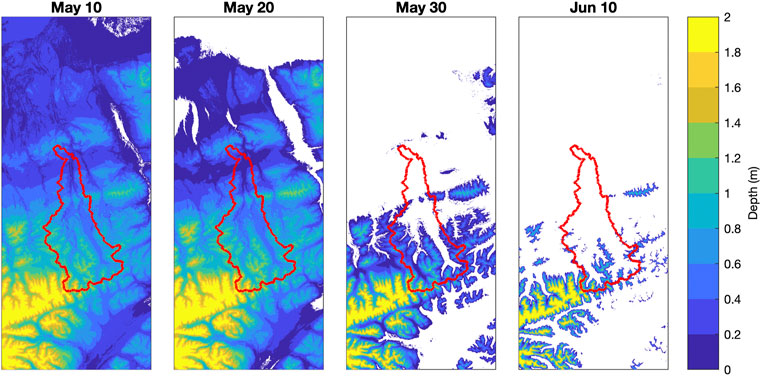
FIGURE 12. Distributions of snow depth in the model domain and the Teklanika watershed (red boundary) during late spring 1992.
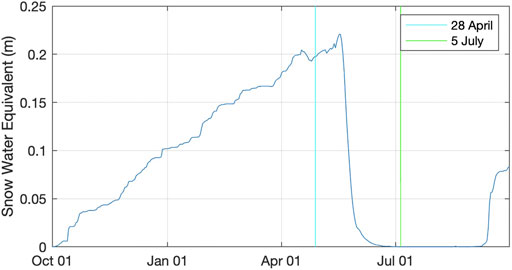
FIGURE 13. Average depth of snow water equivalent (SWE) over the Teklanika watershed during the 1992 water year.
Figure 14 provides the estimated hydrograph for the Teklanika Watershed. For various points of comparison, the hydrograph from 1991 is shown in addition to 1992. Also, gray shading is used to show the envelope of values observed for the USGS watershed over the period 1964–1974 (see Figure 5). Remember that the Teklanika watershed is 64% the size of the USGS watershed. Next, note that the hydrograph presented is for the case where the RGI glacier mask was used. Recall that the RGI mask showed greater glacier cover in the Teklanika watershed. A simulation with the NLCD glacier mask (not shown) was also done. During the summer time, it was found that the streamflow from the RGI simulation was about 5 m3s−1 greater than the NLCD simulation. Also recall the historic ice cover shown in Figure 10, which was larger still. It is therefore expected that summer flows during the period of record of the USGS gauge would have been further elevated, compared to the current simulations.
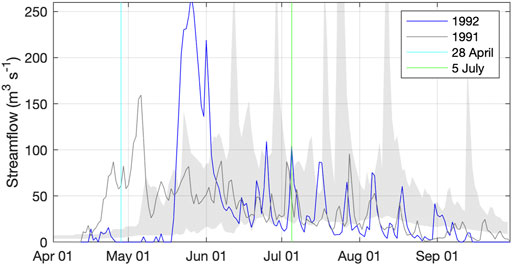
FIGURE 14. Estimated streamflow for the Teklanika watershed during spring and summer of 1991 and 1992. The envelope (1964–1974) of values for the larger USGS watershed is also shown.
The mean discharge in water year 1992 is 16.0 m3s−1 for the RGI simulation, which amounts to a runoff depth of 630 mm. The peak discharge is 260 m3s−1. The green line shows the date of 5 July, and that day corresponds to a high flow of nearly 110 m3s−1. The flows on 3 and 7 July, respectively, are 15 and 50 m3s−1.
The hydrograph for the summer of 1992 is flatter than the 10-years average shown in Figure 5. Part of this is due to reduced glacier cover, from the 1960s to present day, which reduces summer flows. A larger part of it is due to the rapid warming observed in May which quickly melted out much of the snowpack. The hydrograph for summer 1991 demonstrates a more sustained summer flow due to much more gradual warming and snowmelt. It also shows less variability since rainfall events during summer 1991 were less intense.
In summary, the hydrographs estimated in this study show three important results. First, the crossing of the Teklanika river by Mr. McCandless on 28 April 1992 was likely enabled by an extended cold spell, which significantly delayed the streamflow increase associated with the spring snowmelt. Second, streamflow variability in the summer of 1992 was larger than normal due to the spring snowmelt quickly dissipating, and due to intense rainfall events. Finally, the attempted re-crossing of the Teklanika River on 5 July 1992 corresponded with a large runoff event that rose and fell very quickly.
There are several important limitations of and qualifications about this study that should be made clear. First, it is impossible to predict the actual patterns of water elevation and velocity at the Stampede Trail crossing of the Teklanika River in July of 1992. To do so would require an accurate hydraulic model which, in turn, would require accurate information about river cross sectional shape. In braided Alaskan rivers, cross sections constantly evolve in response to strong currents and a heavy sediment load, so the cross sections of 1992 are long gone. This article has largely applied hydrologic modeling techniques, which focus more on water quantities, and less on exact patterns.
Second, this study was not able to resolve the diurnal fluctuations in discharge that can be observed in some Alaskan rivers. Lignite Creek (USGS Station 15518080; category 2B) is a good example of this. Inspection of the 15-min data during the summer of 1992 at that site shows strong diurnal fluctuations in late May. These fluctuations become quite small in later summer, as the spring snowmelt pulse dissipates and the hydrograph becomes dominated by strong peaks associated with rainfall. The CFSv2 data used to force the model for this study were on a 6-h time step and this temporal resolution is too coarse to capture these diurnal signals.
Most significantly, this study is complicated by the lack of contemporaneous in-situ datasets. Hydrologic studies require weather, elevation, and various land characteristic datasets as forcing, and snow telemetry and streamflow datasets for calibration and validation. Unfortunately, there was no temporal overlap between the gauge data and the weather reanalysis data (CFS/CFSv2 period of record is 1979 - present) used in this study. This prevented direct calibration and indirect calibration and simplifications were necessary.
The 10 years of USGS data on the Teklanika (Figure 5) were invaluable to this study and to understanding the hydrologic characteristics of the watershed at that time. The facts that the estimated hydrographs for 1991 and 1992 (Figure 14) are lower than the 1965–1974 average, and that the 1992 peak flow seems anomalously high are the largest potential criticisms of this work and therefore deserve greater discussion.
To investigate the relative magnitudes of peak flows in 1991 and 1992, in the absence of gauge data for the Teklanika, it is useful to consider the gauge records from other USGS stations. Of course, there is no perfect proxy watershed, sharing similar location, elevation, size, and other characteristics. The Chena River (15493000; category 2B) east of Fairbanks has an area of 2,390 km2, but lacks the high elevations of the Teklanika watershed. Its hydrograph in 1992 shows a later and much strong spring snowmelt than in 1991. The same is true for the Salcha River (15484000; 5,600 km2; category 2B) southeast of Fairbanks and Lignite Creek (15518080; 125 km2; category 2B). In this way, these watersheds reinforce some of the features in Figure 14. Watersheds such as the Nenana River at Healy (15518040; 5,380 km2; category 3B) are appealing points of comparison since they include high mountains in the Alaska Range, but the Nenana has discharge data for 1991 only (not 1992). It is worth noting that long-term water surface elevation (stage, not discharge) data for the Nenana are available through the Alaska-Pacific River Forecast Center of the National Weather Service. These stage data (Supplementary Figure S1A) show comparable peaks in 1991 and 1992, but they also confirm a delayed and very rapid rise in the river in 1992 compared to 1991. The Nenana also shows a broader, more consistent hydrograph in summer months, due to its larger size and its higher mean elevation than the Teklanika.
To address the differences in hydrograph shape between the model results for the Teklanika watershed and the observations for the USGS watershed, we looked at several things. First, it should be noted that climatological (long-term averages) hydrographs are not static. As an illustration of this, we considered (Supplementary Figure S1B) the Little Susitna (15290000; 158 km2; category 3B) for two different 30-years periods. Note that the more current hydrograph has significantly less flow in the summer months than the historic one. This could be due to a number of influences, including reduced extent of the Mint Glacier and warmer temperatures. Additionally, the spring freshet occurs about a week earlier in the current hydrograph compared to the historic one.
We also applied our modeling workflow to the Little Susitna watershed in order to gain an understanding of its ability to reproduce discharge in a gauged watershed. This domain is again, not a perfect proxy for the Teklanika, as it is at the southern end of the Talkeetna Range, and not part of the Alaska Range. However, it has temporally overlapping snow telemetry and streamflow data, and both it and the Teklanika are 3B catchments. Modeled and observed discharges are shown in Supplementary Figure S1C. The results show that the model is able to capture many of the peaks in the runoff and the overall performance metrics (R2 = 0.84, NSE = 0.7) are fairly good.
The limitations raised in this discussion do not necessarily discount the present findings. In ways, the appropriate tool for a study scales with ambition, i.e., the type and the accuracy of the information sought. The goal of this study was not to pinpoint the precise discharge on 5 July 1992. Rather, it was to investigate how the hydrology of 1992 compared to other years and to see how the discharge on 5 July compared to the days prior and after. And, connecting these relative changes in streamflow to hydraulic estimates (Equations 1, 2) of how velocity and stage vary with streamflow is a useful second step on a path towards understanding the literal ups and downs of the Teklanika River.
To return to Chris McCandless’ summer, it is clear that the spring snowmelt in 1992 was delayed and rapid, making it possible for him to reach Bus 142 at the end of April. Following this rapid snowmelt, the river rose and fell every week or so, in response to rainfall events. Attempting to re-cross the river on July 5th therefore appears to have been a case of bad timing by Mr. McCandless. Had he returned to the river just a few days earlier or later, the conditions for crossing may have been more favorable.
Publicly available datasets were analyzed in this study. This data can be found here: USGS Streamflow data for the Teklanika River: https://waterdata.usgs.gov/nwis/inventory/?site_no=15518350. USGS Streamflow data for the Little Susitna River: https://waterdata.usgs.gov/nwis/inventory/?site_no=15290000. Downscaled (SNAP) 771m monthly precipitation grids: http://ckan.snap.uaf.edu/dataset/historical-monthly-and-derived-precipitation-products-771m-cru-ts. Snow Telemetry (SNOTEL) data for Independence Mine: https://wcc.sc.egov.usda.gov/nwcc/site?sitenum=1091. MODIS 8-days evapotranspiration data: https://opendap.cr.usgs.gov/opendap/hyrax/MOD16A2GF.006/contents.html. 1/3 arc-second digital elevation model: https://data.usgs.gov/datacatalog/data/USGS:3a81321b-c153-416f-98b7-cc8e5f0e17c3. NLCD 2011 Alaska data: https://www.mrlc.gov/data/nlcd-2011-land-cover-alaska-0. RGI (version 6) glacier cover: https://www.glims.org/RGI/. Climate Forecast System (CFS) data: https://www.ncei.noaa.gov/data/climate-forecast-system/access/reanalysis/6-hourly-flux/.
DH developed the idea for this study and carried out initial model analysis and manuscript writing. CA helped develop many of the modeling tools that were used in the final work and also contributed to data acquisition, model calibration, and other aspects.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Thank you Fiona for renewing my interest in this story.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.902226/full#supplementary-material
Beamer, J. P., Hill, D. F., Arendt, A., and Liston, G. E. (2016). High-resolution Modeling of Coastal Freshwater Discharge and Glacier Mass Balance in the Gulf of Alaska Watershed. Water Resour. Res. 52, 3888–3909. doi:10.1002/2015WR018457
Beamer, J. P., Hill, D. F., McGrath, D., Arendt, A., and Kienholz, C. (2017). Hydrologic Impacts of Changes in Climate and Glacier Extent in the Gulf of Alaska Watershed. Water Resour. Res. 53, 7502–7520. doi:10.1002/2016WR020033
Crumley, R. L., Hill, D. F., Beamer, J. P., and Holzenthal, E. R. (2019). Seasonal Components of Freshwater Runoff in Glacier Bay, Alaska: Diverse Spatial Patterns and Temporal Change. Cryosphere 13, 1597–1619. Publisher: Copernicus GmbH. doi:10.5194/tc-13-1597-2019
Crumley, R. L., Hill, D. F., Wikstrom Jones, K., Wolken, G. J., Arendt, A. A., Aragon, C. M., et al. (2021). EnglishAssimilation of Citizen Science Data in Snowpack Modeling Using a New Snow Data Set: Community Snow Observations. Hydrology Earth Syst. Sci. 25, 4651–4680. Publisher: Copernicus GmbH. doi:10.5194/hess-25-4651-2021
Curran, J. H., and Biles, F. E. (2021). enIdentification of Seasonal Streamflow Regimes and Streamflow Drivers for Daily and Peak Flows in Alaska. Water Resour. Res. 57, e2020WR028425. doi:10.1029/2020WR028425
Farstad, D. J., and Luttrell, J. M. (2020). EnglishFlush Drowning as a Cause of Whitewater Deaths. Wilderness & Environ. Med. 31, 11–15. Publisher: Elsevier. doi:10.1016/j.wem.2019.09.006
Faulhaber, M., Ruedl, G., Schneider, F., Walter, D., Sterr, R., Schobersberger, W., et al. (2020). Characteristics of Victims of Fall-Related Accidents during Mountain Hiking. Int. J. Environ. Res. Public Health 17, 1115. doi:10.3390/ijerph17031115
Harris, I., Jones, P., Osborn, T., and Lister, D. (2014). enUpdated High-Resolution Grids of Monthly Climatic Observations – the CRU TS3.10 Dataset. Int. J. Climatol. 34, 623–642. doi:10.1002/joc.3711
Heggie, T. W., and Amundson, M. E. (2009). engDead Men Walking: Search and Rescue in US National Parks. Wilderness & Environ. Med. 20, 244–249. doi:10.1580/08-WEME-OR-299R.1
Hill, D. F., Bruhis, N., Calos, S. E., Arendt, A., and Beamer, J. (2015). enSpatial and Temporal Variability of Freshwater Discharge into the Gulf of Alaska. J. Geophys. Res. Oceans 120, 634–646. doi:10.1002/2014JC010395
Homer, C., Dewitz, J., Yang, L., Jin, S., Danielson, P., Xian, G., et al. (2015). Completion of the 2011 National Land Cover Database for the Conterminous United States – Representing a Decade of Land Cover Change Information. Photogrammetric Eng. Remote Sens. 81, 345–354. doi:10.14358/PERS.81.5.345
Krakauer, J., Long, Y., Kolbert, A., Thanedar, S., and Southard, J. (2015). EnglishPresence of L-Canavanine in Hedysarum Alpinum Seeds and its Potential Role in the Death of Chris McCandless. Wilderness & Environ. Med. 26, 36–42. Publisher: Elsevier. doi:10.1016/j.wem.2014.08.014
Liston, G. E., and Elder, K. (2006a). A Distributed Snow-Evolution Modeling System (SnowModel). J. Hydrometeorol. 7, 1259–1276. doi:10.1175/JHM548.1
Liston, G. E., and Elder, K. (2006b). A Meteorological Distribution System for High-Resolution Terrestrial Modeling (MicroMet). J. Hydrometeorol. 7, 217–234. doi:10.1175/JHM486.1
Liston, G. E., and Mernild, S. H. (2012). Greenland Freshwater Runoff. Part I: A Runoff Routing Model for Glaciated and Nonglaciated Landscapes (HydroFlow). J. Clim. 25, 5997–6014. doi:10.1175/JCLI-D-11-00591.1
Mernild, S. H., and Liston, G. E. (2012). Greenland Freshwater Runoff. Part II: Distribution and Trends, 1960–2010. J. Clim. 25, 6015–6035. doi:10.1175/JCLI-D-11-00592.1
Monteith, J. L. (1965). “enEvaporation and Environment,” in Symposia of the Society for Experimental Biology (Cambridge: Publisher: Cambridge University Press, 19, 205–234.
Mu, Q., Zhao, M., and Running, S. W. (2011). enImprovements to a MODIS Global Terrestrial Evapotranspiration Algorithm. Remote Sens. Environ. 115, 1781–1800. doi:10.1016/j.rse.2011.02.019
Peden, A. E., Franklin, R. C., and Leggat, P. A. (2016). The Hidden Tragedy of Rivers: A Decade of Unintentional Fatal Drowning in Australia. PLoS ONE 11, e0160709. doi:10.1371/journal.pone.0160709
Saha, S., Moorthi, S., Pan, H.-L., Wu, X., Wang, J., Nadiga, S., et al. (2010). The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorological Soc. 91, 1015–1057. doi:10.1175/2010BAMS3001.1
Schalk, B. (2005). “Floodplain Assessment for the Teklanika and Toklat River Project Reaches,” (Alaska: University of Alaska Fairbanks). Ph.D. thesis.Denali National Park and Preserve
The Mangi Environmental Group (2005). Water Resources Information and Issues Overview Report - Denali National Park and Preserve. Technical Report NPS/NRWRD/NRTR- 2005/341. United States Department of the Interior.
US Geological Survey (2020). 1/3rd Arc-Second Digital Elevation Models (DEMs) - USGS National Map 3DEP Downloadable Data Collection. ItemType: dataset.
Keywords: snow-melt, energy-balance modeling, glacier runoff, Alaska, river crossings
Citation: Hill DF and Aragon C (2022) Stuck in the Wild—The Hydrology of the Teklanika River (Alaska) in the Summer of 1992. Front. Earth Sci. 10:902226. doi: 10.3389/feart.2022.902226
Received: 22 March 2022; Accepted: 21 June 2022;
Published: 15 July 2022.
Edited by:
Wouter Buytaert, Imperial College London, United KingdomReviewed by:
John Pomeroy, University of Saskatchewan, CanadaCopyright © 2022 Hill and Aragon. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David F. Hill, ZGZoQG9yZWdvbnN0YXRlLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.