Geodynamics Based on Solidification of Liquid/Molten Substances in the Earth’s Interior

Since its formation, the Earth has cooled from molten magma to the present layered structure. The liquid and molten substance in the interior of the Earth continuously solidifies, radiating heat to the outer space and causing changes in the pressure and density inside the Earth. Constrained by the rigid lithosphere, the change in density decreases the pressure at the bottom of the crust, and thereby supports the rigid lithosphere. Under the effect of gravity, there is an increased interaction between tectonic plates, which leads to local stress accumulation. Eventually, this stress exceeds the strength of the rock and makes the mechanical structure of the crustal lithosphere unstable. This process is iterative, and the Earth continuously adjusts to new mechanical equilibria by releasing the accumulated stress through geological events such as earthquakes. In this study, using three sets of observations (Global Positioning System data, length of day data, and the latent heat of Earth solidification), we show that these observations are consistent with the aforementioned assumption that the solidification of liquid cause changes in density and volume in the Earth’s interior. Mechanical analyses indicate that liquid solidification in the interior of the Earth leads to decrease in the Earth’s volume. This increases the intensity of plate interactions, which leads to the movement of large plates, triggering geological events such as earthquakes. Thus, it is determined that liquid solidification in the Earth’s interior is the main source for the movement of plates.

Introduction

The Earth has evolved from a molten state (magma ocean) to today’s layered structure via large-scale cooling and solidification (Elkins-Tanton, 2012). The cooling and solidification continue as the Earth keeps evolving and emitting energy (46 ± 3 TW, as estimated from the current global heat flow) (Lay et al., 2008). The difference between then and now is that the early magma ocean might have solidified faster. These contents of the Earth’s core go through molten-solid transitions at physical conditions (pressure and temperature) that change according to the thermodynamics and evolution of the Earth. Solidification is a universal and crucial phenomenon, and it leads to noticeable changes in density accompanied by heat release and volume contraction (Dziewonski and Anderson, 1981; Massonne et al., 2007; Sakamaki et al., 2010; Hirose et al., 2013). Global magmatism, reaching a rate of 25.8–33.6 km³ yr⁻¹, is caused due to magma solidification at the shallow Earth (Wilson, 2007). At deep Earth, the inner core grows at a rate of 0.5–2.4 mm yr⁻¹ due to crystallization of molten iron (Labrosse et al., 2001; Ohta et al., 2016; Bono et al., 2019). Released latent heat is a key heat source that influences the processes such as inner core growth and the geodynamo. Thus, solidification governs the thermodynamics of the Earth (Buffett et al., 1992; Buffett, 2000). The lithosphere, the topmost layer of the Earth, is a poor conductor of heat, and it is mechanically rigid and brittle (Shimada and Cho, 1990; Rychert and Shearer, 2009; Whittington et al., 2009). It operates like a ceramic outer shell, constraining the ductile mantle beneath it. The energy released by the solidification of melts in the Earth powers the dynamics of the Earth’s lithosphere and plate tectonics. The liquid–solid conversion in the Earth’s interior is a continuous process, and it leads to continuous heat dissipation to the outer space. Under the law of conservation of mass, the change in density due to solidification reflects a volume change, which eventually leads to the geometric variation of the Earth.

Modern space geodesy techniques have revealed that the Earth’s geometry is continuously changing and is not constant. Geodetic studies employing the data obtained from various techniques, such as Global Positioning System (GPS), Satellite Laser Ranging (SLR), Very Long Baseline Interferometry (VLBI), and Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS), suggest that the current rate of change of the Earth’s radius spans from −4.0 to 1.3 mm yr⁻¹. Because of this, it is unclear whether the Earth is expanding or contracting and also difficult to determine the extent of the change (Huang et al., 2002; Sun et al., 2006; Wu et al., 2011; Zhu et al., 2013). The paleomagnetic data indicate that the radius of the ancient Earth was 0.99–1.12 times of that of the present radius in the late Paleozoic and early Mesozoic Era (Cox and Doell, 1961; Ward, 1963). Another evidence of the varying nature of the Earth’s geometry is the Earth’s rotation rate, which has been observed to fluctuate in the interdecadal and longer periods as recorded based on the values of length of day (LOD). The changes in LOD are associated with the change of the Earth’s moment of inertia and impacts of large earthquakes (Stephenson and Morrison, 1984; Chao and Gross, 1987; Holme and De Viron, 2013).

The liquid and molten substance inside the Earth continues to solidify with the latent heat release and volume and density changes. Heat radiates to the surface via conduction, convective, radiation, and so on, and the volume change macroscopically manifests as volume contraction of the Earth. The volume contraction causes the tectonic plates to squeeze together, making them move under the influence of gravity, which in turn leads to various geological events. The traditional plate motion driving force model (mantle convection, slab pull, and ridge push) (Forsyth and Uyeda, 1975; Bott, 1991; Bokelmann, 2002a; Bokelmann, 2002b; van Summeren et al., 2012) has some limitations, as it cannot reasonably explain the plate motion cycle (Sun, 2019). Herein, we propose that the solidification of the Earth drives the dynamics of the Earth’s crust and gives rise to the volume variation of the Earth, and this theory is verified via the analyses of GPS data, LOD observations, and global heat flow estimates.

Theory Validation

Global Positioning System Data Analysis

The solidification of molten substance leads to changes in the internal volume, and it macroscopically manifests as the collapse of the Earth’s volume. If this happened, akin to a deflating balloon, the Earth’s radius would decrease, thereby decreasing the distance between the corresponding points on the Earth’s surface. When the Earth is considered a standard sphere, there is a definite relationship between the reduction of the Earth’s radius and any changes in distance between the two points on the surface, as shown in Figure 1.

FIGURE 1

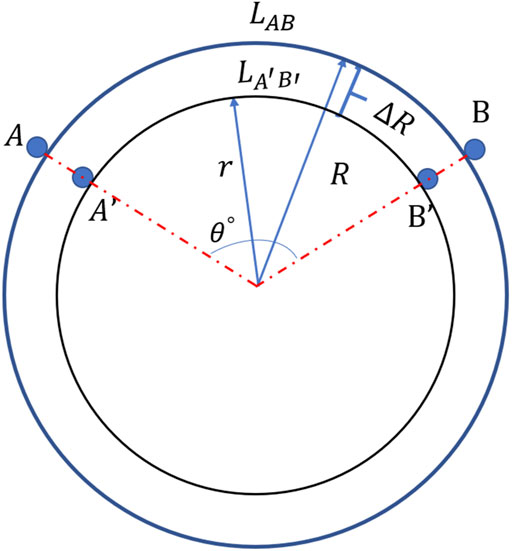
FIGURE 1. Simplified model of the Earth. $A$, $B$ and $A^{\text{'}}$, $B^{\text{'}}$ denote the two points on the ground before and after the contraction of the Earth, respectively; $R$ and $r$ represent the radius of the Earth before and after contraction, respectively; $L_{AB}$ and $L_{A\text{'}B\text{'}}$ represent the distances between the two points before and after Earth’s contraction, respectively; and $\theta$ is the spherical angle corresponding to the two points. $\mathrm{\Delta }R=\frac{360}{2\pi \theta }\mathrm{\Delta }L=\frac{R}{L_{AB}}\mathrm{\Delta }L=\frac{r}{L_{A\text{'}B\text{'}}}\mathrm{\Delta }L=C\mathrm{\Delta }L$.

Herein, variations in the radius and volume of the Earth are derived from the GPS data of 2,674 ground-based receivers during 1995–2019. A detailed site information is presented in Figure 2. These GPS data, recorded by NASA and processed by the Jet Propulsion Laboratory, provide the time series of longitude, latitude, and altitude of the individual sites over time (Heflin, 1994). The relationship between the change in distance $\left(\mathrm{\Delta }L\right)$ of two receivers and the change in the Earth’s radius $\left(\mathrm{\Delta }R\right)$ is given using Eq. 1:

$\mathrm{\Delta }R=C\mathrm{\Delta }L,(1)$

where $\mathrm{\Delta }R=r-R\text{ and }$ $\Delta L=L_{AB}-L_{A\text{'}B\text{'}}$ $C=R/L$ (Figure 1). $R$ is the current radius of the Earth (= 6,371 km), and $d$ is the distance between the two receivers. The Haversine formula (Eq. 2) is used to calculate the distance $\left(L\right)$ between the two receivers (Josiah, 2010):

$haversin\left(\frac{L}{R}\right)=haversin\left({\phi }_2-{\phi }_1\right)+\mathit{cos}{\phi }_2\mathit{cos}{\phi }_{1}haversin\left(\mathrm{\Delta }\lambda \right),(2)$

where $haversin\left(\frac{L}{R}\right)=\sin {\left(\frac{L}{R}/2\right)}^2$, ${\phi }_2$ and ${\phi }_1$ denote the latitudes of two points, and $\Delta \lambda$ denotes the difference in their longitudes.

FIGURE 2

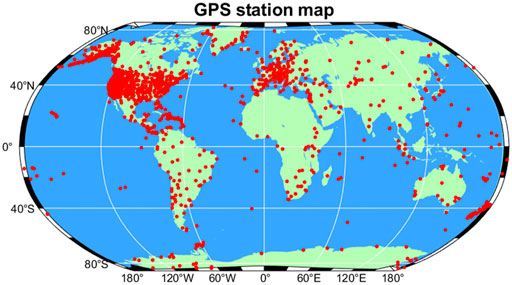
FIGURE 2. Locations of 2,764 GPS stations. The stations in North America (the United States) are relatively closer than the stations elsewhere in the world.

The data are processed by a self-written Python code. The arc length between any two stations on the Earth is calculated. Then, the relation between the annual radius change of the Earth and the change in the arc length between the two sites is given using Eq. 3:

$\mathrm{\Delta }\overline{R}=\frac{1}{n}{\displaystyle \sum _i^n\left\{\frac{1}{m}{\displaystyle \sum _j^m}\left[\frac{R}{L_j}\left(L_j-L_j^{\prime }\right)\right]\right\}},(3)$

where $i$ is the $i$-th year of calculation, $n$ is the total number of years, $j$ denotes the $j$-th pair of sites, $m$ is the total number of $j$ in year $i$, and $L_j$ $L_j^{\text{'}}$ are the arc distance of the $j$-th pair at the beginning of the $i$-th year and the end of $i$-th year, respectively. By using the error propagation law and GPS positioning error estimation, the accuracy estimate of the annual radius variation of the Earth can be obtained, and the average relative error is 15%.

During data processing, the data from sites whose observation time was less than 12 months for any year are omitted. To reduce errors caused by certain geological factors at close range, only those points are considered for which the distance is ≥100 km. For example, taking the calculation of 1995, we draw a diagram of one of the points (VILL) as shown in Figure 3. According to the longitude and latitude information of each station, the change of distance between the two sites with time is obtained, and the corresponding change in radius is determined. The average of the change in the Earth’s radius for 1995 is obtained by traversing the distances among all the points, and the value is −2.4 ± 0.27 mm.

FIGURE 3

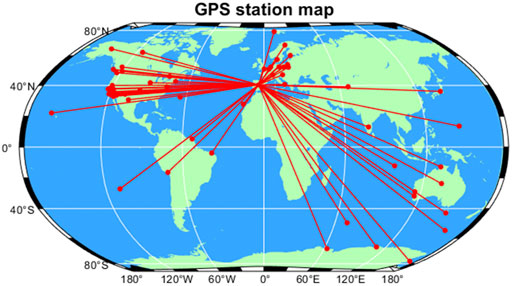
FIGURE 3. Diagram of the distance between VILL and the remaining points. The VILL site in 1995 is taken as an example. The red spot represents the location of each site, and the line segment represents the distance between the sites. The distance between the pairs of receivers at the beginning and the end of the year is calculated, and the change in this value is calculated. The average radius change in 1995 is −2.4 mm.

A total number of 14 million calculations are carried out for $\Delta R$, and 25 annual average radius changes from 1995 to 2019 are derived, among which, 20 results are negative, as shown in Figure 4. The annual average $\Delta \overline{R}$ is −1.65 ± 0.25 mm yr⁻¹, which corresponds to a volume decrease of −841.60 ± 127.5 km³ yr⁻¹.

FIGURE 4

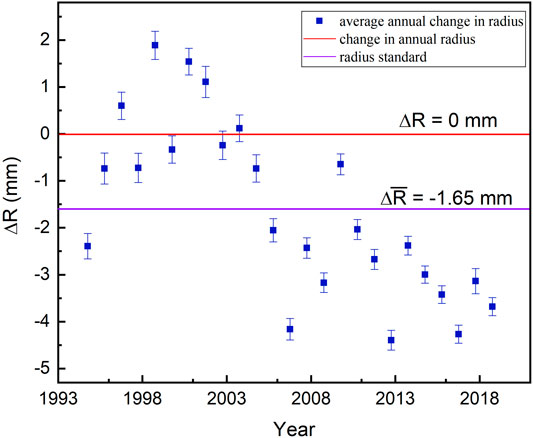
FIGURE 4. Annual average radius changes of the Earth from 1995 to 2019. Black circles: average change of Earth’s radius in that year; red and purple lines represent the annual average radius change (0 and −1.65 mm yr⁻¹, respectively). 20 out of 25 results are negative.

Latent Heat of Earth Solidification

The global heat flow is estimated to be 46 TW, and it mainly comprises radiogenic heat and heat from the core and mantle (Lay et al., 2008). The most accessible integrative energy for the planet is the total amount released at the surface. However, there may be uncertainties in the present-day energy budget. Specifically, there is considerable uncertainty in the radiogenic concentrations (Gessmann and Wood, 2002; Murthy et al., 2003) and the present-day mantle and core secular cooling rates (Lay et al., 2008; Herzberg et al., 2010). Although geoneutrino detectors promise new constraints in the near future (Araki et al., 2005; Dye, 2012), macroscopically, the Earth’s internal temperature distribution is constant, and secular cooling can be neglected over a short period of time. The results of Chang ’e-5 samples research showed that the characteristics of kreep-potassium enrichment in the basalt were formed in the late magmatic period, thus ruling out the main hypothesis that this moon mantle source region is rich in radioactive thermogenic elements (Hu et al., 2021; Li et al., 2021; Tian et al., 2021). The world’s uranium deposits do not overlap with the geothermal anomalies. This suggests that there is not a lot of radioactive material in the Earth’s crust. Thus, radioactive heat may not be a major source of heat loss on the Earth.

According to the thermal evolution of the Earth, the latent heat released from solidification of molten substance is considered an important heat source on the Earth. Herein, to simplify the calculation, the total energy budget of the Earth is assumed to comprise only latent and crustal radiogenic heat. The latent heat released from solidification of the Earth is calculated using Eq. 4:

$Q_t=Q_m+Q_c+Q_r,(4)$

where $Q_t$ is the total heat flow, $Q_m$ is the latent heat of the mantle and crust, $Q_c$ is the latent heat of the core, and $Q_r$ is the radioactive heat from the Earth’s crust (from direct sample sources). The volume change caused by solidification is calculated using Eq. 5:

$\mathrm{\Delta }V=\frac{m}{{\rho }_{molten}}-\frac{m}{{\rho }_{solid}},(5)$

where $m=Q/L$ is the mass of solidified substance, $Q$ stands for $Q_c$ and $Q_m$, respectively, $L$ is the specific latent heat, and ${\rho }_{molten}$ ${\rho }_{solid}$ are the densities of melts and solids, respectively. The specific values are shown in Table 1.

TABLE 1

TABLE 1. Values of the specific latent heat and densities of the melt and solid used for latent heat analysis (Ohtani and Maeda, 2001; Suzuki and Ohtani, 2003; Massonne et al., 2007; Sakamaki et al., 2009; Zhang et al., 2014; Zhang et al., 2020).

When $Q_{\text{c}}=3$ TW (Stacey and Loper, 2007), the mass of the solidified iron alloy is 1.6 × 10¹⁴ kg yr⁻¹, and it corresponds to $\Delta V=-0.24 k{m}^3 y{r}^{-1}$. $\Delta R=-1.6\times {10}^{-3} mm y{r}^{-1}$ corresponds to the amount of solidification in the core. Because of the uncertainty of the radioactive heat in the mantle and core and the nonoverlap between uranium deposits and geothermal anomalies around the world, we consider the crustal radioactive heat from the direct rock samples as the entire radioactive heat, omitting other radioactive heat for the time being. Thus, $Q_r$ is assumed to be 7 TW (Lay et al., 2008), and we get $Q_{\text{m}}=Q_t-Q_r-Q_c=36$ TW. The mass of the magma solidified at the shallow Earth is 2.7 × 10¹⁵ kg yr⁻¹, which corresponds to a volume change of −120 km³ yr⁻¹ and a radius change of $-0.24 mm y{r}^{-1}$. Overall, the heat flow of the Earth is in agreement with a shrinkage of −120.24 km³ yr⁻¹ in the Earth’s volume. This process considers the total solidification rather than the net solidification. However, if melting is also considered when computing the contributions of the crystallization process, it will make the calculation more complex and the volume changes involved may be smaller.

Analysis of Diurnal Length Variation

The variation of the Earth’s moment of inertia is calculated using the LOD data and angular momentum conservation. Based on occultation and solar and lunar eclipses, the long-term average change rate of LOD in the last 1,000 years is determined to be approximately −0.01 $ms y{r}^{-1}$ (Stephenson and Morrison, 1984). The LOD variation associated with large earthquakes is estimated to be approximately 0.0102 $ms y{r}^{-1}$, and the direct LOD observation suggests a rate of −0.0371 $ms y{r}^{-1}$ (O'Connell and Dziewonski, 1976).

When the conservation of angular momentum is achieved, the variation in LOD manifests as the variation of the radius (Eq. 6):

$L=m\omega r^2=I_1{\omega }_1=I_2{\omega }_2,(6)$

where $m$ is the mass of the Earth, $r$ is its radius, $I$ and $\omega$ are its moment of inertia and angular velocity, 1 and 2 denote the first state of the Earth with a radius of 6,371 km and the second state where the Earth’s radius is decreased by an annual average radius change, respectively. The moment of inertia of the Earth is calculated by dividing it into several shells and approximating the integral with respect to $r$ by summation, as shown in Eq. 7:

$I_{total}={\displaystyle {\sum }_{i=1}^n{I}_i},(7)$

where $I_i$ is the moment of inertia of each layer and ${\omega }_1$ ${\omega }_2$ are calculated using Eqs 8, 9:

${\omega }_1=\frac{2\pi }{86400}=7.27\times {10}^{-5} \left(rad s^{-1}\right),(8)$

${\omega }_2=\frac{2\pi }{86400-\mathrm{\Delta }LOD},(9)$

where $\Delta LOD$ is the average variation of LOD. Herein, the Earth is divided into 638 shells, each with a thickness of 10 km and a homogeneous density distribution. The moment of inertia of the ith shell is calculated using Eq. 10:

$I_i=\frac{2}{5}{m}_i\left(\frac{r_{i2}^5-r_{i1}^5}{r_{i2}^3-r_{i1}^3}\right),(10)$

where $r_{i1}$ and $r_{i2}$ are the inner and outer radii of ith shell, respectively, and $m_i$ is its mass, which is calculated as $m_i=\frac{4}{3}\pi \left(r_{i2}^3-r_{i1}^3\right){\text{ρ}}_i$. The density $\left({\text{ρ}}_i\right)$ of each shell is obtained using the PREM model (Dziewonski and Anderson, 1981). The total moment of inertia of the Earth in the first state $\left(I_1\right)$ is $7.98\times {10}^{37} kg{\text{ m}}^2$. For the second state, the annual average radius change for the Earth’s core is set to $-1.6\times {10}^{-6} m y{r}^{-1}$ at the topmost outer core in accordance with the latent heat analysis and that for the Earth’s crust is a variable $\left(\text{Δ}r\right)$. The inner and outer radii of shells in the second state ($r{\mathrm{\text{'}}}_{i1}$ and $r{\mathrm{\text{'}}}_{i2}$) are less than that in the first state owing to change in the Earth’s radius. The moment of inertia of the 348th shell (the first shell is the center of Earth) at the topmost outer core where the radius is 3,471 km $\left(r_2\right)$ is calculated using Eq. 11:

$I_i=\frac{2}{5}{m}_{348}\left(\frac{r{\prime }_{i2}^5-r_{i1}^5}{r{\prime }_{i2}^3-r_{i1}^3}\right),(11)$

where $r{\text{'}}_{i2}=r_2-1.6\times {10}^{-3} mm$. The moments of inertia of shells from 349th to 637th are calculated using Eq. 12:

$I_i=\frac{2}{5}{m}_i\left(\frac{r{\prime }_{i2}^5-r{\prime }_{i1}^5}{r{\prime }_{i2}^3-r{\text{'}}_{i1}^3}\right),(12)$

where $r{\prime }_{i1}=r_{i1}-1.6\times {10}^{-6}{\left(\frac{3471}{r_{i1}}\right)}^2$ and $r{\prime }_{i2}=r_{i2}-1.6\times {10}^{-6}{\left(\frac{3471}{r_{i2}}\right)}^2$. The moment of inertia of the last shell (638th) is calculated using Eq. 13:

$I_{638}=\frac{2}{5}{m}_{638}\left(\frac{{\left(r{\mathrm{\prime }}_{{638}_2}-\Delta r\right)}^5-r{\mathrm{\prime }}_{{638}_1}^5}{{\left(r{\mathrm{\prime }}_{{638}_2}-\Delta r\right)}^3-r{\mathrm{\prime }}_{{638}_1}^3}\right).(13)$

The total moments of inertia of the Earth in the first and second states are quite similar due to minute changes in the radius, and thus, $\left(1-I_{2nd}/I_{1st}\right){10}^{13}$ and $\left(1-{\omega }_1/{\omega }_2\right){10}^{13}$ are introduced for comparison in Figure 5. When the angular momentum conservation is realized, the radius change is −0.2 to −3.3 mm yr⁻¹, which corresponds to a volume change of −111 to −1,676 km³ yr⁻¹.

FIGURE 5

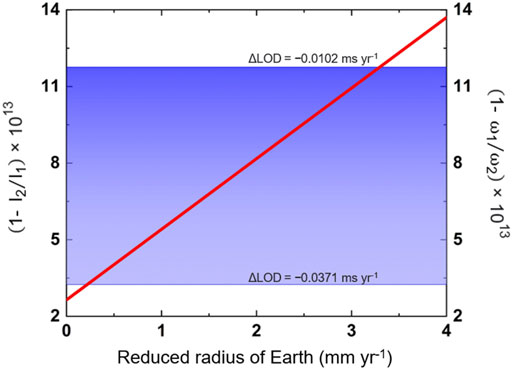
FIGURE 5. Changes in the moment of inertia of Earth as a function of reduced radius of the crust. Red line: change of the moment of inertia of Earth; blue shading: range of variation of the Earth’s angular velocity. Changes of the moment of inertia and angular velocity are extremely small, and thus, they are expressed as the vertical axis title. The subscripts 1 and 2 represent the states before and after the radius of the Earth has decreased, respectively.

Summary

The annual average volume variation of the Earth obtained from the analysis of GPS data, LOD observations, and global heat flux estimates are −841.60 km³ yr⁻¹, −120.24 km³ yr⁻¹, and −111 to −1,676 km³ yr⁻¹, respectively, and these are in good agreement with each other. The values are on the same order of magnitude but with some differences, which can be attributed to the uncertainty of global heat flux estimates and the specific latent heat reported in previous studies. The density profile of the Earth and density of iron under high pressure and high temperature are also likely sources of uncertainty. Moreover, the GPS tracking stations are sparsely distributed in some regions, which could have led to the gaps in data. Nevertheless, these results are sufficient for validating the theory of solidification-driven dynamics of the Earth.

Mechanical Analysis

The molten substance in the Earth’s interior continues to solidify. When the volume change at the shallow Earth due to solidification accumulates, after a specific peak value is reached, the pressure changes because of which the rigid lithosphere become mechanically unstable and eventually fails, decreasing the Earth’s radius and volume. The volume shrinkage increases the influence of gravity on the crust, triggering a pressure drop at the bottom of the lithosphere and a large-scale fracture and dislocation of the overlying strata, which induces geological events such as earthquakes. This is similar to the elastic bucking load that an ordinary spherical shell model can bear under external pressure. The Earth’s crust is thus simplified by a spherical shell model, and the ultimate load of the spherical shell is calculated. For a spherical shell, the ultimate load is only 70% of the ideal case because of the accuracy, and the ultimate load $P_c$ that can sustain under external pressure is calculated using Eq. 14 (Pan and Cui, 2010),

$P_c=0.7\times \frac{2E}{\sqrt{3\left(1-{\mu }^2\right)}}{\left(\frac{t}{R}\right)}^2,(14)$

where $E$ and $\mu$ are Young’s modulus and Poisson’s ratio of crustal rocks, $t$ is the mean thickness of the crust (30 km), and $R$ is the mean radius of the sphere (6,371 km). For most crustal rocks, values of Poisson’s ratio are between 0.2 and 0.3 (Hyndman, 1979; Zandt and Ammon, 1995; Wang, 2009). Herein, an average value of 0.25 is selected to simplify the calculation. For most crustal rocks, values of Young’s moduli vary in the range 20–100 GPa (Wang, 2009); we selected the maximum and minimum values to get a range. Therefore, according to the crustal temperature and pressure conditions at different depths (≤30 km), we obtained $P_C=0.37–1.85$ MPa.

The results show that the limit load of the overlying crust is small and much less than the stress caused by self-weight ($\sim 1000 MPa)$. However, it can exist stably because of the support of the lower shell. When the magma solidifies, more magma diffuses up to occupy the newly available volume, which decreases the density and pressure and increases the influence of gravity on the crust, as shown in Figure 6. Eventually, for the new shell to reach mechanical equilibrium, the builtup strain is released in the form of earthquakes and other geologic activities. The pressure change $\left(\Delta P\right)$ caused by the increase of gravity of the solidified magma $\left(\Delta G\right)$ is calculated using Eq. 15:

$\mathrm{\Delta }P=\frac{\mathrm{\Delta }G}{S}=\frac{mg}{S},(15)$

where $g$ is the gravitational constant, $m$ is the mass of the solidified magma, and $S$ is the solidified area. Since the stress accumulated by magma solidification is released by earthquakes, herein, we assume that the area of solidified magma is equal to the area of the earthquake’s hardest-hit area. The relationship between the radius and intensity in the worst-hit area is given using Eq. 16 (Bath, 2013):

$I_0-I=3\mathit{log}\frac{d^2+h^2}{h^2},(16)$

where $I_0$ is the maximum intensity, $I$ is the intensity of the site located at distance $d$ from the epicenter, and $h$ is the mean focal depth. The maximum intensity can be obtained from the magnitude $\left(M\right)$ (Båth, 1975) using Eq. 17:

$M=0.62I_0+1.68{log}_{10}h-0.95.(17)$

FIGURE 6

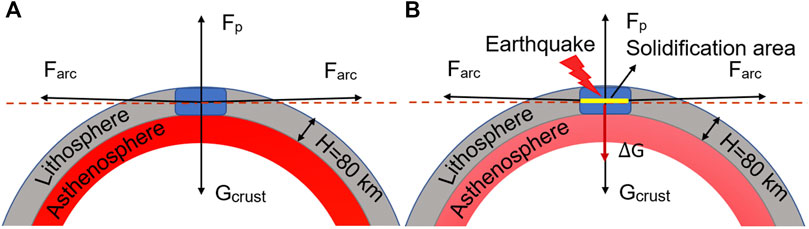
FIGURE 6. The mechanical models of the Earth before and after solidification. Red shading: density of magma, a darker color implies greater density; F_P denotes supporting the force of asthenosphere, and F_arc denotes the circumferential force. (A) The mechanical structure of the overlying crust is balanced before solidification. (B) When the magma continues solidifying, it accumulates the weight of the overlying crust, and the mechanical structure of the overlying crust becomes unstable when its limit load is reached, causing collapse and rupture and triggering an earthquake.

Taking the hardest-hit area of Mw 8 earthquake as an example, the results show that the pressure change $\left(\Delta P\right)$ is 1.84–5.51 MPa, and it decreases with increasing depth. As shown in Figure 7, the pressure variation within a depth of 30 km exceeds the ultimate load of the crust. Small changes in the interior can cause the mechanical structure of the Earth’s crust to break down, and when the strain is beyond the strength limit of the crust, geological movements such as earthquakes are triggered. This finding is consistent with the depth and frequency of the shallow earthquakes.

FIGURE 7

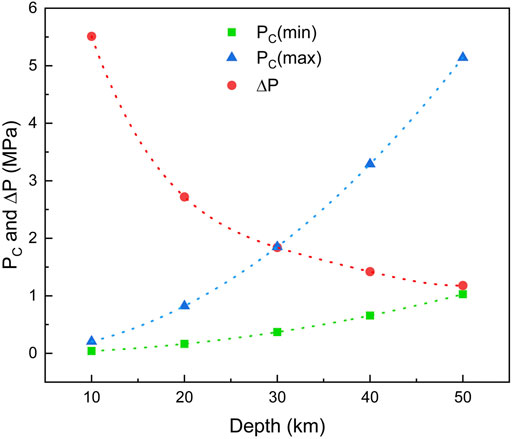
FIGURE 7. Relationship between the pressure change caused by the magma solidification and the ultimate load of the overlying crust. P_c(max) and P_c(min) are obtained from the average maximum and minimum Young’s moduli of the main components of the crust (basalt and granite), respectively (Schultz, 1993; Yang et al., 2019).

Discussion and Conclusion

Based on the analysis of the GPS data, changes in the total volume and radius of the Earth are determined, and these changes demonstrate that the Earth is undergoing contraction at an average rate of 1.65 mm yr⁻¹. The change in the radius causes changes in the moment of inertia of the Earth, which increases the Earth’s rotation speed. This can explain the physical phenomenon of the change in the Earth’s speed and the change in LOD. The change of the Earth’s radius is mainly attributed to the solidification of molten substance in the Earth’s interior, and this liquid–solid transformation is the main power source for geodynamics. The abovementioned phenomena and principles can be extended to other planets whose structures are similar to that of the Earth, that is, planets on which the liquid–solid transformation of the inner material is not yet complete.

The pressure-volume work ($W=P\times \Delta V$), as a result of solidification, is a critical energy source for geodynamics and earthquakes. At the shallow Earth (10 km), W = ∼2.3 TW. For major earthquakes (Mw > 7), W = ∼2 TW (Kanamori, 1978). Therefore, the estimated energy from the pressure–volume work is sufficient to generate earthquakes, and the remaining energy contributes to power plate tectonics and other geologic movements. At the Earth’s core, W = ∼1 TW, which contributes to the geodynamic processes.

Based on the previous discussion, earthquakes can be predicted based on the energy provided by solidification and the energy required for earthquakes. The expectation of energy of earthquakes from Mw $M_1$ to $M_2$ can be calculated using Eq. 18:

$E\left[X\right]={\displaystyle {\int }_{M_1}^{M_2}e\left(x\right)f\left(x\right)dx},(18)$

where $E\left[X\right]$ is the expected value of the energy released by earthquakes from Mw $M_1$ to $M_2$, $e\left(x\right)$ is the energy released by an Mw x earthquake, and $f\left(x\right)$ is the probability density function of earthquakes (derived from the Gutenberg–Richter relationship). The frequency of earthquakes $\left(N\right)$ of a certain magnitude range within a period is thus calculated using Eq. 19:

$N=f\left(x\right)W/E\left[X\right] ,(19)$

where $W$ is the pressure–volume work at the shallow Earth. If more sufficient LOD and GPS data are available, the volume change of the Earth can be calculated more accurately, which will enable precise earthquake prediction.

In conclusion, the Earth has been going through a nonlinear solidification process since the magma ocean stage, which has been accompanied by the release of latent heat and volume contraction. Our analyses based on the GPS data, LOD observations, and heat flux estimates demonstrate that the current rate of change of the Earth’s volume is −841 km³ yr⁻¹. The decrease in the Earth’s internal volume reduces the pressure at the bottom of the crust and rock layers. Under the action of gravity, the interactions between the crustal plates intensify, which makes the mechanical structure unstable. Our mechanical model shows that the decrease of pressure (1.84–5.51 MPa) is greater than the ultimate load (0.37–1.85 MPa) that most of the Earth’s crust can bear. Therefore, volume shrinkage leads to stress buildup followed by mechanical failure, which manifests as earthquakes and powers the geodynamics of the crust. The findings of this study reveal the connection between the liquid–solid transformation inside the Earth and geodynamics and provides a new perspective for predicting earthquakes.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

DH contributed to conception of the study; DH and XL designed the study; XL and MT collected the data and performed the analysis; XL wrote the first draft of the article; DH and XL revised the article. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank all the reviewers who participated in the review, as well as MJEditor (www.mjeditor.com) for providing English editing services during the preparation of this manuscript.

References

Araki, T., Enomoto, S., Furuno, K., Gando, Y., Ichimura, K., Ikeda, H., et al. (2005). Experimental Investigation of Geologically Produced Antineutrinos with KamLAND. Nature 436 (7050), 499–503. doi:10.1038/nature03980

PubMed Abstract | CrossRef Full Text | Google Scholar

Bath, M. (2013). Introduction to Seismology. Basel: Birkhäuser.

Google Scholar

Båth, M. (1975). Seismicity of the Tanzania Region. Tectonophysics 27 (4), 353–379. doi:10.1016/0040-1951(75)90004-9

CrossRef Full Text | Google Scholar

Bokelmann, G. H. R. (2002b). Convection-driven Motion of the North American Craton: Evidence from P-Wave Anisotropy. Geophys. J. Int. 148 (2), 278–287. doi:10.1046/j.1365-246X.2002.01614.x

CrossRef Full Text | Google Scholar

Bokelmann, G. H. R. (2002a). Which Forces Drive North America? Geol 30 (11), 1027–1030. doi:10.1130/0091-7613(2002)030<1027:wfdna>2.0.co;2

CrossRef Full Text | Google Scholar

Bono, R. K., Tarduno, J. A., Nimmo, F., and Cottrell, R. D. (2019). Young Inner Core Inferred from Ediacaran Ultra-low Geomagnetic Field Intensity. Nat. Geosci 12 (2), 143–147. doi:10.1038/s41561-018-0288-0

CrossRef Full Text | Google Scholar

Bott, M. (1991). Ridge Push and Associated Plate interior Stress in normal and Hot Spot Regions. Tectonophysics 200 (1-3), 17–32. doi:10.1016/0040-1951(91)90003-B

CrossRef Full Text | Google Scholar

Buffett, B. A. (2000). Earth's Core and the Geodynamo. Science 288 (5473), 2007–2012. doi:10.1126/science.288.5473.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Buffett, B. A., Huppert, H. E., Lister, J. R., and Woods, A. W. (1992). Analytical Model for Solidification of the Earth's Core. Nature 356 (6367), 329–331. doi:10.1038/356329a0

CrossRef Full Text | Google Scholar

Chao, B. F., and Gross, R. S. (1987). Changes in the Earth's Rotation and Low-Degree Gravitational Field Induced by Earthquakes. Geophys. J. Int. 91 (3), 569–596. doi:10.1111/j.1365-246X.1987.tb01659.x

CrossRef Full Text | Google Scholar

Cox, A., and Doell, R. R. (1961). Palæomagnetic Evidence Relevant to a Change in the Earth's Radius. Nature 189 (4758), 45–47. doi:10.1038/189045a0

CrossRef Full Text | Google Scholar

Dye, S. (2012). Geoneutrinos and the Radioactive Power of the Earth. Rev. Geophys. 50 (3), 1–19. doi:10.1029/2012RG000400

CrossRef Full Text | Google Scholar

Dziewonski, A. M., and Anderson, D. L. (1981). Preliminary Reference Earth Model. Phys. Earth Planet. Interiors 25 (4), 297–356. doi:10.1016/0031-9201(81)90046-7

CrossRef Full Text | Google Scholar

Elkins-Tanton, L. T. (2012). Magma Oceans in the Inner Solar System. Annu. Rev. Earth Planet. Sci. 40, 113–139. doi:10.1146/annurev-earth-042711-105503

CrossRef Full Text | Google Scholar

Forsyth, D., and Uyeda, S. (1975). On the Relative Importance of the Driving Forces of Plate Motion. Geophys. J. Int. 43 (1), 163–200. doi:10.1111/j.1365-246X.1975.tb00631.x

CrossRef Full Text | Google Scholar

Gessmann, C., and Wood, B. (2002). Potassium in the Earth’s Core? Earth Planet. Sci. Lett. 200 (1-2), 63–78. doi:10.1016/S0012-821X(02)00593-9

CrossRef Full Text | Google Scholar

Heflin, M. (1994). GNSS Time Series. Available: https://www.frontiersin.org/about/author-guidelines (Accessed May 20, 2021).

Google Scholar

Herzberg, C., Condie, K., and Korenaga, J. (2010). Thermal History of the Earth and its Petrological Expression. Earth Planet. Sci. Lett. 292 (1-2), 79–88. doi:10.1016/j.epsl.2010.01.022

CrossRef Full Text | Google Scholar

Hirose, K., Labrosse, S., and Hernlund, J. (2013). Composition and State of the Core. Annu. Rev. Earth Planet. Sci. 41, 657–691. doi:10.1146/annurev-earth-050212-124007

CrossRef Full Text | Google Scholar

Holme, R., and De Viron, O. (2013). Characterization and Implications of Intradecadal Variations in Length of Day. Nature 499 (7457), 202–204. doi:10.1038/nature12282

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, S., He, H., Ji, J., Lin, Y., Hui, H., Anand, M., et al. (2021). A Dry Lunar Mantle Reservoir for Young Mare Basalts of Chang'e-5. Nature 600, 49–53. doi:10.1038/s41586-021-04107-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, L.-r., Ma, Z.-j., and Zhu, J.-x. (2002). The Newest Observational Evidence on Asymmetrical Deformation of the Earth. Acta Seimol. Sin. 15 (2), 210–213. doi:10.1007/s11589-002-0010-5

CrossRef Full Text | Google Scholar

Hyndman, R. (1979). Poisson’s Ratio in the Oceanic Crusta Review. Developments in Geotectonics 15, 321–333. doi:10.1016/B978-0-444-41851-7.50022-4

CrossRef Full Text | Google Scholar

Josiah, R. (2010). Distance Calculation Using Haversine Formula. Available: https://www.mathworks.com/matlabcentral/fileexchange/27785-distance-calculation-using-haversine-formula (Accessed August 18, 2021).

Google Scholar

Kanamori, H. (1978). Quantification of Earthquakes. Nature 271 (5644), 411–414. doi:10.1038/271411a0

CrossRef Full Text | Google Scholar

Labrosse, S., Poirier, J.-P., and Le Mouël, J.-L. (2001). The Age of the Inner Core. Earth Planet. Sci. Lett. 190 (3-4), 111–123. doi:10.1016/S0012-821X(01)00387-9

CrossRef Full Text | Google Scholar

Lay, T., Hernlund, J., and Buffett, B. A. (2008). Core-mantle Boundary Heat Flow. Nat. Geosci 1 (1), 25–32. doi:10.1038/ngeo.2007.44

CrossRef Full Text | Google Scholar

Li, Q.-L., Zhou, Q., Liu, Y., Xiao, Z., Lin, Y., Li, J.-H., et al. (2021). Two-billion-year-old Volcanism on the Moon from Chang'e-5 Basalts. Nature 600, 54–58. doi:10.1038/s41586-021-04100-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Massonne, H., Willner, A., and Gerya, T. (2007). Densities of Metapelitic Rocks at High to Ultrahigh Pressure Conditions: What Are the Geodynamic Consequences? Earth Planet. Sci. Lett. 256 (1-2), 12–27. doi:10.1016/j.epsl.2007.01.013

CrossRef Full Text | Google Scholar

Murthy, V. R., Van Westrenen, W., and Fei, Y. (2003). Experimental Evidence that Potassium Is a Substantial Radioactive Heat Source in Planetary Cores. Nature 423 (6936), 163–165. doi:10.1038/nature01560

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Connell, R. J., and Dziewonski, A. M. (1976). Excitation of the Chandler Wobble by Large Earthquakes. Nature 262 (5566), 259–262. doi:10.1038/262259a0

CrossRef Full Text | Google Scholar

Ohta, K., Kuwayama, Y., Hirose, K., Shimizu, K., and Ohishi, Y. (2016). Experimental Determination of the Electrical Resistivity of Iron at Earth's Core Conditions. Nature 534 (7605), 95–98. doi:10.1038/nature17957

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohtani, E., and Maeda, M. (2001). Density of Basaltic Melt at High Pressure and Stability of the Melt at the Base of the Lower Mantle. Earth Planet. Sci. Lett. 193 (1-2), 69–75. doi:10.1016/S0012-821X(01)00505-2

CrossRef Full Text | Google Scholar

Pan, B., and Cui, W. (2010). An Overview of Buckling and Ultimate Strength of Spherical Pressure hull under External Pressure. Mar. Structures 23 (3), 227–240. doi:10.1016/j.marstruc.2010.07.005

CrossRef Full Text | Google Scholar

Rychert, C. A., and Shearer, P. M. (2009). A Global View of the Lithosphere-Asthenosphere Boundary. Science 324 (5926), 495–498. doi:10.1126/science.1169754

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakamaki, T., Ohtani, E., Urakawa, S., Suzuki, A., and Katayama, Y. (2010). Density of Dry Peridotite Magma at High Pressure Using an X-ray Absorption Method. Am. Mineral. 95 (1), 144–147. doi:10.2138/am.2010.3143

CrossRef Full Text | Google Scholar

Sakamaki, T., Ohtani, E., Urakawa, S., Suzuki, A., and Katayama, Y. (2009). Measurement of Hydrous Peridotite Magma Density at High Pressure Using the X-ray Absorption Method. Earth Planet. Sci. Lett. 287 (3-4), 293–297. doi:10.1016/j.epsl.2009.07.030

CrossRef Full Text | Google Scholar

Schultz, R. A. (1993). Brittle Strength of Basaltic Rock Masses with Applications to Venus. J. Geophys. Res. 98 (E6), 10883–10895. doi:10.1029/93JE00691

CrossRef Full Text | Google Scholar

Shimada, M., and Cho, A. (1990). Two Types of Brittle Fracture of Silicate Rocks under Confining Pressure and Their Implications in the Earth's Crust. Tectonophysics 175 (1-3), 221–235. doi:10.1016/0040-1951(90)90139-Y

CrossRef Full Text | Google Scholar

Stacey, F. D., and Loper, D. E. (2007). A Revised Estimate of the Conductivity of Iron alloy at High Pressure and Implications for the Core Energy Balance. Phys. Earth Planet. Interiors 161 (1-2), 13–18. doi:10.1016/j.pepi.2006.12.001

CrossRef Full Text | Google Scholar

Stephenson, F. R., and Morrison, L. V. (1984). Long-term Changes in the Rotation of the Earth : 700 B.C. To A.D. 1980. Phil. Trans. R. Soc. Lond. A. 313 (1524), 47–70. doi:10.1098/rsta.1984.0082

CrossRef Full Text | Google Scholar

Sun, F.-P., Zhu, X.-H., Wang, R., and Li, J.-T. (2006). Detection of Changes of the Earth's Volume and Geometry by Using GPS and VLBI Data. Chin. J. Geophys. 49 (4), 900–906. doi:10.1002/cjg2.910

CrossRef Full Text | Google Scholar

Sun, W. (2019). The Magma Engine and the Driving Force of Plate Tectonics. Chin. Sci. Bull. 64 (28-29), 2988–3006. doi:10.1360/n972019-00274

CrossRef Full Text | Google Scholar

Suzuki, A., and Ohtani, E. (2003). Density of Peridotite Melts at High Pressure. Phys. Chem. Minerals 30 (8), 449–456. doi:10.1007/s00269-003-0322-6

CrossRef Full Text | Google Scholar

Tian, H.-C., Wang, H., Chen, Y., Yang, W., Zhou, Q., Zhang, C., et al. (2021). Non-KREEP Origin for Chang'e-5 Basalts in the Procellarum KREEP Terrane. Nature 600, 59–63. doi:10.1038/s41586-021-04119-5

PubMed Abstract | CrossRef Full Text | Google Scholar

van Summeren, J., Conrad, C. P., and Lithgow-Bertelloni, C. (2012). The Importance of Slab Pull and a Global Asthenosphere to Plate Motions. Geochem. Geophys. Geosyst. 13 (2), a–n. doi:10.1029/2011GC003873

CrossRef Full Text | Google Scholar

Wang, Q. (2009). Seismic Velocities, Anisotropy, Hysteresis and Poisson's Ratio of Ultrahigh Pressure (UHP) Metamorphic Rocks. Quebec: École Polytechnique de Montréal.

Google Scholar

Ward, M. A. (1963). On Detecting Changes in the Earth's Radius. Geophys. J. Int. 8 (2), 217–225. doi:10.1111/j.1365-246X.1963.tb06285.x

CrossRef Full Text | Google Scholar

Whittington, A. G., Hofmeister, A. M., and Nabelek, P. I. (2009). Temperature-dependent thermal Diffusivity of the Earth's Crust and Implications for Magmatism. Nature 458 (7236), 319–321. doi:10.1038/nature07818

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, B. M. (2007). Igneous Petrogenesis a Global Tectonic Approach. Berlin: Springer Science & Business Media.

Google Scholar

Wu, X., Collilieux, X., Altamimi, Z., Vermeersen, B. L. A., Gross, R. S., and Fukumori, I. (2011). Accuracy of the International Terrestrial Reference Frame Origin and Earth Expansion. Geophys. Res. Lett. 38 (13), a–n. doi:10.1029/2011GL047450

CrossRef Full Text | Google Scholar

Yang, L., Feng, X., and Sun, Y. (2019). Predicting the Young's Modulus of Granites Using the Bayesian Model Selection Approach. Bull. Eng. Geol. Environ. 78 (5), 3413–3423. doi:10.1007/s10064-018-1326-2

CrossRef Full Text | Google Scholar

Zandt, G., and Ammon, C. J. (1995). Continental Crust Composition Constrained by Measurements of Crustal Poisson's Ratio. Nature 374 (6518), 152–154. doi:10.1038/374152a0

CrossRef Full Text | Google Scholar

Zhang, Y., Hou, M., Liu, G., Zhang, C., Prakapenka, V. B., Greenberg, E., et al. (2020). Reconciliation of Experiments and Theory on Transport Properties of Iron and the Geodynamo. Phys. Rev. Lett. 125 (7), 078501. doi:10.1103/PhysRevLett.125.078501

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Sekine, T., He, H., Yu, Y., Liu, F., and Zhang, M. (2014). Shock Compression of Fe-Ni-Si System to 280 GPa: Implications for the Composition of the Earth's Outer Core. Geophys. Res. Lett. 41 (13), 4554–4559. doi:10.1002/2014GL060670

CrossRef Full Text | Google Scholar

Zhu, X., Sun, F., and Wang, R. (2013).Study on the Earth’s Volume Change by Using Space Observed Technology.” in China Satellite Navigation Conference (CSNC) 2013 Proceedings, Wuhan, May 15–17 (Berlin, Heidelberg: Springer), 15–24.

CrossRef Full Text | Google Scholar