
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 24 May 2022
Sec. Geohazards and Georisks
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.893882
This article is part of the Research Topic Volcanic Forecasting, Crisis Management, and Risk Communication View all 8 articles
Auckland, a city of 1.6 million people, is situated atop the active monogenetic Auckland Volcanic Field (AVF). Thus, short-term eruption forecasting is critical to support crisis management in a future event, especially to inform decisions such as calling evacuations. Here we present an updated BET_EF for the AVF incorporating new data and the results of an expert-opinion workshop, and test the performance of the resulting BETEF_AVF on eight hypothetical eruption scenarios with pre-eruptive sequences. We carry out a sensitivity analysis into the selection of prior distributions for key model parameters to explore the utility of using BET_EF outputs as a potential input for evacuation decision making in areas of distributed volcanism such as the AVF. BETEF_AVF performed well based on the synthetic unrest dataset for assessing the probability of eruption, with the vent outbreaks eventuating within the zone of high spatial likelihood. Our analysis found that the selection of different spatial prior model inputs affects the estimated vent location due to the weighting between prior models and monitoring inputs within the BET_EF, which as unrest escalates may not be appropriate for distributed volcanic fields. This issue is compounded when the outputs are combined with cost-benefit analysis to inform evacuation decisions, leading to areas well beyond those with observed precursory activity being included in evacuation zones. We find that several default settings used in past work for the application of BET_EF and CBA to inform evacuation decision-support are not suitable for distributed volcanism; in particular, the default 50-50 weighting between priors and monitoring inputs for assessing spatial vent location does not produce useful results. We conclude by suggesting future cost-benefit analysis applications in volcanic fields appropriately consider the spatial and temporal variability and uncertainty characteristic of such systems.
Eruption forecasting is one of the key goals for volcanology (Sparks, 2003). Eruption forecasting aims to support decision-makers faced with challenges ranging in timescale from evacuation calls in the short-term to land-use planning in the long-term (Sparks, 2003; Marzocchi and Bebbington, 2012). During periods of volcanic unrest, there is a high degree of uncertainty due to the complexity of volcanic systems and the variability in eruption characteristics, such as eruption vent location and eruptive style and size (Marzocchi et al., 2012). Volcanoes can exhibit a range of geophysical, geochemical and geodetic changes during unrest periods, which can be captured using a range of monitoring techniques as magma ascends towards the surface (Marzocchi et al., 2008; Newhall et al., 2017; Gottsmann et al., 2019). However, the interpretation of these changes can place significant pressure on monitoring volcanologists, especially when critical emergency management decisions depend on them (Marzocchi and Woo, 2007; Marzocchi et al., 2012; Papale, 2017). The high stakes have encouraged the development of quantitative models to support increasingly complex eruption forecasting (Connor et al., 2003; Lindsay et al., 2010; Sandri et al., 2012; Selva et al., 2012; Aspinall and Woo, 2014; Sobradelo et al., 2014; Newhall and Pallister, 2015; Cassisi et al., 2016; Sheldrake et al., 2017). Recent reviews can be found in Poland and Anderson (2020) and Whitehead and Bebbington (2021).
One approach gaining prominence for conducting short-term quantitative eruption forecasting assessments is the use of event trees, first proposed by Newhall and Hoblitt (2002). Event trees provide a graphical representation of a volcanic event with branches connecting nodes representing mutually exclusive and exhaustive behaviours with conditional probabilities based on the previously observed behaviour (Marzocchi et al., 2004, Marzocchi et al., 2008). The idea of an event tree is to provide a generic framework that can be applied to any volcano, where the required input data can be derived from any or all of: knowledge of past eruptions, insights from expert opinions, data from analogous volcanoes, and monitoring data. Event trees can consider the aleatoric and epistemic uncertainty for the volcanic behaviour by applying Bayesian inference (Marzocchi et al., 2004, Marzocchi et al., 2008; Neri et al., 2008; Marzocchi and Bebbington, 2012; Sobradelo et al., 2014; Bartolini et al., 2016). There are two prominent short-term event tree frameworks that incorporate Bayesian inference, Bayesian Event Tree for Eruption Forecasting (BET_EF; Marzocchi et al., 2008) and ST_HASSET (Bartolini et al., 2016). These tools are designed to be developed during quiescence, and thus contrast with other event tree structures for assessing short-term volcanic eruption likelihood, such as the USGS Volcano Disaster Assistance Program (VDAP) event tree approach (Newhall and Pallister, 2015), which is designed to document the volcanologist’s understanding of what is occurring in the midst of a crisis.
The output of an eruption forecasting assessment can inform an evacuation call when combined with cost-benefit analysis (CBA; Marzocchi and Woo, 2007; Woo, 2008; Marzocchi and Woo, 2009; Bebbington and Zitikis, 2016). CBA has been applied in conjunction with BET outputs to support evacuation decision-making based on risk-to-life in the AVF from base-surge phenomena (Sandri et al., 2012) and for other volcanoes (Marzocchi and Woo, 2009; Wild et al., 2019). CBA defines a threshold for an action by weighing the cost of action (C) versus the loss from no action (L) and compares this to the probability of impact (p). When the probability of impact reaches or exceeds the CBA threshold, i.e., p => C/L, the action, e.g., evacuation, is cost-beneficial.
This paper explores the challenges of integrating short-term eruption forecasting with cost-benefit analysis for crisis decision making in areas of distributed volcanism by developing and testing a BET_EF for the AVF. First, we present the model set-up, including the parameter selection methodology. Following this, we conduct a sensitivity analysis of key model parameters. In the absence of observed activity in the AVF, the performance of the developed BET_EF is examined using a published synthetic unrest dataset from multiple eruptive scenarios. Finally, we review the integration of BET_EF with CBA to assess its utility for short-term eruption forecasting and evacuation decision-support for distributed volcanic fields such as the AVF.
Auckland, located in New Zealand’s North Island (Figure 1), is the country’s largest city (population ∼1.6 million; Statistics New Zealand 2018) and produces 37.9% (NZ$2018 107.8 billion; Statistics New Zealand 2019) of the nation’s GDP. Auckland is also situated upon the basaltic monogenetic Auckland Volcanic Field (AVF). The monogenetic nature of the AVF poses a significant challenge to forecasting the next eruption location (Allen and Smith, 1994; Lindsay et al., 2010). The AVF has an estimated 53 eruptive centres formed in the last 193 kyr, with the last eruption occurring 550–600 years ago (Allen and Smith, 1994; Lindsay et al., 2011; Leonard et al., 2017; Hopkins et al., 2020). Most AVF eruptions have been <0.1 km2 in volume; however, the most recent two eruptions, namely Mt Wellington and Rangitoto, have been significantly larger than average (Kereszturi et al., 2013). The magma source supplying the AVF is thought to originate from 70 to 90 km depth based on seismic tomography revealing a zone of anomalously low P-wave velocities (Horspool et al., 2006) as well as geochemical evidence (McGee et al., 2013). The mantle-crust boundary is thought to be at 25–30 km depth (Horspool et al., 2006). This is an important parameter in the context of eruption forecasting, as it is considered that seismicity might not be observed until the magma ascends into the crust (Sherburn et al., 2007).
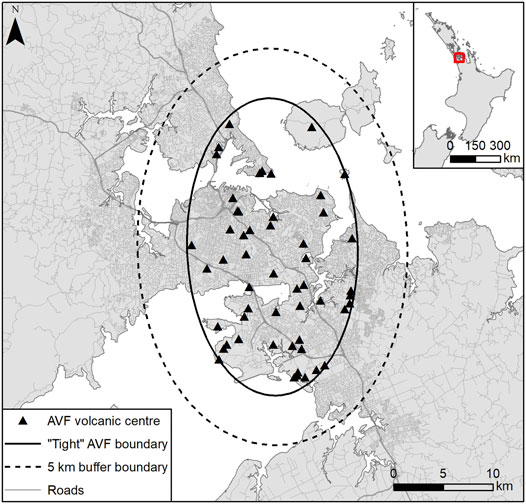
FIGURE 1. Auckland Volcanic Field vent locations with “tight” and 5 km buffer boundaries from Runge et al. (2015) to illustrate the current understanding of the AVF extent. The 5 km buffer is a conservative estimate of the spatial extent of the AVF.
Given the monogenetic nature of the AVF, there are significant uncertainties around the spatial location of the next eruption and its likely volcanic hazards (Magill et al., 2005; Sherburn et al., 2007; Lindsay et al., 2010; Ashenden et al., 2011; Bebbington and Cronin, 2011; Bebbington, 2013, Bebbington, 2015; Kereszturi et al., 2017). Therefore, a critical issue with evaluating the hazard during the next AVF eruption is identifying the vent location. The AVF is thought to be bounded N-S by the mantle source geometry at depth, and E-W by faults associated with the Dun Mountain Ophiolite Belt (Spörli and Eastwood, 1997; Le Corvec et al., 2013). Runge et al. (2015) defined the spatial extent of the AVF using an ellipsoid around past vents (Figure 1), and recommend that a buffer is applied to this boundary given the most recent eruption was anomalous both in terms of polygenetic behaviour and comparatively large erupted volume. Previous studies have looked at the spatial distribution of the next vent location in the AVF using probabilistic approaches for long-term assessments (Magill et al., 2005; Bebbington and Cronin, 2011; Bebbington, 2013, Bebbington, 2015).
The geologic record indicates two primary eruptive styles in the AVF: magmatic and phreatomagmatic (Allen and Smith, 1994; Lindsay et al., 2010; Kereszturi et al., 2014). Approximately 83% of past eruptions have initiated with an explosive phreatomagmatic phase due to magma interacting with groundwater and/or surface water (Morrissey et al., 2000; Kereszturi et al., 2014; Ang et al., 2020); this eruptive style forms maar craters and tuff rings and produces base-surges (which can extend up to 6 km from the vent in a large eruption; Brand et al., 2014), ballistics and tephra fall. Past AVF magmatic eruptions were primarily Hawaiian or Strombolian in style, forming scoria cones, ballistics and lava flows. At least 60% of past AVF eruptions have transitioned from a phreatomagmatic phase into a magmatic phase. The likelihood of future transitions varies spatially across the field, depending on near surface geology and hydrology (Kereszturi et al., 2014, 2017). Due to the eruption hazards, primarily base-surge phenomena, the Auckland Volcano Field Contingency Plan (Auckland Council, 2015) outlines two evacuation zones: the primary evacuation zone, which extends radially from the vent uncertainty zone; and the secondary evacuation zone, which extends 2 km from the primary. Although the two-zones allow for prioritization, in a future crisis both zones are required to evacuate (Auckland Council, 2015).
The likely expected magma ascent time is poorly constrained in the AVF. Blake et al. (2006) estimate magma ascent rates of 0.03–6 ms−1 for the AVF, based on modeling dyke propagation, xenolith settling speeds and xenocryst host reaction speeds from analogous volcanoes. In the AVF, seismicity associated with magma ascent is unlikely to be detected until it reaches the crust-mantle boundary (Sherburn et al., 2007). If detection occurs at this boundary, i.e., 25–30 km depth, these ascent rates would yield ascent times from this depth of <2 h to 12 days. Brenna et al. (2018) evaluated diffusion gradients in AVF xenocrysts and derived magma ascent rates of 0.01–0.03 ms−1, producing ascent times of 9–35 days. Based on the current understanding of the AVF, in which there is no evidence of magma storage in the crust, magma ascent rates are thought to be too quick to support stalling for significant periods (Lindsay et al., 2010; Mazot et al., 2013; Hopkins et al., 2016, Hopkins et al., 2020). Brenna et al. (2018) also suggested that once magma had reached 1–2 km depth, an eruption is likely in less than 12 h. Estimating ascent times is complex, as a single magma batch may ascend at variable rates (Hopkins et al., 2020).
GNS Science conducts volcanic monitoring in New Zealand as part of the GeoNet monitoring program. Auckland’s current seismic monitoring network consists of 10 short-period seismographs, seven of which are buried to reduce anthropogenic noise, and one broadband station (van Wijk et al., 2021). In 2007 it was thought that recorded seismicity might have to be as shallow as 5 km before being useful to estimate potential vent location (Sherburn et al., 2007). There is no permanent geochemistry or geodesy monitoring equipment within the AVF. At the time of writing, there had been no observed volcanic unrest episodes in the AVF.
A previous BET_EF for the AVF was developed by Lindsay et al. (2010) and run as part of the 2008 Exercise Rūaumoko, a national Civil Defence exercise conducted in Auckland, in which the lead-up phase to an AVF eruption was simulated (Auckland Region CDEM Group, 2008; Horrocks, 2008; Brunsdon and Park, 2009). While the Lindsay et al. (2010) BET_EF performed well as part of the exercise, there have been significant subsequent improvements in the scientific understanding of the AVF, which include new constraints on its geographic extent (Runge et al., 2015), spatial vent likelihood (Bebbington and Cronin, 2011; Bebbington, 2013, Bebbington, 2015), eruptive style and the age of past eruptions (Kereszturi et al., 2013, Kereszturi et al., 2014; Leonard et al., 2017; Ang et al., 2020). These improvements have supported the development of seven additional AVF scenarios (Hayes et al., 2018, Hayes et al., 2019). In addition, the Lindsay et al. (2010) consultation with monitoring scientists to inform parameter selection was minimal and informal. In contrast, this study has taken a more formal approach to elicit expert opinion.
Sandri et al. (2012) applied CBA in conjunction with BET outputs in the AVF to support evacuation decision-making based on risk-to-life safety from base-surge phenomena. That study applied the evacuation-specific CBA approach by Woo (2008), which defines the cost of evacuation as the average socio-economic loss per-capita for the evacuation duration, and the loss from no action as the product of the statistical value of life and the proportion of the population that evacuates that owes its life to the decision. Sandri et al. (2012) produced three thresholds based on the evacuation lasting 2 weeks, 2 months and 6 months, and used a proportion of evacuees that owe their life to the evacuation call of 0.5. This made use of the spatial vent likelihood outputs from Lindsay et al. (2010) to produce evacuation zones for the Exercise Rūaumoko sequence.
Bayesian Event Tree for Eruption Forecasting (BET_EF), originally developed by Marzocchi et al. (2008), is an event tree structure developed to assess short-term probabilities of eruption, thereby allowing it to support crisis management (Figure 2). BET_EF was selected as the most appropriate tool for estimating short-term volcanic hazard for crisis decision-support in the AVF context after evaluating a range of available approaches (Wild et al., 2020).
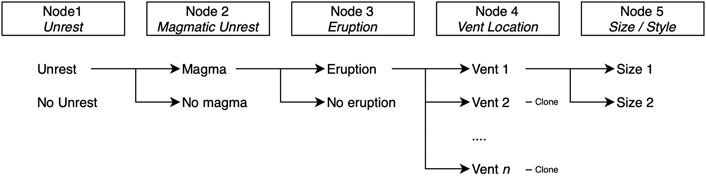
FIGURE 2. Schematic diagram of BET_EF framework. The probability of the selected path is the product of conditional probability θi at all selected branches: [θ]path = [θ1] • [θ2] • [θ3] • [θ4] • [θ5]. Any branch that terminates with “clone” is identical to that of the top branch for that node.
The BET_EF defined structure comprises five nodes (Figure 2):
Node 1: there is either unrest or no unrest, in the time interval (t0, t0 + τ), where t0 is the present time, and τ is the time window considered;
Node 2: the unrest is due to magma, conditional on unrest being detected;
Node 3: the magma will (or will not) erupt) in the time interval (t0, t0 + τ), conditional on the unrest detected is magmatic in origin;
Node 4: the eruption will occur in a specific location, conditional of an eruption; and
Node 5: the eruption will be of a certain size/style (e.g., VEI), conditional of an eruption in a certain location.
At each node, there are three types of inputs:
• Priori beliefs
• Past data
• Monitoring components
Priori beliefs are derived from theoretical models or expert judgment, such as the recurrence rate of unrest or eruption at the volcano. At each node, the priori mean belief input is accompanied by an “equivalent number of data” parameter to reflect the weighting, where a value of 1 indicates low confidence and results in a wider distribution to represent the uncertainty. Past data relates to previous observations of activity at the volcano, for example, the number of observed unrest periods.
Each branch is assigned a probability employing a Bayesian approach, represented by a probability density function, formed by the priori information and weighting values, and past data to produce a distribution representing the uncertainty (both aleatoric and epistemic). The more available data, the more uncertainty is reduced, and subsequently, the variability in each node’s calculated output can potentially be reduced. The output from an event tree is an estimated probability for each outcome node.
Key inputs into a BET_EF for short-term eruption forecasting are monitoring data parameters and threshold values for Nodes 1, 2, and 3 (Marzocchi et al., 2008). In previous implementations of the BET_EF, parameters and thresholds have been determined through expert judgement by evaluating available and theoretical streams of monitoring data (e.g., seismic tremor, gas concentrations) and considering what behavior would be considered anomalous at each node. When setting up a BET_EF, the user can either provide one or two thresholds. A single threshold is reached when the parameter is observed, regardless of the magnitude, e.g., “detection of SO2.” For some parameters, two thresholds are established: one for “background behavior” and another for “anomalous behaviour.” In this case, when observed input data is between the two thresholds, the gradual transition between the two states is modeled using a fuzzy procedure. An example could be “number of long-period earthquakes,” where the lower bound of 3 would indicate potentially anomalous activity for unrest, whereas the upper bound of 8 would be a strong indicator of unrest. Two thresholds can be beneficial as it can be challenging to determine whether the recorded behaviour indicates anomalous diversion from background levels (Gottsmann et al., 2019).
At Node 1, observing a single anomalous parameter sets the probability to 1. Monitoring parameters at Nodes 2 and 3 include a weight. A parameter with an associated weight of 2 means that it is considered to have the same weight as two parameters with a weight value of 1. For Nodes 2 and 3, (Eq. 1) is used to calculate the total degree of anomaly (Z) at a node:
where z is the anomaly and w is the weight for parameter i.
The degree of anomaly is used to calculate the conditional probability distribution for a node. The mean, P, of a Beta distribution is estimated using
where a and b represent the minimum bound (1−a) and the sensitivity to monitoring (b) used to form the Beta distribution. Prior distributions are input for these two parameters, which are updated within the BET_EF framework using data from available observed unrest periods at the volcano in question to form posterior distributions.
BET_EF has been retrospectively applied to the volcanic activity between 2001–2005 at Mt. Etna (Brancato et al., 2011), and between 1981–2009 at Campi Flegrei, Italy (Selva et al., 2012) and to the 1,631 eruption of Mt. Vesuvius (Sandri et al., 2009). The framework has also been used in the emergency management exercise MESIMEX for Mt. Vesuvius, Italy (Marzocchi et al., 2008), Exercise Rūaumoko for the Auckland Volcanic Field (AVF), New Zealand (Lindsay et al., 2010) and the simulation of Cotopaxi, Ecuador (Constantinescu et al., 2015). In all these exercises, estimated probabilities from the BET_EF were consistent with the observed (or simulated) timing and location of eruption and aligned with monitoring scientists’ judgement during the exercise, demonstrating the merits of the framework. An application of BET during the VUELCO Simulation Exercise in Dominica, Lesser Antilles (Constantinescu et al., 2016) demonstrated the importance of users of BET outputs being familiar with probabilistic frameworks in advance of any operational use to ensure the outputs are trusted and applied appropriately.
The BET_EF framework is executed within the PyBETUnrest application (Tonini et al., 2016). This implements both the BET_EF and the BET_UNREST framework (Rouwet et al., 2014; Tonini et al., 2016), the latter of which also considers non-magmatic eruptive phenomena, e.g., hydrothermal eruptions (refer to Tonini et al., 2016 for more detail). PyBETUnrest is an update to the old application form of the BET_EF framework. PyBETUnrest is implemented using the Python programming language, allowing code to be easily modified. Previous testing of the PyBETUnrest application found some discrepancies in how the BET_EF framework is applied between PyBETUnrest and the original application (Wild et al., 2020). In particular, Eq. 2 was not calculated using probability distributions (prior or posterior) but instead used single values of a and b, meaning the procedure is no longer Bayesian, as in the original BET_EF application. In addition, the same values of a and b were used for all three nodes. In the original BET_EF application, prior distributions for a and b are U (0.5, 1) and U (0, 2). For this study, the PyBETUnrest code was modified to reflect the original Bayesian functionality and thus allow uncertainty to be assigned and estimated in the sensitivity analyses. The inputs and outputs from Lindsay et al. (2010) were used to validate the modified PyBETUnrest against the original BET_EF.
To set up the BET_EF for the AVF (hereinafter, BETEF_AVF), both monitoring and non-monitoring components need to be considered for parameter selection. The non-monitoring components were informed by previously published studies for the AVF, following Lindsay et al. (2010).
To inform the monitoring parameters, a scientific consensus approach was applied; this is an approach that has been used to define inputs in past studies for developing volcanic event trees (e.g., Lindsay et al., 2010; Selva et al., 2012; Constantinescu et al., 2016; Tierz et al., 2020) and applied operationally by the USGS’s VDAP team to inform volcanic event-trees in past crises (Newhall and Pallister, 2015). There are alternate methods for collecting expert opinion data, such as Cooke’s classical model (Cooke, 1991), that have been applied in volcanology (e.g., Aspinall, 2006; Neri et al., 2008; Hincks et al., 2014; Bebbington et al., 2018). However, in our case, given the limited number of participants with expertise in each given topic area (e.g., seismic unrest in the AVF), a quantitative elicitation method may have led to very distributed and non-useable data. Furthermore, volcanologists in New Zealand and internationally have operational experience with reaching a consensus for estimating volcanic activity (Potter et al., 2014; Fearnley and Beaven, 2018), while the closely connected nature of the volcanological community suggested a significant risk of a narrow perspective or cognitive bias if a formal elicitation was conducted (Morgan, 2014). As such, the consensus approach within subject matter areas, combined with open discussion, moderated through facilitation, was deemed appropriate for our study.
An expert opinion workshop was thus conducted to define monitoring parameters for the BETEF_AVF. The workshop aimed to establish monitoring parameters and thresholds for the BETEF_AVF for Nodes 1 to 3. The workshop, including preparation, was conducted in four steps:
1. Identify workshop participants
2. Ensure participants have a shared conceptual model of volcanism in the AVF, as well as an understanding of BET_EF and how the workshop output feeds into BETEF_AVF
3. Establish the monitoring parameters and thresholds
4. Run the model using the Exercise Rūaumoko unrest sequence and review outputs with participants
Participants were identified following engagement with the Determining Volcanic Risk in Auckland (DEVORA) research programme management group (Step 1). Specific areas of expertise were targeted amongst the monitoring team from GeoNet and volcanologists from New Zealand universities to ensure representation of participants with expertise in both the AVF and volcanic monitoring. A total of 28 individuals accepted the invitation to participate. Before the workshop, participants attended a virtual presentation on the current understanding of the conceptual model of volcanism in the AVF, what a BET_EF is, and how the data collected from the workshop would be incorporated in BETEF_AVF (Step 2).
At the workshop itself, participants were divided into three groups: seismology, geochemistry and geodesy, based on their respective expertise. Each group was provided with the Lindsay et al. (2010) monitoring parameters and thresholds and asked to record any updates or additional parameters, thresholds or weights for each of Nodes 1–3. Following this, an all-workshop discussion was held to allow all participants to discuss and provide any feedback (Step 3).
A virtual follow-up discussion was conducted to present the results, illustrated through the Exercise Rūaumoko scenario and against the Lindsay et al. (2010) parameters, thresholds and weights (Step 4). This was an opportunity for participants to provide any further feedback. The output of this process was subsequently used to inform the monitoring parameter inputs for the BETEF_AVF. These are collated in Table 1.
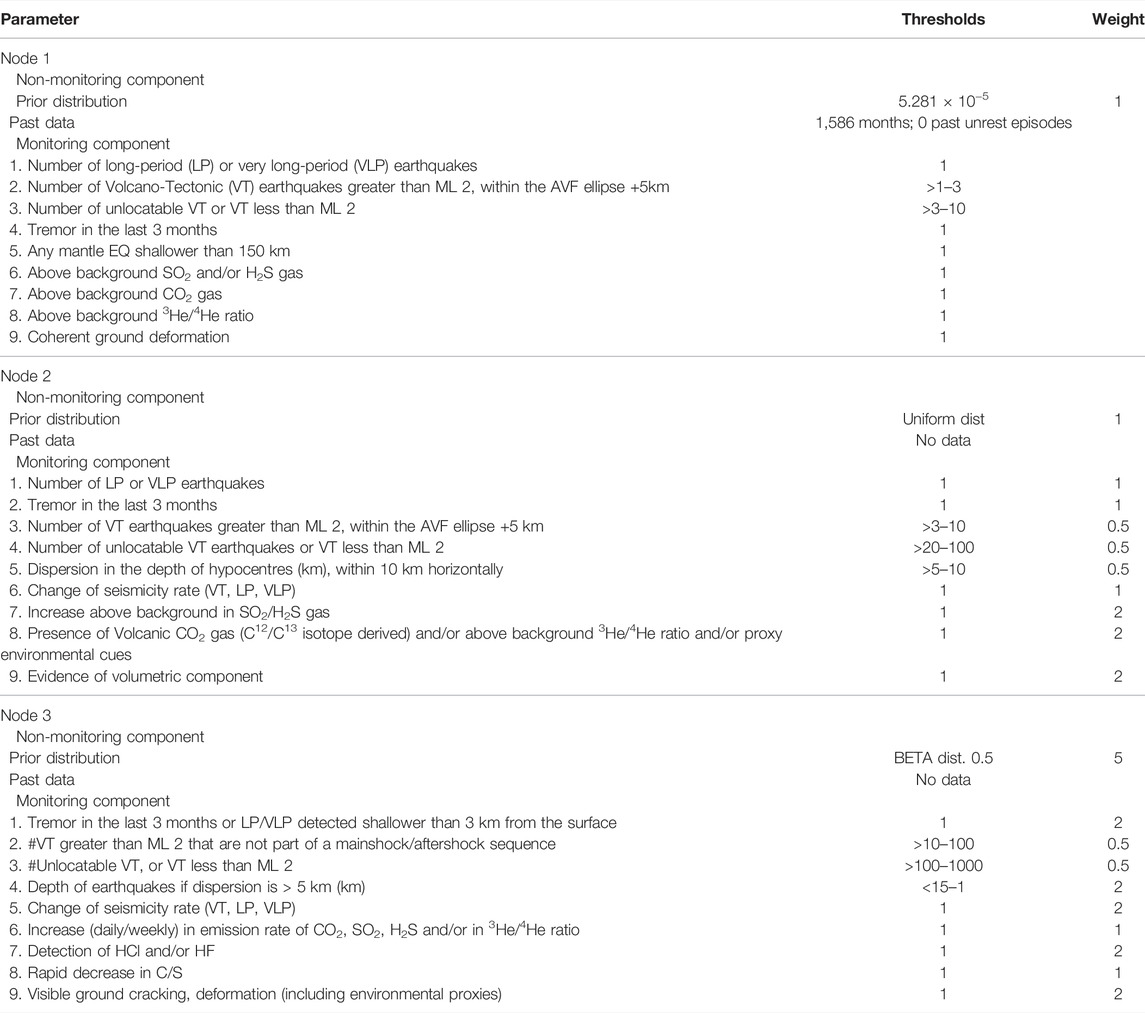
TABLE 1. The volcanological and monitoring BETEF_AVF input data for each node. Refer to text for an explanation of parameters, thresholds and weights.
Nodes 1–4 are considered in BETEF_AVF (Figure 2). Node 5—eruption style is not considered in this particular application. This is because although forecasting the style of an eruption is extremely important in decision making, the Auckland Volcanic Contingency Plan recommends an evacuation of everyone within 5 km of the inferred eruption centre/area (Auckland Council, 2015), irrespective of eruption style.
BETEF_AVF requires some general parameters to be input for the volcano. The field extent is defined as the bounding box around the AVF boundary +5 km buffer (Runge et al., 2015), and the field is divided into 500 × 500 m cells forming a 53 × 79 grid. Participants at the expert opinion workshop decided that the forecasting “look forward” time window (τ) for BETEF_AVF should be reduced from 1 month (Lindsay et al., 2010) to 14 days, to reflect the requirements for a shorter forecast window for crisis decision-support.
The critical parameters a and b (Eq. 2) were reviewed as part of the set-up for BETEF_AVF. In the initial BET_EF (Marzocchi et al., 2008), these were set as prior uniform distributions a = U (0.5, 1) and b = U (0, 2). However, in the case of well-monitored volcanoes (and the AVF can be considered as such), a could be increased to reflect the decrease in likelihood of either Node 2 or Node 3 occurring without observing any anomalous behaviour (W. Marzocchi, personal communication, 31 August 2020). An increase in b would reflect greater monitoring sensitivity. To test the sensitivity of outputs to variations in a and b, four uniform distribution pairs with different lower and upper bounds were considered:
• a = U (0.5, 1) and b = U (0, 2)—Default settings from BET_EF 2.0 (Marzocchi et al., 2008)
• a = U (0.75, 1) and b = U (0, 2)—Increase a and keep b as default
• a = U (0.75, 1) and b = U (0.5, 2)—Increase a and b
• a = U (0.75, 1) and b = U (1, 2)—Increase a and b
The model was run for each combination of a and b priors to provide the input parameters for each node within BETEF_AVF; these are presented Table 1, with further detail provided for each node in the subsections below. Unless stated, the time window for collecting data is 1 month.
We define a prior a Beta distribution with mean = B/A, where B is the eruption frequency per 2 weeks (τ), and A is the expected ratio of eruption to unrest. This is the same approach applied in Lindsay et al. (2010); however, the values are updated based on recent research identifying 53 volcanic centres having erupted over the past 193 ka (Leonard et al., 2017). Hence, B = 53/(193,000*26), and A remains 0.2, i.e., 1 in 5 periods of unrest result in an eruption in monogenetic volcanic fields (Lindsay et al., 2010). The number of equivalent data (Λ) for this distribution remains 1, to reflect it is a rough estimate with high uncertainty.
For the past data, there has been no observed seismic unrest since seismic monitoring began in Auckland in 1960 (Sherburn et al., 2007), therefore n = 61*26, with 0 eruptions.
Seismic parameters: Given the low level of seismicity in the AVF, it is considered that one or more long-period or very-long-period (VLP) event would be indicative of unrest in the AVF. This is the same as in Lindsay et al. (2010), but with the addition of the VLPs.
Observing >1 volcano-tectonic (VT) earthquake is considered anomalous in the AVF. As in Lindsay et al. (2010), the threshold transitions from 1 (normal) to 3 (anomalous). However, in our application, we define these as ML >2 and within the AVF GeoNet monitoring extent. A new parameter is added to capture the number of VT events that are either unlocatable, or of ML < 2, with that threshold transitioning from 10 to 20.
It is considered that the observation of seismic tremor within the past 3 months would be indicative of unrest. Additionally, any seismicity observed in the mantle <100 km, considered the maximum depth of the magma source in the AVF (Horspool et al., 2006), would indicate unrest. These are both new parameters compared to Lindsay et al. (2010).
Geochemistry parameters: There are three parameters in that capture anomalous geochemical behaviour that indicates unrest. These are above-background levels of SO2/H2S, CO2 and 3He/4He ratio. Lindsay et al. (2010) had parameters for the first two; the consideration of 3He/4He ratio is new.
Geodetic parameter: The observation of coherent ground deformation is considered to indicate unrest within the AVF. This represents a slight wording change from Lindsay et al. (2010) “observation of significant ground deformation.”
The Lindsay et al. (2010) parameter related to change in groundwater reservoirs is removed from the revised BETEF_AVF. This is considered no longer required as any change would likely be represented within the other geochemical and geodetic parameters.
As there have been no observed magmatic unrest episodes within the AVF, the prior is considered uniform (mean 0.5) to represent maximum ignorance, with a Λ = 1, with no past data. This is consistent with the input for this component at Node 2 in Lindsay et al. (2010).
Seismic parameters: The observation of a single LP and/or VLP earthquake is thought to be indicative of magmatic unrest (weight of 1). VLP is here added to the original LP of Lindsay et al. (2010) for this parameter.
VT events of ML >2 within the AVF GeoNet monitoring extent threshold transition from 3 (normal) to 10 (anomalous). VT events that are either unlocatable or ML <2 have a threshold transitioning from 20 to 100. Both parameters are assigned a weight of 0.5 each, as it is considered these will likely be observed in tandem. This diverges from the associated parameter Lindsay et al. (2010), whereby it was the maximum magnitude of the observed VT that was considered indicative [transitioning from ML 3.5 (normal) to 4.5 (anomalous), with a weight of 1].
The observation of seismic tremor within the past 3 months is considered indicative of magmatic unrest (weight 1). As with Node 1, this is a new parameter not captured in Lindsay et al. (2010).
A dispersion in the depths of seismic hypocentres is considered an indicator of magma causing the unrest. The threshold transitions from 5 km (normal) to 10 km (anomalous). While the thresholds are the same as in Lindsay et al. (2010), the parameter is modified to constrain the dispersion area to within 10 km horizontally, and the weight is reduced to 0.5.
A change in the rate of seismicity (VLP, LP and/or VT) can be indicative of magma ascent (Kilburn, 2003). This is reflected in the change of seismicity rate parameter which has been given a weight of 1. This is a modification in wording to the Lindsay et al. (2010) parameter which assessed “acceleration of seismicity” of LP or VT events.
Geochemistry parameters: Above background levels of SO2 and/or H2S is considered to reflect magma and thus a strong indicator of magmatic unrest. This is reflected in the parameter with a weight of 2 carried over from Lindsay et al. (2010).
Three indicative monitoring measurements are combined using “and/or” statements in a second geochemistry parameter covering CO2, 3He/4He ratio, and other proxy environmental cues. As magma ascends, it may release CO2. However, CO2 is also common in non-magmatic unrest. It is considered that the presence of above-background volcanic CO2, derived using 12C/13C isotope analysis, is anomalous. Above background levels of 3He/4He ratios are also considered indicative of magmatic unrest. Environmental cues such as residents reporting gaseous smells (Marzocchi et al., 2012), contaminated water (Gottsmann et al., 2019) and the death of vegetation and animals (Edmonds et al., 2018) could be crucial, especially in the absence of monitoring equipment. This parameter has a weight of 2. While the observation of CO2 was considered at Node 2 by Lindsay et al. (2010), the further classification of it being volcanic in origin is new, along with consideration of 3He/4He ratios and environmental cues at this Node.
Geodetic parameter: Evidence of a volumetric component of ground deformation is considered a strong indication of magmatic intrusion. As such, this parameter has a weight of 2. This diverges from the associated parameter in Lindsay et al. (2010), which stated observation of significant ground deformation.
The prior was set as a Beta distribution with an average of 0.5 as in Lindsay et al. (2010), which is based on basaltic field observations (Newhall and Hoblitt, 2002), with Λ = 5. No past data is used as there remain no observed historical eruptions within the AVF.
Seismic parameters: Seismic tremor within the last 3 months could indicate that the magmatic unrest might lead to an eruption. Additionally, the presence of any LP/VLP at shallow depths (<3 km) could indicate magma interaction with groundwater reservoirs. The observation of either of these, once magmatic unrest is confirmed, is considered strongly indicative of an eruption (weight 2). This differs from the associated parameter in Lindsay et al. (2010), which only considered a look-back time for seismic tremor of 1 month, and did not consider the shallowing of LP/VLP.
An increase in the number of VT events from Node 2 is considered an indicator of eruption. Two parameters are used to reflect this. The first is VT events with ML >2 not attributed to a mainshock/aftershock sequence within the AVF GeoNet monitoring extent, with a threshold transitioning from 10 (normal) to 100 (anomalous). The second is VT events that are either unlocatable or ML <2, with a threshold transitioning from 100 to 1,000. Both of these parameters have a weight of 0.5. These are new parameters as Lindsay et al. (2010) did not include a VT parameter at Node 3.
The shallowing of seismicity with a dispersion of hypocentres where the dispersion is >5 km is considered a strong indicator of magma ascending to the surface. The depth threshold for this parameter transitions from 15 km (normal) to 1 km (anomalous). Given the significance, a weight of 2 is used. This parameter differs slightly from Lindsay et al. (2010), where the upper threshold was set at 5 km depth.
The parameter for attributing any observed change, either increase or decrease, in the rate of seismicity is carried over from Lindsay et al. (2010). However, the weight is increased from 1 to 2.
Geochemistry parameters: An increase in gas emission rates of any monitored gases (CO2, SO2, and H2S) or in 3He/4He ratios is considered indicative that magmatic unrest might lead to an eruption (weight 1). This is more detailed than the parameter presented in Lindsay et al. (2010), as it specifies the monitored gas.
Given that it is not uncommon to observe a decrease in gas emissions in the lead-up to an eruption, the parameter “rapid decrease in C/S” (assessed qualitatively) has been included, with a weight of 1. This is a modification to the parameter Lindsay et al. (2010), which did not specify gases.
Detection of HCl and/or HF in fumaroles can be indicative of an eruption; this is captured in a new parameter with a weight of 2.
Geodetic parameter: Observed visible ground cracking from deformation is a strong indicator of a magmatic eruption as magma nears the surface (weight 2). However, this should not be confused with tectonically triggered ground cracking, which is why this parameter is not included at Node 2. This replaces the “acceleration of deformation” parameter from Lindsay et al. (2010).
Lindsay et al. (2010) applied a uniform distribution for the prior model input to represent maximum ignorance at node 4. At that time, there was a limited suite of reliable ages with which to generate a reliable spatial-temporal model to inform the prior distribution. However, since that study, a suite of spatial vent likelihood models have been published (e.g., Bebbington and Cronin 2011; Bebbington 2013, Bebbington 2015). Here we assess the sensitivity of BETEF_AVF to two priors: uniform distribution and the Bebbington (2013) Gaussian anisotropic kernel least-squares cross-validation (LSCV) model, the latter selected as it uses past vent location to inform the spatial likelihood, and differs the most from the uniform distribution. The uniform distribution is applied to 3,312 cells within the AVF boundary +5 km buffer (Runge et al., 2015). For each prior Λ remains 10, as in Lindsay et al. (2010), to reflect the understanding of the extent and monogenetic nature of AVF.
Localization of seismicity can indicate the area of the next vent (Marzocchi et al., 2008). The approach applied for calculating vent location likelihood in BETEF_AVF is based on that outlined in Lindsay et al. (2010). Each seismic event is assigned a weight inversely proportional to its depth, as shallower earthquakes are assumed to be more indicative of vent location than deeper ones. The seismic events’ weights are aggregated back up to the grid before applying a Gaussian filter using 2.5 km of (1σ) standard deviation, to account for earthquake location error. At Node 4, the spatial vent likelihood is evaluated based on 50% monitoring data and 50% the prior (Marzocchi et al., 2008).
The seven “DEVORA” scenarios (Hayes et al., 2018, 2019) and the original Exercise Rūaumoko scenario (Lindsay et al., 2010) are examined to assess the performance of the BETEF_AVF (Figure 3 and Table 2). Six of the eight scenarios (Rūaumoko, Birkenhead, Waitematā, Ōtāhuhu, Auckland Airport, and Rangitoto Channel) have a pre-eruptive sequence of fewer than 15 days. The Mt Eden scenario has an unrest duration of 45 days prior to eruption onset. The Rangitoto Island scenario has a protracted unrest period over 2 years, with two failed eruptions each followed by a year’s quiescence before finally erupting after 31 days of seismic activity. Refer to Hayes et al. (2018) for more information on the scenarios’ pre-eruptive sequences.
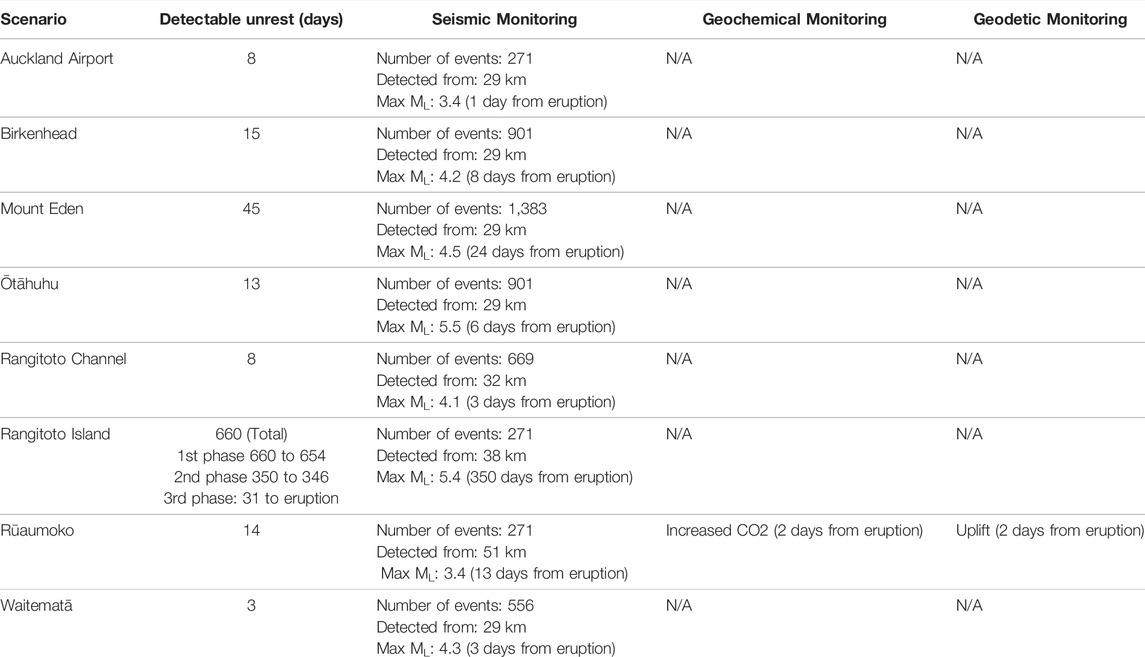
TABLE 2. Overview of the eight AVF scenarios’ pre-eruptive sequences. Refer to Hayes et al. (2018) for more information.
The pre-eruptive sequences for the seven DEVORA scenarios are limited to seismic activity and ground cracking (the latter on the day of the eruption). While this is an apparent limitation of the unrest sequence dataset, seismic monitoring is in fact the only monitoring technique with a permanently installed network in the AVF. Additional monitoring equipment will likely take time to position appropriately within the field (e.g., for geochemical or ground-based GPS measurements), or be limited by the 6-day InSAR satellite repeat pass time for Auckland (Hayes et al., 2018). Geochemical and geodetic monitoring are likely to be initiated only later in a sequence following increased episodes of seismicity, particularly when an area of interest has been identified to support more spatially constrained real-time monitoring (Sherburn et al., 2007; Lindsay et al., 2010; Ashenden et al., 2011; Hayes et al., 2018). This could result in a delay to receive information. As such, the DEVORA scenarios, which are limited to only seismic unrest inputs, are considered appropriate to test the BETEF_AVF. For the Rūaumoko scenario, the spatial earthquake dataset of earthquake epicentres and depths could not be obtained, therefore limiting the BETEF_AVF analysis for that scenario to Nodes 1–3.
Here we have adapted the CBA approach to define an evacuation zone presented for volcanic fields by Marzocchi and Woo (2009), which considers the need to evacuate any given cell (X) within a region. First, we extend out the 500 m × 500 m spaced grid used within BETEF_AVF by an additional 5 km to accommodate for a potential eruption on the edge of the AVF. This is to align with the AVF Contingency Plan (Auckland Council, 2015), whereby an evacuation zone is defined as 5 km radius from a vent. The probability that an evacuation of a given cell X is required
Where k is all possible vents within 5 km of X and p1to4 are outputs from BETEF_AVF at nodes 1 to 4 respectively.
The 6-months evacuation duration CBA threshold from Sandri et al. (2012) is used to demonstrate the establishment of a pre-eruption AVF evacuation zone. Sandri et al. (2012) applied the evacuation-specific CBA approach of Woo (2008), which defines the cost of evacuation (C) as the average socio-economic loss per-capita for the evacuation duration (R), and the loss from no action (L) as the product of the value of statistical life (V) and the proportion of the population that evacuates that owes its life to the decision (E). This results in C/L = R/(E.V). Sandri et al. (2012) set R as $21,500 given the average contribution per capita was $43,000 per annum, V to $3million and E was considered to be 0.5. This application indicated that when
The Rūaumoko and Birkenhead scenarios were selected to assess the sensitivity in BETEF_AVF output probabilities to the four sets of a and b priors. Figure 4 presents the changes in output probabilities for Nodes 2 and 3 of the Rūaumoko scenario, illustrating the effect on the shape of the curve for assessing eruption probability as a function of the degree of anomalous behavior (Z) (Eq. 2). An increase in a decreases the output probability at Nodes 2 and 3 when there are no observed monitoring anomalies, for example, at Node 3 between 15 and 7 days before the eruption. An increase in b increases the calculated probabilities (Eq. 2).
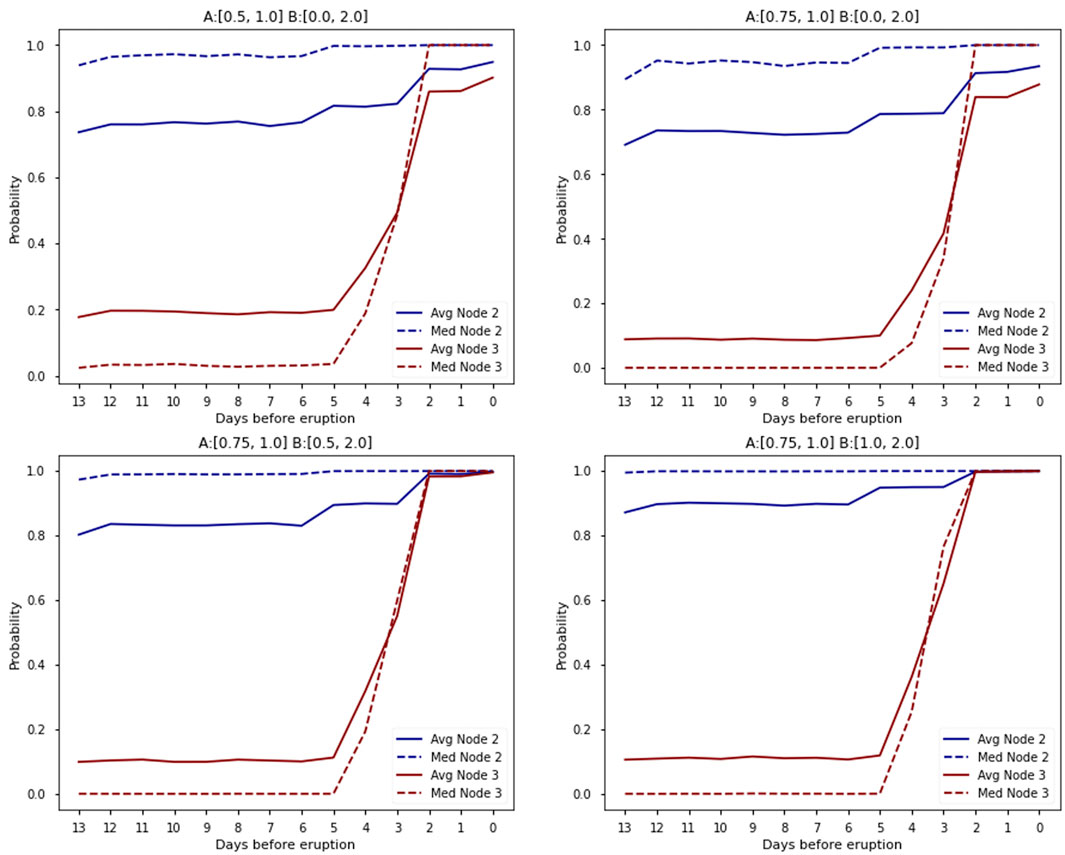
FIGURE 4. Time evolution of BETEF_AVF output probabilities for magmatic unrest and eruption forecasting for the Rūaumoko scenario for a range of a and b parameter combinations. N.B the probability is a distribution at each time step, but because multiple nodes are presented, we only present the average and median.
A similar exercise was conducted for the Birkenhead scenario to evaluate the influence of the a and b priors on an unrest scenario dataset limited to seismicity. The probabilities calculated by BETEF_AVF for the Birkenhead scenario are not as high as those calculated for the Rūaumoko scenario (Figure 5); this is due to the limited observed unrest phenomena, thereby restricting the Z value. The reduction of a is shown to reduce the output probabilities when observing no monitoring observations. With the increase in b, with more observed monitoring parameters, there is a noticeable increase in the output probabilities, notably the median and average probabilities get to 1 in the Rūaumoko sequence. Given that the seismic network is continuously detecting seismic activity in the AVF, the likelihood of volcanic activity occurring without detecting any anomalous behaviour is considered low. For this reason, an argument can be made for increasing a from the original BET_EF distribution of U (0.5, 1). We have therefore chosen to use a = U (0.75, 1) in the modelling presented in the rest of the paper. We retain the original U (0, 2) distribution of b in the absence of any clear justification for change.
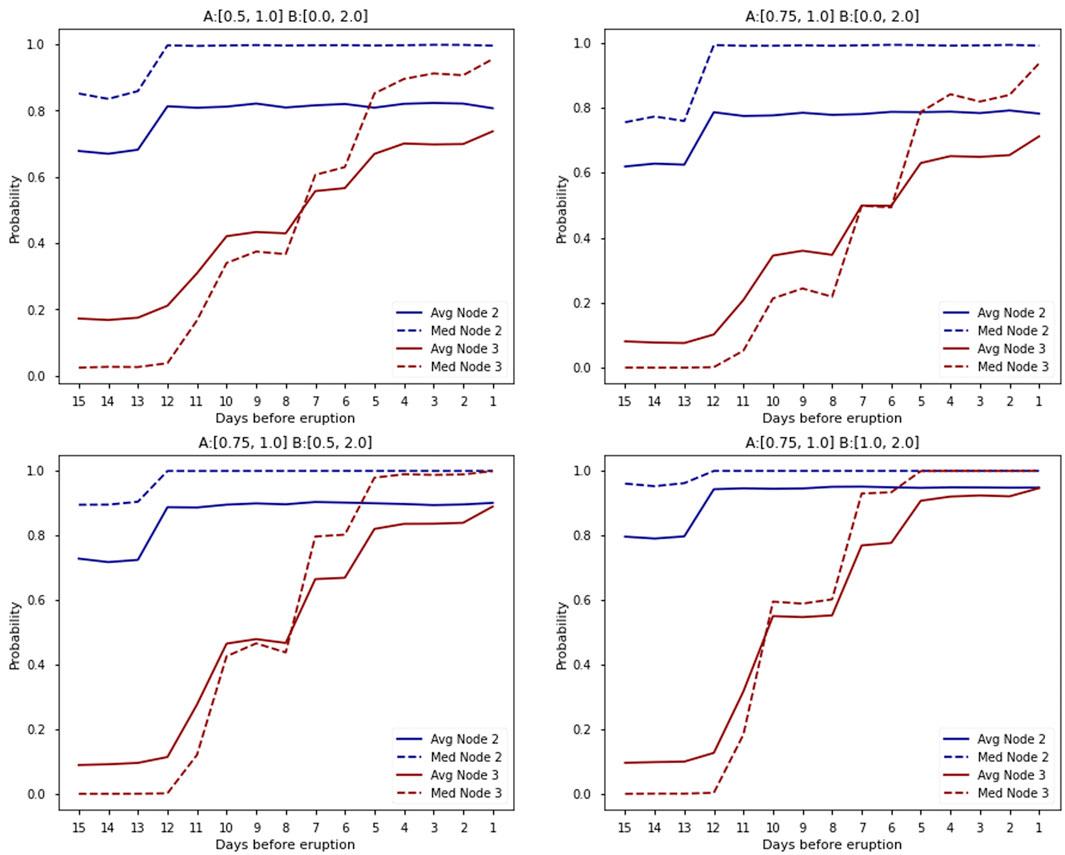
FIGURE 5. Time evolution of BETEF_AVF output probabilities for magmatic unrest and eruption forecasting for the Birkenhead scenario for a range of a and b parameter combinations.
BETEF_AVF was executed for the unrest sequences of all seven DEVORA scenarios to calculate probabilities at Nodes 2 and 3 (Figure 6). In all scenarios, from the onset of anomalous activity, the probability of unrest (Node 1) is 1, i.e., unrest is observed, as at least one of the thresholds is exceeded. As anomalous activity escalates during the lead-up to the eruption, the probabilities at Nodes 2 and 3 increase in all scenarios.
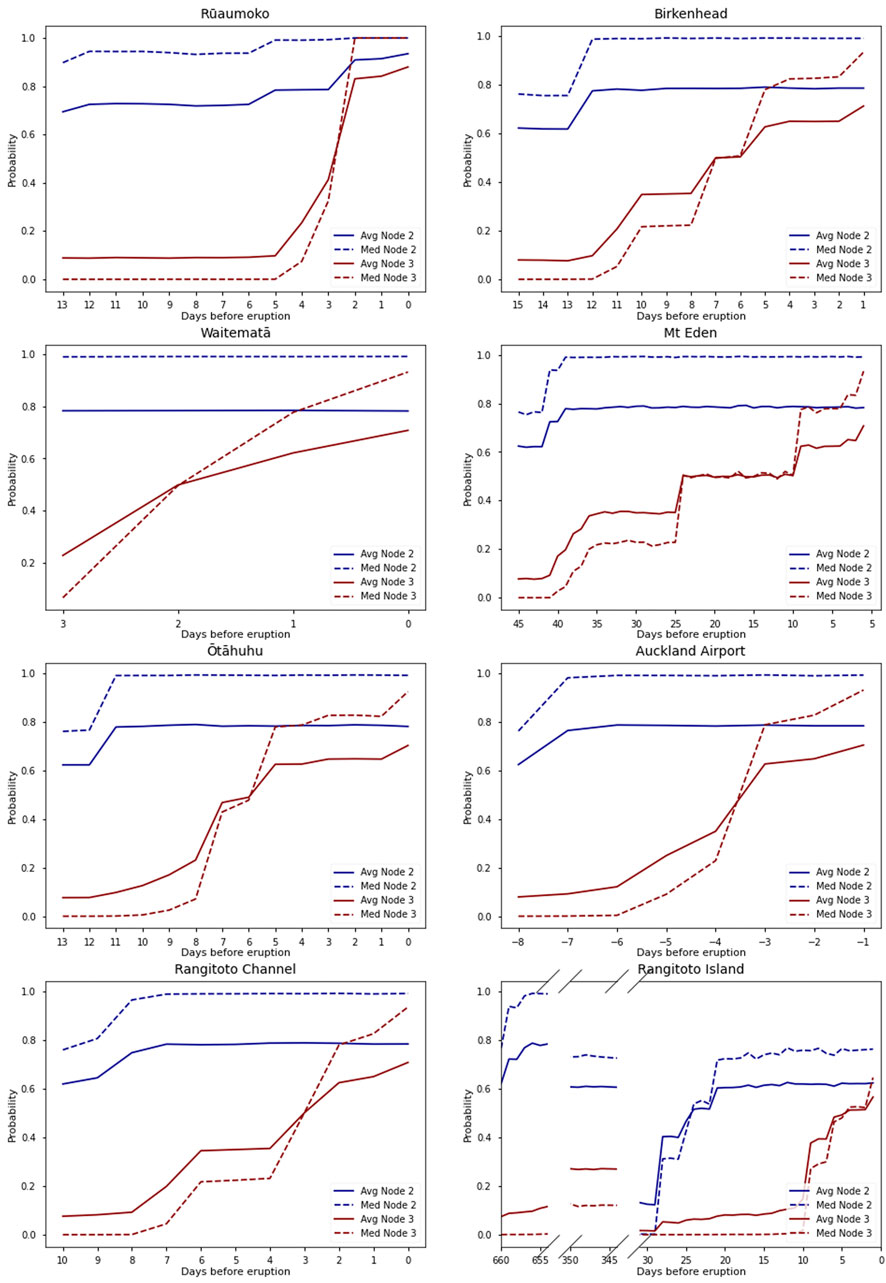
FIGURE 6. Time evolution of BETEF_AVF output probabilities for magmatic unrest and eruption forecasting for each of the eight AVF eruption scenarios. This application uses the distributions a = U (0.75, 1) and b = U (0, 2).
For each scenario, the mean probability of magmatic unrest (Pm) is limited to ≤0.8. This is because the pre-eruptive datasets only consist of LP earthquakes and ML >2 VT earthquakes, which results in a maximum Z-value of 2, based on three monitoring parameters at Node 2. This Z-value, combined with the a and b priors applied here, results in a maximum Pm of ∼0.8. In each of the seven DEVORA scenarios, the observation of LP earthquakes and more than 10 VT earthquakes with an ML >2 with a dispersion in depth of >10 km typically occurs in the first few days of the unrest sequence, thereby reaching the model maximum Pm (Node 2) early in the unrest sequence. This is true for all scenarios, except for the Rangitoto Island sequence, as there are no LP earthquakes during the second and third periods of activity, so the Z-value for Node 2 is limited to 1, and thus the maximum Pm is ∼0.6.
For each of the seven DEVORA scenarios, Node 3, like Node 2, is affected by the limited number of observations in non-seismic phenomena. The maximum Z-value is not observed until 24 h from the eruption when surface ground cracking is observed, increasing the Z-value by 2. The reduced maximum Pm subsequently limits the mean absolute probability of eruption (Pe), given that it is conditional on Pm.
In contrast, the Rūaumoko unrest sequence includes more monitoring parameter types, resulting in a higher Z-value at both Nodes 2 and 3. This results in Pm and Pe reaching ∼0.9 and ∼0.85 in the days leading up to the eruption.
Using the earthquake hypocentres, weights for each earthquake event are attributed based on the inverse of the hypocentral depth, and used to estimate the spatial probability of vent location across the AVF grid cells. To demonstrate the outputs from BETEF_AVF Node 4, we present the absolute average probability of spatial eruption probabilities for the Birkenhead (Figures 7, 8) and Waitematā (Figures 9, 10) scenarios, for both prior spatial models. Outputs are at a 0.25 km2 resolution. In the case of the Birkenhead scenario, the vent eventuated in the centre of the identified likely vent hotspot (warm-coloured cells), while the Waitematā eventual vent location was adjacent to the identified zone of high eruption probability values.
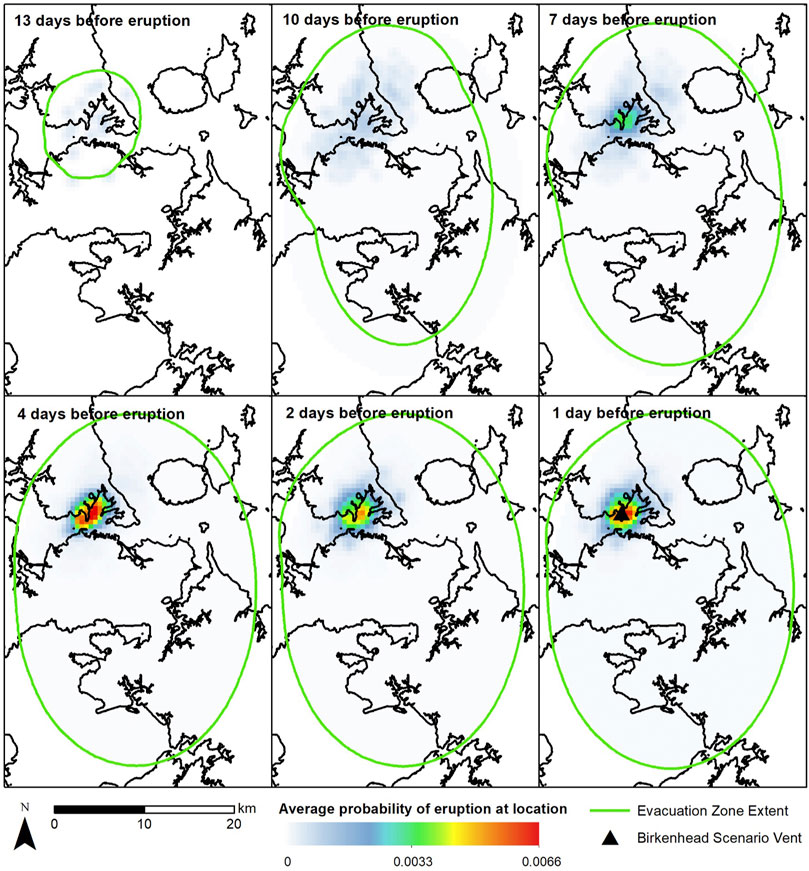
FIGURE 7. Spatial distribution of absolute eruption probabilities for the Birkenhead scenario from BETEF_AVF with a uniform prior vent model for selected days leading up to the eruption. The green contour encompasses the evacuation zone extent based on cost-benefit analysis.
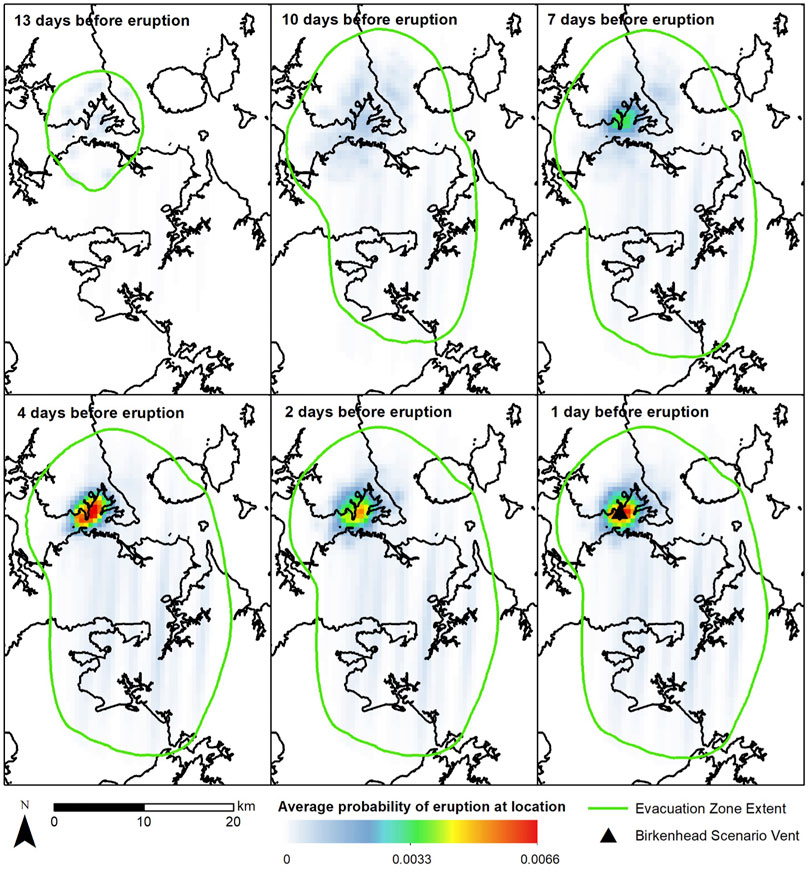
FIGURE 8. Spatial distribution of absolute eruption probabilities for the Birkenhead scenario from BETEF_AVF with the Bebbington 2013 LSCV prior vent model for selected days leading up to the eruption. The green contour encompasses the evacuation zone extent based on cost-benefit analysis.
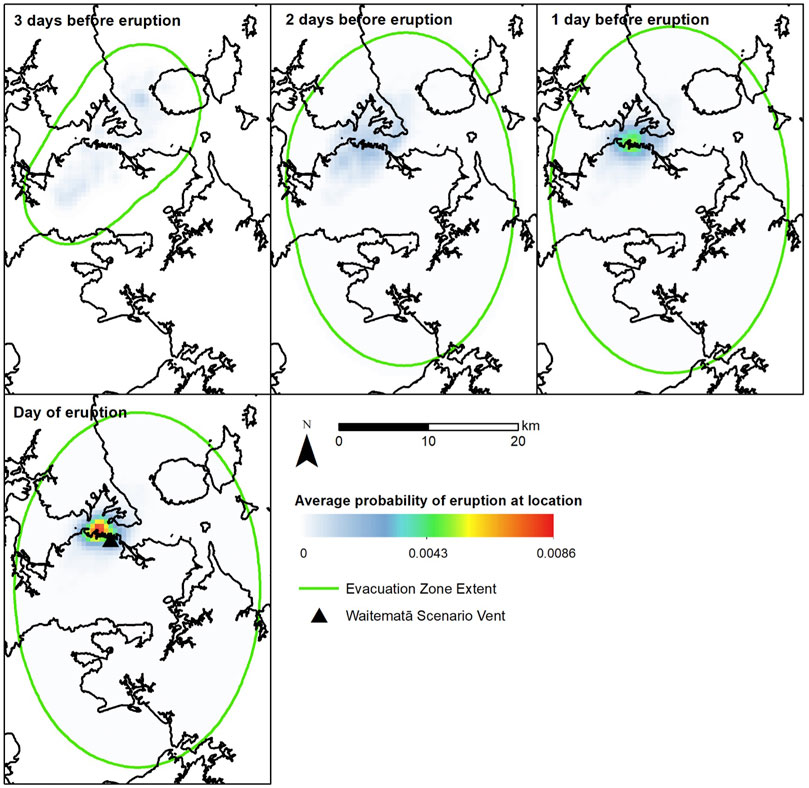
FIGURE 9. Spatial distribution of absolute eruption probabilities for the Waitematā scenario from BETEF_AVF with a uniform prior vent model for selected days leading up to the eruption. The green contour encompasses the evacuation zone extent based on cost-benefit analysis.
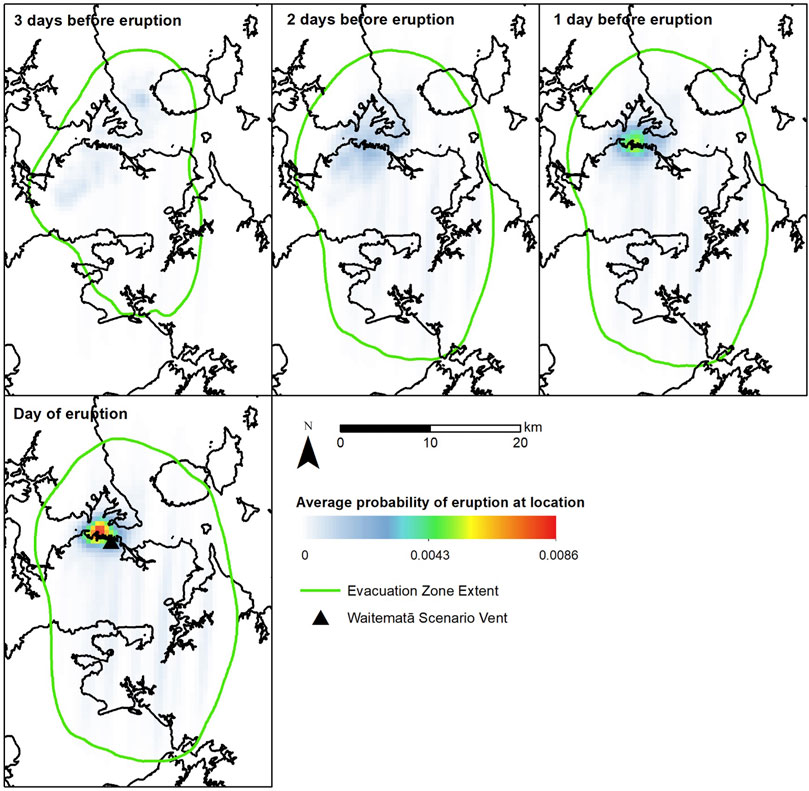
FIGURE 10. Spatial distribution of absolute eruption probabilities for the Waitematā scenario from BETEF_AVF with the Bebbington 2013 LSCV prior vent model for selected days leading up to the eruption. The green contour encompasses the evacuation zone extent based on cost-benefit analysis.
Based on the BETEF_AVF outputs, the CBA threshold presented by Sandri et al. (2012) (p = 0.0143) is exceeded for one or more grid cells following the first day of activity for each of the scenarios, except for the final phase of the Rangitoto Island scenario, where an evacuation would be called after 4 days of unrest.
Figures 7–10 show the evacuation areas (green line) for the Birkenhead and Waitematā scenarios for both considered prior models at different stages of the unrest sequence. Notably, the evacuation area increases in size over the unrest period, due to the increasing probability of eruption (refer to Eq. 3).
In the absence of observed activity in the AVF, Exercise Rūaumoko and the seven DEVORA scenarios provide a synthetic unrest dataset to validate the performance of the BETEF_AVF. While we cannot definitively state BETEF_AVF would detect an eruption, if a future event manifested with similar precursory activity signals as those from the synthetic dataset, the code as set up would identify anomalous behaviour. Our application to these scenarios results in output probabilities of BETEF_AVF for both Pm and Pe that trend upwards as the unrest escalates in the lead up to an eruption.
In the case of the Rūaumoko scenario, the Z-value increases for Nodes 2 and 3 throughout, resulting in a Pe of ∼0.9 the day before the eruption. The output eruption probabilities started to increase 5 days out as the number of VT earthquakes increased and seismicity began shallowing. In contrast, in the DEVORA scenarios, the Node 2 Z-value was limited to 2, which resulted in a maximum Pm of ∼0.8. This subsequently restricted the upper limit for Pe, leading to a Pe of ∼0.72 the day before the eruption. These low Z-values are attributed to the scenarios only containing seismic phenomena (LP and VT events). The final phase of the Rangitoto Island scenario yielded even lower Pe values, due to the low Z-value of 1 at Node 2, given the absence of LP earthquakes following the first phase of activity. Hence, if LP earthquakes are not going to be characteristic of future AVF eruptions or monitoring capability does not detect them, the BETEF_AVF will depend on VT events and the data from any campaign gas and or geodesy monitoring. Whilst this leads to lower probabilities than seen in the Rūaumoko scenario, an initial sequence consisting only of seismic phenomena is highly likely in a future unrest episode in the AVF, thus this application can be considered to reflect what might be derived if BETEF_AVF were applied in a real event.
The number of unlocatable VT events with ML <2 is not provided in the scenario seismicity datasets. Inputs for this parameter (weight of 0.5) would likely be observed in an actual event, with (small) consequent increases in Z-value.
The BETEF_AVF output eruption location probabilities are shown to be sensitive to the input prior model. This is as BET_EF applies a 50% weighting to each of the monitoring and prior model components at Node 4. In both the Birkenhead (Figure 8) and Waitematā (Figure 10) scenarios, the output spatial vent eruption probabilities contain linear N-S features from the Bebbington (2013) LSCV model of higher probability than the uniform distribution counterpart in areas where there is no observed seismicity (Figures 7, 9), demonstrating the influence of the prior input. A notable feature is that the prior distribution remains 50% of the mix regardless of how many (or how few) earthquakes are observed. Hence an obvious avenue is to base the contribution on the level of observed monitored parameters, e.g., the number of earthquakes. A clear avenue for future work would thus be a re-evaluation of the sensitivity of BET model outputs to the weighting of monitoring and prior components at Node 4 in the case of distributed volcanism.
Additional investigations could include changing the inverse (by depth) weighting of earthquakes, using an exponential smoother to weight the elapsed time since the earthquake to capture the lateral migration of earthquakes, or expanding the approach to include additional monitoring parameters such as deformation. While we have presented one approach for informing the Node 4 monitoring component input, other approaches using additional or alternate monitoring techniques can be used. One such input that could be considered is using areas of deformation as an indication of potential vent location (e.g., Rosi et al., 2022). Alternate approaches for informing the Node 4 monitoring components have been presented in other BET implementations. For example, Constantinescu et al. (2016) attempt to localise all observed anomalies in Node 1-3 seismic, geochemical and geodetic parameters across their area of interest to inform the vent likelihood. In contrast, in an application at the stratovolcano Kawah Ijen, Korea, the number of VT events in each of the five considered vent locations were used to weight the likely vent location of a magmatic eruption, as depth of earthquakes is not routinely estimated at that volcano (Tonini et al., 2016). This demonstrates the potential for further work to be undertaken to inform how the various available monitoring techniques and observations can be used to inform the vent likelihood in the AVF and beyond.
A fundamental model component is the prior distributions defining the a and b parameters used to calculate the node’s monitoring-informed probability (Eq. 2). We examined how varying these priors alters the output probabilities, demonstrating the importance of selecting appropriate priors (Figures 4, 5). We found that reducing a and increasing b significantly increases output probability when Z is small. After a certain Z-value, the function becomes saturated, and minimal differences are observed between the different a and b parameter combinations.
While exploration of the scenario suite shows that BETEF_AVF appropriately assesses the eruption likelihood for the AVF, there are known limitations with the BET_EF framework. BET_EF outputs probabilities of a volcanic state for a prescribed look ahead window τ. In contrast, other models such as the failure forecast model (Voight and Cornelius, 1991; Cornelius and Voight, 1994) produce estimates of eruption onset time, which could be viewed as a more desirable outcome for crisis decision-support (Wild et al., 2020; Whitehead and Bebbington, 2021), although the probability of eruption is less concrete, and it does not lend itself to CBA approaches. Additionally, to inform the development of a BET_EF for a volcano, there needs to be a good conceptual model of volcanism, and appropriate experts with a good understanding of the volcano included in monitoring parameter and threshold selection (Whitehead and Bebbington, 2021). While it is considered that there was adequate understanding of the AVF and representation of expertise involved in the development of the BETEF_AVF, the monitoring parameters and thresholds were established based on limited empirical knowledge of how pre-eruptive unrest might progress in the AVF. Furthermore, BETEF_AVF was tested on simulated unrest sequences that may or may not represent what might precede a future eruption. Despite these limitations, it is considered BETEF_AVF performed well, with Pm and Pe increasing appropriately with elevated levels of activity.
Comparison between the original AVF BET_EF from Lindsay et al. (2010) and BETEF_AVF using the Exercise Rūaumoko injects demonstrates that they perform very similarly, even with the modification of the parameters, thresholds and weights (Figure 11). While both models yield similar outputs and follow the same trend for Pm and Pe, the notable differences are due to the weight of a seismic parameter at Node 2 and a change in thresholds for a seismic parameter at Node 3.
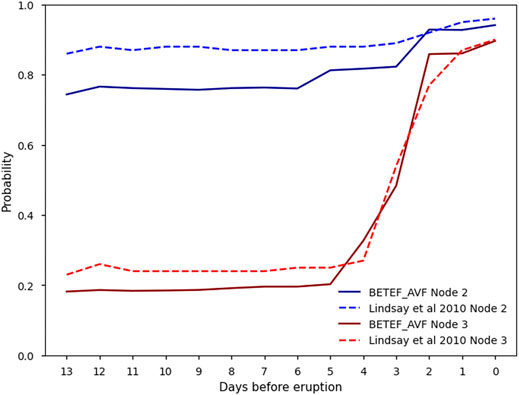
FIGURE 11. Time evolution of BETEF_AVF for magmatic unrest and eruption forecasting compared to the Lindsay et al. (2010) output for the Exercise Rūaumoko sequence. N.B for this comparison, BETEF_AVF uses the distributions a = U (0.5, 1) and b = U (0, 2) to align with the Lindsay et al. (2010) output probabilities.
Tools such as BET_EF have the potential to support crisis decision making, for example, to inform evacuation decisions (Marzocchi et al., 2008; Lindsay et al., 2010; Selva et al., 2012) and zones (Sandri et al., 2012) by means of CBA. However, our analysis yielded a surprising result, namely that the “evacuation area” increased in size as the sequence developed, even extending to include areas far from any observed seismicity (Figures 7–10). This seems to be illogical, i.e., one would think that as seismicity shallows and the spatial vent likelihood increases and converges, the required evacuation zone should decrease. We found two contributing causes to the increasing size of the “evacuation area,”, namely the fixed 50:50 Node 4 weighting between prior and monitoring components, and the CBA approach (and evacuation threshold) applied.
At present, the Node 4 50:50 weighting for monitoring inputs: prior model results in areas that are not affected by seismicity being identified as cost-beneficial to evacuate at increasing levels of unrest. When Pe ≥ ∼0.31, with a CBA ratio of p = 0.0143, it becomes cost-beneficial to evacuate a location in which all potential vents within a 5 km radius are only informed by a uniform prior model (i.e., no monitoring activity). Similar behavior is observed when using the Bebbington (2013) LSCV as the prior location input. This contradicts the expected behavior which might suggest that, as confidence in the vent location increases, the evacuation zone should decrease. As discussed above, increasing the weight of the monitoring component as unrest escalates should progressively lower the spatial vent probabilities of cells beyond the unrest area, thereby reducing the extent of the derived evacuation area.
Our application has highlighted some limitations in the CBA approach applied by Sandri et al. (2012) and in this study. The CBA approach used a fixed value for the proportion of evacuees that owe their life to the evacuation call (E), based on the estimated proportion that would self-evacuate. At present, this value is fixed, irrespective of how the event unfolds. However, actions such as self-evacuation would in fact change the E parameter. Wild et al. (2021) examined population exposure and estimated clearance times within evacuation zones across Auckland, considering increasing vent uncertainty size. Such information could be used to modify E across an event, and can support the decision to call an evacuation as the spatial variability changes with increased monitoring information. This could be a focus for future work.
The 5 km distance around the vent uncertainty area applied by the AVF contingency plan (Auckland Council, 2015) is informed by a maximum considered base-surge run out. However, this assumes an equal risk to life safety within that zone, i.e., the same risk for someone at the vent and someone at 5 km distance, which does not reflect reality with respect to spatial extent and run out distance of a base surge (Sandri et al., 2012) and likelihood of casualty with distance (Baxter et al., 2005). In addition, the eruptive style varies across the AVF (Ang et al., 2020), which in turn effects the phenomena produced and thus the extent of impact (Sandri et al., 2012; Hayes et al., 2018). These factors will confound with the evacuation zone in a complex manner, and need to be assessed.
This paper presents the set-up and application of a revised BET_EF for the AVF to assess the short-term eruption probability and spatial vent likelihood when applied to eight hypothetical unrest scenarios. While not designed to supplant monitoring and advisory groups, output from such models as BETEF_AVF can provide an initial starting point for discussions between volcanic science advisory group members regarding the current unrest and state of the volcano, and can be prepared in advance of a future crisis (Lindsay et al., 2010; Papale, 2017). Additionally, expert elicitation workshops during the development of a BET_EF are opportunities to bring together monitoring and research volcanologists to discuss and share insights to develop a common conceptual understanding of a volcano, and to highlight areas for future research and monitoring enhancements. For example, many of the parameters captured and subsequently applied in BETEF_AVF are not routinely monitored for in the AVF, given it is a distributed volcanic field with no target for geochemical and geodetic monitoring. However, expert opinion revealed that these parameters could be important indicators of unrest, magmatic unrest and eruption, at nodes 1–3, respectively. These insights are valuable in that they can inform the direction of future upgrades of the monitoring network.
Based on our development and application of the BETEF_AVF we offer the following key general conclusions regarding BET_EF as a tool for volcanic eruption forecasting:
• There is value in reviewing previous BET_EF and similar frameworks as the understanding of a volcano or monitoring capability is improved. This can include evaluation and updating the prior datasets, as well as the input monitoring parameters and thresholds. In our case, we conducted our evaluation and update of the latter via an expert opinion workshop using a consensus approach.
• The BET_EF outputs are sensitive to prior distributions for a and b, and as such volcano specific consideration is required when selecting these priors. For the BETEF_AVF implementation, we have selected a = U (0.75, 1) to reflect the low likelihood of a volcano being in a given state (e.g., magmatic unrest) without any monitoring observations, given the fact that the AVF is continually monitored through the seismic network. The outputs of BET_EF can be explained based on the model inputs and transparent methodology using a consensus model in advance without the pressure of ongoing unrest. This can be advantageous in litigious environments.
• The tool can be executed in near real-time, meaning it can readily provide outputs to support decision-making. In particular, the outputs for both eruption probability and vent likelihood can be combined with CBA to support crisis decision-making, such as when and where to evacuate (e.g., Sandri et al., 2012; Wild et al., 2019).
Furthermore, our application of BETEF_AVF and comparison with past work in the AVF by Lindsay et al. (2010) and Sandri et al. (2012) also yielded some interesting insights into potential challenges when applying the tool in areas of distributed volcanism:
• The fixed BET_EF Node 4 50:50 weighting of monitoring: prior inputs (Marzocchi et al., 2008; Sandri et al., 2012) may not be suitable for distributed volcanic fields. The spatial vent location probabilities were higher near the eruption outbreak location. However, when aggregating the spatial eruption probability at each vent across the grid to inform the probability of impact, the evacuation CBA threshold was unrealistically exceeded far from monitoring observations
• Without addressing this issue, the CBA approach applied in this study and previous studies does not appear to be suitable for distributed volcanic fields due to the spatial uncertainty regarding the eruption location.
In summary, this study highlighted several key challenges when applying BET_EF for crisis decision-support to distributed volcanic fields, especially where there have been no past monitored eruptions. We demonstrated that BETEF_AVF performed well based on the synthetic unrest dataset from scenario unrest sequences, yielding increasing probabilities of magmatic unrest and eruption as the unrest sequence progressed, and generating spatial probability maps that highlighted higher probability in the areas of eventual vent formation. Although these were synthetic eruption sequences and thus not real, we believe the results still provide important insights. In particular, we highlight the value of the process of continuous refinement of parameters and thresholds by monitoring and research scientists, and how this contributes to a shared understanding of the conceptual model for a particular volcano.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
This workshop component of this study was carried out under ethics approval issued to the researchers by the University of Auckland (reference number 021876). All participants gave written informed consent.
All authors (AW, MB, and JL) conceived the study. AW and MB developed the study’s methodology. AW conducted the analysis and wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
AW and JL are supported by Determining Volcanic Risk in Auckland (DEVORA) research programme and the New Zealand Earthquake Commission (EQC). MB is supported by the Resilience to Nature’s Challenges Volcano Programme, Grant GNS-RNC047.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co-authorship with one of the authors JL.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The authors would like to thank all workshop participants for their valuable input to support the model development. We are grateful for the valuable insights of Roberto Tonini, Warner Marzocchi and Laura Sandri. Finally, we greatly appreciate the thoughtful reviews of two reviewers, and the journal’s supportive editorial work by Heather Wright.
Allen, S. R., and Smith, I. E. M. (1994). Eruption Styles and Volcanic Hazard in the Auckland Volcanic Field, New Zealand. Geosci. Rep. Shizuoka Univ. 20, 5–14.
Ang, P. S., Bebbington, M. S., Lindsay, J. M., and Jenkins, S. F. (2020). From Eruption Scenarios to Probabilistic Volcanic Hazard Analysis: An Example of the Auckland Volcanic Field, New Zealand. J. Volcanol. Geotherm. Res. 397, 106871. doi:10.1016/j.jvolgeores.2020.106871
Ashenden, C. L., Lindsay, J. M., Sherburn, S., Smith, I. E. M., Miller, C. A., and Malin, P. E. (2011). Some Challenges of Monitoring a Potentially Active Volcanic Field in a Large Urban Area: Auckland Volcanic Field, New Zealand. Nat. Hazards 59, 507–528. doi:10.1007/s11069-011-9773-0
Aspinall, W. P., and Woo, G. (2014). Santorini Unrest 2011-2012: an Immediate Bayesian Belief Network Analysis of Eruption Scenario Probabilities for Urgent Decision Support under Uncertainty. J. Appl. Volcanol. 3, 12. doi:10.1186/s13617-014-0012-8
Aspinall, W. P. (2006). “Structured Elicitation of Expert Judgment for Probabilistic Hazard and Risk Assessment in Volcanic Eruptions,” in Statistics in Volcanology. Editors H. M. Mader, S. G. Coles, C. B. Connor, and L. J. Connor (London: Special publication of IAVCEI; Geological Society), 15–30.
Auckland Council (2015). Auckland Volcanic Field Contingency Plan. Available at: http://www.aucklandcivildefence.org.nz/media/48896/2015-03-27-Auckland-Volcanic-Field-Contingency-Plan-Version-2-.pdf (Accessed February 6, 2016).
Auckland Region CDEM Group (2008). Final Exercise Report. Exercise Ruaumoko ‘08. Auckland, New Zealand: Ministry of Civil Defence & Emergency Management.
Bartolini, S., Sobradelo, R., and Martí, J. (2016). ST-HASSET for Volcanic Hazard Assessment: A Python Tool for Evaluating the Evolution of Unrest Indicators. Comput. Geosci. 93, 77–87. doi:10.1016/j.cageo.2016.05.002
Baxter, P. J., Boyle, R., Cole, P., Neri, A., Spence, R., and Zuccaro, G. (2005). The Impacts of Pyroclastic Surges on Buildings at the Eruption of the Soufrière Hills Volcano, Montserrat. Bull. Volcanol. 67, 292–313. doi:10.1007/s00445-004-0365-7
Bebbington, M. S., and Cronin, S. J. (2011). Spatio-temporal Hazard Estimation in the Auckland Volcanic Field, New Zealand, with a New Event-Order Model. Bull. Volcanol. 73, 55–72. doi:10.1007/s00445-010-0403-6
Bebbington, M., and Zitikis, R. (2016). Dynamic Uncertainty in Cost-Benefit Analysis of Evacuation Prior to a Volcanic Eruption. Math. Geosci. 48, 123–148. doi:10.1007/s11004-015-9615-9
Bebbington, M. S., Stirling, M. W., Cronin, S., Wang, T., and Jolly, G. (2018). National-level Long-Term Eruption Forecasts by Expert Elicitation. Bull. Volcanol. 80, 56. doi:10.1007/s00445-018-1230-4
Bebbington, M. S. (2013). Assessing Probabilistic Forecasts of Volcanic Eruption Onsets. Bull. Volcanol. 75, 1–13. doi:10.1007/s00445-013-0783-5
Bebbington, M. S. (2015). Spatio-volumetric Hazard Estimation in the Auckland Volcanic Field. Bull. Volcanol. 77, 39. doi:10.1007/s00445-015-0921-3
Blake, S., Wilson, C. J. N., Smith, I. E. M., and Leonard, G. S. (2006). Lead Times and Precursors of Eruptions in the Auckland Volcanic Field, New Zealand: Indications from Historical Analogues and Theoretical Modelling. Lower Hutt, N.Z.: GNS Science. Available at: http://books.google.com/books?id=C4BPAQAAIAAJ (Accessed November 22, 2020).
Brancato, A., Gresta, S., Alparone, S., Andronico, D., Bonforte, A., Caltabiano, T., et al. (2011). Application of BET_EF at Mount Etna: a Retrospective Analysis (Years 2001-2005). Ann. Geophys. 54, 642–661. doi:10.4401/ag-5346
Brand, B. D., Gravley, D. M., Clarke, A. B., Lindsay, J. M., Bloomberg, S. H., Agustin-Flores, J., et al. (2014). A Combined Field and Numerical Approach to Understanding Dilute Pyroclastic Density Current Dynamics and Hazard Potential: Auckland Volcanic Field, New Zealand. J. Volcanol. Geotherm. Res. 276, 215–232. doi:10.1016/j.jvolgeores.2014.01.008
Brenna, M., Cronin, S. J., Smith, I. E. M., Tollan, P. M. E., Scott, J. M., Prior, D. J., et al. (2018). Olivine Xenocryst Diffusion Reveals Rapid Monogenetic Basaltic Magma Ascent Following Complex Storage at Pupuke Maar, Auckland Volcanic Field, New Zealand. Earth Planet. Sci. Lett. 499, 13–22. doi:10.1016/j.epsl.2018.07.015
Brunsdon, D., and Park, B. (2009). “Lifeline Vulnerability to Volcanic Eruption: Learnings from a National Simulation Exercise,” in TCLEE 2009: Lifeline Earthquake Engineering in a Multihazard Environment, 1–12. doi:10.1061/41050(357)70
Cassisi, C., Prestifilippo, M., Cannata, A., Montalto, P., Patanè, D., and Privitera, E. (2016). Probabilistic Reasoning over Seismic Time Series: Volcano Monitoring by Hidden Markov Models at Mt. Etna. Pure Appl. Geophys. 173, 2365–2386. doi:10.1007/s00024-016-1284-1
Connor, C. B., Sparks, R. S. J., Mason, R. M., Bonadonna, C., and Young, S. R. (2003). Exploring Links between Physical and Probabilistic Models of Volcanic Eruptions: The Soufrière Hills Volcano, Montserrat. Geophys. Res. Lett. 30, 1997–2000. doi:10.1029/2003GL017384
Constantinescu, R., Rouwet, D., Gottsmann, J., Sandri, L., and Tonini, R. (2015). “Tracking Volcanic Unrest at Cotopaxi, Ecuador: - The Use of the BET_EF Tool During an Unrest Simulation Exercise,” EGU General Assembly, Viena, Austria, April 12–17, 2015.
Constantinescu, R., Robertson, R., Lindsay, J. M., Tonini, R., Sandri, L., Rouwet, D., et al. (2016). Application of the Probabilistic Model BET_UNREST during a Volcanic Unrest Simulation Exercise in Dominica, Lesser Antilles. Geochem. Geophys. Geosyst. 17, 4438–4456. doi:10.1002/2016gc006485
Cooke, R. (1991). Experts in Uncertainty: Opinion and Subjective Probability in Science. Oxford: Oxford University Press on Demand.
Cornelius, R. R., and Voight, B. (1994). Seismological Aspects of the 1989-1990 Eruption at Redoubt Volcano, Alaska: the Materials Failure Forecast Method (FFM) with RSAM and SSAM Seismic Data. J. Volcanol. Geotherm. Res. 62, 469–498. doi:10.1016/0377-0273(94)90048-5
Edmonds, M., Grattan, J., and Michnowicz, S. (2018). “Volcanic Gases: Silent Killers,” in Observing the Volcano World: Volcano Crisis Communication. Editors C. J. Fearnley, D. K. Bird, K. Haynes, W. J. McGuire, and G. Jolly (Cham: Springer International Publishing), 65–83. doi:10.1007/11157_2015_14
Fearnley, C. J., and Beaven, S. (2018). Volcano Alert Level Systems: Managing the Challenges of Effective Volcanic Crisis Communication. Bull. Volcanol. 80, 46. doi:10.1007/s00445-018-1219-z
Gottsmann, J., Komorowski, J.-C., and Barclay, J. (2019). “Volcanic Unrest and Pre-eruptive Processes: A Hazard and Risk Perspective,” in Volcanic Unrest : From Science to Society. Editors J. Gottsmann, J. Neuberg, and B. Scheu (Cham: Springer International Publishing), 1–21. doi:10.1007/11157_2017_19
Hayes, J. L., Tsang, S. W., Fitzgerald, R. H., Blake, D. M., Deligne, N. I., Doherty, A., et al. (2018). The DEVORA Scenarios: Multi-Hazard Eruption Scenarios for the Auckland Volcanic Field. GNS Science Report 2018/29, 138. doi:10.21420/G20652
Hayes, J. L., Wilson, T. M., Deligne, N. I., Lindsay, J. M., Leonard, G. S., Tsang, S. W. R., et al. (2019). Developing a Suite of Multi-Hazard Volcanic Eruption Scenarios Using an Interdisciplinary Approach. J. Volcanol. Geotherm. Res. 392, 106763. doi:10.1016/j.jvolgeores.2019.106763
Hincks, T. K., Komorowski, J.-C., Sparks, S. R., and Aspinall, W. P. (2014). Retrospective Analysis of Uncertain Eruption Precursors at La Soufrière Volcano, Guadeloupe, 1975–77: Volcanic Hazard Assessment Using a Bayesian Belief Network Approach. J. Appl. Volcanol. 3, 3. doi:10.1186/2191-5040-3-3
Hopkins, J. L., Timm, C., Millet, M.-A., Poirier, A., Wilson, C. J. N., and Leonard, G. S. (2016). Os Isotopic Constraints on Crustal Contamination in Auckland Volcanic Field Basalts, New Zealand. Chem. Geol. 439, 83–97. doi:10.1016/j.chemgeo.2016.06.019
Hopkins, J. L., Smid, E. R., Eccles, J. D., Hayes, J. L., Hayward, B. W., McGee, L. E., et al. (2020). Auckland Volcanic Field Magmatism, Volcanism, and Hazard: a Review. N. Z. J. Geol. Geophys., 1–22. doi:10.1080/00288306.2020.1736102
Horrocks, J. (2008). Learning from Exercise Ruaumoko, Exercise Ruaumoko 2008. New Zealand: Ministry of Civil Defence and Emergency Management.
Horspool, N. A., Savage, M. K., and Bannister, S. (2006). Implications for Intraplate Volcanism and Back-Arc Deformation in Northwestern New Zealand, from Joint Inversion of Receiver Functions and Surface Waves. Geophys. J. Int. 166, 1466–1483. doi:10.1111/j.1365-246X.2006.03016.x
Kereszturi, G., Németh, K., Cronin, S. J., Agustín-Flores, J., Smith, I. E. M., and Lindsay, J. (2013). A Model for Calculating Eruptive Volumes for Monogenetic Volcanoes - Implication for the Quaternary Auckland Volcanic Field, New Zealand. J. Volcanol. Geotherm. Res. 266, 16–33. doi:10.1016/j.jvolgeores.2013.09.003
Kereszturi, G., Németh, K., Cronin, S. J., Procter, J., and Agustín-Flores, J. (2014). Influences on the Variability of Eruption Sequences and Style Transitions in the Auckland Volcanic Field, New Zealand. J. Volcanol. Geotherm. Res. 286, 101–115. doi:10.1016/j.jvolgeores.2014.09.002
Kereszturi, G., Bebbington, M., and Németh, K. (2017). Forecasting Transitions in Monogenetic Eruptions Using the Geologic Record. Geology 45, 283–286. doi:10.1130/G38596.1
Kilburn, C. R. J. (2003). Multiscale Fracturing as a Key to Forecasting Volcanic Eruptions. J. Volcanol. Geotherm. Res. 125, 271–289. doi:10.1016/S0377-0273(03)00117-3
Le Corvec, N., Bebbington, M. S., Lindsay, J. M., and McGee, L. E. (2013). Age, Distance, and Geochemical Evolution within a Monogenetic Volcanic Field: Analyzing Patterns in the Auckland Volcanic Field Eruption Sequence. Geochem. Geophys. Geosyst. 14, 3648–3665. doi:10.1002/ggge.20223
Leonard, G. S., Calvert, A. T., Hopkins, J. L., Wilson, C. J. N., Smid, E. R., Lindsay, J. M., et al. (2017). High-precision 40Ar/39Ar Dating of Quaternary Basalts from Auckland Volcanic Field, New Zealand, with Implications for Eruption Rates and Paleomagnetic Correlations. J. Volcanol. Geotherm. Res. 343, 60–74. doi:10.1016/j.jvolgeores.2017.05.033
Lindsay, J., Marzocchi, W., Jolly, G., Constantinescu, R., Selva, J., and Sandri, L. (2010). Towards Real-Time Eruption Forecasting in the Auckland Volcanic Field: Application of BET_EF during the New Zealand National Disaster Exercise 'Ruaumoko'. Bull. Volcanol. 72, 185–204. doi:10.1007/s00445-009-0311-9
Lindsay, J., Leonard, G., Smid, E., and Hayward, B. (2011). Age of the Auckland Volcanic Field: a Review of Existing Data. N. Z. J. Geol. Geophys. 54, 379–401. doi:10.1080/00288306.2011.595805
Magill, C. R., McAneney, K. J., and Smith, I. E. M. (2005). Probabilistic Assessment of Vent Locations for the Next Auckland Volcanic Field Event. Math. Geol. 37, 227–242. doi:10.1007/s11004-005-1556-2
Marzocchi, W., and Bebbington, M. S. (2012). Probabilistic Eruption Forecasting at Short and Long Time Scales. Bull. Volcanol. 74, 1777–1805. doi:10.1007/s00445-012-0633-x
Marzocchi, W., and Woo, G. (2007). Probabilistic Eruption Forecasting and the Call for an Evacuation. Geophys. Res. Lett. 34, 2–5. doi:10.1029/2007GL031922
Marzocchi, W., and Woo, G. (2009). Principles of Volcanic Risk Metrics: Theory and the Case Study of Mount Vesuvius and Campi Flegrei, Italy. J. Geophys. Res. Solid Earth 114 (B03213), 1–12. doi:10.1029/2008jb005908
Marzocchi, W., Sandri, L., Gasparini, P., Newhall, C., and Boschi, E. (2004). Quantifying Probabilities of Volcanic Events: The Example of Volcanic Hazard at Mount Vesuvius. J. Geophys. Res. 109, 1–18. doi:10.1029/2004JB003155
Marzocchi, W., Sandri, L., and Selva, J. (2008). BET_EF: A Probabilistic Tool for Long- and Short-Term Eruption Forecasting. Bull. Volcanol. 70, 623–632. doi:10.1007/s00445-007-0157-y
Marzocchi, W., Newhall, C., and Woo, G. (2012). The Scientific Management of Volcanic Crises. J. Volcanol. Geotherm. Res. 247-248, 181–189. doi:10.1016/j.jvolgeores.2012.08.016
Mazot, A., Smid, E. R., Schwendenmann, L., Delgado-Granados, H., and Lindsay, J. (2013). Soil CO2 Flux Baseline in an Urban Monogenetic Volcanic Field: the Auckland Volcanic Field, New Zealand. Bull. Volcanol. 75, 757. doi:10.1007/s00445-013-0757-7
McGee, L. E., Smith, I. E. M., Millet, M.-A., Handley, H. K., and Lindsay, J. M. (2013). Asthenospheric Control of Melting Processes in a Monogenetic Basaltic System: a Case Study of the Auckland Volcanic Field, New Zealand. J. Pet. 54, 2125–2153. doi:10.1093/petrology/egt043
Morgan, M. G. (2014). Use (And Abuse) of Expert Elicitation in Support of Decision Making for Public Policy. Proc. Natl. Acad. Sci. U.S.A. 111, 7176–7184. doi:10.1073/pnas.1319946111
Morrissey, M., Zimanowski, B., Wohletz, K., and Buettner, R. (2000). “Phreatomagmatic Fragmentation,” in Encyclopedia of Volcanoes. Editors H. Sigurdsson, B. Houghton, S. R. McNutt, H. Rymer, and J. Stix (Academic Press), 431–445.
Neri, A., Aspinall, W. P., Cioni, R., Bertagnini, A., Baxter, P. J., Zuccaro, G., et al. (2008). Developing an Event Tree for Probabilistic Hazard and Risk Assessment at Vesuvius. J. Volcanol. Geotherm. Res. 178, 397–415. doi:10.1016/j.jvolgeores.2008.05.014
Newhall, C., and Hoblitt, R. (2002). Constructing Event Trees for Volcanic Crises. Bull. Volcanol. 64, 3–20. doi:10.1007/s004450100173
Newhall, C. G., and Pallister, J. S. (2015). “Using Multiple Data Sets to Populate Probabilistic Volcanic Event Trees,” in Volcanic Hazards, Risks, and Disasters (Elsevier), 203–232. doi:10.1016/B978-0-12-396453-3.00008-3
Newhall, C. G., Costa, F., Ratdomopurbo, A., Venezky, D. Y., Widiwijayanti, C., Win, N. T. Z., et al. (2017). WOVOdat - an Online, Growing Library of Worldwide Volcanic Unrest. J. Volcanol. Geotherm. Res. 345, 184–199. doi:10.1016/j.jvolgeores.2017.08.003
Papale, P. (2017). Rational Volcanic Hazard Forecasts and the Use of Volcanic Alert Levels. J. Appl. Volcanol. 6, 1–13. doi:10.1186/s13617-017-0064-7
Poland, M. P., and Anderson, K. R. (2020). Partly Cloudy with a Chance of Lava Flows: Forecasting Volcanic Eruptions in the Twenty‐First Century. J. Geophys. Res. Solid Earth 125. doi:10.1029/2018JB016974
Potter, S. H., Jolly, G. E., Neall, V. E., Johnston, D. M., and Scott, B. J. (2014). Communicating the Status of Volcanic Activity: Revising New Zealand's Volcanic Alert Level System. J. Appl. Volcanol. 3, 13. doi:10.1186/s13617-014-0013-7
Rosi, M., Acocella, V., Cioni, R., Bianco, F., Costa, A., De Martino, P., et al. (2022). Defining the Pre-Eruptive States of Active Volcanoes for Improving Eruption Forecasting. Front. Earth Sci. 10, 795700. doi:10.3389/feart.2022.795700
Rouwet, D., Sandri, L., Marzocchi, W., Gottsmann, J., Selva, J., Tonini, R., et al. (2014). Recognizing and Tracking Volcanic Hazards Related to Non-magmatic Unrest: a Review. J. Appl. Volcanol. 3, 1–17. doi:10.1186/s13617-014-0017-3
Runge, M. G., Bebbington, M. S., Cronin, S. J., Lindsay, J. M., and Moufti, M. R. (2015). Sensitivity to Volcanic Field Boundary. J. Appl. Volcanol. 4, 22. doi:10.1186/s13617-015-0040-z
Sandri, L., Guidoboni, E., Marzocchi, W., and Selva, J. (2009). Bayesian Event Tree for Eruption Forecasting (BET_EF) at Vesuvius, Italy: a Retrospective Forward Application to the 1631 Eruption. Bull. Volcanol. 71, 729–745. doi:10.1007/s00445-008-0261-7
Sandri, L., Jolly, G., Lindsay, J., Howe, T., and Marzocchi, W. (2012). Combining Long- and Short-Term Probabilistic Volcanic Hazard Assessment with Cost-Benefit Analysis to Support Decision Making in a Volcanic Crisis from the Auckland Volcanic Field, New Zealand. Bull. Volcanol. 74, 705–723. doi:10.1007/s00445-011-0556-y
Selva, J., Marzocchi, W., Papale, P., and Sandri, L. (2012). Operational Eruption Forecasting at High-Risk Volcanoes: The Case of Campi Flegrei, Naples. J. Appl. Volcanol. 1, 1–14. doi:10.1186/2191-5040-1-5
Sheldrake, T. E., Aspinall, W. P., Odbert, H. M., Wadge, G., and Sparks, R. S. J. (2017). Understanding Causality and Uncertainty in Volcanic Observations: An Example of Forecasting Eruptive Activity on Soufrière Hills Volcano, Montserrat. J. Volcanol. Geotherm. Res. 341, 287–300. doi:10.1016/j.jvolgeores.2017.06.007
Sherburn, S., Scott, B. J., Olsen, J., and Miller, C. (2007). Monitoring Seismic Precursors to an Eruption from the Auckland Volcanic Field, New Zealand. N. Z. J. Geol. Geophys. 50, 1–11. doi:10.1080/00288300709509814
Sobradelo, R., Bartolini, S., and Martí, J. (2014). HASSET: a Probability Event Tree Tool to Evaluate Future Volcanic Scenarios Using Bayesian Inference. Bull. Volcanol. 76, 1–15. doi:10.1007/s00445-013-0770-x
Sparks, R. S. J. (2003). Forecasting Volcanic Eruptions. Earth Planet. Sci. Lett. 210, 1–15. doi:10.1016/S0012-821X(03)00124-9
Spörli, K. B., and Eastwood, V. R. (1997). Elliptical Boundary of an Intraplate Volcanic Field, Auckland, New Zealand. J. Volcanol. Geotherm. Res. 79, 169–179. doi:10.1016/S0377-0273(97)00030-9
Statistics New Zealand (2018). Auckland Region. Available at: https://www.stats.govt.nz/tools/2018-census-place-summaries/auckland-region (Accessed November 10, 2020).
Statistics New Zealand (2019). Regional Gross Domestic Product: Year Ended March 2018. Available at: https://www.stats.govt.nz/information-releases/regional-gross-domestic-product-year-ended-march-2018 (Accessed November 10, 2020).
Tierz, P., Clarke, B., Calder, E. S., Dessalegn, F., Lewi, E., Yirgu, G., et al. (2020). Event Trees and Epistemic Uncertainty in Long‐term Volcanic Hazard Assessment of Rift Volcanoes: the Example of Aluto (Central Ethiopia). Geochem. Geophys. Geosyst. 21. doi:10.1029/2020GC009219
Tonini, R., Sandri, L., Rouwet, D., Caudron, C., Marzocchi, W., and Suparjan, (2016). A New Bayesian Event Tree Tool to Track and Quantify Volcanic Unrest and its Application to Kawah Ijen Volcano. Geochem. Geophys. Geosyst. 17, 2539–2555. doi:10.1002/2016GC006327
van Wijk, K., Chamberlain, C. J., Lecocq, T., and Van Noten, K. (2021). Seismic Monitoring of the Auckland Volcanic Field During New Zealand’s COVID-19 Lockdown. Solid Earth 12 (2), 363–373.
Voight, B., and Cornelius, R. R. (1991). Prospects for Eruption Prediction in Near Real-Time. Nature 350, 695–698. doi:10.1038/350695a0
Whitehead, M. G., and Bebbington, M. S. (2021). Method Selection in Short-Term Eruption Forecasting. J. Volcanol. Geotherm. Res. 419, 107386. doi:10.1016/j.jvolgeores.2021.107386
Wild, A. J., Wilson, T. M., Bebbington, M. S., Cole, J. W., and Craig, H. M. (2019). Probabilistic Volcanic Impact Assessment and Cost-Benefit Analysis on Network Infrastructure for Secondary Evacuation of Farm Livestock : A Case Study from the Dairy Industry , Taranaki , New Zealand. J. Volcanol. Geotherm. Res. 387, 106670. doi:10.1016/j.jvolgeores.2019.106670
Wild, A. J., Lindsay, J. M., Bebbington, M. S., Clive, M. A., and Wilson, T. M. (2020). Suitability of Quantitative Volcanic Hazard and Risk Assessment Methods and Tools for Crisis Management in Auckland, New Zealand. GNS Science. Available at: 10.21420/NGM3-5R75 (Accessed October 23, 2020).
Wild, A. J., Bebbington, M. S., Lindsay, J. M., and Charlton, D. H. (2021). Modelling Spatial Population Exposure and Evacuation Clearance Time for the Auckland Volcanic Field, New Zealand. J. Volcanol. Geotherm. Res. 416, 107282. doi:10.1016/j.jvolgeores.2021.107282
Keywords: eruption forecasting, bayesian event tree, volcanic hazard, decision-support, evacuation, event tree
Citation: Wild AJ, Bebbington MS and Lindsay JM (2022) Short-Term Eruption Forecasting for Crisis Decision-Support in the Auckland Volcanic Field, New Zealand. Front. Earth Sci. 10:893882. doi: 10.3389/feart.2022.893882
Received: 11 March 2022; Accepted: 06 May 2022;
Published: 24 May 2022.
Edited by:
Heather Michelle Wright, United States Geological Survey (USGS), United StatesReviewed by:
Raffaello Cioni, University of Florence, ItalyCopyright © 2022 Wild, Bebbington and Lindsay. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alec J. Wild, YXdpbDMwMkBhdWNrbGFuZHVuaS5hYy5ueg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.