
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 15 June 2022
Sec. Geohazards and Georisks
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.889504
This article is part of the Research Topic Applications of Geotechnical Mechanics in Underground Engineering View all 41 articles
The conventional empirical Sadowski formula has low prediction accuracy for the vibration velocity of the mass point in the near zone of the blast source, which makes it challenging to evaluate the damage of the building structures accurately. Considering the main influencing factors of blast vibration, the blast vibration attenuation law of deeply buried small clearance tunnels is investigated using dimensional analysis, and the Sadowski expansion formula is established considering the resistance line and free face. The regression analysis and fitting results were evaluated by combining the actual blast vibration data measured at the excavation site of the three separated tunnels at Badaling Great Wall Station with the post-expansion formula and the Sadowski formula, respectively. The results show that the correlation coefficients of the blast vibration expansion formulae based on the gauge theory for the fitted predictions of blast vibration isotropic velocities in a practical engineering context (0.92, 0.81, and 0.88, respectively) are higher than those of the conventional attenuation formulae, by 12, 10.5, and 6.3%, respectively, indicating that the expanded Sadowski formulae can better predict the blast vibration attenuation generated by the described deeply buried small clearance tunneling project.
With the continuous development of tunnel excavation technology, it has been found that, from the aspects of construction efficiency and economy, etc., the drilling–blasting method has unparalleled advantages and will still play an essential role in the construction of various new types of tunnels in the future. With the development and upgrading of China’s transport facilities, new tunnel projects such as continuous arch tunnels, deeply buried small clearance tunnels, and overlapping cross tunnels have been launched. These projects are more susceptible to topography, geological conditions, and route alignment during construction, and the mutual spatial and positional relationships with existing tunnels are becoming more complex (Hong, 2017). In terms of efficiency and economy of construction, the drilling–blasting method has unparalleled advantages and will continue to play an essential role in the construction of new types of tunnels in the future (Guo, 2018). However, when using the drilling–blasting method for practical blasting engineering, the energy released is used in addition to rock fragmentation, part of which will also cause damage to the surrounding buildings (structures) in the form of waves (Tan et al., 2003). To accurately evaluate the extent of damage caused by seismic blast vibration to adjacent buildings and structures and control blast vibration within safe limits by appropriate means, it is essential to carry out a study of blast vibration propagation attenuation laws.
The Sadowski formula can describe blast vibration decay laws, which has been a great convenience in previous blast engineering studies (Sadowski and Chen, 1986). However, with the application of this formula in practical engineering, scholars have found that Sadowski’s formula is more suitable for predicting the decay of vibration velocities in the far zone of the blast source, while blast vibration in the near zone of the blast source is difficult to predict with the required accuracy (Fu et al., 2011). Due to the special construction environment of deeply buried small clearance tunnels, there is a great need for a more accurate prediction of blast vibration in the near zone of the source to ensure the safety of existing tunnels.
Based on the above practical situation, this paper combines the actual engineering blasting vibration data with the theory of dimensional analysis and proposes an expanded blasting vibration formula that considers the resistance line based on the traditional Sadowski formula. The expanded formula is further demonstrated by comparing the results of the expanded formula with those of the Sadowski formula.
At present, the Sadowski formula is a semi-empirical formula widely used in practical blasting engineering in the world, by characterizing the relationship between the peak velocity of mass point vibration, the charge weight of blasting, and the blasting center distance to calculate the decay law of blast vibration velocity (Xiong and Gu, 2002):
where
The traditional formula for calculating blasting vibration velocity is the relationship between the peak vibration velocity and the proportional blasting charge. It can be seen from the Sadowski formula that when the blast source distance is certain, the vibration velocity increases with the increase in charge. However, Xin-kuan Zou (Zou et al., 2016) pointed out that, in a tunnel underground boring, blasting often shows a different situation from this, that is, when the free face and the minimum resistance line of influence are large enough, they will also have a certain impact on the blasting vibration velocity.
For the study of blasting vibration, relevant experts have used various research methods such as theoretical analysis, numerical simulation, and field examples. According to Ming-ya Bi (Mingya et al., 2009), the prediction of blasting vibration intensity is affected by various factors including geological and topographical conditions, material quantity, packet shape, and loading form, which are prone to significant errors. Tang et al. (2007) analyzed the influence of concave and convex geomorphology on the propagation of blasting vibration waves by taking geomorphological factors into account in the Guangdong Ling’ao nuclear power plant project. Wang et al. (2017) investigated the propagation of blasting vibration waves within a specific range of the adjacent surface based on investigating the reflection superposition law and the attenuation law of surface vibration velocity of blasting seismic waves in a specific range of the adjacent surface in tunnels with different burial depths based on numerical simulation, verification of measured data, and dimensional analysis and proposed that the calculation formula of surface vibration velocity attenuation considering the influence of burial depth can better reflect the attenuation law of surface vibration velocity. Zhang (2019) considered the influence of elevation and rock damage on the propagation pattern of blast vibration and, combined with actual engineering, concluded that rock damage has a significant weakening effect on the peak velocity of blast vibration.
In the deeply buried small clear distance tunnel projects, the distance between the excavated tunnel and the existing tunnel will be less than the buried depth of the tunnel. The length of the resistance line is the distance from the center of the blasting charge to the outer surface of the side wall lining of the existing tunnel. (In practical deeply buried small clearance tunneling projects, where the distance between the excavated tunnel and the existing tunnel is less than the tunnel depth, the length of the resistance line usually corresponds to the distance from the package to the lining of the existing tunnel sidewall.) To prevent damage to the existing tunnel lining caused by blasting vibrations during tunnel excavation, it is essential that the influence of the resistance line is considered in the actual predictions. The physical quantities associated with tunnel blasting and excavation are presented below. And through theoretical analysis of the magnitudes, a formula is derived for calculating the vibration velocity of tunnel blasting excavation, considering the effects of free face and resistance lines (Yang et al., 1994; Song et al., 2013).
In tunnel excavation blasting vibration velocity analysis, there are two main variables: one is the dependent variable, that is, the variable brought about by the different blasting design, mainly including the peak vibration velocity, single section blasting charge, and blast source distance, and the second is the independent variable, which includes the characteristics of the rock itself, rock density, and wave velocity. The main variables involved in the calculation of the model for studying the decay of vibration velocity in deeply buried small clearance tunnel blasting excavation are summarized in Table 1.
The above influencing factors were selected as the main physical quantities affecting the peak velocity of blast vibration to be studied. It can be seen that the seven physical quantities affecting the propagation law of blast vibration velocity are all related to time
Here,
The scale matrix
In order to determine the rank of the dimensional matrix
Calculate the determinant △≠0, so the rank of the dimensional matrix
It is known that, in the above equation,
The above equation corresponds to the sum of powers of
According to the theory of dimensional analysis (π theorem), the physical relations can be transformed into dimensionless form and the number of independent variables in the function is reduced. So, the relationship between the vibration velocity and the physical quantities in the tunnel when blasting excavation is carried out can be expressed as follows:
In practical engineering, the density of the rock mass
Simplifying the equation above, we get
Observe that the first term of the above equation is found to be consistent with the proportional charge quantity of Sadowski formula
The corresponding relationships between the coefficients in the above equations are as follows:
Analyzing the final expression, the first term on the right-hand side of the equation,
A sample of actual blasting data from Badaling Great Wall Station was used for analysis. The station has many levels, many cavities, and complex cavity types, making it the most complex concealed cavity group station in China. There are multiple spatial relationships in the construction of sections and areas affected by close blasting construction.
Mountain tunnels with a burial depth
The three separate cavern sections are part of a three-line parallel tunnel group, with the right line 2 months behind the mainline and the mainline 3 months behind the left line. Their actual excavation dimensions and chamber spacing are shown in Figure 1. As the net distance between the rock columns of the three parallel tunnels is only 2.27–6 m, blasting in the mainline will cause vibration effects or even damage to the left and right line tunnel structures on both sides where the initial support or secondary lining has been completed. Blasting vibration control is required to ensure that the support effect of the existing support is not affected.
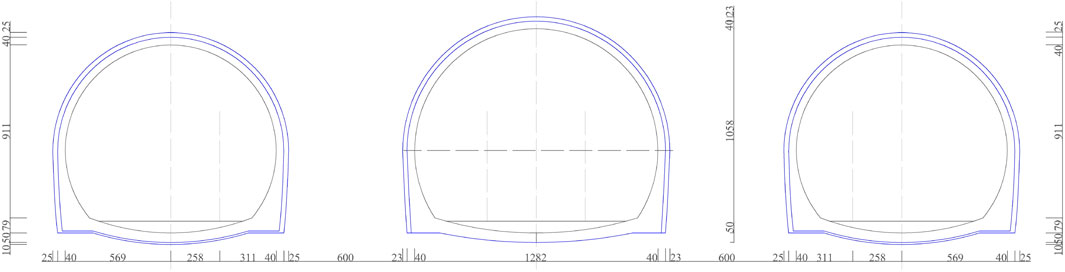
FIGURE 1. Schematic diagram of the cross-sectional dimensions and spacing of the three-hole separation section.
The section of the Great Wall Station at Badaling is 398 m in length, and the surrounding rock level is mainly Grade III. In the actual blasting construction, the section of Grade III surrounding rock is constructed by the step method, with a step length of 5∼8 m, in the order of up- and down-blasting construction. The holes were drilled by hand-held wind drill with a diameter of 42 mm, and the blasting explosive was Φ32 mm rock emulsion explosive. The layered explosive loading structure and uncoupled explosive loading structure are adopted.
Physical measures of blast vibration intensity include the mass vibration velocity, displacement, acceleration, and energy ratio. Following the Safety Regulations for Blasting, this paper uses mass point vibration velocity as the basis for measurement. TC-4850 blasting vibration meter is shown in Figure 2. By importing the vibration data into the software and analyzing the analysis, the vibration velocity of the mass at each monitoring point can be directly obtained as
The vibration test was used to monitor the changes in blast vibration velocity and acceleration at the foot and waist of the left-hand side of the excavated chamber and at various points in the same plane as the palm face during the blasting construction of the cavern. The actual measurement points are shown in Figure 3 and Figure 4, with a total of seven measurement points, of which measurement point 2 is facing the blast charging section of the tunnel palm face; measurement point 1 is placed in the excavated section and measurement point 2 is 5 m away; measurement points 3, 4, and 5 are placed in the unexplored area and the distance from measurement point 2 is 5, 13, and 23 m; and measurement points 6 and 7 are in the same plane as measurement point 2 but 0.8 m lower than measurement point 2. The blast vibration velocities at different locations were analyzed by monitoring the vibration velocities of one line and the same plane of measurement points.
The measured vibration sensors were recorded in all three directions at the same time, and the measured vibration data are listed in Table 3.
In examining the accuracy of the predictions, the correlation coefficient
where
In practical engineering based on the traditional empirical formula to regress the blast vibration peak velocity and proportional charge into a linear relationship and to obtain the decay law of the blast vibration peak velocity, based on the monitoring data in Table 3, the peak vibration velocities of tangential, radial, and vectorial synthesis in measurement points 1 to 5 were calculated to obtain the fitted curves and the corresponding Sadowski empirical decay formulae, as listed in Table 4 for each direction of the fitted results.
The predictions of the above two equations were evaluated through correlation coefficients, and the comparison shown in Figure 5 shows that the correlation coefficient R^2 of the attenuation indices calculated using the gauge calculation model has improved, regardless of radial, tangential, or combined velocities.
The above data show that the tunnel blasting vibration velocity calculation model based on this method can better reflect the existing tunnel lining vibration attenuation pattern when blasting deeply buried small clearance tunnels. In comparison with the traditional blasting vibration velocity calculation formula, it is found that the traditional empirical formula mainly considers the influence of the proportional dose, although the proportional dose is the main factor of blasting vibration velocity, but in actual engineering, it is found that the peak mass vibration velocity is inversely related to the free surface area
This paper combines measured blast vibration monitoring data from the tunnel excavation at Badaling Great Wall Station, systematically analyzes the propagation and attenuation laws of blast seismic waves in deeply buried small clearance tunnels, and draws the following conclusions:
1. By analyzing the relevant factors affecting the vibration velocity of the actual engineering blasting mass, including the length of the resistance line and the area of the free surface, combined with the exhaustive derivation of the dimensional analysis, the expanded blasting vibration velocity decay formula is
2. Based on the results of fitting the measured vibration data, it can be concluded that compared to the traditional Sadowski empirical formula, the correlation coefficient of the extended formula proposed in this paper has been improved, and the correlation of the fit is better, which can better reflect the impact of blasting vibration on the existing tunnel lining when blasting a deeply buried tunnel with small clearances.
When blasting other deeply buried small clearance tunneling projects, the expanded vibration velocity decay formula derived in this paper can be used for calculations in the near zone of the blast, and the explosive unit consumption can be adjusted in a timely manner according to the gun hole diameter, free surface area, and other factors.
The original contributions presented in the study are included in the article/supplementary material, and further inquiries can be directed to the corresponding author.
J-JS conceptualized the research idea, supervised the work, and reviewed and edited the paper. S-CG and J-JS performed the methodology. S-CG and WZ wrote the original draft. All authors have read and agreed to the published version of the manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Fu, H-X., Zhao, Y., and Jin, S. X. (2011). Study of Blasting Vibration Test of Area Near Tunnel Blasting Source. Chin. J. Rock Mech. Eng. 30 (2), 335–340.
Guo, S-Y. (2018). Technical Development and Outlook of the Tunnels and Underground Works in China. Mod. Tunn. Technol. 55 (S2), 1.
Hong, K-R. (2017). Development and Prospects of Tunnels and Underground Works in China in Recent Two Years. Tunn. Constr. 37 (2), 123.
Mingya, B., Li, M., and Liu, C. (2009). Analysis of Forecasting Error for Blasting Vibration. Blasting 26 (2), 96–98.
Rao, Y., and Wang, H. (2013). Multiple Linear Regression Analysis of Blasting Vibration Velocity Attenuation. Metal. Mine (12), 46–47.
Sadowski, M. A., and Chen, Y-F. (1986). Earthquake Prediction. translated. Beijing, China: Seismological Press.
Song, Y., Zhang, Z., and He, H. (2013). Wavelet Packet Energy Analysis of the Vibration and Vibration of the Chamber. Eng. Blasting 19 (4), 14–20.
Tan, Z-S., Yang, X-L., and Wang, M-S. (2003). Effect of Blast in Double Line Tunnel on Existing Tunnel. Chin. J. Rock Mech. Eng. 22 (2), 281–285.
Tang, H., Li, H. B., Jiang, P. C., and Wang, X. (2007). Experimental Study on Effect of Topography on Propagation of Blasting Waves. Chin. J. Rock Mech. Eng. 26 (9), 1817–1823.
Wang, C., Zhou, C., and Lu, S. (2017). Propagation Pattern of Blasting Vibration in the Surrounding Rock of Metro Tunnel. Sci. Technol. Eng. 17 (6), 158–162.
Xiong, D-Y., and Gu, Y-C. (2002). New Progress in Rock Blasting Theory and Technology. Beijing, China: Metallurgical Industry Press.
Yang, G. L., Rocque, P., and Bawden, W. F. (1994). Measyrement and Analysis of Near-Field Blast Vibration and Damage. Geotechnical Geol. Eng. 12 (2), 169–182.
Zhang, Q. B. (2019). Research on Blasting Vibration Propagation Law and its Control Technology Considering Elevation and Rock Mass Damage. Nanning Guangxi Univ.
Keywords: blast vibration, dimensional analysis, deeply buried small clearance tunnels, attenuation law, expansion formulae
Citation: Shi J-J, Guo S-C and Zhang W (2022) Expansion of Blast Vibration Attenuation Equations for Deeply Buried Small Clearance Tunnels Based on Dimensional Analysis. Front. Earth Sci. 10:889504. doi: 10.3389/feart.2022.889504
Received: 04 March 2022; Accepted: 25 April 2022;
Published: 15 June 2022.
Edited by:
Yun Jia, Université de Lille, FranceReviewed by:
Huayan Yao, Hefei University of Technology, ChinaCopyright © 2022 Shi, Guo and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jian-Jun Shi, ZzIwMTk4MDEyQHhzLnVzdGIuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.