
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 17 June 2022
Sec. Solid Earth Geophysics
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.884100
This article is part of the Research Topic The Structure of the Central Mediterranean: Insights from Seismological and Geophysical Data View all 5 articles
The Central-Western Mediterranean (CWM) is one of the most complex tectonic setting on Earth. Episodes of slab rollback, break-off and tearing, the opening of back-arc extensional basins (i.e., Liguro-Provencal, Alborean, Algerian and Tyrrhenian basins), the presence of large mountain ranges, active volcanoes and violent earthquakes have made the Mediterranean an ideal environment to study a wide range of geodynamic processes and an important target for seismological studies (e.g, seismic tomography). Here we build a geodynamic model which, although it does not reproduce its exact tectonic structure (e.g., due to the limits of the numerical method, approximations in the initial setup, etc), presents multiple and geometrically complex subduction systems analogous to those found in the CWM. The tectonic evolution of this model is estimated with petrological-thermo-mechanical 3D simulations, then, we dynamically compute the upper mantle fabrics and seismic anisotropy as a function of the strain history and local P-T conditions. After comparing the model with SKS splitting observations in order to quantify the discrepancies with the true Central-Western Mediterranean, we use the elastic tensors predicted for the modeled configuration to perform 3D P-wave anisotropic tomography by inverting synthetic P-wave delay times. Using the geodynamic model as reference, we evaluate the capabilities of a recently developed seismic tomography technique to recover the isotropic anomalies and anisotropy patterns related to a complex subduction environment in different conditions, such as poor data coverage and bad data quality. We observe that, although P-wave tomography still remains a powerful tool to investigate the upper mantle, the reliability of the retrieved structures strongly depends on data quality and data density. Furthermore, the recovered anisotropic patterns are consistent with those of the target model, but in general an underestimation of the anisotropy magnitude in the upper mantle is observed. In the light of future developments, our study suggests that by combining micro- and macro-scale geodynamic simulations and seismological modeling of seismic anisotropy it will be possible to reproduce, at least to a first order, the tectonic evolution of real study regions (e.g., the Mediterranean) thus providing fundamental constraints on the processes that have contributed in shaping their current geological scenario.
Since the early 1990s numerous seismological studies have been carried out to image the Earth’s upper mantle and seismic tomography proved to be a fundamental tool for constraining the past and present-day mantle dynamics and structure (Liu and Gu, 2012; Rawlinson et al., 2014; Van der Meer et al., 2018; Romanowicz, 2021). Tomographic methods (e.g. P-, S- and surface-wave tomography) yield wave velocity models that are commonly used to infer distributions in physical and chemical properties affecting seismic-wave propagation such as density, temperature, melt fraction and volatile content.
At the same time, petrophysical analysis of exhumed rock samples and micromechanical laboratory experiments (Ribe, 1989; Savage, 1999; Blackman and Kendall, 2002; Kaminski et al., 2004; Karato et al., 2008; Karato et al., 2008; Long and Becker, 2010; Faccenda, 2014; Skemer and Hansen, 2016) have shown that the development of mineral and compositional fabrics mainly associated with rock deformation can create significant directional variations in seismic velocities known as seismic anisotropy. Although the presence of seismic anisotropy in Earth’s upper mantle is well-established, scientists have often assumed the Earth’s interior as seismically isotropic. This approximation certainly simplifies the computational approach but at the same time it can introduce notable imaging artefacts and, consequently, errors in the interpretation of the tomographic results (Kendall, 1994; Blackman et al., 1996; Blackman and Kendall, 1997; Sobolev et al., 1999; Lloyd and Van Der Lee, 2008; Menke, 2015; Bezada et al., 2016; VanderBeek and Faccenda, 2021).
Recently, VanderBeek and Faccenda (2021) and Wang and Zhao (2021), have independently developed a methodology to invert for P-wave isotropic (mean velocity) and anisotropic (magnitude of hexagonal anisotropy, azimuth and dip of the symmetry axis) parameters. When tested on a relatively simple, 3D geodynamic model of subduction, VanderBeek and Faccenda (2021) found that the new inversion technique produces a much more accurate reconstruction of the upper mantle isotropic and anisotropic structures. In contrast, ignoring for seismic anisotropy (isotropic approximation) or allowing for only azimuthal variations in seismic velocity (i.e., no dipping fabrics) generates strong imaging artifacts. From these tests it follows that taking into account seismic anisotropy can provide new insights into the 3D upper mantle structure and dynamics. Despite these encouraging results, it remains unclear whether isotropic and anisotropic structures of the Earth’s mantle can be simultaneously recovered by P-wave anisotropic inversions in real and more complex tectonic settings.
Along with seismic imaging techniques, over the last decades numerical geodynamic modelling became an essential approach for understanding the long-term and deep evolution of a wide range of geological processes, which otherwise would remain unconstrained due to the lack of geological data (Gerya, 2019). Owing to the development of increasingly high performance computers and more advanced numerical techniques, it is nowadays possible to simulate the multiscale tectonic evolution of 3D complex settings for 10s or 100s of millions of years (van Zelst et al., 2021). However, despite being a powerful tool, numerical modeling is also affected by several limitations that could potentially bias the final output, such as uncertainties in the employed initial model geometry, physical parameters (mainly viscosity), chemical compositions, and limited computational power.
In order to test the limitations of the tomographic and numerical modeling methods, a promising approach is combining micro- and macro-scale geodynamic modeling simulations of mantle flow to predict mantle isotropic and anisotropic structures and then perform seismological synthetics (Faccenda and Capitanio, 2012, 2013; Hu et al., 2017; Confal et al., 2018; Zhou et al., 2018; Lo Bue et al., 2021). We decided to apply this combined methodology to the Central-Western Mediterranean (CWM) region (Supplementary Figure S1). In the last 20–30 million years, this area has experienced a complex tectonic activity characterized by back-arc extension related to slab retreat in the Liguro-Provençal, Alborean, Algerian and Tyrrhenian basins and episodes of slab break-off, lateral tearing and interactions between slabs (Spakman et al., 1988; Platt and Vissers, 1989; Lonergan and White, 1997; Carminati et al., 1998; Wortel and Spakman, 2000; Rosenbaum et al., 2002; Faccenna et al., 2004; Mauffret et al., 2004; Spakman and Wortel, 2004; Jolivet et al., 2006; Faccenna et al., 2007; Jolivet et al., 2008; Vignaroli et al., 2008; Jolivet et al., 2009; Carminati et al., 2012; Faccenna et al., 2014; van Hinsbergen et al., 2014; Király et al., 2018; Van Hinsbergen et al., 2020) and a wealth of geological and geophysical data are available. Numerous tomographic models and geodynamic studies focusing on the CWM upper mantle are available, which can be used here to test the reliability of our approach.
We first extend the modeling methodology of Lo Bue et al. (2021) to create a geodynamic model that resemble observed slabs morphology and anisotropic mantle fabrics of the CWM. The geodynamic model is then exploited as synthetic case study to test the capabilities and limitations of P-waves isotropic and anisotropic inversions in recovering complex geological scenarios using the methodology of VanderBeek and Faccenda (2021).
In this work, we attempt to answer some fundamental questions. How well does P-wave anisotropic tomography recover the modeled isotropic and anisotropic structures? How reliable are the inferred anisotropic patterns with respect to the upper mantle fabrics? Which are the main artefacts introduced in the tomographic image when neglecting seismic anisotropy? To which extent vertical smearing bias the inverted structures when only using teleseismic P-wave travel times?
We construct a 3D petrological-thermo-mechanical numerical model of the Central-Western Mediterranean convergent margin using I3MG (Gerya, 2019), which is based on the finite difference method (FDM) combined with a marker-in-cell (MIC) technique. The mass, momentum and energy conservation equations are solved on a staggered Eulerian grid while the physical properties are interpolated to the Lagrangian markers for advection. The Earth’s mantle is treated as a highly viscous incompressible medium. Visco-plastic deformation is simulated by combining a Drucker-Prager yielding criterion with dislocation, diffusion and Peierls creep mechanisms.
In this paper we refer to our geodynamic model as Model CWM (Central-Western Mediterranean Model). This model is an updated version of the Reference Model CM of Lo Bue et al. (2021). Here, the computational domain has been enlarged and has dimensions of 3700 x 700 x 2200 km (373 x 101 x 229 nodes) along the x − y − z coordinates, with y being the vertical direction. As in Model CM, subduction modeling is self-consistent, driven only by internal buoyancy forces. Velocity boundary conditions are free slip everywhere. We impose a constant incoming heat flux of 2 mW/m2 at the bottom boundary, while the top boundary is characterized by a constant temperature of 273 K. The side boundaries are insulating. The models account for frictional and adiabatic heating, and for thermal and dynamic effects of phase changes (except that the medium is assumed to be incompressible).
We used the MATLAB toolbox geomIO (Bauville and Baumann, 2019) to create the 3D initial temperature and compositional fields. The tectonic plate geometry has been designed according to the paleogeographic and tectonic reconstructions at ∼30 Ma proposed by Lucente and Speranza (2001); Lucente et al. (2006); Faccenna et al. (2014); van Hinsbergen et al. (2014); Romagny et al. (2020) although some simplifications were required due to limitations imposed by numerical modeling.
In the initial setup (Figure 1), a subducting oceanic plate, that represents the Ionian Ocean, is surrounded by lateral continental blocks corresponding to the Adria, Africa, Iberia and European plates. The position of the plates in the Oligocene-Miocene was adapted from a reconstruction of van Hinsbergen et al. (2014). It is worth noting that, not having applied a convergence rate between the plates (self-consistent subduction), their relative position slightly differs from the present-day one. However, an initial geometry defined in the Oligocene-Miocene should not have a strong impact on mantle flow directions and splitting parameters as the slow Africa-Europe plates convergence has not caused a drastic change in plates position over this time span.
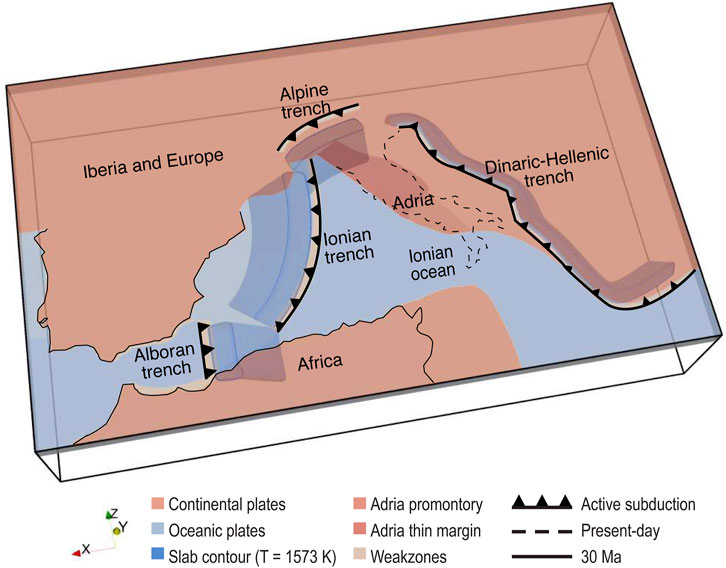
FIGURE 1. Initial model setup for Model CWM. It consists of a subducting oceanic plate (Ionian Ocean; light blue) surrounded by lateral continental blocks (Adria, Africa, Iberia and Europe; salmon pink) drawn according to paleogeographic reconstructions at ∼30 Ma proposed by Faccenna et al. (2014); van Hinsbergen et al. (2014); Romagny et al. (2020). The Adria plate is characterized by the presence of a stiffer continental promontory (peach pink) and a thin continental margin (red) as proposed by Lucente and Speranza (2001); Lucente et al. (2006); Lo Bue et al. (2021). Multiple subducting slabs are positioned according to the chosen reconstructions (i.e., Alboran and Ionian trenches as in Romagny et al. (2020); Alpine and Dinaric-Hellenic trenches as in Faccenna et al. (2014)) and taking into account the limitations imposed by numerical modeling. The solid black line indicates the coastlines at ∼30 Ma as in van Hinsbergen et al. (2014), while the dashed black line the present-day coastlines of peninsular Italy. The plates are opacified for a better visualization of the subducted slab.
In Model CWM, we considered a more realistic paleo-tectonic configuration of the region, which is characterized by the presence of multiple subducting slabs rather than a single one as in Model CM.
Subduction in the Ionian plate occurs along two trenches as in Romagny et al. (2020). The longest one stretches from the Alps to the southeast of the Baleares and is associated with a slab dipping 40°NW and extending down to 300 km in the upper mantle. A second one is placed in the Alboran domain, where a slab with the same dipping angle but an opposite vergence extends down to 350 km in the upper mantle (Romagny et al., 2020). Throughout the manuscript we use “Ionian slab and Ionian trench” to indicate the former subduction zone and “Alboran slab and Alboran trench” when referring to the latter. It is worth noting that to trigger slab roll-back self-consistently, the Ionian trench has been positioned further south as in Lo Bue et al. (2021) and the initial depth of the Alboran and Ionian slabs has been increased compared to tectonic reconstructions. This could cause a difference in rates of slabs retreat when compared to those reported in the literature and be representative of a more recent stage of the Central-Western Mediterranean history rather than the 30 Ma assumed here.
Two large collisional suture zones, are present in the continental Adria and European plates as in Faccenna et al. (2014). To the north, we find the Alpine trench with its characteristic arcuate shape and, to the east of the model, the Dinaric-Hellenic trench that extends from Eastern Alps to the southernmost tip of the Hellenic peninsula (Faccenna et al., 2014). In both trenches the slab dips almost vertically into the upper mantle to a depth of about 350 km to simulate locked collision zones. In this area slabs extended down to 350 km depth to model flow barriers due to the presence of subducted slab.
In the area of the model corresponding to the present-day Apenninic chain, we use the same initial configuration as in Lo Bue et al. (2021), characterized by lithospheric heterogeneities which are fundamental for the development of key tectonic features such as a prolonged eastward retreat of the Ionian plate and the formation of a slab window below the modelled central Apennines. The Adria plate consists of a thin continental lithosphere in the Umbria-Marche region and of a stiffer continental promontory in its central portion corresponding to the Abruzzo-Laziale platform (Calcagnile and Panza, 1980; Geiss, 1987; Lucente and Speranza, 2001; Panza et al., 2003; Lucente et al., 2006; Miller and Piana Agostinetti, 2012; Maino et al., 2013; Lo Bue et al., 2021). The African plate structure, nearby Sicily and the Sicilian Channel area, is characterized by a slightly thinner margin (Arab et al., 2020; Lo Bue et al., 2021).
The initial lithosphere thermal structure was modeled using the half-space cooling equation (Turcotte and Schubert, 2014), while the underlying asthenosphere consists of a 0.5 K/km constant adiabatic temperature gradient. The thermal age of the Ionian oceanic plate is 80 Myr, while that of the two slabs is 70 Myr to simulate partial heating upon subduction. The age of the continental plates (Africa, Africa eastern margin, Iberia, Adria and Adria promontory) is 150 Myr while an age of 90 Myr was imposed for the thinned portion of Adria continental lithosphere. To activate a self-consistent subduction, the Ionian plate north of the two trenches is composed of a young lithospheric portion (1 Myr - the young age is justified by assuming a well-developed continental rifting system North of the Balearics and Corsica-Sardinia block). Furthermore, rheologically weak zones (constant viscosity of 1018 Pa s and constant density of 3200 kg/m3) have been inserted 1) on the slabs top surface to lubricate the initial contact between the overriding and the subducting plates, and 2) around southwest Iberia and northwest Africa to facilitate the Alboran trench retreat (e.g., Chertova et al. (2014)). The plates thermal structures and flow law parameters have been tuned to allow a self-consistently subduction and simultaneously to reproduce the main tectonic events as close as possible to the geological reconstructions. This may cause a too weak rheology and faster rates of mantle convection once self-sustained subduction has started due to the non-linear viscous behaviour of the mantle.
The density is computed using the thermodynamic databases generated with PERPLE_X (Connolly, 2005) and tested by Mishin et al. (2008) for a pyrolytic mantle composition. The continental crust density is calculated as being that of the mantle minus 400 kg/m3, except for the Adria thin margin where we subtract 200 kg/m3 to model a less buoyant continental lithosphere. Instead, for the crust of the Adria promontory we use a constant value of 2700 kg/m3. More details about the physical parameters used in the geodynamic model can be found in Lo Bue et al. (2021).
The development of seismic anisotropy in the upper mantle is calculated using a modified version of D-Rex (Kaminski et al., 2004), which incorporates the deformation mechanisms inducing LPO (plastic deformation, dynamic recrystallization and grain-boundary sliding) and accounts for deformation history and non-steady-state evolution of geodynamic systems (Faccenda and Capitanio, 2013; Faccenda, 2014).
A large number of Lagrangian particles representing mineral aggregates are regularly distributed throughout the numerical domain (25 km reciprocal distance along the three directions, for a total of 364,672 aggregates). Each particle consists of 1024 randomly oriented crystals, which results in an initially isotropic upper mantle. We use a harzburgitic upper mantle composition (70% olivine and 30% orthopyroxene modal abundance) and a more fertile pyrolitic mantle composition in the transition zone (60% spinel and 40% majoritic garnet) (Faccenda, 2014). The Eulerian velocity field obtained by the macro-flow simulation is then used to passively advect the particles and LPO is generated at each time step through the re-orientation of such particles in response to the gradients in the velocity field. Since SKS splitting parameters are mostly sensitive to the upper mantle (Sieminski et al., 2008), we only model the anisotropy from the Moho to the 410 km discontinuity. We use the same dimensionless crystallographic parameters as in (Rappisi and Faccenda, 2019) with the nucleation rate λ = 5, the grain-boundary-mobility M = 1 and the threshold volume fraction χ = 0.9, which generate weaker fabrics and seismic anisotropy more consistent with the observations.
Synthetic SKS splitting parameters are computed using the software package FSTRACK (Becker, 2006). Through the stiffness matrix the code recovers the elastic tensors for each aggregate and then, below each station and down to 400 km, it builds a vertical stack of horizontal layers (minimum thickness of 25 km) where the elastic tensor of each layer is radially averaged within a distance of 50 km. Next, assuming an incident plane wave (5° for typical SKS arrivals) into the mantle over a range of frequencies from 0 to 25 Hz, using the inverse Fourier transform, it computes a pulse seismogram that will be further filtered to construct SKS waves (i.e. from 0.1 to 0.3 Hz). Finally, by applying the cross-correlation method of Menke and Levin (2003) and averaging all the fast azimuths and delay times at each station measured by rotating the vertical stack of elastic tensors by 5° intervals around the y-axis, the SKS splitting parameters are determined. The software for computing mantle aggregates fabrics and SKS splitting can be found in the open source software package ECOMAN (https://newtonproject.geoscienze.unipd.it/ecoman/).
We use the anisotropic seismic imaging method by VanderBeek and Faccenda (2021), that solves for perturbations to P-wave slowness and three additional parameters that define the anisotropic magnitude, azimuth, and dip in a hexagonally symmetric medium. The tomographic algorithm does not require an anisotropic starting model which could potentially distort the results if not close enough to the true solution as in the case of the anisotropic imaging method of Munzarová et al. (2018). Additionally, changes in elevation and surface velocity are explicitly addressed in teleseismic imaging using 3D ray tracing through a user-defined 3D velocity model that incorporates elevation (Toomey et al., 1994).
Ray theoretical travel-times are estimated 1) with the shortest-path algorithm (Moser, 1991) through Model CWM described in the previous section using the mantle aggregates full elastic tensor at ∼21 Myr, and 2) with the tau-p method (Crotwell et al., 1999) outside the study area using a 1D radial Earth velocity model. The geodynamic model was centered on 42°N 12.5°E to match the main seismic structures with the real positions observed in current tomographic images.
Partial derivatives of the travel-times with respect to the model parameters are computed along the discretized ray paths. The LSQR method (Paige and Saunders, 1982) is used to solve the resulting linear system of equations relating changes in model parameters to changes in travel-times. To regularize the ill-posed inverse problem, damping and smoothing constraints are used. The choice of the regularization parameters that limit the norm of the model perturbational vector and enforce the Laplacian spatial smoothness of the model perturbations, thus controlling the length and the roughness of the solution vector relative to the length of the data residual vector, i.e. λd and λs respectively, is discussed in Section 2.3.1.
We use a regular grid with uniform 10 km node spacing for the forward calculation of travel-times. The initial mantle velocity model is the isotropic 1D AK135 model (Kennett et al., 1995). We applied an Earth flattening transform (Müller, 1971) to account for Earth’s curvature in our Cartesian model domain.
Perturbations to the three anisotropic parameters and the mean P-wave slowness (i.e. inverse of velocity, u = 1/v) are solved on a coarser regular grid with 40 km node spacing and then, at each iteration, linearly mapped to the finer model used for travel-times calculation. Model CWM was considered down to 700 km depth, however, to limit the number of inversion parameters, anisotropic perturbations were restricted to the upper 400 km where there is the best ray crossing and mineral physics predicts mantle anisotropy to be most significant (Karato et al., 2008).
To resemble realistic conditions a first inversion was performed using delay times calculated through our Model CWM with the same distribution of sources (Supplementary Figure S2A) and receivers (Figure 2A), and the same regularization parameters as in the anisotropic tomography model of the Central Mediterranean by Rappisi et al. (2022) (Test 1). For this first test normally distributed errors with a standard deviation of 450 ms was added to the seismic data.

FIGURE 2. Plot of the real land (as in Rappisi et al., 2022) (A), ideal land (B) and ideal marine and land (C) station distribution.
Next, several sets of inversions were run imposing a 1-sigma error of 125 ms applied to synthetic data and a smoothing-to-damping ratio (λs/λd) of 100 and damping values (λd) of 1,2, … 9,10 with different synthetic datasets. For these sets of tests we used: 1) same sources (Supplementary Figure S2A) and station array as in Test 1 (Test2); 2) an ideal on land receivers distribution (Figure 2B) (Test 3); 3) an ideal marine and on land receivers distribution (Figure 2C) (Test 4). In the last two cases (Test three and 4) the receivers are equally spaced 75 km apart and the teleseismic events are placed at a distance from the center of the domain from a minimum of 35 up to a maximum of 110°, every 10°of azimuth (Supplementary Figure S2B), guaranteeing a perfectly homogeneous azimuthal events distribution, thus removing any bias associated with preferential sampling of certain back azimuths.
In addition we performed 4) purely isotropic inversions in order to evaluate the effect of neglecting seismic anisotropy on the tomographic image (Test5), and 5) an inversion where the Model CWM is considered to be isotropic below 200 km to address vertical smearing of anisotropic structures (Test 6).
We constructed L-curves (Aster et al., 2018) plotting the squared model norm (|dm|2) as a function of the squared norm of the delay time residuals normalized by the estimated data uncertainty (χ2) for different values of damping factor (λdu) (Supplementary Figure S3). Ideal solutions are considered those near the corner of the L-curve where an increase in model norm does not result in an appreciable decrease in data residuals. For each test, convergence is usually reached before or at iteration 3. All the inversions performed are summarized in Table 1.
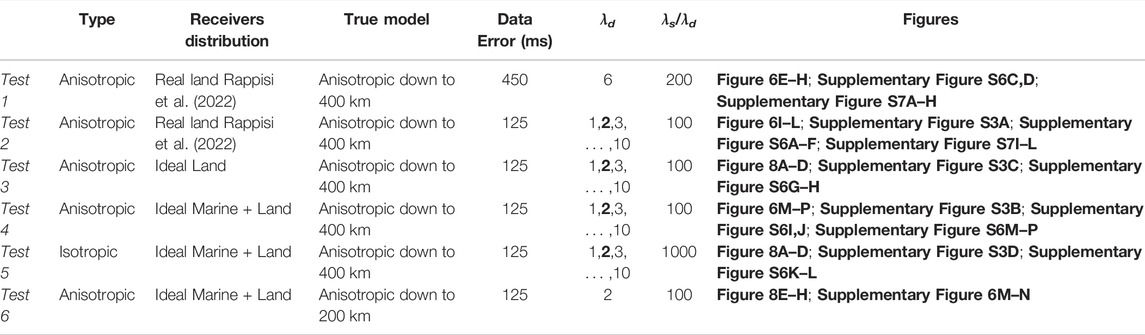
TABLE 1. Inversions summary table. The type of inversion (isotropic/anisotropic), receivers distribution, true model, standard deviation of normally distributed data errors, damping and smoothing factors and relevant figures for each inversion are listed. In bold the λd corresponding to the preferred solution.
To explore possible trade-offs between isotropic and anisotropic parameters, a synthetic inversion was aimed at reconstructing the isotropic component of model CWM. To test if velocity anomalies present in our preferred isotropic model could yield erroneous anisotropy, delays predicted through this model–not considering the anisotropic components–were inverted for both isotropic and anisotropic parameters. The result is showed in Figure 3. Isotropic anomalies were faithfully recovered with minimal anisotropic perturbations throughout the entire study area (generally
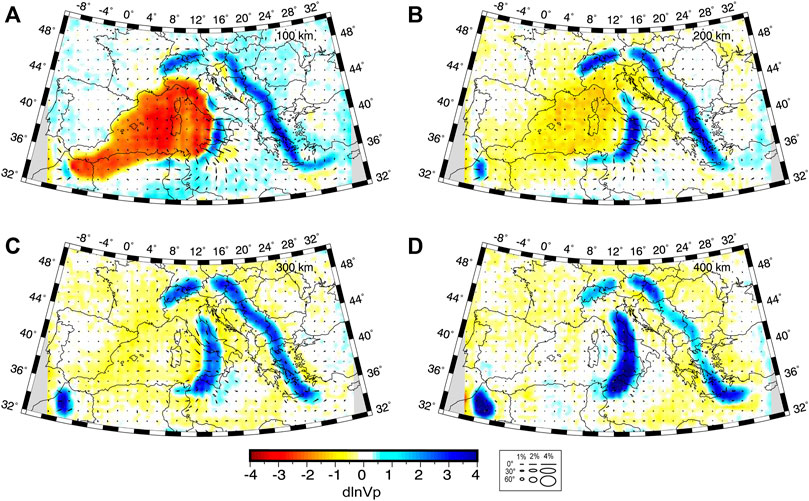
FIGURE 3. Depth slices at (A) 100 km, (B) 200 km, (C) 300 Km and (D) 400 km depth. Isotropic restoration synthetic test. Anisotropic inversion of purely isotropic synthetic data calculated through our model CWM, i.e., non taking into account the anisotropic patterns. While no anisotropic structures have been considered when performing the forward problem, the inversion does introduce some anisotropic perturbations. Anisotropy is represented by ellipse symbols where the major axis of the ellipse parallels the fast-direction and the minor axis scales linearly with the symmetry axis dip into the view plane such that fabrics parallel and normal to the cross-sections plot as lines and circles, respectively. Anisotropic perturbations were restricted to the upper 400 km. See legend. Areas of poor data coverage are masked in grey.
Permuted data test similar to Spakman (1991); Bijwaard et al. (1998); Rawlinson and Spakman (2016) was performed in order to assess the model amplitude error as the anomaly amplitudes are interpreted in terms of geodynamic features and errors could potentially bring to wrong interpretations. The inverted dataset is the data vector of the last iteration of Test 2, randomly permuted. The “permuted dataset” can be considered noise that has the same average, standard deviation and distribution of the delay times “not permuted” used for Test 2. By permuting the data vector order, there is no more correlation between the delay times and the raypaths. The starting model is the tomography obtained at the last iteration of Test 2. This choice allows to guarantee that the ray geometry of the permuted data test is comparable to that in Test 2. The result is showed in Figure 4. We do not observe regions with systematic anomaly patterns, on the contrary, random anomalies are recovered with delay time residual χ2 ≈ 8.8 and the RMS amplitude variations
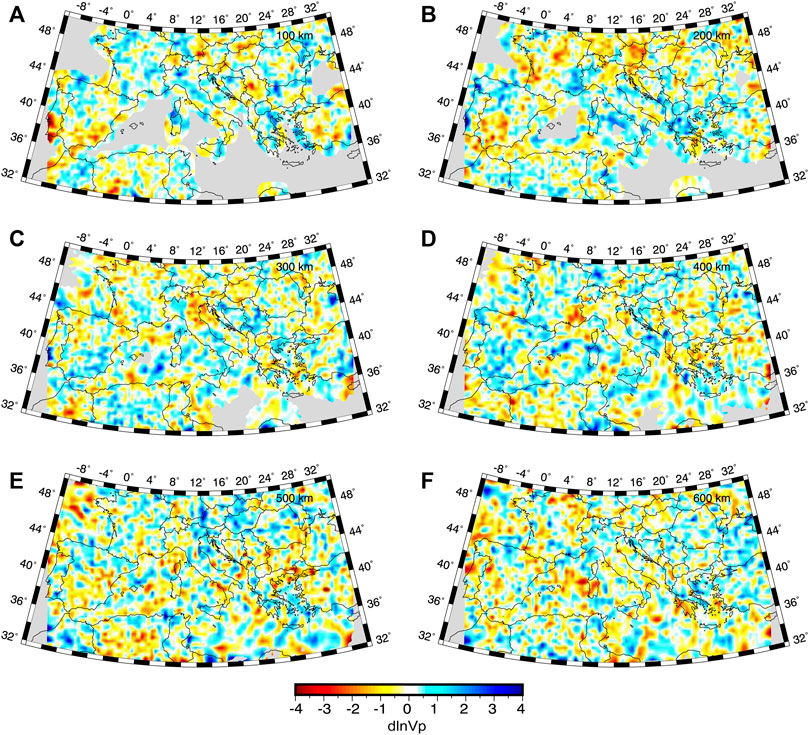
FIGURE 4. Depth slices at (A) 100 km, (B) 200 km, (C) 300 Km, (D) 400 km, (E) 500 km and (F) 600 km depth. Permuted data test. P-wave velocity anomalies obtained from the inversion of randomly permuted delay times.
In this section the geodynamic evolution of Model CWM is addressed (Supplementary Movie S1). The following discussion focuses on a mere description of our geodynamic model evolution. Analogies and differences between Model CWM and the real tectonic evolution of the Central-Western Mediterranean region will be discussed in Section 4.1. The Alpine and Dinaric slabs have been included in the Model CWM only to evaluate their influence in the mantle flow below the Adria plate surrounding regions, but they also represent important targets to be recovered by our tomographic inversions. Their geodynamic evolution is characterized by further slab verticalization and final break-off.
The slabs negative buoyancy drives the evolution of the two active oceanic subductions. The oceanic plates progressively sink down to the mantle transition zone and after bending start to rollback accompanied by a stretching of the overriding lithosphere. The Ionian slab migrates south-eastward while the Alboran slab south-westward. The rollback of the two slabs evolves with episodes of lateral tearing, segmentation and break-off when trenches impact with a continental margin.
The tectonic evolution of the Ionian slab is similar to that of Model CM (Lo Bue et al., 2021). In a few million years (∼ 4 Myr), the western part of the Ionian trench collides with the African plate inducing slab tearing along the passive margin and subduction of continental crust fragments. The tear propagates along the African margin, favouring the eastward slab rollback (Figure 5A). Subsequently, the northeastern edge of the trench reaches the thin northwestern Adria margin progressively causing subduction of the Adria continental crust, slab lateral tearing along the oceanic-continental lithosphere transition, and the formation of a curved trench due to the variations of buoyancy along it. Meanwhile, the Alboran slab rapidly rolls back westward, accommodated by lithosphere tearing along the African and Iberian margins (Figure 5A,B). In ∼10 Myr, both subducting slabs are already stagnating horizontally in the mantle transition zone at the bottom of the model.
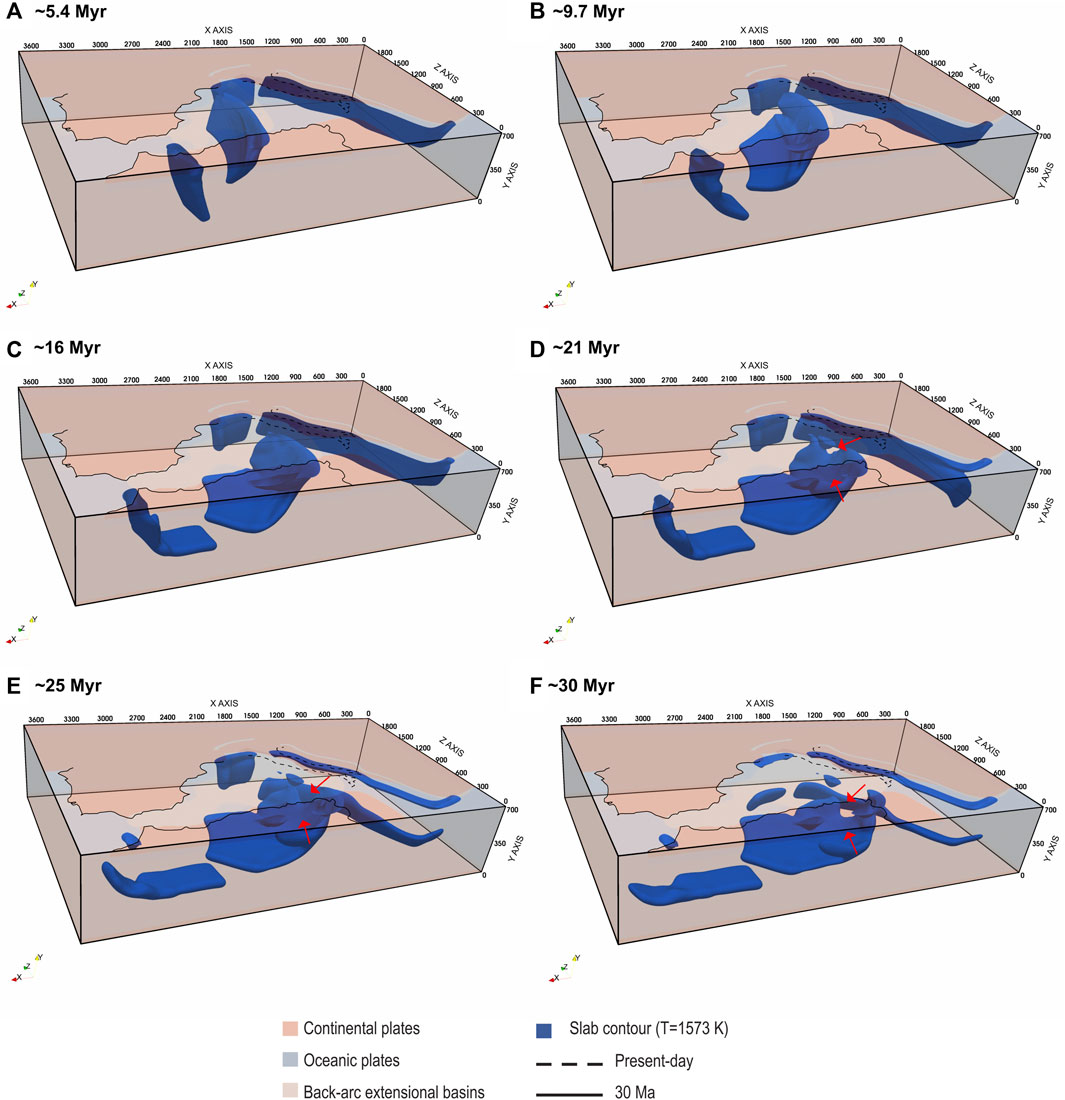
FIGURE 5. Snapshots of the Model CWM geodynamic evolution at (A) ∼5.4 Myr, (B) ∼9.7 Myr, (C) ∼16 Myr, (D) ∼21 Myr, (E) ∼25 Myr, (F) ∼30 Myr. In blue the subducted. Snapshots of the Model CWM geodynamic evolution. In blue the subducted slabs (contour at T=1573 K) below ∼100 km depth. The plates are partially transparent for a better visualization of the subducted slabs. The solid black line indicates the coastlines in the Oligocene-Miocene (van Hinsbergen et al., 2014), while the dashed black line indicates the present-day coastlines of peninsular Italy. The red arrows indicate the two slab windows beneath the Central Apennines and the Africa continental plate.
After ∼16 Myr (Figure 5C), the Alboran slab reaches the area of the model corresponding to the current Gibraltar region, after which a very slow trench retreat is observed until the complete detachment at ∼23 Myr.
The late evolution of the Ionian slab is instead more complex and important differences occur compared to the Model CM (Lo Bue et al., 2021). When the Ionian trench reaches Central Adria, part of the stiffer continental promontory subducts causing slab break-off. As in Lo Bue et al. (2021), this rupture generates a large slab window that splits the Ionian slab in two separate slabs. Contrary to Lo Bue et al. (2021), here, this phenomenon also occurs on the side of the African continent. This leads to a final geometry of the Ionian slab characterized by the presence of two wide windows, one below the area corresponding to the current Central Apennines and one beneath the north-eastern African margin (Figure 5D).
After ∼20 Myr (Figure 5D–F), slab remnants are found in model areas corresponding to the present-day Northern Apennines, Southern Tyrrhenian sea, Alboran sea and Kabylides. At ∼20 Myr, the Ionian slab (portions beneath the Northern Apennines and south of the Tyrrhenian Sea - Supplementary Figure S4A) and the Alboran slab extend continuously from the surface down to the mantle transition zone.
At ∼ 25 Myr, the Northern Apenninic and Kabylides slabs hang down to ∼150 km depth (Supplementary Figure S4B). The first one extends further deeper from ∼180 km down to about ∼660 km depth while a horizontal segment of the Kabylides slab is still joined to the Ionian slab from ∼180 km down to about ∼300. The remaining portion of the Ionian slab (south of the Tyrrhenian Sea) instead extends continuously from the surface down to the mantle transition zone. The Alboran slab is already detached. At ∼ 30 Myr, the Calabrian slab appears still anchored to the surface (Supplementary Figure S4C) showing clear evidences of break-off. The model evolves with the complete detachment of all the slabs (Figure 5F).
The subduction and rollback of the Ionian and Alboran slabs in the Model CWM induces a complex flow in the surrounding mantle characterized by the presence of poloidal and toroidal components (Supplementary Movie S1). The initial sinking of the two slabs (i.e. Ionian and Alboran) generates a dominant poloidal flow component and mantle upwelling in the mantle wedge (i.e., arrows pointing downward or upward in correspondence of slabs and basins, respectively - Supplementary Movie S1). Subsequently, toroidal cells are also generated by slab rollback that forces the mantle to flow circularly around the edges of the two slabs and through the slab windows that are formed at later stages.
Here, compared to Model CM (Lo Bue et al., 2021), the complexity of the mantle flow increases due to the presence of the multiple subducting slabs. We observe the mantle flowing mainly horizontally toward southeast and west directions in response to the horizontal motion of the Ionian and Alboran slabs, respectively. The Dinaric and Alpine slabs act as a barrier to the large toroidal flow patterns induced by the retreat of the Ionian plate found in Model CM of Lo Bue et al. (2021). As a result, the mantle flows parallel to the Dinaric slab in the region corresponding to the Adriatic sea and Dinarides, as well parallel to the Alpine slab. The strongest upper mantle fabrics are observed in the area surrounded by the Alboran and Ionian slabs, down to 400 km depth, while east of the Dinaric slab and in the eastern Ionian sea mainly isotropic structures are found (Figure 6A–D). This is because Model CWM only partially reproduces the retreat of the Aegean slab over the Cenozoic. Trench-perpendicular azimuths are observed in the supra-slab upper mantle, corresponding to the Tyrrhenian and Alboran basins. The sub-slab upper mantle portions (i.e. below Calabrian, Alboran and Alpine slabs) are instead characterized by the presence of trench-parallel fabrics. Near-horizontal fabrics are found in the area of the Ionian sea and in the continental European plate. More steeply dipping fabrics are instead observed in the Tyrrhenian sea, Alboran basin and Northern Italy in correspondence of the subducting slabs.
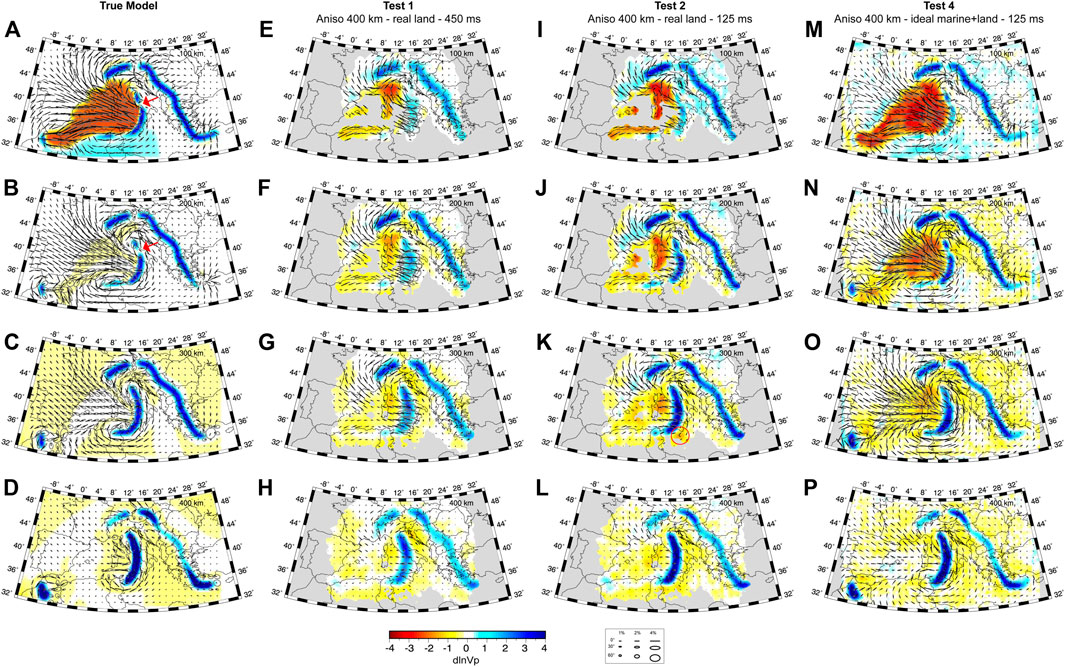
FIGURE 6. True model and anisotropic tomography results. Depth slices are shown at 100 km, 200 km, 300 km and 400 km depth for the true model (A–D), the model resulting from Test 1 (E–H), Test 2 (I–L) and Test 4 (M–P). Isotropic anomalies are plotted with respect to the reference velocity model. We plot anisotropic fabrics as ellipses where the major axis of the ellipse parallels the fast-direction of anisotropy in the view plane and scales with the anisotropic magnitude while the minor axis scales linearly with the symmetry axis dip into the view plane. Thus, fabrics parallel and normal to the view plane plot as lines and circles, respectively; see legend. Areas of poor data coverage are masked in grey. The red arrows in panels a and b indicate the position of the slab window below the Central Apennines. The red circle in panel k indicates a low velocity artefact.
The upper mantle fabrics patterns are reflected in those of the synthetic SKS splitting measurements shown in Figure 7. In the back-arc regions, the fast azimuths orient parallel to the trajectory of the Ionian and Alboran trenches migration. The delay times in these regions are very high (δt = 2–3.2 s), reflecting fabrics that are consistent within the entire upper mantle, and are reduced in the areas near the two trenches (δt = 1–1.5 s) due to the superposition of mantle domains with contrasting fabric patterns. In the fore arc regions, the teleseismic fast shear wave components align trench-parallel, while around the slabs edges, they form a circular pattern highlighting the underlying return flow (δt = 1–1.5 s).
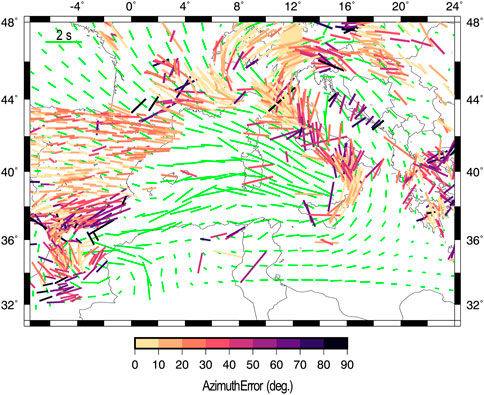
FIGURE 7. SKS-splitting measurements in the Central-Western Mediterranean (Becker et al., 2012) color-coded by the angular misfit compared with synthetic SKS splitting measurements for Model CWM at ∼20 Myr (green bars). The EW green bar in the upper left corner indicates 2 s. Time-delay misfits are shown in Supplementary Figure S5A.
Tomography results are shown in Figures 6, 8, with additional maps at 500 and 600 km depth in Supplementary Figure S6 and narrower colorscale limits (i.e [−2%—+2%]) in Supplementary Figure S7.
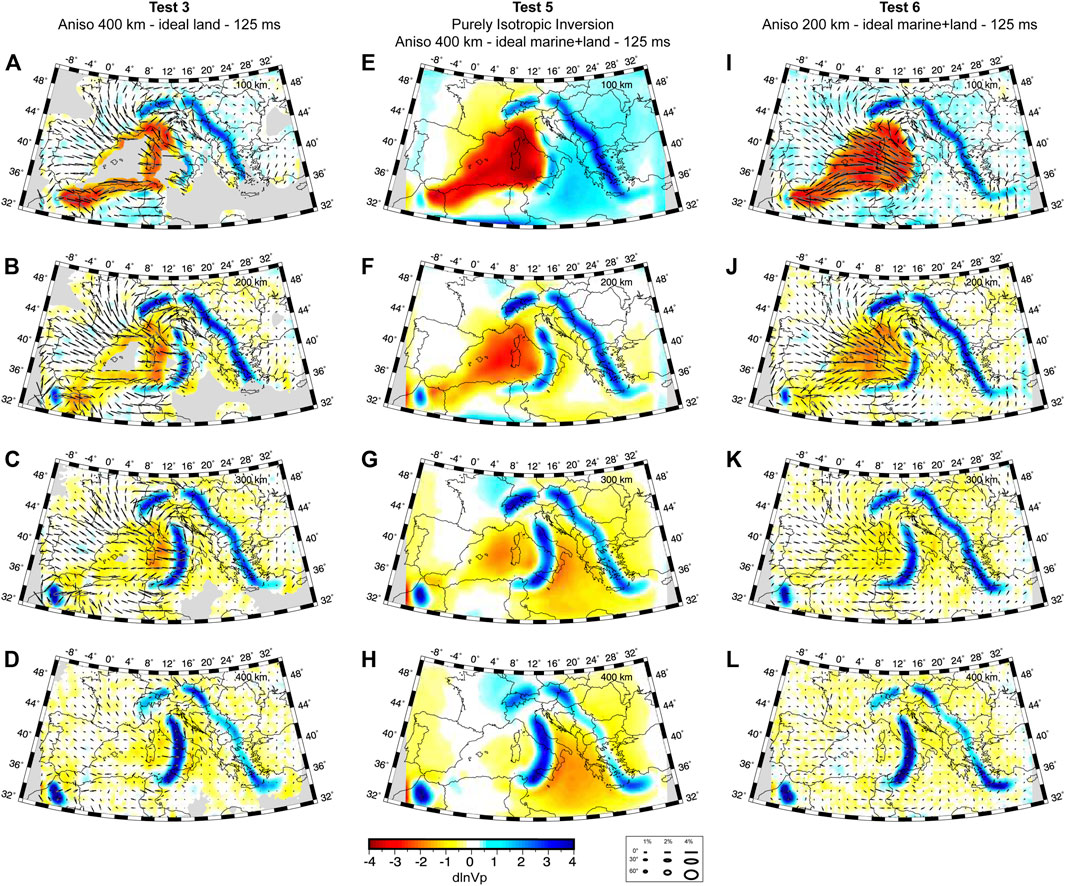
FIGURE 8. Depth slices at 100 km, 200 km, 300 km and 400 km depth for the tomographic results from Test 3 (A–D), Test 5 (E–H) and Test 6 (I–L). Isotropic anomalies are plotted with respect to the starting model. Anisotropy is plotted using ellipses as described in Figure 6. Areas of poor data coverage are masked in grey.
Following the workflow described in Section 2.3.1, we first inverted a set of time delays computed through Model CWM using the distribution of sources and receivers as in Rappisi et al. (2022) (see Supplementary Figure S2A and Figure 2A; Test 1). We added random errors with a standard deviation of 450 ms to the data (i.e. a value corresponding to the amount of error usually encountered in real case studies). This solution reproduces realistic study conditions to test the ability of our method in recovering the main isotropic and anisotropic structures of the target (Figure 6E–H).
The marine areas of the Tyrrhenian, Adriatic, Ionian Sea and Strait of Sicily are poorly sampled, resulting in a general loss of fast and slow anomaly amplitude. Nevertheless, the main isotropic structures (i.e. the Alpine, Northern Apennines, Calabrian and Dinaric-Hellenic slabs) are well recovered. The Northern Apenninic and Calabrian slabs are imaged as a single weak fast anomaly stretching along the N-S direction, while in the geodynamic model a ∼150 km wide window is present at shallow depth, i. e ∼100–200 km beneath central Italy (Figure 5D, Supplementary Figure S4A and Figure 6A,B).
Test 1 exhibits a ∼-2% low velocity artefact in correspondence of the northern Tyrrhenian basin and Corsica-Sardinia block at ∼200 km depth (Figure 6F), indicating some vertical smearing of the true low velocity structure confined in the upper 100 km of the domain. Anisotropy patterns are well recovered where seismic ray coverage is relatively abundant, e.g., the near-horizontal circular pattern of P-wave fast azimuths around the Western Alps in Southern France. Trench perpendicular steeply dipping fabrics are imaged above the Calabrian slab in the Tyrrhenian Sea, while E-W oriented fabrics are found in the Northern African margin.
The recovered isotropic and anisotropic structures from the model resulting from Test 2 (Figure 6I-L) indicate that a better quality dataset increases the probability of better retrieving the magnitude and sharpness of the true anomalies. However, at the same time new and increased in magnitude tomography artefacts are observed. For example, the low velocity artefact at 200 km depth (Figure 6J) in the Tyrrhenian sea, east of the Sardinia-Corsica block, is in Test 2 much stronger than it was in Test 1 (Figure 6F) with an increase in magnitude of ∼1%. And also, a new ∼100 km wide low velocity artefact (∼-2%) appears at 300 km depth south of Sicily (Figure 6K). High velocity artefacts already observed in Test 1, such as the one in Spain and west of the Alps, are in Test 2 much bigger (i.e. joined in a single broader anomaly) and slightly stronger in amplitude, covering the entire southern portion of France at 100 and 200 km depth (Figures 6I,J). Although the anisotropy patterns do not differ from the ones of Test 1, a reduction in their magnitude is observed above the Calabrian slab (i.e. in the Tyrrhenian Sea dipping fabrics). Probably due to the trade-off between isotropic and anisotropic components, it is worth noting that this reduction is associated with an increase in the magnitude of the isotropic fast anomaly.
In Test 4, with an ideal distribution of sources (Supplementary Figure S2B) and marine and land receivers (Figure 2C), the fast anomalies are better retrieved in terms of amplitude and spatial distribution (i.e. size and geographic position). However, many artefacts still persist, for example, at 100 km depth (Figure 6M) the Calabrian fast anomaly exhibits a weak magnitude (i.e., ∼1% vs ∼3% in the true model). More importantly, at 200 km depth (Figure 6M) the slow velocity artefact located est of the Sardinia-Corsica block in the previous tests now affects the entire Liguro-Provencal and Tyrrhenian basins. Although the weak magnitude of the Calabrian fast anomaly, the gap between Northern Apennines and Calabrian slab is better retrieved at 100 and 200 km depth (Figure 6M,N) with respect to the previous Test 1 and Test 2. The Alboran fast anomaly is recovered as well and placed in the correct geographic position (Figure 6P). The high velocity artefact imaged in Test 2 beneath the southern France at shallow depth (100–200 km; Figure 6I,J), now disappears and the recovered model better resembles the target. The ideal station coverage also helps in retrieving anisotropic patterns and magnitude at every depth slice, including the well sampled marine areas where the NW-SE fabrics are now recovered in the Tyrrhenian Sea. Similar results, i.e. about sensitivity of teleseismic P-wave tomography under different conditions, have been previously described (e.g., Spakman and Nolet (1988); Lévěque et al. (1993); Rawlinson and Spakman (2016)).
Considering that placing marine receivers is a costly procedure, we also performed a set of inversions with an ideal distribution of on-land receivers only (Figure 2B). The result is shown in Figure 8A–D. The main effect of having reduced the number of receivers is the underestimation of anisotropy in poorly sampled areas. For example, the trench-parallel patterns bordering the eastern side of the Apenninic fast anomaly in Test 3 (Figure 8A–D) appears weaker than it is in the true model and in Test 4 (Figure 6A–D, M–P).
Figure 8 also shows the results of Test 5 and 6 performed, respectively, in isotropic approximation (Figure 8E–H; i.e. ignoring seismic anisotropy) or with a model that is anisotropic only in the top 200 km (Figure 8I-L). In both cases, we observe that the isotropic solution contains a number of fast anomaly features broadly consistent with the true model (Figure 6A–D). However, several slow velocity artefacts are imaged around and above the main slabs (i.e. Alpine and Calabrian slabs) especially when not considering seismic anisotropy (Figure 8E–H). Figure 8I–L indicate that seismic anisotropy is retrieved also at depths below 200 km where the true model is instead isotropic. This suggests that when only using teleseismic P-waves anisotropic structures are vertically smeared similarly to isotropic anomalies.
In this work we have extended the modeling methodology of Lo Bue et al. (2021) to build a structurally complex geodynamic model which was then exploited to test the capabilities of anisotropic P-wave seismic tomography to recover a Mediterranean-like subduction environment. With respect to Model CM of Lo Bue et al. (2021), the new geodynamic model CWM has been updated by using a different paleo-tectonic configuration characterized by the presence of additional subducting plates (i.e., Alboran, Alpine and Dinaric subduction zones).
Similarly to previous studies (Luth et al., 2013; Jagoutz et al., 2015; Holt et al., 2017, 2018; Király et al., 2018; Peral et al., 2020), here we notice that the presence of multiple subducting slabs influences the overall force balance, the geometry and kinematics of the subduction systems, as well as the mantle flow patterns. The inclusion of additional subduction zones has partly improved the prediction of the mantle dynamics leading to a better correspondence between the modeled and observed surface and deep isotropic structures, and seismic anisotropy patterns when compared to Model CM of Lo Bue et al. (2021). A quantitative comparison between predicted and observed SKS splitting measurements (Figure 7; Becker et al. (2012); (updated 6 December 2020) database updated 6 December 2020) shows a moderate improvement in terms of the average misfit angle from
Uncertainties in the initial model geometry and in the modeled mantle rheology are likely responsible for the major discrepancies. Other sources of mismatch could be related to the modeling of the mantle textures, and to the presence of fossil fabrics within the oceanic and continental subducted lithosphere that have not been included here. Furthermore, the employed free slip boundary conditions prevent lateral mantle flow across the bottom and vertical boundaries. The large discrepancy in the area of the southern Iberian Peninsula may be partly due to the fact that the model does not account for the Cenozoic Eurasia-Africa convergence, and the relative position of the African plate has remained fixed since ∼30 Ma differing slightly from the present-day one. As such, the Alboran arc is positioned further south than its present-day position (under Morocco).
Although Model CWM is based on paleogeographic and tectonic reconstructions of the region in the Oligocene-Miocene (Lucente and Speranza, 2001; Lucente et al., 2006; Faccenna et al., 2014; van Hinsbergen et al., 2014; Romagny et al., 2020), geometrical assumptions, that could potentially bias the final output, were required due to limitations imposed by numerical modeling. First, the initial geometry and thermal ages of the subducting slabs were partly simplified and this could strongly influence the comparison with seismological data. This could be the case of the Alps and Dinarides where a simplified initial portion of the subducted lithosphere was imposed to model flow barriers. We note that the detachment of Alpine slabs prior to collision is still debated in some areas, such as the Western Alps where Kästle et al. (2020) favor the interpretation of a recent European slab break-off, consistent with observations of strong exhumation and sedimentation that started around 2–7 Ma ago and is still ongoing (Escher and Beaumont, 1997; Kuhlemann, 2007; Fox et al., 2016; Nocquet et al., 2016). On the contrary, Zhao et al. (2016) document the lateral continuity of the European slab from the Western Alps to the Central Alps, and the downdip slab continuity beneath the Central Alps, ruling out the hypothesis of slab break-off to explain Cenozoic Alpine magmatism. The teleseismic P-wave tomography of Rappisi et al. (2022), referred as model ani-NEWTON21, exhibits a continuous slab beneath the Alps, divided into an Eastern, Central, and Western segment characterised by changes in dip. Similarly, the extent of the Dinaric slab at ∼30 Ma is largely debated. Post-collisional uplift and contemporaneous emplacement of igneous rocks (33–22 Ma) in the internal Dinarides may suggest either 1) “that the Oligocene-Miocene orogen-wide uplift was driven by post-break-off delamination of the Adriatic lithospheric mantle” Balling et al. (2021), or 2) verticalization of the Adria slab driven by slab pull and consequent upper plate extension, which is exactly what is modeled in our Model CWM. In conclusion, the available geophysical and geological data do not allow to discriminate between a model of post-collisional slab break-off and one of post-collisional slab verticalization (as modelled for the Alps and Dinarides in our Model CWM), as both would imply upper plate extension, uplift and magma emplacement (Faccenda et al., 2008, 2009).
Secondly, the tectonic reconstruction of Romagny et al. (2020) shows that ∼30 Ma the Mesozoic Tethyan lithosphere was consumed in two different trenches located from the Alps to the southeast of the Baleares and in the Alboran domain, respectively. Two incipient slabs (∼150–200 km) were already subducted in the upper mantle. However, to trigger a “spontaneous” subduction system, the Ionian trench has been initially positioned further south with the slab extending to a depth of 300 km, while the Alboran one further west with a 350 km deep slab, in order to model a more developed subduction and increase the slab negative buoyancy. This could cause a difference in rates of Ionian and Alboran slabs retreat at the model early stage when compared to those reported in the literature. However, we note that in the reconstructions by Faccenna et al. (2014) and Romagny et al. (2020) the initial plate geometry at ∼23 Ma does not differ substantially from that at ∼35 Ma, and from our initial setup. This is likely related to the slow dynamics typical of incipient subduction systems.
Despite the modeling limitations, Model CWM reproduces several episodes of slab lateral tearing and break-off that have been proposed according to geological and seismological data. The model is partly able to recover the main features found in the seismic tomography models. After ∼20 Myr (Figure 5D–F and Supplementary Figure S4) subducted lithospheric portions are found below the areas corresponding to the Alboran, Kabylides and Calabria-Apennine region where seismic tomographic methods have revealed several positive velocities anomalies (Spakman, 1991; Spakman et al., 1993; Wortel and Spakman, 2000; Gutscher et al., 2002; Piromallo and Morelli, 2003; Spakman and Wortel, 2004; Wortel et al., 2009; Bezada et al., 2013; Van der Meer et al., 2018). For example, Model CWM retrieves 1) the high-velocity body arranged horizontally over the 660 km discontinuity interpreted as the Ionian slab lying and broadening at the base of the upper mantle by P-wave tomographic models (Amato et al., 1993; Spakman et al., 1993; Selvaggi and Chiarabba, 1995; Lucente et al., 1999; Piromallo and Morelli, 2003; Spakman and Wortel, 2004; Van der Meer et al., 2018); 2) the portion of the slab under the Northern Apennines extending down to 150 km depth and from ∼180 km down to about 660 km depth (Supplementary Figure S4B) (Spakman and Wortel, 2004; Giacomuzzi et al., 2012; El-Sharkawy et al., 2020) and 3) the Calabrian slab continuous from the surface down to a depth of 660 km (Giacomuzzi et al., 2012; Neri et al., 2012; Scarfì et al., 2018; Presti et al., 2019; El-Sharkawy et al., 2020; Rappisi et al., 2022); 4) the portion of slab imaged under the north African margin of Algeria, hanging down to ∼150 km depth and from ∼200 km joining to the Calabrian slab (Supplementary Figure S4B) (Chertova et al., 2014; Van der Meer et al., 2018); 5) the presence of two wide windows in the Ionian slabs, one below the area corresponding to the present-day Central Apennines and one beneath the north-eastern African margin (Amato et al., 1993; Piromallo and Morelli, 1997; Carminati et al., 1998; Lucente and Speranza, 2001; Piromallo and Morelli, 2003; Spakman and Wortel, 2004; Faccenna et al., 2007, 2014; Magni et al., 2014; Van der Meer et al., 2018).
On the contrary, the modeled Alboran slab, in addition to being in a wrong position (i.e. further south than its current position), possesses a morphology which is not entirely realistic. This is probably due to the imposed initially 350 km long slab and to the slab tearing occurring as soon as the trench interacts with the continental margins, thus preventing any arcuate shape of the margin. However, we note that the geometry and length of the Alboran slab in model CWM at 0 (initial conditions; Figure 1) and ∼20 Ma (Figure 5D) are similar to those obtained by (Chertova et al., 2014) at −20 and 0 Ma (see Figures 8, 10 of Chertova et al. (2014)). The flat portion of our Alboran slab at ∼20 Ma (Figure 5) is consistent with the Spakman and Wortel (2004) model (as presented in Figure 3 of Chertova et al. (2014)).
We performed seismological forward and inverse simulations by testing different types of data coverage and quality. To help the comparison between the different tests and evaluating their capabilities in recovering model CWM, Figure 9 shows the difference between the true model and the solution of Test 1, Test 2, Test three and Test 4, both in terms of isotropic and anisotropic structures (i.e. dlnVp = dlnVp true model - dlnVp tomography model). We observe that the average difference in retrieved isotropic velocity is in general low (∼[−1%,+1%]) and gradually decreases moving from Test 1 to Test 4. For example, Figure 9A–D shows maximum values of dlnVp of ∼3% for Test 1, i.e. in the Apenninic slab at 400 km depth (Figure 9D), that gradually decrease to ∼1% for Test 4. For Test 4 (i.e. test with perfect data coverage), higher values are observed in the western side of the model, with peaks of
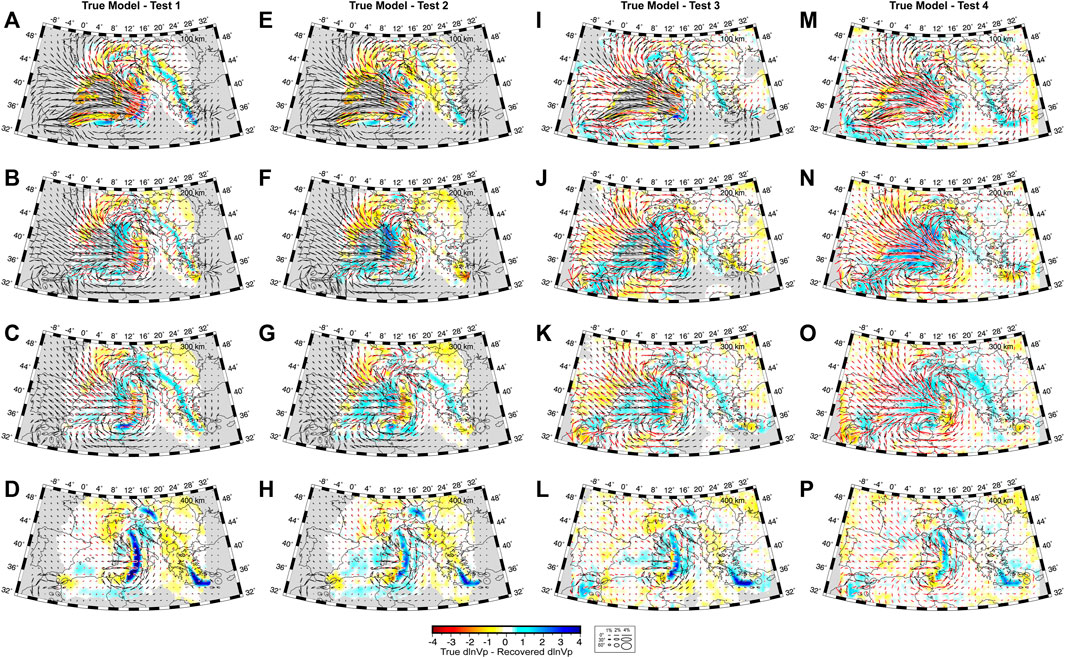
FIGURE 9. Depth slices at 100 km, 200 km, 300 km and 400 km showing the differences between the true model and (A–D) Test 1, (E–H) Test 2 (I–L) Test three and (M–P) Test 4. Anisotropy is plotted using ellipses as described in Figure 6. Areas of poor data coverage are masked in grey.
From our results it emerged that even with a non-ideal source-station coverage the recovery of isotropic structures and anisotropic patterns is quite good, although anisotropy magnitude is overall underestimated (especially in poorly sampled areas). This suggests that the amount of mantle anisotropy could be higher than that retrieved by tomographic models with commonly uneven source-receiver distributions. The consequences of the inhomogeneous distribution of seismicity and stations on ray coverage and on retrieved tomographic images is known in isotropic tomographic models (e.g., Bozdağ et al. (2016); Boschi and Dziewonski (1999); Masters et al. (1996); Antolik et al. (2003); Dalton and Ekström (2006); Ruan et al. (2019)). Here we show that similar problems are also found in anisotropic seismic tomographic models (e.g., causing underestimation of anisotropy magnitude). In addition, it emerged that tomographic images calculated from data with a scarce seismic coverage are potentially affected by the presence of anomalies placed in a wrong geographic position. This is the case of the Alboran slab that in Figure 6E–L appears shifted toward the east. This kind of artefacts could bring errors in the tomographic model interpretation when fast anomalies are present close to the boundaries of the sampled area. Increasing data quality (i.e., decreasing data error; Test 2) helps in better retrieving the magnitude of the isotropic and anisotropic structures, but at the same time leads to an increase in the magnitude and size of the artefacts in poorly sampled areas (Figure 6E–L). In addition, Figure 6M–P shows that ideal data coverage allows for a more accurate retrieval of anomaly magnitudes without increasing artefact amplitudes. However, we note that the higher number of receivers (e.g., in the Tyrrhenian and Liguro-Provencal basins) at 200 km depth amplifies the smearing of the upper low-velocity layer with respect to Test three where, on the contrary, the limited number of stations (i.e. limited rays) reduces this effect.
In the inversions where seismic anisotropy is ignored (Test 5), we observe that several slow anomalies appear in the tomographic sections (Figure 8E-H). This is especially evident in the area north of the Alps (Figure 8A) and below the Calabrian slab (i.e. in the Ionian Sea, Figure 8B–D). Considering that these anomalies are not present in the true model and indeed completely disappear in the anisotropic inversions (Figure 6), it follows that they are seismic artefacts due to the isotropic approximation.
Lastly, the test carried out on the model isotropic only from 200 km depth down (Test 6), showed that both the isotropic and anisotropic features are subjected to vertical smearing (8g,h). This should be taken into account when interpreting teleseismic P-wave anisotropic tomography.
In order to further characterize model differences between true and tomographic models, we have computed the average misfit values for fraction of anisotropy (df), azimuth and dip angles (i.e. dψ and dγ) with increasing depth (Figure 10A–C) with respect to the true values. We observe that the average solution gradually improves, better resembling the true model, with decreasing data error and improving data coverage. The higher values of misfit are in fact observed for the model obtained from the inversion performed with the bigger data error (i.e. 450 ms, Test 1) and the worst receiver distribution. This is true for both df and dψ, while for dγ is valid below ∼70 km depth (Figure 10C). For all models the average azimuthal misfit is highest in the upper 50 km (due to the poor ray coverage at these depths by teleseismic P-waves), below which it rapidly decreases and remains roughly constant with depth except for a slight increase toward the bottom of the anisotropic domain. In contrast, the dip angle average misfit gradually increases with depth. The misfit curves for Test 4 and Test 6 show similar shapes but with shifted absolute values in the upper 150 km. This indicates that the presence of deeper anisotropy (Test 4) associated with poor vertical resolution deteriorates the quality of the retrieved shallower structures.
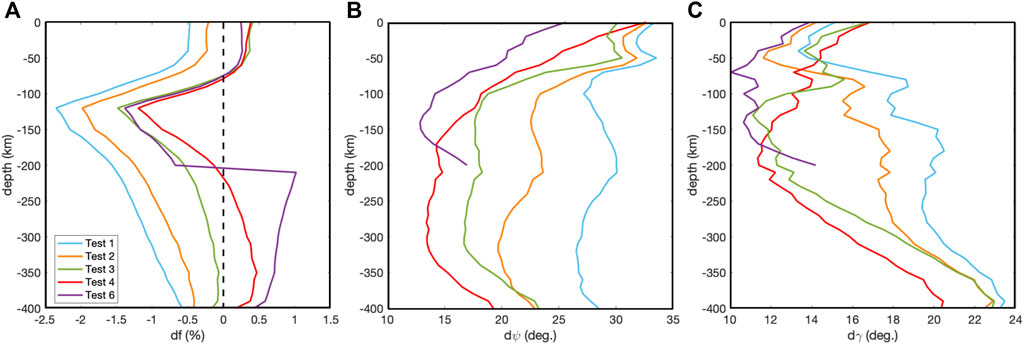
FIGURE 10. Errors in recovered anisotropic parameters. Mean errors in the anisotropic (A) fraction, (B) azimuth, and (C) elevation as a function of depth are shown for Test 1 (blue line), Test 2 (orange line), Test 3 (green line), Test 4 (red line) and Test 6 (purple line).
We applied the modeling methodology of Lo Bue et al. (2021) to simulate the geodynamic evolution over ∼20–30 Myr of a model that presents similar characteristics to those currently observed in the Central-Western Mediterranean region (e.g., detached or stagnating slabs, slab windows, etc). To quantify similarities and discrepancies between the obtained geodynamic model and the current tectonic setting, the model results were verified by comparing seismological synthetics (isotropic P-wave anomalies, P-wave anisotropy and SKS splitting) and major tectonic features (i.e., slab and trench geometry) with observations. This comparison confirms that, with respect to the previous study of Lo Bue et al. (2021), using a more complex initial geometry (i.e. including the Alboran, Alpine and Dinaric-Hellenic slabs) allows us to perform a step forward toward the better recovering of the mantle flow, overall evolution and current tectonic beneath this region. However, we note that model CWM is still far from reproducing the exact evolution and present-day tectonic setting of the area and further studies need to be performed in this direction. For example, next-level numerical studies should attempt to improve the model geometry by considering the Earth’s sphericity and the Africa-Eurasia plates convergence.
Despite the several limitation of the numerical methods (e.g., Cartesian coordinates system, no plates convergence, no fossil LPO, fabrics within the lithosphere, free slip boundaries, no mantle in/outflow, etc.) and the assumptions necessary to start and drive the simulation self-consistently (e.g., initial slab depths, mantle rheology parameters, etc.), we observe that at ∼20 Myr model CWM exhibits interesting geological features resembling those found in the Central-Western Mediterranean (e.g., Calabrian slab continuous from the surface down to the base of the upper mantle, the presence of two wide windows in the Ionian slab, etc). For this reason, we used the modeled elastic properties at this stage (i.e. the elastic tensors at ∼20 Myr), to perform 3D P-wave anisotropic tomography using the approach proposed by VanderBeek and Faccenda (2021). Using the geodynamic model as reference model, we evaluated the capabilities of seismic tomography to recover a complex subduction environment in different conditions, such as poor station coverage and bad data quality. From the seismological inversions and the comparison between purely isotropic and anisotropic solutions it emerges that 1) it is fundamental to invert for anisotropy to improve the reliability of the tomographic result and 2) even a non-ideal source-station coverage allows to recover isotropic structures and anisotropic patterns from teleseismic P-wave tomography. Anisotropy magnitude, although consistent with those of the synthetic target model, is overall underestimated in the upper mantle especially in poorly sampled areas. In light of this, it is recommended to increase the number of marine and land stations and improve the accuracy of teleseismic arrival time measurements. However, it should be noted that perfect coverage of receivers does not guarantee an ideal tomographic solution. For example, Test 4, despite being performed with receivers distributed over the entire study area, presents various imaging artefacts. Future steps aiming at recreating a “perfect coverage” should be characterized by a good ray sampling, thus to include seismic rays that cover different directions in order to guarantee an excellent resolution (e.g., not only teleseismic events). Furthermore, although the synthetic inversions confirm that the developed methodology for P-wave anisotropic tomography is capable of retrieving with a good approximation the modeled upper mantle structures, the employed geodynamic simulations do not account for compositional variations, presence of fluids/melt and lithospheric fossil fabrics that can affect the seismic properties of natural tectonic settings. The presence of these further complexities remains to be tested, and it will be considered in future studies.
The synthetic tomography results demonstrated that using a combination of geodynamic and seismological numerical modeling techniques could represent a powerful tool to investigate mantle dynamics. Although the modeling limitations, we obtained a 3D complex mantle structure that partly resemble some main characteristics of the actual present-day mantle in the Central-Western Mediterranean. This opens new perspectives towards the future possibility of creating models of the geodynamic evolution that can be constrained by the structure and mantle anisotropy obtained from P-travel time anisotropic tomography. To better constrain the initial tectonic configuration, an interesting future development would be to formulate a fluid dynamic inverse problem to reproduce unknown mantle flow back in time from seismic tomographic observations of the mantle and reconstructions of past plate motions using variational data assimilation (Bunge et al., 2003). Adjoint modeling is in fact a great opportunity to produce realistic mantle retrodictions models. However, the development of testing of this methodology is still far from being applicable to complex 3D tectonic settings such as the Mediterranean. This technique has been successfully applied to reproduce the recent dynamics in the South America and North America subduction zones (Hu et al., 2017; Zhou et al., 2018), However, we believe that exhumation back in time of the slabs stagnating in the mantle transition zone is non-trivial when the plate convergence rate is quite small (basically, by inverting gravity there is not easy way to exhume back at the surface these slabs), which is one of the reason why we choose to model forward in time the Central-Western Mediterranean dynamics. Reuber and Simons (2020), although showing the potentials (and limitations) of this technique on quite simple 2D and static (not dynamic) model configurations, concluded that the method “needs to be thoroughly tried and tested on real-world examples”. Adding mantle fabrics to improve the mantle flow retrodictions is an ongoing research activity in our group, that we hope to include in our models in the near future.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
All authors conceived the study. RLB performed the geodynamic and seismological (i.e. strain-induced fabric estimation and SKS splitting calculations) numerical modelling. FR performed the seismological forward and P-wave tomography. BPV and MF supervised the findings of this work. All the authors contributed equally to the discussion of the results and to the conclusions of this study.
This study is supported by the ERC StG 758199 NEWTON.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
T. Gerya provided the I3MG code used for the subduction modeling. The modified version of the D-Rex code used for the fabric modeling, and the routines used to calculate SKS splitting parameters, P-wave and Rayleigh wave anisotropy can be found inside the ECOMAN software package (https://newtonproject.geoscienze.unipd.it/ecoman/). The MATLAB toolbox geomIO used to define the geometry of the model initial setup can be found at https://geomio.bitbucket.io/. Paraview was used for graphic visualization of the model output (https://www.paraview.org/). Tomographic maps were created using Generic Mapping Tools (Wessel et al., 2019) with colormaps developed by Crameri (2018a,b). The manuscript was significantly improved thanks to the constructive feedback and comments from the editor, Wim Spakman and Claudia Piromallo.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.884100/full#supplementary-material
Amato, A., Alessandrini, B., Cimini, G., Frepoli, A., and Selvaggi, G. (1993). Active and Remnant Subducted Slabs beneath italy: Evidence from Seismic Tomography and Seismicity. Ann. Geophys. 36. doi:10.4401/ag-4272
Antolik, M., Gu, Y. J., Ekström, G., and Dziewonski, A. M. (2003). J362D28: a New Joint Model of Compressional and Shear Velocity in the Earth's Mantle. Geophys. J. Int. 153, 443–466. doi:10.1046/j.1365-246x.2003.01910.x
Arab, M., Maherssi, C. E., Granjeon, D., Roure, F., Déverchère, J., Cuilhé, L., et al. (2020). On the Origin and Consequences of Crustal-Scale Extension between Africa and Sicily since Late Miocene: Insights from the Kaboudia Area, Western Pelagian Sea. Tectonophysics 795, 228565. doi:10.1016/j.tecto.2020.228565
Aster, R. C., Borchers, B., and Thurber, C. H. (2018). Parameter Estimation and Inverse Problems. Elsevier.
Balling, P., Grützner, C., Tomljenović, B., Spakman, W., and Ustaszewski, K. (2021). Post-collisional Mantle Delamination in the Dinarides Implied from Staircases of Oligo-Miocene Uplifted Marine Terraces. Sci. Rep. 11, 1–11. doi:10.1038/s41598-021-81561-5
Bauville, A., and Baumann, T. S. (2019). geomIO: An Open‐Source MATLAB Toolbox to Create the Initial Configuration of 2‐D/3‐D Thermo‐Mechanical Simulations from 2‐D Vector Drawings. Geochem. Geophys. Geosyst. 20, 1665–1675. doi:10.1029/2018gc008057
Becker, T. W., Lebedev, S., and Long, M. (2012). Updated December 6, 2020On the Relationship between Azimuthal Anisotropy from Shear Wave Splitting and Surface Wave Tomography. J. Geophys. Res. Solid Earth 117. doi:10.1029/2011jb008705
Becker, T. W. (2006). On the Effect of Temperature and Strain-Rate Dependent Viscosity on Global Mantle Flow, Net Rotation, and Plate-Driving Forces. Geophys. J. Int. 167, 943–957. doi:10.1111/j.1365-246x.2006.03172.x
Bezada, M. J., Faccenda, M., and Toomey, D. R. (2016). Representing Anisotropic Subduction Zones with Isotropic Velocity Models: A Characterization of the Problem and Some Steps on a Possible Path Forward. Geochem. Geophys. Geosyst. 17, 3164–3189. doi:10.1002/2016gc006507
Bezada, M. J., Humphreys, E. D., Toomey, D. R., Harnafi, M., Dávila, J. M., and Gallart, J. (2013). Evidence for Slab Rollback in Westernmost Mediterranean from Improved Upper Mantle Imaging. Earth Planet. Sci. Lett. 368, 51–60. doi:10.1016/j.epsl.2013.02.024
Bijwaard, H., Spakman, W., and Engdahl, E. R. (1998). Closing the Gap between Regional and Global Travel Time Tomography. J. Geophys. Res. 103, 30055–30078. doi:10.1029/98jb02467
Blackman, D. K., Kendall, J.-M., Dawson, P. R., Wenk, H.-R., Boyce, D., and Morgan, J. P. (1996). Teleseismic Imaging of Subaxial Flow at Mid-ocean Ridges: Traveltime Effects of Anisotropic Mineral Texture in the Mantle. Geophys. J. Int. 127, 415–426. doi:10.1111/j.1365-246x.1996.tb04730.x
Blackman, D. K., and Kendall, J.-M. (1997). Sensitivity of Teleseismic Body Waves to Mineral Texture and Melt in the Mantle beneath a Mid-ocean Ridge. Philosophical Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 355, 217–231. doi:10.1098/rsta.1997.0007
Blackman, D. K., Wenk, H.-R., and Kendall, J. M. (2002). Seismic Anisotropy of the Upper Mantle 1. Factors that Affect Mineral Texture and Effective Elastic Properties. Geochem.-Geophys.-Geosyst. 3, 1–24. doi:10.1029/2001gc000248
Boschi, L., and Dziewonski, A. M. (1999). High- and Low-Resolution Images of the Earth's Mantle: Implications of Different Approaches to Tomographic Modeling. J. Geophys. Res. 104, 25567–25594. doi:10.1029/1999jb900166
Bozdağ, E., Peter, D., Lefebvre, M., Komatitsch, D., Tromp, J., Hill, J., et al. (2016). Global Adjoint Tomography: First-Generation Model. Geophys. J. Int. 207, 1739–1766.
Bunge, H.-P., Hagelberg, C. R., and Travis, B. J. (2003). Mantle Circulation Models with Variational Data Assimilation: Inferring Past Mantle Flow and Structure from Plate Motion Histories and Seismic Tomography. Geophys. J. Int. 152, 280–301. doi:10.1046/j.1365-246x.2003.01823.x
Calcagnile, G., and Panza, G. (1980). The Main Characteristics of the Lithosphere-Asthenosphere System in italy and Surrounding Regions. Pure Appl. Geophys. 119, 865–879.
Carminati, E., Lustrino, M., and Doglioni, C. (2012). Geodynamic Evolution of the Central and Western Mediterranean: Tectonics vs. Igneous Petrology Constraints. Tectonophysics 579, 173–192. doi:10.1016/j.tecto.2012.01.026
Carminati, E., Wortel, M. J. R., Spakman, W., and Sabadini, R. (1998). The Role of Slab Detachment Processes in the Opening of the Western-Central Mediterranean Basins: Some Geological and Geophysical Evidence. Earth Planet. Sci. Lett. 160, 651–665. doi:10.1016/s0012-821x(98)00118-6
Chertova, M. V., Spakman, W., Geenen, T., Van Den Berg, A. P., and Van Hinsbergen, D. J. J. (2014). Underpinning Tectonic Reconstructions of the Western Mediterranean Region with Dynamic Slab Evolution from 3-d Numerical Modeling. J. Geophys. Res. Solid Earth 119, 5876–5902. doi:10.1002/2014jb011150
Confal, J. M., Faccenda, M., Eken, T., and Taymaz, T. (2018). Numerical Simulation of 3-d Mantle Flow Evolution in Subduction Zone Environments in Relation to Seismic Anisotropy beneath the Eastern Mediterranean Region. Earth Planet. Sci. Lett. 497, 50–61. doi:10.1016/j.epsl.2018.06.005
Connolly, J. A. D. (2005). Computation of Phase Equilibria by Linear Programming: a Tool for Geodynamic Modeling and its Application to Subduction Zone Decarbonation. Earth Planet. Sci. Lett. 236, 524–541. doi:10.1016/j.epsl.2005.04.033
Crameri, F. (2018a). Geodynamic Diagnostics, Scientific Visualisation and Staglab 3.0. Geosci. Model Dev. 11, 2541–2562. doi:10.5194/gmd-11-2541-2018
Crotwell, H. P., Owens, T. J., and Ritsema, J. (1999). The Taup Toolkit: Flexible Seismic Travel-Time and Ray-Path Utilities. Seismol. Res. Lett. 70, 154–160. doi:10.1785/gssrl.70.2.154
Dalton, C. A., and Ekström, G. (2006). Global Models of Surface Wave Attenuation. J. Geophys. Res. Solid Earth 111. doi:10.1029/2005jb003997
El-Sharkawy, A., Meier, T., Lebedev, S., Behrmann, J. H., Hamada, M., Cristiano, L., et al. (2020). The Slab Puzzle of the Alpine-Mediterranean Region: Insights from a New, High-Resolution, Shear Wave Velocity Model of the Upper Mantle. Geochem. Geophys. Geosystems 21, e2020GC008993.
Escher, A., and Beaumont, C. (1997). Formation, Burial and Exhumation of Basement Nappes at Crustal Scale: a Geometric Model Based on the Western Swiss-Italian Alps. J. Struct. Geol. 19, 955–974. doi:10.1016/s0191-8141(97)00022-9
Faccenda, M., and Capitanio, F. A. (2012). Development of Mantle Seismic Anisotropy during Subduction-Induced 3-d Flow. Geophys. Res. Lett. 39. doi:10.1029/2012gl051988
Faccenda, M., and Capitanio, F. A. (2013). Seismic Anisotropy Around Subduction Zones: Insights from Three-Dimensional Modeling of Upper Mantle Deformation and Sks Splitting Calculations. Geochem. Geophys. Geosyst. 14, 243–262. doi:10.1002/ggge.20055
Faccenda, M., Gerya, T. V., and Chakraborty, S. (2008). Styles of Post-subduction Collisional Orogeny: Influence of Convergence Velocity, Crustal Rheology and Radiogenic Heat Production. Lithos 103, 257–287. doi:10.1016/j.lithos.2007.09.009
Faccenda, M. (2014). Mid Mantle Seismic Anisotropy Around Subduction Zones. Phys. Earth Planet. Interiors 227, 1–19. doi:10.1016/j.pepi.2013.11.015
Faccenda, M., Minelli, G., and Gerya, T. V. (2009). Coupled and Decoupled Regimes of Continental Collision: Numerical Modeling. Earth Planet. Sci. Lett. 278, 337–349. doi:10.1016/j.epsl.2008.12.021
Faccenna, C., Becker, T. W., Auer, L., Billi, A., Boschi, L., Brun, J. P., et al. (2014). Mantle Dynamics in the Mediterranean. Rev. Geophys. 52, 283–332. doi:10.1002/2013rg000444
Faccenna, C., Funiciello, F., Civetta, L., D Antonio, M., Moroni, M., and Piromallo, C. (2007). Slab Disruption, Mantle Circulation, and the Opening of the Tyrrhenian Basins. Special Papers-Geological Soc. Am. 418, 153. doi:10.1130/2007.2418(08)
Faccenna, C., Piromallo, C., Crespo-Blanc, A., Jolivet, L., and Rossetti, F. (2004). Lateral Slab Deformation and the Origin of the Western Mediterranean Arcs. Tectonics 23. doi:10.1029/2002tc001488
Fox, M., Herman, F., Willett, S. D., and Schmid, S. M. (2016). The Exhumation History of the European Alps Inferred from Linear Inversion of Thermochronometric Data. Am. J. Sci. 316, 505–541. doi:10.2475/06.2016.01
Geiss, E. (1987). A New Compilation of Crustal Thickness Data for the Mediterranean Area. Ann. Geophys. Ser. B. Terr. Planet. Phys. 5, 623–630.
Gerya, T. (2019). Introduction to Numerical Geodynamic Modelling. 2nd Edn. Cambridge: Cambridge University Press. doi:10.1017/9781316534243
Giacomuzzi, G., Civalleri, M., De Gori, P., and Chiarabba, C. (2012). A 3d vs Model of the Upper Mantle beneath italy: Insight on the Geodynamics of Central Mediterranean. Earth Planet. Sci. Lett. 335-336, 105–120. doi:10.1016/j.epsl.2012.05.004
Gutscher, M.-A., Malod, J., Rehault, J.-P., Contrucci, I., Klingelhoefer, F., Mendes-Victor, L., et al. (2002). Evidence for Active Subduction beneath gibraltar. Geol 30, 1071–1074. doi:10.1130/0091-7613(2002)030<1071:efasbg>2.0.co;2
Holt, A. F., Royden, L. H., Becker, T. W., and Faccenna, C. (2018). Slab Interactions in 3-d Subduction Settings: The Philippine Sea Plate Region. Earth Planet. Sci. Lett. 489, 72–83. doi:10.1016/j.epsl.2018.02.024
Holt, A., Royden, L., and Becker, T. (2017). The Dynamics of Double Slab Subduction. Geophys. J. Int. 209, 250–265. doi:10.1093/gji/ggw496
Hu, J., Faccenda, M., and Liu, L. (2017). Subduction-controlled Mantle Flow and Seismic Anisotropy in South america. Earth Planet. Sci. Lett. 470, 13–24. doi:10.1016/j.epsl.2017.04.027
Jagoutz, O., Royden, L., Holt, A. F., and Becker, T. W. (2015). Anomalously Fast Convergence of india and Eurasia Caused by Double Subduction. Nat. Geosci. 8, 475–478. doi:10.1038/ngeo2418
Jolivet, L., Augier, R., Faccenna, C., Negro, F., Rimmele, G., Agard, P., et al. (2008). Subduction, Convergence and the Mode of Backarc Extension in the Mediterranean Region. Bull. Société Géologique Fr. 179, 525–550. doi:10.2113/gssgfbull.179.6.525
Jolivet, L., Augier, R., Robin, C., Suc, J.-P., and Rouchy, J. M. (2006). Lithospheric-scale Geodynamic Context of the Messinian Salinity Crisis. Sediment. Geol. 188-189, 9–33. doi:10.1016/j.sedgeo.2006.02.004
Jolivet, L., Faccenna, C., and Piromallo, C. (2009). From Mantle to Crust: Stretching the Mediterranean. Earth Planet. Sci. Lett. 285, 198–209. doi:10.1016/j.epsl.2009.06.017
Kaminski, É., Ribe, N. M., and Browaeys, J. T. (2004). D-rex, a Program for Calculation of Seismic Anisotropy Due to Crystal Lattice Preferred Orientation in the Convective Upper Mantle. Geophys. J. Int. 158, 744–752. doi:10.1111/j.1365-246x.2004.02308.x
Karato, S.-i., Jung, H., Katayama, I., and Skemer, P. (2008). Geodynamic Significance of Seismic Anisotropy of the Upper Mantle: New Insights from Laboratory Studies. Annu. Rev. Earth Planet. Sci. 36, 59–95. doi:10.1146/annurev.earth.36.031207.124120
Kästle, E. D., Rosenberg, C., Boschi, L., Bellahsen, N., Meier, T., and El-Sharkawy, A. (2020). Slab Break-Offs in the Alpine Subduction Zone. Int. J. Earth Sci. Geol. Rundsch) 109, 587–603. doi:10.1007/s00531-020-01821-z
Kendall, J.-M. (1994). Teleseismic Arrivals at a Mid-ocean Ridge: Effects of Mantle Melt and Anisotropy. Geophys. Res. Lett. 21, 301–304. doi:10.1029/93gl02791
Kennett, B. L. N., Engdahl, E. R., and Buland, R. (1995). Constraints on Seismic Velocities in the Earth from Traveltimes. Geophys. J. Int. 122, 108–124. doi:10.1111/j.1365-246x.1995.tb03540.x
Király, Á., Faccenna, C., and Funiciello, F. (2018). Subduction Zones Interaction Around the Adria Microplate and the Origin of the Apenninic Arc. Tectonics 37, 3941–3953. doi:10.1029/2018tc005211
Kuhlemann, J. (2007). Paleogeographic and Paleotopographic Evolution of the Swiss and Eastern Alps since the Oligocene. Glob. Planet. Change 58, 224–236. doi:10.1016/j.gloplacha.2007.03.007
Lévěque, J.-J., Rivera, L., and Wittlinger, G. (1993). On the Use of the Checker-Board Test to Assess the Resolution of Tomographic Inversions. Geophys. J. Int. 115, 313–318.
Liu, Q., and Gu, Y. J. (2012). Seismic Imaging: From Classical to Adjoint Tomography. Tectonophysics 566-567, 31–66. doi:10.1016/j.tecto.2012.07.006
Lloyd, S., and Van Der Lee, S. (2008). Influence of Observed Mantle Anisotropy on Isotropic Tomographic Models. Geochem. Geophys. Geosystems 9. doi:10.1029/2008gc001997
Lo Bue, R., Faccenda, M., and Yang, J. (2021). The Role of Adria Plate Lithospheric Structures on the Recent Dynamics of the Central Mediterranean Region. JGR Solid Earth 126, e2021JB022377. doi:10.1029/2021JB022377
Lonergan, L., and White, N. (1997). Origin of the Betic-Rif Mountain Belt. Tectonics 16, 504–522. doi:10.1029/96tc03937
Long, M. D., and Becker, T. W. (2010). Mantle Dynamics and Seismic Anisotropy. Earth Planet. Sci. Lett. 297, 341–354. doi:10.1016/j.epsl.2010.06.036
Lucente, F. P., Chiarabba, C., Cimini, G. B., and Giardini, D. (1999). Tomographic Constraints on the Geodynamic Evolution of the Italian Region. J. Geophys. Res. 104, 20307–20327. doi:10.1029/1999jb900147
Lucente, F. P., Margheriti, L., Piromallo, C., and Barruol, G. (2006). Seismic Anisotropy Reveals the Long Route of the Slab through the Western-Central Mediterranean Mantle. Earth Planet. Sci. Lett. 241, 517–529. doi:10.1016/j.epsl.2005.10.041
Lucente, F. P., and Speranza, F. (2001). Belt Bending Driven by Lateral Bending of Subducting Lithospheric Slab: Geophysical Evidences from the Northern Apennines (italy). Tectonophysics 337, 53–64. doi:10.1016/s0040-1951(00)00286-9
Luth, S., Willingshofer, E., Sokoutis, D., and Cloetingh, S. (2013). Does Subduction Polarity Changes below the Alps? Inferences from Analogue Modelling. Tectonophysics 582, 140–161. doi:10.1016/j.tecto.2012.09.028
Magni, V., Faccenna, C., van Hunen, J., and Funiciello, F. (2014). How Collision Triggers Backarc Extension: Insight into Mediterranean Style of Extension from 3-d Numerical Models. Geology 42, 511–514. doi:10.1130/g35446.1
Maino, M., Decarlis, A., Felletti, F., and Seno, S. (2013). Tectono-sedimentary Evolution of the Tertiary Piedmont Basin (NW Italy) within the Oligo-Miocene Central Mediterranean Geodynamics. Tectonics 32, 593–619. doi:10.1002/tect.20047
Masters, T. G., Johnson, S., Laske, G., and Bolton, H. (1996). A Shear-Velocity Model of the Mantle. Philosophical Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 354, 1385–1411.
Mauffret, A., Frizon de Lamotte, D., Lallemant, S., Gorini, C., and Maillard, A. (2004). E-W Opening of the Algerian Basin (Western Mediterranean). Terra nova. 16, 257–264. doi:10.1111/j.1365-3121.2004.00559.x
Menke, W. (2015). Equivalent Heterogeneity Analysis as a Tool for Understanding the Resolving Power of Anisotropic Travel‐Time Tomography. Bull. Seismol. Soc. Am. 105, 719–733. doi:10.1785/0120140150
Menke, W., and Levin, V. (2003). The Cross-Convolution Method for interpretingSKSsplitting Observations, with Application to One and Two-Layer Anisotropic Earth Models. Geophys. J. Int. 154, 379–392. doi:10.1046/j.1365-246x.2003.01937.x
Miller, M. S., and Piana Agostinetti, N. (2012). Insights into the Evolution of the Italian Lithospheric Structure from S Receiver Function Analysis. Earth Planet. Sci. Lett. 345-348, 49–59. doi:10.1016/j.epsl.2012.06.028
Mishin, Y. A., Gerya, T. V., Burg, J.-P., and Connolly, J. A. D. (2008). Dynamics of Double Subduction: Numerical Modeling. Phys. Earth Planet. Interiors 171, 280–295. doi:10.1016/j.pepi.2008.06.012
Moser, T. J. (1991). Shortest Path Calculation of Seismic Rays. Geophysics 56, 59–67. doi:10.1190/1.1442958
Müller, G. (1971). Approximate Treatment of Elastic Body Waves in Media with Spherical Symmetry. Geophys. J. Int. 23, 435–449. doi:10.1111/j.1365-246x.1971.tb01835.x
Munzarová, H., Plomerová, J., and Kissling, E. (2018). Novel Anisotropic Teleseismic Body-Wave Tomography Code AniTomo to Illuminate Heterogeneous Anisotropic Upper Mantle: Part I - Theory and Inversion Tuning with Realistic Synthetic Data. Geophys. J. Int. 215, 524–545. doi:10.1093/gji/ggy296
Neri, G., Marotta, A. M., Orecchio, B., Presti, D., Totaro, C., Barzaghi, R., et al. (2012). How Lithospheric Subduction Changes along the Calabrian Arc in Southern italy: Geophysical Evidences. Int. J. Earth Sci. Geol. Rundsch) 101, 1949–1969. doi:10.1007/s00531-012-0762-7
Nocquet, J. M., Sue, C., Walpersdorf, A., Tran, T., Lenôtre, N., Vernant, P., et al. (2016). Present-day Uplift of the Western Alps. Sci. Rep. 6, 28404–28406. doi:10.1038/srep28404
Paige, C. C., and Saunders, M. A. (1982). Lsqr: An Algorithm for Sparse Linear Equations and Sparse Least Squares. ACM Trans. Math. Softw. 8, 43–71. doi:10.1145/355984.355989
Panza, G. F., Pontevivo, A., Chimera, G., Raykova, R., and Aoudia, A. (2003). The Lithosphere-Asthenosphere: Italy and Surroundings. Episodes 26, 169–174. doi:10.18814/epiiugs/2003/v26i3/003
Peral, M., Ruh, J., Zlotnik, S., Funiciello, F., Fernàndez, M., Vergés, J., et al. (2020). Analog and Numerical Experiments of Double Subduction Systems with Opposite Polarity in Adjacent Segments. Geochem. Geophys. Geosystems 21, e2020GC009035. doi:10.1029/2020gc009035
Piromallo, C., and Morelli, A. (1997). Imaging the Mediterranean Upper Mantle by P-Wave Travel Time Tomography. Ann. Geophys. 40. doi:10.4401/ag-3890
Piromallo, C., and Morelli, A. (2003). P Wave Tomography of the Mantle under the Alpine-Mediterranean Area. J. Geophys. Res. Solid Earth 108. doi:10.1029/2002jb001757
Platt, J. P., and Vissers, R. L. M. (1989). Extensional Collapse of Thickened Continental Lithosphere: A Working Hypothesis for the Alboran Sea and gibraltar Arc. Geol 17, 540–543. doi:10.1130/0091-7613(1989)017<0540:ecotcl>2.3.co;2
Presti, D., Totaro, C., Neri, G., and Orecchio, B. (2019). New Earthquake Data in the Calabrian Subduction Zone, italy, Suggest Revision of the Presumed Dynamics in the Upper Part of the Subducting Slab. Seismol. Res. Lett. 90, 1994–2004. doi:10.1785/0220190024
Rappisi, F., and Faccenda, M. (2019). Geodynamic and Seismological Numerical Modelling for Seismic Anisotropy Studies. AGUFM 2019, DI21B–0038.
Rappisi, F., VanderBeek, B., Faccenda, M., Morelli, A., and Molinari, I. (2022). Slab Geometry and Upper Mantle Flow Patterns in the Central Mediterranean from 3d Anisotropic P-Wave Tomography. J. Geophys. Res. Solid Earth 127 (5), e2021JB023488.
Rawlinson, N., Fichtner, A., Sambridge, M., and Young, M. K. (2014). Seismic Tomography and the Assessment of Uncertainty. Adv. Geophys. 55, 1–76. doi:10.1016/bs.agph.2014.08.001
Rawlinson, N., and Spakman, W. (2016). On the Use of Sensitivity Tests in Seismic Tomography. Geophys. J. Int. 205, 1221–1243. doi:10.1093/gji/ggw084
Reuber, G. S., and Simons, F. J. (2020). Multi-physics Adjoint Modeling of Earth Structure: Combining Gravimetric, Seismic, and Geodynamic Inversions. GEM-International J. Geomathematics 11, 1–38. doi:10.1007/s13137-020-00166-8
Ribe, N. M. (1989). Seismic Anisotropy and Mantle Flow. J. Geophys. Res. 94, 4213–4223. doi:10.1029/jb094ib04p04213
Romagny, A., Jolivet, L., Menant, A., Bessière, E., Maillard, A., Canva, A., et al. (2020). Detailed Tectonic Reconstructions of the Western Mediterranean Region for the Last 35 Ma, Insights on Driving Mechanisms. BSGF - Earth Sci. Bull. 191, 37. doi:10.1051/bsgf/2020040
Romanowicz, B. A. (2021). “Seismic Tomography of the Earth's Mantle,” in Encyclopedia of Geology. Editors D. Alderton,, and S. A. Elias. Second EditionSecond edition edn. (Oxford: Academic Press), 587–609. doi:10.1016/B978-0-08-102908-4.00169-7
Rosenbaum, G., Lister, G. S., and Duboz, C. (2002). Reconstruction of the Tectonic Evolution of the Western Mediterranean since the Oligocene. J. Virtual Explor. 8. doi:10.3809/jvirtex.2002.00053
Ruan, Y., Lei, W., Modrak, R., Örsvuran, R., Bozdağ, E., and Tromp, J. (2019). Balancing Unevenly Distributed Data in Seismic Tomography: a Global Adjoint Tomography Example. Geophys. J. Int. 219, 1225–1236. doi:10.1093/gji/ggz356
Savage, M. K. (1999). Seismic Anisotropy and Mantle Deformation: what Have We Learned from Shear Wave Splitting? Rev. Geophys. 37, 65–106. doi:10.1029/98rg02075
Scarfì, L., Barberi, G., Barreca, G., Cannavò, F., Koulakov, I., and Patanè, D. (2018). Slab Narrowing in the Central Mediterranean: the Calabro-Ionian Subduction Zone as Imaged by High Resolution Seismic Tomography. Sci. Rep. 8 (1), 1–12. doi:10.1038/s41598-018-23543-8
Selvaggi, G., and Chiarabba, C. (1995). Seismicity and P-Wave Velocity Image of the Southern Tyrrhenian Subduction Zone. Geophys. J. Int. 121, 818–826. doi:10.1111/j.1365-246x.1995.tb06441.x
Sieminski, A., Paulssen, H., Trampert, J., and Tromp, J. (2008). Finite-frequency Sks Splitting: Measurement and Sensitivity Kernels. Bull. Seismol. Soc. Am. 98, 1797–1810. doi:10.1785/0120070297
Skemer, P., and Hansen, L. N. (2016). Inferring Upper-Mantle Flow from Seismic Anisotropy: an Experimental Perspective. Tectonophysics 668-669, 1–14. doi:10.1016/j.tecto.2015.12.003
Sobolev, S. V., Grésillaud, A., and Cara, M. (1999). How Robust Is Isotropic Delay Time Tomography for Anisotropic Mantle? Geophys. Res. Lett. 26, 509–512. doi:10.1029/1998gl900206
Spakman, W. (1991). Delay-time Tomography of the Upper Mantle below Europe, the Mediterranean, and Asia Minor. Geophys. J. Int. 107, 309–332.
Spakman, W., and Nolet, G. (1988). “Imaging Algorithms, Accuracy and Resolution in Delay Time Tomography,” in Mathematical Geophysics. Modern Approaches in Geophysics, Editors N. J. Vlaar, G. Nolet, M. J. R. Wortel, and S. A. P. L. Cloetingh (Dordrecht: Springer), Vol. 3, 155–187. doi:10.1007/978-94-009-2857-2_8
Spakman, W., van der Lee, S., and van der Hilst, R. (1993). Travel-time Tomography of the European-Mediterranean Mantle Down to 1400 Km. Phys. Earth Planet. Interiors 79, 3–74. doi:10.1016/0031-9201(93)90142-v
Spakman, W., Wortel, M. J. R., and Vlaar, N. J. (1988). The Hellenic Subduction Zone: a Tomographic Image and its Geodynamic Implications. Geophys. Res. Lett. 15, 60–63. doi:10.1029/gl015i001p00060
Spakman, W., and Wortel, R. (2004). “A Tomographic View on Western Mediterranean Geodynamics,” in The TRANSMED Atlas. The Mediterranean Region from Crust to Mantle (Berlin, Heidelberg: Springer), 31–52. doi:10.1007/978-3-642-18919-7_2
Toomey, D. R., Solomon, S. C., and Purdy, G. M. (1994). Tomographic Imaging of the Shallow Crustal Structure of the East Pacific Rise at 9°30′N. J. Geophys. Res. 99, 24135–24157. doi:10.1029/94jb01942
Van der Meer, D. G., Van Hinsbergen, D. J. J., and Spakman, W. (2018). Atlas of the Underworld: Slab Remnants in the Mantle, Their Sinking History, and a New Outlook on Lower Mantle Viscosity. Tectonophysics 723, 309–448. doi:10.1016/j.tecto.2017.10.004
Van Hinsbergen, D. J. J., Torsvik, T. H., Schmid, S. M., Maţenco, L. C., Maffione, M., Vissers, R. L. M., et al. (2020). Orogenic Architecture of the Mediterranean Region and Kinematic Reconstruction of its Tectonic Evolution since the Triassic. Gondwana Res. 81, 79–229. doi:10.1016/j.gr.2019.07.009
van Hinsbergen, D. J. J., Vissers, R. L. M., and Spakman, W. (2014). Origin and Consequences of Western Mediterranean Subduction, Rollback, and Slab Segmentation. Tectonics 33, 393–419. doi:10.1002/2013tc003349
van Zelst, I., Crameri, F., Pusok, A. E., Glerum, A., Dannberg, J., and Thieulot, C. (2021). 101 Geodynamic Modelling: How to Design, Carry Out, and Interpret Numerical Studies. Solid Earth Discuss. 2021, 1–80.
VanderBeek, B. P., and Faccenda, M. (2021). Imaging Upper Mantle Anisotropy with Teleseismic P-Wave Delays: Insights from Tomographic Reconstructions of Subduction Simulations. Geophys. J. Int. 225, 2097–2119. doi:10.1093/gji/ggab081
Vignaroli, G., Faccenna, C., Jolivet, L., Piromallo, C., and Rossetti, F. (2008). Subduction Polarity Reversal at the Junction between the Western Alps and the Northern Apennines, italy. Tectonophysics 450, 34–50. doi:10.1016/j.tecto.2007.12.012
Wang, Z., and Zhao, D. (2021). 3d Anisotropic Structure of the japan Subduction Zone. Sci. Adv. 7, eabc9620. doi:10.1126/sciadv.abc9620
Wessel, P., Luis, J. F., Uieda, L., Scharroo, R., Wobbe, F., Smith, W. H. F., et al. (2019). The Generic Mapping Tools Version 6. Geochem. Geophys. Geosyst. 20, 5556–5564. doi:10.1029/2019gc008515
Wortel, M. J. R., and Spakman, W. (2000). Subduction and Slab Detachment in the Mediterranean-Carpathian Region. Science 290, 1910–1917. doi:10.1126/science.290.5498.1910
Wortel, R., Govers, R., and Spakman, W. (2009). “Continental Collision and the Step-wise Evolution of Convergent Plate Boundaries: From Structure to Dynamics,” in Subduction Zone Geodynamics (Berlin, Heidelberg: Springer), 47–59. doi:10.1007/978-3-540-87974-9_3
Zhao, L., Paul, A., Malusà, M. G., Xu, X., Zheng, T., Solarino, S., et al. (2016). Continuity of the Alpine Slab Unraveled by High-Resolution P Wave Tomography. J. Geophys. Res. Solid Earth 121, 8720–8737. doi:10.1002/2016jb013310
Keywords: central-western mediterranean, geodynamic modeling, composition and structure of the mantle, seismic anisotropy, seismic tomography, body waves
Citation: Lo Bue R, Rappisi F, Vanderbeek BP and Faccenda M (2022) Tomographic Image Interpretation and Central-Western Mediterranean-Like Upper Mantle Dynamics From Coupled Seismological and Geodynamic Modeling Approach. Front. Earth Sci. 10:884100. doi: 10.3389/feart.2022.884100
Received: 25 February 2022; Accepted: 31 May 2022;
Published: 17 June 2022.
Edited by:
Giuliana Rossi, Istituto Nazionale di Oceanografia e di Geofisica Sperimentale, ItalyReviewed by:
Claudia Piromallo, Istituto Nazionale di Geofisica e Vulcanologia (INGV), ItalyCopyright © 2022 Lo Bue, Rappisi, Vanderbeek and Faccenda. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rosalia Lo Bue, cm9zYWxpYS5sb2J1ZUBwaGQudW5pcGQuaXQ=; Francesco Rappisi, ZnJhbmNlc2NvLnJhcHBpc2lAcGhkLnVuaXBkLml0
†These authors have contributed equally to this work and share first authorship
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.