Ab Initio Molecular–Dynamics Study of Structural and Bonding Properties of Liquid Fe–Light–Element–O Systems Under High Pressure

The structural and bonding properties of liquid iron–light–element–oxygen ternary systems such as Fe–H–O, Fe–C–O, Fe–Si–O, and Fe–S–O under high pressure are studied by ab initio molecular dynamics simulations. H, C, O, Si, and S are the candidate light elements in the Earth’s outer core (liquid iron is a major constituent). From our simulations, it is found that H, C, and O show “interstitial” type behavior while Si and S show “substitutional” type behavior in the liquid iron–light–element–O ternary systems. For the interactions between light elements, C–C, Si–Si, and Si–O show covalent–like interactions even under high–pressure condition. The Si–O covalent bond causes a shift in the ionic charge of Si to more positive, which could be related to the immiscibility of liquid Fe–Si–O.

1 Introduction

Light elements (LEs) such as hydrogen, carbon, oxygen, silicon, and sulfur are expected to exist in the Earth’s core (Birch, 1964; Poirier, 1994; Mcdonough, 2003) because the core density is approximately 10% smaller than that of pure iron (Birch, 1964; Anderson and Isaak, 2002). In addition to the density, LE have a strong influence on the structural and transport properties of liquid iron under high pressure. However, there are still many uncertainties regarding the influence of LE.

To fully understand the thermal and magnetic behavior of the Earth, information about transport properties such as electrical and thermal conductivities of the Earth’s outer core are required. Therefore, several experimental and theoretical studies were reported on liquid Fe alloys under high pressure, such as shock wave compression experiments (Keeler and Royce, 1971; Matassov, 1977; Stacey and Anderson, 2001; Yan et al., 2002), and first–principle calculations (de Koker et al., 2012; Pozzo et al., 2012; Pozzo et al., 2013; Wagle et al., 2018).

The transport properties of liquid systems are strongly related to their liquid structures. The structural properties of liquid Fe–LE binary systems under high pressure have therefore been investigated both theoretically and experimentally. Recently, Morard et al. clarified the compression mechanism of liquid Fe–C from X–ray diffraction measurements and demonstrated that the compression rate for the first coordination shell was higher than that for the second and third (Morard et al., 2017). Theoretically, the structures of liquid Fe–H, Fe–C, Fe–N, Fe–O, Fe–Mg, Fe–Si, and Fe–S under high pressure were investigated using ab initio molecular dynamics (MD) simulations (Alfe and Gillan, 1998; Alfe et al., 1999; Morard et al., 2014; Ichikawa and Tsuchiya, 2015; Posner and Steinle–Neumann, 2019; Ohmura et al., 2020). Alfe et al. investigated the structure of liquid Fe–S at 330 GPa and 6000 K and suggested that there was no tendency for S atoms to form chains (Alfe and Gillan, 1998). The structural properties of liquid Fe–O under high pressure were also investigated by ab initio MD simulations (Alfe et al., 1999). The distance between neighboring iron and oxygen atoms was found to be significantly shorter than the Fe–Fe and O–O distances. Morard et al. investigated the structural properties of liquid Fe–O, Fe–Si, and Fe–S under low (5 GPa and 2500 K) and high (330 GPa and 6000 K) pressure conditions using ab initio MD simulations (Morard et al., 2014). From the peak positions of the radial distribution functions obtained from these simulations, it was discovered that Si was incorporated in the liquid state via substitution of Fe atoms, even at 330 GPa. Recently, Posner et al. also performed first–principles MD simulations for liquid Fe–X (X = H, C, N, O, Mg, Si, S, and Ni with 4 at%) (Posner and Steinle–Neumann, 2019), investigating diffusion coefficients and structural properties. The results showed that Si and Ni are “iron–like” elements while H, C, N, O, and S were “small non–iron–like” elements. However, it was suggested that the incorporation mechanism of S shifts to substitutional when the pressure increases.

More recently, a systematic theoretical investigation based on ab initio MD simulations for the LE–effect on the structural properties of liquid Fe–LE binary systems under high pressure was reported (Ohmura et al., 2020). The simulation clarified that H, C, and O are incorporated into liquid Fe interstitially, while Si and S are “substitutional” type impurities.

For the Fe–Si–O ternary system, Pozzo et al. reported the structural properties under high pressure (Pozzo et al., 2013). The distance between the iron and oxygen atoms in the liquid Fe–Si–O was clarified to be almost the same as that in the Fe–O binary liquid, and the Fe–Si distance was almost the same as the iron–iron distance. It was also found that the distance between the silicon and oxygen atoms was shorter than the distance between iron and oxygen. They additionally reported the thermal and electrical conductivities of liquid Fe (Pozzo et al., 2012) and Fe–Si–O mixtures (Pozzo et al., 2013) obtained from density functional theory calculations with the Kubo–Greenwood formula at outer core conditions.

Recently, the immiscibility of liquid Fe–Si–O systems under high pressure was investigated (Arveson et al., 2019; Huang et al., 2019). Arveson et al. found immiscibility between liquid Fe–Si and Fe–Si–O under high pressure, using a combination of laser–heated diamond–anvil cell experiments and first–principles MD simulations. The results suggested that silicon and oxygen can coexist in the Earth’s outer core and SiO₂ does not crystallize at the core–mantle boundary (Arveson et al., 2019). Huang et al. also suggested that SiO₂ crystallization is unlikely under Earth’s core conditions from their ab initio MD simulations (Huang et al., 2019).

In addition to Fe–Si–O, the liquid immiscibility of Fe–S–O has also been discussed. Tsuno et al. suggested that liquid–liquid immiscibility is not expected in liquid Fe–S–O under high pressure, such as in the outer core condition (Tsuno et al., 2007). In contrast, based on thermodynamic modeling, liquid immiscibility would be still possible under the outer core conditions (Helffrich and Kaneshima, 2004). Recently, melting experiments of liquid Fe–S–O were reported, and the liquid core composition system was discussed (Yokoo et al., 2019).

Several experimental and theoretical studies on the properties of liquid Fe–LE–O have been reported, including the immiscibility of liquid Fe–Si–O and Fe–S–O. However, the detailed local structures, including properties of atomic bond in liquid Fe–LE–O ternary systems, from which various properties of the liquids originate, remain unclear. In this study to fully understand the properties of liquid Fe–LE–oxide ternary systems, we investigate the structural and bonding properties of liquid Fe–O with H, C, S, and Si using ab initio MD simulations. The purpose of this study is to find unique properties of liquid ternary systems under high pressure, which cannot be observed in binary systems.

2 Numerical Details

In our ab initio MD simulations, atomic forces were obtained from the electronic states calculated by the projector–augmented plane–wave (PAW) method (Blochl, 1994; Kresse and Joubert, 1999) within the framework of density functional theory (DFT). In the calculations, the generalized gradient approximation formulated by Perdew, Burke, and Ernzerhof (GGA–PBE) was used for the exchange–correlation potential (Perdew et al., 1996). The cutoff energies of the plane wave were 30 and 300 Ry for the pseudo–wavefunctions and pseudo–charge density, respectively. These cutoff energies were the same as those used in a previous study (Ohmura et al., 2020). The energy functional was minimized using an iterative scheme based on the preconditioned conjugate–gradient method (Kresse and Hafner, 1994; Shimojo et al., 2001). The gamma point was used for the k–point sampling. As valence electrons, 3d, 4s, and 4p states of Fe, 1s state of H, 2s and 2p states of C and O, and 3s, 3p, and 3d states of Si and S were used. We used 200 atoms in a cubic supercell under periodic boundary conditions. The thermodynamic states investigated in this study were 140 GPa and 5000 K. Properties of liquid Fe–LE (LE = H, O, C, Si and S) binary systems have been previously investigated at 140 GPa and 5000 K using AIMD (Ohmura et al., 2020). To be able to compare the results of the present work with those of the binary systems, we have used the same pressure and temperature (140 GPa and 5000 K). Four alloy compositions were studied: Fe160H20O20 (Fe–H–O), Fe160C20O20 (Fe–C–O), Fe160Si20O20 (Fe–Si–O), and Fe160S20O20 (Fe–S–O). Since this study does not aim to clarify the properties of liquid Fe alloy under the actual outer core condition, the compositions of the four liquids in this study were also not set to reproduce the density of outer core. To obtain each liquid state, we first prepared pure liquid Fe (liquid Fe₂₀₀), and 40 Fe atoms in the liquid were randomly replaced by LEs. To make the system reach a completely disordered state without the effects of the initial configuration, we carried out MD simulations for approximately 2 ps at a temperature 10,000 K. Then, we decreased the temperature of the systems gradually to a target temperature to 5000 K. After these preprocessing, to determine the density of each liquid system, a constant–pressure MD simulations was performed for 2.4 ps. By averaging over 1.8 ps after equilibration, we determined the densities (volumes) in each liquid. The structural properties were investigated using MD simulations in a canonical ensemble (Nose, 1984; Hoover, 1985). Using the Nose–Hoover thermostat technique, the equations of motion were solved via an explicit reversible integrator (Tuckerman et al., 1992) with a time step of Δt = 1.2 fs for all systems except the system including hydrogen, in which the time step was 0.48 fs. The quantities of interest were obtained by averaging over approximately 4.8–9.6 ps after an initial equilibration taking approximately 2 ps. In all the calculations, spin polarization was not considered.

3 Results and Discussion

Structural Properties

Figure 1 shows the densities of liquid Fe–H–O, Fe–C–O, Fe–Si–O, and Fe–S–O at 140 GPa and 5000 K obtained from the simulations. The densities of liquid Fe and Fe160O40 (Fe–O) at the same P,T are also shown as solid and dashed lines, respectively. The densities of all ternary liquids are smaller than that of liquid Fe. However, in comparison with liquid Fe–O, the densities of liquid Fe–H–O and Fe–C–O are larger than that of liquid Fe–O, while the densities of liquid Fe–Si–O and Fe–S–O are smaller than that of liquid Fe–O. At a lower temperature condition (T = 3700 K), the same behaviors can be observed (Supplementary Figure S1).

FIGURE 1

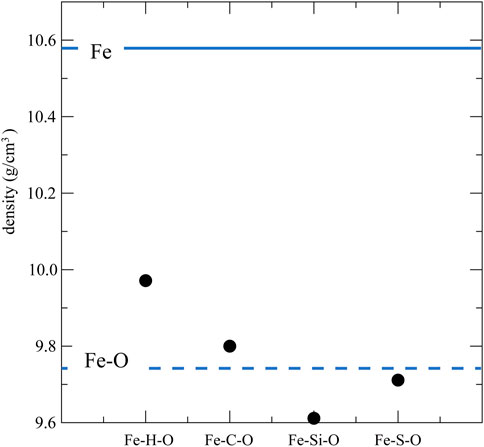
FIGURE 1. Densities of liquid Fe₁₆₀H₂₀O₂₀ (Fe–H–O), Fe₁₆₀C₂₀O₂₀ (Fe–C–O), Fe₁₆₀Si₂₀O₂₀ (Fe–Si–O), and Fe₁₆₀S₂₀O₂₀ (Fe–S–O) at 140 GPa and 5000 K. Densities of liquid Fe and Fe₁₆₀O₄₀ (Fe–O) at 140 GPa and 5000 K are also displayed as solid and dashed lines, respectively.

The partial pair distribution functions gαβ(r) for liquid Fe–H–O (A), Fe–C–O (B), Fe–Si–O (C), and Fe–S–O (D) are shown in Figure 2. The g_Fe–Fe(r) has the first peak at approximately 2.2 Å and the second peak at approximately 4 Å in all the liquid systems. For g_O–O(r), the profile is almost the same in each liquid, in which we can see the first peak at approximately 2.2 Å and a small second peak at approximately 3.5 Å. For the interactions between Fe and light elements, the first peak positions of Fe–H, Fe–C, and Fe–O are smaller than that of Fe–Fe, and the first peak positions of Fe–Si and Fe–S are almost the same as that of Fe–Fe. These features are also seen in the Fe–LE binary systems (Ohmura et al., 2020). The results of densities and gαβ(r) indicate that H, C, and O are interstitial, and that Si and S show substitutional properties in the liquid Fe–LE–O ternary systems as well as the liquid Fe–LE binary systems.

FIGURE 2

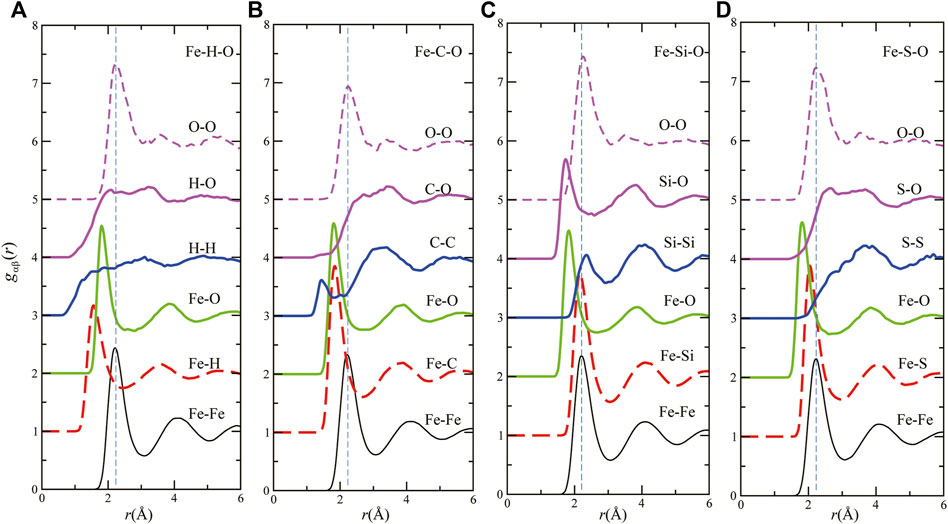
FIGURE 2. Partial pair distribution functions of liquids (A) Fe₁₆₀H₂₀O₂₀ (Fe–H–O), (B) Fe₁₆₀C₂₀O₂₀ (Fe–C–O), (C) Fe₁₆₀Si₂₀O₂₀ (Fe–Si–O) and (D) Fe₁₆₀S₂₀O₂₀ (Fe–S–O) at 140 GPa and 5000 K.

Regarding the LE–LE interactions, we can see the different features of each liquid. For homoatomic interactions, H–H does not have clear correlations. In contrast, C–C shows strong interactions in the sense that there is a first peak at approximately 1.5 Å, which is the smallest first peak position in all gαβ(r). The strong C–C interaction is found in liquid Fe–C–H system as well (Belonoshko et al., 2015). The first peak positions of g_O–O(r) are almost the same as those of g_Fe–Fe(r) in all liquids. However, the second–peak positions are smaller than those of g_Fe–Fe(r). For Si–Si interactions, the first–and second–peak positions of Si–Si are almost the same as those of Fe–Fe or Fe–Si. These features align with the results of earlier studies for liquid Fe–O or Fe–Si binary (Alfe et al., 1999; Morard et al., 2014; Posner and Steinle–Neumann, 2019; Ohmura et al., 2020) and for Fe–Si–O ternary systems (Pozzo et al., 2013; Arveson et al., 2019; Huang et al., 2019). For S–S interactions, the first peak is broad, and its position is much farther than those of other gαβ(r) in liquid Fe–S–O. In terms of the heteroatomic interactions, H–O, C–O, and S–O have similar behaviors in the sense that there are broad first peaks. In contrast, the first peak of g_Si–O(r) is located at 1.8 Å and sharp, meaning strong interactions between Si and O.

Bonding Properties

To clarify the detailed bonding nature in the liquid Fe–LE–O ternary systems, we use the Mulliken population analysis, where the electronic wave functions are expanded in an atomic orbital basis set (Mulliken, 1955; Shimojo et al., 2008). Figure 3 shows the time–averaged distribution $p_{\alpha \beta }\left(\overline{O}\right)$ of the bond overlap population $O_{i\in \alpha ,j\in \beta }$, which gives a semiquantitative estimate of the covalent–like bonding between the α and β atomic types in liquid Fe–H–O (A), Fe–C–O (B), Fe–Si–O (C), and Fe–S–O (D). It should be noted that, since the atomic–orbital basis used in the expansion of the wavefunctions is not unique, the absolute magnitudes of $O_{ij}$ are little physical meaning. However, the trends remain unchanged for any choice of atomic–orbital basis sets, and therefore we can discuss their relative variations meaningfully.

FIGURE 3

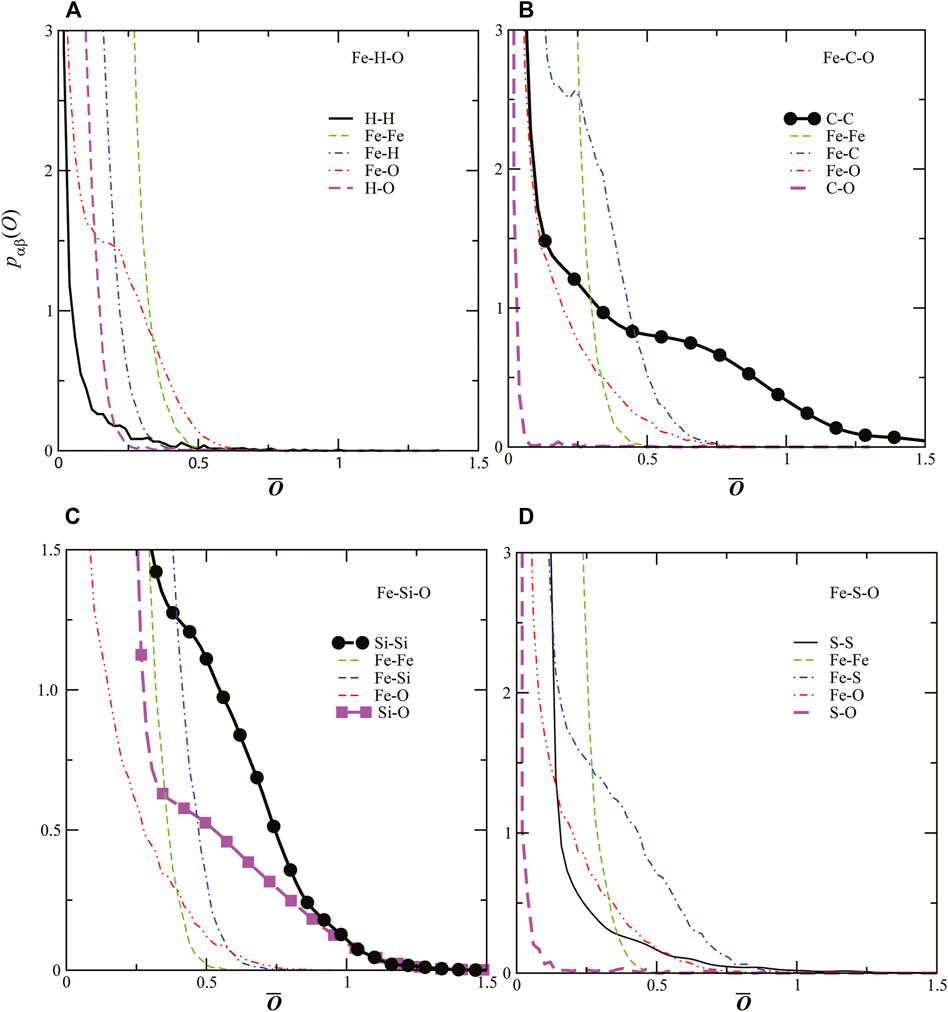
FIGURE 3. Distributions $p_{\alpha \beta }\left(\overline{O}\right)$ of the overlap populations Oij for five pairs of α–atomic and β–atomic types of liquids (A) Fe-H-O, (B) Fe-C-O, (C) Fe-Si-O and (D) Fe-S-O. Thick solid, thin dashed, dotted dashed, double–dotted dashed and thick dased lines show $p_{\alpha \beta }\left(\overline{O}\right)$ for LE–LE, Fe–Fe, Fe–LE, Fe–O and LE–O, respectively. Circles in Fe–C–O (B) and Fe–_Si–O (C) show p_C–C $\left(\overline{O}\right)$ and pSi–Si $\left(\overline{O}\right)$, respectively. Squares show pSi–O $\left(\overline{O}\right)$ in liquid Fe–Si–O.

Figure 3A shows $p_{\alpha \beta }\left(\overline{O}\right)$ in liquid Fe–H–O. All of $p_{\alpha \beta }\left(\overline{O}\right)$ in liquid Fe–H–O do not show strong overlaps. In contrast, as shown in Figures 3B,C, $p_{C-C}\left(\overline{O}\right)$, $p_{Si-Si}\left(\overline{O}\right)$, and $p_{Si-O}\left(\overline{O}\right)$ have values in the regions $\overline{O}$ > 1.0, while other $p_{\alpha \beta }\left(\overline{O}\right)$ are almost zero in the same region. For liquid Fe–S–O, $p_{S-S}\left(\overline{O}\right)$ shows a relatively stronger interaction in the sense that there is a shoulder at approximately $\overline{O}$ = 0.5, but $p_{S-S}\left(\overline{O}\right)$ = 0 in the region $\overline{O}$ > 1.0. Although the Si–O and Si–Si atomic distances are almost the same as those for Fe–O and Fe–Fe, respectively (Figure 2C), the bonding nature is different. Covalency are clearly found between Si–O and Si–Si, whereas not between Fe–O and Fe–Fe. These results indicate that C–C, Si–Si, and Si–O have covalent–like interactions in liquid Fe mixtures even under high–pressure conditions (>100 GPa).

In order to analyze the covalent–like interactions of C–C, Si–Si, and Si–O in more detail, we investigate the time evolution of the bond overlap population $O_{ij}\left(t\right)$. Figure 4 shows $O_{\text{C}1-\text{C}2}\left(t\right)$ (overlap population between C1 and C2 atoms) displayed with the time evolution of the atomic distance between C1 and C2 atoms, d_C1–C2(t), and the snapshots of atomic configurations. At t = 0.00 ps, d_C1–C2(t) is more than 2.0 Å and $O_{C1-C2}\left(t\right)$ is zero, meaning no covalent bonding between C1 and C2. $O_{C1-C2}\left(t\right)$ increases when d_C1–C2(t) decreases, meaning that a covalent bond forms between C1 and C2 (the snapshot at t = 0.13 ps). After $O_{C1-C2}\left(t\right)$ and d_C1–C2(t) oscillate approximately 10 times, $O_{C1-C2}\left(t\right)$ becomes almost 0 and d_C1–C2(t) becomes more than 2.5 Å at approximately 0.40 ps, meaning that the covalent bond between C1 and C2 is lost, as shown in the snapshot at t = 0.40 ps. From the result, the lifetime of the C–C covalent bond is estimated to be approximately 0.3 ps at this P,T.

FIGURE 4

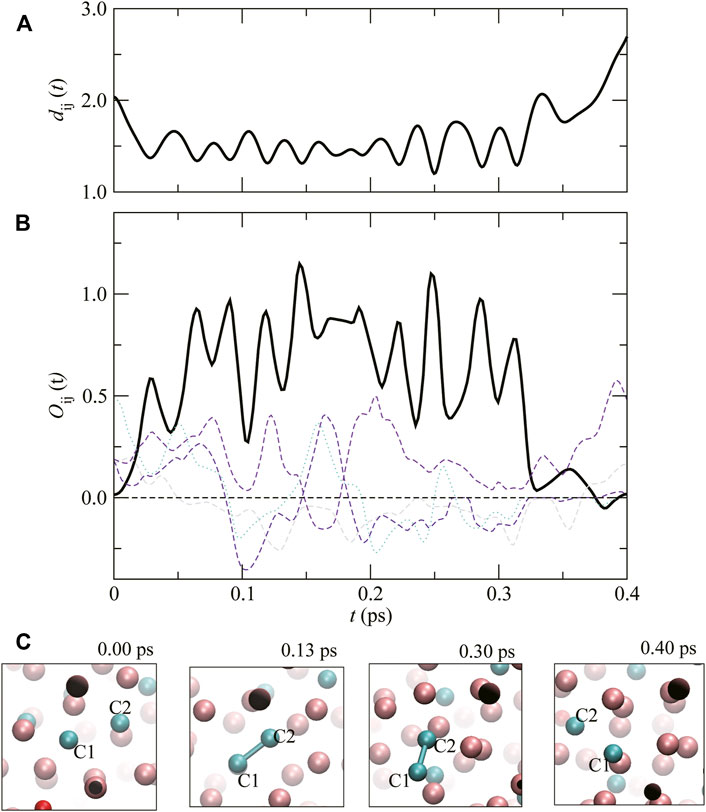
FIGURE 4. (A) The time evolution of atomic distance between C1 and C2, d_C1–C2(t), and (B) the overlap population, $O_{\text{C}1-\text{C}2}\left(t\right)$ (Thick solid line). Dashed lines show $O_{\text{C}1-\text{Fe}}\left(t\right)$. (C) Atomic configurations around C1 and C2 at t = 0.00, 0.13, 0.30 and 0.40 ps. The pink, green and red spheres correspond to Fe, C and O atoms, respectively. The dark spheres represent Fe atoms that are in the process of moving outside the frame, and towards the paper boundary.

Figure 5 shows the time evolution of the distance and overlap population of focusing atomic pair (Si1 and Si2), dSi1–Si2(t) and the $O_{\text{Si}1-\text{Si}2}\left(t\right)$, with the snapshots of atomic configuration in liquid Fe–Si–O. At t = 0.00 ps, dSi1–Si2(t) is almost 3.5 Å, and $O_{\text{Si}1-\text{Si}2}\left(t\right)$ is almost 0. Similar to the C–C interactions shown in Figure 4, with time, an Si–Si covalent–like bond forms (the snapshot at 0.70 ps), and the Si–Si bond oscillates several times, then the bond dissolves (at 1.30 ps).

FIGURE 5

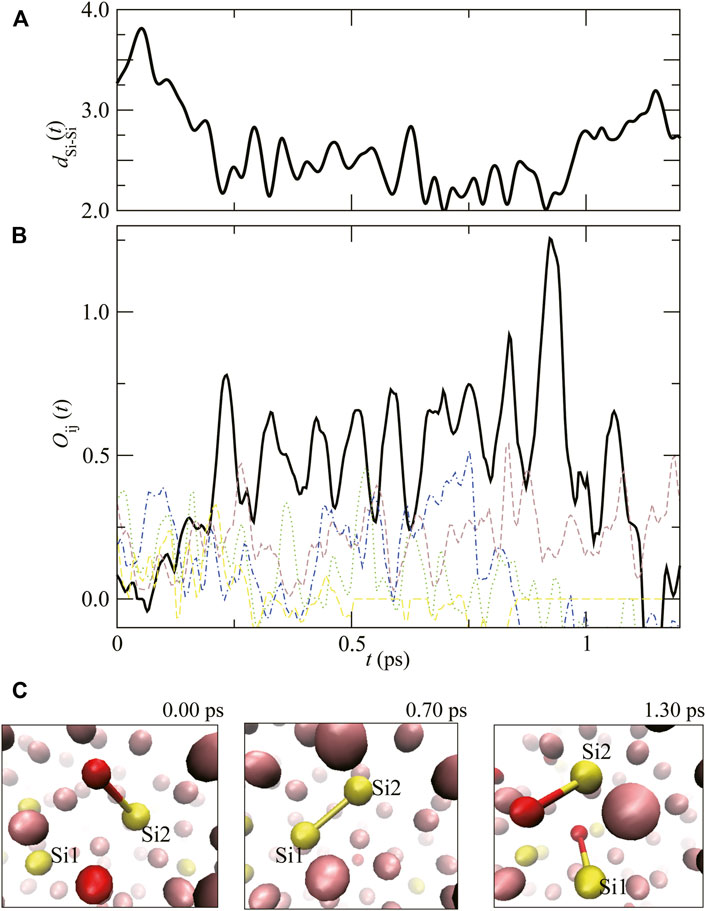
FIGURE 5. (A) The time evolution of atomic distance between Si1 and Si2, d_Si1–Si2(t), and (B) the overlap population, $O_{\text{Si}1-\text{Si}2}\left(t\right)$ (Thick solid line). Dashed lines show $O_{\text{Si}1-\text{Fe}}\left(t\right)$. (C) Atomic configurations around Si1 and Si2 at t = 0.00, 0.70 and 1.30 ps. The pink, yellow and red spheres correspond to Fe, Si and O atoms, respectively.

In liquid Fe–Si–O, Si–O covalent bonding can also be observed. OSi–O(t), dSi–O(t), and snapshots of the atomic configuration are shown in Figure 6. At t = 0.00 ps, OSi–O(t) is almost 0, meaning no covalent bond between Si and O (the snapshot at t = 0.00 ps). OSi–O(t) begins to increase at approximately 0.05 ps, meaning the covalent bond formation between Si and O. Similar to C–C and Si–Si covalent bonds, after the Si–O bond oscillates several times, OSi–O(t) decreases drastically at approximately 0.22 ps. At the same time. dSi–O(t) increases, meaning that covalent bond between Si–O dissolves (the snapshot at 0.25 ps). From this result, we can estimate the lifetime of the Si–O covalent bond to be approximately 0.15 ps at this P,T.

FIGURE 6

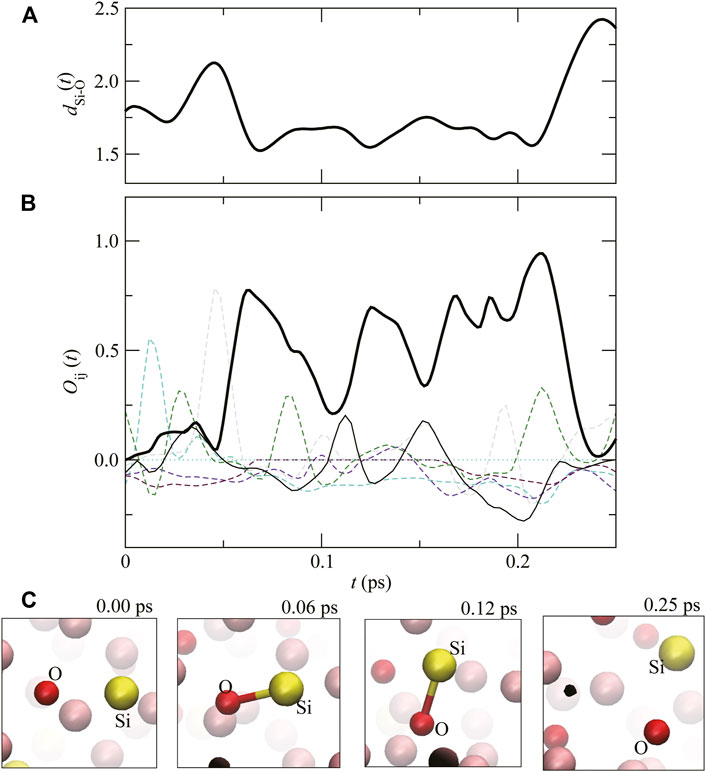
FIGURE 6. (A) The time evolution of distance between Si and O atoms, d_Si–O(t), and (B) the overlap population $O_{\text{Si}-\text{O}}\left(t\right)$ (Thick solid line). Dashed lines show $O_{\text{Si}-\text{Fe}}\left(t\right)$. (C) Atomic configurations around Si and O at t = 0.00, 0.06, 0.12 and 0.25 ps. The pink, yellow and red spheres correspond to Fe, Si and O atoms, respectively.

Our calculations clearly indicate that in liquid Fe–Si–O and Fe–C–O, covalent–like interactions with finite lifetimes exist between C and C, Si and Si, and also Si and O under high–pressure more than 100 GPa.

Charge distribution of Si atoms in liquid Fe–Si–O.

Figure 7A shows the averaged distribution qα(Q) of the gross charge $Q_{i\in \alpha }$ for α type atoms in liquid Fe–Si–O obtained by population analysis as same as $O_{ij}$. As shown in Figure 7A, the peak positions of q_Fe(Q), q_Si(Q), and q_O(Q) are approximately Q = 0.1, –0.2, and –0.7, respectively. While the Si–O covalent bond affects the atomic charge of the Si atom, the C–C and Si–Si interactions have no effects on the atomic charge of C and Si (Supplementary Figure S2). To analyze q_Si(Q) in more detail, we decompose q_Si(Q) into q_Si–O(Q) and q_Si–nonO(Q). Here, q_Si–O(Q) means the distribution of the atomic charge for Si atoms coordinated to O atoms, which is displayed as a thick dashed line in Figure 7B and q_Si–nonO(Q) means the distribution of the atomic charge for Si atoms unbonded to O atoms, which is displayed as a thin solid line in Figure 7B. As shown in Figure 7B, q_Si–O(Q) is distributed to a relatively large Q region, which means that Si atoms have more positive charges when bonded to the O atom compared to the charges when the Si atoms are unbonded to O.

FIGURE 7

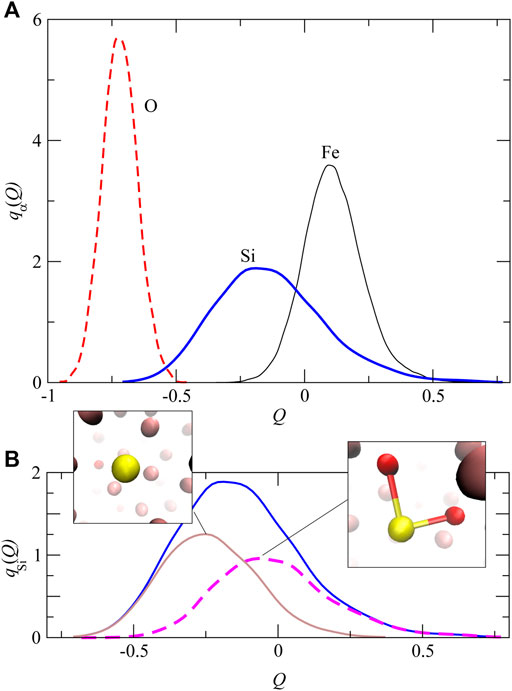
FIGURE 7. (A) The distribution of qα(Q) of the gross charges $Q_{i \in \text{α}}$. The thin solid, thick solid and dashed lines represent q_Fe(Q), q_Si(Q) and q_O(Q), respectively. (B) The distribution of q_Si(Q) decomposed into q_Si–O(Q) and q_Si–nonO(Q). The former represents the charge distribution for Si atoms coordinated to O atoms (a pink thin–dashed line) and the latter represents the charge distribution of Si atoms unbonded to O atoms (a brown thin–solid line).

According to an earlier study (Arveson et al., 2019), liquid Fe–Si–O shows might have immiscibility between liquid Fe–Si–O and Fe–Si (there are two domains with and without oxygen in liquid Fe–Si–O) just above their solidus temperatures at Earth’s outer core pressures. Atomic configurations in our simulation also seem to be suggestive of this phase separation though the actual immiscibility region might exist at some lower temperatures (Supplementary Figure S3). The shift of atomic charge due to the Si–O covalent bond is possibly related to the gathering of oxygen atoms with negative charges around Si, leading to the separation of ionic Fe–Si–O and metallic Fe–Si domains in liquid Fe–Si–O. However, at the moment, the upper temperature bound of the immiscibility region at the outer core pressures is yet to be determined. In addition to these atomic perspectives, energetic information regarding thermodynamic stability of miscible and immiscible liquids has to be determined to understand the immiscibility of liquid Fe–Si–O in more detail.

4 Conclusion

The structural and bonding properties of liquid Fe–H–O, Fe–C–O, Fe–Si–O and Fe–S–O ternary systems under high pressure have been investigated by ab initio molecular–dynamics simulations. The pair distribution functions indicated the interstitial nature for H, C, and O but the substitutional one for Si and S, similar to liquid Fe–LE binary systems. Regarding the interactions between light elements, bond–overlap populations showed covalent characters in C–C, Si–Si, and Si–O interactions in liquid Fe–C–O and Fe–Si–O even under high–pressure condition. Mulliken charge analyses clarified that the Si–O covalent bond caused a shift in the atomic charge of Si to more positive. This might be related to the phase separation between the Fe–Si–O and Fe–Si domains in liquid Fe–Si–O. To further understand immiscibility of multi–component liquid Fe mixtures such as liquid Fe–Si–O, thermodynamic stability should be explored.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SO: Methodology, formal analysis, investigation, writing–original draft, project administration. FS: Software, writing–review and editing. TT: Validation, supervision, writing–review and editing.

Funding

This work was supported by KAKENHI (Nos. 21K03705 and 20H00198).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank the Supercomputer Center, Institute for Solid State Physics, the University of Tokyo for the use of the facilities. The computation was also carried out using the computer facilities at the Research Institute for Information Technology, Kyushu University.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.873088/full#supplementary–material

References

Alfe, D., and Gillan, M. J. (1998). First–principles Simulations of Liquid Fe–S under Earth's Core Conditions. Phys. Rev. B 58, 8248–8256. doi:10.1103/physrevb.58.8248

CrossRef Full Text | Google Scholar

Alfe, D., Price, G. D., and Gillan, M. J. (1999). Oxygen in the Earth's Core: a First–Principles Study. Phys. Earth Planet. Inter. 110, 191–210. doi:10.1016/s0031–9201(98)00134–4

CrossRef Full Text | Google Scholar

Anderson, O. L., and Isaak, D. G. (2002). Another Look at the Core Density Deficit of Earth's Outer Core. Phys. Earth Planet. Interiors 131, 19–27. doi:10.1016/s0031–9201(02)00017–1

CrossRef Full Text | Google Scholar

Arveson, S. M., Deng, J., Karki, B. B., and Lee, K. K. M. (2019). Evidence for Fe–Si–O Liquid Immiscibility at Deep Earth Pressures. Proc. Natl. Acad. Sci. U.S.A. 116, 10238–10243. doi:10.1073/pnas.1821712116

PubMed Abstract | CrossRef Full Text | Google Scholar

Belonoshko, A. B., Lukinov, T., Rosengren, A., Bryk, T., and Litasov, K. D. (2015). Synthesis of Heavy Hydrocarbons at the Core–Mantle Boundary. Sci. Rep. 5, 18382–18416. doi:10.1038/srep18382

PubMed Abstract | CrossRef Full Text | Google Scholar

Birch, F. (1964). Density and Composition of Mantle and Core. J. Geophys. Res. 69, 4377–4388. doi:10.1029/jz069i020p04377

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector Augmented–Wave Method. Phys. Rev. B 50, 17953–17979. doi:10.1021/acs.jctc.7b00404.s001

CrossRef Full Text | Google Scholar

De Koker, N., Steinle–Neumann, G., and Vlček, V. (2012). Electrical Resistivity and thermal Conductivity of Liquid Fe Alloys at High P and T , and Heat Flux in Earth's Core. Proc. Natl. Acad. Sci. U.S.A. 109, 4070–4073. doi:10.1073/pnas.1111841109

PubMed Abstract | CrossRef Full Text | Google Scholar

Helffrich, G., and Kaneshima, S. (2004). Seismological Constraints on Core Composition from Fe–O–S Liquid Immiscibility. Science 306, 2239–2242. doi:10.1126/science.1101109

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoover, W. G. (1985). Canonical Dynamics: Equilibrium Phase–Space Distributions. Phys. Rev. A. 31, 1695–1697. doi:10.1103/physreva.31.1695

CrossRef Full Text | Google Scholar

Huang, D., Badro, J., Brodholt, J., and Li, Y. (2019). Ab Initio Molecular Dynamics Investigation of Molten Fe–Si–O in Earth's Core. Geophys. Res. Lett. 46, 6397–6405. doi:10.1029/2019gl082722

CrossRef Full Text | Google Scholar

Ichikawa, H., and Tsuchiya, T. (2015). Atomic Transport Property of Fe–O Liquid Alloys in the Earth's Outer Core P, T Condition. Phys. Earth Planet. Interiors 247, 27–35. doi:10.1016/j.pepi.2015.03.006

CrossRef Full Text | Google Scholar

Keeler, R. N., and Royce, E. B. (1971). Shock Waves in Condensed mediaPhysics of High Energy Density. Proc. Int. Sch. Phys. "Enrico Fermi", Course XLVIII, 51.

Google Scholar

Kresse, G., and Hafner, J. (1994). Ab Initiomolecular–Dynamics Simulation of the Liquid–Metal–Amorphous–Semiconductor Transition in Germanium. Phys. Rev. B 49, 14251–14269. doi:10.1103/physrevb.49.14251

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented–Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Matassov, G. (1977). Electrical Conductivity of Iron––silicon alloys at high pressures and the earth's core. Livermore (USA)United States): California Univ.Lawrence Livermore Lab.

Google Scholar

Mcdonough, W. F. (2003). “Compositional Model for the Earth's Core” in Treatise on Geochemistry. Editor K. K. Turekian (Oxford: Pergamon), 547–568. doi:10.1016/b0–08–043751–6/02015–6

CrossRef Full Text | Google Scholar

Morard, G., Andrault, D., Antonangeli, D., and Bouchet, J. (2014). Properties of Iron Alloys under the Earth's Core Conditions. Comptes Rendus Geosci. 346, 130–139. doi:10.1016/j.crte.2014.04.007

CrossRef Full Text | Google Scholar

Morard, G., Nakajima, Y., Andrault, D., Antonangeli, D., Auzende, A. L., Boulard, E., et al. (2017). Structure and Density of Fe–C Liquid Alloys under High Pressure. J. Geophys. Res. Solid Earth 122, 7813–7823. doi:10.1002/2017jb014779

CrossRef Full Text | Google Scholar

Mulliken, R. S. (1955). Electronic Population Analysis on LCAO–MO Molecular Wave Functions. II. Overlap Populations, Bond Orders, and Covalent Bond Energies. J. Chem. Phys. 23, 1841–1846. doi:10.1063/1.1740589

CrossRef Full Text | Google Scholar

Nosé, S. (1984). A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 52, 255–268. doi:10.1080/00268978400101201

CrossRef Full Text | Google Scholar

Ohmura, S., Tsuchiya, T., and Shimojo, F. (2020). Structures of Liquid Iron–Light Element Mixtures under High Pressure. Phys. Status Solidi B 257, 2000098. doi:10.1002/pssb.202000098

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Poirier, J.–P. (1994). Light Elements in the Earth's Outer Core: A Critical Review. Phys. Earth Planet. Interiors 85, 319–337. doi:10.1016/0031–9201(94)90120–1

CrossRef Full Text | Google Scholar

Posner, E. S., and Steinle-Neumann, G. (2019). Mass Transport and Structural Properties of Binary Liquid Iron Alloys at High Pressure. Geochem. Geophys. Geosyst. 20, 3556–3568. doi:10.1029/2019gc008393

CrossRef Full Text | Google Scholar

Pozzo, M., Davies, C., Gubbins, D., and Alfe, D. (2012). Thermal and Electrical Conductivity of Iron at Earth's Core Conditions. Nature 485, 355–358. doi:10.1038/nature11031

PubMed Abstract | CrossRef Full Text | Google Scholar

Pozzo, M., Davies, C., Gubbins, D., and Alfe, D. (2013). Transport Properties for Liquid Silicon–Oxygen–Iron Mixtures at Earth's Core Conditions. Phys. Rev. B 87, 014110. doi:10.1103/physrevb.87.014110

CrossRef Full Text | Google Scholar

Shimojo, F., Nakano, A., Kalia, R. K., and Vashishta, P. (2008). Electronic Processes in Fast Thermite Chemical Reactions: A First–Principles Molecular Dynamics Study. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 77, 066103. doi:10.1103/PhysRevE.77.066103

PubMed Abstract | CrossRef Full Text | Google Scholar

Shimojo, F., Kalia, R. K., Nakano, A., and Vashishta, P. (2001). Linear–scaling Density–Functional–Theory Calculations of Electronic Structure Based on Real–Space Grids: Design, Analysis, and Scalability Test of Parallel Algorithms. Comput. Phys. Commun. 140, 303–314. doi:10.1016/s0010–4655(01)00247–8

CrossRef Full Text | Google Scholar

Stacey, F. D., and Anderson, O. L. (2001). Electrical and thermal Conductivities of Fe–Ni–Si alloy under Core Conditions. Phys. Earth Planet. Interiors 124, 153–162. doi:10.1016/s0031–9201(01)00186–8

CrossRef Full Text | Google Scholar

Tsuno, K., Ohtani, E., and Terasaki, H. (2007). Immiscible Two–Liquid Regions in the Fe–O–S System at High Pressure: Implications for Planetary Cores. Phys. Earth Planet. Interiors 160, 75–85. doi:10.1016/j.pepi.2006.09.004

CrossRef Full Text | Google Scholar

Tuckerman, M., Berne, B. J., and Martyna, G. J. (1992). Reversible Multiple Time Scale Molecular Dynamics. J. Chem. Phys. 97, 1990–2001. doi:10.1063/1.463137

CrossRef Full Text | Google Scholar

Wagle, F., Steinle–Neumann, G., and De Koker, N. (2018). Saturation and Negative Temperature Coefficient of Electrical Resistivity in Liquid Iron–Sulfur Alloys at High Densities from First–Principles Calculations. Phys. Rev. B 97, 094307. doi:10.1103/physrevb.97.094307

CrossRef Full Text | Google Scholar

Yan, B., Hua, T., and Fuqian, J. (2002). Electrical Conductivity of Iron under Shock Compression up to 200 GPa. J. Phys. Cond. Matter 14, 10849. doi:10.1088/0953-8984/14/44/389

CrossRef Full Text | Google Scholar

Yokoo, S., Hirose, K., Sinmyo, R., and Tagawa, S. (2019). Melting Experiments on Liquidus Phase Relations in the Fe–S–O Ternary System under Core Pressures. Geophys. Res. Lett. 46, 5137–5145. doi:10.1029/2019gl082277

CrossRef Full Text | Google Scholar