Boron Incorporation in Silicate Melt: Pressure-induced Coordination Changes and Implications for B Isotope Fractionation

Drewitt, James W. E.; Bromiley, Geoffrey D.

doi:10.3389/feart.2022.870892

ORIGINAL RESEARCH article

Front. Earth Sci., 26 April 2022

Sec. Earth and Planetary Materials

Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.870892

This article is part of the Research Topic Advances in the Study of Fluids and Melts Under Extreme Conditions View all 5 articles

Boron Incorporation in Silicate Melt: Pressure-induced Coordination Changes and Implications for B Isotope Fractionation

James W. E. Drewitt¹*

Geoffrey D. Bromiley^2,3

¹H.H. Wills Physics Laboratory, School of Physics, University of Bristol, Bristol, United Kingdom
²School of GeoSciences, Grant Institute, University of Edinburgh, Edinburgh, United Kingdom
³Centre for Science at Extreme Conditions, University of Edinburgh, Edinburgh, United Kingdom

Ab initio molecular dynamics simulations have been employed to investigate the nature of boron incorporation in a haplobasalt melt at pressures up to 8 GPa. At ambient pressure, boron is predominantly incorporated as trigonal planar BO₃ units. With increasing pressure, the proportion of tetrahedral BO₄ increases markedly in parallel with increases in the coordination of other cations in silicate liquids. In contrast to studies of high-pressure boron-rich silicate glasses and liquids where boron units are polymerized, simulations of low B-concentration liquid here indicate that boron does not adopt a significant role as a network-forming cation. Marked changes in the proportion of BO₄ in silicate melt at even moderate pressures (from 5 to 20%, over the pressure range 0–3 GPa) imply that pressure may significantly affect the extent of melt/fluid and melt/crystal boron isotope fractionation. This pressure-effect should be considered when using boron isotope data to elucidate processes occurring within the mantle.

Introduction

Although boron is a minor component in most silicates, the concentration of boron, and proportion of its two stable isotopes ¹⁰B and ¹¹B, are important tracers of geological processes (Marschall and Foster, 2018). B is typically incompatible and concentrated in silicate liquids, especially more evolved magmas, but is also fluid mobile and a useful tracer of rock-fluid interaction (Barth, 1993; Leeman, 1996; Peacock and Hervig, 1999; Kowalski et al., 2013; Palmer, 2017). There is growing interest in the use of B and its isotopes to constrain fluid-mediated processes within Earth’s mantle, especially volatile transport and release within subduction zones (Peacock and Hervig, 1999; Palmer, 2017; De Hoog and Savov, 2018). Differences in B coordination between aqueous fluids, minerals and silicate melts, and the large mass difference between ¹⁰B and ¹¹B, result in considerable fractionation of B isotopes, even up to magmatic temperatures, and the ready identification of signatures of fluid-rock interaction (Kowalski et al., 2013; Kowalski and Wunder, 2018). However, there is limited experimental data on fractionation of B isotopes under high-pressure/temperature conditions, and interpretation of B isotope data often relies on assumed isotopic fractionation based on differences in B coordination between phases. In turn, although B coordination and bonding environment in many crystalline phases and in borosilicate glasses is well constrained (see Kowalski and Wunder (2018) for a recent review of controls of B coordination on isotopic fractionation), our understanding of B coordination in silicate liquids is limited, especially in basaltic magmas formed by mantle melting.

In natural silicates, B occurs in either [3] or [4] coordination with oxygen, forming BO₃ or BO₄ units (Sanchez-Valle et al., 2005; Schmidt et al., 2005; Wunder et al., 2005; Ertl et al., 2010; Hålenius et al., 2010; Gatta et al., 2012; Edwards et al., 2014; Ingrin et al., 2014; Kilymis et al., 2015; Yamada et al., 2018). Insight into boron incorporation in terrestrial systems builds on a wealth of studies of the technological important borosilicate glasses. These studies, and simulations of B-rich silicate liquids, demonstrate progressive changes in boron coordination up to at least 20 GPa, with BO₃ being the dominant species at ambient pressure and the proportion of BO₄ increasing markedly even over moderate pressure increases, although there are also strong compositional controls on boron coordination in glasses (e.g. Dell et al., 1983; Dingwell et al., 1996; Martens and Muller-Warmuth, 2000; Du et al., 2004; Wondraczek et al., 2007; Edwards et al., 2014; Smedskjaer et al., 2014; Zeidler et al., 2014; Kilymis et al., 2015; Kapoor et al., 2017; Stevensson et al., 2018; Yamada et al., 2018; Lee and Lee, 2020). By comparison, changes in coordination of B, and progressive changes in melt structure and composition with pressure, are expected to have a considerable influence on mineral/melt/fluid fractionation of B isotopes in terrestrial systems (Kowalski and Wunder, 2018; Lee and Lee, 2020). However, although both compositional controls on B speciation in B-rich and Si-rich liquids/glasses and pressure-induced structural changes have been the subject of numerous investigations, there is a lack of information on B incorporation and speciation in more basaltic composition liquids characteristic of subduction magmatism and mantle melting, especially at realistic, low B concentrations. Importantly, on the basis of melt/fluid B isotope partitioning data it has been suggested that B structural environment in low B melts could differ significantly from B-rich systems, with a significant proportion of B incorporated as BO₄ (Hervig et al., 2002; Maner and London, 2018).

Here we have performed ab initio molecular dynamics calculations to simulate B-bearing, basaltic liquids over a range of pressures relevant to mantle melting, and to constrain B-O coordination environment. The simulation results are used to consider the effects of B coordination changes, and other pressure-induced changes in silicate melts, on B isotope fractionation.

Methodology

Ab initio molecular dynamics (MD) calculations based on density functional theory (DFT) were performed using the Vienna Ab Initio Software Package (VASP) (Kresse and Furthmüller, 1996a; Kresse and Furthmüller, 1996b) compiled on the BlueCrystal Phase 4 parallel computing cluster at the Advanced Computing Research Centre, Bristol. The electronic interactions were described by the projector-augmented wave (PAW) (Blochl, 1994; Kresse and Joubert, 1999) pseudopotentials using the Perdew-Burke-Ernzerhof (PBE) formulation of the generalised gradient approximation (GGA) exchange correlation functional (Perdew et al., 1996). The Brillouin zone was sampled at the Γ-point with an energy cut-off value of 550 eV. MD trajectories were computed in the canonical (NVT) ensemble with periodic boundary conditions and a Nosé thermostat (Nosé, 1984).

The simulations are based on a haplobasalt melt composition, diopside-anorthite (Di-An), chosen as a simplified model primary mantle melt. This composition consists of 64% diopside (CaAl₂Si₂O₆), 36% anorthite (CaAl₂Si₂O₆). For simulations of the boron-bearing basaltic melts, 22 Ca, 14 Mg, 16 Al, 44 Si, 154 O, and 4 B atoms were used, corresponding to 14, 8, and 2 formula units of diopside, anorthite and boron trioxide (B₂O₃), respectively, and 1.6 atomic % B. Additional calculations were made for boron free Di-An melt. Starting configurations with a range of volumes were constructed from randomly generated cubic cells, with closest approaches defined from crystallographic bond lengths. The initial configurations were super-heated to 10,000 K for 2 ps, cooled isochorically to 2500 K over 4 ps, and equilibrated at both 2500 and 1800 K for 30 ps with a time-step of 1 fs. The total CPU time for each 30 ps simulation was approximately 5 days running on 280 cores. Only the final 25 ps of the equilibrated trajectories were considered for the melt structure analysis using the R.I.N.G.S (Le Roux and Jund, 2010) and MAGMA codes (Drewitt, 2022).

In order to account for the under-binding of chemical bonds inherent to GGA calculations, several of the B-bearing melt simulations were repeated using the Strongly Constrained and Appropriately Normed (SCAN) meta-GGA functional (Sun et al., 2015), which has been shown to provide more accurate volumes (Chen et al., 2017). The pressure dependence of the melt density derived from the SCAN calculations is in good general agreement with the Birch-Murnaghan equation of state previously reported from shock-compression measurements of molten Di₆₄An₃₆ (Rigden et al., 1988). An empirical correction $p_{e m p} = - 2.5 - 0.18 p$ was applied to the PBE-GGA data to bring the results into agreement with the computed SCAN values and shock-compression data.

Results

Melt Density and Structure

The densities of the simulated melts are shown as a function of pressure in Figure 1, together with the equation of state of molten Di₆₄An₃₆ previously reported from shock-compression experiments (Rigden et al., 1988). A third order Birch-Murnaghan equation of state with a Berman thermal expansion model was fitted to the B-bearing melt data using EoSFit7-GUI (Gonzalez-Platas et al., 2016). Fit parameters using temperature reference $T_{0} = 1800 K$ are: zero pressure density $ρ_{0} = 2.67 g c m^{- 3}$ , bulk modulus $K_{0} = 20.8 (9) G P a$ , pressure derivative $K^{'} = 5.7 (5)$ , constant of thermal expansion $α_{0} = 6.1 (3) \times 10^{5} K^{- 1}$ , and non-linear thermal expansion term $α_{1} = - 2.3 (5) \times 10^{8} K^{- 2}$ .

FIGURE 1

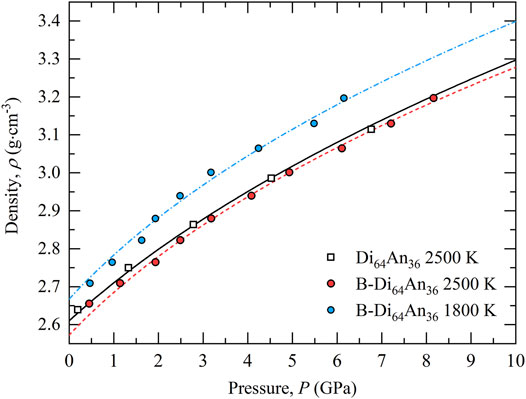
FIGURE 1. Mass density of the simulated pure (B-free) Di₆₄An₃₆ and B-bearing melts as a function of pressure (symbols defined in legend). The blue chained and red dashed curves are Birch-Murnaghan equations of state for the B-bearing melts at 1800 and 2500 K, respectively (for fit parameters see main text). The Birch-Murnaghan equation of state for pure liquid Di₆₄An₃₆ with ambient pressure bulk modulus K₀ = 24.2 GPa and pressure derivative K’ = 4.85, as derived from shock-compression measurements by Rigden et al. (1988), is also shown (solid black curve).

The pressure dependence of the average coordination by oxygen of the major cations and are shown in Figure 2, as calculated using a cut-off distance r_cut corresponding to the first minimum following the nearest neighbour peak in the corresponding partial $g_{X O} (r)$ functions, shown for the selected B-bearing melts in Figure 3. The average coordination numbers for pure Di₆₄An₃₆ and B-bearing melts at 2500 K are comparable, indicating that the local coordination environments in the melt are not altered substantially by the addition of 1.6 at.% B atoms. However, further analysis of the oxygen-cation coordination does reveal a small depolymerization effect among SiO₄ polyhedra on the addition of boron, where the number of oxygens not bonded to Si increases from 7 to 10%, with a concomitant 3% reduction in the number Si-O-Si bridges. With increasing pressure, Al, Mg, and Ca local structure environments undergo significant change, with average coordination numbers increasing linearly from ${\bar{n}}_{A l}^{O} = 4.4 (1)$ , ${\bar{n}}_{M g}^{O} = 5.2 (1)$ , and ${\bar{n}}_{C a}^{O} = 7.1 (1)$ at ambient pressure to ${\bar{n}}_{Al}^{O} = 5.2 (1)$ , ${\bar{n}}_{Mg}^{O} = 6.3 (1)$ , and ${\bar{n}}_{Ca}^{O} = 8.8 (1)$ at 8.2 GPa and 2500 K. This pressure effect is enhanced at lower temperature giving rise to a more rapid increase in coordination at 1800 K. In contrast, Si experiences only a very gradual increase in average coordination from ${\bar{n}}_{Si}^{O} = 4.05 (5)$ at ambient pressure to ${\bar{n}}_{Si}^{O} = 4.25 (5)$ at 8.2 GPa and 2500 K, with negligible differences in coordination at 1800 K cf. 2500 K.

FIGURE 2

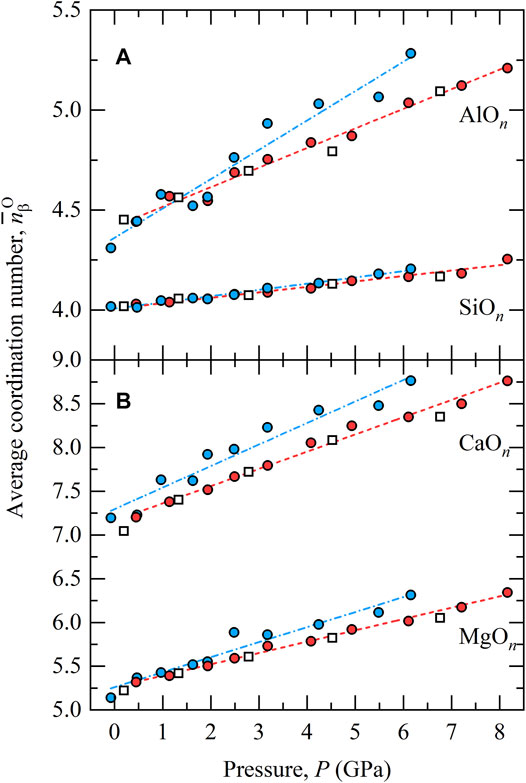
FIGURE 2. Average coordination numbers ${\bar{n}}_{β}^{O}$ of the major cations in the B-bearing melt simulations at 1800K (blue circles) and 2500 K (red circles) for (A) Al-, Si-, and (B) Ca-, and Mg-centred units evaluated at fixed cut-off distances of 2.25 Å (Si-O), 2.65 Å (Al-O), 2.95 Å (Mg-O), and 3.35 Å (Ca-O) as a function of pressure. The blue chained and red dashed lines are linear fits to the data at 1800 and 2500 K, respectively. The corresponding coordination numbers from the pure Di₆₄An₃₆ melt simulations are also shown (open squares).

FIGURE 3

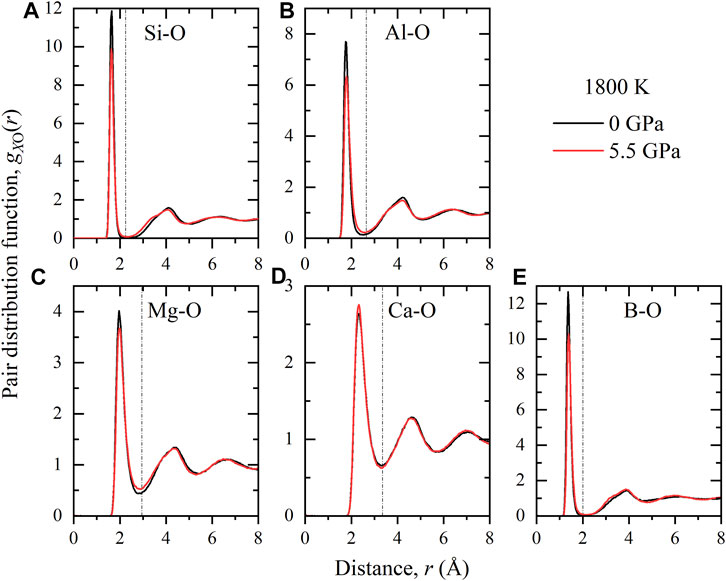
FIGURE 3. Pair distribution functions g_XO(r), where X = Si (A), Al (B), Mg (C), Ca (D), B (E), for the B-bearing melt simulations at 1800 K and 0 GPa or 5.5 GPa. The cut-off distance used to compute coordination numbers and other local structure analysis are indicated by the vertical lines.

The fractional distribution of partial coordination numbers for the major cations are shown in Figure 4. At ambient pressure silicon is almost entirely 4-fold coordinated by oxygen, SiO₄. With increasing pressure there is a gradual development in the fraction of SiO₅ units, reaching 20% by ∼ 8 GPa. Very small fractions (<2%) of SiO₆ are present in the melt at ∼ 8 GPa. The O-Si-O bond angle distributions for SiO₄ or SiO₅ units in the B-bearing melts at 1800 K are shown in Figure 5A). The peak O-Si-O bond angle of 109° for SiO₄ units is consistent with tetrahedral geometry (ideal tetrahedral angle is equal to $\cos^{- 1} (1 / 3) = 109.47 °$ ) (Feuston and Garofalini, 1988). For SiO₅ units, the O-Si-O bond angle of 90° is consistent with square pyramidal geometry (Badro et al., 1997).

FIGURE 4

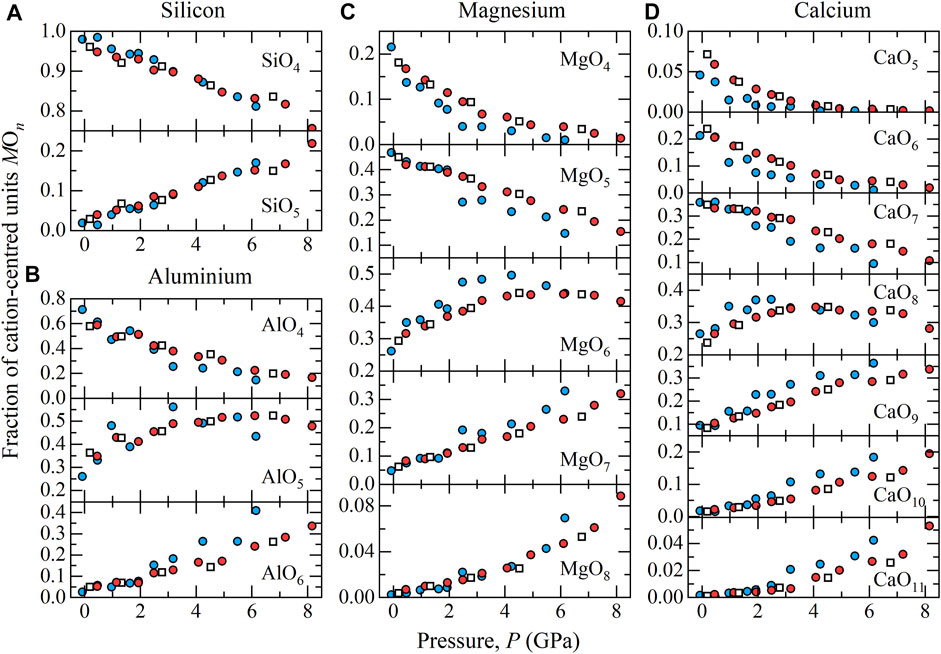
FIGURE 4. Fraction of cation centred MO_n units (A) SiO_n, (B) AlO_n, (C) MgO_n, and (D) CaO_n units in the simulated B-bearing melts at 1800 K (blue circles) and 2500 K (red circles) shown as a function of pressure, together with corresponding fractions present in pure Di₆₄An₃₆ melts (open squares).

FIGURE 5

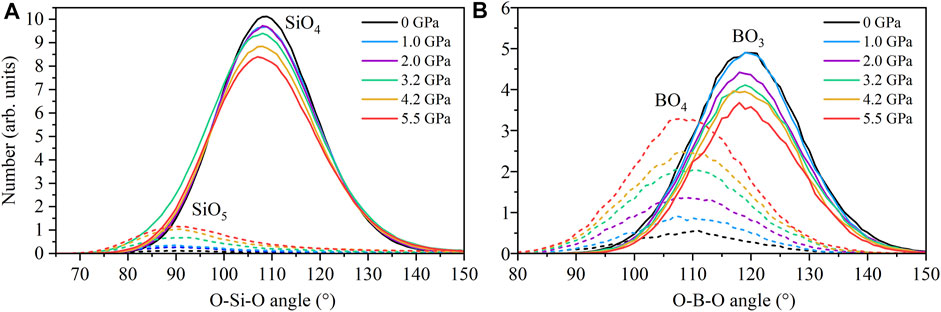
FIGURE 5. Bond angle distributions (A) O-Si-O in 4-fold SiO₄ and 5-fold SiO₅ units and (B) O-B-O in BO₃ and BO₄ units in the B-bearing melt simulations at 1800K and approximate pressures indicated by the colours as defined in the legend.

At ambient pressure, Al predominantly resides in 4-fold coordination by oxygen, with approximately 20% AlO₅ units. With increasing pressure, AlO₄ units transform rapidly with approximately 80% of the structure dominated by AlO₅ and AlO₆ units at 6–8 GPa. At ambient pressure, Mg occupies a mixture of predominantly MgO₄ (20%), MgO₅ (50%), and MgO₆ (25%). By 8.2 GPa at 2500 K, MgO₄ units are almost entirely absent, MgO₅ units are diminished to ∼10%, with MgO₆ (∼45%) and MgO₇ (∼35%) units becoming dominant units, and MgO₈ units present in an appreciable fraction (∼9%). As the largest cation in the melt, Ca adopts a wide distribution of coordination polyhedra, CaO_n, with n = 5, 6, 7, 8, 9, 10, and 11. At ambient pressure, CaO₆ (∼25%), CaO₇ (∼35%), and CaO₈ (∼25%) units predominate, with CaO₈ (∼30%), CaO₉ (∼35%), CaO₁₀ (∼20%) dominant at 8.2 GPa and 2500 K.

Boron Coordination Environment

The average coordination of boron by oxygen ${\bar{n}}_{B}^{O}$ are shown as a function of pressure in Figure 6A. At ambient pressure, ${\bar{n}}_{B}^{O} = 3.05 (5)$ at 1800 K, increasing to 3.25(10) at 6.2 GPa. Similar coordination numbers are observed at 2500 K although, as for the major cations, there is a slight enhancement in coordination at lower temperatures. Over the entire pressure range investigated, only BO₃ and BO₄ units have significant populations and their fractional distributions are shown in Figures 6B,C. At ambient pressure, BO₃ units dominate, with only around 5% BO₄. With increasing pressure, BO₃ units are gradually replaced by BO₄ units, with 15–20% BO₄ at ∼2–3 GPa, and approximately 30% BO₄ at ∼ 8 GPa. O-B-O bond angle distributions for BO₃ or BO₄ units are shown in Figure 5B). For BO₃ units, the peak O-B-O angle of 120° is consistent with ideal trigonal planar geometry. As observed for SiO₄ units, the peak of 109° in the O-B-O bond angle distribution for BO₄ units is consistent with tetrahedral geometry. These two coordination environments are illustrated in the simulation snapshots in Figure 7. At high-pressure, there is a slight contraction in the mean nearest neighbor B-O bond distance from 1.41 Å in BO₃ units and 1.54 Å in BO₄ units at ambient pressure to 1.39 Å in BO₃ units and 1.51 Å in BO₄ units at 6.2 GPa and 1800 K.

FIGURE 6

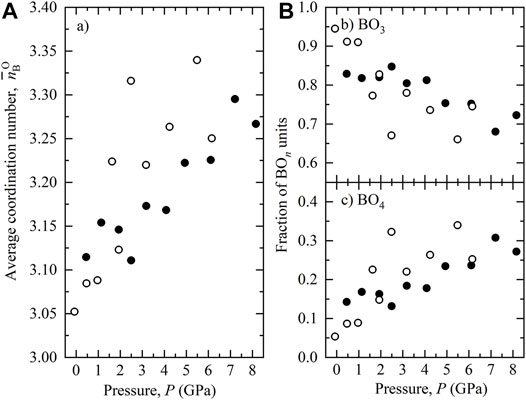
FIGURE 6. (A) Average coordination number ${\bar{n}}_{B}^{O}$ for the B-bearing melts as a function of pressure at 1800K (open circles) and 2500 K (solid circles) together with the corresponding fractions of (B) BO₃ and (C) BO₄ units.

FIGURE 7

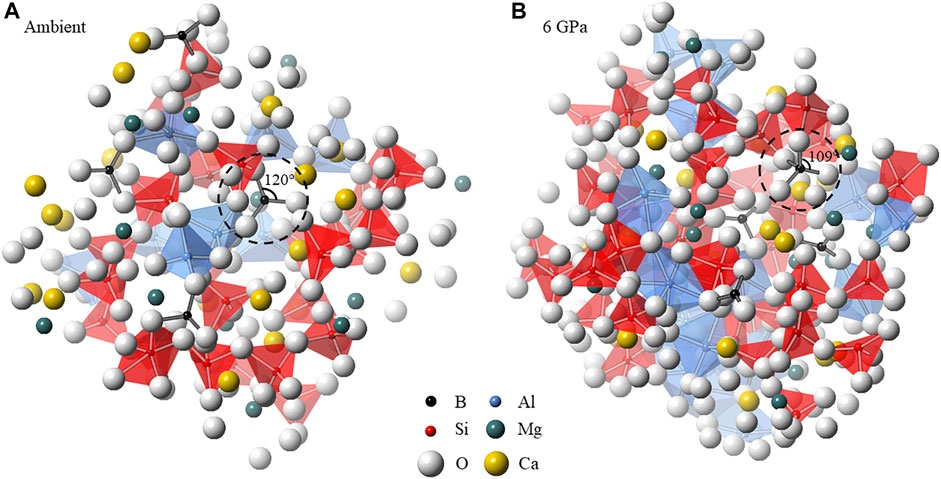
FIGURE 7. Simulation snapshots of the B-bearing melts at (A) ambient and (B) 6.2 GPa at 1800 K. Trigonal planar BO₃ and tetrahedral BO₄ units are highlighted, illustrating the origin of the peak O-B-O bond angle distributions in Figure 5B.

The lifetime of individual trigonal planar BO₃ units reduces as a function of pressure from approximately 1.6 ps at ambient pressure to 0.5 ps at 6.2 GPa and 1800 K. These lifetimes reduce by two thirds at 2500 K. Lifetimes of individual tetrahedral BO₄ units increase slightly from 0.1 ps at ambient pressure to 0.2 ps at 6.2 GPa and 1800 K, remaining relatively constant at 0.1 ps as a function of pressure at 2500 K. For comparison, the lifetimes of individual SiO₄ tetrahedra reduce from 0.7 to 0.2 ps at 1800 K and 0.2 to 0.1 ps at 2500 K over the studied pressure range.

The average O-B coordination remains close to 1 across the entire pressure and temperature range, with only a small fraction of 1–2% B-O-B bridges present in the melt at the highest pressures, indicating that B-centred units are largely isolated from one another. There is, however, significant sharing between oxygen atoms bound to boron (hereafter denoted O_B atoms) and adjacent major cations, as expected for charge compensation and as also observed in B-bearing silicate minerals. At ambient pressure, ∼ 60% of all O_B atoms share bonds with Ca at both 1800 and 2500 K. With increasing pressure, the fraction increases to ∼80%. These are predominantly single O_B-Ca bonds with 20–30% O_B atoms involved in Ca-O_B-Ca bridges. Approximately 60% O_B atoms are bound to Al (40% O_B-Al, 20% Al-O_B-Al) across the studied P-T range. In contrast, only 30–40% O_B atoms are bound to Mg as single O_B-Mg bonds with zero Mg-O_B-Mg linkages. This is likely due to the smaller atomic radius and lower atomic fraction of Mg cf. Ca in the melt making it less accommodating for charge compensation. Similarly, only 40% O_B atoms are bound to Si, with constant proportions of 30% O_B-Si and 10% Si-O_B-Si linkages across the studied P-T range.

Discussion

Pressure-Induced Changes in Silicate Liquid Structure

Compression of Di-An melt results in progressive increases in coordination of all cations, as opposed to abrupt changes in coordination observed in crystalline silicate minerals. For all cations, changes in overall coordination number arise from the progressive increase in fraction of higher coordinated species at the expense of lower coordination species, consistent with previous experimental (Sanloup et al., 2013a; Sanloup et al., 2013b; Wang et al., 2014; Drewitt et al., 2015; Drewitt, 2021) and simulation (Stixrude and Karki, 2005; Adjaoud et al., 2008; de Koker et al., 2008; Spera et al., 2009; de Koker 2010; Bajgain et al., 2015a; Bajgain et al., 2015b) studies of silicate melts. The presence of B has a small depolymerizing effect on the silicate network melt structure, evidenced by the ∼3% reduction in Si-O-Si bridges.

The rate of increase in Si coordination with increasing pressure up to ∼8 GPa is notably less than other cations, presumably due to the relatively strong Si-O bond, and the presence of softer cation sites whose conversion to higher coordination is energetically more favorable. Adjaoud et al. (2008) noted largely insignificant pressure-induced changes in Si coordination in classical MD simulations using an aspherical ion model potential of Mg₂SiO₄ liquid to considerably higher pressures. However, they acknowledged that Si-O coordination in their simulations is underestimated by comparison to ab initio calculations reported by de Koker et al. (2008) and to classical MD results from Guillot and Sator (2007) using rigid ion model potentials, both of which are consistent with the development in Si coordination observed in Figure 4. Drewitt et al. (2015) directly compared classical MD, using the same aspherical ion model potential as Adjaoud et al. (2008), and ab initio MD calculations, the latter of which show a similar development in Si-O coordination to that noted here and in ab initio MD simulations of other Ca-bearing aluminosilicate liquids (Bajgain et al., 2015b).

Adjaoud et al. (2008) did note concomitant increases in Mg coordination in their simulations, from ∼5 at room pressure to ∼7 at 24 GPa, which are broadly comparable to Mg coordination changes up to 8 GPa in this study. Similarly, MD simulations of CaSiO₃ liquid by Bajgain et al. (2015b) show a substantial increase in Ca coordination with pressure, with progressive changes in the proportions of 5–11 coordinated Ca up to 8 GPa. Clear differences in relative changes for specific Ca coordinations in CaSiO₃ and Di-An liquids (here), especially Ca^[8], likely arise from marked differences in liquid composition, although as noted here temperature is also a key control. The progressive changes in Al coordination observed here are also in broad agreement with previous studies. For example, Allwardt et al. (2007) used Nuclear Magnetic Resonance (NMR) spectroscopy to constrain an increase in Al coordination in quenched, high-pressure silicate glasses, from 4.0 at ambient pressure to between 4.2 and 5.1 at 8 GPa. They noted that the extent of Al coordination changes with pressure is highly composition-dependent, with their CMAS (CaO-MgO-Al₂O₃-SiO₂) glass, as expected, most closely resembling the trends for Di-An melt observed in Figure 4. Similarly, they also noted a progressive decrease in proportion of Al^[4], increase in proportion of Al^[6], and an increase, plateauing, and then decrease in proportion of Al^[5] with increasing pressure up to 8 GPa. Drewitt et al. (2015) employed in-situ X-ray diffraction combined with classical and ab initio MD calculations to directly constrain the development of Al-O coordination in anorthite melt and glass at high-pressures up to ∼30 GPa. The coordination numbers reported for these diffraction measurements and ab initio MD results are broadly consistent with the results presented here. Overall, the progressive changes in cation coordination reported here are in broad agreement with previous investigations, both for simplified compositions and in more complex basaltic liquids (Bajgain et al., 2015a). There are progressive, approximately linear, increases in coordination for all cations during densification of Di-An liquid, which are more pronounced at lower temperatures. As previously noted, pressure-induced coordination increases for all cation sites implies a progressive reduction in the proportion of non-bridging oxygen sites (NBOs), and the resultant formation of more bridging oxygens (Bajgain et al., 2015a).

B Incorporation in Silicate Liquid

There have been numerous structural investigations of borosilicate glasses/liquids and B-rich silicate glasses/liquids (e.g. Geisinger et al., 1998; Dingwell et al., 1996; Schmidt et al., 2004, 2005). Considerable insight into boron incorporation in oxides has been provided by a wealth of spectroscopic studies of the technologically important borosilicate glasses. A consistent finding of previous research is that B, due to its small ionic radius and high-charge, is found in either [3] or [4] coordination with O, forming quasi-planar [BO₃]³⁻ triangles and near-regular [BO₄]⁵⁻ tetrahedra (see Kowalski and Wunder (2018) for a recent review). Higher coordinations of B have not, so far, been reported, at least up to 20 GPa (Kilymis et al., 2015). In borosilicate glasses, boron acts as a network-forming cation, and boron species polymerize to form various combinations with other boron units and with other network-forming components, such as [SiO₄]⁴⁻ and [AlO₄]⁵⁻ (Kowalski and Wunder, 2018). Pressure stabilizes B^[4] over B^[3], although B-rich glasses are structurally complex, with variations in short to long range order which extend far beyond simple distribution and proportions of BO₃ and BO₄ (e.g. Dell et al., 1983; Geisinger et al., 1988; Dingwell et al., 1996; Martens and Muller-Warmuth, 2000; Wondraczek et al., 2007; Smedskjaer et al., 2014; Guerette and Huang, 2015; Kapoor et al., 2017; Jolivet et al., 2019; Jolivet et al., 2021; Lu et al., 2021). In particular, there is a strong compositional control on B coordination (Dell et al., 1983; Martens and Muller-Warmuth, 2000; Jolivet et al., 2019; Lu et al., 2021). As alkali content of borosilicate glasses is increased, the proportion of B^[4] initially increases due to charge balancing of [BO₄] units, although B^[4] reaches a maximum and then decreases at higher alkali contents. Presence of Al₂O₃ in borosilicate glasses reduces the proportion of B^[4], at least at lower pressures where Al is assumed to play the same structural role as B^[4], and proportions of B^[4] are also dependent on the ratio SiO₂/B₂O₃ (Lu et al., 2021).

Similarly, the extent to which pressure modifies B coordination in quenched borosilicate glasses is variable and dependent on composition (Wondraczek et al., 2007; Smedskjaer et al., 2014; Guerette and Huang, 2015; Kapoor et al., 2017; Jolivet et al., 2021). Yamada et al. (2018) noted, based on in-situ X-ray absorption data, that borosilicate glasses synthesized at ambient pressure with 72% of boron as BO₃, underwent considerable changes in structure up to 8.5 GPa, including a progressive increase in B coordination within compressed, fully-polymerized boron frameworks. This is consistent with high-resolution NMR spectroscopy data on high-pressure, quenched borosilicate glasses, which also demonstrated an increase in polymerization and B-Si disordering at pressure (Du et al., 2004). Similarly, MD simulations of pressure-induced changes in borosilicate liquids show progressive increases in both the proportion of B^[4], and in average coordination of Na, with increasing pressure (Kilymis et al., 2015). That study also noted that the relative proportions of B^[3] and B^[4], and extent of pressure-induced coordination changes, in sodium-bearing borosilicate glasses is strongly composition dependent, with simulations again suggesting that B, and especially BO₄, is a network-former.

Investigations of B-incorporation in silicate glasses/liquids (i.e. less B-rich systems) are more limited, but similarly suggest that boron is dominantly B^[3]. An NMR spectroscopy study of natural rhyolitic glasses (Tonarini et al., 2003) demonstrated that 74–92% of B is trigonal, and suggested a compositional control on B coordination. On the basis of NMR spectroscopy data of a series of rhyolitic glasses, Lee and Lee (2020) suggested a similar increase in B coordination and proportion of B^[4] with increasing B/Al and Si/B ratios. This implies that the proportion of B^[4] should be lower in basaltic glasses than in rhyolitic glasses, within which they identified ∼75% B^[3]. Lee and Lee (2020) also concluded that B acts as a network-former, noting that B units avoid interaction with Al within aluminosilicate frameworks. As a note of caution, based on a review of available data, Kowalski and Wunder (2018) suggested that quenching may result in structural modification of B-rich silicate liquid, with B changing from a network-modifier to a network-former, again consistent with structural characterization of borosilicate glasses which demonstrate the importance of thermal history (Lu et al., 2021). Regardless, all data supports the dominance of B^[3] over B^[4] in silicate and borosilicate liquids, with an increase in B^[4] with increasing pressure, and strong compositional controls on B coordination, including an increase in B^[4] in more Si-rich and Na-rich systems, and reduction in B^[4] due to a destabilising effect of Al^[4].

In contrast, it has been suggested that isotopic fractionation of B implies that tetrahedral BO₄ is the dominant B-species in silicate melts with low B contents (Hervig et al., 2002). There is a mass difference of approximately 10% between the two stable isotopes of boron, ¹⁰B and ¹¹B, and boron isotopes are readily fractionated by geological processes. The smaller, heavier ¹¹B prefers trigonal coordination, with ¹⁰B preferring tetrahedral coordination with O (Kowalski and Wunder, 2018). In aqueous fluids, trigonal BO₃ is the dominant species, forming the [B(OH)3]⁰ complex, with a fraction of B^[4], i.e. [B(OH)₄]⁻, only becoming important in neutral to basic fluids at greater depths (Sanchez-Valle et al., 2005; Schmidt et al., 2005; Kowalski et al., 2013; Kowalski and Wunder, 2018). In silicate minerals, boron can be both trigonally or tetrahedrally coordinated to O. The coordination difference between aqueous fluids and silicate minerals can result in strong isotopic fractionation of B, with fluids in equilibrium with silicates typically strongly enriched in ¹¹B (Kowalski and Wunder, 2018). Based on a common temperature dependence for both mineral-fluid and silicate melt-fluid B isotopic fractionation, Hervig et al. (2002) suggested that trace amounts of B characteristic of natural systems are incorporated into silicate melts onto tetrahedral BO₄ sites, in marked contrast to B coordination in B-rich liquids. Mineral-fluid isotope partitioning data supports a strong, first order control of B coordination changes on isotopic fractionation, with B-O strength/distance an important additional control (Kowalski et al., 2013). Maner and London (2018) similarly noted comparable temperature dependences for boron isotope fractionation for granitic melt, illite and boromuscovite in equilibrium with aqueous fluids, and again suggested that the fraction of B^[4] in granitic melts must be significant, at least at elevated pressure/temperature.

In the lower B concentration Di-An liquids studied here, B is predominantly 3-fold coordinated by O at ambient pressure with only approximately 5% of B existing as BO₄. As such, our simulations support assertions based on characterisation of B-rich liquids and glasses. However, the proportion of B^[4] in Di-An liquid increases markedly with pressure, up to 30% at ∼ 8 GPa. This demonstrates that: 1) in low Si systems (i.e. characteristic of natural basalts), B^[3] dominates, and the proportion of B^[4] is actually slightly lower than predicted based on borosilicate glass data, as formulated by Lee and Lee (2020), and much lower than in Si-rich systems; and that 2) pressure has a strong control on B coordination in silicate liquids of all compositions. As such, any formalisation of controls on B coordination and B isotope fractionation should additionally consider the role of pressure. O-B-O angle data (Figure 5) are consistent with near-ideal planar trigonal BO₃ and near-ideal tetrahedral BO₄ groups. In contrast to investigations of B-rich systems, the average O-B coordination of ∼1 and B-O bond lengths imply that B within D-An liquid is not a network-forming cation. B-centred units do not form an integral part of silicate tetrahedral framework, and O-B coordinations imply that B-centred units are generally isolated from each other. Due to the need to charge-balance O_B atoms are bonded to other cations, principally to Ca. There is no evidence that O_B avoids interaction with Al, in contrast to B-rich silicate liquids.

Average B-O bond lengths for BO₃ groups in Di-An liquid at 1800 K are ∼1.4 Å, which is broadly consistent with B-O bond lengths in crystalline minerals containing BO₃ groups. B-O bond lengths in hambergite, Be₂BO₃(OH,F), containing near-ideal planar trigonal BO₃ groups, are approximately 1.37 Å at room temperature/pressure. BO₃ groups in hambergite share O sites with adjacent beryllium tetrahedra, but are not part of the Be tetrahedral network. In the B-bearing tourmaline dravite, B-O distances within BO₃ planar trigonal units are 1.37–1.38 Å (Ertl et al., 2010). BO₃ units in tourmaline again have O atoms associated with adjacent [6] and [9] coordinated cation polyhedral sites, but not silicon tetrahedra. B also forms trigonal planar BO₃ units in olivine (Ingrin et al., 2014), with B located on a vacant Si tetrahedral site, coordinated to 3 of the adjacent O atoms. The remaining O atom about this site is protonated (i.e. forms an O-H group), resulting in formation of a BO₃ substitutional defect coupled to, but not directly bonded to, an OH defect. These BO₃ groups are approximately trigonal planar, although with slightly asymmetric B-O bond distances. Again, in contrast to Di-An liquid, in B-bearing olivine, O atoms in BO₃ groups are associated with adjacent Mg^[6] cation sites. Corresponding B-O distances are, in accordance, longer, ranging from 1.40 to 1.42 Å at ambient conditions (Ingrin et al., 2014).

The average B-O bond distance for BO₄ groups in Di-An- liquid is 1.54 Å at 0 GPa, 1800 K, i.e. an 8.6% increase from the bond distance in BO₃ groups. This increase in bond distance with increasing coordination of B is well established in the literature, and close to the 7.8% increase calculated by Kowalski et al. (2013) for isolated B(OH)₃ and B(OH)₄^- units. However, even at 8 GPa, there is only a very small fraction of B-O-B bridges and, as discussed above, the addition of B into the Di-An melt results in a slight (3%) reduction in Si-O_B-Si connections. Pressure does not promote a significant increase in the proportion of Si-O_B-Si bridges over the range of conditions studied here. This implies that at high pressures B tends to behave more as a network-modifying cation rather than a network-forming cation in low B concentration silicate liquids.

Pressure-Induced Changes in B Coordination

From 0 to 3 GPa, the proportion of B^[4] in Di-An liquid at 1800 K increases markedly, from approximately 5–20%. This increase in B coordination is more pronounced at lower temperature, as is the case for coordination changes for all other cations in silicate liquids. As such, for basaltic liquids produced by mantle melting, a substantial proportion of B is likely to be in higher coordination.

Available data suggests that both the proportion of B^[4], and increase in proportion of B^[4] in silicate liquids/glasses with pressure are composition dependent and highly variable (e.g. Kilymis et al., 2015; Kowalski and Wunder, 2018; Stevensson et al., 2018). Proportions of B^[4] in Di-An liquid appear to be somewhat lower than in both borosilicate and rhyolitic glass/liquids at ambient pressure, likely due to lower B and SiO₂ content. However, the extent of increases in B coordination in Di-An liquid are broadly in-line with studies of borosilicate glasses (Kilymis et al., 2015), highlighting the importance of pressure-induced coordination changes in B in all systems. Some studies have noted that the presence of Al^[4] on tetrahedral sites inhibits formation of BO₄ in silicate/borosilicate glasses (Kowalski and Wunder, 2018). However, simulations here do not support assertions that B-centred units avoid interacting with Al-centred units.

On the basis of NMR spectroscopy measurements of glasses and ab initio calculations, Edwards et al. (2014) concluded that pressure-induced increases in B coordination in borosilicate glass arise due to out-of-plane displacement of the central B atom in BO₃ units. Formation of BO₄ units then depends of the availability of an O site in the structural neighbourhood, and presumably, the proportion of underbonded O atoms/NBOs. Although caution is required applying observations of B-rich glasses to silicate melts in which B may not act as a network-forming cation, the mechanism proposed by Edwards et al. (2014) is consistent with the high-pressure behaviour of silicate glasses generally, where the effect of compression and coordination changes is to markedly reduce the concentration of NBOs (Bajgain et al., 2015b). A relationship between the proportion of B^[4] and the silica content of B-rich liquids/glasses (i.e. the extent of melt polymerisation and proportion of NBO sites) as commonly noted in structural studies (Lee and Lee, 2020) is also consistent with this mechanism of B coordination change.

If conversion of BO₃ to BO₄ in silicate liquids is dependent on the proportion of NBOs, the pressure dependence of coordination should be greater in basaltic, i.e. less polymerised, systems. However, the extent of B coordination change is also dependent on coordination changes for other cations, and structural changes in liquids generally, which are complex and constantly evolving with pressure (Figures 3, 4). For example, studies of borosilicate glass demonstrate that Al₂O₃ decreases the proportion of BO₄ units, presumably because Al^[4] plays a similar structural role to B^[4] (Lu et al., 2021). Whether this is true at higher pressures, where proportion of Al^[4] decreases at the expense of Al^[5] and Al^[6] is unclear. One additional factor in controlling the extent of B coordination change in silicate liquids not considered here is the presence of water. Small amounts of water are incorporated in silicate liquids and many nominally anhydrous minerals as OH⁻, i.e. via protonation of underbonded O atoms. B incorporation in olivine results in the formation of trigonal BO₃⁻ on vacant tetrahedral sites, and protonation of an adjacent O atom (Ingrin et al., 2014). If coupled B and H defects are also stable in silicate melts, protonation of O atoms might reduce the extent of B coordination changes at pressure by inhibiting formation of BO₄ units, at least in relatively hydrous silicate liquids. Schmidt et al. (2004) found spectroscopic evidence for the formation of B-OH complexes in albite glasses synthesised at 1 GPa, with the presence of B in glasses resulting in the formation of OH units at the expense of molecular water. However, Schmidt et al. (2004) also found that the presence of water results in a slight increase in proportion of B^[4]/(B^[3]+B^[4]), from 2 to 6%, instead suggesting that the presence of water and coupling of B and OH, at least in albitic glass, results in increases the proportion of tetrahedral coordinated B.

Implications for B Isotope Fractionation

B is readily mobilised during fluid-rock interaction, and concentrations of B, and proportions of its two stable isotopes ¹⁰B and ¹¹B, are powerful tracers of fluid-mediated processes. By extension, B contents and isotopic compositions in silicate magmas record processes of fluid transport deep within the Earth. Peacock and Hervig (1999) noted that in subduction zone environments, across arc variations in both B concentrations and in isotopic fractionation of B, can be explained by progressive ¹¹B-enriched fluid loss from the subducting slab. In fluids at ambient pressure, trigonal B dominates, i.e. B(OH)₃ (Schmidt et al., 2005). Although slight changes in average B coordination in fluids are noted with increasing pressure up to 2 GPa (Sanchez-Valle et al., 2005; Schmidt et al., 2005) trigonal B is proposed to dominate in higher pressure fluids as well, at least under the conditions of sub-arc magmatism. In contrast, most hydrous phases stable in subducting compositions have B in tetrahedral coordination. A strong preference predicted for ¹¹B for trigonal coordination, and ¹⁰B for tetrahedral coordination is, therefore, proposed to account for marked trends in B isotopic composition (Peacock and Hervig, 1999; Hervig et al., 2002). Progressive dehydration of subducting slabs (mineral-fluid equilibration) depletes slabs in B, and especially in ¹¹B, such that fluids expelled at greater depths are isotopically lighter. If this signature is inherited by magmas formed by flux of slab-derived fluids into the mantle wedge, arc magmas will be isotopically light, with a predictable relationship between B content and isotopic composition with depth of the subducting slab (De Hoog and Savov, 2018).

For some other silicates, such as olivine and clinopyroxene (Hålenius et al., 2010; Ingrin et al., 2014) B is preferentially incorporated as B^[3]. Equilibration of B between residual olivine and clinopyroxene and fluids at sub-arc conditions, for example during serpentine dehydration, could result in the opposite signature of ¹¹B enrichment in slabs (De Hoog and Savov, 2018). Recent studies also consider the effect of multiple fluid extraction events and B isotopic disequilibria during slab dehydration (Clarke et al., 2020), the extent to which melt inclusions record multiple isotopic signatures of slab-derived material (Iveson et al., 2021), and even the extent to which ocean island basalts record a signature of boron subduction beyond the depths of sub-arc magmatism and into the deep mantle (Walowski et al., 2021). However, interpretation of geochemical data is typically reliant on simple assumptions of the extent of B isotope fractionation, and B coordination environments. In particular, there is a broad lack of data on B coordination under high pressure conditions, and the ability of melts to record isotopic signatures from subduction-derived fluids.

Hervig et al. (2002) noted only minor partitioning of B between silicate melt and fluids, but preferential partitioning of ¹¹B into fluids. Importantly, they noted large isotopic fractionation between basaltic melt and aqueous fluid at magmatic temperatures (approx. 3‰ at 1,100°C). Based on comparisons of melt-fluid and mineral-fluid fractionation, Hervig et al. (2002) suggested that B is incorporated into silicate melt as B^[4]. This is, however, inconsistent with data presented here, highlighting 1) the importance of secondary effects on melt/fluid B isotope fractionation, and/or 2) that fractionation is simply dependent on the proportion on B^[4] in silicate melt. As an aside, B isotopic compositions of natural tourmaline are similarly inconsistent with fractionation trends suggested by Hervig et al. (2002). For example, data predict that hydrothermal (late-stage) tourmaline should be systematically and strongly enriched in ¹¹B relative to magmatic (early) tourmaline. This is counter to studies of Tonarini et al. (1998) and Trumbull et al. (2013) which instead indicate minimal fractionation of boron isotope during magmatic-hydrothermal processes, or the importance of complex and local fractionation effects. Regardless of the exact cause of liquid/fluid B isotope partitioning, an additional effect of pressure on B coordination in magmas cannot be ignored. Aqueous fluids in equilibrium with silicate liquids will be isotopically heavy, and silicate liquids will be isotopically light, even at magmatic conditions. Experimental data on B isotope partitioning for basaltic melt/fluid from Hervig et al. (2002) was obtained from experiments conducted at < 0.2 GPa. Even over the modest pressure range 0–3 GPa, the fraction of B^[4] in comparable Di-An liquids increases from approximately 5–20% at 1800K. This increase may be significantly greater at lower temperatures. As such, under conditions of subarc magmatism, fractionation of B isotopes during fluid/melt should be significantly greater than predicted by Hervig et al. (2002).

Similarly, progressive changes in B coordination in melt could also result in a control of pressure on isotopic exchange between silicate melts and minerals. For example, preferential incorporation of B^[3] in olivine (Ingrin et al., 2014), and an increase in proportion of B^[3] in silicate liquids could result in increased isotopic fractionation of B, and increasingly isotopically light magma with pressure/depth of melting. The extent of any fractionation of B isotopes in magmatic systems will depend on the strong control of temperature, with limited fractionation at temperatures approaching 1,400°C based on data from Hervig et al. (2002). However, the simulations presented here highlight an important effect of pressure on B coordination in silicate melts which cannot be ignored. Further research on the incorporation mechanisms of B in silicate systems and aqueous fluids at high pressure, and on the controls of crystal/melt/fluid chemistry on B isotope fractionation are required if the true potential of B as a tracer of fluid-mediated processes in the deep Earth is to be realised.

Data Availability Statement

Data are available at the University of Bristol data repository, data.bris, at https://doi.org/10.5523/bris.2h8j2lkec4mms20a5z0kpsrght.

Author Contributions

GB and JD jointly devised the concept for work presented here. JD conducted the simulations and data analysis, and GB assisted in data interpretation. Both authors contributed equally to the preparation of this manuscript.

Funding

This work was supported by NERC standard grant NE/P002951/1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

JD thanks Dr Oliver Lord (Bristol) for funding provision. This work was carried out using the computational facilities of the Advanced Computing Research Centre (ACRC), University of Bristol—http://www/.bris.ac.uk/acrc/. JD thanks Callum Wright (ACRC) for HPC sysadmin support.

References

Adjaoud, O., Steinle-Neumann, G., and Jahn, S. (2008). Mg₂SiO₄ Liquid under High Pressure from Molecular Dynamics. Chem. Geol. 256, 185–192. doi:10.1016/j.chemgeo.2008.06.031