- 1CIC-FEMD/ILCEC, Key Laboratory of Meteorological Disaster of Ministry of Education (KLME), Nanjing University of Information Science and Technology, Nanjing, China
- 2School of Atmospheric Sciences, Nanjing University of Information Science and Technology, Nanjing, China
- 3Shaoxing Meteorological Burea, Shaoxing, China
It is well known that the El Niño-Southern Oscillation (ENSO) could affect the precipitation anomalies in the central-western Indian Ocean (CWIP) through modifying the Walker circulation, with an El Niño generally accompanied by an enhanced CWIP. In this study, we find that this positive association is modulated by the Atlantic Multidecadal Oscillation (AMO). When ENSO and AMO are out-of-phase combinations (i.e., AMO-/El Niño and AMO+/La Niña), the CWIP is significantly stronger than that when they are in-phase cooperated. It is suggested that the AMO’s modulating effect mainly comprises two pathways that influence ENSO’s linkage with the CWIP. On one hand, AMO could modulate the SST variability in the central-eastern tropical Pacific with a stronger ENSO SST amplitude during its negative phase, thus influencing the ENSO-CWIP relationship. On the other hand, AMO is associated with a multidecadal atmospheric variation in the Walker circulation. The weakened circulation during the negative AMO phase favors an anomalous ascending flow over the central-western Indian Ocean, thereby favoring an enhanced CWIP there. Therefore, El Niño is accompanied by a more pronounced CWIP during the negative AMO phase compared to that during a positive AMO phase. For La Niña episodes, however, these two pathways have opposite modulation effects. Although AMO+/La Niña is weaker than AMO-/La Niña, the accompanied CWIP is relatively stronger as an multidecadal dry background induced by the Atlantic warming reinforces the negative CWIP anomaly generated by La Niña. We here highlight that the AMO decadal forcing needs to be considered when investigating the Indian Ocean atmospheric variabilities during ENSO events.
Introduction
As the predominant year-to-year climate variability on the planet, El Niño-Southern Oscillation (ENSO) arises through the coupled air-sea interactions in the tropical Pacific. Although rooted in the tropical Pacific, ENSO can lead to global atmospheric circulation and patterns of climate variability worldwide (e.g., van Loon and Madden, 1981; Ropelewski and Halpert, 1987; Trenberth et al., 1998; Trenberth and Caron, 2000; McPhaden et al., 2006). When El Niño events occur, the atmospheric anomalies are first felt in the tropical Pacific. The warm sea surface temperature (SST) anomalies cause the edge of the Pacific warm pool extending eastward, leading to a reorganization of tropical atmospheric convection with the heating source moving farther east of its normal position. Thus, anomalous ascending motions and wet conditions occur in the central-eastern Pacific, while subsidence and precipitation deficits emerge in the west, weakening the Walker circulation (Ropelewski and Halpert, 1987). These reorganizations of the Walker circulation and atmospheric convection are further responsible for generating remote atmospheric or SST teleconnections (e.g., Klein et al., 1999; Lau and Nath, 2003). For example, the eastward shift of the Walker cell during El Niño events induces anomalous subsidence over the central-western Indian Ocean (Trenberth et al., 1998; Xie et al., 2016; Wang, 2019), reducing precipitation and cloudiness there with anticyclonic anomalies, which contribute to increasing SST with a warm Indian Ocean basin mode (IOBM) pattern through both enhanced downward solar and reduced latent upward heat fluxes (Klein et al., 1999; Lau and Nath, 2003; Tokinaga and Tanimoto, 2004).
However, observations have shown that ENSO teleconnections exhibit considerable multi-scale spatio-temporal variabilities (e.g., Wang et al., 2000; Mariotti et al., 2002; Chen et al., 2014; Geng et al., 2017; 2020). For instance, the anomalous western North Pacific (WNP) anticyclone, which bridges ENSO and the East Asian monsoon, is detected to have been weakened since the mid-1990s (Chen et al., 2014; Geng et al., 2020). The decadal variations in ENSO teleconnections are demonstrated to be closely associated with the change of ENSO properties modulated by interdecadal natural variabilities (e.g., Lu and Dong, 2008; Zhang et al., 2014; Geng et al., 2020). It is argued that the Pacific Decadal Oscillation (PDO) could play some role in modulating ENSO decadal behaviors (Fedorov and Philander, 2000, 2001; Verdon and Franks, 2006; Kravtsov, 2012; Chung and Li, 2013) and thus modifying ENSO teleconnections (Feng et al., 2014; Watanabe and Yamazaki, 2014; Liu et al., 2021). However, these viewpoints are challenged by the argument that the Pacific multidecadal mean state changes could result from averaging over the skewed ENSO system (Schopf and Burgman, 2006) and thus a substantial fraction of the PDO signal may be caused by ENSO (Alexander et al., 2002; Newman et al., 2003; Wang et al., 2012; Di Lorenzo et al., 2015).
As the basin-wide SST mode in the North Atlantic region with a period of 60–80 years, the Atlantic Multidecadal Oscillation (AMO) has also been widely proposed as an important forcing modulating ENSO’s decadal variabilities (Dong et al., 2006; Dong and Sutton, 2007; Kang et al., 2014; Yu et al., 2015; Levine et al., 2017; Wang et al., 2017; Cai et al., 2019; Wang, 2019). A multidecadal Atlantic warming is associated with strengthened Walker circulation and trade winds in the western and central tropical Pacific. This background change is conducive to a deepened thermocline and weakened vertical stratification in the equatorial Pacific, which weakens the coupled instability via which ENSO events grow (Zebiak and Cane, 1987; Jin et al., 2006), thus reducing the ENSO SST amplitude (Dong et al., 2006; Dong and Sutton, 2007; Timmermann et al., 2007; Li et al., 2016; Levine et al., 2017; Gong et al., 2020). In addition, there may also exists a physical linkage between the North Atlantic warming and the zonal structure change of El Niño SST anomalies (Yu et al., 2015). Correspondingly, ENSO teleconnections are also found to be modulated by the AMO through modifying the amplitude or zonal structure of ENSO SST anomalies (e.g., Lu and Dong., 2008; Chen et al., 2014; Geng et al., 2017, 2020).
Although previous studies have demonstrated that ENSO could affect the central-western Indian Ocean precipitation (CWIP), but the nonstationary features of this teleconnection have not been sufficiently elucidated. In particular, previous studies have revealed that ENSO amplitude and spatial pattern is modulated by the AMO forcing on decadal time scales (e.g., Dong et al., 2006; Kang et al., 2014; Gong et al., 2020), it is interesting to explore whether the relation of ENSO with the CWIP is modulated by the AMO. Because of a larger amplitude of ENSO SST anomaly in the negative AMO phase, the CWIP anomaly during ENSO mature winters is expected to be stronger than those in the positive phase. However, in this paper, we find that the intensity of CWIP anomaly during ENSO winters is not necessarily consistent with the decadal amplitude changes in the ENSO SST anomaly. This mismatch between ENSO SST and CWIP anomaly can be largely attributed to AMO’s another modulating pathway through generating a multidecadal atmospheric variation in the Walker circulation. In the remainder of this paper, Data and Methodology describes the utilized datasets, methodologies, and model simulations. In The Relation of ENSO With the CWIP Modulated by AMO, we explore the modulation effect of the relation between ENSO and CWIP by the AMO. Next, based on observations and a suit of idealized pacemaker experiments from a coupled general circulation model (CGCM), the possible mechanisms that can explain this AMO modulation effect are presented in Possible Mechanisms. Conclusion and Discussion presents the main conclusion discussions.
Data and Methodology
Datasets
We primarily utilize monthly datasets (1948–2019) in this work. Global SST is derived from the National Oceanic and Atmospheric Administration (NOAA) Extended Reconstructed SST analysis, version 3 (ERSST, Smith et al., 2008). Atmospheric circulations are analyzed based on the National Centers for the Environmental Prediction/National Center for the Atmospheric Research (NCEP/NCAR) reanalysis data (Kalnay et al., 1996). The precipitation anomalies are examined using the NOAA’s precipitation reconstruction dataset (PREC) (Chen et al., 2002). To further test our results, we also utilize the atmospheric circulations from the NOAA-CIRES-DOE 20th Century Reanalysis version 3 (20CRv3) (Slivinski et al., 2019) and the precipitation provided by the Climate Prediction Center (CPC) Merged Analysis of Precipitation (CMAP) (Xie et al., 1997). The horizontal spatial resolutions are 2 × 2° for the SST dataset and 2.5 × 2.5° for the atmospheric circulation and precipitation datasets, respectively.
Methodologies
Several climatic indices are used to facilitate our analysis. We define an AMO index as the area-averaged SST anomalies within the domain of 0°–60°N and 0°–80°W (Trenberth and Shea, 2006). A 10-year low-pass fast Fourier transform (FFT) filter is utilized to extract its inherent decadal variability (conclusion does not change when other filters, such as 9- and 11-year low-pass filters, is used). Based on the time evolution of the AMO index, we select the 1948–1967 and 1998–2018 periods as positive AMO phases and the 1968–1997 period as a negative AMO phase according to the filtered AMO index. The Niño-3.4 index, which is calculated as the area-averaged SST anomalies in the Niño-3.4 region (5°S–5°N, 120°–170°W), is adopted to describe ENSO intensity. Following conventions, ENSO events are defined by a threshold of ±0.5 standard deviation of the Niño-3.4 index during the boreal winter season (December-February: DJF). With this method, we can identify 23 El Niño and 26 La Niña events (Table 1). Note that all the datasets are analyzed for the boreal winter season (December-February: DJF) and the winter of 1948 represents December 1948-February 1949. All the above indices are normalized before our investigations. The linear trends have been removed from all anomalies to avoid possible interferences associated with the long-term trend. Statistical significance tests are all performed based on the two-tailed Student’s t test. It should be mentioned that the filtered decadal data are highly autocorrelated and thus the effective number of degrees of freedom, Neff, is adjusted and calculated as:
where N is the sample size and
Model Simulations
Due to the relatively short observational period, we further verify our hypotheses by employing the idealized Atlantic Multidecadal Variability (AMV, referred to as the Atlantic Multidecadal Oscillation or AMO in this paper) pacemaker simulations with the Earth System coupled climate model EC-Earth3 (EC-Earth3; Döscher et al., 2021), which were performed as part of the Decadal Climate Prediction Project (DCPP). Following the DCPP-C protocol (Boer et al., 2016), two sets of ensemble simulations have been performed, in which time-invariant SST anomalies corresponding to the warm (AMO+) and cold (AMO-) phases of the observed AMO were imposed upon the 12-months model climatology over the North Atlantic (from 10° to 65°N) using SST nudging. The model is allowed to evolve freely outside this target region. An 8°-wide buffer zone is applied at the edge of the nudging area to minimize shocks and to suppress instabilities due to artificial SST gradients. All the external forcings are set to their preindustrial values. An ensemble of 32 members is conducted for each AMO phase and each realization is integrated over a 10-year period. The first 11 months of integration are considered as a spin-up period and are discarded for the current analysis. We can thus obtain 9 winters in each ensemble of the simulations. More extensive description of the experimental protocol is provided in the technical note for AMV DCPP-C simulations: https://www.wcrpclimate.org/wgsip/documents/Tech-Note-1.pdf. We note that, when calculating anomalies in this suit of model simulations, the average of AMO+ and AMO- experiments for each realization is considered as the corresponding reference state. If the DJF SST departure from the reference state is greater than 0.5°C or less than −0.5°C, we define it as an ENSO winter.
The Relation of ENSO With the CWIP Modulated by AMO
We first display the regressed precipitation and atmospheric anomalies onto the DJF Niño-3.4 index from 1948 to 2018 in Figure 1. It can be seen that an El Niño winter is accompanied by anomalous ascending flows in the central-eastern tropical Pacific and in the western tropical Indian Ocean. And the western tropical Pacific is controlled by an evident descending flow (Figure 1B). This Walker circulation reorganization leads to low-level easterly wind anomalies over the tropical Indian Ocean, causing enhanced precipitation in the central-western part of the Ocean (Figure 1A). To show the temporal variability, we define a CWIP index as the area-average precipitation anomalies in the region of 30°S-6°N, 50°E-90°E and then display its time evolution with the Niño-3.4 index in Figure 2. It is clear that the CWIP index exhibits conspicuous interannual variability, which is significantly correlated the Niño-3.4 index. Their temporal correlation coefficient reaches up to 0.50 (exceeding the 99% confidence level), suggesting that the CWIP intensity is positively proportional to the ENSO SST amplitude. These results are in well agreements with many previous studies (e.g., Xie et al., 2002; Kao and Yu, 2009; Liu and Alexander, 2007).
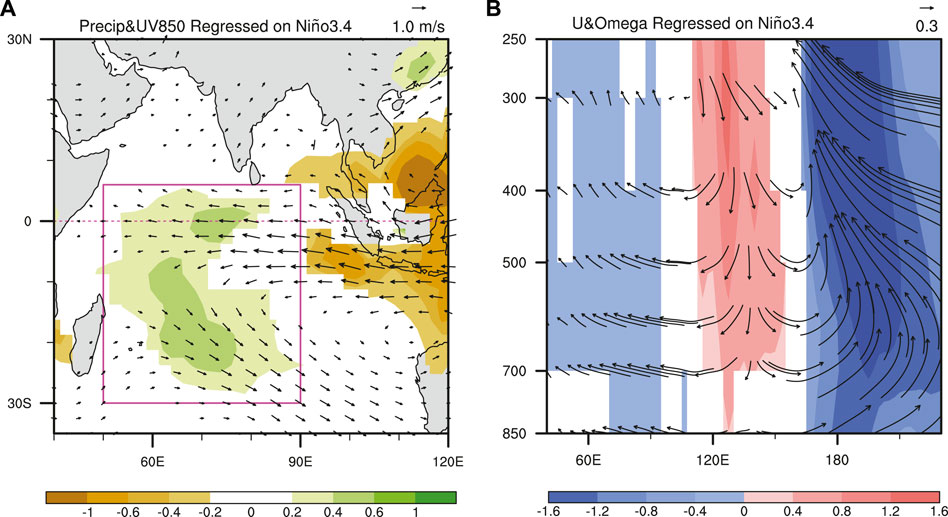
FIGURE 1. Regressed DJF anomalous (A) 850-hPa wind (vectors in m s−1), precipitation (shading in mm day−1), (B) Walker circulation and vertical velocity (shading in Pa s−1) onto the Niño-3.4 index for the 1948–2018 period. Note that the vertical velocity anomalies are multiplied by a factor of -100 for better visualization. The magenta box outlines the domain used as the definition of the CWIP index. The precipitation, 850-hPa wind and vertical velocity anomalies are only displayed when they are significant at the 90% confidence level.
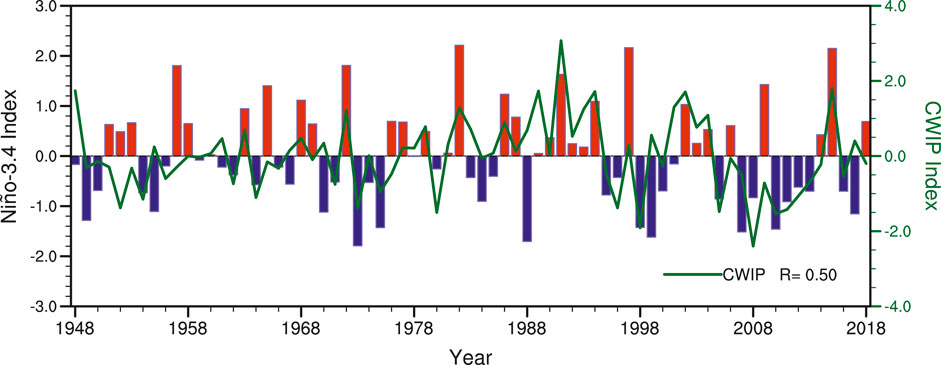
FIGURE 2. Time evolution of the DJF Niño-3.4 (bar) and CWIP (green curve) indices for the 1948–2018 period. The correlation coefficient (R) is also displayed and is significant at the 99% confidence level.
Previous studies have suggested that ENSO SST amplitude shows considerable decadal variations and is significantly modulated by the AMO. ENSO events during the negative AMO phase are generally stronger than those during the positive phase (e.g., Dong et al., 2006; Kang et al., 2014; Gong et al., 2020). Thus, it is compelling to expect that the CWIP anomaly in ENSO winters is stronger during the AMO negative phase. To verify this hypothesis, we first categorize the ENSO events into four types according to the AMO phase, that is, El Niño events with a positive AMO phase (AMO+/El Niño), El Niño events with a negative AMO phase (AMO-/El Niño), La Niña events with a positive AMO phase (AMO+/La Niña), and La Niña events with a negative AMO phase (AMO-/La Niña) (Table 2). And then display the composite SST (Figure 3) and precipitation (Figure 5) anomalies for these four cases. It can be seen that, compared with those during the positive AMO phase, both El Niño and La Niña events during the negative AMO phase mature with weaker SST anomalies in the central-eastern tropical Pacific. The composite Niño-3.4 indices in AMO+/El Niño, AMO-/El Niño, AMO+/La Niña and AMO-/La Niña winters are 1.05, 1.28, −0.95 and −1.11, respectively (Figure 4), consistent well with previous studies (Dong et al., 2006; Kang et al., 2014; Gong et al., 2020). In accordance with this decadal amplitude change in ENSO SST anomaly due to AMO modulation, we speculate that the accompanied CWIP anomaly during ENSO winters exhibit similar intensity difference. However, an unexpected result is obtained when checking the composite precipitation anomalies (Figure 5). For El Niño episodes, the DJF CWIP anomalies are more pronounced during the negative AMO phase compared to those during the positive phase. The composite CWIP indices for the AMO+/El Niño and AMO-/El Niño cases are 0.27 and 0.79 respectively (Figure 9), corresponding well to ENSO SST amplitude difference for these two cases. In contrast, La Niña winters during the negative AMO phase are accompanied by a weaker CWIP (Figures 5C,D), although their Niño-3.4 SST anomalies are stronger than those during the positive phase (Figure 4). In other words, the intensity difference of the CWIP anomalies does not match the amplitude difference of La Niña tropical Pacific SST anomalies associated with the AMO modulation.
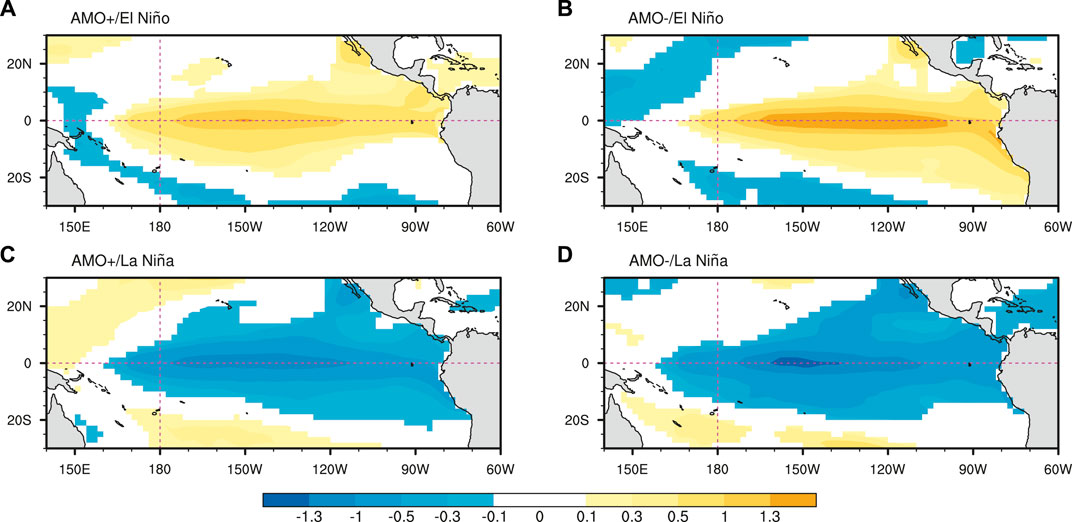
FIGURE 3. Composite SST anomalies (shading in°C) during the (A) AMO+/El Niño, (B) AMO-/El Niño, (C) AMO+/La Niña, and (D) AMO-/La Niña boreal winters. The SST anomalies are only displayed when they are significant at the 90% confidence level.
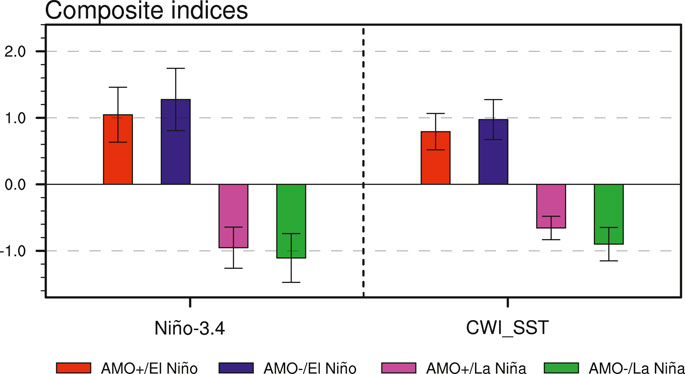
FIGURE 4. Composite Niño-3.4 and central-western Indian Ocean SST (30°S-6°N, 50°E-90°E) indices during the AMO+/El Niño (red bar), AMO-/El Niño (blue bar), AMO+/La Niña (magenta bar), and AMO-/La Niña (green bar) boreal winters. The solid bars indicate the composites exceeding the 90% confidence level. The error bars represent one standard deviation for the indices during four ENSO cases.
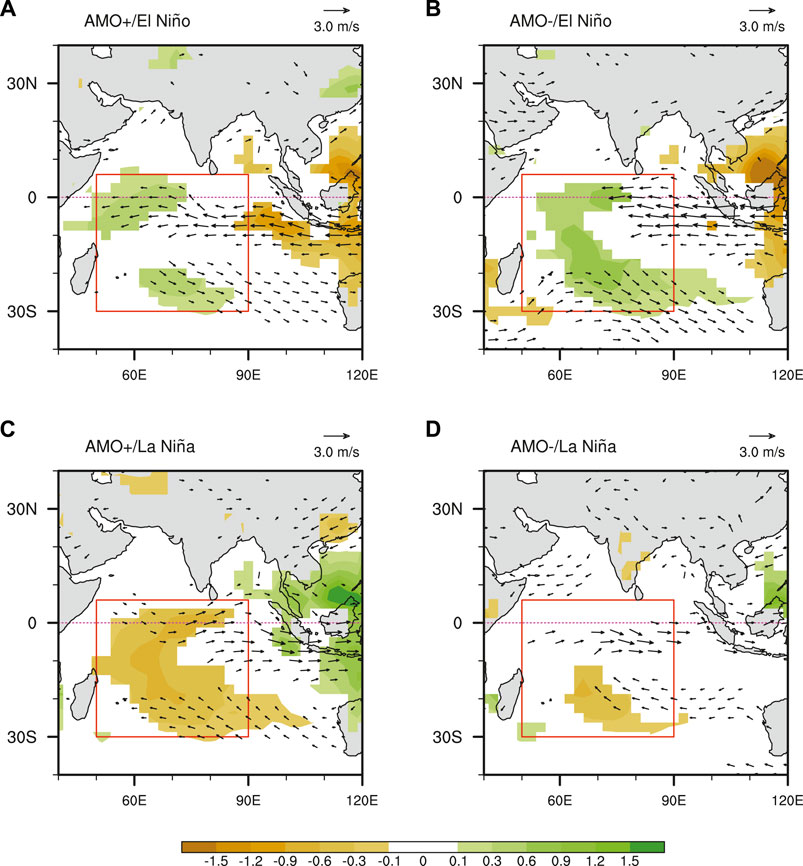
FIGURE 5. Composite 850-hPa wind (vectors in m s−1) and precipitation (shading in mm day−1) anomalies during the (A) AMO+/El Niño, (B) AMO-/El Niño, (C) AMO+/La Niña, and (D) AMO-/La Niña boreal winters. The red box outlines the domain used as the definition of the CWIP index. The wind and precipitation anomalies are only displayed when they are significant at the 90% confidence level.
Then, to examine the possible roles of local air-sea interaction, the Indian Ocean local SST indices (30°S-6°N, 50°E-90°E) during the four cases are also displayed in Figure 4. They show similar features as the Niño-3.4 indices. The SST anomaly in the tropical Indian Ocean is stronger for AMO-/La Niña winters, inconsistent with the weaker CWIP anomaly, either. It seems that, apart from via modifying ENSO-related SST amplitudes, AMO may also modulate the relation of ENSO with the CWIP in a different pathway.
Possible Mechanisms
Previous studies have shown that the AMO are closely connected with the climate variabilities in Indian Ocean region (e.g., Sun et al., 2019; Xie et al., 2021). A positive AMO could generate an anomalous descending flow in the central Indian Ocean via Atlantic-Indian Ocean multidecadal atmospheric teleconnections (Xie et al., 2021). Therefore, we speculate that there may also exist an atmospheric pathway through which AMO modifies the relation of ENSO with the CWIP. Figure 6 shows the regression patterns of DJF precipitation anomalies onto the AMO index. We can see that the precipitation anomalies in tropical Pacific and central-western Indian Ocean are both significantly associated with AMO. A positive AMO favors weakened precipitation anomalies in the central tropical Pacific and in the central-western Indian Ocean, but leads to strengthened precipitation anomalies in the western tropical Pacific. The anomalies are generally reversed during a negative AMO phase.
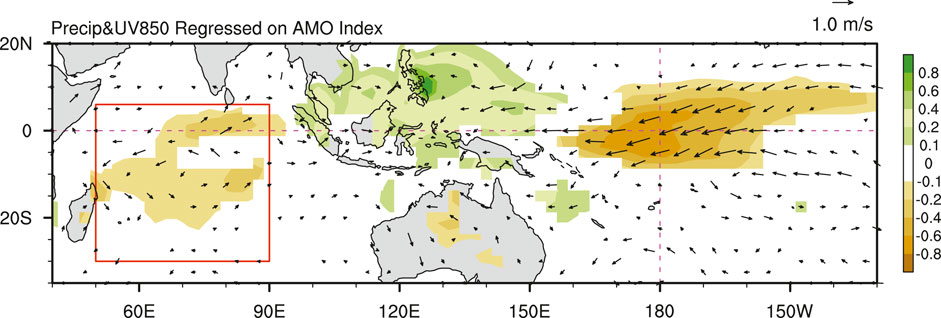
FIGURE 6. Regressed DJF 850-hPa wind (vectors in m s−1) and precipitation (shading in mm day−1) anomalies onto the AMO index for the 1948–2018 period. The red box outlines the domain used as the definition of the CWIP index. The precipitation and 850-hPa wind anomalies are only displayed when they are significant at the 90% confidence level.
To understand how the AMO physically affects the CWIP multidecadal variability, we display the regression profiles of DJF Walker circulation onto the AMO index in Figure 7. An Atlantic SST warming is accompanied by anomalous ascending flows in the western equatorial Atlantic and western equatorial Pacific regions. Meanwhile, descending flows can be observed over the central-eastern equatorial Pacific and central-western Indian Ocean. As a result of the local descending flows over the central-western Indian Ocean, the CWIP is reduced. These results are well consistent with previous studies (McGregor et al., 2014; Xie et al., 2021). Previous studies have demonstrated that the AMO is also positively correlated with the SST anomalies in the WNP region through extratropical inter-basin atmospheric teleconnections (Sun et al., 2017; 2021). During the positive AMO phase, the induced WNP warming may establish positive feedback with the anomalous Walker circulation, which could also play a role in AMO’s influence on the CWIP. This can also explain why we observe a relatively stronger WNP SST anomaly in the AMO-/El Niño and AMO+/La Niña winters in Figure 3. Nevertheless, by comparing Figure 1 with Figures 6, 7, we can find that the tropical Walker circulation and CWIP anomalies are significantly associated with both ENSO and AMO. But the impacts seem to be opposite in phase. An El Niño and a negative AMO favor ascending flows and enhanced precipitation anomalies in the central-western Indian Ocean, while La Niña events and positive AMO phases are conducive to atmospheric sinking motions and reduced precipitation anomalies there. As a result, compared with those during the positive AMO phase, El Niño winters during the negative AMO phase are accompanied by more robust ascending motions the precipitation anomalies due to their in-phase impacts (Figures 8A,B). This amplitude difference of the atmospheric anomalies between AMO+/El Niño and AMO-/El Niño winters are further reinforced because stronger El Niño events in the negative AMO phase (Figures 3A,B) also leads to more robust ascending motions and stronger CWIP. On the other hand, although La Niña events in the negative AMO phase are stronger than those in the positive phase (Figures 3C,D), the atmospheric perturbations induced by La Niña anomalous SST are partly counteracted by the opposite impacts by the remote Atlantic multidecadal forcing, thereby resulting in weaker anomaly amplitudes (Figure 8D). In comparison, AMO+/La Niña winters are accompanied by stronger descending flows and precipitation anomalies in the central-western Indian Ocean due to the in-phase influences from ENSO and AMO SST forcings (Figure 8C). These results suggest that the AMO may exert two different pathways modifying the ENSO-CWIP relationship. While AMO’s indirect modulation effect on the relation of ENSO with the CWIP is through modifying the ENSO SST anomaly amplitude, AMO’s direct influence is via generating a multidecadal atmospheric variation in the Walker circulation, which leads to the mismatch between intensities of La Niña anomalous SST and the accompanied CWIP anomaly.
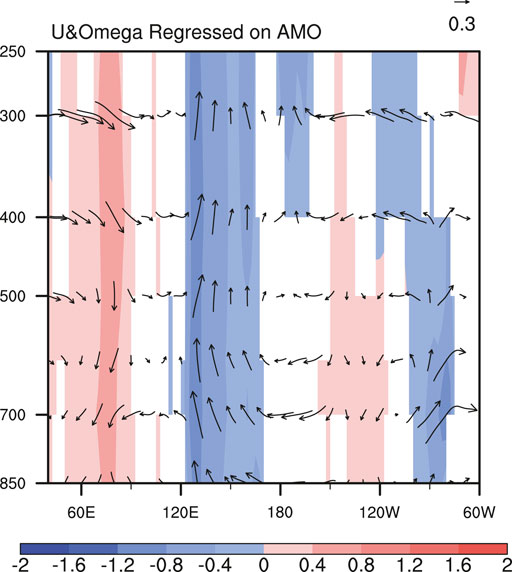
FIGURE 7. Regressed DJF Walker circulation and vertical velocity (shading in Pa s−1) anomalies onto the AMO index for the 1948–2018 period. Note that the vertical velocity anomalies are multiplied by a factor of −100 for better visualization and are displayed only when they are significant at the 90% confidence level.
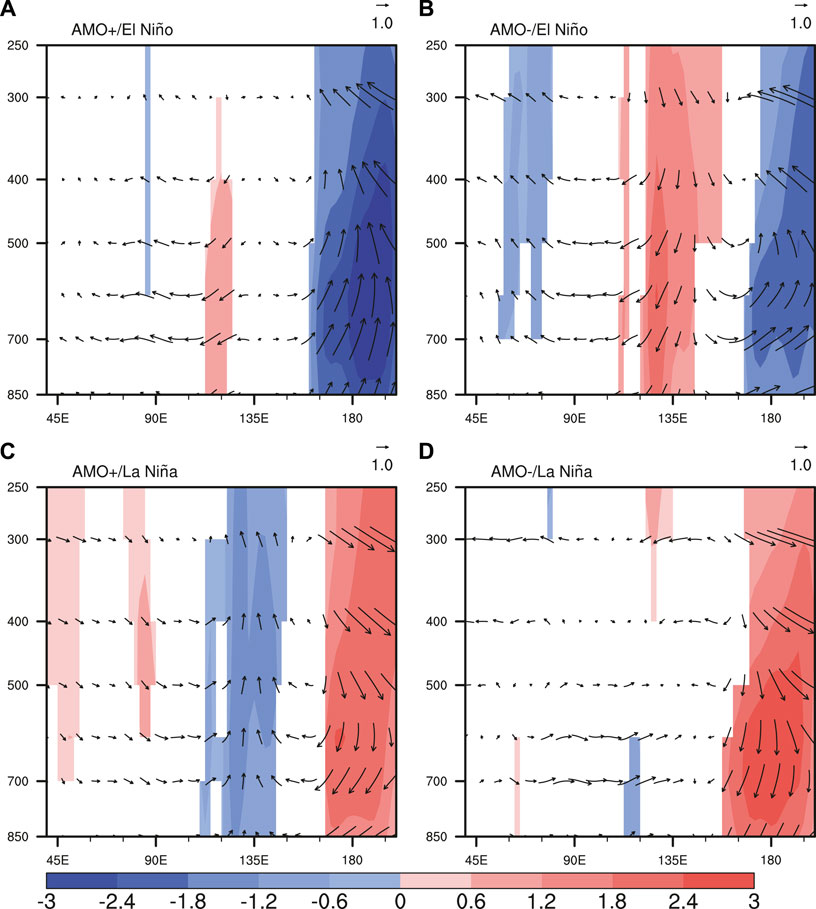
FIGURE 8. Composite Walker circulation and vertical velocity (shading in Pa s−1) anomalies during the (A) AMO+/El Niño, (B) AMO-/El Niño, (C) AMO+/La Niña, and (D) AMO-/La Niña boreal winters. Note that the anomalous vertical velocity anomalies are multiplied by a factor of −100 for better visualization and are displayed only when they are significant at the 90% confidence level.
We next compare the composite DJF CWIP indices for the four cases based on the original (i.e., observational), single-factor (Niño-3.4 index) and two-factor (Niño-3.4 and AMO indices) reconstructed anomalies in Figure 9. When only the Niño-3.4 index is considered, the reconstructed DJF CWIP anomalies during ENSO events are stronger in the AMO negative phase because of a stronger ENSO SST anomaly amplitude, which is consistent with our observed composite results for El Niño winters, suggesting a role of AMO’s indirect modulation effect via modifying the ENSO SST anomaly amplitude. This effect can be quantificationally expressed by the difference between the AMO+/El Niño and AMO-/El Niño (or the AMO+/La Niña and AMO-/La Niña) composites based on this single-factor (Niño-3.4) reconstructed CWIP index, which are −0.11 and −0.06 for El Niño and La Niña winters, respectively. However, for La Niña episodes, the single-factor reconstructed composite CWIP indices are inconsistent with the observational results, which indicates that pure ENSO SST impacts cannot explain why the CWIP anomaly in AMO+/La Niña winters is stronger than that in AMO-/La Niña winters. Only when the AMO decadal influence is considered together can the composite CWIP anomalies for the four ENSO cases show better agreements with the observational results. To quantitatively express this AMO direct decadal modulation, we first subtract the single-factor reconstructed composite CWIP indices from the two-factor reconstructed composite CWIP indices for these four ENSO cases (i.e., −0.18, 0.18, −0.11, and 0.27 respectively for AMO+/El Niño, AMO-/El Niño, AMO+/La Niña, and AMO-/La Niña winters). Then, we calculate the differences between the AMO+/El Niño and AMO-/El Niño values (or the AMO+/La Niña and AMO-/La Niña values), which are −0.36 and −0.38 for El Niño and La Niña, respectively. By comparing the direct and indirect AMO effects on the CWIP anomaly during ENSO winters, we further suggest that the AMO’s direct decadal modulation pathway through modifying the Walker circulation plays a key role in causing the observed relation of ENSO with the CWIP.
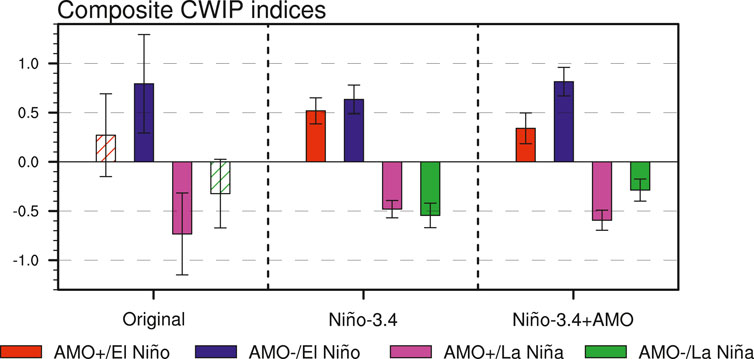
FIGURE 9. Composite CWIP indices based on the original, single-factor (i.e., Niño-3.4 index) and two-factor (i.e., Niño-3.4 and AMO indices) reconstructed anomalies for the AMO+/El Niño (red bar), AMO-/El Niño (blue curve), AMO+/La Niña (magenta bar), and AMO-/La Niña (green bar) boreal winters. The solid bars indicate the composites significant at the 90% confidence level. The error bars represent one standard deviation for the indices during four ENSO cases.
To further consolidate our conclusion, we conduct a parallel analysis based on the atmospheric circulations derived from the NOAA-CIRES-DOE 20CRv3 dataset (Supplementary Figures S1–S5). It should be noted that the obtained Walker circulation anomalies induced by ENSO and AMO in the Indian Ocean (Supplementary Figures S1B, S4) are slightly weaker than the results based on the NCEP/NCAR dataset (Figures 1B, 7), which may be related to the different schemes of data assimilation or model performance of these two reanalysis datasets (Yang et al., 2022). Despite some discrepancy, the features of precipitation and atmospheric circulation anomalies based on this NOAA-CIRES-DOE 20CRv3 dataset remain qualitatively unchanged compared to the NCEP/NCAR results. We also use the precipitation dataset from the CPC CMAP to test our hypotheses. Although the time period is relatively short (i.e., 1979–2018), similar AMO’s modulation effect can also be qualitatively reproduced (Supplementary Figures S6–S9). Next, we use a suit of idealized AMO pacemaker simulations with the coupled model EC-Earth3 that comply with the Model Intercomparison phase six (CMIP6)/DCPP-C protocol (Boer et al., 2016, see Data and Methodology for details). The ENSO events in each AMO + or AMO- realization is first identified, and then the spatial distributions of composite SST anomaly for the four ENSO cases in all AMO + or AMO- realizations are displayed in Figure 10. We can see that in the AMO- simulations, both El Niño and La Niña events are stronger than those in the AMO- experiments, which is consistent with the observational results. The simulated DJF atmospheric anomalies in the central-western Indian Ocean for the four cased are then displayed in Figure 11. Despite a relatively large spreads in the EC-Earth3 DCPP-C model simulations, both the vertical velocity and the precipitation anomalies in the central-western Indian Ocean are also relatively stronger in AMO-/El Niño and AMO+/La Niña winters, qualitatively consistent with the observational results. This consistency between the observations and model experiments further increases our confidence for the aforementioned hypothesis about the AMO modulation effects on DJF ENSO-CWIP relationship.
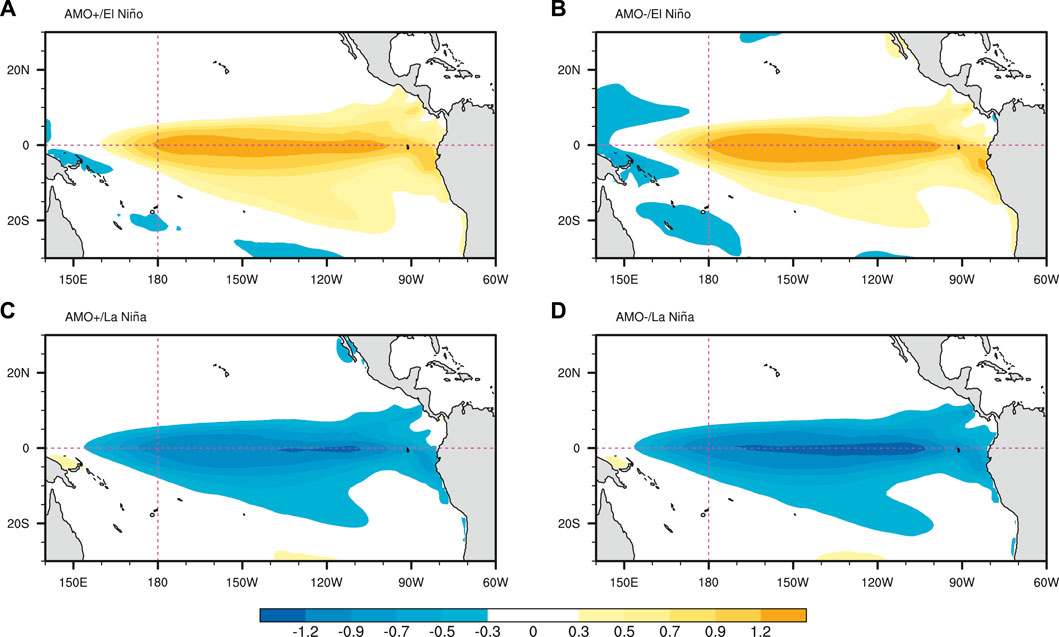
FIGURE 10. The same as Figure 3 but for the composite SST anomalies based on the EC-Earth3 DCPP-C simulations.
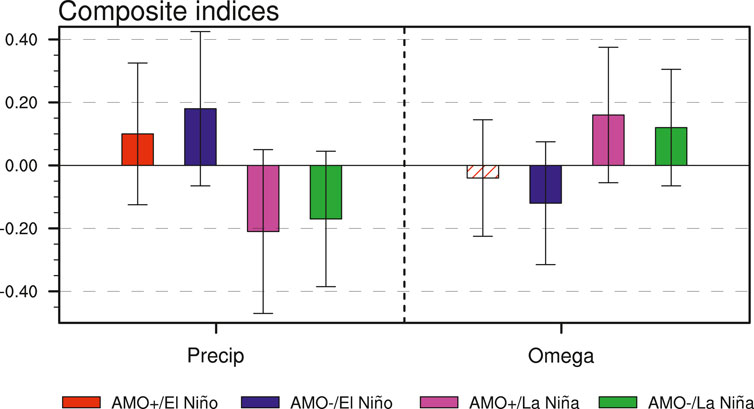
FIGURE 11. Composite anomalous precipitation and vertical velocity indices in central-western Indian Ocean (30°S-6°N, 50°E-90°E) for the AMO+/El Niño (red bar), AMO-/El Niño (blue curve), AMO+/La Niña (magenta bar), and AMO-/La Niña (green bar) boreal winters in the EC-Earth3 DCPP-C simulations. The solid bars indicate that the composite significant at the 90% confidence level. The error bars represent one standard deviation for the indices during four ENSO cases.
Conclusion and Discussion
It has been well known that ENSO can exert significant impacts on the CWIP via modifying the Walker circulation. Based on both observations and a suit of coupled model idealized pacemaker simulations, the present study demonstrates that this positive ENSO-CWIP association is modulated of by the AMO. We suggest that AMO’s modulation effects include two pathways. On the one hand, AMO could affect ENSO SST variability through “atmospheric bridge-thermocline feedback” (e.g., Dong et al., 2006; Dong and Lu, 2013; Gong et al., 2020). During a negative AMO phase, ENSO events mature with stronger SST anomalies in the central-eastern tropical Pacific. Therefore, the relation of ENSO with the CWIP should be enhanced during the negative AMO phase, with stronger CWIP anomalies in the AMO-/El Niño and AMO-/La Niña winters. However, we find that the CWIP anomalies of ENSO winters during different AMO phases are not necessarily consistent with the ENSO SST amplitude changes. While El Niño in the negative AMO phase corresponds to stronger CWIP anomalies due to its stronger central-eastern tropical Pacific SST anomaly than that in the positive AMO phase, a different picture is observed for La Niña. Compared with those in the positive AMO phase, La Niña events in the negative AMO phase are accompanied by a weaker CWIP, although their SST anomalies in the central-eastern tropical Pacific are stronger. There exists a mismatch between the intensities of La Niña tropical SST and central-western Indian Ocean atmospheric anomalies. Strong La Niña SST anomaly during the negative AMO phase does not necessarily concur with strong CWIP anomalies.
We suggest that this mismatch for La Niña events are largely attributed to AMO’s another direct decadal modulation pathway through the atmospheric teleconnection in Walker circulation. Besides the significant relationship with ENSO on the interannual time scale, The DJF CWIP anomaly is also significantly associated with the AMO SST forcing on decadal time scales. But the influences from AMO and ENSO are opposite in phase. An AMO warming could generate an anomalous descending flow in the central-western Indian Ocean through changing the Walker circulation, thus reducing the CWIP anomalies there. Therefore, when La Niña coincides with a positive AMO, the anomalous descending flows in central-western Indian Ocean is superimposed, which gives rise to a stronger negative CWIP anomaly. In contrast, during AMO-/La Niña winters, the atmospheric descending anomalies in central-western Indian Ocean induced by La Niña anomalous SST are partly counteracted by the multidecadal anomalous ascending flow associated with the AMO, thus resulting in weaker CWIP anomaly. For El Niño episodes, the enhanced precipitation is strengthened and weakened during the negative and positive AMO phases, respectively, which further reinforces the amplitude difference of the CWIP anomaly caused by El Niño SST anomaly in the central-eastern tropical Pacific. The idealized AMO pacemaker experiments based on the coupled model EC-Earth3 can well capture these observational results, further consolidating the two pathways through which AMO modulates the relation of ENSO with the CWIP.
In the present study, we emphasize the Atlantic multidecadal (i.e., AMO) SST modulation effects on the relation of ENSO with the CWIP during the boreal winter. The conclusions carry important implications for our climate research community. To accurately simulate the atmospheric anomalies in the Indian Ocean during ENSO events, especially during La Niña events, the remote AMO decadal modulation needs to be considered besides the contribution from ENSO interannual SST variability itself. It should be noted that, we basically regard the atmospheric anomalies in the central-western Indian Ocean as passive responses to the anomalous ENSO-related SST during the mature winter in this study. It would be interesting to investigate whether these atmospheric anomalies can feedback on the subsequent SST evolution characteristics in the tropical oceans. In addition, as an important source of atmospheric perturbations, different atmospheric anomalies in the Indian Ocean will certainly produce different ENSO extra-tropical teleconnections and climate impacts, which are also important targets for further investigations.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
XG conceived the idea. CZ and XG conducted the data analysis and prepared the tables and figures. All authors discussed the results. CZ wrote the original draft and XG reviewed and edited this paper.
Funding
This work is supported by the National Natural Science Foundation of China (42088101, 41905073).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to thank the editor and two reviewers for their constructive suggestions and comments that significantly improved this paper.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.866241/full#supplementary-material
References
Alexander, M. A., Bladé, I., Newman, M., Lanzante, J. R., Lau, N.-C., and Scott, J. D. (2002). The Atmospheric Bridge: The Influence of ENSO Teleconnections on Air-Sea Interaction over the Global Oceans. J. Clim. 15 (16), 2205–2231. doi:10.1175/1520-0442(2002)015<2205:TABTIO>2.0.CO
Boer, G. J., Smith, D. M., Cassou, C., Doblas-Reyes, F., Danabasoglu, G., Kirtman, B., et al. (2016). The Decadal Climate Prediction Project (DCPP) Contribution to CMIP6. Geosci. Model. Dev. 9 (10), 3751–3777. doi:10.5194/gmd-9-3751-2016
Cai, W., Wu, L., Lengaigne, M., Li, T., McGregor, S., Kug, J.-S., et al. (2019). Pantropical Climate Interactions. Science 363 (6430). doi:10.1126/science.aav4236
Chen, M., Xie, P., Janowiak, J. E., and Arkin, P. A. (2002). Global Land Precipitation: A 50-yr Monthly Analysis Based on Gauge Observations. J. Hydrometeor 3 (3), 249–266. doi:10.1175/1525-7541(2002)003%3c0249:GLPAYM%3e2.0
Chen, W., Lu, R., and Dong, B. (2014). Intensified Anticyclonic Anomaly over the Western North Pacific during El Niño Decaying Summer under a Weakened Atlantic Thermohaline Circulation. J. Geophys. Res. Atmos. 119 (24), 13637–13650. doi:10.1002/2014JD022199
Chung, P.-H., and Li, T. (2013). Interdecadal Relationship between the Mean State and El Niño Types*. J. Clim. 26 (2), 361–379. doi:10.1175/JCLI-D-12-00106.1
Di Lorenzo, E., Liguori, G., Schneider, N., Furtado, J. C., Anderson, B. T., and Alexander, M. A. (2015). ENSO and Meridional Modes: A Null Hypothesis for Pacific Climate Variability. Geophys. Res. Lett. 42 (21), 9440–9448. doi:10.1002/2015GL066281
Dong, B., and Lu, R. (2013). Interdecadal Enhancement of the Walker Circulation over the Tropical Pacific in the Late 1990s. Adv. Atmos. Sci. 30 (2), 247–262. doi:10.1007/s00376-012-2069-9
Dong, B., and Sutton, R. T. (2007). Enhancement of ENSO Variability by a Weakened Atlantic Thermohaline Circulation in a Coupled GCM. J. Clim. 20 (19), 4920–4939. doi:10.1175/JCLI4284.1
Dong, B., Sutton, R. T., and Scaife, A. A. (2006). Multidecadal Modulation of El Niño-Southern Oscillation (ENSO) Variance by Atlantic Ocean Sea Surface Temperatures. Geophys. Res. Lett. 33 (8). doi:10.1029/2006GL025766
Döscher, R., Acosta, M., Alessandri, A., Anthoni, P., Arneth, A., Arsouze, T., et al. (2021). The EC-Earth3 Earth System Model for the Climate Model Intercomparison Project 6. Geoscientific Model. Develop. Discuss., 1–90.
Fedorov, A. V., and Philander, S. G. (2001). A Stability Analysis of Tropical Ocean-Atmosphere Interactions: Bridging Measurements and Theory for El Niño. J. Clim. 14 (14), 3086–3101. doi:10.1175/1520-0442(2001)014%3c3086:ASAOTO%3e2.0
Fedorov, A. V., and Philander, S. G. (2000). Is El Nino Changing? Science 288 (5473), 1997–2002. doi:10.1126/science.288.5473.1997
Feng, J., Wang, L., and Chen, W. (2014). How Does the East Asian Summer Monsoon Behave in the Decaying Phase of El Niño during Different PDO Phases? J. Clim. 27 (7), 2682–2698. doi:10.1175/jcli-d-13-00015.1
Geng, X., Zhang, W., Jin, F.-F., Stuecker, M. F., and Levine, A. F. Z. (2020). Modulation of the Relationship between ENSO and its Combination Mode by the Atlantic Multidecadal Oscillation. J. Clim. 33 (11), 4679–4695. doi:10.1175/JCLI-D-19-0740.1
Geng, X., Zhang, W., Stuecker, M. F., Liu, P., Jin, F.-F., and Tan, G. (2017). Decadal Modulation of the ENSO-East Asian winter Monsoon Relationship by the Atlantic Multidecadal Oscillation. Clim. Dyn. 49 (7), 2531–2544. doi:10.1007/s00382-016-3465-0
Gong, Y., Li, T., and Chen, L. (2020). Interdecadal Modulation of ENSO Amplitude by the Atlantic Multi-Decadal Oscillation (AMO). Clim. Dyn. 55 (9), 2689–2702. doi:10.1007/s00382-020-05408-x
Jin, F.-F., Kim, S. T., and Bejarano, L. (2006). A Coupled-Stability index for ENSO. Geophys. Res. Lett. 33 (23). doi:10.1029/2006GL027221
Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., et al. (1996). The NCEP/NCAR 40-year Reanalysis Project. Bull. Amer. Meteorol. Soc. 77 (3), 437–471. doi:10.1029/2006GL02722110.1175/1520-0477(1996)077<0437:tnyrp>2.0.co;2
Kang, I.-S., No, H.-h., and Kucharski, F. (2014). ENSO Amplitude Modulation Associated with the Mean SST Changes in the Tropical central Pacific Induced by Atlantic Multidecadal Oscillation. J. Clim. 27 (20), 7911–7920. doi:10.1175/JCLI-D-14-00018.1
Kao, H.-Y., and Yu, J.-Y. (2009). Contrasting Eastern-Pacific and central-Pacific Types of ENSO. J. Clim. 22 (3), 615–632. doi:10.1175/2008JCLI2309.1
Klein, S. A., Soden, B. J., and Lau, N.-C. (1999). Remote Sea Surface Temperature Variations during ENSO: Evidence for a Tropical Atmospheric Bridge. J. Clim. 12 (4), 917–932. doi:10.1175/1520-0442(1999)012<0917:RSSTVD>2.0.CO
Kravtsov, S. (2012). An Empirical Model of Decadal ENSO Variability. Clim. Dyn. 39 (9), 2377–2391. doi:10.1007/s00382-012-1424-y
Lau, N.-C., and Nath, M. J. (2003). Atmosphere-Ocean Variations in the Indo-Pacific Sector during ENSO Episodes. J. Clim. 16 (1), 3–20. doi:10.1175/1520-0442(2003)016<0003:AOVITI>2.0.CO
Levine, A. F. Z., McPhaden, M. J., and Frierson, D. M. W. (2017). The Impact of the AMO on Multidecadal ENSO Variability. Geophys. Res. Lett. 44 (8), 3877–3886. doi:10.1002/2017GL072524
Li, X., Xie, S.-P., Gille, S. T., and Yoo, C. (2016). Atlantic-induced Pan-Tropical Climate Change over the Past Three Decades. Nat. Clim Change 6 (3), 275–279. doi:10.1038/nclimate2840
Liu, F., Zhang, W., Jin, F.-F., and Hu, S. (2021). Decadal Modulation of the ENSO-Indian Ocean Basin Warming Relationship during the Decaying Summer by the Interdecadal Pacific Oscillation. J. Clim. 34 (7), 2685–2699. doi:10.1175/jcli-d-20-0457.1
Liu, Z., and Alexander, M. (2007). Atmospheric Bridge, Oceanic Tunnel, and Global Climatic Teleconnections. Rev. Geophys. 45 (2). doi:10.1029/2005RG000172
Lu, R., and Dong, B. (2008). Response of the Asian Summer Monsoon to Weakening of Atlantic Thermohaline Circulation. Adv. Atmos. Sci. 25 (5), 723–736. doi:10.1007/s00376-008-0723-z
Mariotti, A., Zeng, N., and Lau, K. M. (2002). Euro-Mediterranean Rainfall and ENSO-A Seasonally Varying Relationship. Geophys. Res. Lett. 29 (12), 59–515954. doi:10.1029/2001GL014248
McGregor, S., Timmermann, A., Stuecker, M. F., England, M. H., Merrifield, M., Jin, F.-F., et al. (2014). Recent Walker Circulation Strengthening and Pacific Cooling Amplified by Atlantic Warming. Nat. Clim Change 4 (10), 888–892. doi:10.1038/nclimate2330
McPhaden, M. J., Zebiak, S. E., and Glantz, M. H. (2006). ENSO as an Integrating Concept in Earth Science. science 314 (5806), 1740–1745. doi:10.1126/science.1132588
Newman, M., Compo, G. P., and Alexander, M. A. (2003). ENSO-forced Variability of the Pacific Decadal Oscillation. J. Clim. 16 (23), 3853–3857. doi:10.1175/1520-0442(2003)016<3853:EVOTPD>2.0.CO
Pyper, B. J., and Peterman, R. M. (1998). Comparison of Methods to Account for Autocorrelation in Correlation Analyses of Fish Data. Can. J. Fish. Aquat. Sci. 55 (9), 2127–2140. doi:10.1139/f98-104
Ropelewski, C. F., and Halpert, M. S. (1987). Global and Regional Scale Precipitation Patterns Associated with the El Niño/Southern Oscillation. Mon. Wea. Rev. 115 (8), 1606–1626. doi:10.1175/1520-0493(1987)115%3c1606
Schopf, P. S., and Burgman, R. J. (2006). A Simple Mechanism for ENSO Residuals and Asymmetry. J. Clim. 19 (13), 3167–3179. doi:10.1175/JCLI3765.1
Slivinski, L. C., Compo, G. P., Whitaker, J. S., Sardeshmukh, P. D., Giese, B. S., McColl, C., et al. (2019). Towards a More Reliable Historical Reanalysis: Improvements for Version 3 of the Twentieth century Reanalysis System. Q. J. R. Meteorol. Soc. 145 (724), 2876–2908. doi:10.1002/qj.3598
Smith, T. M., Reynolds, R. W., Peterson, T. C., and Lawrimore, J. (2008). Improvements to NOAA's Historical Merged Land-Ocean Surface Temperature Analysis (1880-2006). J. Clim. 21 (10), 2283–2296. doi:10.1175/2007JCLI2100.1
Sun, C., Kucharski, F., Li, J., Jin, F. F., Kang, I. S., and Ding, R. (2017). Western Tropical Pacific Multidecadal Variability Forced by the Atlantic Multidecadal Oscillation. Nat. Commun. 8 (1), 15998. doi:10.1038/ncomms15998
Sun, C., Li, J., Kucharski, F., Kang, I. S., Jin, F. F., Wang, K., et al. (2019). Recent Acceleration of Arabian Sea Warming Induced by the Atlantic‐Western Pacific Trans‐basin Multidecadal Variability. Geophys. Res. Lett. 46 (3), 1662–1671. doi:10.1029/2018GL081175
Sun, C., Liu, Y., Xue, J., Kucharski, F., Li, J., and Li, X. (2021). The Importance of Inter‐basin Atmospheric Teleconnection in the SST Footprint of Atlantic Multidecadal Oscillation over Western Pacific. Clim. Dyn. 57 (1), 239–252. doi:10.1007/s00382-021-05705-z
Timmermann, A., Okumura, Y., An, S.-I., Clement, A., Dong, B., Guilyardi, E., et al. (2007). The Influence of a Weakening of the Atlantic Meridional Overturning Circulation on ENSO. J. Clim. 20 (19), 4899–4919. doi:10.1175/JCLI4283.1
Tokinaga, H., and Tanimoto, Y. (2004). Seasonal Transition of SST Anomalies in the Tropical Indian Ocean during El Nino and Indian Ocean Dipole Years. J. Meteorol. Soc. Jpn. 82 (4), 1007–1018. doi:10.2151/jmsj.2004.1007
Trenberth, K. E., Branstator, G. W., Karoly, D., Kumar, A., Lau, N.-C., and Ropelewski, C. (1998). Progress during TOGA in Understanding and Modeling Global Teleconnections Associated with Tropical Sea Surface Temperatures. J. Geophys. Res. 103 (C7), 14291–14324. doi:10.1029/97JC01444
Trenberth, K. E., and Caron, J. M. (2000). The Southern Oscillation Revisited: Sea Level Pressures, Surface Temperatures, and Precipitation. J. Clim. 13 (24), 4358–4365. doi:10.1175/1520-0442(2000)013%3c4358:TSORSL%3e2.0
Trenberth, K. E., and Shea, D. J. (2006). Atlantic Hurricanes and Natural Variability in 2005. Geophys. Res. Lett. 33 (12). doi:10.1029/2006GL026894
van Loon, H., and Madden, R. A. (1981). The Southern Oscillation. Part I: Global Associations with Pressure and Temperature in Northern winter. Mon. Wea. Rev. 109 (6), 1150–1162. doi:10.1175/1520-0493(1981)109%3c1150
Verdon, D. C., and Franks, S. W. (2006). Long-term Behaviour of ENSO: Interactions with the PDO over the Past 400 Years Inferred from Paleoclimate Records. Geophys. Res. Lett. 33 (6). doi:10.1029/2005GL025052
Wang, B., Wu, R., and Fu, X. (2000). Pacific-east Asian Teleconnection: How Does ENSO Affect East Asian Climate? J. Clim. 13 (9), 1517–1536. doi:10.1175/1520-0442(2000)013<1517:PEATHD>2.0.CO
Wang, C. (2019). Three-ocean Interactions and Climate Variability: A Review and Perspective. Clim. Dyn. 53 (7), 5119–5136. doi:10.1007/s00382-019-04930-x
Wang, H., Kumar, A., Wang, W., and Xue, Y. (2012). Seasonality of the Pacific Decadal Oscillation. J. Clim. 25 (1), 25–38. doi:10.1175/2011JCLI4092.1
Wang, L., Yu, J. Y., and Paek, H. (2017). Enhanced Biennial Variability in the Pacific Due to Atlantic Capacitor Effect. Nat. Commun. 8 (1), 14887–7. doi:10.1038/ncomms14887
Watanabe, T., and Yamazaki, K. (2014). Decadal-Scale Variation of South Asian Summer Monsoon Onset and its Relationship with the Pacific Decadal Oscillation. J. Clim. 27 (13), 5163–5173. doi:10.1175/jcli-d-13-00541.1
Xie, P., and Arkin, P. A. (1997). Global Precipitation: A 17-year Monthly Analysis Based on Gauge Observations, Satellite Estimates, and Numerical Model Outputs. Bull. Amer. Meteorol. Soc. 78 (11), 2539–2558. doi:10.1175/1520-0477(1997)078<2539:GPAYMA>2
Xie, S.-P., Annamalai, H., Schott, F. A., and McCreary, J. P. (2002). Structure and Mechanisms of South Indian Ocean Climate Variability. J. Clim. 15 (8), 864–878. doi:10.1175/1520-0442(2002)015<0864:SAMOSI>2.0
Xie, S.-P., Kosaka, Y., Du, Y., Hu, K., Chowdary, J. S., and Huang, G. (2016). Indo-western Pacific Ocean Capacitor and Coherent Climate Anomalies in post-ENSO Summer: A Review. Adv. Atmos. Sci. 33 (4), 411–432. doi:10.1007/s00376-015-5192-6
Xie, T., Li, J., Chen, K., Zhang, Y., and Sun, C. (2021). Origin of Indian Ocean Multidecadal Climate Variability: Role of the North Atlantic Oscillation. Clim. Dyn. 56 (9), 3277–3294. doi:10.1007/s00382-021-05643-w
Yang, Y., Li, Q., Song, Z., Sun, W., and Dong, W. (2022). A Comparison of Global Surface Temperature Variability, Extremes and Warming Trend Using Reanalysis Datasets and CMST‐Interim. Intl J. Climatology. doi:10.1002/joc.7551
Yu, J.-Y., Kao, P.-k., Paek, H., Hsu, H.-H., Hung, C.-w., Lu, M.-M., et al. (2015). Linking Emergence of the Central Pacific El Niño to the Atlantic Multidecadal Oscillation. J. Clim. 28 (2), 651–662. doi:10.1175/JCLI-D-14-00347.1
Zebiak, S. E., and Cane, M. A. (1987). A Model El Niñ-Southern Oscillation. Mon. Wea. Rev. 115 (10), 2262–2278. doi:10.1175/1520-0493(1987)115<2262:ameno>2.0.co;2
Keywords: enso, Indian ocean precipitation, walker circulation, atlantic multidecadal oscillation, teleconnection
Citation: Zhao C, Geng X and Qi L (2022) Atlantic Multidecadal Oscillation Modulates the Relation of ENSO With the Precipitation in the Central-Western Indian Ocean. Front. Earth Sci. 10:866241. doi: 10.3389/feart.2022.866241
Received: 31 January 2022; Accepted: 28 February 2022;
Published: 31 March 2022.
Edited by:
Hong-Li Ren, Chinese Academy of Meteorological Sciences, ChinaReviewed by:
Youichi Kamae, University of Tsukuba, JapanSen Zhao, University of Hawaii at Manoa, United States
Copyright © 2022 Zhao, Geng and Qi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xin Geng, Z2VuZ3hpbkBudWlzdC5lZHUuY24=
 Chiyu Zhao
Chiyu Zhao Xin Geng
Xin Geng Li Qi
Li Qi
