- 1School of Traffic & Transportation Engineering, Changsha University of Science & Technology, Changsha, China
- 2Department of Civil and Environmental Engineering, Hong Kong Polytechnic University, Hung Hom, Hong Kong SAR, China
Freeze-thaw (FT) cycling is a crucial issue in seasonal frozen regions and it will influence the mechanical properties of soils, which must be strictly considered for embankment engineering. This study conducted a series of unconsolidated and undrained triaxial tests under various closed-system FT cycles to investigate the mechanical properties of a typical embankment clay from China. Results indicated that the stress-strain curves changed from strain hardening or stabilization to softening during FT cycles. The elastic modulus was obviously weakened by FT cycles and declined sharply after the first FT action. The failure strength gradually reduced with the accumulation of FT cycles and eventually tended to be stable when the FT cycles reached 10, and the attenuation range was approximately 6–22% compared with the condition before FT cycles. Moreover, a phenomenological model on the failure strength was established by results of the tested clay in this study and validated to be robust through multiple sets of different clays data from other published literatures. Based on that, combined with the Mohr stress circle equation and envelope theory, an innovative method for rapidly obtaining the shear strength was proposed. The ensuing discoveries were that the cohesion was damaged in the course of the first few FT cycles and then kept basically constant after 10 cycles, while the internal friction angle was not sensitive to FT cycles. The normalized empirical formula was deduced and can simultaneously apply to the strain hardening, stabilization, and softening curves given the effect of FT cycles.
Introduction
In geotechnical and road areas, the mechanical properties of embankment soils have been paid sustained attention of related researchers and engineers. Moreover, given the stability and durability during the operation period, a complex and changeable climate environment is a foreseeable latent threat to the service performance of embankment soils. According to the available statistical data, the distribution area of seasonal frozen regions widely accounts for approximately 53.5 and 23% of China’s and the world’s total land area (Zhou et al., 2018). In such areas, every year the embankments are subjected to short-term or even continuous high-frequency freeze-thaw (FT) cycles (Hao et al., 2022). The violent weathering attributed to FT cycles attenuates mechanical properties of soils to varying degrees, as many failures of subsistent embankments are due to this phenomenon, e.g., uneven frost heave (Miao et al., 2020), thaw subsidence (Wang et al., 2015), slope destabilization (Gowthaman et al., 2020), and retaining wall collapse (Rui et al., 2016). Thus, it is of great academic and pragmatic significance to explore the mechanical properties of embankment soils considering repeated FT cycles.
For embankment soils suffering from FT cycles, the investigations focused on mechanical properties can be acquired in previous documents. At present, it has been generally agreed that the mechanism of soil damage owing to FT cycles is as follows: 1) on the macroscopic scale, the cryogenic suction induced unfrozen water to migrate toward the frozen area and produce ice lenses; these ice lenses thawed at the positive temperature and formed cracks in the compacted soils (Zhang et al., 2014; Aldaood et al., 2016); and 2) on the microscopic scale, the growth of pore ice makes the particles be uplifted, which is the primary reason that changes soil internal structure and thus deteriorates soil properties (Nguyen et al., 2019; Liu et al., 2020). In terms of specific properties, such as the stress-strain curve transformation as well as the failure strength, shear strength, and elastic modulus, they fluctuate with the FT cycles. By the direct shear apparatus, He et al. (2020) studied the shear behavior occurs on frozen soils-concrete interface. The results indicated the relationship between shear stress and horizontal strain generally presents a strain softening type. In particular, three characteristic stages can be observed on the curve: pre-peak, post-peak, and residual can be observed on the curve. Also, for the test environment at −5°C, the peak cohesion declines with the increase of FT cycles, while the law of peak friction angle is the opposite. In the same vein, Wang et al. (2020) discovered that the internal friction angle of soft soils was not sensitive to FT cycles. Meanwhile, the first FT action weakened the cohesion weakly, then the attenuation continued to accumulate, and the 10th FT cycle was the threshold for it to achieve stability. In parallel, the mechanical properties of soils are usually revealed via the unconfined (uniaxial) compression test. As pure expansive soils suffer the entire FT cycle, Lu et al. (2020) claimed that the stress-strain curves did not change in type. At the same time, when the cycles exceed 9, the curves basically overlap, and this rule was also obtained between the failure strengths. When Ding et al. (2018) chose improved clay as the object; they showed that under the intricate impacts of FT cycles, polypropylene fibers, and cement, the stress-strain curves exhibited two forms, namely, strain softening and strain stabilization. They also reported that the failure strengths of the clay treated by various methods were reduced by 42–69% after 10 FT cycles, and then the fluctuation was negligible. In addition, Wang et al. (2017) measured the elastic modulus of fine-grained soils using a lever pressure gauge. Within the conclusions, they suggested taking the value after 6 FT cycles for designing the pavement structure in seasonal frozen areas and proposed 0.5–0.6 as the range of FT reduction coefficients. To reflect the actual engineering states more comprehensively, the researchers added considerations about the confining pressure in the test conditions. Zhou et al. (2019) carried out the orthogonal consolidated and undrained tests to underline the effect degrees on multiple factors for statics mechanical characteristics of the soil-rock mixtures. Their results highlighted that the cohesion and internal friction angle continued to decrease during the consecutive FT processes. Moreover, under the higher confining pressure, the attenuation of the failure strengths caused by FT cycles is relatively slight. Wei et al. (2019) uncovered a similar phenomenon with a series of unconsolidated and undrained (UU) tests, and three load response types, strain softening, strain stabilization, and strain hardening, all appeared in the experimental results. However, in an earlier work by Liu et al. (2016), they conducted UU tests on the silty sand at confining pressures of 100, 200, and 300 kPa, where it was noticed that the internal friction angle did not seem to reduce regularly with FT cycles and only two stress-strain relationships of strain hardening and stabilization occurred. More importantly, the authors established a normalized equation based on the Konder hyperbolic model and it can well describe the stress-strain relationship for their selected soils given the effect of FT cycles as well as confining pressures. This breakthrough was believed to be significant for predicting the stress-strain curve of other soils such as the plain or lime-treated loess in Xining, Qinghai province, China (Zhang et al., 2019).
In conclusion, these published literatures served insightful and valuable understandings on the mechanical properties of embankment soils suffering FT cycles. Nonetheless, due to the disparate soil types and test methods, the findings, especially the stress-strain relationships and shear strength indexes affected by FT cycles, are not generally unified, which limits the guidance for embankment construction. Also, existing research has concentrated on the influence factors and variation rules for mechanical properties of soils, but the corresponding evaluation models have rarely been discussed. Furthermore, the constitutive equation originating from the Konder model was applicable to hardening or stabilization soils, while the prediction for strain softening curves remains poorly understood.
To address the aforementioned imperfections, in this paper, a typical embankment clay was investigated through a series of UU tests under different FT cycles. From the experimental results, the evolution and phenomenological models for the mechanical properties of the tested clay were elucidated. In particular, in conjunction with the published data and the envelope theory, a creative method for rapidly predicting the shear strength indexes of embankment clay was highlighted. Not only that, the comprehensive normalized constitutive relationship considering the effect of FT cycles was presented and can predict the stress-strain curves with different types, especially the strain softening. These main findings can provide novel contributions to engineering construction in seasonal frozen regions.
Laboratory Experiments
Properties of Materials
This study selected typical clay from China as the tested soil. According to the Chinese Specification of JTG 3430-2020, Test Methods of Soils for Highway Engineering, the main basic physical properties of the tested soils were listed in Table 1. On the basis of these parameters, the soils were determined as low liquid limit clay (CL) in accordance with the Unified Soil Classification System.
Specimen Preparation
Limited by the difficulty of achieving undisturbed soils, and in order to ensure consistent humidity and density levels between specimens, the soils were remolded and tested in the laboratory. Firstly, the soils were crushed and collected after filtering by the 2-mm sieve, then dried at 105°C for 12 h. Subsequently, the dry soils were mixed with distilled water at the optimum moisture content and then stored in a sealed plastic bag for 24 h so that the moisture was uniform. The principle of this specimen preparation method is to simulate the actual humidity inside most embankments (Lin et al., 2017; Bozbey et al., 2018). At the same time, the dry density of the specimens was maintained at 1.73 g/cm3. Afterwards, the wet soil with the calculated mass was compacted by five layers into a cylinder that was 68 mm in diameter and 140 mm in height. The rationale behind this was that ASTM D2850 states the height-to-diameter ratio should be greater than 2. Finally, the specimens were wrapped to avoid water evaporation and waited for the next tasks.
Freeze-Thaw Cycles
The closed-system FT cycle experiments were applied in this study. This method is suitable for depicting the condition that there are no obvious differences in the in-situ moisture content all year round. Meanwhile, given the low permeability of clay, the rate of frost penetration is significantly faster than moisture transportation, so that there is no adequate time to achieve persistent replenishment of moisture to the frozen front during the freezing process (Güllü and Khudir, 2014). Thus, it is reasonable to adopt the closed FT type here.
As shown in Figure 1, the entire FT cycle tests were performed in the automatic refrigerator (the range was from −60 to 150°C) with internal temperature sensors (the precision was ±0.5°C). The prepared specimens were encased in preservative film to prevent moisture exchange. The specimens were first frozen at −20°C for 12 h, and following this period, they were thawed at 20°C for 12 h. The two processes were integrated into one FT cycle, and so on. In earlier pertinent reports, it can be found that these temperatures and durations were approved by some scholars (Orakoglu and Liu, 2017; Nguyen et al., 2019; Gowthaman et al., 2020; He et al., 2020; Lu et al., 2020). The numbers of FT cycles in this study were designed as 0, 1, 3, 6, 10, and 15.
Unconsolidated and Undrained Triaxial Tests
DYNATRIAX-100/14 (Figure 2), a triaxial test apparatus, was employed to investigate the mechanical properties of clay in this study. Its axial load limit was 100 kN, the confining pressure could be adjusted from 0 to 1000 kPa, and the maximum axial distance of the actuator was 100 mm. The external transducer with the highest frequency of 1000 Hz collected real-time displacement and load data for the computer.
When the specimens had been subjected to the preset FT cycles, they were transferred to the triaxial chamber for UU tests. The axial loading rate was 0.8% per min and the values of confining pressures were set at 50, 100, 150, 200, 300, and 400 kPa, respectively. Once the axial strain of the specimens reached 20%, the test ended.
Experimental Results and Discussions
The stress-strain response, elastic modulus, failure strength, and shear strength are attractive indicators for the mechanical properties of soils in engineering (Zhou et al., 2015; Wei et al., 2019; Xiao et al., 2019). This section set out to present the test curves and excavated their implied information to research characteristics of the other three parameters. At the same time, a practical and innovative method for rapidly predicting the cohesion and internal friction angle of soils under FT cycles was established.
Stress-Strain Response Affected by Freeze-Thaw Cycles
Figure 3 displays the stress-strain curves of the tested soils with various FT cycles and confining pressures (σ3). For strain softening soils, with the development of axial strain, the deviator stress first reaches its peak point and then declines gradually. While soils exhibit strain hardening characteristics, the deviator stress increases along the axial. As for strain stabilization curves, the deviator stress rise to a stable value with the accumulation of axial strain, and then continues to stabilize. Accordingly, three types of stress-strain responses can be observed in the experimental results. Moreover, at the identical confining pressures, it can be found that the more FT cycles, the smaller the peak value of softening curves, and after the 10th FT cycle, this change is not considerable.
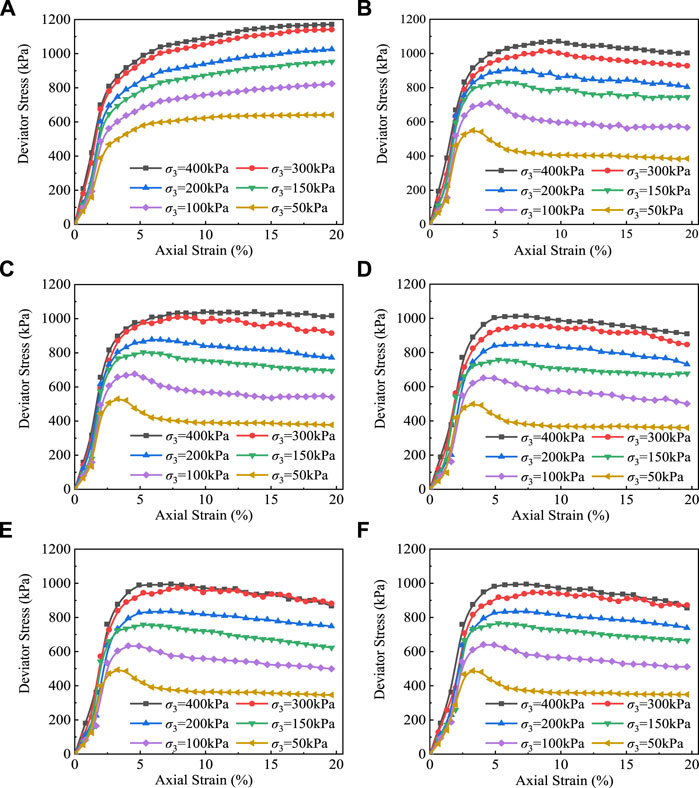
FIGURE 3. Stress-strain curves of the tested clay suffering from various FT cycles. (A) 0 FT cycle. (B) 1 FT cycle. (C) 3 FT cycles. (D) 6 FT cycles. (E) 10 FT cycles. (F) 15 FT cycles.
Figure 3 also shows that, with the given FT cycles, the rise in confining pressures causes greater deviator stress when the soils achieve the same axial strain. This indicates that the constraint effect contributed by confining pressures strengthens the soils to better resist axial loads. In addition, the behaviors of strain hardening or stabilization occurred in the absence of FT cycles while the softening appeared with FT cycles. In other words, FT cycles can transform the types of stress-strain curves of the soils in this study. This phenomenon is consistent with the findings reported by Roustaei et al. (2015) and Orakoglu and Liu (2017), but different from Xian et al. (2019). One possible explanation is that the different clays with their own diverse properties were selected in this research, resulting in differences in the numbers of FT cycles and confining pressures corresponding to the critical conditions when the stress-strain curves transition.
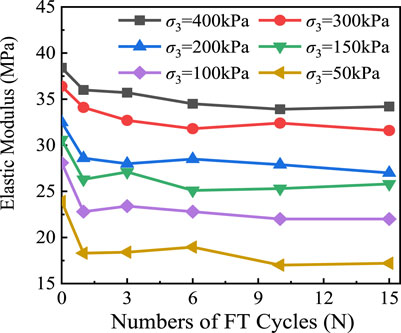
Elastic Modulus Changes Affected by Freeze-Thaw Cycles
Elastic modulus is a key indicator for describing the stiffness and anti-deformation ability of soils. For instance, in a recent study, Ling et al. (2020) discovered that railway coarse-grained materials that had undergone 10 FT cycles lost 68, 57, and 50% of their elastic modulus at confining pressures of 30, 60, and 90 kPa, respectively. For simplicity, the stress-strain curves were considered to be linear within the 2.0% axial strain, and the slope of this point was defined as the elastic modulus value (Wei et al., 2019; Liu et al., 2021), which can be determined in Eq. 1:
where E denotes the elastic modulus; σ2.0% is the deviator stress when the axial strain reaches 2.0% (ε2.0%); and σ0 and ε0 are the initial stress and strain, respectively.
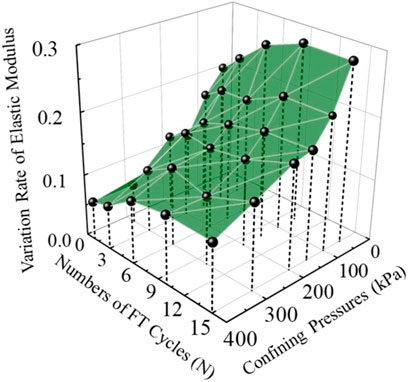
Figure 4 reveals the relationship between the elastic modulus and confining pressures with different FT cycles. Taking the state of 6 FT cycles as an instance, when the confining pressure ranged from 50 kPa to 100, 150, 200, 300, and 400 kPa, the elastic modulus increased by 20, 33, 51, 67, and 85%, respectively. This analysis result means that the confining pressure has a considerable positive effect on the elastic modulus of the studied clay. On the other hand, it can be observed that the accumulated FT cycles declined the elastic modulus. Furthermore, the value decayed sharply during the first FT cycle and stabilized after a certain number of cycles, in agreement with most research on clay in the past decade (Roustaei et al., 2015; Wang et al., 2007; Xian et al., 2019). Based on the foregoing analysis, to better understand the elastic modulus of the studied clay, this study suggested a novel empirical model through the multiple regression modeling of all 36 data points in Figure 4, especially adopting the modificatory logarithmic form to embody the effect of FT cycles, as shown in Eq. 2. The result is satisfactory in reference to the recommended criteria for evaluating the determination coefficient (R2) in geotechnical engineering (Zhang et al., 2020b; Zhang et al., 2021; Yao et al., 2022), namely, a fair fit is defined as 0.4 ≤ R2 ≤ 0.69, a good fit is R2 = 0.7–0.89 and an excellent fit is R2 ≥ 0.9.
where N is the number of FT cycles.
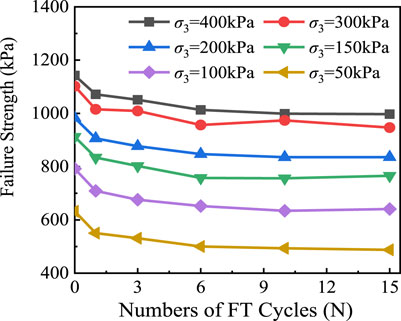
Failure Strength Affected by Freeze-Thaw Cycles
This study ascertained the failure strength of clay in accordance with the instructions of ASTM D2166: for strain softening clay, the deviator stress corresponding to the peak of the stress-strain curve is the failure strength; and if strain hardening or stabilization occurs, the deviator stress at 15% of the axial strain is taken as the failure strength. The results of the failure strength due to various confining pressures and FT cycles are presented in Figure 5. It can be seen that the addition of confining pressures continuously improved the failure strength. Also, the failure strength weakened throughout the FT cycles and then basically tended to be stable after 10 FT cycles with an approximate attenuation rate of 6–22% compared to the state before FT cycles. This law may be produced as follows: the water in pores freezes into ice at a negative temperature, and the volume of ice is roughly 9% larger than liquid water (Zhou and Wei, 2020). The growth of ice crystals uplifted the soil particles, but when ice crystals thaw at positive temperatures, the lifted particles cannot be completely restored (Zhou et al., 2018). Thus, a complete process comprising freezing and thawing resulted in the expansion of pores between particles and the attenuation of failure strength. Furthermore, with increasing FT cycles, the contribution of ice crystals to the lifting of particles decreased gradually until the pores between the particles were expanded by repeated FT cycles were large enough to endure the volume growth due to the phase transitions in water, the failure strength was no longer attenuated. Given the above discussions, a new model can be conceived as Eq. 3.
where
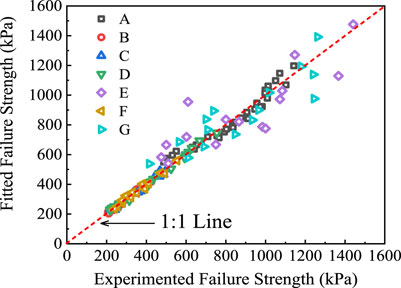
In the stability analysis of embankments, the failure strength of soils must be strictly considered (Zhao et al., 2020). Obviously, it is necessary and meaningful to verify the robustness and accuracy of Eq. 3. As for regression coefficients, k1 is the adjustment coefficient, that is, proportional to the failure strength, which can be ascertained to be a positive number because the failure strength cannot be negative. k2 as an exponent must be a negative number given that with the increase in the number of FT cycles, the failure strength decreases. In order to reflect the influence of confining pressures, k3 is a positive number as well as an exponent, since the higher the confining pressure, the larger the failure strength. This study adopted all 36 data points in Figure 5 and, in conjunction with previous data from other researchers, fitted Eq. 3 accordingly. The specific regression coefficients are summarized in Table 2, and the intuitionistic fitting effect is presented in Figure 6. The results demonstrated that the signs of regression coefficients in each group were consistent with the discussions, and the accuracies were mainly excellent. Simultaneously, the values of the fitted and experimented failure strength were close. The verification analysis concludes that the model established as Eq. 3 is suitable for different clays, although it was proposed only on the basis of test results from the low liquid limit clay in this study.

TABLE 2. Regression coefficients in Eq. 3 of different clays.
Shear Strength Affected by Freeze-Thaw Cycles and Its Rapid Prediction
The shear strength of soils, specifically cohesion and internal friction angle, are the most popular parameters in embankment engineering, as they are the basic inputs necessary for calculating the slope safety factor. Currently, the common practice is to plot the Mohr semicircles and envelopes based on the failure strength determined by triaxial tests to obtain the shear strength (Zhou et al., 2019). Nonetheless, triaxial instruments are still far from universal due to their high cost. Furthermore, triaxial tests require experienced personnel to operate procedures and analyze test data, which is a complex and time-consuming process. Contrary to this, trying to propose a method for rapidly predicting the shear strength through performance-related soil basic parameters is advisable due to the measurements of these parameters being faster, more simple, reliable, and accurate.
In the above scenario, the weight percent of soils passing through 0.075-mm sieve (P0.075), the plastic limit (wp) and the liquid limit (wL) were selected as physical parameters; relative humidity (RH, the ratio of actual moisture content to optimal moisture content) and relative compaction (RC, the ratio of actual dry density to maximum dry density) were taken as status parameters, because they had a considerable effect on the mechanical properties of soils (Nazzal and Mohammad, 2010). Corresponding to the various soils in Table 2, these detailed parameters were summarized in Table 3. Subsequently, an excellent multiple regression relationship between these basic parameters and the model regression coefficients (k1, k2 and k3) of Eq. 3 was developed utilizing the JMP statistical analysis software, as presented in Eq. 4.
For the particular moment when the soils reach the failure state, the failure strength expressed by Eq. 3 can also be rewritten into Eq. 5:
where
Most failures in geotechnical engineering can be attributed to shear action, and thus it is meaningful to describe the failure state by the normal stress and shear stress. This study adopted the widely used Mohr stress circle to reflect this relationship, as shown in Eq. 6:
where
On the basis of the envelope theory, the
Substituting Eq. 5, Eq. 6 into Eq. 7, the normal stress and shear stress on the shear plane can be derived as given in Eq. 8:
The rationality of Eq. 8 is logical, and the reasons are analyzed as follows. The regression model of failure strength established in this study, as shown in Eq. 3, has been verified to be reliable by multiple groups of clay data. Meanwhile, the Mohr stress circle and envelope theory have been proven to be successful in existing documents. Therefore, the normal stress and shear stress obtained by them together should be accurate. In order to have confidence in Eq. 8, the measured failure strength data of this study were used to draw the Mohr semicircles, and the set numbers of FT cycles (N), confining pressures (σ3), fitted k1, k2 and k3 in Table 2, and Eq 5 and Eq. 8 of this study were adopted to calculate the envelope, as shown in Figure 7. It can be observed that the calculated envelopes were basically anastomotic with the Mohr semicircles, which indicates that the Eq. 8 obtained in this section can well describe the nonlinear relationship between the shear strength of clay and the numbers of FT cycles and confining pressures.
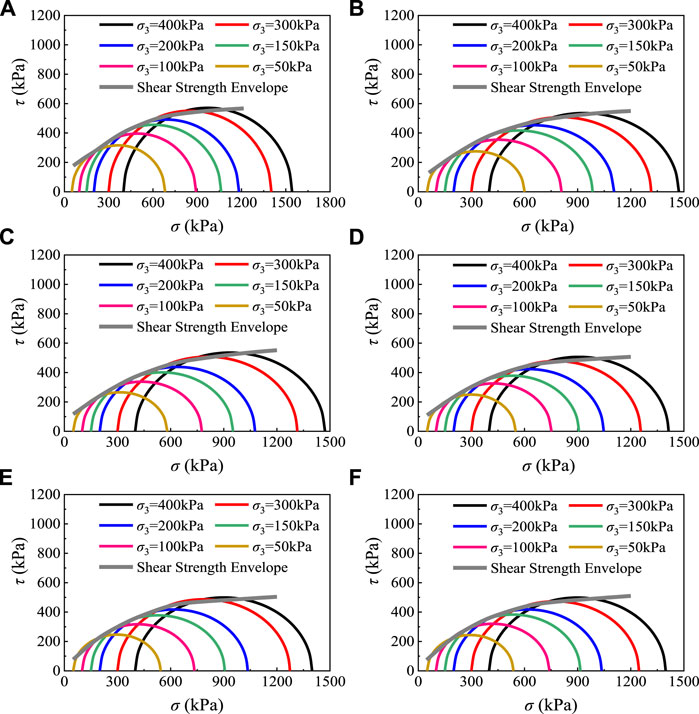
FIGURE 7. Mohr semicircles and calculated envelopes in this study. (A) 0 FT cycle. (B) 1 FT cycle. (C) 3 FT cycles. (D) 6 FT cycles. (E) 10 FT cycles. (F) 15 FT cycles.
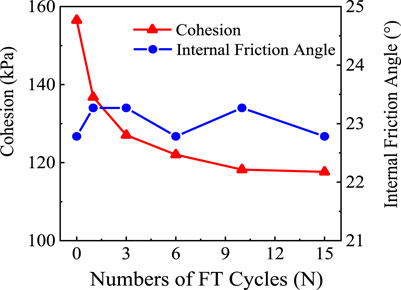
To sum up, the critical steps in the rapid prediction method for the shear strength of clay considering FT cycles were summarized and organized as follows:
1) Through a few simple laboratory basic physical tests to determine the values of P0.075, wp, wL, RH and RC, and then substitute them into Eq. 4 to calculate k1, k2 and k3;
2) Investigate the climate conditions of the engineering site to determine the number of FT cycles (N), and select several confining pressure levels (σ3, 1 m is equivalent to 20 kPa) in combination with the embankment filling height. Then, substitute k1, k2, k3, N and σ3 into Eq. 5 to calculate the corresponding σ1 at the failure state;
3) Substitute each group k1, k2, k3, σ1, σ3 and N into Eq. 8 to calculate the corresponding σ and τ, and then use the Mohr-Coulomb linear equation to fit them to obtain the shear strength indicators under various FT cycles.
Following the above steps, the results of the cohesion and internal friction angle were summarized in Figure 8. It can be observed that the cohesion of the tested clay decayed throughout a whole FT cycles, and the rate of attenuation gradually decreased until it became flat. This phenomenon has also been found in previous studies (Orakoglu and Liu, 2017; Wei et al., 2019). Figure 8 also showed that the internal friction angle of the tested clay was not sensitive to the numbers of FT cycle, that is, it fluctuated repeatedly around 23°, which was consistent with the studies from Liu et al. (2016), Orakoglu and Liu (2017) and Zhang et al. (2019), but unlike the findings from Zhou et al. (2019) and Xian et al. (2019). The difference was likely due to the effect of FT cycles do not cause particles rearrangement in the tested clay such as interlocking or slipping. Not long ago, a measurement on the micro-structure of pavement recycled materials seemed to indicate that the X-ray Micro-Computed Tomography technology might be an effective means of exploring this difference (Afshar et al., 2018), however it is beyond the scope of this study.
It is noteworthy that the method proposed in this work for rapidly predicting the shear strength of embankment clay under FT cycles is generally applicable. Concretely, when this method is applied to other clay, it is only necessary to carry out several simple basic physical tests and follow the above steps 1)–3) to achieve the purpose. For situations where the triaxial tests are limited or the shear strength of clay is urgently needed, this method has satisfactory engineering practicability.
Empirical Constitutive Equation for Freeze-Thaw Clay
Stress-strain curves are the source and foundation for investigating the mechanical properties of soils. In addition to the experimental studies, the constitutive equations also help to grasp the stress-strain relationship well (Zhang et al., 2020a). This part selected reasonable normalized factors, starting from the situation before FT cycles, and derived the empirical constitutive equation of the studied clay considering FT cycles.
Stress-Strain Relationships Before Freeze-Thaw Cycles
The studied clay before FT cycles in Figure 3A exhibited obvious strain hardening or stabilization behavior. Here the Konder hyperbolic model as shown in Eq 9a, Eq. 9b was adopted to describe the stress-strain relationship, and the results were listed in Table 4. Although this model showed high accuracy, it could not easily reflect the influence of confining pressures. In other words, for different confining pressure levels, corresponding model coefficients need to be fitted separately, which increases the difficulty and complexity of operation.
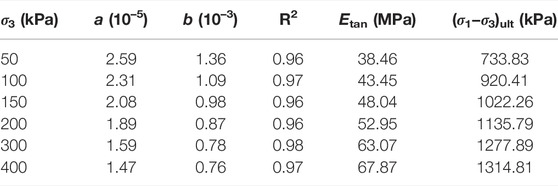
where ε1 represents the axial strain; 1/a is the initial tangent modulus Etan; and 1/b is the ultimate deviator stress (σ1−σ3)ult.
Casey and Germaine (2013) reported that the stress-strain relationship of soils under different conditions can be expressed by a normalized function. Based on this idea, multiply both sides of Eq. 9b by a normalized factor of N to obtain Eq. 10:
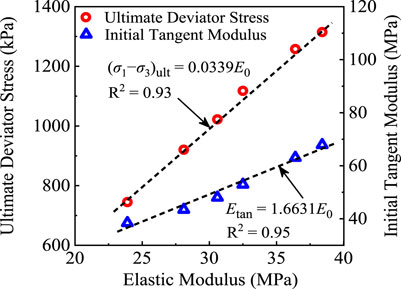
To implement the normalized function, the N should satisfy a linear relationship with the Etan and (σ1−σ3)ult, respectively. Through a series of attempts on the mechanical indicators obtained in Section 3, it was found that the elastic modulus before FT cycles (E0) met this normalized condition, as shown in Figure 9.
E0 was selected as the normalized factor N, based on Eq. 10, and Eq. 11 can be deduced:
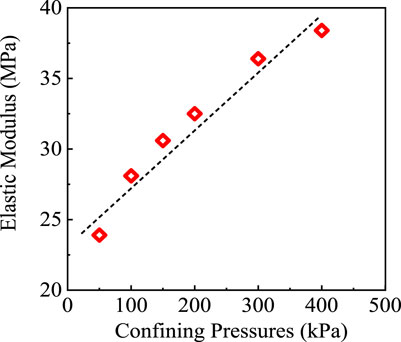
In addition, the E0 also had a relationship with confining pressures as shown in Figure 10 can be depicted by Eq. 12:
Substituting Eq. 12 into Eq. 11, the stress-strain relationship of the studied clay before FT cycles can be expressed as Eq. 13:
Stress-Strain Relationships Considering Freeze-Thaw Cycles
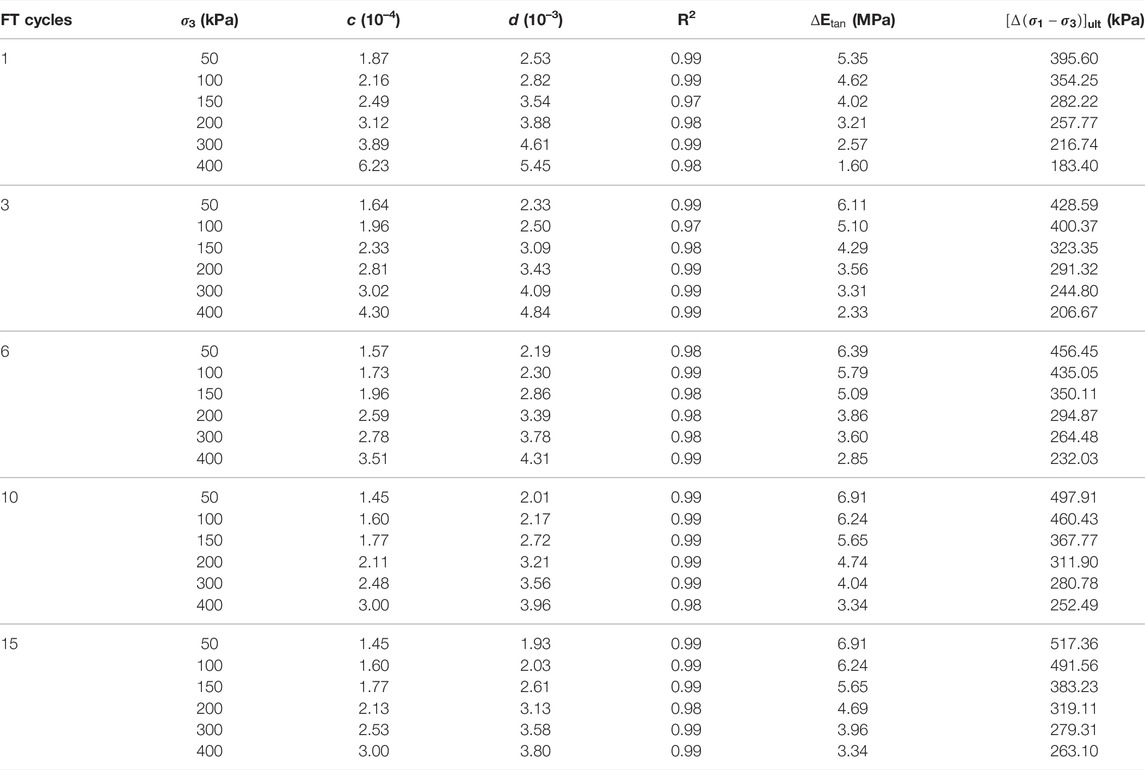
The studied clay under FT cycles in Figure 3B to Figure 4F demonstrated strain softening behavior, and thus the Konder model cannot be adopted to describe their stress-strain relationship directly. For this reason, this study introduced a new variable, namely, the deviator stress differences caused by FT cycles, and defined it in Eq. 14. The results of deviator stress differences with various FT cycles are plotted in Figure 11.
where
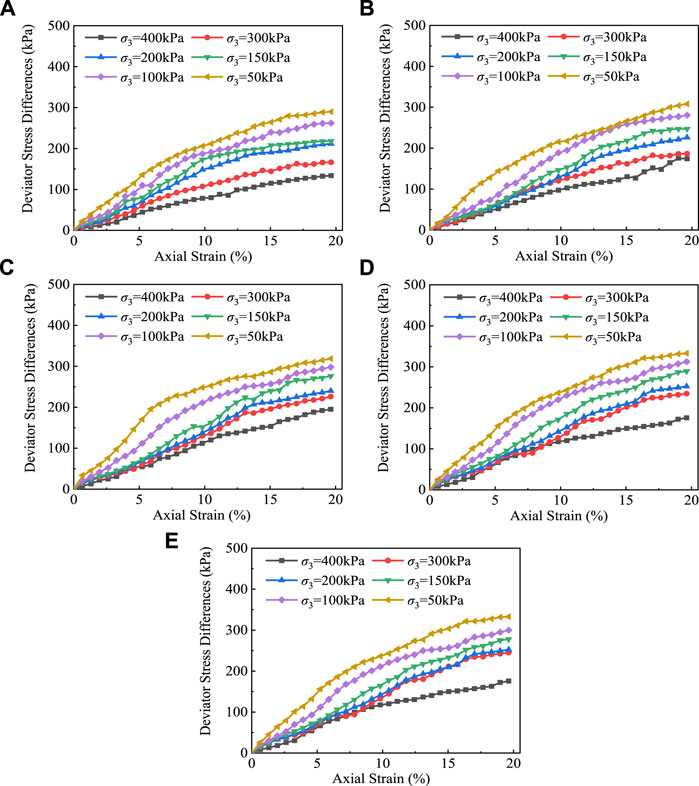
FIGURE 11. Deviator stress differences of the tested clay with various FT cycles. (A) 1 FT cycle. (B) 3 FT cycles. (C) 6 FT cycles. (D) 10 FT cycles. (E) 15 FT cycles
From Figure 11, the strain hardening behavior was found. Hence, the Konder model was applied to them, as expressed in Eq. 15, and the results are exhibited in Table 5.
where 1/c denotes the initial tangent modulus
Following the processing method in Section 4.1, in order to obtain a normalized relationship between the deviator stress differences and axial strain, the normalized factor here needs to have a good linear relationship with both the
∆E0 was chosen as the normalized factor, and Eq. 16 can be given:
To eliminate the intermediate variable
Combining Eqs 12–14, 16–18, the normalized empirical constitutive equation for the tested clay considering FT cycles can be obtained as:
For the special case N = 0, the Eq. 19 is completely transformed to Eq. 13, and thus Eq. 19 is also applicable to the condition before FT cycles. Then Eq. 19 was selected to calculate the stress-strain curves with the corresponding confining pressures and numbers of FT cycles. The tested and calculated results are shown in Figure 14, demonstrating that the normalized Eq. 19 can preliminarily describe the stress-strain relationship of the tested clay affected by FT cycles, including strain hardening, stabilization, and softening forms.
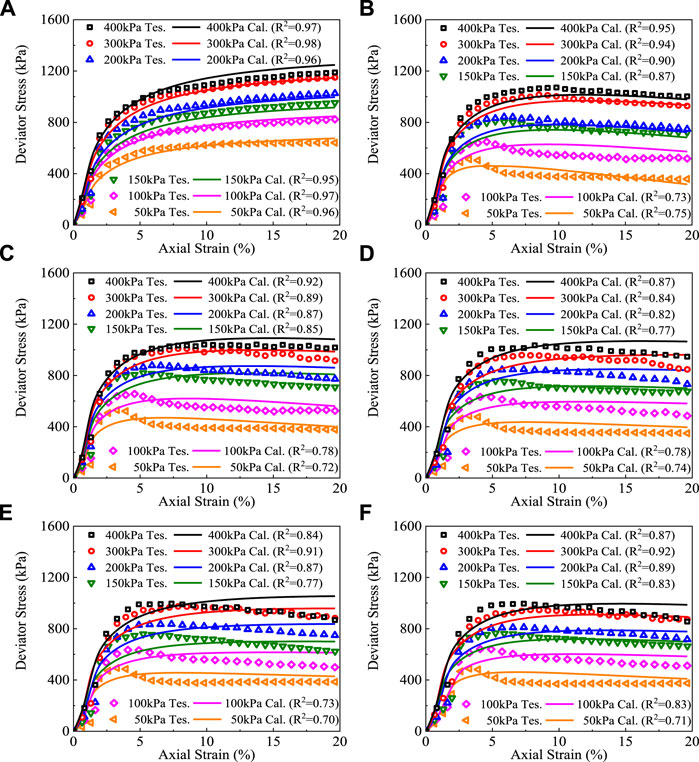
FIGURE 14. Tested and calculated stress-strain results of tested clay. (A) 0 FT cycle. (B) 1 FT cycle. (C) 3 FT cycles. (D) 6 FT cycles. (E) 10 FT cycles. (F) 15 FT cycles.
Conclusion
This study aimed at gaining a better understanding of the mechanical properties of embankment clay subjected to FT cycles. For this purpose, a series of UU tests on a typical clay sample from China were conducted under various confining pressures as well as FT cycles. On the basis of the test results, several key findings were synthesized here:
1) With the accumulation of FT cycles, the stress-strain curves transformed from strain hardening (or stabilization) to strain softening. Meanwhile, under the same number of FT cycles, the greater the confining pressure, the higher the stress-strain curve. After 10 FT cycles, the curves with corresponding confining pressures have no obvious difference.
2) The elastic modulus was significantly affected by FT cycles and decreased sharply after the first FT action. The reduction of confining pressures also weakened the elastic modulus. From this, a phenomenological regression model was established by the modificatory logarithmic form to reflect the effect of FT cycles.
3) The failure strength was damaged by about 6–22% compared with that before the FT cycles, and the change can be ignored when the number of FT cycles exceeds 10. At the same time, the increase in confining pressure enhanced the failure strength. Similarly, a regression model for the failure strength was built and proved to be reliable by experimental results from other researchers.
4) In conjunction with the existing experimental data and the envelope theory, a method for rapidly predicting the shear strength through performance-related basic parameters was proposed. Besides, during the process of FT cycles, the cohesion gradually decreased but eventually became stable and the internal friction angle fluctuated slightly.
5) According to the Konder model, the elastic modulus before FT cycles was selected as the normalized factor to derive the empirical stress-strain formula without FT cycles. Then, by means of the elastic modulus differences, the relationship between the deviator stress differences and axial strain was normalized. Based on this, the empirical constitutive equation was deduced, which can concurrently describe the strain hardening, stabilization, and softening behaviors considering the effect of FT cycles.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All the authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
The National Science Fund for Distinguished Young Scholars (52025085), the National Key Research and Development Program (2021YFB2600900), the National Natural Science Foundation of China (51927814, 51878078), the Key Research and Development Program of Hunan Province (2022SK 2083), the Science and Technology Innovation Program of Hunan Province (2020RC4048), the Project of Scientific Research of Hunan Provincial Department of Education (21C0187), and the Graduate Research Innovation Project of Hunan Province (CX20210748).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or any claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Afshar, T., Disfani, M. M., Narsilio, G. A., and Arulrajah, A. (2018). Post-breakage Changes in Particle Properties Using Synchrotron Tomography. Powder Technol. 325, 530–544. doi:10.1016/j.powtec.2017.11.039
Aldaood, A., Bouasker, M., and Al-Mukhtar, M. (2016). Effect of Water during Freeze-Thaw Cycles on the Performance and Durability of Lime-Treated Gypseous Soil. Cold Regions Sci. Technol. 123, 155–163. doi:10.1016/j.coldregions.2015.12.008
Bozbey, I., Kelesoglu, M. K., Demir, B., Komut, M., Comez, S., Ozturk, T., et al. (2018). Effects of Soil Pulverization Level on Resilient Modulus and Freeze and Thaw Resistance of a Lime Stabilized clay. Cold Regions Sci. Technol. 151, 323–334. doi:10.1016/j.coldregions.2018.03.023
Casey, B., and Germaine, J. T. (2013). Stress Dependence of Shear Strength in Fine-Grained Soils and Correlations with Liquid Limit. J. Geotech. Geoenviron. Eng. 139, 1709–1717. doi:10.1061/(ASCE)GT.1943-5606.0000896
Ding, M., Zhang, F., Ling, X., and Lin, B. (2018). Effects of Freeze-Thaw Cycles on Mechanical Properties of Polypropylene Fiber and Cement Stabilized clay. Cold Regions Sci. Technol. 154, 155–165. doi:10.1016/j.coldregions.2018.07.004
Gowthaman, S., Nakashima, K., and Kawasaki, S. (2020). Freeze-thaw Durability and Shear Responses of Cemented Slope Soil Treated by Microbial Induced Carbonate Precipitation. Soils and Foundations 60, 840–855. doi:10.1016/j.sandf.2020.05.012
Güllü, H., and Khudir, A. (2014). Effect of Freeze–Thaw Cycles on Unconfined Compressive Strength of fine-grained Soil Treated with Jute Fiber, Steel Fiber and Lime. Cold Reg. Sci. Tech. 106 (107), 55–65. doi:10.1016/j.coldregions.2014.06.008
Hao, J., Cui, X., Qi, H., Zheng, Y., and Bao, Z. (2022). Dynamic Behavior of Thawed Saturated saline silt Subjected to Freeze-Thaw Cycles. Cold Regions Sci. Technol. 194, 103464. doi:10.1016/j.coldregions.2021.103464
He, P., Mu, Y., Yang, Z., Ma, W., Dong, J., and Huang, Y. (2020). Freeze-thaw Cycling Impact on the Shear Behavior of Frozen Soil-concrete Interface. Cold Regions Sci. Technol. 173, 103024. doi:10.1016/j.coldregions.2020.103024
Lin, B., Zhang, F., Feng, D., Tang, K., and Feng, X. (2017). Accumulative Plastic Strain of Thawed Saturated clay under Long-Term Cyclic Loading. Eng. Geology. 231, 230–237. doi:10.1016/j.enggeo.2017.09.028
Ling, X., Tian, S., Tang, L., and Li, S. (2020). A Damage-Softening and Dilatancy Prediction Model of Coarse-Grained Materials Considering Freeze-Thaw Effects. Transportation Geotechnics 22, 100307. doi:10.1016/j.trgeo.2019.100307
Liu, H.-b., Sun, S., Wei, H.-b., and Li, W.-j. (2021). Effect of Freeze-Thaw Cycles on Static Properties of Cement Stabilised Subgrade Silty Soil. Int. J. Pavement Eng., 1–13. doi:10.1080/10298436.2021.1919306
Liu, J., Chang, D., and Yu, Q. (2016). Influence of Freeze-Thaw Cycles on Mechanical Properties of a Silty Sand. Eng. Geology. 210, 23–32. doi:10.1016/j.enggeo.2016.05.019
Liu, J., Zha, F., Xu, L., Kang, B., Yang, C., Feng, Q., et al. (2020). Strength and Microstructure Characteristics of Cement-Soda Residue Solidified/stabilized Zinc Contaminated Soil Subjected to Freezing-Thawing Cycles. Cold Regions Sci. Technol. 172, 102992. doi:10.1016/j.coldregions.2020
Liu, X.-q., Liu, J.-k., Tian, Y.-h., Chang, D., and Hu, T.-f. (2019). Influence of the Freeze-Thaw Effect on the Duncan-Chang Model Parameter for Lean clay. Transportation Geotechnics 21, 100273. doi:10.1016/j.trgeo.2019.100273
Lu, Y., Liu, S., Zhang, Y., Li, Z., and Xu, L. (2020). Freeze-thaw Performance of a Cement-Treated Expansive Soil. Cold Regions Sci. Technol. 170, 102926. doi:10.1016/j.coldregions.2019.102926
Miao, Q., Niu, F., Lin, Z., Luo, J., and Liu, M. (2020). Comparing Frost Heave Characteristics in Cut and Embankment Sections along a High-Speed Railway in Seasonally Frozen Ground of Northeast China. Cold Regions Sci. Technol. 170, 102921. doi:10.1016/j.coldregions.2019.102921
Nazzal, M. D., and Mohammad, L. N. (2010). Estimation of Resilient Modulus of Subgrade Soils for Design of Pavement Structures. J. Mater. Civ. Eng. 22, 726–734. doi:10.1061/(asce)mt.1943-5533.0000073
Nguyen, T. T. H., Cui, Y.-J., Ferber, V., Herrier, G., Ozturk, T., Plier, F., et al. (2019). Effect of Freeze-Thaw Cycles on Mechanical Strength of Lime-Treated fine-grained Soils. Transportation Geotechnics 21, 100281. doi:10.1016/j.trgeo.2019.100281
Orakoglu, M. E., and Liu, J. (2017). Effect of Freeze-Thaw Cycles on Triaxial Strength Properties of Fiber-Reinforced Clayey Soil. KSCE J. Civ. Eng. 21, 2128–2140. doi:10.1007/s12205-017-0960-8
Roustaei, M., Eslami, A., and Ghazavi, M. (2015). Effects of Freeze-Thaw Cycles on a Fiber Reinforced fine Grained Soil in Relation to Geotechnical Parameters. Cold Regions Sci. Technol. 120, 127–137. doi:10.1016/j.coldregions.2015.09.011
Rui, D., Deng, H., Nakamura, D., Yamashita, S., Suzuki, T., and Zhao, H. (2016). Full-scale Model Test on Prevention of Frost Heave of L-type Retaining wall. Cold Regions Sci. Technol. 132, 89–104. doi:10.1016/j.coldregions.2016.07.010
Wang, D.-y., Ma, W., Niu, Y.-h., Chang, X.-x., and Wen, Z. (2007). Effects of Cyclic Freezing and Thawing on Mechanical Properties of Qinghai-Tibet clay. Cold Regions Sci. Technol. 48, 34–43. doi:10.1016/j.coldregions.2006.09.008
Wang, L., Zuo, X., Zheng, F., Wilson, G. V., Zhang, X. J., Wang, Y., et al. (2020). The Effects of Freeze-Thaw Cycles at Different Initial Soil Water Contents on Soil Erodibility in Chinese Mollisol Region. Catena 193, 104615. doi:10.1016/j.catena.2020.104615
Wang, T.-l., Liu, Y.-j., Yan, H., and Xu, L. (2015). An Experimental Study on the Mechanical Properties of Silty Soils under Repeated Freeze-Thaw Cycles. Cold Regions Sci. Technol. 112, 51–65. doi:10.1016/j.coldregions.2015.01.004
Wang, W., Qin, Y., Lei, M., and Zhi, X. (2017). Effect of Repeated Freeze-Thaw Cycles on the Resilient Modulus for fine-grained Subgrade Soils with Low Plasticity index. Road Mater. Pavement Des. 19, 898–911. doi:10.1080/14680629.2017.1283352
Wei, C., Apel, D. B., and Zhang, Y. (2019). Shear Behavior of Ultrafine Magnetite Tailings Subjected to Freeze-Thaw Cycles. Int. J. Mining Sci. Technol. 29, 609–616. doi:10.1016/j.ijmst.2019.06.007
Xian, S., Lu, Z., Yao, H., Fang, R., and She, J. (20192019). Comparative Study on Mechanical Properties of Compacted Clay under Freeze-Thaw Cycles with Closed and Open Systems. Adv. Mater. Sci. Eng. 2019, 1–13. doi:10.1155/2019/9206372
Xiao, Y., Long, L., Matthew Evans, T., Zhou, H., Liu, H., and Stuedlein, A. W. (2019). Effect of Particle Shape on Stress-Dilatancy Responses of Medium-Dense Sands. J. Geotech. Geoenviron. Eng. 145, 04018105. doi:10.1061/(ASCE)GT.1943-5606.0001994
Yang, Y., Gao, F., and Lai, Y. (2013). Modified Hoek?Brown Criterion for Nonlinear Strength of Frozen Soil. Cold Regions Sci. Technol. 86, 98–103. doi:10.1016/j.coldregions.2012.10.01010.1016/j.coldregions.2012.10.010
Yao, Y., Li, J., Ni, J., Liang, C., and Zhang, A. (2022). Effects of Gravel Content and Shape on Shear Behaviour of Soil-Rock Mixture: Experiment and DEM Modelling. Comput. Geotechnics 141, 104476. doi:10.1016/j.compgeo.2021.104476
Zhang, J., Fan, H., Zhang, S., Liu, J., and Peng, J. (2020a). Back-Calculation of Elastic Modulus of High Liquid Limit Clay Subgrades Based on Viscoelastic Theory and Multipopulation Genetic Algorithm. Int. J. Geomech. 20, 04020194. doi:10.1061/(ASCE)GM.1943-5622.0001841
Zhang, J., Peng, J., Zhang, A., and Li, J. (2020b). Prediction of Permanent Deformation for Subgrade Soils under Traffic Loading in Southern China. Int. J. Pavement Eng. 23, 673–682. doi:10.1080/10298436.2020.1765244
Zhang, J., Zhang, A., Huang, C., Yu, H., and Zhou, C. (2021). Characterising the Resilient Behaviour of Pavement Subgrade with Construction and Demolition Waste under Freeze-Thaw Cycles. J. Clean. Prod. 300, 126702. doi:10.1016/j.jclepro.2021.126702
Zhang, L., Ma, W., Yang, C., and Yuan, C. (2014). Investigation of the Pore Water Pressures of Coarse-Grained sandy Soil during Open-System Step-Freezing and Thawing Tests. Eng. Geology. 181, 233–248. doi:10.1016/j.enggeo.2014.07.020
Zhang, W., Guo, A., and Lin, C. (2019). Effects of Cyclic Freeze and Thaw on Engineering Properties of Compacted Loess and Lime-Stabilized Loess. J. Mater. Civ. Eng. 31, 04019205. doi:10.1061/(ASCE)MT.1943-5533.0002858
Zhao, Y., Ling, X., Gong, W., Li, P., Li, G., and Wang, L. (2020). Mechanical Properties of Fiber-Reinforced Soil under Triaxial Compression and Parameter Determination Based on the Duncan-Chang Model. Appl. Sci. 10, 9043. doi:10.3390/app10249043
Zhou, C., Xu, J., and Ng, C. W. W. (2015). Effects of Temperature and Suction on Secant Shear Modulus of Unsaturated Soil. Géotechnique Lett. 5, 123–128. doi:10.1680/jgele.14.0009610.1680/jgele.14.00096
Zhou, J., and Wei, C. (2020). Ice Lens Induced Interfacial Hydraulic Resistance in Frost Heave. Cold Regions Sci. Technol. 171, 102964. doi:10.1016/j.coldregions.2019.102964
Zhou, Z., Li, F., Yang, H., Gao, W., and Miao, L. (2019). Orthogonal Experimental Study of Soil-Rock Mixtures under the Freeze-Thaw Cycle Environment. Int. J. Pavement Eng. 22, 1376–1388. doi:10.1080/10298436.2019.1686634
Keywords: embankment clay, mechanical properties, freeze-thaw cycles, static triaxial tests, strain softening curve
Citation: Zhang A, Zhang J, Peng J, Huang C and Zhou C (2022) Effect of Freeze-Thaw Cycles on Mechanical Properties of an Embankment Clay: Laboratory Tests and Model Evaluations. Front. Earth Sci. 10:865348. doi: 10.3389/feart.2022.865348
Received: 29 January 2022; Accepted: 11 March 2022;
Published: 14 April 2022.
Edited by:
Yun Zheng, Institute of Rock and Soil Mechanics (CAS), ChinaCopyright © 2022 Zhang, Zhang, Peng, Huang and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Junhui Zhang, empoc2V1QGNzdXN0LmVkdS5jbg==
 Anshun Zhang1
Anshun Zhang1 Junhui Zhang
Junhui Zhang