The number of joints existing in the rock affects the elastic modulus of the rock, and the relationship has not been obtained. In this paper, 10 numerical models are established by numerical simulations to study the effect of the number of parallel joints on the size effect of rock elastic modulus. The research shows that there is a power function relationship between the elastic modulus and the number of parallel joints, and a negative exponential relationship between the elastic modulus and the rock size, and their special mathematical models are given. The paper also obtains special form of the relationships between the characteristic size of rock elastic modulus, the characteristic elastic modulus and the number of parallel joints.

1 Introduction

Parallel-joints (PJs) are widespread in rock masses and influence the strength and deformation characteristics of rocks. The elastic modulus of rock reflects the deformability of the rock (Yang et al., 2016). The elastic modulus has size effect. Therefore, studying the influence of PJs on rock deformation capacity and size effect is of great important for rock engineering design (Wu et al., 2020).

Elastic modulus is an important mechanical parameter of rock. Scholars have studied the influence of different joint parameters on the elastic modulus. For example, Chen et al. (2019) studied the influence of confining pressure on the elastic modulus of coal by conducting triaxial compression tests on coal. Liu et al. (2021) studied the influence of joint angle on rock elastic modulus by uniaxial compression test too and obtained that the elastic modulus gradually increases with the increase of joint angle. Yu et al. (2020) conducted a uniaxial compression test on siltstone samples and found that the elastic modulus is positively correlated with the crack inclination angle. Scholars have studied the influence of two or more joint parameters on the elastic modulus. For example, Liu et al. (2020) conducted uniaxial compression tests on five types of rough jointed rocks, and studied the influence of joint angle and joint length on the elastic modulus. Wang et al. (2020a) used triaxial compression test to analyze the influence of joint angle and confining pressure on the elastic modulus of rock mass. It is obtained that the elastic modulus changes in a “U” shape with the increase of the joint angle. Lin et al. (2020) studied the affect of joint angle and spacing on elastic modulus. Huang et al. (2019) used a combination of uniaxial compression test and DEM to study the influence of joint angle, joint spacing, joint length, and rock bridge length on the elastic modulus. The joint angle has the greatest impact.

As a key parameter of jointed rock, the number of parallel-joints (NPJs) also has influence on elastic modulus (Wu et al., 2022). For example, Wang et al. (2019) found that the elastic modulus decreases as NPJs increases by studied the influence of NPJs on elastic modulus. Zhao et al. (2020) used DEM to study the influence of joint density on the elastic modulus. Peng et al. (2019), Zhang et al. (2017) used Particle Flow Code (PFC) to study the influence of joint density on the elastic modulus, and found that the elastic modulus decreases with the increase of joint density. Wang et al. (2017) studied the change of elastic modulus under the combination of joint density and angle, and obtained that the elastic modulus changes in a “V” shape with the increase of joint density. Shu et al. (2019) studied the influence of joint inclination, spacing, intersection angle, and density on the elastic modulus of rock mass based on DEM. Among them, the joint density has the greatest influence on the elastic modulus. The joint parameters involved in the above studies are joint angle, length, spacing, and numbers, etc., but rarely involve the influence of size changes on the elastic modulus.

Elastic modulus reflects the deformation characteristics of the rock (Yang et al., 2021), and the elastic modulus has a size effect. For example, Liu et al. (2019a), Han et al. (2019) used PFC to study the influence of rock-size on the elastic modulus and found that the elastic modulus has size effect. Zhang et al. (2020) studied the influence of different height-diameter ratios on the mechanical properties of rocks by using PFC2D, and found that the elastic modulus increases with the increase of the height-diameter ratio. Scholars have studied the size effect of rock elastic modulus by establishing different material models. Wang et al. (2020b) used Synthetic Rock Mass to study the influence of specimen size on the elastic modulus of jointed rock mass, and found that the elastic modulus of rock mass has size effect. Liu et al. (2019b) established a coal-rock assembly with different height-ratios by using PFC, and obtained that the elastic modulus increased with the increase of height-ratios. The above studies on the size effect of rock elastic modulus mostly use numerical simulation. In recent years, with the innovation of numerical methods, the use of numerical simulation to study the mechanical properties of jointed rocks has become a popular trend. There are many types of numerical simulation software, among which a new numerical code–Realistic Failure Process Analysis (RFPA) developed by Tang (1997). RFPA has a good effect in simulating the strength and deformation of rock materials in geomechanically problems. Sun et al. (2019) obtained a positive correlation between elastic modulus and gravel size using RFPA. size effect of rock elastic modulus is obtained to solve engineering problems by finding the functional expression of rock elastic modulus and rock-size. For example, Zhang et al. (2019) established different mineral size models by using the DEM, and obtained a fourth-order polynomial relationship between the rock elastic modulus and the model radius. Dai et al. (2020) found that the relationship between the elastic modulus and the slenderness ratio accords with a logarithmic function using uniaxial compression tests. Ma et al. (2021) used PFC to simulate the uniaxial compression of coal and rock composite samples with different height-ratios, and obtained that the elastic modulus has an exponential relationship with the height-ratios of coal-rock. The above studies have obtained the functional formula of rock elastic modulus and rock-size from a quantitative perspective. The size effect of elastic modulus is obtained more accurately. But studies seldom involved the influence of NPJs on the elastic modulus.

The elastic modulus changes with the size of the jointed rock, and eventually tends to a stable value, which is defined as representative elementary volume (REV) (Bear, 1972). Scholars have studied the characteristic-size of rocks. Ying et al. (2018) found a calculation method of rock mass REV. Peng et al. (2020) used PFC to conduct numerical experiments on multi-scale rocks and analyzed the scale effect of rocks and found that the REV is 16 m × 16 m × 16 m. Scholars have studied the characteristic-size of elastic modulus (CSEM). Loyola et al. (2021) evaluated the REV of the elastic modulus of fractured rocks. Liang et al. (2019) obtained the CSEM of the jointed rock mass to be 14 m × 14 m. With the deepening of research, scholars have studied the characteristic elastic modulus (CEM) of rock based on the CSEM. For example, Cui et al. (2020) took the schist of the Danba Hydropower Project as an example, and the elastic modulus at the REV scale was about 6.8 GPa. Although scholars have done a lot of research on the CSEM and CEM, they rarely study the relationship between the CSEM and PJs from a quantitative perspective. Mathematical models of CSEM and NPJs are rerely established by scholars.

This paper sets up 10 simulation programs by using numerical simulations and RFPA. The influence of NPJs and rock-size on the elastic modulus is studied. The stress-strain curves of different NPJs and sizes of rock are analyzed. A mathematical model of the elastic modulus and NPJs and a mathematical model of the elastic modulus and rock-size are established. A mathematical model of the CSEM and NPJs and a mathematical model of rock CEM and NPJs are established.

2 Establishment of Numerical Model

2.1 Simulation Program and Model Establishment

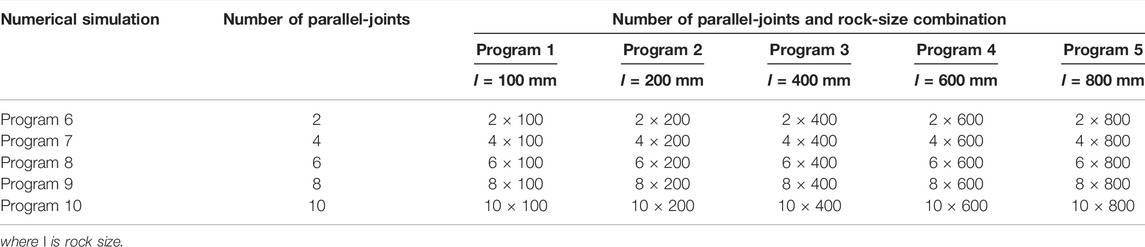
This numerical simulation contained two parts (ⅰ) The influence of the NPJs on elastic modulus, including Program 6 to Program 10 (ⅱ) The influence of rock size with PJs on elastic modulus, including Program 1 to Program 5. The numerical simulation programs are given in Table 1.

TABLE 1

TABLE 1. Number of parallel-joints and rock-size combination.

The angle of parallel joints in rocks may be arbitrary, therefore, this paper sets up a set of verification program to verify the accuracy of the research content. The number of parallel joints in this verification program is 2, and the angle of parallel joints is 45°.

2.2 Boundary Conditions and Rock Joint Parameters

2.2.1 Boundary Conditions and Loading Methods

The software used in this study is RFPA, which is a numerical calculation method for simulating inhomogeneous materials developed based on finite-element theory and statistical damage theory (Hu and Ma, 2021).

This study adopted uniaxial compression deformation theory and the plane stress model (Hu and Ma, 2021). The constraint conditions were that the load was not borne by the two sides of the model but by its upper surfaces, the displacement loading method was adopted for numerical simulation, the displacement loading on both sides of the model was zero, and that on its upper and lower surfaces was 0.01 mm (Hu and Ma, 2021).

2.2.2 Rock Mechanical Parameters and Joint Parameters

The rock mechanics parameters used in the article are selected from literature (Hu and Ma, 2021). The elastic modulus of the joint used in the numerical simulation was 1.1 MPa, Poisson’s ratio was 0.3, compressive strength was 1.5 MPa, friction angle was 30°, and JRC value was 2.

2.3 Research on the Influence of the Number of Parallel-Joints on the Rock Elastic Modulus

According to the numerical simulation program and results of research content (ⅰ): the influence of the NPJs on elastic modulus, the stress–strain variation law of rock with different NPJs was analyzed. A fitting method for the relationship between the elastic modulus and NPJs was proposed. A mathematical model of elastic modulus and NPJs was established.

2.3.1 Analysis of Rock Stress–Strain Curve With Different Numbers of Parallel-Joints

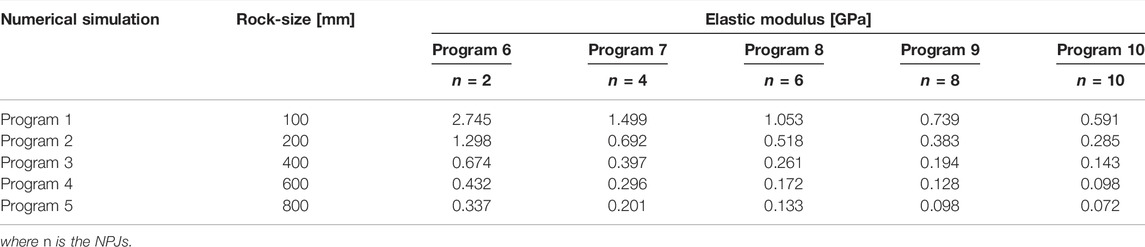
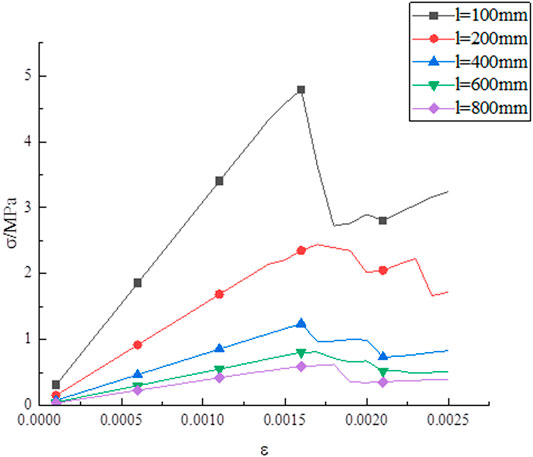
The stress-strain curve rules in program 1 to 5 were output in Figure 1. And according to Figure 1, the elastic modulus under each working condition was solved in Table 2.

FIGURE 1

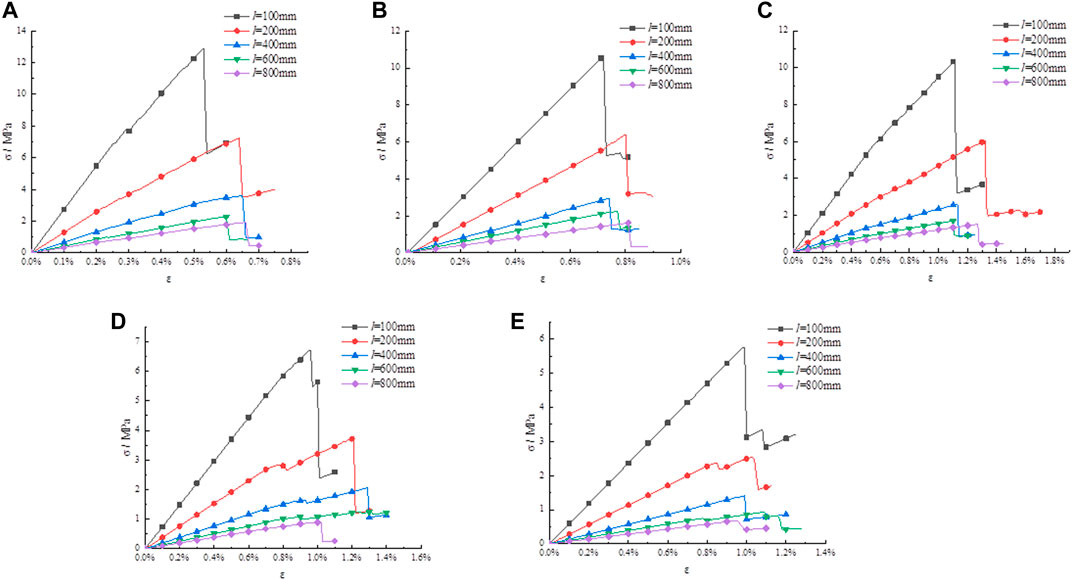
FIGURE 1. Stress–strain curves with different numbers of parallel-joint. (A) l = 100 mm, (B) l = 200 mm, (C) l = 400 mm, (D) l = 600 mm, (E) l = 800 mm.

TABLE 2

TABLE 2. Elastic modulus of rock with different numbers of parallel-joints.

Figure 1 shows that the laws of stress-strain curves are similar when NPJs is different. All obey the following laws: with the increase of strain, the stress gradually increases, and the rock changes from elastic deformation to plastic failure.

Taking Figure 1A as an example to analyze the effect of NPJs on the elastic modulus. With the increase of NPJs, the elastic modulus gradually decreased from 2.745 to 0.591 GPa. It shows that the elastic modulus is affected by the NPJs. Similarly, the same law can still be obtained when the rock size is increased.

Taking program 6 in Table 2 as an example to analyze the effect of rock size on elastic modulus. With the increase of rock size, the elastic modulus gradually decreased from 2.745 to 0.337 Gpa. This phenomenon shows that elastic modulus is affected by rock size. From program 7 to Program 10 also obey the same law, indicating that the elastic modulus of the rock with NPJs has a size effect.

In short, the elastic modulus of the rock with joints decreases with the increase of NPJs, and decreases with the increase of the size of the rock.

2.3.2 Fitting Method for Relationship Between Rock Elastic Modulus and the Number of Parallel-Joints

The stress-strain curve of rock under different NPJs is a macroscopic manifestation of the rock failure process, which can reflect the changing trend of the rock at various stages. However, the relationship between NPJs and the elastic modulus cannot be analyzed quantitatively. Therefore, From the stress-strain curve, it becomes particularly important to obtain the relationship between the elastic modulus and NPJs.

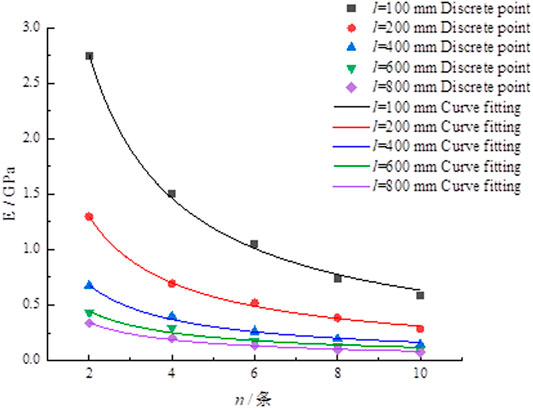
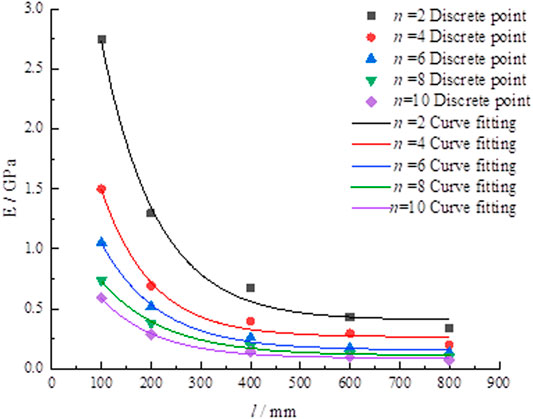
According to the data in Table 2, the fitting curve of the elastic modulus of rocks with different NPJs was drawn, as shown in Figure 2.

FIGURE 2

FIGURE 2. Fitting curves of rock elastic modulus with different number of parallel-joint.

Figure 2 shows that when the rock size is the same, as NPJs increases, the elastic modulus gradually decreases. Rocks of different sizes have the same changing law. However, under the same NPJs, the elastic modulus decreases with the increase of the rock-size, and the curve shows a downward movement trend. It shows that the elastic modulus with joints is negatively correlated with the NPJs and the rock-size.

The relationship between the elastic modulus of different sizes of rocks and NPJs in Figure 2 is regressed in Eqs 1–5. Among them, Eqs 1–5 are the regression functions for rock sizes of 100, 200, 300, 400, and 500 mm, respectively, and the fitting coefficients are 0.998, 0.997, 0.993, 0.963, and 0.991.

$E\left(n\right)=5.201n^{-0.908},(1)$

$E\left(n\right)=2.404n^{-0.888},(2)$

$E\left(n\right)=1.258n^{-0.853},(3)$

$E\left(n\right)=0.790n^{-0.828}(4)$

$E\left(n\right)=0.625n^{-0.821}(5)$

Analyzing the fitting formula, the elastic modulus fits well with the NPJs. It can provide a method for quantitative analysis of NPJs and the elastic modulus for engineering practice.

2.3.3 Relationship Between Rock Elastic Modulus and Number of Parallel-Joints

According to the fitting formula, the mathematical model for elastic modulus and NPJs is proposed as:

$E\left(n\right)=a{n}^{-b}(6)$

where E(n) [GPa] is the elastic modulus when the NPJs is n, n is the NPJs, and a, b are parameters.

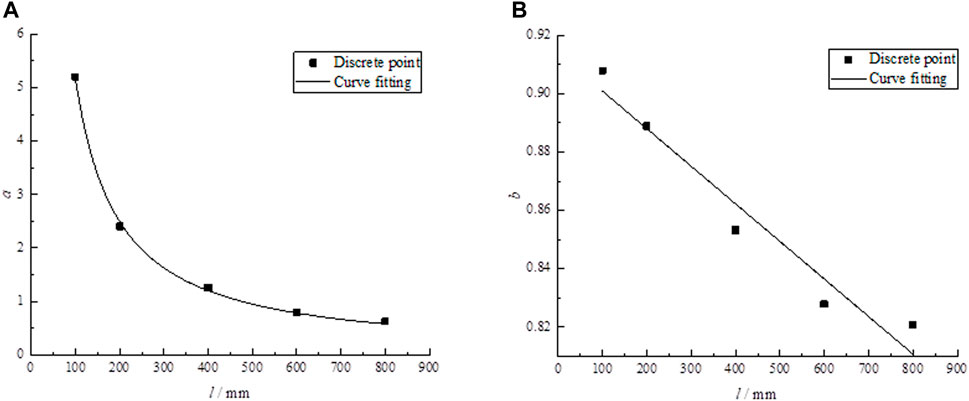
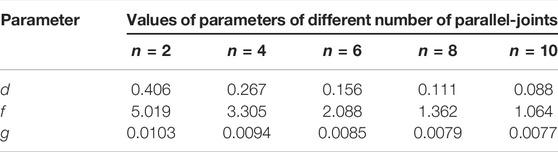
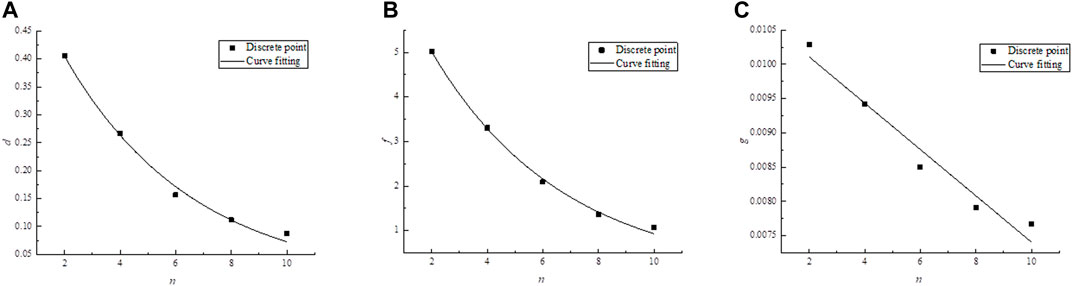
According to the formula, the values of parameters a and b are found in Table 3. The fitting curves of parameters a and b and rock size are drawn, as shown in Figure 3.

TABLE 3

TABLE 3. Value of parameters a and b of different rock-size.

FIGURE 3

FIGURE 3. Fitting curve diagram of parameter. (A) parameter a, (B) parameter b.

From Figure 3, the following formulas for the relationship between a and b and rock size can be obtained.

$a=661.549l^{-1.053}(7)$

$b=-1.289l+0.914(8)$

From Eqs 6–8, a special relational formula for elastic modulus can be obtained as:

$E\left(n\right)=661.549l^{-1.053}{n}^{1.289\times {10}^{-4}l-0.914},(9)$

where E(n) [GPa] is the elastic modulus when the NPJs is n, n is the NPJs, and l [mm] is the rock-size.

Eq 9 is a special formula about the elastic modulus and NPJs, which can quantitatively analyze the elastic modulus of rock.

2.4 Research on the Influence of Rock-Size on Rock Elastic Modulus

According to the numerical simulation program and results of research content (ⅱ) the influence of rock size with PJs on elastic modulus, the stress–strain variation law of rock under different rock-size was analyzed. A fitting method for the relationship between the elastic modulus and rock-size was proposed. The mathematical model between elastic modulus and rock-size was established.

2.4.1 Analysis of Rock Stress–Strain Curve With Different Rock-Sizes

The stress-strain curve rules in program 6 to 10 were output in Figure 4. And according to Figure 4, the elastic modulus under each working condition was solved in Table 1.

FIGURE 4

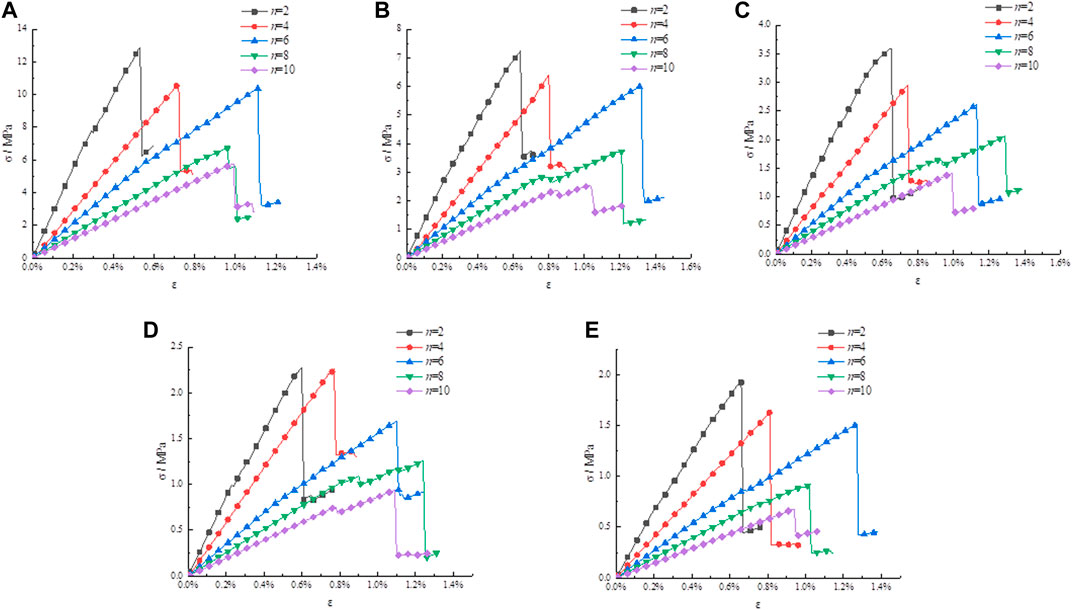
FIGURE 4. Stress–strain curves of different rock-sizes. (A) n = 2, (B) n = 4, (C) n = 6, (D) n = 8, (E) n = 10.

Figure 4 shows that the laws of stress-strain curves are similar when the rock size is different. All obey the following laws: with the increase of strain, the stress gradually increases, and the rock changes from elastic deformation to plastic failure. The destruction of rocks is a gradual process. Firstly, compaction occurs inside the rock under the action of external load. Secondly, the rock strength reaches its peak and fluctuates around the peak strength. Finally, the rock reaches macroscopic destruction.

Taking Figure 4A as an example to analyze the effect of rock size on elastic modulus. With the increase of rock size, the elastic modulus gradually decreased from 2.745 to 0.337 GPa. It shows that the elastic modulus is affected by rock size. Similarly, the same law can still be obtained when the NPJs is increased.

Taking program 1 in Table 1 as an example to analyze the effect of NPJs on elastic modulus. With the increase of NPJs, the elastic modulus gradually decreased from 2.745 to 0.591 Gpa. This phenomenon shows that elastic modulus is affected by NPJs. From program 2 to 5 also have the same law, indicating that the NPJs has an important influence on the elastic modulus.

In short, the elastic modulus with joints decreases with the increase of NPJs, and decreases with the increase of the size of the rock.

2.4.2 Fitting Method for Relationship Between Rock Elastic Modulus and Rock-Size

According to the data in Table 1, the fitting curve of the elastic modulus of rocks with different rock sizes was drawn, as shown in Figure 5.

FIGURE 5

FIGURE 5. Fitting curve of elastic modulus of rock under different rock-size.

Figure 5 shows that when NPJs is the same, as the rock size increases, the elastic modulus gradually decreases. Rocks with different NPJs have the same variation law. The variation law of elastic modulus with different sizes is the same. However, with different NPJs, the elastic modulus decreases at different rates. It shows that the elastic modulus is not only related to the size of the rock, but also related to the NPJs. That is to say, the elastic modulus with different NPJs has size effect.

Numerical simulation was performed on rocks with NPJs of 4, 6, 8, and 10, respectively under the same conditions, and the fitting relationships between the elastic modulus and the rock-size were obtained as follows. Among them, Eqs 10–14 are the regression functions for NPJs of 2, 4, 6, 8, and 10, respectively, and the fitting coefficients are 0.995, 0.991, 0.996, 0.996, and 0.996.

$E\left(l\right)=0.406+5.019e^{-0.0103l},(10)$

$E\left(l\right)=0.267+3.305e^{-0.0094l},(11)$

$E\left(l\right)=0.156+2.088e^{-0.0085l},(12)$

$E\left(l\right)=0.111+1.362e^{-0.0079l},(13)$

$E\left(l\right)=0.088+1.064e^{-0.0077l}.(14)$

Analyzing the fitting formula, the relationships between the elastic modulus and the rock-size fit well, showing a negative exponential function relationship. It can provide a way to quantitative analyze the elastic modulus and rock-size for engineering practice.

2.4.3 Relationship Between Elastic Modulus of Rock and Parallel-Jointed Rock-Size

According to the fitting formula, the fitting curve of the elastic modulus versus different sizes is proposed:

$E\left(l\right)=d+f{e}^{-gl}(15)$

where E(l) [GPa] is the elastic modulus when the rock-size is l, l [mm] is the rock size, and d, f, and g are undetermined parameters.

According to the formula, the values of parameters d, f and g are found in Table 4. The fitting curves of parameters d, f and g and rock size are drawn, as shown in Figure 6.

TABLE 4

TABLE 4. Values of parameters d, f, and g of different number of parallel-joints.

FIGURE 6

FIGURE 6. Fitting curve diagram of parameter. (A) parameter d, (B) parameter f, (C) parameter g.

From Figure 6, the following formulas for the relationship between d, f, and g and NPJs can be obtained.

$d=0.621e^{-0.2145n},(16)$

$f=7.626e^{-0.2103n},(17)$

$g=-3.375\times {10}^{-4}n+\mathrm{0.011.}(18)$

From Eqs 15–18, a special relational formula for elastic modulus can be obtained as:

$E\left(l\right)=0.621e^{-0.2145n}+7.626e^{\left(3.375\times {10}^{-4}nl-0.0108l-0.2103n\right)}(19)$

where E(l) [GPa] is the elastic modulus when the rock-size is l, n is the NPJs, and l [mm] is the rock-size.

Eq 19 is a special formula about the elastic modulus and rock size, which can quantitatively analyze the elastic modulus.

2.5 Established Relationship of Characteristic-Size of Elastic Modulus, Characteristic Elastic Modulus and Number of Parallel-Joints

Usually, the characteristic-size is used to quantitatively analyze the size effect of rock. The elastic modulus has size effect. Therefore, the size effect of the elastic modulus can be characterized by the CSEM. It is of great meaningful to analyze the influence of NPJs on the CSEM.

2.5.1 Derived Formula of Characteristic-Size of Elastic Modulus

The size effect of the elastic modulus can be characterized by the CSEM. The quantitative calculation of characteristic-size is given a minute description in the literature (Ling et al., 2013). The formula to solve the characteristic-size is as follows:

$\left|k\right|=\left|gf{e}^{\left(-gl\right)}\right|(20)$

$\left|k\right|\le \gamma (21)$

$l\ge \frac{\ln \left(gf\right)-\ln \gamma }{g}(22)$

where k and γ are the slope value, f and g are undetermined parameters.

2.5.2 Relationship Between Characteristic-Size of Elastic Modulus and Number of Parallel-Joints

When the NPJs was 2, 4, 6, 8, and 10, the CSEM were calculated as summarized in Table 5. According to the data in Table 5, the fitting curve of the CSEM and NPJs is regressed, as shown in Figure 7A.

TABLE 5

TABLE 5. Relationship between characteristic-size of elastic modulus and number of parallel-joints.

FIGURE 7

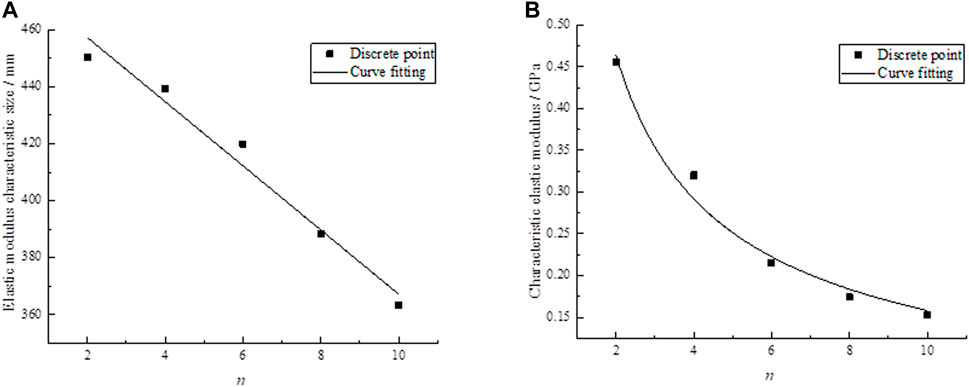
FIGURE 7. Fitting curve. (A) characteristic-size of elastic modulus, (B) characteristic elastic modulus.

The slope of the curve in Figure 7A is negative, indicating that the CSEM gradually decreases with the increase of NPJs. They are linearly related, and the function type conforms to a linear functional relationship. Therefore, the following special relation is obtained:

$L\left(n\right)=-11.26n+479.787,(23)$

where L(n) [mm] is the CSEM, n is the NPJs.

Eq 23 can be used to describe the mathematical relationship between the CSEM and NPJs, and can be extended to similar rocks with parallel joints.

2.5.3 Relationship Between the Characteristic-Elastic-Modulus of Rock and the Number of Parallel-Joints

Substituting the value of the CSEM into Eq 15, the CEM of the rock when the NPJs was 2,4, 6, 8, 10 was obtained in Table 5. According to the data in Table 5, the fitting curve of the CEM and NPJs is regressed, as shown in Figure 7B.

Figure 7B shows that with the increase of NPJs, the CEM gradually decreases. They are in a power function relationship. Therefore, the following special relation is obtained:

$E_w\left(n\right)=0.736n^{-0.667}(24)$

where E_w(n) [GPa] is the CEM of rock, n is the NPJs.

Eq 24 can be used to describe the mathematical relationship between the CEM and NPJs, and the fitting coefficient R² = 0.983. It can be extended to similar rocks with parallel joints.

2.6 Verification Analysis of Research Content (ⅱ)

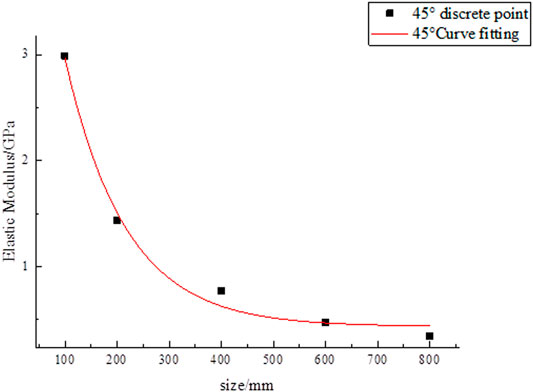
To verify the correctness and general applicability of Eq 15 obtained in research content (ⅱ), a new set of numerical simulations with two parallel joints with an angle of 45° was added for verification. According to the numerical simulations, the stress-strain curves of different rock sizes were drawn, as shown in Figure 8.

FIGURE 8

FIGURE 8. The stress-strain curve of different rock sizes.

According to the slope of the stress-strain curves in Figure 8, the elastic modulus of rocks with different sizes are calculated in Table 6. The functional relationship between elastic modulus and rock size was found from the data in Table 6, and their fitting curves were drawn, as shown in Figure 9.

TABLE 6

TABLE 6. Elastic modulus of different rock sizes at joint angles of 45°.

FIGURE 9

FIGURE 9. Fitting curve of elastic modulus with different rock sizes.

Figure 9 shows the relationship between elastic modulus and rock size when the parallel joint angle is 45°:

$\begin{array}{cc}E\left(l\right)=0.434+5.97e^{-l/116.64}& \left({\mathrm{R}}^2=0.983\right)\end{array}(25)$

Both the function type of Eq. 25 and the mathematical model proposed in Eq 15 conform to the negative exponential function relationship. Therefore, it is proved that Eq 15 is still applicable when the angle of the parallel joint changes. The verification shows that the mathematical model proposed in Eq 15 is suitable to the elastic modulus of rocks with parallel joints of arbitrary angles.

3 Discussion

The NPJs has an influence on the size effect of elastic modulus, but the relationship is yet to be obtained. This study established the following four relationships: 1) elastic modulus and NPJs; 2) elastic modulus and rock size; 3) CSEM and NPJs; 4) CEM and NPJs.

3.1 Relationship Between Elastic Modulus and NPJs

The establishment of this relationship is to first establish the general formula of the relationship between elastic modulus and NPJs by analyzing the influence of the change of the NPJs on elastic modulus. Then combined with the change of rock size, the solution method of the parameters in the general formula is given, and the specific relational formula is obtained. In the existing research, few scholars have discussed the effect of NPJs on elastic modulus, and rarely considered the effect of the change of rock size on the elastic modulus with PJs.

3.2 Relationship Between Elastic Modulus and Rock Size

The establishment of this relationship is to first establish the general formula of the relationship between elastic modulus and rock size by analyzing the influence of the change of the rock size on elastic modulus. Then combined with the change of NPJs, the solution method of the parameters in the general formula is given, and the specific relational formula is obtained. In the existing research, few scholars have discussed the size effect of rock with PJs on elastic modulus, and rarely considered the influence of the change of NPJs on the size effect of elastic modulus.

3.3 Relationship Between CSEM, CEM and NPJs

The establishment of these two relationships is based on the relationship (1). In the existing research, scholars rarely have carried out the research on the relationship between the CSEM, CEM and NPJs.

The establishment of these four relationships in this study reveals the law of size effect of rocks with NPJs, which has important engineering application value.

4 Conclusion

In this paper, numerical simulation is used to study the size effect of NPJs on elastic modulus, and the following conclusions are obtained:

1) The relationship between the elastic modulus and NPJs conforms to a linear function relationship, and the general formula of their relationship is as follows:

$E\left(n\right)=-an+b,$

Further, we find that the parameters a and b are affected by the size of the rock. Through regression analysis, we obtain a special relationship:

$E\left(n\right)=\left(23.67e^{-0.0008l}-1.366n\right)e^{-0.0056l}-0.135n+\mathrm{2.07.}$

2) The relationship between the elastic modulus and rock size conforms to a negative exponential relationship, and the general formula of their relationship is as follows:

$E\left(l\right)=d+f{e}^{-gl}$

Further, we find that the parameters d, f, and g are affected by the NPJs. Through regression analysis, we obtain a special relationship:

$E\left(l\right)=\left(24.237-1.379n\right)e^{-0.0055l{e}^{0.0463n}}-0.139n+\mathrm{2.222.}$

3) We find that the CSEM is linearly related to the NPJs, and our simulation gives the following special form:

$L\left(n\right)=-28.98n+\mathrm{978.442.}$

4) We find that the relationship between the CEM and NPJs is linear, and our simulation gives the following special form:

$E_w\left(n\right)=-0.143n+\mathrm{2.321.}$

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

GH: Conceptualization, formal analysis, methodology, funding acquisition, writing and original draft preparation. GM: Investigation, software, writing and original draft preparation. WL: Data curation, formal analysis. LS: Investigation, data curation. WF: Data curation, formal analysis.

Funding

This work was supported by the National Natural Science Foundation of China (42002275), the Natural Science Foundation of Zhejiang Province (LQ21D020001), the China Postdoctoral Science Foundation (2021M692319), Zhejiang Collaborative Innovation Center for Prevention and Control of Mountain Geological Hazards (PCMGH-2017-Y-05), Key Laboratory of Rock Mechanics and Geohazards of Zhejiang Province (ZGRMG-2019-07), and Shaoxing City Public Welfare Technology Application Research Project (2018C30006).

Conflict of Interest

Author WL and WF were employed by China Coal Technology and Engineering Group.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors appreciate the support of the National Natural Science Foundation of China (42002275), the Natural Science Foundation of Zhejiang Province (LQ21D020001), the China Postdoctoral Science Foundation (2021M692319), Zhejiang Collaborative Innovation Center for Prevention and Control of Mountain Geological Hazards (PCMGH-2017-Y-05), Key Laboratory of Rock Mechanics and Geohazards of Zhejiang Province (ZGRMG-2019-07), and Shaoxing City Public Welfare Technology Application Research Project (2018C30006). The authors also appreciate the help of China Coal Technology and Engineering Group.

References

Bear, J. (1972). Dynamics of Fluids in Porous Media. Amsterdam, Netherlands: American Elsevier Pub. Co.

Google Scholar

Chen, D., Guo, Z., Huang, H., Sun, B., Lu, H., and Zhu, W. (2019). Triaxial Test of Coal-Rock under Effective Confining Pressure. IOP Conf. Ser. Mater. Sci. Eng. 592, 012175. doi:10.1088/1757-899x/592/1/012175

CrossRef Full Text | Google Scholar

Cui, Z., Chen, P. Z., and Sheng, Q. (2020). Estimation of REV for Danba Schist Based on 3D Synthetic Rock Mass Technique. IOP Conf. Ser. Earth Environ. Sci. 570 (3), 032001. doi:10.1088/1755-1315/570/3/032001

CrossRef Full Text | Google Scholar

Dai, B., Zhao, X., Zhang, S., Kang, Q., and Zhu, Z. (2020). Mechanical Behavior and Energy Evolution of Sandstone Considering Slenderness Ratio Effect. Adv. Civil Eng. 2020 (9), 1–13. doi:10.1155/2020/8881416

CrossRef Full Text | Google Scholar

Han, Z., Zhang, L., and Zhou, J. (2019). Effect of mineral Particle Size Heterogeneity on Mechanical Properties in PFC- (2D) Simulation. J. Eng. Geology. 27 (4), 706–716. doi:10.13544/j.cnki.jeg.2017-148

CrossRef Full Text | Google Scholar

Hu, G., and Ma, G. (2021). Size Effect of Parallel-Joint Spacing on Uniaxial Compressive Strength of Rock. PLoS One 16 (9), 1–16. doi:10.1371/journal.pone.0257245

CrossRef Full Text | Google Scholar

Huang, C., Yang, W., Duan, K., Fang, L., Wang, L., and Bo, C. (2019). Mechanical Behaviors of the Brittle Rock-like Specimens with Multi-Non-Persistent Joints under Uniaxial Compression. Construction Building Mater. 220 (30), 426–443. doi:10.1016/j.conbuildmat.2019.05.159

CrossRef Full Text | Google Scholar

Liang, Z., Wu, N., Li, Y., and Li, W. (2019). Numerical Study on Anisotropy of the Representative Elementary Volume of Strength and Deformability of Jointed Rock Masses. Rock Mech. Rock Eng. 52 (3), 4387–4402. doi:10.1007/s00603-019-01859-9

CrossRef Full Text | Google Scholar

Lin, Q., Cao, P., Meng, J., Cao, R., and Zhao, Z. (2020). Strength and Failure Characteristics of Jointed Rock Mass with Double Circular Holes under Uniaxial Compression: Insights from Discrete Element Method Modelling. Theor. Appl. Fracture Mech. 109, 102692. doi:10.1016/j.tafmec.2020.102692

CrossRef Full Text | Google Scholar

Ling, Z. Z., Zhang, Y. B., Tang, S. B., Li, L., and Tang, C. (2013). Size Effect of Rock Masses and Associated Representative Element Properties. Chin. J. Rock Mech. Eng. 32 (6), 1157–1166. doi:10.3969/j.issn.1000-6915.2013.06.009

CrossRef Full Text | Google Scholar

Liu, J., Su, H., Jing, H., Hu, C., and Yin, Q. (2020). Experimental Study on the Fracture Evolution Processof Rock-like Specimens Containing a Closed RoughJoint Based on 3D-Printing Technology. Adv. Civil Eng. 2020 (1), 1–16. doi:10.1155/2020/8889606

CrossRef Full Text | Google Scholar

Liu, W.-r., Liu, J.-k., and Zhu, C. (2019). Multi-scale Effect of Acoustic Emission Characteristics of 3D Rock Damage. Arab J. Geosci. 12 (22), 668–680. doi:10.1007/s12517-019-4864-4

CrossRef Full Text | Google Scholar

Liu, W., Yuan, W., Yan, Y., and Wang, X. (2019). Analysis of Acoustic Emission Characteristics and Damage Constitutive Model of Coal-Rock Combined Body Based on Particle Flow Code. Symmetry 11 (8), 1040. doi:10.3390/sym11081040

CrossRef Full Text | Google Scholar

Liu, Z., Ma, C., Wei, X. a., and Xie, W. (2021). Experimental Study on Mechanical Properties and Failure Modes of Pre-existing Cracks in sandstone during Uniaxial Tension/compression Testing. Eng. Fracture Mech. 255 (3), 107966. doi:10.1016/j.engfracmech.2021.107966

CrossRef Full Text | Google Scholar

Loyola, A. C., Pereira, J. M., and Neto, M. (2021). General Statistics-Based Methodology for the Determination of the Geometrical and Mechanical Representative Elementary Volumes of Fractured Media[J]. Rock Mech. Rock Eng. 54 (2), 1841–1861. doi:10.1007/s00603-021-02374-6

CrossRef Full Text | Google Scholar

Ma, Q., Tan, Y.-l., Liu, X.-s., Zhao, Z.-h., and Fan, D.-y. (2021). Mechanical and Energy Characteristics of Coal-Rock Composite Sample with Different Height Ratios: a Numerical Study Based on Particle Flow Code. Environ. Earth Sci. 80 (8), 309. doi:10.1007/s12665-021-09453-5

CrossRef Full Text | Google Scholar

Peng, C., Guo, Q., Yan, Z., Wang, M., and Pan, J. (2020). Investigating the Failure Mechanism of Jointed Rock Slopes Based on Discrete Element Method. Adv. Civil Eng. 2020 (9), 1–19. doi:10.1155/2020/8820158

CrossRef Full Text | Google Scholar

Peng, J., Wong, L. N. Y., Liu, G., and Teh, C. I. (2019). Influence of Initial Micro-crack Damage on Strength and Micro-cracking Behavior of an Intrusive Crystalline Rock. Bull. Eng. Geol. Environ. 78 (4), 2957–2971. doi:10.1007/s10064-018-1317-3

CrossRef Full Text | Google Scholar

Shu, J., Jiang, L., Kong, P., and Wang, Q. (2019). Numerical Analysis of the Mechanical Behaviors of Various Jointed Rocks under Uniaxial Tension Loading. Appl. Sci. 9 (9), 1824. doi:10.3390/app9091824

CrossRef Full Text | Google Scholar

Sun, Y., Hao, Y., Peng, G., Wang, Y., Dong, S., and Cheng, Y. (2019). Investigation on the Effect of Gravel on the Fracture of Sand Conglomerate Based on RFPA. J. Petrochemical Universities 32 (3), 71–75. doi:10.3969/j.issn.1006-396X.2019.03.012

CrossRef Full Text | Google Scholar

Tang, C. (1997). Numerical Simulation of Progressive Rock Failure and Associated Seismicity. Int. J. Rock Mech. Mining Sci. 34 (2), 249–261. doi:10.1016/s0148-9062(96)00039-3

CrossRef Full Text | Google Scholar

Wang, G.-L., Zhang, L., Wang, Z., Zhang, J.-Z., Sun, F., and Qiu, P.-Y. (2019). Acoustic-Mechanical Responses of Intact and Flaw-Contained Rock Deformation under Uniaxial Compression: A Comparison. Adv. Civil Eng. 2019, 1–12. doi:10.1155/2019/7940923

CrossRef Full Text | Google Scholar

Wang, L., Tang, K., Li, J., and Xu, X. (2020). Experimental Research on the Anisotropic Properties of sandy Slate. IOP Conf. Ser. Earth Environ. Sci. 570 (3), 032055. doi:10.1088/1755-1315/570/3/032055

CrossRef Full Text | Google Scholar

Wang, P. X., Cao, P., Pu, C. Z., Fan, X., Chen, Y., and Wang, C. C. (2017). Effect of the Density and Inclination of Joints on the Strength and Deformation Properties of Rock-like Specimens under Uniaxial Compression. Chin. J. Eng. 39 (04), 494–501. doi:10.13374/j.issn2095-9389.2017.04.003

CrossRef Full Text | Google Scholar

Wang, X., Yuan, W., Yan, Y., and Zhang, X. (2020). Scale Effect of Mechanical Properties of Jointed Rock Mass: A Numerical Study Based on Particle Flow Code. Geomechanics Eng. 21 (3), 259–268. doi:10.12989/gae.2020.21.3.259

CrossRef Full Text | Google Scholar

Wu, W., Yang, Y., and Zheng, H. (2020). Hydro-mechanical Simulation of the Saturated and Semi-saturated Porous Soil-Rock Mixtures Using the Numerical Manifold Method. Comput. Methods Appl. Mech. Eng. 370 (3), 113238. doi:10.1016/j.cma.2020.113238

CrossRef Full Text | Google Scholar

Wu, W., Yang, Y., Zheng, H., Zhang, L., and Zhang, N. (2022). Numerical Manifold Computational Homogenization for Hydro-Dynamic Analysis of Discontinuous Heterogeneous Porous media. Comput. Methods Appl. Mech. Eng. 388, 114254. doi:10.1016/j.cma.2021.114254

CrossRef Full Text | Google Scholar

Yang, Y., Tang, X.-H., Zheng, H., Liu, Q., and He, L. (2016). Three-dimensional Fracture Propagation with Numerical Manifold Method. Eng. Anal. Boundary Elem. 72, 65–77. doi:10.1016/j.enganabound.2016.08.008

CrossRef Full Text | Google Scholar

Yang, Y., Wu, W., and Zheng, H. (2021). An Uzawa-type Augmented Lagrangian Numerical Manifold Method for Frictional Discontinuities in Rock Masses. Int. J. Rock Mech. Mining Sci. 148, 104970. doi:10.1016/j.ijrmms.2021.104970

CrossRef Full Text | Google Scholar

Ying, L., Wang, Q., Chen, J., Song, S., Zhan, J., and Han, X. (2018). Determination of Geometrical REVs Based on Volumetric Fracture Intensity and Statistical Tests. Appl. Sci. 8 (5), 800. doi:10.3390/app8050800

CrossRef Full Text | Google Scholar

Yu, L., Yao, Q., Li, X., Wang, W., Han, H., and Zhang, M. (2020). Experimental Study of Failure Characteristics and Fissure Propagation in Hydrous Siltstone. Arab J. Geosci. 13 (13), 527. doi:10.1007/s12517-020-05522-4

CrossRef Full Text | Google Scholar

Zhang, H., Zhang, X., and Zhou, H. (2020). Research on Acoustic Emission Characteristics and Constitutive Model of Rock Damage Evolution with Different Sizes. Adv. Civil Eng. 2020 (16), 1–8. doi:10.1155/2020/6660595

CrossRef Full Text | Google Scholar

Zhang, S., Zhang, D., Zhao, Q., Chi, M., Zhang, W., and Yu, W. (2019). DEM Investigation of the Influence of Minerals on Crack Patterns and Mechanical Properties of Red Mudstone. Processes 7 (3), 162. doi:10.3390/pr7030162

CrossRef Full Text | Google Scholar

Zhang, X., Fatahi, B., Khabbaz, H., and Zhang, H. (2017). “Investigating Effects of Fracture Density on Stress-Strain Behaviour of Jointed Rocks Using Discrete Element Method,” in Proceedings of the 15th IACMAG. ACM, China , Wuhan, October 2017.

Google Scholar

Zhao, Y., Wu, Y., Xu, Q., Jiang, L., Huang, W., Zhang, P., et al. (2020). Numerical Analysis of the Mechanical Behavior and Failure Mode of Jointed Rock under Uniaxial Tensile Loading. Adv. Civil Eng. 2020 (4), 1–13. doi:10.1155/2020/8811282

CrossRef Full Text | Google Scholar