Anisotropic Elastic Properties of Montmorillonite With Different Layer Charge Densities and Layer Charge Distributions Through Molecular Dynamic Simulation

The knowledge of the anisotropic elastic properties of clay minerals is of crucial importance for the exploration and development of shale oil and gas. Montmorillonite (MMT) is a common natural clay mineral with different layer charge densities and layer charge distributions due to different geological conditions. Therefore, it is important to understand the currently poorly known effect of layer charge density and layer charge distribution on the anisotropic elastic properties of MMTs. This work aims to obtain such knowledge by studying the anisotropic elastic properties of different MMTs under stratigraphic conditions through molecular dynamic simulations. We showed that the in-plane compressional coefficients C₁₁, C₂₂ and C₁₂ decrease with the increasing layer charge density for MMTs with different layer charge distributions, and the MMTs with the layer charges distributed on the two tetrahedral (T) sheets were found to have the smallest C₁₁, C₂₂ and C₁₂. We also showed that the out-of-plane compressional coefficients C₃₃, C₁₃ and C₂₃ of the MMTs with the layer charges distributed in the two T sheets decrease, while those with the layer charges in the octahedral (O) sheet increase and those with layer charges distributed in both the O sheet and the T sheets do not vary much with the increasing layer charge density. The variations of the anisotropic compressional elastic coefficients with different layer charge densities and layer charge distributions were found to be a result of the impact of the density and distribution of layer charges on the molecular interactions within the MMT layer. We further demonstrated that the layer charge density and layer charge distribution do not influence significantly the shear coefficients C₄₄, C₅₅, and C₆₆. The results revealed the mechanisms of how the density and distribution of layer charges affect the anisotropic elastic properties of MMTs and will contribute to the more successful exploration and development of unconventional resources in MMT bearing shale reservoirs.

Introduction

In recent years, shale oil and gas have a contribution to a country’s energy security by lowering the dependence on imported energy (Kobek et al., 2015; Raszewski, 2016), and specifically the shale gas is considered to play a role as a bridging fuel to a low-carbon future (Kirkland, 2010; Few et al., 2017). Exploration and development of shale oil and gas are drawing a lot of attentions (Chen et al., 2021; Pu et al., 2021), in which the knowledge about the elastic properties of shale is of vital importance because the elastic properties provide crucial geomechanical information required by seismic inversion to predict “sweet spot” (Han et al., 2021) and by hydraulic fracturing projects to increase permeability for the flow of the hydrocarbon (Rahm, 2011; Bian et al., 2019). Clay minerals, as the main mineral type and the matrix of shale, cause shale to be elastically anisotropic because of their layered structure (Bailey, 1966; Weaver and Pollard, 2011). In the process of shale oil and gas exploration and development, problems such as poor fracturing effect, high development cost, and great difficulty in finding sweet spot and stabilizing the borehole wall would arise if the influence of anisotropy is ignored (Gao et al., 2021). Therefore, it is of great significance to study the anisotropic elastic properties of clay minerals for the exploration and development of shale oil and gas.

Clay minerals, any of a group of important hydrous aluminum silicates with a layer (sheet-like) structure (Grim and Kodama, 2014), consist of some combinations of silicon tetrahedra (T) and aluminum octahedra (O) (Ebrahimi et al., 2012). This work considers montmorillonite (MMT), a kind of clay mineral that has more significant swelling properties and expands more considerably than the other clay minerals, and therefore can more seriously affect the anisotropic elastic properties of shale (Dewhurst and Siggins, 2006; Sridharan, 2014; Sayers and den Boer, 2016). The experimental measurement of the anisotropic elastic properties of MMTs can be challenging because of their small grain particle size (Vanorio et al., 2003; Zartman et al., 2010). Alternatively, all-atom molecular simulation makes it possible to study the anisotropic elastic parameters of MMTs by simulating the motion of the MMT molecular system based on Newtonian mechanics. Many successful results, to date, have been obtained reporting the anisotropic elastic properties of MMTs under the effect of pressure, temperature, water content and interlayer cation types (Ebrahimi et al., 2012; Carrier et al., 2014; Zhao et al., 2021), which are of significance to understand the elastic anisotropy of clay minerals.

However, isomorphous substitution is always associated with MMTs, making them contain different layer charge densities and different layer charge distributions because of the number and locations of the isomorphous substitution (Zartman et al., 2010; Herling et al., 2012). Previous researches show that the different layer charge densities and layer charge distributions can significantly affect the physicochemical properties of MMTs such as the exfoliation performance (Zhong et al., 2021), the adsorption capacity (Lee et al., 2005; Barrientos-Velázquez et al., 2016; Koutsopoulou et al., 2020), the hydration performance (Qiu et al., 2019), the swelling properties (Teich-McGoldrick et al., 2015; Daab et al., 2018; Ghasemi and Sharifi, 2021), and the thermal stability (Qin et al., 2021) among others. Moreover, the structures of MMTs are also influenced by different layer charge densities and layer charge distributions. For instance, the basal layer spacing and interlayer spacing can be affected by different layer charge densities and distributions (Peng et al., 2021) and the introduction of the substitutions generates structural tension to the layer structure leading to the structure expansion (Lavikainen et al., 2016). Since the anisotropic elastic properties of MMTs are strongly correlated with their structure (Zhong et al., 2021), the variation of structure may potentially cause a change in the anisotropic elastic properties of MMTs. However, there are very few studies reporting the anisotropic elastic properties of MMTs with different layer charge densities and layer charge distributions. Therefore, it is necessary to study the influences of different layer charge densities and layer charge distributions on the anisotropic elastic properties of MMTs to strengthen our understanding of the elastic properties of clay minerals.

This work aims to investigate the influence of different layer charge densities and layer charge distributions on the anisotropic elastic properties of MMTs through dedicated molecular dynamic simulation. To achieve this goal, we first build a series of MMT models with different layer charge densities and layer charge distributions by molecular mechanics. The anisotropic elastic parameters of the different MMT models are subsequently calculated under stratigraphic conditions using molecular dynamic simulation. The relationships between the anisotropic elastic parameters and the different charge densities and layer charge distributions are finally analyzed and interpreted.

Methods

Model Establishment

In this study, we construct the MMT model from the structure of pyrophyllite unit cell with the crystal constant a = 0.5160 nm, b = 0.8966 nm, c = 0.9347 nm, and α = 91.18°, β = 100.46°, and γ = 89.64° (Lee and Guggenheim, 1981; Skipper et al., 1995). The pyrophyllite unit cell ${(\text{Al}}_4{\text{O}}_4{\left(\text{OH}\right)}_4{\left)\right(\text{Si}}_8{\text{O}}_{12})$ is then replicated (8 × 6 × 2) along the a, b, and c crystallographic directions, respectively to form a supercell of two TOT clay layers. The sizes of the replicated cell are Lx = 4.1280 nm, Ly = 5.3796 nm and Lz = 1.8694 nm. The constructed supercell not only decreases the subsequent excessive ordering of isomorphous substitution but also ensures that the atom in MMTs does not interact with its image in the next cell, when three-dimensional periodic boundary conditions are applied.

Based on the formed supercell, the isomorphous substitutions of octahedral Mg atom for Al atom and tetrahedral Al atom for Si atom with various compositions are introduced to establish different MMT models needed in this paper. Since one isomorphous substitution produces one negative charge (referring to the Supporting Information for details), which is referred to as the layer charge (Karnland, 2010), we introduce 48, 60, 72, 96, and 108 isomorphous substitutions to obtain the MMT models with the layer charge density (defined as the ratio between the number of layer charge to the number of unit cell, which is 96) of −0.5, −0.625, −0.75, −1.0, and −1.125 e/uc, respectively. For the MMT models with each layer charge density, three different isomorphous substitution positions, i.e., complete tetrahedral substitutions in the T sheet, entire octahedral substitutions in the O sheet and the ratio of the tetrahedral to octahedral substitutions is 1:1, are designed and the corresponding MMT models are denoted as M1, M2, and M3, respectively. All isomorphous substitutions obey Lowenstein’s substitution rule (i.e., the substitution sites cannot be adjacent to each other). We finally add the same number of Na cations as the layer charge between the layers of the MMT models to make sure that each MMT system is electrically neutral. Eventually, fifteen MMT models are established. Figure 1 shows the schematic view of the three MMT models and the snapshot of the molecular dynamic simulation supercell for the M3 Model with the layer charge of 0.75 e/uc.

FIGURE 1

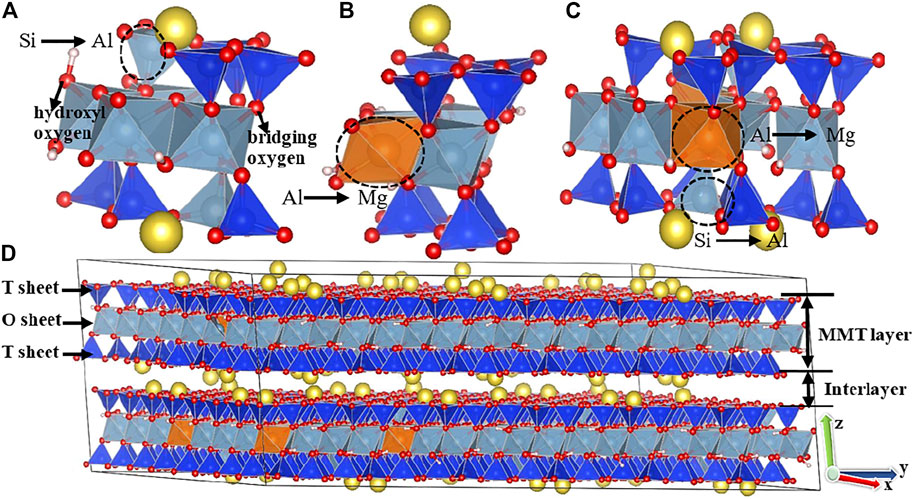
FIGURE 1. Schematic views of (A) the two unit cells for the M1 Model, (B) the unit cell for the M2 Model, and (C) the four unit cells for the M3 Model and snapshot of (D) the molecular dynamic simulation supercell for the M3 Model with the layer charge of 0.75 e/uc. The color code is Si (blue), Al (blue-grey), Mg (orange), O (red), H (pink), and Na (yellow). The atoms in the black circle are the representative atoms of replacement.

Elastic Tensor Computation

In our molecular dynamic simulation, the Parinello−Rahman (PR) strain fluctuation formula (Ray and Rahman, 1985; Cui et al., 2007; Carrier et al., 2014) is used to calculate the anisotropic elastic parameters in the constant-pressure and constant-temperature (NPT) ensemble. The PR strain fluctuation formula is given as

$C_{ijkl}=\frac{K_{B}T}{\langle V\rangle }{\left[\langle {\epsilon }_{ij}{\epsilon }_{kl}\rangle -\langle {\epsilon }_{ij}\rangle \langle {\epsilon }_{kl}\rangle \right]}^{-1}(1)$

where $K_B$ is the Boltzmann constant, equal to 1.38065 × 10^–23 J/K, T is the temperature in Kelvin, V is the volume in cubic meters, ${\epsilon }_{ij}$ is the strain tensor, and $\langle \mathit{\blacksquare }\rangle$ denotes the ensemble average. The subscripts i, j, k and l run from one to three and represent the three dimensions in the Cartesian coordinates. The indexes one and two correspond to the x- and y-axes, respectively, which are parallel to the MMT layer, and the index three corresponds to the z-axis, which is perpendicular to the MMT layer. The strain tensor ${\epsilon }_{ij}$ can be determined by

${\epsilon }_{ij}=\frac{1}{2}\left[{\langle h\rangle }_{ik}^{-T}{h}_{kl}^T{h}_{lm}{h}_{mj}^{-1}-{\delta }_{ij}\right](2)$

where ${\delta }_{ij}$ is the Kronecker tensor, and h is the scaling matrix, which can be obtained through molecular dynamic simulation.

In this work, the LAMMPS code (Plimpton, 1995) is employed to perform the molecular dynamic simulation to obtain the scaling matrix h. In the simulation, a force field is required to describe the interactions of the atoms in the MMT, and we use the CLAYFF force field (Cygan et al., 2004) for this purpose (the interaction parameters and charge of the relevant atoms are shown in the Supporting Information). The CLAYFF force field consists solely of the electrostatic terms, the Lennard-Jones terms and the O-H bond constrained by a harmonic bond stretch potential and is widely used in the simulations of clay minerals (Ebrahimi et al., 2012; Carrier et al., 2014). In our molecular dynamic simulations, we set the time step to be 1 fs in the NPT ensemble under stratigraphic conditions (i.e., p = 10 MPa, and T = 323 K). The Langevin dynamics and Nosé−Hoover barostat are used to control the pressure and temperature, respectively. The cutoff distance of the nonbonded interaction is set to be 10.0 Å, and the long-range electrostatic interactions are calculated employing the particle-particle particle mesh (PPPM) method with an accuracy of 10^–4. The system is equilibrated for 2 ns. The box size (lx, ly, lz), tilt factors (xy, xz, yz) and volume of box (V) are then sampled every ten steps for 8 ns. After that, the sample data (lx, ly, lz, xy, xz, yz) are sorted to form the scaling matrix h in the form of

$h=\left[\begin{array}{c}lx xy xz\\ 0lyyz\\ 00lz\end{array}\right](3)$

Then the resulting scaling matrix h is substituted into Eq. 2 to obtain the strain tensor ${\epsilon }_{ij}$, which are further integrated into Eq. 1 with V and T to determine the elastic tensors $C_{ijkl}$ of the MMTs.

When we show the elastic tensors, the Voigt notation is used to represent the calculated fourth-order stiffness tensor $C_{ijkl}$ by the second-order tensors $C_{ij}$ . The indexes change as follows: $11\to 1$, $22\to 2$, $33\to 3$, $23\to 4$, $13\to 5$, and $12\to 6$. The indexes 1, 2, and three correspond to the compressions in the x, y, and z directions, respectively, and the indexes 4, 5, and six correspond to the shears in the yz-, xz-, and xy-planes, respectively. Although 36 coefficients of the stiffness tensor are computed, we only report the nine coefficients C₁₁, C₂₂, C₁₂, C₃₃, C₁₃, C₂₃, C₄₄, C₅₅, and C₆₆ because of the transverse isotropic characteristics of MMT (Ebrahimi et al., 2012; Carrier et al., 2014). According to the deformation modes involving the crystalline structure of the clay layer and interlayer space, the nine data are divided into three groups: the in-plane compressional coefficients C₁₁, C₂₂, and C₁₂, the out-of-plane compressional coefficients C₃₃, C₁₃, C₂₃, and the shear coefficients C₄₄, C₅₅, and C₆₆.

Results and Discussion

Before presenting the simulation results of the anisotropic elastic coefficient with varying layer charge density and layer charge distribution, we need to test the validity of the employed method for the computation of the anisotropic elastic tensors. This is achieved by performing the calculation on the elastic coefficients of the MMT model [${(\text{Na}}_6{[\text{Si}}_{62}{\text{Al}}_2{\left]\right[\text{Al}}_{28}{\text{Mg}}_4{]\text{O}}_{160}{\left(\text{OH}\right)}_{32})$] at the pressure and temperature of 1 Bar and 300 K, respectively, and comparing the results with those published by Carrier et al. (2014) using the same model at the same pressure and temperature. The comparison of the calculated elastic coefficients is given in Table 1, from which we can see that our calculated elastic coefficients are in good agreement with those of Carrier et al. (2014). The excellent agreement validates the computation method for the elastic tensors, and lays the foundation for the study of the anisotropic elastic properties of MMTs with different layer charge densities and layer charge distributions.

TABLE 1

TABLE 1. Comparison of calculated the elastic coefficients of the MMT at 1 Bar and 300 K by Carrier et al. (2014) and by the method provided in this work.

In-Plane Compressional Coefficients

The variations of the in-plane compressional coefficients C₁₁, C₂₂, and C₁₂ with different layer charge densities for the three models with different layer charge distributions are shown in Figure 2. It is interesting that all the three in-plane compressional coefficients decrease approximately linearly with the increasing layer charge density in the three models. The reduction in the three coefficients indicates that the compressional resistance of the three models decreases with the increasing layer charge density. Specifically, the decreasing C₁₁ and C₂₂ represents the reduction in the compressional resistance in the x-axis and y-axis, respectively, and the declining C₁₂ stands for the decrease of the compressional resistance in the y-direction when a given positive pressure is applied to the x-axis.

FIGURE 2

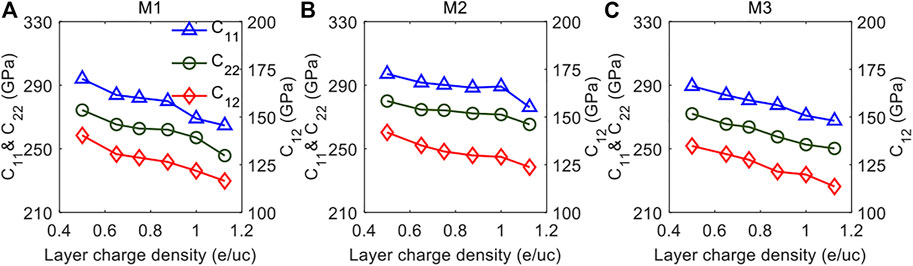
FIGURE 2. The in-line compressional elastic constants C₁₁, C₂₂, and C₁₂ as a function of layer charge density for the (A) M1 Model, (B) M2 Model and (C) M3 Model.

Since C₁₁ and C₂₂ reflect the strength of the intermolecular interactions of the MMT molecules in the x-axis and y-axis, respectively, and C₁₂ reflects the strength of the intermolecular interactions in the xy-plane, the decrease of C₁₁, C_22, and C₁₂ can be explained by the weakening of the intermolecular interactions of the MMT in these directions. The intermolecular interaction is inversely proportional to the atomic distance (Cygan et al., 2004; Davarcioglu, 2011), and thus the decrease of the three coefficients with the increasing layer charge density may be related to the increase in the atomic distance of the MMT. Figure 3 shows the atomic distances (distance between the replaced atom or replacement atom and the adjacent oxygen atom) before and after the substitutions, and the results clearly demonstrate that the atomic distances in the MMT layer (composed of three sheets) after the substitutions are increasing, no matter whether the tetrahedral substitutions or the octahedral substitutions are introduced into the MMT. The increase in the atomic distance in the MMT layer may lead to the weakening of the intermolecular interactions within the MMT layer in all directions.

FIGURE 3

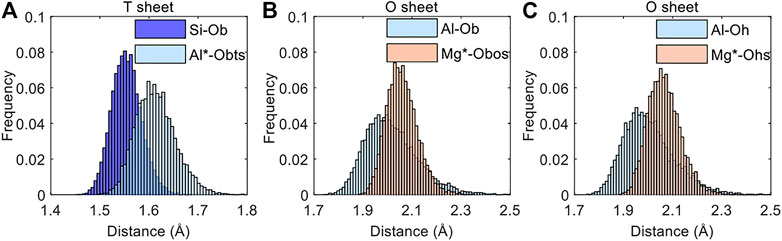
FIGURE 3. The frequency of the distance between the substituted atom or replacement atom and the adjacent oxygen atom in the (A) T sheet and (B, C) O sheet of the MMT layer before and after the isomorphous substitution. The symbol * represents the atoms after substitution. In the O sheet, the Al/Mg-O distances are classified into the Al/Mg-Ob(os) and Al/Mg-Oh(s) distances according to the type of the connected oxygen atoms (i.e., bridging oxygen or hydroxyl oxygen) as shown in Figure 1.

To further support the explained variation of the interaction strength, we also calculate the interaction energy (the difference between the molecules’ combined energy and all of their isolated energies) between the replaced atom or replacement atom and the adjacent oxygen atom (i.e., the forming atom pair) as shown in Figure 4. It can be seen that the interaction energy between the atom pair increases after the tetrahedral substitutions or the octahedral substitutions, directly indicating that the interaction within the MMT layer is weakened (Šponer et al., 1999; Lovelock, 2017). Considering the in-plane compressional coefficients are related to the intermolecular interactions in the x- and y-axes of the MMT layer (Carrier et al., 2014), the increase in the atomic distances will reduce these intermolecular interactions in these directions and hence the in-line compressional elastic coefficient C₁₁, C₂₂, and C₁₂.

FIGURE 4

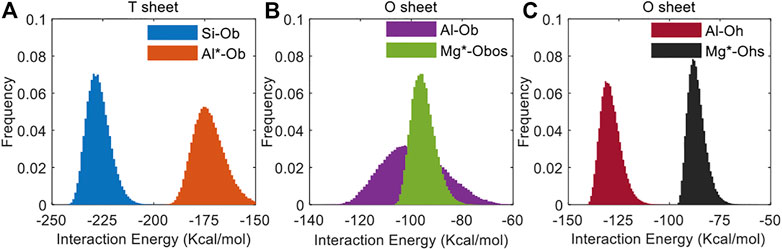
FIGURE 4. The frequency of the interaction energy between the replaced atom or replacement atom and the adjacent oxygen atom in the (A) T sheet and (B,C) O sheet of the MMT layer before and after the isomorphous substitution.

It is worth noting that although C₁₁, C₂₂, and C₁₂ of all the models are decreasing, we find the values and the variations of C₁₁, C₂₂, and C₁₂ in the three models are different. First, it is evident that C₁₁, C₂₂, and C₁₂ in the M2 Model are larger than those in the other two models when the layer charge densities are the same. This means that C₁₁, C₂₂, and C₁₂ of the MMT with the layer charges distributed in the O sheet are greater than those of the MMT with the layer charges distributed in the two T sheets and in both the O sheet and the T sheets. This result can be closely related to the structure of the MMT. As shown in Figure 1D, the MMT consists of a sandwich of one O sheet between two T sheets, called a TOT structure. Since the O sheet is constrained by the two T sheets and there are interactions among the sheets, the increase in the atomic distance and in the interaction energy between the atomic pairs in the O sheet after the octahedral substitution is weakened. As a result, the intermolecular interactions in the xy-plane are less reduced, leading to a greater C₁₁, C₂₂, and C₁₂ in the M2 model.

In addition to the difference in the values of the three in-plane compressional coefficients, it is also interesting to note that the changing rates of the compressional coefficient with layer charge densities in the three models are different. Table 2 tabulates the slopes of C₁₁, C₂₂, and C₁₂ after linear fitting for the three models. By comparing the slopes of the same parameter in the three models, we find that the M1 model has the largest slopes of C₁₁, C₂₂, and C₁₂, followed by the M3 model and the M2 model. This result implies that the layer charge density has a greater effect on C₁₁, C₂₂, and C₁₂ of MMT with the layer charges distributed in the T sheet. The difference in the slopes of the in-plane compressional coefficients in the three models can again be explained through the structure of the MMT, where the TOT architecture will confine the expansion of the O sheet, and hence the octahedral substitution has less impaction on the elastic properties, resulting in a gentler slope of the in-plane compressional coefficients with varying layer charge density.

TABLE 2

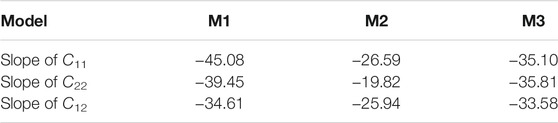
TABLE 2. The linear-fit slopes of the compressional elastic constants C₁₁, C₂₂, and C₁₂ with the varying layer charge density for the three models.

Out-of-Plane Compressional Coefficients

Figure 5 shows the variations of the out-of-plane compressional coefficients C₃₃, C₁₃, and C₂₃ with the increase of layer charge density for the three models with different layer charge distributions. Unlike the in-plane compressional coefficients that show consistent downward trends in the three models, the out-of-plane compressional coefficients show very different variations with layer charge density in the three models. Therefore, to more conveniently understand the influences of the layer charge distribution on the out-of-plane compressional coefficients, we choose to analyze the same elastic coefficient in the different models.

FIGURE 5

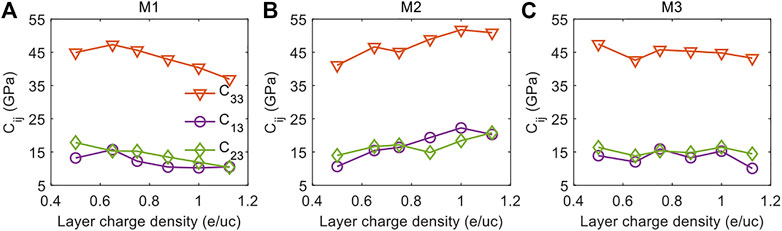
FIGURE 5. The out-of-plane compressional elastic constants C₃₃, C₁₃, and C₂₃ as a function of layer charge density for the (A) M1 Model, (B) M2 Model and (C) M3 Model.

We first compare the variations of C₃₃ with layer charge density in the three models that represents the compressional resistance of the MMT in the z-axis. As shown in Figure 5A, C₃₃ of the M1 Model increases slightly and then decreases linearly with the increase of layer charge density. The initial increasing and then decreasing C₃₃ indicates that the increasing layer charge density first increases and then reduces the compressional resistance of the M1 Model in the z-axis. In a different manner, C₃₃ of the M2 Model consistently increases with increasing layer charge density, suggesting that the compressional resistance of the M2 Model in the z-axis is increasing with the increasing layer charge density. For the M3 Model, C₃₃ doesn’t vary much as the layer charge density increases, implying that the layer charge density is not affecting significantly the compressional resistance of the M3 Model in the z-axis.

Because C₃₃ reflects the strength of the intermolecular interactions of the MMT in the z-axis, the different trends of C₃₃ with the increase of layer charge density in the different models can be explained by the difference in the z-axis intermolecular interaction strength of the MMT caused by the layer charge distributions. The intermolecular interactions of the MMT in the z-axis involve the intermolecular interactions in the z-axis both within the MMT layer (each layer is composed of three sheets) and between the neighboring MMT layers because the MMT contains the MMT layers and the interlayers in the z-axis as shown in Figure 1D. We have employed atomic distance inversely to represent the strength of the intermolecular interactions in the previous section, however, the atomic distance can only reflect the intermolecular strength of the MMT layer in the x- and y-axes, but will not fully represent the intermolecular strength in the z-axis. This is because the z-axis intermolecular interaction includes not only the z-axis intermolecular interaction within each MMT layer but also that between the MMT layers (i.e., the interlayers). To characterize the strength of the intermolecular interactions of the MMT in the z-axis, we will use the interaction energy of the MMT layer and the interlayer. However, the interaction energy will not directly quantify the interaction strength in a particular direction because it contains the information of the intermolecular interactions in all directions. Therefore, we combine the interaction energy with the calculated atomic distance (as shown in Figure 3) that reflects the intermolecular interactions in the x- and y-axes for the better characterization of the intermolecular strength in the z-axis.

Figure 6 shows the simulated interaction energy in the MMT layer and the interlayer as a function of layer charge density for the three models. In the three models, the interaction energy in the interlayer all decreases with the increasing layer charge density, indicating enhanced interlayer interactions (Shiu and Tsai, 2014; Wang et al., 2018). The decreasing interlayer interaction energy with increasing layer charge density can be explained by the fact that with increasing layer charge density there are more compensating Na cations in the interlayer that bind stronger the MMT layers (Zhong et al., 2021), resulting in lower interlayer interaction energy. On the contrary, the interaction energy in the MMT layer varies differently with the increase of layer charge density in the three models. The layer interaction energy of the MMT increases remarkably with the increasing layer charge density in the M1 model, and the increase becomes less significant in the M3 model, indicating the strength of the intermolecular interactions within the MMT layer are reducing significantly and gently in the M1 Model and M3 Model, respectively. In a different way, the interaction energy of the MMT layer reduces with the increasing layer charge density in the M2 Model, suggesting an increasing interaction strength of the intermolecular within the MMT layer with the increasing layer charge density.

FIGURE 6

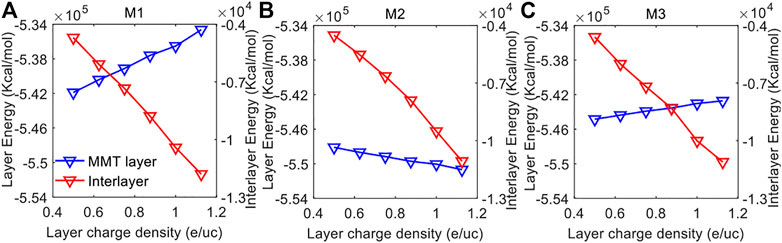
FIGURE 6. The interaction energy of each MMT layer and interlayer as a function of layer charge density for the (A) M1 Model, (B) M2 Model and (C) M3 Model.

The decreasing interaction strength of the MMT layer (the increasing layer interaction energy) in the M1 Model can be understandable, because the isomorphous substitutions in the T sheet will increase the atomic distance (as shown in Figure 3A) and hence reduce the interaction strength, and therefore more isomorphous substitutions with greater layer charge density will result in the more significant reduction in the interaction strength. However, the increasing atomic distance due to the isomorphous substitutions cannot explain the obtained increasing interaction strength (decreasing layer interaction energy) in the M2 Model. Although the isomorphous substitutions in the O sheet (M2 Model) will increase the atomic distance, the increase occurs only in the O sheet, and with the increasing atomic distance in the O sheet, the distance of the atoms between the O and T sheets is reduced. As a result, the interaction strength between the O sheet and the T sheets gets enhanced, leading to an increasing layer interaction strength. Accordingly, the obtained increasing layer interaction strength with layer charge density in the M2 Model implies that the increasing interaction strength between the O sheet and the T sheets overwhelms the decreasing interaction strength in the O sheet. Similarly, the gently decreasing interaction strength of the MMT layer with layer charge density in the M3 Model indicates that the effects of the increasing interaction strength between the O sheet and the T sheets are less significant than the decreasing interaction strength in the O and T sheets.

After analyzing the impact of the layer charge density on the two interactions and on the interactions in the x- and y-axes (which can be represented by the in-plane compressional coefficients presented above) in the three models, the variations of the calculated C₃₃ in the three models that reflect the interaction strength in the z-axis can be more understandable. For the M2 Model, the interaction strength in the x- and y-axes decreases with increasing layer charge density, however, the total interaction strength (i.e., the interaction strength in both the MMT layer and the interlayer) increases with layer charge density, and accordingly the z-axis interaction strength (i.e., C₃₃) must increase with the increasing layer charge density. Unlike C₃₃ in the M2 Models, C₃₃ in the M1 Model and M3 Model can not be directly explained by the total interaction strength and the interaction strength in the x- and y-axes, but can reflect the competition between the interaction strength of the layer and interlayer in the z-axis (i.e., the difference between the layer and interlayer interaction strength and their contribution from the x- and y-axes, respectively).

For the M1 Model, because the total interlayer interaction strength increases while the interaction strength in the x- and y-axes decreases with increasing layer charge density, the z-axis interlayer interaction strength must increase with the increasing layer charge density. On the other hand, the variation of the layer interaction strength in the z-axis with the increasing layer charge density cannot be determined because both the layer interaction strength and the interaction strength in the x- and y-axes decrease with layer charge density. When the layer charge density is low, it can be difficult to deduce the variation of the layer interaction strength in the z-axis from the increasing C₃₃, because the interlayer interaction strength in the z-axis also increases with increasing layer charge density. However, when the layer charge density increases from 0.625 e/uc, the decreasing C₃₃ indicates the layer interaction strength in the z-axis also decreases and the decreasing of the layer interaction strength in the z-axis is playing a more significant role than the increasing interlayer interaction strength in the z-axis.

Since the trends of the interlayer interaction strength and the layer interaction strength in the M3 Model are similar to those in the M1 Model, it is reasonable that the z-axis interlayer interaction strength increases (because the interaction strength in the x- and y-axes decreases) and the layer interaction strength in the z-axis can not be determined (because both the layer interaction strength and the interaction strength in the x- and y-axes decrease) in the M3 Model. However, according to the fact that the C₃₃ of the M3 Model doesn’t vary much with the increase of the layer charge density and the z-axis interlayer interaction strength increases, we can infer that the layer interaction strength in the z-axis decreases and the decreasing interlayer interaction in the z-axis balances with the increasing layer interaction in the z-axis.

Having analyzed the variations of C₃₃ with layer charge density and provided a plausible explanation through the interaction energy, we proceed to present and interpret the variations of C₁₃ and C₂₃ with layer charge density in the three models with different layer charge distributions. Interestingly, although the values are much smaller, C₁₃ and C₂₃ show very similar trends with C₃₃ in each model, and this indicates that the interaction strength in the z-axis that determines C₃₃, may also be the main factor influencing C₁₃ and C₂₃. Therefore, it can be reasonable that the difference in variations of the out-of-plane compressional coefficients with layer charge density in the three models with different layer charge distributions is controlled mainly by the layer interaction strength in the z-axis.

Shear Coefficients

Figure 7 shows the variations of the in-plane shear coefficient C₆₆ and the out-of-plane shear coefficients C₄₄ and C₅₅ with the increasing layer charge density. We can see that C₆₆ of the three models keeps almost constant at around 80 GPa as the layer charge density increases, indicating the shear deformation resistance in the xy-plane is independent of the density and distribution of the layer charges. Unlike the flat in-plane shear coefficient C₆₆, the out-of-plane shear parameters C₄₄ and C₅₅ are fluctuant with the increasing layer charge density in all the three models, and their values in each model are approximately the same. This suggests the shear deformation resistance in the yz-plane and xz-plane is not significantly affected by the layer charge density and the layer charge distribution. Since the shear coefficients are mainly reflecting the torsion interaction of the bonding atoms at the molecular level (Sridharan, 2014; Yang and Xu, 2021), the unchanging shear coefficients indicate that the torsion interaction of the bonding atoms is independent of the varying layer charge density and layer charge distribution.

FIGURE 7

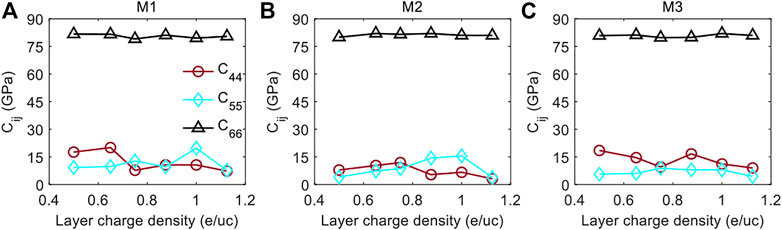
FIGURE 7. The shear elastic constants C₄₄, C₅₅, and C₆₆ as a function of layer charge density for the (A) M1 Model, (B) M2 Model, and (C) M3 Model.

Although the layer charge density and layer charge distribution are not impacting greatly the shear coefficients, it is found that the out-of-plane shear elastic coefficients C₄₄ and C₅₅ are considerably smaller than the in-plane shear elastic constant C₆₆. This result indicates that the shear deformation is more likely to occur in the yz-plane and xz-plane than in the xy-plane of the MMTs. This may be related to the interlayer structure of the MMTs as shown in Figure 1D. Because the interlayer structure is perpendicular to the z-axis and the interlayer interactions are much weaker than the intermolecular interactions within the MMT layer (Zhang et al., 2018; Zhao et al., 2021), the yz- and xz-planes are easier to form slip deformation than the xy-plane when a shear force is applied, resulting in the smaller shear coefficients C₄₄ and C₅₅ than C₆₆.

Conclusion

We have studied the elastic coefficients of MMTs with different charge densities and different charge distributions under stratigraphic conditions using molecular dynamic simulations. The following conclusions can be drawn from the results and analyses presented in the context.

1) The in-plane compressional coefficients C₁₁, C₂₂ and C₁₂ decrease with increasing layer charge density in the MMTs with different layer charge distributions. The C₁₁, C₂₂ and C₁₂ of the MMTs with the layer charges distributed in the octahedral (O) sheet are respectively greater than those distributed in both the octahedral (O) sheet and the tetrahedral (T) sheets, which in turn are greater than those distributed in the tetrahedral (T) sheets.

2) The out-of-plane compressional coefficient C₃₃ shows different trends with increasing layer charge density in the MMTs with different layer charge distributions. C₃₃ decreases overall with the increasing layer charge density when the layer charges are on the two tetrahedral (T) sheets, whereas it shows an increasing trend with layer charge density when the layer charges are distributed on the octahedral (O) sheet. For the MMTs with the layer charges distributed on both the octahedral (O) sheet and the tetrahedral (T) sheets, the increasing layer charge density shows a weak impact on C₃₃. The variations of C₁₃ and C₂₃ with the layer charge density in the MMTs with different layer charge distributions are similar to that of C₃₃.

3) All the shear coefficients C₄₄, C₅₅, and C₆₆ of MMT show no strong correlation with the layer charge density and layer charge distribution, and C₆₆ is considerably greater than C₄₄ and C₅₅.

4) The variations of the anisotropic compressional elastic coefficients with different layer charge densities and layer charge distributions are found to be a result of the impact of the density and distribution of layer charges on the molecular interactions within the MMT layer.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

XW and TH conceive this research. XW writes the manuscript and prepares the figures. TH reviews and supervises the manuscript. The co-author L-YF is involved in the discussion of the manuscript. All authors finally approve the manuscript and thus agree to be accountable for this work.

Funding

The research is supported by the National Natural Science Foundation of China (41821002, 42174136, and 41874151), the Shandong Provincial Natural Science Foundation, China (ZR2021JQ14), and the Postgraduate Innovation Project of China University of Petroleum (East China) (YCX2021009).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bailey, S. W. (1966). The Status of clay mineral Structures. Clay. Clay Miner. 14, 1–23. doi:10.1016/B978-0-08-011908-3.50003-7

CrossRef Full Text | Google Scholar

Barrientos-Velázquez, A. L., MarroquinCardona, A., Liu, L., Phillips, T., and Deng, Y. (2016). Influence of Layer Charge Origin and Layer Charge Density of Smectites on Their Aflatoxin Adsorption. Appl. Clay Sci. 132-133, 281–289. doi:10.1016/j.clay.2016.06.014

CrossRef Full Text | Google Scholar

Carrier, B., Vandamme, M., Pellenq, R. J.-M., and Van Damme, H. (2014). Elastic Properties of Swelling clay Particles at Finite Temperature upon Hydration. J. Phys. Chem. C 118, 8933–8943. doi:10.1021/jp412160e

CrossRef Full Text | Google Scholar

Chen, G., Li, C., Lu, S., Guo, T., Wang, M., Xue, Q., et al. (2021). Critical Factors Controlling Adsorption Capacity of Shale Gas in Wufeng-Longmaxi Formation, Sichuan Basin: Evidences from Both Experiments and Molecular Simulations. J. Nat. Gas Sci. Eng. 88, 103774. doi:10.1016/j.jngse.2020.103774

CrossRef Full Text | Google Scholar

Cui, Z., Sun, Y., Li, J., and Qu, J. (2007). Combination Method for the Calculation of Elastic Constants. Phys. Rev. B 75, 214101. doi:10.1103/PhysRevB.75.214101

CrossRef Full Text | Google Scholar

Cygan, R. T., Liang, J.-J., and Kalinichev, A. G. (2004). Molecular Models of Hydroxide, Oxyhydroxide, and clay Phases and the Development of a General Force Field. J. Phys. Chem. B 108, 1255–1266. doi:10.1021/jp0363287

CrossRef Full Text | Google Scholar

Daab, M., Eichstaedt, N. J., Habel, C., Rosenfeldt, S., Kalo, H., Schießling, H., et al. (2018). Onset of Osmotic Swelling in Highly Charged clay Minerals. Langmuir 34, 8215–8222. doi:10.1021/acs.langmuir.8b00492

PubMed Abstract | CrossRef Full Text | Google Scholar

Davarcioglu, B. (2011). The General Characteristic of Weak Intermolecular Interactions in Liquids and Crystals [Online]. Int. J. Eng. Sci. 1, 443–454. Available at: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.416.5044&rep=rep1&type=pdf

Google Scholar

Dewhurst, D. N., and Siggins, A. F. (2006). Impact of Fabric, Microcracks and Stress Field on Shale Anisotropy. Geophys. J. Int. 165, 135–148. doi:10.1111/j.1365-246X.2006.02834.x

CrossRef Full Text | Google Scholar

Ebrahimi, D., Pellenq, R. J.-M., and Whittle, A. J. (2012). Nanoscale Elastic Properties of Montmorillonite upon Water Adsorption. Langmuir 28, 16855–16863. doi:10.1021/la302997g

PubMed Abstract | CrossRef Full Text | Google Scholar

Few, S., Gambhir, A., Napp, T., Hawkes, A., Mangeon, S., Bernie, D., et al. (2017). The Impact of Shale Gas on the Cost and Feasibility of Meeting Climate Targets-A Global Energy System Model Analysis and an Exploration of Uncertainties. Energies 10, 158. doi:10.3390/en10020158

CrossRef Full Text | Google Scholar

Gao, K., Liu, X., Xiong, J., and Liang, L. (2021). Elastic Parameter Inversion of Longmaxi Formation Shale Based on the Least Squares Method. Arab. J. Geosci. 14, 1–10. doi:10.1007/s12517-021-06657-8

CrossRef Full Text | Google Scholar

Ghasemi, M., and Sharifi, M. (2021). Effects of Layer-Charge Distribution on Swelling Behavior of Mixed-Layer Illite-Montmorillonite Clays: A Molecular Dynamics Simulation Study. J. Mol. Liquids 335, 116188. doi:10.1016/j.molliq.2021.116188

CrossRef Full Text | Google Scholar

Grim, R. E., and Kodama, H. (2014). Clay Mineral [Online]. Available at: https://www.britannica.com/science/clay-mineral.

Google Scholar

Han, T., Yu, H., and Fu, L.-Y. (2021). Correlations between the Static and Anisotropic Dynamic Elastic Properties of Lacustrine Shales under Triaxial Stress: Examples from the Ordos Basin, China. Geophysics 86, MR191–MR202. doi:10.1190/geo2020-0761.1

CrossRef Full Text | Google Scholar

Hantal, G., Brochard, L., Laubie, H., Ebrahimi, D., Pellenq, R. J.-M., Ulm, F.-J., et al. (2014). Atomic-scale Modelling of Elastic and Failure Properties of Clays. Mol. Phys. 112, 1294–1305. doi:10.1080/00268976.2014.897393

CrossRef Full Text | Google Scholar

Herling, M. M., Kalo, H., Seibt, S., Schobert, R., and Breu, J. (2012). Tailoring the Pore Sizes of Microporous Pillared Interlayered Clays through Layer Charge Reduction. Langmuir 28, 14713–14719. doi:10.1021/la303573e

PubMed Abstract | CrossRef Full Text | Google Scholar

Huiyuan, B., Wang, F., Chengen, Z., Gao, X., Zhang, Y., Duan, C., et al. (2019). A New Model between Dynamic and Static Elastic Parameters of Shale Based on Experimental Studies. Arab. J. Geosci. 12, 1–10. doi:10.1007/s12517-019-4777-2

CrossRef Full Text | Google Scholar

Karnland, O. (2010). Chemical and Mineralogical Characterization of the Bentonite Buffer for the Acceptance Control Procedure in a KBS-3 Repository [Online]. Available at: https://www.skb.com/publication/2137257/TR-10-60.pdf.

Google Scholar

Kirkland, J. (2010). Natural Gas Could Serve as a ‘bridge’ Fuel to Low-Carbon Future [Online]. Available at: https://www.scientificamerican.com/article/natural-gas-could-serve-as-bridge-fuel-to-low-carbon-future/.

Google Scholar

Knowles, K. M., and Howie, P. R. (2014). The Directional Dependence of Elastic Stiffness and Compliance Shear Coefficients and Shear Moduli in Cubic Materials. J. Elasticity 120, 87–108. doi:10.1007/s10659-014-9506-1

CrossRef Full Text | Google Scholar

Koutsopoulou, E., Koutselas, I., Christidis, G. E., Papagiannopoulos, A., and Marantos, I. (2020). Effect of Layer Charge and Charge Distribution on the Formation of Chitosan - Smectite Bionanocomposites. Appl. Clay Sci. 190, 105583. doi:10.1016/j.clay.2020.105583

CrossRef Full Text | Google Scholar

Lavikainen, L. P., Hirvi, J. T., Kasa, S., and Pakkanen, T. A. (2016). Interaction of Octahedral Mg(II) and Tetrahedral Al(III) Substitutions in Aluminium-Rich Dioctahedral Smectites. Theor. Chem. Acc. 135, 85. doi:10.1007/s00214-016-1846-4

CrossRef Full Text | Google Scholar

Lee, J. H., and Guggenheim, S. (1981). Single Crystal X-ray Refinement of Pyrophyllite-1T. Am. Mineral. 66, 350–357.

Google Scholar

Lee, S. Y., Cho, W. J., Hahn, P. S., Lee, M., Lee, Y. B., and Kim, K. J. (2005). Microstructural Changes of Reference Montmorillonites by Cationic Surfactants. Appl. Clay Sci. 30, 174–180. doi:10.1016/j.clay.2005.03.009

CrossRef Full Text | Google Scholar

Lovelock, K. R. J. (2017). Quantifying Intermolecular Interactions of Ionic Liquids Using Cohesive Energy Densities. R. Soc. Open Sci. 4, 171223. doi:10.1098/rsos.171223

PubMed Abstract | CrossRef Full Text | Google Scholar

Parraguez Kobek, M. L., Ugarte, A., Ugarte, A., and Campero Aguilar, G. (2015). Shale Gas in the united states: Transforming Energy Security in the Twenty-First century. Norteamérica 10, 7–38. doi:10.20999/nam.2015.a001

CrossRef Full Text | Google Scholar

Peng, C., Wang, G., Zhang, C., Qin, L., Zhu, X., and Luo, S. (2021). Molecular Dynamics Simulation of NH4+-smectite Interlayer Hydration: Influence of Layer Charge Density and Location. J. Mol. Liquids 336, 116232. doi:10.1016/j.molliq.2021.116232

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Pu, B., Wang, F.-q., Dong, D.-z., and Sun, J.-b. (2021). Challenges of Terrestrial Shale Gas Exploration and Development from Chang 7 Shale in the Ordos Basin. Arab. J. Geosci. 14, 1–14. doi:10.1007/s12517-021-06914-w

CrossRef Full Text | Google Scholar

Qin, Y., Peng, T., Sun, H., Zeng, L., Li, Y., and Zhou, C. (2021). Effect of Montmorillonite Layer Charge on the thermal Stability of Bentonite. Clay. Clay Miner. 69, 328–338. doi:10.1007/s42860-021-00117-w

CrossRef Full Text | Google Scholar

Qiu, J., Li, G., Liu, D., Jiang, S., Wang, G., Chen, P., et al. (2019). Effect of Layer Charge Density on Hydration Properties of Montmorillonite: Molecular Dynamics Simulation and Experimental Study. Ijms 20, 3997. doi:10.3390/ijms20163997

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahm, D. (2011). Regulating Hydraulic Fracturing in Shale Gas Plays: The Case of Texas. Energy Policy 39, 2974–2981. doi:10.1016/j.enpol.2011.03.009

CrossRef Full Text | Google Scholar

Raszewski, S. (2016). Shale Gas and Energy Security [Online]. Available at: https://www.academia.edu/34900304/Shale_Gas_and_Energy_Security.

Google Scholar

Ray, J. R., and Rahman, A. (1985). Statistical Ensembles and Molecular Dynamics Studies of Anisotropic Solids. II. J. Chem. Phys. 82, 4243–4247. doi:10.1063/1.448813

CrossRef Full Text | Google Scholar

Sayers, C. M., and den Boer, L. D. (2016). The Elastic Anisotropy of clay Minerals. Geophysics 81, C193–C203. doi:10.1190/geo2016-0005.1

CrossRef Full Text | Google Scholar

Shiu, S.-C., and Tsai, J.-L. (2014). Characterizing thermal and Mechanical Properties of Graphene/epoxy Nanocomposites. Composites B: Eng. 56, 691–697. doi:10.1016/j.compositesb.2013.09.007

CrossRef Full Text | Google Scholar

Skipper, N. T., Sposito, G., and Chang, F. R. C. (1995). Monte Carlo Simulation of Interlayer Molecular Structure in Swelling clay Minerals. 2. Monolayer Hydrates. Clay. Clay Miner. 43, 294–303. doi:10.1346/CCMN.1995.043030310.1346/ccmn.1995.0430304

CrossRef Full Text | Google Scholar

Šponer, J., Hobza, P., and Leszczynski, J. (1999). “Computational Approaches to the Studies of the Interactions of Nucleic Acid Bases,” in Computational Molecular Biology. Editor J. Leszczynski (Amsterdam: Elsevier), 8, 85–117.

Google Scholar

Sridharan, A. (2014). Fourth IGS-Ferroco Terzaghi Oration: 2014. Indian Geotech. J. 44, 371–399. doi:10.1007/s40098-014-0136-0

CrossRef Full Text | Google Scholar

Teich-McGoldrick, S. L., Greathouse, J. A., Jové-Colón, C. F., and Cygan, R. T. (2015). Swelling Properties of Montmorillonite and Beidellite clay Minerals from Molecular Simulation: Comparison of Temperature, Interlayer Cation, and Charge Location Effects. J. Phys. Chem. C 119, 20880–20891. doi:10.1021/acs.jpcc.5b03253

CrossRef Full Text | Google Scholar

Vanorio, T., Prasad, M., and Nur, A. (2003). Elastic Properties of Dry clay mineral Aggregates, Suspensions and Sandstones. Geophys. J. Int. 155, 319–326. doi:10.1046/j.1365-246X.2003.02046.x

CrossRef Full Text | Google Scholar

Wang, Y., Liao, B., Kong, Z., Sun, Z., Qiu, L., and Wang, D. (2018). Oscillating Electric Field Effects on Adsorption of the Methane-Water System on Kaolinite Surface. Energy Fuels 32, 11440–11451. doi:10.1021/acs.energyfuels.8b02961

CrossRef Full Text | Google Scholar

Weaver, C. E., and Pollard, L. D. (2011). The Chemistry of clay Minerals. Amsterdam: Elsevier.

Google Scholar

Yang, Y., and Xu, G. (20212011). Molecular Dynamics Simulation of the Mechanical Behavior of Mixed-Layer clay upon Hydration. J. Phys. Conf. Ser. 2011, 012053. doi:10.1088/1742-6596/2011/1/012053

CrossRef Full Text | Google Scholar

Zartman, G. D., Liu, H., Akdim, B., Pachter, R., and Heinz, H. (2010). Nanoscale Tensile, Shear, and Failure Properties of Layered Silicates as a Function of Cation Density and Stress. J. Phys. Chem. C 114, 1763–1772. doi:10.1021/jp907012w

CrossRef Full Text | Google Scholar

Zhang, J., Pervukhina, M., and Clennell, M. B. (2018). Nanoscale Elastic Properties of Dry and Wet Smectite. Clay. Clay Miner. 66, 209–219. doi:10.1346/CCMN.2018.064094

CrossRef Full Text | Google Scholar

Zhao, J., Cao, Y., Wang, L., Zhang, H.-J., and He, M.-C. (2021). Investigation on Atomic Structure and Mechanical Property of Na- and Mg-Montmorillonite under High Pressure by First-Principles Calculations. Minerals 11, 613. doi:10.3390/min11060613

CrossRef Full Text | Google Scholar

Zhong, L., Hu, S., Yang, X., Yang, M., Zhang, T., Chen, L., et al. (2021). Difference in the Preparation of Two-Dimensional Nanosheets of Montmorillonite from Different Regions: Role of the Layer Charge Density. Colloids Surf. A: Physicochemical Eng. Aspects 617, 126364. doi:10.1016/j.colsurfa.2021.126364

CrossRef Full Text | Google Scholar