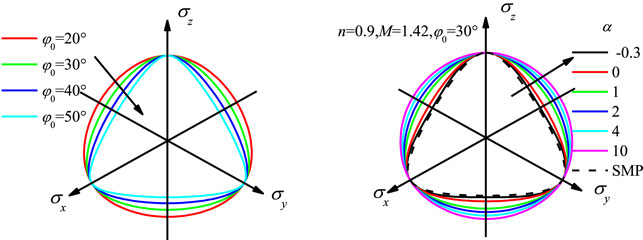Developing a Three Dimensional (3D) Elastoplastic Constitutive Model for Soils Based on Unified Nonlinear Strength (UNS) Criterion

To achieve versatility, a unified nonlinear strength (UNS) criterion is put forward for capturing the complicated strength behaviors exhibited by geomaterials under three dimensional (3D) stress paths. The UNS criterion, widely covering meridian planes and octahedral planes, can serve for describing the nonlinear strength behaviors exhibited by soils, as well as confirm how the intermediate principal stress affects the strength of different materials. Based on UNS strength criterion, an elastoplastic constitutive model is presented, with the purpose of predicting the strength as well as deformation behavior exhibited by soils under 3D stress conditions. Besides, although the proposed model is extremely simple, it is fit for predicting the results of true triaxial tests in related literature with the help of the UNS criterion, and meanwhile can confirm how intermediate principal stress affects material strength and material deformation when the stresses are different.

1 Introduction

Geotechnical engineering has been paid much attention on studies of failure criterion and constitutive model. During the past century, researchers put forward numerous strength criteria (Matsuoka and Nakai, 1974; Matsuoka, 1976; Lade and Duncan, 1975; Lade, 1977; Hoek and Brown, 1980; Yu et al., 1985; Yu et al., 1992) for explaining properties regarding soils and rocks, namely the failure and the strength. For meridian plane, these proposed criteria appear linear. For octahedral plane, criteria put forward by Matsuoka-Nakai and Lade-Duncan are round triangular curves. In spite of this, they are not generally suitable for different soils when stresses are different. Consequently, some researchers (Yu et al., 2002; Liu et al., 2003; Yao et al., 2004; Li et al., 2005; Mortara, 2008; Mortara, 2009; Su et al., 2009; Xiao et al., 2011a; Lu et al., 2016; Tan et al., 2022) attempted to put forward a unified one to fit various soils. For example, Liu and Carter (2003), taking into account the well-known Mohr-Coulomb criterion, came up with a different strength criterion for explaining the strength of soils at peak and in critical state, and applied it to test the strength of rock, sand, cemented sand as well as clay. Yao et al. (2004), partially taking into account of the SMP criterion and Mises criterion, put forward a new unified nonlinear strength (UNS) criterion, meanwhile used it for testing the properties of rock, sand as well as clay. A different UNS was obtained based on shape function changing. Lu et al. (2016) came up with another one considering the D-P criterion together with the stress space transforming method, meanwhile, for proving that if was better than other criteria, comparison was performed.

Unified strength theories used currently were on the basis of the adjustment of failure plane position as well as outer normal direction, of which the expressions show a strong complication, thus are inconvenient to use. To be specific, twin-shear unified strength theory is expressed as a piecewise linear function, and has a discontinuous partial derivative. The generalized nonlinear strength theory adopted the interpolation approach for determining the failure plane outer normal direction. A variable is needed for reflecting the intermediate principal stress effects regarding different geomaterial types. The variable can be the adjustment of failure plane or the adjustment of acting stress.

When considering how intermediate principal stress affects soil strength and deformation, the constitutive model shall be extended into the 3D stress space, where the Extended Mises criterion (i.e., Cam-Clay model) is the mostly used. Nevertheless, as found by the experiments, the Extended Mises criterion always overestimated the strength when performing triaxial extension, therefore, when performing plane strain, the intermediate stress ratio is inaccurate (Wroth and Houlsby 1985; Wang et al., 2022a). Generally, on octahedral plane, soils exhibit a strength shape of round triangular curve as presented in the Matsuoka-Nakai criterion or Lade-Duncan criterion, and not a circular curve presented in the Extended Mises criterion. On that account, the constitutive model was tentatively extended into 3D stress space. For a more reasonable description of soil strength and deformation behaviors when the stress is normal, a yield function or plastic potential function was developed by adopting various dilatancy equations (Rowe 1962). Other researchers conducted corresponding experiments and numerical analysis on the strength of materials (Jiang et al., 2016; Fan et al., 2019; Liu et al., 2020a; Liu et al., 2020b; Fan et al., 2020; Wang et al., 2020; Kang et al., 2021; Wang et al. 2021a; Wang et al. 2021b; Wang J. et al., 2022; Wang L. et al., 2022; Zhou et al., 2022). Researchers adopted a tedious process for switching the flow rules in the process of the mutual change of load extension and compression. Thus a complex constitutive model was obtained. In the research by Chang and Yin (2010), the micromechanics approach helped to obtain dilatancy equation to deal with stress extension and compression. The dilatancy of soils was uniform, however, it is difficult to determine the equation parameters.

Since the Mohr-Coulomb criteria, the Lade-Duncan criteria, the Matsuoka-Nakai criteria, etc. can not effectively capture the soil strength behaviors in normal stress conditions, this paper pays attention to a the unified nonlinear strength (UNS) criterion, etc. the round triangular curve on the octahedral plane. UNS criterion is capable of presenting soil nonlinear strength behavior on the meridian plane, as well as the intermediate stress behaviors on the octahedral plane. On this basis, a simple but effective soil elastoplastic constitutive model was presented regardless of the changing stress conditions. At last, experimental results of authors together with literature data were used for testing whether the model is applicable.

2 Unified Nonlinear Strength (UNS) Criterion

2.1 The Form of the UNS

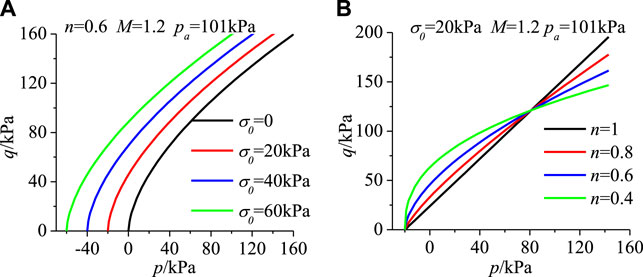
It is not allowed to uniformly apply the criteria of Tresca, the Mohr-Coulomb, the Mises, the Lade-Duncan and the Matsuoka-Nakai to different soil types when the stresses are different. Refer to the form of strength criterion given in literatures (Liu et al., 2010; Xiao et al., 2010; Xiao et al., 2011a; Xiao et al., 2011b; Xiao et al., 2012a; Xiao et al., 2012b; Xiao et al., 2012c; Sun et al., 2013), a simple UNS criterion is given. The formulation can be expressed as:

$q=Mg\left(\theta \right)p_a{\left(\frac{p+{\sigma }_0}{p_a}\right)}^n(\mathrm{1a})$

or

$\ln \left(\frac{q}{p_a}\right)=n\ln \left(\frac{p+{\sigma }_0}{p_a}\right)+\ln \left[Mg\left(\theta \right)\right](\mathrm{1b})$

where:

$p=\frac{{\sigma }_1+{\sigma }_2+{\sigma }_3}{3}(2)$

$q=\frac{\sqrt{2}}{2}\sqrt{{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2}(3)$

$g\left(\theta \right)=\frac{\frac{\sqrt{3}}{2\sqrt{L_1}\cos {\delta }_{\theta }}+\frac{6\alpha \sin {\phi }_0}{3-\sin {\phi }_0}}{\frac{\sqrt{3}}{2\sqrt{L_1}\cos {\delta }_0}+\frac{6\alpha \sin {\phi }_0}{3-\sin {\phi }_0}}(4)$

$\begin{array}{l}{\delta }_{\theta }=\frac{1}{3}\arccos \left(-\frac{3\sqrt{3}{L}_2\cos (3\theta )}{2L_1^{3/2}}\right)\\ {\delta }_0=\frac{1}{3}\arccos \left(-\frac{3\sqrt{3}{L}_2}{2L_1^{3/2}}\right)\end{array}\}(5)$

$\begin{array}{l}{L}_1=\frac{{\left(3-\sin {\phi }_0\right)}^3}{3{\left(3-\sin {\phi }_0\right)}^3-81\left(1-\sin {\phi }_0-{\sin }^2{\phi }_0+{\sin }^3{\phi }_0\right)}\\ L_2=\frac{2{\left(3-\sin {\phi }_0\right)}^3}{27{\left(3-\sin {\phi }_0\right)}^3-729\left(1-\sin {\phi }_0-{\sin }^2{\phi }_0+{\sin }^3{\phi }_0\right)}\end{array}\}(6)$

σ₀ denotes the bonding stress, reflecting the cohesive property exhibited by the cohesive-frictional material, σ₀ = ccotφ₀ (where c is cohesion, φ₀ is friction angle). n denotes the slope in the $\ln \left(\frac{q}{p_a}\right)-\ln \left(\frac{p+{\sigma }_0}{p_a}\right)$ plane. $\ln \left[Mg\left(\theta \right)\right]$ denotes the intercept, the effect of geomaterial frictional characteristic. The exponent n serves for describing how hydrostatic pressure affects material failure. α, denotes the combination coefficient, and it is able to confirm its value based on triaxial compression strength and any strength when b ≠ 0. Figure 1 illustrates how φ₀ and α affect the curve change of the linear strength criterion in the deviatoric plane when other conditions are the same. It can be seen from the figure that, in theory, the criterion shape is a circular firstly when the friction angle is 20°, and then changes into a curved triangle when it gradually changes to 50°. In an increasing range of −0.3 to 10, the criterion is firstly a SMP curved triangle and then becomes the Mises circle, which approximates all the curves between the SMP curved triangle and the Mises circle. Specifically, with n = 1 and α = 0, we adopt the Lade-Duncan criterion as the UNS criterion. With n = 1 and α = −0.3, we adopt the SMP criterion as the UNS criterion. With n = 1 and α → +∞, it is the Extended Mises criterion. Figure 2 illustrates how σ₀ and n affect the failure curves. Accordingly, parallel failure curves can be obtained if other parameters are equal. Figure 2B illustrates how n affects the failure curves in meridian plane and octahedral plane. We can see expanding failure planes with n increase.

FIGURE 1

FIGURE 1. Criterion variation with different parameters on the deviatoric plane.

FIGURE 2

FIGURE 2. UNS criterion variation with the parameter σ0 and n on the meridian plane.

2.2 Experimental Verification

In the consolidated drained true triaxial strength experiments performed by Toyota et al. (2004) on saturated silty sand, they set the hydrostatic pressures to values of 100, 200, and 300 kPa. In the process of loading, in a given experiment, b held a constant value of 0, 0.25, 0.5, 0.75, and 1.0. Figure 3 shows the experimental results, and as calculated by the proposed criterion, σ₀ = 0 kPa, M = 1.509, and n = 1, α = 0.229. Figure 3 also shows the curves under theoretical prediction, which well fit experimental data, showing that the developed criterion is capable of well describing silty sand strength behavior, namely the variations of b and p. In the deviatoric plane, when the hydrostatic pressure is the same, the shear strength shows a downtrend when b increases, showing how the intermediate principal stress affects the shear strength (Figure 3B).

FIGURE 3

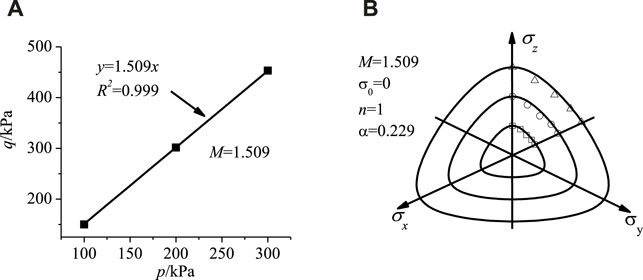
FIGURE 3. UNS criterion variation (test data from Toyota et al., 2004).

3 Constitutive Model Incorporating UNS Criterion

3.1 Model Description

In general, there are many factors that decide soil yielding and soil strength, namely the current stress state, the loading history, the internal structure and the loading direction regarding internal structure as well. Also, the yield function shall be objective and not affect or be affected by the coordinate system. In this paper, the yield function is proposed following for describing soil yielding when the intermediate principal stress is taken into account (Gao, 2012):

$f=q-Hg\left(\theta \right)p=0(7)$

The above yield function is modified from the UNS criterion proposed this paper, then a hardening parameter H is used to replace the originally constant frictional coefficient M. The other parameters (p, g(θ), q) are shown in Eq. 2 and 3 and Eq. 4, respectively. In the true triaxial tests, on the deviatoric plane, θ denotes the angle between the current stress state and the vertical stress axes, Figure 4A partitions the deviatoric plane; Figure 4B is the yield surface; Figure 4C is the yield loci with different hardening parameter values.

FIGURE 4

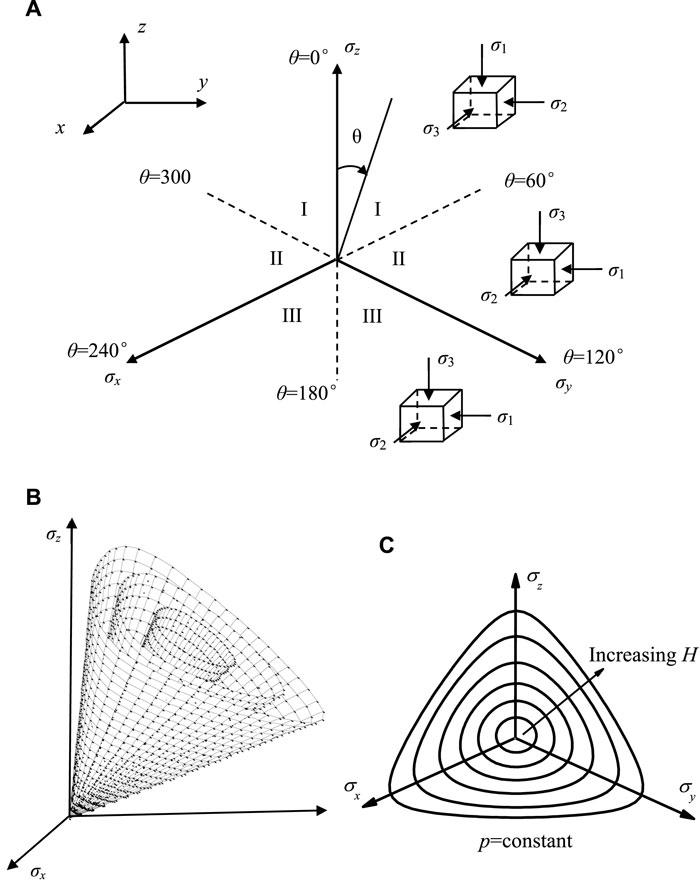
FIGURE 4. (A) Angle θ definitionand the deviatoric plane partition under the true triaxial test; (B) the yield surface in the 3D space and (C) the yield loci in the deviatoric plane.

3.2 Hardening Law

The H evolution law is proposed as follows:

$dH=\langle dL\rangle r_H=\langle dL\rangle \frac{G{c}_h}{H{p}_a}\left(M_f-H\right)(8)$

In the equation, r_H shows the H evolution direction, and r_H ≥ 0; dL is a loading index. <x> = 0 is the Macauley bracket, and x ≤ 0 when x > 0, and <x> = x when x > 0; c_h denotes a positive constant.

3.3 Dilatancy and Flow Rule

Dilatancy relation supports the soil constitutive model. The dilatancy is described by the dilatancy relation found in the literature of Li and Dafalias (2004):

$D=\frac{d{\epsilon }_v^p}{\sqrt{2/3d{e}_{ij}^{p}d{e}_{ij}^p}}=\frac{d_1}{\exp \left({\displaystyle \int \langle dL\rangle }\right)}\left(M_p-H\right)(9)$

In the equation, $d{\epsilon }_v^p$ shows the plastic volumetric strain increment; the plastic deviatoric strain increment is denoted as $d{e}_{ij}^p\left(=d{\epsilon }_{ij}^p-d{\epsilon }_v^p{\delta }_{ij}/3\right)$; d₁ denotes a positive parameter of model; The phase transformation stress ratio is expressed as M_p which is obtained from the conventional triaxial compression tests about remolded samples. The denominator in Eq. 9 serves for controlling the change of volume, particularly in the case of high strain level. With the sample being sheared to critical state, the plastic deviatoric strain increase can be unlimited. Hence, when the flow is unlimited, the denominator term can be infinite, thus the value of D goes to 0.

Besides, considering the yield function of Eq. 7, we propose the associated flow rule:

$d{e}_{ij}^p=\langle dL\rangle n_{ij}(10)$

In Equation 10, n_ij denotes a unit tensor, which is defined by:

$n_{ij}=\frac{1}{C}\left(\frac{\partial f}{\partial {\sigma }_{ij}}-\frac{1}{3}\frac{\partial f}{\partial {\sigma }_{mn}}{\delta }_{mn}{\delta }_{ij}\right)(11)$

where C can be explained as the quantity norm in the parentheses in Eq. 11. Of particular note is that Pietruszczak (1999) also has adopted a similar flow rule.

3.4 Constitutive Equation

By applying the consistency condition to the general yield function form in Eq. 7, we can obtain:

$df=\frac{\partial f}{\partial {\sigma }_{ij}}d{\sigma }_{ij}+\frac{\partial f}{\partial H}dH=0(\mathrm{12a})$

or:

$df=\frac{\partial f}{\partial {\sigma }_{ij}}d{\sigma }_{ij}+\langle dL\rangle \frac{\partial f}{\partial H}{r}_H=\frac{\partial f}{\partial {\sigma }_{ij}}d{\sigma }_{ij}-\langle dL\rangle K_p=0(\mathrm{12b})$

K_p is the plastic modulus,

$K_p=-\frac{\partial f}{\partial H}{r}_H(13)$

The constitutive relations can be derived by following the classical plasticity theory. Regarding the deviatoric and volumetric elastic strain increments, the present model makes a postulation on the $d{e}_{ij}^e$ and $d{\epsilon }_v^e$, an isotropic hypoelastic relation:

$\begin{array}{l}d{e}_{ij}^e=\frac{d{s}_{ij}}{G}\\ d{\epsilon }_v^e=\frac{dp}{K}\end{array}\}(14)$

wherein the expressions regarding the elastic moduli K and G are employed according to:

$\begin{array}{l}K=\frac{E}{3\left(1-2\nu \right)}\\ G=\frac{E}{2\left(1+\nu \right)}\end{array}\}(15)$

Regarding the relevant plastic strain increments, the dilatancy equation together with the flow rule assist in obtaining the relations as follows:

$d{e}_{ij}^p=\langle dL\rangle n_{ij}(16)$

and

$d{\epsilon }_v^p=D\sqrt{2/3d{e}_{ij}^{p}d{e}_{ij}^p}=\langle dL\rangle \sqrt{2/3}D(17)$

Equation 11 already gives the definition of n_ij. Calculation of the incremental stress–strain relation can be achieved with the help of equations mentioned above. Then,

$\begin{array}{l}d{\sigma }_{ij}=d{s}_{ij}+dp{\delta }_{ij}\\ =2Gd{e}_{ij}^e+Kd{\epsilon }_v^e{\delta }_{ij}\\ =2G\left(d{e}_{ij}-d{e}_{ij}^p\right)+K\left(d{\epsilon }_v-d{\epsilon }_v^p\right){\delta }_{ij}\\ =2G\left(d{e}_{ij}-\langle dL\rangle n_{ij}\right)+K\left(d{\epsilon }_v-\langle dL\rangle \sqrt{2/3}D\right){\delta }_{ij}\end{array}(18)$

Eq. 18 assumes an additive decomposition regarding the total strain increment $d{\epsilon }_{ij}=d{\epsilon }_{ij}^e+d{\epsilon }_{ij}^p$. Eq. 19 gives the loading index expression on the basis of Eqs 12–18,

$\langle dL\rangle =\frac{2G\frac{\partial f}{\partial {\sigma }_{ij}}+\left(K-\frac{2}{3}G\right)\frac{\partial f}{\partial {\sigma }_{kl}}{\delta }_{kl}{\delta }_{ij}}{\frac{\partial f}{\partial {\sigma }_{ij}}\left(2G{n}_{ij}+\sqrt{\frac{2}{3}}KD{\delta }_{ij}\right)+K_p}d{\epsilon }_{ij}\sqrt{2/3}D={\mathrm{\Theta }}_{ij}d{\epsilon }_{ij}(19)$

The chain rule serves for obtaining

$\frac{\partial f}{\partial {\sigma }_{ij}}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial {\sigma }_{ij}}+\frac{\partial f}{\partial p}\frac{\partial p}{\partial {\sigma }_{ij}}+\frac{\partial f}{\partial g\left(\theta \right)}\frac{\partial g\left(\theta \right)}{\partial \theta }\frac{\partial \theta }{\partial {\sigma }_{ij}}(20)$

where

$\frac{\partial f}{\partial q}=1(21)$

$\frac{\partial q}{\partial {\sigma }_{ij}}=\frac{\left(q^2-I_1^2\right)\frac{\partial I_1}{\partial {\sigma }_{ij}}+9\frac{\partial I_3}{\partial {\sigma }_{ij}}}{2q\left(q-I_1\right)}(22)$

$\frac{\partial f}{\partial p}=-Hg\left(\theta \right)(23)$

$\frac{\partial p}{\partial {\sigma }_{ij}}=\frac{1}{3}{\delta }_{ij}(24)$

$\frac{\partial f}{\partial g\left(\theta \right)}=-Hp(25)$

$\frac{\partial g\left(\theta \right)}{\partial \theta }=-\frac{3\sqrt{3}}{2}\frac{m{l}_3}{r_0\sqrt{1-n^2}}\frac{\sin \left({\delta }_{\theta }\right)\sin \left(3\theta \right)}{l_2^{3/2}\cos \left({\delta }_{\theta }\right)}(26)$

$m=\frac{\sqrt{3}}{2\sqrt{l_1}}(27)$

$n=-\frac{3\sqrt{3}{l}_2}{2l_1^{3/2}}\cos \left(3\theta \right)(28)$

Combining Eqs 18, 19, the obtained constitutive relation regarding incremental form serves for the following numerical computations.

$d{\sigma }_{ij}={\mathrm{\Lambda }}_{ijkl}d{\epsilon }_{kl}(29)$

where

${\mathrm{\Lambda }}_{ijkl}=G\left({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}\right)+\left(K-\frac{2}{3}G\right){\delta }_{ij}{\delta }_{kl}-h\left(dL\right)\left(2G{n}_{ij}+\sqrt{\frac{2}{3}}KD{\delta }_{ij}\right){\mathrm{\Theta }}_{kl}(30)$

The Heaviside step function is expressed as h (dL), and h (dL > 0) = 1, h (dL ≤ 0) = 0.

3.5 Model Calibration and Verification

3.5.1 Calibration of Model Parameters

At first, the discussion about the model parameter calibration shows its value in guiding. Relevant parameters regarding the failure criterion are determined in Section 2. We classified the other parameters into elastic moduli parameter, hardening law parameter and dilatancy relation parameter, of which the calibration can be achieved in conventional triaxial extension and compression tests on the basis of the process given as follows.

(a) Elastic parameters E, G and are ν determined by equal p test.

(b) M_p: The conventional triaxial compression tests can serve for obtaining the phase transformation stress ratio M_p.

(c) d₁: When the weak elastic deformation is not taken into account, drained triaxial compression test can help to get the relation as follows,

$\frac{d{\epsilon }_v^p}{d{\epsilon }_q^p}\approx \frac{d{\epsilon }_v}{d{\epsilon }_q}=\frac{d_1}{\exp \left(\sqrt{3/2}{\epsilon }_q\right)}\left(M_p-\eta \right)(31)$

where $\eta =q/p$. Only d₁ can affect the model response. Thus, corresponding ε_q - ε_v curves can be fit in the tests to calibrate d₁.

(d) c_h: When the weak elastic deformation is not considered, drained triaxial compression test can help to get the relation as follows,

$\begin{array}{l}d{\epsilon }_q\approx \sqrt{2/3}\langle dL\rangle =\sqrt{2/3}\frac{1-a\eta }{K_p}dq\\ =\sqrt{2/3}\frac{\left(1-a\eta \right)\left(1+e\right)p_a}{G_0{c}_h{\left(2.97-e\right)}^{2}p\sqrt{p{p}_a}\left(M_f/\eta -1\right)}\end{array}(32)$

Regarding the constant-mean-stress test and the conventional triaxial compression test, variable a is 0 and 1/3, respectively. Then, c_h becomes the only parameter in Eq. 32, and fitting it to the ε_q - q curves can assist in achieving its calibration. All parameters can be slightly adjusted by using ε_q - q results obtained by performing undrained triaxial compression tests.

3.5.2 Experimental Verification and Discussion

Nakai et al. (1986) performed many tests to examine the properties related to Fujinomori clay, and sheared samples under the drainage condition when the effective mean pressure is constant at 196 kPa. They set b at 0, 0.268, 0.5, 0.732 and 1, and corresponding Lode angles at 0°, 15°, 30°, 45°and 60°, respectively. In the established model, material parameters are φ₀ = 34.3°, α = -0.23, M_f = 1.39, M_p = 1.39, κ/(1 + e₀) = 0.0112, c_h = 0.32, d₁ = 1.0.

Figure 5 shows both the predictions of the model using Mises criterion and UNS criterion in this study. When the stress paths are different, the failure ratio regarding the model that uses Mises criterion dose not change (constant M) as the failure function is the Mises cycle. Hence, the Mises model predicted a higher strength compared with the test data when b value is 0.268, 0.5, 0.732 or 1. In comparison, the failure function of the proposed model is the UNS, thus, the failure ratio changes when the stress paths are different. Accordingly, the proposed model is capable of better describing the strength and deformation when performing true triaxial compression tests.

FIGURE 5

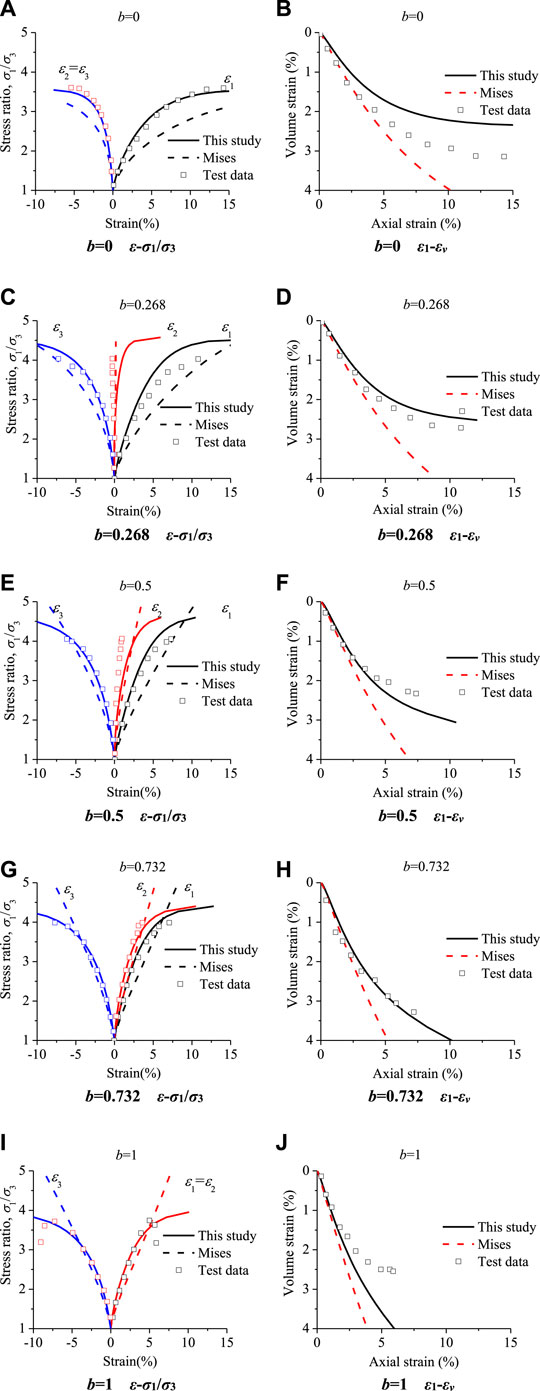
FIGURE 5. Comparisons of the test results and predictions for true triaxial conditions (data from Nakai et al., 1986).

4 Conclusion

(1) UNS criterion is proposed for gaining complicated strength behaviors regarding geomaterials. A lot of other criteria can be found in UNS criterion, like the Extended Mises criterion (n = 1 and α→ +∞), the Lade criterion (n = 1 and α = 0) as well as approximate SMP criterion (n = 1 and α = −0.3). On the meridian plane, UNS criterion is capable of well reflecting soil nonlinear strength behavior considering the material parameter n.

(2) The paper put forward a 3D constitutive model using the UNS criterion as the shear failure condition. It is capable of better predicting the results of true triaxial test found in related literature, and helps to confirm how the intermediate principal stress affects soil strength and deformation when stresses are different.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SW propose the unified nonlinear strength criterion and constitutive model, ZZ and XL verified the accuracy of the unified nonlinear strength criterion, BC and BW verified the accuracy of the constitutive model.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The work presented in this paper was sponsored by the Supported by Systematic Project of Key Laboratory of New Technology for Construction of Cities in Mountain Area (No. LNTCCMA-20200104), the Systematic Project of Guangxi Key Laboratory of Disaster Prevention and Structural Safety (No. 2019ZDK005), the Initial Scientific Research Fund of Young Teachers in Ningbo University of technology (2019A610394), the Ningbo Public Welfare Science and Technology Planning Project (No. 2019C50012). These financial supports are gratefully acknowledged.

References

Chang, C. S., and Yin, Z.-Y. (2010). Modeling Stress-Dilatancy for Sand under Compression and Extension Loading Conditions. J. Eng. Mech. 136, 777–786. doi:10.1061/(asce)em.1943-7889.0000116

CrossRef Full Text | Google Scholar

Fan, J., Jiang, D., Liu, W., Wu, F., Chen, J., and Daemen, J. (2019). Discontinuous Fatigue of Salt Rock with Low-Stress Intervals. Int. J. Rock Mech. Mining Sci. 115 (3), 77–86. doi:10.1016/j.ijrmms.2019.01.013

CrossRef Full Text | Google Scholar

Fan, J., Liu, W., Jiang, D., Chen, J., Tiedeu, W. N., and Daemen, J. J. K. (2020). Time Interval Effect in Triaxial Discontinuous Cyclic Compression Tests and Simulations for the Residual Stress in Rock Salt. Rock Mech. Rock Eng. 53, 4061–4076. doi:10.1007/s00603-020-02150-y

CrossRef Full Text | Google Scholar

Gao, Z. (2012). Constitutive Modeling of Anisotropic Behavior in Geomaterials: The Role of Fabric. [Doctoral dissertation]. Hong Kong: Hong Kong University of Science and Technology.

Google Scholar

Hoek, E., and Brown, E. T. (1980). Empirical Strength Criterion for Rock Masses. J. Geotech. Engrg. Div. 106 (9), 1013–1035. doi:10.1061/ajgeb6.0001029

CrossRef Full Text | Google Scholar

Jiang, D., Fan, J., Chen, J., Li, L., and Cui, Y. (2016). A Mechanism of Fatigue in Salt under Discontinuous Cycle Loading. Int. J. Rock Mech. Mining Sci. 86 (7), 255–260. doi:10.1016/j.ijrmms.2016.05.004

CrossRef Full Text | Google Scholar

Kang, Y., Fan, J., Jiang, D., and Li, Z. (2021). Influence of Geological and Environmental Factors on the Reconsolidation Behavior of fine Granular Salt. Nat. Resour. Res. 30 (1), 805–826. doi:10.1007/s11053-020-09732-1

CrossRef Full Text | Google Scholar

Lade, P. V., and Duncan, J. M. (1975). Elastoplastic Stess-Strain Theory for Cohesionless Soil. J. Geotech. Eng. Div. 101 (GT10), 1037–1053. doi:10.1061/ajgeb6.0000204

CrossRef Full Text | Google Scholar

Lade, P. V. (1977). Elasto-Plastic Stress-Strain Theory for Cohesionless Soil with Curved Yield Surfaces. Int. J. Sol. Structures 13 (11), 1019–1035. doi:10.1016/0020-7683(77)90073-7

CrossRef Full Text | Google Scholar

Li, L., Aubertin, M., Simon, R., and Bussière, B. (2005). Formulation and Application of a General Inelastic Locus for Geomaterials with Variable Porosity. Can. Geotech. J. 42 (2), 601–623. doi:10.1139/t04-113

CrossRef Full Text | Google Scholar

Li, X. S., and Dafalias, Y. F. (2004). A Constitutive Framework for Anisotropic Sand Including Non-Proportional Loading. Géotechnique 54 (1), 41–55. doi:10.1680/geot.2004.54.1.41

CrossRef Full Text | Google Scholar

Liu, H., Xiao, Y., Liu, J., and Li, G. (2010). A New Elliptic-Parabolic Yield Surface Model Revised by an Adaptive Criterion for Granular Soils. Sci. China Tech. Sci. 53, 2152−2159. doi:10.1007/s11431-010-4014-4

CrossRef Full Text | Google Scholar

Liu, M. C., Gao, Y. F., and Liu, H. L. (2003). Large Scale Triaxial Test Study on Deformation and Strength Characteristics of Rockfill Materials. Chin. J. Rock Mech. Eng. 22 (7), 1104–1111. doi:10.1142/S0252959903000104

CrossRef Full Text | Google Scholar

Liu, M. D., and Carter, J. P. (2003). General Strength Criterion for Geomaterials. Int. J. Geomech. 3 (2), 253–259. doi:10.1061/(asce)1532-3641(2003)3:2(253)

CrossRef Full Text | Google Scholar

Liu, W., Zhang, X., Fan, J., Zuo, J., Zhang, Z., and Chen, J. (2020a). Study on the Mechanical Properties of Man-Made Salt Rock Samples with Impurities. J. Nat. Gas Sci. Eng. 84, 103683. doi:10.1016/j.jngse.2020.103683

CrossRef Full Text | Google Scholar

Liu, W., Zhang, Z., Fan, J., Jiang, D., Li, Z., and Chen, J. (2020b). Research on Gas Leakage and Collapse in the Cavern Roof of Underground Natural Gas Storage in Thinly Bedded Salt Rocks. J. Energ. Storage 31, 101669. doi:10.1016/j.est.2020.101669

CrossRef Full Text | Google Scholar

Lu, D. C., Ma, C., Du, X. L., and Jin, L. (2016). Development of a New Nonlinear Unified Strength Theory for Geomaterials Based on the Characteristic Stress Concept. Int. J. Geomech. 17 (2), 04016058. doi:10.1061/(ASCE)GM.1943-5622.0000729

CrossRef Full Text | Google Scholar

Matsuoka, H., and Nakai, T. (1974). Stress-Deformation and Strength Characteristics of Soil under Three Different Principal Stresses. Proc. Jpn. Soc. Civil Eng. 1974, 59–70. doi:10.2208/jscej1969.1974.232_59

CrossRef Full Text | Google Scholar

Matsuoka, H. (1976). On the Significance of the "Spatial Mobilized Plane". Soils Found. 16 (1), 91–100. doi:10.3208/sandf1972.16.91

CrossRef Full Text | Google Scholar

Mortara, G. (2009). A Hierarchical Single Yield Surface for Frictional Materials. Comput. Geotechnics 36 (6), 960–967. doi:10.1016/j.compgeo.2009.03.007

CrossRef Full Text | Google Scholar

Mortara, G. (2008). A New Yield and Failure Criterion for Geomaterials. Géotechnique 58 (2), 125–132. doi:10.1680/geot.2008.58.2.125

CrossRef Full Text | Google Scholar

Nakai, T., Matsuoka, H., Okuno, N., and Tsuzuki, K. (1986). True Triaxial Tests on Normally Consolidated clay and Analysis of the Observed Shear Behavior Using Elastoplastic Constitutive Models. Soils and Foundations 26 (4), 67–78. doi:10.3208/sandf1972.26.4_67

CrossRef Full Text | Google Scholar

Pietruszczak, S. (1999). On Inelastic Behaviour of Anisotropic Frictional Materials. Mech. Cohes.‐Frict. Mater. 4, 281–293. doi:10.1002/(sici)1099-1484(199905)4:3<281::aid-cfm63>3.0.co;2-m

CrossRef Full Text | Google Scholar

Rowe, P. W. (1962). The Stress-Dilatancy Relation for Static Equilibrium of an Assembly of Particles in Contact. Proc. Math. Phys. Eng. Sci. 269, 500–527.

Google Scholar

Su, D., Wang, Z.-L., and Xing, F. (2009). A Two-Parameter Expression for Failure Surfaces. Comput. Geotechnics 36 (3), 517–524. doi:10.1016/j.compgeo.2008.09.001

CrossRef Full Text | Google Scholar

Sun, Y, Liu, H., Gui, Y., and Xiao, Y. (2013). Formulation of Cross-Anisotropic Failure Criterion for Soils. Water Sci. Eng. 6 (4), 456–468. doi:10.3882/j.issn.1674-2370.2013.04.009

CrossRef Full Text | Google Scholar

Tan, Y., Xu, X., Ming, H., and Sun, D. A. (2022). Analysis of Double-Layered Buffer in High-Level Waste Repository. Ann. Nucl. Energ. 165, 108660. doi:10.1016/j.anucene.2021.108660

CrossRef Full Text | Google Scholar

Toyota, H., Nakamura, K., and Sramoon, W. (2004). Failure Criterion of Unsaturated Soil Considering Tensile Stress under Three-Dimensional Stress Conditions. Soils and Foundations 44 (5), 1–13. doi:10.3208/sandf.44.5_1

CrossRef Full Text | Google Scholar

Wang, J., Wang, T., Song, Z., Zhang, Y., and Zhang, Q. (2021a). Improved Maxwell Model Describing the Whole Creep Process of Salt Rock and its Programming. Int. J. Appl. Mech. 13, 21501131. doi:10.1142/S1758825121501131

CrossRef Full Text | Google Scholar

Wang, J., Wang, X., Zhang, Q., Song, Z., and Zhang, Y. (2021b). Dynamic Prediction Model for Surface Settlement of Horizontal Salt Rock Energy Storage. Energy 235, 121421. doi:10.1016/j.energy.2021.121421

CrossRef Full Text | Google Scholar

Wang, J., Zhang, Q., Song, Z., Feng, S., and Zhang, Y. (2022a). Nonlinear Creep Model of Salt Rock Used for Displacement Prediction of Salt Cavern Gas Storage. J. Energ. Storage 48, 103951. doi:10.1016/j.est.2021.103951

CrossRef Full Text | Google Scholar

Wang, J., Zhang, Q., Song, Z., and Zhang, Y. (2020). Creep Properties and Damage Constitutive Model of Salt Rock under Uniaxial Compression. Int. J. Damage Mech. 29 (6), 902–922. doi:10.1177/1056789519891768

CrossRef Full Text | Google Scholar

Wang, L., Zhou, A., Xu, Y., and Xia, X. (2022b). Consolidation of Partially Saturated Ground Improved by Impervious Column Inclusion: Governing Equations and Semi-analytical Solutions. J. Rock Mech. Geotechnical Eng. doi:10.1016/j.jrmge.2021.09.017

CrossRef Full Text | Google Scholar

Wroth, C. P., and Houlsby, G. T. (1985). “Soil Mechanics- Property Characterization and Analysis Procedures,” in Proc 11th Int Conf Soil Mech and Found Engrg., San Francisco, California, August 11-15, 1985, 1, 1–55.

Google Scholar

Xiao, Y., Liu, H., and Chen, Y. (2012a). Unified Relationship Between Intermediate Principal Stress and Internal Friction Angle for Sand. Chinese J. Geotech. Eng. 34 (6), 1102–1108.

Google Scholar

Xiao, Y., Liu, H., and Gui, Y. (2011b). A United Anisotropic Strength Criterion for Soils. Soils[C]. Contemporary Topics on Testing, Modeling, and Case Studies of Geomaterials, Pavements, and Tunnels, ASCE, GSP 215, 23–31. doi:10.1061/47626(405)4

CrossRef Full Text | Google Scholar

Xiao, Y., Liu, H., and Gui, Y. (2012b). Formulation of Cross-Anisotropic Failure Criterion for Geomaterial. Int. J. Geomech. 12 (2), 182–188. doi:10.1061/(ASCE)GM.1943-5622.0000136

CrossRef Full Text | Google Scholar

Xiao, Y., Liu, H., and Liang, R. Y. (2011a). Modified Cam-Clay Model Incorporating Unified Nonlinear Strength Criterion. Sci. China Technol. Sci. 54 (4), 805–810. doi:10.1007/s11431-011-4313-4

CrossRef Full Text | Google Scholar

Xiao, Y., Liu, H., and Zhu, J. (2010). Study on The Failure Criterion of Granular Soils. Chinese J. Geotech. Eng. 32 (4), 586–591.

Google Scholar

Xiao, Y., Liu, H., and Zhu, J. (2012c). Modeling and Behaviours of Rockfill Materials in Three-Dimensional Stress Space. Sci. China Tech. Sci. 55, 2877–2892. doi:10.1007/s11431-012-4979-2

CrossRef Full Text | Google Scholar

Yao, Y. P., Lu, D. C., Zhou, A. N., and Zou, B. (2004). Generalized Non-linear Strength Theory and Transformed Stress Space. Sci. China Ser. E-Tech Sci. 47 (6), 691–709. doi:10.1360/04ye0199

CrossRef Full Text | Google Scholar

Yu, M. H., He, L. N., and Liu, C. Y. (1992). Generalized Twin Shear Stress Yield Criterion and its Generalization. Chin. Sci. Bull. 37 (24), 2085–2089.

Google Scholar

Yu, M. H., He, L. N., and Song, L. Y. (1985). Twin Shear Stress Theory and its Generalization. Sci. Sin (Sci China) Ser. A. 28 (11), 1174–1183.

Google Scholar

Yu, M.-H., Zan, Y.-W., Zhao, J., and Yoshimine, M. (2002). A Unified Strength Criterion for Rock Material. Int. J. Rock Mech. Mining Sci. 39 (8), 975–989. doi:10.1016/s1365-1609(02)00097-7

CrossRef Full Text | Google Scholar

Zhou, P., Wang, J., Song, Z., Cao, Z., and Pei, Z. (2022). Construction Method Optimization for Transfer Section between Cross Passage and Main Tunnel of Metro Station. Front. Earth Sci. 10, 770888. doi:10.3389/feart.2022.770888

CrossRef Full Text | Google Scholar