Gaussian Beam Migration for Free-Surface Multiples in VSP

The vertical seismic profiling (VSP) Gaussian beam migration is a seismic imaging method with both computational efficiency and imaging precision. It can get high-resolution structural features near the well. However, the VSP migration based on primary reflection imaging is limited by the observation system, which makes it unable to image for the shallow structure at far offset. The free-surface multiples in VSP can expand the illumination range for far offset effectively. Therefore, Gaussian beam migration (GBM) for free-surface multiples imaging in VSP is proposed. Firstly, based on the ground Gaussian beam pre-stack depth migration, the method for decomposing the plane wave is improved and adapted into VSP geometry. We decompose the seismic records received by the well into plane waves in different directions according to different window centers and image the plane wave of each direction independently. Secondly, through the mirror image of both the velocity model and VSP receivers, the VSP free-surface multiples are converted into VSP primary reflections which are involved in the VSP Gaussian beam migration method, and thus, the method of the primaries is used to image the free-surface multiples. Finally, the effectiveness and robustness of the proposed method are verified by the theoretical model and practical data.

Introduction

There are many difficulties in exploration and development, such as surface-complicated, complex underground structure, strong reservoir heterogeneity, thin reservoir thickness, and small reservoir traps. Seismic imaging technology needs a high-precision method which can broaden the frequency band so as to improve spatial resolution and identify thinner reservoirs and faults as well as some complex structures. The receivers of VSP exploration are close to the geologic objects, and seismic wave information from VSP can directly reflect the geological attributes of strata, reservoirs, or targets. The exploration precision and detection range of VSP are between ground seismic and logging methods. VSP is the spatial expansion and effective supplement of these two technologies, which is mainly used to study the formation process and the spatial structure around the well. Compared with ground seismic migration, VSP migration improves the resolution and provides the corresponding relationship between the underground strata structure and subsurface measurement parameters.

For a long time, the primaries have been used in imaging and the multiples have been suppressed as interference waves. However, the multiples also contain plentiful geological structure information. Reiter et al. (1991) tried to mine the useful information from the multiples and added the first-order water-bottom reflection operator into Kirchhoff pre-stack time migration. The method is difficult to obtain the up-going and down-going components of the towline data in submarine, so it is limited to deep water data processing. Based on this idea, many researchers have done much research on multiples imaging. Until now, the multiples have been regarded as effective information and applied effectively, which are significant to the fine description of underground structure information. Berkhout and Verschuur (1994) proposed a method to realize multiples imaging by using the received records as the sources and the separated multiples as the received records. Based on this idea, Guitton (2002) used the shot-profile method to migrate the multiples. Shan (2003) used source–receiver depth migration to realize multiples imaging. Shan and Guitton (2004) used the multiples to construct a pseudo-primary wave and realize the imaging of the multiples and proved that this method is equivalent to the above method which images the multiples by modifying boundary conditions. Berkhout and Verschuur (2006) combined surface-related multiple elimination (SRME) theory and focal transformation theory to convert the multiples into the primaries, and thus, multiples imaging can also be realized indirectly by extracting the multiples in the focal transformation domain. Lou et al. (2007) presented a new method to perform the 3C vector Kirchhoff pre-stack depth migration for the first-order free-surface multiples in VSP data by the velocity mirror image and the virtual receivers. It can accurately produce a much wider seismic image zone than the conventional VSP migration which uses primary reflections only. Liu et al. (2011) used the reverse time migration (RTM) to image the multiples by separating the multiples to realize multiples imaging through the primaries imaging method. However, the precision of separating the primaries and the multiples may reduce the quality of multiples imaging. Zhang and Schuster (2014) did multiples imaging and achieved the results based on the least square reverse time migration (LSRTM). But it involves huge calculation cost and the elimination of the noise. Liu et al. (2018) proposed the fast LSRTM to image the down-going free-surface multiples in VSP, which greatly expands the imaging illumination range of VSP.

Non-zero offset VSP imaging commonly uses VSP-CDP transform and Kirchhoff migration. Since the VSP-CDP transform and stack method use the ray method for model building in the depth domain and are based on the hypothesis of layered and uniform medium, it is difficult to image the complex structures. The Kirchhoff migration also leads to poor amplitude conservation and low imaging precision. To solve these problems, wave equation pre-stack depth migration was proposed, and it has been demonstrated effective when imaging complex structures (Wang J et al., 2008; Fang et al., 2016). RTM is based on the two-way wave equation and is distinguished by its high imaging and migration homing accuracy (Chen et al., 2018). The Gaussian beam migration (GBM) overcomes the shortcomings of Kirchhoff migration and retains its flexibility and efficiency at the same time. It also leads to the results as accurate as these by RTM. In summary, it has a fast calculation speed and high accuracy (Hill, 1990; Huang et al., 2014; Yu et al., 2018). In order to improve the quality of VSP imaging, Wang Y. G et al. (2008) applied the GBM to VSP for the first time (VSP-GBM for short). VSP-GBM not only considers both computational efficiency and imaging accuracy but also calculates multi-arrival travel time. Besides, it is a ray method, which has a weak dependence on the velocity model, so it has strong imaging ability. In this paper, VSP-GBM is used to calculate the free-surface multiples, and this method is verified by forward seismic data and actual seismic data.

Methods

VSP-GBM

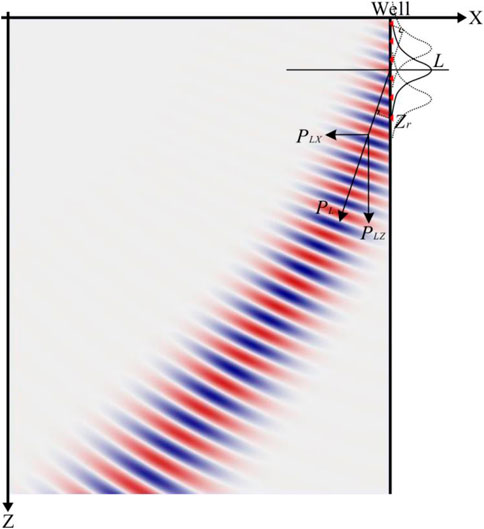
In a 2D scalar isotropic medium, the surface is horizontal and the receiving well is vertical. ${{\rm X}}_s=\left(x_s,0\right)$ is the seismic source, ${{\rm X}}_r=\left(x_r,z_r\right)$ is the receiver point, ${\rm X}=\left(x,z\right)$ is the imaging point, $\omega$ is the angular frequency, and $U\left({{\rm X}}_r,{{\rm X}}_s,\omega \right)$ is the received seismic wave field. According to the method of Gaussian beam characterizing Green’s function, Green’s function of the ray beam propagating from the seismic source to the imaging point can be described as

$G\left(\mathbf{X,}{\mathbf{X}}_s,\omega \right)=\frac{i}{4\pi }{\displaystyle \int \frac{d{p}_x}{p_z}{u}_{GB}\left(\mathbf{X,}{\mathbf{X}}_s,\mathit{P},\omega \right)=\frac{i}{4\pi }{\displaystyle \int \frac{d{p}_x}{p_z}A\exp \left(i\omega T\right)}},(1)$

where $p_x$ and $p_z$ represent the horizontal and vertical components of initial slowness in the central ray, respectively; $\mathit{P}=\left(p_x,p_z\right)$; and $T=\tau \left(s\right)+\frac{1}{2}\frac{P\left(s\right)}{Q\left(s\right)}{n}^2$ and $A=\sqrt{\frac{\epsilon V\left(s\right)}{V\left(0\right)Q\left(s\right)}}$ represent the complex-valued travel time and amplitude, respectively. The reverse continuation seismic wave field $U\left(\mathrm{X,}{\mathrm{X}}_{\mathrm{s}},\omega \right)$ from the source point to the imaging point can be shown by Rayleigh II integral as

$U\left(\mathbf{X,}{\mathbf{X}}_s,\omega \right)=2i\omega {\displaystyle \int d{x}_r\frac{\cos {\theta }_r}{V_r}}{G}^{\ast }\left(\mathbf{X,}{\mathbf{X}}_r,\omega \right)U\left({\mathbf{X}}_r\mathbf{,}{\mathbf{X}}_s,\omega \right),(2)$

where $\mathrm{G}\left(\mathrm{X,}{\mathrm{X}}_{\mathrm{r}}\mathrm{,\omega }\right)$ is Green’s function from the receiving point ${\mathrm{X}}_{\mathrm{r}}$ to the imaging point $\mathrm{X}$, ${\theta }_r$ is the emergent angle of ray, $V_r$ is the velocity of the receiver point, and * represents the complex conjugate.

If we add Gaussian window into the seismic records $\mathrm{U}\left({\mathrm{X}}_{\mathrm{r}}\mathrm{,}{\mathrm{X}}_{\mathrm{s}}\mathrm{,\omega }\right)$ received from receivers, and use the emitted Gaussian beam from the window center to represent Green’s function $\mathrm{G}\left(\mathrm{X,}{\mathrm{X}}_{\mathrm{r}}\mathrm{,\omega }\right)$ (as shown in Figure 1), then Eq. 2 can be transformed into

$U\left(\mathbf{X,}{\mathbf{X}}_s,\omega \right)\approx \frac{\mathrm{\Delta }L{\omega }_r}{{\left(2\pi \right)}^{3/2}{\omega }_0}\frac{\cos {\theta }_L}{V_L}{\displaystyle \sum _L{\displaystyle \int \frac{d{p}_{Lx}}{p_{Lz}}}}{A}_L^{\ast }\exp \left(-i\omega T_L^{\ast }\right)D_s\left(L,p_{Lz},\omega \right),(3)$

where the one-dimensional (1D) Gaussian window function in the vertical well VSP has the properties shown in

$\frac{\mathrm{\Delta }L}{\sqrt{2\pi }{\omega }_0}\sqrt{\left|\frac{\omega }{{\omega }_r}\right|}{\displaystyle \sum _L\exp \left[-\left|\frac{\omega }{{\omega }_r}\right|\frac{\left(z_r-L\right)}{2{\omega }_0^2}\right]}\approx 1.(4)$

$D_s\left(L,p_{Lz},\omega \right)$ is the slant stacking of seismic wave field in the Gaussian window which takes $\left(x_r,L\right)$ as its center. It is expressed as

$D_s\left(L,p_{Lz},\omega \right)={\left|\frac{\omega }{{\omega }_r}\right|}^{3/2}{\displaystyle \int d{z}_r}U\left({\mathbf{X}}_{\mathit{r}}\mathbf{,}{\mathbf{X}}_{\mathit{s}}\mathit{,\omega }\right)\exp \left[i\omega p_{Lz}\left(z_r-L\right)-\left|\frac{\omega }{{\omega }_r}\right|\frac{{\left(z_r-L\right)}^2}{2{\omega }_0^2}\right].(5)$

FIGURE 1

FIGURE 1. Local plane wave decomposition.

Here, we need to use the deconvolution imaging conditions in order to get the amplitude-preserving migration results in the shot domain:

$\mathit{I}\mathbf{(X,}{\mathbf{X}}_{\mathrm{s}}\mathrm{)=}\frac{\mathrm{1}}{\mathrm{2}\mathrm{\pi }}{\displaystyle \int \frac{U\mathbf{(X,}{\mathbf{X}}_{\mathit{s}}\mathit{,\omega )}{G}^{\mathrm{*}}\mathbf{(X,}{\mathbf{X}}_{\mathit{s}}\mathrm{,\omega )}}{G\mathbf{(X,}{\mathbf{X}}_{\mathit{s}}\mathrm{,\omega )}{G}^{\mathrm{*}}\mathbf{(X,}{\mathbf{X}}_{\mathit{s}}\mathit{,\omega )}}}\mathit{d\omega },(6)$

where $\mathrm{I}\left(\mathrm{X,}{\mathrm{X}}_{\mathrm{s}}\right)$ is the imaging value of one shot and $\mathrm{G}\left(\mathrm{X,}{\mathrm{X}}_{\mathrm{s}}\mathrm{,\omega }\right)$ is Green’s function of the source spreading in the forward direction. Upon substituting Eqs 1, 3 into Eq. 6, we get

$\begin{array}{l}\mathit{I}\left(\mathbf{X,}{\mathbf{X}}_{\mathit{s}}\right)\mathrm{=-}\frac{\mathrm{\Delta }\mathit{L}{\omega }_r}{\mathrm{16}{\mathit{\pi }}^{\mathrm{3}}\sqrt{\mathrm{2\pi }}{\mathit{\omega }}_{\mathrm{0}}}{\displaystyle \sum _{\mathit{L}}{\displaystyle \int \mathrm{d\omega }\frac{\mathit{i}}{\mathit{G}\left(\mathbf{X,}{\mathbf{X}}_{\mathbf{s}}\mathit{,\omega }\right){\mathrm{G}}^{\mathrm{*}}\left(\mathbf{X,}{\mathbf{X}}_{\mathit{s}}\mathit{,\omega }\right)}}}{\displaystyle \int \frac{\mathit{d}{\mathit{p}}_{\mathit{sx}}}{{\mathit{p}}_{\mathit{sz}}}}{\mathrm{A}}_{\mathit{s}}^{\mathrm{*}}\exp \left(\mathit{-i\omega }{\mathit{T}}_{\mathit{s}}^{\mathrm{*}}\right)\\ \mathrm{\times }\frac{\mathit{cos}{\mathit{\theta }}_{\mathit{L}}}{V_{\mathit{L}}}{\displaystyle \sum _L{\displaystyle \int \frac{d{p}_{\mathit{Lx}}}{p_{\mathit{Lz}}}}}{\mathrm{A}}_{\mathit{L}}^{\mathrm{*}}\exp \left(\mathit{-i\omega }{\mathit{T}}_{\mathit{L}}^{\mathrm{*}}\right){\mathit{D}}_{\mathit{s}}\left(\mathit{L,}{\mathit{p}}_{\mathit{Lz}}\mathit{,\omega }\right).\end{array}(7)$

Eq. 7 is the 2D VSP amplitude-preserving Gaussian beam imaging formula in the shot domain.

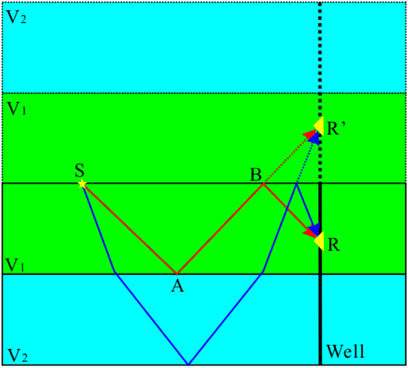
Velocity Mirror

In order to solve the issue of first-order free-surface multiples migration, we convert VSP first-order free-surface multiples into primary reflections based on the idea of velocity mirror image. As shown in Figure 2, the mirror point of the receiver point R is R’. The path of first-order free-surface multiples ($\overrightarrow{\text{SABR}}$) can be converted to the travel path of primary reflection ($\overrightarrow{{\text{SAR}}^{’}}$). VSP-GBM is employed in first-order free-surface multiples, and thus, the beam center is located at the mirror point R’. First, the seismic records are divided into a series of local regions. Then, the seismic records of local regions are decomposed into plane waves (amount to the beam) in different directions by using slant stacking. Finally, we map imaging the plane wave through the travel time and amplitude of rays (as shown in Figure 3).

FIGURE 2

FIGURE 2. Ray path of VSP first-order free-surface multiples.

FIGURE 3

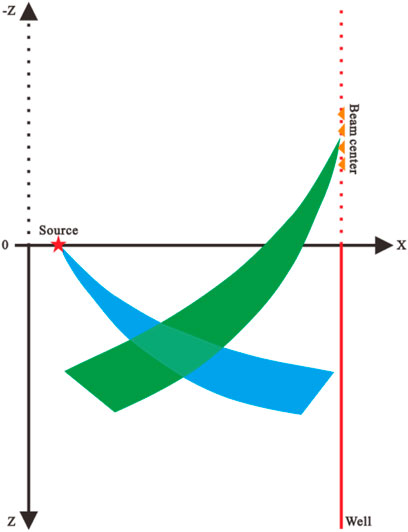
FIGURE 3. Arrangement of the receivers in GBM for VSP free-surface multiples imaging. The red star indicates the source location, orange inverted triangles indicate the receivers in the velocity mirror image, the blue beam is emitted from the source, the green beam is emitted from the window center point, and the light green area is the region where the ray pairs coincide.

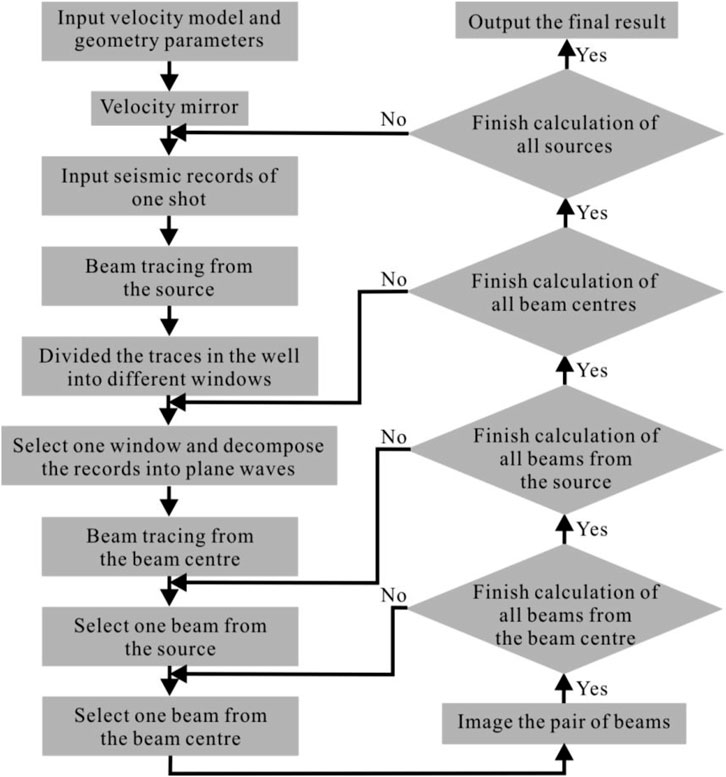
The workflow of the VSP-GBM algorithm is shown in Figure 4.

FIGURE 4

FIGURE 4. Workflow of GBM for VSP imaging.

Numerical Example

This section employs the complex model to test the VSP-GBM in free-surface multiples.

Figure 5A is the complex model, which is composed of a 301 (in the x dimension) by 3,001 (in the z dimension) grid, with grid spacings 10.0 m (in the x dimension) and 1.0 m (in the z dimension), respectively. The well is vertical and locates at the position of (1500 m, 0 m), and the triangles represent part of the receivers. The dataset has 16 shots at intervals of 200 m. The first shot locates at the position of (0 m, 0 m), and the stars represent part of the shot points. Each shot consists of 151 traces, and the receiver interval is 20.0 m (as shown in Figure 5B). It can be found from Figures 5C,D that the VSP free-surface multiples effectively expand the lateral imaging range, especially in the shallow structure at the far offset. Therefore, it not only fully utilizes VSP free-surface multiples but also effectively compensates the deficiency of primaries imaging in the shallow structure at the far offset.

FIGURE 5

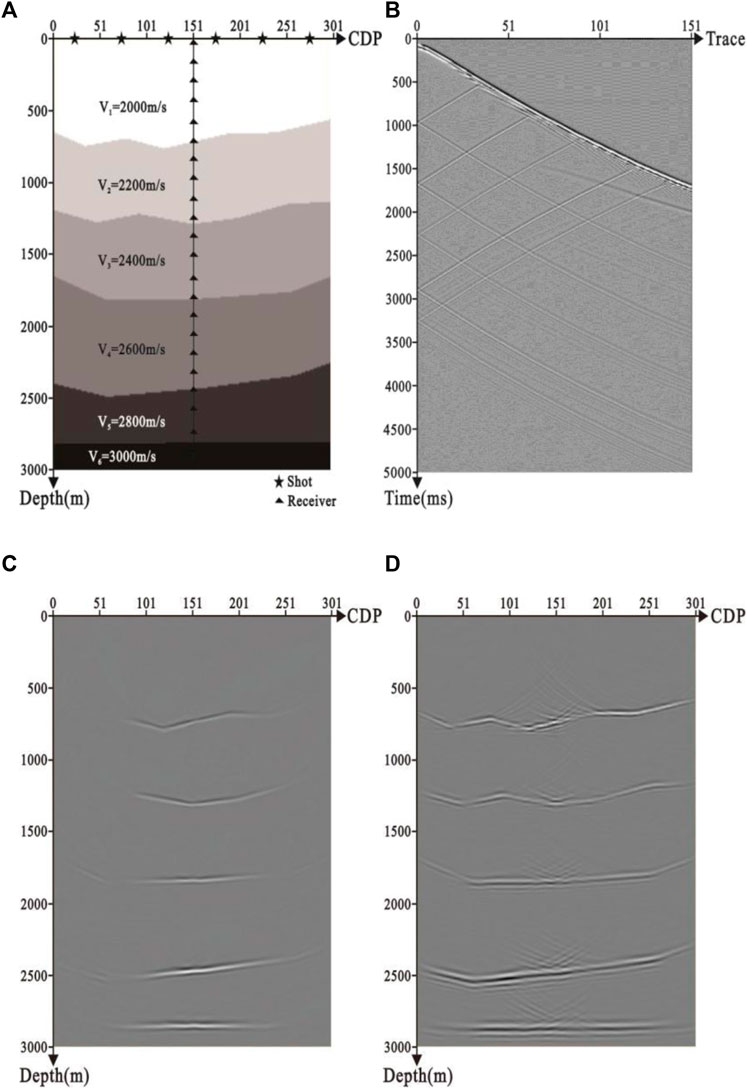
FIGURE 5. VSP-GBM result of the complex model: (A) complex model, (B) shot record of the numerical example, (C) migration result of the primaries, and (D) combined migration result of the first-order free-surface multiples and the primaries.

Practical Data Test

This section employs the practical data to test the effectiveness between primaries and first-order free-surface multiples in the VSP-GBM method.

The geological model is shown in Figure 6A with a size of 10000 m × 6000 m. The grid spacing is 10.0 m in the x dimension and 10.0 m in the z dimension. The well is not vertical, and the black curve indicates the receivers’ distribution range. The dataset has 110 shots, and the first shot locates at (1929 m, 0 m); note that the shot intervals are unequal and that the explosion signs are part of the shot points. The minimum offset is 130 m, and the maximum offset is 3070 m. The shot consists of 171 traces, and the receivers locate from 297 to 1967 m in depth. Note that the receiver intervals are also unequal. The wave field is shown in Figure 6B. The method can effectively avoid the errors from wave field separation. Figures 6C,D show the VSP-GBM results of primaries and first-order free-surface multiples. It can be seen that the VSP-GBM result of first-order free-surface multiples effectively compensates the imaging deficiency of VSP primaries in the shallow structure at the far offset. By comparing the VSP-GBM results shown in Figures 6C,D, the feasibility and effectiveness of the proposed method are verified.

FIGURE 6

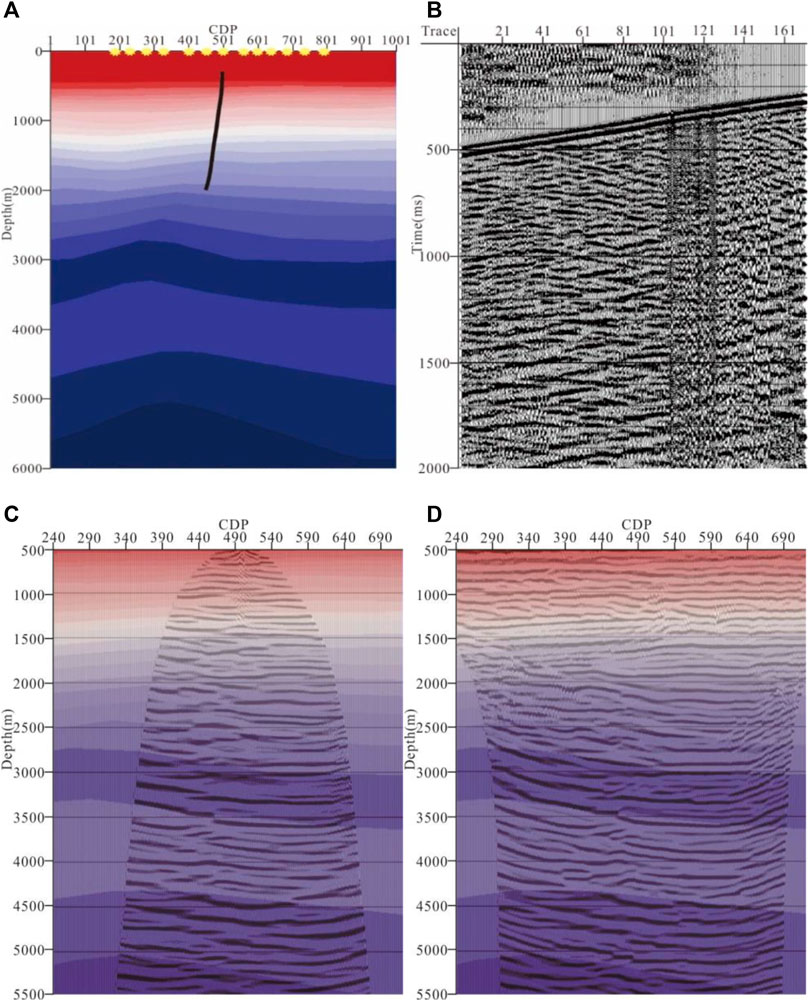
FIGURE 6. VSP-GBM result of the practical data: (A) velocity model, (B) shot record, (C) migration result of the primaries, and (D) combined migration result of the first-order free-surface multiples and the primaries.

Conclusion

In this paper, the ground GBM method is extended to VSP geometry, and the idea of velocity mirror image is applied to VSP-GBM. This method can directly image the primary reflection waves and first-order free-surface multiple waves of VSP without wave field separation and effectively use the multiples wave field information of VSP to improve the imaging accuracy of VSP. The results of the theoretical model and practical data show that the first-order free-surface multiples can expand the lateral imaging range of VSP-GBM and effectively compensate the imaging deficiency of VSP primaries in the shallow structure at the far offset.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

FY and DY contributed to conception and design of the study and wrote the first draft of the manuscript. BW provided practical data. YW and DH performed data analysis. BW, YW, and CZ wrote sections of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This research was funded by the Natural Science Basic Research Plan in the Shaanxi Province of China (No. 2021JQ-588).

Conflict of Interest

BW was employed by BGP Offshore of China National Petroleum Corporation. YW was employed by Docan Tech (Xi’an) Co., Ltd. CZ was employed by Sinopec Northwest Oilfield Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Berkhout, A. J., and Verschuur, D. J. (1994). “Multiple Technology: Part 2 ,migration of Multiple Reflections[C],” in 64th Annual International Meeting, Los Angeles, CA, October 23-28, 1994 (SEG, Expanded Abstracts), 1497–1500.

Google Scholar

Berkhout, A. J., and Verschuur, D. J. (2006). Imaging of Multiple Reflections. Geophysics 71 (4), SI209–SI220. doi:10.1190/1.2215359

CrossRef Full Text | Google Scholar

Chen, Y. Z., Zhang, R. F., Tang, C. Z., Zhang, Y. B., Wang, X. J., and Wang, G. (2018). A Joint VSP and Surface Seismic Survey for Marlstones in Shulu, Huabei Oilfield[J]. Oil Geophys. Prospecting (in Chinese) 53 (Suppl. 2), 50–57. doi:10.13810/j.cnki.issn.1000-7210.2018.S2.009

CrossRef Full Text | Google Scholar

Fang, T. E., Huang, X. R., and Ma, S. F. (2016). VSP Migration Based on High Angle One-Way Wave Equation in Time-Space Domain and its Applications[J]. Chin. J. Geophys. (in Chinese) 59 (9), 3459–3469. doi:10.6038/cjg20160928

CrossRef Full Text | Google Scholar

Guitton, A. (2002). “Shot-profile Migration of Multiple Reflections[C],” in 72th Annual International Meeting, Salt Lake City, UT, October 6-11, 2002 (SEG, Expanded Abstracts), 1296–1299.

Google Scholar

Hill, N. R. (1990). Gaussian Beam Migration. Geophysics 55 (11), 1416–1428. doi:10.1190/1.1442788

CrossRef Full Text | Google Scholar

Huang, J. P., Zhang, Q., Zhang, K., Li, Z. C., Yue, Y. B., and Yuan, M. L. (2014). Reverse Time Migration with Gaussian Beams Based on the Green Function[J]. Oil Geophys. Prospecting (in Chinese) 49 (1), 101–106. doi:10.13810/j.cnki.issn.1000-7210.2014.01.012

CrossRef Full Text | Google Scholar

Liu, X. J., Liu, Y. K., and Khan, M. (2018). Fast Least-Squares Reverse Time Migration of VSP Free-Surface Multiples with Dynamic Phase-Encoding Schemes[J]. Geophysics 83, 321–332. doi:10.1190/geo2017-0419.1

CrossRef Full Text | Google Scholar

Liu, Y. K., Chang, X., Jin, D., He, R. Q., Sun, H. C., and Zheng, Y. C. (2011). “Reverse Time Migration of Multiples[C],” in 81st Annual International Meeting, San Antonio, TX, September 18-23, 2011 (SEG, Expanded Abstracts), 3326–3331.

Google Scholar

Lou, M., Zhao, X., Doherty, F., and Jackson, J. (2007). “Vector Kirchhoff Migration of First Order Downgoing Multiples from VSP Data [C],” in 77th Annual International Meeting, San Antonio, TX, September 23-28, 2007 (SEG, Expanded Abstracts), 3059–3063.

Google Scholar

Reiter, E. C., Toksöz, M. N., Keho, T. H., and Purdy, G. M. (1991). Imaging with Deep‐water Multiples. Geophysics 56 (7), 1081–1086. doi:10.1190/1.1443119

CrossRef Full Text | Google Scholar

Shan, G. J., and Guitton, A. (2004). “Migration of Surface-Related Multiples: Tests on the Sigsbee2B Dataset[C],” in 74th Annual International Meeting, Denver, CO, October 10-15, 2004 (SEG, Expanded Abstracts), 1285–1288.

Google Scholar

Shan, G. J. (2003). “Source-receiver Migration of Multiple Reflections[C],” in 73nd Annual International Meeting, Dallas, TX, October 26-31, 2003 (SEG, Expanded Abstracts), 1008–1011.

Google Scholar

Wang, J., Qiao, Y. L., Yao, Z. R., and Li, R. Z. (2008). Vertical Seismic Profile Imaging by Gaussian Beam Migration [J]. J. China Univ. Pet. 32 (4), 29–33. (in Chinese). doi:10.3969/j.issn.1673-5005.2008.04.006

CrossRef Full Text | Google Scholar

Wang, Y. G., Wang, Y. C., Wei, X. C., Yang, Z. R., and Zhang, D. L. (2008). Improvement of Non-zero Offset VSP Imaging Method[J]. Oil Geophys. Prospecting (in Chinese) 43 (6), 641–644. doi:10.13810/j.cnki.issn.1000-7210.2008.06.015

CrossRef Full Text | Google Scholar

Yu, D., Yang, F. L., Sun, Y., Bian, R. F., and Wang, Y. (2018). The Study of Cross-Well Seismic Gaussian Beam Pre-stack Migration Imaging in Depth Domain[J]. Comput. Tech. Geophys. Geochemical Exploration (in Chinese) 40 (2), 141–149. doi:10.3969/j.issn.1001-1749.2018.02.01

CrossRef Full Text | Google Scholar

Zhang, D., and Schuster, G. T. (2014). Least-squares Reverse Time Migration of Multiples. Geophysics 79 (1), S11–S21. doi:10.1190/geo2013-0156.1

CrossRef Full Text | Google Scholar