Bearing Capacity Calculation of Soft Foundation of Waste Dumps—A Case of Open-Pit Mine

For a waste dump with soft foundation, the foundation bearing capacity has an important impact on slope stability. According to the load distribution and stress characteristics of a waste dump, combining the gravity load of the triangular slope of the waste dump and the passive Earth pressure exerted by the foundation soil with an improved Plandtl formula, the foundation bearing capacity and the ultimate pile height of a waste dump are calculated and determined. The concept of foundation bearing capacity of a waste dump is redefined, that is, the ultimate pile height corresponding to a certain slope angle. A method for determining the ultimate pile height of a waste dump based on the slope angle of the waste dump is proposed, and the relation function between dump slope angle and waste height is established. The results show that the sliding moment increment (∆M_S) caused by the gravity load of the triangular slope after waste increase is positively proportional to the pile height increment (∆H); the anti-sliding moment increment (∆M_AS) is positively proportional to or positively correlated with the pile height increment (∆H); the slope angle of the waste dump decreases with the increase of the thickness of soft bedrocks, and the smaller thickness of soft bedrocks is more favorable to the ultimate pile height of the waste dump. The research results can provide reference for the calculation of the bearing capacity of soft foundation and the optimal design of slope shape of waste dumps.

1 Introduction

The stability of waste dumps is one of the critical factors for the safe production of an open-pit mine (Behera et al., 2016; Wang et al., 2017; Gong et al., 2021). As a joint product of geological processing and artificial landfilling, the slope stability of a waste dump is mainly affected by the mechanical properties of the foundation (Gao et al., 2021; Zhang Y et al., 2021), the shape of the slope, and the properties of the discharged materials (Han et al., 2016; Wang et al., 2019; Jiang et al., 2021).

The mechanical properties of the foundation are an internal influencing factor and cannot be artificially altered, especially the soft foundation with a low bearing capacity (Tao et al., 2018; Zhang Z et al., 2021). Under the action of granular material pressure, the slope/waste dump may slip along the smooth base, further causing the mess to collapse and triggering a retrogressive landslide (Jorge, 2017; Wang et al., 2020; Zhang et al., 2022). Slope failure is an inevitable aspect of economic mine slope design in the mining industry (Neil et al., 2020); large landslides or floor heaves have occurred at the south dump of the Antaibao Openpit Mine, the east dump of the Pingshuo Opencast Mine, the external waste dump at the “South Field” lignite mine, Northern Greece, the Jianshan dump of the Lanjian Iron Mine, etc. due to insufficient bearing capacity of foundations (Steiakakis et al., 2009; Cao et al., 2021; Huang F et al., 2021), which is a serious threat to mine safety and sustained operation. Hence, it is necessary to systematically study the bearing capacity of the foundation to ensure the safety and stability of the waste dump (Zhang et al., 2011; Chakraborty 2013; Park et al., 2017).

Currently, the calculation of the bearing capacity of dump foundations is usually based on the calculation method of the bearing capacity of building foundations in soil mechanics (Castelli, 2012; Moayedi et al., 2018), such as the formulae proposed by Prandtl (Roy et al., 2017), Terzaghi, and Hansen (Terzaghi, 1943; Georgiadis, 1985; Luo, 1986; Huang, 1991; Griffiths, 2001). In recent years, scholars have conducted a series of studies on ultimate bearing capacity in view of the instability caused by the soft foundation of waste dumps (Wang et al., 2012; Li L et al., 2021). Divya et al. (2020) used Bell’s approach to study the foundation bearing capacity of discontinuous rock slope in the Garhwal Himalayas of India. Karrech (2021) used the generalized Hoek–Brown criterion to analyze the seismic stability of three-dimensional rock slopes. Zhou (2002)deduced a theoretical formula of foundation bearing capacity based on the ultimate bearing capacity theory of foundations and the statics theory of loose medium. Zhai et al. (2015) analyzed the base bearing capacity according to foundation thickness and failure mode and determined the ultimate pile height through physical and mechanical tests. He et al. (1999) studied the topsoil thickness of the foundation and the contact conditions with the waste rocks in the dump, revealed the influencing mechanism of the foundation topsoil under loading, and obtained the critical topsoil thickness formula for determining the ultimate pile height. Zhong et al. (2017) adopted the leading bearing capacity theory to derive a theoretical formula for calculating the ultimate bearing capacity of foundations considering the foundation thickness and verified the calculation results by using FLAC^3D.

To sum up, many scholars presently calculate the bearing capacity of the foundation base; some are theoretical derivation, and some are empirical formulas. However, these formulas and methods do not consider the inhibition of the anti-sliding force generated by the gravity load of the triangular slope of the waste dump slope on the foundation failure, and the influence of the foundation thickness on the foundation bearing capacity is rarely involved. Therefore, according to the actual conditions of an open-pit waste dump, based on the improved Prandtl calculation method, this paper analyzes the influence of basement rock thickness and slope angle on slope stability and determines the limit discharge height corresponding to different slope angles.

In a word, the traditional test method and stability analysis theory of ultimate bearing capacity research consider the influence of basement rock condition or basement state on the maximum bearing capacity and top dumping height of waste dump, respectively, but they do not form a law. Once the lithology of the waste dump basement and the angle of the waste dump slope change, the waste dump slope will become unstable. To change this situation, it is also necessary to further understand the relationship between the dumping height of the waste dump and the bearing capacity of the foundation and establish a scientific calculation method of the ultimate bearing capacity of the foundation of the waste dump. In this paper, a particular discussion is carried out. A new theory, practice, and formula for calculating the bearing capacity of weak foundations according to the actual load distribution and stress characteristics are given.

2 Prandtl Calculation Method on Ultimate Vertical Load

2.1 Analysis of Prandtl’s Vertical Load Calculation Principle

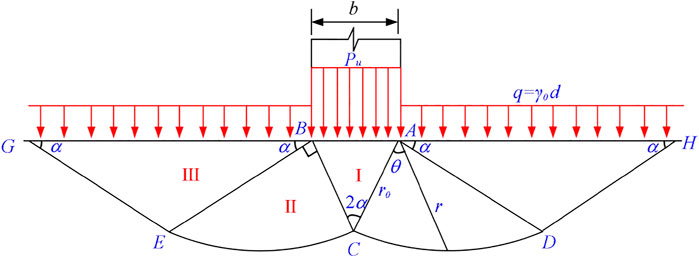
Due to the simple calculation principle and convenient application (Pakdel et al., 2021; Wang et al., 2010), Prandtl’s formula is widely used to calculate the bearing capacity of dump foundations and the ultimate pile height of open-pit waste dumps (Li et al., 2017a). The failure pattern of foundations proposed by Prandtl is shown in Figure 1 (Kyle et al., 2013; Jiang et al., 2019). The vertical stress in Zone Ⅰ is the maximum principal stress, namely, the ultimate bearing capacity of the foundation (P_u) (Amin et al., 2018; Huang et al., 2020). It is a Rankine active zone. The sliding planes AC and BC are 45°+φ/2 with the horizontal plane. Soil wedges ADH and BEG in Zone Ⅲ are in a passive state after being pressed downward by the wedge in Zone Ⅰ, and they are Rankine passive zones. The sliding planes DH and EG form α = 45°−φ/2 with the horizontal plane. Between the active zone and the passive zone, the transition zones ACD and BEC (Zone Ⅱ) are composed of a group of logarithmic spiral curves and a group of radiation lines. The equation of the logarithmic spiral curve (CD) is expressed as:

$r=r_0\cdot e^{\theta tan\phi }(1)$

Where r is the vector radius from the origin of the spiral curve to any point on CD, (m); r₀ is the initial radius, namely, the line segments AC and BC, (m); θ is the angle between rays r and r₀, (°); φ is the internal friction angle of the foundation soil, (°).

FIGURE 1

FIGURE 1. Schematic diagram of the Prandtl foundation sliding model.

2.2 Prandtl Vertical Load Calculation Formula

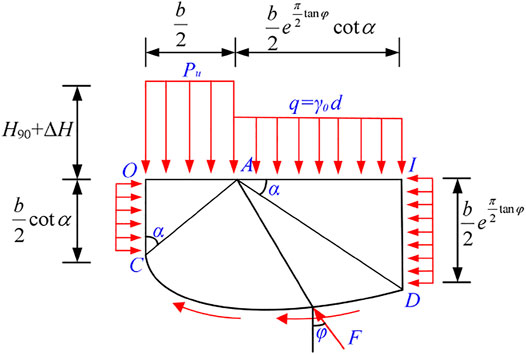
In Figure 1, a part of sliding soil OCDI is regarded as a rigid body, as shown in Figure 2. According to the balanced state of the force system on OCDI, the ultimate load Pu per unit length on OA (base surface) and its moment to point A can be calculated by Eq. (2):

$M_1=\frac{P_{u}b}{2}\cdot \frac{b}{4}=\frac{1}{8}{b}^2{P}_u(2)$

FIGURE 2

FIGURE 2. Force analysis of isolators.

The resultant force of the active Earth pressure on OC plane is:

$E_a=P_u{\tan }^2\alpha -2\cdot c\tan \alpha (3)$

Its moment about point A is:

$M_2=\frac{1}{2}{E}_a{\left(\frac{b}{2}\cot \alpha \right)}^2=\frac{1}{8}{b}^2{\cot }^2\alpha \left(P_u{\tan }^2\alpha -2c\tan \alpha \right)=\frac{1}{8}{b}^2{P}_u-\frac{1}{4}\mathit{ }{b}^{2}c\cot \alpha (4)$

The moment of the resultant force of the soil weight on AI plane about point A is:

$M_3=\frac{1}{2}q{\left(\frac{b}{2}{e}^{\frac{\pi }{2}\tan \phi }\cot \alpha \right)}^2=\frac{b^2}{8}{\gamma }_{0}d{e}^{\pi \tan \phi }{\cot }^2\alpha (5)$

The Prandtl formula assumes that the soil mass beneath the foundation is weightless and ignores that the passive Earth pressure generated by the soil mass on the right side of surface ID can produce an anti-sliding moment. According to Rankine’s Earth pressure theory, the passive Earth pressure on ID surface is:

$E_p={\gamma }_{1}d{\cot }^2\alpha +2c\cot \alpha (6)$

Its moment about point A is calculated by:

$\begin{array}{l}{M}_4=\frac{1}{2}{E}_p\overline{I{D}^2}=\frac{1}{2}{E}_p{\left(\frac{b}{2}{e}^{\frac{\pi }{2}\tan \phi }\right)}^2=\frac{1}{2}{\left(\frac{b}{2}{e}^{\frac{\pi }{2}\tan \phi }\right)}^2\left({\gamma }_{1}d{{\displaystyle \cot }}^2\alpha +2c\cot \alpha \right)\\ =\frac{1}{8}{\gamma }_{1}d{b}^2{e}^{\pi \tan \phi }{{\displaystyle \cot }}^2\alpha +\frac{1}{4}b{}^{2}c{e}^{\pi \tan \phi }\cot \alpha \end{array}(7)$

The moment of the resultant force of the cohesion on CD about point A is:

$M_5={\displaystyle {\int }_0^{1}cdsr\cos \phi }={\displaystyle {\int }_0^{\pi /2}c{r}^{2}d\theta }={\displaystyle {\int }_0^{\pi /2}c\frac{rd\theta }{\cos \phi }}=\frac{b^{2}c\cot \phi \left(e\pi \tan \phi -1\right)}{8{\sin }^2\alpha }(8)$

The resultant resistance force (F) on CD passes through the center point A of the logarithmic spiral curve, and then its moment about point A is zero. According to the equilibrium condition for the moment about point A, the following equation is obtained.

${\displaystyle \sum M_A}=M_1+M_2-M_3-M_4-M_5=0(9)$

Eqs. 1–8 are substituted into Eq. 9 to obtain:

$\begin{array}{l}{P}_u=\frac{4}{b^2}\left(\frac{1}{4}{b}^{2}c\cot \alpha +\frac{b^2}{8}{\gamma }_{0}d{e}^{\pi \tan \phi }{{\displaystyle \cot }}^2\alpha +\frac{1}{8}{\gamma }_{1}d{b}^2{e}^{\pi \tan \phi }+{\cot }^2\alpha \frac{1}{4}{b}^{2}c{e}^{\pi \tan \phi }\cot \alpha \right)\\ +\frac{c\left(e^{\pi \tan \phi }-1\right)}{2\tan \phi {\sin }^2\alpha }=c\cot \alpha \left(1+e^{\pi \tan \phi }\right)+\frac{c\left(e^{\pi \tan \phi }-1\right)}{2\tan \phi {\sin }^2\alpha }\end{array}(10)$

where γ₀ represents the weighting average volumetric weight of the soil above the foundation, (kN/m³).

γ₁ means the volumetric weight of the foundation soil, (kN/m³); d is the burial depth of the foundation, (m); c is the soil cohesion above the foundation, (kPa); b is the foundation width, (m). P_u refers to the ultimate load, (kPa); E_a indicates the active Earth pressure, (kPa); E_p denotes the passive Earth pressure, (kPa).

3 Dump Foundation Bearing Capacity Calculation Using a Revised Prandtl Formula

When Prandtl’s formula is used to calculate the ultimate bearing capacity of the dump foundation (Abhishek et al., 2015), only the soil above the foundation is regarded as uniformly distributed on the foundation plane and specific load distribution of the slope is ignored. However, the actual load distribution of the dump should be considered during calculation. The resistance force to the ultimate bearing capacity of the foundation is composed of the gravity load of the triangular slope and the passive Earth pressure of the foundation soil. Therefore, according to the load distribution characteristics of the dump foundation, the foundation bearing capacity and the ultimate pile height of the slope can be calculated and determined based on a revised Prandtl formula.

3.1 Analysis of Foundation Bearing Capacity Under Non-Uniform Loading

Combined with the practical conditions of the dump slope in an open-pit mine, when the foundation of a vertical gradient with a slope angle of 90° reaches the ultimate bearing capacity (H₉₀), a continuous sliding surface will occur in the foundation, indicating that the foundation is in the limit equilibrium state and further loading will cause overall shear failure to the dump foundation. The actual dump slope is set at a certain angle with the horizontal surface. When the mine waste is discharged at a certain angle on the vertical slope, which is under the limit equilibrium condition, the vertical slope foundation will not slide along the sliding surface because a triangular slope is produced at the side of the slope, namely, triangular slope gravity load is induced and also provides additional resistance to the foundation sliding surface. The foundation is in a stable state, allowing another certain pile height on the vertical slope. When the discharging reaches a certain height (i.e., the height increment, ∆H), the slope is in a new limit equilibrium state (Deng et al., 2019). At this time, the sliding moment of the newly increased slope is equal to the anti-sliding moment. As a result, the slope has a new ultimate pile height (Huang et al., 2017; Wang J et al., 2021).

3.2 Improved Formula for Calculating Prandtl’s Ultimate Bearing Capacity

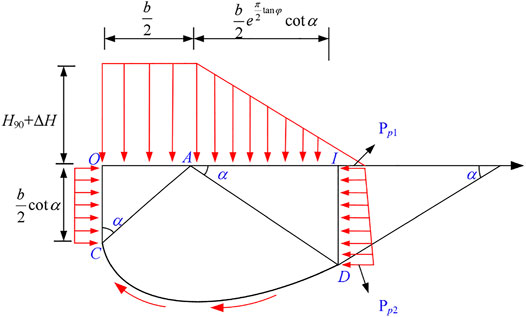
By analyzing the isolator OCDI, the moment increment ΔL caused by the gravity load of the triangular dump slope is associated with the difference value between (H₉₀+ΔH)/tanβ and $\overline{AI}$, where β is the slope angle. Thus, the passive Earth pressure on ID surface is discussed in two aspects.

3.2.1 The Gravity Load of the Triangular Slope is on the Inner Side of the Foundation Sliding Surface

When the value of (H₉₀+ΔH)/tanβ is smaller than $\overline{AI}$, the gravity load of the triangular slope at the side of the dump is distributed in the inner part of the sliding surface of the foundation (within the ID surface) on the horizontal axis, and moment increment is generated on the OA, OC, and AI planes separately, as shown in Figure 3.

FIGURE 3

FIGURE 3. Sliding mode diagram when (H₉₀+ΔH)/tanβ < $\overline{AI}$

The resultant force increment of the ultimate bearing capacity is generated on OA (foundation surface) and its moment increment about point A is:

$\text{Δ}{M}_1=\frac{P_u^{\prime }b}{2}\cdot \frac{b}{4}=\frac{1}{8}{b}^2{P}_u^{\prime }=\frac{1}{8}{b}^2\left(\text{Δ}H\cdot {\gamma }_0\right)(11)$

The resultant force increment of the active Earth pressure on OC surface can be calculated by:

$\text{Δ}{E}_a=P_u^{\prime }{\tan }^2\alpha -2\cdot c\tan \alpha (12)$

Its moment increment about point A is:

$\begin{array}{l}\text{Δ}{M}_2=\frac{1}{2}\text{Δ}{E}_a{\left(\frac{b}{2}\cot \alpha \right)}^2=\left(P_u^{\prime }{\tan }^2\alpha -2c\tan \alpha \right)\left(\frac{b^2}{8}{{\displaystyle \cot }}^2\alpha \right)\\ =\frac{1}{8}{b}^2{P}_u^{\prime }-\frac{1}{4}{b}^{2}c\cot \alpha =\frac{1}{8}{b}^2\left(\text{Δ}H\cdot {\gamma }_0\right)-\frac{1}{4}{b}^{2}c\cot \alpha \end{array}(13)$

The resultant force increment of the soil weight on AI surface is obtained:

$\text{Δ}q=\frac{1}{2}\left(H_{90}+\text{Δ}H\right){\gamma }_0(14)$

Its moment increment relative to point A is:

$\text{Δ}{M}_3=\frac{1}{3}\text{Δ}q{\left(\frac{H_{90}+\text{Δ}H}{\tan \beta }\right)}^2=\frac{1}{6}{\gamma }_0{\left(\frac{H_{90}+\text{Δ}H}{\tan \beta }\right)}^2\left(H_{90}+\text{Δ}H\right)(15)$

The moment of the resultant force of the cohesion on CD about point A is that:

$\begin{array}{l}\text{Δ}{M}_5={\displaystyle {\int }_0^{l}cdsr\cos \phi }={\displaystyle {\int }_0^{\pi /2}c{r}^{2}d\theta }={\displaystyle {\int }_0^{\pi /2}c\cdot \frac{rd\theta }{\text{cos}\phi }\cdot }\text{cos}\phi r\\ =\frac{b^2\cdot c\cdot \cot \phi \cdot \left(e^{\pi \tan \phi }-1\right)}{8{\sin }^2\alpha }\end{array}(16)$

When the dump slope reaches a new limit equilibrium state and the pile height increment (∆H) produces ∆M_S equal to ∆M_AS, then:

$\begin{array}{l}\text{Δ}{M}_S=\text{Δ}{M}_1+\text{Δ}{M}_2=\frac{1}{8}{b}^2\left(\text{Δ}H{\gamma }_0\right)+\frac{1}{8}{b}^2\left(\text{Δ}H{\gamma }_0\right)-\frac{1}{4}{b}^{2}c\cot \alpha \\ =\frac{1}{4}{b}^2\left(\text{Δ}H{\gamma }_0-c\cot \alpha \right)\end{array}(17)$

$\text{Δ}{M}_{AS}=\text{Δ}{M}_3+\text{Δ}{M}_5=\frac{1}{6}{\gamma }_0{\left(\frac{H_{90}+\text{Δ}H}{\tan \beta }\right)}^2\left(H_{90}+\text{Δ}H\right)+\frac{b^2\cdot c\cdot \cot \phi \cdot \left(e^{\pi \tan \phi }-1\right)}{8{\sin }^2\alpha }(18)$

$\text{Δ}M=\text{Δ}{M}_{AS}-\text{Δ}{M}_S=\frac{1}{6}{\gamma }_0{\left(\frac{H_{90}+\text{Δ}H}{\tan \beta }\right)}^2\left(H_{90}+\text{Δ}H\right)+\frac{b^2\cdot c\cdot \cot \phi \cdot \left(e^{\pi \tan \phi }-1\right)}{8{\sin }^2\alpha }-\frac{1}{4}{b}^2\left(\text{Δ}H{\gamma }_0-c\cot \alpha \right)(19)$

3.2.2 The Sliding Surface Is Covered by the Gravity Load of the Triangular Slope

When the value of (H₉₀+ΔH)/tanβ is bigger than $\overline{AI}$, the gravity load on the triangular slope covers the sliding surface AI, leading to passive Earth pressure on ID surface, as expressed in Figure 4.

FIGURE 4

FIGURE 4. Slip mode diagram when (H₉₀+ΔH)/tanβ > $\overline{AI}$

The resultant force increment of the ultimate bearing capacity is generated by OA (foundation surface), and its moment increment about point A is:

$\text{Δ}{M}_1=\frac{P_u^{\prime }b}{2}\cdot \frac{b}{4}=\frac{1}{8}{b}^2{P}_u^{\prime }=\frac{1}{8}{b}^2\left(\text{Δ}H\cdot {\gamma }_0\right)(20)$

The resultant force increment of the active pressure on OC surface is achieved by:

$\text{Δ}{E}_a=P_u^{\prime }{\tan }^2\alpha -2\cdot c\tan \alpha (21)$

Its incremental moment relative to point A is:

$\begin{array}{l}\text{Δ}{M}_2=\frac{1}{2}\text{Δ}{E}_a{\left(\frac{b}{2}\cot \alpha \right)}^2=\left(P_u^{\prime }{\tan }^2\alpha -2c\tan \alpha \right)\left(\frac{b^2}{8}{{\displaystyle \cot }}^2\alpha \right)\\ =\frac{1}{8}{b}^2{P}_u^{\prime }-\frac{1}{4}{b}^{2}c\cot \alpha =\frac{1}{8}{b}^2\left(\text{Δ}H\cdot {\gamma }_0\right)-\frac{1}{4}{b}^{2}c\cot \alpha \end{array}(22)$

The resultant force of the soil weight on AI surface presents trapezoidal loading distribution and its resultant force increment about point A is as follows:

$\text{Δ}q={\gamma }_0\left(H_{90}+\text{Δ}H\right)-\frac{b}{4}{\gamma }_0{e}^{\frac{\pi }{2}\tan \phi }\cot \alpha \tan \beta (23)$

Its moment increment relative to point A can be obtained:

$\begin{array}{l}\text{Δ}{M}_3=\frac{1}{2}{\gamma }_0\left(H_{90}+\text{Δ}H\right){\left(\frac{b}{2}{e}^{\frac{\pi }{2}\tan \phi }\cot \alpha \right)}^2-\frac{b}{6}{e}^{\frac{\pi }{2}\tan \phi }{\gamma }_0\cot \alpha \tan \beta {\left(\frac{b}{2}{e}^{\frac{\pi }{2}\tan \phi }\cot \alpha \right)}^2\\ =\frac{b^2}{8}{\gamma }_0\left(H_{90}+\text{Δ}H\right)e^{\pi \tan \phi }{{\displaystyle \cot }}^2\alpha -\frac{b^3}{24}{e}^{\frac{3\pi }{2}\tan \phi }{\gamma }_0{{\displaystyle \cot }}^3\alpha \tan \beta \end{array}(24)$

Both the gravity load of the soil on the right side of the ID surface and the gravity load of the triangular slope acting on the AI surface produce passive Earth pressure on the ID surface. The passive Earth pressure on the ID surface is a superposition. According to Rankine’s passive Earth pressure theory (Etezad et al., 2015; Xu et al., 2019; Yang et al., 2019), it can be concluded that:

The Earth pressure at the top of the bedrocks is:

$P_{p1}=2c\cot \alpha (25)$

The Earth pressure at the bottom of the bedrocks is:

$P_{p2}={\gamma }_1\left(H_{90}+\text{Δ}H\right){{\displaystyle \cot }}^2\alpha +2c\cot \alpha (26)$

Its moment relative to point A is shown below:

$\begin{array}{l}\text{Δ}{M}_4=\frac{1}{3}{P}_{p1}{\left(\frac{b}{2}{e}^{\frac{\pi }{2}\tan \phi }\right)}^2+\frac{2}{3}{P}_{p2}{\left(\frac{b}{2}{e}^{\frac{\pi }{2}\tan \phi }\right)}^2\\ =\frac{b^2}{6}c\cot \alpha e^{\pi \tan \phi }+\frac{b^2}{6}{e}^{\pi \tan \phi }\left({\gamma }_1\left(H_{90}+\text{Δ}H\right){{\displaystyle \cot }}^2\alpha +2c\cot \alpha \right)\\ =\frac{b^2}{2}c\cot \alpha e^{\pi \tan \phi }+\frac{b^2}{6}{\gamma }_1{e}^{\pi \tan \phi }\left(H_{90}+\text{Δ}H\right){{\displaystyle \cot }}^2\alpha \end{array}(27)$

The moment of the resultant force of the cohesion on CD about point A can be achieved by:

$\text{Δ}{M}_5={\displaystyle \underset{0}{\overset{l}{\int }}cdsr\cos \mathit{\varphi }}={\displaystyle {\int }_0^{\pi /2}c{r}^{2}d\theta =}{\displaystyle {\int }_0^{\pi /2}c\frac{rd\theta }{\cos \varphi }\cos \varphi r}=\frac{b^2\cdot c\cdot \cot \varphi \cdot \left(e^{\pi \tan \varphi }-1\right)}{8{\sin }^2\alpha }(28)$

When the dump slope reaches a new limit equilibrium state, the pile height increment ∆H produces ∆M_S equal to ∆M_AS, and the waste height at this time is the ultimate pile height.

$\begin{array}{l}\text{Δ}{M}_S=\text{Δ}{M}_1+\text{Δ}{M}_2=\frac{1}{8}\cdot b^2\left(\text{Δ}H\cdot {\gamma }_0\right)+\frac{1}{8}\cdot b^2\left(\text{Δ}H\cdot {\gamma }_0\right)-\frac{1}{4}\cdot b^2\cdot c\cdot \cot \alpha \\ =\frac{1}{4}{b}^2\left(\text{Δ}H\cdot {\gamma }_0\right)-\frac{1}{4}{b}^2\cdot c\cdot \cot \alpha \end{array}(29)$

$\begin{array}{l}\text{Δ}{M}_{AS}=\text{Δ}{M}_3+\text{Δ}{M}_4+\text{Δ}{M}_5=\frac{b^2}{8}\left(H_{90}+\text{Δ}H\right){\gamma }_0{e}^{\pi \tan \phi }{{\displaystyle \cot }}^2\alpha +\frac{b^2}{2}c\cot \alpha e^{\pi \tan \phi }+\frac{b^2}{6}\left(H_{90}+\text{Δ}H\right){\gamma }_1{e}^{\pi \tan \phi }{{\displaystyle \cot }}^2\alpha \\ -\frac{b^3}{24}{e}^{\frac{3\pi }{2}\tan \phi }{\gamma }_0{{\displaystyle \cot }}^3\alpha \tan \beta +\frac{b^2\cdot c\cdot \cot \phi \cdot \left(e^{\pi \tan \phi }-1\right)}{8{\sin }^2\alpha }\end{array}(30)$

$\text{Δ}M=\text{Δ}{M}_{AS}-\text{Δ}{M}_S(31)$

3.3 Analysis of the Base State of Waste Dump

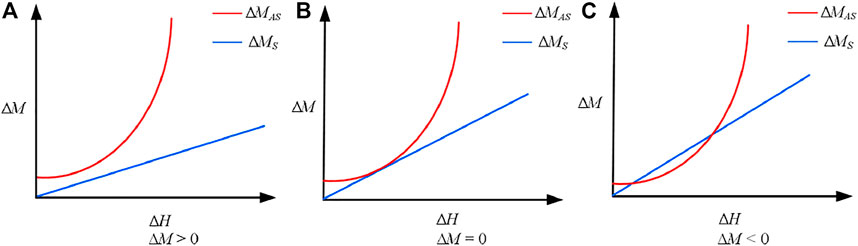
According to Eqs. 11–30, based on the elastic–plastic limit equilibrium analysis, the relation between the sliding moment increment (∆M_S) and the pile height increment (∆H) presents a proportional function, and the anti-sliding moment increment (∆M_AS) shows proportional or positively correlated cubic function relation with the pile height increment (∆H). By discussing Eq. 31 and from Figure 5, it can be found that when ∆M > 0, the anti-sliding moment of the ultimate bearing capacity of the dump foundation is bigger than the sliding moment, shear failure of the foundation will not occur, and the bearing capacity of the foundation meets the requirements. When ∆M = 0, the anti-sliding moment of the ultimate bearing capacity of the dump foundation is equal to the sliding moment and the foundation is in the limit equilibrium state. As ∆M < 0, the anti-sliding moment of the ultimate bearing capacity of the dump foundation is smaller than the sliding force and overall shear failure of the dump foundation takes place.

FIGURE 5

FIGURE 5. Relationship curves of ΔM and ΔH. (A) ΔM > 0, (B) ΔM = 0, (C) ΔM < 0.

3.4 Determination of Allowable Pile Height Based on Ultimate Bearing Capacity of Foundation

As specified in the foundation engineering specification (Zheng, 2019; Chen H H et al., 2021), when the foundation width b > 6 m, take b = 6 m. When the foundation width b < 3 m, take b = 3 m. Since the length and width of the dump are both thousands of kilometers, the influencing width of the initial uniform vertical load is deemed as 6 m in this study when the improved Prandtl method is utilized to calculate the bearing capacity of the foundation. Based on the revised Prandtl algorithm, the effect of the gravity load of the triangular slope on the foundation bearing capacity dominantly depends on the slope angle. When the discharging angle is changed, the corresponding ultimate bearing capacity is certainly different. Therefore, calculating the maximum load per unit area of the foundation body is transformed into solving the ultimate pile height corresponding to a certain slope angle, and the latter is more beneficial to the calculation of the foundation bearing capacity.

The improved Prandtl formula is used to calculate the ultimate bearing capacity of the dump foundation. The influence depth of the foundation bearing capacity is considered as the thickness of the soft foundation (D), and the foundation width (b) in the limit equilibrium state can be obtained (Poulsen et al., 2014; Ismail Ibrahim et al., 2016):

$b=\frac{2D\sin \alpha }{e^{\theta \tan \phi }\cos \left(\theta -\alpha \right)}(32)$

According to Eqs. 11–31, it can be seen that different foundation widths under non-uniform loading condition correspond to slope angles of the dump in the limit equilibrium state. By judging the relationship between the horizontal length of the gravity load of the triangular slope and the sliding surface length of the foundation, the pile height increment ∆H is obtained based on the moment equilibrium condition.

$\text{Δ}H=\overline{AI}\cdot \tan \beta -H_{90}(33)$

$H_{90}=\frac{P_u}{{\gamma }_0}(34)$

$H=H_{90}+\text{Δ}H(35)$

For the dump with affirmable lithology, the foundation thickness is a constant and the corresponding foundation width is confirmed. When the slope angle (β) is different, the corresponding ultimate pile height can be calculated, and then the allowable height of the dump can be determined. When the discharging angle is smaller than β, the pile height can be infinitely high in theory.

3.5 Influence of Different Foundation Lithology and Thickness on Foundation Bearing Capacity

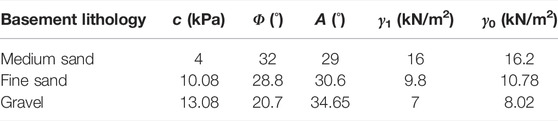
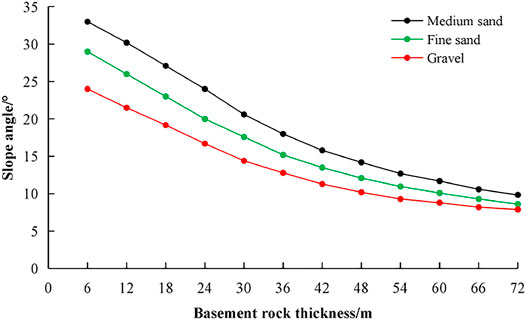
Compared with the dump size, the foundation width (b) is a small constant (6 m). According to Eq. 32, the value of b can be determined according to the thickness of the foundation strata (D), and the corresponding slope angle (β) and the ultimate pile height can be obtained (Li et al., 2017b; Zheng et al., 2020; Ma et al., 2021). Physical and mechanical properties of the foundation strata are given in Table 1 (Jiang et al., 2020; Wang L J et al., 2021). By substituting these parameters into Eqs. 11–34, the relationship between D and β can be achieved as presented in Figure 6.

TABLE 1

TABLE 1. Physical and mechanical properties of base strata.

FIGURE 6

FIGURE 6. Relationship between base strata thickness and dump slope angle.

It can be seen from Figure 6 that the slope angle and the ultimate pile height are different under different foundation lithology. The ultimate pile height is calculated according to the revised Prandtl formula. When the foundation thickness is constant, better foundation lithology allows smaller dump slop angle. Meanwhile, the corresponding ultimate pile height is larger. As the foundation lithology is constant, the slope angle decreases with the increasing thickness of soft foundation strata. In other words, better rock lithology and smaller thickness of foundation are more favorable to the ultimate pile height.

4 Engineering Case Study and Discussion

4.1 Engineering Case Study

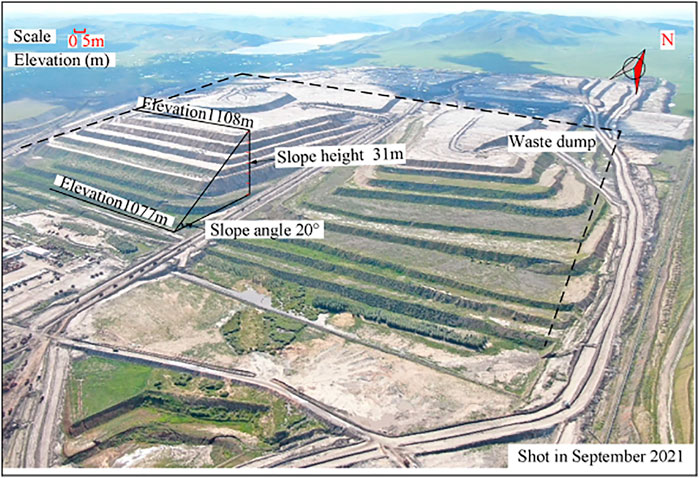
The bedrocks of an open-pit dump are mainly quaternary medium sand with loose structure, strong compressibility, and poor mechanical properties. Shear failure is easy to occur under the loading of waste materials, resulting in instability of the dump and large landslides due to improper treatment. Therefore, the dump stability cannot be ignored. The elevation of the dump is about 1,077 m, and the average thickness of the bedrocks is about 20 m in Figure 7.

FIGURE 7

FIGURE 7. Schematic diagram of external waste dump.

According to the stress characteristics and load distribution of the dump, the ultimate load, the ultimate height of the vertical slope, and the ultimate pile height are calculated by employing the revised Prandtl formula. The ultimate vertical load and the ultimate height of the vertical slope are 505.44 kPa and 31.2 m, respectively. Figure 8 presents the relation curves between ∆M and ∆H at different slope angles. It is noted that when the slope angle is 33°, ∆H is 2.06 m and the ultimate pile height is 33.26 m. When the slope angle is 27.1°, ∆H is 5 m and the ultimate pile height is 36.2 m. If the slope angle is less than 27.1°, the two curves have no intersection and ∆H has no solution. This implies that the anti-sliding moment of the dump is greater than the sliding moment, and the pile height can be infinitely high.

FIGURE 8

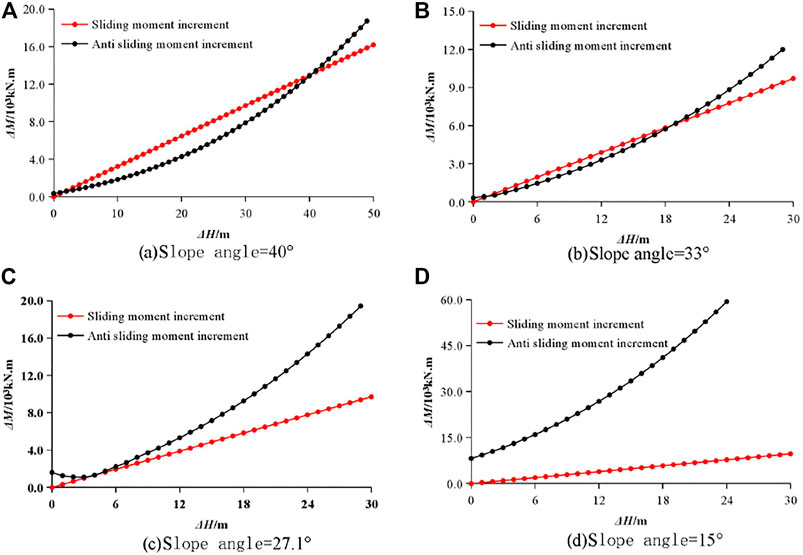
FIGURE 8. The maximum pile height of the dump at different slope angles. (A) Slope angle = 40°, (B) slope angle = 33°, (C) slope angle = 27.1°, (D) slope angle = 15°.

The slope angle, the elevation, and the slope height of an open-pit dump are 20°, 1,108 m, and 31 m, respectively, in Figure 8. The slope and the foundation are both in a stable state. By using the improved Prandtl formula, it is obtained that when the dump slope angle is less than 27.1°, the pile height can be infinitely high under the premise of only considering the foundation stability, which is consistent with the engineering practice. This verifies the rationality and reliability of the improved Prandtl formula proposed in this paper.

4.2 Discussion

The stability of waste dumps is a long-term research topic of slope engineering. Therefore, considering the bearing capacity of the waste dump foundation, the angle and limit of the height of the waste dump slope are calculated, which provides a basis for the stability analysis of the waste dump foundation (Cho et al., 2014; Chen H et al., 2021). The traditional analysis methods mainly focus on the stability evaluation of waste dump (Huang F M et al., 2021), and less consideration is given to the bearing capacity of the waste dump base. This study provides an excellent supplement to the slope stability of the open-pit waste dump.

This study focuses on the analysis of the actual load distribution and stress characteristics and puts forward an improved Prandtl foundation bearing capacity calculation method. The calculation of the foundation bearing capacity of the waste dump is transformed into the relationship function problem of solving the limit dumping height corresponding to a specific slope angle. The angle of waste dump slope, base lithology, and base rock thickness are three key factors affecting the base stability of waste dump.

In the stability analysis of the waste dump, the mechanical state of the waste dump and the physical and mechanical parameters of the base rock layer of the waste dump should be considered (Kainthola et al., 2015; Zástěrová et al., 2015). When the basement’s lithology and the rock stratum’s thickness are different, the dumping angle and the limit dumping height will change under the gravity stacking of the upper dumping materials. This paper considers the influence of the basement conditions on the stability of the waste dump. The better the lithology of the basement, the greater the dumping slope angle, and the dumping slope angle of the waste dump decreases with the increase of the thickness of the weak basement rock stratum. The lithology of the vulnerable basement rock stratum is better. The consistency is smaller, which is more favorable to the limited height of the waste dump.

In this study, the waste dump of an open-pit mine is analyzed. On the premise of considering the base lithology and rock thickness, the base stability of the waste dump is guaranteed, and the optimal waste angle and height of the waste dump are calculated. The bearing capacity of the weak foundation of the waste dump will change significantly under the action of pressure, water, and time for a long time, which is very important to the stability of the waste dump and needs further research in the future (Li X S et al., 2021). This study applies to the calculation of bearing capacity of the weak foundation of the waste dump, provides technical support for the stability evaluation of waste dump, has good application value, and will achieve good engineering results in the application of open-pit waste dump.

5 Conclusion

In this study, a calculation method of bearing capacity of waste dump base based on the improved Prandtl formula is proposed. The ultimate bearing capacity of the base is defined as the ultimate dumping height corresponding to a specific slope angle, and the influence laws of different base lithology and base thickness on the maximum bearing capacity of the base of the waste dump are analyzed. The rationality and reliability of the calculation method of foundation bearing capacity of waste dump proposed in this paper are verified through an engineering example.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

JJ: Conceptualization, Methodology, Software, Investigation, Formal Analysis, and Writing—Original Draft; HY: Data Curation and Writing—Original Draft and Writing—Review and Editing. LC: Visualization and Investigation; DW: Conceptualization, Funding Acquisition, Resources, Supervision; LW: Software and Validation. ZJ: Visualization and Writing—Review and Editing. YL:Resources and Supervision.

Funding

This project was supported by the National Natural Science Foundation of China under Project No. 51874160, LNTU20TD-01, and the “Millions of Talents Project” of Liaoning Province China.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abhishek, S. V., Rajyalakshmi, K., and Madhav, M. R. (2015). Bearing Capacity of Strip Footing on Reinforced Foundation Bed over Soft Ground with Granular Trench. Indian Geotech J. 45 (3), 304–317. doi:10.1007/s40098-014-0138-y

CrossRef Full Text | Google Scholar

Amin, K., and Kumar, J. (2018). Bearing Capacity of Foundations on Rock Mass Using the Method of Characteristics. Int. J. Numer. Anal. Methods Geomech 42, 542–557. doi:10.1002/nag.2754

CrossRef Full Text | Google Scholar

Bar, N., Kostadinovski, M., Tucker, M., Byng, G., Rachmatullah, R., Maldonado, A., et al. (2020). Rapid and Robust Slope Failure Appraisal Using Aerial Photogrammetry and 3D Slope Stability Models. Int. J. Mining Sci. Technol. 30 (5), 651–658. doi:10.1016/j.ijmst.2020.05.013

CrossRef Full Text | Google Scholar

Behera, P. K., Sarkar, K., Singh, A. K., Verma, A. K., and Singh, T. N. (2016). Dump Slope Stability Analysis - A Case Study. J. Geol. Soc. India 88, 725–735. doi:10.1007/s12594-016-0540-4

CrossRef Full Text | Google Scholar

Cao, B., Wang, S., Song, D., Du, H., and Guo, W. (2021). Investigation on the Deformation Law of Inner Waste Dump Slope in an Open-Pit Coal Mine: A Case Study in Southeast Inner Mongolia of China. Adv. Civil Eng. 2021, 18. doi:10.1155/2021/9953554

CrossRef Full Text | Google Scholar

Castelli, F., and Lentini, V. (2012). Evaluation of the Bearing Capacity of Footings on Slopes. Int. J. Phys. Model. Geotechnics 12 (3), 112–118. doi:10.1680/ijpmg.11.00015

CrossRef Full Text | Google Scholar

Chakraborty, D., and Kumar, J. (2013). Bearing Capacity of Foundations on Slopes. Geomechanics and Geoengineering 8 (4), 274–285. doi:10.1080/17486025.2013.770172

CrossRef Full Text | Google Scholar

Chen, H. H., Li, L., Li, J. P., and Sun, D. (2021). A Generic Analytical Elastic Solution for Excavation Responses of an Arbitrarily-Shaped Deep Opening under Biaxial In-Situ Stresses. Int. J. Geomechanics. doi:10.1061/(ASCE)GM.1943-5622.0002335

CrossRef Full Text | Google Scholar

Chen, H., Li, L., Li, J., and Sun, D. a. (2021). A Rigorous Elastoplastic Load-Transfer Model for Axially Loaded Pile Installed in Saturated Modified Cam-clay Soils. Acta Geotech.doi:10.1007/s11440-021-01248-z

CrossRef Full Text | Google Scholar

Cho, Y.-C., and Song, Y.-S. (2014). Deformation Measurements and a Stability Analysis of the Slope at a Coal Mine Waste Dump. Ecol. Eng. 68 (7), 189–199. doi:10.1016/j.ecoleng.2014.03.005

CrossRef Full Text | Google Scholar

Deng, B., and Yang, M. H. (2019). Analysis of Passive Earth Pressure for Unsaturated Retaining Structures. Int. J. Geomech. 19 (12), 1518. doi:10.1061/(asce)gm.1943-5622.0001518

CrossRef Full Text | Google Scholar

Divya, S., and Mahendra, S. (2020). Bearing Capacity of Foundations on Rock Slopes Intersected by Non-persistent Discontinuity. Int. J. Mining Sci. Technol. 30 (5), 669–674. doi:10.1016/j.ijmst.2020.03.018

CrossRef Full Text | Google Scholar

Etezad, A. M., Hanna, M., Asce, F., and Ayadat, T. (2015). Bearing Capacity of a Group of Stone Columns in Soft Soil. Int. J. Geomech 15 (2), 393. doi:10.1061/(asce)gm.1943-5622.0000393

CrossRef Full Text | Google Scholar

Gao, M., Xie, J., Gao, Y., Wang, W., Li, C., Yang, B., et al. (2021). Mechanical Behavior of Coal under Different Mining Rates: A Case Study from Laboratory Experiments to Field Testing. Int. J. Mining Sci. Technol. 31 (5), 825–841. doi:10.1016/j.ijmst.2021.06.007

CrossRef Full Text | Google Scholar

Georgiadis, M., and Michalopoulos, A. P. (1985). Bearing Capacity of Gravity Bases on Layered Soil [J]. J. Geotechnical Eng. 11 (6).

Google Scholar

Gong, C., Lei, S., Bian, Z., Tian, Y., Zhang, Z., Guo, H., et al. (2021). Using Time Series InSAR to Assess the Deformation Activity of Open-Pit Mine Dump Site in Severe Cold areaUsing Time Series InSAR to Assess the Deformation Activity of Open-Pit Dump Site in Severe Cold Area. J. Soils Sediments 21, 3717–3732. doi:10.1007/s11368-021-03040-8

CrossRef Full Text | Google Scholar

Griffiths, D. V., and Fenton, G. A. (2001). Bearing Capacity of Spatially Random Soil: the Undrained clay Prandtl Problem Revisited. Géotechnique 51 (4), 351–359. doi:10.1680/geot.2001.51.4.351

CrossRef Full Text | Google Scholar

Han, L., Shu, J., Cai, Q., Jing, H., and Tian, H. (2016). Mechanical Characteristics of Dip Basement Effects on Dump Stability in the Shengli Open Pit Mine in Inner Mongolia, China. Arab J. Geosci. 9, 750. doi:10.1007/s12517-016-2774-2

CrossRef Full Text | Google Scholar

He, Y. G., Yan, R. G., and Zeng, Z. Q. (1999). Bearing Capacity and Ultimate Pile Height of Dump Foundation [J]. Chin. J. Nonferrous Met. 9 (3), 672–676.

Google Scholar

Huang, F., Cao, Z., Jiang, S.-H., Zhou, C., Huang, J., Guo, Z., et al. (2020). Landslide Susceptibility Prediction Based on a Semi-supervised Multiple-Layer Perceptron Model. Landslides. 17, 2919–2930. doi:10.1007/s10346-020-01473-9

CrossRef Full Text | Google Scholar

Huang, F., Huang, J., Jiang, S., and Zhou, C. (2017). Landslide Displacement Prediction Based on Multivariate Chaotic Model and Extreme Learning machineLandslide Displacement Prediction Based on Multivariable Chaotic Model and Extreme Learning Machine [J]. Eng. Geology. 218, 173–186. doi:10.1016/j.enggeo.2017.01.016

CrossRef Full Text | Google Scholar

Huang, F. M., Yan, J., Fan, X. M., Yao, C., Huang, J. S., Chen, W., et al. (2021). Uncertainty Law of Landslide Susceptibility Prediction Modelling: Effects of Different Landslide Boundaries and Spatial Shape Expressions [J]. Geosciences Front. 12 (2). doi:10.1016/j.gsf.2021.101317

CrossRef Full Text | Google Scholar

Huang, F., Tao, S., Chang, Z., Huang, J., Fan, X., Jiang, S.-H., et al. (2021). Efficient and Automatic Extraction of Slope Units Based on Multi-Scale Segmentation Method for Landslide Assessments. Landslides 18, 3715–3731. doi:10.1007/s10346-021-01756-9

CrossRef Full Text | Google Scholar

Huang, J. (1991). Causes of Landslide and Control Measures of Jianshan Dump. [J]. Sichuan Metall. 1991 (04), 1–4.

Google Scholar

Ismail Ibrahim, K. M. H. (2016). Bearing Capacity of Circular Footing Resting on Granular Soil Overlying Soft clay. HBRC J. 12 (1), 71–77. doi:10.1016/j.hbrcj.2014.07.004

CrossRef Full Text | Google Scholar

Jiang, J. Y., Wang, D., and Han, X. P. (2019). Analysis of Progressive Rupture Process Insurrounding Rock for a Deep Homogeneous and Circular Opening. Energy Sourc. A: Recovery Utilization Environ. Effects 1556-7036 (Print), 1556–7230. doi:10.1080/15567036.2019.1645766

CrossRef Full Text | Google Scholar

Jiang, J. Y., Wang, D., Han, X. P., and Di, S. (2020). Relationship between Brittleness Index and Crack Initiation Stress Ratio for Different Rock Types. Adv. Civil Eng. 2020 (12). doi:10.1155/2020/8091895

CrossRef Full Text | Google Scholar

Jiang, J. Y., Yang, H. W., Wang, D., Wang, L. G., and Han, X. P. (2021). Experimental Study on Instability Evolution Mechanism of Supporting Coal Pillar in End wall Mining [J]. Chin. J. Saf. Sci. 31 (10), 89–96.

Google Scholar

Jorge, P. O. (2017). Methodology for a Dump Design Optimization in Large-Scale Open Pit Mines. Cogent Eng. 4 (1), 1387955. doi:10.1080/23311916.2017.1387955

CrossRef Full Text | Google Scholar

Kainthola, A., Singh, P. K., and Singh, T. N. (2015). Stability Investigation of Road Cut Slope in Basaltic Rockmass, Mahabaleshwar, India. Geosci. Front. 6, 837–845. doi:10.1016/j.gsf.2014.03.002

CrossRef Full Text | Google Scholar

Karrech, A., Dong, X., Elchalakani, M., Basarir, H., Shahin, M. A., and Regenauer-Lieb, K. (2021). Limit Analysis for the Seismic Stability of Three-Dimensional Rock Slopes Using the Generalized Hoek-Brown Criterion. Int. J. Mining Sci. Technol.doi:10.1016/j.ijmst.2021.10.005

CrossRef Full Text | Google Scholar

Kyle, E. O., Margaret, M. D., Scott, L. H., and Gang, C. (2013). Site Investigation and Slope Stability Analysis of the Chitina Dump Slide (CDS), Alaska. Environ. Eng. Geosci. 19 (1), 27–40. doi:10.2113/gseegeosci.19.1.27

CrossRef Full Text | Google Scholar

Li, L., Chen, H., Li, J., and Sun, D. a. (2021). An Elastoplastic Solution to Undrained Expansion of a Cylindrical Cavity in SANICLAY under Plane Stress Condition. Comput. Geotechnics 132, 103990. doi:10.1016/j.compgeo.2020.103990

CrossRef Full Text | Google Scholar

Li, L., Li, J., Sun, D. A., and Gong, W. (2017b). Semi-analytical Approach for Time-dependent Load-Settlement Response of a Jacked Pile in clay Strata. Can. Geotech. J. 54 (12), 1682–1692. doi:10.1139/cgj-2016-0561

CrossRef Full Text | Google Scholar

Li, L., Li, J., Sun, D. a., and Zhang, L. (2017a). Time-dependent Bearing Capacity of a Jacked Pile: An Analytical Approach Based on Effective Stress Method. Ocean Eng. 143 (1), 177–185. doi:10.1016/j.oceaneng.2017.08.010

CrossRef Full Text | Google Scholar

Li, X. S., Yang, S., Wang, Y. M., Nie, W., and Liu, Z. F. (2021). Macro-Micro Response Characteristics of Surrounding Rock andOverlying Strata towards the Transition from Open-Pit to Underground Mining. Geoflfluids 2021 (18). doi:10.1155/2021/5582218

CrossRef Full Text | Google Scholar

Luo, Z. Z. (1986). Opencast Mining (I)[M]. Xu zhou: China Institute of Mining Press.

Google Scholar

Ma, J., Li, X. L., Wang, J. G., Tao, Z. H., Zuo, T., Li, Q., et al. (2021). Experimental Study on Vibration Reduction Technology of Hole-By-Hole Presplitting Blasting. Geofluids 20. doi:10.1155/2021/5403969

CrossRef Full Text | Google Scholar

Moayedi, H., and Hayati, S. (2018). Modelling and Optimization of Ultimate Bearing Capacity of Strip Footing Near a Slope by Soft Computing Methods. Appl. Soft Comput. 66, 208–219. doi:10.1016/j.asoc.2018.02.027

CrossRef Full Text | Google Scholar

Pakdel, P., Jamshidi Chenari, R., and Veiskarami, M. (2021). Seismic Bearing Capacity of Shallow Foundations Rested on Anisotropic Deposits. Int. J. Geotechnical Eng. 15 (2), 181–192. doi:10.1080/19386362.2019.1655983

CrossRef Full Text | Google Scholar

Park, J.-S., and Park, D. (2017). Vertical Bearing Capacity of Bucket Foundation in Sand Overlying clay. Ocean Eng. 134, 62–76. doi:10.1016/j.oceaneng.2017.02.015

CrossRef Full Text | Google Scholar

Poulsen, B., Khanal, M., Rao, A. M., Adhikary, D., and Balusu, R. (2014). Mine Overburden Dump Failure: A Case Study. Geotech Geol. Eng. 32, 297–309. doi:10.1007/s10706-013-9714-7

CrossRef Full Text | Google Scholar

Roy, S. S., and Deb, K. (2017). Effects of Aspect Ratio of Footings on Bearing Capacity for Geogrid-Reinforced Sand over Soft Soil. Geosynthetics Int. 2017, 1072–6349. doi:10.1680/jgein.17.00008

CrossRef Full Text | Google Scholar

Steiakakis, E., Kavouridis, K., and Monopolis, D. (2009). Large Scale Failure of the External Waste Dump at the "South Field" lignite Mine, Northern Greece. Eng. Geology. 104, 269–279. doi:10.1016/j.enggeo.2008.11.008

CrossRef Full Text | Google Scholar

Terzaghi, K. (1943). Theoretical Soil mechanics[M]. New York: John Wiley and Son, 5–96.

Google Scholar

Wang, C. Y., Wang, B. J., and Jiang, S. Z. (2012). Theory of the Ultimate Bearing Capacity Calculation. Esr 1, 1. doi:10.5539/esr.v1n1p109

CrossRef Full Text | Google Scholar

Wang, D., Jiang, J. Y., Han, X. P., Nan, C. Q., and He, X. G. T. (2017). Research on Stability of Supporting Coal Pillar in Endwall Mining Slope of lignite Open-Pit Mine [J]. China Saf. Sci. J. 27 (12), 62–67.

Google Scholar

Wang, J., Zuo, T., Li, X., Tao, Z., and Ma, J. (2021). Study on the Fractal Characteristics of the Pomegranate Biotite Schist under Impact Loading. Geofluids 2021, 1–8. doi:10.1155/2021/1570160

CrossRef Full Text | Google Scholar

Wang, L. J., Zhao, Q. H., and Wu, J. J. (2021). Influence of Different Geological Geotechnical Structureson the Bearing Properties of Underground Continuous wall Base. Arabian J. Geosciences 14, 633. doi:10.1007/s12517-021-06919-5

CrossRef Full Text | Google Scholar

Wang, W. L., Zhao, D. J., and Wang, L. (2010). Influence of Lateral Fill Load on Foundation Bearing Capacity of Culvert[J]. China J. Highw. Transport 23 (06), 1–6. doi:10.19721/j.cnki.1001-7372.2010.06.001

CrossRef Full Text | Google Scholar

Wang, Y.-k., Sun, S.-w., and Liu, L. (2019). Mechanism, Stability and Remediation of a Large Scale External Waste Dump in China. Geotech Geol. Eng. 37 (6), 5147–5166. doi:10.1007/s10706-019-00969-z

CrossRef Full Text | Google Scholar

Wang, Y., Sun, S., Pang, B., and Liu, L. (2020). Base Friction Test on Unloading Deformation Mechanism of Soft Foundation Waste Dump under Gravity. Measurement 163, 108054. doi:10.1016/j.measurement.2020.108054

CrossRef Full Text | Google Scholar

Xu, S.-Y., Lawal, A. I., Shamsabadi, A., and Taciroglu, E. (2019). Estimation of Static Earth Pressures for a Sloping Cohesive Backfill Using Extended Rankine Theory with a Composite Log-Spiral Failure Surface. Acta Geotech. 14, 579–594. doi:10.1007/s11440-018-0673-2

CrossRef Full Text | Google Scholar

Yang, S. C., Leshchinsky, B., Cui, K., and Zhang, F. (2019). Unified Approach toward Evaluating Bearing Capacity of Shallow Foundations Near Slopes. J. Geotech. Geoenviron. Eng. 145 (12). doi:10.1061/(asce)gt.1943-5606.0002178

CrossRef Full Text | Google Scholar

Zástěrová, P., Marschalko, M., Niemiec, D., Durďák, J., Bulko, R., and Vlček, J. (2015). Analysis of Possibilities of Reclamation Waste Dumps after Coal Mining. Proced. Earth Planet. Sci. 15, 656–662. doi:10.1016/j.proeps.2015.08.077

CrossRef Full Text | Google Scholar

Zhai, W. L., Zhou, H. M., and Chen, B. (2015). Analysis of the Base Bearing Capacity and Ultimate Pile Height of a High-Bench Dump[J]. Non-ferrous Met. (Mining Section). 67 (06), 89–92.

Google Scholar

Zhang, Y., Bienen, B., Cassidy, M. J., and Gourvenec, S. (2011). The Undrained Bearing Capacity of a Spudcan Foundation under Combined Loading in Soft clay. Mar. Structures. 24, 459–477. doi:10.1016/j.marstruc.2011.06.002

CrossRef Full Text | Google Scholar

Zhang, Y. G., Tang, J., Cheng, Y., Huang, L., Guo, F., Yin, X., et al. (2022). Prediction of Landslide Displacement with Dynamic Features Using Intelligent Approaches. Int. J. Mining Sci. Technol. 12 (1), 368–382.

CrossRef Full Text | Google Scholar

Zhang, Y., Qiu, J. B., Zhang, Y. G., and Xie, Y. L. (2021). The Adoption of a Support Vector Machine Optimized by GWO to the Prediction of Soil Liquefaction. Environ. Earth Sci. 80 (9). doi:10.1007/s12665-021-09648-w

CrossRef Full Text | Google Scholar

Zhang, Z., Deng, M., Bai, J., Yan, S., and Yu, X. (2021). Stability Control of Gob-Side Entry Retained under the Gob with Close Distance Coal Seams. Int. J. Mining Sci. Technol. 31 (2), 321–332. doi:10.1016/j.ijmst.2020.11.002

CrossRef Full Text | Google Scholar

Zheng, L., Li, L., and Li, J. (2020). Development of Three-Dimensional Failure Mechanisms and Genetic Algorithm for Limit Analysis of Two-Layer Slopes. Nat. Hazards 103, 3181–3212. doi:10.1007/s11069-020-04126-1

CrossRef Full Text | Google Scholar

Zheng, Q. (2019). Discussion on Parameter Value and Application of Foundation Bearing Capacity Calculation Formula in Code for Design of Building Foundation. IOP Conf. Ser. Earth Environ. Sci. 358, 042032. doi:10.1088/1755-1315/358/4/042032

CrossRef Full Text | Google Scholar

Zhigang, T., Chun, Z., Yong, W., Jiamin, W., Manchao, H., and Bo, Z. (2018). Research on Stability of an Open-Pit Mine Dump with Fiber Optic Monitoring. Geofluids 2018, 1–20. doi:10.1155/2018/9631706

CrossRef Full Text | Google Scholar

Zhong, S. H., and Zhang, J. (2017). Analysis of the Ultimate Bearing Capacity of the Weak Basement of the Open-Pit Dump[J]. Coal Eng. 49 (12), 145–148.

Google Scholar

Zhou, R. J. (2002). Analysis of Base Bearing Capacity of Soft Base High Dumping Site[J]. Rock Soil Eng. Technol. 2, 79–109.

Google Scholar