Sandstone Slope Stability Analysis Under Wetting-Drying Cycles Based on Generalized Hoek-Brown Failure Criterion

The deterioration of rock strength due to cyclic fluctuations in the groundwater level in drawdown regions influences bank slope stability. Based on wetting–drying cycling and uniaxial compression tests of sandstone specimens, the intact rock strength deterioration characteristics were analyzed. Considering different types of rock mass discontinuities, the rock mass strength deterioration features were shown. The results of rock mass strength deterioration characteristics were then applied in sandstone slope stability analysis. Using the finite element method, the safety factors of the slope under different wetting–drying cycles were computed based on the generalized Hoek–Brown failure criterion. Meanwhile, statistical distribution features of strength parameters were considered, and safety factor distribution of studied slopes was obtained with Monte Carlo simulation. The results show that rock mass deformation modulus decreased during wetting–drying cycling. The mean safety factors of the slope with any type of discontinuities were reduced by wetting–drying cycling in probabilistic analyses. Wetting–drying cycling plays an important role in damaging slope stability at initial stages since the degree of rock mass strength deterioration is remarkable during initial wetting–drying cycles. However, the rock mass strength and safety factor of the slope are reduced gently after 10 wetting–drying cycles. This research presents the phases of the effect of wetting–drying cycles on sandstone slope stability in drawdown regions.

Introduction

Bank slopes in drawdown regions are prone to be damaged by wetting–drying effects due to cyclic fluctuations in the groundwater level. Wetting–drying cycling would soften the geologic materials on the banks, decrease their shear strength, and in turn affect the stability of bank slopes (Sun et al., 2015; Liao et al., 2020).

Most studies focused on the multiple-layer landslides, whose failure mostly depends on existing sliding zone or soil-bedrock interlayer (Tang et al., 2016; Zhang et al., 2020; Li et al., 2021). Such landslides usually have relatively obvious sliding surfaces, and the slope failure occurred due to structurally controlled surfaces. However, few studies particularly assessed the stability of jointed rock slopes only defined by intersecting discontinuity systems, whose type of slope failure does not depend on structurally controlled surfaces. This sort of slope can be considered homogeneous and isotropic when discontinuity sets are sufficiently closely spaced relative to the size of the structure (Hoek and Brown, 2019). The steep homogeneous-like sandstone slopes, which spread widely in Three Gorges Reservoir bank, are the focus of this research.

Regarding quantitative approaches, the deterministic analysis is a common method adopted for assessing slope stability. However, due to the randomness and uncertainty of the parameters affecting slope stability, it is more reasonable to use probabilistic analysis (Miao et al., 2016; Guo et al., 2020; Kang et al., 2021). Therefore, the dispersion of sandstone strength properties will be considered in current quantitative assessment of slope stability.

In the present study, a typical rock slope composed of sandstone on the bank of Three Gorges Reservoir was selected. Based on the strength deterioration law of intact sandstone, the strength characteristics of rock masses due to wetting–drying cycles were explored. Meanwhile, statistical distribution features of strength parameters were considered with Monte Carlo simulation. Accordingly, with the help of the RS2 program (Rocscience, 2021), finite element analysis (FEM) based on the generalized Hoek–Brown failure criterion was conducted to investigate the changing rule of safety factors of sandstone banks.

Methods

Cyclic Wetting–Drying Tests of Intact Sandstone

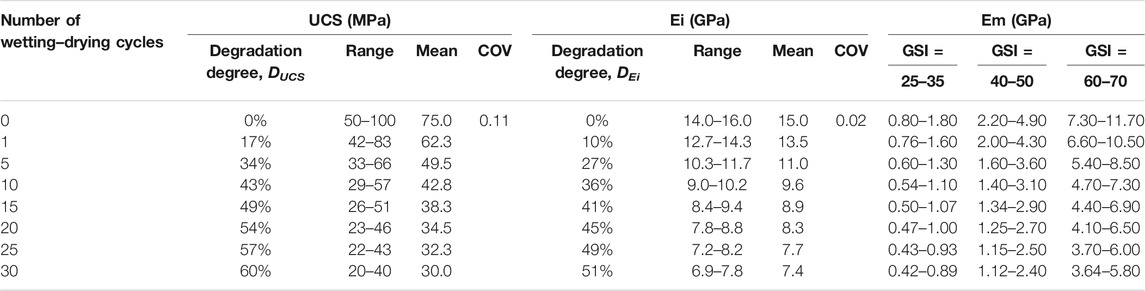
The sandstone specimens in the Chongqing Reservoir area were selected for strength tests under wetting–drying cycles (Huang et al., 2018). A uniaxial compression test in the laboratory was carried out to observe the effects of cyclic wetting–drying on uniaxial compressive strength (UCS) and deformation modulus (E_i) of intact rocks. Before the test, sandstone specimens were subjected to 1–30 wetting and drying cycles. Meanwhile, 3 untreated sandstone specimens were also tested to determine the initial mechanical properties of the specimens without wetting–drying cycles. The material’s damage due to wetting–drying cycling can be defined as a value of “Degradation Degree (DD)”. DD indicates the change of the material strength, which refers to UCS and E_i in this study. Degradation Degree was calculated as

${\mathit{DD}}_{\mathit{UCS}}=\left(1-\mathit{UC}{\mathit{S}}_{\mathit{N}}\text{/}\mathit{UC}{\mathit{S}}_{\mathit{0}}\right)\text{×}100\text{\% }(1)$

$\mathit{D}{\mathit{D}}_{\mathit{Ei}}=\left(1-\mathit{E}{\mathit{i}}_{\mathit{N}}\mathit{/E}{\mathit{i}}_{\mathit{0}}\right)\text{×}100\text{\% }(2)$

where DD_UCS and DD_Ei are the total degradation degree of UCS and E_i, respectively; UCS_N and E_iN are the compressive strength and deformation modulus of specimens after N wetting–drying cycles, and UCS₀ and E_i0 are the uniaxial compressive strength without wetting–drying cycling.

The change of the Degradation Degree represents that sandstone had a different amount of degradation with increasing number (N) of wetting–drying cycles. The relationships between DD_UCS and DD_Ei of intact sandstone and “N + 1” could be fitted by a logarithmic curve as follows (Huang et al., 2018):

${\mathit{DD}}_{\mathit{UCS}}=15\text{.}548\text{ ln}\left(\mathit{N}+1\right)+6\text{.}198(3)$

${\mathit{DD}}_{\mathit{Ei}}=14\text{.}872\text{ ln}\left(\mathit{N}+1\right)+\text{ 0}\text{.}186(4)$

Regarding the limitation of specimen selection location, the rock strength without wetting–drying cycles in the above tests could not be representative enough. To solve that, the more presentative UCS and E_i of sandstone were adopted in following calculation. The strength deterioration relationships obtained above were then applied to compute UCS and E_i with different wetting–drying cycles.

Generalized Hoek–Brown Criterion

The generalized Hoek–Brown criterion reported by Hoek et al. (2002) was developed as a means to estimate rock mass strength. The Hoek–Brown criterion is based on the assumption of isotropic behavior, which is considered reasonable for rock masses composed of blocks of intact rock separated by intersecting discontinuities. It integrates the intact rock properties from laboratory tests and geological characteristics from the field observations. Based on rock mass quality, the intact rock strength is quantitatively downgraded in order to estimate the strength of rock mass. The generalized Hoek–Brown criterion is expressed as

${\sigma }_1={\sigma }_3+{\sigma }_{ci}{\left(m_b\frac{{\sigma }_3}{{\sigma }_{ci}}+s\right)}^a(5)$

where σ₁ and σ₃ are Major and Minor principal stress, respectively; σ_ci is uniaxial compressive strength (UCS) of the intact rock; and s, a, and m_b are Hoek–Brown material constants determined by a constant m_i, geological strength index (GSI), and disturbance factor D:

$m_b=m_{i}exp\left(\frac{GSI-100}{28-14D}\right)(6)$

$s=exp\left(\frac{GSI-100}{9-3D}\right)(7)$

$a=\frac{1}{2}+\frac{1}{6}\left(e^{GSI/15}-e^{20/3}\right)(8)$

Rock mass deformation modulus E_m could be estimated by the following equation (Hoek and Diederichs, 2006):

$E_{\text{m}}=E_{\text{i}}\left(0.02+\frac{1-D/2}{1+{\text{e}}^{(60+15D-\text{GSI})/11)}}\right)(9)$

where E_i is the intact rock deformation modulus (MPa).

Through the field observations, the value of GSI can be obtained via the basic GSI chart (Hoek and Marinos, 2000). The selection of GSI value depends on structure and surface conditions of the discontinuities. Note that assigning a range of values to GSI is more realistic than a precise value.

The geotechnical software RS2 (Rocscience, 2021) for slope stability analysis allows the nonlinear generalized Hoek–Brown criterion to be used directly, rather than equivalent linear Mohr-Coulomb criterion to be obtained firstly. Therefore, the RS2 program was used to assess the slope stability in this research.

Finite Element Modeling With Strength Reduction Analysis

A typical 100-m-high rock slope composed of sandstone on the bank of Three Gorges Reservoir was selected, shown in Figure 1A. The numerical model of slope stability was set up using the FEM software RS2 (Rocscience, 2021). In this model, the total height of the slope is 100 m, and slope angle is 60° (see Figure 1B). Considering that the reservoir water level rises and falls between 145 and 175 m (Huang et al., 2020), the middle part of sandstone slope with a height of 30 m is regarded as a cyclic wetting–drying layer, the mechanical properties of which were the focus of this research, presented in Table 1. The material properties of the upper layer and the lower layer are regarded natural and saturated, respectively. The input parameters for slope stability analysis included unit weight (γ), Poisson’s ratio (μ), E_i, UCS, GSI, m_i, and D. The values of the following parameters were set to be constant: γ = 24 kN/m³; μ = 0.3; m_i = 17; and D = 0. The other parameters were set to be variables, which will be presented in the following content.

FIGURE 1

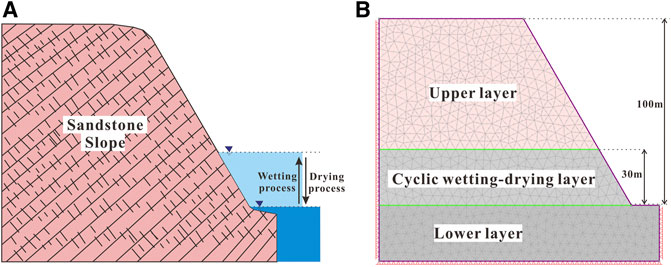
FIGURE 1. (A) A typical 100-m-high slope consisting of sandstone with slope angle of 60° on the bank of Three Gorges Reservoir. (B) The numerical slope model.

TABLE 1

TABLE 1. Values of mechanical parameters of the intact rock and the rock masses.

Only the effect of gravity was considered in this slope model. The model was meshed with six-noded triangles with 1,369 elements. In terms of boundary conditions, the lateral sides and the bottom were totally restrained, while free boundary condition was applied to ground surface.

Note that the study slope was without dominant sliding zone or structural surface. The rock mass could be considered homogeneous and isotropic, whose failure pattern is sliding and rotation, according to the generalize Hoek–Brown criterion.

Strength reduction analysis does not require any assumptions about the shape or location of the failure surface. The critical strength reduction factor is regarded as the safety factor of a slope. The strength reduction method will automatically determine the most critical failure mode and the corresponding safety factor.

Monte Carlo Method

Monte Carlo simulation is one of the most popular probabilistic methods developed to incorporate uncertainties in slope stability (Griffiths and Fenton, 2004). In this study, the Monte Carlo method is employed to the probabilistic slope stability analysis. Fundamental to the Monte Carlo method are the randomly generated input parameters that are fed into a deterministic model. This needs to be done using a random number generation function. The random numbers generated from the function are uniformly distributed with values between 0 and 1. The generated random number is then used to get a new parameter value for the sampling function. In this study, the normal distribution function is selected as the sampling function, depending on mean value and coefficient of variation (COV).

As previously mentioned, assigning a range of values to GSI is more realistic than a precise value. The GSI could be seen as an uncertain parameter. Meanwhile, UCS can vary from point to point in one rock slope. UCS can also be assigned to a range of values. Therefore, two uncertain parameters related to the generalized Hoek–Brown failure criterion are modeled as random variables. These are the Geological Strength Index (GSI) and the uniaxial compressive strength of the intact rock (UCS). Besides, deformation modulus (E_i) of intact rocks related to finite element calculation is also selected as random variables. According to different types of rock mass discontinuities, GSI range of sandstone slope was roughly classified into 3 groups: 60–70 for massive slope, 40–50 for thin bedded slope with interlocking blocks, and 25–35 for bedded slope with complex folding. The GSI range selection was referring to some typical rock mass examples for different rock formations in Hoek and Brown (2019). The range of UCS and E_i of natural sandstone without wetting–drying cycling was set up to 50–100 MPa and 14–16 GPa, respectively (Hoek and Brown, 1997). The COV of sandstone material properties (UCS and E_i) before and after wetting–drying cycles is assumed to be constant, as shown in Table 1. The statistics of UCS and E_i subjected to 1, 5, 10, 15, 20, 25, and 30 wetting–drying cycles are presented in Figure 2A and Figure 2B, respectively. In current probabilistic analysis, the safety factor of slope will be recomputed 1,000 times (number of samples = 1,000), using a different set of randomly generated input variables for each analysis.

FIGURE 2

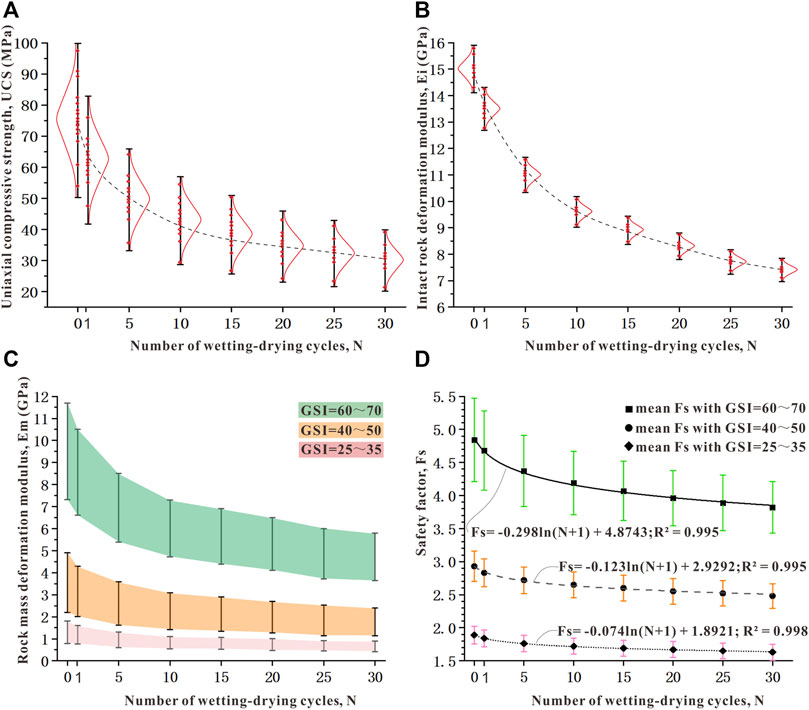
FIGURE 2. (A) Uniaxial compressive strength range and (B) deformation modulus range of intact sandstone exposed to 1, 5, 10, 15, 20, 25, and 30 wetting–drying cycles incorporating normal distribution. (C) Rock mass deformation modulus changing trend at different stages of wetting–drying cycling. (D) Relationships between the number of wetting–drying cycles and the safety factor of the slope.

Results

Rock Mass Deformation Modulus Deterioration

As mentioned above, the deterioration law of intact rock deformation modulus (E_i) has been presented as Eq. 4. Using Eq. 9, the rock mass deformation modulus (E_m) in the sandstone slopes at different stages of wetting–drying cycling was obtained. The range of rock masses E_m considering various GSI groups is shown in Table 1. From Figure 2C, it can be seen that with the value of N increasing, E_m decreased gradually. At the initial wetting and drying cycles, the E_m of sandstone rock mass degenerated rapidly. With the increase in the value of N, the rate of E_m decrease had a tendency to slow down. The main deterioration process occurred before 10 wetting–drying cycles. Taking the slope with GSI of 25–35 as an example, the range of E_m value is 0.8–1.8 GPa without wetting–drying cycling. When the value of N was respectively 1, 5, 10, 15, 20, 25, and 30, the E_m of sandstone was reduced to 0.76–1.60, 0.60–1.30, 0.54–1.10, 0.5–1.07, 0.47–1.00, 0.43–0.93, and 0.42–0.89 GPa. It shows that E_m dropped dramatically as N was 1, 5, and 10, then E_m decreased gently after 10 cycles. It is also clear that E_m was decreasing as GSI was decreasing. E_m with a GSI of 60–70 is approximately 10 times of that with a GSI of 25–35.

Safety Factor of Sandstone Slope

Safety factors (F_s) of the study slope were computed though FEM software RS2 based on the generalized Hoek–Brown criterion. Figure 2D shows the safety factor of sandstone slope after different numbers of wetting–drying cycles. As Monte Carlo simulation was carried out, the results of safety factor show dispersion, which includes maximum, mean, and minimum values. It can be seen from Figure 2D that after 30 wetting–drying cycles, the mean F_s of the slope with a GSI of 60–70 drops from 4.84 to 3.82; the mean F_s with a GSI of 50–70 drops from 2.93 to 2.48; the mean F_s with a GSI of 50–70 drops from 1.89 to 1.63. The changing trend of mean safety factors indicated that sandstone slope stability had undergone different amounts of degradation after wetting–drying cycling.

For sandstone slope with different GSI ranges, the relationship between mean F_s and “N+1” could be fitted by logarithmic curves as follows:

$\text{For GSI}=\text{60}-\text{70:Fs}=-\text{0}\text{.}298\text{ln}\left(\text{N}+1\right)+4{\text{.}8743\text{ ; R}}^2=\text{ 0}\text{.}995(10)$

$\text{For GSI}=\text{40}-\text{50: Fs}=-\text{0}\text{.}123\text{ln}\left(\text{N}+1\right)+2{\text{.}9292\text{ ; R}}^2=\text{ 0}\text{.}995(11)$

$\text{For GSI}=\text{25}-\text{35: Fs}=-\text{0}\text{.}074\text{ln}\left(\text{N}+1\right)+1{\text{.}8921\text{; R}}^2=\text{ 0}\text{.}998(12)$

Taking the slope with a GSI of 25–35 as an example, Figure 3 displays a plot of the shear strain of the slope with the strength reduction method after different numbers of wetting–drying cycling. Once the slope failure happens in FEM, the well-formed shear band would be presented as shown in Figure 3. The maximum shear strain occurs at both the upper layer and the cyclic wetting–drying layer when subjected to 1, 5, and 10 wetting–drying cycles, while it mainly occurs at the cyclic wetting–drying layer when subjected to 15, 20, 25, and 30 wetting–drying cycles. The mean safety factor of the slope without wetting–drying cycling (0 wetting–drying cycle) is 1.89. While, the mean safety factors of the slope subjected to 1, 5, 10, 15, 20, 25, and 30 wetting–drying cycles are 1.84, 1.76, 1.72, 1.69, 1.67, 1.65, and 1.63, respectively. As shown in Figure 3, the slope stability decreases as the number of wetting–drying cycles increases.

FIGURE 3

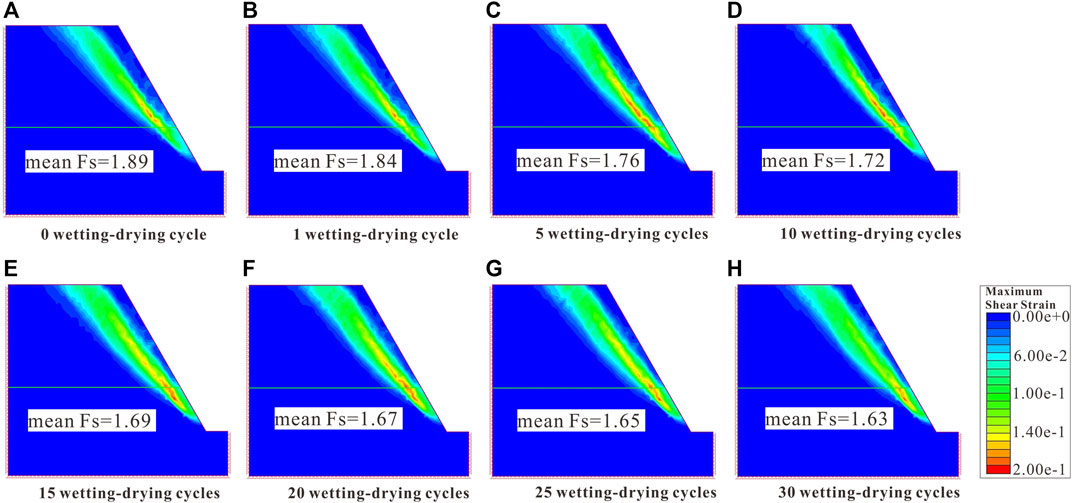
FIGURE 3. Plots of the shear strain of the slope using the strength reduction method with mean Fs: (A) before wetting–drying cycling; (B) after 1 wetting–drying cycle; (C) after 5 wetting–drying cycles; (D) after 10 wetting–drying cycles; (E) after 15 wetting–drying cycles; (F) after 20 wetting–drying cycles; (G) after 25 wetting–drying cycles; (H) after 30 wetting–drying cycles.

Discussion

As mentioned above, considering different types of rock mass discontinuities, the slope composed by sandstone was classified into 3 categories in this study: massive slope of high GSI values, thin bedded slope with interlocking blocks of medium GSI values, and bedded slope with complex folding of low GSI values. From Figure 2D, it is clear that F_s with a certain GSI range decreases as the number of wetting–drying cycles increases, and that F_s was reduced with the decrease in GSI during a certain wetting–drying cycle. In probabilistic analysis, the F_s of the slope with a high GSI varies more widely than that with a low GSI. It indicates that both wetting–drying cycling and rock mass discontinuities affect slope stability. However, the influence of wetting–drying cycling on slope stability deterioration becomes small after 10 wetting–drying cycles, while GSI is the dominant factor of slope stability.

It could be understood that wetting–drying cycling affects the microstructure of sandstone, while GSI affects the macrostructure of the whole rock slope. As known, wetting–drying cycles can dissolve some minerals and weaken the cement among grains in sandstone. However, the remaining minerals are not easy to dissolve after 10 wetting–drying cycles. Meanwhile, the pore structure in rock is hard to expand during subsequent wetting–drying cycling. Therefore, the strength of the sandstone and F_s of the slope with the same GSI is slightly reduced after 10 wetting–drying cycles. When the influence of wetting–drying cycling on slope stability is limited, the GSI turns out to be the dominant factor affecting slope stability.

In this study, the range of natural sandstone mechanical properties is selected to be representative of those referred to in the literature, and applied in strength deterioration relationships (see Eqs 3 and 4) developed by authors, and then the rock mass mechanical properties and safety factor were obtained. However, the mechanical properties of intact sandstone in a specific site could be different from the values selected in this study. The only normal distribution was assumed for GSI and mechanical properties in the probabilistic analysis. Other distribution types like lognormal could be applied in future research.

Conclusion

The rock mass mechanical properties and the safety factors of the slope under different wetting–drying cycles were analyzed based on generalized Hoek–Brown failure criterion. Some conclusions have been drawn:

1) Wetting–drying cycles have a remarkable influence on mechanical properties of sandstone rock mass at initial stages (N = 1, 5, and 10). After that, the rock mass strength is reduced gently or nearly kept constant with increasing number of wetting–drying cycles.

2) With the number of wetting–drying cycles (N) increasing, the F_s of sandstone slope at different GSI ranges decreases, and the relationship between F_s and the value of N+1 could be fitted by logarithmic curves. The most deteriorating process of F_s of sandstone slope with constant GSI happens during the initial stages of wetting–drying cycles.

3) Both wetting–drying cycling and GSI influence slope stability. The influence of wetting–drying cycling on slope stability becomes small after 10 wetting–drying cycles, while GSI then becomes the dominant factor of slope stability.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

Drafting of article: KK; experiment design: SH; analysis and interpretation of data: KK and SH; numerical modeling: KK and IF; revisions of the manuscript: WL, HC, and YZ.

Funding

This research is financially supported by Jiangsu Shuangchuang Doctoral Program (Grant No. JSSCBS20210825), the Fundamental Research Funds for the Central Universities (Grant No. JUSRP121059), Chongqing Natural Science Foundation (Grant No. cstc2021jcyj-msxmX1114), Major science and technology projects of Anhui Province (Grant No. 201903a07020008), and the Scientific Research Fund of Institute of Engineering Mechanics, China Earthquake Administration (Grant No. 2019D08). These sources of funding are all gratefully acknowledged.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Griffiths, D. V., and Fenton, G. A. (2004). Probabilistic Slope Stability Analysis by Finite Elements. J. Geotechnical Geoenvironmental Eng. 130 (5), 507–518. doi:10.1061/(ASCE)1090-0241(2004)130:5(507)

CrossRef Full Text | Google Scholar

Guo, Z., Chen, L., Yin, K., Shrestha, D. P., and Zhang, L. (2020). Quantitative Risk Assessment of Slow-Moving Landslides from the Viewpoint of Decision-Making: A Case Study of the Three Gorges Reservoir in China. Eng. Geology. 273, 105667. doi:10.1016/j.enggeo.2020.105667

CrossRef Full Text | Google Scholar

Hoek, E., and Brown, E. T. (1997). Practical Estimates of Rock Mass Strength. Int. J. Rock Mech. Mining Sci. 34, 1165–1186. doi:10.1016/S1365-1609(97)80069-X

CrossRef Full Text | Google Scholar

Hoek, E., and Brown, E. T. (2019). The Hoek-Brown Failure Criterion and GSI - 2018 Edition. J. Rock Mech. Geotechnical Eng. 11, 445–463. doi:10.1016/j.jrmge.2018.08.001

CrossRef Full Text | Google Scholar

Hoek, E., Carranza-Torres, C., and Corkum, B. (2002). “Hoek-Brown Failure Criterion-2002 Edition,” in Proceedings of the 5th North American rock mechanics symposium and 17th tunnelling association of Canada conference, Toronto, Canada: Toronto: University of Toronto, 1, 267–273.

Google Scholar

Hoek, E., and Diederichs, M. S. (2006). Empirical Estimation of Rock Mass Modulus. Int. J. Rock Mech. Mining Sci. 43, 203–215. doi:10.1016/j.ijrmms.2005.06.005

CrossRef Full Text | Google Scholar

Hoek, E., and Marinos, P. (2000). Predicting Tunnel Squeezing Problems in Weak Heterogeneous Rock Masses. Tunnels tunnelling Int. 32 (11), 45–51.

Google Scholar

Huang, S., Wang, J., Qiu, Z., and Kang, K. (2018). Effects of Cyclic Wetting-Drying Conditions on Elastic Modulus and Compressive Strength of Sandstone and Mudstone. Processes 6 (12), 234. doi:10.3390/pr6120234

CrossRef Full Text | Google Scholar

Huang, X., Guo, F., Deng, M., Yi, W., and Huang, H. (2020). Understanding the Deformation Mechanism and Threshold Reservoir Level of the Floating Weight-Reducing Landslide in the Three Gorges Reservoir Area, China. Landslides 17, 2879–2894. doi:10.1007/s10346-020-01435-1

CrossRef Full Text | Google Scholar

Kang, K., Zerkal, O. V., Ponomarev, A. A., and Fomenko, I. K. (2021). Probabilistic Slope Stability Assessment under Seismic Conditions Based on the Generalized Hoek-Brown Criterion. Soil Mech. Found. Eng. 58, 223–229. doi:10.1007/s11204-021-09732-0

CrossRef Full Text | Google Scholar

Li, C., Criss, R. E., Fu, Z., Long, J., and Tan, Q. (2021). Evolution Characteristics and Displacement Forecasting Model of Landslides with Stair-step Sliding Surface along the Xiangxi River, Three Gorges Reservoir Region, China. Eng. Geology. 283, 105961. doi:10.1016/j.enggeo.2020.105961

CrossRef Full Text | Google Scholar

Liao, K., Wu, Y., Miao, F., Li, L., and Xue, Y. (2020). Time-varying Reliability Analysis of Majiagou Landslide Based on Weakening of Hydro-Fluctuation belt under Wetting-Drying Cycles. Landslides 18, 267–280. doi:10.1007/s10346-020-01496-2

CrossRef Full Text | Google Scholar

Miao, F., Wu, Y., Xie, Y., Yu, F., and Peng, L. (2016). Research on Progressive Failure Process of Baishuihe Landslide Based on Monte Carlo Model. Stoch Environ. Res. Risk Assess. 31, 1683–1696. doi:10.1007/s00477-016-1224-8

CrossRef Full Text | Google Scholar

Rocscience (2021). Rocscience RS2, 11, 012.

Google Scholar

Sun, G., Zheng, H., Tang, H., and Dai, F. (2015). Huangtupo Landslide Stability under Water Level Fluctuations of the Three Gorges Reservoir. Landslides 13, 1167–1179. doi:10.1007/s10346-015-0637-7

CrossRef Full Text | Google Scholar

Tang, H., Yong, R., and Ez Eldin, M. A. M. (2016). Stability Analysis of Stratified Rock Slopes with Spatially Variable Strength Parameters: the Case of Qianjiangping Landslide. Bull. Eng. Geol. Environ. 76, 839–853. doi:10.1007/s10064-016-0876-4

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, Z., Xue, S., Wang, R., and Xiao, M. (2020). Stability Analysis of a Typical Landslide Mass in the Three Gorges Reservoir under Varying Reservoir Water Levels. Environ. Earth Sci. 79 (1). doi:10.1007/s12665-019-8779-x

CrossRef Full Text | Google Scholar