Influence of Inter-Particle Friction and Damping on the Dynamics of Spherical Projectile Impacting Onto a Soil Bed

This study investigates the dynamics of a spherical projectile impact onto a granular bed via numerical simulations by discrete element method (DEM). The granular bed is modeled as an assembly of polydisperse spherical particles and the projectile is represented by a rigid sphere. The DEM model is used to investigate the cratering process, including the dynamics of the projectile and energy transformation and dissipation. The cratering process is illustrated by tracking the motion of the projectile and granular particles in the bed. The numerical results show that the dynamics of the projectile follows the generalized Poncelet law that the final penetration depth is a power-law function of the falling height. The numerical results can match well the experimental data reported in the literature, demonstrating the reliability of the DEM model in analyzing the impact of a spherical projectile on a granular bed. Further analyses illustrate that the impact process consists of three main stages, namely the impact, penetration and collapse, as characterized by the evolution of projective velocity, strong force chains and crater shape. The initial kinetic and potential energy of the projectile is dissipated mainly by inter-particle friction which governs the projectile dynamics. The stopping time of projectile decreases as the initial impact velocity increases. The final penetration depth scales as one-third the power of total falling height and is inversely proportional to the macroscopic granular friction coefficient.

Introduction

The impact of projectiles on granular media are widespread phenomena in nature, such as asteroids colliding onto planetary surfaces (Senft and Stewart, 2009), raindrops falling into soil (Marston et al., 2010), people walking on sand beaches (Uehara et al., 2003) and rockfalls impacting onto soil buffering layers (Wang and Cavers, 2008; Calvetti and di Prisco, 2012; Su et al., 2018; Shen et al., 2019). The related research contributes to a better understanding of the formation of impact craters and the design of efficient shock absorbers. Though it has been studied via experiments, numerical simulations and analytical theories (Newhall and Durian, 2003; Wada et al., 2006; Crassous et al., 2007; Katsuragi and Durian, 2007; Clark et al., 2015; Li et al., 2016; Ye et al., 2016; Horabik et al., 2018; Ye et al., 2018; Zhang et al., 2021) in the past several decades, the understanding of impact process is still limited owing to the complexities of such events (Wada et al., 2006; Tiwari et al., 2014; Horabik et al., 2018).

The dynamic interaction between projectiles and granular media is complex because it depends on the kinematics of the projectile (e.g. size, density, velocity and shape) and the mechanical properties of the granular media (e.g. bulk density, inter-particle friction, inter-particle damping and particle size). A part of these factors have been systematically analyzed by a series of experimental tests (Newhall and Durian, 2003; Uehara et al., 2003; Katsuragi and Durian, 2013). The focus of these tests is on the ejection process, the crater morphology and the penetration dynamics, aiming to find a scaling law for crater size and penetration depth. For a spherical projectile impacting onto granular media, it is well established that the crater diameter scales with the power of 1/4 the kinetic energy of the projectile and the final penetration depth scales with the power of 1/3 the falling height (Uehara et al., 2003). The observed deceleration of the impacting sphere can be interpreted by the generalized Poncelet force law (Uehara et al., 2003). The stopping time of a spherical projectile has also been studied in different experiments (Ciamarra et al., 2004; Katsuragi and Durian, 2007). It was found to be a decreasing function of the impact velocity with an asymptotic plateau at high impact velocities. Newhall and Durian (2003) investigated the effect of projectile shape on the penetration of a projectile into a granular layer. Their results indicate that for low velocity impacts, the projectile shape plays a crucial role such that the sharper/elongated objects can penetrate more deeply. Recently, with the help of photo-elastic particles and high speed camera, the microscopic inter-particle force networks in the granular media have been clearly identified by Clark et al. (2012). Based on the obtained results of force networks, the propagation and topology of the force networks were investigated (Clark et al., 2015; Takahashi et al., 2018). However, researchers are still far from a comprehensive understanding of the cratering mechanisms and the mechanical responses of the granular media (Wada et al., 2006; Tiwari et al., 2014), because it is difficult to control some physical parameters without changing other crucial parameters during the experiments. In particular, the influence of inter-particle friction and damping on the dynamics of projectile has not been investigated (Clark et al., 2015).

The aforementioned micro- and macro-mechanical responses of granular media can also be addressed by the discrete element method (DEM) (Cundall and Strack, 1979), especially for their loose and discontinuous natures (Wada et al., 2006; Li et al., 2016; Shen et al., 2018). With careful calibrations, the DEM modeling allows researchers to quantitatively analyze some physical processes that are nearly impossible to obtain in experiments (Utili et al., 2015; Zhang et al., 2015; Gao G. and Meguid M., 2018; Gao G. and Meguid M. A., 2018; Shen et al., 2021a), e.g. force wave propagation, energy evolution. In addition, the DEM allows a parametric analysis on one factor without altering other factors (Seguin et al., 2009). In the literature, both two- and three-dimensional (i.e., 2D and 3D) DEM models have been employed to study the projectile impacts on granular media (Tanaka et al., 2002; Ciamarra et al., 2004; Wada et al., 2006; Seguin et al., 2009; Kondic et al., 2012; Tiwari et al., 2014; Li et al., 2016; Horabik et al., 2018). Bourrier et al. (2010) and Zhang et al. (2017) investigated the impact-induced force chain evolution and its relation to the global mechanical response of granular media by 2D DEM. Wada et al. (2006) and Li et al. (2016) investigated the impact cratering processes of granular materials by 3D DEM models, reproducing the total mass and the velocity distribution of the impact-induced ejecta. The above studies show that the DEM is an effective and efficient method to investigate the impact of projectiles onto granular media. It is worth to note that the inter-particle friction and damping can be changed easily but not change the geometrical and mechanical properties of granular particles by using DEM.

The present study employs a 3D DEM model to investigate the dynamics of projectile impact onto granular media, with detailed parametric analyses of inter-particle friction and material damping. The paper is organized as follows: Section 2 presents a brief introduction of the DEM theory and the numerical model configurations. Section 3 summarizes the numerical results and discusses the dynamics of projectile and the energy transformation and dissipation during the impact process. Finally, conclusions on the projectile impact process are provided in Section 4.

Methodology and Numerical Model Configurations

Discrete Element Method Theory

The open-source DEM code ESyS-Particle (Wang and Mora, 2009; Weatherley et al., 2014) is employed to run all simulations presented herein. This code has been widely employed to study the mechanical behavior of soil and rock (Utili et al., 2015; Zhao et al., 2017; Shen et al., 2018; Zhao et al., 2018; Shen et al., 2021b; Gao and Meguid, 2021). In DEM, the granular material is mimicked as an assembly of closely packed rigid spherical particles. The translational and rotational motions of each particle are governed by the Newton’s second law of motion as expressed in Eqs 1, 2.

${\mathit{F}}_{\mathit{i}}=m_i\frac{d^2}{d{t}^2}{\mathit{r}}_{\mathit{i}}(1)$

${\mathit{T}}_{\mathit{i}}=I_i\frac{d{\mathit{\omega }}_{\mathit{i}}}{dt}(2)$

where F_i is the resultant force acting on particle i; r_i is the position of its centroid; m_i is the particle mass; T_i is the resultant moment acting on the particle; ω_i is the angular velocity and I_i is the moment of inertia.

In DEM, the inter-particle interactions are computed by the cohesionless frictional model. This employs a linear elastic-spring model to calculate the normal and tangential contact forces (Figure 1). In order to replicate the energy dissipation by particle asperities being sheared off and the plastic deformations at contacts, a linear viscous damping model (dashpot model) is employed in the normal direction. Thus, the normal contact force (F_n) is calculated as,

$F_{\mathbf{n}}=k_{\mathbf{n}}{u}_{\mathbf{n}}+F_{\mathbf{n}}^{\mathbf{d}}(3)$

where u_n is the overlapping length between two particles in the normal contact direction; k_n is the normal contact stiffness and $F_{\text{n}}^{\text{d}}$ is the normal damping force. The stiffness of particle normal contact is defined as $k_{\text{n}}=\text{π}E\left(R_{\text{A}}+R_{\text{B}}\right)/4$ with E being the Young’s modulus of particles, R_A and R_B being the radii of the two contacting particles, respectively.

FIGURE 1

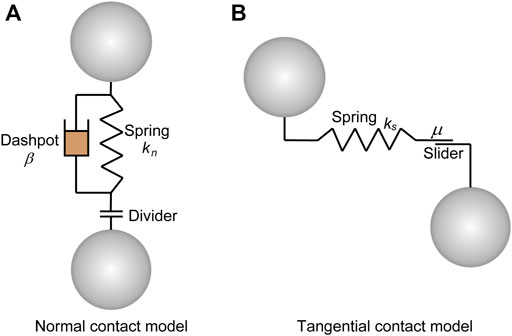
FIGURE 1. The DEM contact model between two contacting particles. (A) Normal contact model, (B) Tangential contact model.

The damping force ($F_{\text{n}}^{\text{d}}$) is calculated as

$F_{\mathbf{n}}^{\mathbf{d}}=-2\beta \sqrt{0.5\left(m_{\mathbf{A}}+m_{\mathbf{B}}\right)k_{\mathbf{n}}}{v}_{\mathbf{n}}(4)$

where β is the damping ratio; m_A and m_B are the mass of the two contacting particles, and v_n is the relative velocity between the particles in the normal direction.

The shear force at the current time step ($F_s^n$) is calculated incrementally as,

$F_s^n=F_s^{n-1}+\left(\Delta F_{s1}+\Delta F_{s2}\right)(5)$

where $F_s^{n-1}$ is the shear force at the previous iteration time step. $\Delta F_{s1}$ is calculated as △u_sk_s with k_s being the shear contact stiffness and △u_s being the incremental shear displacement. The shear stiffness is calculated as $k_s=\pi E\left(R_A+R_B\right)/\left(8\left(1+\upsilon \right)\right)$ with $\upsilon$ being the particle Poisson’s ratio. $\Delta F_{s2}$ is the shear force related to the rotation of particle contact plane. A detailed description of these two shear force terms can be found in Wang and Mora (2009).

The magnitude of the shear force is limited by the Coulomb’s friction law as,

$\left|F_{\mathbf{s}}\right|\le \mu \left|F_{\mathbf{n}}\right|(6)$

where μ is the friction coefficient of particle.

The shear induced moment is computed as:

$M=F_s{\mathit{r}}_{\mathit{i}}(7)$

Numerical Model Configurations

The numerical model configuration of a projectile colliding onto a granular bed is shown in Figure 2. The projectile is modeled as a rigid sphere of diameter (D) 2.54 cm. The granular bed is represented by an assembly of rigid spherical particles with radius uniformly ranging from 1.6 to 3.0 mm. It is prepared by randomly generating a loose packing of spherical particles in a cubic container space confined by rigid boundary walls. These particles are then released to settle downward under gravity until the kinetic energy of the system becomes nil. The acceleration due to gravity (g) is equal to 9.81 m/s². After the gravitational deposition, the granular bed has dimensions of 22.1 cm in thickness (T), 20.0 cm in length (L) and width (W). The solid volume fraction is 0.58 and the bulk density (ρ_g) is 1.54 g/cm³. Consequently, it can be calculated T/D = 8.7, L/D = 7.9 and W/D = 7.9. According to Seguin et al. (2008), the influence of model size on granular penetration can be neglected if T/D > 2.6, L/D > 5.0 and W/D > 5.0. Hence, the boundary conditions employed in the present study are acceptable.

FIGURE 2

FIGURE 2. Numerical model configurations. Particles are colored on the basis of their radii.

The input parameters of the DEM model are listed in Table 1. The material properties of the projectile and particles in the granular bed are chosen according to the well-documented experimental data reported in Katsuragi and Durian (Katsuragi and Durian, 2007; Katsuragi and Durian, 2013). For the granular particles, the inter-particle friction coefficient (μ) is obtained by measuring the material angle of repose (θ_r) in the DEM to match approximately that of glass beads commonly used in experiments (≈22°). For the projectile, the Young’s modulus and friction angle are set the same as those of the bed particles. The density of the projectile is set the same as that of a steel ball. During simulations, the projectile is positioned in the middle and just above the granular bed with an initial downward velocity (v₀). Each simulation lasts around 20 h on a standard desktop computer (Intel® Core™ i7 CPU, 4.00 GHz × 8, and 16 GB RAM).

TABLE 1

TABLE 1. Input parameters used in the DEM simulations.

Results

The DEM model has been employed to investigate the dynamic response of the projectile and granular bed during the impact process. A series of simulations are computed under conditions of various initial impact velocities (v₀). The obtained numerical results are compared with the well-documented experimental and numerical data reported in the literature (Uehara et al., 2003; Katsuragi and Durian, 2007; Tiwari et al., 2014), in terms of the formation of crater, the dynamics of projectile, the penetration depth and the stopping time of projectile. In addition, the energy transformation and dissipation during the impact are analyzed quantitatively.

Formation of Crater

Figure 3 illustrates the dynamic cratering process of the projectile colliding on and penetrating into the granular bed for test with v₀ = 5.0 m/s. For visualization purpose, the granular bed has been divided into seven equal-sized sub-layers with distinct colors at t = 0 (Figure 3). To plot the velocity field, the bed has been divided into 20 × 21 equal-sized grid cells along a vertical plane and then the average velocity of all the particles in each grid cell can be obtained. From Figure 3, it can be observed that after t = 0, the projectile gradually penetrates the granular bed. The granular particles around the projectile are significantly disturbed. In the meantime, the deformation of granular bed is still small, and no obvious crater can be observed. As the simulation continues, particles beneath the projectile move downward and the side particles move laterally, forming a bowl-shaped crater. After a few milliseconds, the projectile enters the granular bed completely (Figure 3). Meanwhile, the particles above the projectile continually move laterally and the diameter of the crater increases gradually (Figure 3). After the projectile penetrates into the granular bed, the top and lateral particles are still in dynamic motion with relatively small velocities (Figure 3). At 50 ms, the projectile stops moving, and an instantaneous deep crater is formed (Figure 3). Then, this transient crater begins to collapse. The collapsed particles gradually bury the projectile, forming a final stable crater (Figure 3). The numerical observations of the cratering process reveal three distinct stages: impact, penetration and side collapse. The impact stage is featured by the initial collision of a projectile onto the granular medium with very small bed deformation (e.g., Figure 3). The penetration stage is characterized by the rapid downward movement of the projectile in the granular media and the gradual expansion of the crater size (e.g., Figures 3a3–a5). The collapse stage involves the toppling of the transient crater and the formation of a final stable crater (e.g. Figures 3a6, b6). These observations agree with some well-documented experimental and numerical results reported in the literature (Ciamarra et al., 2004; Wada et al., 2006; Li et al., 2016).

FIGURE 3

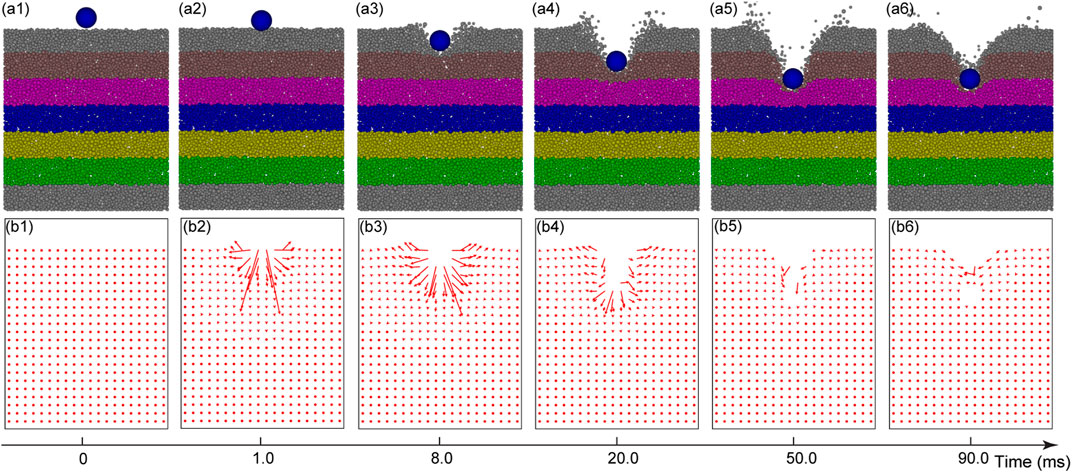
FIGURE 3. Snapshots of a projectile colliding into a granular bed from t = 0–90 ms (v₀ = 5.0 m/s). The series (a1–a6) are snapshots of a 1 cm thick vertical slice of the model through the axisymmetric center of the granular bed. The series (b1–b6) are the corresponding velocity fields. The length of the arrow is scaled by the velocity magnitude. The velocities smaller than 0.01 m/s are plotted as dots.

The corresponding compressive force wave propagation within the impacted granular bed can be represented by the evolution of force chains, as shown in Figure 4. Here, the force chain is defined as a network of straight lines connecting the centers of contacting particles. The thickness of these lines is proportional to the magnitude of normal contact force. According to Bourrier et al. (2008), the propagation of force chains within an assembly of granular materials can be used to analyze the propagation of compressive stress waves. From Figure 4, it can be observed that before impact, the force chains are uniformly distributed within the granular bed, as determined by the gravity force (Figure 4A). At impact, large contact forces occur immediately beneath the projectile and small contact forces distribute in the propagation front (Figure 4B), indicating the propagation of compressive wave. Over time, a clear and intact force chain network is formed in the granular bed (Figure 4C). After a certain time, the force chains stop propagating and begin to destruct (Figures 4D, E). As the projectile penetrates into the granular bed, the force chain beneath the projectile is almost totally broken, but a small number of force chains still exist at the bottom edge of the projectile (Figures 4F–H). During the collapse stage, the large contact force chains (red lines) totally disappear (Figures 4I, J).

FIGURE 4

FIGURE 4. Evolutions of contact force chains during the impact process (v₀ = 5.0 m/s). The thickness of force chains is proportional to the force magnitude, and red if force is larger than 0.6 N, otherwise gray. Note that the threshold value (0.6 N) is the largest contact force at t = 0.0 s. (A) t = 0.0 ms, (B) t = 0.08 ms, (C) t = 0.16 ms, (D) t = 0.20 ms, (E) t = 0.24 ms, (F) t = 4.0 ms, (G) t = 8.0 ms, (H) t = 20.0 ms, (I) t = 50.0 ms. (J) t = 90.0 ms.

Projectile Dynamics

Figures 5A, B show the evolution of velocity (v) and penetration depth (y) of the projectile during the cratering process, respectively, for simulations of different initial velocities. The positive directions of the position and velocity are defined vertically down. Once the projectile impacts on the granular bed, the velocity firstly exhibits a rapid decrease and then slows down gradually to zero. According to Tiwari et al. (2014), the rapid decrease of the projectile velocity is due to the formation of strong force chain network in the granular bed. During the impact, the projectile must overcome the resistant force exerted by the bed materials (i.e. the force chain network), resulting in the rapid decrease of its velocity. In general, the time at which the projectile stops moving is defined as the stopping time (t_s). The stopping time decreases with the initial impact velocity. An impact at a high velocity exhibits a short stopping time. This phenomenon has also been observed by some experimental and numerical studies (Katsuragi and Durian, 2007; Seguin et al., 2009). For the evolution of projectile penetration depth (Figure 5B), it increases gradually to the final penetration depth (h_f). As expected, it increases with the impact velocity. The impact at low velocity can lead to a relatively shallow crater, and specifically, the final penetration depth may be less than the projectile diameter (i.e. 0.0254 m). By contrast, the projectile with a relatively high speed can be entirely submerged in the granular bed, as implied in Figure 5B.

FIGURE 5

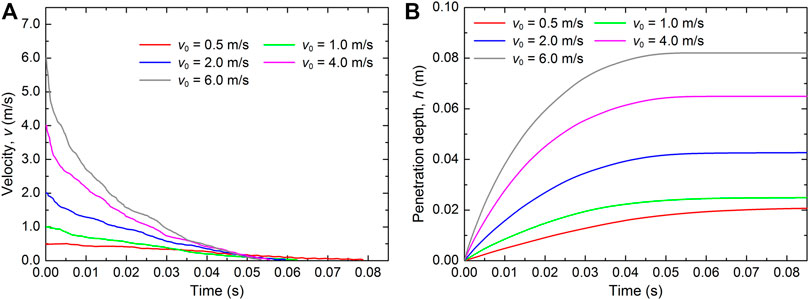
FIGURE 5. Evolutions of the (A) velocity (v) and (B) penetration depth (h) of projectiles for the numerical tests with different impact velocities. y = 0 corresponds to the position at which the projectile just contacts with the granular bed.

According to Uehara et al. (2003), the final penetration depth of a projectile can be estimated by an empirical formula $h_f=\left(0.14/{\mu }^{\prime }\right){\left({\rho }_p/{\rho }_g\right)}^{1/2}{D}^{2/3}{H}^{1/3}$ with ${\mu }^{\prime }$ being the macroscopic friction coefficient of bed particles and H being the falling height. ${\mu }^{\prime }$ is calculated as the tangent of the repose angle (θ_r). H is representative falling height calculated as the sum of the final penetration depth and the free fall height ($H=h_f+v_0^2/2g$). Figure 6 shows the relationship between the final penetration depth and the total falling height from the current DEM simulations. The black curve shows the analytical results predicted by the empirical formula by Uehara et al. (2003). As shown in this figure, the numerical results can match well the empirical formula, demonstrating the accuracy of the empirical formula.

FIGURE 6

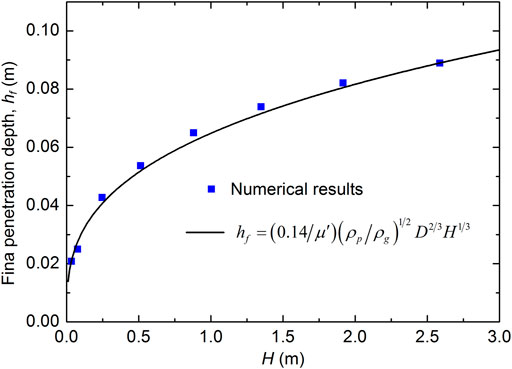
FIGURE 6. Relationship between the final penetration depth (h_f) and the total falling height ($H=h_f+v_0^2/2g$). The black line corresponds to the empirical equation obtained by Uehara et al. (3) in their experimental studies.

In the literature, several studies reported that the dynamics of a projectile can be assumed to follow the generalized Poncelet law (Katsuragi and Durian, 2007; Seguin et al., 2009),

$m\ddot{h}=mg-m{v}^2/d_1-kh(8)$

where h is the penetration depth of the projectile, m is the projectile mass; g is the gravity acceleration of value 9.8 m/s²; d₁ is the material parameter of unit length; k is the elastic constant of contact. The solution of this equation shows the relationship between the velocity and penetration depth, as:

$\frac{v^2}{v_0^2}=e^{-\frac{2h}{d_1}}-\frac{k{d}_{1}h}{m{v}_0^2}+\left(\frac{g{d}_1}{v_0^2}+\frac{k{d}_1^2}{2m{v}_0^2}\right)\left(1-e^{-\frac{2h}{d_1}}\right)(9)$

Figure 7 illustrates the relationships between the velocity and penetration depth for numerical simulations with different impact velocities. These curves exhibit the trend of a progressive change from a concave-down to a convex-up shape. Generally, there is a rapid decrease of velocity to zero at the end of penetration stage. These behaviors have also been observed in experiments by Katsuragi and Durian (2013) and DEM simulations by Tiwari et al. (2014). In addition, as shown in Figure 7, the numerical results can be well fitted by Eq. 9. This indicates that the dynamics of projectile in the present DEM study obeys well the generalized Poncelet law.

FIGURE 7

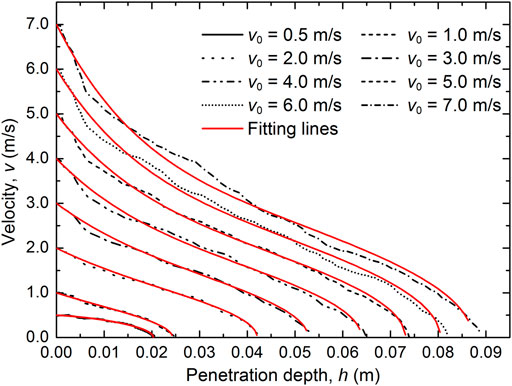
FIGURE 7. Relationships between the velocity and penetration depth of projectiles for the numerical tests of different impact velocities. The black curves represent the numerical results and the red curves are obtained by fitting the numerical results using Eq. 9.

According to Katsuragi and Durian (2013), the fitting parameters d₁ and k in Eq. 8 can be approximately calculated as

$d_1=D\left(0.25/{\mu }^{\prime }\right)\left({\rho }_p/{\rho }_g\right)(10)$

$k=12mg{D}^{-1}{\mu }^{\prime }{\left({\rho }_g/{\rho }_p\right)}^{1/2}(11)$

Thus, d₁ and k are estimated as 0.0831 m and 56.049 N/m, respectively. By substituting these values into Eq. 8, the final penetration depth and stopping time of the projectiles with different impact velocities can be predicted and compared with the numerical results (Figure 8). It can be seen that the final penetration depths predicted by Eq. 8 using the parameters d₁ and k calculated from Eqs 10, 11 are larger than the numerical results. However, the increasing trend of the data obtained in numerical modeling is in accordance with the prediction of Eq. 8. The stopping time firstly shows a rapid decrease as the impact velocity increases from 0 to 1.0 m/s, and then it gradually approaches a stable value. For low impact velocities (v₀ < 1.0 m/s), the stopping time can be well predicted by Eq. 8, while for higher impact velocities, Eq. 8 would underestimate the stopping time. However, the general decreasing trend of the stopping time matches well the prediction of Eq. 8. In addition, according to Katsuragi and Durian (2007), the ultimate stopping time can be estimated using $\sqrt{D/\text{g}}$. This theoretical estimation is plotted as a gray dashed line in Figure 8B.

FIGURE 8

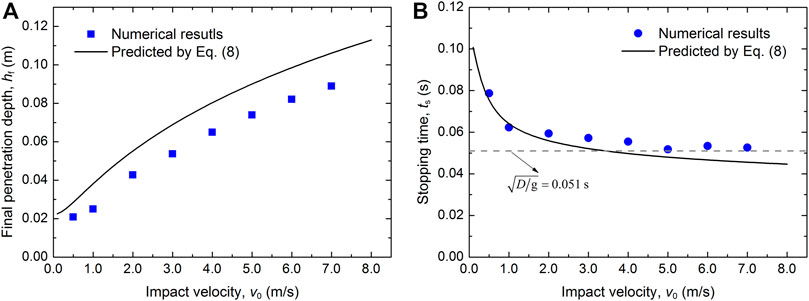
FIGURE 8. Dependences of (A) the final penetration depth and (B) the stopping time on the impact velocity. The black curves show the final penetration depth and stopping time predicted by Eq. 8 using the parameters d₁ and k calculated from Eqs 10, 11.

Energy Transformation and Dissipation

Analyses of the energy evolution, transformation and dissipation are important for a comprehensive understanding of the interaction process between the projectile and granular bed. The analyses also allow a quantitative evaluation of the role of inter-particle friction and damping on the projectile dynamics. The total energy (E_T) of the granular system consists of potential energy (E_P), kinetic energy (E_K), elastic strain energy (E_S) and the energy loss due to inter-particle friction (E_F) and local contact viscous damping (E_D). The method to calculate these energy components in the context of DEM has been detailed in (Shen et al., 2018). In this study, all these energy components were recorded during the simulations and subsequently analyzed regarding the energy evolution, transformation and dissipation, as shown in Figure 9. The kinetic energy of the projectile ($E_K^p$) and the granular bed ($E_K^g$), the potential energy of the projectile ($E_P^p$), the energy dissipated by friction between the projectile and granular bed ($E_F^p$), the energy dissipated by damping ($E_D^g$) and friction ($E_F^g$) are recorded separately. The potential energy ($E_P^p$) is defined with respect to the bottom of the granular bed. The strain energy ($E_S$) is not plotted because its value is negligibly small. All these energy components are normalized by the initial mechanical energy of the projectile (E₀: the initial kinetic energy plus potential energy). As illustrated in Figure 9, the whole system involves a cascade of energy evolution which begins when the projectile impacts onto the granular bed. After the collision occurs (t = 0), the kinetic energy of the projectile decreases rapidly, while that of the granular bed increases rapidly to the peak value at t = 1.5 ms. During this period, only a small amount of energy is dissipated by inter-particle friction and damping. After t = 1.5 ms, the kinetic energy of both the projectile and granular bed decreases slowly. However, the decreasing rate of kinetic energy of the granular bed is smaller than that of the projectile. This is because during the penetration stage of the projectile, a certain portion of projectile kinetic energy can still be transferred to the granular bed. To limit the computation time, the calculation is terminated when the projectile stops. Hence, at t = 51.8 ms, the kinetic energy of the projectile vanishes, while the granular bed still has a little of kinetic energy. From Figure 9, it also can be seen that nearly 70% of the mechanical energy of the projectile is dissipated by the inter-particle friction in the granular bed. The energy consumed by the friction of projectile and the damping of granular bed is less than 10% of E_0. Thus, from the perspective of energy consumption, it can be speculated that compared with the particle damping, the inter-particle friction plays a dominant role in the mechanical response of granular bed against the projectile impact. However, in addition to the energy consumption, it is also necessary to study the influences of inter-particle friction and damping on the projectile dynamics.

FIGURE 9

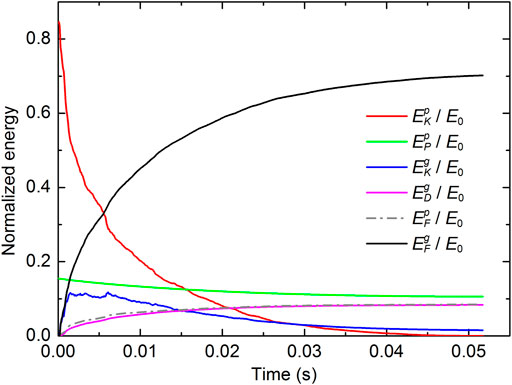
FIGURE 9. Evolution and transformation of energy components during a simulation of v₀ = 5.0 m/s. All the energy components are normalized by the initial mechanical energy (kinetic energy plus potential energy) of the projectile (E₀).

Influence of Inter-Particle Friction on Projectile Dynamics

To investigate the influence of inter-particle friction (μ_b), a series of impact tests are performed with the bed particle friction coefficient (μ_b) ranging from 0.1 to 0.6. In these numerical tests, the granular bed is also generated by gravitational deposition as described in Section 2.2. Since the porosity of the granular bed depends on the inter-particle friction, the value of μ_b is set as 0.1 during the gravitational deposition, such that the inter-particle friction can be varied to investigate its influence on the projectile dynamics without changing the initial stable state and especially the porosity of the granular bed. After the gravitational deposition, the volume fraction and bulk density (ρ_g) of the granular bed are 0.61 and 1.61 g/cm³, respectively.

Figure 10 shows the evolutions of velocities and penetration depths of the projectiles for the numerical tests with various inter-particle friction coefficients. Generally, the velocity first shows a rapid decrease at the initial impact and then decreases gradually to zero. As the inter-particle friction increases, the stopping time of projectile decreases. For μ_b ≥ 0.4, the evolutions of velocities are almost identical and the projectiles stop at the same time. As for the penetration depth, it increases gradually to a peak value after the collision is initiated. The final penetration depth decreases as the inter-particle friction increases. For the tests with μ_b ≥ 0.4, the evolution of the projectile penetration depth is nearly identical and the projectiles almost stop at the same position. These results indicate that the inter-particle friction indeed has a significant influence on the projectile dynamics. However, it has a relatively negligible influence on the velocity and penetrating depth of the projectile after the inter-particle friction is beyond 0.4. The dependence of the final penetration depth and stopping time on the friction coefficient of particles are illustrated in Figures 11A, B, respectively. It can be seen that both the final penetration depth and stopping time decrease as the inter-particle friction increases. After the inter-particle friction increases to 0.4, both the final penetration depth and stopping time become relatively stable. This is in accord with the general trend of the prediction by Eq. 8. Actually, such a phenomenon is related to the dependence of the macroscopic friction coefficient of the granular bed (${\mu }^{\prime }$) on the microscopic inter-particle friction. For spherical particles, if particle rotation is allowed, the macroscopic friction (${\mu }^{\prime }$) increases with the inter-particle friction (μ_b) and reaches the peak value after μ_b increases to 0.45 (Suiker and Fleck, 2004). According to Eqs 10, 11, d₁ and k tend to be constant values when the macroscopic friction coefficient reaches its limit. Thus, the dynamics of projectile is not sensitive to μ_b when it increases beyond 0.45.

FIGURE 10

FIGURE 10. Evolutions of (A) velocity and (B) penetration depth of projectiles for the numerical tests of various friction coefficients of bed particles (under the condition of v₀ = 4.0 m/s).

FIGURE 11

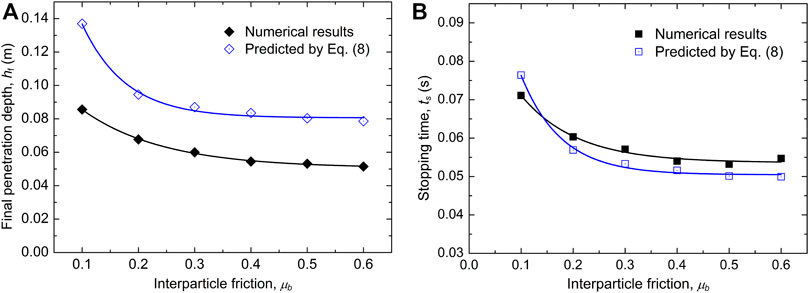
FIGURE 11. Dependences of (A) final penetration depth and (B) stopping time of projectile on the friction coefficient of particles in granular bed.

Influence of Particle Damping on Projectile Dynamics

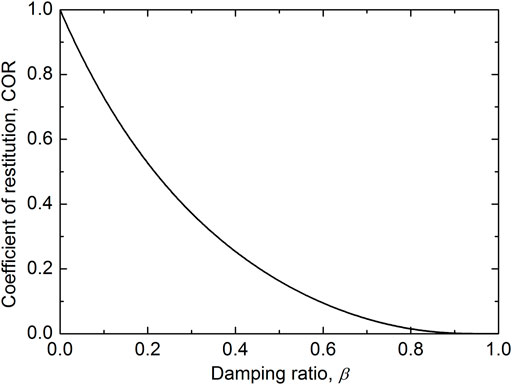
In this study, the linear dashpot model Eq. (4) is used in DEM to simulate the energy dissipation due to elastic wave propagation through a solid particle. This kind of model has been widely applied to numerical simulations of granular materials (Mao et al., 2004; Zhou et al., 2016; Gao G. and Meguid M. A., 2018; Li and Zhao, 2018; Shen et al., 2018). The damping ratio (β) in this model quantifies the plastic properties of particles. In the laboratory, the coefficient of restitution (COR) is commonly used as an index of this plastic property of solid materials. It can be measured in the laboratory from a series of drop tests (Imre et al., 2008). The relationship between the COR and the damping ratio (β) is depicted in Figure 12. The derivation of this equation can be found in (Gao G. and Meguid M., 2018). Thus, by varying the damping ratio, the influence of material damping of the granular bed on the projectile dynamics can be investigated. Figure 13 gives the evolution of velocity and penetration depth of the projectiles for the numerical tests at various damping ratios (i.e. 0.01, 0.1, 0.2 and 0.3). The corresponding COR values are 0.97, 0.73, 0.53 and 0.37, respectively. From Figure 13A, it can be observed that the damping ratio has little influence on the projectile velocity. For the tests with different damping ratios, the evolutions of velocity of the projectiles are nearly the same and the projectiles nearly stop at the same time. From Figure 13B, it can be observed that in the cases of β < 0.2, the final penetration depth decreases with the increase of the damping ratio. However, an increase of β from 0.01 to 0.2 leads to only 7.3% decrease of the final penetration depth. In addition, for the cases of β ≥ 0.2, the evolution of penetration depth of is nearly the same. Thus, it can be concluded that the main factor determining the dynamics of projectile is the inter-particle friction rather than the particle damping of a granular material.

FIGURE 12

FIGURE 12. Relationship between the coefficient of restitution (COR) and the damping ratio (β).

FIGURE 13

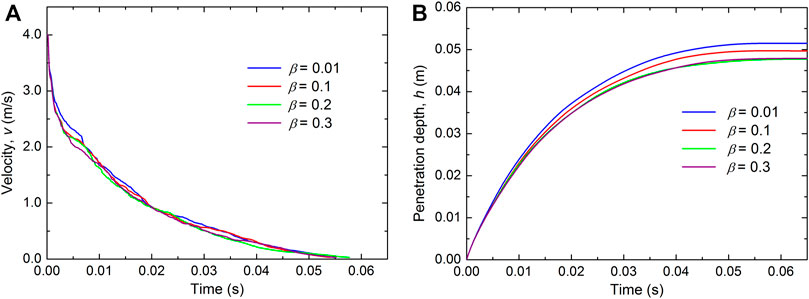
FIGURE 13. Evolutions of (A) velocity and (B) penetration depth of projectiles for the numerical tests of various damping ratios (under the condition of v₀ = 4.0 m/s).

Conclusions

The impact of a spherical projectile into a granular bed is analyzed via three-dimensional numerical modeling by the discrete element method. This model is validated by comparing the numerical and experimental results reported in the literature. The validated model is then used to investigate the influence of inter-particle friction and material damping on the dynamics of projectile. The main conclusions of this study are as follows:

1. Based on the numerical modeling, three key interaction stages, namely the impact, penetration and collapse, are identified. The impact stage is characterized by the initial collision of projectile onto the granular bed, the rapid decrease of projectile velocity and the formation of strong force chain networks. The penetration stage is featured by the movement of the projectile inside the granular bed and the crater expansion. The collapse stage involves the toppling of the deepest transient crater and the formation of a final static crater.

2. During the whole impact process, the initial kinetic and potential energy of the projectile is dissipated mainly by inter-particle friction, while only a small part of energy loss is induced by projectile-particle friction and inter-particle damping.

3. The parametric study on the inter-particle friction and damping shows that the inter-particle friction is the main factor determining the projectile dynamics.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

TZ, GC, and FD contributed to conception and design of the study. WS performed the numerical simulations and organized the database. WS wrote the first draft of the manuscript. TZ, WS, GC, FD, and GD contributed to manuscript revision, read, and approved the submitted version.

Funding

This research was supported, in whole or in part, by the National Natural Science Foundation of China (No. 42107155), the Royal Society, Sino-British Fellowship Trust International Exchanges Award (No. IES\R2\202023), the Fundamental Research Funds for the Central Universities (No. 2682021CX061), the National Key R&D Program of China (No. 2017YFC1502500).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bourrier, F., Nicot, F., and Darve, F. (2010). Evolution of the Micromechanical Properties of Impacted Granular Materials. Comptes Rendus Mécanique 338, 639–647. doi:10.1016/j.crme.2010.09.007

CrossRef Full Text | Google Scholar

Bourrier, F., Nicot, F., and Darve, F. (2008). Physical Processes within a 2D Granular Layer during an Impact. Granular Matter 10 (6), 415–437. doi:10.1007/s10035-008-0108-0

CrossRef Full Text | Google Scholar

Calvetti, F., and di Prisco, C. (2012). Rockfall Impacts on Sheltering Tunnels: Real-Scale Experiments. Géotechnique 62 (10), 865–876. doi:10.1680/geot.9.p.036

CrossRef Full Text | Google Scholar

Clark, A. H., Kondic, L., and Behringer, R. P. (2012). Particle Scale Dynamics in Granular Impact. Phys. Rev. Lett. 109 (23), 238302. doi:10.1103/physrevlett.109.238302

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, A. H., Petersen, A. J., Kondic, L., and Behringer, R. P. (2015). Nonlinear Force Propagation during Granular Impact. Phys. Rev. Lett. 114 (14), 144502. doi:10.1103/physrevlett.114.144502

PubMed Abstract | CrossRef Full Text | Google Scholar

Crassous, J., Beladjine, D., and Valance, A. (2007). Impact of a Projectile on a Granular Medium Described by a Collision Model. Phys. Rev. Lett. 99 (24), 248001. doi:10.1103/physrevlett.99.248001

PubMed Abstract | CrossRef Full Text | Google Scholar

Cundall, P. A., and Strack, O. D. L. (1979). A Discrete Numerical Model for Granular Assemblies. Géotechnique 29 (1), 47–65. doi:10.1680/geot.1979.29.1.47

CrossRef Full Text | Google Scholar

Gao, G., and Meguid, M. A. (2021). On the Role of Joint Roughness on the Micromechanics of Rock Fracturing Process: a Numerical Study. Acta Geotech. doi:10.1007/s11440-021-01401-8

CrossRef Full Text | Google Scholar

Gao, G., and Meguid, M. A. (2018b). On the Role of Sphericity of Falling Rock Clusters-Insights from Experimental and Numerical Investigations. Landslides 15 (2), 219–232. doi:10.1007/s10346-017-0874-z

CrossRef Full Text | Google Scholar

Gao, G., and Meguid, M. (2018a). Modeling the Impact of a Falling Rock Cluster on Rigid Structures. Int. J. Geomech. 18 (2), 1–15. doi:10.1061/(asce)gm.1943-5622.0001045

CrossRef Full Text | Google Scholar

Horabik, J., Sochan, A., Beczek, M., Mazur, R., Ryżak, M., Parafiniuk, P., et al. (2018). Discrete Element Method Simulations and Experimental Study of Interactions in 3D Granular Bedding during Low-Velocity Impact. Powder Tech. 340, 52–67. doi:10.1016/j.powtec.2018.09.004

CrossRef Full Text | Google Scholar

Imre, B., Räbsamen, S., and Springman, S. M. (2008). A Coefficient of Restitution of Rock Materials. Comput. Geosciences 34 (4), 339–350. doi:10.1016/j.cageo.2007.04.004

CrossRef Full Text | Google Scholar

Katsuragi, H., and Durian, D. J. (2013). Drag Force Scaling for Penetration into Granular media. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 87 (5), 052208. doi:10.1103/PhysRevE.87.052208

PubMed Abstract | CrossRef Full Text | Google Scholar

Katsuragi, H., and Durian, D. J. (2007). Unified Force Law for Granular Impact Cratering. Nat. Phys 3 (6), 420–423. doi:10.1038/nphys583

CrossRef Full Text | Google Scholar

Kondic, L., Fang, X., Losert, W., O'Hern, C. S., and Behringer, R. P. (2012). Microstructure Evolution during Impact on Granular Matter. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 85 (1), 011305. doi:10.1103/PhysRevE.85.011305

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., and Zhao, J. (2018). Dam-break of Mixtures Consisting of Non-newtonian Liquids and Granular Particles. Powder Tech. 338, 493–505. doi:10.1016/j.powtec.2018.07.021

CrossRef Full Text | Google Scholar

Li, Y., Dove, A., Curtis, J. S., and Colwell, J. E. (2016). 3D DEM Simulations and Experiments Exploring Low-Velocity Projectile Impacts into a Granular Bed. Powder Tech. 288, 303–314. doi:10.1016/j.powtec.2015.11.022

CrossRef Full Text | Google Scholar

Mao, K., Wang, M. Y., Xu, Z., and Chen, T. (2004). DEM Simulation of Particle Damping. Powder Technol. 142 (2), 154–165. doi:10.1016/j.powtec.2004.04.031

CrossRef Full Text | Google Scholar

Marston, J. O., Thoroddsen, S. T., Ng, W. K., and Tan, R. B. H. (2010). Experimental Study of Liquid Drop Impact onto a Powder Surface. Powder Tech. 203 (2), 223–236. doi:10.1016/j.powtec.2010.05.012

CrossRef Full Text | Google Scholar

Newhall, K. A., and Durian, D. J. (2003). Projectile-shape Dependence of Impact Craters in Loose Granular media. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 68 (6), 060301. doi:10.1103/PhysRevE.68.060301

PubMed Abstract | CrossRef Full Text | Google Scholar

Pica Ciamarra, M., Lara, A. H., Lee, A. T., Goldman, D. I., Vishik, I., and Swinney, H. L. (2004). Dynamics of Drag and Force Distributions for Projectile Impact in a Granular Medium. Phys. Rev. Lett. 92 (19), 194301. doi:10.1103/physrevlett.92.194301

PubMed Abstract | CrossRef Full Text | Google Scholar

Seguin, A., Bertho, Y., and Gondret, P. (2008). Influence of Confinement on Granular Penetration by Impact. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 78 (1), 010301. doi:10.1103/PhysRevE.78.010301

PubMed Abstract | CrossRef Full Text | Google Scholar

Seguin, A., Bertho, Y., Gondret, P., and Crassous, J. (2009). Sphere Penetration by Impact in a Granular Medium: a Collisional Process. Europhys. Lett. 88, 44002. doi:10.1209/0295-5075/88/44002

CrossRef Full Text | Google Scholar

Senft, L. E., and Stewart, S. T. (2009). Dynamic Fault Weakening and the Formation of Large Impact Craters. Earth Planet. Sci. Lett. 287 (3), 471–482. doi:10.1016/j.epsl.2009.08.033

CrossRef Full Text | Google Scholar

Shen, W., Luo, G., and Zhao, X. (2021a). On the Impact of Dry Granular Flow against a Rigid Barrier with Basal Clearance via Discrete Element Method. Landslides. doi:10.1007/s10346-021-01805-3

CrossRef Full Text | Google Scholar

Shen, W., Zhao, T., and Dai, F. (2021b). Influence of Particle Size on the Buffering Efficiency of Soil Cushion Layer against rockfall Impact. Nat. Hazards 108 (2), 1469–1488. doi:10.1007/s11069-021-04741-6

CrossRef Full Text | Google Scholar

Shen, W., Zhao, T., Dai, F., Jiang, M., and Zhou, G. G. D. (2019). DEM Analyses of Rock Block Shape Effect on the Response of rockfall Impact against a Soil Buffering Layer. Eng. Geology. 249, 60–70. doi:10.1016/j.enggeo.2018.12.011

CrossRef Full Text | Google Scholar

Shen, W., Zhao, T., Zhao, J., Dai, F., and Zhou, G. G. D. (2018). Quantifying the Impact of Dry Debris Flow against a Rigid Barrier by DEM Analyses. Eng. Geology. 241, 86–96. doi:10.1016/j.enggeo.2018.05.011

CrossRef Full Text | Google Scholar

Su, Y., Cui, Y., Ng, C. W. W., Choi, C. E., and Kwan, J. S. H. (2018). Effects of Particle Size and Cushioning Thickness on the Performance of Rock-Filled Gabions Used in protection against boulder Impact. Can. Geotech. J. 56 (2), 198–207. doi:10.1139/cgj-2017-0370

CrossRef Full Text | Google Scholar

Suiker, A. S. J., and Fleck, N. A. (2004). Frictional Collapse of Granular Assemblies. J. Appl. Mech. 71 (3), 350–358. doi:10.1115/1.1753266

CrossRef Full Text | Google Scholar

Takahashi, T., Clark, A. H., Majmudar, T., and Kondic, L. (2018). Granular Response to Impact: Topology of the Force Networks. Phys. Rev. E 97 (1), 012906. doi:10.1103/PhysRevE.97.012906

PubMed Abstract | CrossRef Full Text | Google Scholar

Tanaka, K., Nishida, M., Kunimochi, T., and Takagi, T. (2002). Discrete Element Simulation and experiment for Dynamic Response of Two-Dimensional Granular Matter to the Impact of a Spherical Projectile. Powder Technol. 124 (1), 160–173. doi:10.1016/s0032-5910(01)00489-2

CrossRef Full Text | Google Scholar

Tiwari, M., Mohan, T. R., and Sen, S. (2014). Drag-force Regimes in Granular Impact. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 90 (6), 062202. doi:10.1103/PhysRevE.90.062202

PubMed Abstract | CrossRef Full Text | Google Scholar

Uehara, J. S., Ambroso, M. A., Ojha, R. P., and Durian, D. J. (2003). Low-speed Impact Craters in Loose Granular media. Phys. Rev. Lett. 90 (19), 194301. doi:10.1103/physrevlett.90.194301

PubMed Abstract | CrossRef Full Text | Google Scholar

Utili, S., Zhao, T., and Houlsby, G. T. (2015). 3D DEM Investigation of Granular Column Collapse: Evaluation of Debris Motion and its Destructive Power. Eng. Geology. 186, 3–16. doi:10.1016/j.enggeo.2014.08.018

CrossRef Full Text | Google Scholar

Wada, K., Senshu, H., and Matsui, T. (2006). Numerical Simulation of Impact Cratering on Granular Material. Icarus 180 (2), 528–545. doi:10.1016/j.icarus.2005.10.002

CrossRef Full Text | Google Scholar

Wang, B., and Cavers, D. S. (2008). A Simplified Approach for rockfall Ground Penetration and Impact Stress Calculations. Landslides 5 (3), 305–310. doi:10.1007/s10346-008-0123-6

CrossRef Full Text | Google Scholar

Wang, Y., and Mora, P. (2009). “The ESyS_Particle: A New 3-D Discrete Element Model with Single Particle Rotation,” in Advances in Geocomputing. Editor H. Xing (Berlin, Heidelberg: Springer Berlin Heidelberg), 183–228. doi:10.1007/978-3-540-85879-9_6

CrossRef Full Text | Google Scholar

Weatherley, D., Hancock, W., and Boris, V. (2014). “ESyS-Particle Tutorial and User's Guide Version 2.1,” in Earth Systems Science Computational Centre (Brisbane, Australia: The University of Queensland).

Google Scholar

Ye, X., Wang, D., and Zheng, X. (2016). Criticality of post-impact Motions of a Projectile Obliquely Impacting a Granular Medium. Powder Tech. 301, 1044–1053. doi:10.1016/j.powtec.2016.07.043

CrossRef Full Text | Google Scholar

Ye, X., Wang, D., and Zheng, X. (2018). Effect of Packing Fraction on Dynamic Characteristics of Granular Materials under Oblique Impact. Powder Tech. 339, 211–222. doi:10.1016/j.powtec.2018.07.099

CrossRef Full Text | Google Scholar

Zhang, G., Tang, H., Xiang, X., Karakus, M., and Wu, J. (2015). Theoretical Study of rockfall Impacts Based on Logistic Curves. Int. J. Rock Mech. Min. Sci. 78, 133–143. doi:10.1016/j.ijrmms.2015.06.001

CrossRef Full Text | Google Scholar

Zhang, L., Nguyen, N. G. H., Lambert, S., Nicot, F., Prunier, F., and Djeran-Maigre, I. (2017). The Role of Force Chains in Granular Materials: from Statics to Dynamics. Eur. J. Environ. Civ. En. 21 (7-8), 874–895. doi:10.1080/19648189.2016.1194332

CrossRef Full Text | Google Scholar

Zhao, T., Crosta, G. B., Utili, S., and De Blasio, F. V. (2017). Investigation of Rock Fragmentation during Rockfalls and Rock Avalanches via 3‐D Discrete Element Analyses. J. Geophys. Res. Earth Surf. 122 (3), 678–695. doi:10.1002/2016jf004060

CrossRef Full Text | Google Scholar

Zhang, Y., Dai, Y., Wang, Y., Huang, X., Xiao, Y., and Pei, Q. (2021). Hydrochemistry, Quality and Potential Health Risk Appraisal of Nitrate Enriched Groundwater in the Nanchong area, Southwestern China. Sci. Total Environ. 784, 147186. doi:10.1016/j.scitotenv.2021.147186

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, T., Crosta, G., Dattola, G., and Utili, S. (2018). Dynamic Fragmentation of Jointed Rock Blocks during Rockslide-Avalanches: Insights from Discrete Element Analyses. J. Geophys. Res. Sol.Ea. 123, 1–20. doi:10.1002/2017jb015210

CrossRef Full Text | Google Scholar

Zhou, W., Ma, X., Ng, T.-T., Ma, G., and Li, S.-L. (2016). Numerical and Experimental Verification of a Damping Model Used in DEM. Granular Matter 18 (1), 1. doi:10.1007/s10035-015-0597-6

CrossRef Full Text | Google Scholar