- Dr. Moses Strauss Department of Marine Geosciences, Leon H. Charney School of Marine Science, University of Haifa, Haifa, Israel
Methane (CH4) transport from organic-rich fine-grained (muddy) shallow aquatic sediments to water column is mediated dominantly by discrete bubbles, which is an important natural source of greenhouse CH4. The lifespan of these bubbles within the sediment comprises two successive stages: growth from nucleation up to a mature size and then buoyant ascent toward the sediment–water interface. Bubbles often experience an oscillating overburden load due to the passage of winds and/or storm-induced short period surface waves or long-period tides, which can potentially affect both stages of the bubble’s lifespan. However, little is known about the wave effects over bubble growth phase. In the present work, this subject is investigated using a numerical single-bubble mechanical/solute transport model, which quantifies the effects of different parameters (amplitude and period) of the wave loading and of the water depth, over the bubble growth pattern in sediments and its specific characteristics. It was found that bubbles induce early sediment fracturing in the presence of waves, attributed to the low overburden load appearing at wave troughs. Bubbles at shallow depth rapidly grow at wave troughs by inducing multiple intense fracturing events. However, this ability decreases with an increasing water depth because of a slower solute influx. In the presence of waves, bubbles mature in shorter time, whose contrast to the no wave case is controlled by the ratio of wave amplitude to equilibrium water depth. Due to the higher frequency of occurrence of wave troughs for shorter-period waves, bubble growth is accelerated compared with the case of longer-period waves. Overall, our modeling suggests that the fastest bubble growth can be predicted for higher amplitude, short-period waves traveling in shallow water. We further infer that accelerated bubble growth, along with subsequent wave-induced ascent can sufficiently shorten the bubble’s total lifespan in sediment, which explains the observed episodic in situ ebullitions correlated with wind- or storm-induced waves.
Introduction
Formation of methane (CH4) bubbles in shallow aquatic sediments is a widespread phenomenon (Bastviken et al., 2011), which is usually associated with synthesis of CH4 during microbial remineralization of organic matter. Fine-grained cohesive (muddy) aquatic sediments develop discrete diffusion-fed bubbles (markedly larger than pore scale; Wheeler, 1988; Anderson et al., 1998), which elastically deform the sediment matrix and grow by fracturing (Abegg and Anderson, 1997; Johnson et al., 2002; Van Kesteren and van Kessel, 2002; Best et al., 2004; Boudreau et al., 2005; Reed et al., 2005; Jain and Juanes, 2009; Boudreau, 2012; Katsman et al., 2013). They rise in the sediment toward the water column due to buoyancy forces (Wheeler, 1990; Van Kesteren and van Kessel, 2002; Boudreau et al., 2005; Algar et al., 2011a; Algar et al., 2011b; Boudreau, 2012; Sirhan et al., 2019). Within aquatic environments, their entire life cycle is a matter of a great concern, due to the significant contribution of shallow aquatic sites to the global atmospheric CH4 budget (USEPA, 2010; Saunois et al., 2016), and the bubbles ability to alter effective properties of gassy sediments—compressibility (Nageswaran, 1983; Sills and Wheeler, 1992) and undrained shear strength (Sills et al., 1991; Sills and Wheeler, 1992), which may induce slope failure in aquatic environments (Esrig and Kirby, 1977; Hovland et al., 2002; Bünz et al., 2005; Best et al., 2006).
The life cycle of a bubble within the sediment includes two subsequent stages: 1) bubble growth from its nucleation to mature size and configuration (with a closed tail, just prior to its ascent) (Abegg and Anderson, 1997; Johnson et al., 2002; Van Kesteren and van Kessel, 2002; Best et al., 2004; Reed et al., 2005; Barry et al., 2010; Katsman et al., 2013); and 2) subsequent rise of mature bubble from its place of nucleation toward the sediment - water interface (Wheeler, 1990; Van Kessel and Van Kesteren, 2002; Van Kesteren and van Kessel, 2002; Haeckel et al., 2004; Shin and Santamarina, 2010; Algar et al., 2011a; Algar et al., 2011b; Boudreau, 2012; Sirhan et al., 2019). Both of these stages within the sediment layers are governed by a complex interplay between geochemical properties of the ambient pore fluids (Martens and Klump, 1980; Abegg and Anderson, 1997) and the mechanical properties (fracture toughness, Young’s modulus, and Poisson’s ratio) of the sediment (Johnson et al., 2002; Algar and Boudreau, 2010; Boudreau, 2012; Katsman, 2015).
In addition, aquatic sediments often experience fluctuating loads, produced, for instance, by surface waves due to winds or storms, by swells or tides, and seasonal water level changes. Bubbles react to the mechanical energy of the varying hydrostatic load by rectifying their sizes and adjusting inner pressure, in accordance with the fluctuating overburden load. This is coupled with the process of CH4 diffusion to a growing bubble from within the ambient sediments, responsible for bubble growth (Algar and Boudreau, 2009). Field studies often discern a correlation between episodic ebullition from aquatic sediments with variations in hydrostatic pressure (Martens and Klump, 1980; Miller and Oremland, 1988; Chanton et al., 1989; Mattson and Likens, 1990; Keller and Stallard, 1994; Scandella et al., 2011; Chen and Slater, 2016; Scandella et al., 2016; Chen et al., 2017), which was also recently confirmed by lab observations (Scandella et al., 2017) and numerical studies (Algar et al., 2011b; Katsman, 2019).
However, despite its importance, little is known about the effects of varying wave loading over the bubble growth phase, i.e., from its nucleation to mature configuration at the start of its ascent. A strong coupling between the net solute transport from the ambient sediment to the growing bubble with fluctuating size, along with difficulties in precise measuring and assessing bubble growth rates due to mud opacity, make it extremely complicated to explore this process in situ and to define its controls in aquatic sediments. Only a few studies based on numerical modeling quantified bubble growth under periodic wave loadings in muddy aquatic sediments (e.g., Boudreau et al., 2001; Algar and Boudreau, 2009; Algar et al., 2011b). These studies focused on bubble growth under a semidiurnal tidal loading (wave periods of 12 h) and its effect on processes of rectified diffusion and solute transport (due to pressure oscillations) to the growing bubble. The rectified diffusion was suggested to become important as (∆P/P)2
In the present study, an underlying general quantitative mechanistic pattern and specific features of bubble growth in aquatic sediments, prior to bubble’s ascent, under the action of surface wave loadings, are explored. Bubble growth is simulated under distinct wave characteristics (wave amplitude and period) at various ambient water depths. Results indicate that under the wave action, the bubbles grow faster compared with the no wave case, especially at shallow water depths and under higher amplitude and shorter wave periods. This is attributed to an early appearance of sediment fracturing, and in some cases to intense and frequent fracturing events that appear at the wave trough. Our findings associate this mechanism of accelerated bubble growth with episodic ebullitions at various aquatic sites to be correlated with wind or storm-induced surface waves, which is important in the context of a long-persisting uncertainty related to net CH4 fluxes from shallow aquatic sediments.
Materials and Methods
To analyze the effects of wave-induced periodic loadings on CH4 bubble growth within muddy sediment, we used a coupled mechanical/solute transport numerical model, previously developed in Katsman et al. (2013) and Katsman (2015). This single-bubble model is applicable to fine-grained cohesive (muddy) sediments, where a bubble grows by a crack propagation within the framework of linear elastic fracture mechanics (LEFM) (e.g., Johnson et al., 2002; Boudreau et al., 2005; Best et al., 2006; Barry et al., 2010; Boudreau, 2012). The model simulates the coupled process of diffusion-driven bubble expansion due to a concentration gradient of dissolved CH4 at the bubble surface, and the sediment’s elastic-fracture mechanical response (Broek, 1982; Lawn, 1993; Gross and Seelig, 2017) to bubble growth. The modeling setup (Figure 1A) includes a small penny-shaped bubble seed with dimensions larger than a pore scale, embedded at the symmetry plane of a 3D sediment cell. The bubble’s (crack’s) spatial opening implicitly depends upon the inner bubble pressure, which continuously mounts due to an uninterrupted solute supply from the ambient sediment. This causes the bubble to grow elastically and gain stress intensity factor (Mode I SIF,
where
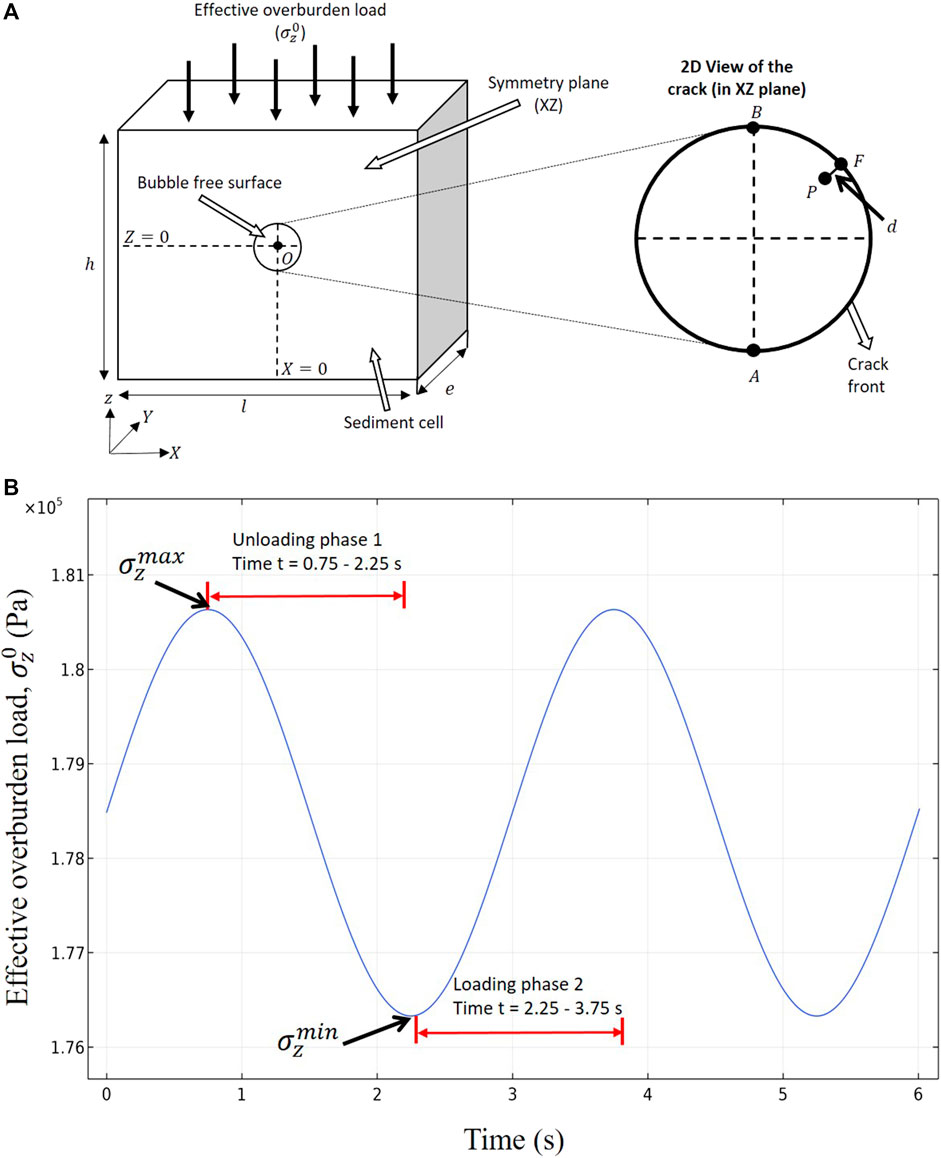
FIGURE 1. Schematic illustration of modeling setup: (A) Computational domain consists of a 3D sediment box cut by a symmetry plane (XZ), with an embedded penny-shaped bubble seed (centered at origin, O). (X, Y, Z) depicts the global coordinate system. Top boundary of sediment is subjected to an effective overburden load,
Under the action of surface waves, the effective water column height
where A is the amplitude, T is the period of pulsation of the surface wave, and t is the time. A corresponding effective overburden load,
For clarity of further analysis, the periodic oscillations in the effective overburden load
Simulations are initiated with a small penny-shaped bubble having a radius of 4 mm (Figure 1A) and continue until the bubble attains mature size and configuration with closed tail (Katsman et al., 2013). This time period is specified as “Bubble maturity time” designated by
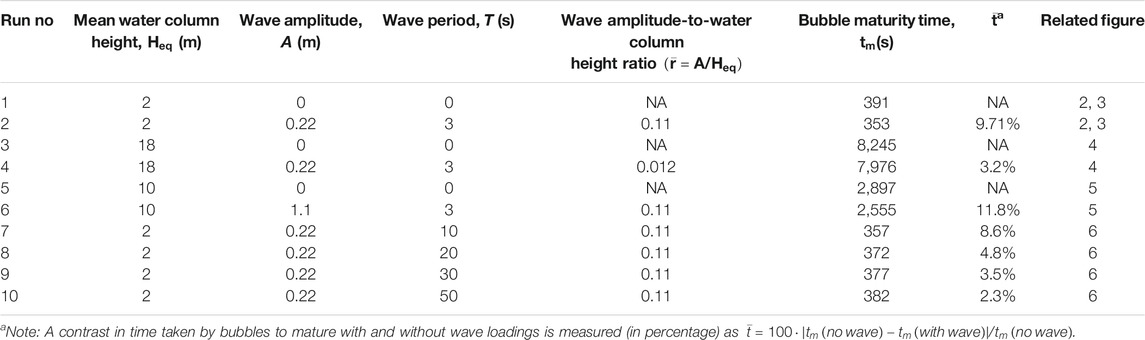
TABLE 1. Input conditions used in simulations: to illustrate 1) a general pattern of bubble growth without and with (runs 1, 2) waves; 2) an effect of water depth (runs 3, 4) over the bubble growth; 3) an effect of wave amplitude-to-water depth ratio (runs 5, 6); and 4) an effect of wave periods (runs 7–10).
Results
Pattern of Bubble Growth Under the Wave Loading
First, we explore the general pattern and specific features of bubble growth under the wave action. In parallel and for comparison, bubble growth is simulated in the absence and presence of wave loadings, with conditions summarized in Table 1 (runs 1, 2, respectively). Corresponding results of evolution of Mode I stress intensity factor at the bubble head,
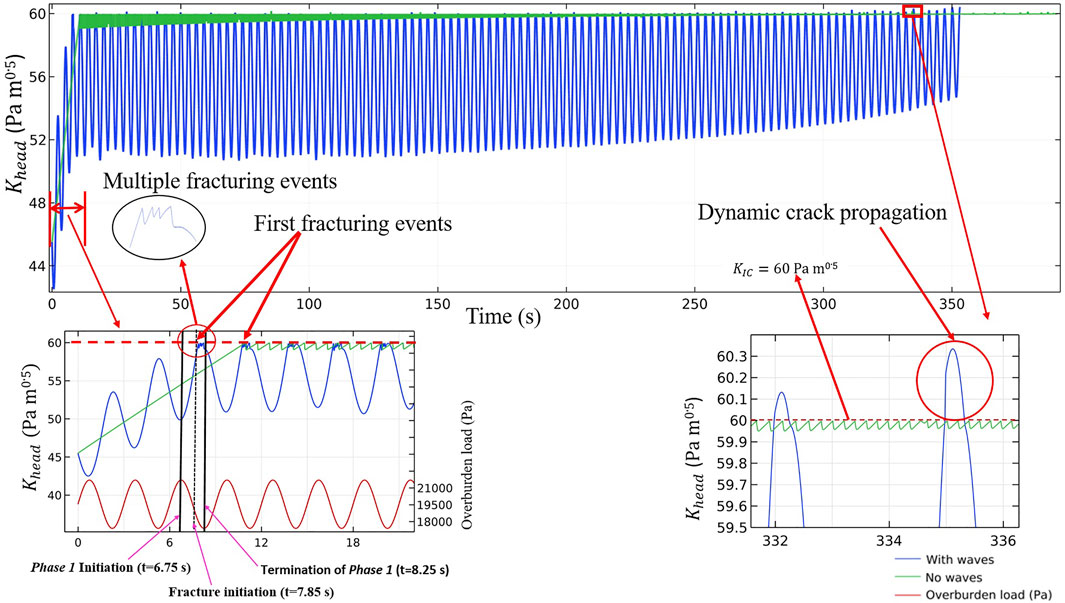
FIGURE 2. The evolution of stress intensity factor at bubble head,
In contrast, in the presence of waves, the stress intensity factor at the bubble head
1. Early fracture initiation due to decline in
2. Intense multiple fracturing events in the unloading stage (phase 1) near the wave trough.
Early fracturing appearance due to a
Intense multiple fracturing events in the unloading stage (phase 1) near wave trough: Under the action of wave loadings, the
As a result of the appearance of these early and multiple fracturing features, the bubble in run 2 earlier attains a larger surface area (e.g., between t = 7.85 and 10.95 s, Figure 2) and thus, grows with a higher total diffusive flux over its surface as compared with the bubble growing under no waves in run 1 (Figure 3). Therefore, bubbles growing under the wave action are able to mature in less time (
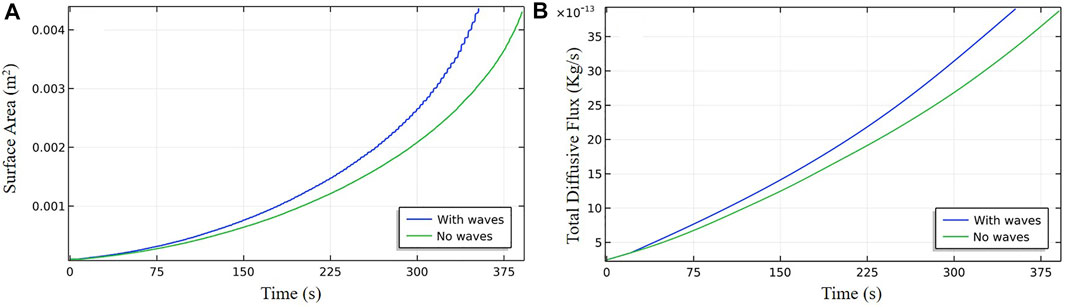
FIGURE 3. Temporal growth of surface area [panel (A)] and total diffusive flux [panel (B)] for bubbles growing in sediment under a 2 m water depth, in the presence (run 2, blue curve) and absence (run 1, green curve) of waves. Attributed to early and multiple fracturing, bubbles growing in the presence of waves gain surface area and total diffusive flux comparatively faster, thus, maturing in less time (
Effect of the Water Depth on Bubble Growth
To explicitly demonstrate the effect of water depth on bubble maturity time,
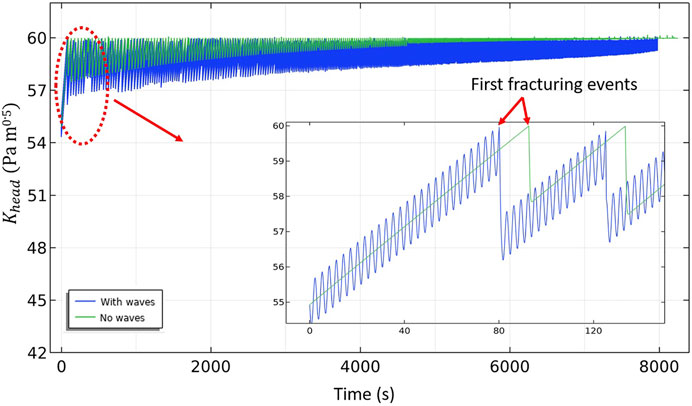
FIGURE 4. Evolution of
Bubbles in deeper water (i.e., under the higher overburden load,
Therefore, in sediments submerged under shallow water depths (as modeled in run 2), bubbles incur early fracturing as well as induce multiple fracturing events (as described in Figure 2) near the wave troughs, sometimes supplemented by a dynamic fracturing regime at a later stage of the bubble growth, which expedites bubble growth (Figure 2). Therefore, a bubble under 2 m of water was able to mature in nearly ∼9.71% (
Role of Ratio of Wave Amplitude to Water Depth Over Bubble Growth
To further explore the role of the ratio of wave amplitude to water depth
The magnitude of fluctuations in
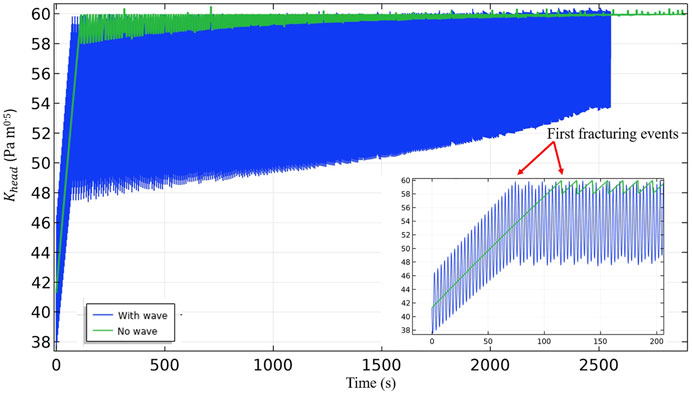
FIGURE 5. Evolution of
Furthermore, following Eq. 2, the rate of change in scaled hydrostatic overburden load (
where
Notably, as attributed to increased water depths, the total solute flux to bubble in run 6 (of orders of ∼
Role of Wave Periods Over Bubble Growth
In order to understand the effect of wave periods (T) over bubble growth, we simulate bubble growth under fixed water column height (
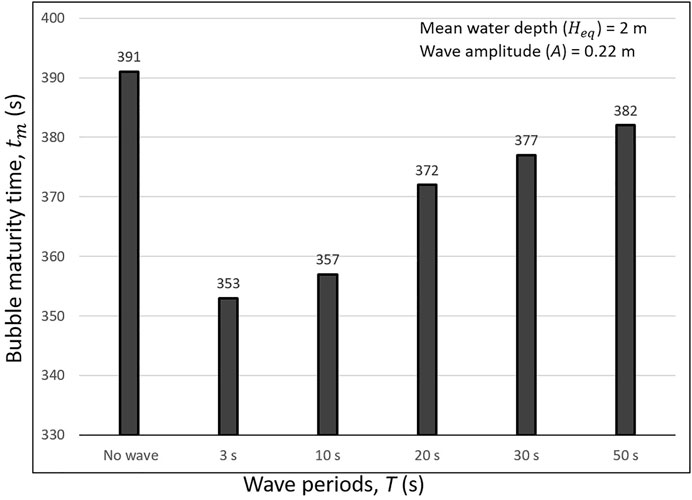
FIGURE 6. Maturity time,
Simulations reveal that smaller period waves expedite bubble growth (Figure 6): for instance, a bubble matures in 353 s when T = 3 s (run 2), compared with 382 s when T = 50 s (run 10). For smaller wave periods, the bubble is exposed to wave trough loadings (i.e., low overburden load) more frequently, over the entire period of its growth. Thus, bubble growth via early and/or multiple fracturing events occurs more frequently in the presence of short period waves. This facilitates bubbles attaining mature size in less time, as seen in Figure 6.
Discussion
Our calculations assert that surface waves developed in the water column with the passage of winds or storms, reduce the duration of the growth phase of bubbles, and thus allow early upward buoyant bubble rise. For instance, the water depth and surface wave characteristics simulated in runs 1 and 2 (Table 1) may be associated with the usual ambient conditions in the shallow littoral zone of Lake Constance, Europe, in the presence of synoptic scale winds from the southwest-west and northeast (Appt et al., 2004; Hofmann et al., 2008). The data in runs 3 and 4 agree with ambient conditions at the 18 m isobaths of Lake Kinneret, Israel, in the presence of Mediterranean summer sea breezes (Serruya, 1975; Zohary et al., 2014). There is a reduction of ∼9% and 3% in the time duration of the bubble growth period at the respective sites in the presence of the surface waves under the modeled conditions.
In shallow water sites (e.g., under water depth 2 m, run 2), at the stage when bubbles gain sufficiently large heights, they are able to grow by inducing a dynamic fracturing style at each wave trough (right inset of Figure 2). This agrees with the principles of LEFM (Broek, 1982; Lawn, 1993; Gross and Seelig, 2017; Sirhan et al., 2019), which assert that a crack grows dynamically (runs unrestrictedly) when mechanical energy dissipated per unit crack increment exceeds the energy required to create new crack surfaces (Lawn, 1993). In our simulation (run 2), the dynamic crack propagation appeared when the crack’s vertical height and total size grew beyond a critical limit (see Sirhan et al., 2019, for details). Such bubbles can unrestrictedly proceed from a dynamic growth stage to a dynamic ascent toward the sediment–water interface and can potentially escape from the sediment (Sirhan et al., 2019), if the wave action halts. Quantifying these processes provides a valuable insight into understanding the observed correlation between winds and enhanced gas effluxes at various sites with microbially mediated CH4 (Miller and Oremland, 1988; Mattson and Likens, 1990; Keller and Stallard, 1994). For example, at Lake Gatun (Panama) average winds of 4–7 m s−1 appear to enhance gas fluxes up to ∼500 ml m−2 h−1. This is about ∼20 ml m−2 h−1 under no wind conditions (in 1.4–4.5 m water depth), ∼98% of which occurred by bubbling (Keller and Stallard, 1994). A gas flux of ∼500 ml m−2 h−1 indicates liberation of nearly 24 × 103 mature bubbles per square meter of the lake surface per hour (assuming a volume of one mature bubble as 21 × 10−9 m3, following the current model) and nearly 960 bubbles in the absence of winds (neglecting CH4 bubble volume loss in the oxidizing zone, which is negligible for rapidly rising bubbles in shallow waters, Katsman, 2019). The high contrast in the amount of the escaping bubbles indicates that they rapidly grow in size, gain maturity in the presence of waves, and are effectively able to escape the sediments. Also, the continuous persistence of intensive bubbling up to 4–6 h (Keller and Stallard, 1994) is indirect evidence of the accelerated permanent bubbles growth that ultimately reach their maturity sizes under the waves. This is especially important for cases when bubble “no-growth” condition (Algar and Boudreau, 2010) occurs within the sediment under no waves, wherein the wave action may induce a persistent bubble growth.
Moreover, intense ebullition in the presence of surface waves can be attributed to a dynamic ascent of mature bubbles, which are pulled out from their stationary positions at a gas horizon and propagate unrestrictedly toward the sediment–water interface (Katsman, 2019). In shallow water depths where wave height is comparable with the water column height (as in run S2, Supplementary Table S3), acceleration in bubble growth (prior to its ascent) is significant (∼30% contrast in the maturity times) and can also significantly decrease the bubble lifespan. However, in other cases simulated in this study, it is smaller (∼2%–12% contrast in the maturity times, Table 1) and contributes to the enhanced ebullition fluxes via the mechanisms discussed above.
Our results indicate that waves with large periods (for example, tides) would have a very marginal effect over the bubble maturity time (as indicated in Figure 6, runs 7–10), as was also suggested previously by Boudreau et al. (2001), Algar and Boudreau (2009), and Algar et al. (2011b). However, a correlation of gas emissions with falling tides observed at a cold seep offshore Vancouver Island, British Columbia, Canada, was attributed to a decreasing pressure on the sub-bottom fluid system (Römer et al., 2016). According to our study, this should shorten the bubble growth period due to the enhanced solute transport (run 2 compared with run 4). Decreased CH4 solubility under the decreasing tidal load can fairly enhance the bubble exsolution (Römer et al., 2016; Blouin et al., 2019).
Moreover, a long period of tidal loading could affect migration of mature bubbles toward the sediment–water interface. For example, Chanton et al. (1989) found at White Oak River estuary, North Carolina, that bubbles release from sediment were closely coupled with daily tidal activities. The rate of bubble liberation rate to the water column was found to increase significantly, when the water column declined from its highest to its lowest water level (at an ambient water depth of ∼70 cm, wave amplitude ∼20 cm;
Bubble growth in muds is linked to the available dissolved CH4 concentration in the ambient sediment, which is site specific, depending on local CH4 production rate (Martens and Klump, 1980; Abegg and Anderson, 1997; Liu et al., 2020), and also to the diffusion process, supplying solute to the bubble (see Supplementary Equation S3). This process is controlled by: 1) the concentration gradient of CH4 at the bubble surface and the ambient dissolved CH4 concentration in the pore waters; and 2) the tortuosity-corrected CH4 diffusion coefficient in the bulk sediment. Under deeper waters, bubbles in mud grow by developing higher inner pressures,
Ambient dissolved CH4 concentrations in pore waters of shallow sediments is a result of a long term CH4 production. Zero CH4 local production rate (Supplementary Equation S2) is used in our simulations to avoid a permanent increase in concentrations within our small computational domain where no CH4 consumption is prescribed. Identical CH4 concentration boundary conditions are prescribed in all the simulations to allow a consistent comparison, associated with supersaturation under all the modeled overburden loads. In the natural settings, such quasi-steady state CH4 concentrations (Adler et al., 2011) as those simulated in this study are produced by spatially separated CH4 production and consumption zones under a small temporal variability in their rates that interchange the solute by diffusion (Martens and Berner, 1977). Modeling these more complex settings in a larger computational domain seem unnecessary for the bubble growth problem studied here in contrast to the bubble migration.
Additionally, the local production rates that rely on a variety of geochemical and environmental factors predefine the ambient CH4 pore water concentrations and differ significantly between the environments (Zamanpour et al., 2020). Persistent fracture-driven bubble growth is also dependent on muddy sediment mechanical properties, suggesting that weaker sediments along with larger CH4 production may significantly expedite bubble growth and induce its ebullition (Zamanpour et al., 2020). Wave action studied in this paper also contributes to this process.
Mud constitutes a mixture of clay- and silt-sized (<63 μm; NEN, 1989; Winterwerp and van Kesteren, 2004) particles. The hygroscopic properties of flat, small clay particles with large surface areas reduce the effective porosity and, thus, mobility of water content through the sediment’s pore structure (Mitchell and Soga, 2005; Sevee, 2010). Therefore, the effective porosity of clayey muds can be much smaller than that of sandy sediment (see Sirhan et al., 2019 and references therein). It can be smaller than 20% of the effective porosity specified in the current paper (Supplementary Table S2). This will hamper the supply of dissolved CH4 and will yield a slower diffusive flux to the growing bubble and, hence, slower bubble growth in muds (e.g., a week-long scale of a bubble’s growth was suggested by Algar et al., 2011b). In this case, even the tides (with shorter periods than the bubble growth time scale) may expedite the bubble growth, by a more frequent exposure to the tide/wave trough loadings, according to our study.
Muddy in situ sediments can maintain partially annealed rise paths (Martens, 1976; Martens and Klump, 1980) formed by the upward migration of older bubbles, leading to the partial breakage of cohesive interparticle bonds (Algar et al., 2011b; Boudreau, 2012). After the initial bubbles leave the sediment, subsequent bubbles with smaller volumes may rise through these tracts, correlated with a temporal reduction in fracture toughness (Algar et al., 2011b) or tensile strength (Scandella et al., 2017) of these conduits or channels. Subsequent bubbles can have mean volumes as low as 1/200 compared with the initially rising bubble in intact sediment (Algar et al., 2011b). In the presence of wave loadings, not only the subsequent bubbles could grow faster, but the vertical conduits or channels through which they rise are also forced to dilate periodically (Scandella et al., 2011), in response to fluctuations in the effective overburden load; paving the way for their “easy” liberation into the water column (e.g., Martens and Klump, 1980; Scandella et al., 2011; Algar et al., 2011b; Scandella et al., 2017). This facilitates a “dynamic” bubble escape from the shallow gas horizon within the sediment under shorter-period waves of higher amplitude traveling in shallow water (Katsman, 2019), and explains the rise of multiple bubbles observed in the field in the presence of wind- or storm-induced surface waves (Martens, 1976; Martens and Klump, 1980; Mattson and Likens, 1990).
Natural lakes occasionally have regions with irregular bathymetry with significant depth changes, for instance, Lake Kinneret in Israel, with a maximum depth of ∼40 m (Zohary et al., 2014). This enforces spatially distinct hydrostatic conditions over the lake (when the ratio,
There is a persistent uncertainty associated with atmospheric CH4 contributed from shallow aquatic sediments (Kirschke et al., 2013). This is largely due to the heterogeneous spatiotemporal nature of bubble growth and migration in aquatic sediments. The current work is intended to better characterize the bubble growth in sediments subjected to periodic wave actions, which allows an evaluation of their connections to bubble emissions to the water column.
Conclusion
We demonstrate that periodic wave loading accelerates growth of bubbles incubated within cohesive fine-grained aquatic sediments. We analyze the specific mechanisms by means of which bubble growth is altered, compared with the calm water/no wave case. The following conclusions can be drawn:
1. Under shallow water depth, bubbles induce early as well as induce multiple fracturing under the troughs of waves passing overhead. At a later stage bubble growth can be supplemented by a dynamic fracturing regime that may contribute to initiation of unrestricted upward migration of bubbles in sediment. However, under deeper water, bubbles induce only early fracturing and no multiple fracturing from passage of wave troughs. Therefore, as the water depth increases, the effectivity of wave loadings to expedite bubble growth decreases.
2. Similar values of the wave amplitude to water depth ratio
3. With an increase in wave periods, the frequency of wave trough unloading (when early fracturing and/or multiple fracturing events occur) decreases over the entire time of bubble growth. Therefore, the time of bubble maturity increases with the increase in wave period.
4. Overall, our modeling suggests that the fastest bubble growth can be predicted when higher-amplitude short-period waves travel in shallow water (i.e., high
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, Further inquiries can be directed to the corresponding author.
Author Contributions
Conceptualization, AP and RK; numerical computations, AP; result validation, RK; formal analysis, AP and RK; original draft preparation, AP; review and editing, funding acquisition and resources, RK. All authors have read and agreed to the published version of the manuscript.
Funding
This project was supported by the Israel Science Foundation, Grant No. 1441-14, by United States-Israel Binational Science Foundation, Grant No. 2018150, and by the Institutional Postdoctoral Fellowships from the University of Haifa, Israel.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed nor endorsed by the publisher.
Acknowledgments
We would like to thank the Editor and two Reviewers for their contributions in enhancing this paper. Improvement of the text by Dr. John K. Hall is greatly appreciated.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.833918/full#supplementary-material
References
Abegg, F., and Anderson, A. L. (1997). The Acoustic Turbid Layer in Muddy Sediments of Eckernföerde Bay, Western Baltic: Methane Concentration, Saturation and Bubble Characteristics. Mar. Geology. 137 (1-2), 137–147. doi:10.1016/S0025-3227(96)00084-9
Adler, M., Eckert, W., and Sivan, O. (2011). Quantifying Rates of Methanogenesis and Methanotrophy in Lake Kinneret Sediments (Israel) Using Pore-Water Profiles. Limnol. Oceanogr. 56 (4), 1525–1535. doi:10.4319/lo.2011.56.4.1525
Algar, C. K., Boudreau, B. P., and Barry, M. A. (2011a). Initial Rise of Bubbles in Cohesive Sediments by a Process of Viscoelastic Fracture. J. Geophys. Res. 116, B04207. doi:10.1029/2010JB008133
Algar, C. K., Boudreau, B. P., and Barry, M. A. (2011b). Release of Multiple Bubbles from Cohesive Sediments. Geophys. Res. Lett. 38, L08606. doi:10.1029/2011GL046870
Algar, C. K., and Boudreau, B. P. (2010). Stability of Bubbles in a Linear Elastic Medium: Implications for Bubble Growth in marine Sediments. J. Geophys. Res. 115, F03012. doi:10.1029/2009JF001312
Algar, C. K., and Boudreau, B. P. (2009). Transient Growth of an Isolated Bubble in Muddy, fine-grained Sediments. Geochimica et Cosmochimica Acta 73 (9), 2581–2591. doi:10.1016/j.gca.2009.02.008
Anderson, A. L., Abegg, F., Hawkins, J. A., Duncan, M. E., and Lyons, A. P. (1998). Bubble Populations and Acoustic Interaction with the Gassy Floor of Eckernförde Bay. Continental Shelf Res. 18 (14-15), 1807–1838. doi:10.1016/S0278-4343(98)00059-4
Appt, J., Imberger, J., and Kobus, H. (2004). Basin-scale Motion in Stratified Upper Lake Constance. Limnol. Oceanogr. 49 (4), 919–933. doi:10.4319/lo.2004.49.4.0919
Barry, M. A., Boudreau, B. P., Johnson, B. D., and Reed, A. H. (2010). First-order Description of the Mechanical Fracture Behavior of fine-grained Surficial marine Sediments during Gas Bubble Growth. J. Geophys. Res. 115, F04029. doi:10.1029/2010JF001833
Bastviken, D., Tranvik, L. J., Downing, J. A., Crill, P. M., and Enrich-Prast, A. (2011). Freshwater Methane Emissions Offset the continental Carbon Sink. Science 331 (6013), 50. doi:10.1126/science.1196808
Best, A. I., Richardson, M. D., Boudreau, B. P., Judd, A. G., Leifer, I., Lyons, A. P., et al. (2006). Shallow Seabed Methane Gas Could Pose Coastal hazard. Eos Trans. AGU 87 (22), 213–217. doi:10.1029/2006EO220001
Best, A. I., Tuffin, M. D. J., Dix, J. K., and Bull, J. M. (2004). Tidal Height and Frequency Dependence of Acoustic Velocity and Attenuation in Shallow Gassy marine Sediments. J. Geophys. Res. 109, B08101. doi:10.1029/2003JB002748
Blouin, A., Sultan, N., Callot, J.-P., and Imbert, P. (2019). Sediment Damage Caused by Gas Exsolution: A Key Mechanism for Mud Volcano Formation. Eng. Geology. 263, 105313. doi:10.1016/j.enggeo.2019.105313
Boudreau, B. P., Algar, C., Johnson, B. D., Croudace, I., Reed, A., Furukawa, Y., et al. (2005). Bubble Growth and Rise in Soft Sediments. Geol 33 (6), 517–520. doi:10.1130/G21259.1
Boudreau, B. P., Gardiner, B. S., and Johnson, B. D. (2001). Rate of Growth of Isolated Bubbles in Sediments with a Diagenetic Source of Methane. Limnol. Oceanogr. 46 (3), 616–622. doi:10.4319/lo.2001.46.3.0616
Boudreau, B. P. (2012). The Physics of Bubbles in Surficial, Soft, Cohesive Sediments. Mar. Pet. Geology. 38 (1), 1–18. doi:10.1016/j.marpetgeo.2012.07.002
Broek, D. (1982). Elementary Engineering Fracture Mechanics. 3rd ed. Boston, Mass: Kluwer Academic Publishers.
Bunz, S., Mienert, J., Bryn, P., and Berg, K. (2005). Fluid Flow Impact on Slope Failure from 3D Seismic Data: a Case Study in the Storegga Slide. Basin Res. 17 (1), 109–122. doi:10.1111/j.1365-2117.2005.00256.x
Chanton, J. P., Martens, C. S., and Kelley, C. A. (1989). Gas Transport from Methane-Saturated, Tidal Freshwater and Wetland Sediments. Limnol. Oceanogr. 34 (5), 807–819. doi:10.4319/lo.1989.34.5.0807
Chen, X., Schäfer, K. V. R., and Slater, L. (2017). Methane Emission through Ebullition from an Estuarine Mudflat: 2. Field Observations and Modeling of Occurrence Probability. Water Resour. Res. 53 (8), 6439–6453. doi:10.1002/2016WR019720
Chen, X., and Slater, L. (2016). Methane Emission through Ebullition from an Estuarine Mudflat: 1. A Conceptual Model to Explain Tidal Forcing Based on Effective Stress Changes. Water Resour. Res. 52 (6), 4469–4485. doi:10.1002/2015WR018058
Citarella, R., and Cricrì, G. (2010). Comparison of DBEM and FEM Crack Path Predictions in a Notched Shaft under Torsion. Eng. Fracture Mech. 77 (11), 1730–1749. doi:10.1016/j.engfracmech.2010.03.012
Coche, A. G. (1974). “Limnological Study of a Tropical Reservoir,” in Lake Kariba: A Man-Made Tropical Ecosystem in Central Africa. Editors E. K. Balon, and A. G. Coche (The Hague, Netherlands: Dr. W. Junk Publishers).
DelSontro, T., Kunz, M. J., Kempter, T., Wüest, A., Wehrli, B., and Senn, D. B. (2011). Spatial Heterogeneity of Methane Ebullition in a Large Tropical Reservoir. Environ. Sci. Technol. 45 (23), 9866–9873. doi:10.1021/es2005545
Esrig, M. I., and Kirby, R. C. (1977). Implications of Gas Content for Predicting the Stability of Submarine Slopes. Mar. Geotechnology 2 (1-4), 81–100. doi:10.1080/10641197709379771
Gross, D., and Seelig, T. (2017). Fracture Mechanics: With an Introduction to Micromechanics. 3rd ed. Berlin: Springer.
Haeckel, M., Suess, E., Wallmann, K., and Rickert, D. (2004). Rising Methane Gas Bubbles Form Massive Hydrate Layers at the Seafloor. Geochimica et Cosmochimica Acta 68, 4335–4345. doi:10.1016/j.gca.2004.01.018
Hofmann, H., Lorke, A., and Peeters, F. (2008). The Relative Importance of Wind and Ship Waves in the Littoral Zone of a Large lake. Limnol. Oceanogr. 53 (1), 368–380. doi:10.4319/lo.2008.53.1.0368
Hovland, M., Gardner, J. V., and Judd, A. G. (2002). The Significance of Pockmarks to Understanding Fluid Flow Processes and Geohazards. Geofluids 2 (2), 127–136. doi:10.1046/j.1468-8123.2002.00028.x
Jain, A. K., and Juanes, R. (2009). Preferential Mode of Gas Invasion in Sediments: Grain-Scale Mechanistic Model of Coupled Multiphase Fluid Flow and Sediment Mechanics. J. Geophys. Res. 114, B08101. doi:10.1029/2008JB006002
Johnson, B. D., Boudreau, B. P., Gardiner, B. S., and Maass, R. (2002). Mechanical Response of Sediments to Bubble Growth. Mar. Geology. 187 (3-4), 347–363. doi:10.1016/S0025-3227(02)00383-3
Katsman, R. (2015). Correlation of Shape and Size of Methane Bubbles in fine-grained Muddy Aquatic Sediments with Sediment Fracture Toughness. J. Struct. Geology. 70, 56–64. doi:10.1016/j.jsg.2014.11.002
Katsman, R. (2019). Methane Bubble Escape from Gas Horizon in Muddy Aquatic Sediment under Periodic Wave Loading. Geophys. Res. Lett. 46 (12), 6507–6515. doi:10.1029/2019GL083100
Katsman, R., Ostrovsky, I., and Makovsky, Y. (2013). Methane Bubble Growth in fine-grained Muddy Aquatic Sediment: Insight from Modeling. Earth Planet. Sci. Lett. 377-378, 336–346. doi:10.1016/j.epsl.2013.07.011
Keller, M., and Stallard, R. F. (1994). Methane Emission by Bubbling from Gatun Lake, Panama. J. Geophys. Res. 99 (D4), 8307–8319. doi:10.1029/92JD02170
Kirschke, S., Bousquet, P., Ciais, P., Saunois, M., Canadell, J. G., Dlugokencky, E. J., et al. (2013). Three Decades of Global Methane Sources and Sinks. Nat. Geosci 6, 813–823. doi:10.1038/ngeo1955
Liu, L., Sotiri, K., Dück, Y., Hilgert, S., Ostrovsky, I., Uzhansky, E., et al. (2020). The Control of Sediment Gas Accumulation on Spatial Distribution of Ebullition in Lake Kinneret. Geo-mar Lett. 40 (4), 453–466. doi:10.1007/s00367-019-00612-z
Martens, C. S., and Berner, R. A. (1977). Interstitial Water Chemistry of Anoxic Long Island Sound Sediments. 1. Dissolved Gases1. Limnol. Oceanogr. 22 (1), 10–25. doi:10.4319/lo.1977.22.1.0010
Martens, C. S. (1976). Control of Methane Sediment-Water Bubble Transport by Macroinfaunal Irrigation in Cape Lookout Bight, North Carolina. Science 192 (4243), 998–1000. doi:10.1126/science.192.4243.998
Martens, C. S., and Val Klump, J. (1980). Biogeochemical Cycling in an Organic-Rich Coastal marine basin-I. Methane Sediment-Water Exchange Processes. Geochimica et Cosmochimica Acta 44 (3), 471–490. doi:10.1016/0016-7037(80)90045-9
Mattson, M. D., and Likens, G. E. (1990). Air Pressure and Methane Fluxes. Nature 347 (6295), 718–719. doi:10.1038/347718b0
Miller, L. G., and Oremland, R. S. (1988). Methane Efflux from the Pelagic Regions of Four Lakes. Glob. Biogeochem. Cycles 2 (3), 269–277. doi:10.1029/GB002i003p00269
Mitchell, J. K., and Soga, K. (2005). Fundamentals of Soil Behavior. 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Nageswaran, S. (1983). Effect of Gas Bubbles on the Seabed Behaviour. Oxford, England: Oxford University. PhD thesis.
NEN (1989). Geotechniek - Classificatie Van Onverharde Grondmonsters, NEN 5104. Delft: Nederlands Normalisatie-instituut.
Ostrovsky, I., and Tęgowski, J. (2010). Hydroacoustic Analysis of Spatial and Temporal Variability of Bottom Sediment Characteristics in Lake Kinneret in Relation to Water Level Fluctuation. Geo-mar Lett. 30 (3), 261–269. doi:10.1007/s00367-009-0180-4
Reed, A. H., Boudreau, B. P., Algar, C., and Furukawa, Y. (2005). “Morphology of Gas Bubbles in Mud: A Microcomputed Tomographic Evaluation,” in Proceedings of The International Conference “Underwater Acoustic Measurements: Technologies & Results”, Heraklion, Crete, Greece, 28th June -1st July 2005. https://apps.dtic.mil/sti/citations/ADA454883.
Römer, M., Riedel, M., Scherwath, M., Heesemann, M., and Spence, G. D. (2016). Tidally Controlled Gas Bubble Emissions: A Comprehensive Study Using Long-Term Monitoring Data from the NEPTUNE Cabled Observatory Offshore Vancouver Island. Geochem. Geophys. Geosyst. 17 (9), 3797–3814. doi:10.1002/2016GC006528
Saunois, M., Bousquet, P., Poulter, B., Peregon, A., Ciais, P., Canadell, J. G., et al. (2016). The Global Methane Budget 2000–2012. Earth Syst. Sci. Data 8 (2), 697–751. doi:10.5194/essd-8-697-2016
Scandella, B. P., Delwiche, K., Hemond, H. F., and Juanes, R. (2017). Persistence of Bubble Outlets in Soft, Methane‐generating Sediments. J. Geophys. Res. Biogeosci. 122 (6), 1298–1320. doi:10.1002/2016JG003717
Scandella, B. P., Pillsbury, L., Weber, T., Ruppel, C., Hemond, H. F., and Juanes, R. (2016). Ephemerality of Discrete Methane Vents in lake Sediments. Geophys. Res. Lett. 43 (9), 4374–4381. doi:10.1002/2016GL068668
Scandella, B. P., Varadharajan, C., Hemond, H. F., Ruppel, C., and Juanes, R. (2011). A Conduit Dilation Model of Methane Venting from lake Sediments. Geophys. Res. Lett. 38 (6), L06408. doi:10.1029/2011GL046768
Serruya, S. (1975). Wind, Water Temperature and Motions in Lake Kinneret: General Pattern. SIL Proc 19 (1), 73–87. doi:10.1080/03680770.1974.11896041
Sevee, J. E. (2010). Effective Porosity Measurement of a marine clay. J. Environ. Eng. 136 (7), 674–681. doi:10.1061/(ASCE)EE.1943-7870.0000205
Shin, H., and Santamarina, J. C. (2010). Fluid-driven Fractures in Uncemented Sediments: Underlying Particle-Level Processes. Earth Planet. Sci. Lett. 299 (1-2), 180–189. doi:10.1016/j.epsl.2010.08.033
Sills, G. C., and Wheeler, S. J. (1992). The Significance of Gas for Offshore Operations. Continental Shelf Res. 12 (10), 1239–1250. doi:10.1016/0278-4343(92)90083-V
Sills, G. C., Wheeler, S. J., Thomas, S. D., and Gardner, T. N. (1991). Behaviour of Offshore Soils Containing Gas Bubbles. Géotechnique 41 (2), 227–241. doi:10.1680/geot.1991.41.2.227
Sirhan, S. T., Katsman, R., and Lazar, M. (2019). Methane Bubble Ascent within fine-grained Cohesive Aquatic Sediments: Dynamics and Controlling Factors. Environ. Sci. Technol. 53 (11), 6320–6329. doi:10.1021/acs.est.8b06848
T. Zohary, A. Sukenik, T. Berman, and A. Nishri (Editors) (2014). Lake Kinneret: Ecology and Management (New York, Heidelberg, Dordrecht and London: Springer), 6.
USEPA (2010). Methane and Nitrous Oxide Emissions from Natural Sources. Washington DC: US Environmental Protection Agency. EPA 430-R-10–001.
Uzhansky, E., Katsnelson, B., Lunkov, A., and Ostrovsky, I. (2020). Spatial and Temporal Variability of Free Gas Content in Shallow Sediments: Lake Kinneret as a Case Study. Geo-mar Lett. 40 (4), 491–505. doi:10.1007/s00367-019-00629-4
Van Kessel, T., and Van Kesteren, W. G. M. (2002). Gas Production and Transport in Artificial Sludge Depots. Waste Manag. 22 (1), 19–28. doi:10.1016/S0956-053X(01)00021-6
Van Kesteren, W., and van Kessel, T. (2002). “Gas Bubble Nucleation and Growth in Cohesive Sediments,” in Finite Sediment Dynamics in the marine Environment. Proceedings in Marine Science. Editors J. C. Winterwerp, and C. Kranenburg (Amsterdam: Elsevier), 5 329–341. doi:10.1016/s1568-2692(02)80025-0
Wheeler, S. J. (1988). A Conceptual Model for Soils Containing Large Gas Bubbles. Géotechnique 38 (3), 389–397. doi:10.1680/geot.1988.38.3.389
Wheeler, S. J. (1990). Movement of Large Gas Bubbles in Unsaturated fine‐grained Sediments. Mar. Geotechnology 9 (2), 113–129. doi:10.1080/10641199009388234
Winterwerp, J. C., and van Kesteren, W. G. M. (2004). Introduction to the Physics of Cohesive Sediment Dynamics in the marine Environment, 6. Amsterdam, Netherlands: Elsevier.
Keywords: methane bubbles, gassy sediment, muddy sediment, bubble growth, sediment fracturing, fracture mechanics, modeling
Citation: Painuly A and Katsman R (2022) Mechanism of Faster CH4 Bubble Growth Under Surface Waves in Muddy Aquatic Sediments: Effects of Wave Amplitude, Period, and Water Depth. Front. Earth Sci. 10:833918. doi: 10.3389/feart.2022.833918
Received: 12 December 2021; Accepted: 21 January 2022;
Published: 17 March 2022.
Edited by:
Michel Michaelovitch Mahiques, University of São Paulo, BrazilReviewed by:
Bernhard Wehrli, ETH Zürich, SwitzerlandVictor Mikhailovich Stepanenko, Lomonosov Moscow State University, Russia
Copyright © 2022 Painuly and Katsman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Regina Katsman, cmthdHNtYW5AdW5pdi5oYWlmYS5hYy5pbA==
 Abhishek Painuly
Abhishek Painuly Regina Katsman
Regina Katsman