Modelling of Critical Acceleration for Regional Seismic Landslide Hazard Assessments by Finite Element Limit Analysis

The critical acceleration model plays an important role in seismic slope stability and determines the predictive accuracy of regional seismic landslide hazard assessments. Recently, the critical acceleration model based on the limit equilibrium method has been used to evaluate the seismic stability of regional slopes. However, when the Hoek-Brown failure criterion is used to evaluate the seismic stability of slopes with angles greater than 60°, the results obtained is unconservative by limit equilibrium method. Therefore, based on the simulation of a typical slope model with finite element limit analysis, prediction equations of the critical acceleration are established. The corresponding results are compared with the prediction results from the limit equilibrium method. This comparison shows that the proposed critical acceleration model has higher predictive accuracy than the limit equilibrium method, especially when the Hoek-Brown failure criterion is used to evaluate the slopes with angles greater than 60°. The proposed model is applicable to the global scope and can be effectively applied to regional seismic landslide hazard assessments.

1 Introduction

Earthquakes have induced a large number of landslides, which buried towns and farmland and damaged infrastructure, causing substantial economic losses and casualties in the disaster area (Qi et al., 2010; Xu et al., 2015; Chen et al., 2018; Fan et al., 2018). Therefore, seismic landslides have been widely studied by geoscience experts. Relevant researchers have made beneficial exploration in the evaluation of slope stability and deformation (Yang et al., 2019a; Yang et al., 2019b; Wu et al., 2020; Yang et al., 2021), the compilation of landslide database (Xu et al., 2012; Xu et al., 2013) and landslide hazard assessment (Caccavale et al., 2017; Chen et al., 2018; Wang et al., 2018; Li and Su, 2021), which provided important theoretical scientific support for exploring the mechanisms driving seismic landslides and reducing seismic landslide disasters. Regional seismic landslide hazard assessment is one of the most important research directions, and the results from these assessments can provide a reference for reconstructing post-earthquake disaster areas and predicting future earthquake-induced landslides.

Traditionally, there are two quantitative methods to evaluate the hazards of regional seismic landslides, including statistical analysis methods and mechanical model methods based on physical slope models. The statistical analysis method mainly uses seismic landslides that have occurred, establishes a mathematical statistical model of these landslides and the related landslide influence factors, and then applies this model to the whole earthquake area. The advantages of this method are that it is based on actual landslides and that the evaluation results are objective; however, this method lacks an understanding of the mechanism of seismic landslides (Xu et al., 2012; Xu et al., 2013). In the mechanical model method, Newmark’s sliding block analysis (Newmark, 1965) (referred to hereinafter as the Newmark method) is commonly used to estimate regional seismic landslide hazards (Jibson et al., 2000; Jibson, 2007; Rodríguez-Peces et al., 2011; Bozzano et al., 2013; Dreyfus et al., 2013; Rodríguez-Peces et al., 2014; Caccavale et al., 2017; Liu et al., 2017; Shinoda and Miyata 2017; Chen et al., 2018; Wang et al., 2018; Li and Su, 2021). In the Newmark method, the slope model should be assumed to be an infinite plane (i.e., an infinite slope), and the failure depth of the slope should be known in advance (usually assumed to be less than 3 m) (Jibson et al., 2000). However, according to previous studies (Wilson and Keefer 1983; Keefer 1984; Huang et al., 2011; Wartman et al., 2013; Li et al., 2021), seismic landslides are widely developed in soil and rock units, and there are many failure modes. This shows that the assumption of an infinite slope may be too simplistic in many cases, thereby underestimating the risk area of sliding. Some scholars have realized the limitations of the Newmark method in regional seismic landslide hazard assessment and put forward measures to improve the predictive accuracy of the Newmark method (Shinoda and Miyata 2017; Jin et al., 2019; Zang et al., 2020). Although the predictive accuracy of the Newmark method has been improved through some measures (e.g., modified strength parameters), the limitations of the Newmark method are still difficult to overcome (Shinoda and Miyata 2017; Jin et al., 2019; Zang et al., 2020). Therefore, it is urgent and important to develop new mechanical model methods for regional seismic landslide hazard assessments.

Some scholars have recently proposed new mechanical models and used these models to carry out regional seismic landslide hazard assessments (Saade et al., 2016; Yuqiao et al., 2019; Tsai et al., 2019). Compared with the traditional Newmark model, the mechanical models proposed by these scholars have made the following improvements. 1) The modified models are not limited to a single shallow sliding mode. 2) The failure depth of the slope does not need to be assumed. 3) The strength parameters do not need to be reduced to improve the predictive accuracy of the model. 4) Moreover, the modified models have obvious advantages in predicting the potential sliding area. Although these mechanical models provide a new perspective for regional earthquake landslide hazard assessments, they are still not sufficiently comprehensive as they have the following shortcomings. 1) For Saade et al., 2016 and Yuqiao et al., 2019, obtaining the critical acceleration of the slope with the limit equilibrium method (LEM) and the finite element method (FEM) requires many iterative calculations, which are estimated by trial and error and may therefore affect the calculation efficiency. 2) Saade et al., 2016, the safety factor and critical acceleration of the slope calculated by the Hoek-Brown (HB) criterion will be overestimated for steep slopes (Li et al., 2009; Li et al., 2019). 3) For Yuqiao et al., 2019, the mechanical model requires a slope angle <45°. 4) For Tsai et al., 2019, 12 equations and six steps are needed to evaluate the permanent displacement of landslides caused by earthquakes, which makes it difficult for engineers to quickly evaluate earthquake-induced landslide hazards.

A modified model of the critical acceleration for regional seismic landslide hazard assessments is proposed based on the work of Saade et al. (2016) to overcome the limitations of the above mechanical models. In this model, finite element limit analysis (FELA) is used to build a simplified slope model, and the material strength parameter and slope angle are taken as variables to conduct simulations of the slopes. Through two-step regression analysis, the prediction equations for the strength parameters, slope angle and critical acceleration are obtained. The predicted results of the proposed model are compared with those of the Newmark method and the LEM (Saade et al., 2016). The validity of the proposed model is verified through this comparison. In addition, the proposed model can be effectively applied to regional seismic landslide hazard assessments.

2 Modelling of Slope Critical Acceleration Model

2.1 Review of the Mechanical Modelling Methods

2.1.1 LEM

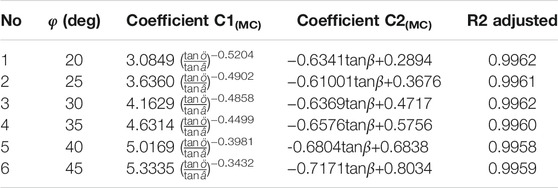
Saade et al. (2016) conducted a series of numerical simulations to establish the predicted equations of linear function between the slope angle β, the unit weight γ, strength parameters and the critical acceleration (A_c). In addition, Saade et al. (2016) used the Mohr-Coulomb (MC) failure criterion and the HB failure criterion to calculate the critical acceleration when the slope angle <45° and when the slope angle ≥45°, respectively. The prediction equations of two linear functions for critical acceleration is as follows:

$A_{c\left(MC\right)}=C{1}_{\left(MC\right)}\frac{c}{\gamma H}+C{2}_{\left(MC\right)}(1)$

$A_{c\left(HB\right)}=C{1}_{\left(HB\right)}\ln \frac{{\sigma }_{ci}}{\gamma H}+C{2}_{\left(HB\right)}(2)$

Where A_c(MC) is the critical acceleration for the MC failure criterion, c is the cohesion, γ is the unit weight, H is the slope height, C1_(MC) is the coefficient related to slope angle β and friction angle φ for the MC failure criterion, and C2_(MC) is the coefficient related to slope angle β for the MC failure criterion, A_c(HB) is the critical acceleration for the HB failure criterion, σ_ci is unconfined compressive strength, and C1_(HB) and C2_(HB) are the coefficient related to slope angle β for the HB failure criterion.

2.1.2 FELA

In this study, FELA can be used to obtain the collapse load of slope (Lyamin et al., 2005; Sloan 2013; Ali et al., 2016). By establishing strict upper and lower bounds with a certain level of error, it is possible to accurately estimate the collapse load. For a given problem, L is the lower limit of the collapse load and U is the upper limit of the collapse load. Then, the estimate of the exact solution is simply taken as the average of the upper and lower limits:

$M=\frac{L+U}{2}(3)$

In addition, the exact solution is denoted e. Since L ≤ e ≤ U, the following expressions can be derived:

$M\left(1-\epsilon \right)\le e\le M\left(1+\epsilon \right)(4)$

$\epsilon =\frac{U-L}{U+L}(5)$

where ε is the relative error. Previous experience shows that when appropriate upper and lower bounds are used, the actual error of the average value is usually less than the estimated value. Hence, the average value is an excellent estimate of the exact solution. Therefore, we calculate the upper—and lower-limit solutions of the critical acceleration in this paper. The average bound solution of the critical acceleration is obtained according to the upper- and lower-limit solutions of the critical acceleration. The critical accelerations mentioned hereinafter are all average bound solutions. Detailed information about the technologies and solution algorithms used in FELA can be found in the literature (Sloan 1988; Sloan 1989; Lyamin and Sloan 2002a; Lyamin and Sloan 2002b; Lyamin et al., 2005; Sloan 2013; Krabbenhoft and Lyamin, 2015; Li et al., 2019).

3 Parametric Study

3.1 Calculation Settings and Input Parameters

At present, the design using pseudostatic analysis is usually based on the horizontal seismic coefficient (k_h). The critical acceleration mentioned hereafter corresponds to the critical horizontal seismic coefficient (k_c) multiplied by the gravitational acceleration. FELA can directly solve the ultimate load of a slope subjected to an earthquake (such as the critical horizontal acceleration) without requiring iterative calculations, thereby significantly reducing the computational effort (Sloan 2013; Utili and Abd 2016).

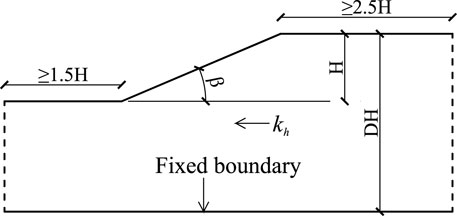
A typical slope model (slope height H is 30 m; unit weight γ is 22 kN/m³) is applied for parametric study (Figure 1). To obtain the minimum critical acceleration for the MC failure criterion, DH is set as 100 m when the slope height is 30 m (Loukidis et al., 2003; Saade et al., 2016). Besides, to eliminate the influence of the lateral boundary on the sliding surface of the slope, the lateral boundary is set away from the slope surface. The bottom boundary of the slope model is fixed. The numerical model uses the adaptive mesh generation method, in which the number of adaptive iterations is 3, the initial number of elements is 2,000, and the maximum number of elements is 4,000. The control variable of adaptive meshing is shear dissipation. The mesh refinement factor is 0.25, and the mesh coarsening factor is 1.50.

FIGURE 1

FIGURE 1. Simple slope model.

Based on Saade et al., 2016, we also use the MC failure criterion and HB failure criterion to calculate the critical acceleration of the slope when the slope is less than 45° and when the slope is greater than or equal to 45°, respectively. Table 1 and Table 2 show the slope angle and strength parameters for the two failure criteria. For each combination described in Table 1 and Table 2, two slope models (including the upper-limit solution and lower-limit solution) are established. While keeping the gravity load constant, the horizontal load multiplier is maximized (lower-bound simulation) and minimized (upper-bound simulation), and the critical horizontal acceleration is calculated. The results of finite element discretization of the upper- and lower-limit solutions of the MC failure criterion and HB failure criterion are shown in Figure 2.

TABLE 1

TABLE 1. Calculation parameters of the MC failure criterion.

TABLE 2

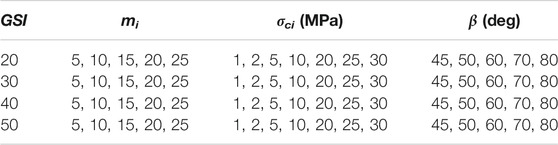
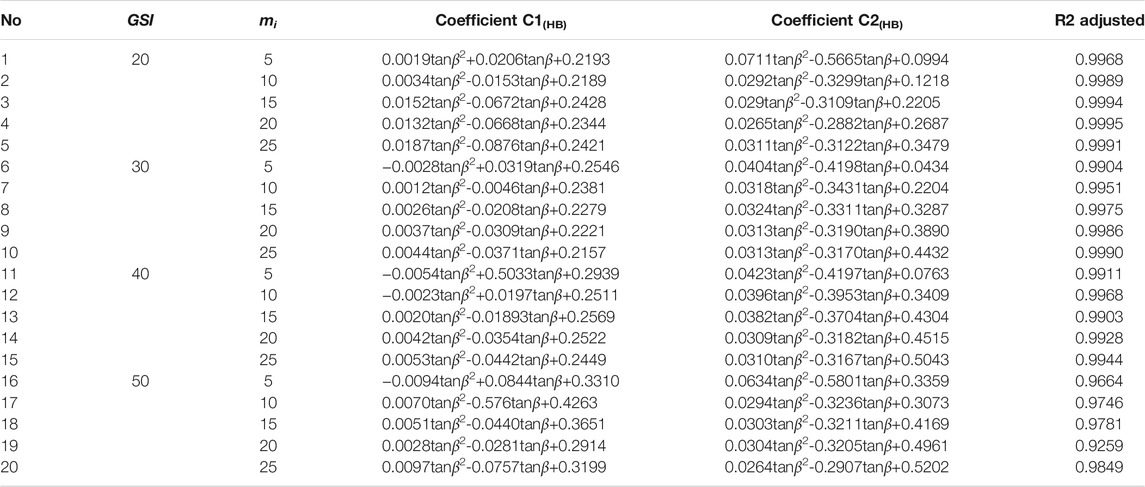
TABLE 2. Calculation parameters of the HB failure criterion.GSI is geological strength index and m_i is rock-type constant.

FIGURE 2

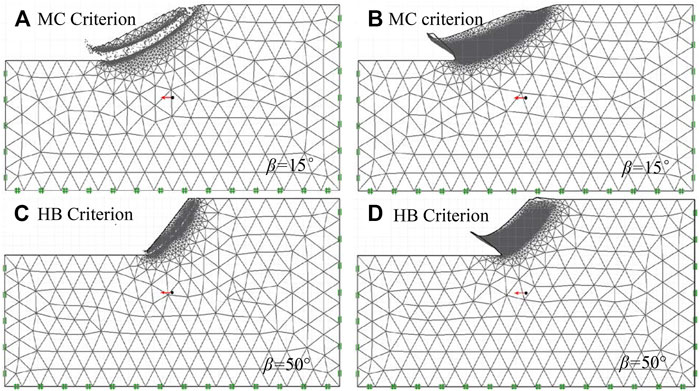
FIGURE 2. Examples of finite element discretization: (A–C) lower-bound simulations and (B–D) upper-bound simulations.

3.2 Regression Equations

3.2.1MC Failure Criterion

Based on the Saade et al., 2016, we use the same linear function, as shown in Eq 1. Figure 3A shows the relationship between the critical acceleration and non-dimensional term (c/γH) when the friction angle is 33°. For each friction angle between 25° and 45°, similar curves are generated (with increments of 5°). According to different functions of slope angle β, the C1_(MC) and C2_(MC) are obtained respectively, as shown in Figures 3B,C. In addition, the optimal fit equations of the C1_(MC) and C2_(MC) for other friction angles are considered in this study, as shown in Table 3. The C1_(MC) and C2_(MC) of any other friction angle can be calculated by interpolation method. The fit index (R2 adjusted) is greater than 0.99 for any condition. Figure 4 shows the predicted and calculated results of critical acceleration using LEM, Newmark method and FELA when the friction angle is 30°, cohesion is 20 kPa and 15°≤β < 45°. From Figure 4, the results of the Newmark method seriously overestimate the critical acceleration: A_cNewmark = 1.6707A_c(MC)-0.0179 (Saade et al., 2016). However, the results when using FELA are in good agreement with the critical acceleration: A_cFELA = 1.0827A_c(MC)-0.0233. This is very consistent with the results reported by Saade et al. (2016) using the LEM: A_cLEM = 1.0262A_c(MC)-0.0207.

FIGURE 3

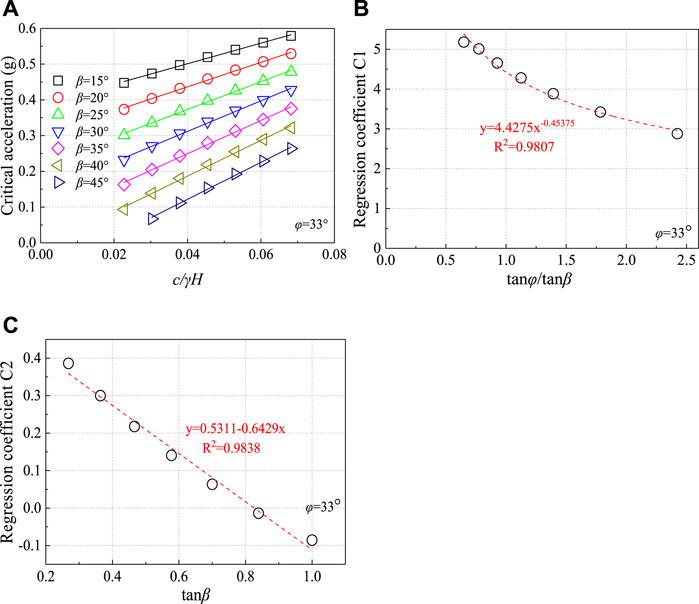
FIGURE 3. Example of (A) A_c versus c/γH and (B) coefficient C1_(MC) and (C) coefficient C2_(MC) when friction angle is 33°.

TABLE 3

TABLE 3. Equations of C1_(MC) and C2_(MC) (slope angle β < 45°).

FIGURE 4

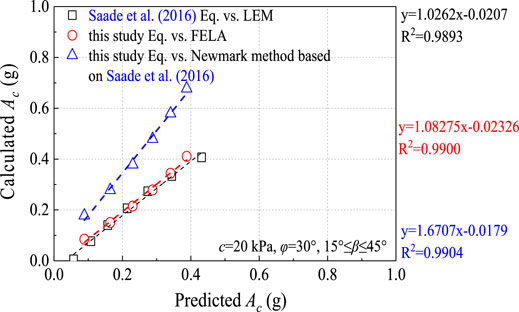
FIGURE 4. Comparison between the A_c values predicted and calculated with the LEM, Newmark method, and FELA for c = 20 kPa, φ = 30° and 15°≤β < 45°.

3.2.2 HB Failure Criterion

Based on Saade et al., 2016, we also use the same linear function, as shown in Eq 2. Figure 5A shows the relationship between the critical acceleration and non-dimensional term (σ_ci/γH) when the GSI is 20 and m_i is 25. For each GSI (20, 30, 40, 50) and m_i (5, 10, 15, 20, 25), similar curves are generated. According to different functions of slope angle β, the C1_(HB) and C2_(HB) are obtained respectively, as shown in Figures 5B,C. In addition, the optimal fit equations of the C1_(HB) and C2_(HB) for other GSI-m_i conditions are considered in this study, as shown in Table 4. The C1_(HB) and C2_(HB) of any other conditions can be calculated by interpolation method. The fit index (R2 adjusted) is greater than 0.92 for any conditions. Figure 6 shows the predicted and calculated results of critical acceleration using the LEM, the Newmark method and FELA when the GSI is 20, m_i is 25, σ_ci is 5 MPa and 45°≤β ≤ 80°. As shown in Figure 6, the results of the Newmark method substantially overestimate the critical acceleration: A_cNewmark = 1.8819A_c(HB)+0.0006 (Saade et al., 2016). However, the results when using FELA are in good agreement with the critical acceleration: A_cFELA = 1.02454A_c(HB)−0.00134. This is very consistent with the results reported by Saade et al. (2016) using the LEM: A_cLEM = 1.0218A_c(HB)+0.0006.

FIGURE 5

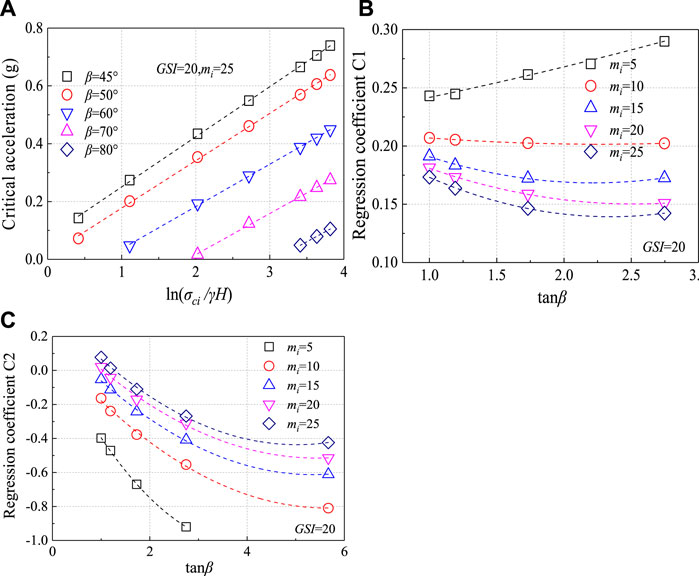
FIGURE 5. Example of (A) A_c versus ln (σ_ci/γH), (B) coefficient C1 and (C) coefficient C2 for GSI = 20 and m_i = 25.

TABLE 4

TABLE 4. Equations of C1_(HB) and C2_(HB) (slope angle β ≥ 45°).

FIGURE 6

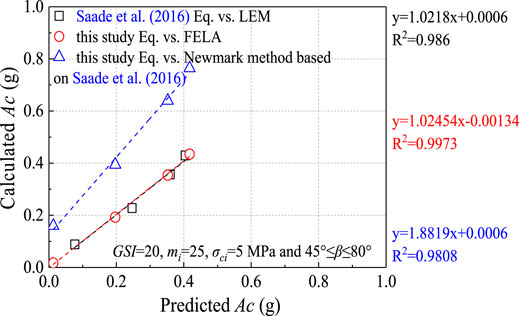
FIGURE 6. Comparison between the A_c values predicted and calculated with the LEM, Newmark method, and FELA for GSI = 20, m_i = 25, σ_ci = 5 MPa and 45°≤β ≤ 80°.

3.3 Comparison of the LEM and FELA Results

From Section 3.2, specific strength parameters are selected to compare the critical acceleration values predicted by the LEM and FELA. This shows that the two methods have good consistency. However, to extend the predicted regression equation to additional conditions, the results of other strength parameters and geometric parameters need to be further tested to assess their validity, especially when used the HB failure criterion. Notably, since the FELA results are closer to the real solution than the LEM results, the calculated critical accelerations adopt the results from the FELA simulation (Li et al., 2009; Sloan 2013; Li et al., 2019) as the Y-axis in Figure 7 and Figure 8. Figure 7 compares the results of predicted A_c and FELA simulation for c = 20kPa, and φ = 25° and φ = 45° at variable β when use MC failure criterion. This shows that the regression equations from the LEM and FELA are in good agreement under different strength parameters. This is consistent with the conclusion of Loukidis et al. (2003).

FIGURE 7

FIGURE 7. Comparison between the A_c values predicted and calculated with FELA for c = 20 kPa, φ = 25° and 45° and 15°≤β < 45° when using the MC failure criterion.

FIGURE 8

FIGURE 8. Comparison between the A_c values predicted and calculated with FELA for m_i = 25, σ_ci = 5 and 25 MPa, 45°≤β ≤ 80° and GSI = 20, 30, 40 and 50 when using the HB failure criterion. (A) GSI = 20 and 30 and σ_ci = 5 MPa; (B) GSI = 40 and 50 and σ_ci = 5 MPa; (C) GSI = 20 and 30 and σ_ci = 25 MPa; and (D) GSI = 40 and 50 and σ_ci = 25 MPa.

Figure 8 compares the Ac values predicted and calculated with FELA for m_i = 25, σ_ci = 5 and 25 MPa, 45°≤β ≤ 80° and GSI = 20, 30, 40 and 50 when using the HB failure criterion. Figure 8 shows that the A_c(HB) values predicted and calculated with FELA are very consistent under any combination of parameters (the relationship is almost one to one). However, the A_c(HB) values predicted with the LEM and FELA are not consistent, and the difference between these values increases gradually as the strength parameter and slope angle increase. Taking Figures 8A,D as an example, when GSI = 20, m_i = 25, and σ_ci = 5 MPa, the regression equation from Saade et al. (2016) is y = 1.2594x-0.1004, whereas when GSI = 50, m_i = 25, and σ_ci = 25 MPa, the regression equation from Saade et al. (2016) is y = 1.9568x-1.1260. When the slope angle β is 70°, the predicted critical acceleration obtained by the LEM regression equation is 29.76–86.58% higher than that obtained by the FELA regression equation. In addition, the FELA regression equation can accurately estimate the critical acceleration of slopes with 60°<β ≤ 80°, which is difficult to determine with the regression equation from Saade et al. (2016).

4 Examples

From Sections 3.2 and 3.3, we compare the A_c values predicted and calculated with FELA when H is 30 m and γ is 22 kN/m³. To further test the influence of the slope height and unit weight on the regression equation, Table 5 and Table 6 compares the A_c values predicted and calculated with FELA for different slope heights (H is 10 and 50 m) and unit weights (γ is 18 kN/m³ and 28 kN/m³). From Table 5 and Table 6, at a certain slope height and unit weight, the larger the slope angle is, the larger the error in the critical acceleration predicted by the LEM. The critical acceleration predicted and calculated by FELA are in good agreement.

TABLE 5

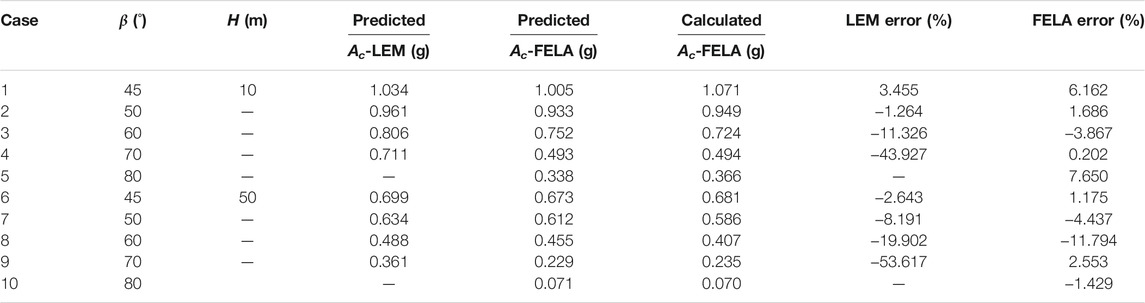
TABLE 5. Comparison between the results of predicted A_c and FELA simulation for different slope heights and slope angles (Note: GSI is 40, m_i is 25, γ is 22 kN/m³, σ_ci is 10 MPa).

TABLE 6

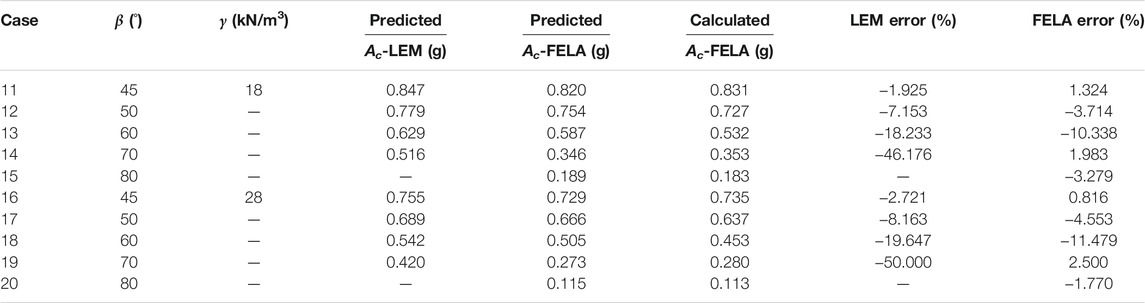
TABLE 6. Comparison between the results of predicted A_c and FELA simulation for different unit weights and slope angles (Note:GSI is 40, m_i is 25, H is 30 m, σ_ci is 10 MPa).

Case

Case 1. is a 10-m-tall slope with β = 45° composed of rock with GSI is 40, m_i is 25, γ is 22 kN/m³, σ_ci is 10 MPa.

1) The process for predicted critical acceleration of LEM from the regression coefficient (Saade et al., 2016) and Eq 2 is as follows:

$\begin{array}{l}\mathrm{Pr}edicted{A}_{cLEM\left(HB\right)}=C{1}_{\left(HB\right)}\ln \frac{{\sigma }_{ci}}{\gamma H}+C{2}_{\left(HB\right)}\\ =\left(0.020\tan {45}^2-0.070\tan 45+0.258\right)\ln \frac{10000}{22\times 10}+\left(0.048\tan {45}^2-0.387\tan 45+0.578\right)\\ =1.034\end{array}$

2) The process for predicted critical acceleration of FELA from the 15th regression coefficient in Table 4 in combination with Eq 2 is as follows:

$\begin{array}{l}\mathrm{Pr}edicted{A}_{cFELA\left(HB\right)}=C{1}_{\left(HB\right)}\ln \frac{{\sigma }_{ci}}{\gamma H}+C{2}_{\left(HB\right)}\\ =\left(0.005\tan {45}^2-0.044\tan 45+0.245\right)\ln \frac{10000}{22\times 10}+\left(0.031\tan {45}^2-0.317\tan 45+0.504\right)\\ =1.005\end{array}$

5 Discussion

In the existing mechanical model framework of earthquake-induced permanent displacements, there are four crucial factors that determine the final predicted results for a fixed study area: the digital elevation model resolution, the material strength parameter, the empirical sliding displacement model and the critical acceleration model. The digital elevation model, material strength parameter and empirical sliding displacement model are subjective factors determined by engineers. Every engineer may obtain different values for the material strength parameter in the same region, and there are also differences in the empirical sliding displacement models in each region. However, the critical acceleration model is an objective and unified factor that can serve global applications and plays an important role in the framework of earthquake-induced permanent displacements. In addition, critical acceleration can not only be used as a criterion to evaluate the susceptibility of seismic landslides (Chen et al., 2014), but also be used to evaluate the hazard of seismic landslides by comparing with known peak ground acceleration (Chen et al., 2018). Therefore, it is of great significance to establish a reliable critical acceleration model for regional seismic landslide hazard assessments.

In previous studies, due to the inherent limitations of the traditional Newmark method and its modified versions, the calculated critical accelerations are substantially different from the numerical simulations. Compared with the Newmark method, the critical acceleration models from Saade et al. (2016), Yuqiao et al., 2019, Tsai et al. (2019) and this study offer obviously higher predictive accuracy, providing strong support for regional seismic landslide hazard assessments. In addition, in the regional scale analysis, the vertical acceleration, slope direction, groundwater conditions, water content, material degradation and rock slope disturbance coefficient may affect the critical acceleration model, which were not discussed in this study. Therefore, the development of a more comprehensive critical acceleration model should be the direction of future research. However, our model can directly estimate strength parameters from a good engineering geological description while still providing an accurate quantitative index, which can quickly measure the behaviour of a seismic slope at a regional scale.

On the other hand, Li et al. (2008) found that the difference of safety factor from limit analyses and LEM is less than 4% for steep slopes when used the HB failure criterion. However, Li et al. (2008) reported this conclusion when the safety factor of the slope is near 1. Saade et al. (2016) did not seem to notice this phenomenon. In addition, for lower GSI values (GSI ≤ 50), the stability numbers of slope (the stability number is equal to σ_ci/γHF, wherein F is the safety factor of slope) obtained using the LEM are 18–30% lower than the average bound solutions obtained with FELA (Li et al., 2009). Moreover, the σ_ci/γHF from the LEM are close to the results of FELA when β ≤ 60°. However, the difference of the σ_ci/γHF between FELA and the LEM tends to be substantial when β ≥ 75° (Li et al., 2019). Therefore, according to the research of Li et al. (2009, 2019), we revised the model from Saade et al. (2016).

6 Conclusion

Our model improves the limitations of previous mechanical models for regional seismic landslide hazard assessments. Herein, FELA is used to calculate the average bound solution of the critical acceleration of the simplified slope model. The proposed model of critical acceleration is not limited to failures of shallow sliding slopes nor does it require the failure depth to be assumed in advance. The MC failure criterion and the HB failure criterion are used to simulate the seismic behaviour of soil and rock slopes. The prediction equations for the critical horizontal acceleration, material strength and slope gradient are established. The corresponding results are compared with the prediction results from the Newmark sliding analysis and the LEM. The results show that the predictive accuracy of FELA and the LEM is significantly higher than that of the Newmark sliding analysis. When the MC failure criterion is used, the prediction results from the FELA and LEM regression equations are consistent. However, the prediction results from the FELA and LEM regression equations are significantly different, especially when the slope gradient is greater than 60° and uses HB failure criterion. In general, the predictive accuracy of our model is higher than that of the LEM. Therefore, the proposed model can be effectively applied to regional seismic landslide hazard assessments.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material further inquiries can be directed to the corresponding authors.

Author Contributions

CL: Conceptualization, Investigation, Writing—original draft, Writing—review and editing. SW: Formal analysis, Investigation, Writing—review and editing, XX: Methodology, Resources, Writing—review and editing, Supervision, XQ: Formal analysis, Investigation, Writing—review and editing, Project administration, Funding acquisition.

Funding

This study has been financially supported by National Natural Science Foundation of China (Grant No. 41867040), Qiandongnan Science and Technology plan project: Study on the consistency of Hoek Brown parameter and equivalent Mohr Coulomb parameter in slope stability calculation, Qiandongnan Science and technology plan project ((2019)No.107), National Natural Science Foundation of China (Grant No.42107195) and National Natural Science Foundation of China (Grant No. 52069007).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, A., Lyamin, A. V., Huang, J., Li, J. H., Cassidy, M. J., and Sloan, S. W. (2016). Probabilistic Stability Assessment Using Adaptive Limit Analysis and Random fields. Acta Geotech. 12, 937–948. doi:10.1007/s11440-016-0505-1

CrossRef Full Text | Google Scholar

Bozzano, F., Esposito, C., Martini, G., Martino, S., Prestininzi, A., Rinaldis, D., et al. (2013). Earthquake-reactivated Landslide Scenarios in Southern Italy Based on Spectral-Matching Input Analysis. Bull. Earthquake Eng. 11 (6), 1927–1948. doi:10.1007/s10518-013-9477-9

CrossRef Full Text | Google Scholar

Caccavale, M., Matano, F., and Sacchi, M. (2017). An Integrated Approach to Earthquake-Induced Landslide hazard Zoning Based on Probabilistic Seismic Scenario for Phlegrean Islands (Ischia, Procida and Vivara), Italy. Geomorphology 295, 235–259. doi:10.1016/j.geomorph.2017.07.010

CrossRef Full Text | Google Scholar

Chen, X.-L., Liu, C.-G., Yu, L., and Lin, C.-X. (2014). Critical Acceleration as a Criterion in Seismic Landslide Susceptibility Assessment. Geomorphology 217 (15), 15–22. doi:10.1016/j.geomorph.2014.04.011

CrossRef Full Text | Google Scholar

Chen, X., Liu, C., and Wang, M. (2018). A Method for Quick Assessment of Earthquake-Triggered Landslide Hazards: a Case Study of the Mw6.1 2014 Ludian, China Earthquake. Bull. Eng. Geol. Environ. 78 (4), 2449–2458. doi:10.1007/s10064-018-1313-7

CrossRef Full Text | Google Scholar

Dreyfus, D., Rathje, E. M., and Jibson, R. W. (2013). The Influence of Different Simplified Sliding-Block Models and Input Parameters on Regional Predictions of Seismic Landslides Triggered by the Northridge Earthquake. Eng. Geology. 163, 41–54. doi:10.1016/j.enggeo.2013.05.015

CrossRef Full Text | Google Scholar

Fan, X., Scaringi, G., Xu, Q., Zhan, W., Dai, L., Li, Y., et al. (2018). Coseismic Landslides Triggered by the 8th August 2017 Ms 7.0 Jiuzhaigou Earthquake (Sichuan, China): Factors Controlling Their Spatial Distribution and Implications for the Seismogenic Blind Fault Identification. Landslides 15 (5), 967–983. doi:10.1007/s10346-018-0960-x

CrossRef Full Text | Google Scholar

Huang, R., Xu, Q., and Huo, J. (2011). Mechanism and Geo-Mechanics Models of Landslides Triggered by 5.12 Wenchuan Earthquake. J. Mt. Sci. 8 (2), 200–210. doi:10.1007/s11629-011-2104-9

CrossRef Full Text | Google Scholar

Jibson, R. W., Harp, E. L., and Michael, J. A. (2000). A Method for Producing Digital Probabilistic Seismic Landslide hazard Maps. Eng. Geol. 58 (3), 271–289. doi:10.1016/s0013-7952(00)00039-9

CrossRef Full Text | Google Scholar

Jibson, R. W. (2007). Regression Models for Estimating Coseismic Landslide Displacement. Eng. Geol. 91 (2), 209–218. doi:10.1016/j.enggeo.2007.01.013

CrossRef Full Text | Google Scholar

Jin, K. P., Yao, L. K., Cheng, Q. G., Xing, A. G., and Xing, A. G. (2019). Seismic Landslides hazard Zoning Based on the Modified Newmark Model: a Case Study from the Lushan Earthquake, China. Nat. Hazards 99 (1), 493–509. doi:10.1007/s11069-019-03754-6

CrossRef Full Text | Google Scholar

Keefer, D. K. (1984). Landslides Caused by Earthquakes. Geol. Soc. America Bull. 95 (4), 406–421. doi:10.1130/0016-7606(1984)95<406:lcbe>2.0.co;2

CrossRef Full Text | Google Scholar

Krabbenhoft, K., and Lyamin, A. V. (2015). Strength Reduction Finite-Element Limit Analysis. Géotechnique Lett. 5 (4), 250–253. doi:10.1680/jgele.15.00110

CrossRef Full Text | Google Scholar

Li, A.-J., Qian, Z., Jiang, J.-C., and Lyamin, A. (2019). Seismic Slope Stability Evaluation Considering Rock Mass Disturbance Varying in the Slope. KSCE. J. Civ. Eng. 23 (3), 1043–1054. doi:10.1007/s12205-019-0963-8

CrossRef Full Text | Google Scholar

Li, A. J., Lyamin, A. V., and Merifield, R. S. (2009). Seismic Rock Slope Stability Charts Based on Limit Analysis Methods. Comput. Geotech. 36 (1–2), 135–148. doi:10.1016/j.compgeo.2008.01.004

CrossRef Full Text | Google Scholar

Li, A. J., Merifield, R. S., and Lyamin, A. V. (2008). Stability Charts for Rock Slopes Based on the Hoek-Brown Failure Criterion. Int. J. Rock Mech. Mining Sci. 45 (5), 689–700. doi:10.1016/j.ijrmms.2007.08.010

CrossRef Full Text | Google Scholar

Li, C., and Su, L. (2021). Influence of Critical Acceleration Model on Assessments of Potential Earthquake-Induced Landslide Hazards in Shimian County, Sichuan Province, China. Landslides 18, 1659–1674. doi:10.1007/s10346-020-01578-1

CrossRef Full Text | Google Scholar

Li, C., Su, L., Liao, H., Zhang, C., and Xiao, S. (2021). Modeling of Rapid Evaluation for Seismic Stability of Soil Slope by Finite Element Limit Analysis. Comput. Geotechnics 133 (9), 104074. doi:10.1016/j.compgeo.2021.104074

CrossRef Full Text | Google Scholar

Liu, J., Shi, J., Wang, T., and Wu, S. (2017). Seismic Landslide hazard Assessment in the Tianshui Area, China, Based on Scenario Earthquakes. Bull. Eng. Geol. Environ. 77 (3), 1263–1272. doi:10.1007/s10064-016-0998-8

CrossRef Full Text | Google Scholar

Loukidis, D., Bandini, P., and Salgado, R. (2003). Stability of Seismically Loaded Slopes Using Limit Analysis. Géotechnique 53 (5), 463–479. doi:10.1680/geot.53.5.463.37509

CrossRef Full Text | Google Scholar

Lyamin, A. V., Sloan, S. W., Krabbenhøft, K., and Hjiaj, M. (2005). Lower Bound Limit Analysis with Adaptive Remeshing. Int. J. Numer. Meth. Engng 63 (14), 1961–1974. doi:10.1002/nme.1352

CrossRef Full Text | Google Scholar

Lyamin, A. V., and Sloan, S. W. (2002a). Lower Bound Limit Analysis Using Non-linear Programming. Int. J. Numer. Meth. Engng. 55, 573–611. doi:10.1002/nme.511

CrossRef Full Text | Google Scholar

Lyamin, A. V., and Sloan, S. W. (2002b). Upper Bound Limit Analysis Using Linear Finite Elements and Non-linear Programming. Int. J. Numer. Anal. Meth. Geomech. 26, 181–216. doi:10.1002/nag.198

CrossRef Full Text | Google Scholar

Newmark, N. M. (1965). Effects of Earthquakes on Dams and Embankments. Géotechnique 15, 139–160. doi:10.1680/geot.1965.15.2.139

CrossRef Full Text | Google Scholar

Qi, S. W., Xu, Q., Lan, H. X., Zhang, B., and Liu, J. Y. (2010). Spatial Distribution Analysis of Landslides Triggered by 2008.5.12 Wenchuan Earthquake, China. Eng. Geol. 116 (1-2), 95–108. doi:10.1016/j.enggeo.2010.07.011

CrossRef Full Text | Google Scholar

Rodríguez-Peces, M. J., García-Mayordomo, J., Azañòn, J. M., and Jabaloy, A. (2014). GIS Application for Regional Assessment of Seismically Induced Slope Failures in the Sierra Nevada Range, South Spain, along the Padul Fault. Environ. Earth. Sci. 72 (7), 2423–2435. doi:10.1007/s12665-014-3151-7

CrossRef Full Text | Google Scholar

Rodríguez-Peces, M. J., Pérez García, J. L., García-Mayordomo, J., Azañòn, J. M., sua-Arévalo, J. M., and Delgado-García, J. (2011). Applicability of Newmark Method at Re-gional, Sub-regional and Site Scales: Seismically Induced Bullas and La Paca Rock-Slidecases (Murcia, SE Spain). Nat. Hazards 59, 1109–1124. doi:10.1007/s11069-011-9820-x

CrossRef Full Text | Google Scholar

Saade, A., Abou-Jaoude, G., and Wartman, J. (2016). Regional-scale Co-seismic Landslide Assessment Using Limit Equilibrium Analysis. Eng. Geology. 204, 53–64. doi:10.1016/j.enggeo.2016.02.004

CrossRef Full Text | Google Scholar

Shinoda, M., and Miyata, Y. (2017). Regional Landslide Susceptibility Following the Mid NIIGATA Prefecture Earthquake in 2004 with NEWMARK'S Sliding Block Analysis. Landslides 14 (6), 1887–1899. doi:10.1007/s10346-017-0833-8

CrossRef Full Text | Google Scholar

Sloan, S. W. (2013). Geotechnical Stability Analysis. Géotechnique 63 (7), 531–571. doi:10.1680/geot.12.rl.001

CrossRef Full Text | Google Scholar

Sloan, S. W. (1988). Lower Bound Limit Analysis Using Finite Elements and Linear Programming. Int. J. Numer. Anal. Methods Geomech. 12 (1), 61–77. doi:10.1002/nag.1610120105

CrossRef Full Text | Google Scholar

Sloan, S. W. (1989). Upper Bound Limit Analysis Using Finite Elements and Linear Programming. Int. J. Numer. Anal. Methods Geomech. 13 (3), 263–282. doi:10.1002/nag.1610130304

CrossRef Full Text | Google Scholar

Tsai, H.-Y., Tsai, C.-C., and Chang, W.-C. (2019). Slope Unit-Based Approach for Assessing Regional Seismic Landslide Displacement for Deep and Shallow Failure. Eng. Geology. 248, 124–139. doi:10.1016/j.enggeo.2018.11.015

CrossRef Full Text | Google Scholar

Utili, S., and Abd, A. H. (2016). On the Stability of Fissured Slopes Subject to Seismic Action. Int. J. Numer. Anal. Meth. Geomech. 40 (5), 785–806. doi:10.1002/nag.2498

CrossRef Full Text | Google Scholar

Wang, T., Wu, S. R., Shi, J. S., Xin, P., and Wu, L. Z. (2018). Assessment of the Effects of Historical strong Earthquakes on Large-Scale Landslide Groupings in the Wei River Midstream. Eng. Geology. 235, 11–19. doi:10.1016/j.enggeo.2018.01.020

CrossRef Full Text | Google Scholar

Wartman, J., Dunham, L., Tiwari, B., and Pradel, D. (2013). Landslides in Eastern Honshu Induced by the 2011 Tohoku Earthquake. Bull. Seismological Soc. America 103 (2B), 1503–1521. doi:10.1785/0120120128

CrossRef Full Text | Google Scholar

Wilson, R. C., and Keefer, D. K. (1983). Dynamic Analysis of a Slope Failure from the 6 August 1979 Coyote Lake, California, Earthquake. Bull. Seismol. Soc. Am. 73 (3), 863–877. doi:10.1785/bssa0730030863

CrossRef Full Text | Google Scholar

Wu, W., Yang, Y., and Zheng, H. (2020). Hydro-mechanical Simulation of the Saturated and Semi-saturated Porous Soil-Rock Mixtures Using the Numerical Manifold Method. Comput. Methods Appl. Mech. Eng. 370 (3), 113238. doi:10.1016/j.cma.2020.113238

CrossRef Full Text | Google Scholar

Xu, C., Dai, F., Xu, X., and Lee, Y. H. (2012). GIS-based Support Vector Machine Modeling of Earthquake-Triggered Landslide Susceptibility in the Jianjiang River Watershed, China. Geomorphology 145-146 (2), 70–80. doi:10.1016/j.geomorph.2011.12.040

CrossRef Full Text | Google Scholar

Xu, C., Xu, X., Dai, F., Wu, Z., He, H., Shi, F., et al. (2013). Application of an Incomplete Landslide Inventory, Logistic Regression Model and its Validation for Landslide Susceptibility Mapping Related to the May 12, 2008 Wenchuan Earthquake of China. Nat. Hazards. 68 (2), 883–900. doi:10.1007/s11069-013-0661-7

CrossRef Full Text | Google Scholar

Xu, C., Xu, X., and Shyu, J. B. H. (2015). Database and Spatial Distribution of Landslides Triggered by the Lushan, China Mw 6.6 Earthquake of 20 April 2013. Geomorphology 248, 77–92. doi:10.1016/j.geomorph.2015.07.002

CrossRef Full Text | Google Scholar

Yang, Y., Sun, G., Zheng, H., and Qi, Y. (2019b). Investigation of the Sequential Excavation of a Soil-Rock-Mixture Slope Using the Numerical Manifold Method. Eng. Geology. 256, 93–109. doi:10.1016/j.enggeo.2019.05.005

CrossRef Full Text | Google Scholar

Yang, Y., Sun, G., Zheng, H., and Yan, C. (2019a). An Improved Numerical Manifold Method with Multiple Layers of Mathematical Cover Systems for the Stability Analysis of Soil-Rock-Mixture Slopes. Eng. Geol. 264, 105373. doi:10.1016/j.enggeo.2019.105373

CrossRef Full Text | Google Scholar

Yang, Y., Wu, W., and Zheng, H. (2021). An Uzawa-type Augmented Lagrangian Numerical Manifold Method for Frictional Discontinuities in Rock Masses. Int. J. Rock Mech. Mining Sci. 148, 104970. doi:10.1016/j.ijrmms.2021.104970

CrossRef Full Text | Google Scholar

Yuqiao, Q, Hua, T, Qin, D, Xiaotao, Y, and Dongying, W (2019). Regional Seismic Slope Assessment Improvements Considering Slope Aspect and Vertical Ground Motion. Eng. Geology. 259, 105148. doi:10.1016/j.enggeo.2019.105148

CrossRef Full Text | Google Scholar

Zang, M., Qi, S., Zou, Y., Sheng, Z., and Zamora, B. S. (2020). An Improved Method of Newmark Analysis for Mapping Hazards of Coseismic Landslides. Nat. Hazards Earth Syst. Sci. 20 (3), 713–726. doi:10.5194/nhess-20-713-2020

CrossRef Full Text | Google Scholar