Water Migration and Segregated Ice Formation in Frozen Ground: Current Advances and Future Perspectives

A characteristic of frozen ground is a tendency to form banded sequences of particle-free ice lenses separated by layers of ice-infiltrated soil, which produce frost heave. In permafrost, the deformation of the ground surface caused by segregated ice harms engineering facilities and has considerable influences on regional hydrology, ecology, and climate changes. For predicting the impacts of permafrost degradation under global warming and segregated ice transformation on engineering and environmental, establishing appropriate mathematical models to describe water migration and ice behavior in frozen soil is necessary. This requires an essential understanding of water migration and segregated ice formation in frozen ground. This article reviewed mechanisms of water migration and ice formation in frozen soils and their model construction and introduced the effects of segregated ice on the permafrost environment included landforms, regional hydrological patterns, and ecosystems. Currently, the soil water potential has been widely accepted to characterize the energy state of liquid water, to further study the direction and water flux of water moisture migration. Models aimed to describe the dynamics of ice formation have successfully predicted the macroscopic processes of segregated ice, such as the rigid ice model and segregation potential model, which has been widely used and further developed. However, some difficulties to describe their theoretical basis of microscope physics still need further study. Besides, how to describe the ice lens in the landscape models is another interesting challenge that helps to understand the interaction between soil ice segregation and the permafrost environment. In the final of this review, some concerns overlooked by current research have been summarized which should be the central focus in future study.

Introduction

Frozen ground, defined as soil or rock containing ice that remains at or below 0°C, is widely distributed globally (Qin, 2016). About 50.5% of the long-term average maximum extent of frozen ground in the northern hemisphere undergoes seasonal freezing and thawing, and about 13–18% of the area in the northern hemisphere is occupied by permafrost (Zhang et al., 2003; Gruber, 2012). Permafrost is soil or rock that remains at or below 0°C for at least two consecutive years (Subcommittee, 1988; Qin, 2016). The topsoil that overlays permafrost and undergoes seasonal freezing and thawing is known as the active layer. Changes in permafrost temperature and the active layer thickness (ALT) have significant environmental and socioeconomic implications from the local to global scales. At the local scale, soil freezing and thawing directly affect the physical properties of water and heat transfer in the active layer, eventually altering the heat and water exchange between the land surface and the atmosphere (Frey and McClelland, 2009; Vonk et al., 2019). At the global scale, permafrost thaw impacts are attributed to their influences on biogeochemical processes and greenhouse gas emissions. The total carbon stored in the permafrost regions is estimated to be twice that in the atmosphere (Schuur et al., 2015). The vast amount of carbon stored in permafrost is likely to be released into the atmosphere under a warming climate, exacerbating climate change due to positive greenhouse gas feedbacks.

How permafrost thaws in response to climatic warming and its associated impacts on ecological and hydrological aspects have gained global attention in the scientific community (Shur and Jorgenson, 2007; Koven et al., 2011; Schuur et al., 2015; Streletskiy et al., 2015). Several permafrost monitoring networks, such as the Global Terrestrial Network for Permafrost (GTN-P) (https://gtnp.arcticportal.org/about-the-gtnp), Circumpolar Active Layer Monitoring (CALM) (https://ipa.arcticportal.org/products/gtn-p/calm), and Permafrost and Climate in Europe (PACE) (https://doi.org/10.1002/ppp.377), have been established to record changes in permafrost temperature and ALT regionally and globally (Fagan and Nelson, 2017; Streletskiy et al., 2017; Etzelmuller et al., 2020; Tregubov et al., 2020). In addition to extensive field monitoring, process-based modeling is a complementary approach to understanding water and heat transfer processes and mechanisms in the biogeochemical cycle in permafrost regions. In this regard, land surface models (LSMs), soil-vegetation-atmosphere transfer (SVAT) models, and hydrological or frozen soil water-heat models have been used to simulate permafrost hydrothermal conditions (Flerchinger and Saxton, 1989; Cherkauer and Lettenmaier, 1999; Gouttevin et al., 2012; Swenson et al., 2012; Che et al., 2014; Yi et al., 2014; Wang et al., 2017).

There are various forms of ground ice in permafrost with different sizes, structures, and formation patterns at spatial and temporal scales. The former Soviet Union scholar Ershov et al. (2015) first divided permafrost ground ice into two main types according to the formation causes: intrasedimental ice and buried ice (Ershov et al., 2015). Mackay (1972) further provided a more detailed classification of intrasedimental ice based upon the water source immediately prior to freezing and the principle of water migration. Figure 1 shows the various types of ground ice exhibit significant differences in thickness and duration of formation and existence. Segregated ice formed by water migration ranges in thickness from hairline width to more than 10 m (Subcommittee, 1988; Mackay and Dallimore, 1992), and it plays a critical role in changing soil structure, affecting the hydrothermal properties of frozen ground (Van Huissteden, 2020). Seasonal segregated ice lens formation and thaw cause frost heaves and thawing settlement. In permafrost, repeated-segregation ice near the permafrost table significantly affects the topographic features and soil hydrologic conditions. Segregated ice formation and water migration cause mass and energy transfer within the active layers to be extremely complex (Xu et al., 2010). In addition, the barrier effect and water migration caused by ice formation alter soil hydrothermal properties, microstructure, and ventilation conditions (He et al., 2020; He et al., 2021). These processes influence the mass and energy exchange between the land surface and the atmosphere, leading to the redistribution of soil carbon and nutrients and impacting vegetation dynamics (Walker et al., 2004). To reveal the physical mechanisms of mass and energy transfer in frozen soil and the environmental impacts of frozen soils, representing the mechanisms that explicitly describe these processes is one of the main challenges in state-of-the-art LSMs.

FIGURE 1

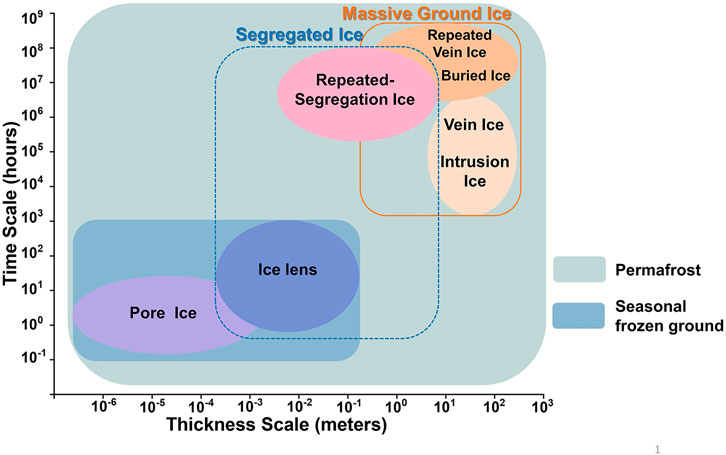
FIGURE 1. The types of ice in frozen soil range from the pore size to the massive ground ice size at the spatial scale, and their formation ranges from sub-daily to centennial at the temporal scale. The study focuses on the segregated ice and water migration with medium and minor scales (blue dotted line), which exist in permafrost and seasonally frozen ground.

Frost heave models based on the frozen fringe theory (Miller, 1972) have been used to simulate ice formation (Konrad and Morgenstern, 1980; Sheng et al., 1995; Michalowski and Zhu, 2006; Ji et al., 2019; Zhou and Wei, 2020). These models have detailed descriptions to simulate the ice segregation process in soil freezing. However, it is difficult to apply frost heave model in fieldwork because the empirical work has principally been conducted in highly controlled laboratory conditions (Smith et al., 1985). At the landscape scale, LSMs that involve processes such as hydrogeology, biochemistry, and vegetation dynamics focus more on frozen soil parameterization schemes rather than a specific mechanism in the freeze-thaw processes, such as the segregated ice formed by water migration and freezing front movement (Oleson et al., 2010; Che et al., 2014; Sun, 2015; Andresen et al., 2019; Li et al., 2020). The lack of detailed representation of water migration and ice formation in models probably increases uncertainty in the simulation of soil water content and temperature conditions (Pitman et al., 1999), leading to deviations in the assessment of the ecological and hydrological effects of permafrost at the landscape scale. (Xue et al., 1996; Koren et al., 1999; Liang et al., 2003; Oleson et al., 2013).

The overall framework and linkage between different sections are shown in Figure 2. This review discusses the theories of water migration and ice formation and their current modeling methods. Their impacts on the land surface processes (such as the landform, hydrological patterns, and biogeochemical processes) in permafrost regions are involved. Based on the discussion of the water migration and segregated ice formation and their model construction, this review puts forward some reference opinions on developing present theories and permafrost modeling in the future. The summary review will help facilitate studies accounting for the interaction between permafrost, ecosystems, and climate systems.

FIGURE 2

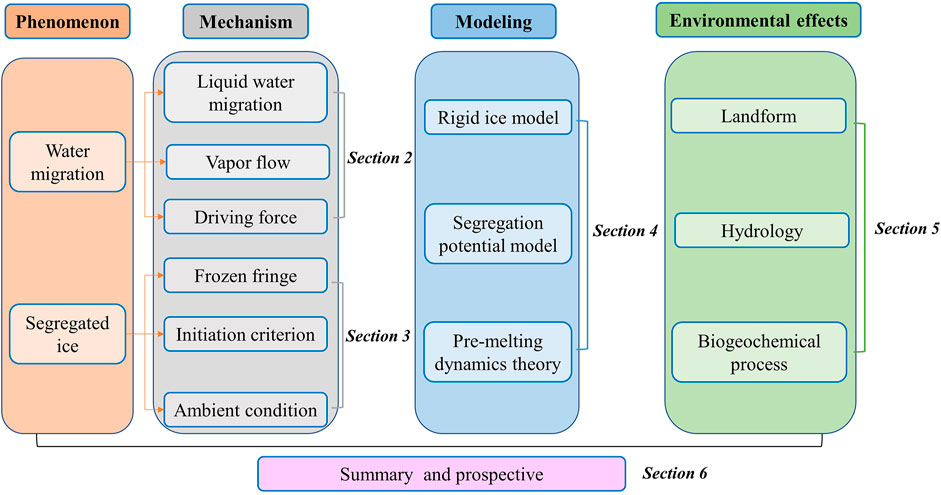
FIGURE 2. A diagram illustrating the overall framework and linkages of different sections in this article.

Water Migration During the Soil Freezing-Thawing Process

Unfrozen Water Migration

When the temperature drops to the freezing point, where water and ice are in equilibrium with equal free energy, the water is transformed into ice. For pure water under normal conditions, the freezing point equals 0°C, while the freezing point has a depression in soil due to soil salinity, the capillary effect, and adsorption of soil particles (Anderson and Tice, 1972; Banin and Anderson, 1974; Scherer, 1999). Many studies have shown that liquid water exists in the soil pore in equilibrium with ice at temperatures considerably below 0°C (Burt and Williams, 1976; Horiguchi and Miller, 1983; Smith, 1985; Zhang et al., 2020). This water is known as unfrozen water. Burt and Williams (1976) first measured hydraulic conductivity in freezing soils and demonstrated that the hydraulic conductivity decreased with temperature decreases but did not fall to zero, even at relatively low temperatures.

In general, the water-energy state and movement direction in soil mainly determined by the soil matric potential, which is created by the capillary and adsorption forces of the soil matrix (Or et al., 2002). The matric potential is usually related to soil properties. However, regardless of the soil type, the unfrozen water alongside the ice lens has a matric potential proportional to the temperature depression below 0°C, described by the Clausius-Clapeyron equation (Edlefsen and Anderson, 1943; Williams and Smith, 1989). This equation shows that the potential decreases by approximately 1.2 MPa per °C below 0°C. This potential is significant and creates suction that makes unfrozen water migrate to zones of lower temperature and then accumulate there, leading to the growth of ice lenses (Ferguson et al., 1964; Biermans et al., 1978). The development of ice lenses, called segregated ice, causes considerable volumetric expansion, which is the primary reason for soil frost heave (Hoekstra and Miller, 1963; Kanevskiy et al., 2013). (Taber, 1929; Taber, 1930) was the earliest to deduce that frost heave is caused by liquid migration that supplies growing ice lenses through a series of experiments. This is the first basic theoretical explanation of frost heave, and is typically referred to as the capillary theory (Smith et al., 1985). The growth rate of segregated ice depends on the freezing speed (Station et al., 1915; Bouyoucos, 1920; Watanabe et al., 1997). Besides, when frozen soil thaws unidirectionally, water also migrates from thawed regions to the thawing front, decreasing the water content through dehydration (Cheng, 1982).

Thick segregated ice is one of the main components of ground ice near the permafrost table (Williams, 1968; French, 2017). In permafrost regions, more than 50% of the volumetric ice content of massive ground ice is located near the bottom of the active layer or permafrost table (Mackay, 1972; Hughes, 1974). Mackay (1972) called this kind of ground ice “aggradational ice” and attributed it to the syngenetic growth of permafrost (with the continuous deposition of surface sediments, the upper limit of permafrost rises with the rise of the ground). Cheng (1982) considered that the downward migration of unfrozen water content is always greater than the upward migration in the active layer during a freeze-thaw cycle, accounting for moisture accumulation at the permafrost table. He proposed that accumulation of ice at the permafrost table might occur under all conditions and thus form a thick ground ice layer, namely repeated ice-segregation (Cheng, 1983). This mechanism was verified by Burn and Michel (1988) and Yang et al. (2017) using an isotope technology.

Vapor Flow in Frozen Soil

Unfrozen water migration in frozen soil is more likely to occur in soil with fine particles and high moisture content than dry coarse-grained soil (Burt and Williams, 1976; Fisher et al., 2020). Therefore, in cold regions, replacing the foundation soil of roadbeds or airport runways with dry coarse-grained soil is considered an effective engineering measure to prevent frost heaves (Vinson et al., 1996). However, frost heaves can also occur in high-speed railway embankments and airport runways padded with unsaturated coarse-grained soils (Zhang et al., 2016; Teng et al., 2020). It has been confirmed that gaseous water (vapor) migrates from the warm and humectant side of the soil layer to the cold and dry layer below the closed/impermeable ground surface in coarse-grained soil and then condenses into ice, causing frost heaving (Guthrie et al., 2006; Niu et al., 2017; Yuzhi et al., 2020). This phenomenon is called the “pot effect” or “canopy effect” (Bai et al., 2018). The water vapor migration rate is controlled by the pressure gradient and soil diffusion rate related to the relative humidity (Philip and Vries, 1957). In general, soil with an initial moisture content of less than 30% is more prone to showing the “pot effect” (Bai et al., 2018).

Some results showed that more water comes out of the soil in winter than can be reconciled with the theory for vapor flux (Farouki, 1981; Currie, 1983; Smith and Burn, 1987). Smith and Burn (1987) pointed out that unfrozen water migration is still the dominant mode of transport in contrast with vapor flow by comparing field observations and calculation values. Even so, vapor migration in frozen still has potentially considerable impacts on engineering facilities and the environment. Numerical simulation results indicate that if vapor migration is not considered in unsaturated coarse-grained soils, the predicted value of frost heaving is underestimated by 60% compared to the measured value (Teng et al., 2020). In sandy soils, although the larger soil pores reduce capillarity, it is very conductive to vapor migration (Yu et al., 2018). Intense evaporation occurs on the surface of sandy soil, leading to soil water loss. Without replenishment, the continuous loss of surface soil moisture can cause land desertification, especially in regions with lower groundwater tables (Zhanrong and Shuangping, 2002; Cui and Shao, 2005; Wang et al., 2006b).

Driving Forces of Water Migration

The capillary theory indicates that water migrates toward the freezing front along with the pores among soil particles because of the primary mover of capillary force during freezing. Based on the capillary theory (Everett, 1961), illustrated frost heaving and estimated the amount of frost heaving quantitatively. However, the theoretical value calculated by capillary theory is always smaller than the experimental value, and there is no plausible mechanism within the capillary theory for explaining the initiation of new lenses (Miller, 1972; Peppin and Style, 2013).

With the development of the theory, the hypothesis of film water migration was proposed to make up for these deficiencies (Beskow and Fil, 1935). The film theory suggested that the water film on soil particle surfaces shows asymmetry under temperature gradients, causing a thinner film at the end with low temperature and a thicker film at the opposite end, resulting in the unfrozen imbalance in the water-ice-soil particle system. Suppose the soil particles have identical radii but different water film thicknesses. In that case, the film water will migrate from the place with a thicker film (with more extensive water molecular activity) to the place with a thinner film (with lower water molecular activity) to reach a new thermodynamic equilibrium under the water potential gradients (Figure 3). There is a 1/3 power function relationship between water film thickness and temperature (Dash, 1989):

$d=\left(\frac{-{\rm A}}{6\pi {\rho }_{s}L}\right){\left(\frac{T_0-T}{T_0}\right)}^{-1/3},(1)$

where d is the film thickness, T is the temperature, A is the Hamker constant, ${\rho }_s$ is the density of soil particles, L is the latent heat of ice, and T₀ is the freezing temperature of soil water. The film theory that relates unfrozen water migration to temperature gradients has been confirmed in subsequent studies and once substituted the capillary theory as the mainstream theory (Hoekstra, 1966; Hoekstra, 1969; Takagi, 1980; Wilen and Dash, 1995).

FIGURE 3

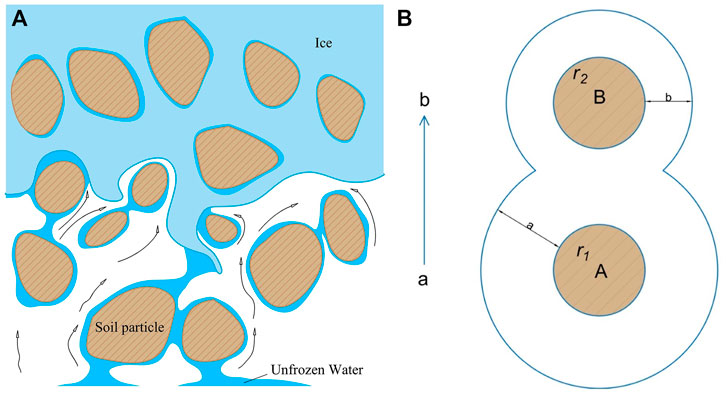
FIGURE 3. A schematic diagram of film water migration: (A) the direction of film water migration; (B) the principle of film water migration around soil particles (i.e., A and B are soil particles with equal radius, a and b are water film thickness (a > b), and particle B is closer to the freezing front).

In 1963, the International Union of Soil Sciences (IUSS) clarified the definition of soil water potential, pointing out that water migration can be caused by any component (such as pressure, temperature, matric, osmotic, or gravity) of soil water potential (Shao et al., 2006). However, the water potential gradient is difficult to determine in frozen soil because the surficial films are too small. The temperature gradient is the only driving gradient that could be determined directly. Using a thermodynamic approach, A linear relation between temperature below 0°C and soil water potential is derived from the generalized Clausius Clapeyron equation (GCCE) (Gilpin, 1982; Spaans and Baker, 1996; Hansson et al., 2004). GCCE indicates that the temperature specifically controls the difference in potential between solid and liquid phases, and if ice pressure rises, water potential rises too. Therefore, a linear relation is only considered reliable under static conditions (Takashi et al., 1982). However, the freezing and thawing of an open system is more likely to be a non-equilibrium thermodynamic process in many cases (Bronfenbrener, 2013). Wood (1990) suggested a pressure difference between the ice and aqueous phases throughout the freeze-thaw cycle and ice deformation consecutively, making it difficult to approach equilibrium. Li et al. (2001) pointed out that GCCE must satisfy the assumption that temperature and pressure do not change with time. The depression of pore water pressure under open-system freezing is approximately half of that under closed-system freezing while considering the dynamic flow of soil freezing (Miyata and Akagawa, 1997). There are inconsistencies between experiments results and the calculation of GCCE (McGaw et al., 1983; Zhang et al., 2014b). Style and Peppin (2012) suggested that using the GCCE to determine the water pressure at the ice-lens front and applying it to Darcy’s law will overestimate the ice growth rate. Ma et al. (2015) discussed the applicability of GCCE and proposed a static and a dynamic model, respectively. The dynamic GCCE model may be closer to the actual freezing process. Thus, it can better describe nonlinear variations in pore water pressure and address inconsistency between calculated values and experiments.

In addition to the above theories, various hypotheses of water migration driving force have been proposed, such as crystallization force, suction force, barometric vacuole, and ice pressure gradient (Xu et al., 2010). These hypotheses explain the mechanism of moisture migration in frozen soil from the perspectives of thermodynamics, mechanics, and physical chemistry. However, each view has its limitations (Table 1), representing the driving force under specific conditions (Bouyoucos, 1920; Taber, 1930; Korkina, 1965; Hoekstra, 1969; Gilpin, 1980). There is now a consensus that the water migration in frozen soil is due to multiple factors (such as thermodynamic, mechanics, and physicochemical) that need comprehensive analysis from various perspectives.

TABLE 1

TABLE 1. Hypotheses on the driving force of water migration in frozen soil.

Ice Segregation in Frozen Soil

The Structure of Frozen Fringe

In the early stage of research on frozen soil, the capillary theory (primary frost heave) was used to illustrate the formation mechanism of segregated ice (Taber, 1930; Gold, 1957; Everett, 1961; Haynes, 1965). Primary heave occurs when there is no frost penetration into the soil, leading to needle ice and for some of the very large lenses of massive ice (Miller, 1972; Goulet, 1995). However, the primary frost heave theory still did not answer the questions: 1) mechanisms to explain the initiation of new ice lenses; and 2) the frost heaving force estimated by the theory does not match the experimental data (Sheppard et al., 1978; Jansson and Halldin, 1979; Guymon et al., 1980). Peppin and Style (2013) considered that the flow rate toward the ice lens tends to be overestimated due to the Clapeyron equation breaking down outside equilibrium under the assumption of local equilibrium at the ice-lens-soil boundary.

Miller (1972) proposed the concept of frozen fringe (secondary frost heave). The frozen fringe is defined as the partially frozen zone between the ice lens and the warmest soil with pore ice, i.e., the soil volume in which the water pressure declines due to coexisting with ice (Figure 4) (Gilpin, 1982; Konrad, 1999; Miller, 1972; ONeill and Miller, 1985). Therefore, any internal and external factors that can change soil unfrozen water content will influence the thickness of the frozen fringe, such as soil texture, soil salinity, and the external load (Radd and Oertle, 1973; Loch and Miller, 1975; Konrad and Morgenstern, 1981; Akagawa, 1988; Ma et al., 2015). Some reports have stated that the frozen fringe is non-existent in saturated soil with a particle size larger than 0.1 mm (Liu et al., 2005). However, if the soil water has high salinity, there may well be the coexistence of ice and water below 0°C (Chamberlain, 1983). The ice lens growth rate at the frozen fringe depends on the freezing velocity (Watanabe et al., 1997). During fast freezing, the freezing front moves so rapidly that water cannot migrate towards the freezing front immediately, and the water freezes in situ without forming a frozen fringe (Xu and Deng, 1991). Overall, the internal structure of the frozen fringe is complex, and various physical parameters change significantly in different freezing stages, making it challenging to accurately determine different parameters (Akagawa et al., 2006; Akagawa and Nishisato, 2009).

FIGURE 4

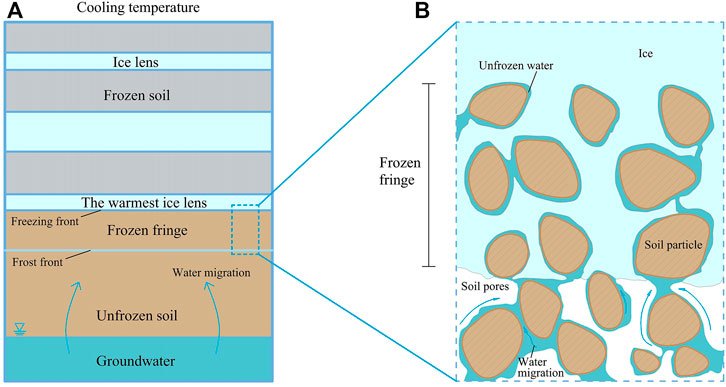
FIGURE 4. A schematic diagram (not to scale) of frozen fringe: (A) shows the relative position of the frozen, frozen fringe, and unfrozen zones within freezing soil and, (B) is the magnified views of the frozen fringe zone.

Initiation Criteria of Ice Lenses

The conditions of moisture, temperature, and stress conditions in the frozen fringe can determine when and where ice lens initiation occurs (Xu et al., 2010). In the frozen fringe, although the permeability decreases rapidly with the formation of porous ice during the freezing process, moisture still migrates to the frozen zone continuously under the pressure gradient caused by the depression of pore water pressure (Peppin and Style, 2013). However, the permeability in the frozen fringe is so poor that moisture accumulates, forming ice lenses at the back of the freezing front (Figure 4A) (Rempel, 2007). Ice lenses undergo sustained grow with enough water supply. The location of new ice lenses is related to the hydraulic conductivity of the currently frozen fringe. The growth or stagnation of the ice lenses depends on the temperature at the warmest end of the ice lens, i.e., the segregation temperature (Figure 4B) (Konrad and Morgenstern, 1980). Akagawa (1988) found that the segregation temperature was around −0.8°C through experiments. Based on a simple method to determine the segregation temperature and the ice lens location, Xu et al. (2010) found that segregated ice was most likely to form in soil with structural connections. The temperature gradient and water migration caused uneven soil shrinkage, resulting in the appearance of cracks in the frozen fringe (Arenson et al., 2007). In addition to stress and temperature criteria, there are also some other possible criteria for the formation of ice lens. Style et al. (2011) claimed that a new ice lens occurs at a location where supercooling reaches maximum. Zhou and Li (2012) modelled ice lens formation with the concept of separating void ratio, a critical void ratio that enables pore ice to connect into an ice lens.

Figure 5B and Figure 5C show the temperature and pressure profiles around the frozen fringe. When discussing the ice lens initiation criteria, typically only the stress conditions are considered to facilitate practical calculation and application (Ma et al., 2015). The stress conditions include pore pressure ${\sigma }_{por}$ (Sheng et al., 1995), pore water pressure $u_w$ (Hazirbaba et al., 2011), ice pressure $u_i$, and overburden ${\sigma }_{R }$ (Nixon, 1991) (Figure 5C). ONeill and Miller, 1985 pointed out that a new ice lens forms when the ice pressure in the frozen fringe is greater than or equal to the external load at the cold end of the frozen fringe. Gilpin (1980) proposed critical segregation pressure, in which ice pressure is regarded as the destructive force of soil structures that determines the ice lens formation. An increasing number of studies have shown that the formation of new ice lenses and the halt in the growth of old ice lenses may not occur at the same time, which can be determined using mechanical and thermophysical methods, respectively (Konrad and Duquennoi, 1993; Zhang et al., 2014a). A previous study showed that the stress conditions of ice lens initiation should include two stresses: the driving force of soil fracturing as well as ice lens formation and the constraining force preventing soil fracturing (Ma et al., 2015). Ice lens initiation can only occur when the pore pressure is greater than or equal to the restraining force, and the effective stress (${\sigma }^{\text{'} }$ in Figure 5C) equals zero (Ma et al., 2015).

FIGURE 5

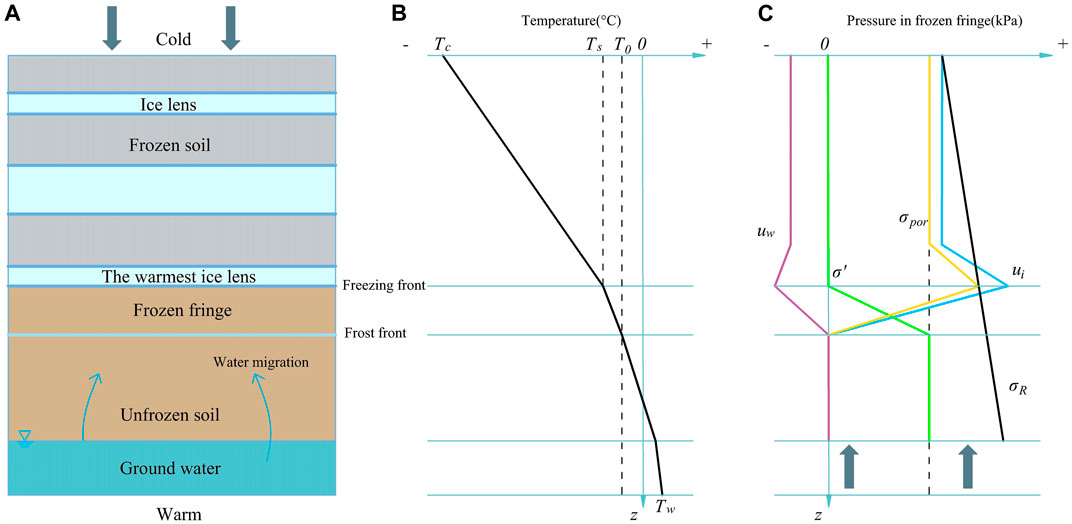
FIGURE 5. The temperature and pressure of the frozen fringe (based on a static model of the frozen fringe by Ma et al. (2015): (A) the location of the ice lens and frozen fringe; (B) temperature in the frozen fringe. ${\mathit{T}}_{\mathit{C}}$ and ${\mathit{T}}_{\mathit{W}}$ are the upper and lower boundary temperatures, respectively; ${\mathit{T}}_{\mathit{S}}$ is the segregated temperature; and ${\mathit{T}}_{\mathit{0}}$ is the soil freezing point; (C) pressure in the frozen fringe.

Environment for the Development of Segregated Ice

The natural formation of massive segregated ice is mainly affected by soil properties. Fine-grained soils generally promote segregated ice formation due to their high unfrozen water content (Van Huissteden, 2020). However, Burt and Williams (1976) showed that although clays have the highest unfrozen water content, their low permeability leads to a lower hydraulic conductivity than silts below 0°C. For this reason, silts have a high frost susceptibility compared to clay and are easy to occur the segregated ice (Burt and Williams, 1976; Chamberlain, 1981). The change in soil structures due to frost cracking is another essential mechanism for ground ice formation (Azmatch et al., 2008). During the freezing process, vertical cracks may occur in the frozen fringe and unfrozen areas, leading to appropriate soil local stress conditions for segregated ice growth. Segregated ice may also occur in rocks by accelerating cracking and physical weathering, especially in stratums prone to fission, such as shale or fine-grained porous rocks (Murton and Lautridou, 2003; French and Shur, 2010). Higher soil water content is critical factor for the growth of segregated ice in some permafrost regions. The results of Calmels and Allard (2008) showed that ice content could exceed 50% after frost heaving in wet peat. Segregated ice formation brings about water migration and accumulation in soil with enough groundwater supply recharge. Without sufficient water, segregated ice ceases to grow, and the soil finally becomes consolidated and contracted due to dehydration under freeze-thaw cycles (Van Huissteden, 2020).

Laboratory Studies and Simulations of Segregated Ice

Mathematical models of the soil ice formation process have attracted much attention in the past decades (Harlan, 1973; Jame and Norum, 1980; Hansson et al., 2004; Lai et al., 2014; Liu et al., 2019). These studies help elucidate the mechanism of frost heaving and provide practical measures for frost heave prediction and prevention for engineering. The review does not try to comprehensively discuss all aspects related to soil frost heave, such as the distinction of primary, secondary, and tertiary heave (Miller, 1978; Mackay et al., 1979; Horiguchi, 1980; Smith et al., 1985). Instead, we focus on the processes involved in segregated ice formation, which mostly describes the warmest or first ice lens ice based on the frozen fringe. They can be broadly divided into three types: rigid ice models (ONeill and Miller, 1985; Sheng et al., 1995; Zhou et al., 2018), models based on segregation potential (Gilpin, 1980; Koren et al., 1999; Ji et al., 2019), and pre-melting dynamic models (Wettlaufer et al., 1996; Rempel et al., 2004; Michalowski and Zhu, 2006; Zhou and Wei, 2020). These models differ in practical applications due to different theoretical assumptions and bases.

Rigid Ice Model and Separated Ice Model

The rigid ice model was first proposed by Miller (1972), who considered that ice lens and pore ice in the frozen fringe is a rigid ensemble that moves at a uniform velocity. The pore ice in the frozen fringe is attached to the growing lens above and moves relative to the surrounding soil particles by melting and refreezing as necessary. ONeill and Miller (1985) developed it into a complete model, aiming to directly predict the characteristics of ice lenses and the rate of frost heave as a function of environmental conditions and sediment constitutive behavior. In the model, the relationship between ice content I (%) and water pore pressure P_w (Pa), and temperature T (°C) was connected by the soil-water characteristic curve and integral form of the Clapeyron equation:

$I=I\left(A{P}_w+BT\right),(2)$

where A and B are known constants. In addition, the movement of the ice lens is considered in basic transport equations:

$\left({\rho }_i-{\rho }_w\right)\frac{\partial {\theta }_i}{\partial t}-\frac{\partial }{\partial x}\left[\frac{K_h}{g}\left(\frac{\partial P_w}{\partial x}-{\rho }_{w}g\right)-{\rho }_i{V}_I{\theta }_i\right]=0(3)$

${\displaystyle \sum {\rho }_n{c}_n{\theta }_n\frac{\partial T}{\partial t}}-\frac{\partial }{\partial x}\left(\lambda \frac{\partial T}{\partial x}\right)-{\rho }_{i}L\left(\frac{\partial {\theta }_{\text{i}}}{\partial t}+V_I\frac{\partial {\theta }_{\text{i}}}{\partial x}\right)=0,(4)$

where ρ_i and ρ_w are ice and water density (kg m⁻³), respectively; $n$ represents different soil components; c_n is the thermal conductivity of different components (J m⁻¹ s⁻¹ K⁻¹); θ_n is the volume fraction of the nth component including soil solids (%); V_I is the segregation rate of ice (m s⁻¹); g is gravitational acceleration (m s⁻²); K_h is the hydraulic conductivity (m s⁻¹), and the function of unfrozen water content in frozen fringe and can be regarded as the saturated hydraulic conductivity in the unfrozen zone; and λ is the thermal conductivity of the soil skeleton (J m⁻¹ s⁻¹ K⁻¹), which is related to the content of soil components. The segregation rate V_I can be obtained from the conservation of mass in the frozen fringe as

$V_I=-K_h\left(\frac{\partial P_w}{\partial x}-{\rho }_{w}g\right)\frac{1}{{\rho }_{w}g\left(1-{\theta }_i\right)}.(5)$

Soil particles lose contact and new ice lenses form when the effective stress of pores in the frozen fringe is greater than or equal to the total load at the end of the frozen fringe:

${\sigma }_n=\chi P_w+\left(1-\chi \right)P_i\ge P_0,(6)$

where σ_n is the effective stress (Pa), and $\chi ={\left({\theta }_u/\rho \right)}^{1.5}$ is the stress-partition parameter (Pa) (Miller, 1978), where ${\theta }_u$ is the unfrozen water content (%) and $\rho$ is the soil density.

The rigid ice model can describe frost-heave behavior by keeping track of only two essential parameters of the ice content in the frozen fringe: 1) spatial variations in the volume fraction of the pore space that is occupied by ice; and 2) spatial variations in the effective permeability caused by these changes in ice saturation (Rempel, 2010). Both parameters can be obtained from independent laboratory studies (Watanabe and Flury, 2008; Watanabe and Wake, 2009). However, there are still considerable workloads to put it into practical application (Ming and Li, 2016). Many researchers have devoted attention to simplifying the model (Black, 1985; Ishizaki and Nishio, 1988; Sheng et al., 1995). Fowler and Krantz (1994) reduced the computational amount of the rigid-ice model by using asymptotic analysis to reformulate the model and greatly improve its practical implementation. Sheng et al. (1995) modified the governing equation and interruption stress expression, establishing an operable simplified model (PCheave). This model can solve variables such as soil frost heave rate, freeze-thaw front movement speed, and ice volume content, which is helpful for frost heave monitoring in the field (Zhang et al., 2014a).

Segregation Potential Model

The segregation potential model is a semi-empirical model describing the growth of a single ice lens (Konrad and Morgenstern, 1980; Konrad and Morgenstern, 1982b). The basic assumption is that for any identical soil, while the one-dimensional freeze is steady-state, the ratio of the velocity of water migration at the bottom of the last ice lens and the soil temperature gradient below ice lens is a constant, namely, segregation potential $SP$：

$V=SP\cdot \mathrm{\Delta }T,(7)$

where $V$ is the velocity of water migration and $\text{Δ}T$ is temperature gradient (K cm⁻¹), and the segregated ice content can be calculated by (Konrad et al., 1995):

$H=1.09{\displaystyle {\int }_0^{t}SP\mathrm{\Delta }Tdt}.(8)$

The SP, in effect, is a conductivity driven by temperature, and depends on external pressure, suction at the frost front, and rate of cooling of the frozen fringe (Konrad and Morgenstern, 1980; Konrad and Morgenstern, 1982a). All of these parameters may be obtained directly from laboratory frost heave tests at the macroscopic scale. Konrad (2005) reported values of SP ranging 160 to 410 (mm²/°C·d) for saturated sand–silt–clay mixtures, 52 to 325 (mm²/°C·d) for till samples, and 84 to 329 (mm²/°C·d) for fine quarry materials. Water migration and segregated ice can be directly predicted as long as $SP$ has been measured by experiments. (Nixon, 1982; Fukuda et al., 1988; Saarelainen, 1992; Tiedje and Guo, 2012). Konrad and Morgenstern (1984) predicted the frost heave caused by a frozen pipe buried in an unfrozen region using the segregation potential model. The simulation was in good agreement with long-term field observation results. However, Nixon (1987) and Ishizaki and Nishio (1988) pointed out that the model could not describe the ice lens growth under unstable thermal conditions. The model cannot predict the dewatering at the initial stage of freezing. Furthermore, the model did not involve the parameters related to basic soil properties (Li et al., 2000). Based on the segregation potential model and the water activity criteria, Ji et al. (2019) proposed a quasi-static model for ice lens growth to describe the ice lens growth under slowly changing segregation temperature.

Pre-Melting Dynamics Theory

The rigid-ice model and the segregated potential model give a successful prediction of the macroscopic processes of segregated ice. At the microscale, the force-balance condition of the initiation of new lenses still lacks a firm theoretical basis. Römkens and Miller (1973) observed the migration of particles in freezing soil and attributed it to the osmotic transport of water in the film surrounding the particles. The authors explained the force between ice and soil particles based on two models: 1) electrical double-layer effects and the viscous flow of water, and 2) a brine pocket enclosing the particle and diffusion phenomena. Wettlaufer et al. (1996), Wettlaufer et al. (1997) found that due to the thermal molecular repulsion between the porous medium and ice, there is interfacial melting between the ice lens and the matrix. This melting forms a thin liquid water film on the surface of the substrate called pre-melting film (Lu et al., 2017). The net force between the ice and sediment particles can be explained quantitatively as a result of the intermolecular forces that act between them and produce the intervening pre-melting films (Williams, 1995). The intermolecular force changes the thickness of the film between the soil particles and surrounding ice, and increases with the decreasing distance and increasing temperature between soil particles and ice (Rempel et al., 2001). In the presence of pre-melting film, the total surface energy of the soil particle-water and liquid water-ice interface is lower than that of the soil particle-ice surface (Zhou and Meschke, 2013).

Rempel et al. (2004) concluded that the thermal molecular repulsion of both the cold and warm ends of soil particles is imbalanced. Owing to the difference in water film thickness, the force of the cold end is greater than that of the warm end. This force will drive soil particles away from the ice lens, causing ice to melt on the warmer side and water to refreeze on the colder side through thermal regelation. Rempel et al. (2004) developed a model based on mechanical equilibrium and conservation to describe the formation and evolution of ice lenses. Based on the micro thermodynamic theory of ice soil particle interaction, different forms of macro frost heaving processes can be described, including the growth of single ice lens or needle ice, the successive growth of multiple lenses, and the situation with only pore ice (Rempel et al., 2004; Rempel, 2007). It should be noted that the pre-melting film is still affected by thermal molecular forces while the frozen fringe disappears because the warm side coincides with the freezing front. Therefore, the frozen fringe is not always considered in the pre-melting film model (Lu et al., 2017). The derivation and development of pre-melting film originated from the micro-physical mechanism, discussing the essence of soil water and heat change during the freeze-thaw process, opening up a new direction for the macroscopic ice formation process model (Rempel et al., 2004; Zhou and Wei, 2020).

In the 1990s, Fremond and Mikkola (1991) proposed a thermodynamic model based on the law of energy conservation and entropy increase balance. This model was derived from a series of thermodynamic equations based on the basic axioms. The model can describe the suction caused by pore water freezing and moisture and heat transfer (Ran et al., 2019). However, the application of this model has not been extensive due to its large number of parameters, which are too difficult to obtain in experiments. The model still needs to be further improved and developed in the future.

Environment Effects Caused by the Segregated Ice Formation

Segregated ice is a vital factor affecting the permafrost environment. It is widespread in the active layer from the permafrost table to the ground surface (Figure 6A), where there are acute water and heat transports among soil, vegetation, and the atmosphere. These energy exchange processes are significantly affected by segregated ice formation, growing, and melting via changes in the soil hydrothermal properties and soil structures (Wu et al., 2003). Thus, segregated ice formation shapes the unique frozen land morphology, changing the regional topography and hydrological processes, and causes soil and vegetation reorganization in the cold region ecosystems, affecting the carbon and nitrogen cycle and other biogeochemical processes.

FIGURE 6

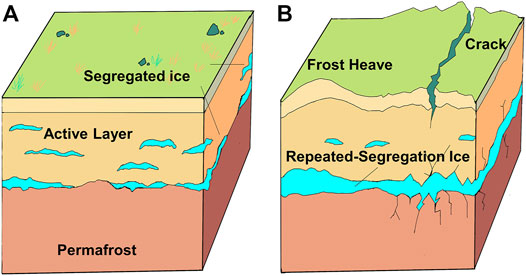
FIGURE 6. A schematic diagram of landforms in permafrost regions. (A) Segregated ice forms in the active layer at first, and the ice lens at the permafrost table is preserved after a freeze-thaw cycle. (B) Under a cooling climate, the permafrost table is raised, and the accumulation of segregated ice forms massive repeated-segregation ice, causing frost heave and frost crack.

Permafrost Landforms

The ice in permafrost has an important role in the formation of topography, or at least, in the origin of minor relief in permafrost regions. Segregated ice development causes frost heave and modifies topography (Figure 6B). Sometimes segregated ice development causes polygonal cracks because of the uneven distribution of ice in the soil mass (Walker et al., 2004). Segregated ice is also an essential factor in frost mounds formation (Van Huissteden, 2020). Hummocks are widely distributed in arctic and subarctic permafrost regions (Washburn, 1980), and are caused by the long-term seasonal freeze-thaw of ice lenses at the top and bottom of the active layer (Mackay, 1980). When permafrost degrades, the inhomogeneous melting of segregated ice causes the ground surface to collapse unevenly (Streletskiy et al., 2015; French, 2017). The hollows caused by the subsidence of the ground surface easily collect precipitation, runoff, and meltwater, forming ponds or lakes, changing the surface heat balance (Boike et al., 2015).

Regional Hydrological Processes

Segregated ice affects the hydrological process mainly by changing the hydrological properties and micro-topography by reducing soil permeability (Woo, 2012; Walvoord and Kurylyk, 2016). Massive segregated ice near the permafrost table causes a sharp decrease in permeability of this area. The zone with massive segregated ice can be regarded as a regional aquifer or impermeable layer. The impermeable layer obstructs or weakens the hydraulic connection between groundwater and active layer water, runoff, and even atmospheric precipitation on a seasonal scale (Zhao et al., 2019). In addition, the formation and melting processes of segregated ice accompanied by water migration significantly affect the spatiotemporal characteristics of the hydrological conditions of the active layer (Woo, 2012; Walvoord and Kurylyk, 2016). During warm seasons, the moisture content of the active layer increases due to the influence of rainfall, snowmelt water and excessive ice melting of the ice-rich permafrost table. Before percolating into the deep soil, most of this melted water, is discharged into rivers or lakes through surface runoff or subsurface lateral flow. The runoff variation is related to slope, ALT, and saturation, as well as the supply due to the seasonal melt of segregated ice (Van Huissteden, 2020). During periods of alternating warmth and cold, snow meltwater permeates through the surrounding soil. However, because the soil temperature is still below 0°C, a portion of the meltwater will refreeze, reducing the permeability of the ground surface. Meltwater generates runoff easily, forming ponds (Woo, 2012). In the cold season, there is bidirectional freezing in the active layer, and water migrates toward the freezing front, dehydrating the soil in the middle unfrozen layer (Woo, 2012). Soil fractures due to frost heaves, increasing the infiltration of precipitation and meltwater downward in the warm season (Ostroumov et al., 2001).

Ecosystem and Biogeochemical Processes

Segregated ice affects the growth dynamics of plants indirectly in cold regions by changing soil microstructure, soil ventilation, and thermal conductivity. Meanwhile, the water migration affects the nutrient and water distribution of the active layer, transforming the succession of the whole cold region ecosystem (Wang et al., 2006a). For example, during the development of frost mound, frost heave causes the central location to move upward year by year with the growth of segregated ice. In this process, the organic matter and nutrients at the bottom of active layer are pushed to the center of frost mound, and then transported and accumulated to the surrounding edge by leaching and soil movement (Peterson and Krantz, 2003). It will result in sparse vegetation in the center over time and luxuriant vegetation in the edge of frost mound, respectively, forming the unique honeycomb vegetation characteristics in permafrost regions (Walker et al., 2004). In the Qinghai Tibet Plateau, thawing segregated ice near the permafrost table weakened its role as an impermeable layer, which lowers water table and dries surface soil (Niu et al., 2011), thus decreasing the water available to plants and the productivity of the ecosystem (Wang et al., 2006a; Yi et al., 2014).

Large amounts of soil organic carbon (SOC) and soil organic nitrogen (SON) are stored in the active layer and underlying permafrost (Tarnocai et al., 2009; Koch et al., 2013; Zubrzycki et al., 2014; Ping et al., 2015). These organic matters easily develop into dissolved organic carbon (DOC) and dissolved organic or inorganic nitrogen (DON, and DIN, respectively) while the segregated ice melts (Wickland et al., 2018). Moreover, various soluble ions migrate to the freeze-thaw front with water migration, increasing their concentration near the ice lens (Ostroumov et al., 2001). Studies have shown that the DOC concentration in the soil solution ranges from 2 to 30 mg C L⁻¹ (White, 2020), while that in the segregated ice meltwater is as high as 4–128 mg C L⁻¹ (Ewing et al., 2015). Other types of dissolved organic matter (such as root exudates) produced by vegetation may accumulate due to the restriction of subsurface drainage by segregated ice (Michaelson and Ping, 2003). This organic matter is then transported to rivers through runoff (Prokushkin et al., 2009; Ma et al., 2019), strongly affecting oxidation-reduction, decomposition, and other biogeochemical processes.

Ice lenses in frozen soil also affect the below-ground gas transport process. When the soil changes between the freezing and thawing state, the SOC stored in permafrost will be decomposed by soil microbes, generating carbon dioxide (CO₂), methane (CH₄), nitrous oxide (N₂O), or other greenhouse gases (Yang et al., 2014; Zona et al., 2016). Owing to the ice lens barrier, the frozen soil delays the emission of N₂O and CO₂ in winter (Van Bochove et al., 2001; Song et al., 2012). The large autumn burst of CH₄ from the tundra in high latitudes may be related to the freezing and thawing process of permafrost in the Arctic (Mastepanov et al., 2008; Zona et al., 2016; Byun et al., 2017). Because gas solubility is significantly lower in ice than in liquid water, the formation of segregated ice at the freezing front during the bidirectional freezing process in autumn may lead to the efflux of methane previously dissolved in soil water (Byun et al., 2017). However, segregated ice blocks the pores and hinders the gas discharge, leading to the retention of CH₄. Subsequently, frost heaving due to the continuous formation of segregated ice destroys the mechanical structure of soil and causes ground cracking, providing a channel for gas to escape, thus producing a CH₄ peak (Mastepanov et al., 2013). Under a cold climate, the seasonal segregated ice and the trapped CH₄ in the active layer may be permanently incorporated into near-surface or even deeper permafrost (Byun et al., 2017). The reverse is also possible upon climate warming. Higher soil temperature will promote the activity of soil organisms and thus aggravate the decomposition of SOC to release more carbon dioxide (Natali et al., 2015).

Summary and Future Perspectives

Since Taber realized that frost heaving mainly comes from liquid water migration that supplies growing ice lenses, people have put forward to various theoretical models to improve the understanding of their mechanism. Now the processes of ice lenses have been explained by mathematical models that successfully verified from the macroscopic features. In permafrost regions, water migration and segregated ice shapes spectacular permafrost topographic features, changes regional hydrological patterns, even makes their carbon cycle differ from that of other soils. Under a warming climate, researchers have much renewed interest in how the processes of water migration and ice formation play roles in the interaction between frozen ground and the environment. This article reviewed the mechanism of water migration and segregated ice formation and different models developed to account for their physical processes, as well as an overview of their impact on the permafrost environment. Given the aspects that current research regarding water migration and ice formation has overlooked, we suggest the following perspectives should be the central focus in future research.

(1) It is the basis for understanding the mechanism of ice segregation to explicitly know the driving forces of unfrozen water migration. Since the theory of unfrozen water film was brought up, the concept of soil water potential has been widely accepted to characterize the energy state of liquid water, to further study the direction and water flux during water moisture migration. Current methods are hard to directly measure the soil water potential in frozen soil, so researchers rely on the Clapeyron equation based on phase equilibrium to convert the temperature gradient to water potential (Loch, 1978; Gilpin, 1980; Drotz et al., 2009; Thomas et al., 2009). However, one of the primary assumptions invoked when employing the Clapeyron equation and its modified versions is that the pore water pressure is measured relative to the pressure in the ice phase, which is often implicitly assumed to be atmospheric (Kurylyk and Watanabe, 2013). In fact, soil increases its strength as temperature declines and as ice progressively fills the pores in the freezing process. This means the ice pressure must rise for a growing ice lens and the potential gradient will no longer be linearly related to the temperature gradient (Wood, 1990). If we can only measure the temperature gradient, it is difficult to fully interpret the reason why the growth rate of ice lenses decreases with temperature. Therefore, the applicability of the Clapeyron equation in frozen soil still needs to be further verified by accurately measuring the pore water pressure and ice pressure in the laboratory, which depends on the progress of measurement technologies. Another concern is the calculation and determination of unfrozen water content, which is also important for the study of water migration. At present, a commonly used method to calculate unfrozen water content in frozen soil is the empirical formula or relate soil frozen characteristic curve (SFCC) and the soil water characteristic curve (SWCC) by the Clausius-Clapeyron equation (Spaans and Baker, 1996; Kurylyk and Watanabe, 2013; Fu et al., 2021). The latter is inappropriate to apply this equation at disequilibrium, such as during rapid early-stage freezing. The accuracy of the empirical formula largely depends on the calibration dataset size and characteristics. However, because of the possibility of ice be melted by the temperature or moisture probes, it is difficult to conduct long-term monitoring of the energy state of unfrozen water or unfrozen water and ice content in frozen ground under field conditions (He et al., 2018). Many new theories and methods emerged to partition water and ice in partially frozen soil to estimate unfrozen water content and ice content (Gang and Si, 2011; Kojima et al., 2016; Kojima et al., 2020). New theories and methods are in their infancy and have limitations at present. Still, they potentially could greatly improve the measurement techniques and our understanding of unfrozen water migration and ice formation.

2) The measurement of ice content is essential for studying the water migration in frozen soil and is very important for understanding the mechanism of frost heave or thaw settlement. In laboratory experiments, the ice content is usually estimated by subtracting the unfrozen water content from the total water content. The latter could be directly measured by mature methods, such as the neutron moisture meter method (NMM) (Sun et al., 2021) and gamma-ray attenuation method (Zhou et al., 2014) for the total water content, TDR (time-domain reflectometer) method, FDR (frequency-domain reflectometer) method, and NMR (Nuclear Magnetic Resonance) method for unfrozen water content (Feng et al., 2021). However, there is still no suitable method to monitor the ice content, water migration, and their spatial variation under field conditions. One of the critical problems is that we cannot monitor the change of ice content during freezing and thawing without damaging the soil structure. Although some improved methods have been verified in the field (Cheng et al., 2013; Kojima et al., 2020; Wang et al., 2021), there is still no commercial sensor available. Another way is to estimate the ice content by geophysical technology or remote sensing methods, such as ground-penetrating radar (GPR) (Daniels et al., 1995; Lamoureux et al., 2018). However, the GPR method prefers to resolve wedge ice, massive ice, and ice-rich sediments rather than the individual ice lenses with small volume, and it needs to be combined with other means to improve the accuracy of detection (Fortier and Savard, 2010; Sokolov et al., 2020). Satellite remote sensing provides another method to continuously monitor the surface water condition of frozen soil in space via data assimilation (Mwangi et al., 2020; Szczykulska et al., 2021). Cosmic-ray neutron probes (CRNP) allows continuous monitoring of soil ice content at the field scale averaged over several hectares in shallow soil profiles (Mwangi et al., 2020). However, it is still unable to reasonably estimate the ice content of deep soil layer due to soil heterogeneities (Stevanato et al., 2019). With the ever-expanding use of geophysical methods for permafrost and ground ice studies, new inversion means or improved methods should be verified by boreholes or test pits to estimate the spatiotemporal variation and distribution. This will be a new challenge for engineering geologists and shallow geophysicists.

(3) Models aimed to describe the dynamics of ice formation have given a successful prediction of the macroscopic processes of segregated ice, such as the rigid ice model, which has been widely used and further developed. However, the pre-hypothesis of the rigid ice model used to predict the heave rate and the initiation of new lenses still lack a firm theoretical basis at the microscope physics. This means it will produce uncertainty when applying the model in different physical environments by modifying the model parameters. The rigid-ice model assumes that lenses initiate within ice that is connected through the frozen fringe to the active lens. However, experiments showed that there are variety of ice growth forms in addition to lenses (Peppin et al., 2006; Rempel, 2011), and their initiation mechanisms should also be considered. Premelting theory began with surface interface physics provides a new sight in understanding the microphysical interactions that occur between the soil particles, the ice and the liquid (Rempel et al., 2004; Rempel, 2007). The net ice-particle force within the fringe can be calculated by applying the concept of thermodynamic buoyancy (Rempel, 2010). However, as it still employed a few simplifying assumptions in constructing theoretical model, the premelting model needs further development. Engineering applications of the ice formation models is another critical problem. Many works verified the model simulations through laboratory measurements (Williams and Smith, 1989), Unfortunately, relatively little field research has been conducted on frost heave. The empirical work has principally been conducted under highly controlled laboratory conditions, making it difficult to apply theoretical models in field conditions. These difficulties include but are not limited to the following: a) the complex form and various parameters of the model make it difficult for it to be popularized in actual application, b) most models are based on saturated soils, and they are not well suited to application in unsaturated permafrost and c) the considerable diversities of soil particle characteristics in different soils cause it is hard to find a uniform method to evaluate the parameters regard to frost susceptibility, such as the parameterization scheme of soil thermal conductivity and hydraulic conductivity (Gelfan, 2006; He et al., 2020). In the future, simplifying existing models or developing new ice formation models will be an exciting challenge that will facilitate field application. Additionally, combined with more observational data, developing the comprehensive and systematic scheme of permafrost soil thermal and hydraulic conductivity will also help improve the description of soil thermal properties in models.

(4) The development and decline of segregated ice at the permafrost table is an important feature in the change of permafrost, which exerts a strong influence on the development of landforms, hydrology and biochemical processes (Van Huissteden, 2020). Sustained climate warming is accelerating the degradation of permafrost and the thawing of ice lenses near the permafrost table. Under this condition, landscape models were developed to predict the influences of permafrost degradation on hydrological, ecological, and climatic effects (Flerchinger and Saxton, 1989; Cherkauer and Lettenmaier, 1999; Gouttevin et al., 2012; Yang et al., 2018a; Yang et al., 2018b). However, there were significant deviations of simulations when the models applied to permafrost, especially the unfrozen soil moisture during the freezing and thawing process (Swenson et al., 2012; Xiao et al., 2013; Chadburn et al., 2015; Yang et al., 2018a; Luo et al., 2018). One possible reason is the inadequate consideration of the water migration and segregated ice in models. Most landscape models that we have checked simplify, even ignore the process of water migration and ice lenses formation in constructing the model (Dai et al., 2003; Liang et al., 2003; Chen et al., 2007; Swenson et al., 2012; Zheng et al., 2017). Of course, it is necessary and understandable because the factors that control segregated ice formation operate at a sub-mm scale, and are primarily affected by soil properties. This makes incorporating segregated ice behavior into models operating with 1- or 10-km grid cells difficult due to soil spatial heterogeneity. However, when discussing the long-term effects of the permafrost changes, the development and thawing of ice lenses is still an inseparable feature. Some researchers have added excess ground ice to the model for simulating thermal karst caused by permafrost degradation in recent years, but they are not concerned with the long-term process of excess ice formation (Lee et al., 2014; Cai et al., 2020). In the future, we may be able to find methods to connect segregated ice models with landscape models to achieve the modeling of ice lenses that through the hundreds or even ten thousand years of evolvement. This will be a challenging and interesting work that will help us to understand the interaction between soil ice segregation and the permafrost environment, and improve the accuracy of landscape models in permafrost regions.

Author Contributions

QW contributed to the conception of the study, supervision and funding acquisition; ZF: contributed to literature synthesis and wrote the manuscript; WZ, HH, and LW helped perform the analysis with constructive discussions.

Funding

This work was supported by the Key Program for Frontier Sciences of the Chinese Academy of Sciences (grant numbers QYZDJ-SSW-DQC011), the National Natural Science Foundation of China (grant numbers 41690144), the funding by the Swedish Nation Space Agency 209/19 and Swedish Research Council VR 2020-05338, and the National Natural Science Foundation of China (grant numbers 41877015).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akagawa, S. (1988). Experimental Study of Frozen Fringe Characteristics. Cold Regions Sci. Technology 15 (3), 209–223. doi:10.1016/0165-232X(88)90068-7

CrossRef Full Text | Google Scholar

Akagawa, S., and Nishisato, K. (2009). Tensile Strength of Frozen Soil in the Temperature Range of the Frozen Fringe. Cold Regions Sci. Technology 57 (1), 13–22. doi:10.1016/j.coldregions.2009.01.002

CrossRef Full Text | Google Scholar

Akagawa, S., Satoh, M., Kanie, S., and Mikami, T. (2006). Effect of Tensile Strength on Ice Lens Initiation Temperature. Curr. Practices Cold Regions Eng., 1–12. doi:10.1061/40836(210)43

CrossRef Full Text | Google Scholar

Anderson, D. M., and Tice, A. R. (1972). Predicting Unfrozen Water Contents in Frozen Soils from Surface Area Measurements. Highw. Res. Rec. 393, 12–18. doi:10.1016/0022-4898(73)90017-7

CrossRef Full Text | Google Scholar

Andresen, C. G., Lawrence, D. M., Wilson, C. J., McGuire, A. D., Koven, C., Schaefer, K., et al. (2019). Soil Moisture and Hydrology Projections of the Permafrost Region: A Model Intercomparison. Cryosphere Discuss., 1–20. doi:10.5194/tc-2019-144

CrossRef Full Text | Google Scholar

Arenson, L. U., Sego, D. C., and Take, W. A. (2007). “Measurement of Ice Lens Growth and Soil Consolidation during Frost Penetration Using Particle Image Velocimetry (PIV),” in 60th Canadian Geotechnical Conference (Ottawa, ON, 2046–2053.

Google Scholar

Azmatch, T. F., Arenson, L. U., Sego, D. C., and Biggar, K. W. (2008). “Measuring Ice Lens Growth and Development of Soil Strains during Frost Penetration Using Particle Image Velocimetery (GeoPIV),” in Proceedings of the Ninth International Conference on Permafrost, 89–94.

Google Scholar

Bai, R., Lai, Y., Zhang, M., and Gao, J. (2018). Water-vapor-heat Behavior in a Freezing Unsaturated Coarse-Grained Soil with a Closed Top. Cold Regions Sci. Technology 155, 120–126. doi:10.1016/j.coldregions.2018.08.007

CrossRef Full Text | Google Scholar

Banin, A., and Anderson, D. M. (1974). Effects of Salt Concentration Changes during Freezing on the Unfrozen Water Content of Porous Materials. Water Resour. Res. 10 (1), 124–128. doi:10.1029/wr010i001p00124

CrossRef Full Text | Google Scholar

Beskow, D. G., and Fil, B. (1935). Soil Freezing and Frost Heaving with Special Application to Roads and Railroads. Soil Sci. 65 (4), 355. doi:10.1097/00010694-194804000-00

CrossRef Full Text | Google Scholar

Biermans, M. B. G. M., Dijkema, K. M., and De Vries, D. A. (1976). Water Movement in Porous media towards an Ice Front. Nature 264 (1-2), 166–167. doi:10.1038/264166a0

CrossRef Full Text | Google Scholar

Black, P. B. (1985). The Rigidice Model of Frost Heave and its Input Functions (Frozen Soil, Unfrozen Water Content, Regelation). Cornell University.

Google Scholar

Boike, J., Georgi, C., Kirilin, G., Muster, S., Abramova, K., Fedorova, I., et al. (2015). Thermal Processes of Thermokarst Lakes in the Continuous Permafrost Zone of Northern Siberia - Observations and Modeling (Lena River Delta, Siberia). Biogeosciences 12 (20), 5941–5965. doi:10.5194/bg-12-5941-2015

CrossRef Full Text | Google Scholar

Bouyoucos, G. (1920). Degree of Temperature to Which Soils Can Be Cooled without Freezing. Mon. Wea. Rev. 48 (12), 718. doi:10.1038/scientificamerican04011910.1175/1520-0493(1920)48<718a:dottws>2.0.co;2

CrossRef Full Text | Google Scholar

Bronfenbrener, L. (2013). Non-equilibrium Crystallization in Freezing Porous media: Numerical Solution. Cold Regions Sci. Technology 85 (JAN), 137–149. doi:10.1016/j.coldregions.2012.09.002

CrossRef Full Text | Google Scholar

Burn, C. R., and Michel, F. A. (1988). Evidence for Recent Temperature-Induced Water Migration into Permafrost from the Tritium Content of Ground Ice Near Mayo, Yukon Territory, Canada. Can. J. Earth Sci. 25 (6), 909–915. doi:10.1139/e88-087

CrossRef Full Text | Google Scholar

Burt, T. P., and Williams, P. J. (1976). Hydraulic Conductivity in Frozen Soils. Earth Surf. Process. 1 (4), 349–360. doi:10.1002/esp.3290010404

CrossRef Full Text | Google Scholar

Byun, E., Yang, J.-W., Kim, Y., and Ahn, J. (2017). Trapped Greenhouse Gases in the Permafrost Active Layer: Preliminary Results for Methane Peaks in Vertical Profiles of Frozen Alaskan Soil Cores. Permafrost Periglac. Process. 28 (2), 477–484. doi:10.1002/ppp.1935

CrossRef Full Text | Google Scholar

Cai, L., Lee, H., Westermann, S., and Aas, K. S. (2020). Projecting Circum-Arctic Excess Ground Ice Melt with a Sub-grid Representation in the Community Land Model. Cryosphere Discuss., 1–28. doi:10.5194/tc-2019-230

CrossRef Full Text | Google Scholar

Calmels, F., and Allard, M. (2008). Segregated Ice Structures in Various Heaved Permafrost Landforms through CT Scan. Earth Surf. Process. Landforms 33 (2), 209–225. doi:10.1002/esp.1538

CrossRef Full Text | Google Scholar

Chadburn, S., Burke, E., Essery, R., Boike, J., Langer, M., Heikenfeld, M., et al. (2015). An Improved Representation of Physical Permafrost Dynamics in the JULES Land-Surface Model. Geosci. Model. Dev. 8 (5), 1493–1508. doi:10.5194/gmd-8-1493-2015

CrossRef Full Text | Google Scholar

Chamberlain, E. (1983). “Frost Heave of saline Soils,” in Proceedings 4th International Conference on Permafrost, Fairbanks, Alaska, 121–126.

Google Scholar

Chamberlain, E. J. (1981). Frost Susceptibility of Soil, Review of index Tests. Hanover, NH: Cold Regions Research and Engineering Lab.

Google Scholar

Che, M., Chen, B., Chen, J., and Wang, Y. (2014). Parameterization of Deciduous Vegetation Phenology for the Dynamic Land Model (DLM). San Francisco: Agu Fall Meeting.

Google Scholar

Chen, B., Chen, J. M., and Ju, W. (2007). Remote Sensing-Based Ecosystem-Atmosphere Simulation Scheme (EASS)-Model Formulation and Test with Multiple-Year Data. Ecol. Model. 209 (2), 277–300. doi:10.1016/j.ecolmodel.2007.06.032

CrossRef Full Text | Google Scholar

Cheng, G. (1982). Effect of Uni-Direction Accumulation of Unfrozen Water in Seasonally Frozen and Thawed Ground. Chin. Sci. Bull. (23), 42–45.

Google Scholar

Cheng, Q., Sun, Y., Qin, Y., Xue, X., Cai, X., Sheng, W., et al. (2013). In Situ measuring Soil Ice Content with a Combined Use of Dielectric Tube Sensor and Neutron Moisture Meter in a Common Access Tube. Agric. For. Meteorology 171-172, 249–255. doi:10.1016/j.agrformet.2012.12.004

CrossRef Full Text | Google Scholar

Cherkauer, K. A., and Lettenmaier, D. P. (1999). Hydrologic Effects of Frozen Soils in the Upper Mississippi River basin. J. Geophys. Res. 104 (D16), 19599–19610. doi:10.1029/1999jd900337

CrossRef Full Text | Google Scholar

Cui, Y., and Shao, J. (2005). The Role of Ground Water in Arid/Semiarid Ecosystems, Northwest China. Ground Water 43 (4), 471–477. doi:10.1111/j.1745-6584.2005.0063.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Currie, J. A. (1983). Gas Diffusion through Soil Crumbs: the Effects of Wetting and Swelling. J. Soil Sci. 34 (2), 217–232. doi:10.1111/j.1365-2389.1983.tb01029.x

CrossRef Full Text | Google Scholar

Dai, Y., Zeng, X., Dickinson, R. E., Baker, I., Bonan, G. B., Bosilovich, M. G., et al. (2003). The Common Land Model. Bull. Am. Meteorol. Soc. 84 (8), 1013–1024. doi:10.1175/BAMS-84-8-1013

CrossRef Full Text | Google Scholar

Daniels, J. J., Roberts, R., and Vendl, M. (1995). Ground Penetrating Radar for the Detection of Liquid Contaminants. J. Appl. Geophys. 33 (1), 195–207. doi:10.1016/0926-9851(95)90041-1

CrossRef Full Text | Google Scholar

Dash, J. G. (1989). Thermomolecular Pressure in Surface Melting: Motivation for Frost Heave. Science 246 (4937), 1591–1593. doi:10.1126/science.246.4937.1591

PubMed Abstract | CrossRef Full Text | Google Scholar

Drotz, S. H., Tilston, E. L., Sparrman, T., Schleucher, J., Nilsson, M., and Öquist, M. G. (2009). Contributions of Matric and Osmotic Potentials to the Unfrozen Water Content of Frozen Soils. Geoderma 148 (3-4), 392–398. doi:10.1016/j.geoderma.2008.11.007

CrossRef Full Text | Google Scholar

Edlefsen, N. E., and Anderson, A. B. C. (1943). Thermodynamics of Soil Moisture. Hilg 15 (2), 31–298. doi:10.3733/hilg.v15n02p031

CrossRef Full Text | Google Scholar

Ershov, E. D., Zhestkova, T. N., Kuchukov, E. Z., Malinovskii, D. V., Chuvilin, E. M., Komarov, I. A., et al. (2015). Principles of Geocryology. Lithogenetic Geocryology, 2. Lanzhou, China: Lanzhou University Press.

Google Scholar

Etzelmüller, B., Guglielmin, M., Hauck, C., Hilbich, C., Hoelzle, M., Isaksen, K., et al. (2020). Twenty Years of European Mountain Permafrost Dynamics-The PACE Legacy. Environ. Res. Lett. 15, 104070. doi:10.1088/1748-9326/abae9d

CrossRef Full Text | Google Scholar

Everett, D. H. (1961). The Thermodynamics of Frost Damage to Porous Solids. Trans. Faraday Soc. 57, 1541. doi:10.1039/tf9615701541

CrossRef Full Text | Google Scholar

Everett, K. R. (1989). Glossary of Permafrost and Related Ground-Ice Terms. Arctic Alpine Res. 21, 213. doi:10.2307/1551636

CrossRef Full Text | Google Scholar

Ewing, S. A., O'Donnell, J. A., Aiken, G. R., Butler, K., Butman, D., Windham‐Myers, L., et al. (2015). Long‐term Anoxia and Release of Ancient, Labile Carbon upon Thaw of Pleistocene Permafrost. Geophys. Res. Lett. 42 (2410), 10,730–10,738. doi:10.1002/2015gl066296

CrossRef Full Text | Google Scholar

Fagan, J. D., and Nelson, F. E. (2017). Spatial Sampling Design in the Circumpolar Active Layer Monitoring Programme. Permafrost Periglac. Process. 28 (1), 42–51. doi:10.1002/ppp.1904

CrossRef Full Text | Google Scholar

Farouki, O. T. (1981). Thermal Properties of Soils. Hanover, NH: Cold Regions Research and Engineering Lab.

Google Scholar

Feng, S., Zhang, H., Lv, J., Dyck, M., Wu, Q., and He, H. (2021). A Scientometric Review of Research Status on Unfrozen Soil Water. Water 13 (5), 708. doi:10.3390/w13050708

CrossRef Full Text | Google Scholar

Ferguson, H., Brown, P. L., and Dickey, D. D. (1964). Water Movement and Loss under Frozen Soil Conditions. Soil Sci. Soc. America J. 28 (5), 700–703. doi:10.2136/sssaj1964.03615995002800050034x

CrossRef Full Text | Google Scholar

Fisher, D. A., Lacelle, D., and Pollard, W. (2020). A Model of Unfrozen Water Content and its Transport in Icy Permafrost Soils: Effects on Ground Ice Content and Permafrost Stability. Permafrost and Periglac Process 31 (1), 184–199. doi:10.1002/ppp.2031

CrossRef Full Text | Google Scholar

Fortier, R., and Savard, C. (2010). “Engineering Geophysical Investigation of Permafrost Conditions underneath Airfield Embankments in Northern Quebec (Canada),” in Geo-2010. Confer. Proceed. Calgary, 1307–1316. Availableat: https://pubs.aina.ucalgary.ca//cpc/CPC6-1307.pdf.

Google Scholar

Fowler, A. C., and Krantz, W. B. (1994). A Generalized Secondary Frost Heave Model. SIAM J. Appl. Math. 54 (6), 1650–1675. doi:10.1137/s0036139993252554

CrossRef Full Text | Google Scholar

Fremond, M., and Mikkola, M. (1991). “Thermomechanical Modelling of Freezing Soil,” in International symposium on ground freezing, 17–24.

Google Scholar

French, H. M. (2017). The Periglacial Environment. John Wiley & Sons.

Google Scholar

French, H., and Shur, Y. (2010). The Principles of Cryostratigraphy. Earth-Science Rev. 101 (3-4), 190–206. doi:10.1016/j.earscirev.2010.04.002

CrossRef Full Text | Google Scholar

Frey, K. E., and McClelland, J. W. (2009). Impacts of Permafrost Degradation on Arctic River Biogeochemistry. Hydrol. Process. 23 (1), 169–182. doi:10.1002/hyp.7196

CrossRef Full Text | Google Scholar

Fu, Z., Wu, Q., Miles, D., and He, H. (2021). A New Model to Describe Soil Freezing and Thawing Characteristic Curve. J. Glaciology Geocryology 43 (02), 437–452. doi:10.7522/j.issn.1000-0240.2020.0090

CrossRef Full Text | Google Scholar

Fukuda, m., Ogawa, s., and Kamei, t. (1988). Prediction of Field Frost Heave Using the Segregation Potential Theory. Doboku Gakkai Ronbunshu 1988 (400), 253–259. doi:10.2208/jscej.1988.400_253

CrossRef Full Text | Google Scholar

Gelfan, A. (2006). Physically-based Model of Heat and Water Transfer in Frozen Soil and its Parameterization by Basic Soil Data, 303. Wallingford, UK: IAHS publication, 293.

Google Scholar

Gilpin, R. (1982). “A Frost Heave Interface Condition for Use in Numerical Modelling,” in Proc. 4th Canadian Permafrost Conference, Calgary, Canada, 459–465.

Google Scholar

Gilpin, R. R. (1980). A Model for the Prediction of Ice Lensing and Frost Heave in Soils. Water Resour. Res. 16 (5), 918–930. doi:10.1029/WR016i005p00918

CrossRef Full Text | Google Scholar

G. N. Flerchinger, G. N., and K. E. Saxton, K. E. (1989). Simultaneous Heat and Water Model of a Freezing Snow-Residue-Soil System I. Theory and Development. Trans. ASAE 32 (2), 0565–0571. doi:10.13031/2013.3104110.13031/2013.31040

CrossRef Full Text | Google Scholar

Gold, L. W. (1957). A Possible Force Mechanism Associated with the Freezing of Water in Porous Materials. High. Res. Board Bull. 168, 65–72.

Google Scholar

Goulet, F. (1995). Frost Heaving of forest Tree Seedlings: a Review. New For. 9 (1), 67–94. doi:10.1007/bf00028927

CrossRef Full Text | Google Scholar

Gouttevin, I., Krinner, G., Ciais, P., Polcher, J., and Legout, C. (2012). Multi-scale Validation of a New Soil Freezing Scheme for a Land-Surface Model with Physically-Based Hydrology. The Cryosphere 6 (2), 407–430. doi:10.5194/tc-6-407-2012

CrossRef Full Text | Google Scholar

Gruber, S. (2012). Derivation and Analysis of a High-Resolution Estimate of Global Permafrost Zonation. The Cryosphere 6 (1), 221–233. doi:10.5194/tc-6-221-2012

CrossRef Full Text | Google Scholar

Guodong, C. (1983). The Mechanism of Repeated-Segregation for the Formation of Thick Layered Ground Ice. Cold Regions Sci. Technology 8 (1), 57–66. doi:10.1016/0165-232X(83)90017-4

CrossRef Full Text | Google Scholar

Guthrie, W. S., Hermansson, A., and Woffinden, K. H. (2006). “Saturation of Granular Base Material Due to Water Vapor Flow during Freezing: Laboratory Experimentation and Numerical Modeling,” in 13th International Conference on Cold Regions Engineering. doi:10.1061/40836(210)66

CrossRef Full Text | Google Scholar

Guymon, G., Hromadka Ii, T., and Berg, R. (1980). A One Dimensional Frost Heave Model Based upon Simulation of Simultaneous Heat and Water Flux. Cold Regions Sci. Technology 3 (2-3), 253–262. doi:10.1016/0165-232X(80)90032-4

CrossRef Full Text | Google Scholar

Hansson, K., Simunek, J., Mizoguchi, M., Lundin, L.-C., and Van Genuchten, M. T. (2004). Water Flow and Heat Transport in Frozen Soil: Numerical Solution and Freeze-Thaw Applications. Vadose Zone J. 3 (2), 693–704. doi:10.2136/vzj2004.069310.2113/3.2.693

CrossRef Full Text | Google Scholar

Harlan, R. L. (1973). Analysis of Coupled Heat-Fluid Transport in Partially Frozen Soil. Water Resour. Res. 9 (5), 1314–1323. doi:10.1029/WR009i005p01314

CrossRef Full Text | Google Scholar

Haynes, J. M. (1965). Capillary Properties of Some Model Pore Systems. Bristol, England: University of Bristol.

Google Scholar

Hazirbaba, K., Zhang, Y., and Leroy Hulsey, J. (2011). Evaluation of Temperature and Freeze-Thaw Effects on Excess Pore Pressure Generation of fine-grained Soils. Soil Dyn. Earthquake Eng. 31 (3), 372–384. doi:10.1016/j.soildyn.2010.09.006

CrossRef Full Text | Google Scholar

He, H., Dyck, M. F., Horton, R., Ren, T., Bristow, K. L., Lv, J., et al. (2018). Development and Application of the Heat Pulse Method for Soil Physical Measurements. Rev. Geophys. 56 (4), 567–620. doi:10.1029/2017RG000584

CrossRef Full Text | Google Scholar

He, H., Flerchinger, G. N., Kojima, Y., Dyck, M., and Lv, J. (2021). A Review and Evaluation of 39 thermal Conductivity Models for Frozen Soils. Geoderma 382, 114694. doi:10.1016/j.geoderma.2020.114694

CrossRef Full Text | Google Scholar

He, H., He, D., Jin, J., Smits, K. M., Dyck, M., Wu, Q., et al. (2020). Room for Improvement: A Review and Evaluation of 24 Soil thermal Conductivity Parameterization Schemes Commonly Used in Land-Surface, Hydrological, and Soil-Vegetation-Atmosphere Transfer Models. Earth-Science Rev. 211, 103419. doi:10.1016/j.earscirev.2020.103419

CrossRef Full Text | Google Scholar

Hoekstra, P., and Miller, R. (1963). Movement of Water in a Film between Glass and Ice. Cornell University.

Google Scholar

Hoekstra, P. (1966). Moisture Movement in Soils under Temperature Gradients with the Cold-Side Temperature below Freezing. Water Resour. Res. 2 (2), 241–250. doi:10.1029/WR002i002p00241

CrossRef Full Text | Google Scholar

Hoekstra, P. (1969). Water Movement and Freezing Pressures. Soil Sci. Soc. America J. 33 (4), 512–518. doi:10.2136/sssaj1969.03615995003300040011x

CrossRef Full Text | Google Scholar

Horiguchi, K. (1980). Experimental Studies with Frozen Soil in an Ice Sandwich Permeameter. Cold Regions Sci. Technology 3 (2-3), 177–183. doi:10.1016/0165-232X(80)90023-3

CrossRef Full Text | Google Scholar

Horiguchi, K., and Miller, R. D. (1983). Hydraulic Conductivity Functions of Frozen Materials. Washington, DC: National Academy Press.

Google Scholar

Hughes, O. L. (1974). Geology and Permafrost in Relation to Hydrology and Geophysics. PERMAFROST HYDROLOGY. doi:10.2307/1551636

CrossRef Full Text | Google Scholar

Ishizaki, T., and Nishio, N. (1988). “Experimental Study of Frost Heaving of a Saturated Soil,” in Proceedings: 5th International Symposium on Ground Freezing, Nottingham, UK, 65–72.

Google Scholar

Jame, Y.-W., and Norum, D. I. (1980). Heat and Mass Transfer in a Freezing Unsaturated Porous Medium. Water Resour. Res. 16 (4), 811–819. doi:10.1029/WR016i004p00811

CrossRef Full Text | Google Scholar

Jansson, P.-E., and Halldin, S. (1979). Model for Annual Water and Energy Flow in a Layered Soil. Dev. Agric. Manag. For. Ecol. 9, 145–163. doi:10.1016/B978-0-444-41844-9.50017-2

CrossRef Full Text | Google Scholar

Ji, Y., Zhou, G., Zhou, Y., and Vandeginste, V. (2019). Frost Heave in Freezing Soils: A Quasi-Static Model for Ice Lens Growth. Cold Regions Sci. Technology 158, 10–17. doi:10.1016/j.coldregions.2018.11.003

CrossRef Full Text | Google Scholar

Kanevskiy, M., Shur, Y., Jorgenson, M. T., Ping, C.-L., Michaelson, G. J., Fortier, D., et al. (2013). Ground Ice in the Upper Permafrost of the Beaufort Sea Coast of Alaska. Cold Regions Sci. Technology 85 (JAN), 56–70. doi:10.1016/j.coldregions.2012.08.002

CrossRef Full Text | Google Scholar

Koch, J. C., Runkel, R. L., Striegl, R., and McKnight, D. M. (2013). Hydrologic Controls on the Transport and Cycling of Carbon and Nitrogen in a Boreal Catchment Underlain by Continuous Permafrost. J. Geophys. Res. Biogeosci. 118 (2), 698–712. doi:10.1002/jgrg.20058

CrossRef Full Text | Google Scholar

Kojima, Y., Heitman, J. L., Flerchinger, G. N., Ren, T., and Horton, R. (2016). Sensible Heat Balance Estimates of Transient Soil Ice Contents. Vadose zone j. 15 (5), 1–11. doi:10.2136/vzj2015.10.0134

CrossRef Full Text | Google Scholar

Kojima, Y., Nakano, Y., Kato, C., Noborio, K., Kamiya, K., and Horton, R. (2020). A New Thermo-Time Domain Reflectometry Approach to Quantify Soil Ice Content at Temperatures Near the Freezing point. Cold Regions Sci. Technology 174, 103060. doi:10.1016/j.coldregions.2020.103060

CrossRef Full Text | Google Scholar

Konrad, J.-M., and Duquennoi, C. (1993). A Model for Water Transport and Ice Lensing in Freezing Soils. Water Resour. Res. 29 (19), 3109–3124. doi:10.1029/93WR00773

CrossRef Full Text | Google Scholar

Konrad, J.-M. (2005). Estimation of the Segregation Potential of fine-grained Soils Using the Frost Heave Response of Two Reference Soils. Can. Geotech. J. 42 (1), 38–50. doi:10.1139/t04-080

CrossRef Full Text | Google Scholar

Konrad, J.-M. (1999). Frost Susceptibility Related to Soil index Properties. Can. Geotech. J. 36 (3), 403–417. doi:10.1139/cgj-36-3-40310.1139/t99-008

CrossRef Full Text | Google Scholar

Konrad, J.-M., and Morgenstern, N. R. (1980). A Mechanistic Theory of Ice Lens Formation in fine-grained Soils. Can. Geotech. J. 17 (4), 473–486. doi:10.1139/t80-056

CrossRef Full Text | Google Scholar

Konrad, J.-M., and Morgenstern, N. R. (1982a). Effects of Applied Pressure on Freezing Soils. Can. Geotech. J. 19 (4), 494–505. doi:10.1139/t82-053

CrossRef Full Text | Google Scholar

Konrad, J.-M., and Morgenstern, N. R. (1984). Frost Heave Prediction of Chilled Pipelines Buried in Unfrozen Soils. Can. Geotech. J. 21 (1), 100–115. doi:10.1139/t84-008

CrossRef Full Text | Google Scholar

Konrad, J.-M., and Morgenstern, N. R. (1982b). Prediction of Frost Heave in the Laboratory during Transient Freezing. Can. Geotech. J. 19 (3), 250–259. doi:10.1139/t82-032

CrossRef Full Text | Google Scholar

Konrad, J.-M., and Morgenstern, N. R. (1981). The Segregation Potential of a Freezing Soil. Can. Geotech. J. 18 (4), 482–491. doi:10.1139/t81-059

CrossRef Full Text | Google Scholar

Konrad, J.-M., Roy, M., Rochelle, P. L., Leroueil, S., and Bergeron, G. (1995). Field Observations of Frost Action in Intact and Weathered Champlain Sea clay. Can. Geotech. J. 32 (4), 689–700. doi:10.1139/t95-068

CrossRef Full Text | Google Scholar

Koren, V., Schaake, J., Mitchell, K., Duan, Q.-Y., Chen, F., and Baker, J. M. (1999). A Parameterization of Snowpack and Frozen Ground Intended for NCEP Weather and Climate Models. J. Geophys. Res. 104 (D16), 19569–19585. doi:10.1029/1999JD900232

CrossRef Full Text | Google Scholar

Korkina, R. (1965). Electrical Potentials in Freezing Solutions and Their Effect on Migration, Protsessy Tepla I Massoobmena Y Merzlykh Gornykh Porodakh. Cold Regions Res. Eng. Lab. Draft Translation 490, 56–65.

Google Scholar

Koven, C. D., Ringeval, B., Friedlingstein, P., Ciais, P., Cadule, P., Khvorostyanov, D., et al. (2011). Permafrost Carbon-Climate Feedbacks Accelerate Global Warming. Proc. Natl. Acad. Sci. 108 (36), 14769–14774. doi:10.1073/pnas.1103910108

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurylyk, B. L., and Watanabe, K. (2013). The Mathematical Representation of Freezing and Thawing Processes in Variably-Saturated, Non-deformable Soils. Adv. Water Resour. 60 (oct), 160–177. doi:10.1016/j.advwatres.2013.07.016

CrossRef Full Text | Google Scholar

Lai, Y., Pei, W., Zhang, M., and Zhou, J. (2014). Study on Theory Model of hydro-thermal-mechanical Interaction Process in Saturated Freezing Silty Soil. Int. J. Heat Mass Transfer 78, 805–819. doi:10.1016/j.ijheatmasstransfer.2014.07.035

CrossRef Full Text | Google Scholar

Lamoureux, S. F., McFadden, S. I., Bevan, G., Rudy, A., Paquette, M., and Fortier, D. (2018). Localized Ground Ice Subsidence and Soil Water Dynamics as Indicators of Near-Surface Ice Content in the High Arctic. Washington, DC: AGU Fall Meeting Abstracts, C54A–C05.

Google Scholar

Lee, H., Swenson, S. C., Slater, A. G., and Lawrence, D. M. (2014). Effects of Excess Ground Ice on Projections of Permafrost in a Warming Climate. Environ. Res. Lett. 9 (12), 124006. doi:10.1088/1748-9326/9/12/124006

CrossRef Full Text | Google Scholar

Li, N., Cheng, G., Xu, X., and Zhu, Y. (2001). The advance and Review on Frozen Soil Mechanics. Adv. Mech. 031 (1), 95–102.

Google Scholar

Li, P., Xu, X., and Cheng, F. (2000). State and Progress of Research on the Frozen Finge and Frost Heave Prediction Models. J. Glaciology Geocryology V22 (1), 90–85.

Google Scholar

Li, X., Wu, T., Wu, X., Zhu, X., Hu, G., Li, R., et al. (2020). Assessing the Simulated Soil thermal Regime from Noah-MPLSM v1.1 for Near-Surface Permafrost Modeling on the Qinghai-Tibet Plateau. Geosci. Model. Dev. Discuss. 2020, 1–29. doi:10.5194/gmd-2020-142

CrossRef Full Text | Google Scholar

Liang, X., Xie, Z., and Huang, M. (2003). A New Parameterization for Surface and Groundwater Interactions and its Impact on Water Budgets with the Variable Infiltration Capacity (VIC) Land Surface Model. J. Geophys. Res. 108 (D16). doi:10.1029/2002JD003090

CrossRef Full Text | Google Scholar

Liu, G., and Si, B. C. (2011). Single- and Dual-Probe Heat Pulse Probe for Determining Thermal Properties of Dry Soils. Soil Sci. Soc. America J. 75, 787–794. doi:10.2136/sssaj2010.0241

CrossRef Full Text | Google Scholar

Liu, J., Tong, C., and Fang, J. (2005). Introduction to Geotechnical Engineering in Cold Region. Beijing, China: China Railway Publishing House.

Google Scholar

Liu, Q., Wang, Z., Li, Z., and Wang, Y. (2019). Transversely Isotropic Frost Heave Modeling with Heat-Moisture-Deformation Coupling. Acta Geotech. 15, 1273–1287. doi:10.1007/s11440-019-00774-1

CrossRef Full Text | Google Scholar

Loch, J. P. G., and Miller, R. D. (1975). Tests of the Concept of Secondary Frost Heaving. Soil Sci. Soc. America J. 39 (6), 1036–1041. doi:10.2136/sssaj1975.03615995003900060012x

CrossRef Full Text | Google Scholar

Loch, J. P. G. (1978). Thermodynamic Equilibrium between Ice and Water in Porous media. Soil Sci. 126 (2), 77–80. doi:10.1097/00010694-197808000-00002

CrossRef Full Text | Google Scholar

Lu, J., Zhang, M., Zhang, X., and Pei, W. (2017). Review of the Coupled Hydrothermo-Mechanical Interaction of Frozen Soil. J. Glaciology Geocryology 39 (1), 102–111.

Google Scholar

Luo, S., Chen, B., Lyu, S., Fang, X., Wang, J., Meng, X., et al. (2018). An Improvement of Soil Temperature Simulations on the Tibetan Plateau. Sci. Cold Arid Regions 10 (1), 80–94. doi:10.3724/SP.J.1226.2018.00080

CrossRef Full Text | Google Scholar

Ma, Q., Jin, H., Yu, C., and Bense, V. F. (2019). Dissolved Organic Carbon in Permafrost Regions: A Review. Sci. China Earth Sci. 62 (2), 349–364. doi:10.1007/s11430-018-9309-6

CrossRef Full Text | Google Scholar

Ma, W., Zhang, L., and Yang, C. (2015). Discussion of the Applicability of the Generalized Clausius-Clapeyron Equation and the Frozen Fringe Process. Earth-Science Rev. 142, 47–59. doi:10.1016/j.earscirev.2015.01.003

CrossRef Full Text | Google Scholar

Mackay, J., Ostrick, J., Lewis, C., and MacKay, D. (1979). Frost Heave at Ground Temperatures below 0 °C, Inuvik, Northwest Territories. Ottawa, Canada: Geological Survey of Canada Paper, 403–406.

Google Scholar

Mackay, J. R., and Dallimore, S. R. (1992). Massive Ice of the Tuktoyaktuk Area, Western Arctic Coast, Canada. Can. J. Earth Sci. 29 (6), 1235–1249. doi:10.1139/e92-099

CrossRef Full Text | Google Scholar

Mackay, J. R. (1980). The Origin of Hummocks, Western Arctic Coast, Canada. Can. J. Earth Sci. 17 (8), 996–1006. doi:10.1139/e80-100

CrossRef Full Text | Google Scholar

Mackay, J. R. (1972). The World of Underground Ice. Ann. Assoc. Am. Geogr. 62 (1), 1–22. doi:10.1111/j.1467-8306.1972.tb00839.x

CrossRef Full Text | Google Scholar

Mastepanov, M., Sigsgaard, C., Dlugokencky, E. J., Houweling, S., Ström, L., Tamstorf, M. P., et al. (2008). Large Tundra Methane Burst during Onset of Freezing. Nature 456 (7222), 628–630. doi:10.1038/nature07464

PubMed Abstract | CrossRef Full Text | Google Scholar

Mastepanov, M., Sigsgaard, C., Tagesson, T., Ström, L., Tamstorf, M. P., Lund, M., et al. (2013). Revisiting Factors Controlling Methane Emissions from High-Arctic Tundra. Biogeosciences 10 (7), 5139–5158. doi:10.5194/bg-10-5139-2013

CrossRef Full Text | Google Scholar

McGaw, R., Berg, R., and Ingersoll, J. (1983). An Investigation of Transient Processes in an Advancing Zone of Freezing. Proc. 4th Int. Conf. Permafrost, 821–825.

Google Scholar

Michaelson, G. J., and Ping, C. (2003). Soil Organic Carbon and CO2 respiration at Subzero Temperature in Soils of Arctic Alaska. J. Geophys. Res. 108 (D2), ALT 5-1-ALT 5–10. doi:10.1029/2001JD000920

CrossRef Full Text | Google Scholar

Michalowski, R. L., and Zhu, M. (2006). Frost Heave Modelling Using Porosity Rate Function. Int. J. Numer. Anal. Meth. Geomech. 30 (8), 703–722. doi:10.1002/nag.497

CrossRef Full Text | Google Scholar

Miller, R. D. (1972). Freezing and Heaving of Saturated and Unsaturated Soils. Highw. Res. Rec. 393 (1), 1–11. doi:10.1021/ba-1972-0110.ap001

CrossRef Full Text | Google Scholar

Miller, R. D. (1978). “Frost Heaving in Non-colloidal Siols,” in Proceedings of the Third International Conference on Permafrost, Edmonton, Canada, 708–713.

Google Scholar

Ming, F., and Li, D.-q. (2016). A Model of Migration Potential for Moisture Migration during Soil Freezing. Cold Regions Sci. Technology 124 (Apr), 87–94. doi:10.1016/j.coldregions.2015.12.015

CrossRef Full Text | Google Scholar

Miyata, Y., and Akagawa, S. (1997). An Experimental Study of Dynamic Solid-Liquid Phase Equilibrium in the Pores of a Porous Medium. Trans. Jpn. Soc. Mech. Eng. B 63 (611), 2421–2429. doi:10.1299/jsmeb.41.590

CrossRef Full Text | Google Scholar

Murton, J. B., and Lautridou, J.-P. (2003). Recent Advances in the Understanding of Quaternary Periglacial Features of the English Channel Coastlands. J. Quat. Sci. 18 (3-4), 301–307. doi:10.1002/jqs.748

CrossRef Full Text | Google Scholar

Mwangi, S., Zeng, Y., Montzka, C., Yu, L., and Su, Z. (2020). Assimilation of Cosmic‐Ray Neutron Counts for the Estimation of Soil Ice Content on the Eastern Tibetan Plateau. J. Geophys. Res. Atmos. 125 (3), e2019JD031529. doi:10.1029/2019JD031529

CrossRef Full Text | Google Scholar

Natali, S. M., Schuur, E. A. G., Mauritz, M., Schade, J. D., Celis, G., Crummer, K. G., et al. (2015). Permafrost Thaw and Soil Moisture Driving CO2 and CH4 Release from upland Tundra. J. Geophys. Res. Biogeosci. 120 (3), 525–537. doi:10.1002/2014JG002872

CrossRef Full Text | Google Scholar

Niu, F., Li, A., Luo, J., Lin, Z., Yin, G., Liu, M., et al. (2017). Soil Moisture, Ground Temperatures, and Deformation of a High-Speed Railway Embankment in Northeast China. Cold Regions Sci. Technology 133 (133), 7–14. doi:10.1016/j.coldregions.2016.10.007

CrossRef Full Text | Google Scholar

Niu, L., Ye, B., Li, J., and Sheng, Y. (2011). Effect of Permafrost Degradation on Hydrological Processes in Typical Basins with Various Permafrost Coverage in Western China. Sci. China Earth Sci. 54 (4), 615–624. doi:10.1007/s11430-010-4073-1

CrossRef Full Text | Google Scholar

Nixon, J. F. (1991). Discrete Ice Lens Theory for Frost Heave in Soils. Can. Geotech. J. 28 (6), 843–859. doi:10.1139/t91-102

CrossRef Full Text | Google Scholar

Nixon, J. F. (1982). Field Frost Heave Predictions Using the Segregation Potential Concept. Can. Geotech. J. 19 (4), 526–529. doi:10.1139/t82-059

CrossRef Full Text | Google Scholar

Nixon, J. F. (1987). Thermally Induced Heave beneath Chilled Pipelines in Frozen Ground. Can. Geotech. J. 24 (2), 260–266. doi:10.1139/t87-031

CrossRef Full Text | Google Scholar

O'Neill, K., and Miller, R. D. (1985). Exploration of a Rigid Ice Model of Frost Heave. Water Resour. Res. 21 (3), 281–296. doi:10.1029/WR021i003p00281

CrossRef Full Text | Google Scholar

Oleson, K., Lawrence, D., Bonan, G., Drewniak, B., Huang, M., Koven, C., et al. (2013). Technical Description of Version 4.5 of the Community Land Model (CLM), NCAR Technical Note: NCAR/TN-503+ STR. Boulder, CO: National Center for Atmospheric Research. doi:10.5065/D6RR1W7M

CrossRef Full Text | Google Scholar

Oleson, K. W., Lawrence, D. M., Gordon, B., Flanner, M. G., Kluzek, E., Peter, J., et al. (2010). Technical Description of Version 4.0 of the Community Land Model (CLM). doi:10.1029/2010GL042430

CrossRef Full Text | Google Scholar

Ostroumov, V., Hoover, R., Ostroumova, N., Van Vliet-Lanoë, B., Siegert, C., and Sorokovikov, V. (2001). Redistribution of Soluble Components during Ice Segregation in Freezing Ground. Cold Regions Sci. Technology 32 (2), 175–182. doi:10.1016/S0165-232X(01)00031-3

CrossRef Full Text | Google Scholar

Peppin, S. S. L., Elliott, J. A. W., and Worster, M. G. (2006). Solidification of Colloidal Suspensions. J. Fluid Mech. 554, 147–166. doi:10.1017/S0022112006009268

CrossRef Full Text | Google Scholar

Peppin, S. S. L., and Style, R. W. (2013). The Physics of Frost Heave and Ice-Lens Growth. Vadose Zone J. 12 (1), vzj20120049–0049. doi:10.2136/vzj2012.0049

CrossRef Full Text | Google Scholar

Peterson, R. A., and Krantz, W. B. (2003). A Mechanism for Differential Frost Heave and its Implications for Patterned-Ground Formation. J. Glaciol. 49 (164), 69–80. doi:10.3189/172756503781830854

CrossRef Full Text | Google Scholar

Philip, J. R., and De Vries, D. A. (1957). Moisture Movement in Porous Materials under Temperature Gradients. Trans. AGU 38 (2), 222–232. doi:10.1029/TR038i002p00222

CrossRef Full Text | Google Scholar

Ping, C. L., Jastrow, J. D., Jorgenson, M. T., Michaelson, G. J., and Shur, Y. L. (2015). Permafrost Soils and Carbon Cycling. SOIL 1 (1), 147–171. doi:10.5194/soil-1-147-2015

CrossRef Full Text | Google Scholar

Pitman, A. J., Slater, A. G., Desborough, C. E., and Zhao, M. (1999). Uncertainty in the Simulation of Runoff Due to the Parameterization of Frozen Soil Moisture Using the Global Soil Wetness Project Methodology. J. Geophys. Res. 104 (D14), 16879–16888. doi:10.1029/1999JD900261

CrossRef Full Text | Google Scholar

Prokushkin, A. S., Kawahigashi, M., and Tokareva, I. V. (2009). Global Warming and Dissolved Organic Carbon Release from Permafrost Soils, Permafrost Soils. Berlin, Heidelberg: Springer, 237–250. doi:10.1007/978-3-540-69371-0_16

CrossRef Full Text | Google Scholar

Qin, D. (2016). Glossary of Cryospheric Science. Beijing, China: China Meteorological Press.

Google Scholar

Radd, F., and Oertle, D. (1973). Experimental Pressure Studies of Frost Heave Mechanisms and the Growth-Fusion Behavior of Ice in Proceeding of the Second International Conference on Permafrost, Washington DC Yakutsk, USSR (North American Contribution, publication National Academy of Science), 377–384.

Ran, H., Fan, J., and Huang, Q. (2019). Review of the Coupling of Water and Heat in the Freeze-Thaw Process and its Model of Frozen Soil. Pratacultural Sci. 036 (004), 991–999.

Google Scholar

Rempel, A. W. (2007). Formation of Ice Lenses and Frost Heave. J. Geophys. Res. 112 (F2). doi:10.1029/2006jf000525

CrossRef Full Text | Google Scholar

Rempel, A. W. (2010). Frost Heave. J. Glaciol. 56 (200), 1122–1128. doi:10.3189/002214311796406149

CrossRef Full Text | Google Scholar

Rempel, A. W. (2011). Microscopic and Environmental Controls on the Spacing and Thickness of Segregated Ice Lenses. Quat. Res. 75 (2), 316–324. doi:10.1016/j.yqres.2010.07.005

CrossRef Full Text | Google Scholar

Rempel, A. W., Wettlaufer, J. S., and Worster, M. G. (2001). Interfacial Premelting and the Thermomolecular Force: Thermodynamic Buoyancy. Phys. Rev. Lett. 87 (8), 088501. doi:10.1103/PhysRevLett.87.088501

PubMed Abstract | CrossRef Full Text | Google Scholar

Rempel, A. W., Wettlaufer, J. S., and Worster, M. G. (2004). Premelting Dynamics in a Continuum Model of Frost Heave. J. Fluid Mech. 498, 227–244. doi:10.1017/S0022112003006761

CrossRef Full Text | Google Scholar

Römkens, M. J. M., and Miller, R. D. (1973). Migration of mineral Particles in Ice with a Temperature Gradient. J. Colloid Interf. Sci. 42 (1), 103–111. doi:10.1016/0021-9797(73)90012-X

CrossRef Full Text | Google Scholar

Saarelainen, S. (1992). Modelling Frost Heaving and Frost Penetration in Soils at Some Observation Sites in Finland: The SSR Model. Espoo, Finland: Tampere University of Technology TUT, 120.

Google Scholar

Scherer, G. W. (1999). Crystallization in Pores. Cement Concrete Res. 29 (8), 1347–1358. doi:10.1016/S0008-8846(99)00002-2

CrossRef Full Text | Google Scholar

Schuur, E. A. G., McGuire, A. D., Schädel, C., Grosse, G., Harden, J. W., Hayes, D. J., et al. (2015). Climate Change and the Permafrost Carbon Feedback. Nature 520 (7546), 171–179. doi:10.1038/nature14338

PubMed Abstract | CrossRef Full Text | Google Scholar

Shao, M., Wang, Q., and Huang, M. (2006). Soil Physics. Beijing, China: Higher Education Press.

Google Scholar

Sheng, D., Axelsson, K., and Knutsson, S. (1995). Frost Heave Due to Ice Lens Formation in Freezing Soils. Hydrol. Res. 26 (2), 125–146. doi:10.2166/nh.1995.000910.2166/nh.1995.0008

CrossRef Full Text | Google Scholar

Sheppard, M. I., Mi, S., and Bd, K. (1978). Development and Testing of a Computer Model for Heat and Mass Flow in Freezing Soils, In: proceedings of the 3rd International Conference on Permafrost, Edmonton, Alberta (Edmonton: National research council of Canada) 1, 75–81.

Google Scholar

Shur, Y. L., and Jorgenson, M. T. (2007). Patterns of Permafrost Formation and Degradation in Relation to Climate and Ecosystems. Permafrost Periglac. Process. 18 (1), 7–19. doi:10.1002/ppp.582

CrossRef Full Text | Google Scholar

Smith, M., Church, M., and Slaymaker, O. (1985). “Models of Soil Freezing,” in Field and Theory: Lectures in Geocryology. Editors M. Church, and O. Slaymaker (Vancouver, British Columbia: University of British Columbia Press Vancouver).

Google Scholar

Smith, M. W., and Burn, C. R. (1987). Outward Flux of Vapour from Frozen Soils at Mayo, Yukon, Canada: Results and Interpretation. Cold Regions Sci. Technology 13 (2), 143–152. doi:10.1016/0165-232x(87)90052-8

CrossRef Full Text | Google Scholar

Smith, M. W. (1985). Observations of Soil Freezing and Frost Heave at Inuvik, Northwest Territories, Canada. Can. J. Earth Sci. 22 (2), 283–290. doi:10.1139/e85-024

CrossRef Full Text | Google Scholar

Sokolov, K., Fedorova, L., and Fedorov, M. (2020). Prospecting and Evaluation of Underground Massive Ice by Ground-Penetrating Radar. Geosciences 10 (7), 274. doi:10.3390/geosciences10070274

CrossRef Full Text | Google Scholar

Song, C., Xu, X., Sun, X., Tian, H., Sun, L., Miao, Y., et al. (2012). Large Methane Emission upon spring Thaw from Natural Wetlands in the Northern Permafrost Region. Environ. Res. Lett. 7 (3), 034009. doi:10.1088/1748-9326/7/3/034009

CrossRef Full Text | Google Scholar

Spaans, E. J. A., and Baker, J. M. (1996). The Soil Freezing Characteristic: Its Measurement and Similarity to the Soil Moisture Characteristic. Soil Sci. Soc. America J. 60 (1), 13–19. doi:10.2136/sssaj1996.03615995006000010005x

CrossRef Full Text | Google Scholar

Station, M. S. U. A. E., McCool, M., and Bouyoucos, G. (1915). Freezing Point Method as a New Means of Measuring the Concentration of the Soil Solution Directly in the Soil.

Google Scholar

Stevanato, L., Baroni, G., Cohen, Y., Fontana, C. L., Gatto, S., Lunardon, M., et al. (2019). A Novel Cosmic-ray Neutron Sensor for Soil Moisture Estimation over Large Areas. Agriculture 9 (9), 202. doi:10.3390/agriculture9090202

CrossRef Full Text | Google Scholar

Streletskiy, D., Anisimov, O., and Vasiliev, A. (2015). Permafrost Degradation. Snow & Ice Related Hazards Risks & Disasters, 303–344. doi:10.1016/B978-0-12-394849-6.00010-X

CrossRef Full Text | Google Scholar

Streletskiy, D., Biskaborn, B. K., Smith, S., Noetzli, J., Viera, G., and Schoeneich, P. (2017). Strategy and Implementation Plan 2016-2020 for the Global Terrestrial Network for Permafrost (GTN-P). Washington DC: The George Washington University.

Google Scholar

Style, R. W., Peppin, S. S. L., Cocks, A. C. F., and Wettlaufer, J. S. (2011). Ice-lens Formation and Geometrical Supercooling in Soils and Other Colloidal Materials. Phys. Rev. E 84 (4), 041402. doi:10.1103/PhysRevE.84.041402

CrossRef Full Text | Google Scholar

Style, R. W., and Peppin, S. S. L. (2012). The Kinetics of Ice-Lens Growth in Porous media. J. Fluid Mech. 692, 482–498. doi:10.1017/jfm.2011.545

CrossRef Full Text | Google Scholar

Sun, L. (2015). Development of the Distributed Hydrological Model Coupled Snow and Frozen Soil. Beijing: Chinese Academy of Sciences, 14.

Google Scholar

Sun, M., Shi, B., Zhang, C., Liu, J., Guo, J., Zheng, X., et al. (2021). Quantifying the Spatio-Temporal Variability of Total Water Content in Seasonally Frozen Soil Using Actively Heated Fiber Bragg Grating Sensing. J. Hydrol., 127386. doi:10.1016/j.jhydrol.2021.127386

CrossRef Full Text | Google Scholar

Swenson, S. C., Lawrence, D. M., and Lee, H. (2012). Improved Simulation of the Terrestrial Hydrological Cycle in Permafrost Regions by the Community Land Model. J. Adv. Model. Earth Syst. 4 (3), a–n. doi:10.1029/2012ms000165

CrossRef Full Text | Google Scholar

Szczykulska, M., Boorman, D., Blake, J., and Evans, J. G. (2021). Technical Note: A Revised Incoming Neutron Intensity Correction Factor for Soil Moisture Monitoring Using Cosmic-ray Neutron Sensors. Hydrol. Earth Syst. Sci. Discuss., 1–11. doi:10.5194/hess-2021-564

CrossRef Full Text | Google Scholar

Taber, S. (1929). Frost Heaving. J. Geology. 37 (5), 428–461. doi:10.1086/623637

CrossRef Full Text | Google Scholar

Taber, S. (1930). The Mechanics of Frost Heaving. J. Geology. 38 (4), 303–317. doi:10.1086/623720

CrossRef Full Text | Google Scholar

Takagi, S. (1980). The Adsorption Force Theory of Frost Heaving. Cold Regions Sci. Technology 3 (1), 57–81. doi:10.1016/0165-232X(80)90007-5

CrossRef Full Text | Google Scholar

Takashi, T., Ohrai, T., Yamamoto, H., and Okamoto, J. (1982). Upper Limit of Heaving Pressure Derived by Pore-Water Pressure Measurements of Partially Frozen Soil. Dev. Geotechnical Eng. 18, 245–257. doi:10.1016/0013-7952(81)90064-8

CrossRef Full Text | Google Scholar

Tarnocai, C., Canadell, J. G., Schuur, E. A. G., Kuhry, P., Mazhitova, G., and Zimov, S. (2009). Soil Organic Carbon Pools in the Northern Circumpolar Permafrost Region. Glob. Biogeochem. Cycles 23 (2), a–n. doi:10.1029/2008GB003327

CrossRef Full Text | Google Scholar

Teng, J., Liu, J., Zhang, S., and Sheng, D. (2020). Modelling Frost Heave in Unsaturated Coarse-Grained Soils. Acta Geotech. 15 (1), 3307–3320. doi:10.1007/s11440-020-00956-2

CrossRef Full Text | Google Scholar

Thomas, H. R., Cleall, P., Li, Y.-C., Harris, C., and Kern-Luetschg, M. (2009). Modelling of Cryogenic Processes in Permafrost and Seasonally Frozen Soils. Géotechnique 59 (3), 173–184. doi:10.1680/geot.2009.59.3.173

CrossRef Full Text | Google Scholar

Tiedje, E., and Guo, P. (2012). Frost Heave Modeling Using a Modified Segregation Potential Approach. Cold Regions Eng. 2012, 686–696. doi:10.1061/9780784412473.068

CrossRef Full Text | Google Scholar

Tregubov, O., Uyaganskii, K., and Nuteveket, M. (2020). Monitoring of Permafrost and Climate Conditions of the Anadyr lowland. Geogr. Nat. Resour. (2), 143–152. doi:10.21782/GiPR0206-1619-2020-2(143-152

CrossRef Full Text | Google Scholar

Van Bochove, E., Thériault, G., Rochette, P., Jones, H. G., and Pomeroy, J. W. (2001). Thick Ice Layers in Snow and Frozen Soil Affecting Gas Emissions from Agricultural Soils during winter. J. Geophys. Res. 106 (D19), 23061–23071. doi:10.1029/2000JD000044

CrossRef Full Text | Google Scholar

Van Huissteden, J. (2020). The Role of Ground Ice, Thawing Permafrost: Permafrost Carbon in a Warming Arctic. Cham: Springer International Publishing, 107–177. doi:10.1007/978-3-030-31379-1_3

CrossRef Full Text | Google Scholar

Vinson, T. S., Rooney, J. W., and Haas, W. H. (1996). Roads and Airfields in Cold Regions : A State of the Practice Report. American Society of Civil Engineers.

Google Scholar

Vonk, J. E., Tank, S. E., and Walvoord, M. A. (2019). Integrating Hydrology and Biogeochemistry across Frozen Landscapes. Nat. Commun. 10 (1), 1–4. doi:10.1038/s41467-019-13361-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Walker, D. A., Epstein, H. E., Gould, W. A., Kelley, A. M., Kade, A. N., Knudson, J. A., et al. (2004). Frost-boil Ecosystems: Complex Interactions between Landforms, Soils, Vegetation and Climate. Permafrost Periglac. Process. 15 (2), 171–188. doi:10.1002/ppp.487

CrossRef Full Text | Google Scholar

Walvoord, M. A., and Kurylyk, B. L. (2016). Hydrologic Impacts of Thawing Permafrost-A Review. Vadose Zone J. 15 (6), vzj2016010010–2001. doi:10.2136/vzj2016.01.0010

CrossRef Full Text | Google Scholar

Wang, G., Li, Y., Wu, Q., and Wang, Y. (2006a). Impacts of Permafrost Changes on alpine Ecosystem in Qinghai-Tibet Plateau. Sci. China Ser. D 49 (011), 1156–1169. doi:10.1007/s11430-006-1156-0

CrossRef Full Text | Google Scholar

Wang, L., Zhou, J., Qi, J., Sun, L., Yang, K., Tian, L., et al. (2017). Development of a Land Surface Model with Coupled Snow and Frozen Soil Physics. Water Resour. Res. 53 (6), 5085–5103. doi:10.1002/2017WR020451

CrossRef Full Text | Google Scholar

Wang, M., Li, X., and Xu, X. (2021). An Implicit Heat-Pulse-Probe Method for Measuring the Soil Ice Content. Appl. Therm. Eng. 196, 117186. doi:10.1016/j.applthermaleng.2021.117186

CrossRef Full Text | Google Scholar

Wang, z., Liang, X., Wang, D., Wang, J., and Wang, L. (2006b). Experiment Research on Soil Dew of in the Windy beach Area of Ordos Ground Water 28(006), 28–31.

Google Scholar

Washburn, A. L. (1980). Geocryology: A Survey of Periglacial Processes and Environments. Wiley. doi:10.1111/j.1745-7939.1981.tb0094

CrossRef Full Text | Google Scholar

Watanabe, K., and Flury, M. (2008). Capillary Bundle Model of Hydraulic Conductivity for Frozen Soil. Water Resour. Res. 44 (12). doi:10.1029/2008WR007012

CrossRef Full Text | Google Scholar

Watanabe, K., Mizoguchi, M., Ishizaki, T., Fukuda, M., and Knutsson, S. (1997). Experimental Study on Microstructure Near Freezing Front during Soil Freezing. Transactions-Japanese Soc. Irrigation Drainage Reclamation Eng. 191, 53–58.

Google Scholar

Watanabe, K., and Wake, T. (2009). Measurement of Unfrozen Water Content and Relative Permittivity of Frozen Unsaturated Soil Using NMR and TDR. Cold Regions Sci. Technology 59 (1), 34–41. doi:10.1016/j.coldregions.2009.05.011

CrossRef Full Text | Google Scholar

Wettlaufer, J. S., Worster, M. G., Wilen, L. A., and Dash, J. G. (1996). A Theory of Premelting Dynamics for All Power Law Forces. Phys. Rev. Lett. 76 (19), 3602–3605. doi:10.1103/PhysRevLett.76.3602

PubMed Abstract | CrossRef Full Text | Google Scholar

Wettlaufer, J. S., Worster, M. G., and Wilen, L. A. (1997). Premelting Dynamics: Geometry and Interactions. J. Phys. Chem. B 101 (32), 6137–6141. doi:10.1021/jp9632201

CrossRef Full Text | Google Scholar

White, W. M. (2020). Geochemistry. John Wiley & Sons.

Google Scholar

Wickland, K. P., Waldrop, M. P., Aiken, G. R., Koch, J. C., Jorgenson, M. T., and Striegl, R. G. (2018). Dissolved Organic Carbon and Nitrogen Release from Boreal Holocene Permafrost and Seasonally Frozen Soils of Alaska. Environ. Res. Lett. 13 (6), 065011. doi:10.1088/1748-9326/aac4ad

CrossRef Full Text | Google Scholar

Wilen, L. A., and Dash, J. G. (1995). Frost Heave Dynamics at a Single crystal Interface. Phys. Rev. Lett. 74 (25), 5076–5079. doi:10.1103/PhysRevLett.74.5076

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, P. J. (1968). Ice Distribution in Permafrost Profiles. Can. J. Earth Sci. 5 (6), 1381–1386. doi:10.1139/e68-136

CrossRef Full Text | Google Scholar

Williams, P. J. (1995). Permafrost and Climate Change: Geotechnical Implications. Phil. Trans. R. Soc. Lond. A. 352 (1699), 347–358. doi:10.1098/rsta.1995.0075

CrossRef Full Text | Google Scholar

Williams, P. J., and Smith, M. W. (1989). The Frozen Earth: Fundamentals of Geocryology. Cambridge: Cambridge University Press. doi:10.2307/1551597

CrossRef Full Text | Google Scholar

Woo, M.-k. (2012). Active Layer Dynamics. Permafrost Hydrology. Springer Science & Business Media, 163–227. doi:10.1007/978-3-642-23462-010.1007/978-3-642-23462-0_5

CrossRef Full Text | Google Scholar

Wood, J. A. (1990). The Role of Irreversible Thermodynamics and Rheology in the Regelation-Flow Phenomenon. Cold regions Sci. Technol. 18 (2), 133–145. doi:10.1016/0165-232X(90)90003-F

CrossRef Full Text | Google Scholar

Wraith, J., Or, D., and Warrick, A. (2001). Soil Water Content and Water Potential Relationships. Soil Phys. companion 1, 49–84. doi:10.1201/9781420041651.ch3

CrossRef Full Text | Google Scholar

Wu, Q., Sheng, Y., and Shi, B. (2003). Relationship between Frozen Soil Together with its Water-Heat Process and Ecological Environment in the Tibetan Plateau. J. Glaciology Geocryology 25 (3), 250–255.

Google Scholar

Wu, Y. Y. Q., Jiang, G., Zhang, P., and Zhang, P. (2017). Stable Isotopic Stratification and Growth Patterns of Ground Ice in Permafrost on the Qinghai-Tibet Plateau, China. Permafrost Periglac. Process. 28 (1), 119–129. doi:10.1002/ppp.1892

CrossRef Full Text | Google Scholar

Xiao, Y., Zhao, L., Dai, Y., Li, R., Pang, Q., and Yao, J. (2013). Representing Permafrost Properties in CoLM for the Qinghai-Xizang (Tibetan) Plateau. Cold Regions Sci. Technology 87, 68–77. doi:10.1016/j.coldregions.2012.12.004

CrossRef Full Text | Google Scholar

Xu, X., and Deng, Y. (1991). Experimental Study on Water Migration in Frozen Soil. Beijing: Science Press.

Google Scholar

Xu, X., Wang, J., and Zhang, L. (2010). Frozen Soil Physics. Beijing: Science Press.

Google Scholar

Xue, Y., Zeng, F. J., and Schlosser, C. A. (1996). SSiB and its Sensitivity to Soil Properties—A Case Study Using HAPEX-Mobilhy Data. Glob. Planet. Change 13 (1-4), 0–194. doi:10.1016/0921-8181(95)00045-3

CrossRef Full Text | Google Scholar

Yang, J., Zhou, W., Liu, J., and Hu, X. (2014). Dynamics of Greenhouse Gas Formation in Relation to Freeze/thaw Soil Depth in a Flooded Peat Marsh of Northeast China. Soil Biol. Biochem. 75, 202–210. doi:10.1016/j.soilbio.2014.04.006

CrossRef Full Text | Google Scholar

Yang, K., Wang, C., and Li, S. (2018a). Improved Simulation of Frozen‐Thawing Process in Land Surface Model (CLM4.5). J. Geophys. Res. Atmos. 123 (2313), 13,238–13,258. doi:10.1029/2017JD028260

CrossRef Full Text | Google Scholar

Yang, Q., Dan, L., Wu, J., Jiang, R., Dan, J., Li, W., et al. (2018b). The Improved Freeze-Thaw Process of a Climate‐Vegetation Model: Calibration and Validation Tests in the Source Region of the Yellow River. J. Geophys. Res. Atmos. 123, 13,346–13,367. doi:10.1029/2017JD028050

CrossRef Full Text | Google Scholar

Yi, S., Wang, X., Qin, Y., Xiang, B., and Ding, Y. (2014). Responses of alpine Grassland on Qinghai-Tibetan Plateau to Climate Warming and Permafrost Degradation: a Modeling Perspective. Environ. Res. Lett. 9 (7), 074014. doi:10.1088/1748-9326/9/7/074014

CrossRef Full Text | Google Scholar

Yu, L., Zeng, Y., Wen, J., and Su, Z. (2018). Liquid-Vapor-Air Flow in the Frozen Soil. J. Geophys. Res. Atmos. 123 (14), 7393–7415. doi:10.1029/2018JD028502

CrossRef Full Text | Google Scholar

Zhang, L., Ma, W., Yang, C., and Dong, S. (2014a). A Review and prospect of the Thermodyamics of Soils Subjected to Freezing and Thawing. J. Glaciology Geocryology 35 (6), 1505–1518. doi:10.7522/j.issn.1000-0240.2013.0167

CrossRef Full Text | Google Scholar

Zhang, L., Ma, W., Yang, C., and Yuan, C. (2014b). Investigation of the Pore Water Pressures of Coarse-Grained sandy Soil during Open-System Step-Freezing and Thawing Tests. Eng. Geology. 181, 233–248. doi:10.1016/j.enggeo.2014.07.020

CrossRef Full Text | Google Scholar

Zhang, M., Zhang, X., Lai, Y., Lu, J., and Wang, C. (2020). Variations of the Temperatures and Volumetric Unfrozen Water Contents of fine-grained Soils during a Freezing-Thawing Process. Acta Geotech. 15 (3), 595–601. doi:10.1007/s11440-018-0720-z

CrossRef Full Text | Google Scholar

Zhang, S., Teng, J., He, Z., Liu, Y., Liang, S., Yao, Y., et al. (2016). Canopy Effect Caused by Vapour Transfer in Covered Freezing Soils. Géotechnique 66 (11), 927–940. doi:10.1680/jgeot.16.P.016

CrossRef Full Text | Google Scholar

Zhang, T., Barry, R., Knowles, K., Ling, F., and Armstrong, R. (2003). “Distribution of Seasonally and Perennially Frozen Ground in the Northern Hemisphere,” in Proceedings of the 8th International Conference on Permafrost, Switzerland (Boca Raton, Florida: AA Balkema Publishers Zürich), 1289–1294.

Google Scholar

Zhang, Y., Wen, A., Zhao, W., Liang, X., Li, P., and Černý, R. (2020). Influence of Compaction Level on the Water-Heat-Vapor Characteristics of Unsaturated Coarse-Grained Fillings Exposed to Freezing and Thawing. Adv. Civil Eng. 2020 (1), 1–10. doi:10.1155/2020/4536301

CrossRef Full Text | Google Scholar

Zhanrong, G., and Shuangping, H. (2002). Experimental Study on the Condensation Water in Arid Area, Northwestern China. Adv. Water Sci. 13 (5), 623–628. doi:10.1002/aic.10277

CrossRef Full Text | Google Scholar

Zhao, L., Hu, G., Zou, D.-f., and Wu, X. (2019). Permafrost Changes and its Effects on Hydrological Processes on Qinghai-Tibet Plateau. China Acad. J. Electron. Publishing House 34 (11). doi:10.16418/j.issn.1000-3045.2019.11.006

CrossRef Full Text | Google Scholar

Zheng, D., Van der Velde, R., Su, Z., Wen, J., Wang, X., and Yang, K. (2017). Evaluation of Noah Frozen Soil Parameterization for Application to a Tibetan Meadow Ecosystem. J. hydrometeorology 18 (6), 1749–1763. doi:10.1175/jhm-d-16-0199.1

CrossRef Full Text | Google Scholar

Zhou, G.-q., Zhou, Y., Hu, K., Wang, Y.-j., and Shang, X.-y. (2018). Separate-ice Frost Heave Model for One-Dimensional Soil Freezing Process. Acta Geotech. 13 (1), 207–217. doi:10.1007/s11440-017-0579-4

CrossRef Full Text | Google Scholar

Zhou, J., and Li, D. (2012). Numerical Analysis of Coupled Water, Heat and Stress in Saturated Freezing Soil. Cold Regions Sci. Technology 72, 43–49. doi:10.1016/j.coldregions.2011.11.006

CrossRef Full Text | Google Scholar

Zhou, J., and Wei, C. (2020). Ice Lens Induced Interfacial Hydraulic Resistance in Frost Heave. Cold Regions Sci. Technology 171, 102964. doi:10.1016/j.coldregions.2019.102964

CrossRef Full Text | Google Scholar

Zhou, M. M., and Meschke, G. (2013). A Three-phase Thermo-Hydro-Mechanical Finite Element Model for Freezing Soils. Int. J. Numer. Anal. Meth. Geomech. 37 (18), 3173–3193. doi:10.1002/nag.2184

CrossRef Full Text | Google Scholar

Zhou, X., Zhou, J., Kinzelbach, W., and Stauffer, F. (2014). Simultaneous Measurement of Unfrozen Water Content and Ice Content in Frozen Soil Using Gamma ray Attenuation and TDR. Water Resour. Res. 50 (12), 9630–9655. doi:10.1002/2014WR015640

CrossRef Full Text | Google Scholar

Zona, D., Gioli, B., Commane, R., Lindaas, J., Wofsy, S. C., Miller, C. E., et al. (2016). Cold Season Emissions Dominate the Arctic Tundra Methane Budget. Proc. Natl. Acad. Sci. USA 113 (1), 40–45. doi:10.1073/pnas.1516017113

CrossRef Full Text | Google Scholar

Zubrzycki, S., Kutzbach, L., and Pfeiffer, E.-M. (2014). Permafrost-affected Soils and Their Carbon Pools with a Focus on the Russian Arctic. Solid Earth 5 (2), 595–609. doi:10.5194/se-5-595-2014

CrossRef Full Text | Google Scholar