Floc Size Distributions of Cohesive Sediment in Homogeneous Isotropic Turbulence

Floc size distribution is one of the key parameters to characterize flocculating cohesive sediment. An Eulerian–Lagrangian framework has been implemented to study the flocculation dynamics of cohesive sediments in homogeneous isotropic turbulent flows. Fine cohesive sediment particles are modeled as the dispersed phase by the discrete element method, which tracks the motion of individual particles. An adhesive contact model with rolling friction is applied to simulate the particle–particle interactions. By varying the physicochemical properties (i.e., stickiness and stiffness) of the primary particles, the dependence of the mathematical form of the floc size distribution on sediment properties is investigated. At the equilibrium state, the aggregation and breakup processes reach a dynamic equilibrium, in which construction by aggregation is balanced with destruction by breakup, and construction by breakup is balanced with destruction by aggregation. When the primary particles are less sticky, floc size distribution fits better with the lognormal distribution. When the primary particles are very sticky, both the aggregation of smaller flocs and breakup from larger flocs play an equally important role in the construction of the intermediate-sized flocs, and the equilibrium floc size distribution can be better fitted by the Weibull distribution. When the Weibull distribution develops, a shape parameter around 2.5 has been observed, suggesting a statistically self-similar floc size distribution at the equilibrium state.

1 Introduction

The transport of fine-grained cohesive sediment in nearshore and estuarine environments plays a critical role in ecosystem dynamics, water quality, bed morphology, and engineering applications, for example, the rapid siltation in navigation channels and harbors (Hayter and Mehta, 1986; Winterwerp et al., 2000), cohesive sediment transport in salt marsh (Graham and Manning, 2007), depositional rates of contaminated muddy sediments (Ye et al., 2020), and long-term morphology of deltas (Edmonds and Slingerland, 2010). Cohesive sediment can bind together through both physical (van Olphen, 1964; Winterwerp and van Kesteren, 2004) and biological (Tolhurst et al., 2002) cohesion to form large aggregates, namely, flocs. A floc size distribution develops in sediment suspension (Sheremet et al., 2017). Due to the variability in floc’s structure and effective density, flocs of different size settle at different velocities (Manning, 2004; Mehta et al., 2014). The larger, low-density macroflocs (van Leussen, 1994) tend to settle faster than smaller microflocs (Eisma, 1986; Manning, 2001), but they are more fragile and more prone to break up by turbulent shear. Macroflocs often dominate the depositional mass flux (Mehta and Lott, 1987; Manning et al., 2006). The floc size distribution is therefore of crucial importance in understanding the spatiotemporal transport patterns of cohesive sediment (e.g., Geyer et al. (2000); Baugh and Manning (2007); Prandle et al. (2005)).

Turbulence plays an important role in the flocculation process of cohesive sediment in natural environments (Dyer, 1989; van Leussen, 1997; Winterwerp, 1998; McAnally and Mehta, 2001; Manning, 2004). On the one hand, turbulence enhances the aggregation through the collision frequency, which scales with the turbulent dissipation rate (Sundaram and Collins, 1997). On the other hand, large flocs break in turbulent flows by turbulent eddies via turbulent shear or hydrodynamic drag (Saha et al., 2016). Several phases exist during the flocculation. Initially, the aggregation dominates with the rapid growth of the floc size. As flocs continue to grow, large flocs with porous structures form. Large flocs are vulnerable to fragmentation by fluid shear (Tambo and Watanabe, 1984). Breakup starts to play an increasingly important role in late stages of flocculation. When the two competing mechanisms, namely, the aggregation and breakup processes, balance, an equilibrium floc size distribution develops (Manning and Dyer, 1999; Soulsby et al., 2013; Mehta et al., 2014).

Due to the large variability in the floc size, cohesive sediment is often characterized by the floc size distribution. The mathematical properties of floc size distributions have drawn a lot of attention from the cohesive sediment transport research community, and the interest in unifying the properties of floc size distribution has remained strong. Various statistics for floc size distribution have been proposed to serve as indices of the quality of sediment flocs, as well as sludge in waste treatment. However, theoretical studies, field observations, and laboratory experiments yield different statistics. It is important to investigate the physical mechanisms that lead to different floc size distributions, and the potential implication of different mathematical forms of the floc size distribution.

By applying a dimensional analysis, Hunt (1982) showed the steady state floc size distribution follows a power law. Pushkin and Aref (2002) later developed a more rigorous self-similarity theory of stationary coagulation and showed the floc size distribution follows a power law in the coagulating system. In these studies, the system is forced with particle injection at small sizes, and breakup is not considered. The breakup of large flocs can lead to a skewed floc size distribution with a peak (Hunt, 1982). Spicer and Pratsinis (1996) conducted laboratory experiments to study the evolution of floc size distribution induced by shear and showed the steady state floc size distribution normalized by the average floc size to be self-preserving, which is independent of the shear rate.

Floc size distribution is skewed and hence does not tend to follow the normal distribution. The lognormal distribution and Weibull distribution are commonly used to model skewed distributions; however, the physical origin of the distribution is not well understood. Brown and Wohletz (1995) derived the Weibull distribution with respect to the fragmentation process, in which a power law was used to describe the breakup of a single particle into smaller particles. The Weibull distribution has been widely used as particle size distribution for coarse grains (Fang et al., 1993; Kondolf and Adhikari, 2000). Previous studies of fiber pulp suspension in a flat channel (Huber et al., 2006) and activated sludge flocs (Li and Ganczarczyk, 1991) showed that Weibull distribution is the best descriptor for the floc size distribution. On the other hand, Kiss et al. (1999) developed a model for particle growth that predicts the lognormal particle distribution. They assumed the rate of change of the particle mass is proportional to the surface area, and the particle residence time in the active zone of particle interactions is lognormally distributed. Floc growth is due to collisions with other flocs, and the collision frequency is proportional to the surface area of the floc. A lognormal distribution of velocity fluctuations (Mouri et al., 2009) or dissipation rate (Yeung et al., 2006) that drive inter-particle collisions could also lead to the lognormal floc size distribution. Byun and Son (2020) applied a stochastic approach to model the size distribution of suspended flocs, in which the breakup process is modeled by a lognormal distribution. They showed the lognormal distribution is the best descriptor for the floc size distribution. Hosoda et al. (2011) showed that a stochastic process of halving followed by addition can yield a stationary lognormal distribution. For cohesive sediment flocs, this suggests the breakup of a large floc into two small flocs of equal size followed by the aggregation with another floc could lead to a lognormal floc size distribution. Overall, it is difficult to distinguish the lognormal and Weibull distribution in floc size distribution curves and hence the physical origin of the size distribution, which requires priori knowledge on both the particle–particle and particle–fluid interactions during flocculation.

In the mathematical approach, the aggregation and breakup processes are parameterized. The accuracy of the predictive cohesive sediment transport model strongly depends on the aggregation and breakup models. The two-phase Eulerian-Lagrangian model can resolve both the particle–particle and particle–fluid interactions and can provide the particle-level information on the aggregation and breakup processes. In Eulerian-Lagrangian two-phase models, the carrier fluid is modeled as the continuous phase and the particles are modeled as the dispersed phase (Balachandar and Eaton, 2010). In total, two approaches, namely, the particle-resolving approach (PR) and the point-particle approach (PP), have been developed and implemented to study cohesive sediment dynamics. In both approaches, the discrete element method (DEM) models the particle–particle interactions. Particles are modeled as soft spheres, allowing a small overlap when two particles collide. When one particle collides with another particle or floc, they may stick together. In DEM, the motion of an individual particle is tracked, along with the aggregation and breakup of flocs. Collisions among particles are modeled by the contact mechanics theory, such as Hookean or Hertzian contact models (Johnson, 1985). In the particle-resolving approach (Vowinckel et al., 2019), flows around individual particles are fully resolved. Due to the large computational cost, the particle resolving approach is often limited to systems with a few thousands of particles, which may not generate satisfactory statistics for flocculation dynamics. On the other hand, in the point-particle approach (Marshall, 2009; Zhou et al., 2010), hydrodynamic forces, such as drag force, lift force, and inertial force, on the particle are modeled. The point-particle approach can be implemented to millions of particles easily. However, the accuracy of the point-particle approach strongly depends on the hydrodynamic force models (Akiki et al., 2017). To investigate the flocculation processes in homogeneous isotropic turbulence, the point-particle approach is implemented to get better statistics of particle dynamics.

In this study, we investigate the floc size distribution in homogeneous isotropic turbulence using a two-phase Eulerian-Lagrangian model, in which the particle–particle interactions are modeled by the discrete element method. Due to the limit of computational resources, we focused on flocculation processes in high-energy estuaries or near-field river plumes with high turbulent shear rate, in which turbulence dictates the aggregation, breakup, and restructuring processes of flocs. We investigated how the primary particle properties affect the aggregation and breakup processes and hence the floc size distribution by varying the stickiness, stiffness, and size of the primary particle while keeping the turbulent shear rate the same. We focus on the physical origin of the floc size distribution and assess the performance of the lognormal distribution and the Weibull distribution at the equilibrium stage. This study is organized as follows. Methods are described in Section 2, including the adhesive contact model and the one-way coupling of the fluid and particle phases. Model validation and model setup are also presented in Section 2. Model results are presented in section 3 followed by the discussion in Section 4 and concluding remarks in Section 5.

2 Model Description

2.1 Direct Numerical Simulation of Homogeneous Isotropic Turbulence

Turbulence is characterized by a wide range of length scales. Interactions between turbulent eddies of different length scales with flocs play a critical role in flocculation dynamics. The primary particles are smaller than the Kolmogorov length scale (Kolmogorov, 1941a,b) in this study. Although the flow around the particle is not resolved, all turbulent scales including the Kolmogorov scale and larger, are fully resolved. Thus, the present approach is the particle-unresolved direct numerical simulations (DNS).The homogeneous isotropic turbulence is implemented in this study, which is an idealized version of the realistic turbulence and a reasonable approximation of the turbulent flow away from bottom boundary. To generate homogeneous isotropic turbulence, the linear forcing model (Lundgren, 2003; Rosales and Meneveau, 2005) was implemented. Instead of applying forces only to low-wavenumber modes, a force proportional to velocity is introduced in the momentum equation in the form of αu. Because the volumetric sediment concentration is dilute (≪ 1%) and the dominant effect is that of the turbulent carrier flow on the particle dynamics, the one-way coupling approach is adopted, and the governing equations of the fluid phase are as follows:

$\nabla \cdot \mathbf{u}=0(1)$

and

$\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}\cdot \nabla \mathbf{u}=-\frac{1}{\rho }\nabla p+\nu {\nabla }^2\mathbf{u}+\alpha \mathbf{u},(2)$

in which u is the fluid velocity, p is the pressure, ρ is the density of the fluid, ν is the kinematic viscosity of the fluid, and α is the linear forcing coefficient. The direct numerical simulations were conducted with the open source code Nek5000 (Fischer et al., 2008; Zwick and Balachandar, 2020), which uses a high-order spectral element method.

2.2 Discrete Element Method for Cohesive Sediment

To resolve particle–particle interactions, the sediment phase is modeled by using the discrete element method (DEM), in which motions of individual particles are tracked.

$\frac{d{\mathbf{x}}_i}{dt}={\mathbf{v}}_i,(3)$

$m_i\frac{d{\mathbf{v}}_i}{dt}=\sum {\mathbf{F}}_i,(4)$

$I_i\frac{d{\mathbf{\omega }}_{\mathbf{i}}}{dt}=\sum {\mathbf{T}}_i.(5)$

x is the position vector, v is the particle velocity vector, F is the force vector, and m is the mass of the particle. The subscript “i” is the particle label. The force on particle “i” is the sum of the collision force (F_c) between particle i and all other particles j, the hydrodynamic force (F_f), and the gravitational force (F_g) as F_i = ∑_jF_c,ij + F_f,i + F_g,i. I is the moment of inertia, ω is the angular velocity of the particle, and T is the torque on the particle. In this study, we coupled the CFD code nek5000 with the molecular dynamic code LAMMPS (Plimpton, 1995). The granular package in LAMMPS provides a variety of options for the normal, tangential, rolling, and twisting forces resulting from the contact between two particles, and hence is used to model the complex interactions among cohesive sediment particles. For soft clay particles, the Johnson–Kendall–Roberts (JKR) model is adopted.

${\mathbf{F}}_{ne,jkr}=\left(\frac{4E{a}^3}{3R}-2\pi a^2\sqrt{\frac{4\gamma E}{\pi a}}\right)\mathbf{n},(6)$

where a is the radius of the contact zone and is related to the overlap δ according to

$\delta =\frac{a^2}{R}-2\sqrt{\frac{\pi \gamma a}{E}},(7)$

where E is the Young’s Modulus, R is the radius of the particle, and γ is the surface energy density. The overlap between particle “i” and particle “j” is given as δ = R_i + R_j − |x_i − x_j|. The JKR model allows for a tensile force beyond contact (δ < 0), up to a maximum of 3πγR. When two particles are not in contact initially, they will not experience this force until they come into contact (δ > 0), then as they move apart, they experience a tensile force up to 3πγR till they lose contact. This force can be used to define the yield strength of the floc. In addition, a viscoelastic damping force model is used.

${\mathbf{F}}_{n,d}=-{\eta }_D{\mathbf{V}}_n,(8)$

where η_D is the viscoelastic damping coefficient, and V_n is the relative velocity along the direction of the vector n, which is the unit vector along the line connecting the centers of the two particles. The total normal force is the sum of the adhesive JKR and viscoelastic damping terms.

${\mathbf{F}}_n={\mathbf{F}}_{ne,kjr}+{\mathbf{F}}_{n,d}.(9)$

The Mindlin no-slip model (Mindlin, 1949) is used to compute the tangential force (F_t), as follows:

${\mathbf{F}}_t=-\min \left({\mu }_t{F}_{n0},|-k_{t}a\mathbf{\xi }+{\mathbf{F}}_{t,d}|\right)\mathbf{t},(10)$

where μ_t is the friction coefficient, k_t is the elastic constant for tangential contact, and ξ is the tangential displacement accumulated during the entire duration of the contact. The vector t is the unit vector in the relative tangential velocity direction. F_t,d is the damping term for the tangential force, which follows the same general form as the normal damping force (Eq. 9) but uses the relative velocity along the direction of the tangential vector t. The normal force value F_n0 used to compute the critical force is given as follows:

$F_{n0}=|{\mathbf{F}}_n+2{\mathbf{F}}_{pulloff}|=|{\mathbf{F}}_{ne,jkr}+6\pi \gamma R|.(11)$

The floc restructuring, in which particles change their relative positions while remaining connected, could also play an important role in the flocculation dynamics. Compaction of flocs by turbulent shear may occur with preferential floc structures. To account for floc restructuring, a rolling friction model of a pseduo-force formulation (Luding, 2008) was implemented. The rolling friction model allows the adjustment of rolling displacement of the contacting pair. The rolling pseudo-force is computed analogously to the tangential force, as follows:

${\mathbf{F}}_{roll,0}=k_{roll}{\mathbf{\xi }}_{roll}-{\gamma }_{roll}{\mathbf{v}}_{roll},(12)$

where k_roll is the elastic constant for rolling, γ_roll is the damping constant for rolling, ξ_roll is the rolling displacement, and v_roll is the relative rolling velocity (Wang et al., 2015). A Coulomb friction criterion truncates the rolling pseudo-force if it exceeds a critical value of

${\mathbf{F}}_{roll}=\min \left({\mu }_{roll}{F}_{n0},|{\mathbf{F}}_{roll,0}|\right)\mathbf{k},(13)$

where k is the direction of the pseudo-force. The rolling pseudo-force does not contribute to the total force on either particle, but it acts only to induce an equal and opposite torque on each particle.

${\mathbf{T}}_{roll,i}=\frac{R_i{R}_j}{R_i+R_j}\mathbf{n}\times {\mathbf{F}}_{roll},(14)$

${\mathbf{T}}_{roll,j}=-{\mathbf{T}}_{roll,i}.(15)$

2.3 Hydrodynamic Force

The total hydrodynamic force on particle “i” is given as follows:

${\mathbf{F}}_{hd,i}={\mathbf{F}}_{d,i}+{\mathbf{F}}_{p,i},(16)$

where F_d and F_p are the quasi-steady force and stress-divergence force, respectively. The added-mass force is neglected in this study assuming the small particle Stokes number. The drag force F_d on particle “i” is given as follows:

${\mathbf{F}}_{d,i}=\frac{1}{2}\rho C_{D}A|\mathbf{u}-{\mathbf{v}}_i|\left(\mathbf{u}-{\mathbf{v}}_i\right).(17)$

where ρ is the fluid density and $A=\pi D_p^2/4$ is the projected area of the spherical particle with D_p as the diameter of the spherical particle. For very dilute flow with sediment concentration ϕ ≪ 0.1%, the standard drag coefficient C_D for an individual particle is used, which is given as follows:

$C_D=\left\{\begin{array}{cc}\frac{24}{R{e}_p}\left(1+0.15R{e}_p^{0.687}\right),\hfill & \text{if}R{e}_p<1000\hfill \\ 0.44,\hfill & \text{otherwise},\hfill \end{array}\right.(18)$

where Re_p = |u − v|D_p/ν is the particle Reynolds number. The stress-divergence force experienced by the particle is calculated as follows:

${\mathbf{F}}_{p,i}=\left(-\nabla p+\nabla \cdot \tau \right)V_{p,i},(19)$

where the pressure gradient and stress divergence are interpolated to the particle center. In the current formulation, only the hydrostatic pressure is used to calculate the force F_p for simplicity. The buoyancy force due to the hydrostatic pressure is F_p,i = −ρ_fgV_p,i, where g is the gravitational acceleration vector and $V_p=\pi D_p^3/6$ is the volume of the particle.

2.4 Model Setup and Model Validation

The aforementioned governing equations are solved in non-dimensional forms. With the characteristic velocity scale U and length scale L, the non-dimensionalized variables are defined as follows:

${\mathbf{x}}^{\ast }=\frac{\mathbf{x}}{L},{\mathbf{u}}^{\ast }=\frac{\mathbf{u}}{U},p^{\ast }=\frac{p}{\rho U^2},{\mathbf{F}}^{\ast }=\frac{\mathbf{F}}{\rho U^2{L}^2}.(20)$

In homogeneous isotropic turbulence, the Reynolds number based on the Taylor microscale (λ) and the root mean square of turbulent velocity fluctuations (u_rms) is commonly used, which is defined as Re_λ = λu_rms/ν. The Taylor microscale is computed by $\lambda =\sqrt{15\nu /ϵ}{u}_{rms}$, where ϵ is the viscous dissipation rate and computed from the simulation results. We varied the properties of primary particles, including the particle diameter $(D_p^{\ast }=D_p/L)$, Young’s modulus (E∗ = E/ρU²), viscoelastic damping coefficient $({\eta }_D^{\ast }={\eta }_D/\rho U{L}^2)$, and the surface energy density (γ∗ = γ/ρU²L). Properties of primary particle used in this study are summarized in Table 1. Coefficients in the tangential force and rolling friction models were kept the same for all simulations. The Young’s modulus of soft clay particle is on the order of 1 MPa, which can significantly restrict the critical time step for DEM simulations. In practice, the Young’s modulus used in the model is often several orders of magnitude smaller than the actual value to accelerate the computation. Tsuji et al. (1993) showed that stiffness can be reduced by orders of magnitude without altering the collisional behaviors of particles. In this study, the Young’s modulus and the surface energy density are scaled down properly to make sure the relative importance of the elastic force and adhesive force is kept the same and the same floc structures can be reproduced. For simplicity, the superscript “*” in the non-dimensionalized variables are omitted in the analysis.

TABLE 1

TABLE 1. Summary of parameters for all simulations, all parameters are normalized. ${\bar{D}}_f$ is the average floc size at the equilibrium state and Ad represents the adhesive number.

The computational domain is a periodic box of size 8 × 8 × 8, and 16 elements of uniform size were used in each direction. A polynomial order P_N = 8 was used within each element, which yields a total resolution of around 2.1 million grid points. The third order Adams–Bashforth method was used for time integration. A fixed time step was chosen in all simulations, which ensures the maximum Courant–Friedrichs–Lewy (CFL) number to remain around 0.2. The “3/2” rule was used for de-aliasing. The PNPN-2 algorithm was applied (Maday et al., 1990; Fischer, 1997), in which pressure is solved on a coarser grid with polynomial order 6.

The DNS Model has been validated with previous DNS study by Rosales and Meneveau (2005) using the time-averaged energy spectrum. Due to the small Reynolds number used in both studies, there is no clear “−5/3” slope. The red solid curve represents the averaged non-dimensional energy spectra over cases with different Reynolds numbers. Our model results agree with the previous DNS study reasonably well (Figure 1). The forcing coefficient (α = 0.033) and the viscosity (ν = 5 × 10^–3) are kept the same for all cases. This gives the Reynolds number of 200 based on unit characteristic velocity and length scales, and Taylor Reynolds number (Re_λ) of 32. For homogeneous isotropic turbulent flow, there are no intrinsic characteristic scales for the mean flow. The Taylor Reynolds number is commonly used in homogeneous isotropic turbulence because it uses the fundamental length scale and velocity scale of turbulence to define the Reynolds number. To relate the idealized simulation conducted in this study with field condition, the Taylor Reynolds number can be used to obtain the turbulent shear rate when characteristic scales in dimensional form are given. The average Kolmogorov length scale is η = 0.049 and the average turbulent kinetic energy is k_t = 0.12.

FIGURE 1

FIGURE 1. Model validation with DNS simulation results from Rosales and Meneveau (2005).

To make results relevant to geophysical or engineering applications, simulation results can be interpreted in the dimensional forms with given characteristic length scale and velocity scale. Due to the limitation of computational resources, the present study focuses on energetic environment with high turbulent shear only. For a characteristic length scale of L = 10^–3 m, the characteristic velocity scale is U = 0.2 m/s, based on the Reynolds number, and the particle diameter is D_p = 12.8 μm for cases P₂. The particles can be interpreted as the smallest clay-based aggregates, namely, flocculi. Flocculi seldom break down to the lowest-level primary particles even at the high turbulent shear and hence are the building blocks of large flocs. The turbulent shear rate based on the characteristic scales is 350 s⁻¹ for all cases. The shear rate is higher than the values in most laboratory experiments and field observations; however, the model captures how turbulence affects flocculation dynamics. The Young’s modulus for soft clay is in the range of 0.5 to 5MPa, and the Poisson ratio of clay is 0.3. The Young’s modulus used in the simulation is between 6.4 and 16 kPa, which is reduced by two order of magnitude to accelerate the computation. In the JKR theory, the pull-off force to separate two particles is 3πγ_JKRD_p/2, which can be used to define the yield strength of the floc. The softness of particles does not affect the yield-strength of flocs directly and hence the aggregation of particles. Detailed measurement on the surface energy density γ is still lacking. In this study, the surface energy density used in the JKR model is in the range of 2 × 10^–4 to 1 × 10^–3 J/m². The stickiness of the particle can be characterized by the adhesive number, which is defined as the ratio of the yield strength of flocs represented by the surface energy density γ to the turbulent kinetic energy Ad = γ/ρk_tD. Because the turbulent intensity remains the same in all cases, the average floc size increases with the adhesive number as expected when the primary particle is kept the same (Table 1). In addition, the averaged floc size is almost three times greater than the Kolmogorov length scale for the cases with the largest adhesive number. However, for cases with relatively small adhesive number (case P₂S₂ and P₂S₃), the floc size is limited by the Kolmogorov length scale, and the average floc size is comparable to the Kolmogorov length scale.

3 Model Results

3.1 Flow Visualization

The flow velocity field from case P₁S₁ is shown in Figure 2A. The horizontal x − y plane is located at z₀ = 0. Only particles whose centers are located between z₀ − D_p/2 and z₀ + D_p/2 are projected to the x − y plane. The zoom in view is shown in Figure 2B to show the detailed structures of the flocs. Clusters of primary particles can be observed as flocs form. The Stokes numbers $St=s{D}_p{u}_{rms}^{*}/18\nu$ are 0.2 and 0.13 for P₁ and P₂ cases with the specific gravity of s = 2.65, therefore we did not observe strong local preferential accumulation of particles.

FIGURE 2

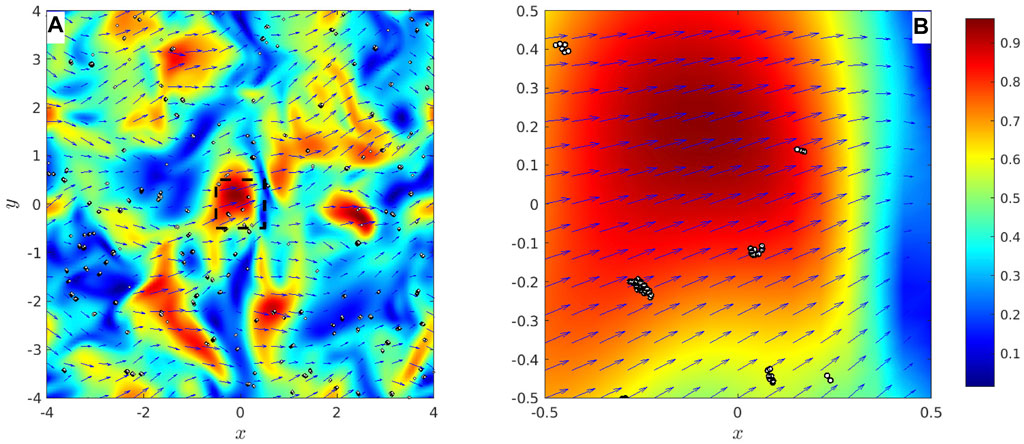
FIGURE 2. Model results. (A) Horizontal (x–y) plane of the flow field with particles from case P₁S₁ with relatively larger primary particles. The streamwise velocity component is used as background color. (B) Zoom in view of the velocity field and particles [black box in panel (A)].

3.2 Time Evolution of the Floc Size Distribution

All simulations are initialized with mono-dispersed spherical particles, which are uniformly distributed in the simulation domain. Initially, the particle velocity is set to zero. Due to collisions driven by turbulence, flocs start to form gradually and the floc size distribution evolves into an equilibrium distribution. In total, two contrasting cases, P₂S₁ (softer and more sticky primary particles) and P₂S₂ (more stiff and less sticky primary particles), are selected to investigate the dynamics. Figure 3 shows the time-evolution of the floc population $(N_{n_f})$ from case P₂S₁, where the primary particles of size D_p = 0.0128 are the stickiest (the adhesive number Ad is the greatest), and n_f represents the number of primary particles consisting the floc. At the beginning stage (t = 2), a power law relation can be observed. With the formation of larger flocs (t = 1000–3000), the power–law relation can still be observed for small flocs, but the slope starts to decrease. The slope is significantly different from the beginning stage. At the early stage, small flocs form mainly due to aggregation, and the power–law relation can well capture the size distribution for those small flocs (Hunt, 1982). At the intermediate stage (t = 4000–6000), we observe the accumulation of intermediate-sized flocs with n_f between 20 and 90, which forms a staircase in the floc size distribution (for instance at t = 5000). At the late stage (t ≥ 7000), the population of floc $(N_{n_f})$ with n_f between 20 and 90 starts to decrease and a peak appears around n_f = 95. $N_{n_f}$ only changes slightly for relatively large flocs at t ≥ 10,000, suggesting the equilibrium floc size distribution is reached. The floc size distribution shows an asymmetric shape with respect to the peak of $N_{n_f}$ at n_f = 95 on the log-log plot.Figure 4 shows the time-evolution of floc size distribution from a contrasting case P₂S₂ with less sticky and more stiff particles. Similarly, at the early stage (t ≤ 2000), the power–law relation between $N_{n_f}$ and n_f can be observed. However, there is no formation of the staircase-shaped structure at the intermediate stage, and the peak around n_f = 16 shows up at a much earlier time and is evident for t ≥ 3000. In addition, the population $(N_{n_f})$ of large flocs of size n_f ≥ 16 does not change with time much. However, the depletions of small flocs of size n_f ≤ 5 due to aggregation can still be observed at the late stage. The floc size distribution shows a more symmetric shape with respect to the peak at n_f = 16 on the log-log plot compared to the case P₂S₁.

FIGURE 3

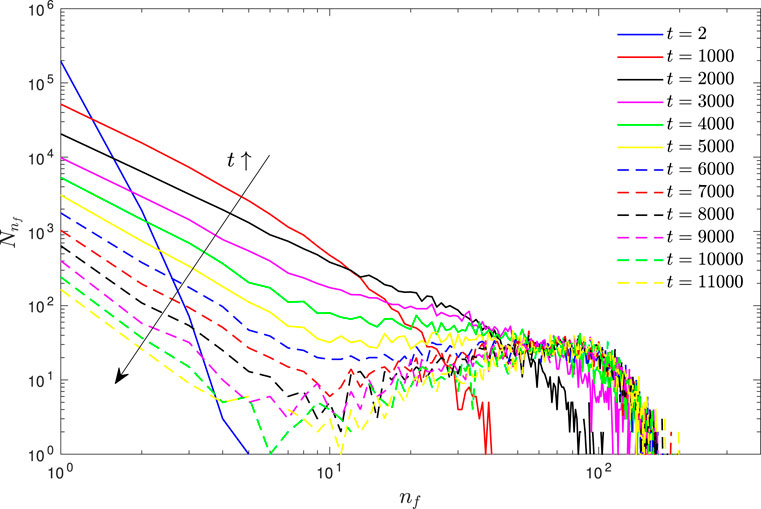
FIGURE 3. Time evolution of the floc population $N_{n_f}$ as function of floc of size n_f from case P₂S₁ with the most sticky primary particles.

FIGURE 4

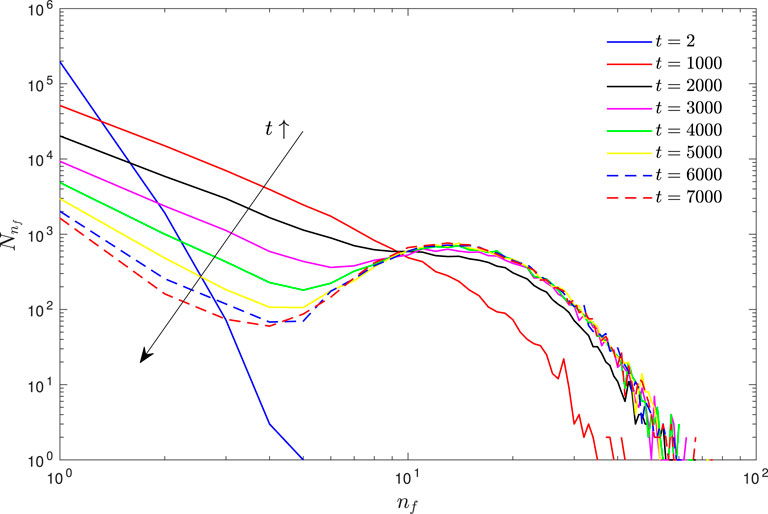
FIGURE 4. Time evolution of the floc population $N_{n_f}$ as function of floc of size n_f from case P₂S₂ with less sticky and more stiff primary particles.

To further investigate the aggregation process of flocs, the time-evolution of the floc population for given floc sizes are shown in Figures 5, 6. For case P₂S₁, small flocs of size n_f between 2 and 5 show a similar pattern (Figure 5A). The population $N_{n_f}$ first increases and reaches a peak, then it drops and approaches to an asymptotic value at the late stage when the equilibrium is reached. For relatively large flocs (Figure 5B), the time of the first appearance of the floc of size n_f increases with floc size n_f, since the flocs are built gradually when the floc grows. For intermediate flocs of size 10 <n_f < 40, we observed a similar pattern to small flocs, $N_{n_f}$ increases, peaks, and then decreases and approaches to the asymptotic value. However, for large flocs of size n_f ≥ 50, $N_{n_f}$ increases to the peak value and then approaches to the asymptotic value. Continuous aggregation and breakup keep occurring at the equilibrium stage. The oscillations in $N_{n_f}$ at the late stage are due to the intermittent nature of turbulence.

FIGURE 5

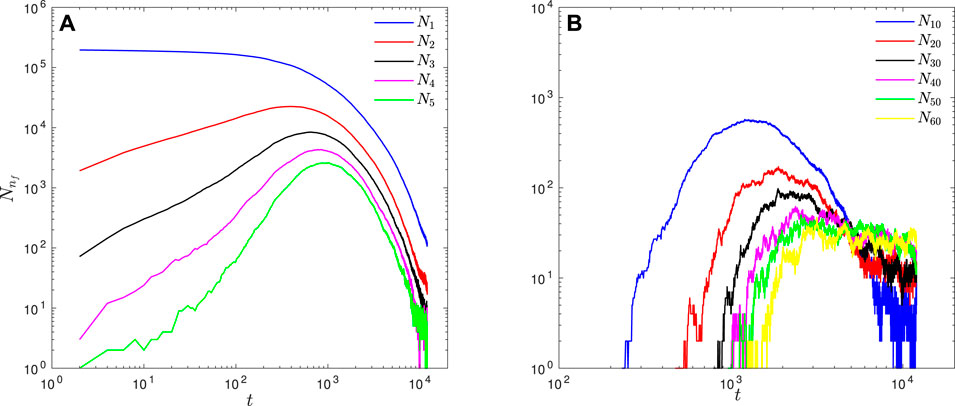
FIGURE 5. Time evolution of floc population $N_{n_f}$ for given floc size n_f from case P₂S₁. (A) Small flocs of size n_f = 1 to 5. (B) Large flocs of size n_f = 10, 20, 30, 40, 50, and 60 and 60.

FIGURE 6

FIGURE 6. Time evolution of floc population $N_{n_f}$ for given floc size n_f from case P₂S₂. (A) Small flocs of size n_f = 1 to 5. (B) Large flocs of size n_f = 10, 20, 30, and 40.

The time evolution of floc population $N_{n_f}$ from case P₂S₂ is shown in Figure 6. Similar patterns for small flocs of size n_f ≤ 5 can be observed. However, large flocs of size n_f ≥ 10 show a different pattern that $N_{n_f}$ first increases and then approaches the asymptotic constant at the equilibrium stage. This is consistent with the time evolution of the floc size distribution that the peak appears in the early case P₂S₂ and the population of large flocs does not change much with time at the late stage (Figure 4). The time of the first appearance of large floc of n_f ≥ 10 also increases with floc size, again suggesting the flocs grow gradually. Again, we observe oscillations of $N_{n_f}$ at the equilibrium stage due to the intermittent nature of turbulence. The oscillation is much stronger for larger flocs because large flocs are more fragile and more susceptible to breakup by turbulent shear.

3.3 Flocculation Dynamics: Breakup and Aggregation

To better understand how physicochemical properties of the primary particle (i.e, stickiness) affect the equilibrium floc size distribution, we examine the flocculation dynamics using the population balance equation as follows:

$\begin{array}{ll}\hfill & \frac{\partial n\left(v,\mathbf{x},t\right)}{\partial t}-\frac{\partial n\left(v,\mathbf{x},t\right)\left[u_i\left(\mathbf{x},t\right)-{\delta }_{i3}{W}_s\right]}{\partial x_i}-\frac{\partial }{\partial x_i}\left(\kappa \frac{\partial n\left(v,\mathbf{x},t\right)}{\partial x_i}\right)\hfill \\ \hfill & =\underset{\text{I:\hspace{0.17em}Construction\hspace{0.17em}by\hspace{0.17em}aggregation}}{\underbrace{\frac{1}{2}{\int }_0^{v}n\left(v-v^{\prime },\mathbf{x},t\right)n\left(v^{\prime },\mathbf{x},t\right)Q\left(v-v^{\prime },\mathbf{x},v^{\prime }\right)d{v}^{\prime }}}+\underset{\text{II:\hspace{0.17em}Construction\hspace{0.17em}by\hspace{0.17em}breakup}}{\underbrace{{\int }_n^{\infty }\beta \left(v,v^{\prime }\right)\mathrm{\Gamma }\left(v^{\prime }\right)n\left(v^{\prime },\mathbf{x},t\right)d{v}^{\prime }}}\hfill \\ \hfill & -\underset{\text{III:\hspace{0.17em}Destruction\hspace{0.17em}by\hspace{0.17em}aggregation}}{\underbrace{{\int }_0^{\infty }n\left(v,\mathbf{x},t\right)n\left(v^{\prime },\mathbf{x},t\right)Q\left(v,v^{\prime }\right)d{v}^{\prime }}}-\underset{\text{IV:\hspace{0.17em}Destruction\hspace{0.17em}by\hspace{0.17em}breakup}}{\underbrace{\mathrm{\Gamma }\left(v\right)n\left(v,\mathbf{x},t\right)}},\hfill \end{array}(21)$

where n (v, x, t) is the number density of flocs with volume (or size) v at time t and location x, W_s is the floc settling velocity, u_i is the fluid velocity component in the i-th direction, and κ is the sum of the molecular and turbulent diffusivity. On the right hand side of the equation, Q is the aggregation kernel and Γ is the breakup kernel. β is the fragmentation distribution, which describes the created number of daughter flocs of volume v after the breakage of a mother floc of volume v′. The aggregation kernel (Q) is a function of the collision frequency and collision efficiency. The collision frequency is a function of the turbulent shear rate and increases with the turbulent shear rate. The collision efficiency is defined as the rate of successful collisions resulting in the aggregation of flocs to the total number of collisions, which is a function of the properties of sediment particles.

The first term (term I) on the right hand side represents the formation of a floc of volume v by the aggregation of two smaller flocs of volume v − v′ and v′. The second term (term II) on the right hand side represents the formation of a floc of volume v from the breakup of a larger floc of volume v′. In both term I and term II, a new floc of volume v is generated, and hence they are the construction terms. The third term (term III) represents the aggregation of a floc of volume v with another floc of volume v′ to form a larger floc of volume v + v′. The last term (term IV) represents the breakup of a floc of volume v. In both term III and term IV, a floc of volume v is consumed, and hence they are the destruction terms.

In Eq. 21, both aggregation and breakup processes in the population balance equation require parameterization, including the aggregation kernel, the breakup kernel, and the fragmentation distribution (Jeldres et al., 2015). By modeling the sediment phase as the dispersed phase using the Lagrangian framework, we can track the time-evolution of individual flocs of different size n_f (or volume v = n_fV_p, with V_p as the volume of the primary particle) to understand the aggregate and breakup processes at the particle scale. By comparing simulation results at two consecutive time instances, aggregation and breakup of flocs can be obtained in the time-driven Lagrangian model. Considering all the flocs of size n_f = 16, we investigate the state of each one of them at a time interval Δt = 2 before. Most of the flocs of size n_f = 16 have remained the same over this small time interval. Some flocs would have been of a smaller size (i.e., n_f < 16) at the previous time (t − Δt) and have grown to flocs of n_f = 16 due to aggregation, while some of the flocs would have been larger at the previous time and have reduced in size to n_f = 16 due to breakup. We refer to the previous time floc size at t − Δt as the “prior-size”. Figure 7A shows the probability density function (PDF) of the prior-size of flocs whose current size is n_f = 16. Most of the flocs of prior-size n_f = 16 that have remained the same without aggregation or breakup and are not included in the analysis. In Figure 7A, the blue circle symbols represent the source of n_f = 16 flocs. The circles to the left of the dash line correspond to the PDF of smaller flocs aggregating and becoming n_f = 16 floc, while circles to the right of the dash line correspond to the PDF of larger flocs breaking up and generating a daughter floc of size n_f=16. These are terms I and II on the right hand side of (21).

FIGURE 7

FIGURE 7. Case P₂S₁ with the largest stickiness. (A) Probability density function (PDF) that a floc of size n_f becomes a floc of size n_f = 16 in a non-dimensional time period of 2 (blue circles) and the PDF that a floc of size n_f = 16 evolves into a floc of size n_f over the same period (red pluses). (B,C) Same as frame-(A) for n_f = 32 and 64.

In a similar manner, the red plus symbols represent the sink of n_f = 16 flocs, i.e., they measure the PDF of what a floc of size n_f = 16 floc becomes after a small time interval of Δt = 2. The pluses to the left of the dash line correspond to the PDF of smaller flocs that form from the breakup of n_f = 16 flocs, while pluses to the right of the dash line correspond to the PDF of larger flocs that are formed by the aggregation of a floc of size n_f = 16 with another floc (or other flocs). These are terms III and IV on the right hand side of (Eq. 21). The collapse of the two curves (circle sources and plus sinks) suggests a dynamic equilibrium with the balance between the aggregation and breakup processes. The PDF is almost uniform for small flocs. A peak is evident at n_f ≈ 80. A power–law distribution of the PDF can be observed for the large flocs with n_f > 80. For small flocs, we observe a drastic drop from the peak to n_f ≈ 30, and the distribution is quite uniform for n_f ≤ 30.

We carried out the same analysis for flocs of size n_f = 32 (Figure 7B), the power–law distribution is evident for large flocs of n_f > 80. A uniform distribution can be observed between n_f = 32 and 80. For smaller flocs of n_f < 32, the distribution shows a minimum around n_f ≈ 9 and peaks around n_f = 32 and n_f = 1 (primary particles). For floc of size n_f = 64 (Figure 7C), the power–law distribution is still evident for large flocs of n_f > 80. In addition, a significant change of the slope for large flocs of size greater than n_f = 150 can be identified. For small flocs of n_f < 64, the distribution shows a uniform distribution between 20 and 60 and two peaks near n_f = 64 and n_f = 1 (primary particles). For case P₂S₂ with less sticky and more stiff primary particles, the terms are plotted for flocs of size n_f = 8, 16, and 24 (Figure 8). The PDFs for flocs of different size are quite similar. It shows a power–law relation for large flocs of n_f ≥ 16. For smaller flocs of n_f < 16, the distribution exhibits a minimum at n_f = 5 and two peaks at n_f = 16 and n_f = 1 (primary particle). Compared to the case P₂S₁ with the stickies primary particles, the presence of the uniform distribution for intermediate-sized flocs (n_f between 30 and 50 in case P₂S₁) is not evident in case P₂S₂.

FIGURE 8

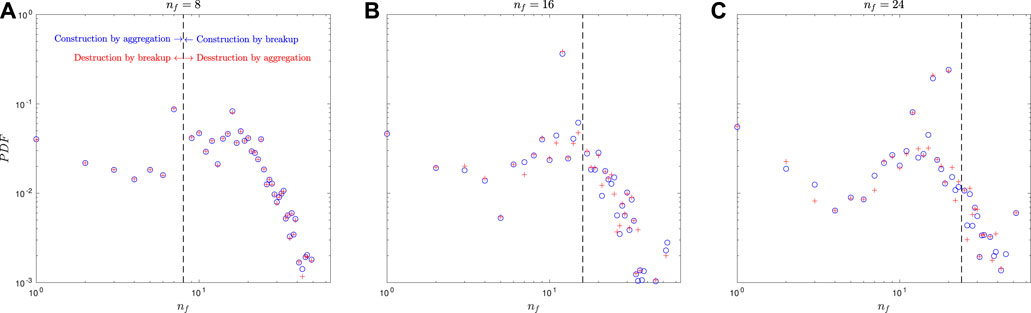
FIGURE 8. Case P₂S₂ with smaller stickiness and larger stiffness. (A) Probability density function (PDF) that a floc of size n_f becomes a floc of size n_f = 8 in a non-dimensional time period of 2 (blue circles) and the PDF that a floc of size n_f = 8 evolves into a floc of size n_f over the same period (red pluses). (B,C) Same as frame-(A) for n_f = 16 and 24.

In both cases, at the equilibrium stage when the breakup and aggregation processes balance with each other, simulation results show that the construction by aggregation is primarily balanced by the destruction by breakup and the construction by breakup is primarily balanced by the destruction by aggregation. At the microscopic level, each aggregation or breakup pathway is reversible and hence in a dynamic equilibrium. With given aggregation and breakup kernels, equilibrium solutions of the floc size distribution exist (Vigil, 2009), and the mathematical form of the equilibrium floc size distribution could be derived.

3.4 Equilibrium Floc Size Distribution

An equilibrium floc size distribution develops when the aggregation process balances with the breakup process. The floc size distribution is modeled as a function of n_f, instead of the floc size D_f, because the number density (n) in Equation (21) is expressed as a function of the floc volume v. In this study, flocs are consisted of slightly overlapping identical spheres, and the volume of a floc consisted of n_f primary particles can be approximated by n_f as $v\approx n_f\pi D_p^3/6$. To calculate the floc volume using the actual floc size D_f requires a priori knowledge of the floc internal structure, which is difficult to obtain. Because of the asymmetry around the peak, we tested the floc size distribution against two widely used asymmetric distributions, namely, the lognormal distribution and the Weibull distribution. The lognormal probability distribution function is expressed as follows:

$f\left(n_f;\mu ,{\sigma }^2\right)=\frac{1}{n_f\sigma \sqrt{2\pi }}\exp \left(-\frac{{\left(\ln n_f-\mu \right)}^2}{2{\sigma }^2}\right),(22)$

where ln n_f follows the normal distribution, μ is the mean, and σ² is the variance.

The Weibull distribution is a special form of Gamma distribution with two parameters, namely, the scaling parameter λ and the shape parameter k.

$f\left(n_f;\lambda ,k\right)=\frac{k}{\lambda }{\left(\frac{n_f}{\lambda }\right)}^{k-1}\exp \left(-{\left(n_f/\lambda \right)}^k\right)n_f\ge 0.(23)$

The Weibull distribution interpolates between the exponential distribution and Rayleigh distribution. The shape parameter k affects the shape of the distribution rather than simply shifting or stretching it. Figure 9 shows the curve fitting for case P₂S₁ (panel a), P₂S₂ (panel b), and P₂S₃ (panel c). For case P₂S₁ with the stickiest primary particles, model results fit better with the Weibull distribution, while results from case P₂S₂ with less sticky but more stiff primary particles fit better with the lognormal distribution. For case P₂S₃, neither lognormal nor Weibull distribution can fit the data for the entire range of the floc size n_f. To assess the performance of different distributions, the Anderson–Darling (AD) test (Anderson and Darling, 1952) was conducted, which is based on the empirical cumulative distribution obtained from the sample. The AD test is commonly used to test if a sample of data comes from a population with a specific distribution. We used the significant level of α = 0.01, which is commonly used in statistical hypothesis test (Fisher, 1992). The results are summarized in Table 2, where E_s is the sum of squared residual errors. The accepted hypothesis for each case is shown with “*” in Table 2, which means the optimal descriptor for the floc size distribution. For the case with less sticky primary particles (case P₂S₂), the lognormal distribution fits better and for the cases with very sticky primary particles (case P₁S₂ and P₂S₁), the Weibull distribution fits better. The AD test rejects both lognormal and Weibull distribution hypothesis for most cases, suggesting neither lognormal nor Weibull distribution can accurately predict the floc size distribution. For instance, the lognormal distribution fits better for small flocs and also captures the peak more accurately in case P₂S₃ (Figure 9C), while the Weibull distribution fits better for large flocs (n_f > 35). The adjusted coefficient of determination $(R_{adj}^2)$ was then used to evaluate the goodness of the fit (Ezekiel, 1930). However, the $R_{adj}^2$ for both distributions are quite close, and hence it is difficult to distinguish the two distributions. Based on curve fitting results, the shape parameter k is around 2.5 for all cases, suggesting a similarity in the floc size distribution.

FIGURE 9

FIGURE 9. Floc size distribution represented by $N_{n_f}$. (A) Case P₂S₁, (B) case P₂S₂, and (C) case P₂S₃.

TABLE 2

TABLE 2. Anderson–Darling test results and the adjusted coefficient of determination $R_{adj}^2$.

Floc size distribution from P₂S₁ fits better with the Weibull distribution. To further investigate the floc size distribution from case P₂S₁, we plotted model results under log-log scale (Figure 10A) and semi-log scale (Figure 10B). We averaged $N_{n_f}$ from t = 11,000 to 12,000, when the equilibrium is achieved for large flocs. For flocs with size n_f between 30 and 75, a power–law relation can be identified when the aggregation and breakup processes balance. For large flocs with n_f greater than 110, we observe an exponential decay of $N_{n_f}$ with n_f. For case P₂S₂ with lognormal distribution, we did not observe the power–law relation, and hence the results are not shown.

FIGURE 10

FIGURE 10. Floc size distribution from case P₂S₁ (A) power-law fit and (B) exponential fit.

4 Discussion

Different mathematical formulas of floc size distribution arise in the aggregation or breakage processes (Huber et al., 2006). Lognormal distribution has been observed in particle growth or coagulation processes (Smoluchowski, 1918; Friedlander and Wang, 1966), in which aggregation process dominates the dynamics. On the other hand, Weibull distribution has been commonly observed in the fragmentation process of large particles (Brown and Wohletz, 1995). In the flocculation process, both the aggregation and fragmentation processes play an important role. At the equilibrium state, a floc can be constructed either by aggregation of smaller flocs or breakup from larger flocs. To further understand under which circumstances a lognormal or Weibull distribution performs better, we analyzed the dominant floc construction mechanisms at the equilibrium stage. Figure 11 shows the relative importance of construction by aggregation and construction by the breakup for flocs of size n_f from the two contrasting cases P₂S₁ and P₂S₂. In case P₂S₁ (Figure 11A), the majority of small flocs are constructed by breakup of larger flocs, while large flocs (n_f > 75) are mainly constructed by aggregation as expected. The aggregation and breakup processes play equally important roles for flocs in the range of 30<n_f < 75. The primary particles first aggregate into microflocs, the microflocs are quite resilient to turbulent shear and serve as the building blocks for larger flocs. For case P₂S₂ (Figure 11B), we observe a monotonic increase in relative importance for aggregation and a decrease for breakup process with respect to n_f. In general, a large portion of flocs (n_f < 75) in case P₂S₁ are generated mainly from breakup of larger flocs. However, in case P₂S₂, breakup only controls the formation of a small portion of flocs with n_f < 15, and the aggregation process dominates the formation of flocs for a wide range of flocs. The lognormal distribution (case P₂S₂) develops when the large flocs grow gradually from primary particles without the intermediate stage (the formation of “microflocs”). This behavior has not been observed in laboratory experiments before, and future laboratory studies are required to test whether this is an artifact of the numerical model or an actual physical process.

FIGURE 11

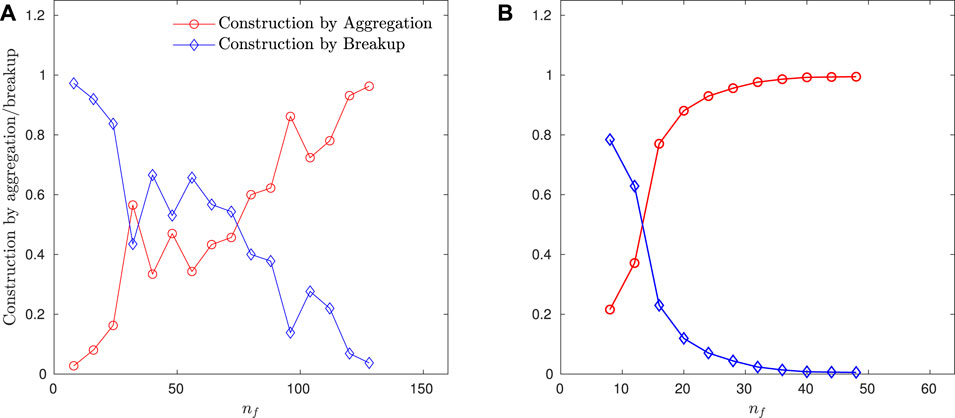
FIGURE 11. Relative importance of the two construction mechanisms for flocs of size n. (A) Case P₂S₁ and (B) P₂S₂.

Mathematical approach of floc modeling that has gained much interest by modelers is the fractal representation of flocs (Kranenburg, 1994; Merckelbach, 2000; Graham and Manning, 2007). Fractal theory is dependent on the successive aggregations of self-similar flocs, thereby producing a structure that is independent of the scale (or scale invariant). This is similar to the order-of-aggregation theory (Krone, 1963). Following the fractal theory, simple power laws can be used to describe floc properties such as floc density and settling velocity, as well as the aggregation and breakup processes (Winterwerp, 1998). Although some studies suggest that individually some natural muddy flocs (particularly those with high organic contents) may not be fully fractal in structure (Zhang et al., 2018; Spencer et al., 2021), the wider examination of in situ floc populations shows that a fractal representation of flocs still has many merits (Dyer and Manning, 1999; Winterwerp et al., 2006). The fractal dimension d₀ used to characterize the floc structure is defined as

$n_f={\left(\frac{D_f}{D_p}\right)}^{d_0},(24)$

where n_f is the total number of the primary particles consisting the floc, D_f is the floc size and D_p is the primary particle diameter. The major axis length (longest axis) is used as floc size D_f, which is obtained by the principal component analysis (PCA). In general, the fractal dimension (d₀) is 1 for chain-like flocs and 2 for flat plane-like flocs. Flocs with fractal dimension close to 3 have compact structure and spherical shape.

Flocs with the same number of primary particles (n_f) can exhibit different structures, and the averaged fractal dimension $(\overline{d_0})$ for flocs with the same n_f is shown in Figure 12. For case P₂S₁, the fractal dimension first increases and reaches a constant value around 2.4 for flocs of size n_f between 50 and 120, suggesting compact and similar floc structures. Fractal dimension $\overline{d_0}$ decreases for large flocs of n_f > 120. The increase in $\overline{d_0}$ for small flocs is due to the limited configurations of floc structure by finite n_f. For instance, the most compact structure for a dimer (aggregate consisted of exact two spheres) is a rod with a fractal dimension of 1, and the most compact structure for a trimer (aggregate consisted of exact three spheres) is an equilateral triangle of fractal dimension of 1.7. The “microflocs” in the range of 30<n_f<75 (Figure 11A) have relatively small fractal dimensions. The primary particles in case P₂S₁ are the stickiest and the turbulent shear stress is less efficient to break these ‘microflocs’ at the scale. The decrease of $\overline{d_0}$ for large flocs suggests that they are more porous. Similar trends can be observed for cases P₁S₂, in which Weibull distribution better describes the flocs size distribution.

FIGURE 12

FIGURE 12. Averaged fractal dimension $(\overline{d_0})$ as function of floc size n_f for different cases.

In contrast, in case P₂S₂ with the least sticky primary particles, the fractal dimension increases to the peak value around 1.95 and then drops for large flocs. The decrease in the fractal dimension for large flocs has also been observed by Khelifa and Hill (2006) and Maggi (2007). Our numerical results suggest the scale-dependence of floc structure as the fractal dimension is not constant for the entire range of the floc size. A variable fractal dimension should be considered to characterize the flocs.

In general, for the cases with the same primary particle diameter, primary particles with small adhesive numbers (or surface energy density) lead to flocs with smaller fractal dimensions, and primary particles with large adhesive numbers generate more compact flocs with fractal dimension as large as 2.4 in case P₂S₁. Floc compaction by the breakage-regrowth and restructuring mechanisms are more pronounced in the case with the stickiest primary particle. By comparing case P₂S₂ and P₂S₃, the stiffness of the particle also affects the floc structures. Primary particles with larger Young’s modulus (case P₂S₂) lead to flocs with smaller fractal dimension.

5 Conclusion

A two-phase Eulerian–Lagrangian framework was implemented to investigate the equilibrium floc size distribution of cohesive sediment in homogeneous isotropic turbulence. The primary particles are modeled as identical sticky soft spheres, and particle–particle interactions are modeled by the discrete element method. The adhesive contact JKR model was implemented to model cohesive sediment particles, which is a tensile force model with hysteretic effect. In the adhesive contact model, the pull-off force to break two particles apart scales with both the particle size and the surface energy density (i.e., the physicochemical properties of the primary particle).

A series of numerical simulations were conducted by varying the size and properties of the primary particles. At the equilibrium state, the construction by breakup is balanced with the destruction by aggregation, and the construction by aggregation is balanced with the destruction by breakup. The equilibrium floc size distribution depends on primary particle properties, including the stiffness and the surface energy density. For cases with more sticky primary particles, the floc size distribution can be better described by the Weibull distribution with a shape parameter around 2.5. In addition, at the intermediate stage, a staircase structure develops in the floc size distribution. The primary particles first form the ‘microflocs’, which serve as the building blocks for large flocs. For the case with less sticky primary particles, the lognormal distribution performs better. Flocs grow gradually from primary particles without the intermediate stage of ‘microflocs’.

By analyzing the construction mechanisms of flocs of different size, when the Weibull distribution develops, construction by breakup and construction by aggregation are of equal importance for the intermediate-sized flocs. The fractal dimension of large flocs then decreases with floc size, suggesting large “macroflocs” are more porous and fragile. For less sticky particles, the lognormal distribution develops, and the aggregation dominates the floc construction for a wide range of flocs. The fractal dimension of flocs first increases with floc size, reaches the peak value, and then decreases with the floc size. However, given the similarity between the lognormal and Weibull distributions and hence the difficulties in distinguishing between them in confidence, it is recommended to choose the floc size distribution and make interpretations in practice with caution.

Due to the limited computational resources, the current simulation focuses on the high-energy environments with large turbulent shear rate (350 s⁻¹ in this study). Simulations with more particles (several millions to billions of particles) are therefore required for more realistic cohesive sediment transport studies in low-to moderate-energy environments. In addition, current model framework oversimplifies the hydrodynamic interactions among particles without the influence from neighboring particles. For cohesive sediment, the particle Reynolds number based on Stokes settling velocity is small, and hence the sheltering and blockage effects from neighboring particles could play an important role. The sheltering effects from neighboring particles lead to reduced hydrodynamic drag, and hence could affect the breakup processes. A more sophisticated efficient model that can accurately predict hydrodynamic interactions among a large amount of particles is required and will be the future work.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://figshare.com/articles/dataset/FlocSizeDistribution/16619734.

Author Contributions

MY: methodology; formal analysis; and writing—original draft, review, and editing. XY: supervision; conceptualization; methodology; formal analysis; writing—original draft, review, and editing. SB: conceptualization; methodology, and writing—review and editing. AM: writing–review and editing.

Funding

This work is funded by the United States Army Engineering Research and Development Center under the Cooperative Ecosystem Studies Unit (CESU) grant W912HZ-21-2-0035. AM’s contribution toward this research was also partly supported by the United States National Science Foundation under grants OCE-1736668 and OCE-1924532, TKI-MUSA project 11204950-000-ZKS-0002, and HR Wallingford company research FineScale project (ACK3013-62).

Conflict of Interest

Author AM was employed by the company HR Wallingford.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

All simulations were carried out on the HiperGator super computer at the University of Florida. Computer resources, technical expertise, and assistance provided by the HiperGator are gratefully acknowledged. The CFD model nek5000 is developed primarily by the Argonne National Laboratory at https://nek5000.mcs.anl.gov/, and the DEM model LAMMPS is developed by Sandia National Laboratories at https://lammps.sandia.gov/.

References

Akiki, G., Moore, W. C., and Balachandar, S. (2017). Pairwise-interaction Extended Point-Particle Model for Particle-Laden Flows. J. Comput. Phys. 351, 329–357. doi:10.1016/j.jcp.2017.07.056

CrossRef Full Text | Google Scholar

Anderson, T. W., and Darling, D. A. (1952). Asymptotic Theory of Certain “Goodness of Fit” Criteria Based on Stochastic Processes. Ann. Math. Stat. 23, 193–212. doi:10.1214/aoms/1177729437

CrossRef Full Text | Google Scholar

Balachandar, S., and Eaton, J. K. (2010). Turbulent Dispersed Multiphase Flow. Annu. Rev. Fluid Mech. 42, 111–133. doi:10.1146/annurev.fluid.010908.165243

CrossRef Full Text | Google Scholar

Baugh, J. V., and Manning, A. J. (2007). An Assessment of a New Settling Velocity Parameterisation for Cohesive Sediment Transport Modeling. Cont. Shelf Res. 27 (13), 1835–1855. doi:10.1016/j.csr.2007.03.003

CrossRef Full Text | Google Scholar

Brown, W. K., and Wohletz, K. H. (1995). Derivation of the Weibull Distribution Based on Physical Principles and its Connection to the Rosin-Rammler and Lognormal Distributions. J. Appl. Phys. 78 (4), 2758–2763. doi:10.1063/1.360073

CrossRef Full Text | Google Scholar

Byun, J., and Son, M. (2020). On the Relationship between Turbulent Motion and Bimodal Size Distribution of Suspended Flocs. Estuar. Coast. Shelf Sci. 245, 106938. doi:10.1016/j.ecss.2020.106938

CrossRef Full Text | Google Scholar

Dyer, K. R., and Manning, A. J. (1999). Observation of the Size, Settling Velocity and Effective Density of Flocs, and Their Fractal Dimensions. J. Sea Res. 41 (1-2), 87–95. doi:10.1016/s1385-1101(98)00036-7

CrossRef Full Text | Google Scholar

Dyer, K. R. (1989). Sediment Processes in Estuaries: Future Research Requirements. J. Geophys. Res. 94 (C10), 14327–14339. doi:10.1029/jc094ic10p14327

CrossRef Full Text | Google Scholar

Edmonds, D. A., and Slingerland, R. L. (2010). Significant Effect of Sediment Cohesion on Delta Morphology. Nat. Geosci. 3, 105–109. doi:10.1038/ngeo730

CrossRef Full Text | Google Scholar

Eisma, D. (1986). Flocculation and De-flocculation of Suspended Matter in Estuaries. Neth. J. Sea Res. 20 (2-3), 183–199. doi:10.1016/0077-7579(86)90041-4

CrossRef Full Text | Google Scholar

Ezekiel, M. (1930). Methods of Correlation Analysis. Oxford, England: Wiley.

Google Scholar

Fang, Z., Patterson, B. R., and Turner, M. E. (1993). Modeling Particle Size Distributions by the Weibull Distribution Function. Mater. Charact. 31 (3), 177–182. doi:10.1016/1044-5803(93)90058-4

CrossRef Full Text | Google Scholar

Fischer, P. F. (1997). An Overlapping Schwarz Method for Spectral Element Solution of the Incompressible Navier-Stokes Equations. J. Comput. Phys. 133 (1), 84–101. doi:10.1006/jcph.1997.5651

CrossRef Full Text | Google Scholar

Fischer, P. F., Lottes, J. W., and Kerkemeier, S. G. (2008). Nek5000. Available at: http://nek5000.mcs.anl.gov.

Google Scholar

Fisher, R. A. (1992). “Statistical Methods for Research Workers,” in Breakthroughs in Statistics (New York, NY: Springer), 66–70. doi:10.1007/978-1-4612-4380-9_6

CrossRef Full Text | Google Scholar

Friedlander, S. K., and Wang, C. S. (1966). The Self-Preserving Particle Size Distribution for Coagulation by Brownian Motion. J. Colloid interface Sci. 22 (2), 126–132. doi:10.1016/0021-9797(66)90073-7

CrossRef Full Text | Google Scholar

Geyer, W. R., Hill, P., Milligan, T., and Traykovski, P. (2000). The Structure of the Eel River Plume during Floods. Cont. Shelf Res. 20 (16), 2067–2093. doi:10.1016/s0278-4343(00)00063-7

CrossRef Full Text | Google Scholar

Graham, G. W., and Manning, A. J. (2007). Floc Size and Settling Velocity within a Spartina Anglica Canopy. Cont. Shelf Res. 27 (8), 1060–1079. doi:10.1016/j.csr.2005.11.017

CrossRef Full Text | Google Scholar

Hayter, E. J., and Mehta, A. J. (1986). Modelling Cohesive Sediment Transport in Estuarial Waters. Appl. Math. Model. 10 (4), 294–303. doi:10.1016/0307-904x(86)90061-2

CrossRef Full Text | Google Scholar

Hill, P. S. (1996). Sectional and Discrete Representations of Floc Breakage in Agitated Suspensions. Deep Sea Res. Part I Oceanogr. Res. Pap. 43 (5), 679–702. doi:10.1016/0967-0637(96)00030-1

CrossRef Full Text | Google Scholar

Hosoda, K., Matsuura, T., Suzuki, H., and Yomo, T. (2011). Origin of Lognormal-like Distributions with a Common Width in a Growth and Division Process. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 83, 031118. doi:10.1103/PhysRevE.83.031118

PubMed Abstract | CrossRef Full Text | Google Scholar

Huber, P., Roux, E., Mauret, J. C., and Carre, B. (2006). Characterising the Floc Size Distribution of Flowing Pulp Suspensions: from Fibre Flocculation to Sheet Formation. Appita Technol. Innov. Manuf. Environ. 59, 37. doi:10.3316/informit.586267214881170

CrossRef Full Text | Google Scholar

Hunt, J. R. (1982). Self-similar Particle-Size Distributions during Coagulation: Theory and Experimental Verification. J. Fluid Mech. 122, 169–185. doi:10.1017/s0022112082002158

CrossRef Full Text | Google Scholar

Jeldres, R. I., Concha, F., and Toledo, P. G. (2015). Population Balance Modelling of Particle Flocculation with Attention to Aggregate Restructuring and Permeability. Adv. colloid interface Sci. 224, 62–71. doi:10.1016/j.cis.2015.07.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, K. L. (1985). Contact Mechanics. Cambridge University Press.

Google Scholar

Khelifa, Ali, and Hill, Paul S. (2006). Models for Effective Density and Settling Velocity of Flocs. J. Hydraulic Res. 44 (3), 390–401. doi:10.1080/00221686.2006.9521690

CrossRef Full Text | Google Scholar

Kiss, L. B., Söderlund, J., Niklasson, G. A., and Granqvist, C. G. (1999). New Approach to the Origin of Lognormal Size Distributions of Nanoparticles. Nanotechnology 10 (1), 25–28. doi:10.1088/0957-4484/10/1/006

CrossRef Full Text | Google Scholar

Kolmogorov, A. N. (1941b). Dissipation of Energy in Locally Iscotropic Turbulence. Proc. USSR Acad. Sci. 32, 16.

Google Scholar

Kolmogorov, A. N. (1941a). The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Numbers. Proc. USSR Acad. Sci. 30, 301.

Google Scholar

Kondolf, G. M., and Adhikari, A. (2000). Weibull vs. Lognormal Distributions for Fluvial Gravels. J. Sediment. Res. 70 (3), 456–460. doi:10.1306/2dc4091e-0e47-11d7-8643000102c1865d

CrossRef Full Text | Google Scholar

Kranenburg, C. (1994). The Fractal Structure of Cohesive Sediment Aggregates. Estuar. Coast. Shelf Sci. 39 (5), 451–460. doi:10.1006/ecss.1994.1075

CrossRef Full Text | Google Scholar

Krone, R. B. (1963). A Study of Rheological Properties of Estuarial Sediments. Report No. 63-68. Berkeley: Hydraulic Engineering Laboratory and Sanitary Engineering Research Laboratory, University of California.

Google Scholar

Li, D., and Ganczarczyk, J. (1991). Size Distribution of Activated Sludge Flocs. Res. J. water Pollut. control Fed. 63 (5), 806–814

Google Scholar

Luding, S. (2008). Cohesive, Frictional Powders: Contact Models for Tension. Granul. matter 10 (4), 235–246. doi:10.1007/s10035-008-0099-x

CrossRef Full Text | Google Scholar

Lundgren, T. S. (2003). Linearly Forces Isotropic Turbulence. Minnesota Univ Minneapolis. Ph.D. thesis.

Google Scholar

Maday, Y., Patera, A. T., and Rnquist, E. M. (1990). An Operator-Integration-Factor Splitting Method for Time-dependent Problems: Application to Incompressible Fluid Flow. J. Sci. Comput. 5, 263–292. doi:10.1007/bf01063118

CrossRef Full Text | Google Scholar

Maggi, F. (2007). Variable Fractal Dimension: A Major Control for Floc Structure and Flocculation Kinematics of Suspended Cohesive Sediment. J. Geophys. Res. Oceans 112 (C7), 3951. doi:10.1029/2006jc003951

CrossRef Full Text | Google Scholar

Manning, A. J. (2001). A Study of the Effects of Turbulence on the Properties of Flocculated Mud. Ph.D. Thesis. Institute of Marine Studies, University of Plymouth.

Google Scholar

Manning, A. J., Bass, S. J., and Dyer, K. R. (2006). Floc Properties in the Turbidity Maximum of a Mesotidal Estuary during Neap and Spring Tidal Conditions. Mar. Geol. 235 (1-2), 193–211. doi:10.1016/j.margeo.2006.10.014

CrossRef Full Text | Google Scholar

Manning, A. J., and Dyer, K. R. (1999). A Laboratory Examination of Floc Characteristics with Regard to Turbulent Shearing. Mar. Geol. 160 (1-2), 147–170. doi:10.1016/s0025-3227(99)00013-4

CrossRef Full Text | Google Scholar

Manning, A. J., and Schoellhamer, D. H. (2013). Factors Controlling Floc Settling Velocity along a Longitudinal Estuarine Transect. Mar. Geol. 345, 266–280. doi:10.1016/j.margeo.2013.06.018

CrossRef Full Text | Google Scholar

Manning, A. J. (2004). The Observed Effects of Turbulence on Estuarine Flocculation. J. Coast. Res. 41, 90–104

Google Scholar

Marshall, J. S. (2009). Discrete-element Modeling of Particulate Aerosol Flows. J. Comput. Phys. 228 (5), 1541–1561. doi:10.1016/j.jcp.2008.10.035

CrossRef Full Text | Google Scholar

McAnally, W. H., and Mehta, A. J. (2001). Collisional Aggregation of Fine Estuarine Sediments. Coast. Estuar. Fine Sediment Process. - Proc. Mar. Sci. 3, 19

Google Scholar

Mehta, A. J., and Lott, J. W. (1987). Sorting of Fine Sediment during Deposition. Proc. Conf. Adv. Underst. Coast. Sediment Process. 1, 348

Google Scholar

Mehta, A. J., Manning, A. J., and Khare, Y. P. (2014). A Note on the Krone Deposition Equation and Significance of Floc Aggregation. Mar. Geol. 354, 34–39. doi:10.1016/j.margeo.2014.04.002

CrossRef Full Text | Google Scholar

Merckelbach, L. (2000). Consolidation and Strength Evolution of Soft Mud Layers.

Google Scholar

Mindlin, R. D. (1949). Compliance of Elastic Bodies in Contact. J. Appl. Mech. ASME 16 (3), 259–268. doi:10.1115/1.4009973

CrossRef Full Text | Google Scholar

Mouri, H., Hori, A., and Takaoka, M. (2009). Large-scale Lognormal Fluctuations in Turbulence Velocity Fields. Phys. fluids 21, 7936. doi:10.1063/1.3147936

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117 (1), 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Prandle, D., Lane, A., and Manning, A. J. (2005). Estuaries Are Not So Unique. Geophys. Res. Lett. 32 (23), 24797. doi:10.1029/2005gl024797

CrossRef Full Text | Google Scholar

Pushkin, D. O., and Aref, H. (2002). Self-similarity Theory of Stationary Coagulation. Phys. fluids 14, 694–703. doi:10.1063/1.1430440

CrossRef Full Text | Google Scholar

Rosales, C., and Meneveau, C. (2005). Linear Forcing in Numerical Simulations of Isotropic Turbulence: Physical Space Implementations and Convergence Properties. Phys. fluids 17 (9), 095106. doi:10.1063/1.2047568

CrossRef Full Text | Google Scholar

Saha, D., Babler, M. U., Holzner, M., Soos, M., Lüthi, B., Liberzon, A., et al. (2016). Breakup of Finite-Size Colloidal Aggregates in Turbulent Flow Investigated by Three-Dimensional (3d) Particle Tracking Velocimetry. Langmuir 32 (1), 55–65. doi:10.1021/acs.langmuir.5b03804

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheremet, A., Sahin, C., and Manning, A. J. (2017). Flocculation: A General Aggregation-Fragmentation Framework. Int. Conf. Coast. Eng. 35, 27. doi:10.9753/icce.v35.sediment.27

CrossRef Full Text | Google Scholar

Smoluchowski, M. v. (1918). Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Z. für Phys. Chem. 92U (1), 129–168. doi:10.1515/zpch-1918-9209

CrossRef Full Text | Google Scholar

Soulsby, R. L., Manning, A. J., Spearman, J., and Whitehouse, R. J. S. (2013). Settling Velocity and Mass Settling Flux of Flocculated Estuarine Sediments. Mar. Geol. 339, 1–12. doi:10.1016/j.margeo.2013.04.006

CrossRef Full Text | Google Scholar

Spencer, K. L., Wheatland, J. A. T., Bushby, A. J., Carr, S. J., Droppo, I. G., and Manning, A. J. (2021). A Structure-Function Based Approach to Floc Hierarchy and Evidence for the Non-fractal Nature of Natural Sediment Flocs. Sci. Rep. 11, 14012. doi:10.1038/s41598-021-93302-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Spicer, P. T., and Pratsinis, S. E. (1996). Coagulation and Fragmentation: Universal Steady-State Particle-Size Distribution. AIChE J. 42 (6), 1612–1620. doi:10.1002/aic.690420612

CrossRef Full Text | Google Scholar

Sun, R., Xiao, H., and Sun, H. (2018). Investigating the Settling Dynamics of Cohesive Silt Particles with Particle-Resolving Simulations. Adv. Water Resour. 111, 406–422. doi:10.1016/j.advwatres.2017.11.012

CrossRef Full Text | Google Scholar

Sundaram, S., and Collins, L. R. (1997). Collision Statistics in an Isotropic Particle-Laden Turbulent Suspension. Part 1. Direct Numerical Simulations. J. Fluid Mech. 335, 75–109. doi:10.1017/s0022112096004454

CrossRef Full Text | Google Scholar

Tambo, N., and Watanabe, Y. (1984). Physical Aspect of Flocculation Process-III. Water Res. 18 (4), 695–707. doi:10.1016/0043-1354(84)90165-9

CrossRef Full Text | Google Scholar

Tolhurst, T. J., Gust, G., and Paterson, D. M. (2002). The Influence of an Extracellular Polymeric Substance (EPS) on Cohesive Sediment Stability. Proc. Mar. Sci. 5, 409–425. doi:10.1016/s1568-2692(02)80030-4

CrossRef Full Text | Google Scholar

Tsuji, Y., Kawaguchi, T., and Tanaka, T. (1993). Discrete Particle Simulation of Two-Dimensional Fluidized Bed. Powder Technol. 77 (1), 79–87. doi:10.1016/0032-5910(93)85010-7

CrossRef Full Text | Google Scholar

van Leussen, W. (1994). Estuarine Macroflocs and Their Role in Fine-Grained Sediment Transport. Ph.D. Thesis. The Netherlands: University of Utrecht.

Google Scholar

van Leussen, W. (1997). “The Kolmogorov Microscale as a Limiting Value for the Floc Sizes of Suspended Fine-Grained Sediments in Estuaries,” in Cohesive Sediments (New York: Wiley), 45–62

Google Scholar

van Olphen, H. (1964). An Introduction to Clay Colloid Chemistry. Soil Sci. 97 (4), 290.

CrossRef Full Text | Google Scholar

Vigil, R. D. (2009). On Equilibrium Solutions of Aggregation-Fragmentation Problems. J. colloid interface Sci. 336 (2), 642–647. doi:10.1016/j.jcis.2009.04.061

CrossRef Full Text | Google Scholar

Vowinckel, B., Withers, J., Luzzatto-Fegiz, P., and Meiburg, E. (2019). Settling of Cohesive Sediment: Particle-Resolved Simulations. J. Fluid Mech. 858, 5–44. doi:10.1017/jfm.2018.757

CrossRef Full Text | Google Scholar

Wang, Y., Alonso-Marroquin, F., and Guo, W. W. (2015). Rolling and Sliding in 3-D Discrete Element Models. Particuology 23, 49–55. doi:10.1016/j.partic.2015.01.006

CrossRef Full Text | Google Scholar

Wen, C. Y. (1966). Mechanics of Fluidization. Chem. Eng. Prog. Symp. Ser. 62, 100

Google Scholar

Winterwerp, J. C. (1998). A Simple Model for Turbulence Induced Flocculation of Cohesive Sediment. J. Hydraulic Res. 36 (3), 309–326. doi:10.1080/00221689809498621

CrossRef Full Text | Google Scholar

Winterwerp, J. C., Manning, A. J., Martens, C., de Mulder, T., and Vanlede, J. (2006). A Heuristic Formula for Turbulence-Induced Flocculation of Cohesive Sediment. Estuar. Coast. Shelf Sci. 68 (1-2), 195–207. doi:10.1016/j.ecss.2006.02.003

CrossRef Full Text | Google Scholar

Winterwerp, J. C., Uittenbogaard, R. E., and De Kok, J. M. (2000). Rapid Siltation from Saturated Mud Suspensions. Proc. Mar. Sci. 3, 125–146. doi:10.1016/s1568-2692(00)80117-5

CrossRef Full Text | Google Scholar

Winterwerp, J. C., and van Kesteren, W. G. M. (2004). Introduction to the Physics of Cohesive Sediment in the Marine Environment, Amsterdam, Netherlands: Elsevier.

Google Scholar

Ye, L., Manning, A. J., and Hsu, T.-J. (2020). Oil-mineral Flocculation and Settling Velocity in Saline Water. Water Res. 173, 115569. doi:10.1016/j.watres.2020.115569

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeung, P. K., Pope, S. B., Lamorgese, A. G., and Donzis, D. A. (2006). Acceleration and Dissipation Statistics of Numerically Simulated Isotropic Turbulence. Phys. Fluids 18, 065103. doi:10.1063/1.2204053

CrossRef Full Text | Google Scholar

Zhang, N., Thompson, C. E. L., Townend, I. H., Rankin, K. E., Paterson, D. M., and Manning, A. J. (2018). Nondestructive 3D Imaging and Quantification of Hydrated Biofilm-Sediment Aggregates Using X-Ray Microcomputed Tomography. Environ. Sci. Technol. 52 (22), 13306–13313. doi:10.1021/acs.est.8b03997

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Z. Y., Kuang, S. B., Chu, K. W., and Yu, A. B. (2010). Discrete Particle Simulation of Particle-Fluid Flow: Model Formulations and Their Applicability. J. Fluid Mech. 661, 482–510. doi:10.1017/s002211201000306x

CrossRef Full Text | Google Scholar

Zwick, D., and Balachandar, S. (2020). A Scalable Euler-Lagrange Approach for Multiphase Flow Simulation on Spectral Elements. Int. J. High Perform. Comput. Appl. 34 (3), 316–339. doi:10.1177/1094342019867756

CrossRef Full Text | Google Scholar