Spectrally Consistent Mean Dynamic Topography by Combining Mean Sea Surface and Global Geopotential Model Through a Least Squares-Based Approach

The filtering procedure is usually mandatory for modeling mean dynamic topography (MDT) when a geodetic approach based on the Mean Sea Surface (MSS) and the Global Geopotential Model (GGM) is used. This is due to the inconsistent spectral contents between MSS and GGM. However, traditional isotropic filtering algorithms (e.g., Gaussian filter) consider neither the MDT locations nor their azimuth when smoothing the signal within the filtering radius. Hence, the isotropic filtering will attenuate the MDT signal near the current and filter the current signal into the surrounding ocean, which may lead to signal contamination and distortion. In this study, we set up a least squares-based (LS) approach to model MDT signal from the altimeter-derived MSS and geoid height using spherical harmonics from GGMs, where MDT is parameterized by Lagrange Basis Functions (LBFs). The design matrix is segmentally established, considering the error information of GGM in various spectral bands. Numerical experiments in the Gulf Stream show that applications of full error variance-covariance matrix or only diagonal error variance of GGM may have marginal effects on the MDT modeling. The MDT computed from this LS-based approach using the latest releases of Gravity Field and Steady-state Ocean Circulation Explorer (GOCE) geoid models, i.e., GO_CONS_GCF_2_DIR_R6 and Gravity Observation Combination 06s model (GOCO06s), have the best agreement with the comparison data, especially near the current region. Deduced geostrophic velocities based on the MDT solutions show that the LS-based approach recovers the current signal better than the Gaussian filtering by 1.8 cm/s. Estimated error map illustrates that errors are more concentrated near the coastal region.

1 Introduction

The mean dynamic topography (MDT) plays a very important role in ocean circulation, global climate change, and vertical datum unification (Le Traon et al., 2015; Woodworth et al., 2015). In the geodetic sense, the MDT is represented as the difference between the mean sea surface (MSS) and the geoid in a specific reference period, which emphasizes the importance of the accurate knowledge of MSS and geoid (Rio, 2004; Andersen and Knudsen, 2009; Knudsen et al., 2011).

Since the first operation of the altimetry satellite in 1970s, there have been more than 20 altimetry missions used for global sea level monitoring, giving a centimeter-level accuracy in the open ocean (Vignudelli et al., 2019; Donlon et al., 2021). The accumulation of satellite altimetry data over 20 years greatly refined the MSS (Hwang et al., 2002; Andersen and Knudsen, 2009). Consequently, the latest models such as Centre National d’Etudes Spatiales - Collect Localisation Satellites 2015 Mean Sea Surface model (CNES-CLS15MSS) (Schaeffer et al., 2016) and Danmarks Tekniske Universitet 2018 Mean Sea Surface model (DTU18MSS) (Andersen et al., 2018b), combining 20 years of altimetric data, can refine MSS at the spatial resolution down to 10 km. With the operation of the Gravity Recovery And Climate Experiment (GRACE) mission (Swenson and Wahr, 2002; Tapley et al., 2004) launched in 2002 and GRACE Follow-on (GRACE-FO) mission launched in 2018 (Flechtner et al., 2014; Landerer et al., 2020), especially the operation of the subsequent Gravity field and steady-state Ocean Circulation Explorer (GOCE) launched in 2009 (Drinkwater et al., 2003; Bock et al., 2014; Brockmann, 2014; Wu et al., 2017), the modeling accuracy and spatial resolution of the global gravity field have been improved unprecedentedly (Pail et al., 2010; Bruinsma et al., 2014; Tziavos et al., 2015). The GRACE and GRACE-FO missions have an initial orbit altitude of about 500 km and can accurately measure the long-wavelength of global gravity field signal, which made it possible for the first time to obtain reasonable MDT results relying solely on satellite gravity data (Vianna et al., 2007; Knudsen et al., 2011). In 2009, the European Space Agency (ESA) launched a GOCE mission that carried a gravity gradient payload for the first time (Drinkwater et al., 2003; Baur and Grafarend, 2006). With an orbit altitude of only ∼250 km, the GOCE mission can sense higher-frequency gravity field signal up to degree and order (d/o) ∼250. Currently, the maximum expansion of the Global Geopotential Model (GGM) based on pure GRACE gravity data is d/o ∼200 (Tapley et al., 2003; Mayer-Gürr et al., 2014; Kvas et al., 2019a), and due to the complementarity of gravity signal from the two gravity satellite missions, the pure satellite GGM integrating data from GRACE/GOCE can be expanded to d/o 300, corresponding to a spatial resolution of about 70 km.

The spatial resolution of GGM is still much lower than that of MSS (Bingham et al., 2014). MSS is furthermore given as a uniform grid over ocean, while GGM needs to be represented as the sum of global Spherical Harmonics (SHs), so the spectral content between MSS and GGM will not be completely matched (Bingham et al., 2008). Deriving the MDT by subtracting the two models will inevitably cause signal leakage problems. To resolve this, several researchers have utilized filtering in either space or spectral domains to obtain smooth MDT solutions by removing high-frequency information. The Gaussian filter, which is essentially an isotropic weighted low-pass filter, was first proposed by Jekeli (1981). It has been widely used in MDT modeling and the choice of filtering parameters has been discussed in detail (Knudsen et al., 2011; Siegismund, 2020). To avoid the signal contamination and attenuation caused by the isotropic filters, Bingham (2010) and Sánchez-Reales (2016) represent the filter as an anisotropic diffusion process reducing the MDT attenuation near currents.

In order to accurately determine a geodetic MDT and comprehensively analyze its error level, it is necessary to take into account the error information of input data in the MDT modeling. On the one hand, the commission error increases significantly with the expansion of GGM, which should be assessed and reweighted in the MDT modeling based on the error information of GGM. On the other hand, the error models of MSS and GGM could help to evaluate the formal errors of the MDT. However, the evaluation of the error characteristic of the MDT would still be hampered due to the filtering procedure; hence, methods that could evaluate errors of the MDT are presented in some studies (Bingham et al., 2014; Bai et al., 2020). For instance, Rio et al. (2011)and Rio et al. (2014) introduced an objective analysis method considering the variance-covariance and the correlation between observations for MDT modeling, which helps suppress the noise level in the MDT solution. Alternatively, Becker et al. (2012)and Becker et al. (2014) established a complete observation equation considering the error characteristics of MSS and GGM. As a result, a smooth MDT solution and its associated errors were estimated without any additional filtering procedure (Chambers et al., 2017).

Inspired by this approach, this study set up a Least Squares-based (LS) approach to combine MSS and GGM for MDT estimation, which avoids additional smoothing filters after the LS adjustment. The satellite-only GGMs are used for MDT modeling. Both the omission error and the commission error information of the GGM are considered segmentally and introduced into observation equations, so that a spectrally consistent MDT could be estimated in the LS system. The MDT solutions using full error variance-covariance information or diagonal error variance information of GGM in the MDT modeling are also compared. The effects of different choices of GGMs are investigated quantitively, and finally geostrophic velocities are validated. This paper starts with a brief introduction of the principle of the LS-based approach for MDT modeling. Section 2 introduces the research area and data used in this study. The construction of the complete observation equations and the weight matrices based on error information provided by input models is detailed in Section 3. Section 4 illustrates estimated MDT solutions based on the LS-based approach, where the effects of different choices of GGMs are analyzed. Deduced geostrophic current velocities are validated, subsequently. Finally, a brief conclusion is drawn in Section 5.

2 Data and Research Area

2.1 Research Area

Our research area is the Gulf Stream (15°N–55°N, 40°W–80°W) illustrated in Figure 1 [image is adapted from the General Bathymetric Chart of Oceans (GEBCO) world map 2014, www.gebco.net], with the distribution of ocean currents. The Gulf Stream is one of the strongest ocean currents in the world and has a significant influence on climate, mass/heat transportation, and ocean fishery (Rossby et al., 2010; Palter, 2015). Formed by the Coriolis force and the trade wind, the Gulf Stream originates from the North equatorial current and is obstructed by the American continent, which flows northward first and then eastward through the Gulf of Mexico, where the maximum speed could reach 2 m/s. When flowing in deep water, a large number of currents shed off from the main current, forming mesoscale eddies (Kang and Curchitser, 2013). As a result, the variation of the MDT around the Gulf Stream is complex, leading to a difficulty in the MDT signal recovery from the geodetic approach (Rio, 2004; Klymak et al., 2016). On the other hand, the complexity of the currents in this area provides favorable conditions for validating the MDT modeling algorithm, especially its performance near current and coast, leading to the Gulf Stream becoming a hot spot in MDT research.

FIGURE 1

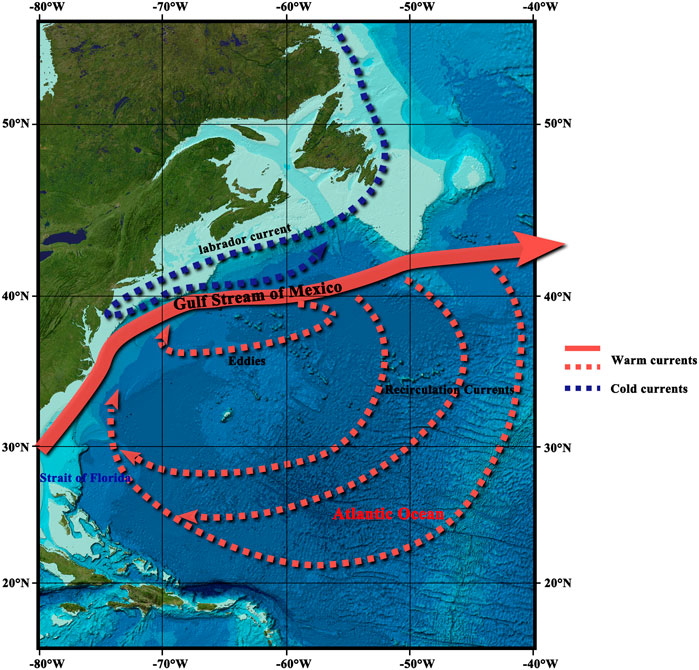
FIGURE 1. The research area and the distribution of the Gulf Stream (image is adapted from the GEBCO world map 2014, www.gebco.net).

2.2 MSS and GGM

In order to accurately separate the MDT signal from MSS and GGM, the latest MSS of CNES-CLS15MSS is introduced for modeling (Schaeffer et al., 2016; Pujol et al., 2018), where 20 years of altimetric data from 1993 to 2012 are assimilated. The CNES-CLS15MSS is represented on a 1/8° spatial resolution grid. The reference time period is 1993–2012, and the reference ellipsoid is the World Geodetic System 1984 (WGS84).

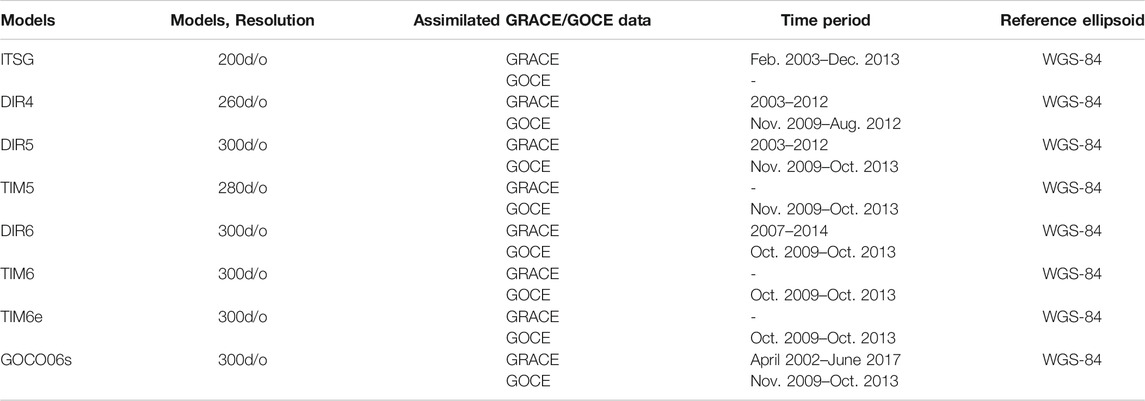
The ITSG-Grace2014s GGM (ITSG), published by the Graz University of Technology, provides full error variance-covariance information that can be conducive to the investigation of the commission error modeling (Mayer-Gürr et al., 2014). However, the ITSG is a GRACE-only GGM with a maximum expansion of d/o 200, which will be a limitation in the MDT modeling, spectrally (Table 1). In the following the ITSG model will be called the “GRACE-only GGM.” In addition, with the completion of a GOCE mission, the accuracy of GGM based on satellite-only gravimetric data has been unprecedently improved, especially in the open ocean. Therefore, the Gravity Observation Combination 06s model (GOCO06s) that provides full error variance-covariance matrix is also introduced for MDT modeling (Kvas et al., 2019b).

TABLE 1

TABLE 1. The summary of the GGMs.

ESA has released six releases of direct GGM solutions based on GRACE/GOCE gravity data, where the fourth-release (GO_CONS_GCF_2_ DIR_R4, DIR4), the fifth-release (GO_CONS_GCF_2_DIR_R5, DIR5), and the sixth-release (GO_CONS_GCF_2_DIR_R6, DIR6) are introduced for MDT modeling. Notably, the DIR6 recalibrates the satellite orbits compared to the DIR5 (Förste et al., 2019). Besides, in order to better assess the performance of the LS-based approach in the MDT estimation, the timewise solutions that only assimilated GOCE data, including the fifth-release (GO_CONS_GCF_2_TIM_R5, TIM5) and the sixth-release (GO_CONS_GCF_2_TIM_R6, TIM6, and GO_CONS_GCF_2_TIM_R6e, TIM6e), are also introduced for MDT estimation. In the following the releases of GOCE GGM will be called the “GOCE-based GGM.” Table 1 summarizes more detailed information about these GGMs.

In addition, the XGM 2019e_2159 combined GGM (Zingerle et al., 2020), provided by Technical University of Munich, is introduced as the complementary information in the weight matrix construction in the LS-based approach. The reason for choosing XGM 2019e_2159 is that the XGM 2019e_2159 assimilated the latest Altimetry data, satellite gravity data, and ground data for modeling, which could be expanded up to 2190d/o. And comparing with the other high d/o GGMs e.g., EIGEN6c4 (Förste et al., 2014) or EGM 2008 (Pavlis et al., 2012), the XGM 2019e_2159 shows a better performance in the ocean, especially in the coastal regions (Zingerle et al., 2020).

This study introduces GOCE-based GGMs, including DIR4, DIR5/TIM5, DIR6/TIM6/TIM6e, and GOCO06s, to evaluate the contribution of GOCE-based gravimetric data for MDT modeling. Notably, all MSS and GGMs are unified to the tide-free and WGS84 reference ellipsoid.

2.3 Synthetic MDT

In order to assess the performance of estimated MDT, the latest Centre National d’Etudes Spatiales - Collect Localisation Satellites 2018 Mean Dynamic Topography model (CNES-CLS18MDT, CLS18) and the Danmarks Tekniske Universitet 2017 Mean Dynamic Topography model (DTUc17MDT, DTU17) with their associated geostrophic velocity fields are introduced for comparison and validation (Knudsen et al., 2021; Mulet et al., 2021). The CLS18 utilized CNES-CLS15MSS and GOCO05S for modeling. All drifting buoy velocities and hydrological profiles from 1993 to 2017 are assimilated in CLS18 for current signal augmentation. Estimated error of the CNES-CLS18 could reach ∼10 cm around current areas and down to ∼2 cm in the other areas (Mulet et al., 2021). The DTU17 has been developed using the DTU15MSS as MSS, and EIGEN-6C4 for geoid modeling. Drifter data from 1992 to 2015 are assimilated in the DTU17, and the quasi-gaussian filter (Knudsen et al., 2021) was implemented to best fit the velocities of oceanographic drifting buoys. The estimated errors of the DTU17cMDT range from a few centimeters to a few decimeters, and they exceed 20 cm in areas of the major ocean currents (Knudsen et al., 2021). The reference period of both CLS18 and DTU17 is 1993–2012, with the spatial resolution of 1/8°. Table 2 shows more details about these two models. In this study, we take geostrophic velocity fields provided by CLS18 and DTU17 as validation data, considering that both models assimilated a large amount of in-situ data. A synthetic MDT model (Synthetic_MDT) and associated geostrophic velocity field (Synthetic_Current) were calculated from the average of the CLS18 and DTU17 for comparison and validation.

TABLE 2

TABLE 2. | The summary of the MDT models.

2.4 Gaussian Filtered MDT

The Gaussian filtered MDT will also be introduced for comparison in this study, which is derived based on a direct solution combining GGM and CNES-CLS15MSS. In this study, the same GGM information are introduced to estimated MDT and the Gaussian filtered MDT to ensure that the content between the two MDT solutions is comparable. The Gaussian filter used in this study is introduced from Jekeli (1981) and Wahr et al. (1998). The MDT values ($\mathrm{X}$) could be Gaussian filtered by

${\widehat{X}}_i=\mathbf{W}\cdot \mathbf{X}/\sum \left(\mathbf{W}\right)(1)$

where ${\widehat{X}}_i\left(i=\mathrm{1,2,3},\mathrm{...}\right)$ represents the filtered MDT value and $\mathrm{W}$ represents the weighting vectors. The weighting factors read based on Wahr et al. (1998) as

$\mathbf{W}\left(\alpha \right)=\frac{\mathbf{b}\cdot \exp \left[-\mathbf{b}\left(1-\cos \left(\alpha \right)\right)\right]}{2\pi \cdot \left(1-e^{-2\mathbf{b}}\right)}(2)$

$b=\frac{\ln \left(2\right)}{1-\cos \left(R_{filter}/\alpha \right)}(3)$

where $\alpha$ and $R_{filter}$ represents the spherical distance of the MDT point and the filtering radius (m). The filtering radius ($R_{filter}$) for the Gaussian filtered MDT is given as (Barthelmes, 2013):

$R_{filter}=20000000/l_{\max }(4)$

where $l_{max}$ denotes the max degree of the expansion of SHs.

3 Methodology

We initially set up an LS-based approach to separate MDT signal from MSS and GGM. The key point is the establishment of a complete observation equation and the associated weight matrix, which will prominently influence the separation of MDT signal from MSS and GGM. Here, we express GGM and MDT in the spatial domain, which is given as (Bingham et al., 2008)

$MSS\left(\theta ,\lambda \right)=Geoid\left(\theta ,\lambda \right)+MDT\left(\theta ,\lambda \right)(5)$

where $\theta$ and $\lambda$ represent the latitude and longitude in spherical coordinate system, respectively. Equation 5 illustrates the model used for MDT reconstruction, and the geoid and the MDT should be parameterized in a uniform grid. Consequently, the geoid is expanded based on a series of SHs, which is given as

$Geoid\left(\theta ,\lambda \right)=\frac{GM}{R\gamma \left(B\right)}{{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{m=0}^n\left(\frac{R}{r}\right)}}}^{n+1}{\overline{P}}_{nm}\left(\cos \theta \right)\left({\overline{C}}_{nm}\cos \left(m\lambda \right)+{\overline{S}}_{nm}\sin \left(m\lambda \right)\right)(6)$

where $GM$ represents the gravitational constant times the Earth’s mass, $R$ denotes the Earth’s radius, $\gamma \left(B\right)$ denotes the normal gravity at geodetic latitude $B$, ${\overline{P}}_{nm}\left(\cos \theta \right)$ denotes the fully normalized Legendre polynomial at degree $n$ and order $m$, and ${\overline{C}}_{nm},{\overline{S}}_{nm}$ is the corresponding Stokes coefficients.

In addition, the MDT is parameterized by the Lagrange Basis Function (LBF) (Becker et al., 2012):

$MDT\left(\overline{\theta },\overline{\lambda }\right)={\displaystyle \sum _{k\in K}{a}_k{b}_k\left(\overline{\theta },\overline{\lambda }\right)}(7)$

where K represents the number of basis function $b_k$ and $a_k$ represents the MDT values at nodes $\left(\overline{\theta },\overline{\lambda }\right)$.

Due to the computer limitation, LBF with 4 parameters was used to interpolate the MDT in this study, despite the recommendation to use 16 parameters in Shi et al. (2020). MSS and GGM are extracted on a 0.5° grid, respectively, in order to reduce the correlation between the grids. For each unknown MDT point, the four points around it in the 0.5° grid are found, and a local coordinate system in this 4-points-rectangle is established. Then, the unknown MDT value in this local system is calculated based on the interpolation using LBF with 4 parameters. Finally, all the unknown MDT values can be parameterized by LBF, and the parameter coefficient matrix (${\mathrm{A}}_{mdt}$) is derived. More details of the MDT parameterization can be seen in Supplementary Appendix SA, Becker et al. (2012), and Shi et al. (2020). Equation 5 can be rewritten as

$\mathbf{MSS}+\mathbf{v}=\left[\begin{array}{cc}{\mathbf{A}}_{cs}& {\mathbf{A}}_{mdt}\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{cs}\\ {\mathbf{x}}_{mdt}\end{array}\right](8)$

where $\mathbf{v}$ represents the residuals derived from the LS system, and ${\mathrm{x}}_{cs}$ and ${\mathrm{x}}_{mdt}$ denote the unknown SH coefficients and the MDT values, which should be estimated based on the LS theory. The determination of ${\mathrm{A}}_{cs}$ and ${\mathrm{A}}_{mdt}$ can be seen in Supplementary Appendix SB.

In this study, we investigate the use of the satellite-only GGM. In principle, SHs from d/o 2 to ∞ should be used for expression of the geoid. However, the Signal to Noise Ratio (SNR) of GGM will decrease with the increase of the expansion of GGM (Tsoulis and Patlakis, 2013; Bruinsma et al., 2014). Consequently, we segmentally construct observation equation and the weight matrix based on the error information provided by GGMs.

The expression of GGM is split into three parts and processed accordingly. The first parameters group of SHs ($cs1$) represents SHs from d/o 2 to an appropriate cut-off frequency of GGM (e.g., where SNR>1), the second group ($cs2$) serves as a buffer between $cs1$ and $cs3$, and the third group ($cs3$) where no GGM information is available expands SHs from max d/o of $cs2$ to infinity d/o, hence:

$\mathrm{MSS}+\mathrm{v}=\left[\begin{array}{cccc}{\mathrm{A}}_{cs\mathbf{1}}& {\mathrm{A}}_{cs\mathbf{2}}& {\mathrm{A}}_{cs\mathbf{3}}& {\mathrm{A}}_{mdt}\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{cs\mathbf{1}}\\ {\mathbf{x}}_{cs\mathbf{2}}\\ {\mathbf{x}}_{cs\mathbf{3}}\\ {\mathbf{x}}_{mdt}\end{array}\right](9)$

In order to better extract the MDT signal from MSS and GGM, more smoothing conditions and a priori information should be added, which will be discussed in the following sub-sections.

3.1 The Construction of the Weight Matrix

We directly introduce SH coefficients ${\overline{C}}_{nm},{\overline{S}}_{nm}$ of GGM as a priori information for $cs1$, which is given as

$\mathbf{GG}{\mathbf{M}}_{cs\mathbf{1}}+{\mathrm{v}}_{cs\mathbf{1}}={\mathrm{x}}_{cs\mathbf{1}}(10)$

Here, the variance information provided in GGM (${\mathrm{K}}_{cs1}$) is considered as error models in the LS system. Accordingly, the commission error introduced by GGM would be reweighted and suppressed in the LS system.

The smoothness information should be introduced through pseudo-observation considering the SNR of GGM. Supposing that the random variables are normally distributed, the degree-wise variance function of the SH coefficients can be expressed based on Kaula’s rule (Kaula, 1966):

${\sigma }_n^2={10}^{-10}\frac{2n+1}{n^4}(11)$

where ${\sigma }_n^2$ represents the variance information at degree n.

The smoothness information is introduced in $cs2\mathbf{and}cs3$, and the variance matrix results in

${\mathbf{K}}_{cs}^{smooth}=\left[\begin{array}{cc}{\mathbf{K}}_{cs\mathbf{2}}^{smooth}& \\ & {\mathbf{K}}_{cs\mathbf{3}}^{smooth}\end{array}\right](12)$

Consequently, the pseudo-observation equations can be expressed as

$\left[\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right]+\left[\begin{array}{c}{\mathbf{v}}_{smooth\mathbf{2}}\\ {\mathbf{v}}_{smooth\mathbf{3}}\end{array}\right]=\left[\begin{array}{cc}\mathbf{I}& \\ & \mathbf{I}\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{cs\mathbf{2}}\\ {\mathbf{x}}_{cs\mathbf{3}}\end{array}\right](13)$

In the combination of MSS and GGM, the main obstruction is the limited spatial resolution of GGM. Consequently, information from $cs3$ is usually neglected or set to zero, and a spatial or spherical filter is introduced for smoothing (Knudsen et al., 2011; Ke et al., 2019). Hence, considering the omission errors of GGM, the combined MDT would suffer from a serious signal leakage problem. As a result, it is important to consider the error information for $cs3$ for a spectral consistent MDT.

In our approach, $cs3$ is treated separately (Eq. 9),

$\mathbf{MSS}+\mathbf{v}=\left[\begin{array}{ccc}{\mathbf{A}}_{\mathbf{c}\mathbf{s}\mathbf{1}}& {\mathbf{A}}_{\mathbf{c}\mathbf{s}\mathbf{2}}& {\mathbf{A}}_{\mathbf{m}\mathbf{d}\mathbf{t}}\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{\mathbf{c}\mathbf{s}\mathbf{1}}\\ {\mathbf{x}}_{\mathbf{c}\mathbf{s}\mathbf{2}}\\ {\mathbf{x}}_{\mathbf{m}\mathbf{d}\mathbf{t}}\end{array}\right]+{\mathbf{A}}_{\mathbf{c}\mathbf{s}\mathbf{3}}\cdot {\mathbf{x}}_{\mathbf{c}\mathbf{s}\mathbf{3}}(14)$

where $\mathbf{S}={\mathbf{A}}_{cs3}\cdot {\mathbf{x}}_{cs3}$ is the signal from $cs3$, thus,

$\overline{\mathbf{MSS}}+\mathbf{v}=\left[\begin{array}{ccc}{\mathbf{A}}_{cs\mathbf{1}}& {\mathbf{A}}_{cs\mathbf{2}}& {\mathbf{A}}_{mdt}\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{cs\mathbf{1}}\\ {\mathbf{x}}_{cs\mathbf{2}}\\ {\mathbf{x}}_{mdt}\end{array}\right](15)$

where $\mathbf{MSS}=\mathbf{MSS}-\mathbf{S}$. In this study, the discrepancy between XGM 2019e_2159 (Zingerle et al., 2020) and GGM used in the LS-based approach as the diagonal variance information of $\mathbf{MSS}$ (${\mathbf{K}}_{\mathbf{MSS}}$).

${\mathbf{K}}_{\overline{\mathbf{MSS}}}={\left(\mathbf{GG}{\mathbf{M}}_{xgm19}-\mathbf{GG}{\mathbf{M}}_{satellite-only}\right)}^{\mathbf{2}}\cdot \mathbf{I}(16)$

3.2 The Additional Smoothness Information

In order to derive a slightly smoother MDT and associated geostrophic current velocity field, additional smoothness information needs to be supplemented in the observation equation. In this study, we try to minimize the norm of the gradient of the MDT (Becker et al., 2014). The parameterization matrix of the MDT part in Eq. 8 can be expressed as

$\mathbf{MDT}={\mathbf{A}}_{mdt}\cdot {\mathbf{X}}_{mdt}(17)$

where ${\mathbf{A}}_{mdt}$ denotes the parameterization matrix based on LBF. The derivative of the parameterized MDT in zonal ($\nabla {\mathbf{A}}_x$) and meridian ($\nabla {\mathbf{A}}_y$) direction can be expressed as

$\begin{array}{c}\nabla \mathbf{MDT}=\nabla \left({\mathbf{A}}_{mdt}\cdot {\mathbf{X}}_{mdt}\right)\\ =\left(\begin{array}{c}\nabla {\mathbf{A}}_x\\ \nabla {\mathbf{A}}_y\end{array}\right){\mathbf{X}}_{mdt}\end{array}(18)$

Hence, the smoothing information that could reduce the norm of the MDT gradient could be supplemented in observation equation by

$\left[\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right]+\left[\begin{array}{c}{\mathbf{v}}_{md{t}_x}\\ {\mathbf{v}}_{md{t}_y}\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{l}\mathbf{0}\\ \mathbf{0}\end{array}& \begin{array}{l}\mathbf{0}\\ \mathbf{0}\end{array}& \begin{array}{l}\nabla {\mathbf{A}}_x\\ \nabla {\mathbf{A}}_y\end{array}\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{cs\mathbf{1}}\\ {\mathbf{x}}_{cs\mathbf{2}}\\ {\mathbf{x}}_{mdt}\end{array}\right](19)$

3.3 The Complete Observation Equation

This study expresses MSS as the combination of the MDT and the geoid, where the geoid is represented as a sum of SH functions and the associated error information provided by GGM is introduced in the modeling. The MDT is parameterized and estimated in a LS system, and observation equations are segmentally established considering the SNR of GGM. It is notable that Eq. 9 may suffer from ill-condition problem, since the SH coefficients are introduced in observation equations. Also, the estimated MDT using the LS-based approach may be coarse, due to the noises introduced from the MDT parameterization and the weight matrix. Therefore, the SH coefficients of the satellite-only GGM (Eq. 10) and the gradient term of the MDT (Eq. 19) are introduced in this study as constraints to help derive a reasonable MDT solution. In the end, the complete observation equation with its weight matrix can be expressed as

$\left[\begin{array}{c}\mathbf{MSS}\\ \mathbf{GG}{\mathbf{M}}_{cs1}\\ \mathbf{0}\\ \mathbf{0}\\ \mathbf{0}\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{A}}_{cs1}& {\mathbf{A}}_{cs2}& {\mathbf{A}}_{mdt}\\ \mathbf{I}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \nabla {\mathbf{A}}_x\\ \mathbf{0}& \mathbf{0}& \nabla {\mathbf{A}}_y\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{cs1}\\ {\mathbf{x}}_{cs2}\\ {\mathbf{x}}_{mdt}\end{array}\right](20)$

$\mathbf{P}=\left[\begin{array}{ccccc}{\mathbf{K}}_{\overline{MSS}}^{-1}& & & & \\ & {\mathbf{K}}_{cs1}^{-1}& & & \\ & & {\mathbf{K}}_{\mathbf{cs2}}^{smooth-1}& & \\ & & & {\mathbf{K}}_I^{-1}& \\ & & & & {\mathbf{K}}_I^{-1}\end{array}\right](21)$

Therefore, observation equation can be solved by the weighted LS method:

$\widehat{\mathbf{x}}={\left({\mathbf{A}}^T\mathbf{PA}\right)}^{-1}{\mathbf{A}}^T\mathbf{PL}(22)$

where $\widehat{x}$ represents the unknown parameters in Eq. 20, and $\mathbf{A},\mathbf{P}$ represent the design matrix and the weight matrix, respectively. However, this study focuses on the estimation of the MDT parameters (${\mathbf{x}}_{mdt}$), so the calculation of Eq. 22 is time consuming and may lead to ill-condition problems. Hence, the Schur decomposition (Lawson and Hanson, 1995) is introduced to help solve the solution. Supplementary Appendix SC shows more information about the derivation of the ${\mathbf{x}}_{mdt}$. As a result, this approach avoids introduction of additional filtering procedure after the LS adjustment and is expected to retain more detailed signal. Further, the posterior variance of the MDT solution can also be estimated by error propagation. This is beneficial to further assimilation by combining information such as ocean numerical data (Freiwald, 2013; Rio et al., 2014).

4 Results

The performance of the LS-based MDT modeling approach is evaluated in the Gulf Stream area (Figure 1). We first investigate the importance of the full variance-covariance information of GGM in the MDT modeling, where GRACE-only GGM and GOCE-based GGM are used. Then, we study the effect of gravity signal in the modeling of MDT using the latest seven releases of GOCE-based GGMs, and estimated errors of the MDT solutions will be analyzed and assessed. Effects of different choices of the cut-off frequency for $cs\mathbf{1}$ will be investigated.

4.1 Importance of the Full Error Variance-Covariance Matrix

As for GRACE-only GGM (ITSG), the choice of the cut-off frequency for segmentation is $cs\mathbf{1}$: d/o 2–160, $cs\mathbf{2}$: d/o 161–180, while the choice of the cut-off frequency for GOCE-based GGM (GOCO06s) is $cs\mathbf{1}$: d/o 2–260, $cs\mathbf{2}$: d/o 261–280. The selection of $cs\mathbf{1}$ is based on the SNR of GGMs (SNR>1), while the selection of $cs\mathbf{2}$ is obtained by trial-and-error analysis. It is notable that signal of the discrepancy between ITSG/GOCO06s and XGM 2019e_2159 is treated as the variance information of $\mathbf{MSS}$ in observation equation, respectively. Considering the cut-off frequency of $cs\mathbf{1}$, the radius of the Gaussian filtered MDT is chosen as 1.1° (∼125 km) for ITSG, and 0.65° (∼75 km) for GOCO06s, based on Eq. 4. The MDT solutions with 1° resolution are estimated and compared in the following experiment.

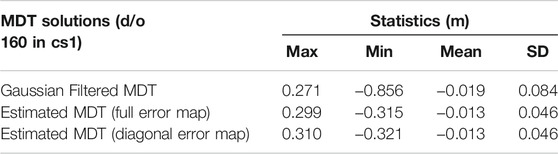
Full error variance-covariance matrix and diagonal error variance matrix from ITSG and GOCO06s are introduced in the LS system, respectively, and the corresponding solutions are compared. The MDT solutions estimated using ITSG are shown in Figure 2. Figure 2A is the Synthetic_MDT, Figures 2B–D are the Gaussian filtered MDT, the estimated MDT with full error information, and diagonal error information of GGM, respectively. Misfits between MDT solutions against the Synthetic_MDT are also illustrated in Figure 2, where Figures 2E–G are the corresponding misfits between Figures 2B–D against the Synthetic_MDT, respectively. The statistics are shown in Table 3. Notice that the land area is ignored in this experiment.

FIGURE 2

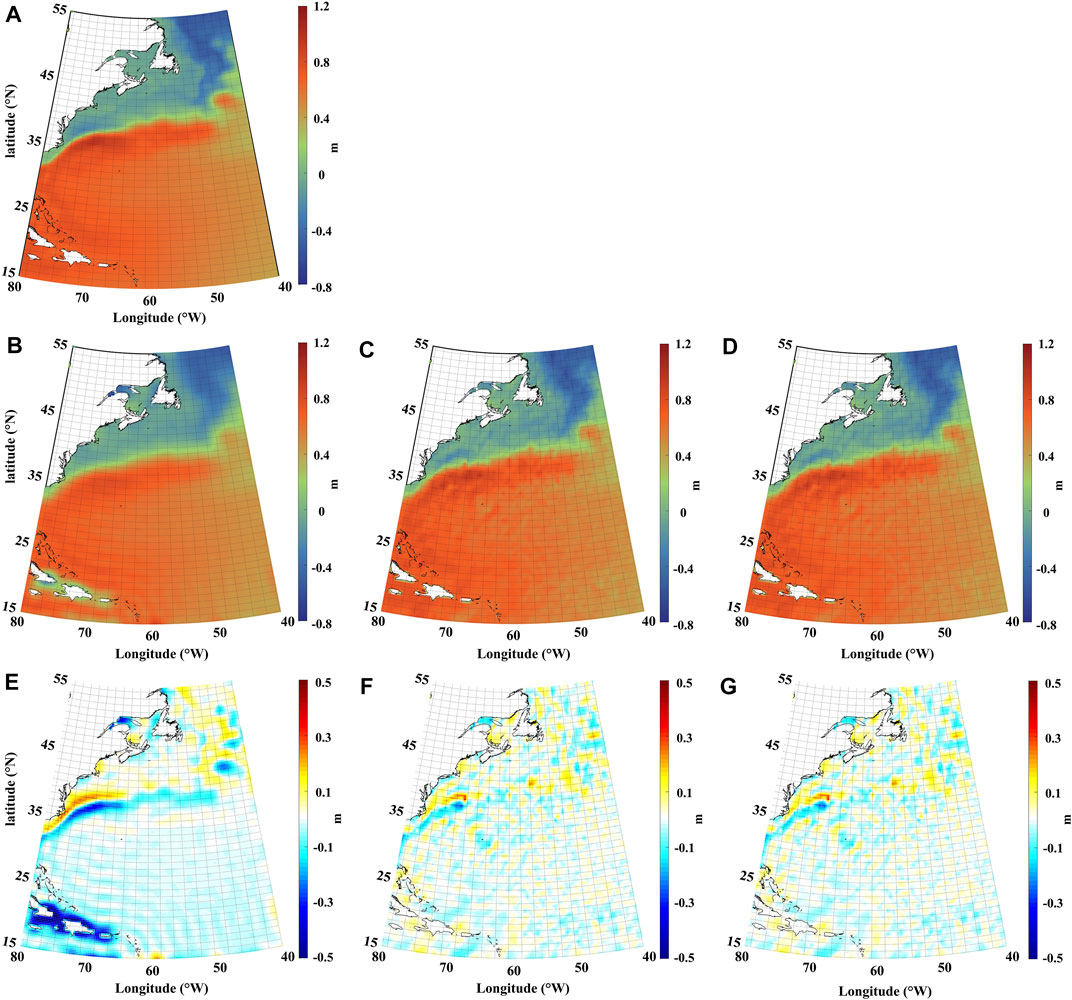
FIGURE 2. (A) the Synthetic_MDT; (B) the Gaussian filtered MDT; estimated MDT with (C) full error information, and (D) diagonal error information of GGM; and (E–G) are the corresponding misfits between (B–D) against the Synthetic_MDT, respectively.

TABLE 3

TABLE 3. Statistics of misfits between MDTs using ITSG against the Synthetic_MDT.

All MDTs provide reasonable solutions, with similar patterns of the signal distribution. Specifically, bounded by the Gulf Stream (Figure 1), the MDT in its southern part is above 0.4 m, while the MDT in the northern part is below 0.4 m. Also, it can be seen from Figure 2A, that the variation of the MDT around (38°N/70°W) is more than 1 m, and we will take it as a comparison point in this study. The MDTs derived by the two approaches could reach the level of -0.8–1.2 m in the research area. The Gaussian filtered MDT is apparently smoother than estimated MDT, while there is sharper signal in the estimated solution. The reason is that the Gaussian filter operates an isotropic spatial weighting average procedure to the signal for a smoother solution (Bingham, 2010). On the contrary, there are no additional filters introduced in estimated MDT after the LS adjustment.

As can be seen from Figures 2E–G, misfits of all three MDT solutions can reach the level of ±0.5 m. However, their distribution is different. Misfits between the Gaussian filtered MDT and the Synthetic_MDT in Figure 2E show a clear signal leakage, especially near the current and the coastal area. Specifically, the signal near current is weakened for about 0.3 m. This is because the isotropic filtering causes attenuation of the MDT gradient signal, resulting in a large discrepancy between the MDT solution and the Synthetic_MDT. The loss of the signal will have an influence not only on the model accuracy but also on further investigation in ocean currents.

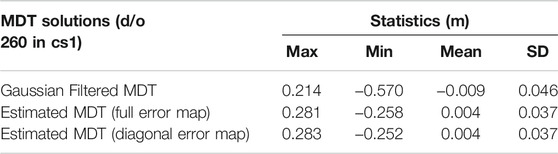
In addition, Figures 3A–C show misfits between Gaussian filtered MDT, estimated MDT with full error information, and diagonal error information of GOCO06s, against the Synthetic_MDT, respectively. The statistics are shown in Table 4. Apparently, the improvement in GOCE-based MDTs is significant compared with the GRACE-only MDT, where the SD of misfits decreases from 0.046 m (ITSG) to 0.037 m (GOCO06s). It is seen from Figure 3B that there are high-frequency misfits along 38°N in the estimated MDT, but it’s apparently better suppressed comparing with that in Figure 2F using the GRACE-only GGM, which is the contribution of GOCE signal.

FIGURE 3

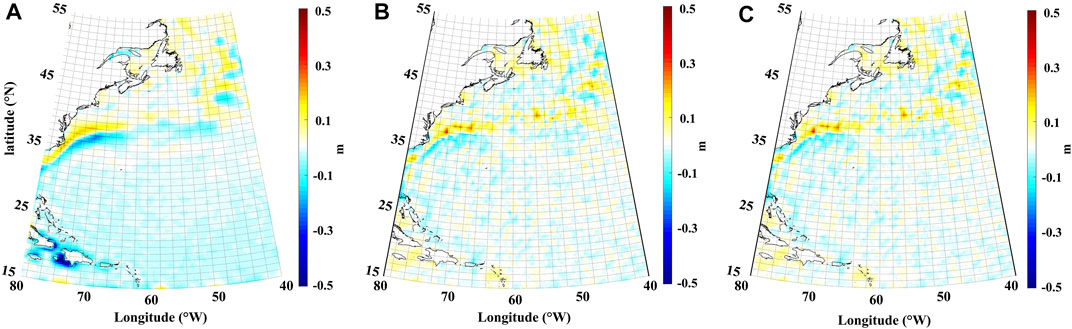
FIGURE 3. Misfits between estimated MDTs using GOCO06s against the Synthetic_MDT. [(A) Gaussian filtered MDT, (B) estimated MDT with full error information of GGM, and (C) diagonal error information of GGM, against the Synthetic_MDT. The $cs1$ is d/o 260.]

TABLE 4

TABLE 4. Statistics of misfits between MDTs using GOCO06s against the Synthetic_MDT.

However, both results obtained from ITSG and GOCO06s show that there are only marginal differences between the MDT solutions using full error variance-covariance of GGM and using only diagonal error variance information for error modeling. Statistics show a maximum difference of 0.6 cm between these two MDT solutions, with a SD of ∼0.05 cm. This is likely because the diagonal elements of SHs coefficients play a major role in GGM signal (Gruber, 2001; Ran et al., 2021). Consequently, only the diagonal error variance information of GGM will be considered in the following MDT modeling using GOCE-based GGM in the next section.

Comparing with the Synthetic_MDT, both the Gaussian filtered solution and estimated MDT solution will show signal attenuation near the current. For example, alternating positive and negative misfits are seen around 30°N–38°N, which is induced by the over-smooth in the Gaussian filtering or the smoothness condition in the LS system. The estimated MDT recovers more signal than the Gaussian filtered one. Misfits of the estimated MDTs (Figures 2F, 3B) around 30–38°N are significantly smaller compared with the Gaussian filtered solution (Figures 2E, 3A). Statistics in Tables 3, 4 show that, although the SD of misfits between Gaussian filtered MDT and the Synthetic_MDT decreases from 0.084 m (ITSG) to 0.046 m (GOCO06s), the MDT estimated by the LS-based approach are still a better fit with the Synthetic_MDT. The SD of misfits between the estimated MDTs and the Synthetic_MDT decreases from 0.046 m (ITSG) to 0.037 m (GOCO06s). In addition, the signals around the coast in the southwestern part of the research area are better recovered than the Gaussian filtered solution, indicating the superiority of the LS-based approach in the MDT modeling.

4.2 Improved GOCE-Based GGMs

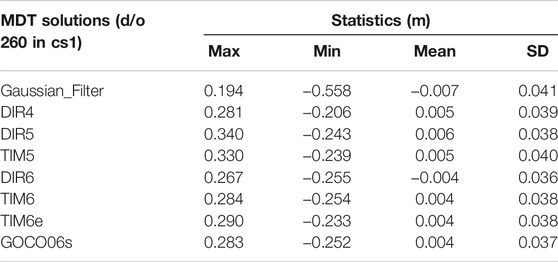
In order to further assess the performance of GOCE-based GGMs in MDT estimation, seven GOCE-based GGMs (i.e., DIR4, DIR5/TIM5, DIR6/TIM6/TIM6e, and GOCO06s) are investigated, and their MDT solutions are compared. The strategies for MDT modeling are the same as in Section 4.1. Considering the SNR of the GGMs, the cut-off frequency for $cs\mathbf{1}$ is chosen as d/o 2–260, and $cs\mathbf{2}$ is chosen as d/o 261–280. Again, the signal using the difference between GOCE-based GGMs and XGM 2019e_2159 are treated as the variance information of $\mathbf{MSS}$ in observation equation. The filtering radius for the Gaussian filtered MDT is 0.65° based on Eq. 4, where $cs\mathbf{1}$ of the DIR6 and the CNES-CLS15MSS are used. Notice that only the diagonal error variance information of GGM is used in this experiment.

Figure 4 shows misfits between the MDT solutions using (A) Gaussian filtering, (B) DIR4, (C) DIR5, (D) TIM5, (E) DIR6, (F) TIM6, (G) TIM6e, and (H) GOCO06S, against the Synthetic_MDT, respectively. The statistics of misfits between the estimated MDT and the Synthetic_MDT are shown in Table 5. The Gaussian filtered MDT still suffers from the severe signal leakage problem near the current and coast region in the southwestern part of the research area. For instance, misfit around 38°N/70°W is ∼±0.1 m in the estimated solutions, while it increases to ∼±0.2 m in the Gaussian filtered solution. The statistics in Table 5 show that the SD of misfits of the MDT solutions using DIR4, DIR5/TIM5, DIR6/TIM6/TIM6e, and GOCO06s is 0.039, 0.038/0.040, 0.036/0.038/0.038, and 0.037 m, respectively. The SD of misfits of the Gaussian filtered MDT increases to 0.041 m. The statistics of misfits show that the estimated MDT using GOCO06s and DIR6 perform the best in this study. However, the MDT based on DIR6 only shows 0.3 cm better agreement with the Synthetic_MDT than that based on DIR4. Besides, when comparing with the same release of the GGM, the estimated MDT using direct GGM solution shows better performance than the timewise GGM solution. For example, the SD of misfits of the estimated MDT using TIM6 show ∼0.2 cm larger than the MDT using DIR6. Estimated errors are deduced based on the error propagation using DIR6, shown in Figure 5, where $cs\mathbf{1}$ is d/o 260. It is seen that most of estimated errors are found near the coast region, especially in the southwestern part of the research area. Statistically, estimated errors (SD) reach ∼0.1 m near the coast area, while they reduce to less than 0.05 m in most of the open sea.

FIGURE 4

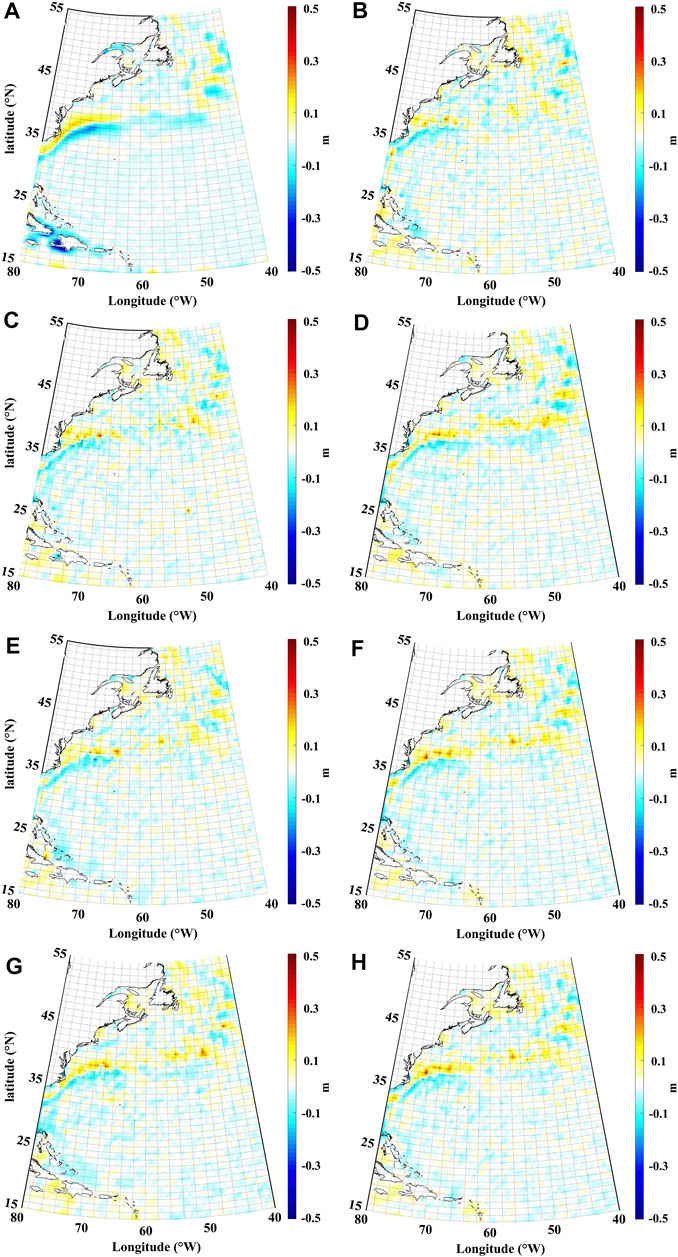
FIGURE 4. Misfits between estimated MDTs against the Synthetic_MDT. (The MDT solutions using (A) Gaussian filtering, (B) DIR4, (C) DIR5, (D) TIM5, (E) DIR6, (F) TIM6, (G) TIM6e, and (H) GOCO06s, against the Synthetic_MDT, respectively. The $cs1$ is d/o 260.)

TABLE 5

TABLE 5. Statistics of misfits between GOCE-based MDTs against the Synthetic_MDT.

FIGURE 5

FIGURE 5. Estimated errors based on DIR6 with $cs1$ of d/o 260.

Further, the effect of different choices of the cut-off frequency for $cs\mathbf{1}$ is investigated, and the SD of misfits between the MDT solution using DIR6 against Synthetic_MDT is shown in Figure 6, where $cs\mathbf{1}$ is selected from d/o 180 to d/o 300 with a step of 10 d/o, corresponding to the expansion of DIR6. The blue dash-line and the orange dash-line in Figure 6 shows the improvement of MDTs using LS-based approach and Gaussian filtering with different choices of $cs\mathbf{1}$. The SD of misfits of estimated MDT solution is always smaller than the Gaussian filtered one, and it decreases gradually with the increase of $cs\mathbf{1}$ and the curve of the SD converges at d/o 260, where the SD of misfits is ∼0.036 m. Misfits for the Gaussian filtered MDTs rapidly decrease from ∼0.070 m (d/o 180) to ∼0.039 m (d/o 300). This is due to the signal contribution from GGM with increasing cut-off frequency. However, the curve of the SD starts to converge after the expansion of d/o 260, and the SD of misfits is improved by less than 1 mm when the expansion of $cs\mathbf{1}$ exceeds d/o 260. The reason for this may be because the SNR of GGM is getting close to 1 with the increase of the expansion, and thus less signal is introduced in the modeling (Bruinsma et al., 2014).

FIGURE 6

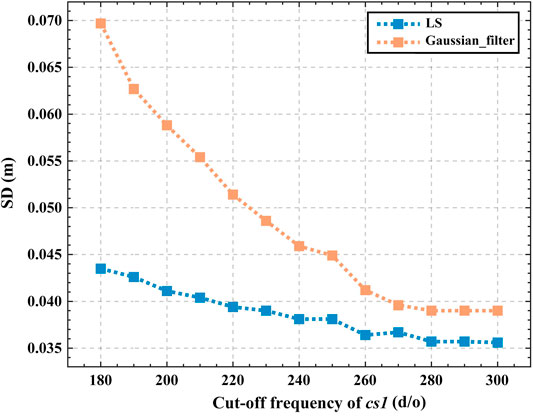
FIGURE 6. The SD of misfits under different cut-off frequency of $cs1$. (The LS represents estimated MDT solution based on the DIR6 GGM; The Gaussian_filter represents the Gaussian filtered solution based on DIR6 GGM.)

4.3 Geostrophic Current Validation

Geostrophic current velocities are calculated based on estimated MDT and the Gaussian filtered MDT, where DIR6 in d/o 260 is used in the calculation. The MDT signal may be smoothed out from the coast or current, and into the surrounding ocean due to filtering, causing current signal attenuation. Accordingly, it is necessary to utilize geostrophic current data for validating deduced geostrophic current using estimated MDT and the Gaussian filtered MDT. Geostrophic current velocities can be given as (Lagerloef et al., 1999):

$u=-\frac{g}{fR}\frac{\partial MDT}{\partial \varphi },v=\frac{g}{fR\cos \varphi }\frac{\partial MDT}{\partial \lambda }(23)$

where u and v denote the eastward and the northward component of geostrophic current velocity, respectively. $f$ denotes the Coriolis force coefficient, and $R\mathbf{,}\varphi \mathbf{,}\lambda \mathbf{,}\mathbf{and}\mathbf{g}$ denote the mean radius of the Earth, the latitude, the longitude, and the acceleration due to gravity, respectively.

In the top panel of Figure 7, estimated geostrophic currents deduced from different MDT solutions are illustrated, where Figures 7A–C represent the geostrophic current derived from Synthetic_Current, estimated MDT, and Gaussian filtered MDT, respectively. And in the bottom panel of Figure 7, misfits between deduced geostrophic current against the Synthetic_Current are illustrated, where Figures 7D,E represent misfits from the estimated MDT (DIR6) and Gaussian filtered MDT, respectively. The Synthetic_Current can reach the level of 0.5–1.0 m/s in the research area, while results obtained from estimated MDT and Gaussian filtered MDT in Figures 7B,C are weaker by 0.3–0.5 m/s. There are two main reasons for this signal attenuation. First, geostrophic velocity information from Synthetic_Current assimilated a large number of in-situ measurements to enhance the current signal in the model. In addition, the expansion of GGM and the imposed spatial filtering or smoothing condition will make an attenuation of geostrophic current signal. It is notable that the signal of geostrophic current in the open ocean in Figure 7B is relatively larger compared to Figures 7A,C. The main reason is that the MDT estimated using the LS-based approach is still not as smooth as the Gaussian filtered MDT, so the geostrophic current signal is amplified where the gradient of the MDT is overestimated.

FIGURE 7

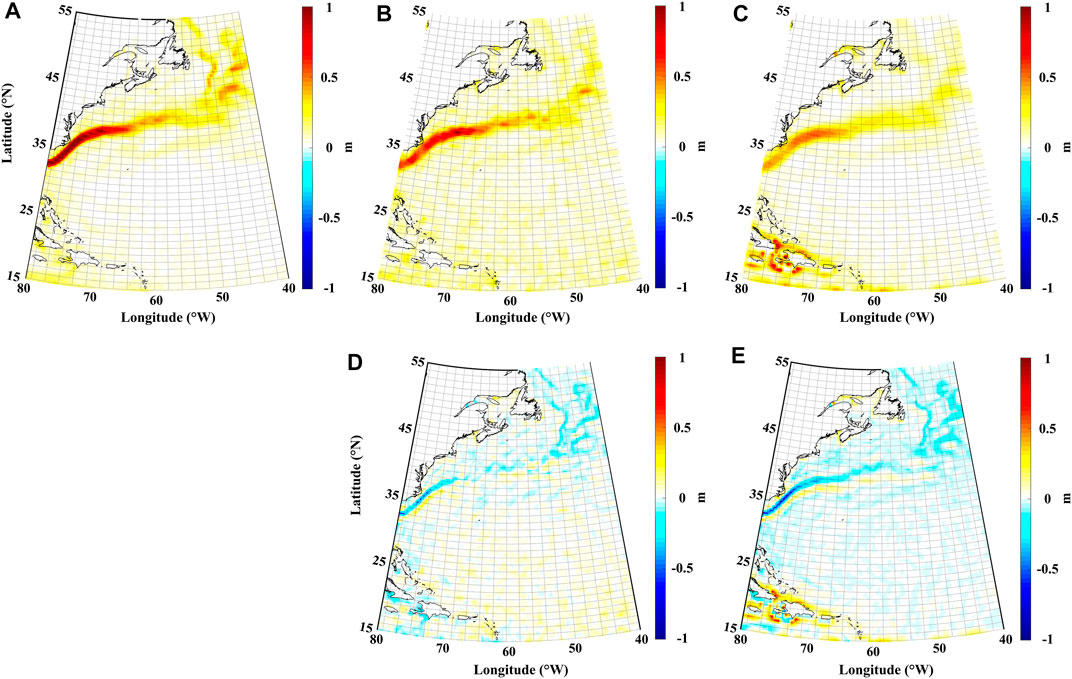
FIGURE 7. Top panel: Estimated geostrophic currents deduced from (A) Synthetic_Current, (B) estimated MDT, and (C) Gaussian filtered MDT are illustrated, respectively. Bottom panel: misfits between deduced geostrophic current against the Synthetic_Current, where the misfits from (D) estimated MDT (DIR6) and (E) Gaussian filtered MDT are illustrated, respectively.

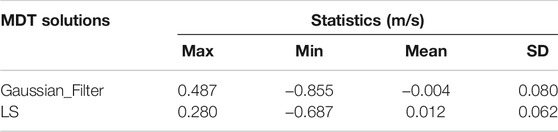
It is seen from the bottom panel of Figure 7 that both deduced geostrophic current fields are relatively weaker than the Synthetic_Current. For instance, geostrophic current velocities derived by the Gaussian filtering approach show significant misfits in the coast of the Gulf Stream. However, by comparing Figures 7D,E, it can be seen that the signal attenuation problem in geostrophic current obtained by the LS-based approach is better suppressed, where misfits are smaller. More importantly, the deduced geostrophic current velocities using Gaussian filtered MDT shows stronger noise signal in the coastal area in the southwestern part of the research area, indicating a signal distortion problem. Estimated MDT recovers better geostrophic current velocities in both the coastal and current regions than the Gaussian filtered MDT. Table 6 shows the statistics of misfits between geostrophic current obtained from the LS-based approach and Gaussian filtering, against the Synthetic_Current. It can be seen that the SD of misfits of geostrophic currents derived by the LS-based approach is 0.062 m/s, which shows 1.8 cm/s better agreement than the Gaussian filtered MDT.

TABLE 6

TABLE 6. Statistics of misfits between geostrophic current against the Synthetic_Current.

5 Conclusion

The traditional geodetic MDT modeling approach requires a filter procedure in the spatial or spectral domain to derive a reasonable solution, which inevitably lead to signal attenuation problems. In this study, we focus on using an LS-based approach for MDT modeling to limit the usage of spatial filtering. This approach constructs observation equations segmentally and carefully models the power matrices of each spectral domain. Further, the unknown parameters of the MDT are estimated in the LS system. Satellite-only GGMs including GRACE-only GGM and seven GOCE-based GGMs with error information are used for MDT modeling, where the effects of the error variance-covariance information from GGM and the contribution of the geoid signal in $cs\mathbf{1}$ are carefully investigated. Finally, deduced geostrophic current velocities based on the MDT solutions are validated and analyzed.

Results show that applications of full error variance-covariance matrix or only diagonal error variance of GGMs may have marginal effects on the MDT modeling. The latest GOCE-based GGMs, i.e., DIR6 and GOCO06s, reveal the best geodetic MDT solution using the LS-based approach, where the SD of the MDT misfits is 0.036 and 0.037 m if d/o 260. The estimated error map based on the error propagation illustrates that errors are more concentrated near the coastal region (∼0.1 m in Figure 5), while it reduces to ∼0.05 m (Figure 5) in the open ocean. The validation using deduced geostrophic velocities shows that estimated MDT recovers better geostrophic current signal in both the coastal and current region than the Gaussian filtered MDT. The SD of geostrophic current misfits by estimated MDT shows an improvement by 1.8 cm/s, comparing with the corresponding ones estimated by the Gaussian filtered MDT.

More future work need to be done to further assess and improve the LS-based MDT modeling approach. First, in order to study the variation of ocean currents due to the global sea level rise over the years, it is necessary to adjust the reference time of the MSS to the last 20 years (e.g., 1997–2018). It is notable that the MDT solutions derived in this study are referenced to the time period 1993–2012. However, with the study of the accumulated altimetry data, it is found that the sea level is rising gradually due to global warming (Hamlington et al., 2020), which will significantly affect the MDT and deduced geostrophic current. Research reveals that there is more prominent sea state variation near ocean current. For example, Gonçalves Neto et al. (2021) showed that the MSS in the Gulf Stream increased by an average of 4.5 cm from 2009 to 2018 compared to 1993–2007, and there is a significant increase (up to 15 cm) in the northern part of the Gulf Stream and a decrease of up to 15 cm in the southern part of the Gulf Stream. This means that the Gulf Stream is moving to the north. Therefore, the MDT and geostrophic current signal referenced to the last 20 years needs to be further investigated. Second, it is important to use independent in-situ data for robust validation of MDT solutions. For example, the drift data from the Argo program should be reprocessed and used as validation data. And in order to facilitate studies on the vertical datum unification, the performance of the estimated MDT in the coastal region needs to be evaluated using tide gauges. What’s more, a comprehensive comparison and analysis of several up-to-date MDT modeling methods, e.g., Andersen et al. (2018a), Karimi et al. (2020), and Wu et al. (2021), together with the LS-based approach need to be performed, and their performance near current and coast region should be further investigated. In this study, the spatial resolution of the MDT is lower than that of DTU15MDT/CNES-CLS18MDT due to the computation limitation of the global SHs. One solution is to replace SHs with a radial basis function (Wu et al., 2018), which could reduce the size of the design matrix and save the computation resources. It is also necessary to evaluate the error information of the altimetric data and introduce altimetric data into the LS system for the MDT modeling.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

HS designed this research, carried out experiments and data analysis, visualized the figures and drafted the manuscript. YW, OA, and PK conceived and coordinated this research. XH and YL participated in research coordination. ZZ participated in figure visualization. All the seven authors contributed to discuss results and reviewed the manuscript.

Funding

The project was funded by the National Natural Science Foundation of China (Nos. 41830110, 42004008, 42004014), the Postgraduate Research and Practice Innovation Program of Jiangsu Province (KYCX21_0530), the Fundamental Research Funds for the Central Universities, the Guangxi Key Laboratory of Spatial Information and Geomatics (NO. 19-185-10-06), the Natural Science Foundation of Jiangsu Province, China (Nos. BK20190498, BK20200530), the National Key Research Development Program of China (No. 2018YFC1503603), Foundation for Returned Overseas Chinese Scholars, Nanjing (No. B2004804), the State Scholarship Fund from Chinese Scholarship Council (Nos. 202006710169, 201306270014).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank DTU space and CNES/CLS for providing the DTU17cMDT and CNES-CLS15MSS/CNES-CLS18MDT products. The authors would also like to thank the ICEGM, the Graz University of Technology and ESA for providing ITSG and releases of GOCE GGM. The authors would like to give sincerest thanks to the reviewers for their beneficial suggestions and comments, which are of great value for improving the manuscript. The authors also thank the Editor ME for the kind assistance and constructive comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.795935/full#supplementary-material

References

Andersen, O. B., and Knudsen, P. (2009). DNSC08 Mean Sea Surface and Mean Dynamic Topography Models. J. Geophys. Res. 114, C11001. doi:10.1029/2008jc005179

CrossRef Full Text | Google Scholar

Andersen, O. B., Nielsen, K., Knudsen, P., Hughes, C. W., Bingham, R., Fenoglio-Marc, L., et al. (2018a). Improving the Coastal Mean Dynamic Topography by Geodetic Combination of Tide Gauge and Satellite Altimetry. Mar. Geodesy 41, 517–545. doi:10.1080/01490419.2018.1530320

CrossRef Full Text | Google Scholar

Andersen, O. B., Rose, S. K., Knudsen, P., and Stenseng, L. (2018b). “The DTU18 MSS Mean Sea Surface Improvement from SAR Altimetry,” in Proceedings of the 25 years of progress in radar altimetry symposium, 24–29 September, Portugal, 24–26.

Google Scholar

Bai, X., Yan, H., Zhu, Y., Peng, P., Yan, Y., and Shen, Y. (2020). Formal Error Assessment of Geodetic Mean Dynamic Topography at Different Spatial Scales. J. Geodynamics 138, 101753. doi:10.1016/j.jog.2020.101753

CrossRef Full Text | Google Scholar

Barthelmes, F. (2013). Definition of Functionals of the Geopotential and Their Calculation from Spherical Harmonic Models: Theory and Formulas Used by the Calculation Service of the International Centre for Global Earth Models (ICGEM). Potsdam: Deutsches GeoForschungsZentrum GFZ. Scientific Technical Report. ISSN 1610-0956, Potsdam, Germany. doi:10.2312/gfz.b103-0902-26

CrossRef Full Text | Google Scholar

Baur, O., and Grafarend, E. W. (2006). “High-Performance GOCE Gravity Field Recovery from Gravity Gradient Tensor Invariants and Kinematic Orbit Information,” in Observation of the Earth System from Space. Editors J. Flury, R. Rummel, C. Reigber, M. Rothacher, G. Boedecker, and U. Schreiber (Berlin/Heidelberg: Springer-Verlag), 239–253. doi:10.1007/3-540-29522-4_17

CrossRef Full Text | Google Scholar

Becker, S., Brockmann, J. M., and Schuh, W.-D. (2014). Mean Dynamic Topography Estimates Purely Based on GOCE Gravity Field Models and Altimetry. Geophys. Res. Lett. 41, 2063–2069. doi:10.1002/2014gl059510

CrossRef Full Text | Google Scholar

Becker, S., Freiwald, G., Losch, M., and Schuh, W.-D. (2012). Rigorous Fusion of Gravity Field, Altimetry and Stationary Ocean Models. J. Geodynamics 59-60 (60), 99–110. doi:10.1016/j.jog.2011.07.006

CrossRef Full Text | Google Scholar

Bingham, R. J., Haines, K., and Hughes, C. W. (2008). Calculating the Ocean's Mean Dynamic Topography from a Mean Sea Surface and a Geoid. J. Atmos. Oceanic Tech. 25, 1808–1822. doi:10.1175/2008jtecho568.1

CrossRef Full Text | Google Scholar

Bingham, R. J., Haines, K., and Lea, D. J. (2014). How Well Can We Measure the Ocean's Mean Dynamic Topography from Space? J. Geophys. Res. Oceans 119, 3336–3356. doi:10.1002/2013jc009354

CrossRef Full Text | Google Scholar

Bingham, R. J. (2010). Nonlinear Anisotropic Diffusive Filtering Applied to the Ocean's Mean Dynamic Topography. Remote Sensing Lett. 1, 205–212. doi:10.1080/01431161003743165

CrossRef Full Text | Google Scholar

Bock, H., Jäggi, A., Beutler, G., and Meyer, U. (2014). GOCE: Precise Orbit Determination for the Entire mission. J. Geod 88, 1047–1060. doi:10.1007/s00190-014-0742-8

CrossRef Full Text | Google Scholar

Brockmann, J. M. (2014). On High Performance Computing in Geodesy : Applications in Global Gravity Field Determination. Dissertation. Bonn: Rheinische Friedrich-Wilhelms-Universität Bonn. Available at: https://nbn-resolving.org/urn:nbn:de:hbz:5n-38608.

Google Scholar

Bruinsma, S. L., Förste, C., Abrikosov, O., Lemoine, J.-M., Marty, J.-C., Mulet, S., et al. (2014). ESA's Satellite-Only Gravity Field Model via the Direct Approach Based on All GOCE Data. Geophys. Res. Lett. 41, 7508–7514. doi:10.1002/2014GL062045

CrossRef Full Text | Google Scholar

Chambers, D., Andersen, O. B., Rio, M.-H., Rummel, R., Wiese, D., et al. (2017). “Auxiliary Space-Based Systems for Interpreting Satellite Altimetry,” in Satellite Altimetry Over Oceans And Land Surfaces. Editors D. Stammer, and A. Cazenave (Boca Raton, FLTaylor & Francis: CRC Press), 149–186. doi:10.1201/9781315151779-4

CrossRef Full Text | Google Scholar

Donlon, C. J., Cullen, R., Giulicchi, L., Vuilleumier, P., Francis, C. R., Kuschnerus, M., et al. (2021). The Copernicus Sentinel-6 Mission: Enhanced Continuity of Satellite Sea Level Measurements from Space. Remote Sensing Environ. 258, 112395. doi:10.1016/j.rse.2021.112395

CrossRef Full Text | Google Scholar

Drinkwater, M. R., Floberghagen, R., Haagmans, R., Muzi, D., and Popescu, A. (2003). “GOCE: ESA's First Earth Explorer Core Mission,” in Earth Gravity Field From Space — From Sensors To Earth Sciences Space Sciences Series of ISSI. Editors G. Beutler, M. R. Drinkwater, R. Rummel, and R. Von Steiger (Dordrecht: Springer Netherlands), 419–432. doi:10.1007/978-94-017-1333-7_36

CrossRef Full Text | Google Scholar

Flechtner, F., Morton, P., Watkins, M., and Webb, F. (2014). “Status of the GRACE Follow-On Mission,” in Gravity, Geoid And Height Systems International Association of Geodesy Symposia. Editor U. Marti (Cham: Springer International Publishing), 117–121. doi:10.1007/978-3-319-10837-7_15

CrossRef Full Text | Google Scholar

Förste, C., Abrykosov, O., Bruinsma, S., Dahle, C., König, R., and Lemoine, J.-M. (2019). ESA’s Release 6 GOCE Gravity Field Model by Means of the Direct Approach Based on Improved Filtering of the Reprocessed Gradients of the Entire mission (GO_CONS_GCF_2_DIR_R6). 3 Files. Potsdam, Germany: GFZ Data Services. doi:10.5880/ICGEM.2019.004

CrossRef Full Text | Google Scholar

Förste, C., Bruinsma, S., Abrikosov, O., Flechtner, F., Marty, J. C., Lemoine, J. M., et al. (2014). EIGEN-6C4-The Latest Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 1949 of GFZ Potsdam and GRGS Toulouse. EGU Gen. Assembly Conf. Abstr. 16, 3707. doi:10.5880/icgem.2015.1

CrossRef Full Text | Google Scholar

Freiwald, G. (2013). A New Filter for the Mean Dynamic Topography of the Ocean Derived Directly from Satellite Observations. J. Geodynamics 72, 67–71. doi:10.1016/j.jog.2013.08.006

CrossRef Full Text | Google Scholar

Gonçalves Neto, A., Langan, J. A., and Palter, J. B. (2021). Changes in the Gulf Stream Preceded Rapid Warming of the Northwest Atlantic Shelf. Commun. Earth Environ. 2, 74. doi:10.1038/s43247-021-00143-5

CrossRef Full Text | Google Scholar

Gruber, T. (2001). High-Resolution Gravity Field Modeling with Full Variance-Covariance Matrices. J. Geodesy 75, 505–514. doi:10.1007/s001900100202

CrossRef Full Text | Google Scholar

Hamlington, B. D., Gardner, A. S., Ivins, E., Lenaerts, J. T. M., Reager, J. T., Trossman, D. S., et al. (2020). Understanding of Contemporary Regional Sea‐Level Change and the Implications for the Future. Rev. Geophys. 58, e2019RG000672. doi:10.1029/2019RG000672

PubMed Abstract | CrossRef Full Text | Google Scholar

Haynsworth, E. V. (1968). On the Schur Complement. Base1 Mathematical Notes, BMN 20, Basel: University of Basel.

Google Scholar

Hwang, C., Hsu, H.-Y., and Jang, R.-J. (2002). Global Mean Sea Surface and marine Gravity Anomaly from Multi-Satellite Altimetry: Applications of Deflection-Geoid and Inverse Vening Meinesz Formulae. J. Geodesy 76, 407–418. doi:10.1007/s00190-002-0265-6

CrossRef Full Text | Google Scholar

Jekeli, C. (1981). Alternative Methods to Smooth the Earth’s Gravity Field. Columbus: Department of Geodetic Science and Surveying, Ohio State University.

Google Scholar

Kang, D., and Curchitser, E. N. (2013). Gulf Stream Eddy Characteristics in a High-Resolution Ocean Model. J. Geophys. Res. Oceans 118, 4474–4487. doi:10.1002/jgrc.20318

CrossRef Full Text | Google Scholar

Karimi, A. A., Andersen, O. B., and Deng, X. (2021). Mean Sea Surface and Mean Dynamic Topography Determination from Cryosat-2 Data Around Australia. Adv. Space Res. 68 (2), 1073–1089. doi:10.1016/j.asr.2020.01.009

CrossRef Full Text | Google Scholar

Kaula, W. M. (1966). Theory of Satellite Geodesy. Waltham, Mass: Blaisdell Publ. Co.

Google Scholar

Ke, B., Zhang, L., Xu, J., Zhang, C., and Dang, Y. (2019). Determination of the Mean Dynamic Ocean Topography Model through Combining Multi-Source Gravity Data and DTU15 MSS Around China's Coast. Adv. Space Res. 63, 203–212. doi:10.1016/j.asr.2018.10.040

CrossRef Full Text | Google Scholar

Klymak, J. M., Shearman, R. K., Gula, J., Lee, C. M., D'Asaro, E. A., Thomas, L. N., et al. (2016). Submesoscale Streamers Exchange Water on the North Wall of the Gulf Stream. Geophys. Res. Lett. 43, 1226–1233. doi:10.1002/2015GL067152

CrossRef Full Text | Google Scholar

Knudsen, P., Andersen, O., and Maximenko, N. (2021). A New Ocean Mean Dynamic Topography Model, Derived from a Combination of Gravity, Altimetry and Drifter Velocity Data. Adv. Space Res. 68, 1090–1102. doi:10.1016/j.asr.2019.12.001

CrossRef Full Text | Google Scholar

Knudsen, P., Bingham, R., Andersen, O., and Rio, M.-H. (2011). A Global Mean Dynamic Topography and Ocean Circulation Estimation Using a Preliminary GOCE Gravity Model. J. Geod 85, 861–879. doi:10.1007/s00190-011-0485-8

CrossRef Full Text | Google Scholar

Kvas, A., Behzadpour, S., Ellmer, M., Klinger, B., Strasser, S., Zehentner, N., et al. (2019a). ITSG‐Grace2018: Overview and Evaluation of a New GRACE‐Only Gravity Field Time Series. J. Geophys. Res. Solid Earth 124, 9332–9344. doi:10.1029/2019JB017415

CrossRef Full Text | Google Scholar

Kvas, A., Mayer-Gürr, T., Krauss, S., Brockmann, J. M., Schubert, T., Schuh, W. D., et al. (2019b). The Satellite-Only Gravity Field Model GOCO06s. Potsdam, Germany: GFZ Data Services. doi:10.5880/ICGEM.2019.002

CrossRef Full Text | Google Scholar

Lagerloef, G. S. E., Mitchum, G. T., Lukas, R. B., and Niiler, P. P. (1999). Tropical Pacific Near-Surface Currents Estimated from Altimeter, Wind, and Drifter Data. J. Geophys. Res. 104, 23313–23326. doi:10.1029/1999jc900197

CrossRef Full Text | Google Scholar

Landerer, F. W., Flechtner, F. M., Save, H., Webb, F. H., Bandikova, T., Bertiger, W. I., et al. (2020). Extending the Global Mass Change Data Record: GRACE Follow‐On Instrument and Science Data Performance. Geophys. Res. Lett. 47, e2020GL088306. doi:10.1029/2020GL088306

CrossRef Full Text | Google Scholar

Lawson, C. L., and Hanson, R. J. (1995). Solving Least Squares Problems. Newyork: Society for Industrial and Applied Mathematics.

Google Scholar

Le Traon, P.-Y., Antoine, D., Bentamy, A., Bonekamp, H., Breivik, L. A., Chapron, B., et al. (2015). Use of Satellite Observations for Operational Oceanography: Recent Achievements and Future Prospects. J. Oper. Oceanography 8, s12–s27. doi:10.1080/1755876x.2015.1022050

CrossRef Full Text | Google Scholar

Mayer-Gürr, T., Norbert, Z., Beate, K., and Andreas, K. (2014). “ITSG-Grace2014: A New GRACE Gravity Field Release Computed in Graz,” in Presented at: Grace Science Team Meeting 2014, Potsdam, Germany, 28-30 September. doi:10.13140/rg.2.1.5098.2805

CrossRef Full Text | Google Scholar

Mulet, S., Rio, M.-H., Etienne, H., Artana, C., Cancet, M., Dibarboure, G., et al. (2021). The New CNES-CLS18 Global Mean Dynamic Topography. Ocean Sci. 13, 789–808. doi:10.5194/os-2020-117

CrossRef Full Text | Google Scholar

Pail, R., Goiginger, H., Schuh, W.-D., Höck, E., Brockmann, J. M., Fecher, T., et al. (2010). Combined Satellite Gravity Field modelGOCO01Sderived from GOCE and GRACE. Geophys. Res. Lett. 37, L20314. doi:10.1029/2010GL044906

CrossRef Full Text | Google Scholar

Palter, J. B. (2015). The Role of the Gulf Stream in European Climate. Annu. Rev. Mar. Sci. 7, 113–137. doi:10.1146/annurev-marine-010814-015656

CrossRef Full Text | Google Scholar

Pavlis, N. K., Holmes, S. A., Kenyon, S. C., and Factor, J. K. (2012). The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. 117, a–n. doi:10.1029/2011jb008916

CrossRef Full Text | Google Scholar

Pujol, M. I., Schaeffer, P., Faugère, Y., Raynal, M., Dibarboure, G., and Picot, N. (2018). Gauging the Improvement of Recent Mean Sea Surface Models: A New Approach for Identifying and Quantifying Their Errors. J. Geophys. Res. Oceans 123, 5889–5911. doi:10.1029/2017jc013503

CrossRef Full Text | Google Scholar

Ran, J., Tangdamrongsub, N., and Wan, X. (2021). The Impact of Error Covariance Matrix Structure of GRACE's Gravity Solution on the Mass Flux Estimates of Greenland Ice Sheet. Adv. Space Res. 67, 163–178. doi:10.1016/j.asr.2020.07.012

CrossRef Full Text | Google Scholar

Rio, M.-H. (2004). A Mean Dynamic Topography Computed over the World Ocean from Altimetry, In Situ Measurements, and a Geoid Model. J. Geophys. Res. 109, C12032. doi:10.1029/2003jc002226

CrossRef Full Text | Google Scholar

Rio, M.-H., Pascual, A., Poulain, P.-M., Menna, M., Barceló, B., and Tintoré, J. (2014). Computation of a New Mean Dynamic Topography for the Mediterranean Sea from Model Outputs, Altimeter Measurements and Oceanographic In Situ Data. Ocean Sci. 10, 731–744. doi:10.5194/os-10-731-2014

CrossRef Full Text | Google Scholar

Rio, M. H., Guinehut, S., and Larnicol, G. (2011). New CNES‐CLS09 Global Mean Dynamic Topography Computed from the Combination of GRACE Data, Altimetry, and In Situ Measurements. J. Geophys. Res. 116, C07018. doi:10.1029/2010jc006505

CrossRef Full Text | Google Scholar

Rossby, T., Flagg, C., and Donohue, K. (2010). On the Variability of Gulf Stream Transport from Seasonal to Decadal Timescales. J Mar. Res. 68, 503–522. doi:10.1357/002224010794657128

CrossRef Full Text | Google Scholar

Sánchez-Reales, J. M., Andersen, O. B., and Vigo, M. I. (2016). Improving Surface Geostrophic Current from a GOCE-Derived Mean Dynamic Topography Using Edge-Enhancing Diffusion Filtering. Pure Appl. Geophys. 173, 871–884. doi:10.1007/s00024-015-1050-9

CrossRef Full Text | Google Scholar

Schaeffer, P., Pujol, I., Faugere, Y., Guillot, A., and Picot, N. (2016). The CNES CLS 2015 Global Mean Sea Surface. Available at: http://meetings.aviso.altimetry.fr/fileadmin/user_upload/tx_ausyclsseminar/files/GEO_03_Pres_OSTST2016_MSS_CNES_CLS2015_V1_16h55.pdf (Accessed January 25, 2022).

Google Scholar

Shi, H., He, X., Wu, Y., and Huang, J. (2020). The Parameterization of Mean Dynamic Topography Based on the Lagrange Basis Functions. Adv. Space Res. 66, 2122–2140. doi:10.1016/j.asr.2020.07.042

CrossRef Full Text | Google Scholar

Siegismund, F. (2020). A Spectrally Consistent Globally Defined Geodetic Mean Dynamic Ocean Topography. J. Geophys. Res. Oceans 125, e2019JC016031. doi:10.1029/2019jc016031

CrossRef Full Text | Google Scholar

Swenson, S., and Wahr, J. (2002). Methods for Inferring Regional Surface-Mass Anomalies from Gravity Recovery and Climate Experiment (GRACE) Measurements of Time-Variable Gravity. J. Geophys. Res. 107, 3–1. doi:10.1029/2001JB000576

CrossRef Full Text | Google Scholar

Tapley, B. D., Bettadpur, S., Watkins, M., and Reigber, C. (2004). The Gravity Recovery and Climate experiment: Mission Overview and Early Results. Geophys. Res. Lett. 31, 4. doi:10.1029/2004GL019920

CrossRef Full Text | Google Scholar

Tapley, B. D., Chambers, D. P., Bettadpur, S., and Ries, J. C. (2003). Large Scale Ocean Circulation from the GRACE GGM01 Geoid. Geophys. Res. Lett. 30, L018622. doi:10.1029/2003GL018622

CrossRef Full Text | Google Scholar

Tsoulis, D., and Patlakis, K. (2013). A Spectral Assessment Review of Current Satellite-Only and Combined Earth Gravity Models. Rev. Geophys. 51, 186–243. doi:10.1002/rog.20012

CrossRef Full Text | Google Scholar

Tziavos, I. N., Vergos, G. S., Grigoriadis, V. N., Tzanou, E. A., and Natsiopoulos, D. A. (2015). “Validation of GOCE/GRACE Satellite Only and Combined Global Geopotential Models over Greece in the Frame of the GOCESeaComb Project,” in IAG 150 Years International Association Of Geodesy Symposia. Editors C. Rizos, and P. Willis (Cham: Springer International Publishing), 297–304. doi:10.1007/1345_2015_160

CrossRef Full Text | Google Scholar

Vianna, M. L., Menezes, V. V., and Chambers, D. P. (2007). A High Resolution Satellite-Only GRACE-Based Mean Dynamic Topography of the South Atlantic Ocean. Geophys. Res. Lett. 34, L24604. doi:10.1029/2007GL031912

CrossRef Full Text | Google Scholar

Vignudelli, S., Birol, F., Benveniste, J., Fu, L.-L., Picot, N., Raynal, M., et al. (2019). Satellite Altimetry Measurements of Sea Level in the Coastal Zone. Surv. Geophys. 40, 1319–1349. doi:10.1007/s10712-019-09569-1

CrossRef Full Text | Google Scholar

Wahr, J., Molenaar, M., and Bryan, F. (1998). Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE. J. Geophys. Res. 103, 30205–30229. doi:10.1029/98JB02844

CrossRef Full Text | Google Scholar

Woodworth, P. L., Gravelle, M., Marcos, M., Wöppelmann, G., and Hughes, C. W. (2015). The Status of Measurement of the Mediterranean Mean Dynamic Topography by Geodetic Techniques. J. Geod 89, 811–827. doi:10.1007/s00190-015-0817-1

CrossRef Full Text | Google Scholar

Wu, Y., Huang, J., Shi, H., and He, X. (2021). Mean Dynamic Topography Modeling Based on Optimal Interpolation from Satellite Gravimetry and Altimetry Data. Appl. Sci. 11, 5286. doi:10.3390/app11115286

CrossRef Full Text | Google Scholar

Wu, Y., Luo, Z., Zhong, B., and Xu, C. (2018). A Multilayer Approach and its Application to Model a Local Gravimetric Quasi-Geoid Model over the North Sea: QGNSea V1.0. Geosci. Model. Dev. 11, 4797–4815. doi:10.5194/gmd-11-4797-2018

CrossRef Full Text | Google Scholar

Wu, Y., Zhou, H., Zhong, B., and Luo, Z. (2017). Regional Gravity Field Recovery Using the GOCE Gravity Gradient Tensor and Heterogeneous Gravimetry and Altimetry Data. J. Geophys. Res. Solid Earth 122, 6928–6952. doi:10.1002/2017jb014196

CrossRef Full Text | Google Scholar

Zingerle, P., Pail, R., Gruber, T., and Oikonomidou, X. (2020). The combined global gravity field model XGM2019e. J. Geod 94, 66. doi:10.1007/s00190-020-01398-0

CrossRef Full Text | Google Scholar